An IPAVSG Control Strategy for Microgrid With Multi-Parallel VSG System

Virtual synchronous generator (VSG) is widely used in various distributed power generation systems due to great simulated inertia and damping support performance. However, when the microgrid (MG) composed of multi-parallel VSG is in both grid-connected and islanded modes with various large disturbances, the control strategy with fixed parameters cannot guarantee the stable operation of the MG under all disturbances. To this end, an improved parameter-adaptive virtual synchronous generator (IPAVSG) control strategy is proposed in this paper to ensure that the virtual inertia and damping are adaptively optimized with the system operating state during the disturbance process. Therefore, the dynamic performance of the power frequency regulation and transient stability are significantly improved. Meanwhile, in order to realize the output active power of each VSG is distributed among the loads according to the ratio of its rated capacity, the active power decoupling control is designed to eliminate the influence of the virtual damping on the output active power of the VSG in islanded MG. The effectiveness and practicability of the proposed control strategy are verified through several experiments.

1 Introduction

In recent years, distributed generation (DG) devices with clean energy such as solar energy and wind energy are widely used in many fields of production and life. The microgrid, which is composed of various distributed generation units with power converter, can be integrated into the power grid or operated in islanded mode (Liserre et al., 2010; Mojica-Nava et al., 2014; Zhao et al., 2016; Meng et al., 2019). Because of the rapid penetration of distributed generation units in power systems, a variety of serious challenges such as poor transient response performance, insufficient inertia and damping have emerged (Weng S. et al., 2019; Tian and Peng, 2020). In order to effectively solve these problems, many reasonable control strategies by Ma et al. (2021c), Hu et al. (2021a) and Wang et al. (2021) have been introduced into interface power converters of DG units.

The droop control is a classical control strategy for distributed generation units. Through simulating the static droop characteristics of synchronous generator, the control of voltage and frequency of the MG system are realized. The DG with droop control can maintain the load voltage and frequency stability according to the droop curve. In addition, power can be reasonably distributed among parallel DG units according to their respective droop curves without externalcommunication (Li et al., 2021). However, the droop control strategy cannot provide inertia and damping similar to synchronous generator (SG) to inverter-interfaced distributed generation (IIDG) units (Li, 2019). Thus, when a large disturbance occurs, if additional power cannot be provided in time to balance the disturbance, the stability of the MG with the droop control strategy is extremely poor (Fang et al., 2019). Although the low-pass filter droop control strategy with equivalent virtual inertia is introduced by Eskandari et al. (2019). the adjustment range of the parameters is small, and the performance of dynamic adjustment needs to be further improved.

Compared with the droop control, the virtual synchronous generator (VSG) control strategy effectively solves the lack of inertia and damping in the MG (Liu et al., 2014; D’Arco and Suul, 2014; Ma et al., 2021a). The basic principle of VSG is to introduce an equivalent rotation equation to emulate the inertia and damping characteristics of synchronous generator (SG). And the concept of VSG is originally proposed by Beck and Hesse (2007) and Driesen and Visscher (2008). Then, the equivalent mathematical model and specific implementation method of VSG based on three-phase inverter are preliminarily studied by Zhong and Weiss (2011) and Zhong et al. (2014). Afterwards, the VSG control is applied in the control of voltage, frequency, power flow and so on (Yang et al., 2011). With further in-depth research, VSG control strategy or improved control strategy based on it are used in various types of equipment or occasions such as energy storage (Rene et al., 2009; Kong et al., 2019), doubly-fed induction generators (Hwang et al., 2017), high voltage direct current transmission (Aouini et al., 2016) and direct current MG (Wu et al., 2017).

VSG can effectively simulate the inertia and damping performance of SG well. Thus, when MG fluctuates violently, the system can alleviate the fluctuation of active power and frequency of DG units. Improving the dynamic characteristics of the MG by designing appropriate virtual inertia and damping coefficients has been demonstrated by Zhong et al. (2014) and Yang et al. (2011). At present, the research on parameter selection based on VSG control is mainly divided into two categories: one is the fixed virtual inertia and damping value represented by Kerdphol et al. (2018), Fang et al. (2018) and Soni et al. (2013), while the (Simpson-Porco et al., 2013; Hou et al., 2016; Meng et al., 2016; Li et al., 2017; Alipoor et al., 2018; Andalib et al., 2018; Wang et al., 2018) focus on the study of adaptive parameters. Obviously, compared with fixed parameter control, adaptive parameter control has a wider adjustment range, which can better cope with various disturbances in the MG. In the parameter adaptive control strategy mentioned above, the damping coefficient is not considered or fixed at zero by Andalib et al. (2018) Hou et al. (2016), Alipoor et al. (2018) and Simpson-Porco et al. (2013). Therefore, the areas and scenarios are easily limited. Theoretical analysis of virtual inertia and damping coefficients is not mentioned by Li et al. (2017), and the realization of the control process is complicated. The design principles of virtual inertia and damping are given by Wang et al. (2018). Therein, the two key parameters change in opposite directions. However, the parameter extremums and optimal damping ratios that satisfy the stability of the system are not explained in any way. A control strategy called Bang-Bang is proposed by Meng et al. (2016). This strategy systematically analyzes the specific effects of virtual inertia and damping on power frequency, and designs the principle of parameter value accordingly. Unfortunately, the Bang-Bang control contains only two virtual inertia values, and the performance of the controller cannot be greatly improved. It is noteworthy that the vast majority of adaptive VSG strategies consider MG in grid-connected mode. However, the MG also needs to operate in islanded mode. In islanded mode, MG is impossible to establish an electrical connection with the power grid. So, the energy supply of the load and the voltage amplitude and frequency adjustment are independently completed by each DG unit (Lin et al., 2017). Once a disturbance occurs, the MG needs better inertia and damping support. Therefore, in order to effectively suppress the power-frequency oscillation of the perturbation process, the parameter-adaptive VSG control strategy needs to be considered for application to the islanded MG. In addition, another core control requirement is that the DG units connected in parallel should distribute the output active power proportionally according to their rated capacity (Huang et al., 2019; Jiang et al., 2020). Therefore, it is necessary to introduce both adaptive VSG and power equalization control in the islanded MG.

In summary, this paper proposes an improved parameter-adaptive VSG control strategy for MG that is suitable for grid-connected and islanded mode. In addition, power decoupling control strategy used in islanded MG is also taken into account. The outstanding features of the IPAVSG control strategy can be summarized as follows.

1) The IPAVSG control strategy proposed in this paper is suitable for grid-connected and islanded MG. In the two modes, the virtual inertia and damping can be optimally selected according to changes in the state of the MG transient adjustment process to improve the power frequency adjustment performance of the system. Especially at the initial moment of disturbance, the virtual inertia and damping quickly respond to larger values to suppress oscillation and fluctuation.

2) An active power proportional distribution control strategy is introduced into the islanded MG to eliminate the influence of damping on the output power of the DG units at steady state. Therefore, the output active power of each DG unit is proportional to its rated capacity.

The structure of this article is arranged as follows. Section The Basic Principle and Mathematical Model of VSG introduces the mathematical model and power controller of the VSG. Section The Transient Response Analysis of Parameter Perturbation analyzes the specific effects of virtual inertia and damping on the power and frequency transient adjustment process. Section The IPAVSG Control Strategy for MPVS presents the virtual inertia adaptive expression and power sharing control block diagram of two parallel VSGs suitable for both grid-connected and islanded mode. Section The Experimental Results analyzes the experimental results and proves the superiority and feasibility of the control strategy proposed in this paper. Section The Conclusion summarizes the advantages and feasibility of the control strategy proposed in this paper.

2 Basic Principle and Mathematical Model of Vsg

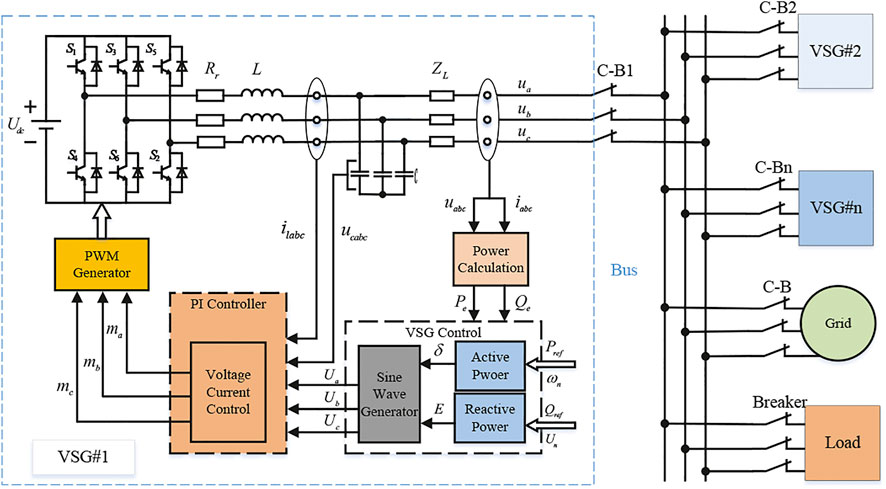
To facilitate the interpretation, the IIDG unit controlled by VSG strategy is referred to as a VSG in this paper. A classic control topology of VSG is shown in Figure 1. It is composed of an inverter triggered by PWM generator and an LC filter set to reduce the current and voltage ripple. Utilizing the current and voltage measurement signals from VSG terminals, the power calculation and frequency measurement could be expediently realized. In order to better investigate the control strategy of the inverter, the dynamic characteristics of DG and energy storages are omitted in this paper. Moreover, the state-of-charge of energy storages is supposed to well satisfy the system requirements. In order to better investigate the control strategy of the inverter, the dynamic characteristics of DG and energy storages are omitted in this paper. Hence, the IIDG containing energy storages can be substituted for a DC voltage source (Simpson-Porco et al., 2013). Moreover, the state-of-charge of energy storages is supposed to well satisfy the system requirements.

FIGURE 1

FIGURE 1. Classic topology and control block of MPVS.

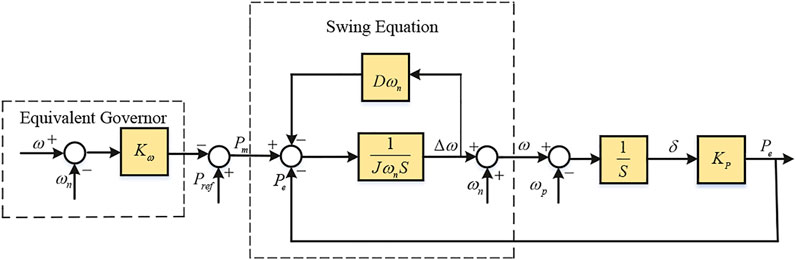
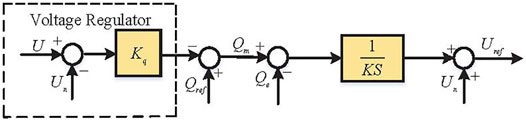
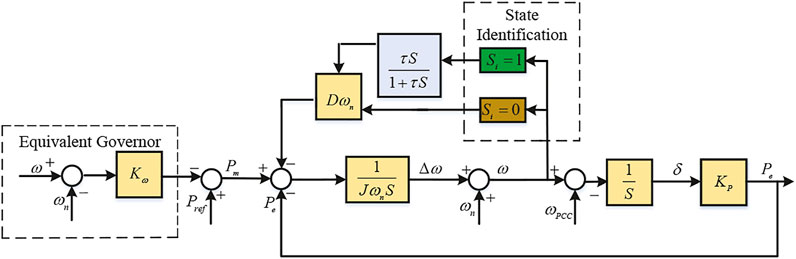
As shown in Figure 1, the core of VSG can be separated into two parts: the active power control module and the reactive power control module. The active power control module is composed of the equivalent governor and mechanical model. The former simulates the prime mover of SG with the feature of primary frequency modulation whereas the latter takes charge of imitating mechanical rotor motion, which is considered as the most essential part of VSG. The reactive power control module is responsible for reactive power regulation. In operation, the active power control module export phase angle and the reactive power control module produce voltage magnitude respectively, then the generated reference sine waves are conveyed to the PWM generator to emit trigger signals. The details of these two parts are shown in Figures 2, 3. The control system depicted in Figure 2 is suitable for both the grid-connected mode and islanded mode. Because the active power control module of the VSG should include the swing equation and the equivalent governor in both modes. The reactive power control module in Figure 3 includes voltage regulator and integrator, which can obtain the amplitude of reference voltage. The total mathematical model can be concluded as

$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_m-P_e-D{\omega }_n\left(\omega -{\omega }_n\right)=J{\omega }_n\frac{d\omega }{dt}\hfill \\ Q_{\mathit{r}\mathit{e}\mathit{f}}-K_p\left(U-U_n\right)-Q_e=K\frac{dU}{dt}\hfill \\ \delta =\int \left(\omega -{\omega }_p\right)dt\hfill \end{array}\right.\end{array}(1)$

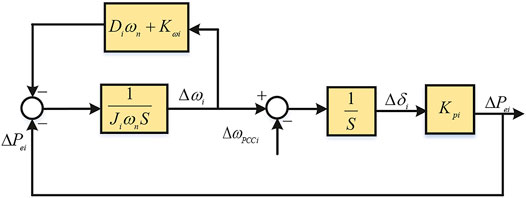
where P_m, P_e, Q_ref, Q_e are the virtual mechanical power, actual output active power, the reactive power reference and actual output reactive power, respectively. J and D represent the virtual inertia and the damping coefficient, respectively. U and U_n represent the voltage of the VSG and the reference voltage, and δ is the phase angle of the voltage. In actual control, the output power angle δ should be connected to the power angle balance compensator, which is shown in Figure 4, where ${\bar{\delta }}_i$, δ_i, ${\delta }_i^{*}$ respectively represent the average output power angle of all VSGs in the system, the actual power angle of the ith VSG, and the power angle of the ith VSG after compensation. This method has been proposed well by Jiang et al. (2020) and Ma et al. (2021b). ω and ω_n indicate the virtual angular frequency and the reference angular frequency, respectively, and Δω = (ω − ω_n) is the frequency deviation. In both grid-connected state and islanded state, ω_p represents the reference angular frequency of the PCC, and it is directly collected by the phase-locked loop. Under this operation, the smooth switching between islanded mode and connected-grid mode can be achieved (Wang et al., 2019). In order to avoid the complex iterative computation of Eq. (1), the controller is designed in the frequency domain.

FIGURE 2

FIGURE 2. Control modules of active power control module.

FIGURE 3

FIGURE 3. Control modules of reactive power control module.

FIGURE 4

FIGURE 4. Block diagram of power angle balance compensator.

Observations obtained from Figure 2 depict that P_m is composed of the active power reference P_ref and the output power regulated by the equivalent governor according to the frequency deviation. It could be expressed as

$P_m=P_{\mathit{r}\mathit{e}\mathit{f}}-K_{\omega }\left(\omega -{\omega }_n\right)(2)$

Then, the whole process of the active power control module is calculated as

$P_{\mathit{r}\mathit{e}\mathit{f}}-K_{\omega }\left(\omega -{\omega }_n\right)-P_e-D{\omega }_n\mathrm{\Delta }\omega =J{\omega }_n\frac{d\omega }{dt}(3)$

where K_ω is the droop coefficient of the equivalent governor.

Eqs. (1)–(3) indicate that the VSG control strategy plays a significant role in imitating the operating characteristics of SG through introducing the rotor motion equation.

3 Transient Response Analysis of Parameter Perturbation

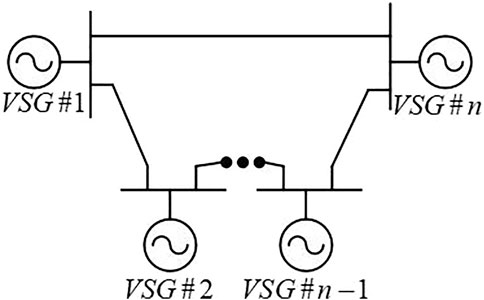
Theoretically, VSG can be operated alone or in parallel. This paper aims to investigate the impact of some key parameters (virtual inertia and damping coefficient) on the frequency and active power outputs of the MG with multiple VSGs connected in parallel, and we called this system as the multi-parallel VSG system (MPVS). The structure of MPVS is depicted in Figure 1, where the VSGs are attached to a point of common coupling (PCC) through a distribution line, then the PCC is connected to the utility grid via circuit breaker (CB). Notice that the capacitor of the output LC filter can be neglected in consequence of the susceptance is inappreciable around the fundamental frequency. Thus, the VSG can be substituted with an ideal DC voltage source with a series output impedance.

For the purpose of deeper analyzing the output characteristics of the MPVS, networked power system, a universally applicable model, is selected for instance. Figure 5 depicts the equivalent model of networked power system, which contains multi-paralleled virtual synchronous generators. To simplify the model, the reactive power output is not considered in this system and these simplifications have no impact on the precision of the model (Zhong et al., 2014).

FIGURE 5

FIGURE 5. Equivalent circuit model of networked power system.

According to Eq. (1) and (3), the mathematical model of VSGi can be expressed as

$\left\{\begin{array}{c}{P}_{\mathit{r}\mathit{e}\mathit{f}\mathit{i}}-K_{\omega i}\left({\omega }_i-{\omega }_n\right)-P_{ei}-D_i{\omega }_n\left({\omega }_i-{\omega }_n\right)=J_i{\omega }_n\frac{d{\omega }_i}{dt}\hfill \\ {\delta }_i=\int \left({\omega }_i-{\omega }_p\right)dt\hfill \end{array}\right.(4)$

where P_ei means the active power of VSGi flowing into PCC. The relationship between the P_ei and the variables at PCC can be expressed as

$P_{ei}=\frac{3E_i{U}_p}{Z_i}\sin {\delta }_i=K_{pi}\sin {\delta }_i(5)$

where K_pi = 3E_iU_p/Z_i, E_i and U_p represent the output voltages of the VSG i and the PCC separately. $P_{e_i}$ denotes the output active power. Z_i represents the equivalent line impedance and the output impedance. sin δ_i represents power angle. Z_L is the load impedance.

The small signal model of the two-parallel VSG system is derived as follows. Let

$\left\{\begin{array}{c}{\omega }_i={\omega }_s+\mathrm{\Delta }{\omega }_i\hfill \\ {\omega }_p={\omega }_{ps}+\mathrm{\Delta }{\omega }_p\hfill \\ {\delta }_i={\delta }_{is}+\mathrm{\Delta }{\delta }_i\hfill \\ P_{ei}=P_{\mathit{e}\mathit{i}\mathit{s}}+\mathrm{\Delta }{P}_{ei}\hfill \end{array}\right.(6)$

Notice that the state variables in Eq. (6) are equivalent to the value of steady state plus a perturbation value. Since Δδ_i is very small, the following equations $\sin \left(\mathrm{\Delta }{\delta }_i\right)\approx \mathrm{\Delta }{\delta }_i$ and $\cos \left(\mathrm{\Delta }{\delta }_i\right)\approx 1$ are satisfied. Furthermore, the second-order perturbation terms could be omitted due to the frequency deviation is comparatively small. Therefore, the small signal model of Figure 2 can be obtained as Figure 6. Then the closed loop transfer function from ΔP_refi to ΔP_ei is obtained as

$\frac{\mathrm{\Delta }{P}_{ei}}{\mathrm{\Delta }{P}_{\mathit{r}\mathit{e}\mathit{f}\mathit{i}}}=\frac{E_{\text{i}}{U}_p}{J_i{\omega }_n{Z}_i{s}^2+D_{pi}{Z}_{i}s+E_i{U}_{\text{p}}}(7)$

where D_pi = K_ωi + D_iω_n.

FIGURE 6

FIGURE 6. Small signal model of active power control module.

In line with Eq. (7), the peak time t_p−p, settling time t_s−p and overshoot M_p−p of the step response of the active power can be expressed as follows:

$t_{p-p}=\frac{2\pi J_i{\omega }_n{Z}_i}{\sqrt{4J_i{\omega }_n{Z}_i{E}_i{U}_p-D_{pi}^2{Z}_i^2}}(8)$

$M_{p-p}=e^{-\pi \sqrt{\frac{D_{pi}^2{Z}_i^2}{4J_i{\omega }_n{Z}_i{E}_i{U}_p-D_{pi}^2{Z}_i^2}}}(9)$

$t_{s-p}=\frac{D_{pi}}{2}\sqrt{\frac{Z_i}{J_i{\omega }_n{E}_i{U}_p}}(10)$

The closed loop transfer function from ΔP_refi to Δω_i can be obtained as

$\frac{\mathrm{\Delta }{\omega }_i}{\mathrm{\Delta }{P}_{\mathit{r}\mathit{e}\mathit{f}\mathit{i}}}=\frac{Z_{i}s}{J_{\text{i}}{\omega }_n{Z}_i{s}^2+D_{pi}{Z}_{i}s+E_i{U}_p}(11)$

According to Eq. (11), the influences on the step response of frequency caused by D_pi can be indicated as.

$t_{p-\omega }=\frac{\arctan \sqrt{\frac{4J_i{\omega }_n{E}_i{U}_p-D_{pi}^2{Z}_i}{D_{pi}^2{Z}_i}}}{\sqrt{\frac{E_i{U}_p}{J_i{\omega }_n{Z}_i}-\frac{D_{pi}^2}{4J_i^2{\omega }_n^2}}}(12)$

$M_{p-\omega }=\sqrt{\frac{4E_i{U}_p}{J_i{\omega }_n{Z}_i}}{e}^{-\sqrt{\frac{D_{pi}^2{Z}_i}{4J_i{\omega }_n{E}_i{U}_p-D_{pi}^2{Z}_i}}\arctan \sqrt{\frac{4J_i{\omega }_n{E}_i{U}_p-D_{pi}^2{Z}_i}{D_{pi}^2{Z}_i}}}(13)$

$t_{s-w}=\frac{8J_i{w}_n}{D_{pi}}(14)$

In line with Eq. (7) and (11), the poles, the natural oscillation angular frequency and damping ratio of the characteristic equation can be calculated as

$s_{\mathrm{1,2}}=\frac{-D_{pi}{Z}_i\pm \sqrt{D_{pi}^2{Z}_i^2-4J_i{\omega }_n{Z}_i{E}_i{U}_p}}{2J_i{\omega }_n{Z}_i}(15)$

$\left\{\begin{array}{c}{\omega }_{ni}=\sqrt{\frac{K_{pi}}{J_i{\omega }_n}}\hfill \\ {\zeta }_{ni}=\frac{D_{pi}}{2}\sqrt{\frac{1}{J_i{\omega }_n{K}_{pi}}}\hfill \end{array}\right.(16)$

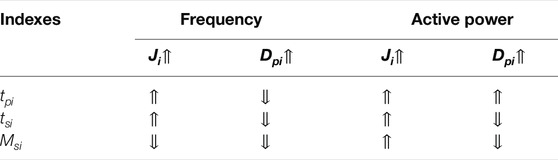
Eqs. (7)–(16) clearly shows that the natural oscillation angular frequency and damping ratio are determined by virtual inertia and damping coefficient. The typical indexes for the dynamic response the peak time (t_p), overshoot (M_s) and settling time (t_s) are directly associated with natural oscillation angular frequency and damping ratio, so that the dynamic responses of frequency and active power of VSG have relation to J_i and D_pi. The specific reflect is summarized in Table 1. Furthermore, the transit stability is affected by the two parameters as well since the poles would be to close to the imaginary axis to arouse oscillations. In other words, when the disturbances occur, not only deteriorated dynamic responses with long settling time, large overshoot and short peak time, but unstable oscillations will be caused if J_i and D_pi are chosen improperly. Therefore, it is of great significance to select appropriate J_i and D_pi to get better dynamic responses and improved transit stability of the MPVS.

TABLE 1

TABLE 1. Influence of parameter perturbation on dynamic responses.

Additionally, Eq. (7) also indicates that the active power outputs of VSGi during the steady state are bound up with D_iω_n + K_ωi when the MG is operated in islanded mode. In other words, the coupled effect between the primary frequency modulation and the damping characteristic results in the coupled effect of K_ωi and D_i on the active power output during steady operation. Whether active power can be shared proportionally by each VSG depends on whether the value of D_iω_n + K_ωi is proportional to its rated capacity. Power sharing error is prone to emerge once the parameters are chosen improperly. Consequently, it is essential to take measures to achieve proportional power sharing during steady state.

4 The IPAVSG Control Strategy for MPVS

In this section, a IPAVSG control strategy appropriate for both grid-connected and islanded MG is proposed, with which the ameliorative dynamic responses of the MPVS can be achieved through adaptively adjusting the virtual inertia and damping coefficient. Furthermore, proportional power sharing during steady operation in islanded mode is accomplished based on decoupling the coupled effect between the damping coefficient and equivalent governor droop coefficient on active power outputs.

4.1 Parameter-Adaptive VSG Control Strategy

In view of above analysis, if the virtual inertia and damping coefficient are selected improperly, deteriorated oscillations with long settling time and large overshoot will be aroused. Therefore, an adaptive virtual inertia and damping control strategy is designed to adaptively adjust inertia and damping to ameliorate the dynamic responses. This strategy is suitable for both grid-connected and islanded MG.

From Table 1, the influences of virtual inertia and damping coefficient on frequency and active power dynamic responses are roughly similar when it changes dynamically, so the dynamic responses of the active power will also be improved if those of frequency is modified. With respect to virtual inertia, in the case of large disturbances and sudden changes, within a limited value range, the smaller the virtual inertia is, the shorter the settling time becomes. In contrast, the larger the virtual inertia is, the smaller the overshoot and the longer the peak time stay, which means the firmer system holds. In order to combine these advantages, the virtual inertia should show a large value when the frequency deviates and a small one when frequency recovers (Andalib et al., 2018). Moreover, Eq. (16) shows that the damping coefficient changes accordantly with the virtual inertia.

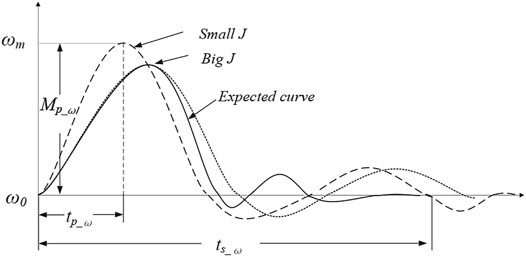
For quantitative selection of virtual inertia, the step responses of the output frequency are plotted, and shown as Figure 7.

FIGURE 7

FIGURE 7. Step response of frequency when J changes.

The two dashed lines represent the step responses of the output frequencies with two fixed rotational inertias J. Furthermore, as indicated by the expected curve (the solid one) in the picture above, if a big J is selected in the rising area and a small J is given in the descending area, the response time of the output frequency is decreased and the overshoot is also reduced. According to the same analysis method, the rules of the selection of virtual inertia and damping coefficient during transient process can be summarized as Table 2.

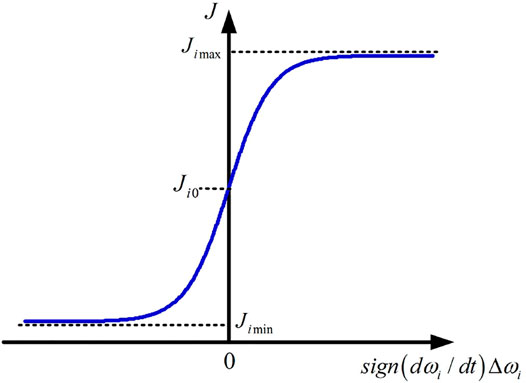
Notice that the large or small virtual inertia value mentioned here is relative to the steady-state virtual inertia. Besides, considering the stability of the system, the upper and lower limits (J_{i max} and J_{i min}) of the virtual inertia need to be taken into consideration, because low frequency oscillations of active power may be caused if inertia exceeds the limits. Based on the aforementioned analysis, the arc-tangent function is employed for adaptive calculation of virtual inertia. The adaptive control strategy with adjustable virtual inertia is designed as follows

$J_i=\left\{\begin{array}{c}{J}_{i0}+\frac{J_{i\max }-J_{i0}}{\pi /2}\arctan \left(\frac{\mathrm{\Delta }{\omega }_i}{2M_i}\times \mathit{s}\mathit{i}\mathit{g}\mathit{n}\left(\frac{d{\omega }_i}{dt}\right)\right),\hfill \\ \left|\mathrm{\Delta }{\omega }_i\right|>M_i\cap \mathrm{\Delta }{\omega }_i\times \mathit{s}\mathit{i}\mathit{g}\mathit{n}\left(\frac{d{\omega }_i}{dt}\right)>0\hfill \\ J_{i0}+\frac{J_{i0}-J_{i\min }}{\pi /2}\arctan \left(\frac{\mathrm{\Delta }{\omega }_i}{2M_i}\times \mathit{s}\mathit{i}\mathit{g}\mathit{n}\left(\frac{d{\omega }_i}{dt}\right)\right),\hfill \\ \left|\mathrm{\Delta }{\omega }_i\right|>M_i\cap \mathrm{\Delta }{\omega }_i\times \mathit{s}\mathit{i}\mathit{g}\mathit{n}\left(\frac{d{\omega }_i}{dt}\right)\le 0\hfill \\ J_{i0},\left|\mathrm{\Delta }{\omega }_i\right|\le M_i\hfill \end{array}\right.(17)$

where J_i0 is the steady-state virtual inertia, which is associated with the rated capacity. M_i is the frequency deviation threshold set to avoid the chattering of J_i during steady state. In theory, there should also be a threshold M_di set for dω_i/dt, and the adaptive control for J_i will be triggered only if both $\left|\mathrm{\Delta }{\omega }_i\right|>M_i$ and dω_i/dt > M_di are satisfied. However, whether the frequency keeps stable or not is mainly determined by Δω_i while the sign of dω_i/dt only represents the trend of frequency changing, and the value of Δω_i is normally smaller than dω_i/dt especially at the initial stage when disturbances occur. Therefore, to facilitate analysis, only the threshold for Δω_i is set in this paper. In actual situations, the change of Δω_i may be small, Δω_i/2M_i is introduced in this paper to amplify the frequency fluctuation value. With the proper threshold setting, the system can effectively filter out small disturbances while keeping sensitive to large disturbances. If the trigger condition $\left|\mathrm{\Delta }{\omega }_i\right|>M_i$ is satisfied, the virtual inertia will be adaptively changed.

TABLE 2

TABLE 2. Rules of J_i and D_pi.

The curve of the virtual inertia is depicted in Figure 8. The right half part represents the period of frequency deviating whereas the left means the period of frequency recovering. As can be seen in Figure 8, different from the bang-bang control, the adaptive control strategy designed here contributes to a continuous and broader range of virtual inertia. When the frequency deviates with the feature of $\mathrm{\Delta }{\omega }_i\times \mathit{s}\mathit{i}\mathit{g}\mathit{n}\left(d{\omega }_i/dt\right)>0$, the larger Δω_i is, the larger virtual inertia correspondingly becomes, which helps to suppress the overshoot and delay the peak time of the frequency oscillation. In reverse, smaller virtual inertia is conducive to shorten the settling time and accelerate the response speed when frequency recovers. In the whole process, the application of the arc-tangent function enables the virtual inertia to be more sensitive to frequency deviation, even for the initial small Δω_i, the J_i obtained from Eq. (17) is capable to be comparatively large to suppress the oscillation effectively at the initial stage of disturbances. With the further increase of the Δω_i, the J_i transits to the limits smoothly without beyond it, which is favorable for ensuring the system transient stability.

FIGURE 8

FIGURE 8. Changing curve of virtual inertia.

In terms of the damping coefficient, according to Table 1, the adjustment of D_i influences frequency and active power dynamic responses in a similar tendency (Hu et al., 2021b). The adaptive control strategy of D_i is designed as

${\zeta }_{ni}=\frac{D_i{\omega }_n+K_{\omega i}}{2}\sqrt{\frac{1}{J_i{\omega }_n{K}_{pi}}}=\text{\hspace{0.17em}constant}(18)$

Equation (18) means that during the transit process, the J_i and D_i are adaptively adjusted in a similar tendency and at the same time with a constant damping ratio. The upper or lower limits of virtual inertia and damping coefficient are obtained when the damping ratio is 0.7 or 1. In practice, the optimal damping ratio (ζ_ni = 0.707) is usually adopted for the best situation of the system. Hence, the damping ratio is kept at 0.707 in this paper to better ameliorate the dynamic responses and improve transient stability.

4.2 Active Power Proportional Distribution Control Strategy

In accordance with the above analysis, the active power outputs P_ei are associated with the coupled effect of primary frequency ω_p modulation and the damping characteristic in steady-state of islanded MG with MPVS. In general, the governor droop coefficient is set as K_ωi = S_ratei/(0.1%ω_n), S_ratei represents the rated capacity of the ith virtual synchronous generator (Zhang et al., 2017), and the value of D_i is supposed to prioritize the requirements of the best dynamic response. As can be seen in Figure 9, to fulfill these requirements, an active power proportional distribution control strategy is proposed to decouple the interaction between the equivalent governor droop coefficient and the damping coefficient in the conventional VSG control and eliminate the effect of D_i on the active power output during steady operation in islanded MG.

FIGURE 9

FIGURE 9. Active power proportional distribution control strategy.

When the system is running in an islanded state and remains stable, the output angular frequency of the inverter ω no longer changes. According to equation Eq. 3 and Figure 9, the active power output by VSGi and VSGj is shared in proportion to formula Eq. (19).

$\frac{P_{ei}}{P_{ej}}=\frac{P_{\mathit{r}\mathit{e}\mathit{f}\mathit{i}}-K_{\omega i}\left({\omega }_i-{\omega }_n\right)}{P_{\mathit{r}\mathit{e}\mathit{f}\mathit{j}}-K_{\omega j}\left({\omega }_j-{\omega }_n\right)}=C(19)$

Therefore, whether the line impedance is resistive, inductive or capacitive, the active power ratio sharing is determined by P_ref, K_ω and (ω − ω_n).

Compared to the conventional VSG control strategy, the principal modification is the introduction of a first-order lead-lag unit in the damping feedback loops. Then, the closed loop transfer function of ΔP_ei is obtained as follows

$\frac{\mathrm{\Delta }{P}_{ei}}{\mathrm{\Delta }{\omega }_p}=\frac{K_{pi}\times \left[J_i{\omega }_n{T}_{ci}{s}^2+\left(J_i{\omega }_n+D_i{T}_{ci}+K_{\omega i}{T}_{ci}\right)s+K_{\omega i}\right]}{J_i{\omega }_n{T}_{ci}{s}^3+\left(J_i{\omega }_n+D_i{T}_{ci}+K_{\omega i}{T}_{ci}\right)s^2+\left(K_{\omega i}+K_{pi}{T}_{ci}\right)s+K_{pi}}(20)$

Equation (20) illustrates that the active power output is only up bounded by K_ωi and the effect of D_i has been eliminated during steady state. The specific implementation process of the whole control strategy is as follows.

$S_i=\left\{\begin{array}{c}1,\left|\mathrm{\Delta }{\omega }_i\right|\le M_i\hfill \\ 0,\left|\mathrm{\Delta }{\omega }_i\right|>M_i\hfill \end{array}\right.(21)$

During steady operation, the switching state value S_i remains at one and the branch included the first-order lead-lag unit is chosen to decouple the effect of D_i on active power output. Subsequent to disturbances, S_i changes to 0 so that the adaptive control of J_i and D_i will be activated. Consequently, the proportional power sharing of the MPVS during steady operation can be ensured while the dynamic responses of the system in transient process is ameliorated.

5 Experiment Results

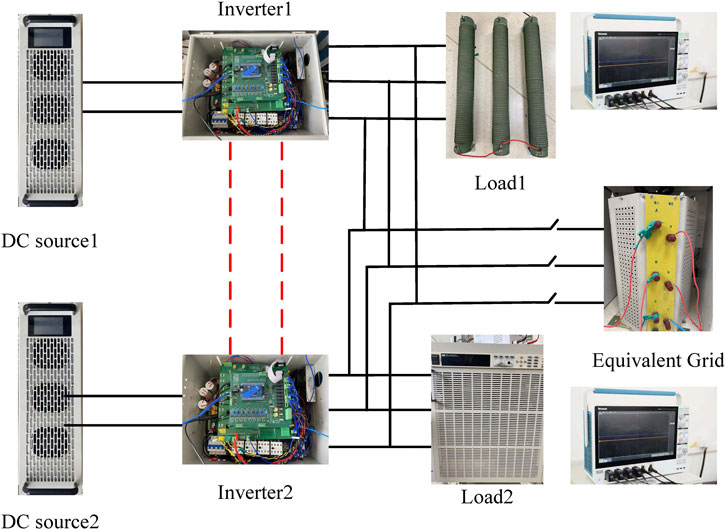
In this section, verifications of the IPAVSG control strategy are conducted through experiment results. As can be seen from Figure 10, the experimental platform contains two IIDG units operated in parallel. The corresponding experimental parameters are shown in Table 3. The parallel hard-switched PWM converters are digitally controlled by TMS28335 fixed-point DSP to implement the power and voltage control algorithm where switching frequency is 20 kHz. In practice, in order to save resource, a discrete table is created in advance. The value of arctan(x) can be directly taken from the table.

FIGURE 10

FIGURE 10. Experimental testbed.

TABLE 3

TABLE 3. Parameters of the TEST system.

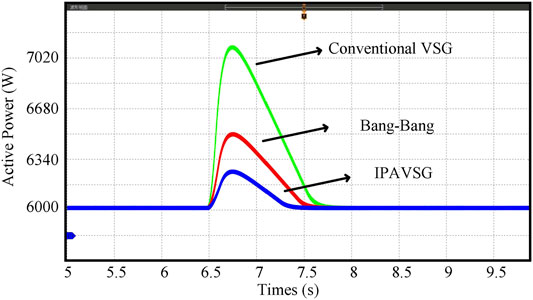
Firstly, an experiment is executed in grid-connected MG to verify the IPAVSG control strategy. The performances of the controllers to follow the power reference and maintain frequency stability are evaluated during a sudden load variation. The references of active and reactive power for each IIDG unit are assigned as 6 kW and 1 kVar. Then a 2 kW, 400 Var PCC load reduction happens at 6.4s.

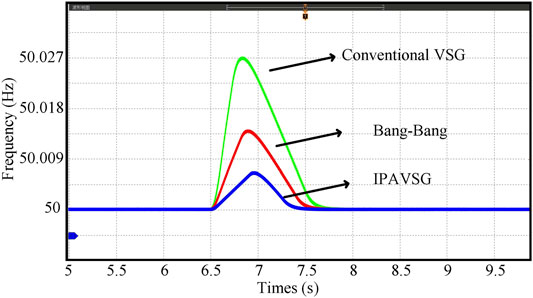
The frequency and active power dynamic responses controlled by the conventional VSG and the Bang-Bang and the IPAVSG control strategies are displayed in Figures 11, 12. Similar to the previous statement, only the results of IIDG1 are displayed here because the parameters of the two IIDG units are identical. When the load decreases suddenly, the frequency deviations of the three control strategies are 0.027, 0.014 and 0.006 Hz, respectively. Besides, the active power overshoot of the three control strategies are 1120, 510 and 250 W, respectively. Obviously, the experiment results have verified that the frequency and active power deviations can be suppressed with the virtual inertia and the damping coefficient in three VSG control strategies, in which the suppression is more effective in the IPAVSG control strategy since the parameters can be adaptively adjusted.

FIGURE 11

FIGURE 11. Frequency outputs of IIDG1.

FIGURE 12

FIGURE 12. Active power outputs of IIDG1.

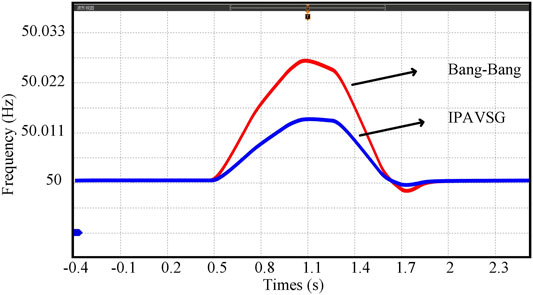
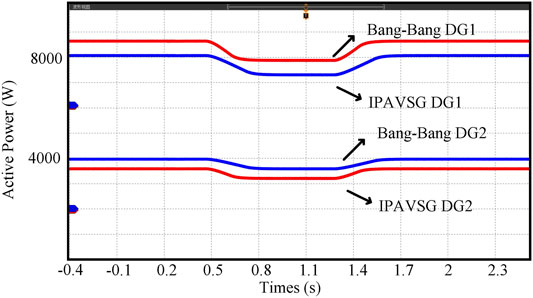
Another experiment is executed in islanded MG. The rated capacities of the two IIDG units are 10kW and 5kW, respectively. The MG is operated steadily with PCC loads rated at 12 kW at frist. A 1.2 kW load step decrease happens at 0.5s, then reconnects to the MG at 1.3 s.

The IPAVSG control strategy in the islanded MG is supposed to not only realize the adaptive tuning of virtual inertia and damping coefficient, but also proportional active power sharing. The former experiment results have illustrated the buffer and suppression effect of virtual inertia and the damping coefficient, and the conventional VSG control strategy has less superiority than the Bang-Bang and IPAVSG control strategies in oscillation suppression. Hence, in this experiment, we focus on the performance comparison of Bang-Bang and IPAVSG control strategies.

The frequency and active power of the system are displayed in Figures 13, 14. To get a clearer illustration, only the frequency responses of IIDG1 are displayed. Figure 13 depictes that the frequency overshoot controlled by IPAVSG is 0.015 Hz, which is much smaller than 0.028 Hz of Bang-Bang control. And the frequency rising trendency controlled by IPAVSG is much slower than that of Bang-Bang. Therefore, the better performances in suppressing frequency dynamic response can be found in the IPAVSG control strategy. Furthermore, during steady operation, the loads connected to IIDG1 and IIDG2 of IPAVSG are 8000 and 4000 W, respectively. During load transition, the loads decrease by 800 W and 400 W, respectively. The active power decrease is even slower. By contract, the loads supported by IIDG1 and IIDG2 of Bang-Bang are 8400 and 3600 W during steady state, then the loads reduction are 840 W and 360 W after 0.5 s. Besides, the active power decrease is slight faster. These experiment results could validate that the IPAVSG control strategy containing adaptive virtual inertia and damping control and decoupling control in islanded MG, has effective impact on ameliorating frequency and active power dynamic responses and has decoupling effect of damping coefficient on power sharing, with which the outputs could transit to a new steady state smoothly and the loads can be shared proportionally no matter before or after the load transition.

FIGURE 13

FIGURE 13. Frequency outputs from IIDG1 and IIDG2.

FIGURE 14

FIGURE 14. Active power outputs from IIDG1 and IIDG2.

6 Conclusion

An IPAVSG control strategy consists of adaptive virtual inertia and damping coefficient control along with decoupling control is proposed in this paper. The IPAVSG strategy can be adopted for MG with multiple IIDG units connected in parallel. The adaptive virtual inertia and damping control of IPAVSG has significantly ameliorated the dynamic responses of the MG in both grid-connected and islanded modes. Additionally, the active power outputs during steady state in islanded MG can be shared proportionally to rated capacities of IIDGs. The virtual inertia and damping coefficient of the IPAVSG control strategy can be adaptively adjusted based on the frequency responses, their proper selections are of great essentiality to the system dynamic resonances. In conclusion, the IPAVSG control strategy is of great benefit to the stability of the system.

Several experiment results in both grid-connected and islanded MG with different contingencies are conducted to validate the advantages and effectiveness of the IPAVSG control strategy. Comparisons between the conventional VSG control and Bang-Bang control are also provided in this paper, which facilitates a thorough acknowledge of these two promising control strategies for the utilization and development of renewable energy.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

XS has done the main theory research work. FZ, XC, and JL conceived the project and wrote the manuscript. RW, YZ and YL designed and participated in the experiment. All authors discussed the results, read, and commented on the manuscript.

Funding

This study is supported by the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources(Grant No.LAPS22002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipoor, J., Miura, Y., and Ise, T. (2018). Stability Assessment and Optimization Methods for Microgrid with Multiple VSG Units. IEEE Trans. Smart Grid 9 (2), 1462–1471. doi:10.1109/TSG.2016.2592508

CrossRef Full Text | Google Scholar

Andalib-Bin-Karim, C., Liang, X., and Zhang, H. (2018). Fuzzy-Secondary-Controller-Based Virtual Synchronous Generator Control Scheme for Interfacing Inverters of Renewable Distributed Generation in Microgrids. IEEE Trans. Ind. Appl. 54 (2), 1047–1061. doi:10.1109/TIA.2017.2773432

CrossRef Full Text | Google Scholar

Aouini, R., Marinescu, B., Ben Kilani, K., and Elleuch, M. (2016). Synchronverter-Based Emulation and Control of HVDC Transmission. IEEE Trans. Power Syst. 31 (1), 278–286. doi:10.1109/tpwrs.2015.2389822

CrossRef Full Text | Google Scholar

Beck, H., and Hesse, R. (2007). “Virtual Synchronous Machine,” in 2007 9th International Conference on Electrical Power Quality and Utilisation (Barcelona, Spain: IEEE), 1–6. doi:10.1109/epqu.2007.4424220

CrossRef Full Text | Google Scholar

D'Arco, S., and Suul, J. A. (2014). Equivalence of Virtual Synchronous Machines and Frequency-Droops for Converter-Based MicroGrids. IEEE Trans. Smart Grid 5 (1), 394–395. doi:10.1109/tsg.2013.2288000

CrossRef Full Text | Google Scholar

Driesen, J., and Visscher, K. (2008). “Virtual Synchronous Generators,” in Proc. IEEE Power Energy Soc. Gen. Meeting-Conversion and Delivery of Electrical Energy in the 21st Century (IEEE), 1–3. doi:10.1109/pes.2008.4596800

CrossRef Full Text | Google Scholar

Eskandari, M., Li, L., Moradi, M. H., Siano, P., and Blaabjerg, F. (2019). Active Power Sharing and Frequency Restoration in an Autonomous Networked Microgrid. IEEE Trans. Power Syst. 34 (6), 4706–4717. doi:10.1109/tpwrs.2019.2923797

CrossRef Full Text | Google Scholar

Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2018). Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 33 (10), 8488–8499. doi:10.1109/tpel.2017.2785218

CrossRef Full Text | Google Scholar

Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2019). On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 7 (4), 2130–2146. doi:10.1109/jestpe.2018.2877766

CrossRef Full Text | Google Scholar

Hou, X., Zhong, C., Yuan, W., Yi, M., and Chen, Y. (2016). “Improvement of Transient Stability in Inverter-Based AC Microgrid via Adaptive Virtual Inertia,” in 2016 IEEE Energy Conversion Congress and Exposition (IEEE), 1–6. doi:10.1109/ecce.2016.7855195

CrossRef Full Text | Google Scholar

Hu, X., Zhang, H., Ma, D., and Wang, R. (2021a). “Hierarchical Pressure Data Recovery for Pipeline Network via Generative Adversarial Networks,” in IEEE Transactions on Automation Science and Engineering (Early Access) (IEEE), 1–11. doi:10.1109/tase.2021.3069003

CrossRef Full Text | Google Scholar

Hu, X., Zhang, H., Ma, D., Wang, R., and Tu, P. (2021b). “Small Leak Location for Intelligent Pipeline System via Action-dependent Heuristic Dynamic Programming,” in IEEE Transactions on Industrial Electronics (Early Access) (IEEE), 1. doi:10.1109/tie.2021.3127016

CrossRef Full Text | Google Scholar

Huang, B., Liu, L., Zhang, H., Li, y., and Sun, Q. (2019). Distributed Optimal Economic Dispatch for Microgrids Considering Communication Delays. IEEE Trans. Syst. Man. Cybern. Syst. 49 (8), 1634–1642. doi:10.1109/tsmc.2019.2900722

CrossRef Full Text | Google Scholar

Hwang, M., Muljadi, E., Jang, G., and Kang, Y. C. (2017). Disturbance-Adaptive Short-Term Frequency Support of a DFIG Associated with the Variable Gain Based on the ROCOF and Rotor Speed. IEEE Trans. Power Syst. 32 (3), 1873–1881. doi:10.1109/tpwrs.2016.2592535

CrossRef Full Text | Google Scholar

Jiang, W., Zhang, X., Guo, F., Chen, J., Wang, P., and Koh, L. H. (2020). Large-Signal Stability of Interleave Boost Converter System with Constant Power Load Using Sliding-Mode Control. IEEE Trans. Ind. Electron. 67 (11), 9450–9459. doi:10.1109/tie.2019.2955401

CrossRef Full Text | Google Scholar

Kerdphol, T., Rahman, F. S., Mitani, Y., Watanabe, M., and Kufeoglu, S. (2018). Robust Virtual Inertia Control of an Islanded Microgrid Considering High Penetration of Renewable Energy. IEEE Access 6, 625–636. doi:10.1109/access.2017.2773486

CrossRef Full Text | Google Scholar

Kong, X., Liu, X., Ma, L., and Lee, K. Y. (2019). Hierarchical Distributed Model Predictive Control of Standalone Wind/Solar/Battery Power System. IEEE Trans. Syst. Man. Cybern. Syst. 49 (8), 1570–1581. doi:10.1109/TSMC.2019.2897646

CrossRef Full Text | Google Scholar

Li, D., Zhu, Q., Lin, S., and Bian, X. Y. (2017). A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 32 (1), 397–398. doi:10.1109/tec.2016.2623982

CrossRef Full Text | Google Scholar

Li, X. (2019). Global Exponential Stability of Impulsive Delay Systems with Flexible Impulse Frequency. IEEE Trans. Syst. Man. Cybern. Syst. 49 (10), 2166–2174. doi:10.1109/tsmc.2017.2766260

CrossRef Full Text | Google Scholar

Li, X., Xu, Q., and Blaabjerg, F. (2021). Adaptive Resilient Secondary Control for Islanded AC Microgrids with Sensor Faults. IEEE J. Emerg. Sel. Top. Power Electron. 9 (5), 5239–5248. doi:10.1109/jestpe.2020.2988509

CrossRef Full Text | Google Scholar

Lin, L., Ma, H., and Bai, Z. (2017). An Improved Proportional Load-Sharing Strategy for Meshed Parallel Inverters System with Complex Impedances. IEEE Trans. Power Electron. 32 (9), 7338–7351. doi:10.1109/tpel.2016.2630709

CrossRef Full Text | Google Scholar

Liserre, M., Sauter, T., and Hung, J. (2010). Future Energy Systems: Integrating Renewable Energy Sources into the Smart Power Grid through Industrial Electronics. EEE Ind. Electron. Mag. 4 (1), 18–37. doi:10.1109/mie.2010.935861

CrossRef Full Text | Google Scholar

Liu, J., Miura, Y., and Ise, T. (2014). “Dynamic Characteristics and Stability Comparisons between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators,” in 2014 International Power Electronics Conference (IPEC-Hiroshima 2014 - ECCE ASIA) (Hiroshima, Japan: IEEE), 1536–1543. doi:10.1109/ipec.2014.6869789

CrossRef Full Text | Google Scholar

Ma, D., Cao, X., Sun, C., Wang, R., Sun, Q., Xie, X., et al. (2021a). “Dual-Predictive Control with Adaptive Error Correction Strategy for AC Microgrids,” in IEEE Transactions on Power Delivery (Early Access) (IEEE), 1. doi:10.1109/tpwrd.2021.3101198

CrossRef Full Text | Google Scholar

Ma, D., Hu, X., Zhang, H., Sun, Q., and Xie, X. (2021b). A Hierarchical Event Detection Method Based on Spectral Theory of Multidimensional Matrix for Power System. IEEE Trans. Syst. Man. Cybern. Syst. 51 (4), 2173–2186. doi:10.1109/tsmc.2019.2931316

CrossRef Full Text | Google Scholar

Ma, D., Liu, M., Zhang, H., Wang, R., and Xie, X. (2021c). “Accurate Power Sharing and Voltage Regulation for AC Microgrids: An Event-Triggered Coordinated Control Approach,” in IEEE Transactions on Cybernetics (Early Access) (IEEE), 1–11. doi:10.1109/tcyb.2021.3095959

CrossRef Full Text | Google Scholar

Meng, J., Wang, Y., Fu, C., and Wang, H. (2016). “Adaptive Virtual Inertia Control of Distributed Generator for Dynamic Frequency Support in Microgrid,” in 2016 IEEE Energy Conversion Congress and Exposition (IEEE), 1–5. doi:10.1109/ecce.2016.7854825

CrossRef Full Text | Google Scholar

Meng, K., Dong, Z. Y., Xu, Z., Zheng, Y., and Hill, D. J. (2019). Coordinated Dispatch of Virtual Energy Storage Systems in Smart Distribution Networks for Loading Management. IEEE Trans. Syst. Man. Cybern. Syst. 49 (4), 776–786. doi:10.1109/tsmc.2017.2690911

CrossRef Full Text | Google Scholar

Mojica-Nava, E., Macana, C. A., and Quijano, N. (2014). Dynamic Population Games for Optimal Dispatch on Hierarchical Microgrid Control. IEEE Trans. Syst. Man. Cybern. Syst. 44 (3), 306–317. doi:10.1109/tsmcc.2013.2266117

CrossRef Full Text | Google Scholar

Rene, V., Sjored, D., Pablo, V., and Klaas, V. (2009). “Grid Tied Converter with Virtual Kinetic Storage,” in 2009 IEEE Bucharest PowerTech (IEEE), 1–7.

Google Scholar

Simpson-Porco, J. W., Dörfler, F., and Bullo, F. (2013). Synchronization and Power Sharing for Droop-Controlled Inverters in Islanded Microgrids. Automatica 49 (9), 2603–2611. doi:10.1016/j.automatica.2013.05.018

CrossRef Full Text | Google Scholar

Soni, N., Doolla, S., and Chandorkar, M. C. (2013). Improvement of Transient Response in Microgrids Using Virtual Inertia. IEEE Trans. Power Deliv. 28 (3), 1830–1838. doi:10.1109/TPWRD.2013.2264738

CrossRef Full Text | Google Scholar

Tian, E., and Peng, C. (2020). Memory-Based Event-Triggering H ∞ Load Frequency Control for Power Systems under Deception Attacks. IEEE Trans. Cybern. 50 (11), 4610–4618. doi:10.1109/tcyb.2020.2972384

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., He, H., and Liu, D. (2017). Adaptive Critic Nonlinear Robust Control: A Survey. IEEE Trans. Cybern. 47 (10), 3429–3451. doi:10.1109/tcyb.2017.2712188.23

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F., Zhang, L., Feng, X., and Guo, H. (2018). An Adaptive Control Strategy for Virtual Synchronous Generator. IEEE Trans. Ind. Appl. 54 (5), 5124–5133. doi:10.1109/TIA.2018.2859384

CrossRef Full Text | Google Scholar

Wang R, R., Sun, Q., Ma, D., and Liu, Z. (2019). The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energy 10 (3), 1459–1469. doi:10.1109/tste.2019.2894633

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 36 (7), 7866–7879. doi:10.1109/tpel.2021.3049241

CrossRef Full Text | Google Scholar

Weng S, S., Yue, D., Dou, C., Shi, J., and Huang, C. (2019). Distributed Event-Triggered Cooperative Control for Frequency and Voltage Stability and Power Sharing in Isolated Inverter-Based Microgrid. IEEE Trans. Cybern. 49 (4), 1427–1439. doi:10.1109/tcyb.2018.2803754

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Chen, Y., Luo, A., Zhou, L., Zhou, X., Yang, L., et al. (2017). A Virtual Inertia Control Strategy for DC Microgrids Analogized with Virtual Synchronous Machines. IEEE Trans. Ind. Electron. 64 (7), 6005–6016. doi:10.1109/tie.2016.2645898

CrossRef Full Text | Google Scholar

Yang, X., Su, J., Ding, M., Li, J., and Du, Y. (2011). “Control Strategy for Virtual Synchronous Generator in Microgrid,” in 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (IEEE), 1633–1637.

Google Scholar

Zhang, X., Mao, F., Xu, H., Liu, F., and Li, M. (2017). An Optimal Coordination Control Strategy of Micro-grid Inverter and Energy Storage Based on Variable Virtual Inertia and Damping of Vsg. Chin. J. Electr. Eng. 3 (3), 25–33.

Google Scholar

Zhong, Q., Nguyen, P., Ma, Z., and Sheng, W. (2014). Self-Synchronized Synchronverters: Inverters without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 29 (2), 617–630. doi:10.1109/tpel.2013.2258684

CrossRef Full Text | Google Scholar

Zhao, Z., Yang, P., Guerrero, J. M., Xu, Z., and Green, T. C. (2016). Multiple-Time-Scales Hierarchical Frequency Stability Control Strategy of Medium-Voltage Isolated Microgrid. IEEE Trans. Power Electron. 31 (8), 5974–5991. doi:10.1109/tple.2015.249686910.1109/tpel.2015.2496869

CrossRef Full Text | Google Scholar

Zhong, Q.-C., and Weiss, G. (2011). Synchronverters: Inverters that Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 58 (4), 1259–1267. doi:10.1109/tie.2010.2048839

CrossRef Full Text | Google Scholar