Distributed Secondary Control Strategy Against Bounded FDI Attacks for Microgrid With Layered Communication Network

This paper investigates FDI attacks in distributed secondary control strategy for low inertia microgrid with a high proportion of renewable energy and power electronics. Adversaries always aim to tamper information exchange between the neighbor distributed generators (DGs) in microgrids, which results in voltage and frequency deviation leading to power breakdown. To enhance the resilience against FDI attacks of microgrid, a control network layer interconnecting with the original data transmission layer is introduced to form a layered communication network. Due to the higher openness of the layered network, the introduced control network layer also faces to potential FDI attacks. This paper proposed a distributed secondary control strategy against double-layered bounded FDI attacks rather than only attacks in the information transmission layer. The strategy can mitigate FDI attacks launched in the control network layer, and adverse influence on the data transmission layer can also be mitigated caused by FDI attacks launched in the control network layer by designing proper interconnecting matrices. In this paper, the Lyapunov theory is used to demonstrate that the strategy can make the low inertia microgrid still maintain stable against double-layered bounded FDI attacks. The effectiveness of the distributed secondary strategy against bounded FDI attacks is validated in a test microgrid consisting of 4 DGs using the Matlab/Simpower system.

1 Introduction

Grid-connected operation of DGs with a high proportion of renewable energy has become a feature of current microgrids (Liang, 2017; Sockeel et al., 2020), which requires more power electronic equipments to replace part of the synchronous generators in microgrids. This trend can improve the efficiency of energy conversion, but reduce the inertia of microgrids. There exists complex uncertainties in microgrids, ensuring frequency stability is essential for low inertia microgrids.

The operation framework of microgrids is proposed in (Bidram and Davoudi, 2012). When the microgrid is connected to the main grid, its operating frequency and voltage are determined by the main grid (Rui et al., 2020). When the microgrid operates in an islanded mode, the hierarchical control framework regulates its standardized operation. The hierarchical control framework dividesthe frequency control in the microgrid into three levels. Primary control strategies mean that when loads are suddenly connected or cut off, the output power of microgrids should be increased or decreased accordingly to maintain the balance between the output power and the power required by loads. According to the droop mechanism, when the output power of the microgrid changes, it will lead to a frequency fluctuation. When the rated frequency is 50 Hz, the frequency of the microgrid is allowed to fluctuate between 49.5 and 50.2 Hz. Without human intervention, the microgrid will accommodate the fluctuation in a small range through its frequency capacity. If the fluctuation exceeds the normal range, the microgrid cannot maintain operating frequency stable only by relying on its frequency capacity. At this point, manual secondary control is required. Secondary control strategies refer to design the primary control reference point, which make the reference point change from a fixed value to a dynamic one, and make the operating frequency and voltage of the microgrid fluctuate around the rated value all the time. Finally, tertiary control strategies involve power flow calculation in the microgrid, which aim to optimize the operation of the microgrid economically and efficiently (Wang et al., 2021). It can be seen from three levels of the control framework that secondary control strategies are crucial for the safe operation and high-quality power supply of microgrids, so the reliability of the secondary control strategies level is particularly important. Microgrids mainly focus on security and reliability analysis. Security is to evaluate the ability of the system to maintain continuous power supply in the cases of open and short circuit. Reliability refers to the evaluation of the performance of microgrids for a long time. As long as there is no power breakdown, the reliability evaluation of microgrids will not be affected. It can be seen that security and reliability are defined for general failures. The resilience research aimed at the extreme disturbance or cyberattacks, which is an effective supplement to the security and reliability of microgrids.

In the past microgrid operation, secondary control strategies usually adopted centralized control methods. Due to the wide distribution and strong fluctuation of renewable energy, it is quite necessary to exchange information between neighbor DGs based on distributed energy resources (DERs). However, centralized point-to-point control strategies impose a great burden on communication facilities in this case. At present, centralized secondary control strategies are gradually transitioning to distributed secondary control strategies, which are inspired by the cooperative control based on multi-agent systems (MASs) (Olfati-Saber and Murray, 2004; Bidram et al., 2014; Shafiee et al., 2014). That is, distributed secondary control strategies applied to the microgrid consider each inverter-based DG as an agent, and DGs carry out a lot of information exchange and calculation through the communication network. However, it should be noted that attacks are quite pervasive in the communication network environment. Especially, transmission and distribution network, an obvious target that will generate huge economic losses after being attacked, will attract the attention of potential attackers. For example, Ukraine’s power grid was attacked in 2015, resulting in a power outage (Liang et al., 2017). Distributed secondary control strategies seldom consider the adverse influence of attacks in the network environment. If the communication network between the neighbor DGs in the microgrid are attacked, they will gradually deviate from the rated frequency due to the lack of accurate information exchange. In this way, the output frequency of each DG in the microgrid will be out of synchronization and then oscillate. The most pervasive and classic cyber attacks in microgrids include false data injection (FDI) (Liu et al., 2011; Hu et al., 2018; Qu et al., 2021; Sinha et al., 2021) and denial of service (DoS) attacks. FDI attacks show that attackers launch false information into the communication network to tamper with real information. DoS attacks show that attackers send a large number of packets to block communication channels for preventing information exchange. In the operation process of microgrids, the application of firewalls (Salah et al., 2012; Zhang et al., 2019), gates (Condry and Nelson, 2016), and other technologies can effectively defend against DoS attacks. In addition to DoS attacks, FDI attacks also often occur in MASs.

A class of more sophisticated FDI attack can be designed after adversaries have known parameters of system matrices. This class of FDI attacks can evade traditional detection methods, such as χ² detection method, while tampering information exchange between neighbor DGs. Therefore, FDI attacks are more destructive and stealthier compared with DoS attacks. Distributed secondary strategies against FDI attacks mainly include detecting and isolating the attacked DG (Manandhar et al., 2014; Beg et al., 2017; Musleh et al., 2020; Xiahou et al., 2022) and designing resilient algorithms to defend against FDI attacks (Jin et al., 2017; Abhinav et al., 2018; Zhou et al., 2020). However, attack detection strategies have large computational burdens, and isolated DG nodes will adversely affect the connectivity of communication networks (Sundaram and Hadjicostis, 2011; Pasqualetti et al., 2012). Attack-resilient strategies have attracted more attention from researchers, which are characterized by improving the resilience of the communication network to effectively mitigate adverse effects caused by stealthy FDI attacks. Through the design of trust-based resilience control protocol in (Abhinav et al., 2018), the adverse influence of FDI attacks on communication links and sensors can be mitigated (Zhou et al., 2020). Adopted aperiodic intermittent control strategy with random switching frequency to improve the resilience of the microgrid against time-varying FDI attacks (Jin et al., 2017). Proposed a communication network structure based on the software-defined network (SDN) of the microgrid, indicating attack-resilient strategies can significantly improve the stability and security of communication networks in the SDN environment. Although (Abhinav et al., 2018) and (Zhou et al., 2020) have improved the resilience of microgrids against FDI attacks, attacked DG nodes still need to be detected and then isolated. However, detection and isolation strategies not only have requirements on the connectivity of communication networks but also have limitations on the number of attacked DGs in the microgrid.

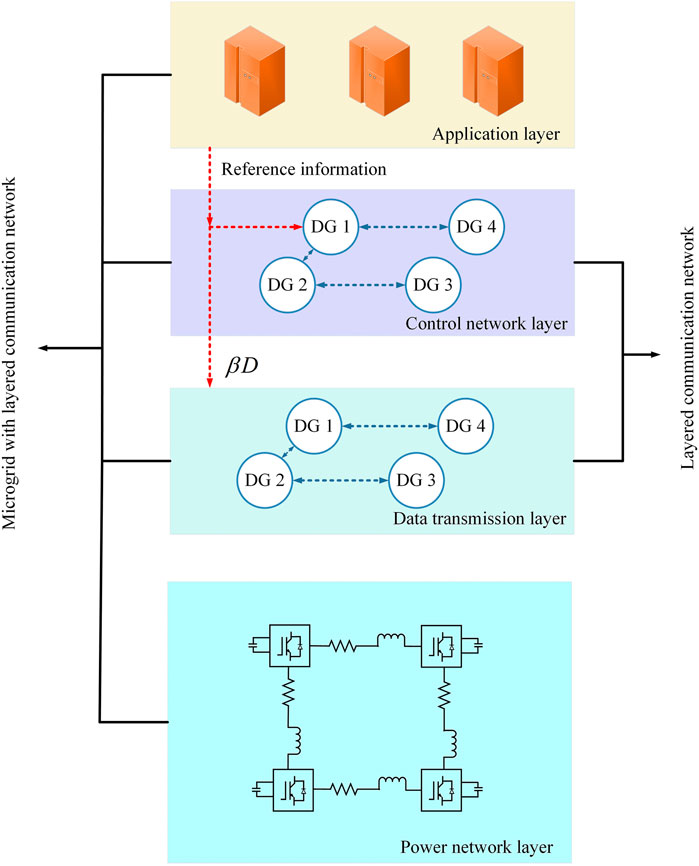
It is worth noting that there exists some work based on a layered communication network against FDI attacks, which is not limited by network connectivity and the number of attacked DGs. The attack-resilient control strategy proposed in (Gusrialdi et al., 2018) introduces a virtual system with a hidden network, so that the whole system consisting of the original consensus system, virtual system, and attack dynamic is stable without any information about attack position. The strategies discussed above depend on the distributed controller and information exchange between the neighbor DGs, which perhaps are in different network layers. Different vendors produce different types of controller hardware. Accordingly, operating systems in these devices are often designed and developed by different vendors. As a result, strategies designed by researchers are difficult to be applied uniformly in each DG, and it consumes a lot of resources to standardize different operating systems. The SDN is an emerging network structure, it aims to separate the data transmission function from the control function of the communication network (Nunes et al., 2014; Kreutz et al., 2015; Mijumbi et al., 2016). The structure of the microgrid with the layered communication network is shown in Figure 1. As can be seen from Figure 1, the microgrid is composed of four layers: application layer, control network layer, data transmission layer, and power network layer. The application layer contains energy management, state estimation, data monitoring, and other functions, which are directly controlled by the users. The control network layer and the data transmission layer constitute the layered communication network. Information in the power network layer is transmitted to the layered communication network through sensors, and finally to SCADA in the application layer. After obtaining the power information, SCADA will send the reference information (frequency, voltage, etc.) required for information exchange between neighbor DGs to the data transmission layer. At the same time, the control network layer also can receive the reference information through the design of interconnection matrices.

FIGURE 1

FIGURE 1. The structure of the microgrid with the layered communication network.

Based on the introduced control network layer using SDN, (Chen et al., 2021; Zhou et al., 2021) apply the resilient control strategy proposed in (Gusrialdi et al., 2018) to distributed secondary control of the microgrid, and demonstrate that this strategy can effectively restrain the adverse influence of FDI attacks on the communication network between DGs (Zuo and Yue, 2022). further proposed a fully distributed control strategy to guarantee the uniformly ultimately bounded containment convergence of multigroup systems to resist unbounded FDI attacks, which have more stronger impact but are more easilier to be detected (Chen et al., 2021; Zhou et al., 2021). believe that the hidden network layer in (Gusrialdi et al., 2018) is less likely to be attacked, but in fact, the control network layer is still possible to be tempered by more stealthier attacks because the openness of the network will become wider after layering the communication network.

To solve this problem, this paper considers the case that bounded FDI attacks are launched in both the data transmission layer and the control network layer, and proposes a distributed secondary control strategy against double-layered bounded FDI attacks in the microgrid. The distributed secondary strategy proposed in this paper can be applied to microgrids with layered communication networks. The data transmission layer is responsible for the transmission of power information, and the control network layer is responsible for the control of information exchange. The layered communication network reduces the requirement on the local controller of each DG, and it is also convenient for managers to replace with advanced control strategies whenever necessary. When both the data transmission layer and control network layer suffered bounded FDI attacks launched by adversaries, angular frequency and active power sharing can maintain stable due to the stronger resilience provided by the layered communication network. And Lyapunov theory is used to demonstrate the strategy can effectively defend against double-layered bounded FDI attacks and maintain the stability of the microgrid.

The rest of this paper is organized as follows. The introduction of the graph theory and the control structure of each DG is presented in Section 2. The stability of the proposed strategy under the influence of bounded FDI attacks is demonstrated using Lyapunov theory in Section 3. The effectiveness of the proposed distributed secondary control strategy against double-layer bounded FDI attacks is validated in a microgrid test system consisting of 4 DGs using Matlab/Simpower system simulations in Section 4, and Section 5 presents the summary of this paper.

2 Preliminaries

This section introduces the communication network between DGs in the microgrid and the control structure of the inverter-based DG. And a nomenclature containing sets, parameters, and abbreviations is shown in Table 1.

TABLE 1

TABLE 1. Nomenclature table.

2.1 Communication Network Between DGs

The microgrid discussed in this paper is a multi-agent cooperative control system containing N inverter-based DGs. Distributed secondary control strategies can maintain stable operating frequency and voltage only with the support of a communication network. Each DG is treated as an agent node, and the information flow between neighbor DGs is modeled by a direct graph $\varsigma =\left(\nu ,\epsilon ,A_a\right)$ consisting of a node set $\nu =\left\{{\nu }_1,{\nu }_2,\dots ,{\nu }_N\right\}$ and an edge set ɛ ⊂ ν × ν. A_a = [a_ij] ∈ R^N×N represents an adjacency matrix with a_ii = 0, (i, j) ∈ ɛ, (i, j) ∈ ɛ. Otherwise, a_ij = 0. A_a = [a_ij] ∈ R^N×N represents an adjacency matrix with a_ii = 0. If (i, j) ∈ ɛ, a_ij = 1. Otherwise, a_ij = 0, (i, j) means information flowing from DG j to DG i. DG j is called DG i’s neighborhood if (i, j) ∈ ɛ, this is the definition of neighbor in this paper. The set of neighbors of DGi called $N_i=\left\{j|(i,j)\in \epsilon \right\}$. The in-degree matrix D_in is a diagonal matrix representing as $D_{in}=diag\left\{d_1,d_2,\dots ,d_N\right\}$, where $d_i=\sum _{j=1}^N{a}_{ij}(i=1,\dots ,N)$ is the number of neighbors of DG i. d_i is also the number of elements in N_i. The corresponding Laplace matrix can be defined as:

$L_{ij}=\left\{\begin{array}{c}\sum _{j=1}^n{a}_{ij}\text{,\hspace{0.17em}}i=j\hfill \\ -a_{ij}\text{,\hspace{0.17em}}i\ne j\hfill \end{array}\right.(1)$

Generally, at least one DG can receive the reference information such as the rated angular frequency ω_ref given by SCADA in the application layer as shown in Figure 1. Such DG is called the leader in this paper, and the rest of DGs will exchange information through the communication network to track the leader’s state. b_i (i = 1, 2, … , N) represents which DG is the leader. If b_i = 1, DG i is the leader, otherwise, DG i is not. The dynamic angular frequency expression in the islanded microgrid can be obtained as:

$\dot{\omega }=-\left(L+G_b\right)\omega +B{\omega }_{ref}(2)$

where $B={(b_1,b_2,\dots ,b_N)}^T$ and G_b = diag (b₁, b₂, … , b_N) here. (2) is a typical distributed secondary control strategy, but it is obvious that the expression does not consider how to restore the microgrid to the rated operation state when the communication network is attacked. The renewable energy facilities in microgrids are very expensive, and the damage of frequency oscillation to devices is permanent. Therefore, it is very important to design a distributed secondary control strategy against FDI attacks to maintain the stable operation of the microgrid.

2.2 Power Electronics Model and Control Structure of Each Inverter-Based DG

It can be seen from Figure 1 that the design of the communication network layer is inseparable from the design of the power network layer (Pogaku et al., 2007; Wang et al., 2019; Ge et al., 2021). In this paper, the power network layer refers to an islanded microgrid consisting of multiple DGs. The control structure of each DG is shown in Figure 2.

FIGURE 2

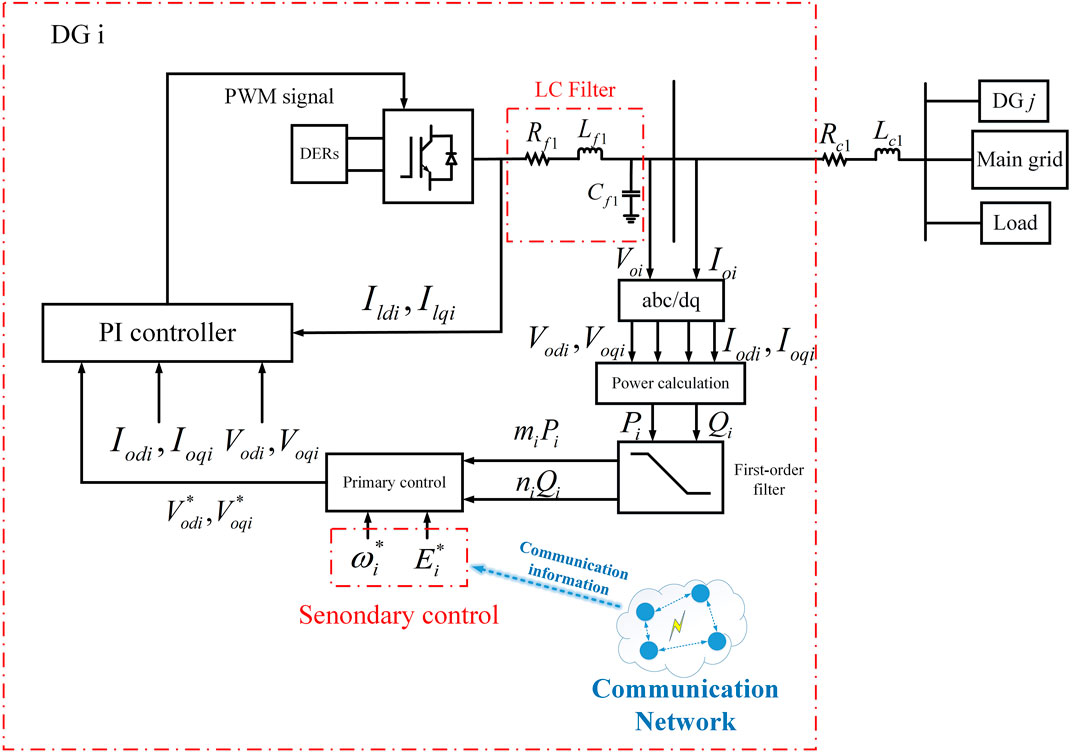
FIGURE 2. The block diagram of the power electronics model and control structure of each inverter-based DG applied distributed secondary control strategy.

As shown in Figure 2, the renewable energy storage device completes the conversion from dc to ac by connecting the port of the voltage source inverter (VSI). The inverter-based DG adopts current voltage double closed loop as control structure. V_oi and I_oi are output voltage and current of the DG, respectively. In order to more conveniently calculate the output power of each DG, V_oi and I_oi need to be transformed from abc axes to dq axes. The droop expression of the primary control strategy in Figure 2 is shown as (3):

$\left\{\begin{array}{c}{\omega }_i={\omega }_i^{*}-m_i{P}_i\hfill \\ V_{odi}^{*}=E^{*}-n_i{Q}_i\hfill \end{array}\right.(3)$

Combining active power P and ${\omega }_i^{*}$ according (3) yields $V_{odi}^{*},V_{oqi}^{*}$ which represents the reference input signal of the voltage loop controller. And how to design ${\omega }_i^{*}$ is the target of the secondary control strategy. Combining $V_{odi}^{*},V_{oqi}^{*},I_{odi},I_{oqi},V_{odi}$ and V_oqi yields the reference input signal of the current loop controller, where I_odi, I_oqi are output current of the DG. Voltage and current loop controller form PI controller together. Combining the reference input signal of the current loop controller and output current I_ldi, I_lqi of the inverter yields PWM signals which controls the sequence of switch actions of the inverter. The control circuit of each DG also has several series filters to mitigate the effect of harmonics. The whole DG connects the main grid and other DGs by R and L.

3 Distributed Secondary Control Strategies Against Bounded FDI Attacks

Primary control strategies of low inertia islanded microgrids mostly adopt the droop control method. The droop control method means that the microgrid balances the load variation by adjusting the output power of DGs. However, the primary control strategy is differential, that is, although the power balance of the microgrid is maintained, the angular frequency cannot be maintained at the rated value. To solve this shortcoming, secondary control strategies are designed to eliminate the difference value. Distributed secondary control strategies perform as cooperative control methods by sharing local power information between neighbor DGs. Generally, the communication network connectivity of microgrids is often high enough to exchange information, which also lays a potential risk for the spread of attacks rapidly in the communication network. Therefore, the potential attacks in the communication network should be considered when designing distributed secondary control strategies.

3.1 The Distributed Secondary Control Strategy Without FDI Attacks

The work in (Bidram et al., 2013, 2014) adopted the MAS-based distributed cooperative control method using input-output feedback linearization to design secondary control strategy of the microgrid. Once the multi-agent system is linearized by input-output feedback, the secondary control strategy of microgrids will lead to a first-order synchronization problem. The distributed secondary control protocol of each DG is shown in (4), whose purpose is to synchronize the angular frequency of each DG to the rated value. The rated frequency in this paper is set to 50Hz, and accordingly, the rated angular frequency w_ref is set to 314 rad/s. The relationship between control protocol and primary control set point is shown in (5):

$\begin{array}{ll}\hfill u_i& =-c\left[\sum _{j\in N_i}{a}_{ij}\left(w_i-w_j\right)+g_i\left(w_i-w_{ref}\right)\right.\hfill \\ \hfill & \left.+\sum _{j\in N_i}{a}_{ij}\left(m_i{P}_i-m_j{P}_j\right)\right]\hfill \end{array}(4)$

$w_i^{*}=\int u_{i}dt(5)$

Combine (3) and (5), the expression ${\dot{P}}_i$ is shown in (6), where w_ci represents the cut-off frequency of each DG. In this way, the angular frequency of microgrids can be obtained after primary control and secondary control adjustment, as shown in (7):

${\dot{P}}_i=-w_{ci}{P}_i+w_{ci}\left(v_{odi}{i}_{odi}+v_{oqi}{i}_{oqi}\right)(6)$

$w_i=\int u_{i}dt-m_i{P}_i(7)$

Distributed secondary control strategies without FDI attacks proposed in (Bidram et al., 2013, 2014) keep the angular frequency running within the rated range effectively under the condition of load disturbance. However, these strategies do not consider the case of external attack injection (Abhinav et al., 2018). Indicates that when the control protocol in (Bidram et al., 2014) suffers external FDI attacks, the frequency of each DG cannot be synchronized to the rated value. The severe frequency oscillation of each DG in the attacked microgrid will cause permanent damage to renewable energy facilities in the station, resulting in unnecessary economic losses. The distributed secondary control strategy exchanges information between neighbor DGs through a communication network to design ${\omega }_i^{*}$ and E^* compensating angular frequency and voltage changes. Obviously, the distributed secondary control strategy without attacks does not consider the adverse influence of cyber attacks when exchanging information between neighbor DGs. The most outstanding innovation of the distributed secondary proposed in this paper compared with the strategy without FDI attacks is that a layered communication network has been considered to enhance the resilience of microgrids against FDI attacks. Therefore, it is necessary to design a distributed secondary control strategy against FDI attacks.

3.2 Distributed Secondary Control Strategy Against FDI Attacks

Researches on cyber attacks in microgrids mainly focus on bounded FDI attacks, because stealthy bounded attacks are easier to disguise and often difficult to be detected by detection algorithms (Liu et al., 2011; Hu et al., 2018). Therefore, a distributed secondary control strategy against double-layered bounded FDI attacks in microgrids with the layered communication network is proposed in this paper, which can be described by

$\left\{\begin{array}{c}\dot{w}=Aw+\beta Kz+B{w}_{ref}+{\mathrm{\Theta }}_1\hfill \\ \dot{z}=Hz-\beta Gw+\beta D{w}_{ref}+{\mathrm{\Theta }}_2\hfill \end{array}\right.(8)$

where $w={[w_1,w_2,\dots ,w_N]}^T$ denotes the angular frequency of each DG in the data transmission layer of the microgrid. $z={[z_1,z_2,\dots ,z_N]}^T$ denotes that each DG node in the data transmission layer corresponds to a control node in the control network layer. A can be calculated by − (L + G_b), and H can be chosen as any sparse Hurwitz matrix. P_s, P_h are diagonal matrices, and the design of P_s, P_h, K, G, D is detailed in (Zhang et al., 2015; Gusrialdi et al., 2018). And (8) can be rewrited as

$\left\{\begin{array}{c}\dot{w}=Aw+\beta Kz+B{w}_{\mathrm{r}\mathrm{e}\mathrm{f}}+{\mathrm{\Theta }}_1\hfill \\ \dot{z}=Hz-\beta P_h^{-1}{K}^T{P}_{s}w+\beta \left(P_h^{-1}{K}^T{P}_{s}1\right)w_{ref}+{\mathrm{\Theta }}_2\hfill \end{array}\right.(9)$

Assumption 1. The FDI attacks Θ₁, Θ₂ in this paper are bounded.It’s worth noting that Θ₁, Θ₂ denote external bounded FDI attacks in the data transmission layer and control network layer, respectively. In other words, $‖{\mathrm{\Theta }}_1‖\le k_1$, $‖{\mathrm{\Theta }}_2‖\le k_2$, and k₁, k₂ are both constants. Define $\tilde{w}=w-w_{ref}\mathbf{1}$ as the difference between w and w_ref, (10) can be obtained combining (9) and $\tilde{w}$, and the equilibrium state of (10) satisfies (11):

$\left\{\begin{array}{c}\dot{\stackrel{̃}{w}}=A\tilde{w}+\beta Kz+{\mathrm{\Theta }}_1\hfill \\ \dot{z}=Hz-\beta P_h^{-1}{K}^T{P}_s\tilde{w}+{\mathrm{\Theta }}_2\hfill \end{array}\right.(10)$

$\left\{\begin{array}{c}0=A{\tilde{w}}^e+\beta K{z}^e+{\mathrm{\Theta }}_1^e\hfill \\ 0=H{z}^e-\beta P_h^{-1}{K}^T{P}_s{\tilde{w}}^e+{\mathrm{\Theta }}_2^e\hfill \end{array}\right.(11)$

Define error vectors $\bar{w}=w-w^e$, $\bar{z}=z-z^e$, the error dynamic can be shown as

$\left\{\begin{array}{c}\dot{\stackrel{̄}{w}}=A\bar{w}+\beta K\bar{z}+\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)\hfill \\ \dot{\stackrel{̄}{z}}=H\bar{z}-\beta P_h^{-1}{K}^T{P}_s\bar{w}+\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\hfill \end{array}\right.(12)$

where Θ₁ satisfies ${\dot{\mathrm{\Theta }}}_1=f({\mathrm{\Theta }}_1,w)$, Θ₂ satisfies ${\dot{\mathrm{\Theta }}}_2=f({\mathrm{\Theta }}_2,z)$. ${\mathrm{\Theta }}_1^e$, ${\mathrm{\Theta }}_2^e$ from $0=f({\mathrm{\Theta }}_1^e,w^e)$, $0=f({\mathrm{\Theta }}_2^e,z^e)$ can be obtained respectively. To solve ${\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e$ in (12), a Lyapunov function need to be determined. By the Lyapunov converse theorem, it is known that there exists a $V_{{\mathrm{\Theta }}_1}({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e)$ satisfies (13). Moreover, by the Lipschitz continuity, (14) can be obtained as

$\left\{\begin{array}{c}{\gamma }_1{‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖}^2\le V_{{\mathrm{\Theta }}_1}\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)\le {\gamma }_2{‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖}^2\hfill \\ \frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}f\left({\mathrm{\Theta }}_1,w^e\right)\le -{\gamma }_3{‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖}^2\hfill \\ ‖\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}‖\le {\gamma }_4‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖\hfill \end{array}\right.(13)$

$\left\{\begin{array}{c}‖f\left({\mathrm{\Theta }}_1,w\right)-f\left({\mathrm{\Theta }}_1,w^e\right)‖\le {\gamma }_5‖w-w^e‖\hfill \\ ‖f\left({\mathrm{\Theta }}_1,w^e\right)-f\left({\mathrm{\Theta }}_1^e,w^e\right)‖\le {\gamma }_6‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖\hfill \end{array}\right.(14)$

Similarly, we have $V_{{\mathrm{\Theta }}_2}({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e)$ satisfies (15) and (16):

$\left\{\begin{array}{c}{\gamma }_7{‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖}^2\le V_{{\mathrm{\Theta }}_2}\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\le {\gamma }_8{‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖}^2\hfill \\ \frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}f\left({\mathrm{\Theta }}_2,w^e\right)\le -{\gamma }_9{‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖}^2\hfill \\ ‖\frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}‖\le {\gamma }_{10}‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖\hfill \end{array}\right.(15)$

$\left\{\begin{array}{c}‖f\left({\mathrm{\Theta }}_2,z\right)-f\left({\mathrm{\Theta }}_2,z^e\right)‖\le {\gamma }_{11}‖z-z^e‖\hfill \\ ‖f\left({\mathrm{\Theta }}_2,z^e\right)-f\left({\mathrm{\Theta }}_2^e,z^e\right)‖\le {\gamma }_{12}‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖\hfill \end{array}\right.(16)$

where γ_i (i = 1, 2, … , 12) are all positive constants. Computing the time derivation of $V_{{\mathrm{\Theta }}_1}({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e)$ yields $\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}f({\mathrm{\Theta }}_1,w)$. Combining (13) and (14) yields (17) as

$\begin{array}{ll}\hfill & \frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}f\left({\mathrm{\Theta }}_1,w\right)\hfill \\ \hfill & =\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}\left[f\left({\mathrm{\Theta }}_1,w^e\right)+f\left({\mathrm{\Theta }}_1,w\right)-f\left({\mathrm{\Theta }}_1,w^e\right)\right]\hfill \\ \hfill & =\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}f\left({\mathrm{\Theta }}_1,w^e\right)+\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}\left[f\left({\mathrm{\Theta }}_1,w\right)-f\left({\mathrm{\Theta }}_1,w^e\right)\right]\hfill \\ \hfill & \le -{\gamma }_3‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖+{\gamma }_4{\gamma }_5‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖‖w-w^e‖\hfill \end{array}(17)$

Similarly, combining (15) and (16) yields (18) as

$\begin{array}{ll}\hfill & \frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}f\left({\mathrm{\Theta }}_2,z\right)\hfill \\ \hfill & =\frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}\left[f\left({\mathrm{\Theta }}_2,z^e\right)+f\left({\mathrm{\Theta }}_2,z\right)-f\left({\mathrm{\Theta }}_2,z^e\right)\right]\hfill \\ \hfill & =\frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}f\left({\mathrm{\Theta }}_2,z^e\right)+\frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}\left[f\left({\mathrm{\Theta }}_2,z\right)-f\left({\mathrm{\Theta }}_2,z^e\right)\right]\hfill \\ \hfill & \le -{\gamma }_7‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖+{\gamma }_8{\gamma }_9‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖‖z-z^e‖\hfill \end{array}(18)$

To demonstrate that the layered communication network is stable against double-layered bounded FDI attacks, we choose a Lyapunov function as

$\begin{array}{ll}\hfill V& =\beta {\bar{w}}^T{P}_s\bar{w}+\beta {\bar{z}}^T{P}_h\bar{z}+V_{{\mathrm{\Theta }}_1}\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)+V_{{\mathrm{\Theta }}_2}\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\hfill \\ \hfill & -2{\bar{z}}^T{P}_h{K}^{-1}\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)-2{\bar{w}}^T{\left(K^T\right)}^{-1}{P}_h\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\hfill \end{array}(19)$

Next, the time derivation of V need to be computed. And ${\dot{V}}_{{\mathrm{\Theta }}_1}({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e)$ and ${\dot{V}}_{{\mathrm{\Theta }}_2}({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e)$ have been known from (17), (18). Define $2{\bar{z}}^T{P}_h{K}^{-1}({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e)$ and $2{\bar{w}}^T{(K^T)}^{-1}{P}_h({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e)$ as V₁, V₂. Then compute the time derivation of V₁, V₂, (20) and (21) can be obtained as

$\begin{array}{ll}\hfill {\dot{V}}_1& =2{\bar{z}}^T{P}_h{K}^{-1}\left[f\left({\mathrm{\Theta }}_1,w\right)-f\left({\mathrm{\Theta }}_1^e,w^e\right)\right]\hfill \\ \hfill & +2{\bar{z}}^T{H}^T{P}_h{K}^{-1}\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)+2{\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)}^T{P}_h{K}^{-1}\hfill \\ \hfill & \times \left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)\hfill \end{array}(20)$

$\begin{array}{ll}\hfill {\dot{V}}_2& =2{\bar{w}}^T{\left(K^T\right)}^{-1}{P}_h\left[f\left({\mathrm{\Theta }}_2,z\right)-f\left({\mathrm{\Theta }}_2^e,z^e\right)\right]\hfill \\ \hfill & +2{\bar{w}}^T{A}^T{\left(K^T\right)}^{-1}{P}_h\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)+2{\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)}^T{\left(K^T\right)}^{-1}\hfill \\ \hfill & \times P_h\left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\hfill \end{array}(21)$

$\begin{array}{ll}\hfill {\dot{V}}_1-{\dot{V}}_2& =2{\bar{z}}^T{P}_h{K}^{-1}\left[f\left({\mathrm{\Theta }}_1,w\right)-f\left({\mathrm{\Theta }}_1,w^e\right)\right]\hfill \\ \hfill & +2{\bar{z}}^T{P}_h{K}^{-1}\left[f\left({\mathrm{\Theta }}_1,w^e\right)-f\left({\mathrm{\Theta }}_1^e,w^e\right)\right]\hfill \\ \hfill & +2{\bar{z}}^T{H}^T{P}_h{K}^{-1}\left({\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e\right)-2{\bar{w}}^T{\left(K^T\right)}^{-1}{P}_h\hfill \\ \hfill & \times \left[f\left({\mathrm{\Theta }}_2^e,z\right)-f\left({\mathrm{\Theta }}_2^e,z^e\right)\right]-2{\bar{x}}^T{\left(K^T\right)}^{-1}{P}_h\hfill \\ \hfill & \times \left[f\left({\mathrm{\Theta }}_2,z^e\right)-f\left({\mathrm{\Theta }}_2^e,z^e\right)\right]-2{\bar{w}}^T{A}^T{\left(K^T\right)}^{-1}{P}_h\hfill \\ \hfill & \times \left({\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e\right)\hfill \end{array}(22)$

Since A is a Hurwitz matrix, there exists a matrix P_s > 0 such that A^TP_s + P_sA < 0. Similarly, we choose a Hurwitz and sparse matrix H, and there exists a matrix P_h > 0 such that H^TP_h + P_hH < 0. Define Q_s = A^TP_s + P_sA and Q_h = H^TP_h + P_hH. The time derivation of V can be obtained as $\dot{V}=\beta {\bar{w}}^T{Q}_s\bar{w}+\beta {\bar{z}}^T{Q}_h\bar{z}+\frac{\partial V_{{\mathrm{\Theta }}_1}}{\partial {\mathrm{\Theta }}_1}f({\mathrm{\Theta }}_1,w)+\frac{\partial V_{{\mathrm{\Theta }}_2}}{\partial {\mathrm{\Theta }}_2}f({\mathrm{\Theta }}_2,z)$. Combining (17) and (18), (23) can be obtained as

$\begin{array}{ll}\hfill \dot{V}& \le \beta {\bar{w}}^T{Q}_s\bar{w}+\beta {\bar{z}}^T{Q}_h\bar{z}-{\gamma }_3‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖\hfill \\ \hfill & +{\gamma }_4{\gamma }_5‖{\mathrm{\Theta }}_1-{\mathrm{\Theta }}_1^e‖‖w-w^e‖-{\gamma }_7‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖\hfill \\ \hfill & +{\gamma }_8{\gamma }_9‖{\mathrm{\Theta }}_2-{\mathrm{\Theta }}_2^e‖‖z-z^e‖+{\dot{V}}_1-{\dot{V}}_2\hfill \end{array}(23)$

where Q_s, Q_h, P_h, P_s, A, H, and K are all known matrices, and β > 0, $\beta {\bar{w}}^T{Q}_s\bar{w}<0$, and $\beta {\bar{z}}^T{Q}_h\bar{z}<0$. It can be observed that $\dot{V}<0$ for all large values of β, hence the equilibrium state of the layered communication network exists as w^e, z^e satisfing (11), in other words, (12) is stable. $z^e=H^{-1}(\beta P_h^{-1}{K}^T{P}_s{\tilde{w}}^e-{\mathrm{\Theta }}_2^e)$ can be obtained from (11), and then ${\tilde{w}}^e={(A+{\beta }^{2}K{H}^{-1}{P}_h^{-1}{K}^T{P}_s)}^{-1}({\beta }^{2}K{H}^{-1}{\mathrm{\Theta }}_2^e-{\mathrm{\Theta }}_1^e)$. And compute the time derivation of ${\tilde{w}}^e$, (24) can be obtained as

$\begin{array}{ll}\hfill \underset{t\to \infty }{\lim }w\left(t\right)& =w_{ref}+{\left(A+{\beta }^{2}K{H}^{-1}{P}_h^{-1}{K}^T{P}_s\right)}^{-1}\hfill \\ \hfill & \times \left({\beta }^{2}K{H}^{-1}{\mathrm{\Theta }}_2^e-{\mathrm{\Theta }}_1^e\right)\hfill \end{array}(24)$

Obviously, the larger β is, the closer the angular frequency of the microgrid with layered communication network is to the rated operating value w_ref when influenced by bounded FDI attacks. How to select the most appropriate β is an optimization problem, which is also the future work of this paper. In conclusion, in the case that both the data transmission layer and the control network layer are influenced by bounded FDI attacks, the angular frequency can be restored to the rated operating value w_ref. In this section, the stability of the proposed strategy against bounded FDI attack is demonstrated using Lyapunov theory.

4 Simulation Analysis

The effectiveness of the proposed distributed secondary control strategy against double-layer bounded FDI attacks is validated in a microgrid test system consisting of 4 DGs using Matlab/Simpower system simulations in this section.

Before initiating the simulation test on the microgrid composed of DGs, this section will verify the influence of bounded FDI attacks on DGs with different inertia shown as Figure 3. Set a set of DG i (i = 1, 2, 3, 4), droop coefficients of them are 3e-4, 4e-4, 5e-4, 6e-4, respectively. As shown in the figure below, with the increase of the active power output of each DG, the operating angular frequency also gradually decreases correspondingly, which is caused by the differential droop control mechanism. When the active power output reaches 2500 W, the same bounded FDI attacks are injected into the controllers of all DGs. Moreover, to ensure the effect of comparison, the location of external attacks are set within the controller of each DG. In this way, the size and position of attacks are guaranteed to be identical for each DG, and then the influence of attacks on DGs with different inertia can be observed distinctly. It can be seen that the operating angular frequency of DG1 is the least affected by attacks, while that of DG4 is the most affected. This shows that the frequency oscillation of the low inertia microgrid composed of DGs is more severe after being attacked. The distributed secondary control strategy designed in this paper can not only eliminate the difference phenomenon caused by droop control mechanism, but also effectively alleviate the influence caused by bounded FDI attacks in the low-inertia microgrid composed of DGs, so that the microgrid can operate at the rated angular frequency.

FIGURE 3

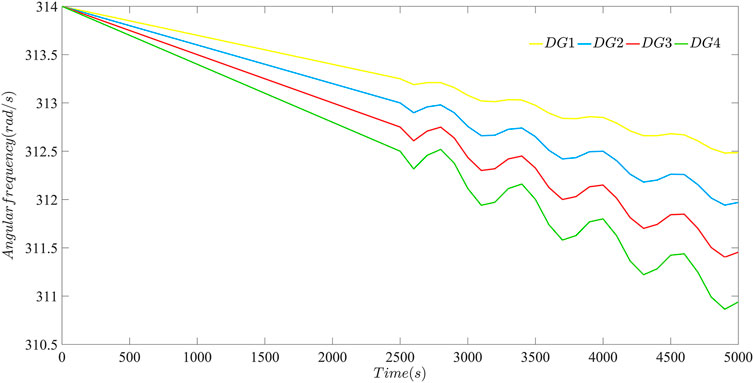
FIGURE 3. Effect of bounded FDI attacks on angular frequency of DG i (i = 1, 2, 3, 4) with different inertia.

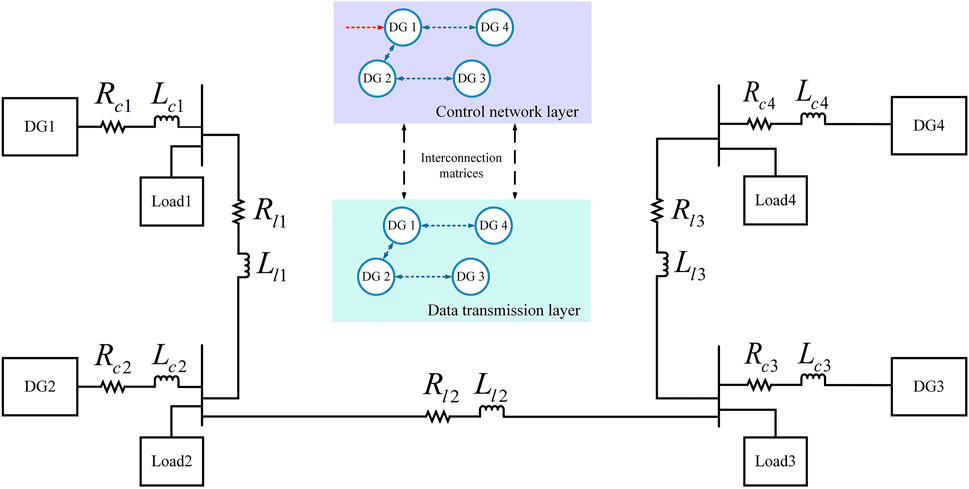
The circuit and communication topology of the microgrid test system are shown in Figure 4. The specifications of the microgrid test system are shown in Table 2, and the time step of the test microgrid test system is set to be 5e-6s.

FIGURE 4

FIGURE 4. The circuit model of the microgrid with the layered communication network.

TABLE 2

TABLE 2. Specifications of the microgrid test system with the layered communication network.

Set DG1 in Figure 4 as the leader, that is, only DG1 can receive the reference information of sent by SCADA. Matrixs of the distributed secondary control strategy proposed in this paper is selected as follows

$A_a=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],D_{in}=\left[\begin{array}{cccc}\hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],B=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right](25)$

$\begin{array}{c}H=\left[\begin{array}{cccc}\hfill -4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 2\hfill & \hfill -5\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill -4\hfill \end{array}\right],K=\left[\begin{array}{cccc}\hfill -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -2\hfill \end{array}\right],\\ A=\left[\begin{array}{cccc}\hfill -3\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right]\end{array}(26)$

where A_a is the adjacency matrix, D_in is the in-degree matrix. B is the pinned matrix, and b₁ = 1 means the DG1 acting as the leader. A can be calculated by − (D_in + G_b − A_a), where G_b = diag(B). K can be chosen to be any invertible sparse matrix. P_s, P_h can be calculated by methods Section 3 introduced. To verify the effectiveness of the distributed secondary control strategy against attacks proposed in this paper, bounded FDI attacks that are not easily detected are defined as

$\mathrm{\Theta }=k\hspace{0.17em}\sin \left(mt+\phi \right)+n(27)$

where k, m, and n are constants, and φ ∈ [0, 2π] represents the phase angle. The bounded FDI attacks in the layered communication network studied in this paper are selected as follows:

${\mathrm{\Theta }}_1=\left[\begin{array}{c}\hfill 4\hspace{0.17em}\sin \left(t\right)\hfill \\ \hfill 4\hspace{0.17em}\sin \left(2t\right)\hfill \\ \hfill -4\hspace{0.17em}\cos \left(t\right)\hfill \\ \hfill -4\hspace{0.17em}\cos \left(2t\right)\hfill \end{array}\right],{\mathrm{\Theta }}_2=\left[\begin{array}{c}\hfill 4\hfill \\ \hfill -4\hspace{0.17em}\sin \left(t\right)\hfill \\ \hfill -4\hfill \\ \hfill 4\hspace{0.17em}\sin \left(t\right)\hfill \end{array}\right](28)$

It is obvious that $‖{\mathrm{\Theta }}_1‖\le 4$, $‖{\mathrm{\Theta }}_2‖\le 4$ are both bounded. This section compares the resilience against bounded FDI attacks for existing distributed secondary strategies through simulation including: 1) the distributed secondary control strategy without FDI attacks; 2) the distributed secondary control strategy with the layered communication network which only considers FDI attacks in the data transmission layer. 3) This paper the distributed secondary control strategy proposes in this paper which considers FDI attacks in both the data transmission layer and the control network layer. The effectiveness of the distributed secondary control strategy designed in 4) is validated in the microgrid test system when the bounded FDI attack is launched at t = 8 s.

4.1 Performance of the Distributed Secondary Control Strategy Without FDI Attacks

The angular frequency of the microgrid when bounded FDI attacks are launched in the communication network is shown in Figure 5. It is obvious that angular frequency of the distributed secondary control strategy with FDI attacks can maintain stable when there exists no attacks before t = 8 s. However, once FDI attacks launched at t = 8 s, angular frequency of the microgrid oscillates violently after t = 8 s in Figure 5A, which deviates from the normal frequency fluctuation range of the microgrid and are unable to maintain stable. Performances of Figure 5A indicates that traditonal distributed secondary strategy lacks the ability against FDI attacks. Therefore, it is necessary to design a distributed secondary control strategy with stronger resilience against bounded FDI attacks to maintain stable of the microgrid.

FIGURE 5

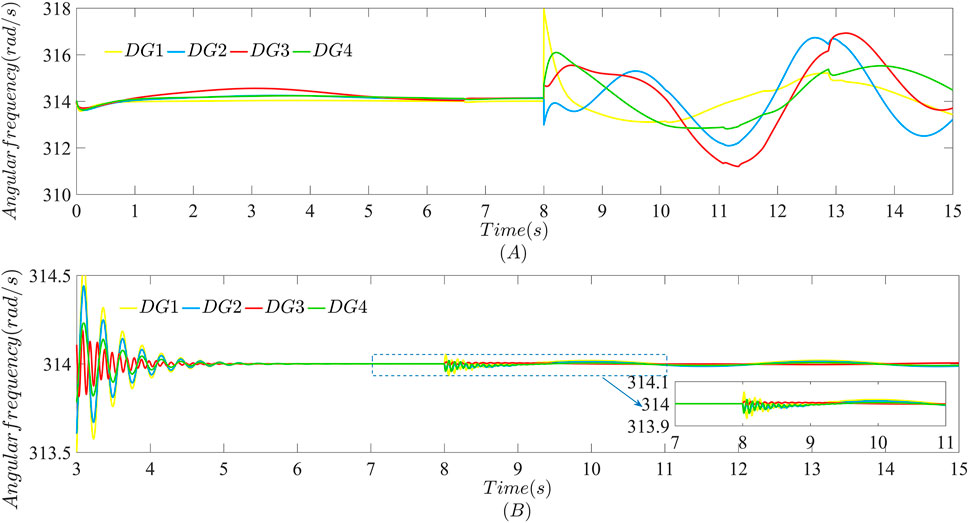
FIGURE 5. Performance of the angular frequency against the bounded FDI attack launched only in the data transmission layer at t = 8 s: (A) Using the distributed secondary strategy without FDI attacks; (B) Using the strategy proposed in this paper.

4.2 The Distributed Secondary Control Strategy With the Layered Communication Network Which Only Considers FDI Attacks in the Data Transmission Layer

The layered communication network separates the data transmission function and the control function from the communication network. The data transmission layer is only responsible for information exchange between neighbor the DGs, such as angular frequency and voltage. The control network layer is responsible for implementing the designed strategy, and the local controller of each DG corresponds to a virtual node control in the control network layer. The privacy of power information is directly related to the security of the microgrid operation. The existing strategies in (Chen et al., 2021; Zhou et al., 2021) consider the attacks only launched in the data transmission layer, but do not discuss how to defend against attacks in the control network layer. The distributed secondary control strategy based on the layered communication network against bounded FDI attacks proposed in this paper has considered cases that FDI attacks launched in the control network layer. At the same time, the distributed secondary strategy proposed in this paper does not affect the case when bounded FDI attacks are launched in the data transmission layer but the control network layer are not. Figure 5B shows it is obvious that the distributed secondary control strategy proposed in this paper can still keep the angular frequency of each DG around the rated value when the bounded FDI attack only launched in the data transmission layer.

4.3 The Distributed Secondary Control Strategy Proposes in This Paper Which Considers FDI Attacks in Both the Data Transmission Layer and the Control Network Layer

Compared with the distributed secondary control strategy without FDI attacks in (4), distributed secondary control strategies with the layered communication network undoubtedly enhances the resilience of the microgrid against external bounded FDI attacks. As can be seen from Figures 6, 7, the consensus angular frequency value of each DG is 314 rad/s, that is, 50 Hz of the corresponding frequency value. The consensus value of the active power sharing is 1.5, which ensures that each DG provides active power for microgrid loads in proportion to droop coefficients. And the consensus value of the control network layer is zero. The control network layer has no practical physical meaning causing a high security level, but it is not completely free of risks. Bounded FDI attacks $‖{\mathrm{\Theta }}_1‖\le 4,‖{\mathrm{\Theta }}_2‖\le 4$ are launched in the data transmission layer and the control network layer respectively. Performances of the microgrid are shown in Figures 6, 7.

FIGURE 6

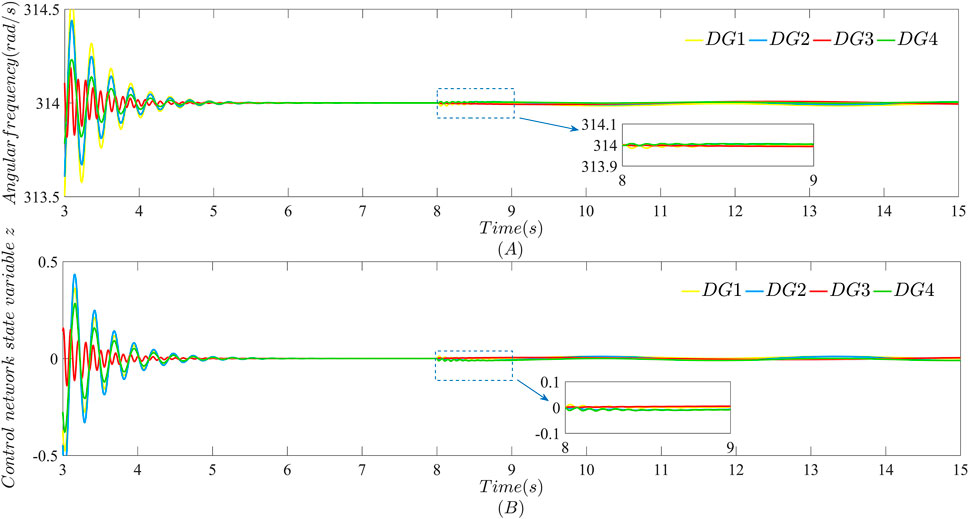
FIGURE 6. Performance of each DG in the microgrid after bounded FDI attacks are launched at t = 8 s in both the data transmission layer and the control network layer with β = 40: (A) Angular frequency; (B) Control network state variable z.

FIGURE 7

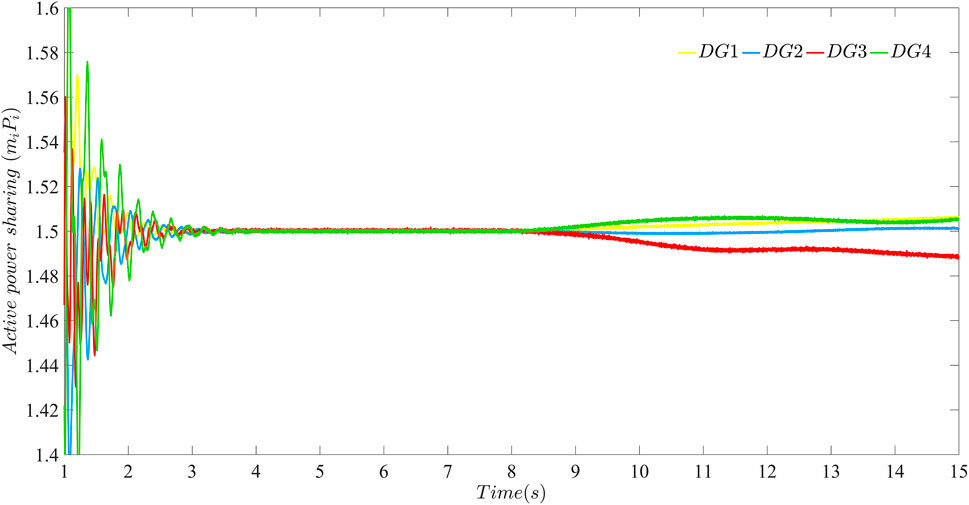
FIGURE 7. The active power sharing of each DG in the microgrid after bounded FDI attacks are launched at t = 8 s in both the data transmission layer and the control network layer with β = 40.

As can be seen from Figures 6, 7, the strategy proposed in this paper can achieve the purpose of the existing work, such as the stability of angular frequency and active power sharing. Moreover, the case that FDI attacks launched in the control network layer also can be solved. In other words, the distributed secondary strategy extends the function of layered communication networks used by existing work. Compared with the existing work, this paper will also consider the influence of FDI attacks in data transmission layer and control network layer on each other. It is worth mentioning that Figures 6, 7 show the case with β = 40 in the distributed secondary strategy proposed in this paper.

According to (24) in Section 3, when β > 0 is a large enough constant value, the larger its value is, the closer the angular frequency of each DG in the microgrid will be to the rated value w_ref. For this purpose, performances of the microgrid using the distributed secondary control strategy proposed in this paper with β = 100 are shown in Figures 8, 9.

FIGURE 8

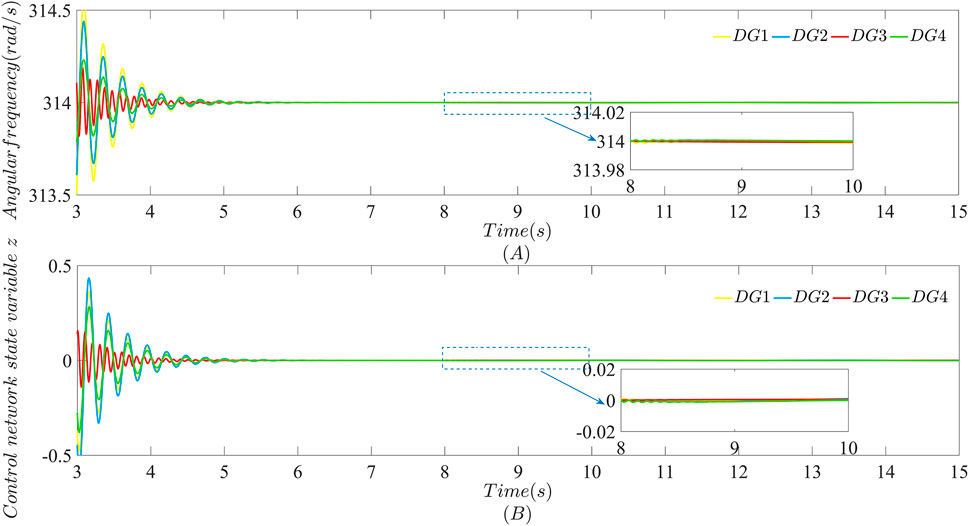
FIGURE 8. Performance of each DG in the microgrid after bounded FDI attacks are launched at t = 8 s in both the data transmission layer and the control network layer with β = 100: (A) Angular frequency; (B) Control network state variable z.

FIGURE 9

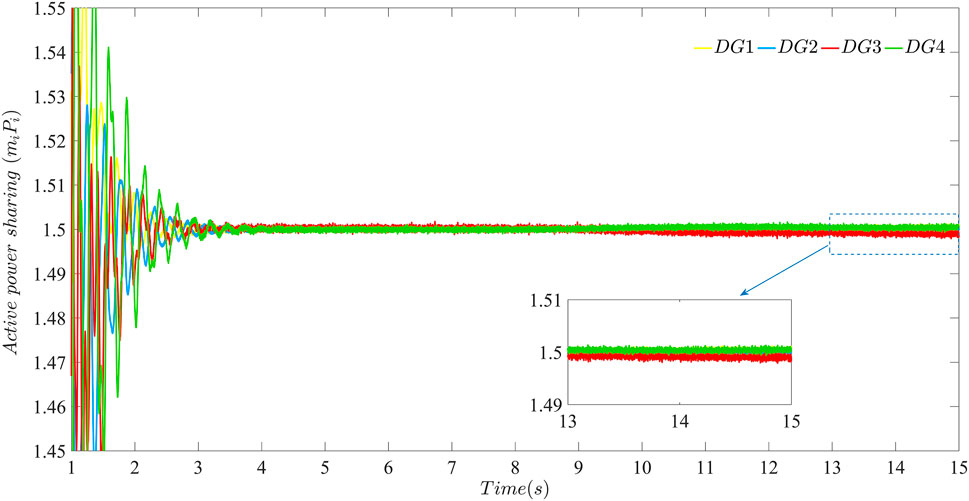
FIGURE 9. The active power sharing of each DG in the microgrid after bounded FDI attacks are launched at t = 8 s in both the data transmission layer and the control network layer with β = 100.

As can be seen from Figures 8, 9, the layered communication network of the microgrid becomes more resilient against bounded FDI attacks launched at t = 8 s using the distributed secondary control strategy proposed in this paper with β = 100. Compare Figures 6, 8 and Figures 7, 9, respectively. It can be seen the oscillations of angular frequency and active power sharing caused by bounded FDI attacks launched at t = 8 s in the data transmission layer using the strategy with β = 100 are mitigated faster than performances in the microgrid using the distributed secondary control strategy proposed in this paper with β = 40. In a word, cases shown in Figures 6–9 are to perform the resilience of the microgrid using the distributed secondary strategy proposed in this paper against bounded FDI attacks only launched at t = 8 s.

However, attacks once launched, can only be sustained and random in the actual network environment. Sustained attacks means that the attacker will not stop the action after launch attacks at one moment, but continue to launch attacks at the next moment so that the accumulated attacks will cause greater impact on the communication network of the microgrid. Information exchange also exists between the data transmission layer and the control network layer. Each DG node in the data transmission layer has a corresponding virtual node in the control network layer. The DG node in the data transmission layer uploads power information such as angular frequency to the virtual node in the control network layer for real-time control. Accordingly, the randomness of attacks means that external attacks will not be launched in the data transmission layer and the control network layer at the same time. That is, attacks in double-layer can be launched separately. And since the information exchange is bidirectional, external attacks launched in the data transmission layer or the control network layer actually affect the other layer, even if the other layer is not attacked.

To validate the resilience of the strategy proposed in this paper to sustained and random attacks in the actual network environment, the simulation process is as follows: The secondary control strategy starts at t = 0 s. The bounded FDI attack Θ₁ is launched in the data transmission layer at t = 7 s. The bounded FDI attack Θ₂ is launched in the network control layer at t = 8 s. The bounded FDI attack 2Θ₁ is launched in the data transmission layer at t = 9 s. The bounded FDI attack 2Θ₂ is launched in the network control layer at t = 10 s. The total simulation time is set to be 15 s.

It is obvious that external sustained and random bounded FDI attacks are launched in the data transmission layer at t = 7 s and t = 9 s from Figure 10 and in the control network layer at t = 8 s and t = 10 s from Figure 11. When, the data transmission layer is attacked but the control network layer is not. The same condition happens at t = 8 s and t = 10 s. Attacks are launched at t = 7 s and t = 9 s in the data transmission layer is attacked but the control network layer is not. And attacks are launched at t = 8 s and t = 10 s in the control network layer is attacked but the data transmission layer is not. As can be seen from Figure 10 and Figure 11, although attacks are not launched in the control network layer, the data transmission layer still are effected by attacks due to the information exchange between the two layers. In this paper, by designing interconnection matrix reasonably, the data transmission layer itself can mitigate the impact of attacks, and the control network layer can also quickly mitigate the influence due to information exchange. After the layered communication network mitigates the impact of direct attacks and the influence of cross-layer information exchange, the angular frequency still converges to 314 rad/s and the state variable z converges to 0. Similarly, the layered communication network using the distributed secondary strategy proposed in this paper can also mitigate the impact of direct attacks and the influence of cross-layer information exchange at t = 8 s and t = 10 s, respectively. The above cases have shown that the distributed secondary strategy proposed in this paper can effectively deal with the randomness of attack in real network environment.

FIGURE 10

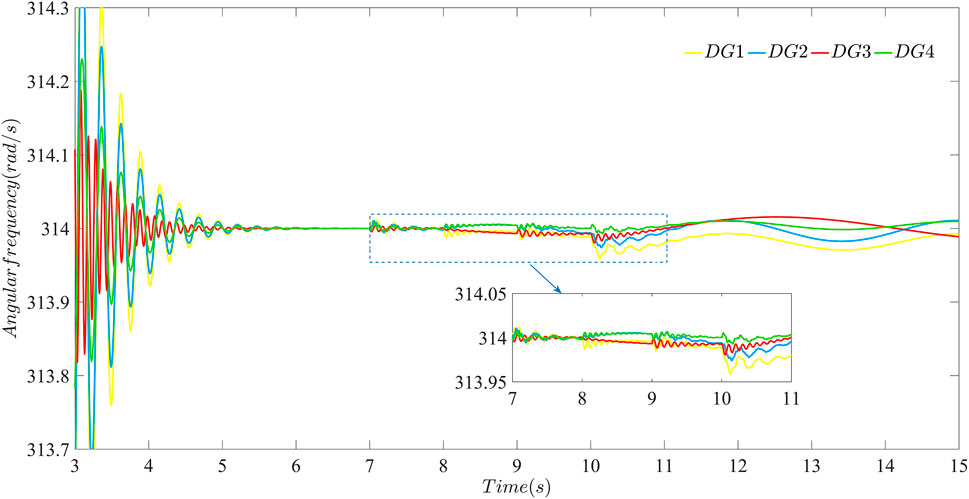
FIGURE 10. The effectiveness of the layered communication network against sustained and random bounded FDI attacks using the distributed secondary strategy proposed in this paper: performance of the data transmission layer against attacks with β = 40.

FIGURE 11

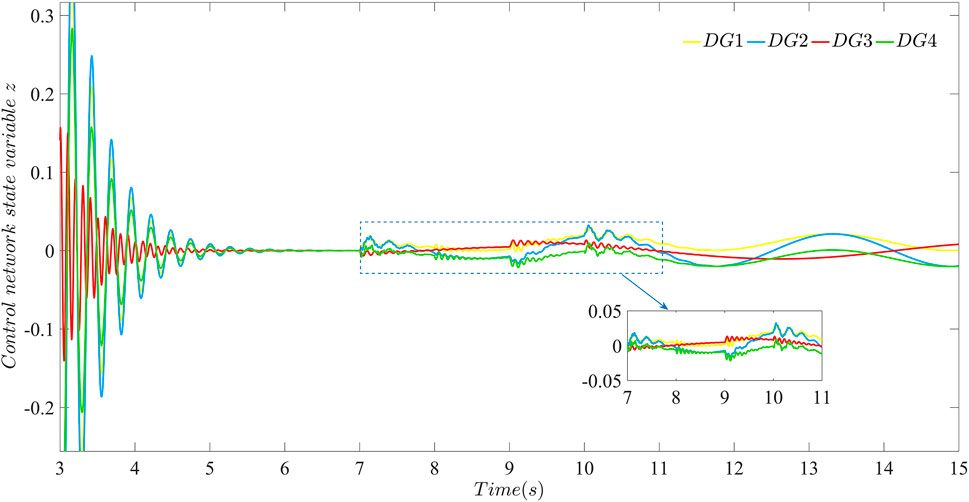
FIGURE 11. The effectiveness of the layered communication network against sustained and random bounded FDI attacks using the distributed secondary strategy proposed in this paper: performance of the control network layer against attacks with β = 40.

Moreover, It can be seen from Figure 10 that the data transmission layer is directly affected by attacks launched at t = 7 s and t = 9 s, and is influenced by attacks from the control network layer due to information exchange at t = 8 s and t = 10 s. Attacks always exist and gradually accumulate in the layered communication network, which can be mitigated using the distributed secondary strategy proposed in this paper. Cases in Figures 12, 13 show that after β increased to 100, the distributed secondary control strategy proposed in this paper becomes more resilient to the sustained and random bounded FDI attack launched in the double-layer communication network from t = 7 s to t = 10 s. Compare Figures 10, 12 and Figures 11, 13, respectively. It can be seen the strategy with β = 100 can strengthen the resilience of the microgrid against sustained and random attacks compared with the condition with β = 40.

FIGURE 12

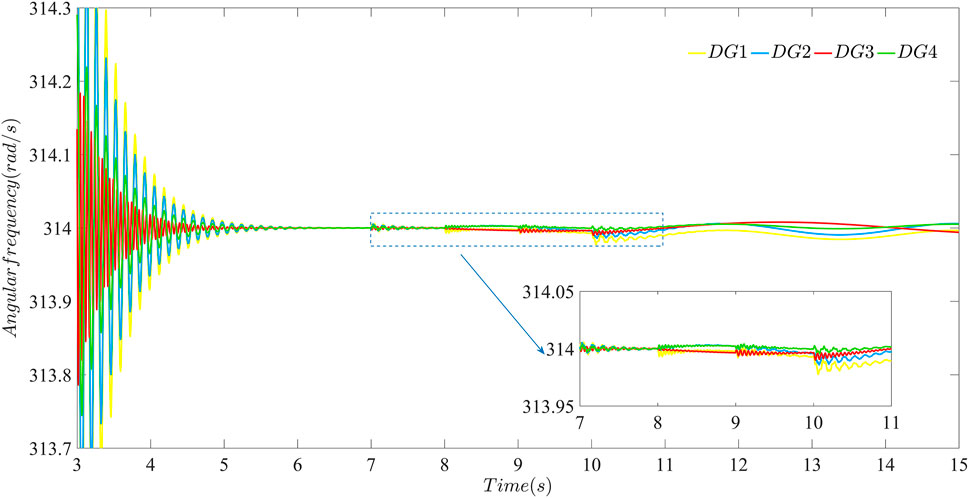
FIGURE 12. The effectiveness of the layered communication network against sustained and random bounded FDI attacks using the distributed secondary strategy proposed in this paper: performance of the data transmission layer against attacks with β = 100.

FIGURE 13

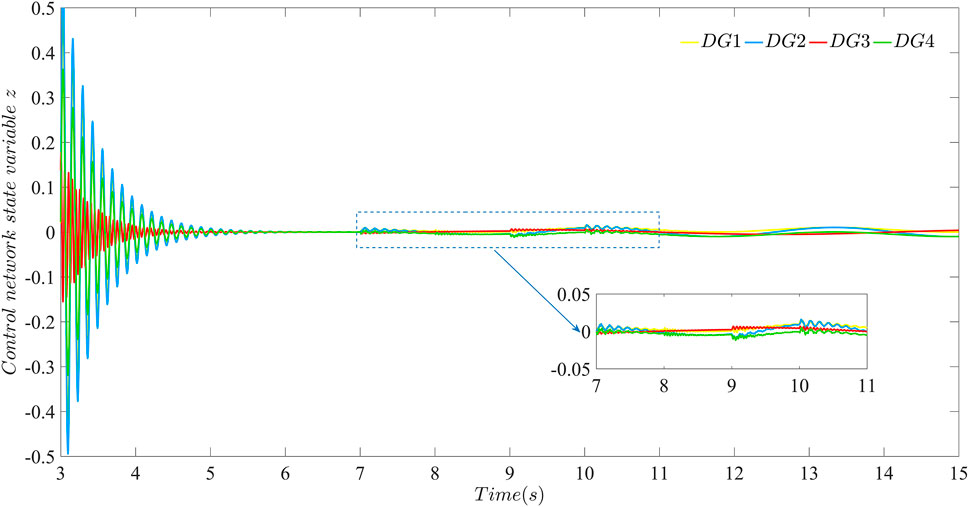
FIGURE 13. The effectiveness of the layered communication network against sustained and random bounded FDI attacks using the distributed secondary strategy proposed in this paper: performance of the control network layer against attacks with β = 100.

All the above cases show that the distributed secondary control strategy in the microgrid with layered communication network proposed in this paper can effectively mitigate external bounded FDI attacks, and the resilience of the strategy against attacks can be enhanced by increasing β. Compared with the simulation results of the distributed secondary control strategy without FDI attacks and the distributed secondary control strategy against FDI attacks in the data transmission layer, the distributed secondary control strategy proposed in this paper is more practical in the case that bounded FDI attacks are launched in both the data transmission layer and the control network layer.

5 Conclusion

In this paper, a distributed secondary control strategy against bounded FDI attacks has been proposed for low inertia microgrids with the layered communication network to enhance the resilience to bounded FDI attacks. For the problem that stealthy bounded FDI attacks have been launched in the layer communication network extensively, the strategy proposed in this paper can keep angular frequency stable against attacks. Moreover, Lyapunov theory has been used to demonstrate that the microgrid consisting of DGs remains stable even when bounded FDI attacks are launched in both the data transmission layer and the control network layer, and the angular frequency can be closer to the rated value by increasing β. Finally, a microgrid test system consisting of four inverter-based DGs has been set up using Matlab/Simpower system. Firstly, simulation results have validated that the distributed secondary control strategy without FDI attacks cannot defend against external bounded FDI attacks. Secondly, simulation results have validated that the distributed secondary control strategy proposed in this paper can maintain the angular frequency stable even when external bounded FDI attacks are launched only in the data transmission layer. Finally, simulation results have shown when sustained and random bounded FDI attacks are launched in both the data transmission layer and the control network layer, the angular frequency also runs within the allowed fluctuation range around the rating value, which validate the effectiveness of the distributed secondary strategy proposed in this paper. In future work, the authors will combine the practical application, such as seaport microgrid, to specify the layered network theory used in this paper to solve more complex attack types.

Data Availability Statement

The datasets presented in this article are not readily available because the original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. Requests to access the datasets should be directed to QS, c2hhbnFpaGVAMTYzLmNvbQ==.

Author Contributions

FW and QS designed the experiments, research methods. QS performed the format analysis. The tools analysis, data processing, and writing the original draft were carried out by FT. ZH solved the application problem of research methods. ZW performed the writing-review on references. YX contributed to proof reading and project/organization management. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported in part by the National Natural Science Foundation of China (under grant nos. 51939001, 61803064, 61751202, 61903092, 61976033, and U1813203); the Science and Technology Innovation Funds of Dalian (under grant no. 2018J11CY022); the Liaoning Revitalization Talents Program (under grant nos. XLYC1908018 and XLYC1807046); the Natural Science Foundation of Liaoning (2019-ZD-0151,20170540098); the Fundamental Research Funds for the Central Universities (under grant nos. 3132019345, 3132020103, and 3132020125).

Conflict of Interest

Author ZH is employed by China Railway Rolling Stock Corporation Zhuzhou Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abhinav, S., Modares, H., Lewis, F. L., Ferrese, F., and Davoudi, A. (2018). Synchrony in Networked Microgrids Under Attacks. IEEE Trans. Smart Grid 9, 6731–6741. doi:10.1109/TSG.2017.2721382

CrossRef Full Text | Google Scholar

Beg, O. A., Johnson, T. T., and Davoudi, A. (2017). Detection of False-Data Injection Attacks in Cyber-Physical Dc Microgrids. IEEE Trans. Ind. Inf. 13, 2693–2703. doi:10.1109/TII.2017.2656905

CrossRef Full Text | Google Scholar

Bidram, A., and Davoudi, A. (2012). Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 3, 1963–1976. doi:10.1109/TSG.2012.2197425

CrossRef Full Text | Google Scholar

Bidram, A., Davoudi, A., Lewis, F. L., and Guerrero, J. M. (2013). Distributed Cooperative Secondary Control of Microgrids Using Feedback Linearization. IEEE Trans. Power Syst. 28, 3462–3470. doi:10.1109/tpwrs.2013.2247071

CrossRef Full Text | Google Scholar

Bidram, A., Lewis, F. L., and Davoudi, A. (2014). Distributed Control Systems for Small-Scale Power Networks: Using Multiagent Cooperative Control Theory. IEEE Control Syst. Mag. 34, 56–77. doi:10.1109/MCS.2014.2350571

CrossRef Full Text | Google Scholar

Chen, Y., Qi, D., Dong, H., Li, C., Li, Z., and Zhang, J. (2021). A Fdi Attack-Resilient Distributed Secondary Control Strategy for Islanded Microgrids. IEEE Trans. Smart Grid 12, 1929–1938. doi:10.1109/TSG.2020.3047949

CrossRef Full Text | Google Scholar

Condry, M. W., and Nelson, C. B. (2016). Using Smart Edge Iot Devices for Safer, Rapid Response with Industry Iot Control Operations. Proc. IEEE 104, 938–946. doi:10.1109/JPROC.2015.2513672

CrossRef Full Text | Google Scholar

Ge, P., Zhu, Y., Green, T. C., and Teng, F. (2021). Resilient Secondary Voltage Control of Islanded Microgrids: An Eskbf-Based Distributed Fast Terminal Sliding Mode Control Approach. IEEE Trans. Power Syst. 36, 1059–1070. doi:10.1109/TPWRS.2020.3012026

CrossRef Full Text | Google Scholar

Gusrialdi, A., Qu, Z., and Simaan, M. A. (2018). Competitive Interaction Design of Cooperative Systems Against Attacks. IEEE Trans. Autom. Contr. 63, 3159–3166. doi:10.1109/TAC.2018.2793164

CrossRef Full Text | Google Scholar

Hu, L., Wang, Z., Han, Q.-L., and Liu, X. (2018). State Estimation Under False Data Injection Attacks: Security Analysis and System Protection. Automatica 87, 176–183. doi:10.1016/j.automatica.2017.09.028

CrossRef Full Text | Google Scholar

Jin, D., Li, Z., Hannon, C., Chen, C., Wang, J., Shahidehpour, M., et al. (2017). Toward a Cyber Resilient and Secure Microgrid Using Software-Defined Networking. IEEE Trans. Smart Grid 8, 2494–2504. doi:10.1109/tsg.2017.2703911

CrossRef Full Text | Google Scholar

Kreutz, D., Ramos, F. M. V., Esteves Verissimo, P., Esteve Rothenberg, C., Azodolmolky, S., and Uhlig, S. (2015). Software-Defined Networking: A Comprehensive Survey. Proc. IEEE 103, 14–76. doi:10.1109/jproc.2014.2371999

CrossRef Full Text | Google Scholar

Liang, G., Weller, S. R., Zhao, J., Luo, F., and Dong, Z. Y. (2017). The 2015 Ukraine Blackout: Implications for False Data Injection Attacks. IEEE Trans. Power Syst. 32, 3317–3318. doi:10.1109/TPWRS.2016.2631891

CrossRef Full Text | Google Scholar

Liang, X. (2017). Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 53, 855–866. doi:10.1109/tia.2016.2626253

CrossRef Full Text | Google Scholar

Liu, Y., Ning, P., and Reiter, M. K. (2011). False Data Injection Attacks Against State Estimation in Electric Power Grids. ACM Trans. Inf. Syst. Secur. 14, 21–32. doi:10.1145/1952982.1952995

CrossRef Full Text | Google Scholar

Manandhar, K., Cao, X., Hu, F., and Liu, Y. (2014). Detection of Faults and Attacks Including False Data Injection Attack in Smart Grid Using Kalman Filter. IEEE Trans. Control Netw. Syst. 1, 370–379. doi:10.1109/tcns.2014.2357531

CrossRef Full Text | Google Scholar

Mijumbi, R., Serrat, J., Gorricho, J.-L., Bouten, N., De Turck, F., and Boutaba, R. (2016). Network Function Virtualization: State-Of-The-Art and Research Challenges. IEEE Commun. Surv. Tutorials 18, 236–262. doi:10.1109/comst.2015.2477041

CrossRef Full Text | Google Scholar

Musleh, A. S., Chen, G., and Dong, Z. Y. (2020). A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Trans. Smart Grid 11, 2218–2234. doi:10.1109/TSG.2019.2949998

CrossRef Full Text | Google Scholar

Nunes, B. A. A., Mendonca, M., Nguyen, X.-N., Obraczka, K., and Turletti, T. (2014). A Survey of Software-Defined Networking: Past, Present, and Future of Programmable Networks. IEEE Commun. Surv. Tutorials 16, 1617–1634. doi:10.1109/SURV.2014.012214.00180

CrossRef Full Text | Google Scholar

Olfati-Saber, R., and Murray, R. M. (2004). Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Autom. Contr. 49, 1520–1533. doi:10.1109/TAC.2004.834113

CrossRef Full Text | Google Scholar

Pasqualetti, F., Bicchi, A., and Bullo, F. (2012). Consensus Computation in Unreliable Networks: A System Theoretic Approach. IEEE Trans. Autom. Contr. 57, 90–104. doi:10.1109/TAC.2011.2158130

CrossRef Full Text | Google Scholar

Pogaku, N., Prodanovic, M., and Green, T. C. (2007). Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 22, 613–625. doi:10.1109/TPEL.2006.890003

CrossRef Full Text | Google Scholar

Qu, Z., Dong, Y., Qu, N., Li, H., Cui, M., Bo, X., et al. (2021). False Data Injection Attack Detection in Power Systems Based on Cyber-Physical Attack Genes. Front. Energy Res. 9. doi:10.3389/fenrg.2021.644489

CrossRef Full Text | Google Scholar

Rui, W., Qiuye, S., Dazhong, M., and Xuguang, H. (2020). Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters under Weak Grids. IEEE Trans. Smart Grid 11, 2856–2866. doi:10.1109/tsg.2020.2970174

CrossRef Full Text | Google Scholar

Salah, K., Elbadawi, K., and Boutaba, R. (2012). Performance Modeling and Analysis of Network Firewalls. IEEE Trans. Netw. Serv. Manage. 9, 12–21. doi:10.1109/TNSM.2011.122011.110151

CrossRef Full Text | Google Scholar

Shafiee, Q., Guerrero, J. M., and Vasquez, J. C. (2014). Distributed Secondary Control for Islanded Microgrids-A Novel Approach. IEEE Trans. Power Electron. 29, 1018–1031. doi:10.1109/TPEL.2013.2259506

CrossRef Full Text | Google Scholar

Sinha, A., Mohandas, M., Pandey, P., and Vyas, O. P. (2021). Cyber Physical Defense Framework for Distributed Smart Grid Applications. Front. Energy Res. 8. doi:10.3389/fenrg.2020.621650

CrossRef Full Text | Google Scholar

Sockeel, N., Gafford, J., Papari, B., and Mazzola, M. (2020). Virtual Inertia Emulator-Based Model Predictive Control for Grid Frequency Regulation Considering High Penetration of Inverter-Based Energy Storage System. IEEE Trans. Sustain. Energy 11, 2932–2939. doi:10.1109/tste.2020.2982348

CrossRef Full Text | Google Scholar

Sundaram, S., and Hadjicostis, C. N. (2011). Distributed Function Calculation via Linear Iterative Strategies in the Presence of Malicious Agents. IEEE Trans. Autom. Contr. 56, 1495–1508. doi:10.1109/tac.2010.2088690

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). Soc-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 36, 7866–7879. doi:10.1109/TPEL.2021.3049241

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Ma, D., and Liu, Z. (2019). The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energy 10, 1459–1469. doi:10.1109/tste.2019.2894633

CrossRef Full Text | Google Scholar

Xiahou, K., Liu, Y., and Wu, Q. H. (2022). Decentralized Detection and Mitigation of Multiple False Data Injection Attacks in Multiarea Power Systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 3, 101–112. doi:10.1109/JESTIE.2021.3112919

CrossRef Full Text | Google Scholar

Zhang, F., Kodituwakku, H. A. D. E., Hines, J. W., and Coble, J. (2019). Multilayer Data-Driven Cyber-Attack Detection System for Industrial Control Systems Based on Network, System, and Process Data. IEEE Trans. Ind. Inf. 15, 4362–4369. doi:10.1109/tii.2019.2891261

CrossRef Full Text | Google Scholar

Zhang, H., Li, Z., Qu, Z., and Lewis, F. L. (2015). On Constructing Lyapunov Functions for Multi-Agent Systems. Automatica 58, 39–42. doi:10.1016/j.automatica.2015.05.006

CrossRef Full Text | Google Scholar

Zhou, Q., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2020). A Cyber-Attack Resilient Distributed Control Strategy in Islanded Microgrids. IEEE Trans. Smart Grid 11, 3690–3701. doi:10.1109/TSG.2020.2979160

CrossRef Full Text | Google Scholar

Zhou, Q., Shahidehpour, M., Alabdulwahab, A., Abusorrah, A., Che, L., and Liu, X. (2021). Cross-Layer Distributed Control Strategy for Cyber Resilient Microgrids. IEEE Trans. Smart Grid 12, 3705–3717. doi:10.1109/tsg.2021.3069331

CrossRef Full Text | Google Scholar

Zuo, S., and Yue, D. (2022). Resilient Containment of Multigroup Systems Against Unknown Unbounded Fdi Attacks. IEEE Trans. Ind. Electron. 69, 2864–2873. doi:10.1109/TIE.2021.3066941

CrossRef Full Text | Google Scholar