- Institute of Systems Engineering, Liaoning Technical University, Fuxin, China
Over the years, the ventilation systems used in coal mines have become more and more complex. Due to a lack of scientific and effective management, the energy consumed by ventilation systems has rapidly increased, resulting in considerable wasted energy. To solve this problem, the authors established a nonlinear optimization model aimed at minimizing the total energy consumption of a mine ventilation network. Furthermore, the authors propose an improved equilibrium optimizer algorithm to solve the model. First, the population is initialized by a chaotic map. Second, the adjustment strategy of a trigonometric function is introduced to improve the index
1 Introduction
A mine’s ventilation system is one of the most essential coal mine safety production systems. Energy consumed by the ventilation system accounts for about one third of the total energy consumption of a coal mine. Over the years, ventilation systems have become more and more complex. Due to the poor planning of mine ventilation systems and a lack of scientific and effective management, there is considerable waste of energy as well as potential safety hazards. To ensure safe production in a mine, improve mine ventilation conditions, and reduce energy waste, ventilation systems must be optimized (Shao et al., 2020; Su and Ouyang, 2021). Ventilation system optimization is a hot topic of research in this field (Wang et al., 2019).
Mine ventilation systems are highly coupled and complex systems. Traditional methods are not only slow to solve the problem but also poor at solving the problem, so we must use new methods to solve this problem. With the ongoing development of intelligent algorithms, many scholars have introduced intelligent algorithms to optimize mine ventilation systems. Liangshan Shao et al. optimized the problem based on simulated annealing and improved the particle swarm optimization algorithm, thus reducing the energy consumed for ventilation by 25.3% (Shao et al., 2021). Xingguo Zhang et al. studied a ventilation network solution based on an ACPSO algorithm, and the air quantity optimization scheme obtained had the minimum total ventilation energy consumption (Zhang and Zhou, 2018). Zhong et al. proposed an efficient mine ventilation solution method based on minimum independent closed loops to effectively optimize the mine ventilation system (Zhong et al., 2020). Yixin Su used the improved genetic algorithm to search the optimal weight and threshold of the network globally, and used BP algorithm to conduct local optimization, and finally obtained the wind speed prediction value (Su et al., 2017). Xinzhong Wu in fireworks algorithm to join the elite reverse learning strategy, strengthen the search algorithm in the field of space, Thus improve the global searchability (Wu et al., 2019).
The above methods have some limitations for solving the nonlinear optimization model of mine ventilation systems. For example, the algorithm has many parameters and this can easily result in local optimization, so the algorithm must be improved. The equilibrium optimizer (EO) is a physics-based meta-heuristic algorithm, proposed by Faramarzi et al., in 2019 (Faramarzi et al., 2020a). Compared with the genetic algorithm (Li et al., 2007), which can easily result in local optimization and has low execution efficiency, the particle swarm optimization (PSO) algorithm (Marini and Walczak, 2015) with premature phenomenon and the ant colony algorithm (Dorigo et al., 2006) which is easy to appear algorithm stagnation, it has the advantages of fewer parameters, high execution efficiency, and outstanding global optimization ability. Therefore, it has been successfully applied to multi-objective optimization (Abdel-Basset et al., 2020), photovoltaic cell parameter optimization (Dinh, 2021), multimodal medical image fusion (Wang et al., 2021), feature selection (Wang et al., 2021), and other fields.
Many experts and scholars have developed improvements to the performance of the equalization optimizer algorithm. Sayed et al. constructed a stable search mechanism by introducing chaotic mapping to improve the feature selection efficiency of the algorithm (Sayed et al., 2020). Fan et al. improved the optimization accuracy of the algorithm through reverse learning and a new concentration update formula (Fan et al., 2021). Dinkar et al. (2021) updated the candidate solution concentration using the random walk of Laplace distribution and then accelerated the development by reverse learning to make the algorithm converge rapidly. However, these improved methods have only improved parts of the equalization optimizer algorithm. To apply the EO algorithm to mine ventilation system optimization, the algorithm must be comprehensively improved. We propose an improved equalization optimizer (IEO) algorithm combined with chaotic mapping, trigonometric function, Gaussian disturbance, and a learning factor, and compare it with other algorithms to verify the ability of the IEO algorithm to optimize mine ventilation systems.
The main contributions of this paper include:
⁃Establishing a nonlinear optimization model aimed at minimizing the total energy consumption of a mine ventilation network to address the problem of mine ventilation optimization.
⁃Proposing an IEO algorithm based on chaotic mapping, trigonometric function, Gaussian disturbance, and a learning factor.
⁃The performance of the proposed IEO algorithm is validated against seven unimodal benchmark functions, six multimodal benchmark functions, and three fixed-dimension multimodal benchmark functions.
⁃Performance comparisons between the proposed IEO and other state-of-the-art algorithms using various performance metrics for the optimization of the ventilation system of Wangjialing mine, belonging to Zhongmei Huajin Energy Co., Ltd.
The remainder of the paper is organized as follows: Section 2 establishes the mine ventilation network model. Section 3 introduces the EO algorithm. Section 4 describes the IEO algorithm. Section 5 tests the IEO algorithm’s performance. Section 6 describes the engineering application analysis. Section 7 gives the conclusion and the future research direction.
2 Mine Ventilation System Modeling
To realize the intellectualization and automation of the regulation and optimization of mine ventilation systems, a mathematical model of mine ventilation network optimization based on minimum power consumption has been established (Hao et al., 2012; Pei et al., 2017). The model constraints are as follows:
(1) The mine ventilation network follows the node air quantity balance law (Wei, 2011). That is, the air quantity flowing into a node is equal to the air quantity flowing out. This can be described as:
Where,
(2) A mine ventilation network follows the loop resistance balance law (Oliveira et al., 2015). That is, the algebraic sum of resistance, natural wind pressure, and mechanical wind pressure of each branch in the
Where
(3) To make the fan work stably and avoid surge (Dong and Li, 2008), it is generally stipulated that the upper limit of the actual working wind pressure of the fan shall not exceed 90% of its maximum wind pressure, and the lower efficiency limit shall not be less than 60%. This can be described as:
Where
(4) Finally, according to the 《The Coal Mine Safety Rules》 and the actual situation of the mine, the lower and upper limits of the regulated air quantity and air pressure of the adjustable branches can be calculated. This can be described as:
where
On the premise of meeting the demand air distribution, the minimum total power of the fan is regarded in the ventilation network as the optimization goal of the model. This can be described as:
where
It is known that the model is a non-convex nonlinear constrained optimization problem. To better apply an intelligent algorithm to solve the problem, the penalty function was used to transform the inequality constraints: it was constructed the objective function and constraints into an augmented objective function with parameters (Jia et al., 2011) and transform the problem into an unconstrained nonlinear programming problem for solution. The augmented objective function consists of two parts: the objective function of the original problem and the penalty term constructed by the constraint function. The function of the penalty term is to restrict illegal points or data. Therefore, the upper and lower limits of adjustable air volume and wind pressure of some branches are known, so the internal penalty function method is adopted to ensure the feasibility of the iteration points. After the above conversion, the objective function is:
where
3 Principle of the Equalization Optimizer Algorithm
The equalization optimizer algorithm is a new physics-based algorithm for solving continuous optimization problems. The advantage of the equalization optimizer algorithm is that the solution can be changed randomly according to high exploration and exploitation. The particle concentration of the equalization optimizer is similar to the particle and position of the PSO algorithm, which represents the search agent. The search agent randomly updates their concentration and names it the equilibrium candidate solution with the best self searched. Finally, it reaches the equilibrium state, when it can be divided into three stages: population initialization, equilibrium pool, and concentration update.
3.1 Inspiration
The EO algorithm was inspired by the physical mass balance equation, which provides the physical basis by controlling the controller’s volume weight input quality, output quality, and production quality. A section of the breeze equation represents the general mass balance equation, in which the change of mass over time is equal to the mass entering the system minus the mass leaving the system plus the original mass. This is described in Eq. 11.
In the equation,
3.2 Equilibrium Pool and Its Candidate Solution
The equilibrium state is the final convergence state of the algorithm and is globally optimal. The EO algorithm constructs a vector called the equilibrium pool, which provides equalization candidate particles. Through experiments, it can be determined in five candidate solutions in the equilibrium pool, four of which are the best particles identified in the whole optimization process. The other is the mathematical average of the other four. The four best particles are helpful to explore the search space, and the average is helpful for exploitation. The equilibrium pool vector can be described as shown in Eq. 12:
where
3.3
Index
where
where
In the formula,
3.4 Generation Rate
The generation rate
where
where:
where
4 Improved Equalization Optimizer Algorithm
4.1 Chaotic Map Initialization Population
The ergodicity and randomness of chaotic mapping sequences are widely used to optimize search problems. To improve the individual diversity and make the initial particles as evenly distributed in the search space as possible, this paper uses cat mapping, because the cat mapping structure is simple and it is not easy to fall into short cycles and periodic fixed points (Peterson, 2020) to generate the initial population. The expression of cat mapping is shown in Eq. 22:
where,
The initial population generated by cat chaotic mapping can be expressed as shown in Eq. 24:
4.2 Improvement Index
In the equilibrium optimization algorithm, the index
where a, b, c, and d are constants.
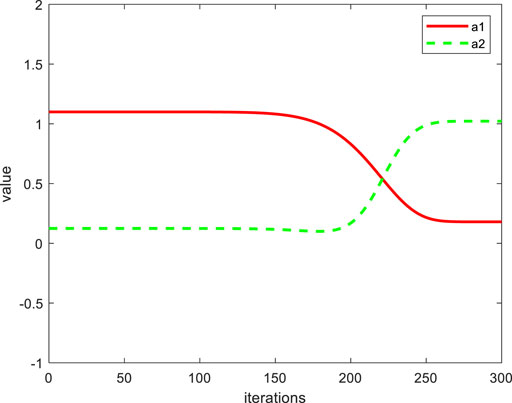
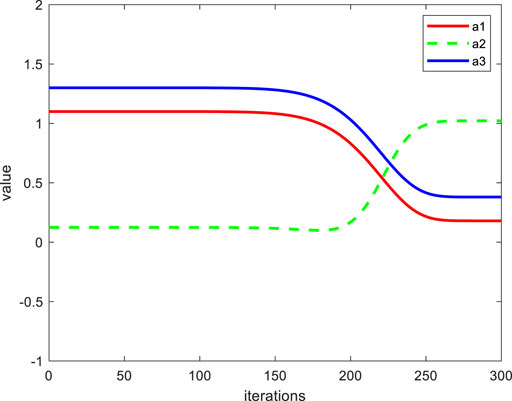
Figure 1 shows the change curves of
4.3 Gaussian Perturbation
Considering that the five candidate solutions in the equilibrium pool constructed by the standard EO algorithm represent the best equilibrium concentration, there is still an ample change space. To avoid falling into local optimization and increase particle diversity, the four best particles are slightly Gaussian perturbed (Gleiser and Dotti, 2005) to improve the algorithm’s ability to explore the optimal value. The expression is:
where
4.4 Improvement Generation Rate
The generation rate
where e and f are constants and, as the number of iterations increases, the learning factor gradually decreases, which increases the optimization accuracy in the later stage of the algorithm.Therefore, Eq. 21 is improved to Eq. 30:
5 Simulation Experiment and Analysis
5.1 Experiment-Related Settings
The experimental environment was a Windows 10, 64-bit operating system, the CPU was an Intel Core i9-11950h, the main frequency was 5.0 GHz, and the memory was 16 GB. The algorithm program was written based on Matlab 2020b. Table 1 shows the full names and abbreviations of the algorithms and their parameter settings.
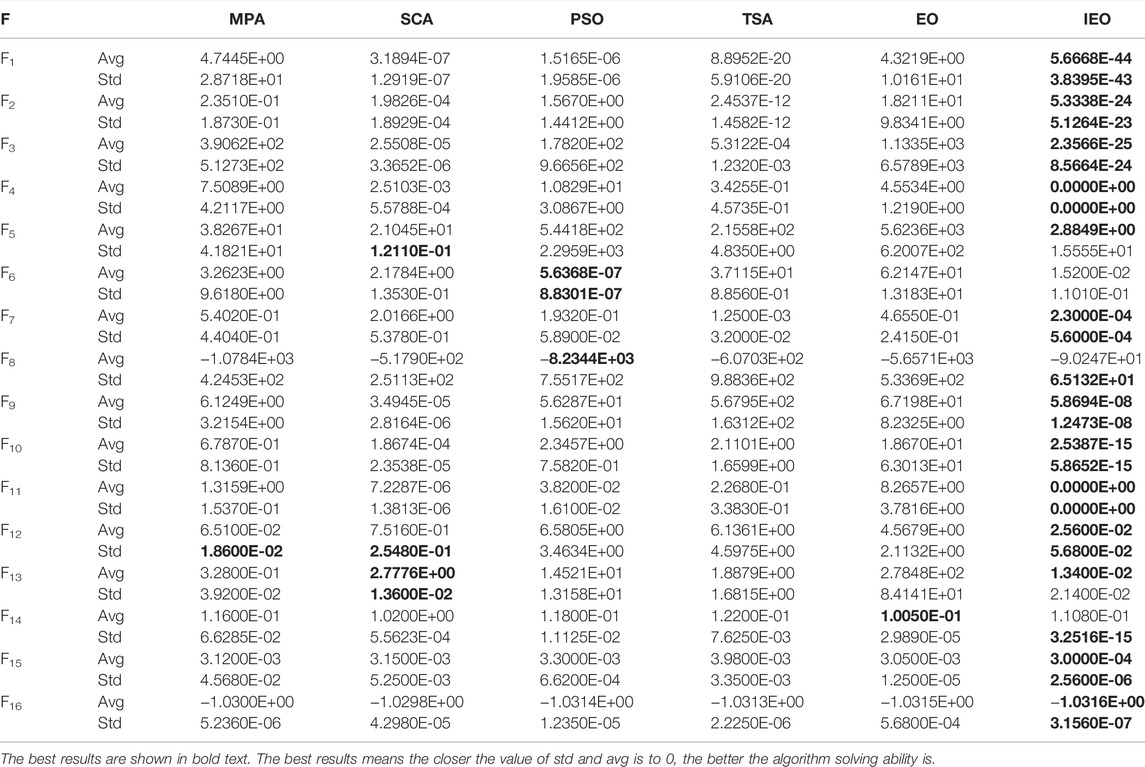
Simulation experiments were carried out on 13 benchmark functions. Table 2 shows the details of the test functions. Among them, functions F1–F7 are unimodal benchmark functions, and there is only one global optimal meridian, used to evaluate the convergence speed of the algorithm. Functions F8–F13 are multimodal benchmark functions used to evaluate the algorithm’s performance in avoiding local optimization and exploration. Functions F14–F16 are fixed-dimension multimodal benchmark functions.
5.2 Experimental Results and Analysis
To prove the effectiveness and robustness of the proposed IEO, the IEO algorithm was compared with the MPA, SCA, PSO, TSA, and EO algorithms. The population number of all algorithms was 30, and the maximum number of iterations was 500. All algorithms were run independently on 13 benchmark functions, 50 times, and the average and standard deviation of these 50 times was taken as the final evaluation index. Table 3 shows the specific experimental data, where Avg represents the average optimal fitness value and Std represents the standard deviation; the best results are shown in bold text.
According to Table 4, in the unimodal function, the proposed IEO algorithm is better than the other algorithms because of the introduction of parameters
5.3 Convergence Analysis
Figure 3 shows the convergence evaluation results of the IEO algorithm and the comparison algorithms in Table 1 for different functions. To facilitate observation, the logarithm with base 10 was taken as the ordinate. From Figure 3, it can be seen that the convergence speed of the proposed IEO algorithm is faster than the other algorithms in both the exploration and exploitation stages. It shows that the three parameters introduced,
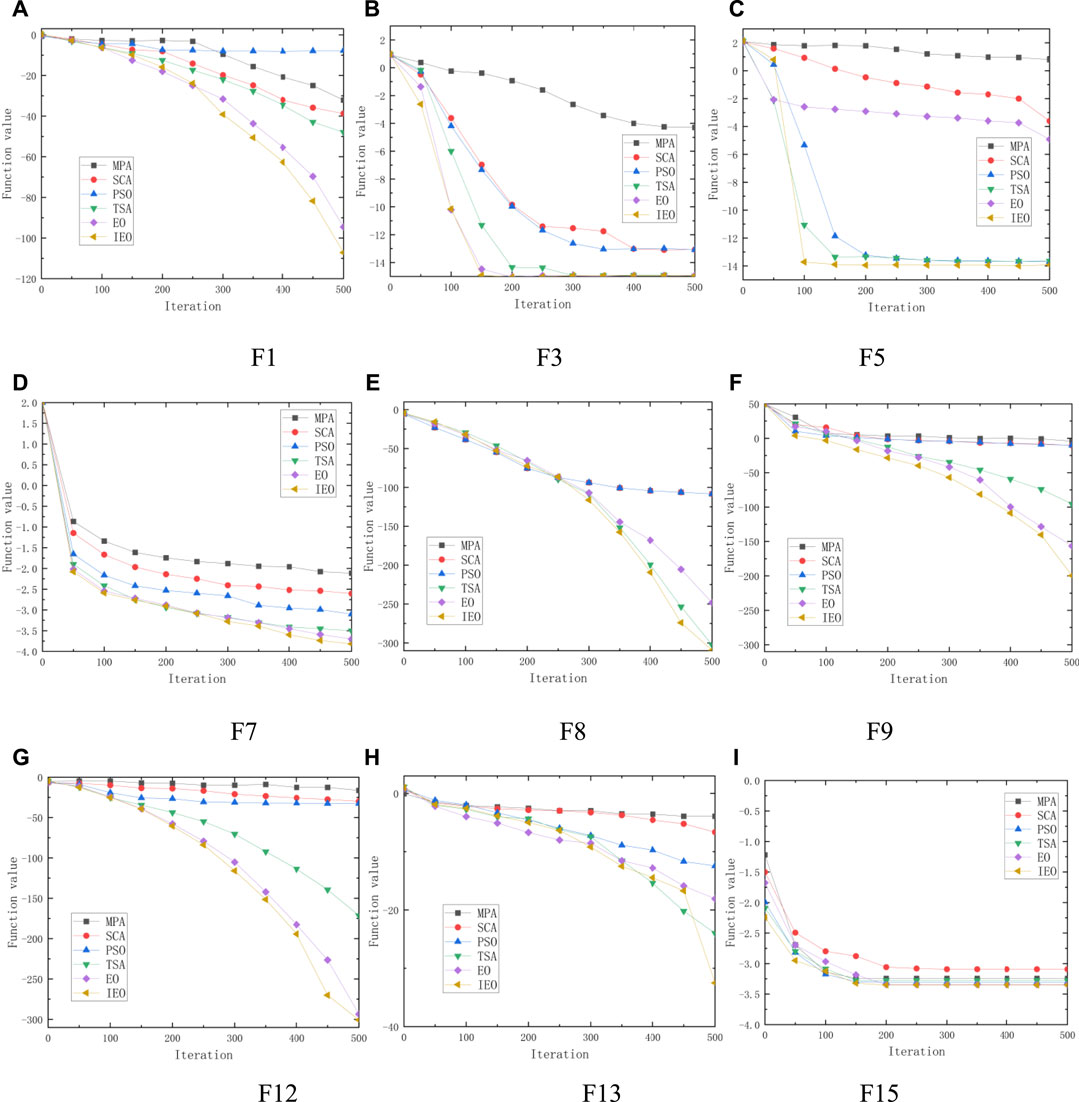
FIGURE 3. Average convergence curve of nine test functions. Graphs showing the convergence of solution at every iteration on test functions using IEO and five classical algorithms.
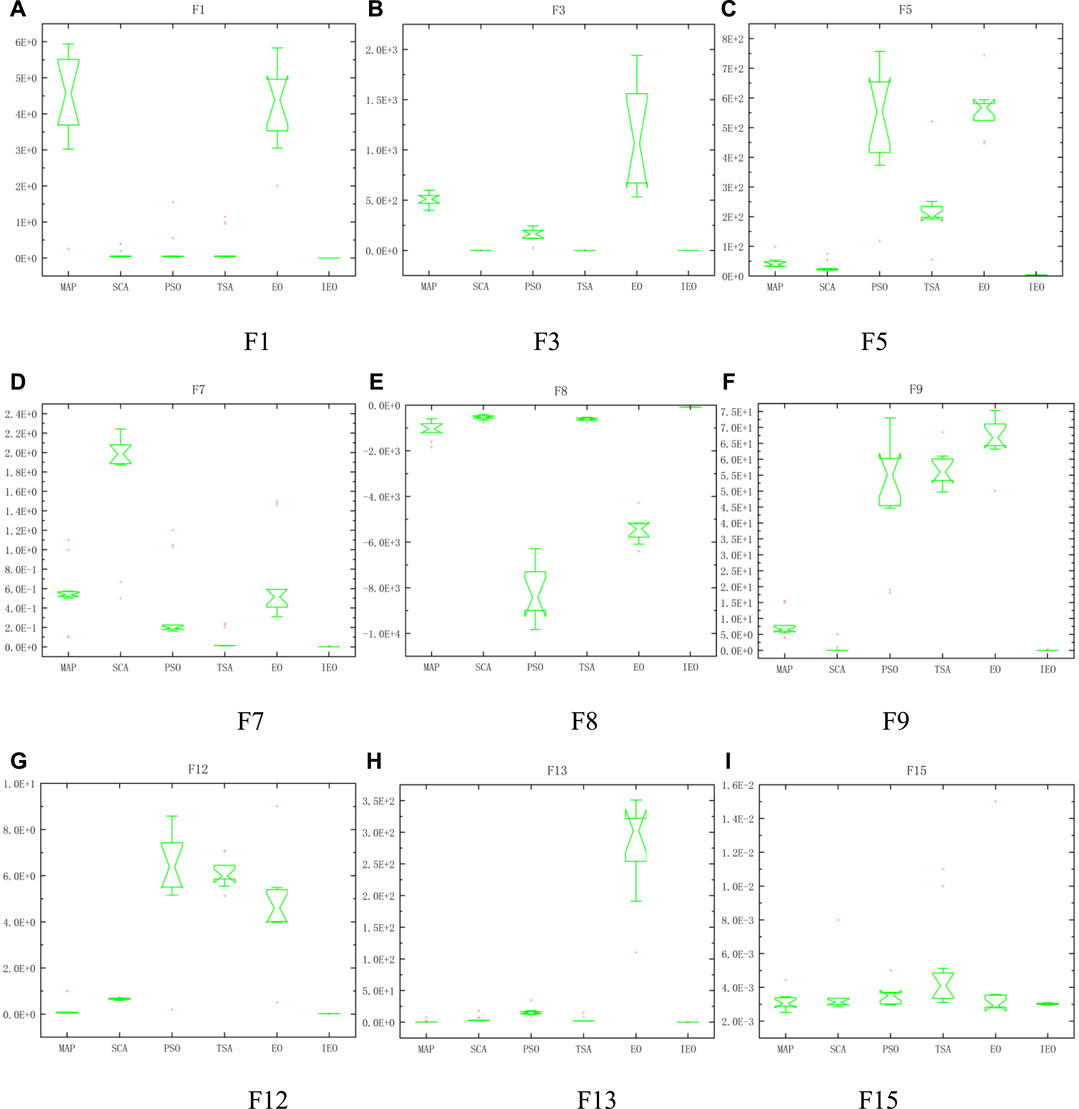
FIGURE 4. Boxplot comparison of nine test functions. IEO and five classical algorithms run independently for 50 times IGD index box diagram.
6 Engineering Application Analysis
6.1 Optimization Algorithm for a Mine Ventilation System Based on the Improved Equalization Optimizer Algorithm
The specific process of the mine ventilation optimization algorithm based on the IEO algorithm is as follows:
Step 1: input population size M; maximum iteration number Tmax; constants a, b, c, d, e, and f; the number of ventilation network nodes and branches; branch air quantity; and wind resistance. Each particle in the equalization optimizer represents the initial air quantity value of the branch.
Step 2: create Ceq1-Ceq4, four empty lists to store four candidate solutions.
Step 3: perform chaotic mapping to initialize the population and obtain a higher quality initial population.
Step 4: determine whether the current iteration number Iter is less than the maximum iteration number Maxiter. If it is less, repeat Steps 1 to 9 until the iteration stop condition is met. Otherwise, go to Step 10.
Step 5: calculate the fitness of each particle in the population.
Step 6: select four particles as candidate solutions according to the fitness of population particles, and calculate the average of the four candidate solutions as the average candidate solutions.
Step 7: build an equilibrium pool and randomly select a candidate solution.
Step 8: perform Gaussian perturbation to perturb the particles in the equilibrium pool to further balance the algorithm’s global and local search capabilities.
Step 9: enter the updating stage of individual concentration and update the particle position. If
Step 10: output the number and amount of adjusting roadway, and calculate the optimal objective function value.
Figure 5 is a flow chart showing this process.
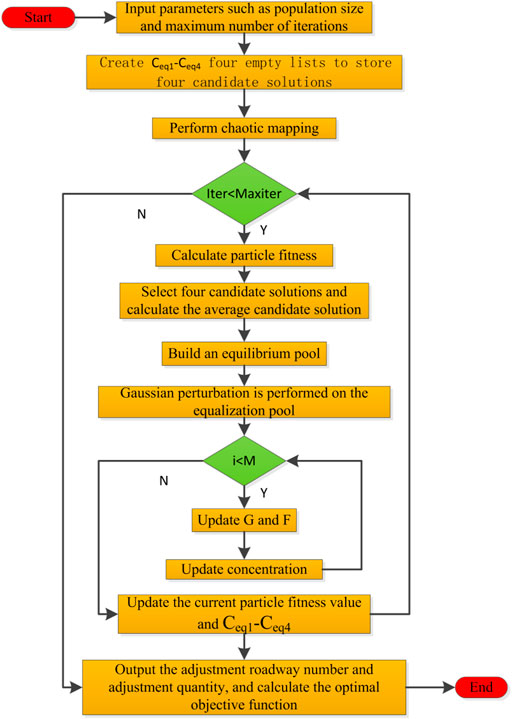
FIGURE 5. Flow chart of the ventilation optimization algorithm based on the improved equalization optimizer algorithm.
6.2 Introduction of a Three-Dimensional Ventilation Simulation System in Wangjialing Mine
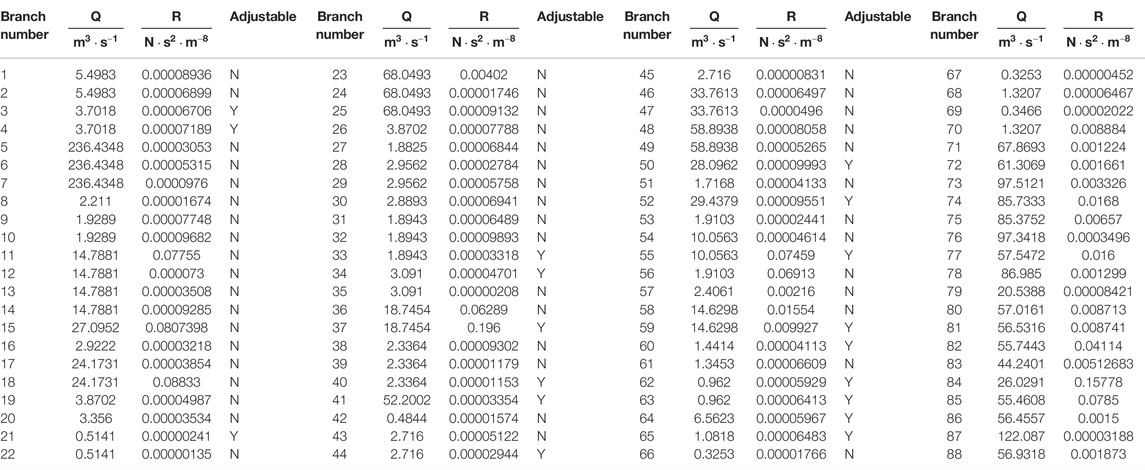
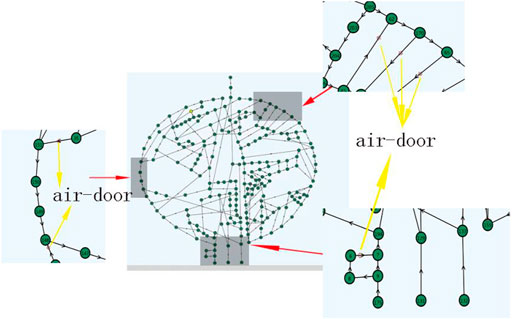
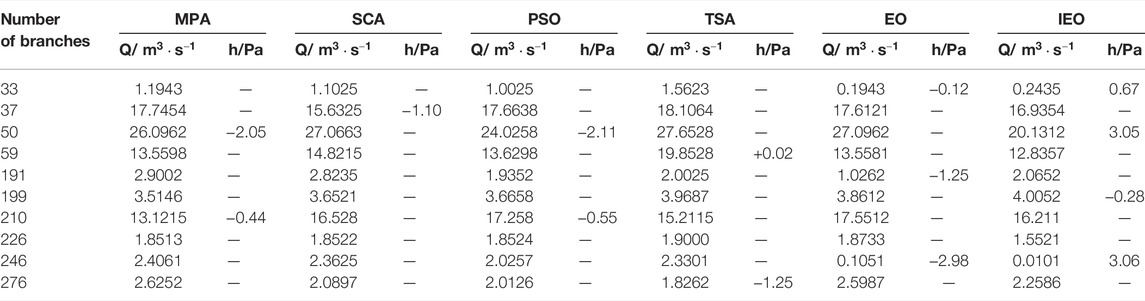
Using the Visual Studio 2019 platform, we developed three-dimensional ventilation simulation and optimization system software using C# and C ++ mixed programming. The optimization method was applied to simulate Wangjialing coal mine belonging to Zhongmei Huajin Energy Co., Ltd. First measurement the resistance of the ventilation system of Wangjialing mine, then imported the measured data and the ventilation system diagram into the software, through the software we can simulated the air quantity distribution of the ventilation system in Wangjialing mine. To improve the calculation speed, simplify the mine ventilation system without affecting the results. Figure 6 shows a simplified mine ventilation system diagram. Figure 7 shows the ventilation system network diagram of Wangjialing mine. Numbering each branch and node in the diagram, the ventilation system of the mine has 213 nodes and 283 branches. Table 4 shows the basic parameters of some of the branches. See Supplementary Appendix SA for the complete data.
At present, there are three intake ventilation shafts in Wangjialing mine. The actual intake air quantities are 1286
Therefore, the method for optimizing mine ventilation systems based on the IEO algorithm proposed in this paper has been adopted by Wangjialing mine to reduce energy waste.
6.3 Analysis of Optimization Results
To verify the effectiveness of the proposed method, we compared the method with the MPA, SCA, PSO, TSA, and EO algorithms. The parameter settings were the same as those described in Section 5.1. Then, Eq. 10 was used as the particle fitness function. Each of the six algorithms was run 50 times. Table 5 shows the statistical results.
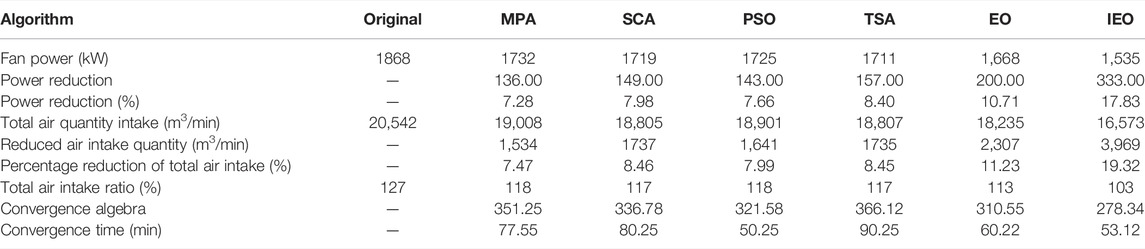
It can be seen from the Table 5 that after the six algorithms were used to optimize the ventilation system of Wangjialing mine, the IEO algorithm reduced the power used by the mine fan by 333 kW, a reduction of 17.83%, which was the most significant among the six algorithms. The intake air quantity was reduced by 3969 m3/min, a reduction of 19.32%. Compared with the other five algorithms, the IEO algorithm can effectively reduce the air quantity, and the total inlet air ratio is reduced to 103%, which greatly reduces the air quantity. The convergence algebra is 278.34 generation, which is the fastest convergence speed among the six algorithms. The convergence time was slightly slower than the PSO algorithm, but the optimization result was much better than with the PSO algorithm. Therefore, the effectiveness and timeliness of the proposed algorithm have been demonstrated. Using this method can effectively reduce the energy consumed by a mine ventilation system and achieve the purpose of energy conservation and emission reduction.
Calculated according to the standard of 0.725 yuan/kWh of power consumption costs in the industrial level period, the annual electricity costs saved after optimization of the air shaft fan using the six algorithms is shown in Table 6. This was calculated by: reduced power × 24 (h) × 0.725 yuan RMB/kWh × 365 (day). It can be seen from Table 6 that the IEO method proposed in this paper can save about 2.11 million yuan for the mine every year, making it the most cost-effective of the six algorithms.
The results of a certain operation are shown in Table 7. A negative sign indicates that the pressure value in the roadway has been reduced. In engineering applications, the corresponding roadway can be found by numbering and the resistance value of the roadway can be adjusted, so as to achieve the purpose of optimizing the mine ventilation system.
7 Conclusion and Future Directions
To conserve energy and reduce emissions in mines, combined with the mine ventilation law, the total power consumption of the ventilation network was minimized. This was achieved by establishing a mine nonlinear optimization model, which was converted into a non-constrained optimization problem by using the penalty function method and solved using the IEO algorithm. The experimental analysis of the algorithm showed that the convergence speed and accuracy of the algorithm are better than those of other algorithms. The engineering application showed that this method can effectively reduce the fan power by 333 kW, saving more than 2 million yuan RMB per year. This will have a pronounced effect on energy conservation and emission reductions.
With the continuous progress of 5G technology, mine ventilation systems will become more intelligent. In the future, various sensors can be arranged in the branches to collect real-time monitoring data. These data can then be input into intelligent decision-making systems to achieve efficient, energy saving, and safe operation of the mine ventilation system. Furthermore, the optimization of mine ventilation systems is not only related to the efficiency of the main fans but can also be considered by establishing a multi-objective optimization model to determine the largest fan shaft power, the highest efficiency of the main fans, and the smallest total resistance of mine ventilation.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
BY contributed to the conception and design of the study, organized the database, performed the statistical analysis, and wrote the first draft of the manuscript. LS wrote sections of the manuscript. All authors contributed to manuscript revision and have read and approved the submitted version.
Funding
The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this paper: this work was supported by National Natural Science Foundation of China: Research on prediction method and application of coal and gas outburst based on big data (71771111).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.913817/full#supplementary-material
References
Abdel-Basset, M., Mohamed, R., Mirjalili, S., Chakrabortty, R. K., and Ryan, M. J. (2020). MOEO-EED: A Multiobjective Equilibrium Optimizer with Exploration-Exploitation Dominance Strategy [J]. Knowledge-Based Syst. 214 (6), 106717. doi:10.1016/j.swevo.2020.100791
Dinh, P.-H. (2021). Multi-modal Medical Image Fusion Based on Equilibrium Optimizer Algorithm and Local Energy Functions. Appl. Intell. 51 (11), 8416–8431. doi:10.1007/s10489-021-02282-w
Dinkar, S. K., Deep, K., Mirjalili, S., and Thapliyal, S. (2021). Opposition-based Laplacian Equilibrium Optimizer with Application in Image Segmentation Using Multilevel Thresholding. Expert Syst. Appl. 174, 114766. doi:10.1016/j.eswa.2021.114766
Dong, M. H., and Li, J. (2008). Analysis on Surging in Axial-Flow Fan and Precautions [J]. Chin. J. Turbomach. (4), 66–67. doi:10.3969/j.issn.1006-8155.2008.04.019
Dorigo, M., Birattari, M., and Stutzle, T. (2006). Ant Colony Optimization. IEEE Comput. Intell. Mag. 1 (4), 28–39. doi:10.1109/mci.2006.329691
Fan, Q., Huang, H., Yang, K., Zhang, S., Yao, L., and Xiong, Q. (2021). A Modified Equilibrium Optimizer Using Opposition-Based Learning and Novel Update Rules. Expert Syst. Appl. 170, 114575. doi:10.1016/j.eswa.2021.114575
Faramarzi, A., Heidarinejad, M., Mirjalili, S., and Gandomi, A. H. (2020b). Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Syst. Appl. 152, 113377. doi:10.1016/j.eswa.2020.113377
Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020a). Equilibrium Optimizer: A Novel Optimization Algorithm. Knowledge-Based Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190
Gleiser, R. J., and Dotti, G. (2005). Linear Stability of Einstein-Gauss-Bonnet Static Spacetimes: Vector and Scalar Perturbations. Phys. Rev. D. 72 (12), 124002. doi:10.1103/physrevd.72.124002
Hao, X. H., Wang, Y. Q., and Wang, L. (2012). Application of Transient Chaotic Network Algorithm to Optimization of Mine Ventilation Network[J]. J. Lanzhou Univ. Tech. 38 (01), 71–74. doi:10.3969/j.issn.1673-5196.2012.01.017
Jia, S. P., Wu, G. J., and Chen, W. Z. (2011). Application of Finite Element Inverse Model Based on Improved Particle Swarm Optimization and Mixed Penalty Function[J]. Rcok Soil Mech. 32 (S2), 598–603. doi:10.16285/j.rsm.2011.s2.042
Kaur, S., Awasthi, L. K., Sangal, A. L., and Dhiman, G. (2020). Tunicate Swarm Algorithm: A New Bio-Inspired Based Metaheuristic Paradigm for Global Optimization. Eng. Appl. Artif. Intell. 90, 103541. doi:10.1016/j.engappai.2020.103541
Li, J., Chen, K., and Lin, B. Q. (2007). Genetic Algorithm for Optimization of Mine Ventilation Network[J]. J. China Univ. Ming Tech. (06), 789–793. doi:10.3321/j.issn:1000-1964.2007.06.015
Marini, F., and Walczak, B. (2015). Particle swarm optimization (PSO). A tutorial. Chemom. Intelligent Laboratory Syst. 149, 153–165. doi:10.1016/j.chemolab.2015.08.020
Mirjalili, S. (2016). SCA: a sine cosine algorithm for solving optimization problems. Knowledge-Based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022
Oliveira, M., Bastos-1'ilho, C. J. A, and Menezes, R. (2015). Gsing network sci-ence to assess particle swarm Optimizers[J]. Soc. Netw. Analysis Min. 5 (1), 1–13. doi:10.1007/s13278-015-0245-5
Pei, X. D., Wang, K., and Li, X. W. (2017). Analysis and Simulation of Intensive Mine Air Regulation Model Based on The Cellular Automation [J]. J. China Univ. Ming Tech. 46 (04), 755–761. doi:10.13247/j.cnki.jcumt.000697
Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization. Swarm Intell. 1 (1), 33–57. doi:10.1007/s11721-007-0002-0
Sayed, G. I., Khoriba, G., and Haggag, M. H. (2020). A novel Chaotic Equilibrium Optimizer Algorithm with S-shaped and V-shaped transfer functions for feature selection [J]. J. Ambient Intell. Humaniz. Comput., 1–26. doi:10.1007/s12652-021-03151-7
Shao, L. S., Wang, Z., and Li, C. M. (2021). Optimization Algorithm of Mine Ventilation Based on SA-IPSO[J]. J. Syst. Simul. 33 (09), 2085–2094.
Shao, L. S., Yu, B. C., and Chen, X. (2020). Key Technique of Mine Intelligent Ventilation[J]. Saf. Coal Mines 51 (11), 121–124. doi:10.13347/j.cnki.mkaq.2020.11.025
Su, S. L., and Ouyang, M. S. (2021). Intelligent Ventilation Management Method of Coal Mine Based on Rough Set and Improved Capsule Network [J/OL]. Coal Sci. Tech., 1–10. [2021-03-10]. doi:10.13199/j.cnki.cst.2021.07.017
Su, Y. X., Ge, L., and Cheng, S. J. (2017). Mine Ventilation Rate Forecasting Based on Improved Genetic Algorithm and BP neural Network[J]. J. Henan Polytech. Univ. Nat. Sci. 36 (4), 20–25. doi:10.16186/j.cnki.1673-9787.2017.04.004
Wang, B., Wang, Y. S., and Hao, J. B. (2019). Optimization of Intelligent Ventilation System in Wanglou Coal Mine. J]. Saf. Coal Mines 50 (02), 105–108. doi:10.13347/j.cnki.mkaq.2019.02.024
Wang, J., Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., et al. (2021). Photovoltaic cell parameter estimation based on improved equilibrium optimizer algorithm. Energy Convers. Manag. 236 (3), 114051. doi:10.1016/j.enconman.2021.114051
Wei, G. (2011). Optimization of Mine Ventilation System Based on Bionics Algorithm. Procedia Eng. 26, 1614–1619. doi:10.1016/j.proeng.2011.11.2345
Wu, X. Z., Hu, J. H., and Wei, L. J. (2019). Research on Opposition Based Enhanced Fireworks Algorithm Optimization for Mine Ventilation Network[J]. Industry Mine Automation 45 (10), 17–22. 67. doi:10.13272/j.issn.1671-251x.17438
Zhang, X. G., and Zhou, Y. (2018). Study on ACPSO algorithm for mine ventilation Network[J]. J. Liaoning Tech. Univ. Sci. Ed. 20 (04), 305–311.
Keywords: ventilation energy consumption, equilibrium optimizer algorithm, ventilation network optimization, Gaussian disturbance, energy saving and emission reduction
Citation: Yu B-c and Shao L-s (2022) A Mine Ventilation System Energy Saving Technique Based on an Improved Equilibrium Optimizer. Front. Energy Res. 10:913817. doi: 10.3389/fenrg.2022.913817
Received: 08 April 2022; Accepted: 31 May 2022;
Published: 11 August 2022.
Edited by:
Ali Bassam, Universidad Autónoma de Yucatán, MexicoReviewed by:
Jingbo Wang, Kunming University of Science and Technology, ChinaRamin Ranjbarzadeh, Dublin City University, Ireland
İsmail Altın, Karadeniz Technical University, Turkey
Copyright © 2022 Yu and Shao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bao-cai Yu, MTM3ODQyNTM2NkBxcS5jb20=
 Bao-cai Yu
Bao-cai Yu Liang-shan Shao
Liang-shan Shao