A Modified Long Short-Term Memory-Deep Deterministic Policy Gradient-Based Scheduling Method for Active Distribution Networks

To improve the decision-making level of active distribution networks (ADNs), this paper proposes a novel framework for coordinated scheduling based on the long short-term memory network (LSTM) with deep reinforcement learning (DRL). Considering the interaction characteristics of ADNs with distributed energy resources (DERs), the scheduling objective is constructed to reduce the operation cost and optimize the voltage distribution. To tackle this problem, a LSTM module is employed to perform feature extraction on the ADN environment, which can realize the recognition and learning of massive temporal structure data. The concerned ADN real-time scheduling model is duly formulated as a finite Markov decision process (FMDP). Moreover, a modified deep deterministic policy gradient (DDPG) algorithm is proposed to solve the complex decision-making problem. Numerous experimental results within a modified IEEE 33-bus system demonstrate the validity and superiority of the proposed method.

1 Introduction

To reduce greenhouse gas emissions, numerous government policies have been established to encourage the development of renewable energy sources. Along with this trend, conventional distribution networks are being transformed into active distribution networks (ADNs) (Wei et al., 2021). Meanwhile, the intermittent and volatility output of high penetration distributed energy resources (DERs), such as photovoltaic generations (PVs), energy storage systems (ESSs), and wind farms, increases the uncertainty of ADNs (Usman et al., 2018; Ehsan and Yang, 2019). Especially, the increasingly severe issues of voltage violation and network loss have attracted widespread attention. Thus, it is necessary to coordinate the scheduling of DERs to promote the flexibility and interaction of ADNs.

Recently, various research efforts have been paid to study coordinated scheduling policies to optimize the decision-making and control of DERs. Studies (Zamzam et al., 2022; Prabawa and Choi, 2021) maintain voltage quality and optimize power losses by coordinating ESSs with charging stations (CSs). In (Zamzam et al., 2022), the scheduling of DERs in a fast time resolution is solved by the interior point method. It is verified that ESSs along with CSs are promising entities for reducing network voltages deviations and system losses. Similarly, Prabawa et al. propose a hierarchical volt/var control (VVC) framework to minimize the total active power losses and voltage deviations through the coordination of smart CSs, PVs, and ESSs at both global and local stages (Prabawa and Choi, 2021). However, limited by the model complexity and computational efficiency, the proposed VVC method may be incapable of handling a large distribution network with various DERs. Additionally, these scholars (Ma et al., 2021; Zhu et al., 2020) dissect the random fluctuation characteristics of PV plants via multi-scenario modeling, improving ADNs’ efficiencies and economics. To reduce the PV curtailment and network loss, a non-dominated sorting genetic algorithm II (NSGA-II)-based voltage regulation method is proposed in (Ma et al., 2021). Although the NSGA-II algorithm is easy to implement, it does not guarantee the global optimum in practical applications. The study reported in (Zhu et al., 2020) constructs a typical scenario set-based approach to address the stochastic economic dispatching, preestablishing charging and discharging schemes for controllable generation units, PV systems, wind farms, and ESSs. However, it suffers a heavy computational burden due to the need to consider many scenarios. Furthermore, studies (Li et al., 2020a; Luo et al., 2021) establish robust optimal operation strategies to deal with the randomness of DERs. In (Luo et al., 2021), the uncertainty of DERs is described based on beta distribution, and a robust optimization model is established to optimize the network loss, power purchase cost, and voltage distribution. Li et al. propose a distributed adaptive robust VVC method (Li et al., 2020a). It robustly mitigates the network loss while keeping voltage within regulation scope. However, the decisions made by the above methods only rely on the current status of ADNs, and the long-term information and objectives are ignored. These scholars (Zhang Z. et al., 2021; Chen et al., 2021; Sheng et al., 2021) consider the cooperative relationship between fast and slow response resources and mainly establish a multi-timescale scheduling architecture to improve the economics of ADNs. For example, studies (Chen et al., 2021; Sheng et al., 2021) propose a day-ahead economic scheduling model and establish a real-time scheduling method using model predictive control (MPC). The authors (Zhang Z. et al., 2021) formulate a double-layer MPC method to achieve minute-level control of mechanical voltage regulation devices and distributed generations (DGs). Furthermore, the MPC method combined with decentralized inter-area coordination is proposed by (Li et al., 2020b) to cope with the high volatility of DGs efficiently.

Although the aforementioned methodologies help us master the nature of coordinated scheduling decision-making for ADNs, the conventional physical model-based methods highly rely on specific optimization models, resulting in low computational efficiency and unstable solution performance. The time-varying DERs gradually infiltrate into ADNs, and it is challenging for the above methods to respond quickly to real-time dispatching demands.

Fortunately, in recent literature, deep reinforcement learning (DRL) has received growing interest in addressing the ADN scheduling issue. The nonlinear programming problem is formulated as a finite Markov decision process (FMDP) in (Cao et al., 2021a), and the proximal policy optimization is utilized to coordinate ESSs and wind farms. Bahrami et al. develop a deep neural network as the approximator of the state-action value function to benefit load aggregators and users (Bahrami et al., 2021). Further, reference (Zhang Y. et al., 2021) controls switchable capacitors, voltage regulators, and smart inverters via a deep Q-network (DQN) and designs a delicate reward function to maintain the voltage range. Besides, these researches (Gao et al., 2021; Cao et al., 2021b; Zhang J. et al., 2021) introduce the multi-agent DRL technology into ADN controlling and decision-making. Based on a multi-agent and multi-objective architecture, DRL is adopted in (Gao et al., 2021) to develop operation schedules for voltage regulators, on-load tap changers, and capacitors, improving the communication efficiency of multi-agent. Research (Cao et al., 2021b) proposes a multi-agent soft actor-critic approach to analyze the impact of PV fluctuation on voltage distribution. However, the state vector consists of node active power, reactive power, and PV output. For optimization problems with a large power system, the perception of the state variables usually leads to low training efficiency and poor optimization solutions. In reference (Zhang J. et al., 2021), DQN and deep deterministic policy gradient (DDPG) are utilized to control discrete and continuous variables, respectively. It rapidly responds to the state changes of distribution networks through the coordinated training of two agents. Other studies (Sun and Qiu, 2021a; Sun and Qiu, 2021b) focus on the collaborative optimization of conventional programming methods and DRL methods. Sun et al. (Sun and Qiu, 2021a) present a two-stage control method to alleviate fast voltage violations. The day-ahead scheduling model is established as a mixed-integer second-order cone programming (MISOCP), while the real-time scheduling problem is solved by a multi-agent DDPG scheme. A similar situation is discussed in (Sun and Qiu, 2021b), where the day-ahead scheduling of ADNs, considering the active and reactive power capacity of electric vehicles (EVs), is constructed as a MISCOCP. Moreover, the DDPG algorithm is adopted to formulate the reactive power control and V2G control schedules.

Given the state-of-the-art ADN scheduling solutions in this field, there are still two significant limitations. Firstly, the DRL algorithms represented by DQN and DDPG still suffer shortcomings in terms of low training efficiency, overlearning, and poor stability. Secondly, in terms of application, DQN-based methods fail to learn the mapping relationship between continuous state and action spaces. Although DDPG-based methods output continuous actions, they lack an understanding of temporal structural characteristics and are incapable of handling large state spaces. It results in a lower perception of the continuous state information of ADNs.

It can be found that methods for extracting high-dimensional temporal characteristics in real-time scheduling of ADNs are limited, and the DRL-based methods lack the assessment of the integration of multi-extension. To fill these research gaps, this paper presents a long short-term memory (LSTM) and modified DDPG (namely, MLDDPG)-based coordinated scheduling solution. The comprehensive optimization objective is constructed to minimize the operating cost and maintain the voltage range of ADNs. The temporal features of the ADN environment are extracted by a LSTM module. While the DDPG agent is leveraged to strategize real-time operation schemes for DERs. The main contributions of this paper are threefold.

1) To our best knowledge, the existing DRL-based approaches are challenging to handle the massive temporal structure data generated by ADNs. Conversely, relying on the high-dimensional understanding and mining ability, we employ a LSTM module to characterize the temporal data of ADNs. It helps the DRL agent extract and learn the changes of temporal characteristics from both the generation and demand sides and improves the modeling ability for node features.

2) Although the classic DDPG can rapidly respond to the scheduling requirements, it still suffers from overlearning, cold start, and poor stability issues. Thus, the learning rate decay strategy is proposed to balance the exploration and exploitation of DRL agents. Besides, the collaborative assistance policy combined with the modified prioritized experience replay mechanism is proposed to prevent the agent from falling into non-optimal strategies. The combination of extensions improves the convergence speed and application stability and enhances agents’ reliability in decision-making scenarios.

3) A modified LSTM-DDPG (MLDDPG) method is developed to tackle the ADN scheduling issue, which is formulated as a FMDP. In this way, the optimal ADN scheduling decisions can better satisfy the real-time response requirements of DERs. The simulation results demonstrate that our approach significantly improves the operation efficiency and economy of ADNs while optimizing voltage distributions.

The remainder of this paper is organized as follows. Problem Formulation Section sketches the modeling process of the ADN coordinated scheduling problem. Then our proposed solution approach is presented in Proposed Real-Time Scheduling Method Section. Case studies are reported in Case Studies Section. Finally, Conclusion Section concludes the paper.

2 Problem Formulation

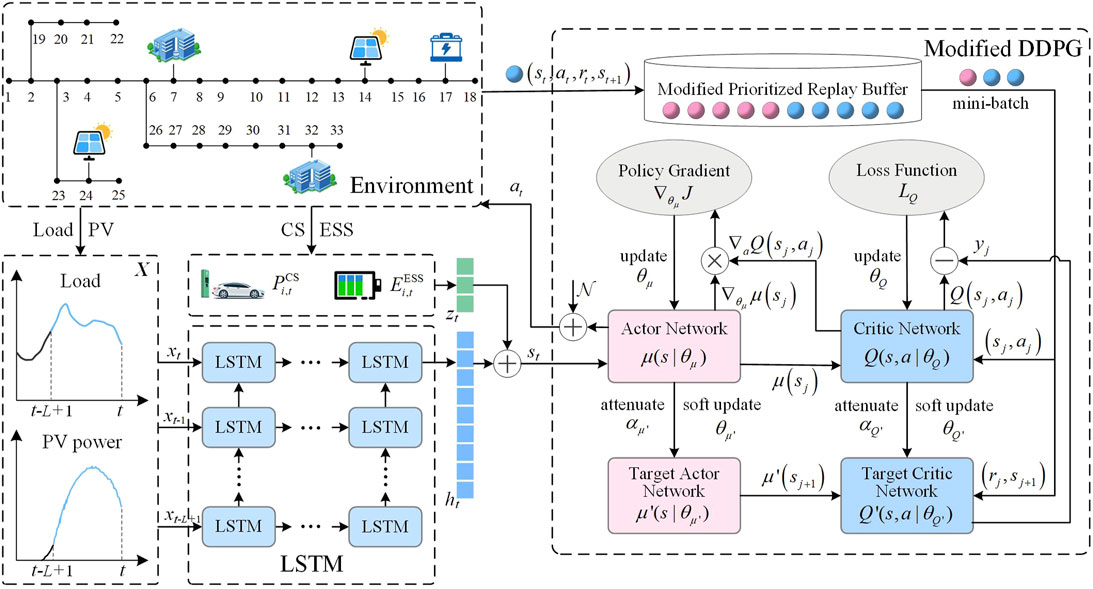
Figure 1 exhibits the established ADN coordinated scheduling architecture based on LSTM and modified DDPG algorithm. The ADN control problem involving DERs is appropriately formulated as a FMDP. Specifically, a LSTM module is utilized to capture the temporal information characteristics of the ADN load and PV output, which, together with the real-time information of CSs and ESSs, constitute the environment state. A DRL-based agent is developed to formulate the ADN control strategy and evaluate the environmental feedback. Further, the agent is trained and optimized based on a modified DDPG module to accelerate the convergence and improve the application stability of the algorithm. Finally, the optimal mapping relationship from the environment state to the control strategy is output to realize the optimal economic operation of ADNs. The details about the modeling process are as follows.

FIGURE 1

FIGURE 1. Overall scheme of the proposed ADN coordinated scheduling method.

2.1 Coordinated Scheduling Model

2.1.1 Objective Function

The sub-objectives consist of substation power purchase cost, ESS charging and discharging degradation cost, and CS response cost to realize the economic operation of ADNs. Mathematically, the comprehensive objective is expressed as:

$\min f={\displaystyle \sum _{t\in {\text{Ω}}_T}{C}_t^{\text{sub}}+C_t^{\text{ESS}}+C_t^{\text{CS}}}(1)$

$C_t^{\text{sub}}={\displaystyle \sum _{i\in {\text{Ω}}_{\text{sub}}}{\pi }_{\text{sub}}{P}_{i,t}^{\text{sub}}}\forall t\in {\text{Ω}}_T(2)$

$C_t^{\text{ESS}}={\displaystyle \sum _{i\in {\text{Ω}}_{\text{ESS}}}{\pi }_{\text{ESS}}\left|P_{i,t}^{\text{ESS}}\right|}\forall t\in {\text{Ω}}_T(3)$

$C_t^{\text{CS}}={\displaystyle \sum _{i\in {\text{Ω}}_{\text{CS}}}{\pi }_{\text{CS}}\text{Δ}{P}_{i,t}^{\text{CS}}}\forall t\in {\text{Ω}}_T(4)$

where: $C_t^{\text{sub}}$, $C_t^{\text{ESS}}$, and $C_t^{\text{CS}}$ separately represent the substation power purchase cost, ESS charging and discharging degradation cost, and CS response cost. ${\Omega }_T$ represents the set of time periods. ${\Omega }_{\text{sub}}$, ${\Omega }_{\text{ESS}}$, and ${\Omega }_{\text{CS}}$ are sets of the substation, ESS, and CS nodes, respectively. ${\pi }_{\text{sub}}$, ${\pi }_{\text{ESS}}$, and ${\pi }_{\text{CS}}$ indicate the electricity price purchased from the transmission network, ESS degradation unit cost, and CS scheduling unit cost, respectively. $P_{i,t}^{\text{sub}}$ is the power interacted with the transmission network. $P_{i,t}^{\text{ESS}}$ indicate the active power of the ESS. $\Delta P_{i,t}^{\text{CS}}$ denote the active power changes of the CS.

2.1.2 Constraints

2.1.2.1 Power Flow Constraints

$P_{j,t}^{\text{PV}}+P_{j,t}^{\text{ESS}}-P_{j,t}^{\text{L}}-P_{j,t}^{\text{CS}}={\displaystyle \sum _{k\in j}{P}_{jk,t}}-{\displaystyle \sum _{i\in j}\left(P_{ij,t}-r_{ij}{\tilde{I}}_{ij,t}\right)}+g_j{\tilde{U}}_{i,t}\forall ij\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(5)$

$Q_{j,t}^{\text{PV}}+Q_{j,t}^{\text{ESS}}-Q_{j,t}^{\text{L}}={\displaystyle \sum _{k\in j}{Q}_{jk,t}}-{\displaystyle \sum _{i\in j}\left(Q_{ij,t}-x_{ij}{\tilde{I}}_{ij,t}\right)}+b_j{\tilde{U}}_{i,t}\forall ij\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(6)$

${\tilde{U}}_{j,t}={\tilde{U}}_{i,t}-2\left(P_{ij,t}{r}_{ij}+Q_{ij,t}{x}_{ij}\right)+{\tilde{I}}_{ij,t}\left(r_{ij}^2+x_{ij}^2\right)\forall ij\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(7)$

${\Vert \begin{array}{l}2P_{ij,t}\\ 2Q_{ij,t}\\ {\tilde{I}}_{ij,t}-{\tilde{U}}_{i,t}\end{array}\Vert }_2\le {\tilde{I}}_{ij,t}+{\tilde{U}}_{i,t}\forall ij\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(8)$

where: ${\Omega }_{\text{bus}}$ is the set of buses in the ADN. $P_{j,t}^{\text{PV}}$, $P_{j,t}^{\text{ESS}}$, $P_{j,t}^{\text{L}}$, and $P_{j,t}^{\text{CS}}$ indicate the active power of the PV, ESS, load, and CS, respectively. $Q_{j,t}^{\text{PV}}$, $Q_{j,t}^{\text{ESS}}$, and $Q_{j,t}^{\text{L}}$ are reactive power of the PV, ESS, and load, respectively. $P_{ij,t}$ and $Q_{ij,t}$ separately represent the active and reactive power injecting from the ith bus to the jth bus. $r_{ij}$ and $x_{ij}$ are the resistance and reactance, respectively. $g_j$ and $b_j$ indicate the conductance and susceptance, respectively. ${\tilde{I}}_{ij,t}$ and ${\tilde{U}}_{i,t}$ represent the square of the branch current and bus voltage, respectively. Constraints (5–8) represent the second order cone programming-based Dist-flow constraints.

2.1.2.2 Safety Operation Constraints

$U_i^{\min }\le U_{i,t}\le U_i^{\max }\forall i\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(9)$

$I_{ij}^{\min }\le I_{ij,t}\le I_{ij}^{\max }\forall ij\in {\text{Ω}}_{\text{bus}},\forall t\in {\text{Ω}}_T(10)$

where: $U_{i,t}$ indicates the voltage of the ith node at time t. $U_i^{\max }$ and $U_i^{\min }$ are the maximum and minimum voltage values, respectively. $I_{ij,t}$ is the branch current at time t. $I_{ij}^{\max }$ and $I_{ij}^{\min }$ represent the maximum and minimum current values, respectively.

2.1.2.3 Operation Constraints of ESSs

$P_{i,\min }^{\text{ESS}}\le P_{i,t}^{\text{ESS}}\le P_{i,\max }^{\text{ESS}}\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(11)$

$Q_{i,\min }^{\text{ESS}}\le Q_{i,t}^{\text{ESS}}\le Q_{i,\max }^{\text{ESS}}\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(12)$

${\Vert \begin{array}{l}{P}_{i,t}^{\text{ESS}}\\ Q_{i,t}^{\text{ESS}}\end{array}\Vert }_2\le S_{i,\max }^{\text{ESS}}\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(13)$

$E_{i,t}^{\text{ESS}}=E_{i,t-1}^{\text{ESS}}+{\eta }_i^{\text{c}}{P}_{i,t}^{\text{ESS}}\text{Δ}t{P}_{i,t}^{\text{ESS}}\ge 0,\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(14)$

$E_{i,t}^{\text{ESS}}=E_{i,t-1}^{\text{ESS}}+P_{i,t}^{\text{ESS}}\text{Δ}t/{\eta }_i^{\text{d}}{P}_{i,t}^{\text{ESS}}<0,\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(15)$

$E_{i,\min }^{\text{ESS}}\le E_{i,t}^{\text{ESS}}\le E_{i,\max }^{\text{ESS}}\forall i\in {\text{Ω}}_{\text{ESS}},\forall t\in {\text{Ω}}_T(16)$

where: $P_{i,\max }^{\text{ESS}}$ and $P_{i,\min }^{\text{ESS}}$ represent the ESS maximum and minimum active power respectively. $Q_{i,\max }^{\text{ESS}}$ and $Q_{i,\min }^{\text{ESS}}$ are the ESS maximum and minimum reactive power, respectively. $S_{i,\max }^{\text{ESS}}$ stands for the maximum apparent power of the ith ESS. $E_{i,t}^{\text{ESS}}$ indicates the stored energy in the ith ESS at time t. $E_{i,\max }^{\text{ESS}}$ and $E_{i,\min }^{\text{ESS}}$ are the maximum and minimum stored energy, respectively. ${\eta }_i^{\text{c}}$ and ${\eta }_i^{\text{d}}$ separately denote the charging and discharging efficiencies. Equations 11–13 limit the power output ranges of ESSs, while Equations 14–16 indicate the energy constraints of ESSs.

2.1.2.4 Operation Constraints of CSs

${\overline{E}}_{ij,t}^{\text{EV}}=\{\begin{array}{l}0t<t_j^{\text{sta}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\\ \min \left({\overline{E}}_{ij,t-1}^{\text{EV}}+P_i^{\text{cha}}\text{Δ}t,E_j^{\exp }\right)\\ t_j^{\text{sta}}\le t\le t_j^{\text{fin}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\\ E_j^{\exp }t>t_j^{\text{fin}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\end{array}(17)$

${\underset{¯}{E}}_{ij,t}^{\text{EV}}=\{\begin{array}{l}0t<t_j^{\text{sta}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\\ \max \left({\underset{¯}{E}}_{ij,t+1}^{\text{EV}}-P_i^{\text{cha}}\text{Δ}t,0\right)\\ t_j^{\text{sta}}\le t\le t_j^{\text{fin}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\\ E_j^{\exp }t>t_j^{\text{fin}},\forall i\in {\text{Ω}}_{\text{CS}},\forall j\in {\text{Ω}}_{\text{EV}}^i\end{array}(18)$

$\{\begin{array}{l}{E}_{i,t,\max }^{\text{CS}}={\displaystyle \sum _{j\in {\text{Ω}}_{\text{EV}}^i}{\overline{E}}_{ij,t}^{\text{EV}}}\forall i\in {\text{Ω}}_{\text{CS}},\forall t\in {\text{Ω}}_T\\ E_{i,t,\min }^{\text{CS}}={\displaystyle \sum _{j\in {\text{Ω}}_{\text{EV}}^i}{\underset{¯}{E}}_{ij,t}^{\text{EV}}\forall i\in {\text{Ω}}_{\text{CS}},\forall t\in {\text{Ω}}_T}\end{array}(19)$

$E_{i,t,\min }^{\text{CS}}\le \text{Δ}{P}_{i,t}^{\text{CS}}\text{Δ}t\le E_{i,t,\max }^{\text{CS}}\forall i\in {\text{Ω}}_{\text{CS}},\forall t\in {\text{Ω}}_T(20)$

${\displaystyle \sum _{t\in {\text{Ω}}_T}\Delta P_{i,t}^{\text{CS}}}=0\forall i\in {\text{Ω}}_{\text{CS}}(21)$

where: ${\Omega }_{\text{EV}}^i$ indicate the EV users set of the ith CS. ${\overline{E}}_{ij,t}^{\text{EV}}$ and ${\underset{¯}{E}}_{ij,t}^{\text{EV}}$ separately denote the upper and lower energy boundaries of the jth EV (Hu et al., 2021). $t_j^{\text{sta}}$ and $t_j^{\text{fin}}$ separately represent the start and finish charging time of the jth EV. $P_i^{\text{cha}}$ is the charging pile output power. $E_j^{\exp }$ represent the expected charging power of the jth EV. $E_{i,t,\max }^{\text{CS}}$ and $E_{i,t,\min }^{\text{CS}}$ separately indicate the upper and lower energy boundaries of the ith CS. Equations 17, 18 limit the energy boundaries of EVs, and Equations 19, 20 constraint the response power capacities of CSs. Eq. 21 represents the time translation characteristics of CSs’ demand response.

2.2 Long Short-Term Memory for Information Perception

DERs with different operating characteristics bring high-dimensional and complex information to ADNs, while DRL agents are challenging to capture their high-dimensional feature changes. On the other hand, ADN load and PV output are less affected by control decisions and show high correlation characteristics on the time scale. As an improved version of recurrent neural network (RNN), LSTM effectively solves gradient disappearance and gradient explosion issues and shows remarkable performance in time series data prediction and feature extraction. Therefore, a LSTM module is employed to extract the temporal characteristics of loads and PVs and further improve the long-term performance of the scheduling model. The temporal structure information input X generated by ADNs can be expressed as:

$\mathit{X}=\left[\begin{array}{cccc}{P}_{i,t}^{\mathrm{L}}& P_{i,t-1}^{\mathrm{L}}& \cdots & P_{i,t-L+1}^{\mathrm{L}}\\ Q_{i,t}^{\mathrm{L}}& Q_{i,t-1}^{\mathrm{L}}& \cdots & Q_{i,t-L+1}^{\mathrm{L}}\\ P_{j,t}^{\mathrm{P}\mathrm{V}}& P_{j,t-1}^{\mathrm{P}\mathrm{V}}& \cdots & P_{j,t-L+1}^{\mathrm{P}\mathrm{V}}\end{array}\right]\forall i\in {\text{Ω}}_{\mathrm{b}\mathrm{u}\mathrm{s}},\forall j\in {\text{Ω}}_{\mathrm{P}\mathrm{V}},\forall t\in {\text{Ω}}_T(22)$

where: L represents the time-step.

LSTM defines the input gate, forget gate, and output gate based on the RNN. The formulations of all nodes in a LSTM structure are given by Equations 23–27.

$f_t=\sigma \left(W_f[h_{t-1},x_t]+b_f\right)(23)$

$i_t=\sigma \left(W_i[h_{t-1},x_t]+b_i\right)(24)$

$\{\begin{array}{l}{\tilde{c}}_t=\tanh \left(W_c[h_{t-1},x_t]+b_c\right)\\ c_t=f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t\end{array}(25)$

$o_t=\sigma \left(W_o[h_{t-1},x_t]+b_o\right)(26)$

$h_t=o_t\odot \tanh \left(c_t\right)(27)$

where: $W_f$, $W_i$, $W_c$, and $W_o$ are the weight matrices of the forget gate, input gate, cell state, and output gate, respectively. $b_f$, $b_i$, $b_c$, and $b_o$ are the bias weights. $\sigma (·)$ and $\tanh (·)$ denote the sigmoid activation function and tanh function, respectively. ${\tilde{c}}_t$ indicates the candidate cell state. Eq. 25 denotes that the forget gate controls what to forget from the previous cell state $c_{t-1}$, while the input gate decides what to preserve from the candidate cell state ${\tilde{c}}_t$. Eq. 27 represents that the output gate controls what to pass from the cell state $c_t$ (Kong et al., 2019).

The temporal characteristics of loads and PVs are captured relying on the feature extraction ability of the LSTM module. The LSTM output $h_t$ is taken as the temporal information perception required by the DRL agent.

2.3 Finite Markov Decision Process-Based Scheduling Model

After the temporal environment information is extracted, the agent completes the scheduling of the ADN by making a sequence of decisions on DERs. We construct the ADN scheduling problem as a FMDP. The details about the FMDP formulation are described as follows.

1) State: the agent captures the real-time environment information. In this study, the environment information is divided into two parts: temporal information and instant information. The temporal information of loads and PVs are extracted by the LSTM module. The instant information consists of the real-time states of ESSs and CSs. Thus, the environment state $s_t$ can be expressed as:

$s_t=\left(h_t,z_t\right)(28)$

where: $z_t$ indicates the feature information of ESSs and CSs as shown in Eq. 29.

$z_t=\left(E_{i,t}^{\text{ESS}},P_{j,t}^{\text{CS}}\right)\forall i\in {\text{Ω}}_{\text{ESS}},\forall j\in {\text{Ω}}_{\text{CS}}(29)$

2) Action: the agent selects the action to be executed according to the ADN state. Slow devices are usually scheduled in an offline manner due to their limited allowable daily switching times (Liu and Wu, 2021). To sufficiently absorb the PV power, thus, the active and reactive output of ESSs and the response power of CSs are regarded as the action $a_t$.

$a_t=\left(P_{i,t}^{\text{ESS}},Q_{i,t}^{\text{ESS}},\text{Δ}{P}_{j,t}^{\text{CS}}\right)\forall i\in {\text{Ω}}_{\text{ESS}},\forall j\in {\text{Ω}}_{\text{CS}}(30)$

3) Reward: the feedback value that the agent obtains from the environment after executing the control action. The substation power purchase cost $C_t^{\text{sub}}$, ESS charging and discharging degradation cost $C_t^{\text{ESS}}$, and CS response cost $C_t^{\text{CS}}$ are taken as the feedback reward. Additionally, given the significance of the safe operation of ADNs, the voltage violation penalty is also considered in the reward $r_t$, expressed as follows:

$r_t=-C_t^{\text{sub}}-C_t^{\text{ESS}}-C_t^{\text{CS}}-D_t(31)$

$D_t=-{\pi }_{\text{vol}}{\displaystyle \sum _{i\in {\Omega }_{\text{bus}}}\left[\max \left(U_{i,t}-U_i^{\max },0\right)+\max \left(U_i^{\min }-U_{i,t},0\right)\right]}(32)$

where: $D_t$ represents the penalty caused by voltage violation, quantizing the voltage deviation level in ADNs (Zhang Y. et al., 2021). ${\pi }_{\text{vol}}$ is a significant penalty coefficient.

4) State-action value function: the total expected rewards that the current policy $\pi$ can bring after executing the action $a_t$. The state-action value function $Q^{\pi }(s,a)$ can be expressed as:

$Q^{\pi }(s,a)=\mathbb{E}\left[{\displaystyle \sum _{k=0}^K{\gamma }^k{r}_{t+k}}|s_t=s,a_t=a\right](33)$

where: $\pi$ is the policy that maps from a comprehensive state to a schedule plan. $K$ represents the horizon of time steps. $\gamma$ indicates the discount rate, balancing future rewards and immediate rewards.

The primary purpose of the ADNs scheduling problem is to find the optimal policy $\pi \ast$, which is equivalent to maximizing the state-action value function:

$Q^{\pi \ast }(s,a)=\underset{\pi }{\max }{Q}^{\pi }(s,a)(34)$

3 Proposed Real-Time Scheduling Method

3.1 Classic Deep Deterministic Policy Gradient

DDPG adopts a classic actor-critic-based architecture and realizes agent learning and training through four deep neural networks. It adopts the actor network $\mu \left(s\right|{\theta }_{\mu })$ and critic network $Q(s,a|{\theta }_Q)$ to realize the policy action and action evaluation. The target actor network ${\mu }^{\prime }\left(s\right|{\theta }_{{\mu }^{\prime }})$ is utilized to select an action $a_{j+1}$ for the state $s_{j+1}$ extracted from the replay buffer, and the target critic network $Q^{\prime }(s,a|{\theta }_{Q^{\prime }})$ is applied to calculate the state-action value function of the historical sample.

The action of DERs can be expressed in the following equation.

$a_t=\mu \left(s_t\right|{\theta }_{\mu })+N(35)$

where: $N$ represents the noise, which is usually the Ornstein-Uhlenbeck (OU) process. The ADN is not a great inertia system (e.g., inverted pendulums and aircraft systems) (Fujimoto et al., 2018). Thus, we adopt the Gaussian noise $N\left(0,{\sigma }_t\right)$ instead of the OU process. The standard deviation of noise decreases linearly to 0 as the training episode increases.

The critic network can be updated by minimizing the loss function $L_Q$:

$L_Q=\frac{1}{N_{\text{b}}}{\displaystyle \sum _{j=1}^{N_{\text{b}}}{\left[y_j-Q\left(s_j,a_j|{\theta }_Q\right)\right]}^2}(36)$

$y_j=\{\begin{array}{l}{r}_j,s_{j+1}\text{is}\text{terminal}\\ r_j+\gamma Q^{\prime }\left(s_{j+1},{\mu }^{\prime }\left(s_{j+1}\right|{\theta }_{{\mu }^{\prime }})|{\theta }_{Q^{\prime }}\right),\text{otherwise}\end{array}(37)$

where: $N_{\text{b}}$ represents the mini-batch size sampled from the replay buffer. $y_j$ is the target value.

The parameter of the actor network can be updated based on the policy gradient, which can be expressed as:

${\nabla }_{{\theta }_{\mu }}J=\frac{1}{N_{\text{b}}}{\displaystyle \sum _{j=1}^{N_{\text{b}}}\left[{\nabla }_{a}Q(s_j,a_j|{\theta }_Q)\cdot {\nabla }_{{\theta }_{\mu }}\mu \left(s_j\right|{\theta }_{\mu })\right]}(38)$

Then, the weights of target networks are soft-updated via Eq. 39.

$\{\begin{array}{l}{\theta }_{{\mu }^{\prime },k+1}=\tau {\theta }_{\mu ,k}+(1-\tau ){\theta }_{{\mu }^{\prime },k}\\ {\theta }_{Q^{\prime },k+1}=\tau {\theta }_{Q,k}+(1-\tau ){\theta }_{Q^{\prime },k}\end{array}(39)$

where: $k$ is the learning iteration. $\tau$ indicates the soft-updated parameter, and $\tau \ll 1$.

3.2 Proposed Modified Strategies

The classic DDPG algorithm is widely applied in continuous action decision processing. Nevertheless, it has the following two significant shortcomings in practical application.

1) DDPG updates the network parameters with a fixed learning rate $\alpha$, expressed as Eq. 40. A larger learning rate may lead to overlearning and affect the agent’s stability, while a lower learning rate slows down the convergence speed.

${\theta }_{j+1}={\theta }_j-\alpha {\nabla }_{\theta }{L}_{\theta }(40)$

2) Based on the experience replay buffer, the prioritized experience replay buffer refines the learning efficiency of the agent (Hou et al., 2017). In the early training stage, however, the samples with the larger deviations are frequently selected for training, which may cause the overfitting issue. The repeated training of such samples makes the agent fall into the locally optimal solution, and the agent’s generalization ability is significantly reduced.

For the shortcomings of the classic DDPG algorithm, we propose three improved strategies as fellows: learning rate decay strategy, collaborative assistance policy, and modified prioritized experience replay to improve the basic agent. The details of the proposed modified model are as below.

3.2.1 Learning Rate Decay

An exponential decay model is introduced to change the learning rate $\alpha$ appropriately and balance the exploration and exploitation abilities (Wang et al., 2022). The learning rate in each episode can be calculated by Eq. 41.

$\alpha ={\alpha }_0{c}_{\text{d}}^{n·n_{\text{d}}^{-1}}(41)$

where: ${\alpha }_0$ is the initial learning rate. $c_{\text{d}}$ indicates the decay rate. $n$ stands for the current training episode. $n_{\text{d}}$ is the decay step.

3.2.2 Collaborative Assistance

Generally, agents can be equipped with a specific scheduling ability to deal with ADNs environment after a long training period. However, considering the importance of ADNs’ security indicators, agents are often difficult to be trusted in some critical decision-making scenarios. To this end, we propose the collaborative assistance mechanism to help the agent efficiently learn the coordinated control strategy. Specifically, we first generate $N_{\text{s}}$ scenes before the training and then capture the environment state $s_t$. The CPLEX solver is applied to calculate the optimal solution of the control variable, namely, the action $a_t$. Next, the reward $r_t$ and new state $s_{t+1}$ are obtained, and the above “successful” samples containing the optimal actions are placed in replay buffer D. These pre-generated samples assist the agent in speeding up convergence and preventing it from sticking into non-optimal strategies. In the training stage, successful samples generated by the CPLEX and historical samples obtained from the FMDP are combined to form the mini-batch to optimize the agent parameters.

3.2.3 Modified Prioritized Experience Replay

The main idea of the modified prioritized experience replay is to reconstruct the replay buffer D and the mini-batch sampling method. Firstly, the replay buffer with a capacity $\left|D\right|$ is divided into two equal pools used to store successful and historical samples, respectively. The cooperative training of different samples speeds up the convergence while avoiding the locally optimal problem. Secondly, successful and historical samples are sampled with different probabilities. The successful samples are extracted from the replay buffer with uniform probability, eliminating the relevance between different scenes. The historical samples are sampled with the specified priority according to the time difference error (TD-error). The proportion of two types of samples participating in training is shown in Eq. 42.

$\begin{array}{l}{N}_{\text{b}}=N_{\text{s}}+N_{\text{h}}\\ =\beta N_{\text{b}}+\left(1-\beta \right)N_{\text{b}},\beta \in \left[0,1\right]\end{array}(42)$

where: $N_{\text{s}}$ and $N_{\text{h}}$ represent the number of successful and historical samples in the mini-batch. $\beta$ is the proportion parameter, which decreases linearly with the increase of episode. In this way, the agent gradually accumulates high-quality historical samples to significantly reduce the possibility of voltage violation.

3.3 Training Process of the Proposed Solution Method

Table 1 demonstrates the training process of our proposed solution approach for solving the ADN scheduling problem as described in Problem Formulation Section. In each episode, we first use LSTM to extract the temporal feature $h_t$ of PVs and loads, which are combined with instant information $z_t$ to serve as the environment state $s_t$. The agent formulates the scheduling strategies of ESSs and CSs using the actor network $\mu \left(s\right|{\theta }_{\mu })$. Upon executing the action $a_t$, the reward $r_t$ is obtained by the agent, and the new state $s_{t+1}$ is observed. The historical samples are accumulated via the above interactions and stored in the replay buffer D. Note that half of the replay buffer has been filled with successful samples via the collaborative assistance policy. Then, a mini-batch is extracted based on the modified prioritized experience replay mechanism, and the network parameters are updated. Specifically, after 24-h scheduling is completed, the learning rate $\alpha$ decays exponentially, and the training proportion $\beta$ is also adjusted. Repeat the above steps until the maximum training episode is reached.

TABLE 1

TABLE 1. Training process of the proposed MLDDPG-based method.

4 Case Studies

4.1 Case Study Setup

In this study, the performance of the proposed approach is illustrated using a modified IEEE 33-bus distribution system. The system consists of two PV plants at buses 14 and 24, two CSs at buses 7 and 32, and an ESS at bus 17. The capacities of all PV plants are 400 kWp, and their power generation characteristics are described by real-world data. The installed capacity of the ESS is 600 kWh, and the charging and discharging capacity limit is 250 kVA. The charging efficiency ${\eta }_i^{\text{c}}$ and discharging efficiency ${\eta }_i^{\text{d}}$ are set as 0.9. The upper and lower boundaries of storage capacity are set as 0.1 and 0.9, respectively. Assume the CSs serve 200 EVs per day, wherein the configuration and operation data of EVs and CSs come from the Charging Bar (http://admin.bjev520.com).

The electricity price for power loss is modeled by the time of use (TOU) price. The unit costs of the CS scheduling ${\pi }_{\text{CS}}$ and ESS degradation ${\pi }_{\text{ESS}}$ are set as 0.2 ¥/kWh and 0.06 ¥/kWh, respectively (Cui et al., 2020). The penalty coefficient ${\pi }_{\text{vol}}$ for voltage violation is -5000. A workstation with an AMD R9 3950X CPU and an NVIDIA GeForce 2080Ti GPU is used for the simulation.

4.2 Training Process

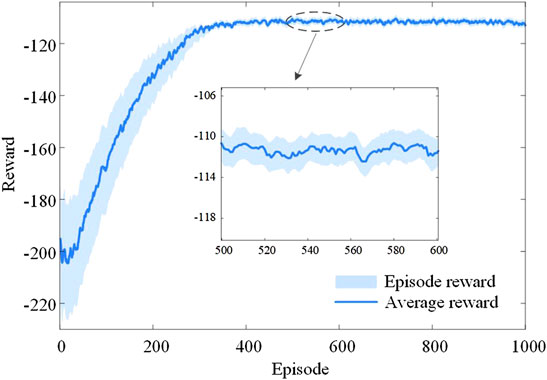
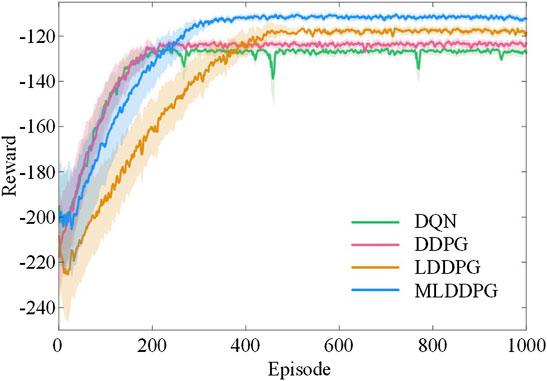
Let the simulation step length be 5 min, and the temporal data over the past 12 time steps are fed into the LSTM module. Table 2 details the parameters of the proposed method, and Figure 2 illustrates the obtained rewards under 1000 training episodes.

TABLE 2

TABLE 2. Parameters of the proposed method.

FIGURE 2

FIGURE 2. Training process of our proposed MLDDPG method.

As attested by Figure 2, the agent learns from the ADN environment by undergoing trials and errors, and the rewards oscillate obviously in the initial stage. Then, the solution process tends to converge steadily from the middle to the final late stage. Especially, the initial learning rate is 0.015, so the agent is encouraged to explore the environment with a high probability in the first 30 episodes. Therefore, the rewards fluctuate obviously, and the average reward in this stage is −201.36. From 30 to 300 episodes, the agent quickly learns successful samples via the collaborative assistance policy and accumulates a certain amount of successful experience. The average reward in this stage increases to −201.36. After that, the agent can learn the optimal mapping from 300 to 1000 episodes. Meanwhile, the learning rate decreases to 8.86 × 10⁻⁴ to steadily exploit the existing experience, and the average reward of the agent is stable at −111.76.

4.3 Practical Application Results

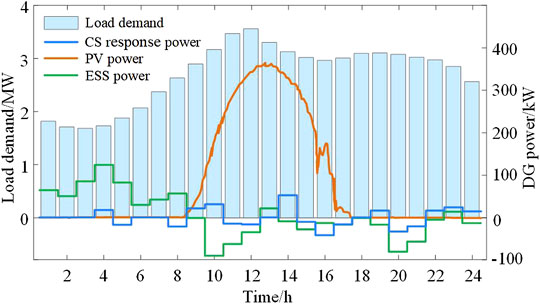
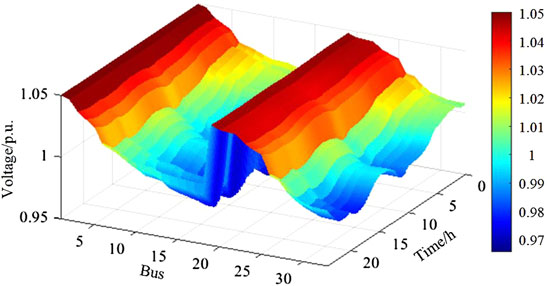
Figures 3, 4 separately exhibit the active power output and voltage amplitude distribution in the testing period. As attested by Figure 3, the well-trained agent can schedule the output of the ESS and CSs as well as cooperate with PVs to respond to the power demand of the ADN. Herein, the agent chooses to charge the ESS during 0:00-7:00 due to the low load level and TOU price. It plays a positive role in reducing the load peak-valley difference and network loss, and the average power loss is 58.06 kW in this period. At around 20:00, the operating pressure of the ADN is alleviated by reducing the charging load and adjusting the ESS discharging power. The final operating cost of the distribution network throughout the day is ¥31,936.62. Moreover, it can be seen from Figure 4 that the operating voltage of each node in the ADN is within the safe range. The minimum voltage is 0.966 3 p.u., which appears on bus 18 at 11:35.

FIGURE 3

FIGURE 3. The active power output of each unit in the ADN.

FIGURE 4

FIGURE 4. Voltage amplitude distribution of the ADN throughout the day.

4.4 Numerical Comparison of Different Methods

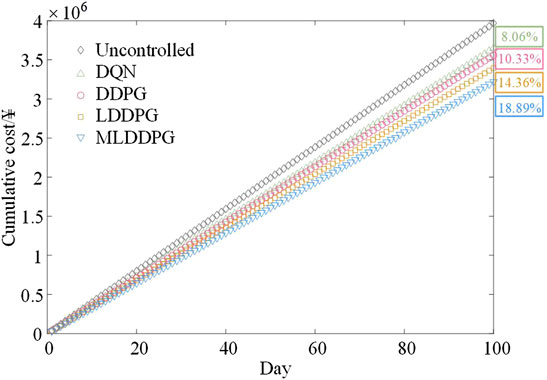
To comprehensively evaluate the implementation effect of our method, DRL algorithms, including DQN, DDPG, and LSTM-DDPG (LDDPG), are taken as benchmark solutions to compare the decision-making capabilities in coordinated scheduling. The parameter settings of DQN, DDPG, and LDDPG are listed in Supplementary Material. Figure 5 details the reward in each episode for different DRL algorithms, and Figure 6 exhibits the cumulative costs of their online testing over 100 days. As depicted, although the DQN algorithm converges rapidly, it has relatively weak convergence and stability in dealing with decision-making problems with high-dimensional state and action spaces. The average convergence reward of DQN is −126.79. Due to the capacity for coping with continuous action spaces, the performance of DDPG is better than that of DQN in terms of convergence performance and stability. Obviously, the LDDPG method initially shows the worst convergence performance, and the reward stabilizes at −117.78 after about 500 episodes. The proposed MLDDPG method improves the convergence performance using three modified mechanisms, and the rewards are stable at −111.59, which is increased by 9.72% compared with the classic DDPG algorithm. Moreover, MLDDPG also achieves excellent decision-making results in the online testing stage, reducing the operation cost by 18.89%.

FIGURE 5

FIGURE 5. Training rewards of different algorithms (DQN, DDPG, LDDPG, and MLDDPG).

FIGURE 6

FIGURE 6. Cumulative total costs of different methods (Uncontrolled, DQN, DDPG, LDDPG, and MLDDPG).

Furthermore, we define the ADN voltage qualification rate $R_{\text{vol}}$ as shown in Eq. 43, and the optimization comparison results are listed in Table 3. The prediction horizon, control horizon, and sampling time interval of the MPC algorithm are 1 h, 20 min, and 5 min, respectively. The DQN and DDPG methods improve the voltage distribution of the ADN, but they still suffer from voltage violation issues. Depending on the information perception ability of the LSTM module for PVs and residential loads, both LDDPG and MLDDPG algorithms successfully restrict the node voltage within an acceptable range. Besides, the MLDDPG agent is capable of adapting to various environments via the collaborative assistance policy combined with the modified prioritized experience replay mechanism. Thus, the proposed method shows remarkable results in reducing power loss and operating cost, and the total operating cost is ¥32,203.17, which is 5.19% lower than that of LDDPG. The MPC can also cope with uncertainties based on rolling optimization, and the algorithm performance is close to that of LDDPG. In addition, the proposed method takes only 0.16 s to solve the scheduling scheme, which is much less than 381.37 s of the CPLEX. Therefore, although the difference between the MLDDPG and the optimal solution is 0.12%, it still achieves an excellent optimization decision-making effect while meeting the real-time scheduling requirements.

$R_{\text{vol}}=1-\frac{{\displaystyle \sum _{t\in {\text{Ω}}_T}{\displaystyle \sum _{i\in {\text{Ω}}_{\text{bus}}}\sigma \left(U_{i,t}\right)}}}{\left|{\text{Ω}}_T\right|\left|{\text{Ω}}_{\text{bus}}\right|}\times 100\%(43)$

$\sigma \left(U_{i,t}\right)=\{\begin{array}{l}0,U_i^{\min }\le U_{i,t}\le U_i^{\max }\\ 1,\text{otherwise}\end{array}(44)$

TABLE 3

TABLE 3. Application results of different methods (Uncontrolled, DQN, DDPG, LDDPG, MLDDPG, MPC, and CPLEX).

4.5 Sensitivity Analysis

Furthermore, the influence of ESS and CS planning schemes and running states on the proposed model is analyzed. Figure 7 illustrates the influence of ESS capacity and CS capacity planning schemes on the ADN operation cost. As attested, the total cost of the ADN gradually decreases with the increase of ESS capacity. For every 100-kWh increase in the ESS capacity, the total operation cost of the ADN is reduced by ¥29.18. Meanwhile, for every 40-kW increase in the CS capacity, the total cost only decreases by ¥6.80. Notably, when the CS capacity is larger than 400 kW, there is little impact on the operating cost of the ADN, indicating that the CS capacity configuration far covers the EV charging demand.

FIGURE 7

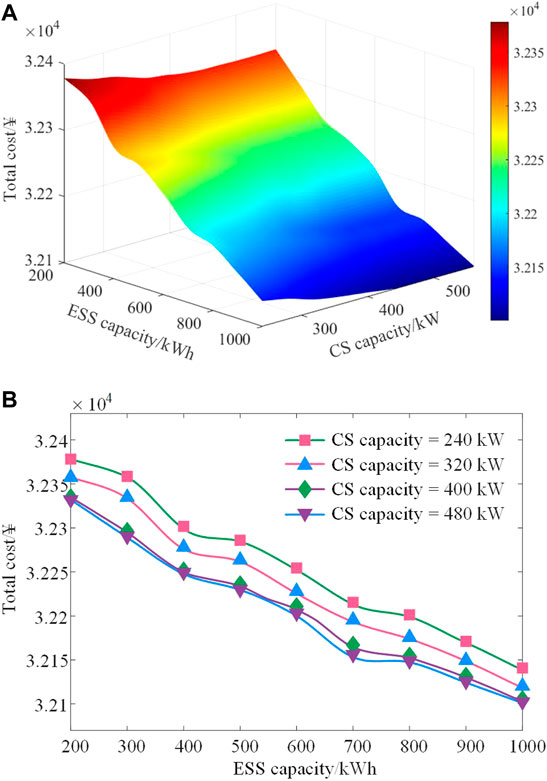
FIGURE 7. Influence of ESS and CS planning schemes on the operation cost of the ADN. (A) Total operation cost of the ADN under different ESS capacity and CS capacity; (B) Total operation cost under different ESS capacity when the CS capacity is 240, 320, 400, and 480 kW, respectively.

Assuming that the number of vehicles is 2 000 in this area, Figure 8 exhibits the impact of EV penetration rates and charger power operation status on the total cost of the ADN. With the EV penetration rate increasing, the total cost increases gradually. For every 1% increase in the EV penetration rate, the operation cost of the ADN increases by ¥31.20. The increase of the charger power improves the carrying capacity of CS but also increases the operation burden of the ADN. For every 1-kW increase in the charger power, the operation cost increases by ¥15.61. Note that the total cost remains stable when the EV penetration rate increases to a specific value. For example, when the charger power is 20 kW, the operation cost is stabilized at around ¥33,998.07 after the EVPR is increased to 20%, which means that the CS carrying capacity and dispatchable potential reach the upper limits.

FIGURE 8

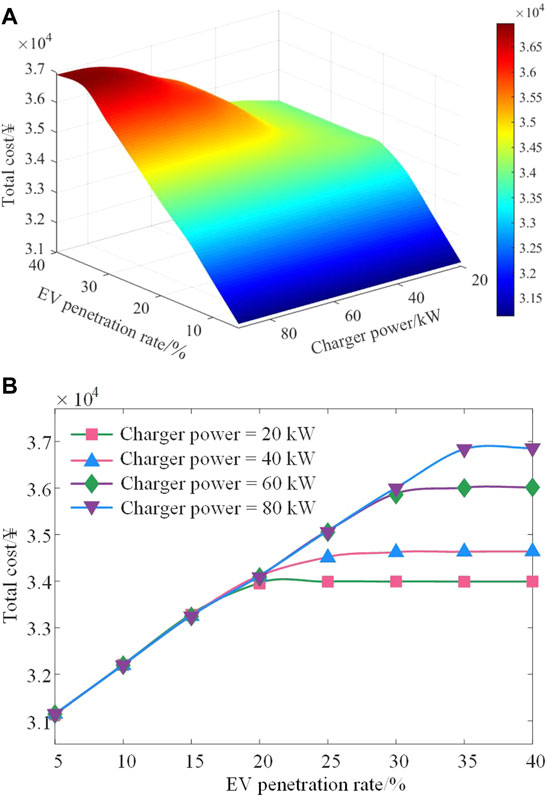
FIGURE 8. Influence of EV and CS running states on the operation cost of the ADN. (A) Total operation cost of the ADN under different EV penetration rates and charger power; (B) Total operation cost under different EV penetration rates when the charger power is 20, 40, 60, and 80 kW, respectively.

4.6 Scalability Performance

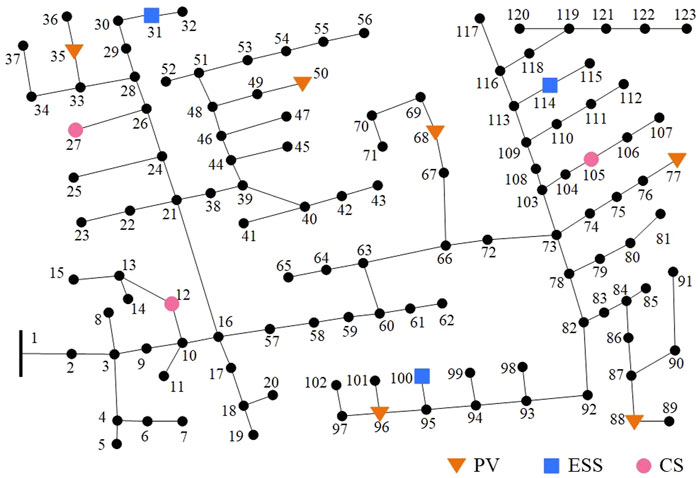
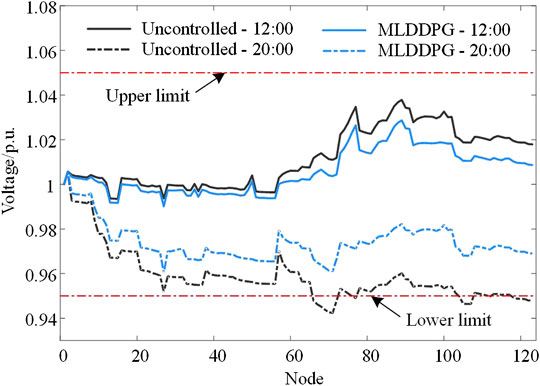
Finally, simulations are also performed on a modified IEEE 123-bus test system to evaluate the scalability of the proposed method. As shown in Figure 9, the test system is modified by integrating 6 PV units, 3 ESSs, and 3 CSs. The parameter setting of each unit is the same as that in Case Study Setup Section. Table 4 lists the numerical results in the modified IEEE 123-bus test system, and Figure 10 exhibits the voltage distribution at peak power consumption.

FIGURE 9

FIGURE 9. Topology of the modified IEEE 123-bus test system.

TABLE 4

TABLE 4. Numerical results in the modified IEEE 123-bus test system.

FIGURE 10

FIGURE 10. Voltage distribution of the test system at 12:00 and 20:00.

It can be observed that there are voltage violation issues when no control is applied, especially during peak power consumption. The uncontrolled method also suffers from high network loss and operating cost issues due to the lack of coordination. Limited by the dimension of environmental states, the DDPG algorithm makes slight improvements in dealing with voltage violation issues. By contrast, the proposed method captures the temporal trends and high-dimensional features of DERs to against uncertainties and provides a basic state for the coordination of each unit. The total operating cost of the MLDDPG method is ¥25,813.86, which is 25.39% lower than that of the uncontrolled mode. The results demonstrate that the proposed MLDDPG method effectively realizes improvements in economic performance and voltage violation mitigation. We conclude that the scalability performance of our method in a large system is validated.

5 Conclusion

Based on the LSTM and modified DDPG algorithm, this paper proposes a novel DRL method for coordinated scheduling of ADNs. Specifically, the LSTM is employed to capture the temporal information of DERs. Then, the extracted state features are fed into the modified DDPG to formulate the operation schedules for CSs and ESSs. Case studies are carried out within a modified IEEE 33-bus system embedded with PVs, ESSs, and CSs. The training and testing results show that the proposed MLDDPG method can not only maintain the safe voltage range but also reduce the economic cost of ADNs. The convergence performance and stability of the proposed method are also improved, which is 9.72% higher than that of the classic DDPG algorithm. Furthermore, the sensitivity analysis is performed, and the scalability of the proposed method is validated in a modified IEEE 123-bus test system. One future direction is to evaluate the sensitivity of DRL-based training parameters and further enhance the robustness of the proposed method. In addition, slow devices will be considered to coordinate with the proposed method and further improve the scalability of the scheduling model.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

ZC: Conceptualization and methodology. RW: Methodology, writing, and original draft preparation. KS: Review and editing. TZ: Formal analysis and visualization. PD: Investigation and review. QZ: Data curation.

Funding

This research was funded by the State Grid Technology Project under Grant 5108-202018026A-0-0-00.

Conflict of Interest

KS and QZ were employed by the company State Grid Jiangsu Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Thanks to the contributions of colleagues and institutions who assisted in this work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.913130/full#supplementary-material

References

Bahrami, S., Chen, Y. C., and Wong, V. W. S. (2021). Deep Reinforcement Learning for Demand Response in Distribution Networks. IEEE Trans. Smart Grid 12 (2), 1496–1506. doi:10.1109/TSG.2020.3037066

CrossRef Full Text | Google Scholar

Cao, D., Hu, W., Xu, X., Wu, Q., Huang, Q., Chen, Z., et al. (2021a). Deep Reinforcement Learning Based Approach for Optimal Power Flow of Distribution Networks Embedded with Renewable Energy and Storage Devices. J. Mod. Power Syst. Clean Energy 9 (5), 1101–1110. doi:10.35833/MPCE.2020.000557

CrossRef Full Text | Google Scholar

Cao, D., Zhao, J., Hu, W., Ding, F., Huang, Q., Chen, Z., et al. (2021b). Data-driven Multi-Agent Deep Reinforcement Learning for Distribution System Decentralized Voltage Control with High Penetration of PVs. IEEE Trans. Smart Grid 12 (5), 4137–4150. doi:10.1109/TSG.2021.3072251

CrossRef Full Text | Google Scholar

Chen, S., Wang, C., and Zhang, Z. (2021). Multitime Scale Active and Reactive Power Coordinated Optimal Dispatch in Active Distribution Network Considering Multiple Correlation of Renewable Energy Sources. IEEE Trans. Ind. Appl. 57 (6), 5614–5625. doi:10.1109/TIA.2021.3100468

CrossRef Full Text | Google Scholar

Cui, S., Wang, Y.-W., Shi, Y., and Xiao, J.-W. (2020). An Efficient Peer-To-Peer Energy-Sharing Framework for Numerous Community Prosumers. IEEE Trans. Ind. Inf. 16 (12), 7402–7412. doi:10.1109/TII.2019.2960802

CrossRef Full Text | Google Scholar

Ehsan, A., and Yang, Q. (2019). State-of-the-art Techniques for Modelling of Uncertainties in Active Distribution Network Planning: A Review. Appl. Energy 239, 1509–1523. doi:10.1016/j.apenergy.2019.01.211

CrossRef Full Text | Google Scholar

Fujimoto, S., van Hoof, H., and Meger, D. (2018). Addressing Function Approximation Error in Actor-Critic Methods. arXiv e-printsarXiv:1802.09477.

Google Scholar

Gao, Y., Wang, W., and Yu, N. (2021). Consensus Multi-Agent Reinforcement Learning for Volt-VAR Control in Power Distribution Networks. IEEE Trans. Smart Grid 12 (4), 3594–3604. doi:10.1109/TSG.2021.3058996

CrossRef Full Text | Google Scholar

Hou, Y., Liu, L., Wei, Q., Xu, X., and Chen, C. (2017). “A Novel DDPG Method with Prioritized Experience Replay,” in 2017 IEEE International Conference on Systems, Man, and Cybernetics (Banff, CanadaIEEE), 316–321. doi:10.1109/SMC.2017.8122622

CrossRef Full Text | Google Scholar

Hu, J., Wu, J., Ai, X., and Liu, N. (2021). Coordinated Energy Management of Prosumers in a Distribution System Considering Network Congestion. IEEE Trans. Smart Grid 12 (1), 468–478. doi:10.1109/TSG.2020.3010260

CrossRef Full Text | Google Scholar

Kong, W., Dong, Z. Y., Jia, Y., Hill, D. J., Xu, Y., and Zhang, Y. (2019). Short-term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 10 (1), 841–851. doi:10.1109/TSG.2017.2753802

CrossRef Full Text | Google Scholar

Li, P., Ji, J., Ji, H., Jian, J., Ding, F., Wu, J., et al. (2020b). MPC-based Local Voltage Control Strategy of DGs in Active Distribution Networks. IEEE Trans. Sustain. Energy 11 (4), 2911–2921. doi:10.1109/TSTE.2020.2981486

CrossRef Full Text | Google Scholar

Li, P., Zhang, C., Wu, Z., Xu, Y., Hu, M., and Dong, Z. (2020a). Distributed Adaptive Robust Voltage/VAR Control with Network Partition in Active Distribution Networks. IEEE Trans. Smart Grid 11 (3), 2245–2256. doi:10.1109/TSG.2019.2950120

CrossRef Full Text | Google Scholar

Liu, H., and Wu, W. (2021). Two-stage Deep Reinforcement Learning for Inverter-Based Volt-VAR Control in Active Distribution Networks. IEEE Trans. Smart Grid 12 (3), 2037–2047. doi:10.1109/TSG.2020.3041620

CrossRef Full Text | Google Scholar

Luo, Y., Nie, Q., Yang, D., and Zhou, B. (2021). Robust Optimal Operation of Active Distribution Network Based on Minimum Confidence Interval of Distributed Energy Beta Distribution. J. Mod. Power Syst. Clean Energy 9 (2), 423–430. doi:10.35833/MPCE.2020.000198

CrossRef Full Text | Google Scholar

Ma, W., Wang, W., Chen, Z., Wu, X., Hu, R., Tang, F., et al. (2021). Voltage Regulation Methods for Active Distribution Networks Considering the Reactive Power Optimization of Substations. Appl. Energy 284, 116347. doi:10.1016/j.apenergy.2020.116347

CrossRef Full Text | Google Scholar

Prabawa, P., and Choi, D.-H. (2021). Hierarchical Volt-VAR Optimization Framework Considering Voltage Control of Smart Electric Vehicle Charging Stations under Uncertainty. IEEE Access 9, 123398–123413. doi:10.1109/ACCESS.2021.3109621

CrossRef Full Text | Google Scholar

Sheng, H., Wang, C., Li, B., Liang, J., Yang, M., and Dong, Y. (2021). Multi-timescale Active Distribution Network Scheduling Considering Demand Response and User Comprehensive Satisfaction. IEEE Trans. Ind. Appl. 57 (3), 1995–2005. doi:10.1109/TIA.2021.3057302

CrossRef Full Text | Google Scholar

Sun, X., and Qiu, J. (2021b). A Customized Voltage Control Strategy for Electric Vehicles in Distribution Networks with Reinforcement Learning Method. IEEE Trans. Ind. Inf. 17 (10), 6852–6863. doi:10.1109/TII.2021.3050039

CrossRef Full Text | Google Scholar

Sun, X., and Qiu, J. (2021a). Two-stage Volt/Var Control in Active Distribution Networks with Multi-Agent Deep Reinforcement Learning Method. IEEE Trans. Smart Grid 12 (4), 2903–2912. doi:10.1109/TSG.2021.3052998

CrossRef Full Text | Google Scholar

Usman, M., Coppo, M., Bignucolo, F., and Turri, R. (2018). Losses Management Strategies in Active Distribution Networks: A Review. Electr. Power Syst. Res. 163, 116–132. doi:10.1016/j.epsr.2018.06.005

CrossRef Full Text | Google Scholar

Wang, R., Chen, Z., Xing, Q., Zhang, Z., and Zhang, T. (2022). A Modified Rainbow-Based Deep Reinforcement Learning Method for Optimal Scheduling of Charging Station. Sustainability 14 (3), 1884. doi:10.3390/su14031884

CrossRef Full Text | Google Scholar

Wei, B., Qiu, Z., and Deconinck, G. (2021). A Mean-Field Voltage Control Approach for Active Distribution Networks with Uncertainties. IEEE Trans. Smart Grid 12 (2), 1455–1466. doi:10.1109/TSG.2020.3033702

CrossRef Full Text | Google Scholar

Zamzam, T., Shaban, K., Gaouda, A., and Massoud, A. (2022). Performance Assessment of Two-Timescale Multi-Objective Volt/VAR Optimization Scheme Considering EV Charging Stations, BESSs, and RESs in Active Distribution Networks. Electr. Power Syst. Res. 207, 107843. doi:10.1016/j.epsr.2022.107843

CrossRef Full Text | Google Scholar

Zhang, J., Li, Y., Wu, Z., Rong, C., Wang, T., Zhang, Z., et al. (2021c). Deep-reinforcement-learning-based Two-Timescale Voltage Control for Distribution Systems. Energies 14 (12), 3540. doi:10.3390/en14123540

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, X., Wang, J., and Zhang, Y. (2021b). Deep Reinforcement Learning Based Volt-VAR Optimization in Smart Distribution Systems. IEEE Trans. Smart Grid 12 (1), 361–371. doi:10.1109/TSG.2020.3010130

CrossRef Full Text | Google Scholar

Zhang, Z., Da Silva, F. F., Guo, Y., Bak, C. L., and Chen, Z. (2021a). Double-layer Stochastic Model Predictive Voltage Control in Active Distribution Networks with High Penetration of Renewables. Appl. Energy 302, 117530. doi:10.1016/j.apenergy.2021.117530

CrossRef Full Text | Google Scholar

Zhu, H., Yuan, S., and Li, C. (2020). Stochastic Economic Dispatching Strategy of the Active Distribution Network Based on Comprehensive Typical Scenario Set. IEEE Access 8, 201147–201157. doi:10.1109/ACCESS.2020.3036092

CrossRef Full Text | Google Scholar