Energy Management Without Iteration—A Regional Dispatch Event-Triggered Algorithm for Energy Internet

Centralized algorithms and distributed algorithms have gained great attention on the energy Internet nowadays. The centralized algorithm presses too much communication and numeration load to its control center in large-scale and neterogeny EI. The distributed algorithm requests too many times of iteration, and the performance and convergence speed is quite slow. The current literature presents a regional dispatch event-triggered algorithm (RDETA). Energy management in RDETA can transform between a centralized model and distributed model. With the effort, the energy management does notrequire iteration times in quantity. And due to event-triggered asynchronous communication, energy management not only relieson a global synchronous clock but also decreasecommunication frequency in most cases and increasecommunication frequency in exigency. In addition, RDETA adopts regional communication and regional energy dispatch, which can automatically modulate the scale of dispatch area by the degree of the energy problem. Finally, simulation results and theoretical demonstration show the aforementioned contributions of the proposed algorithm.

Introduction

Energy is a fundamental guarantee to industrial engineering and human society. With the much more frequent appearance of the fossil energy crisis, global environmental pollution, and multiple energy loads in industry, agriculture, and the daily life of humanity in recent years, it is imperative to create a better strategy to utilize multi-energy in higher efficiency, lower pollution, and more sustainable methods. Energy Internet (EI) and multi-energy systems rise in response to the proper time and conditions (Huang et al., 2010; Sun et al., 2017; Abdella et al., 2021). The key contributions of EI are to realize cooperation (Wang et al., 2020), optimization (Lu et al., 2019), management (Zhang et al., 2017), control (Zhang et al., 2020a), and complementation (Qin et al., 2019) among multiple energy subsystems. Furthermore, EI also contributes greatly in absorbing unstable renewable energy resources through the complex energy networks, enhancing the utilization rate of energy and accelerating energy sustainable development.

However, different from traditional fuel-based centralized power systems, EI is called for effectively coupling various neterogeny energy with different speeds and costs of the manufacture, transmission, and conversion and simultaneously managing large-scale energy systems. In consequence, how to cooperatively allocate energy generation resources including renewable resources that are incapable to control, complex energy conversion among various energy, and satisfying changeable and unpredictable energy loads tends into an exceedingly serious challenge in EI. For handling these issues, recent investigations adopt two main methods. One is centralized algorithms, and another is distributed algorithms.

The centralized algorithm can be subdivided into analytical algorithms (Lin and Viviani, 1984; Lin et al., 1992; Wright, 1997) and heuristic algorithms (Sun et al., 2013; Moeini-Aghtaie et al., 2014). Centralized algorithms have a high quality of performance and a high speed. They can settle small-scale energy trading with no need for iteration. However, the centralized algorithms rely on a strongly centralized communication and control center, are sensitive to single-point failures and modeling errors (Yile et al., 2017), are hard to protect users’ privacy (Pourbabak et al., 2017), etc. To sum up, the centralized algorithm is suitable for small-scale systems, whereas is unfit for large and complex systems in EI. To overcome the aforementioned drawbacks, the distributed algorithm becomes a burgeoning and effective substitute methodology to replace the centralized algorithm to deal with large and complex systems in EI. Demystified by multi-agent systems (Liang et al., 2021), distributed algorithms divide EI into subsystems and subdivide subsystems into energy devices. So Sun (2019) named subsystems in EI we-energy, and defined we-energy as basic energy units with the functions of the multi-energy manufacture, multi-energy consumption, multi-energy conversation, and multi-energy storage. This we-energy has high quality compared with other recent researches in the author’s view, so this study chooses we-energy as a model of energy subsystems.

The distributed algorithm in EI mainly includes four species of rudimentary theoretical knowledge containing price-guide algorithms (Yuang et al., 2022), alternating direction method of multipliers (ADMM) (Zhang et al., 2017), Newton descent algorithms (Li et al., 2020), and consensus-based methods (Sun et al., 2019). Xu et al. (2018) adopted a quasi-Newton algorithm to address economic optimization issues in multi-area. Sun et al. (2015) applied consensus-based methods in multi-agent systems to EI on the first try. Despite distributed algorithms being much fitter to large and complex EI than the centralized algorithm, the synchronous clock bus line is still too long due to the scale of global systems. Therefore, Li et al. (2019) renovated communication strategy to asynchronous event-triggered communication and embedded it into the execution of traditional distributed algorithms. Through its effort, each energy body can asynchronously trigger information exchanging to the global system at discrete instants driven by serious conditions to remove unnecessary communication. Nevertheless, communication and calculation in each time of triggering are still too large to operate. By the way, Li et al. (2019) sacrificed energy balance under the circumstances that communication is not triggered whereas disadvantages of energy mismatch are far more serious than economic loss. So sacrificing economic optimization is a better choice. Huang et al. (2016) raised co-optimization among microgrids. Can et al. (2021) adopted a price-guiding algorithm in EI, whereas the price in it is the energy selling price. The research value of the selling price is much less than that of energy manufacturing and converting costs. Additionally, nonlinear cost functions make energy cost changeable, which greatly increase the difficulty of research.

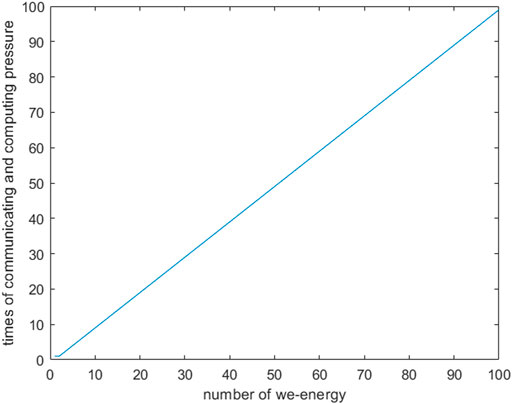
To sum up, recent research on EI has disadvantages hereafter. First, the largest challenge in energy management is all current algorithms require iterations. As we all know, iteration press a great burden on communication and calculation. Communication and calculation times about algorithms with iterations are hundreds of thousands of magnification to that without iterations. So it is a serious matter to invent an algorithm without iteration in EI. Second, because of the large and complex scale of EI, the synchronous clock bus line and global communication consume too much operation cost. The asynchronous communication in the literature (Li et al., 2019) addressed that problem to a certain degree whereas the communication in (Li et al., 2019) was a global communication. Regional communication may be better. Third, price-guiding is an irreplaceable method to alloplastic energy flow issues, because energy price is the only way to estimate value among different types of energy. However, recent research only invests in the selling price. Compared with the selling price, energy cost is far more ponderable in energy conversation. Nevertheless, because of complex cost functions, energy cost is fickle and difficult to be modeled. Finally, distributed algorithms at present are too sensitive to initial values whereas some initial values are difficult to ensure.

These challenges about EI hereinbefore can be settled together. Herein, a regional dispatch event-triggered algorithm (RDETA) comes into being to address the aforementioned issues. Mainly contributions of this article are summarized as following:

1) RDETA does not require iterations. As we all know, iterations press too much burden on communication and calculation. Communication and calculation times about algorithms with iterations are hundreds of thousands of magnification to that without iterations. Therefore, RDETA could increasingly decrease communication and calculation costs in EI.

2) RDETA renovates the communication method to event-triggered asynchronous regional distributed parallel communication, which is exceedingly fit for large EI. Because of the scale of EI, global communication requires too many communicating times. RDETA upsteps communication scope by event-triggered strategy. Furthermore, asynchronous communication does not rely on the synchronous clock bus line. Meanwhile, it decreases communication frequency in most cases to reduce unnecessary costs and increases communication frequency in exigency to aggrandize algorithm adjusting performance to be answerable for emergency circumstances.

3) This study subdivides energy price into energy selling price, energy average cost price, and energy momentary cost price. With this effort, the price-guiding method is better in complex nonlinear cost functions in EI. It is worth noting that these concepts all hereinbefore are originally put forward in this study. They fit energy management whereas may not fit other economic management issues.

4) RDETA adopts high order partial differential equations to centralize dispatch in one or two we-energies. Each energy devices only transmit its partial differential formula and high order partial differential formulas to the control platform inside we-energy. The agents communicate nothing about operating conditions. Therefore, RDETA reinforced the protection of users’ privacy. In addition, because of high order partial differential equations, RDETA is not sensitive to initial values.

5) Three secondary contributions. One is to replace day-ahead forecasting with communication-ahead forecasting to enhance forecasting accuracy. Another is that when the event-triggered system does not activate, RDETA chooses to sacrifice economic optimality rather than energy supply-demand balance because the detriment of energy mismatch is much greater than that of reducing economic earnings. The last contribution is that RDETA entirely handles the issue of energy conversion.

The rest of this study is as follows. Section 2 introduces the proposed mathematical model of EI, we-energies, and energy devices. Section 3 first introduces some fundamental knowledge. Then, it introduces the proposed RDETA. Section 3 demonstrates the optimal performance and avoiding Zeno behavior of RDETA, too. Section 4 analyses several illustrative case studies to show the proposed RDETA applied to a simulated EI. The conclusion drawn from this study is in Section 5.

Mathematical Model of EI

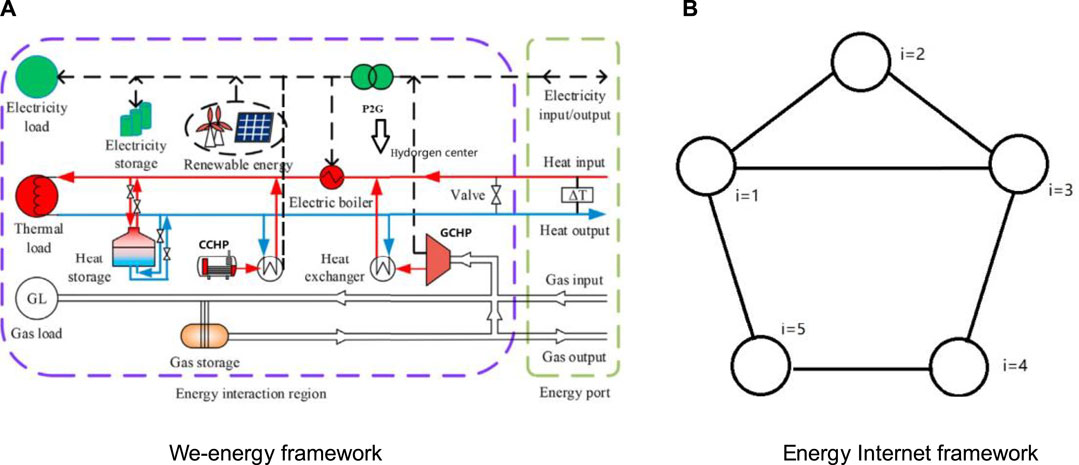
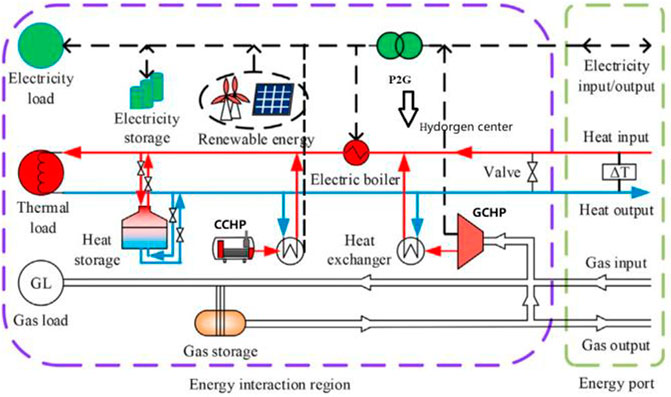
An anticipated construction of single we-energy, employed to couple multiple energy components together, is depicted in Figure 1A. We can divide the energy devices of each we-energy into seven classes, i.e., including the energy manufacturer (EM), the energy transform devices (TD), the energy storage devices (SD), the energy load (EL), the energy transfer path (TP), the information communication path (ICP), and the we-energy control platform (CP). As a small but complex and consummate energy subsystem of the energy prosumer (the conception of prosumer was in (Kubli et al., 2018)), we-energies can play multitudinous roles of energy supplier, energy transformer, and energy terminal user by controlling orders from CP. CP controls its multi-energy generators, multi-energy transform devices, multi-energy storage devices, and multi-energy loads. e.g., each we-energy can sell the part of excess power flow to other we-energies to help we-energies under power shortage circumstances and earn an additional economic profit.

FIGURE 1

FIGURE 1. (A) We-energy framework. (B) Energy Internet framework.

The we-energy is regarded as a power supplier at this moment. In the meantime, the we-energy shall purchase deficit heat energy flow from other we-energies if it is hard to reach its heat supply-demand balance, so it plays a role of the heat terminal user. As shown in Figures 1A, B, the dispatch inside we-energy is centralized dispatch controlled by CP whereas the cooperation among we-energies is implemented under a sparse and distributed communication network based on the theory of multi-agent systems that are topology structures with great promise in the future compositive energy systems. In this mode, each we-energy only needs to exchange information with its corresponding neighbors when an event triggers asynchronous communication to implement their co-management. We can obtain optimal operating conditions through RDETA. To this end, the interconnected EI cyber information structure and physical structure are far different from preceding energy hub models (Sheikhi et al., 2015; Bahrami and Sheikhi, 2016). The energy hub models in previous research are mainly devoted to the energy import side. Each energy hub can reach its energy supply-demand balance. However, we-energies are integrated energy agents constituted of energy hubs and terminal energy users and their co-dispatch can reach further interconnection on both energy entrance sides and energy exit sides. Through these efforts, the system flexibility, scalability, and reliability of EI can be greatly improved. Additionally, it is necessary for energy in the EI network to be transmitted and transformed in easy means. So only power, heat, and gas frequently-used energy conform to the requirement from the network in EI. On this account, EI in this study is power-heat-gas EI. Other types of energy including coal are not discussed in this study. What is noteworthy is that, despite great promise about interconnection among we-energies, the large-scale and complex structure of it brings abundant serious challenges because of the frequency of communication, iterations, and calculations. To handle these issues, RDETA uses various methods such as regional communications, event-triggered asynchronous communications, transitions between distributed model and centralized model, and high-order partial differential equations. The purposes of these methods are to avoid global communications in large EI, reduce unnecessary superfluous communications and rely upon synchronous clock bus lines, settle complex and large EI with the performance-superior centralized algorithm in distributed multi-agent systems, and avoid iterations. In addition, RDETA replaces the day-ahead forecasting (Zhang et al., 2020b) with communication-ahead forecasting to enhance forecasting accuracy.

We-Energy Model

As seen in Figure 1A, at the energy entrance or export side, the received power flow$\left(P^{\text{in}}\right)$, heat flow $\left(H^{\text{in}}\right)$, and gas flow $\left(G^{\text{in}}\right)$ enter into or depart from the we-energy via the solid-state transformers, the caliducts, and the natural gas pipelines. Inside the we-energy structure, the received generated power flow comes from the wind generators (WG) $\left(P^{\text{W}}\right)$, the solar generators (SG) $\left(P^{\text{S}}\right)$, and the power output of the CHP units including coal-based CHP units (CCHP) $\left(P^{\text{CC}}\right)$ and gas-based CHP units (GCHP) $\left(P^{\text{GC}}\right)$. The received dissolved power flow is split into two paths, i.e., the one consumed by the terminal power users and the other one transformed by the power conversion devices including electric boilers (EB) $\left(P^{EB}\right)$ and power-to-gas devices (P2G) $\left(P^{P2G}\right)$. The received generated heat flow comes from the heat output of CHP units incorporating solar heat devices (SH), CCHP $\left(H^{\text{CC}}\right)$, GCHP units $\left(H^{\text{GC}}\right)$, and EB $\left(H^{EB}\right)$. The received consumption of heat flow is utilized by terminal users only because heat is difficult to transform. The received generated gas flow comes from the equivalent gas generators (EGG) and the gas output of P2G $\left(G^{P2G}\right)$. The received dissolved gas flow is subdivided into two paths, i.e., the one consumed by the terminal gas users and the other one transformed by the gas-based CHP units$\left(P^{\text{GC}}\right)$. In addition, the energy (i.e., power, heat, and gas) storage devices (PS, HS, and GS) can adjust their operating conditions of energy supply or demand of the we-energy, which are determined by the discharge/charge states $\left(P^{SD}\right)$,$\left(H^{SD}\right)$, and$\left(G^{SD}\right)$. It is worth noting that, all the aforementioned energy flows are vectors. The positive values of the symbol of energy output, and vice-versa. The energy loads contain two parts including the utilization of terminal users and the transfer loads. The transfer loads mean one type of energy converses with another type of that, e.g., power flow converses to gas flow via P2G, by this method, certain gas load transfers to the power load.

From the preceding part of the study, we can get to know that, the EM includes five kinds of devices, i.e., the WG, the SG, the SH, the CCHP, and the EGG. The TD includes the P2G, the EB, and the GCHP. The SD contains PS, HS, and GS.

Energy flow in we-energies could be calculated as follows:

$\left[\begin{array}{c}{P}_{i,t}^{\text{in }}-P_{i,t}^{\text{U}}\\ H_{i,t}^{\text{in }}-H_{i,t}^{\text{U }}\\ G_{i,t}^{\text{in }}-G_{i,t}^{\text{U }}\end{array}\right]=\left[\begin{array}{ccc}{\mathit{v}}_{\mathrm{PP}}^{\mathrm{SST}}{\mathit{\eta }}_{\mathrm{PP}}^{\mathrm{SST}}& {\mathit{v}}_{\mathrm{PH}}^{\mathrm{EB}}{\mathit{\eta }}_{\mathrm{PH}}^{\mathrm{EB}}& v_{\mathrm{PG}}^{\mathrm{p2G}}{\eta }_{\mathrm{PG}}^{\mathrm{P2G}}\\ 0& 1& 0\\ {\mathit{v}}_{\mathrm{GP}}^{\mathrm{GCHP}}{\eta }_{\mathrm{GP}}^{\mathrm{GCHP}}& {\mathit{v}}_{\mathrm{GP}}^{\mathrm{GCHP}}{\eta }_{\mathrm{GP}}^{\mathrm{GCHP}}& {\mathit{v}}_{\mathrm{GG}}^{\mathrm{EWC}}\end{array}\right]\left[\begin{array}{c}{P}_{i,t}^{\text{in }}+P_{i,t}^{\text{EM}}+P_{i,t}^{\text{SD}}\\ H_{i,t}^{\text{in }}+H_{i,t}^{\text{EM }}+H_{i,t}^{\text{SD }}\\ G_{i,t}^{\text{in }}+G_{i,t}^{\text{EM }}+G_{i,t}^{\text{SD }}\end{array}\right],(1)$

$i$ is the serial number of the we-energy; $t$ is the time; superscript $\text{U}$ is the terminal energy user; $v$ is the proportion of the energy converted from the corresponding energy carrier in the total energy flow; and $\eta$ is the efficiency of energy conversion.

$\{\begin{array}{c}{P}_{i,t}^{\text{EM}}=P_{i,t}^{\text{W}}+P_{i,t}^{\text{S}}+P_{i,t}^{\text{CCHP}}\\ H_{i,t}^{\text{EM}}=H_{i,t}^{\text{S}}+P_{i,t}^{\text{CCHP}}\\ G_{i,t}^{\text{EM}}=G_{i,t}^{\text{EGG}}\end{array}(2)$

We consider an EI as a multi-agent system with $n$ we-energy subsystems, including in each we-energy no more than $\xi$ participants but not limited to energy devices and terminal users. For the simplification of notations, we adopt a three-dimensional vector $\left\{X_{i,j}\in R^3|i=1,\mathrm{...},\epsilon ;j=1,\mathrm{...},{\xi }_i\right\}$ to represent the decision variables of controllable devices in EI and employ $x_{i,j}^m$ to represent the $m$ th element of $X_{ij}$. The three elements$x_{i,j}^1$,$x_{i,j}^2$, and $x_{i,j}^3$ in $X_{ij}$ express power, heat, and gas flow, respectively.

EM Devices Mathematical Model

Renewable Energy Devices Model

One of the main purpose is to promote the utilization of renewable resources because they are clean, environmentally friendly, and low-cost. However, renewable energy resources are scattered in the distribution of geographic position and unpredictable energy production in time. As for better absorbing them, the forecasting accuracy is exceedingly significant. Traditional researchers adopt day-ahead forecasting (Bahrami and Sheikhi, 2016) to predict renewable energy generators. Nevertheless, due to the long time scale (1 day), the accuracy of day-ahead forecasting is exceedingly hard to be assured. For heightening the predicted precision, this study presents communication-ahead forecasting using the day-ahead assist method as follows:

$\left\{{\mu }_{i,j,t_{k+1}}^m=x_{i,j,t_k}^m+s{g}_{i,j,t_k}^m\left(t_{k+1}-t_k\right)+\mathrm{\Delta }{r}_{\left(t_{k+1}-t_k\right)}|x_{i,j}^m\in RE\right\}(3)$

$RE$ mean the set of renewable energy devices; $t_k$ and $t_{k+1}$ mean the present time and the next measuring time; $s{g}_{i,j,t_k}^m$ is the day-ahead subgradient factor which expresses the tendency of $x_{i,j,t_k}^m$ in $t_k$; $\Delta r_{\left(t_{k+1}-t_k\right)}$ is the day-ahead convex or nonconvex compensation from $t_k$ to $t_{k+1}$ because the trend of $x_{i,j}^m$ may not be linear; ${\mu }_{i,j,t_{k+1}}^m$ is the mathematic expectation of $x_{i,j,t_{k+1}}^m$. Note that the accurate value may not be the mathematic expectation because of the forecast error. In this study, we assume that the forecasting error obeys the Gaussian distribution whose feasibility analysis has been introduced in the study by Wu et al. (2015). Then, the probability density function of $x_{i,j,t_{k+1}}^m$ can be modeled as:

$f\left(x_{i,j,t_{k+1}}^m\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{i,j,t_{k+1}}^m}{e}^{-\frac{(x_{i,j,t_{k+1}}^m-{\mu }_{i,j,t_{k+1}}^m)}{2{\left({\sigma }_{i,j,t_{k+1}}^m\right)}^2}}|x_{i,j,t_{k+1}}^m\in RE(4)$

${\sigma }_{i,j,t_{k+1}}^m$ is the standard deviation of $x_{i,j,t_{k+1}}^m$, which shows the dispersed degree of accurate value. ${\sigma }_{i,j,t_{k+1}}^m$ is determined by day-ahead forecasting and measure frequency. It can be calculated as:

${\sigma }_{i,j,t_{k+1}}^m=I_{i,j}^m\left(t_{k+1}-t_k\right)(5)$

$I_{i,j}^m$ is the day-ahead disperse degree forecasting value.

In addition, the confidence intervals of $x_{i,j,t_{k+1}}^m$ can be solved as $\left[x_{i,j,t_{k+1}}^{m-down},x_{i,j,t_{k+1}}^{m-up}\right]$ by the Eq. 4 by the homologous method in probability theory in the confidence level $100\left(1-\partial \right)\%$. We choose $\partial$ as 0.05 in this study. In addition, we adopt TD, SD, and EL to absorb all renewable energies. Then the operating conditions of renewable energy devices can be:

$\left\{x_{i,j,t_{k+1}}^m\in \left[x_{i,j,t_{k+1}}^{m-down},x_{i,j,t_{k+1}}^{m-up}\right]|x_{i,j}^m\in RE\right\}(6)$

Based on the aforementioned reason, the cost of renewable energy devices can be the punishment for energy deficiency. So if we choose the forecasting result higher, the economic optimization will be better, whereas the dependability will be worse, and vice-versa. The cost functions of renewable energy devices can be as following:

$C_{i,j,t_{k+1}}^{m-RE}=a_{i,j}^{RE}{\left(x_{i,j,t_{k+1}}^m-x_{i,j,t_{k+1}}^{m-down}\right)}^2(7)$

$a_{i,j}^{RE}$ is a positive constant.

The limits of renewable energy devices are as follows:

$\left\{x_{i,j,t_{k+1}}^m\in \left[x_{i,j,t_{k+1}}^{m-down},x_{i,j,t_{k+1}}^{m-up}\right]|x_{i,j}^m\in RE\right\}(8)$

That is the same as Eq. 6.

By the way, $\text{Δ}{r}_{\left(t_{k+1}-t_k\right)}$ and ${\sigma }_{i,j,t_{k+1}}^m$ have their trigger conditions. If the trigger condition of $\text{Δ}{r}_{\left(t_{k+1}-t_k\right)}$ is not reached, the tendency of $x_{i,j,t_k}^m$ will be regarded as linear. If the trigger condition of ${\sigma }_{i,j,t_{k+1}}^m$ is not reached, we will regard the mathematic expectation of $x_{i,j,t_{k+1}}^m$ as the accuracy of it and the equations including Eqs 4–8 will be meaningless because the forecasting precision is enough. In this study, the trigger condition of them is that they are more than 4 and 50 s, respectively.

Fossil Fuel Burning Based EM Devices

First, the technology of co-generation combining heat and power has already matured recently. And because of the high-efficient performance, that technology is much better than fuel-based plants and fuel-based boilers in the purpose of environmentally friendly and economic optimal. To sum up, fuel-based plants and fuel-based boilers are all replaced by co-generation combined heat and power devices. Second, to handle and investigate the ramping rate constraints of CCHPs, its form in discrete shape is always modeled into a knapsack mathematical problem. It is worth noting that we only consider the ramping constrain of the bower but not of heat because the response speed of heat is exceedingly slow. That reason is also fit for GCHP. The cost function of CCHP is as follows:

$\begin{array}{l}{C}_{i,j,t_k}={\text{a}}_{i,j}{{\displaystyle x_{i,j}^1}}^2+{\text{b}}_{i,j}{x}_{i,j,t_k}^1+{\text{α}}_{i,j}{{\displaystyle x_{i,j,t_k}^2}}^2\\ +{\text{β}}_{i,j}{x}_{i,j,t_k}^2+{\text{c}}_{i,j}{x}_{i,j,t_k}^1{x}_{i,j,t_k}^2+{\text{χ}}_{i,j}+\\ \left(x_{i,j}^1+x_{i,j,t_k}^2\right)\times {\left({\eta }_{i,j}\right)}^{-1}\times prf\end{array}(9)$

where ${\text{a}}_{i,j},{\text{b}}_{i,j},{\text{α}}_{i,j},{\text{β}}_{i,j},{\text{c}}_{i,j}$, and ${\text{χ}}_{i,j}$ express cost factors, which are controlled by the energy emission of the thermal unit. They are all constants and the second-order coefficients with a single variable are positive constants. ${\eta }_{i,j}$ is the energy conversion efficiency of CCHP. $prf$ represents the price of coal. And the constraints of CCHP are as follows:

$-P_{i,j}^{\text{ramp}}\le x_{i,j,t_k}^1-x_{i,j,t_k}^2\le P_{i,j}^{\text{ramp}}(10)$

${\text{d}}_{i,j}{x}_{i,j,t_k}^1+{\text{e}}_{i,j}{x}_{i,j,t_k}^2+{\text{f}}_{i,j}\ge 0(11)$

${\text{d}}_{i,j}{x}_{i,j,t_k}^1+{\text{e}}_{i,j}{x}_{i,j,t_k}^2\le {\text{g}}_{i,j}(12)$

$P_{i,j}^{\text{ramp}}$ is the ramp rate constraint. Other coefficients without introduction are constants.

EGG Devices

Natural gas is a kind of fossil fuel and there are not any devices that can produce it. The only way to get natural gas is to buy it from related departments. The only thing we need to consider is the natural gas price, which cannot be changed by EI but decided by other departments.

TD Devices Mathematical Model

P2G and EB Models

The model and cost function of P2G are as follows:

$-x_{i,j,t_k}^3={\eta }_{i,j,t_k}{x}_{i,j,t_k}^1(13)$

$C_{i,j,t_k}=-{\theta }_{i,j,t_k}{x}_{i,j,t_k}^1(14)$

${\eta }_{i,j,t_k}$ is the energy transforming the efficiency of P2G. ${\theta }_{i,j,t_k}$ is a positive constant that expresses operating cost. The constraint of DP2G is as follows:

$P_{i,j}^{\text{P}2\text{G}-\text{min}}\le -x_{i,j,t_k}^1(15)$

$P_{i,j}^{\text{P}2\text{G}-\text{min}}$ is the start-stop limit of P2G. Because power energy in the network of EI is limited and the capacity of P2G is very large, we do not consider the energy conversion upper constraint. There is a resemblance between P2G and EB in the model, the operating cost function, and the constraint. We only need to replace the energy type.

GCHP Models

The model and operating cost function of DGC are as follows:

$C_{i,j,t_k}=\left(x_{i,j}^1+x_{i,j,t_k}^2\right)\times {\left({\eta }_{i,j}\right)}^{-1}\times \left(prg+{\theta }_{i,j}\right)(16)$

Where ${\theta }_{i,j}$ is a positive constant that expresses operating cost. ${\eta }_{i,j}$ is the energy conversion efficiency of CCHP. $prg$ represents the price of gas. By the way, some coefficients are shown in the same letters between CCHP and GCHP, whereas the significance of them is different because the subscripts change along with the types of device. The reason is also fit to conditions between other devices.

The constraints of GCHP are as follows:

$-P_{i,j}^{\text{ramp}}\le x_{i,j,t_k}^1-x_{i,j,t_k}^2\le P_{i,j}^{\text{ramp}}(17)$

${\text{d}}_{i,j}{x}_{i,j,t_k}^1+{\text{e}}_{i,j}{x}_{i,j,t_k}^2+{\text{f}}_{i,j}\ge 0(18)$

${\text{d}}_{i,j}{x}_{i,j,t_k}^1+{\text{e}}_{i,j}{x}_{i,j,t_k}^2\le {\text{g}}_{i,j}(19)$

$P_{i,j}^{\text{ramp}}$ is the ramp rate constraint. Other coefficients without introduction are constants.

SD Devices Mathematical Model

There is an optimal reserve in SD. If the stored energy is much less than the optimal reserve, it will press too much stress on SD devices. If things go on like this for too long, it may injure the capacity of SD devices. If the stored energy is much more than the optimal reserve, the stored energy will be under a risk of a leak. So the optimal condition function of SD is as follows:

$O_{i,j,t_{ki,t}}^m{=\text{a}}_{i,j}{x}_{i,j,t_k}^{m-S}\left(x_{i,j,t_k}^{m-S}-2{\mu }_{i,j}^m\right)+{\text{b}}_{i,j}(20)$

$O$ is the optimal function of stored energy in SD, superscript $m$ represents the type of energy, $x_{i,j,t_k}^{m-S}$ is the stored energy in time, $t_k$. ${\mu }_{i,j}^m$ is the optimal reserve of energy in SD, ${\text{a}}_{i,j}$ and ${\text{b}}_{i,j}$ are invariable constants, and ${\text{a}}_{i,j}$ is negative. The cost function of DPSD is as follows:

$C_{i,j,t_k}=O_{i,j,t_k}^m-O_{i,j,t_{k-1}}^m+{\theta }_{i,j}{\Vert x_{i,j,t_k}^m\Vert }_2(21)$

${\theta }_{i,j}$ is a positive constant that expresses operating cost, and $x_{i,j,t_k}^m$ is the energy flow from SD. So we can know the following:

$x_{i,j,t_k}^m=x_{i,j,t_{k-1}}^{m-S}-x_{i,j,t_k}^{m-S}(22)$

The limits of SD are as follows:

${{\displaystyle -x_{i,j}^m}}^{\mathrm{in-SD}}\le x_{i,j,t_k}^m\le {{\displaystyle x_{i,j}^m}}^{\mathrm{out-SD}}(23)$

$x_{i,j}^{m-S-\min }\le x_{i,j,t_k}^{m-S}\le x_{i,j}^{m-S-\max }(24)$

${{\displaystyle x_{i,j}^m}}^{\mathrm{in-SD}}$ and ${{\displaystyle x_{i,j}^m}}^{\mathrm{out-SD}}$ are the maximum energy flow limits about energy input and output rate of DPSD, respectively. $x_{i,j}^{m-S-\min }$ and $x_{i,j}^{m-S-\max }$ are minimum and maximum values of energy capacity, respectively.

EL Mathematical Model

There are two essential challenges in EL. One is the randomness of terminal users, the other is load shifting. Load shifting is analyzed here. RDETA could absorb the randomness of terminal users in the large multi-agent system of EI by RDETA, which will be introduced in Section IV. In the multi-energy system of EI, different energy loads can transform between each other by energy conversion, e.g., power flow converses to gas flow via P2G, through this method certain gas load transfers to the power load. So the model of EL is as follows:

$x_{i,j,t_k}^m=u_{i,j,t_k}^m+t{r}_{i,j,t_k}^m(25)$

$t{r}_{i,j,t_k}^{n_1}+t{r}_{i,j,t_k}^{n_2}+t{r}_{i,j,t_k}^{n_3}+\dots +t{r}_{i,j,t_k}^{n_N}=-{\eta }_{i,j}^{mn}t{r}_{i,j,t_k}^m(26)$

${\eta }_{i,j}^{mn}$ is the energy conversion efficiency from energy $m$ to energy $n$. $m$ is a constant, while $n$ is a set of various numbers because a kind of energy can change into more than one type of energy. By the way, the energy load can also be forecast predicted by communication-ahead forecasting which is similar to renewable energy resources. The only difference is that we regard the mathematic expectation of forecasting value as the accuracy value because the randomness of energy load is much lower than that of renewable energy resources.

Energy Management And RDETA Algorithm

Proposes and Difficulties of Energy Management

Considering an EI with a number of we-energies, the expectation of energy management is to minimize the cost under the circumstance that the total energy demand in the whole society that covers is satisfied by the synergy among all participators. We can model it as a mathematical objective function as:

$\begin{array}{l}\text{min}obj={\displaystyle \sum _{i=1,j=1}^{\epsilon ,{\xi }_i}\left(C_{i,j,t_k}\right)}\\ \{\begin{array}{c}{\displaystyle \sum _{i=1}^{\epsilon }{\displaystyle \sum _{j=1}^{{\xi }_i}I\times X_{i,j}}={\displaystyle \sum _{i=1}^{\epsilon }{\displaystyle \sum _{j=1}^{{\xi }_i}{U}_{i,j}}}}\\ \phi \left(x_{i,j}^m\right)<0\end{array}\end{array}(27)$

The cost not only includes the visualized economic expenditure but also contains some invisible expenditure incorporating but not limited to the inaccurate forecasting of renewable energy resources, undertaking the risk of energy mutation, energy pour and energy shortage, and the like. $U_{i,j}$ is the matrix of terminal users’ energy consumption. $\phi$ is a local closed convex set for $X_{i,j}$. The main difficulties of energy management are as follows:

First, the maximal challenge is too many iterations for the following reason. The complex mathematical issue of energy management is impossible to be solved by continuous math theory. So the only way to settle it is discrete mathematics based on supercomputers. However, that method brings hundreds of thousands of times of iterations. What is more, each time of iteration is accompanied by large communication. Second, the randomness of terminal users and the uncertainty of renewable energy resources cause a mass of trouble. Third, because of the complexity of energy management, recently parallel algorithms in computer math in embedded software are incompatible with EI, which highly limits the high performance of supercomputers. Fourth, because of the large scale of EI, it is exceedingly difficult to build the synchronous clock bus line and global communication. Fifth, although a certain part of EI is uncertain, it does not change tempestuously moment by moment. When participators change a little, the dispatch earnings may be no more than the cost of computing and communicating. Sixth, the principle of multi-energy conversion is complex and multitudinous, and the iteration in the algorithm is incompatible with energy conversion. Seventh, the privacy of we-energies and devices is difficult to protect. Last but not least, the cost of energy generation and conversion is changeable, which causes certain trouble to economic optimization.

The Developing of Energy Management Algorithms

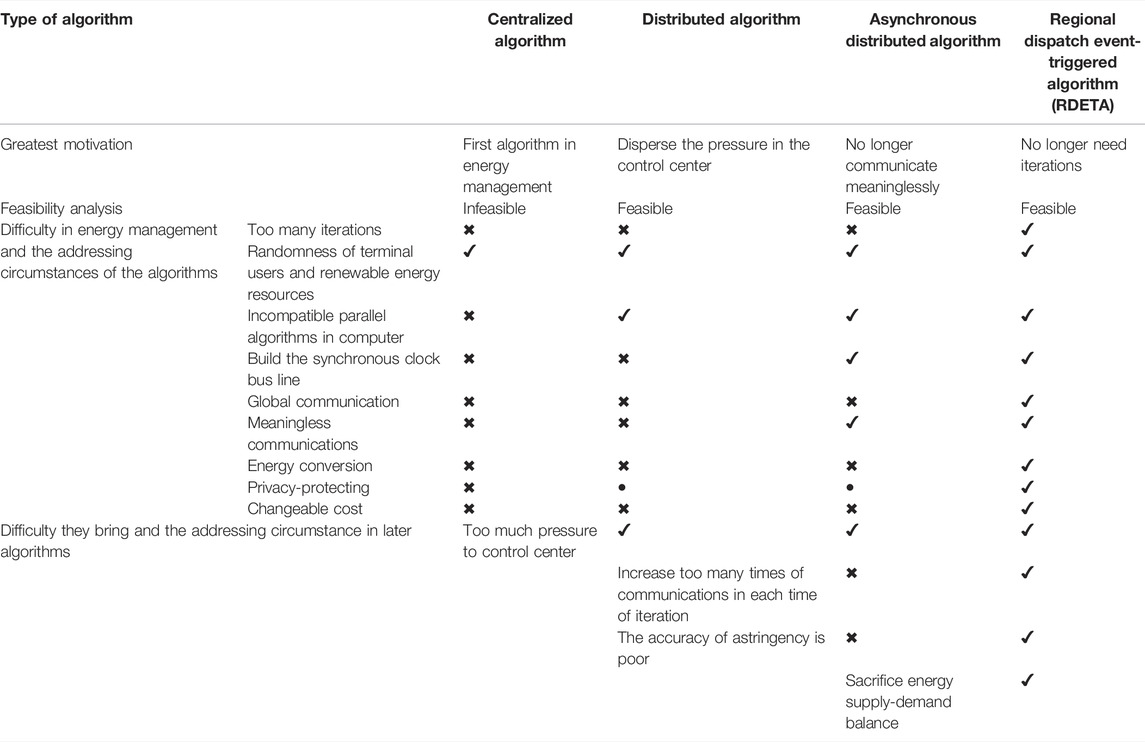
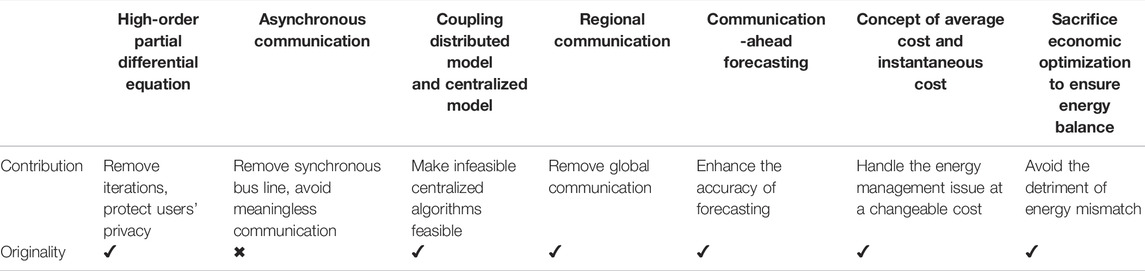
Energy management in a traditional power system adopts the centralized algorithm, which is nearly infeasible because of too much pressure on the control center and communication. So the distributed algorithm rises (Yuang et al., 2022). The distributed algorithm not only greatly reduces the pressure of the control center but also absorbs renewable energy resources in the huge system of EI. Moreover, the issue of privacy protection is half done in it (agents communicate with neighbor agents so their privacy is not entirely protected). Additionally, the incompatible issue is settled on its own. The distributed algorithm is great progress because it is at least a feasible method. However, other disadvantages hereinbefore still exist. What is more, the distributed algorithm requires an excess of iteration times and a large of communications at each time of iteration. What is worth noting is that the computing and communicating times in distributed algorithms are much more than that in centralized algorithms. Whereas the computing and communicating in distributed algorithm allocate to all we-energies, but that in the centralized algorithm are entirely undertaken by the control center. A large number of technology limits including the hardware structure, the size of the microcircuit, and the packaging technology impose certain restrictions on the performance of the supercomputer in the control center, so a centralized algorithm is impracticable. However, the number of the control platforms is not limited, so distributed algorithms can handle much more complex issues. So the distributed algorithm is doable in EI although the computing and communicating cost is large. Li et al. (2019) proposed the asynchronous distributed algorithm which reduces some meaningless communication and does not require the synchronous clock bus line. However, there are still various challenges in energy management, especially the iteration problem and the communicating and computing pressure it brings. Furthermore, the algorithm in the study by Li et al. (2019) sacrifices energy supply-demand balance under certain circumstances, which does great harm to EI. To this end, this study proposed that the RDETA algorithm can handle all aforementioned challenges. The difficulties of energy management, the contributions, and the greatest motivations of all these algorithms are in Table 1 (✔ for entirely addressing, ✖ for not addressing, • for half addressing). RDETA adopts several technologies. Some are original, others are not original. Table 2 shows all technologies and their contributions and their original circumstances (✔ for original, ✖ for not original).

TABLE 1

TABLE 1. The development and contributions of an energy management algorithm.

TABLE 2

TABLE 2. All technologies in RDETA and their contributions and original circumstances.

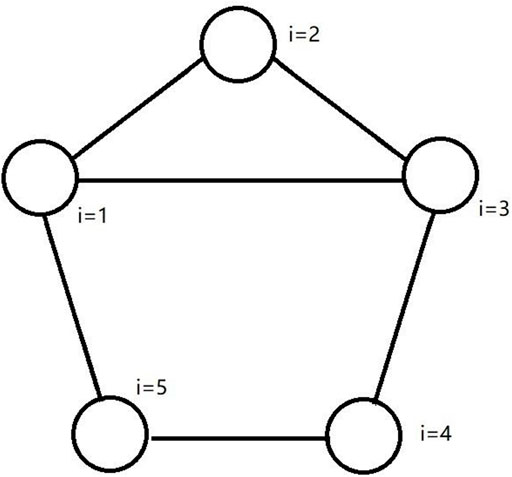
Basic Knowledge of Graph Theory

Consider an EI system with $\epsilon$ we-energies, where $i$ th we-energy has ${\xi }_i$ participators. An undirected graph $Graph=\left(V,E,B\right)$ is adopted to model it, where $V=\left\{v_i|i=\mathrm{1,2},\cdots ,n\right\}$ is a set of nodes representing agents in multi-agent systems and $E\subseteq V\times V$ is a set of undirected edges. Therein, the edge $\left(v_i,v_j\right)$ denotes that $v_i$ node and $v_j$ node can communicate with each other if needed. The relationships between $v_i$ and $v_j$ is shown in $B=\left[b_{i,j}\right]\in R^{m\times n}$. The diagonal elements in that matrix are all zeros constantly. If a non-diagonal element $b_{i,j}>0$, $\left(v_i,v_j\right)\in E$, they are neighbor agents. Whereas if$b_{i,j}=0$,$\left(v_i,v_j\right)\notin E$, they are not neighbor agents. In the undirected graph, sides between nodes are not directed, so $\left(v_i,v_j\right)\in E$ equals to$\left(v_j,v_i\right)\in E$. In this study, we only study connected graph because non-connected graph represents two island energy system that need to be researched, respectively. If we replace a node the graph will be non-connected, that node is called cut-vertex.

RDETA Algorithm

In this study, the main purpose is to minimize all costs under the circumstance that all energy demands and all limits are satisfied. So we can model all participants in each we-energy as a vector space including a lot of vectors including the operating condition vector$\left\{X_{i,j}\in R^3|i=1,\mathrm{...},\epsilon ;j=1,\mathrm{...},{\xi }_i\right\}$, their partial differential, and high-order differentials of cost functions. It is worth noting that, for polynomial functions, their high-order differentials will restrain to zero sooner or later. Whereas for other functions including but not limited to exponential functions, trigonometric functions and logarithmic functions, and their high-order differentials will never restrain. Additionally, some functions may have a too high order, which may greatly increase the computing pressure. So we should use an order supremum $dd$ to avoid these troubles. If a vector is not zero after $\left(dd+1\right)$ order differential, we adopt Chebyshev polynomials to lower the order to $dd$. We establish that in the original state all we-energies operate in the island model in a random condition and that all the energy supply-demand balances are satisfied. Then we will transmit the change value vector of energy resources and the energy loads to the control center inside the we-energy and the control center will solve the energy mismatch vector. Due to the different time scales between different types of energy, we deal with the forecasting results of a different energy in different ways for renewable energy devices and energy loads as follows:

$x_{i,j,t_k}^1=0.5\times \left(z{x}_{i,j,t_k}^1+f{x}_{i,j,t_{k+1}}^1\right)(28)$

$x_{i,j,t_k}^2=z{x}_{i,j,t_k}^2(29)$

$x_{i,j,t_k}^3=f{x}_{i,j,t_k}^3(30)$

$zx$ and $fx$ are the present energy flow and the forecasting energy flow in the next measuring time. The responding speed of power is less than 1 ms and the inductor and capacitance can store or release some power in proper time. So we regard the power flow as the average value of the $zx$ and $fx$ so that the power flow in the time between two measurings will press close to the power demand.

The responding speed of gas may be several seconds or several seconds. We control gas at this time, and because of the slowly responding speed, the control may come into play in the next measuring time. So we regard the gas flow as $fx$ in the next measuring time. . The responding time of heat is too long to consider. For this reason, the forecasting of it is meaningless. So we do not forecast it to reduce computing. Then each device transmits all their condition vectors, their partial differential and high-order partial differentials vectors of cost functions to the control center. Then, the control can solve the issues that all the first-order partial derivative values of the same independent values in EM are equal when the multi-energy balance is reached by high-order partial differential equations. The homologous independent values vector shows their optimal working conditions without TD devices. That first order is the instantaneous cost of the corresponding type of energy for the reason we will introduce in as follows. Then if the instantaneous cost of one type of energy is less than another type of energy and the cheap energy can change into the expensive energy by TD devices, the control center can solve another issue when the instantaneous cost of the expensive energy equals that of the conversion of the cheap energy when the multi-energy is balance. The instantaneous cost of conversion energy is the first-order partial differential of a composite function. The inside function is the cost function of the controllable EM devices of that energy (renewable energy devices are not controllable). The outside function is the cost function of TD. The new independent variable is the new operating conditions of relevant EM devices and the changeable of them is the opposite number of the operating conditions of TD devices. After that, the optimal work of island mode in each we-energy is finished. The next issue is the collaborative optimization among we-energies. First, we should solve all instantaneous costs of each energy and stack them into a price vector $S_i$ with three elements. The instantaneous cost of energy whose load changes to another load is the partial differential of the energy generation about the controllable EM cost functions, while the instantaneous cost of energy whose load changes from another load is the partial differential of part of the energy generation which is utilized by terminal users about that. Then, the we-energy will transmit the energy price vector to neighbor we-energies and compute the trigger vector as follows:

$\begin{array}{l}{\text{T}}_{\mathit{1}}^{\mathit{i}}=S_i\\ {\text{T}}_{\mathit{2}}^{\mathit{i}}=\text{ave}\left\{{\text{T}}_{\mathit{1}}^{\mathit{i}},\text{all}\left({\text{T}}_1^{{\mathit{i}}_2}\right)|i\sim i_2\right\}\\ {\text{T}}_3^{\mathit{i}}=\text{ave}\left\{{\text{T}}_{\mathit{2}}^{\mathit{i}},\text{all}\left({\text{T}}_2^{{\mathit{i}}_2}\right)|i\sim i_2\right\}\\ \mathrm{.......}\\ {\text{T}}_{\text{k}}^{\mathit{i}}=\text{ave}\left\{{\text{T}}_{\text{k}}^{\mathit{i}},\text{all}\left({\text{T}}_{\text{k}}^{i_2}\right)|i\sim i_2\right\}\end{array}(31)$

The symbol $\text{ave}$ means the average vector of all vectors in the set. The symbol $\sim$ means that the two number we-energies between that symbol are neighbor-agents. The symbol $\text{all}$ means a set of all elements under that circumstance. All we-energies will transmit their ${\text{T}}_1^i$ to ${\text{T}}_{\text{q}+1}^i$ to their neighbor-agents. $\text{q}$ is the number of cut-vertex in the EI system. The reason for that is the low connected degree EI needs more control. If the difference value absolute of one of the element in ${\text{T}}_1^i$ to ${\text{T}}_{\text{q}+1}^i$ is larger than the homologous element in the trigger vector $\aleph$ which is very small, the asynchronous communication between their two we-energies will be triggered. Then, two we-energies will be regarded as one big we-energy. They will share one control center and repeat the we-energy partial differential equation dispatch hereinbefore as follows:

$\begin{array}{l}\frac{d\left(C_{i,j,t_k}\right)}{x_{i,j,t_k}^m}=\frac{d\left(C_{i,j\text{'},t_k}\right)}{x_{i,j^{’},t_k}^m}\\ \frac{d\left(C_{i,j,t_k}\right)}{x_{i,j,t_k}^m}=k_1,\frac{d^2\left(C_{i,j,t_k}\right)}{{\left(x_{i,j,t_k}^m\right)}^2}=k_2,\frac{d^3\left(C_{i,j,t_k}\right)}{{\left(x_{i,j,t_k}^m\right)}^3}=k_3\mathrm{...}\frac{d^n\left(C_{i,j,t_k}\right)}{{\left(x_{i,j,t_k}^m\right)}^n}=k_n\\ \frac{d\left(C_{i,j^{\prime },t_k}\right)}{x_{i,j^{\prime },t_k}^m}=k{k}_1,\frac{d^2\left(C_{i,j^{\prime },t_k}\right)}{{\left(x_{i,j^{\prime },t_k}^m\right)}^2}=k{k}_2,\frac{d^3\left(C_{i,j^{\prime },t_k}\right)}{{\left(x_{i,j^{\prime },t_k}^m\right)}^3}=k{k}_3\mathrm{...}\frac{d^n\left(C_{i,j^{\prime },t_k}\right)}{{\left(x_{i,j^{\prime },t_k}^m\right)}^n}=k{k}_n\end{array}(32)$

The partial derivative values are the energy prices for the reason that is expressed hereinafter. $k$ and $kk$ are constants. There are three advantages of this operation. First, this operation is centralized in the two we-energies but is distributed in the whole EI for the reason that the two we-energies are very small to the whole large system of EI. It is worth noting that the method of partial differential equations is unfit for big systems but is fit for small systems. A big we-energy including two we-energies is a small system that is very fit to the method of the partial differential equations. Second, the partial differential equations can solve the issue of energy management without iteration. However, it is unfit for large systems because of the pressure of communication and computing. The RDETA adopts the partial differential equations in two we-energies which not only avoid iteration but also avoid too much computing and communicating pressure.

So the price vector in the two we-energies will be the same. Then, the control center will compute how much energy should be transmitted from one we-energy to another and stack it into an energy flow vector. After that, the asynchronous communication will be cut off, while the energy transmitting value will be reserved in a transmitting vector and the we-energies will transmit energy according to that. There are some points which should be emphasized. First, a we-energy can only asynchronously communicate to only one we-energy at a time. If the price difference still exists between it and another we-energy, that we-energy may communicate to it after it finished the asynchronous communication before. Second, after the asynchronous communication, if another asynchronous communication between them does not appear, the energy transmitting between them will be invariant even if the operating conditions of some energy devices change by the dispatch inside the own we-energy or the asynchronous communication between the we-energy and another we-energy. Third, when the next measuring time is reached, all we-energies will dispatch inside themselves by partial differential equations first, then they may asynchronously communicate and asynchronously dispatch. If one or two we-energies have the energy transmitting assignment between other we-energy, the asynchronous energy dispatch should consider the energy transmitting assignment. Fourth, if one we-energy should asynchronously communicate to two or more we-energies, whose we-energy will be communicated first may be random because there is not an asynchronous clock bus line in EI, so the trigger time may not be same in different we-energies. We cannot control which two we-energies will trigger early. Fifth, if the operating condition of a device is out of its in equation constraint, we will adjust it to a value on the constraint boundary. Then, we will adjust other values to reach the energy balance. By these methods, the energy management of RDETA will be realized. What is more, if the energy conversion efficiency and the operating cost factor of TD devices are all under a trigger condition, we can regard the transmitted load as the terminal users’ load to simplify the computing pressure. In this study, that condition is $70\%$ for energy conversion and $2$ cent for the operating cost factor. It is worth noting that, RDETA cannot adopt KKT. The KKT is a good optimal method and good at handling optimal problems with in equation limits. However, KKT requires entire cost functions. If we adopt KKT, too much pressure will be given on communication and computing. To this end, RDETA adopts partial differential equations rather than KKT conditions. Devices only need to exchange partial differential vectors rather than all cost functions by this means. Generally, the communication needs to end when all the asynchronous communication is not triggered, while if the number of cut-vertex is less than 3, we can stop the communication when all we-energies communicate to all neighbors for one time.

Testification of Optimality and Avoiding Zeno Behaviors

As you can see, we do not prove the astringency of RDETA. The reason for that is there is not any iteration in RDETA, the astringency is obviously meaningless. The optimality is very easy to understand. However, what is the meaning of avoiding Zeno behaviors? The Zeno behavior means the trigger happens infinite times in a limited time. In this study, the Zeno behavior means the asynchronous communication is activated infinite times in one time of measuring.

The cost is changeable, which brings a serious challenge to energy management. For handling that issue, we propose several concepts including average cost, instantaneous cost, and finite difference cost.

The average cost is the specific value of the whole energy generation or conversion cost (can be solved by the cost function) and the energy flow. The finite difference cost is the specific value of a length of energy cost and the energy flow difference. The difference between the average cost and the finite difference cost is that the average cost is a specific value with the whole generation (conversion) energy, which is from zero to an energy flow value. However, the finite difference cost is between energy flow $a$ to energy flow$b$. That value can be solved by the difference value of the cost function value between $a$ and $b$. If we choose a pair of values about $a$ and $b$, in which $a$ is exceedingly similar to$b$, the length finite difference cost can change into a point cost. The point cost is called the instantaneous cost.

Because the absolute value of $\aleph$ is exceedingly small, we can assume it as zero. Only if all trigger vectors are the same, the asynchronous communication will stop. Obviously, if all price vectors in each we-energy are the same, all trigger vectors will be the same, too. If price vectors are not all in the same value, ${\text{T}}_1^i$ will trigger asynchronous communication. So the necessary and sufficient condition of asynchronous communication will stop is that all price vectors are in the same value.

If there are $\epsilon$ we-energies in EI, we can regard them as $\epsilon -1$ we-energies because we can regard two neighbor we-energies as one big we-energy. The neighbor we-energies of the big we-energy are all of the neighbor we-energies of them. The asynchronous communication can adjust their price vectors to the same. Even if another we-energy communicates to one of them, which leads their price vectors different, they can adjust themselves. What is worth noting is if a we-energy communicates to one of them for one time, the change of that we-energy which does not belong to the big we-energy is different from the change while the big we-energy is really one we-energy because that we-energy only communicates to one of them but not to both of them. However, after several times of adjusting inside the big we-energy and between the outside we-energy and one of the we-energy in the big we-energy, the dispatch will be the same of the big we-energy is a really we-energy because the big we-energy will adjust them to one we-energy sooner or later even if other we-energies disturb them. The two we-energies will undertake the perturbance together. Then, we can regard the big we-energy and a neighbor we-energy of it as a bigger we-energy for the same reason. So the big we-energy can enlarge over and over again until adsorbing the whole EI. So the price vectors of each we-energy will be the same after certain communication. The asynchronous communication will stop at the same time. The Zeno behavior of the asynchronous communication time is infinite and will never appear.

The optimization proof of the whole EI is the same as that of one we-energy because we can regard the whole EI as a big we-energy. In that big we-energy, all energy cost functions are convex functions, all price vectors are the same, and all energy conversion instantaneous costs are the same too. Under that circumstance, the energy balance is reached. If some energy devices operate in another condition, other devices also need to change the operating conditions to ensure the energy balance. The price of them will change. According to the theory of convex optimization, the increasing finite difference cost of the devices generating or transforming more energy is more than the decreasing finite difference cost of other devices because all functions are convex functions. (The cost functions of TD devices are also convex functions because they are composite functions.)

There are a large number of contributions of RDETA, which are summarized in Figure 2. Some are obvious while some are vague. We introduce some obscure contributions here. It is worth noting that there is not a relationship between the importance of the contributions and whether to introduce them here. The only reason to introduce them is that they are difficult to understand.

FIGURE 2

FIGURE 2. Heat instantaneous price (cent).

The reason RDETA can enhance privacy protection is that each we-energy only needs to exchange their ${\text{T}}_1^i$ to ${\text{T}}_{\text{q}+1}^i$ to other neighbor agents when the asynchronous communication is not triggered. The information in them is very less. Their operating conditions and a lot of important information do not need to exchange. The reason RDETA can make infeasible centralized algorithms feasible is that centralized algorithms are unsuitable for large systems, while RDETA only adopts it in one or two we-energy. The reason RDETA can remove global communication is that RDETA only communicates in two we-energies at one time.

Simulation Results

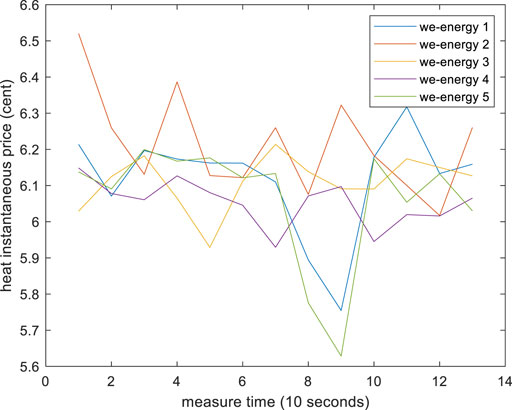
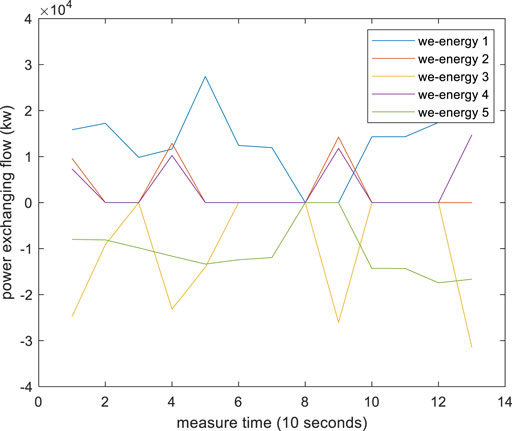
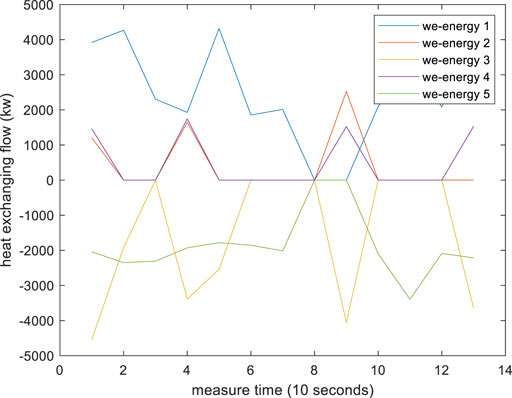
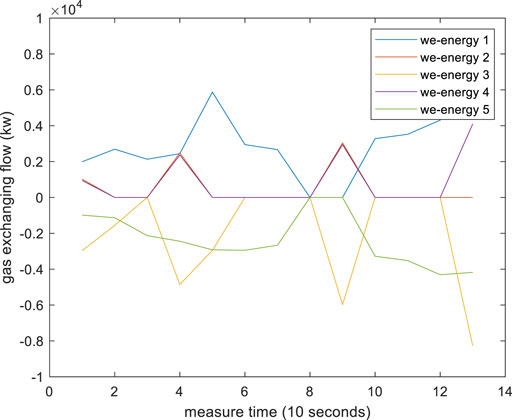
The performance of the proposed RDETA algorithm is tested on an EI system with five we-energies. The simulation platform and all data are shown in the Supplementary Appendix. The measurement interval time is 10 s. The simulation results are as follows.

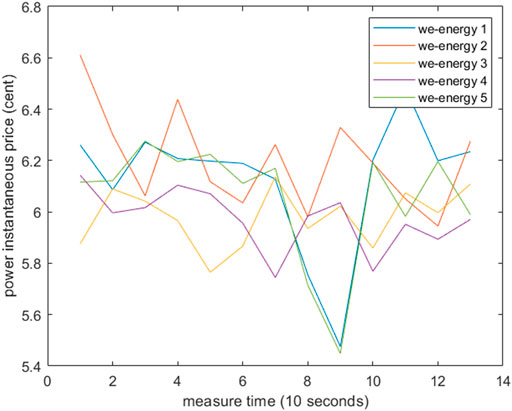
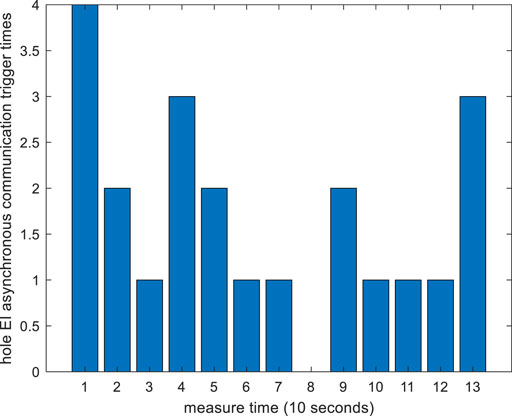
Figures 2, 3 are the instantaneous price of power and heat (the gas price never changes). Figures 4–6 are energy exchanging between each we-energy and others. Figure 7 is the asynchronous communication times in whole EI. What is worth noting is that the communication order is randomized to a certain degree because there is not a synchronous clock bus line. For comparing with the traditional distributed algorithm, we give a distributed Newton algorithm result. Most data and models for the distributed Newton algorithm are the same as that in RDETA, while the gas production cost function is different because without the changing price of gas, the traditional algorithm cannot run. The cost function is as follows:

$C_{i,t}^{\text{DGP}}={\text{a}}_{i,t}^{\text{DGP}}{G}_{i,t}^{\text{DGP}2}+{\text{b}}_{i,t}^{\text{DGP}}{G}_{i,t}^{\text{DGP}}+{\text{c}}_{i,t}^{\text{DGP}}$

FIGURE 3

FIGURE 3. Power instantaneous price (cent).

FIGURE 4

FIGURE 4. Power exchanging flow (kw).

FIGURE 5

FIGURE 5. Heat exchanging flow (kw).

FIGURE 6

FIGURE 6. Gas exchanging flow (kw).

FIGURE 7

FIGURE 7. WholeEI asynchronous communication trigger times.

To differentiate, that device is called DGP in the distributed Newton algorithm but called EGG in RDETA.

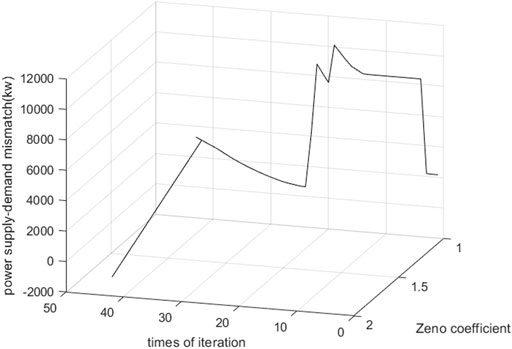
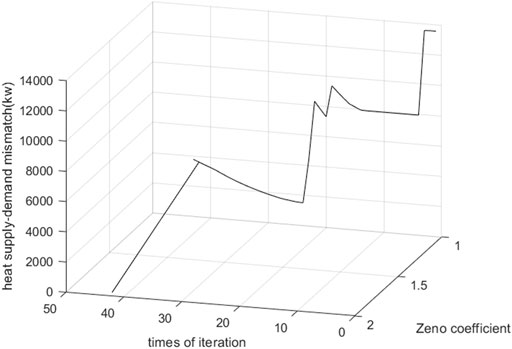
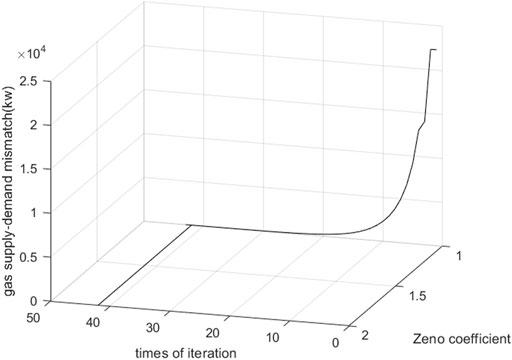
Figures 8–10 are the power-heat-gas mismatch. The Zeno coefficient is the decrease times of the Newton downhill factor. The traditional Newton distributed algorithm goes by 43 times of iteration with global communication to make all types of energy mismatch less than$500kw$. However, RDETA adopts four times of iterations with regional communication (the communication workload of regional communication is one-sixth to that of global communication because there are six sides in the graph of EI in this study.) to make all types of energy match zero. Therefore, RDETA adopts a workload 64.5 times less than that of the traditional distributed algorithm to realize a better energy management result than that in the traditional distributed algorithm. Compared with traditional centralized algorithms, communicating and computing pressure of the control center about RDETA is much less. Figure 11 is the times of communicating and computing pressure of the control center between traditional centralized algorithms and RDETA. As you can see, the communicating and computing pressure times between them are growing sharply with the growth of we-energy numbers. So RDETA is much more suitable for the large EI with lots of we-energies than traditional centralized algorithms.

FIGURE 8

FIGURE 8. Power supply-demand mismatch.

FIGURE 9

FIGURE 9. Heat supply-demand mismatch.

FIGURE 10

FIGURE 10. A gas supply-demand mismatch.

FIGURE 11

FIGURE 11. Times of communicating and computing pressure.

Figure 12 is the we-energy framework. Figure 13 is the EI framework. There are five we-energies in EI in this article. The price of gas is 8 cents per $kwh$. The price of coal is 6 cents per $kwh$. $sg$ for power and gas is0.1 times the initial measure value. $k-1$ means the initial condition. ${\Delta }_r$ is all 2. $I$ is all 4. $sg$ of the energy load is 0.1 times its initial value. Other data is in the following big table. Some data is the same in CCHP and GCHP, so we only introduce it once. The heat load does not change the whole time.

FIGURE 12

FIGURE 12. We-energy framework.

FIGURE 13

FIGURE 13. Energy Internet framework.

Conclusion

In this study, an innovative asynchronous communication energy management framework without iterations has been introduced for the future EI. Along with five we-energies, the EI system can better address the features and requirements of EI in a way with much less workload. By the combination of distributed algorithms and centralized algorithms and the partial differential equations, the cost of RDETA greatly decreases and its performance of that is obviously increased. Simulation results and theoretical identifications have demonstrated the effectiveness of it. However, cyber attacks and nonconvex issues are out of consideration in this study. So they need to address this in future work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author has written the whole article by himself.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.908199/full#supplementary-material

References

Abdella, J., Tari, Z., Anwar, A., Mahmood, A., and Han, F. (2021). An Architecture and Performance Evaluation of Blockchain-Based Peer-To-Peer Energy Trading. IEEE Trans. Smart Grid 12 (99), 1. doi:10.1109/TSG.2021.3056147

CrossRef Full Text | Google Scholar

Bahrami, S., and Sheikhi, A. (2016). From Demand Response in Smart Grid Toward Integrated Demand Response in Smart Energy Hub. IEEE Trans. Smart Grid 7 (2), 650–658.

Google Scholar

Can, W., Zhaohong, B., Qiuwei, W., Gengfeng, L., and Haipeng, X. (2021). Coordinated Post-Contingency Dispatch of Integrated Energy System With Multiple Participants Based on Distributed Energy Trading. Int. J. Electr. Power & Energy Syst. 130, 31. doi:10.1016/j.ijepes.2021.107011

CrossRef Full Text | Google Scholar

Huang, A. Q., Crow, M. L., Heydt, G. T., Zheng, J. P., and Dale, S. J. (2010). The Future Renewable Electric Energy Delivery and Management (FREEDM) System: The Energy Internet. Proc. IEEE 99 (1), 133–148. doi:10.1109/JPROC.2010.2081330

CrossRef Full Text | Google Scholar

Huang, B., Li, Y., Zhang, H., and Sun, Q. (2016). Distributed Optimal Co-Multi-Microgrids Energy Management for Energy Internet. IEEE/CAA J. Automatica Sinica 3 (4), 357. doi:10.1109/JAS.2016.7510073

CrossRef Full Text | Google Scholar

Kubli, M., Loock, M., and Wüstenhagen, R. (2018). The Flexible Prosumer: Measuring the Willingness to Co-Create Distributed Flexibility. Energy Policy 114, 540–548. doi:10.1016/j.enpol.2017.12.044

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 11 (99), 5339. doi:10.1109/TSG.2020.3005179

CrossRef Full Text | Google Scholar

Li, Y., Zhang, H., Liang, X., and Huang, B. (2019). Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inf. 15 (4), 2008–2022. doi:10.1109/tii.2018.2862436

CrossRef Full Text | Google Scholar

Liang, H., Zhang, L., Sun, Y., and Huang, T. (2021). Containment Control of Semi-markovian Multiagent Systems With Switching Topologies. IEEE Trans. Syst. Man, Cybern. Syst. 51 (99), 1–11. doi:10.1109/TSMC.2019.2946248

CrossRef Full Text | Google Scholar

Lin, C, E., and Viviani, G. L. (1984). Hierarchical Economic Dispatch for Piecewise Quadratic Cost Functions. IEEE Power Eng. Rev. 103, 1170. doi:10.1109/TPAS.1984.318445

CrossRef Full Text | Google Scholar

Lin, C. E., Chen, S. T., and Huang, C.-L. (1992). A Direct Newton-Raphson Economic Dispatch. IEEE Trans. Power Syst. 7 (3), 1149–1154. doi:10.1109/59.207328

CrossRef Full Text | Google Scholar

Lu, R., Hong, S. H., and Yu, M. (2019). Demand Response for Home Energy Management Using Reinforcement Learning and Artificial Neural Network. IEEE Trans. Smart Grid 10 (6), 6629–6639. doi:10.1109/tsg.2019.2909266

CrossRef Full Text | Google Scholar

Moeini-Aghtaie, M., Dehghanian, P., Fotuhi-Firuzabad, M., and Abbaspour, A. (2014). Multiagent Genetic Algorithm: An Online Probabilistic View on Economic Dispatch of Energy Hubs Constrained by Wind Availability. IEEE Trans. Sustain. Energy 5 (2), 699–708. doi:10.1109/tste.2013.2271517

CrossRef Full Text | Google Scholar

Pourbabak, H., Luo, J., Tao, C., and Su, W. (2017). A Novel Consensus-Based Distributed Algorithm for Economic Dispatch Based on Local Estimation of Power Mismatch. IEEE Trans. Smart Grid 9 (99), 1. doi:10.1109/TSG.2017.2699084

CrossRef Full Text | Google Scholar

Qin, X., Sun, H., Shen, X., Guo, Y., Guo, Q., and Xia, T. (2019). A Generalized Quasi-Dynamic Model for Electric-Heat Coupling Integrated Energy System with Distributed Energy Resources. Appl. Energy 251, 113270. doi:10.1016/j.apenergy.2019.05.073

CrossRef Full Text | Google Scholar

Sheikhi, A., Rayati, M., Bahrami, S., and Mohammad Ranjbar, A. (2015). Integrated Demand Side Management Game in Smart Energy Hubs. IEEE Trans. Smart Grid 6 (2), 675–683. doi:10.1109/tsg.2014.2377020

CrossRef Full Text | Google Scholar

Sun, J., Palade, V., Wu, X. J., Fang, W., and Wang, Z. (2013). Solving the Power Economic Dispatch Problem With Generator Constraints by Random Drift Particle Swarm Optimization. IEEE Trans. Industrial Inf. 10 (1), 222–232. doi:10.1109/TII.2013.2267392

CrossRef Full Text | Google Scholar

Sun, Q. (2019). Energy Internet and we-energy. Singapore: Springer-Verlag: Springer Nature.

Google Scholar

Sun, Q., Fan, R., Li, Y., Huang, B., and Ma, D. (2019). A Distributed Double-Consensus Algorithm for Residential We-Energy. IEEE Trans. industrial Inf. 15, 4830. doi:10.1109/TII.2019.2921431

CrossRef Full Text | Google Scholar

Sun, Q., Han, R., Zhang, H., Zhou, J., and Guerrero, J. M. (2015). A Multiagent-Based Consensus Algorithm for Distributed Coordinated Control of Distributed Generators in the Energy Internet. IEEE Trans. Smart Grid 6 (6), 3006–3019. doi:10.1109/tsg.2015.2412779

CrossRef Full Text | Google Scholar

Sun, Q., Zhang, Y., He, H., Ma, D., and Zhang, H. (2017). A Novel Energy Function-Based Stability Evaluation and Nonlinear Control Approach for Energy Internet. IEEE Trans. Smart Grid 8, 1195–1210. doi:10.1109/tsg.2015.2497691

CrossRef Full Text | Google Scholar

Wang, Y., Nguyen, T.-L., Xum, Y., Tran, Q. T., Xu, Y., Tran, Q.-T., et al. (2020). Peer-to-Peer Control for Networked Microgrids: Multi-Layer and Multi-Agent Architecture Design. IEEE Trans. Smart Grid 11 (6), 4688–4699. doi:10.1109/tsg.2020.3006883

CrossRef Full Text | Google Scholar

Wright, S. J. (1997). Primal-Dual Interior-Point Methods. Philadelphia, PA: SIAM.

Google Scholar

Wu, J., Zhang, B., Wang, K., Shao, J., Yao, J., Zeng, D., et al. (2015). Optimal Economic Dispatch Model Based on Risk Management for Wind‐integrated Power System. IET Generation, Transm. Distribution 9 (15), 2152–2158. doi:10.1049/iet-gtd.2015.0209

CrossRef Full Text | Google Scholar

Xu, T., Wu, W., Zheng, W., Sun, H., and Wang, L. (2018). Fully Distributed Quasi-Newton Multi-Area Dynamic Economic Dispatch Method for Active Distribution Networks. IEEE Trans. Power Syst. 33, 4253. doi:10.1109/TPWRS.2017.2771950

CrossRef Full Text | Google Scholar

Yile, L., Liu, F., and Mei, S. (2017). Distributed Real-Time Economic Dispatch in Smart Grids: A State-Based Potential Game Approach. IEEE Trans. Smart Grid 9 (5), 4194–4208. doi:10.1109/TSG.2017.2652919

CrossRef Full Text | Google Scholar

Yuang, X., Qingshan, X., Haiya, Q., and Li, C. (2022). Peer-to-Peer Energy Trading Considering the Output Uncertainty of Distributed Energy Resources. Energy Rep. 8, 567. doi:10.1016/j.egyr.2021.11.001

CrossRef Full Text | Google Scholar

Zhang, H., Li, Y., Gao, D. W., and Zhou, J. (2017). Distributed Optimal Energy Management for Energy Internet. IEEE Trans. Ind. Inf. 13 (6), 3081–3097. doi:10.1109/tii.2017.2714199

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q., Wang, J., and Yang, L. (2020a). Distributed Adaptive Dual Control via Consensus Algorithm in the Energy Internet. IEEE Trans. Industrial Inf. 17 (99), 1. doi:10.1109/TII.2020.3031437

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q., and Yang, L. (2020b). A Two-Stage Multi-Objective Optimal Scheduling in the Integrated Energy System with We-Energy Modeling. Energy 215, 119121. doi:10.1016/j.energy.2020.119121

CrossRef Full Text | Google Scholar