A Game Optimization Scheduling Strategy of Active Distribution Network With Multi-Microgrid Sharing Energy Storage

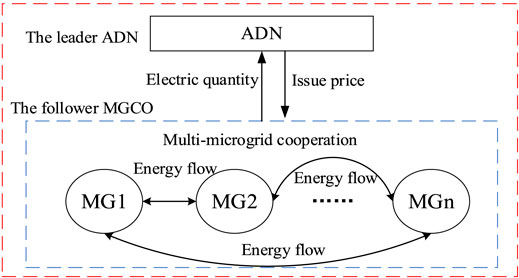
In a multi-microgrid grid-connected system, a MGCO is formed to participate in the optimization scheduling of the ADN by sharing ES, which can promote the efficient utilization of resources and obtain win–win interests for all participants. According to the complementary characteristics of ES behaviors and energy production–consumption of MGs, a game scheduling model of the ADN with the MGCO for sharing ES is established to obtain energy reciprocity and balance the interest of both parties. The ADN formulates the ToU price policy to maximize the operational benefits, and the MGCO responds to the price to obtain each member’s energy-dispatching strategy for minimizing the total operating costs. Furthermore, all members in the MGCO distribute the cooperation surplus based on the Shapley value method. The example results show that the proposed game model can balance the benefits between the ADN and multi-microgrid with sharing ES and maximize the mutual benefits of the MGCO through energy reciprocity.

1 Introduction

The ADN (active distribution network) can actively carry out flexible management of distributed generation, load, and ES, which makes it more open and interactive for new energy access and consumption. Distributed generations with new energy are usually connected to the ADN in the form of all kinds of MGs. ES can be used to improve the flexibility, economy, and security of power systems (Ruiz-Cortes et al., 2019; Dai et al., 2021; Li and Wang, 2021). However, the chaotic charge–discharge behaviors without coordination may cause considerable waste of resources from the overall perspective. According to the complementary characteristics of the ES behaviors and energy production–consumption of MGs, a multi-microgrid joint system with shared ES can be formed as an MGCO obtain energy reciprocity (Feng et al., 2018; Shi et al., 2022). Sharing ES and coalition mechanism in multi-microgrids may change the scheduling strategies and the benefits of the ADN. Consequently, this study is devoted to research on the optimal scheduling strategies of the ADN with the MGCO-sharing ES to promote efficient operation and energy reciprocity.

At present, there are abundant research results on the optimal scheduling of the ADN with MGs, but the scheduling with sharing ES has not been addressed much in literatures. In a study by Fu et al. (2020), an energy management framework of a hybrid AC/DC distribution system with MGs is established, and the benefit equilibrium of various entities is obtained by a master–slave game model. Marzband et al. (2018a) proposed an advanced retail electricity market model for the optimal operation of home MGs and the interaction with the ADN to encourage market participation and improve profits for all participants. In a study by Zhang et al. (2019), a novel data-adaptive robust optimization method for the ADN with renewables is proposed to enhance the economics of the system. Huang et al. (2021) constructed a double-layer distributed optimization model for multi-stakeholders with the ADN as the leader and MGs as the follower. In a study by Sheng et al. (2021), a novel scheduling method with demand response and user satisfaction is proposed to promote the power fluctuation damping and the renewable energy consumption. In a study by Liu et al. (2020), a novel distributed P2P trading method based on the Stackelberg game in the ADN is proposed to improve the economic and technical benefits. Gu (2019) proposed a general model of interactive games to gain more revenue with the cooperation between the MG and ADN. Wei et al. (2014) proposed a game-theoretic coalition formulation strategy for the MGs for minimizing power loss.

Moreover, the research on shared ES is also extensive. In studies by Liu et al. (2019a) and Yang et al. (2021), the energy sharing strategy is supported by a transactive energy mechanism in a regional integrated energy system to achieve distributed optimization of energy sharing. In a study by Cui et al. (2021), a novel bargaining-based benefit-sharing model is proposed for prosumers to share the benefits of energy cooperation based on their contributions. Xiao et al. (2022) proposed a novel ES sharing framework considering ES allocation for prosumers, which can reduce the electricity costs of prosumers and improve the practical feasibility. In a study by Liu et al. (2018a), a decision-making model of cloud ES operators and consumers is established to improve the economic benefits by using their complementary characteristics. In a study by He and Zhang (2021), an adaptive double-side auction mechanism is introduced to obtain the optimal market price for the game equilibrium to save energy-sharing costs and increase agent benefits. In a study by Marzband et al. (2018b), multiple home MGs are integrated into coalitions for gaining competitiveness in the market and obtaining the maximum profits by sharing ES. Tan et al. (2021) proposed a cooperative trading model that is based on a cooperative game, which can improve both the total gains and individual gains of MGs. In a study by Jeon and Hong (2019), an energy-sharing framework between the prosumer and consumer is proposed to handle double-energy spending problems. In a study by Liu et al. (2017), a P2P trading structure is proposed to integrate the PV prosumers into an energy-sharing zone for maximizing the economic benefits. However, the abovementioned studies are mainly focused on market trading in integrated energy systems or community MGs and are rarely related to ADN scheduling.

Based on the abovementioned research, this study proposed an energy optimization scheduling strategy for the ADN with multi-microgrid sharing ES. The main contributions are as follows:

1) An optimal dispatching strategy of the MGCO with shared ES is proposed to obtain energy reciprocity and maximize the mutual benefits of MGs by using their complementary characteristics of ES utilization.

2) A master–slave game model of the ADN with the MGCO is constructed. The price strategy of the ADN and the energy-dispatching strategy of the MGCO are optimized to promote the overall energy utilization and win–win interests for all participants.

2 Energy Reciprocity Strategy of the MGCO Sharing ES

The complementary characteristics of the ES behaviors and energy production–consumption are used to obtain energy reciprocity among MGs and improve the utilization rate of ES. Eq. 1 denotes the amount of residual electricity power before the MG i joins the energy mutual compensation:

$\{\begin{array}{l}\mathrm{\Delta }{P}_{i,B}^t=P_{i\text{,B}}^t-P_{i\text{,C}}^t\\ \mathrm{\Delta }{P}_{i,G}^t=P_{i\text{,G}}^t-P_{i\text{,D}}^t\end{array},(1)$

Energy reciprocity among MGs needs to satisfy the following principles: MGs can transfer or receive the residual electricity power with other members, but the total power exchange shall not exceed their electric power surplus or the shortage power. Eq. 2 represents the constraint conditions of energy reciprocity.

$\{\begin{array}{l}{\displaystyle \sum _{j=1,j\ne i}^n{D}_{ij}{P}_{ij}^t}\le \mathrm{\Delta }{P}_{i,B}^t\\ {\displaystyle \sum _{j=1,j\ne i}^n{D}_{ji}{P}_{ji}^t}\le \mathrm{\Delta }{P}_{i,G}^t\end{array}i=1,\mathrm{...},n,(2)$

where n is the number of MGCO members; ${\displaystyle \sum _{j=1,j\ne i}^n\left(D_{ji}{P}_{ji}^t-D_{ij}{P}_{ij}^t\right)}$ represents the reciprocal power in the coalition; $D_{ji}$ is a binary state variable of [0,1], represents whether transmit the power among MGs.

In the view of MGs, they may sell their energy surplus to the ADN for increasing the revenue. When the MGs are integrated into a coalition, the members obtain energy reciprocity by sharing ES. It seems that energy sharing is free for all members on the surface; however, according to the difference in the ADN’s purchase and sale price in each time sequence, energy reciprocity may greatly reduce the cost of power interaction between MGs and the ADN, and the cooperation surplus obtained by energy reciprocity will bring additional benefits for the coalition. If each member’s revenue is distributed by marginal contributions, the MGs may obtain higher revenues than their independent operation.

3 Optimal Scheduling Strategy of the ADN With Multi-Microgrid Sharing ES

When the MGCO joins in the scheduling of the ADN, the coalition mechanism may change the scheduling strategies and the benefits of the ADN. Since the two participants belong to different entities and have their own operating objectives, based on the game theory (Lee et al., 2015), a master–slave game scheduling relationship is formed with the ADN as the leader and the MGCO as the follower. The ADN implements price incentives with the objective of maximizing operation benefits, and the MGCO responds to the price and optimizes the energy-dispatching strategy to obtain the minimum cost. The cooperation benefits of the coalition can be distributed by the Shapley value method. The game scheduling framework of the ADN and MGCO is built as shown in Figure 1.

FIGURE 1

FIGURE 1. Game scheduling framework of the ADN with the MGCO.

4 Game Optimization Scheduling Model of the ADN With the MGCO Sharing ES

4.1 Optimization Model of the ADN

4.1.1 Objective

The objective is to minimize the total operation costs, including generation costs $C_{\text{G}}^{\text{ADN}}$, operation and maintenance costs of the units $C_{\text{OM}}^{\text{ADN}}$, power interaction costs with the upper grid $C_{\text{g}}$, and power interaction costs with the MGCO $C_{\text{PCC,MGCO}}$, as shown in Eq. 3.

$J_{\text{ADN}}=\min C_{\text{ADN}}=C_{\text{PCC,MGCO}}+C_{\text{G}}^{\text{ADN}}+C_{\text{OM}}^{\text{ADN}}+C_{\text{g}},(3)$

$\{\begin{array}{l}{C}_{\text{g}}={\displaystyle \sum _{t=1}^{24}\left({\lambda }_s^t\cdot P_{\text{ADN},b}^t-{\lambda }_b^t\cdot P_{\text{ADN},s}^t\right)}\\ C_{\text{PCC,MGCO}}={\displaystyle \sum _{t=1}^{24}\left({\rho }_b^t{P}_{\text{PCC,MGCO},s}^t-{\rho }_s^t{P}_{\text{PCC,MGCO},b}^t\right)}\\ C_{\text{G}}^{\text{ADN}}={\displaystyle \sum _{j=1}^k{\displaystyle \sum _{t=1}^{24}\left(a_{mj}{\left(P_{Gj}^t\right)}^2+b_{mj}{P}_{Gj}^t+c_{mj}\right)}}\\ C_{\text{OM}}^{\text{ADN}}={\displaystyle \sum _{j=1}^k{\displaystyle \sum _{t=1}^{24}{k}_{mj}{P}_{Gj}^t}}\end{array},(4)$

where k represents the number of units in the ADN.

4.1.2 Constraints

The constraint conditions of the ADN optimization model mainly include power flow constraints, output constraints of units, and electricity price constraints. The details are as follows:

$\begin{array}{l}\{\begin{array}{l}{P}_{i_1}-U_{i_1}{\displaystyle \sum _{j_1=1,j1\ne i_1}^{n_1}{U}_{j_1}\left(G_{i_1{j}_1}\cos {\delta }_{i_1{j}_1}+B_{i_1{j}_1}\sin {\delta }_{i_1{j}_1}\right)}=0\\ Q_{i_1}-U_{i_1}{\displaystyle \sum _{j_1=1,j_1\ne i_1}^{n1}{U}_{j_1}\left(G_{i_1{j}_1}\sin {\delta }_{i_1{j}_1}-B_{i_1{j}_1}\cos {\delta }_{i_1{j}_1}\right)}=0\end{array}{i}_1=\mathrm{1,2},\mathrm{...},n_1,\\ \end{array}(5)$

$\{\begin{array}{cc}0\le P{l}_{i_1,j_1}^t\le P{l}_{i_1,j_1}^{\max }& i_1,j_1=\mathrm{1,2},\mathrm{...},n_1\\ U_{i_1}^{\min }\le U_{i_1}\le U_{i_1}^{\max }& i_1\ne j_1\\ P_{Gj}^{\min }\le P_{Gj}^t\le P_{Gj}^{\max }& j=1,\mathrm{...},k\end{array},(6)$

$\{\begin{array}{l}{\rho }_s^t=\{\begin{array}{l}{\rho }_{sg},t\in T_g\\ {\rho }_{sp},t\in T_p\\ {\rho }_{sf},t\in T_f\end{array}\\ {\rho }_{sf}\ge {\rho }_{sp}\ge {\rho }_{sg}\end{array},(7)$

$\{\begin{array}{l}{\rho }_b^t=\{\begin{array}{l}{\rho }_{bg},t\in T_g\\ {\rho }_{bp},t\in T_p\\ {\rho }_{bf},t\in T_f\end{array}\\ {\rho }_{bf}\ge {\rho }_{bp}\ge {\rho }_{bg}\end{array},(8)$

where n₁ is the number of the nodes in the ADN.

4.2 Optimization Model of the MGCO

4.2.1 Objective

The objective function of the MGCO includes the total costs of gas turbine generation costs $C_{\text{MT}\mathrm{\Sigma }}$, power interaction costs $C_{\text{PCC,MGCO}}$, and the total costs of unit operation and maintenance $C_{\text{OM}\mathrm{\Sigma }}$, as shown in Eq. 9.

$J_{\text{MGCO}}=\min C_{\text{MGCO}}=\min \left(C_{\text{MT}\mathrm{\Sigma }}+C_{\text{PCC,MGCO}}+C_{\text{OM}\mathrm{\Sigma }}\right),(9)$

$\{\begin{array}{l}{C}_{\text{MT}\mathrm{\Sigma }}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t=1}^{24}{a}_{Mi}{\left(P_{\text{MT,}i}^t\right)}^2+b_{Mi}{P}_{\text{MT,}i}^t+c_{Mi}}}\\ C_{\text{PCC,MGCO}}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t=1}^{24}\left({\rho }_s^t{P}_{\text{PCC}i,\text{buy}}^t-{\rho }_b^t{P}_{\text{PCC}i,\text{sell}}^t\right)}}\\ C_{\text{OMΣ}\sum }={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{\displaystyle \sum _{t=1}^{24}{c}_{\text{OM,}j}^{\text{j}}{P}_{i,j}^t}}}\end{array},(10)$

where m represents the number of units in the MG.

4.2.2 Constraints

The constraint conditions of the MGCO optimization model mainly include power balance constraints, energy reciprocity constraints, tie-line power constraints, and SOC constraints of ES. The detailed constraints of each member in the MGCO are as follows:

$P_{\text{load,}i}^t=P_{\text{new,}i}^t+\left(P_{\text{PCC}i\text{,buy}}^t-P_{\text{PCC}i\text{,sell}}^t\right)+P_{\text{MT,}i}^t+{\displaystyle \sum _{j=1,j\ne i}^n\left(D_{ji}{P}_{ji}^t-D_{ij}{P}_{ij}^t\right)+\left(P_{i\text{,D}}^t-P_{i\text{,C}}^t\right)}i=\mathrm{1,2},\mathrm{...},n(11)$

$\{\begin{array}{l}{P}_{\text{PCC,}i}^{\min }\le P_{\text{PCC}i\text{,buy}}^t,P_{\text{PCC}i\text{,sell}}^t\le P_{\text{PCC,}i}^{\max }\\ P_{\text{MT,}i}^{\min }\le P_{\text{MT,}i}^t\le P_{\text{MT,}i}^{\max }\\ 0\le P_{i\text{,C}}^t,P_{i\text{,D}}^t\le P_i^{\text{Cap}}\\ {\text{SOC}}_i^{\min }{E}_i^{\text{Cap}}\le E_i^t\le E_i^{\text{Cap}}\\ E_i^t=E_i^{t-1}+\mathrm{\Delta }t\left({\eta }_i^{\text{C}}{P}_{i\text{,C}}^t-\frac{P_{i\text{,D}}^t}{{\eta }_i^{\text{D}}}\right)\end{array}i=\mathrm{1,2},\mathrm{...},n.(12)$

4.3 Distribution for the Cooperation Surplus Based on the Shapley Value Method

The Shapley value method is introduced for a fair distribution of cooperation surplus obtained by forming a coalition, which can be interpreted as the average value of marginal contribution related to all possible coalition types (Liu et al., 2018b). The income of member i distributed by the method is shown in Eq. 13.

$\{\begin{array}{l}v\left(i\right)={\displaystyle \sum _{s(i\in s_i)}\omega \left(\left|s\right|\right)\cdot \left[v\left(s\right)-v\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$i$}\right.\right)\right]}\\ \omega \left(\left|s\right|\right)=\frac{\left(n-\left|s\right|\right)!\left(\left|s\right|-1\right)!}{n!}\\ M{C}_i=v\left(s\right)-v\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$i$}\right.\right)\end{array}i=\mathrm{1,2},\mathrm{...},n,(13)$

where s represents the coalition set comprising all members; $v\left(i\right)$ is the revenue distributed for member i; $\left|s\right|$ is the subset number; $\omega \left(\left|s\right|\right)$ is the weight factor; $v\left(s\right)$ is the residual cooperation of coalition s; $v\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$i$}\right.\right)$ is the residual cooperation of sub-alliance excluding member i; and $M{C}_i$ is the marginal contributions of member i in the coalition s.

Cooperation surplus is defined as the difference in the total revenue between all member cooperation and their independent operation. According to the optimization model of the MGCO, the difference of benefits between coalition and independent operation is mainly caused by the model whether considering the energy reciprocity.

5 The Solution of the Proposed Game Model

First, the leader sets the initial price{${\rho }_s^0$, ${\rho }_b^0$}; the follower responds to the price to minimize the total operation cost (Eq. 9) with the constraints (Eqs 2, 11, 12) to obtain the optimal dispatching strategies $\left(P_{\text{PCC,MGCO,}b}^0,P_{\text{PCC,MGCO,}s}^0\right)$; the leader receives the strategies of the follower and re-optimizes the electricity price for minimizing the objective function (Eq. 3) with the constraints (Eqs 5–8), to obtain the new price $\left\{{\rho }_b^1,{\rho }_s^1\right\}$; the follower continues to respond to the price and obtains the new optimal dispatching strategies $\left\{P_{\text{PCC,MGCO,}b}^1,P_{\text{PCC,MGCO,}s}^1\right\}$. In this way, the optimal strategies of the participants in each round are solved by repeated alternating iterations. When the strategies of both sides in the game model are no longer changed, the Nash equilibrium state is achieved.

$\{\begin{array}{l}{\gamma }_1^{\ast }=\left\{{\rho }_s^{\ast },{\rho }_b^{\ast }\right\}=\arg \min J_{\text{ADN}}\left({\rho }_s,{\rho }_b,P_{\text{PCC,MGCO,}b}^{\ast },P_{\text{PCC,MGCO,}s}^{\ast }\right)\\ {\gamma }_2^{\ast }=\left\{P_{\text{PCC,MGCO,}b}^{\ast },P_{\text{PCC,MGCO,}s}^{\ast }\right\}=\arg \min J_{\text{MGCO}}\left({\rho }_s^{\ast },{\rho }_b^{\ast },P_{\text{PCC,MGCO,}b},P_{\text{PCC,MGCO,}s}\right)\end{array}.(14)$

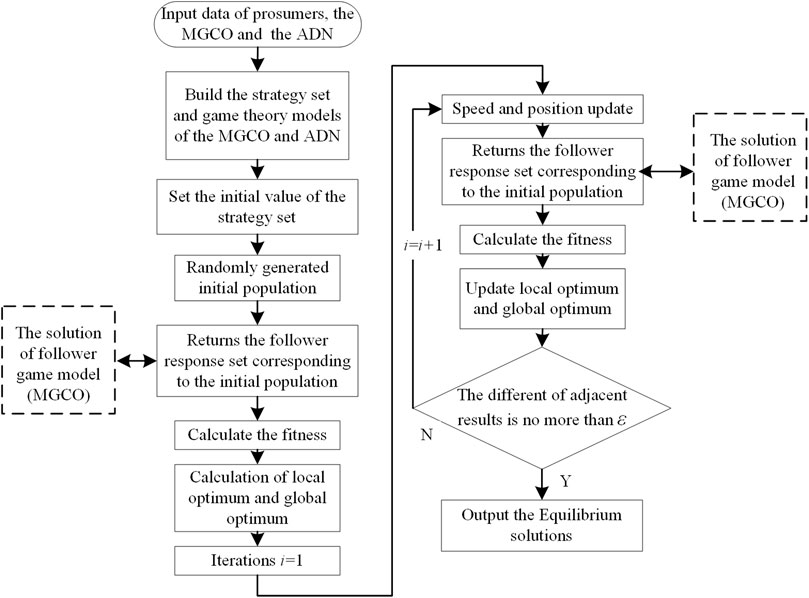
The proposed optimization scheduling model belongs to the category of bi-level optimization game. Based on the bi-level optimization theory (Liu et al., 2017), the solving process of the lower optimization model can be inserted into the upper model: the PSO algorithm is used to solve the upper optimization model within the lower optimization strategy solved using the Yalmip/Cplex toolbox. The optimal solutions are continuously updated with the iteration increase until Nash equilibrium solutions are obtained, as shown in Figure 2, and the main steps are as follows:

FIGURE 2

FIGURE 2. Solving process of the proposed game model.

Step 1: The PSO algorithm randomly generates the ADN’s initial price strategies with a certain number of populations, the initial iterations i = 1;

Step 2: The fitness is calculated considering the influence of the MGCO’s strategy solved using the Cplex toolbox;

Step 3: Local optimum and global optimum are updated, and iterations are updated (i = i +1);

Step 4: The speed and position of the populations are updated, and steps 2–4 are repeated until the difference of the price solutions in adjacent rounds is no more than ε (ε = 0.0001) to obtain the Nash equilibrium and then enter Step 5.

Step 5: The optimal price of the ADN’s strategy corresponding to the Nash equilibrium solution is output. The MGCO’s optimal strategy can be obtained by responding to the ADN’s optimal price.

6 Simulation Results and Analysis

6.1 Case Parameters

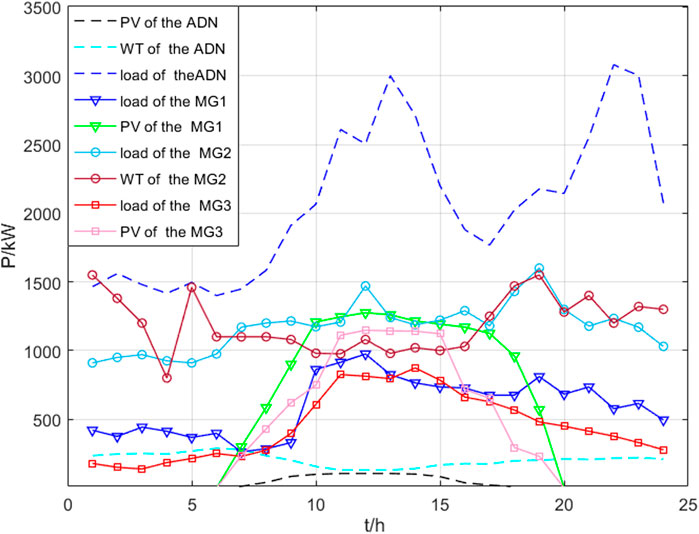
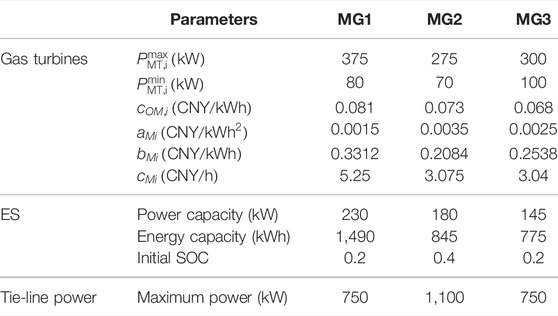
The ADN example is based on the IEEE14-bus system with the parameters shown in the study by Liu et al. (2019b). MG1, MG2, and MG3 are installed on nodes 6,11, and 13, respectively, and the three MGs are integrated into an MGCO. Node 1 is the common connection point between the ADN and the upper grid. PV units, wind turbines, and controllable units are installed on nodes 2, 3, and 8, respectively. The new energy output and load curves of MGs and the ADN on a typical day are shown in Figure 3. The operation and maintenance coefficients of new energies are 0.0096 and 0.0296, respectively. The electricity selling price of the upper grid is 0.55 CNY/kW. The parameters of the gas turbine and ES in MGs are shown in Table 1. The charging–discharging efficiency of ES is 0.95.

FIGURE 3

FIGURE 3. Load and new energy output of the ADN with MGs.

TABLE 1

TABLE 1. Relevant parameters of micro sources in MGs.

The parameters of the PSO algorithm are as follows: population number is 500, maximum iterations are 2000, range in particle velocity is from −1 to 1, learning factor is 1.5, initial inertia weight is 0.9, and final inertia weight is 0.4. The computer is configured as an intel Core i7 processor with a 1.8 GHz main frequency and 16 GB memory capacity.

6.2 Optimization Result Analysis

6.2.1 Analysis of Results Obtained by the Proposed Game Model

The optimized ToU price is shown in Table 2, and the simulation results of MGs are shown in Figure 4.

TABLE 2

TABLE 2. ToU price of the ADN after game equilibrium (CNY/kWh).

FIGURE 4

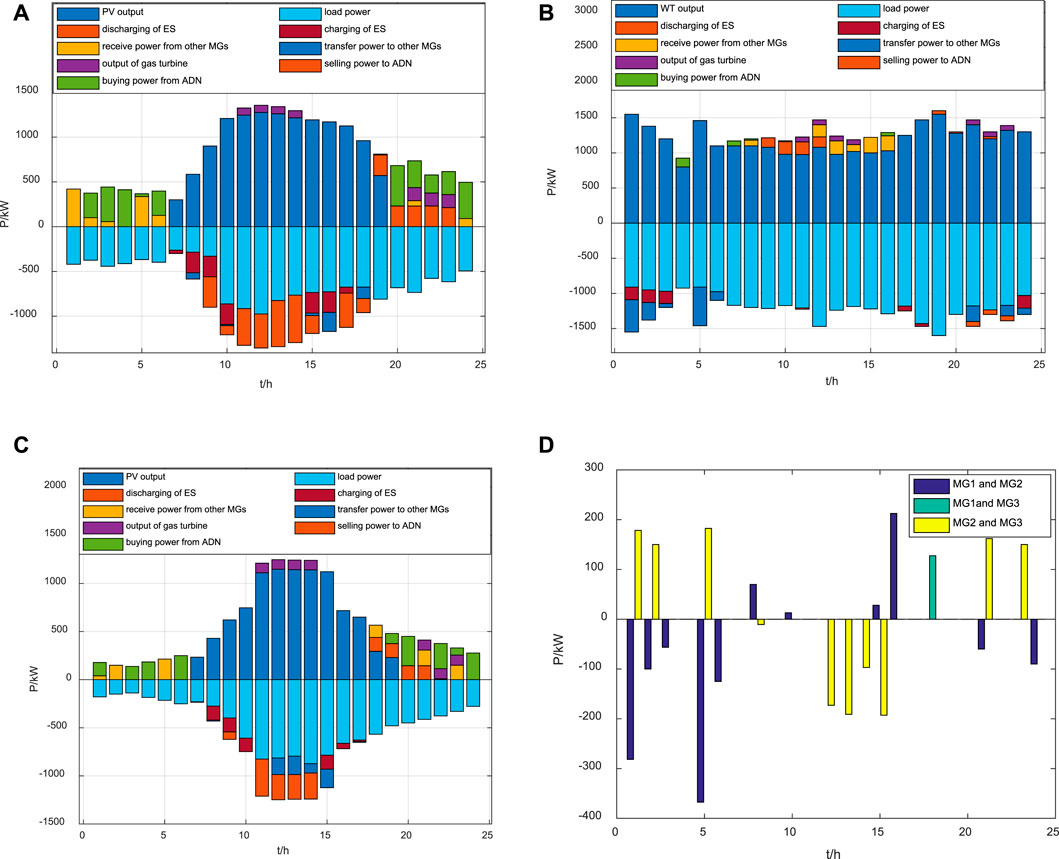
FIGURE 4. Simulation results of MGs. (A) Energy dispatching of MG1. (B) Energy dispatching of MG2. (C) Energy dispatching of MG3. (D) Energy reciprocity among MGs.

Taking MG1 as an example from Figure 4A, the dispatching strategy is as follows: MG1 is mainly supplied by its PV power. In 0:00–7:00 of valley periods, MG1 received the mutual power from other MGs, and the residual power shortage was balanced by the interaction with the ADN. In 19:00–24:00 of flat periods, MG1 is supplied by the gas turbine and purchasing electricity from the ADN after using the ES discharging. In 23:00–24:00 of flat periods, MG1 receives the reciprocal power from other MGs and then compensated by the gas turbine and ADN. In the periods of 7:00–19:00, PV power is enough. MG1 provides mutual assistance to other MGs and then sells residual electricity to the ADN.

The economic benefits and the peak-valley difference of both parties are shown in Table 3. The ADN implements the ToU price policy to stimulate the MGCO to adjust the energy-dispatching strategy for peak load clipping and valley filling, further reducing the peak-valley difference and obtaining win–win interests for both parties.

TABLE 3

TABLE 3. Economic benefits comparison of the ADN and the MGCO.

6.2.2 Mutual Benefits Analysis of the MGCO

Table 4 shows the comparison of the cost with all kinds of coalitions. The coalition type of MG1, MG2, and MG3 obtains the maximum cost saving amount, and the total operation cost is reduced to 4,802.21CNY. Furthermore, each MG’s cost is less than the cost of their independent operation. In addition, MG1 and MG3 are the PV-type MGs, but MG2 is a WT type. Power reciprocity is mainly found between MG2 and MG1 or between MG2 and MG3, as shown in Figure 4D. Therefore, when the benefits are distributed according to the Shapley value method, the cost saving amount shared for MG1 and MG3 is relatively small, while the value of MG2 is relatively more, and the marginal contribution of MG2 is higher than that of other MGs, as shown in Table 4.

TABLE 4

TABLE 4. Comparison of cost in various forms of cooperation (CNY).

7 Conclusion

A game optimization scheduling strategy of the ADN with multi-microgrid sharing ES is proposed in this study. The conclusions can be obtained by the following theoretical analysis and simulations:

1) For the complementary characteristics of the charging–discharging behaviors and energy production–consumption of MGs, the MGCO is formed to obtain energy reciprocity for maximizing the mutual benefit.

2) A master–slave game competition between the ADN and MGCO is proposed to promote overall energy utilization and obtain win–win interests for all participants.

The future study mainly focuses on considering the uncertainty of the new energy output for the proposed model.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

FL: conceptualization, methodology, validation, formal analysis, writing—review and editing, and project administration. XL: writing—review and editing, supervision, and project administration. ZF: methodology, software, validation, investigation, and data curation. LZ: validation, investigation, and funding acquisition.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 52007103, and in part by the Research Fund for Excellent Dissertation of China Three Gorges University under Grant 2021BSPY008.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cui, S., Wang, Y.-W., Liu, X.-K., Wang, Z., and Xiao, J.-W. (2021). Economic Storage Sharing Framework: Asymmetric Bargaining-Based Energy Cooperation. IEEE Trans. Ind. Inf. 17 (11), 7489–7500. doi:10.1109/TII.2021.3053296

CrossRef Full Text | Google Scholar

Dai, R., Esmaeilbeigi, R., and Charkhgard, H. (2021). The Utilization of Shared Energy Storage in Energy Systems: a Comprehensive Review. IEEE Trans. Smart Grid 12 (4), 3163–3174. doi:10.1109/TSG.2021.3061619

CrossRef Full Text | Google Scholar

Feng, X., Gu, J., and Guan, X. (2018). Optimal Allocation of Hybrid Energy Storage for Microgrids Based on Multi-Attribute Utility Theory. J. Mod. Power Syst. Clean. Energy 6 (1), 107–117. doi:10.1007/s40565-017-0310-3

CrossRef Full Text | Google Scholar

Fu, Y., Zhang, Z., Li, Z., and Mi, Y. (2020). Energy Management for Hybrid AC/DC Distribution System with Microgrid Clusters Using Non-cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 11 (2), 1510–1525. doi:10.1109/TSG.2019.2939586

CrossRef Full Text | Google Scholar

Gu, K. (2019). Research on the Cooperation-Competition Mechanism of Microgrid and Active Power Distribution Network Based on Game Theory. IOP Conf. Ser. Earth Environ. Sci. 267 (4), 042052–42052. doi:10.1088/1755-1315/267/4/042052

CrossRef Full Text | Google Scholar

He, L., and Zhang, J. (2021). A Community Sharing Market with PV and Energy Storage: an Adaptive Bidding-Based Double-Side Auction Mechanism. IEEE Trans. Smart Grid 12 (3), 2450–2461. doi:10.1109/TSG.2020.3042190

CrossRef Full Text | Google Scholar

Huang, Z., Zhang, Y., Zheng, F., Lin, J., An, X., and Shi, H. (2021). Day-ahead and Real-Time Energy Management for Active Distribution Network Based on Coordinated Optimization of Different Stakeholders. Power Syst. Technol. 45 (6), 2299–2308. doi:10.13335/j.1000-3673.pst.2020.0410

CrossRef Full Text | Google Scholar

Jeon, J. M., and Hong, C. S. (2019). “A Study on Utilization of Hybrid Blockchain for Energy Sharing in Micro-grid,” in 2019 20th Asia-Pacific Network Operations and Management Symposium (APNOMS), Matsue, Japan.

CrossRef Full Text | Google Scholar

Lee, J., Guo, J., Choi, J. K., and Zukerman, M. (2015). Distributed Energy Trading in Microgrids: a Game-Theoretic Model and its Equilibrium Analysis. IEEE Trans. Ind. Electron. 62 (6), 3524–3533. doi:10.1109/TIE.2014.2387340

CrossRef Full Text | Google Scholar

Li, X., and Wang, S. (2021). Energy Management and Operational Control Methods for Grid Battery Energy Storage Systems. CSEE J. Power Energy Syst. 7 (5), 1026–1040. doi:10.17775/CSEEJPES.2019.00160

CrossRef Full Text | Google Scholar

Liu, B., Liu, F., Zhai, B., and Lan, H. (2019). Investigating Continuous Power Flow Solutions of IEEE 14‐bus System. IEEJ Trans. Elec Electron Eng. 14 (1), 157–159. doi:10.1002/tee.22773

CrossRef Full Text | Google Scholar

Liu, H., Li, J., Ge, S., He, X., Li, F., and Gu, C. (2020). Distributed Day-Ahead Peer-To-Peer Trading for Multi-Microgrid Systems in Active Distribution Networks[J]. IEEE Access 8 (99), 66961–66976. doi:10.1109/ACCESS.2020.2983645

CrossRef Full Text | Google Scholar

Liu, J., Zhang, N., Kang, C., Kirschen, D. S., and Xia, Q. (2018). Decision-making Models for the Participants in Cloud Energy Storage. IEEE Trans. Smart Grid 9 (6), 5512–5521. doi:10.1109/TSG.2017.2689239

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2019). Hybrid Energy Sharing for Multiple Microgrids in an Integrated Heat-Electricity Energy System. IEEE Trans. Sustain. Energy 10 (3), 1139–1151. doi:10.1109/TSTE.2018.2861986

CrossRef Full Text | Google Scholar

Liu, N., Yu, X., Wang, C., Li, C., Ma, L., and Lei, J. (2017). Energy-sharing Model with Price-Based Demand Response for Microgrids of Peer-To-Peer Prosumers. IEEE Trans. Power Syst. 32 (5), 3569–3583. doi:10.1109/TPWRS.2017.2649558

CrossRef Full Text | Google Scholar

Liu, T., Tan, X., Sun, B., Wu, Y., and Tsang, D. H. K. (2018). Energy Management of Cooperative Microgrids: a Distributed Optimization Approach. Int. J. Electr. Power & Energy Syst. 96, 335–346. doi:10.1016/j.ijepes.2017.10.021

CrossRef Full Text | Google Scholar

Marzband, M., Azarinejadian, F., Savaghebi, M., Pouresmaeil, E., Guerrero, J. M., and Lightbody, G. (2018). Smart Transactive Energy Framework in Grid-Connected Multiple Home Microgrids under Independent and Coalition Operations. Renew. Energy 126, 95–106. doi:10.1016/j.renene.2018.03.021

CrossRef Full Text | Google Scholar

Marzband, M., Javadi, M., Pourmousavi, S. A., and Lightbody, G. (2018). An Advanced Retail Electricity Market for Active Distribution Systems and Home Microgrid Interoperability Based on Game Theory. Electr. Power Syst. Res. 157, 187–199. doi:10.1016/j.epsr.2017.12.024

CrossRef Full Text | Google Scholar

Ruiz-Cortes, M., Gonzalez-Romera, E., Amaral-Lopes, R., Romero-Cadaval, E., Martins, J., Milanes-Montero, M. I., et al. (2019). Optimal Charge/discharge Scheduling of Batteries in Microgrids of Prosumers. IEEE Trans. Energy Convers. 34 (1), 468–477. doi:10.1109/TEC.2018.2878351

CrossRef Full Text | Google Scholar

Sheng, H., Wang, C., Li, B., Liang, J., Yang, M., and Dong, Y. (2021). Multi-timescale Active Distribution Network Scheduling Considering Demand Response and User Comprehensive Satisfaction. IEEE Trans. Ind. Appl. 57 (3), 1995–2005. doi:10.1109/TIA.2021.3057302

CrossRef Full Text | Google Scholar

Shi, Z., Wang, W., Huang, Y., Li, P., and Dong, L. (2022). Simultaneous Optimization of Renewable Energy and Energy Storage Capacity with Hierarchical Control. Csee Jpes 8 (1), 95–104. doi:10.17775/CSEEJPES.2019.01470

CrossRef Full Text | Google Scholar

Tan, M., Zhou, Y., Wang, L., Su, Y., Duan, B., and Wang, R. (2021). Fair-efficient Energy Trading for Microgrid Cluster in an Active Distri-Bution Network. Sustain. Energy, Grids Netw. 26, 100453. doi:10.1016/j.segan.2021.100453

CrossRef Full Text | Google Scholar

Wei, C., Fadlullah, Z. M., Kato, N., and Takeuchi, A. (2014). GT-CFS: A Game Theoretic Coalition Formulation Strategy for Reducing Power Loss in Micro Grids. IEEE Trans. Parallel Distrib. Syst. 25 (9), 2307–2317. doi:10.1109/TPDS.2013.178

CrossRef Full Text | Google Scholar

Xiao, J.-W., Yang, Y.-B., Cui, S., and Liu, X.-K. (2022). A New Energy Storage Sharing Framework with Regard to Both Storage Capacity and Power Capacity. Appl. Energy 307, 118171. doi:10.1016/j.apenergy.2021.118171

CrossRef Full Text | Google Scholar

Yang, Z., Hu, J., Ai, X., Wu, J., and Yang, G. (2021). Transactive Energy Supported Economic Operation for Multi-Energy Complementary Microgrids. IEEE Trans. Smart Grid 12 (1), 4–17. doi:10.1109/TSG.2020.3009670

CrossRef Full Text | Google Scholar

Zhang, Y., Ai, X., Wen, J., Fang, J., and He, H. (2019). Data-adaptive Robust Optimization Method for the Economic Dispatch of Active Distribution Networks. IEEE Trans. Smart Grid 10 (4), 3791–3800. doi:10.1109/TSG.2018.2834952

CrossRef Full Text | Google Scholar

Glossary

PV Photovoltaic

SOC state-of-charge

WT wind power

MG microgrid

MGCO microgrid coalition

ES energy storage

ADN active distribution network

ToU time-of-use

$\mathit{\Delta }{\mathit{P}}_{\mathit{i},\mathit{B}}^{\mathit{t}}$, $\mathit{\Delta }{\mathit{P}}_{\mathit{i},\mathit{G}}^t$ power surplus and power shortage of MG i at t time after using its ES

${\mathit{P}}_{\mathit{i}\text{,C}}^{\mathit{t}}$, ${\mathit{P}}_{\mathit{i}\text{,D}}^{\mathit{t}}$ charging and discharging power of MG i at t time

${\mathit{P}}_{\mathit{i},\text{B}}^{\mathit{t}}$, ${\mathit{P}}_{\mathit{i},\text{G}}^{\mathit{t}}$ power surplus and power shortage of MG i at t time

${\mathit{P}}_{\mathit{j}\mathit{i}}^{\mathit{t}}$ active power transmitted from MG j to MG i at t time

${\mathit{\lambda }}_{\mathit{s}}^{\mathit{t}}$, ${\mathit{\lambda }}_{\mathit{b}}^{\mathit{t}}$ the selling price and purchasing price from the upper power grid in t time

${\mathit{P}}_{\text{ADN},\mathit{s}}^{\mathit{t}},{\mathit{P}}_{\text{ADN},\mathit{b}}^{\mathit{t}}$ selling and purchasing quantity with the upper power grid in t time

${\mathit{P}}_{\text{PCC,MGCO,}\mathit{s}}^{\mathit{t}}$, ${\mathit{P}}_{\text{PCC,MGCO,}\mathit{b}}^{\mathit{t}}$ total sale power and purchase power of MGCO at t period

${\mathit{\rho }}_{\mathit{s}}^{\mathit{t}},{\mathit{\rho }}_{\mathit{b}}^{\mathit{t}}$ selling and purchasing price of ADN at t time

${\mathit{a}}_{\mathit{m}\mathit{j}}$, ${\mathit{b}}_{\mathit{m}\mathit{j}}$, ${\mathit{c}}_{\mathit{m}\mathit{j}}$ generation cost coefficients of unit j

${\mathit{P}}_{\mathit{G}\mathit{j}}^{\mathit{t}}$ output of the unit j in t period

${\mathit{P}}_{\mathit{G}\mathit{j}}^{\mathit{min}}$, ${\mathit{P}}_{\mathit{G}\mathit{j}}^{\mathit{max}}$ lower and upper limits of output of the unit j

${\mathit{P}}_{\mathit{i}}\underset{\mathit{x}\to \mathit{\infty }}{\mathit{lim}}$, ${\mathit{Q}}_{\mathit{i}}$ injected active power and active power of node i

${\mathit{U}}_{\mathit{i}}\underset{\mathit{x}\to \mathit{\infty }}{\mathit{lim}}$, ${\mathit{U}}_{\mathit{i}}^{\mathit{min}}$, ${\mathit{U}}_{\mathit{i}}^{\mathit{max}}$ voltage amplitude and lower and upper limits of voltage for node i

${\mathit{G}}_{\mathit{i}\mathit{j}}\underset{\mathit{x}\to \mathit{\infty }}{\mathit{lim}}$, ${\mathit{B}}_{\mathit{i}\mathit{j}}$, ${\mathit{\delta }}_{\mathit{i}\mathit{j}}$ conductance, admittance, and voltage phase angle difference between node i and node j

$\mathit{P}{\mathit{l}}_{\mathit{i},\mathit{j}}^{\mathit{t}}$ active power of branch between i and j at t time in ADN

$\mathit{P}{\mathit{l}}_{\mathit{i},\mathit{j}}^{\mathit{max}}$ maximum transmission power of branch between i and j in ADN

${\mathit{T}}_{\mathit{g}},{\mathit{T}}_{\mathit{p}},{\mathit{T}}_{\mathit{f}}$ valley, flat, and peak periods of TOU price

${\mathit{\rho }}_{\mathit{s}\mathit{g}},{\mathit{\rho }}_{\mathit{s}\mathit{p}},{\mathit{\rho }}_{\mathit{s}\mathit{f}}$ selling price in valley, flat, and peak periods of ADN, respectively

${\mathit{\rho }}_{\mathit{b}\mathit{g}},{\mathit{\rho }}_{\mathit{b}\mathit{p}},{\mathit{\rho }}_{\mathit{b}\mathit{f}}$ buying price in valley, flat, and peak periods of ADN, respectively

${\mathit{a}}_{\mathit{M}\mathit{i}}$, ${\mathit{b}}_{\mathit{M}\mathit{i}}$, ${\mathit{c}}_{\mathit{M}\mathit{i}}$ gas turbine generation cost coefficients of MG i

${\mathit{P}}_{\text{MT,}\mathit{i}}^{\mathit{t}}$ output of gas turbine at t time in MG i

${\mathit{P}}_{\text{MT,}\mathit{i}}^{\mathit{min}}$,${\mathit{P}}_{\text{MT,}\mathit{i}}^{\mathit{max}}$ lower and upper limits of gas turbine output in MG i

${\mathit{P}}_{\text{PCC}\mathit{i},\text{buy}}^{\mathit{t}}$, ${\mathit{P}}_{\text{PCC}\mathit{i},\text{sell}}^{\mathit{t}}$ electricity purchasing quantity and selling quantity of MG i

${\mathit{c}}_{\text{OM,}\mathit{i}}^{\mathit{j}}$ operation and maintenance cost of unit j in MG i

${\mathit{P}}_{\mathit{i},\mathit{j}}^{\mathit{t}}$ output of unit j in MG i

${\mathit{P}}_{\text{load,}\mathit{i}}^{\mathit{t}}$ load power of MG i at t time

${\mathit{P}}_{\text{new,}\mathit{i}}^{\mathit{t}}$ new energy output of MG i at t time

${\mathit{P}}_{\text{PCC,}\mathit{i}}^{\mathit{min}}$, ${\mathit{P}}_{\text{PCC,}\mathit{i}}^{\mathit{max}}$ lower and upper limits of tie-line power between MG i and ADN

${\mathit{P}}_{\mathit{i}}^{\text{Cap}}$, ${\mathit{E}}_{\mathit{i}}^{\text{Cap}}$ power capacity and energy capacity of ES in MG i

${\text{SOC}}_{\mathit{i}}^{\mathit{min}}$ minimum SOC of ES in MG i

${\mathit{E}}_{\mathit{i}}^{\mathit{t}}$ residual capacity of ES in MG i at t time

${\mathit{\eta }}_{\mathit{i}}^{\text{C}},{\mathit{\eta }}_{\mathit{i}}^{\text{D}}$ charging and discharging efficiency of ES in MG i

${\mathit{\gamma }}_1^{\ast }$, ${\mathit{\gamma }}_2^{\ast }$ the equilibrium solutions of the leader and follower, respectively

${\mathit{\rho }}_{\mathit{s}}^{\ast },{\mathit{\rho }}_{\mathit{b}}^{\ast }$ electricity selling price and electricity purchasing price of the equilibrium solutions

${\mathit{P}}_{\text{PCC,MGCO,}\mathit{b}}^{\ast },{\mathit{P}}_{\text{PCC,MGCO,}\mathit{s}}^{\ast }$ electricity purchasing quantity and electricity selling quantity of the equilibrium solutions

argmin (·) set of variables when the objective is minimized