Hill Climbing Artificial Electric Field Algorithm for Maximum Power Point Tracking of Photovoltaics

In this paper, maximum power point tracking (MPPT) of a photovoltaic (PV) system is performed under partial shading conditions (PSCs) using a hill climbing (HC)–artificial electric field algorithm (AEFA) considering a DC/DC buck converter. The AEFA is inspired by Coulomb’s law of electrostatic force and has a high speed and optimization accuracy. Because the traditional HC method cannot perform global search tracking and instead performs local search tracking, the AEFA is used for a global search in the proposed HC-AEFA. The critical advantage of the HC-AEFA is that it is desirable performing local and global searches. The proposed hybrid method is implemented to derive an MPP by tuning the converter duty cycle, considering the objective function for maximizing the PV system extracted power. Its capability is evaluated and compared with well-known particle swarm optimization (PSO), considering standards, PSCs, and radiation changes conditions. The tracking efficiency for the most challenging shading pattern (third pattern) using the HC-AEFA, HC, AEFA and PSO is obtained at 99.93, 90.35, 98.85, 99.80%, respectively. The analysis of the population-based optimization process for different algorithms proved the HC-AEFA faster convergence at lower iterations than the other methods. So, the superiority of the proposed HC-AEFA subjected to different patterns is confirmed with higher tracking efficiency and global power peak, fewer fluctuations, higher convergence speed, and higher dynamic and Static-efficiency compared to the other methods.

1 Introduction

Maximum power point tracking (MPPT) has attracted the attention of many studies as an effective technique to maximize the extracted power of photovoltaic (PV) systems (Al‐Smadi et al., 2021). The MPPT aims to improve and optimize PV systems and maximize the efficiency of the PV plate to ensure the maximum electrical power generation with obtaining global Maximum power point (GMPP) tracking (Arabi Nowdeh et al., 2020; Nowdeh et al., 2019a). The PV plate has a nonlinear curve due to the continuous environmental conditions variations. The power-voltage characteristic has one MPP subjected to uniform radiation. Also, the power–voltage characteristic has a multi-peak PV configuration subjected to partial shading conditions (PSCs). The conventional methods such as open-circuit voltage (Fares et al., 2021), perturb and observe (Kavya and Jayalalitha, 2021), and hill-climbing (HC) (Alajmi et al., 2010), owing to their simplicity, may not be able to track the global maximum power point (GMPP). Despite their good performance regarding the global peak, the unconventional methods (Table 1) are challenging to implement, as they require more software and hardware equipment than the conventional algorithms (Arabi Nowdeh et al., 2020). Thus, several unconventional algorithms have been proposed to enhance simplicity and increase efficiency. Therefore, the traditional algorithms cannot identify the GMPP, and their tracking efficiency is low. The conventional and unconventional methods (or even a combination of them) are applied to improve the ability to track the GMPP. Many researchers have investigated the unconventional methods based on swarm intelligence-based algorithms due to their appropriate convergence towards the GMPP (Nowdeh et al., 2019b; Nasri et al., 2021). Therefore, swarm intelligence is more effective than the conventional methods for achieving the GMPP of the PV systems subjected to the PSCs.

TABLE 1

TABLE 1. State of the art of MPPT solutions.

Intelligent optimization algorithms are developed in MPPT tracking. In (Roy Chowdhury and Saha, 2010), a comparative PSO algorithm was proposed for finding the GMPP. In (Messai et al., 2011), a genetic algorithm integrated with fuzzy logic is developed for tracking the MPP of PV system. In (Miyatake et al., 2011), a new technique for GMPP tracking based on PSO was presented. The proposed method provides better results considering different PSCs; however, it is limited to multi-converter PV production systems. The particle swarm optimization (PSO) algorithm was implemented for tracking the global MPP (GMPP) considering the PSCs (Charin et al., 2021). The applicatins of the evoluationary algorithms in improving the performance of MPPT had been significantly increasing (Ahmed et al., 2022; Fan and Ma, 2022; Lousuwankun and Jantharamin, 2022; Rajesh et al., 2022; Wasim et al., 2022). In (Kulaksız and Akkaya, 2012), a genetic algorithm was proposed for determining the number of neurons in a multilayer artificial neural network for MPPT in a PV system. In (Jiang et al., 2013), the ant colony algorithm was applied for the MPPT solution of a PV system, and the method had an optimal performance for achieving the maximum power. In (Sundareswaran et al., 2014), the artificial bee colony (ABC) method was evaluated for MPPT in a PV system subjected to various shading patterns. It had a good performance and achieved the optimal global point. In (Mohanty et al., 2015), the grey wolf optimizer (GWO) algorithm was applied to track the MPP in a PV. In this study, the effectiveness of the GWO in achieving the maximum power with optimal efficiency was confirmed. In (Benyoucef et al., 2015), the ABC was applied for solving the MPPT subjected to shading pattern conditions. In (Teshome et al., 2016), the firefly algorithm (FA) was developed to design the MPPT for considering PSCs. In (Raman et al., 2016), the dragonfly algorithm (DA) was applied for tracking the MPP for a PV system in PSC. In (Fathy and Rezk, 2016), the mine blast algorithm (MBA) and teaching–learning-based optimization (TLBO) were applied to achieve the GMPP for PV considering PSC. In (Rezk and Fathy, 2017), the TLBO was applied to extract the maximum power of a PV system with PSCs. In (Hu et al., 2019), the improved PSO algorithm was evaluated to achieve the GMPP in a PV system with PSCs. In (Kaced et al., 2017), the bat algorithm was developed for MPPT subjected to different PSC patterns. The bat algorithm is effective for achieving the GMPP of PV systems. In (Re zk et al., 2017), the MPPT of a PV system was performed with different shading patterns based on the cuckoo search algorithm (CSA) method. In (Li et al., 2018), the improved gravitational search algorithm (IGSA) was applied to track the MPP for a PV system considering shading pattern conditions. In (Premkumar and Sowmy a, 2019), the MPPT solution of the PV system is developed using the whale optimization algorithm (WOA) in PSCs. In (Bhukya and Nandiraju, 2020), for the MPPT solution a new hybrid algorithm named grasshopper optimized fuzzy logic control (FLC) method is applied. In (Sukanya Satapathy and Kumar, 2020), weight of set point similarity is applied for the MPPT solution. In (Davoodkhani et al., 2020), designing of grey wolf optimizer-crow search algorithm (GWOCSA) to extract the MPP of PV system is developed in PSCs. In (Kumar et al., 2017a), a battery charging scheme from a solar photovoltaic is presented using a single sensor-based MPPT using Cauchy and Gaussian sine cosine optimization algorithm. In (Kumar et al., 2018), a novel reduced sensor strategy is presented for two-stage single-phase grid connected solar photovoltaic system with a battery using power normalized kernel least mean square algorithm. In (Kumar et al., 2019), damped fifth-order generalized integrator based control algorithm for grid-integrated PV system is studied via Human Psychology optimisation algorithm. In (Kumar et al., 2017b), an intelligent monkey king evolution algorithm for MPP detection under partially shaded condition in a PV system is presented. In (Kumar et al., 2017c), a whale optimization with differential evolution (WODE) method is used for MPPT solving in the dynamic and the steady-state conditions of a partial shading for PV system. The summarize of some studies with controller parameter, controller type, contribution and research gap is presented in Table 1.

So far, according to the literature review, various methods have been investigated to solve the problem of MPPT. This is because the optimization algorithms may work well in solving some of the photovoltaic system configurations in shading conditions to track the MPP. In addition, with the complexity of the problem, they cannot trace the global optimal point. So, today there is still a good incentive to use new optimization methods in the MPPT problem solution. Tracking the MPP in shading conditions due to the presence of multiple peaks in the photovoltaic characteristic, traditional algorithms such as the hill climbing (HC) method cannot detect the global MPP through the local point, which reduces the local the efficiency and overall effectiveness of the photovoltaic system. Therefore, combined methods can be developed to enhance the global MPP. This paper suggests a new MPPT method called hill climbing–artificial electric field algorithm (HC-AEFA) for MPPT of PV system solution with PSCs. The technique is efficient and straightforward. The AEFA is modeled based on Coulomb’s law related to electrostatic force (Anita Yadav, 2019). HC is one of the traditional MPPT methods for PV systems. In the HC-AEFA method, HC is first applied to determine the nearest local answer, and then the AEFA method is evaluated to determine the GMPP. The converter duty cycle is optimized by the combined method to achieve the MPP. The simulation results of the proposed HC-AEFA method were analyzed with different models, including the standard conditions, PSCs, and radiation changes, and compared with those of the HC, AEFA, and PSO methods. The results were evaluated according to the efficiency and convergence time of the algorithms and by comparing the values for the PV, and maximum extracted power among the different methods.

Highlights of this study are listed as follows:

• Global maximum power point tracking of a PV system under partial shading conditions

• Hill climbing (HC)–artificial electric field algorithm to solve the MPPT of PV system

• The superiority of the proposed MPPT method compared with HC, AEFA and PSO

• High tracking speed and efficiency of the proposed MPPT method to obtain the GMPP

• Better performance of the proposed MPPT algorithm compared with last studies

The rest of the paper is organized as follows. The modeling of the PV system is presented in Section 2. The standard and PSC patterns for PV are developed in Section 3. The proposed MPPT algorithm is described in Section 4. The simulation results of different patterns for MPPT solution are presented in Section 5. The results and findings of the paper are outlined in the conclusion section in Section 6.

2 PV Module Under PSCs

The PSC creates multiple power peaks (local and global) in the power-voltage characteristic of the PV. Therefore, it is vital to achieving the MPP subjected to PSCs to maximize PV efficiency. The selected PV module is considered ASMS-167P. The 2S PV parameters applied in this study include GMPP = 167 W, the voltage of the open circuit is 41.7 V, the voltage corresponds to maximum power is 33.4 V, the current of a short circuit is 5.18 A, the current corresponds to maximum power is 5 A, the voltage temperature coefficient is assumed at –0.13 V/°C, and the current’s temperature coefficient is 0.0025 A/°C (Shannan et al., 2013).

In this section, four different models are presented for evaluating the performance of the proposed MPPT method. The patterns are characterized by the 2S configuration (two modules with a series connection). The uniform radiation was 1000 W/m². The first, second, and third patterns correspond to the standard test condition (STC) with GMPP of 331.8 W, PSC with 1,000- and 500-W/m² radiation with GMPP of 182.54 W, and PSC with 300- and 800-W/m² radiation with GMPP of 133.75 W. In the fourth pattern, the conditions for radiation changes are as follows: the modules’ radiation is 800 and 500 W/m² in the first temporal step with MPP of 180.20 W, 600 and 300 W/m² in the second temporal step with GMPP of 108.20 W, and 400 and 200 W/m² in the third temporal step with GMPP of 70.62 W, respectively. Figure 1, show the power-voltage (P-V) and current-voltage (I-V) characteristics for the different patterns.

FIGURE 1

FIGURE 1. PV’s P–V and I–V characteristics at the four patterns.

3 Proposed MPPT Method

The proposed HC-AEFA for optimal tracking of the MPP is presented in various templates. In this method, the HC method is first applied to find the nearest local point, and then the charged particle search method is used to determine the GMPP. Subsequently, the HC-AEFA is described to solve the MPPT. The under-study system includes a PV configuration, a DC/DC buck converter, and load, as depicted in Figure 2. The power of PV is computed using multiplying the calculated voltage and current of the PV, and then the calculated PV power is entered into the MPPT system. Fitness is defined as maximizing the PV system’s power, which is implemented by sampling the voltage and current and determining the best duty cycle of the converter via the proposed method.

FIGURE 2

FIGURE 2. Schematic of MPPT solution system.

3.1 Hill Climbing

The hill climbing (HC) method is like the well-known traditional method of perturb and observation method. The photovoltaic voltage is adjusted to track the maximum voltage regulation point (VMPP) in this method. The photovoltaic output voltage is disturbed by creating a slight increase that changes the power in ∆P. The optimum point corresponding to the maximum power is continuously tracked and updated until the maximum power point is given as dP_PV/dV = 0. The current value of photovoltaic power (P_PV(k)) is continuously compared with the previously calculated value of photovoltaic power (P_PV(k-1)). When the two values ​​are the same, the controller recalculates the voltage and current of the photovoltaic and looks for a point to extract more power for it. Suppose the photovoltaic power fluctuates at the MPP and the duty cycle of the converter changes (Anita Yadav, 2019). Therefore, based on this method, the optimal point to achieve the maximum power of the photovoltaic can be obtained by applying a slight voltage disturbance.

3.2 Artificial Electric Field Algorithm

The artificial electric field algorithm (AEFA) is modeled based on Coulomb’s law in electrostatic force. This law describes the electrostatic reactions between the electrical charges. The magnitude of the electrostatic force is directly related to the magnitude of the charges and is inversely associated with the distance square among them. In the AEFA, the charged particles are selected as agents, and each agent’s resistance is evaluated based on their charges. The AEFA algorithm is modeled based on electrostatic attraction force. In this way, the charged particle with the highest amount of electric charge, with higher power of attraction force, pulls the particles towards it and moves in search spaces. The first law of Coulomb describes that the particles repel each other, and otherwise, the particles pull each other. The second law of Coulomb also states that there is an attractive force among opposing charges and a repulsive force between exact name charges, which is directly related to the multiplication of the charges and inversely related to the distance between them. Moreover, the motion law states that the velocity of each particle is defined as the sum of the last velocities to the velocity changes, or the acceleration of each particle is defined as inserted force divided by its mass.

Suppose the ith particle position considering d-dimension searching as ($x_i=(x_i^1,x_i^1,\mathrm{...},x_i^d),i=\mathrm{1,2},\mathrm{...},N$). The best position with the best fitness obtained from particles is determined. The best value position of the fitness achieved by any particle i is defined by (Anita Yadav, 2019) as follows.

$p_i^d(t+1)=\{\begin{array}{c}{p}_i^d\left(t\right); \mathrm{if} f\left(p_i\left(t\right)\right)<f\left(x_i(t+1)\right)\\ x_i^d(t+1);\mathrm{if} f\left(x_i(t+1)\right)\le f\left(p_i\left(t\right)\right)\end{array}.(1)$

Note that the optimal fitness is defined as P_best = X_best. The force of the charge i inserted by the charge j is calculated by (Anita Yadav, 2019) as follows.

$F_{ij}^d\left(t\right)=K\left(t\right)\frac{Q_i\left(t\right)Q_j\left(t\right)(p_j^d\left(t\right)-x_i^d\left(t\right))}{R_{ij}\left(t\right)+\epsilon },(2)$

Where Q_i(t) and Q_j(t) refer to the charged particles of i and j, K(t) indicates the constant of Coulomb, $\epsilon$ is a small constant, and R_ij (t) is defined as Euclidean distance among two charged particles of i and j is calculated by (Anita Yadav, 2019) as follows.

$R_{ij}\left(t\right)=\Vert X_i\left(t\right),X_j\left(t\right){\Vert }_2.(3)$

The K(t) is based on the iteration number and maximum iteration (max_iter), which is defined by (Anita Yadav, 2019) as expressed as follows.

$K\left(t\right)=K_{0}ex{p}^{(-\alpha \frac{iter}{\mathit{max}\_iter})},(4)$

Where α refers to the parameter and K₀ is the initial value. To explore the AEFA, first, the Coulomb constant value is considered a significant value. Then this value has a decreasing trend to control the accuracy of the AEFA by increasing the iteration. The inserted electric force on particle i via the other particles is defined in d search space at time t as follows adapted from (Anita Yadav, 2019).

$F_i^d\left(t\right)={\displaystyle \sum }_{j=1,j\ne i}^{N}rand\left(\right)F_{ij}^d\left(t\right),(5)$

Where rand () refers to a uniform number randomly in [0, 1], and this value is applied to provide a nature randomly to the AEFA. N indicates the number of the particles, and F_i refers to the force inserted on the charged particle i. Adapted from Anita Yadav (2019). The particle i electrical force in dth dimension search space is defined by

$E_i^d\left(t\right)=\frac{F_i^d\left(t\right)}{Q_i\left(t\right)}.(6)$

So, applying the 2nd Newton law named motion law, the particle i acceleration is defined by

$a_i^d\left(t\right)=\frac{Q_i\left(t\right)E_i^d\left(t\right)}{M_i\left(t\right)}.(7)$

M_i(t) refers to the particle i mass at iteration t. The velocity of the charged particle and its position are updated by (Anita Yadav, 2019).

$V_i^d(t+1)=rand\left(\right)\text{∗}{V}_i^d\left(t\right)+a_i^d\left(t\right),(8)$

$X_i^d(t+1)=X_i^d\left(t\right)+V_i^d(t+1).(9)$

The fitness should have a downward or upward trend for the minimization or maximization problem, respectively [40s].

$Q_i\left(t\right)=Q_i\left(t\right);\forall i,j=\mathrm{1,2},\mathrm{...},N,(10)$

$Q_i\left(t\right)=\frac{q_i\left(t\right)}{{{\displaystyle \sum }}_{i=1}^N{q}_i\left(t\right)},(11)$

$q_i\left(t\right)=\text{exp}\left(\frac{Fi{t}_i\left(t\right)-Worst\left(t\right)}{Best\left(t\right)-Worst\left(t\right)}\right),(12)$

Where Fit_i refers to the fitness of particle i. The Best (t) and Worst (t) values of fitness for the fitness maximization are formulated by

$Best\left(t\right)=\max \left(Fi{t}_j\left(t\right)\right);\forall j=\mathrm{1,2},\mathrm{...},N,(13)$

$Worst\left(t\right)=\min \left(Fi{t}_j\left(t\right)\right);\forall j=\mathrm{1,2},\mathrm{...},N.(14)$

For the problem with the minimization approach, the best (t) and worst (t) values of fitness are presented by

$Best\left(t\right)=\min \left(Fi{t}_j\left(t\right)\right);\forall j=\mathrm{1,2},\mathrm{...},N,(15)$

$Worst\left(t\right)=\max \left(Fi{t}_j\left(t\right)\right);\forall j=\mathrm{1,2},\mathrm{...},N.(16)$

3.3 Hybrid HC-AEFA

Every day new algorithms are presented to solve optimization problems with advantages and disadvantages. No algorithm performs well in most optimization problems and may no longer perform well in solving optimization problems. Therefore, in solving the MPPT problem, the presented algorithms can have different functions. This paper uses a hybrid method based on the AEFA to improve the HC method in optimal global search. The MPPT algorithm based on HC-proposed AEFA seeks to adjust the duty cycle d to extract the MPP optimally. In Figure 3, the flowchart of the hybrid HC-AEFA is depicted for the MPPT solution. The HC method is one of the traditional MPPT methods for PV systems. In the hybrid HC-AEFA, the HC method is first applied to obtain the nearest local solution, and then the AEFA method is implemented to determine the GMPP. The converter duty cycle (d) is optimally defined via the combined method to achieve the MPP. The objective function of the problem involves maximizing the PV system’s power, which is implemented by sampling the voltage and current and determining the best duty cycle of the converter for the proposed method. If disturbance ($\delta$) is minimal, a late convergence may happen before the state is changed to the combined approach. If $\delta$ is too big, the closest peak (local peak, LP) can be rejected. Most HC methods cannot achieve the global peak. So, the hybrid method is applied to search for an LP, and the duty cycle determined optimally via this method is considered the primary value for the AEFA. The steps involving the HC-AEFA in MPPT solution are presented as follows:

• Step 1) The HC is operated to track the PV’s MPP. The PV output voltage is disturbed by creating a slight increase that changes the power in ∆P (power change). The optimum point corresponding to maximum power is continuously tracked and updated until the maximum power point is given as dP_pv/dV = 0.

• Step 2) The present value of PV power (P_pv(k)) is continuously compared with the previously calculated value of photovoltaic power (P_pv (k-1)). When the two values ​​are the same, the MPPT controller looks for a point to extract more power.

• Step 3) If $\mathit{\Delta }{P}_{PV}>0$, d is tuned with the step size increase of the voltage disturbance and if $\mathit{\Delta }{P}_{PV}<0$, d is adjusted by decreasing the step size in the HC.

• Step 4) Initialize the AEFA parameters as $K_0$, $\alpha$, $D$, pop size and iteration number.

• Step 5) In this step, the d determined using the HC is considered the initial value for the AEFA operation.

• Step 6) Calculate the PV power ($P_{PV}$) for each charged particle.

• Step 7) Determine the optimal member of the charged particles. In this step, the optimal charged particle is considered the best particle corresponding to the maximum PV power ($P_{PV}$).

• Step 8) Generate new positions. In this step, the charged particles create a new position in the search space if they are pursued. The duty cycle d is tuned with the step size increasing/decreasing (voltage disturbance) as follows (Inspired by Eq. 7 in AEFA):

$d\left(k\right)=d\left(k\right)+\delta ; \text{if} P_{PV}\left(k\right)>P_{PV}\left(k-1\right)(17)$

$d\left(k\right)=d\left(k\right)-\delta ; \text{if} P_{PV}\left(k\right)<P_{PV}(k-1)(18)$

FIGURE 3

FIGURE 3. Proposed combined HC-AEFA method for solving the MPPT problem.

Here, d(k) refers to the duty cycle at iteration k, and $\delta$ represents the size of the disturbance step at the present position selected after an additional simulation, $P_{PV}$ is PV power, and $\delta$ refers to the disturbance.

• Step 9) Examine the feasibility of the new position for each charged particle. If the particle’s new position is possible, the charged particle updates its position; otherwise, it remains in the current position and does not move towards the newly created position.

• Step 10) Calculate the PV power for the new charged particle positions. In this step, the merit value ($P_{PV}$) is calculated for each member of the newly updated population.

• Step 11) Determine the best solution. Evaluating and comparing the PV power in steps 5–8 indicate that the solution is replaced with a better new solution than the one obtained in step 7.

• Step 12) If the convergence conditions are satisfied (achieving maximum PV power and max iterations of the AEFA), the d with higher PV power is determined to be the optimal solution, and the AEFA is stopped. Otherwise, returning to the AEFA in step 5.

In this paper, the superiority of the HC-AEFA is compared with HC, AEFA and well-known particle swarm optimization methods in MPPT solution. The parameters K₀ and $\alpha$ are assumed equal to 500 and 30 for the AEFA algorithm. $c_1,c_2,w_{\text{min}},$ and $w_{\text{max}}$ are set at 2, 2, 0.1, and 0.9 for PSO algorithm. The similar population size of 6 and maximum number of iterations of 30 are considered in both algorithms. The parameters of the AEFA and PSO Algorithms are selected based on the reference paper and the trial and error method to achieve the best results for each algorithm. Also, the population size and iteration are considered equal based on the trial and error method to achieve the best results for each algorithm.

4 Results and Findings

The results for tracking the MPP in PV system in different conditions such as STC, PSC, and radiation changes (Section 3) obtained using the combined HC-AEFA method with the buck converter are presented. The capability of the HC-AEFA is evaluated using various models. The converter parameters are as follows: fs = 50 kHz, C = 470 µF, L = 6.8 mH, and R = 80 Ω (Shannan et al., 2013).

4.1 Results for the First Pattern (Standard Conditions)

This section investigates the HC-AEFA-based MPCT problem for MPPT solution considering the standard conditions with uniform radiation (1000 W/m² and 25°C). To validate the HC-AEFA method, this problem was also solved using the AEFA, HC, and PSO methods, and the results were compared. Figure 4 show the simulation results, e.g., the power, voltage, current, and the converter duty-cycle curves. The results indicated that the HC-AEFA method reached the global peak value with fewer oscillations and higher velocities than the HC, AEFA, and PSO methods. Furthermore, while the HC method was unable to track the GMPP, the AEFA and PSO methods reached the global peak along with the proposed method. Therefore, the proposed method performed better than the HC method in the MPPT.

FIGURE 4

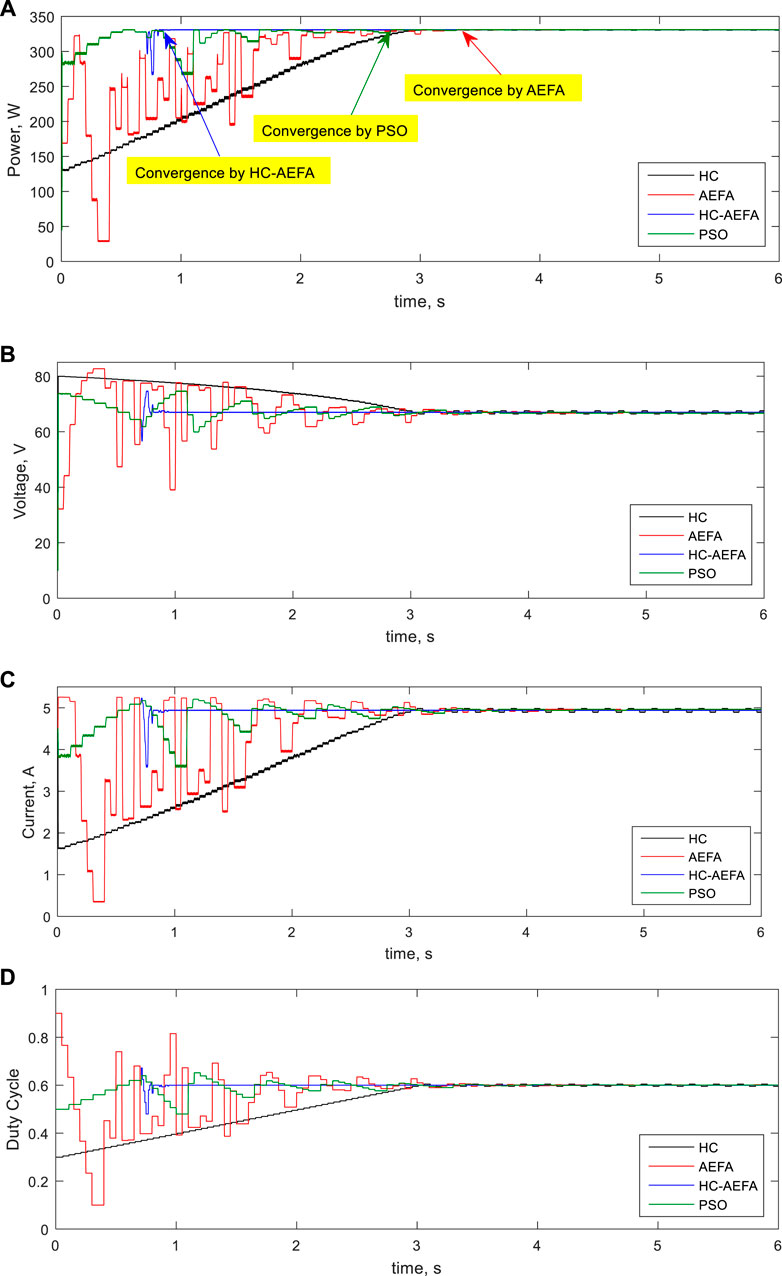
FIGURE 4. Simulation waveforms at the first pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) PV output power, (B) PV output voltage, (C) PV output current, and (D) converter duty-cycle curves.

Figure 5 presents the static and dynamic-efficiency curves of the MPPT for the first pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods, respectively. As shown, the proposed method had higher efficiency than the other methods. The results proved the more static- and dynamic efficiency of the proposed HC-AEFA than the HC, AEFA, and PSO methods. So, the improvement of the HC performance based on the AEFA in problem-solving is confirmed.

FIGURE 5

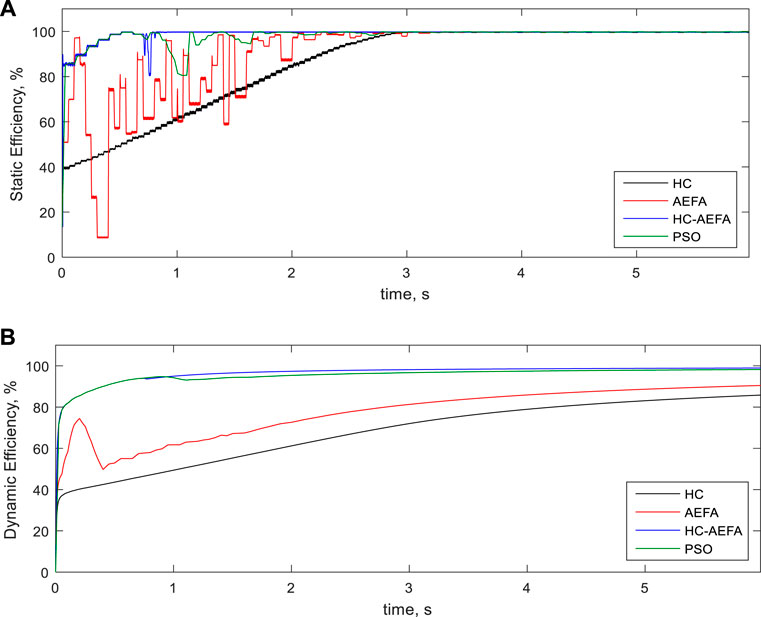
FIGURE 5. Efficiency curves at the first pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) Static-efficiency, and (B) Dynamic- efficiency.

Figure 6 shows the population optimization process in different ways. The proposed method converged to the optimal global value in iteration 5. The AEFA and PSO methods converged to the optimal values in iterations 9 and 8, respectively. The results showed the better performance of the HC-AEFA in achieving GMPP with a fast convergence rate in comparison with the AEFA and PSO methods. Therefore, the convergence rate of the proposed method was higher than those of the other methods.

FIGURE 6

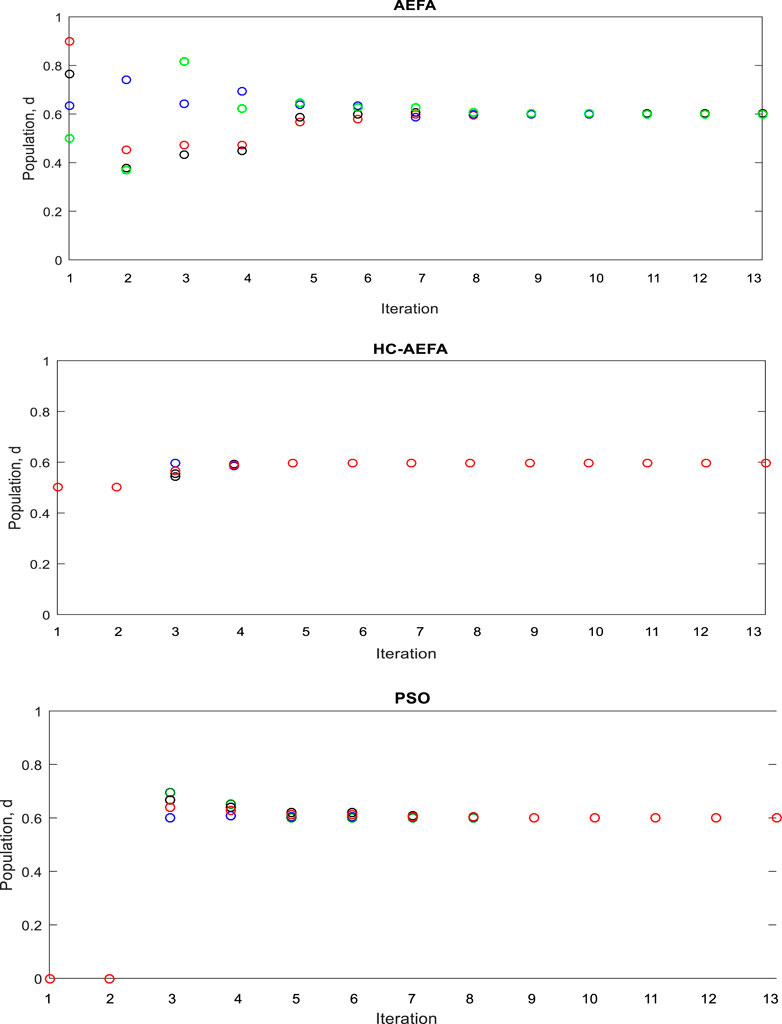
FIGURE 6. Particles’ positions in each iteration for the HC-AEFA, HC, AEFA, and PSO methods in the case of the first pattern.

Table 2 presents the numerical results for the performance of the different methods in the case of the first pattern (standard conditions). The HC-AEFA, AEFA, and PSO-based MPPTs obtained the maximum power, and HC cannot be able to track the GMPP. The tracking efficiencies using HC-AEFA, HC, AEFA, and PSO is obtained at 99.97, 99.82, 99.86 and 99.91%, respectively. Also, the HC-AEFA is converged to the best solution in 0.81 s, and AEFA and PSO have achieved the best solutions in 3.44 and 2.85 s, respectively. However, the results indicated that the proposed HC-AEFA method had the fewest convergence iterations and the highest convergence speed.

TABLE 2

TABLE 2. Results for the different MPPT methods in first pattern.

4.2 Results for the Second Pattern (Under PSCs)

The effectiveness of the HC-AEFA for MPPT solution with PSCs was investigated for the second pattern. In this pattern, the radiation of the modules was 1,000 and 500 W/m². The global peak value was 182.54 W. The capability of the HC-AEFA was compared with that of the HC, AEFA, and PSO methods. The results are shown in Figure 7. The HC method was unable to track the global peak power. Compared with the AEFA and PSO methods, The proposed HC-AEFA method had fewer oscillations and achieved stability and faster global peak power.

FIGURE 7

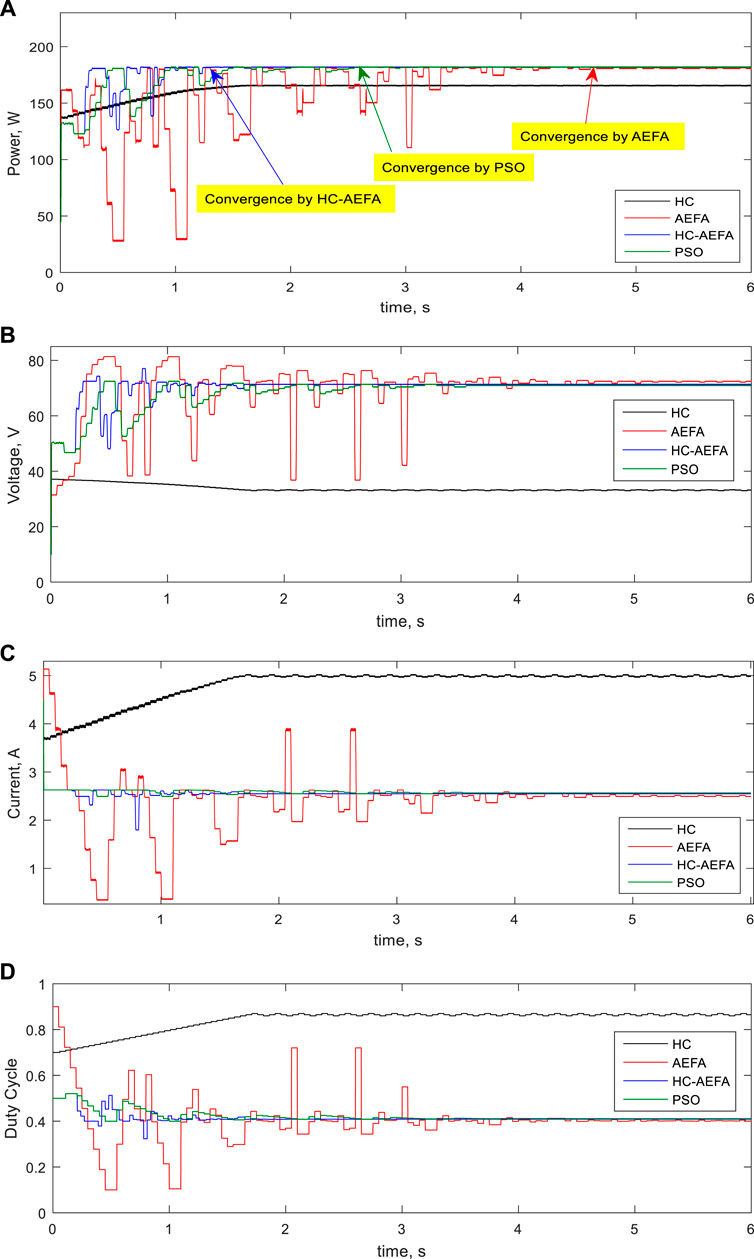
FIGURE 7. Simulation waveforms at the second pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) PV output power, (B) PV output voltage, (C) PV output current, and (D) converter duty-cycle curves.

Figure 8 show the simulation’s dynamic and static efficiencies for the second pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods. The HC-AEFA method had higher dynamic and static efficiencies than the other methods, considering the shading conditions. The results proved the more static- and dynamic efficiency of the proposed HC-AEFA than the HC, AEFA, and PSO methods. So, the improvement of the HC performance based on the AEFA in problem-solving is confirmed.

FIGURE 8

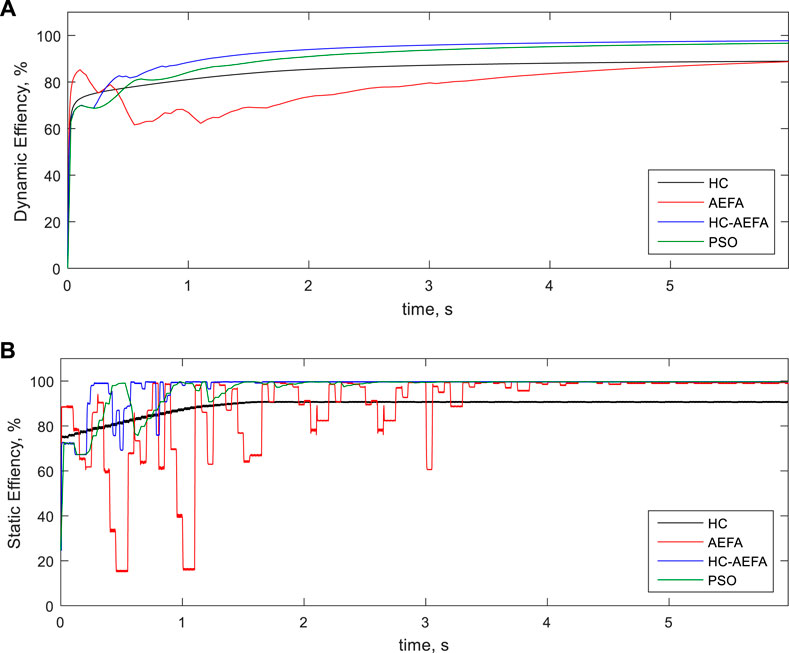
FIGURE 8. Efficiency curves at the second pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) Dynamic -efficiency, and (B) Static-efficiency.

Figure 9 shows the algorithm-based population optimization process for the various MPPT methods in the case of the second pattern. For the AEFA, PSO, and proposed HC-AEFA methods, the population converged to the global peak value in iterations 12, 8, and 5, respectively, indicating that the HC-AEFA method had the highest tracking speed. The results showed the better performance of the HC-AEFA in achieving GMPP with a fast convergence rate compared to the AEFA and PSO methods.

FIGURE 9

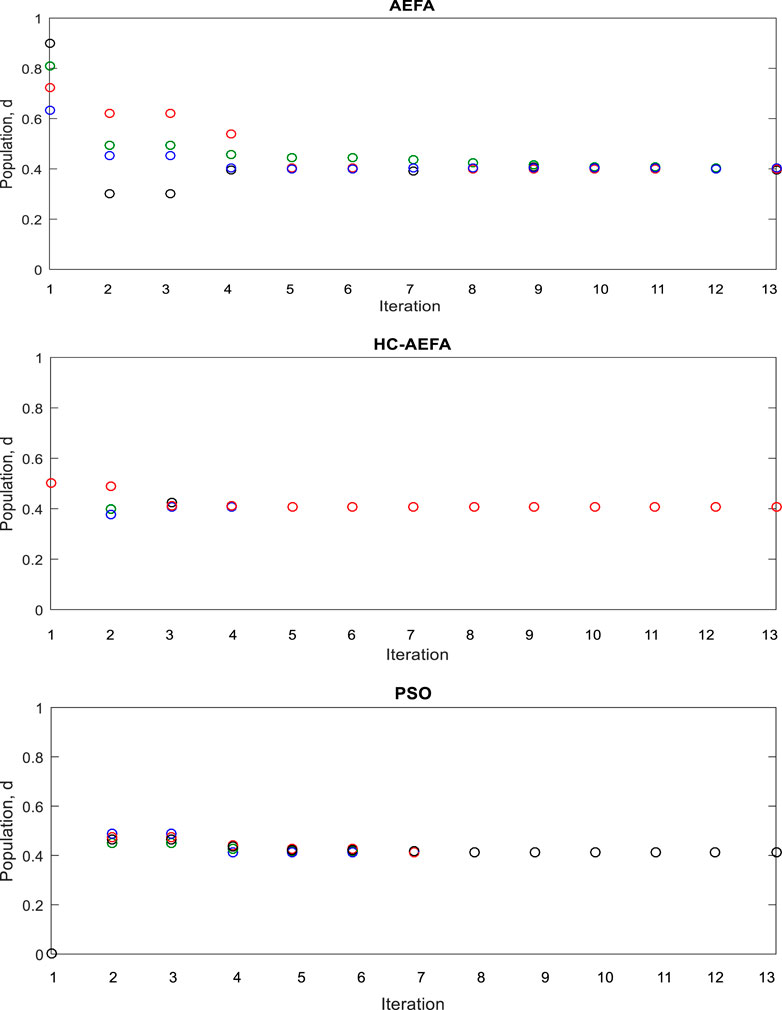
FIGURE 9. Particles’ positions in each iteration for the HC-AEFA, HC, AEFA, and PSO methods in the case of the second pattern.

Table 3 presents the numerical results for different methods for the second pattern. The percentage of tracking efficiency using HC-AEFA, HC, AEFA, and PSO is obtained at 99.95, 88.95, 99.79 and 99.85, respectively. Also, the HC-AEFA converges to GMPP in 1.24 s, and AEFA and PSO have achieved the global power in 4.62 and 2.69 s, respectively. The HC-AEFA-based MPPT method had a higher tracking speed than the other methods with higher tracking efficiency in the MPPT solution.

TABLE 3

TABLE 3. Results for the different MPPT methods in second pattern.

4.3 Results for Third Pattern (Under PSCs)

The capability of the HC-AEFA in MPPT solution with PSCs was investigated for the third pattern. In this pattern, the radiation of the modules was 300 and 800 W/m², and the global peak value was 133.75 W. The capability of the HC-AEFA method was compared with that of the HC, AEFA, and PSO methods. The results are presented in Figure 10. As shown, the HC method could not track the global peak power. The proposed HC-AEFA method had fewer oscillations than the AEFA and PSO methods and achieved stability and the global peak power faster.

FIGURE 10

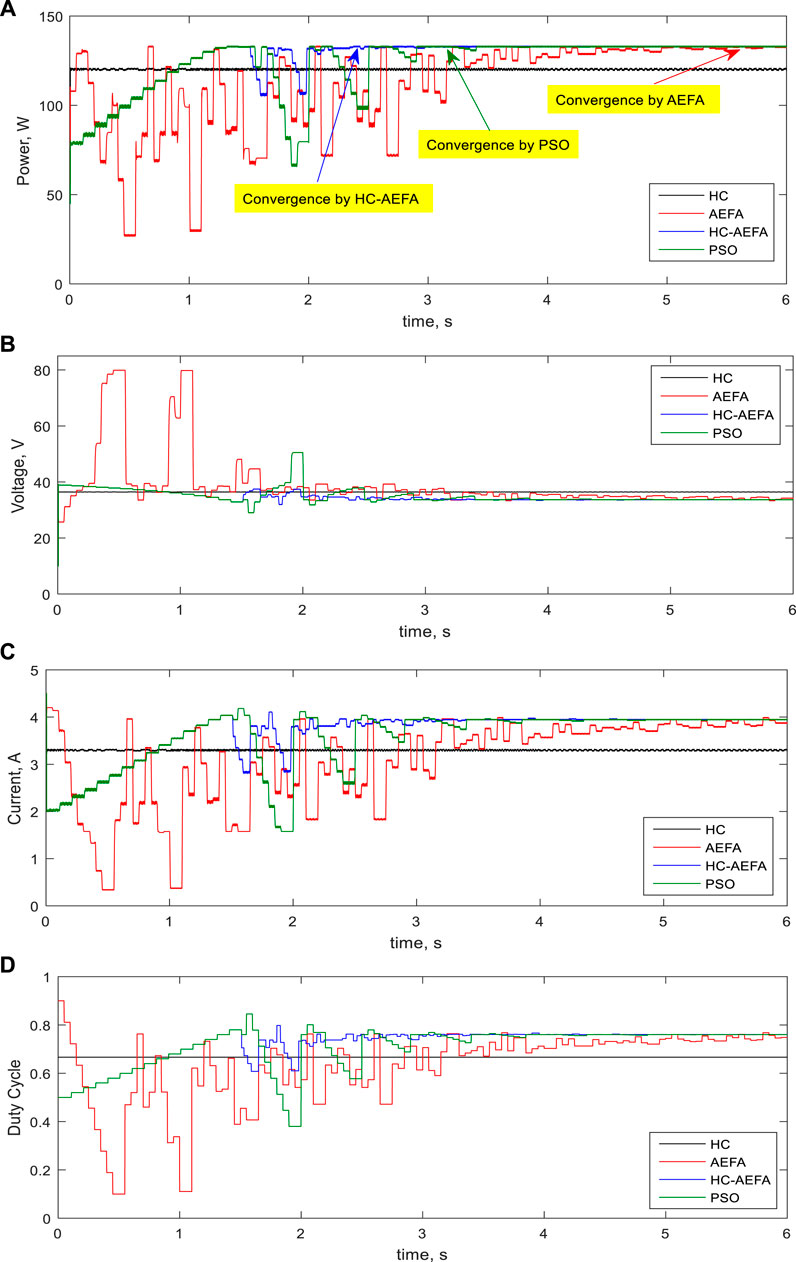
FIGURE 10. Simulation waveforms at the third pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) PV output power, (B) PV output voltage, (C) PV output current, and (D) converter duty-cycle curves.

Figure 11 present the results for the dynamic and static efficiencies of the simulation for the third pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods. The HC-AEFA method had higher dynamic and static efficiencies than the other methods considering the PSCs. The results proved the more static- and dynamic efficiency of the proposed HC-AEFA compared with the HC, AEFA, and PSO methods. So, the improvement of the HC performance based on the AEFA in problem-solving is confirmed.

FIGURE 11

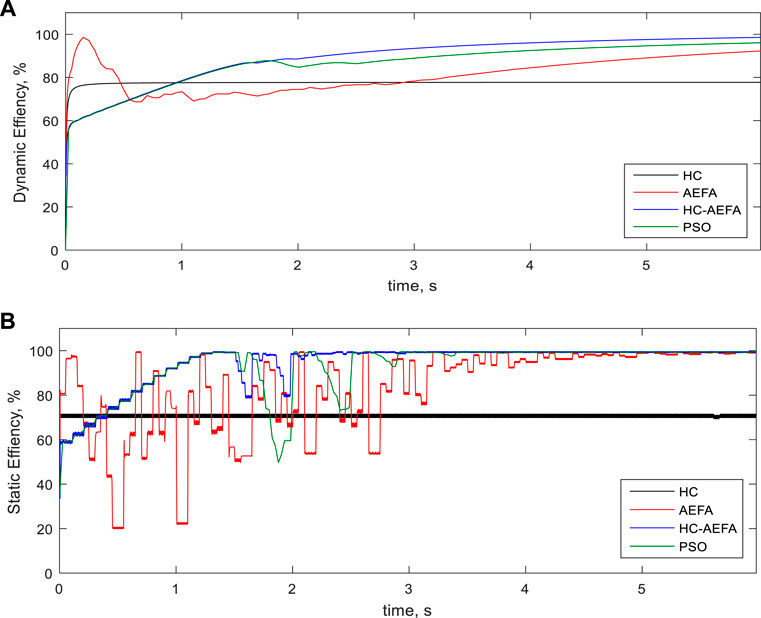
FIGURE 11. Efficiency curves at the third pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) Dynamic- efficiency, and (B) Static-efficiency.

Figure 12 shows the algorithm population-based optimization process for different MPPT methods in the case of the third pattern. For the AEFA, PSO, and proposed HC-AEFA methods, the population converged to the global peak value in iterations 13, 9, and 8, respectively, indicating that the HC-AEFA method had the highest tracking speed. The results showed the better performance of the HC-AEFA in achieving GMPP with a fast convergence rate compared to the AEFA and PSO methods.

FIGURE 12

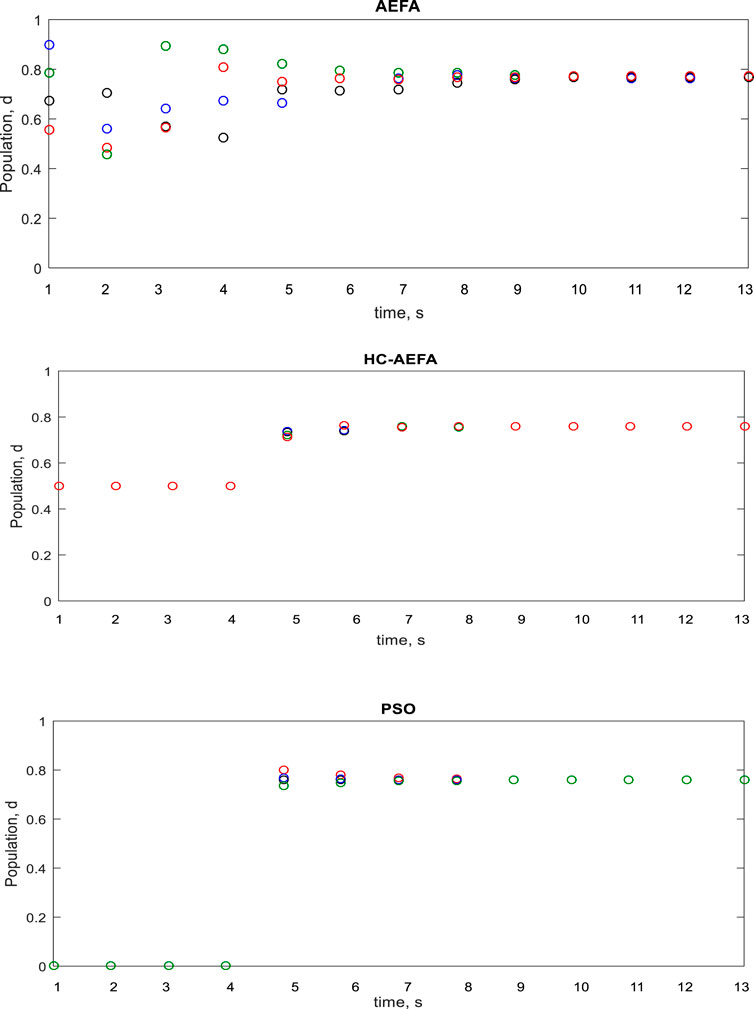
FIGURE 12. Particles’ positions in each iteration for the HC-AEFA, HC, AEFA, and PSO methods in the case of the third pattern.

Table 4 presents the numerical results for the performance of the different methods in the case of the third pattern. The percentage of tracking efficiency using HC-AEFA, HC, AEFA, and PSO is obtained at 99.93, 88.35, 99.85 and 99.80, respectively. Also, the HC-AEFA converges to GMPP in 2.13 s, and also, AEFA and PSO have achieved the global power in 5.28 and 3.48 s, respectively. The results showed that the HC-AEFA-based MPPT obtained higher tracking speed and efficiency than the HC, AEFA, and PSO for the MPPT solution.

TABLE 4

TABLE 4. Results for the different MPPT methods in third pattern.

4.4 Results for the Fourth Pattern (Under Radiation Changes)

The performance of the HC-AEFA in the MPPT problem in the case of the fourth pattern (under radiation changes) was evaluated. The radiation of the modules was 800 and 500 W/m², 600 and 300 W/m², and 400 and 200 W/m² in the first-, second-, and third-time steps, respectively. The simulation time was 6 s. Figure 13 present the simulation results, e.g., the power, voltage, current, and converter duty-cycle curves. As shown, the HC-AEFA method had fewer oscillations than the PSO method. It achieved the peak power faster in all three-time steps, indicating that the performance of the HC-AEFA method for solving the MPPT problem was better than that of the PSO method.

FIGURE 13

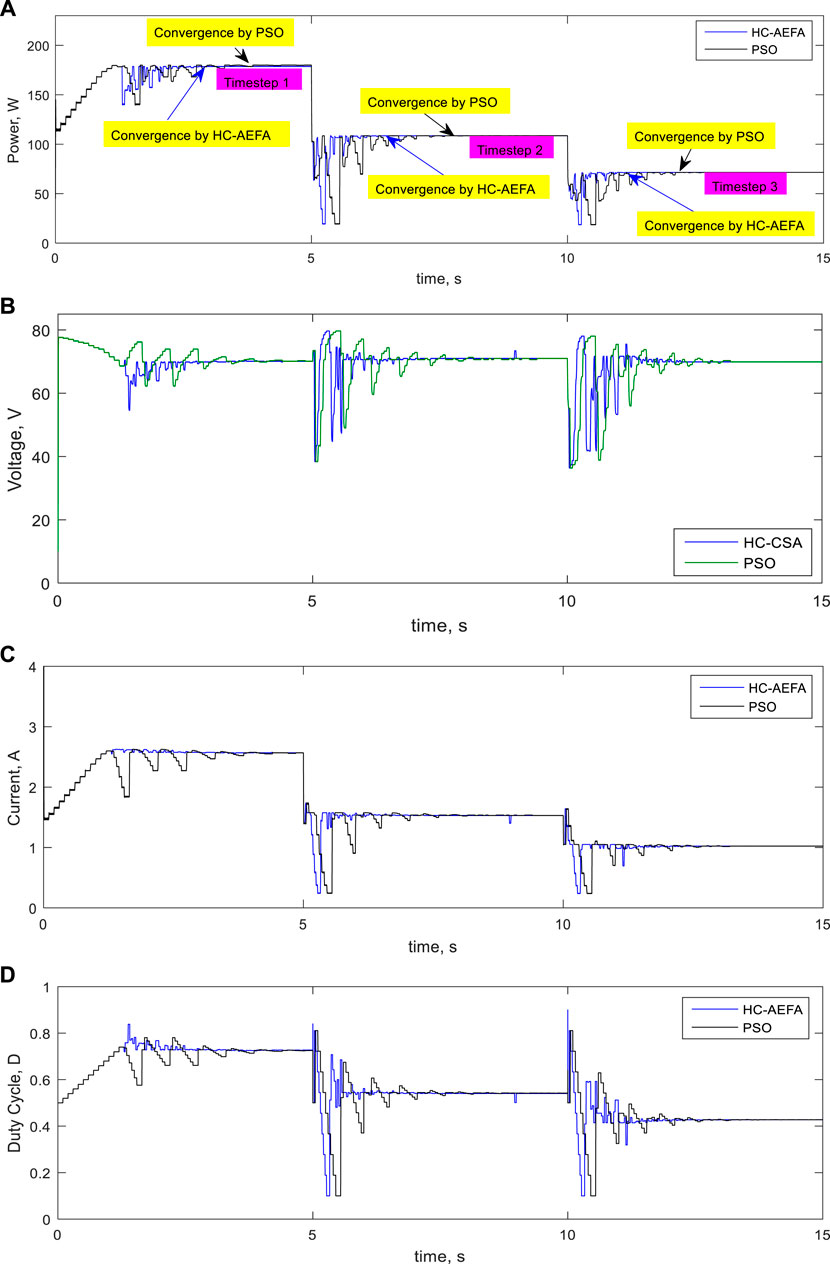
FIGURE 13. Simulation waveforms at the fourth pattern obtained using the HC-AEFA, and PSO methods; (A) PV output power, (B) PV output voltage, (C) PV output current, and (D) converter duty-cycle curves.

Figure 14 present the simulation’s dynamic- and static-efficiency curves for the fourth pattern obtained using the HC-AEFA and PSO methods. The HC-AEFA method had higher dynamic and static efficiencies and fewer oscillations in the radiation conditions at different timesteps compared with the other methods.

FIGURE 14

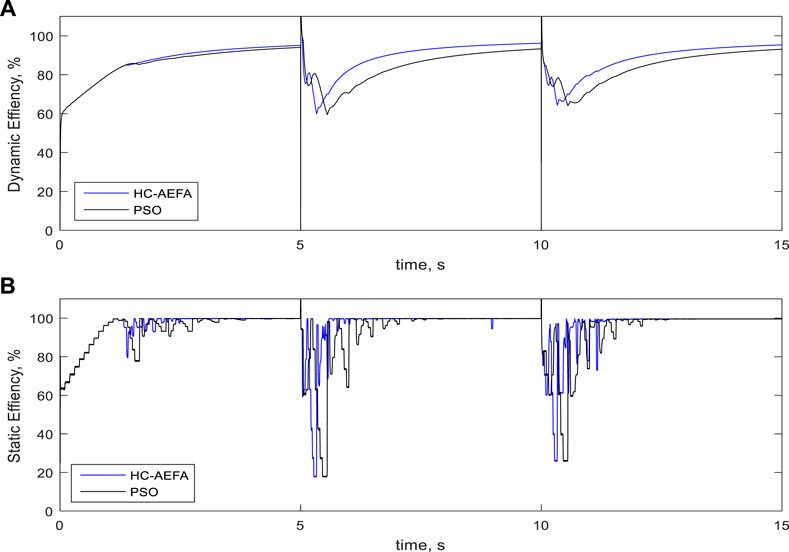
FIGURE 14. Efficiency curves at the fourth pattern obtained using the HC-AEFA, HC, AEFA, and PSO methods; (A) Dynamic- efficiency, and (B) Static-efficiency.

Table 5 presents the numerical results for the performance of the different methods for the fourth pattern at different timesteps. The percentage of tracking efficiency using HC-AEFA and PSO for timestep one is obtained at 99.96 and 99.92. For timestep two is achieved at 99.96 and 99.90, and for timestep three, this value is computed at 99.97 and 99.94, respectively. Among the methods, the HC-AEFA-based method had the highest tracking speed in the MPPT solution. The convergence rate (s) using HC-AEFA and PSO for time step 1 is obtained at 4 and 6 s, for time step 2 is achieved at 3 and 5 s, and for time step 3, this value is computed at 4 and 6 s, respectively. Among the methods, the HC-AEFA-based method had the highest convergence rate in the MPPT solution.

TABLE 5

TABLE 5. Numerical results for the performance of the HC-AEFA and PSO methods in the fourth pattern.

4.5 Results Comparison

In this paper, the proposed HC-AEFA method is applied to solve the MPPT problem of the photovoltaic system in STC and PSCs. The results indicated the proposed method’s effectiveness compared to HC, AEFA and PSO methods with higher tracking efficiency and tracking speed. The performance of the HC-AEFA given tracking efficiency is compared with previous studies in MPPT solution of photovoltaic systems in Tables 6 and 7. As in Table 6, the tracking efficiency of the HC-AEFA is obtained higher than in the previous studies. Also, the capability of the proposed method is compared given tracking speed, steady-state oscillation, complexity, convergence to local peak and tracking efficiency with previous studies in Table 7. As shown in Table 6, the proposed HC-AEFA is a reliable and perfect method to solve the MPPT solution of the photovoltaic system.

TABLE 6

TABLE 6. Comparison of tracking efficiency for HC-AEFA in MPPT solution and previous studies.

TABLE 7

TABLE 7. Comparison of the HC-AEFA performance in MPPT solution with previous studies.

5 Conclusion

This paper developed a combined HC-AEFA algorithm for PV MPPT solution under different conditions as standard patterns, PSCs, and radiation changes integrated with a buck converter. The effectiveness of the HC-AEFA in MPPT solution was evaluated compared to the HC, AEFA, and well-known PSO methods for different patterns. Additionally, for different patterns, the HC, AEFA, HC-AEF, and PSO methods were applied to solve the MPPT problem. The simulation results, e.g., the power, voltage, current, and converter duty-cycle curves, for each method were evaluated. Implementing the MPPT methods for different patterns in the standard and shading conditions indicated that the HC- AEFA method reached the global peak value with fewer oscillations and a higher speed than the HC, AEFA, and PSO methods. The HC method could not track the global power peak, whereas the other techniques achieved the global power peak. Therefore, the HC-AEFA method outperformed the HC method in the MPPT. The optimization process results indicated that among the methods tested, the proposed HC-AEFA had the fewest convergence iterations and the highest convergence speed in the MPPT solution. The simulation results of the MPPT problem for the radiation-change pattern confirmed the superiority of the proposed method (fewer tracking fluctuations and higher convergence speed). Furthermore, the HC-AEFA method outperformed the PSO method in the MPPT solution for the fourth pattern at different timesteps of the radiation changes. The tracking efficiency for the first pattern using the HC-AEFA, HC, AEFA and PSO was obtained at 99.97, 90.82, 98.86 and 99.91%. For the second pattern, these values were achieved at 99.95, 88.95, 99.79 and 99.85%, and for the third pattern, these values were committed at 99.93, 90.35, 98.85 and 99.80%, respectively. The percentage of tracking efficiency for the fourth pattern, using HC-AEFA and PSO for time step 1, was obtained at 99.96 and 99.92, for time step 2 was achieved at 99.96 and 99.90 and for time step 3, this value was computed at 99.97 and 99.94, respectively. The results showed that the HS was not able to achieve global power. Also, the results make clear that improving the HC method based on The AEFA has significantly increased the efficiency of tracking and gaining optimal global power. The results comparison showed the tracking efficiency of the HC-AEFA was obtained higher than in the previous studies, and it is a reliable and perfect method to solve the MPPT solution of the photovoltaic system. The limitations of the research are the fluctuations of the radiations and the PSCs that prevent the achievement of the global peak of the PV power. However, these limitations have been covered using the HC-AEFA. For future work, the MPPT problem solving based on complex series-parallel models of PV configuration in PSCs conditions will be suggested using the combined AEFA-PSO method.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization and methodology, MA, and AA; software, ZM, and MC; validation, MA, and ZM; formal analysis and investigation, MA; writing—original draft preparation, MA, AA, and MC; writing—review and editing, MC, AM, and ZM; visualization, AM; supervision, AM. All authors have read and agreed to the published version of the manuscript.

Funding

The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, for funding this research work through project number "IF_2020_NBU_435".

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to Prince Faisal bin Khalid bin Sultan Research Chair in Renewable Energy Studies and Applications (PFCRE) at Northern Border University, for their support and assistance.

References

Ahmed, S., Mekhilef, S., Mubin, M. B., and Tey, K. S. (2022). Performances of the Adaptive Conventional Maximum Power Point Tracking Algorithms for Solar Photovoltaic System. Sustain. Energy Technol. Assessments 53, 102390. doi:10.1016/j.seta.2022.102390

CrossRef Full Text | Google Scholar

Alajmi, B. N., Ahmed, K. H., Finney, S. J., and Williams, B. W. (2010). Fuzzy-Logic-Control Approach of a Modified Hill-Climbing Method for Maximum Power Point in Microgrid Standalone Photovoltaic System. IEEE Trans. power Electron. 26, 1022–1030. doi:10.1109/TPEL.2010.2090903

CrossRef Full Text | Google Scholar

Al‐Smadi, M. K., Mahmoud, Y., and Xiao, W. (2021). A Fast and Accurate Approach for Power Losses Quantification of Photovoltaic Power Systems under Partial‐shading Conditions. IET Renew. Power Gener. 15, 939–951.

Google Scholar

Anita, A., and Yadav, A. (2019). AEFA: Artificial Electric Field Algorithm for Global Optimization. Swarm Evol. Comput. 48, 93–108. doi:10.1016/j.swevo.2019.03.013

CrossRef Full Text | Google Scholar

Arabi Nowdeh, S., Moghaddam, M. J. H., Nasri, S., Abdelaziz, A. Y., Ghanbari, M., and Faraji, I. (2020). “A New Hybrid Moth Flame Optimizer-Perturb and Observe Method for Maximum Power Point Tracking in Photovoltaic Energy System,” in Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems (Cham: Springer), 401–420. doi:10.1007/978-3-030-05578-3_15

CrossRef Full Text | Google Scholar

Benyoucef, A. S., Chouder, A., Kara, K., Silvestre, S., and sahed, O. A. (2015). Artificial Bee Colony Based Algorithm for Maximum Power Point Tracking (MPPT) for PV Systems Operating under Partial Shaded Conditions. Appl. Soft Comput. 32, 38–48. doi:10.1016/j.asoc.2015.03.047

CrossRef Full Text | Google Scholar

Bhukya, L., and Nandiraju, S. (2020). A Novel Photovoltaic Maximum Power Point Tracking Technique Based on Grasshopper Optimized Fuzzy Logic Approach. Int. J. Hydrogen Energy 45, 9416–9427. doi:10.1016/j.ijhydene.2020.01.219

CrossRef Full Text | Google Scholar

Chaieb, H., and Sakly, A. (2018). A Novel MPPT Method for Photovoltaic Application under Partial Shaded Conditions. Sol. Energy 159, 291–299. doi:10.1016/j.solener.2017.11.001

CrossRef Full Text | Google Scholar

Charin, C., Ishak, D., Mohd Zainuri, M. A. A., Ismail, B., and Mohd Jamil, M. K. (2021). A Hybrid of Bio-Inspired Algorithm Based on Levy Flight and Particle Swarm Optimizations for Photovoltaic System under Partial Shading Conditions. Sol. Energy 217, 1–14. doi:10.1016/j.solener.2021.01.049

CrossRef Full Text | Google Scholar

Davoodkhani, F., Arabi Nowdeh, S., Abdelaziz, A. Y., Mansoori, S., Nasri, S., and Alijani, M. (2020). “A New Hybrid Method Based on Gray Wolf Optimizer-Crow Search Algorithm for Maximum Power Point Tracking of Photovoltaic Energy System,” in Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems (Cham: Springer), 421–438. doi:10.1007/978-3-030-05578-3_16

CrossRef Full Text | Google Scholar

Dileep, G., and Singh, S. N. (2017). An Improved Particle Swarm Optimization Based Maximum Power Point Tracking Algorithm for PV System Operating under Partial Shading Conditions. Sol. Energy 158, 1006–1015. doi:10.1016/j.solener.2017.10.027

CrossRef Full Text | Google Scholar

Fan, L., and Ma, X. (2022). Maximum Power Point Tracking of PEMFC Based on Hybrid Artificial Bee Colony Algorithm with Fuzzy Control. Sci. Rep. 12 (1), 4316. doi:10.1038/s41598-022-08327-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fares, D., Fathi, M., Shams, I., and Mekhilef, S. (2021). A Novel Global MPPT Technique Based on Squirrel Search Algorithm for PV Module under Partial Shading Conditions. Energy Convers. Manag. 230, 113773. doi:10.1016/j.enconman.2020.113773

CrossRef Full Text | Google Scholar

Fathy, A., and Rezk, H. (2016). A Novel Methodology for Simulating Maximum Power Point Trackers Using Mine Blast Optimization and Teaching Learning Based Optimization Algorithms for Partially Shaded Photovoltaic System. J. Renew. Sustain. Energy 8, 23503. doi:10.1063/1.4944971

CrossRef Full Text | Google Scholar

Hu, K., Cao, S., Li, W., and Zhu, F. (2019). An Improved Particle Swarm Optimization Algorithm Suitable for Photovoltaic Power Tracking under Partial Shading Conditions. IEEE Access 7, 143217–143232. doi:10.1109/access.2019.2944964

CrossRef Full Text | Google Scholar

Jiang, L. L., Maskell, D. L., and Patra, J. C. (2013). A Novel Ant Colony Optimization-Based Maximum Power Point Tracking for Photovoltaic Systems under Partially Shaded Conditions. Energy Build. 58, 227–236. doi:10.1016/j.enbuild.2012.12.001

CrossRef Full Text | Google Scholar

Kaced, K., Larbes, C., Ramzan, N., Bounabi, M., and Dahmane, Z. e. (2017). Bat Algorithm Based Maximum Power Point Tracking for Photovoltaic System under Partial Shading Conditions. Sol. Energy 158, 490–503. doi:10.1016/j.solener.2017.09.063

CrossRef Full Text | Google Scholar

Kavya, M., and Jayalalitha, S. (2021). Developments in Perturb and Observe Algorithm for Maximum Power Point Tracking in Photo Voltaic Panel: A Review. Arch. Comput. Methods Eng. 28, 2447–2457. doi:10.1007/s11831-020-09461-x

CrossRef Full Text | Google Scholar

Kulaksız, A. A., and Akkaya, R. (2012). A Genetic Algorithm Optimized ANN-Based MPPT Algorithm for a Stand-Alone PV System with Induction Motor Drive. Sol. Energy 86, 2366–2375. doi:10.1016/j.solener.2012.05.006

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017). Maximum Power Peak Detection of Partially Shaded PV Panel by Using Intelligent Monkey King Evolution Algorithm. IEEE Trans. Ind. Appl. 53 (6), 5734–5743. doi:10.1109/tia.2017.2725954

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017). MPPT in Dynamic Condition of Partially Shaded PV System by Using WODE Technique. IEEE Trans. Sustain. Energy 8 (3), 1204–1214. doi:10.1109/tste.2017.2669525

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2018). Normal Harmonic Search Algorithm-Based MPPT for Solar PV System and Integrated with Grid Using Reduced Sensor Approach and PNKLMS Algorithm. IEEE Trans. Ind. Appl. 54 (6), 6343–6352. doi:10.1109/tia.2018.2853744

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017). Single Sensor-Based MPPT of Partially Shaded PV System for Battery Charging by Using Cauchy and Gaussian Sine Cosine Optimization. IEEE Trans. Energy Convers. 32 (3), 983–992. doi:10.1109/tec.2017.2669518

CrossRef Full Text | Google Scholar

Kumar, N., Singh, B., and Panigrahi, B. K. (2019). Grid Synchronisation Framework for Partially Shaded Solar PV‐based Microgrid Using Intelligent Control Strategy. IET Gener. Transm. &amp; Distrib. 13 (6), 829–837. doi:10.1049/iet-gtd.2018.6079

CrossRef Full Text | Google Scholar

Li, L.-L., Lin, G.-Q., Tseng, M.-L., Tan, K., and Lim, M. K. (2018). A Maximum Power Point Tracking Method for PV System with Improved Gravitational Search Algorithm. Appl. Soft Comput. 65, 333–348. doi:10.1016/j.asoc.2018.01.030

CrossRef Full Text | Google Scholar

Lousuwankun, P., and Jantharamin, N. (2022). Step-Size Adaptation Based on Power and Current Variation for Photovoltaic Maximum-Power-Point Tracking. GMSARN Int. J. 16 (4), 435–441.

Google Scholar

Messai, A., Mellit, A., Guessoum, A., and Kalogirou, S. A. (2011). Maximum Power Point Tracking Using a GA Optimized Fuzzy Logic Controller and its FPGA Implementation. Sol. Energy 85, 265–277. doi:10.1016/j.solener.2010.12.004

CrossRef Full Text | Google Scholar

Miyatake, M., Veerachary, M., Toriumi, F., Fujii, N., and Ko, H. (2011). Maximum Power Point Tracking of Multiple Photovoltaic Arrays: A PSO Approach. IEEE Trans. Aerosp. Electron. Syst. 47, 367–380. doi:10.1109/taes.2011.5705681

CrossRef Full Text | Google Scholar

Mohanty, S., Subudhi, B., and Ray, P. K. (2015). A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System under Partial Shading Conditions. IEEE Trans. Sustain. Energy 7, 181–188. doi:10.1109/TSTE.2015.2482120

CrossRef Full Text | Google Scholar

Nasri, S., Nowdeh, S. A., Davoudkhani, I. F., Moghaddam, M. J., Kalam, A., Shahrokhi, S., et al. (2021). “Maximum Power Point Tracking of Photovoltaic Renewable Energy System Using a New Method Based on Turbulent Flow of Water-Based Optimization (TFWO) under Partial Shading Conditions,” in Fundamentals and Innovations in Solar Energy (Singapore: Springer), 285–310.

CrossRef Full Text | Google Scholar

Nowdeh, S. A., Moghaddam, M. J. H., Babanezhad, M., Davoodkhani, I. F., Kalam, A., Ahmadi, A., et al. (2019). “A Novel Maximum Power Point Tracking Method for Photovoltaic Application Using Secant Incremental Gradient Based on Newton Raphson,” in Solar Photovoltaic Power Plants (Singapore: Springer), 71–96. doi:10.1007/978-981-13-6151-7_4

CrossRef Full Text | Google Scholar

Nowdeh, S. A., Moghaddam, M. J. H., Babanezhad, M., Davoodkhani, I. F., Kalam, A., Ahmadi, A., et al. (2019). A Novel Maximum Power Point Tracking Method for Photovoltaic Application Using Secant Incremental Gradient Based on Newton Raphson. Sol. Photovolt. Power Plants Adv. Control Optim. Tech. 7, 71–96. doi:10.1007/978-981-13-6151-7_4

CrossRef Full Text | Google Scholar

Premkumar, M., and Sowmya, R. (2019). An Effective Maximum Power Point Tracker for Partially Shaded Solar Photovoltaic Systems. Energy Rep. 5, 1445–1462. doi:10.1016/j.egyr.2019.10.006

CrossRef Full Text | Google Scholar

Rajesh, P., Muthubalaji, S., Srinivasan, S., and Shajin, F. H. (2022). Leveraging a Dynamic Differential Annealed Optimization and Recalling Enhanced Recurrent Neural Network for Maximum Power Point Tracking in Wind Energy Conversion System. Technol. Econ. Smart Grids Sustain. Energy 7 (1), 19. doi:10.1007/s40866-022-00144-z

CrossRef Full Text | Google Scholar

Raman, G., Raman, G., Manickam, C., and Ganesan, S. I. (2016). “Dragonfly Algorithm Based Global Maximum Power Point Tracker for Photovoltaic Systems,” in Proceedings of the International Conference on Swarm Intelligence (Cham: Springer), 211–219. doi:10.1007/978-3-319-41000-5_21

CrossRef Full Text | Google Scholar

Rezk, H., Fathy, A., and Abdelaziz, A. Y. (2017). A Comparison of Different Global MPPT Techniques Based on Meta-Heuristic Algorithms for Photovoltaic System Subjected to Partial Shading Conditions. Renew. Sustain. Energy Rev. 74, 377–386. doi:10.1016/j.rser.2017.02.051

CrossRef Full Text | Google Scholar

Rezk, H., and Fathy, A. (2017). Simulation of Global MPPT Based on Teaching-Learning-Based Optimization Technique for Partially Shaded PV System. Electr. Eng. 99, 847–859. doi:10.1007/s00202-016-0449-3

CrossRef Full Text | Google Scholar

Roy Chowdhury, S., and Saha, H. (2010). Maximum Power Point Tracking of Partially Shaded Solar Photovoltaic Arrays. Sol. Energy Mater. Sol. Cells 94, 1441–1447. doi:10.1016/j.solmat.2010.04.011

CrossRef Full Text | Google Scholar

Shannan, N. M. A. A., Yahaya, N. Z., and Singh, B. (2013). “Single-Diode Model and Two-Diode Model of PV Modules: A Comparison,” in 2013 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 29 November 2013 - 01 December 2013, 210–214. doi:10.1109/iccsce.2013.6719960

CrossRef Full Text | Google Scholar

Sukanya Satapathy, S., and Kumar, N. (2020). Framework of Maximum Power Point Tracking for Solar PV Panel Using WSPS Technique. IET Renew. Power Gener. 14, 1668–1676. doi:10.1049/iet-rpg.2019.1132

CrossRef Full Text | Google Scholar

Sundareswaran, K., Sankar, P., Nayak, P. S. R., Simon, S. P., and Palani, S. (2014). Enhanced Energy Output from a PV System under Partial Shaded Conditions through Artificial Bee Colony. IEEE Trans. Sustain. energy 6, 198–209. doi:10.1109/TSTE.2014.2363521

CrossRef Full Text | Google Scholar

Teshome, D. F., Lee, C. H., Lin, Y. W., and Lian, K. L. (2016). A Modified Firefly Algorithm for Photovoltaic Maximum Power Point Tracking Control under Partial Shading. IEEE J. Emerg. Sel. Top. Power Electron. 5, 661–671. doi:10.1109/JESTPE.2016.2581858

CrossRef Full Text | Google Scholar

Wasim, M. S., Amjad, M., Habib, S., Abbasi, M. A., Bhatti, A. R., and Muyeen, S. M. (2022). A Critical Review and Performance Comparisons of Swarm-Based Optimization Algorithms in Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energy Rep. 8, 4871–4898. doi:10.1016/j.egyr.2022.03.175

CrossRef Full Text | Google Scholar