Prediction of Drag Reduction in Slickwater Fracturing by Two General Models

Drag reduction (DR) is critical to the success of hydraulic fracturing operations with slickwater, and it is a challenge to accurately predict DR due to the problem of high injection rates. Although a practical pipe diameter model is frequently used to predict the field DR based on laboratory experimental data, there exist many limitations. This study, on account of dynamic similarity, shows two novel general models for the prediction of field DR, and such two models can give reliable predictions when the laboratory and field Reynolds numbers (Re) are the same. For general model 1, the DR can be predicted by using the laboratory volumetric flow rate, pipe diameter and pressure drop, and the field volumetric flow rate, with a deviation ranging from −10 to 10%. For general model 2, it is simpler than general model 1, and the DR can be predicted by using the laboratory pipe diameter and the field volumetric flow rate, with a deviation ranging from −6 to 6%. The two novel general models can be used for more scenarios than the existing reported ones.

Introduction

As a widely distributed clean and efficient energy source, shale gas has been highly valued by the international energy market and various countries (Peng et al., 2019a). Since the early 21st century, the boom in shale gas development in the United States has significantly advanced the global shale gas development. Since then, the energy landscape in the world has changed gradually (Yuan et al., 2015; Shi et al., 2020). As far as we know, China has abundant shale gas resources and an increasing demand for natural gas. Therefore, a large-scale commercialized development (Ma et al., 2018; Pang, 2018) of hydraulic fracturing shale reservoirs can be expected. Hydraulic fracturing is a necessary technology for developing shale gas (Yu et al., 2020). During the hydraulic fracturing process, the proppant-carrying fracturing fluid is injected into a well at a high pressure and rate to fracture the reservoir rocks. To reduce the friction loss due to tubular roughness, slickwater with drag reducers is often used since it has desirable hydraulic features (Barbot et al., 2013; Shaffer et al., 2013; Al-Muntasheri, 2014; Engle and Rowan, 2014). Numerous studies have focused on various parameters affecting drag reduction (Gallego and Shah, 2009; Chai et al., 2019). Four main parameters can affect the drag reduction of slickwater, including the drag-reducing agent concentration, fluid flow Reynolds number (Re), relative pipe roughness, and water quality (Yang et al., 2019). Meanwhile, two main underlying mechanisms of drag reduction have been identified (Habibpour and Clark, 2017; Habibpour et al., 2017). The first mechanism introduced by Lumley is based on the elongation of coiled polymer molecules, hence increasing the thickness of the viscous sublayer; the other mechanism is the elastic properties of polymers.

Although we have known a lot of the slickwater parameters affecting drag reduction, accurate prediction of drag reduction still remains a challenge. Allahdadi Mehrabadi and Sadeghy (2008) obtained a good drag reduction prediction model called the κ-ε turbulence model for low Reynolds numbers. Al-Sarkhi et al. (2011) developed two correlations to predict the effect of drag-reducing polymers on the friction factor of the two-phase flow for any pipe diameter. Karami and Mowla (2013) presented a general model for predicting drag reduction in crude oil pipelines. Recently, Zhou et al. (2011) proposed a practical pipe diameter model by introducing an effective pipe radius (r_eff) which is defined as follows:

$r_{eff}=\frac{v_f\rho }{\mu },$

where ρ is the fluid density, μ is the fluid viscosity, and v_f is the flow velocity calculated as (dΔp/4ρl)^1/2. To upscale the laboratory experimental results of the drag reduction of slickwater to the field application, two conditions must be met: first, the r_eff value of the field pipe (tubing/casing) must be in the same range as the laboratory pipe; second, the slope of r_eff versus v of the field must match the laboratory setup, where v is the average fluid velocity. We found that as long as the slopes of effective pipe radius versus velocity from the laboratory pipe and the field pipe are numerically close, field drag reduction can be predicted by a modified correlation between DR and velocity established in the laboratory (Zhao et al., 2018; Chen et al., 2021). In this study, two novel general models are proposed using the Reynolds criterion to simplify the prediction condition.

Theoretical Basis

The models presented in this study are based on the similarity principle so as to upscale the laboratory experimental results to the field application. Due to laboratory setting constraints that are different from those in the field application, the experimental results can be upscaled to the field application only under some specific conditions. The laboratory measurements can accurately represent the flow dynamics of the corresponding prototype. Therefore, the similarity between the model and the prototype must be satisfied. There are three types of similarity principles: geometric similarity, kinematic similarity, and dynamic similarity. It is relatively easy to achieve the geometric and kinematic similarities, while the dynamic similarity requires an equal ratio of forces acting on the two systems. Usually, dynamic similarity can be achieved by equating such flow dynamic dimensionless variables as Froude number and Reynolds number. In this study, we chose the Reynolds number as the inherent parameter because it can be easily measured in both the laboratory condition and the field application condition. Reynolds number (Re) is a dimensionless number that is commonly used to characterize flow patterns in different fluid flow situations (Peng et al., 2019b). Because of the similarity of flow viscosity between the prototype and the model, the Reynolds number of the field fracturing flow model should be equal to that of the lab drag reduction experiment model, according to the similarity of flow dynamics.

In previous studies, we have developed a modified Virk’s correlation to accurately characterize the friction factor (λ) under different Reynolds numbers in the turbulent flow pattern for the polyacrylamide polymer drag-reducing agent using laboratory data. The unified model is shown in Eq. 1.

$\frac{1}{\sqrt{\lambda }}=\alpha {\mathrm{D}}^{\beta }\lg \left(\mathrm{Re}\sqrt{\lambda }\right)+\gamma D^{\theta }.(1)$

This equation can be changed to Eq. 2.

${\mathrm{Re}}_{lab}=a{\mathrm{D}}_{lab}^m{\lambda }_{lab}^n,(2)$

where Re_lab is the Reynolds number based on the laboratory data, D_lab is the lab pipe diameter, and λ_lab is the friction factor from the laboratory data. For a given pipe diameter in the field, a similar relationship between the field Re (Re_fie) and the field λ (λ_fie) can be obtained by Eq. 3.

${\mathrm{Re}}_{fie}=b{\lambda }_{fie}^n.(3)$

The Reynolds numbers of the lab and field can be equated by Eq. 4:

${\lambda }_{fie}={\left(\frac{a{D}_{lab}^m}{b}\right)}^{1/n}{\lambda }_{lab}.(4)$

For a slickwater solution, the λ_lab and λ_fie can be determined by the Hagen–Poiseuille equation, respectively, as follows:

${\lambda }_{lab}=\frac{{\pi }^2{\mathrm{D}}_{lab}^5\mathrm{\Delta }{P}_{lab}}{8\rho {\mathrm{L}}_{lab}{\mathrm{Q}}_{lab}^2},(5)$

${\lambda }_{fie}=\frac{{\pi }^2{\mathrm{D}}_{fie}^5\mathrm{\Delta }{P}_{fie}}{8\rho {\mathrm{L}}_{fie}{\mathrm{Q}}_{fie}^2},(6)$

where ∆P_lab is the pressure drop in the laboratory experiment, ρ is the density of slickwater, L_lab is the pipe length in the laboratory experiment, Q_lab is the volumetric flow rate in the laboratory experiment, ∆P_sie is the field friction of slickwater, L_fie is the well depth, and Q_fie is the field volumetric flow rate.

Eq. 5 and 6 are substituted into Eq. 4 to get the predicted ∆P_fie by Eq. 7:

$\mathrm{\Delta }{\mathrm{P}}_{fie}={\left(\frac{a}{b}{D}_{lab}^m\right)}^{1/n}\frac{{\mathrm{D}}_{lab}^5\mathrm{\Delta }{\mathrm{P}}_{lab}{\mathrm{L}}_{fie}{\mathrm{Q}}_{fie}^2}{{\mathrm{L}}_{lab}{\mathrm{Q}}_{lab}^2{\mathrm{D}}_{fie}^5}.(7)$

For the given L_fie, Q_fie, and D_fie, ∆P_fie can be calculated according to the process shown in Figure 1.

FIGURE 1

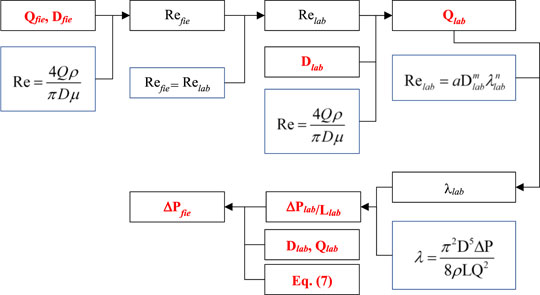
FIGURE 1. Calculation process of ∆P_fie prediction according to Eq. 7.

The field friction of pure water (∆P_pw) can be calculated by Eq. 8, which is obtained by the friction-gradient flow rate diagram of water, as shown in Supplementary Figure S1 in Supporting Information.

$\mathrm{\Delta }{\mathrm{P}}_{pw}=1.385\times {10}^6{D}_{fie}^{-4.8}{\mathrm{Q}}_{fie}^{1.8}{L}_{fie}.(8)$

The drag reduction (DR) is defined as follows:

$\mathrm{D}\mathrm{R}=100-\frac{\mathrm{\Delta }{\mathrm{P}}_{fie}}{\mathrm{\Delta }{\mathrm{P}}_{pw}}\times 100.(9)$

Eq. 7 and 8 are substituted into Eq. 9 to get the DR:

$\mathrm{D}\mathrm{R}=100-7.22\times {10}^{-5}{\left(\frac{a}{b}{D}_{lab}^m\right)}^{1/n}\frac{{\mathrm{D}}_{lab}^5\mathrm{\Delta }{\mathrm{P}}_{lab}{\mathrm{Q}}_{fie}^{0.2}}{{\mathrm{L}}_{lab}{\mathrm{Q}}_{lab}^2{\mathrm{D}}_{fie}^{-9.8}}\times 100.(10)$

Experiment

Materials

The drag-reducing agent, having an average molecular weight of 1.05×10⁷ and a hydrolysis degree of 21.5%, was provided by Chengdu Ringt Technology Development Co., Ltd. In the laboratory experiment, an aqueous solution of 0.1 wt% drag-reducing agent and deionized water as the solvent were used. The experimental setup used to study the drag reduction performance is shown in Supplementary Figure S2 in Supporting Information. The laboratory flow loop was composed of a mixing tank (20 L), a cavity progressive pump (XBY, model: G FG 25-2, range: 0–2 m³h⁻¹), a steel pipe (relative roughness: 3.2), a heater, and a flow meter (SINCERITY, model: DMF-1-M, range: 0–35 kg min⁻¹, accuracy: 0.10–0.20% relative error of the flow meter). It also had two pressure sensors (Sailsors Instruments Ltd., model: V4Db7E, range: -700 to 700 kPa, output: 4–20 mA DC, accuracy: ±0.5% full scale).

Drag Reduction Experiments in the Laboratory

The drag reduction experiments in the laboratory were conducted, following the procedures detailed in the literature (Zhao et al., 2018).

1) Drag-reducing agent and experimental equipment

The drag-reducing agent used in the experiment was the high molecular weight polyacrylamide emulsion prepared by inverse emulsion polymerization. It was a linear polymer with a molecular weight of 1.05×10⁷ and a concentration of 31.2 wt%. The dosage of the linear polymer was 0.1wt%. All experiments were carried out at room temperature. The loop included a 50-L container, and it can circulate at different rates up to 50 L/min under the action of the pump. First, the liquid flowed from the mixing tank through the flow meter having a maximum capacity of 10 t/h and an accuracy of ±0.1%. Then, the liquid flowed through the pipeline, and the pressure was measured by using the pressure sensors with a range of 0–14 MPa. A 30-m long pipe with a diameter of 0.08 m was used in the system. A 50-L container was used to prepare the drag-reducing agent solution, and the solution can be recycled. Then, experiments were conducted at different flow rates.

2) Experimental procedures

1) The water was added to a mixing tank and allowed to circulate for 5 min, followed by filling the pipeline with water and checking the flow meter and pressure sensor to ensure proper and stable range.

2) The water was circulated for 5 min, and the pressure difference (Δ P₀) per second and the flow rate were recorded.

3) A drag-reducing agent was added to the water and allowed to circulate for 5 min, followed by recording the pressure difference (Δ P₁) per second and the flow rate.

4) The system was cleaned with water.

5) The drag reduction was calculated.

6) The drag reduction performance was evaluated by Reynolds number, shear rate, friction coefficient, and average velocity.

Results and Discussion

Construction and Validation of General Model 1

Figure 2 shows the changes of Re_lab with λ_lab of slickwater in pipes with a diameter of 7.8 and 10.15 mm, respectively. We applied numerical regression to the experimental data and obtained the correlation Eq. 11 with coefficients of a = 0.0011, m = 1.76, and n = −2.8.

${\mathrm{Re}}_{lab}=1.1\times {10}^{-3}{\mathrm{D}}_{lab}^{1.76}{\lambda }_{lab}^{-2.8}.(11)$

FIGURE 2

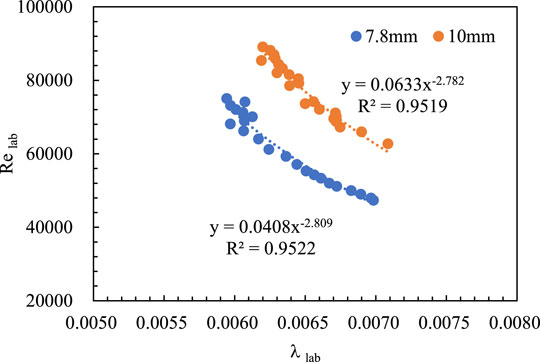
FIGURE 2. Changes in Re_lab with λ_lab of slickwater in pipes with a diameter of 7.8 and 10.15 mm, respectively.

Figure 3 shows the changes of Re_fie with λ_fie of slickwater in the pipe with a diameter of 114.3 mm. For this pipe, the correlation was obtained by Eq. 12.

${\mathrm{Re}}_{fie}=8.8\times {10}^{-4}{\lambda }_{fie}^{-2.8}.(12)$

FIGURE 3

FIGURE 3. Changes in Re_fie with λ_fie of slickwater.

Eq. 11 and 12 should be substituted into Eq. 7 and 10 to obtain the predicted ∆P_fie and drag reduction (by general model 1), respectively, by Eq. 13 and 14:

$\mathrm{\Delta }{\mathrm{P}}_{fie}=\frac{0.66}{{\mathrm{D}}_{lab}^{0.55}}\frac{{\mathrm{D}}_{lab}^5}{{\mathrm{D}}_{fie}^5}\frac{{\mathrm{L}}_{fie}}{3}\frac{{\mathrm{Q}}_{fie}^2}{{\left({\mathrm{Q}}_{lab}/60\times 1000\right)}^2}\mathrm{\Delta }{\mathrm{P}}_{lab},(13)$

$\mathrm{D}\mathrm{R}=100-7.22\times {10}^{-5}{\left(1.25D_{lab}^{1.76}\right)}^{-0.36}\frac{D_{lab}^5\mathrm{\Delta }{\mathrm{P}}_{lab}{Q}_{fie}^{0.2}}{L_{lab}{Q}_{lab}^2{D}_{fie}^{-9.8}}\times 100.(14)$

For the pipe with a diameter of 114.3 mm, the field data, predicted ∆P_fie, and predicted DR are listed in Table 1. Since ∆P_fie predicted using D_lab of 10 mm was higher than that of D_lab of 7.8 mm, the DR predicted using D_lab of 10 mm was lower than that of D_lab of 7.8 mm. Figure 4 shows the DR prediction deviations. In general, the prediction deviation produced by using D_lab of 7.8 mm was lower than that of D_lab of 10 mm, and the deviation was -10–10%.

TABLE 1

TABLE 1. Predicted DRs and deviations obtained by using general model 1.

FIGURE 4

FIGURE 4. DR prediction deviations at different D_lab.

Construction and Validation of General Model 2

As shown in Figure 1 and Eq. 10, the DR prediction using general model 1 is very complicated. Many parameters in the model cannot be measured directly. Therefore, general model 1 should be further simplified. When L_fie and D_fie are known, ∆P_fie is a function of Re_lab, D_lab, and V_fie, as shown in Eq. 7. Therefore, Eq. 10 can be changed to Eq. 15as follows:

$DR=100-x{\mathrm{Re}}_{lab}^y{D}_{lab}^z{V}_{fie}^q.(15)$

Re_lab is also a parameter that cannot be measured directly. Our laboratory experimental results showed that there was a linear relationship between ∆P_lab/V_lab and Re_lab (Figure 5) within our experiment range. In addition, we also found that there was a linear relationship between ∆P_lab/V_lab and ∆P_lab (see Figure 6). As shown in Figure 5 and Figure 6, Re_lab and ∆P_lab also have a linear relationship. In other words, d (ΔP_lab/V)/d (ΔP_lab) and Re_lab have multiple relationships. As a result, Eq. 15 can be converted to Eq. 16as follows:

$\mathrm{D}R=100-x^{\prime }\times {\left[\frac{\mathrm{d}\left(\Delta P_{lab}/V_{lab}\right)}{\mathrm{d}\left(\Delta P_{lab}\right)}\right]}^{y^{\prime }}\times D_{lab}^z{V}_{fie}^q.(16)$

FIGURE 5

FIGURE 5. Relationship between ∆P_lab/V_lab and Re_lab.

FIGURE 6

FIGURE 6. Relationship between ∆P_lab/V_lab and ∆P_lab.

When V_fie is changed from 1.63 m/s to 32.5 m/s, the DR was calculated for different pipe diameters by adjusting the parameters in Eq. 16. The data used for parameter determination are shown in Table 2. Using numerical regression, we obtained general model 2, as shown in Eq. 17.

$\mathrm{D}R=100-56\times {\left[\frac{\mathrm{d}\left(\Delta P_{lab}/V_{lab}\right)}{\mathrm{d}\left(\Delta P_{lab}\right)}\right]}^{0.028}\times D_{lab}^{-0.07}\times V_{fie}^{-0.14}.(17)$

TABLE 2

TABLE 2. Data used for parameter determination.

When the pipe diameter was 114.3 mm, the field data and the predicted ∆P_fie and DR were obtained using general model 2. Figure 7 shows the DR prediction with a deviation ranging from -6 to 6%.

FIGURE 7

FIGURE 7. DR prediction deviations at different velocities.

Deviation Analysis

This study presents models from regression and upscaling laboratory data to predict the field performance of slickwater. The potential deviation from the developed model comes from three different sources: 1) uncertainties of the laboratory measurements and their propagation to the regression correlation. To overcome the system deviation of measurement, multiple measurements on rates, diameters, and pressures were conducted, and the averaged values were used in the laboratory experimental results; 2) numerical regression on a laboratory experiment. To obtain the quantitative relationships between measured quantities and overcome the potential deviations, we applied weighted least squares with data uncertainties determined from experiments; 3) propagation of deviation during upscaling laboratory data to field applications. In this upscaling, we did not consider the potential impact of other differences such as different water quality and changes in fluid flow dynamics or thermodynamic properties, and all of them can contribute to the increased inaccuracy in the upscaling process.

Additionally, Eq. 16 shows that the friction resistance value predicted for the field is related to the linear relationship between the ratio of pressure difference to linear velocity and the differential pressure measured in the laboratory experiment, hydrodynamic radius, and linear velocity designed in the field. The calibration of the hydrodynamic radius is based on the water experiment, and the friction coefficient of water conforms to the Prandtl–Karman law in the hydraulic smooth area, which requires the accurate measurement of the stable pressure difference at different linear velocities under laboratory experimental conditions. Similarly, to establish an accurate linear relationship between the ratio of pressure difference to linear velocity and differential pressure, it is necessary to measure the stable pressure difference of the drag-reducing agent at different linear velocities. Therefore, the most important factor for accurate prediction of field friction is to obtain the stable pressure difference between water and drag-reducing agent solution at different linear velocities under laboratory experimental conditions.

Conclusion

Two novel general models are established to predict the field drag reduction using laboratory experimental data based on the dynamic similarity theory. When the laboratory and field Reynolds numbers are the same and the laboratory and field volumetric flow rates and pipe diameters are known, general model 1 can be used. When the field volumetric flow rates and the laboratory pipe diameter are known, general model 2 can be used. The two proposed mathematical models for field drag reduction prediction are validated by 42 data points. The validation results showed that both models can give high-accuracy predictions, with a deviation ranging from −10 to 10% using general model 1 and a deviation ranging from −6 to 6% using general model 2.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was partially funded by one of the National Key Technology R&D Programs—Research and Application of Generic Technologies for National Quality Infrastructure (2018YFF0213800), specifically research on key technical standards of coalbed methane, shale gas and modern coal chemical industry and that on key technical standards of shale gas resource exploration, geological evaluation and development process.

Conflict of Interest

Authors PC, HC, YF, YT, XH and WY were employed by PetroChina Southwest Oil and Gas Field Company.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Muntasheri, G. (2014). A Critical Review of Hydraulic-Fracturing Fluids for Moderateto Ultralow-Permeability Formations over the Last Decade. SPE Prod. Operations 29, 1–18. doi:10.2118/169552-pa

CrossRef Full Text | Google Scholar

Al-Sarkhi, A., Nakla, M. E., and Ahmed, W. H. (2011). Friction Factor Correlations for Gas-Liquid/liquid-Liquid Flows with Drag-Reducing Polymers in Horizontal Pipes. Int. J. Multiph. Flow 37 (5), 501–506. doi:10.1016/j.ijmultiphaseflow.2011.01.005

CrossRef Full Text | Google Scholar

Allahdadi Mehrabadi, M., and Sadeghy, K. (2008). Simulating Drag Reduction Phenomenon in Turbulent Pipe Flows. Mech. Res. Commun. 35 (8), 609–613. doi:10.1016/j.mechrescom.2008.06.003

CrossRef Full Text | Google Scholar

Barbot, E., Vidic, N. S., Gregory, K. B., and Vidic, R. D. (2013). Spatial and Temporal Correlation of Water Quality Parameters of Produced Waters from Devonian-Age Shale Following Hydraulic Fracturing. Environ. Sci. Technol. 47, 2562–2569. doi:10.1021/es304638h

PubMed Abstract | CrossRef Full Text | Google Scholar

Chai, Y., Li, X., Geng, J., Pan, J., Huang, Y., and Jing, D. (2019). Mechanistic Study of Drag Reduction in Turbulent Pipeline Flow over Anionic Polymer and Surfactant Mixtures. Colloid Polym. Sci. 297, 1025–1035. doi:10.1007/s00396-019-04525-2

CrossRef Full Text | Google Scholar

Chen, P. F., Chang, H. G., Peng, T., Tang, Y. F., Liu, Y. Q., and Xiang, C. (2021). Synthesis and Performance Evaluation of a New Drag Reducer Based on Acrylamide/12-Allyloxydodecyl Acid Sodium. J. Appl. Polym. Sci. 138, e50314. doi:10.1002/app.50314

CrossRef Full Text | Google Scholar

Engle, M. A., and Rowan, E. L. (2014). Geochemical Evolution of Produced Waters from Hydraulic Fracturing of the Marcellus Shale, Northern Appalachian Basin: a Multivariate Compositional Data Analysis Approach. Int. J. Coal Geol. 126, 45–56. doi:10.1016/j.coal.2013.11.010

CrossRef Full Text | Google Scholar

Gallego, F., and Shah, S. N. (2009). Friction Pressure Correlations for Turbulent Flow of Drag Reducing Polymer Solutions in Straight and Coiled Tubing. J. Petroleum Sci. Eng. 65, 147–161. doi:10.1016/j.petrol.2008.12.013

CrossRef Full Text | Google Scholar

Habibpour, M., and Clark, P. E. (2017). Drag Reduction Behavior of Hydrolyzed Polyacrylamide/xanthan Gum Mixed Polymer Solutions. Pet. Sci. 14, 412–423. doi:10.1007/s12182-017-0152-7

CrossRef Full Text | Google Scholar

Habibpour, M., Koteeswaran, S., and Clark, P. E. (2017). Drag Reduction Behavior of Hydrolyzed Polyacrylamide/polysaccharide Mixed Polymer Solutions-Effect of Solution Salinity and Polymer Concentration. Rheol. Acta 56, 7–8. doi:10.1007/s00397-017-1024-1

CrossRef Full Text | Google Scholar

Karami, H. R., and Mowla, D. (2013). A General Model for Predicting Drag Reduction in Crude Oil Pipelines. J. Petroleum Sci. Eng. 111 (21), 78–86. doi:10.1016/j.petrol.2013.08.041

CrossRef Full Text | Google Scholar

Ma, Y. S., Cai, X. Y., and Zhao, P. R. (2018). China’s Shale Gas Exploration and Development: Understanding and Practice. Petroleum Explor. Dev. 45, 561–574. doi:10.1016/s1876-3804(18)30065-x

CrossRef Full Text | Google Scholar

Pang, W. (2018). A Method for Determining the Contribution of Adsorption Gas to the Production of Shale Gas Wells. Pet. Drill. Technol. 46, 86–92.

Google Scholar

Peng, Y., Zhao, J., Sepehrnoori, K., Li, Y., Yu, W., and Zeng, J. (2019). Study of the Heat Transfer in Wellbore during Acid/Hydraulic Fracturing Based on Semi-analytical Transient Model [J]. SPE J. 24 (2), 877–890. doi:10.2118/194206-pa

CrossRef Full Text | Google Scholar

Peng, Y., Zhao, J., Sepehrnoori, K., Li, Z., and Xu, F. (2019). Study of Delayed Creep Fracture Initiation and Propagation Based on Semi-analytical Fractional Model. Appl. Math. Model. 72, 700–715. doi:10.1016/j.apm.2019.03.034

CrossRef Full Text | Google Scholar

Shaffer, D. L., Arias Chavez, L. H., Ben-Sasson, M., Romero-Vargas Castrillón, S., Yip, N. Y., and Elimelech, M. (2013). Desalination and Reuse of High-Salinity Shale Gas Produced Water: Drivers, Technologies, and Future Directions. Environ. Sci. Technol. 47, 9569–9583. doi:10.1021/es401966e

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, W., Wang, X., Guo, M., Shi, Y., Feng, A., Liang, R., et al. (2020). Water Use for Shale Gas Development in China's Fuling Shale Gas Field. J. Clean. Prod. 256, 120680. doi:10.1016/j.jclepro.2020.120680

CrossRef Full Text | Google Scholar

Yang, B., Zhao, J., Mao, J., Tan, H., Zhang, Y., and Song, Z. (2019). Review of Friction Reducers Used in Slickwater Fracturing Fluids for Shale Gas Reservoirs. J. Nat. Gas Sci. Eng. 62, 302–313. doi:10.1016/j.jngse.2018.12.016

CrossRef Full Text | Google Scholar

Yu, P., Zhao, J., Sepehrnoori, K., and Li, Z. (2020). Fractional Model for Simulating the Viscoelastic Behavior of Artificial Fracture in Shale Gas[J]. Eng. Fract. Mech. 228, 106892. doi:10.1016/j.engfracmech.2020.106892

CrossRef Full Text | Google Scholar

Yuan, J., Luo, D., and Feng, L. (2015). A Review of the Technical and Economic Evaluation Techniques for Shale Gas Development. Appl. Energy 148, 49–65. doi:10.1016/j.apenergy.2015.03.040

CrossRef Full Text | Google Scholar

Zhao, J., Chen, P., Liu, Y., Zhao, W., and Mao, J. (2018). Prediction of Field Drag Reduction by a Modified Practical Pipe Diameter Model. Chem. Eng. Technol. 41, 1417–1424. doi:10.1002/ceat.201600570

CrossRef Full Text | Google Scholar

Zhou, J., Sun, H., Stevens, R., Qu, Q., and Bai, B. (2011). “Bridging the Gap between Laboratory Characterization and Field Applications of Friction Reducers,” in SPE Production and Operations symposium. doi:10.2118/140942-ms

CrossRef Full Text | Google Scholar

Nomenclature

Λ: friction factor, dimensionless;

Re: Reynolds numbers, dimensionless;

Re_lab: recalculated by using laboratory data, dimensionless;

D_lab: pipe diameter in the laboratory experiment, mm;

D_fie: pipe diameter in the field application, mm;

λ_lab: λ calculated by using laboratory data, dimensionless;

∆P_lab: pressure drop in the laboratory experiment, MPa;

ρ: density of slickwater, g/cm³;

L_lab: pipe length in the laboratory experiment, mm;

Q_lab: volumetric flow rate in the laboratory experiment, m³/min;

∆P_fie: field friction of slickwater, MPa;

L_fie: well depth, m;

Q_fie: field volumetric flow rate, m³/min;

V_fie: linear velocity, m/s.