Influence of Solid–Liquid Two-Phase Flow on Cavitation of Tubular Turbine Blades Under Combined Conditions

The influence of sediment media on the blade pressure and cavitation of a tubular turbine was investigated in this study. The Zwart–Geber–Belamri cavitation model and the shear stress transport k–w turbulence model were applied to numerically simulate and experimentally validate the full flow path of the tubular turbine under combined conditions for sediment particle sizes of 0.01 and 0.05 mm and concentrations of 1%, 1.5%, and 2%. The results show that the pressure of the blade increases with the sediment concentration. Cavitation mainly occurs between the blade shroud and the leading edge. The higher the sediment concentration, the lower the vapor volume fraction at the same sediment particle size. The presence of sediments inhibits further cavitation development, and the inhibition effect is significant. At the same concentration, the larger the particle size of the sediment, the lower the vapor volume fraction. Thus, the increase in the particle size inhibits cavitation, but the inhibition effect is not significant.

Introduction

China has made ecological civilization construction with Chinese characteristics a vital part of the socialist cause, encouraged ecological civilization promotion, fully implemented the new resource concept, and promoted the economical and efficient use of resources (Li et al., 2022). Hydropower development is economically valuable because it is clean, renewable, and efficient compared to traditional sources of thermal power generation (Wu and Zhu, 2021). Tubular turbines have broad application prospects in developing low-head hydraulic resources (Shu-tang, 2000).

During turbine operations, the fluid exhibits a strong nonlinear motion, that is, turbulent motion, under the influence of the complex turbine structure and three-dimensional transient nonconstant operating conditions. Turbulence is a critical factor that causes pulsations in the physical quantities of the flow field (Li D. et al., 2021; Wangxu et al., 2021). When sediment particles carrying tiny air nuclei enter the rotor area, the existence of a negative pressure fluctuation peak facilitates the rapid expansion and growth of bubbles, which contract and break under the action of the fluid (Xu-na et al., 2019). In addition, the collapse of these bubbles near the solid surface generates microjets and high-pressure waves that directly impact the solid surface and cause deformation. The deformation continues to increase because of the continuous collapse of the bubbles until the surface material breaks down, owing to fatigue and cavitation (Li et al., 2021b). When cavitation occurs, the collapse of the cavitation bubbles changes the amplitude of the pressure fluctuation frequency (Li et al., 2021; Li et al., 2022), increasing the instability of the tubular turbine unit and generating vibration and noise (Fu et al., 2021; Sun, 2022).

In recent years, many scholars have investigated the influence of the sediment inside the turbine on cavitation performance. Lu (1991) investigated the collapse of cavitation bubbles in a solid–liquid two-phase flow and found that the solid particles in the liquid reduced the collapse rate of the bubbles. They observed that the higher the concentration of solids, the more pronounced the effect, which could reduce the destructive capacity of the bubbles. Liao (2012) argued that vortices in fluids are the source of cavitation; large particles in a vortex cannot be pulled into the vortex, and tiny particles cannot be ejected from the vortex. Therefore, appropriate particle size is an induced condition for cavitation. Particle-borne air nuclei facilitate early cavitation initiation, sometimes accompanied by pulsating pressure generation and exacerbating cavitation damage. Zeng and He (2020) simplified sediment particles into spherical shapes and simulated the interaction between cavitation bubbles and sediment particles near the wall. They concluded that the initial bubbles, which were adversely affected by the particles during the growth phase, were mushroom-shaped during the collapse, and bubbles less affected by the particles were pear-shaped. Zhang and Wei (2014) analyzed the distribution patterns of the sediment medium in a hydraulic turbine and the influence of the pressure field. They found that sand-containing water flow resulted in increased pressure load on the surface of turbine runner blades. Dong and Sun (2021) experimentally investigated the mechanism of the effect of different sand contents on the cavitation of high-speed water flow. They concluded that the cavitation factor increased with increasing sediment content at the median particle size (d = 1.09 mm), promoting cavitation. Wang et al. (2019) conducted numerical simulations of a Francis turbine at different sediment concentrations and found that in a high-speed rotating runner, solid particles collided forcefully at the walls because of inertial and centrifugal forces. These forces tended to induce cavitation inside the runner, increasing the head loss in the runner and aggravating blade wear. Teran et al. (2018) combined numerical simulations and experimental tests to investigate the interactions between cavitation bubbles and particles collapsing near the solid wall of a Francis turbine. They found that the initial positions of the solid particles and bubbles could significantly influence the particle velocity, inhibiting or accelerating the damage caused by the cavitation bubble collapses. Liang et al. (1997) investigated the vibration of a vacuolar cloud in a dilute solid–liquid two-phase flow and found that the main frequency of the vibration decreased when solid particles were in the bubble cloud. In addition, the solid particles significantly decreased the high-frequency part. In summary, the sediments inside the turbine induce internal wear and tear, whereas the generated air bubbles cause fatigue damage to the runner. In some cases, both phenomena work synergistically to cause more severe damage than each would cause separately. Although many scholars investigated cavitation under a solid–liquid two-phase flow and established systematic theoretical systems, most studies focused on Francis turbines. The study of cavitation under a solid–liquid two-phase flow in a tubular turbine is crucial, as this research area has not been studied extensively. In this study, the effects of different sediment concentrations and particle sizes on the cavitation characteristics of turbine rotor blades in the inlet flow of a tubular turbine were investigated, considering the combined conditions of a light bulb tubular turbine as a premise (Li et al., 2021a).

Turbulence Models and Control Equations

In terms of turbulence model selection, the k–ε model can simulate complex flows and has the advantages of being efficient and stable (Li W. et al., 2021). The k–ω model replaces the dissipation rate, ε, in the equation with the specific dissipation rate, ω, and is more stable in the viscous sublayer (Deyou et al., 2021). The shear stress transport k–ω equation combines the advantages of both equations and modifies the turbulent viscosity equation to obtain a more accurate simulation (Li et al., 2021). Because fluid compressibility slightly influences the flow field, the fluid domain is used as an incompressible fluid in constant-condition calculations for tubular turbines. No heat exchange between the phases in the fluid is considered. Under adiabatic no-slip conditions, the solid phase is equal in size and contains uniform spherical particles, and the phase change effect is negligible. The volume fraction ${\alpha }_m$ and density ${\rho }_m$ of the mixed phase are expressed as follows:

${\alpha }_m={\alpha }_l+{\alpha }_s+{\alpha }_v(1)$

${\rho }_m=1/\left(\frac{{\text{y}}_v}{{\rho }_v}+\frac{y_s}{{\rho }_s}+\frac{y_l}{{\rho }_l}\right)(2)$

where ${\alpha }_l,{\alpha }_s,{\alpha }_v$ are the liquid-, solid-, and gas-phase volume fractions, respectively, and $y_l$, $y_s$, $y_v$ are the liquid-, solid-, and gas-phase mass fractions, respectively. The mass fraction, y, satisfies the following condition expressed by Eq. 3.

$y_l+y_s+y_v=1(3)$

The continuity equation is a concrete expression of the law of matter indestructibility in fluid mechanics and is expressed by Eq. 4:

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \cdot \overrightarrow{v}\right)=0(4)$

where $\rho$ is the fluid density, and $\overrightarrow{v}$ is the velocity vector.

In hydrodynamic machinery, the entire process of a fluid passing through the flow components obeys the law of conservation of momentum, expressed as follows:

$\frac{\partial }{\partial t}\left(\rho \overrightarrow{v}\right)+\nabla \cdot \left(\text{ρ}\overrightarrow{v}\overrightarrow{v}\right)=-\nabla \cdot p+\nabla \cdot \left(\overrightarrow{\tau }\right)+\rho \overrightarrow{g}+\overrightarrow{F}(5)$

where p is the static pressure, and $\rho \overrightarrow{g}$ and $\overrightarrow{F}$ are the gravitational force and external force, respectively. The shear stress tensor for shear $\overrightarrow{\tau }$ is defined as follows:

$\overrightarrow{\tau }=\mu \left[\left(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T\right)-\frac{2}{3}\nabla \overrightarrow{v}I\right](6)$

where $\mu$ is the dynamic viscosity, and I is the unit tensor. The second term on the right-hand side represents the volume expansion effect.

Model and Its Basic Parameters

In this study, a tubular turbine unit in the upper reaches of the Yellow River was selected. Its basic design parameters are listed in Table 1.

TABLE 1

TABLE 1. Technical parameters of crossflow turbines.

The cavitation performance curve between the cavitation coefficient and turbine efficiency was obtained by determining the different draft tube pressure conditions. When the turbine efficiency decreases by 1%, cavitation of the blades occurs at this pressure, and the draft tube outlet pressure becomes the critical cavitation pressure (Fubing, 2021).

The turbine cavitation coefficient is expressed as follows:

${\sigma }_p=\frac{\frac{P_0}{\rho g}-\frac{P_c}{\rho g}-H_s}{H}(7)$

where $P_0$ is the draft tube outlet pressure, $P_c$ is the saturated vapor pressure of water, $\rho$ is the density of water, g is the acceleration owing to gravity, $H_s$ is the turbine suction height, and H is the working head of the turbine.

Ansys ICEM was used to simulate the hybrid meshing of the overall model. Hexahedral structural meshes were used for the inlet section, bulb body, and draft tube, and tetrahedral structural meshes were used for the complex guide vane and runner sections (Li et al., 2021). The entire flow channel mesh is depicted in Figure 1.

FIGURE 1

FIGURE 1. Overall grid of fluid domain of tubular turbine.

The minimum pressure on the blade surface significantly influences the cavitation performance of the runner during cavitation calculations (Hui et al., 2016). Therefore, the relationship between the overall grid number of the turbine, minimum pressure on the blade surface, and cavitation coefficient of the turbine under combined conditions was analyzed to minimize the influence of the grid number on calculation accuracy (Figure 2). The cavitation coefficient increased with an increasing number of grid nodes, with a maximum difference of 0.0031 (Figure 2). In contrast, the minimum pressure on the blade surface decreased with an increasing number of nodes, with a maximum difference of 8,000 Pa (Figure 2). When the number of grids in the entire fluid domain increased from 5.16 million to 8.84 million, the minimum pressure decreased by 3,000 Pa, and the cavitation coefficient increased by only 0.0001, satisfying the calculation accuracy requirements. Therefore, 8846777 grids and 1973260 nodes were adopted for the calculations.

FIGURE 2

FIGURE 2. Grid independence verification.

This study focused on a solid–liquid two-phase flow, and Ansys CFX was used for numerical simulations. The nonhomogeneous phase model was selected for the multiphase flow, and the particle model was used for interphase transport, which is mainly applicable when a phase is continuous, and the other phase is dispersed or polydispersed. The inlet boundary condition was set as the mass flow, the outlet was set as the average static pressure outlet, and the solid boundary surface was a nonslip wall surface. The rotor speed was set to 68.18 r/min, and the calculation area reflected the effect of gravitational acceleration on the sediments. The guide vane opening and impeller opening were 10° and −34.5°, respectively, for the combined conditions (Li, 2014). The rated flow rate, Q, was 375.2 m³/s, the sediment density was 2,650 kg/m³, the sediment particle sizes were 0.01 and 0.05 mm. Sediment concentrations of 1%, 1.5%, and 2% were selected as discrete phases based on the actual measured data obtained at the upper Yellow River. The drag force during momentum exchange was considered. The high-accuracy solution mode was selected, and the convergence target root mean square was $1\times {10}^{-4}$.

Test Verification

Tests were conducted in a hydropower station at the upper reaches of the Yellow River based on hydrological sediment observation data in May 2019 to obtain an average sediment particle size of approximately 0.05 mm. The tests were conducted at sediment concentrations of 1%, 1.5%, and 2% of the water flow using unit #1 as the test verification unit. The unit paddle and guide vane openings were adjusted to 10° and 34.5°, respectively, and a water head of approximately 8 m was selected. Actual experimental tests were performed to collect data, including the turbine efficiency at different concentrations. Because the sediment content and incoming water flow in the river were different, the measurements were performed at different times.

Water flows with sediment concentrations of 1%, 1.5%, and 2% at a particle size of 0.05 mm were intercepted for observation. The turbine efficiency data were received in the central control room of the power station (Figure 3).

FIGURE 3

FIGURE 3. Crossflow hydropower station at upper Yellow River.

Table 2 lists the experimental monitoring efficiency values for different sediment concentrations with a particle size of 0.05 mm, and Figure 4 shows the corresponding efficiency comparison graph. The efficiency of the test monitoring results was higher than the calculated efficiency, and the efficiency decreased as the sediment concentration increased. Overall, the difference between the efficiency calculated through numerical simulations and the efficiency obtained experimentally was slight. The most significant difference in efficiency was observed for the 2% sediment concentration, with a difference of only 1.1%, indicating that the simulation results are accurate.

TABLE 2

TABLE 2. Experimental monitoring data at different sediment particle concentrations.

FIGURE 4

FIGURE 4. Comparison of efficiency at different sediment concentrations for 0.05 mm particle size.

Figure 5 shows the blade cavitation for the 0.05 mm particle size and 2% concentration for the test performed after maintenance. A part of the damaged area appeared at the back of the blade at the junction between the water inlet edge and the rim. The surface metal was flaked off, and tiny pockmarks, pinhole pits, and cracks appeared, indicating cavitation damage. The cavitation location determined from the test was consistent with that predicted through simulations, demonstrating the accuracy of the simulation model.

FIGURE 5

FIGURE 5. Blade cavitation of tubular turbine (Shengyang, 2020).

Calculation Results and Analysis

Figure 6 shows the relationship between the efficiency and the cavitation coefficient of the turbine. A single sediment on the blade drag force could be neglected. However, an increase in the sediment content impeded the water flow on the blade. The higher the drag force impact on the blade, the lower the efficiency of the turbine. The curve also showed that the lower the sediment concentration, the higher the turbine efficiency (Figure 6). The comparison shows that the turbine efficiency was slightly higher at the sediment particle size of 0.05 mm than at 0.01 mm. Moreover, the larger the sediment concentration, the more significant this phenomenon. At cavitation coefficients ${\sigma }_p$ of 2.35–1.96, the overall efficiency tended to be stable, indicating that cavitation did not occur, and the turbine operated stably. As the outlet pressure decreased, the cavitation coefficient approached 1.96–1.84, and the turbine efficiency decreased. When the cavitation coefficient decreased to 1.84, the turbine efficiency decreased by 1%, suggesting that critical cavitation occurred on the blades at an outlet pressure of 0.6 atm (approximately 60.795 kPa). The outlet pressure continued to decrease, the cavitation coefficient decreased from 1.84 to 1.71, and the overall efficiency decreased. However, the slope of the curve gradually decreased; at this time, the blade had numerous cavitation bubbles, and blade cavitation intensified. After the cavitation coefficient decreased to 1.45, the turbine efficiency decreased sharply, and the cavitation bubble occupied the entire blade and flow channel, obstructing the water flow. If this condition occurs for an extended period, the unit may generate vibration and noise, damaging the blade. Therefore, a critical cavitation factor, ${\sigma }_p$, of 1.84 was adopted to evaluate the effect of solid–liquid two-phase flow on the cavitation characteristics of the blade.

FIGURE 6

FIGURE 6. Relationship between efficiency and cavitation coefficient of hydraulic turbine.

Effects of Concentration and Particle Size on Sediment Velocity on Blades

During the flow of water with sediments inside the turbine, the centrifugal force of the rotating blades caused the sediment particles to gradually gather at the shroud. Here, the sediment was affected by the cavitation bubble blockage, and the sediment flow velocity decreased during this process. This is expressed in the flow line, which is the low-speed area at the shroud, as shown by the dark blue flow line in Figure 7. The sediment velocity of the large particles was lower than that of the small particles because when the sediment particle size was large, the inertial force increased, and the water flow was increasing affected by the sediment particles. At the same inlet concentration, the larger the particle size, the lower the velocity. The difference in flow distribution and absolute velocity between the different particle sizes gradually reduced, and the overall flow velocity tended to be smooth as the sediment concentration and velocity increased for both particle sizes. Thus, the vapor volume fraction might gradually decrease with increasing sediment concentration. Therefore, further verification is required.

FIGURE 7

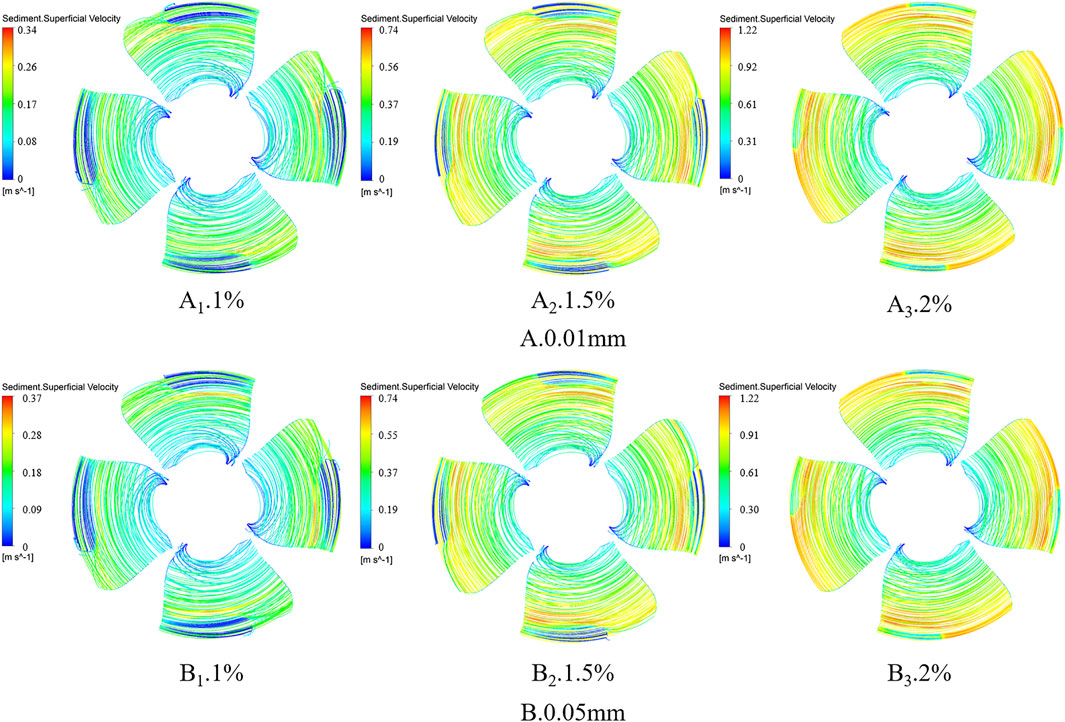
FIGURE 7. Distribution of streamlines on suction side of blade for different sediment particle sizes and concentrations [(A, B) are 0.01 and 0.05 mm particle sizes, respectively; 1, 2, and 3 correspond to 1%, 1.5%, and 2% concentrations, respectively, same as in Figures 8, 9)].

Effects of Concentration and Particle Size on Blade Pressure

Figure 8 shows the pressure distribution on the suction side of the blade. The negative-pressure area gradually decreased from the shroud to the hub. At a sediment concentration of 1%, the negative pressure area for both particle sizes was 23.9 m², confirming that cavitation occurred here. Cavitation was most severe near the shroud (A₁ and B₁ in Figure 8). The width of the negative-pressure area decreased at a concentration of 1.5%, decreasing the pressure area to 20.6 m² for the sediment particle size of 0.01 mm (A₂ in Figure 8) and approximately 20.1 m² for the 0.05 mm sediment (B₂ in Figure 8). When the sediment concentration reached 2%, the negative-pressure area near the hub decreased sharply, and the total area of the negative-pressure region for both particle sizes was 13.3 m². As the sediment concentration increased, the negative-pressure area decreased. Thus, more sediments hit the blade surface as the concentration increased, increasing the overall pressure on the blade.

FIGURE 8

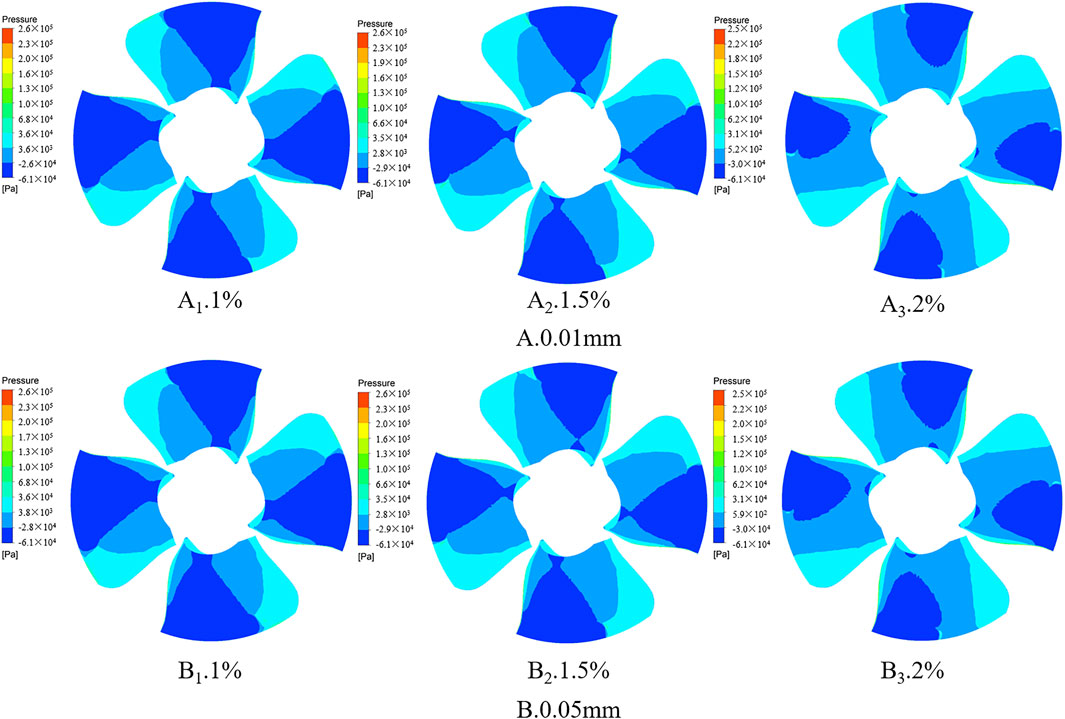
FIGURE 8. Pressure distribution on suction side of blade for different sediment particle sizes and concentrations. (A) and (B) are 0.01 and 0.05 mm particle sizes, respectively; 1, 2, and 3 correspond to 1%, 1.5%, and 2% concentrations, respectively.

The maximum pressures corresponding to the 1%, 1.5%, and 2% concentrations were 2.61 × 10⁵, 2.57 ×10⁵, and 2.46 × 10⁵ Pa for the 0.01 mm sediment particle size and 2.62 ×10⁵, 2.57 ×10⁵, and 2.46 × 10⁵ Pa for the 0.05 mm particle size. The maximum sediment pressure decreased with increasing concentration, probably because of the increase in sediment distribution and the mutual pressure transfer between sediment particles. This resulted in a smoothening of the overall pressure and no pressure peaks, owing to the dispersed distribution of some sediments. The effect of particle size on the magnitude and pressure distribution of the blade pressure was negligible. The results showed that an increase in the sediment content decreased the area of the negative-pressure zone and inhibited cavitation evolution.

Effects of Concentration and Particle Size on Blade Cavitation

As the low-pressure areas of the tubular turbines appeared at the suction side of the runner and were mainly concentrated near the shroud, cavitation mainly occurred at the shroud of the suction side of the blades. For the sediment flow with the runner operating, the cavitation bubble from the center started to collapse outwards when the cavitation bubble just contacted the blade or sediment particles, and the boundary quickly contracted. Here, the pressure gradient of the cavitation bubble edge decreased sharply. The center of the cavitation bubble generated a significant pressure gradient, causing the water to flow towards the blade boundary and sediment particles, forming two microjet flows. Therefore, when sediments were present, a part of the energy generated through the collapse of the cavitation bubbles was transported by the sediment particles. Thus, the higher the sediment content, the lower the bubble distribution on the blade (Figure 9). Extensive cavitation occurred at the shroud, and the bubble distribution was concentrated. A comparison with the pressure distribution graph indicated a significant distribution of bubbles in the area of least pressure at the shroud. The most severe cavitation occurred when the sediment concentration was 1%; at 0.01 mm, the maximum vapor volume fraction was 97.85%, and at 0.05 mm, it was 97.7%. The least significant cavitation was observed at a sediment concentration of 2%; the maximum vapor volume fractions at 0.01 and 0.05 mm were 85.59 and 85.24%, respectively. The calculated cavitation areas were 14.9, 11.3, and 7.39 m² at sediment concentrations of 1%, 1.5%, and 2%, respectively, for the 0.01 mm particle size. For the 0.05 mm particle size, the cavitation areas were 12.61, 10.69, and 7.58 m² at sediment concentrations of 1%, 1.5%, and 2%, respectively. At the same sediment particle size, the sediment concentration increased with decreasing vapor volume, indicating that the sediments significantly inhibited further cavitation development. At the same concentration, the larger the particle size of the sediment, the lower the volume fraction of vapor, indicating that an increase in the particle size had a constraining effect on cavitation. However, the inhibiting effect of the concentration was less significant than that of the particle size.

FIGURE 9

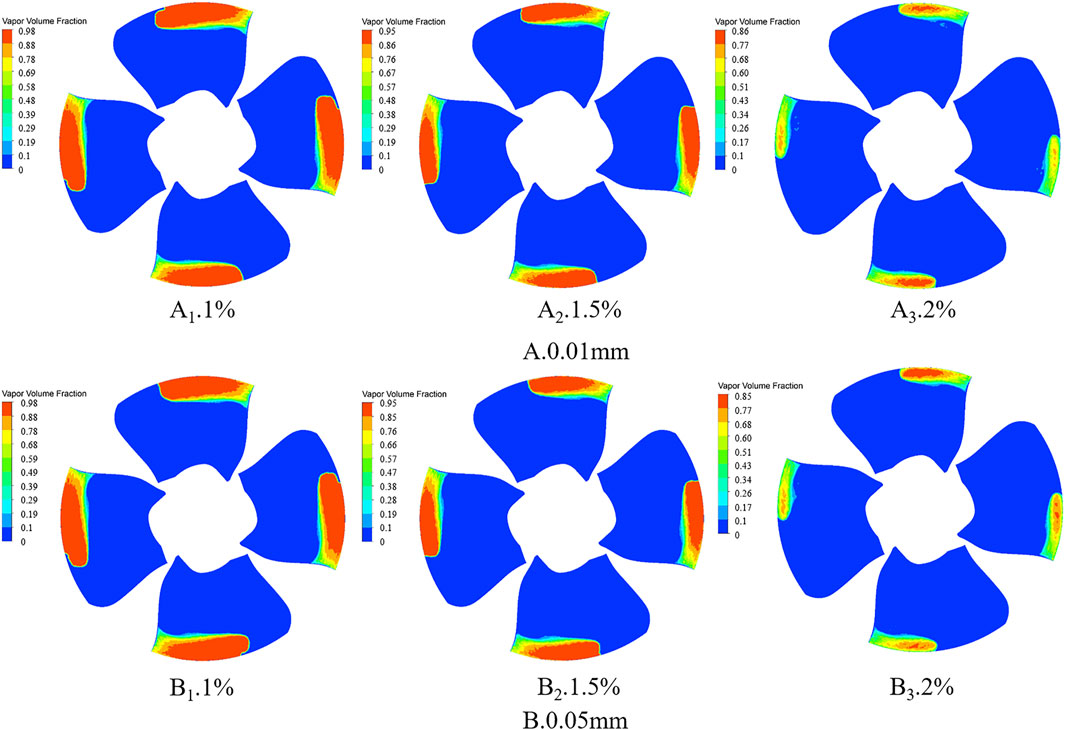
FIGURE 9. Vapor volume distribution on suction side of blade for different sediment particle sizes and concentrations. (A) and (B) are 0.01 and 0.05 mm particle sizes, respectively; 1, 2, and 3 correspond to 1%, 1.5%, and 2% concentrations, respectively.

Discussion

Although the effect of sediment concentration and sediment particle size on the distribution of cavitation bubbles has been analysed in this paper, the size and strength of cavitation bubbles has not been investigated. Much research has been done by some scholars and experts on the occurrence and development of cavitation bubbles, GAO Q (Gao et al., 2021a; Gao et al., 2021b; Gao et al., 2021c) performed numerical simulations using coupled level set and volume of fluid (CLSVOF) method to resolve air-water interface directly and studied the statistics of bubble size distributions; Wang et al. (2021) conducted simulations on the bubbles in the ventilated cavitation and studied the bubble distribution under the effects of breakup and coalescence.

Due to experimental constraints, this paper has some shortcomings below:

1). In the actual operation of hydropower stations, the distribution of sediment particle size and concentration within the sand-bearing water stream is more complex, so the tests carried out in this paper differ to a small extent from the boundary conditions set by the numerical simulation, which is also reflected in the efficiency diagrams derived from the tests.

2). This paper only considers the distribution and size of cavitation under sand-bearing water flow conditions, but lacks the study of other dimensions such as bubble generation, breakage, intensity and size. Although some effects of solid and liquid phases on each other can be obtained, the analysis of the development and evolution of cavitation bubbles is lacking.

We anticipate using a model turbine in future work to test this in order to bring the flow of water with different sediment concentrations and particle sizes within a controlled range and to increase the reliability of the test results. In addition, the solid-water interface will be studied in more detail and the development and evolution of cavitation bubbles will be considered, exploring the specific influence of sediment particles on the size and distribution of cavitation bubbles at the microscopic level.

Conclusion

In this study, a three-dimensional flow-field numerical study of the blade flow and cavitation performance of a tubular turbine was conducted for different sediment particle sizes and concentrations. The blade cavitation and bubble distribution behavior under different working conditions were analyzed. The following conclusions were drawn.

1) The negative-pressure area of the blade decreased with increasing sediment concentration. For the 0.01 mm particle size, the negative-pressure areas were 23.9, 20.6, and 13.3 m² at 1%, 1.5%, and 2% sediment concentrations, respectively. For the 0.05 mm condition, the negative-pressure areas were 23.9, 20.1, and 13.3 m² at 1%, 1.5%, and 2% concentrations, respectively. The larger the concentration of sediments on the blade, the smaller the negative-pressure area. In addition, the maximum pressure decreased with increasing sediment concentration. Apart from the cavitation area, sediment concentration was the main factor influencing the area of the negative-pressure zone on the blade.

2) The vapor area on the blade decreased with increasing sediment concentration. For the 0.01 mm particle size, the vapor areas were 14.9, 11.3, and 7.39 m² at 1%, 1.5%, and 2% sediment concentrations, respectively. For the 0.05 mm size, the vapor areas were 12.61, 10.69, and 7.58 m² at 1%, 1.5%, and 2% sediment concentrations, respectively. The higher the sediment concentration, the lower the volume fraction of vapor. The presence of sediments inhibited further development of cavitation, and the inhibition effect was significant. The inhibition effect of the particle size on cavitation became less significant as the concentration increased.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The CC wrote and improved the paper; ZL provided guidance and advice on writing the paper; FH, SW, and CZ provided guidance on the analysis of the study, KZ provided guidance on the test apparatus, and JZ provided guidance on the tests.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52079118), Central leading local (scientific and technological innovation base construction) project XZ202201YD0017C, National Key Research and Development Program (2018YFE0128500).

Conflict of Interest

FH is employed by Guoneng Dadu River Basin Hydropower Development Co., Ltd. SW is employed by China Three Gorges Construction Engineering (Group) Co., Ltd. CZ is employed by Dongyuan Branch of Shenzhen Water Planning and Design Institute Co., Ltd. KZ is employed by China Gezhouba Group Electromechanical Construction Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Deyou, L., Liang, Y., Xunyu, Y., Hongjie, W., Qian, S., and Xianzhu, W. (2021). Runner Cone Optimization to Reduce Vortex Rope-Induced Pressure Fluctuations in a Francis Turbine. Sci. China Technol. Sci. 64, 1953–1970. doi:10.1007/s11431-021-1867-2

CrossRef Full Text | Google Scholar

Dong, Z-Y., and Sun, J-Y. (2021). Experimental Study of Effects of Sediment Concentration on Cavitation Erosion in High Velocity Flows. J. Hydroelectric Eng. 40 (10), 10–18. doi:10.11660/slfdxb.20211002

CrossRef Full Text | Google Scholar

Fu, X., Zuo, Z., Chang, H., Li, D., Wang, H., and Wei, X. (2021). Mechanism of Low Frequency High Amplitude Pressure Fluctuation in a Pump-Turbine during the Load Rejection Process. J. Hydraulic Res. 59 (2), 280–297. doi:10.1080/00221686.2020.1780488

CrossRef Full Text | Google Scholar

Fubing, H. (2021). Study on Cavitation Characteristics and Flow Field of Tubular under Different Clearances [D]. Chengdu: Xi Hua University.

Google Scholar

Gao, Q., Deane, G. B., Liu, H., and Shen, L. (2021a). A Robust and Accurate Technique for Lagrangian Tracking of Bubbles and Detecting Fragmentation and Coalescence. Int. J. Multiphase Flow 135, 103523. doi:10.1016/j.ijmultiphaseflow.2020.103523

CrossRef Full Text | Google Scholar

Gao, Q., Deane, G. B., and Shen, L. (2021b). Bubble Production by Air Filament and Cavity Breakup in Plunging Breaking Wave Crests. J. Fluid Mech. 929, 890. doi:10.1017/jfm.2021.890

CrossRef Full Text | Google Scholar

Gao, Q., Shen, L., and Deane, G. B. (2021c). A Numerical Simulation Framework for Bubbly Flow and Sound Generation in Laboratory-Scale Breaking Waves. JASA Express Lett. 1 (10), 100801. doi:10.1121/10.0006584

CrossRef Full Text | Google Scholar

Hui, R., Weili, L., Xingqi, L., Yaping, Z., Hongzhe, Q., and Zhongjie, Y. (2016). Effects of Low Pressure Meridional Position on Cavitation Performance for High-Head Pump-Turbine. Trans. Chin. Soc. Agric. Eng. 32 (16), 73–81. doi:10.11975/j.issn.1002-6819.2016.16.011

CrossRef Full Text | Google Scholar

Li, D., Song, Y., Lin, S., Wang, H., Qin, Y., and Wei, X. (2021). Effect Mechanism of Cavitation on the Hump Characteristic of a Pump-Turbine. Renew. Energ. 167, 369–383. doi:10.1016/j.renene.2020.11.095

CrossRef Full Text | Google Scholar

Li, W., Li, Z., Qin, Z., Yan, S., Wang, Z., and Peng, S. (2022). Influence of the Solution pH on the Design of a Hydro-Mechanical Magneto-Hydraulic Sealing Device. Eng. Fail. Anal. 135, 106091. doi:10.1016/j.engfailanal.2022.106091

CrossRef Full Text | Google Scholar

Li, W., Li, Z., Wang, Z., Wu, F., Xu, L., and Peng, S. (2021). Turbulence Intensity Characteristics of a Magnetoliquid Seal Interface in a Liquid Environment. Coatings 11 (11), 1333. doi:10.3390/coatings11111333

CrossRef Full Text | Google Scholar

Li, Z-G. (2014). Research on Co-associated Relation and Performance of Bulb Tubular Turbine [D]. Lanzhou: Lanzhou University of Technology.

Google Scholar

Li, Z., Cheng, C., and Yan, S. (2021a). Theoretical Analysis of Entropy Generation at the Blade Interface of a Tubular Turbine under Cooperative Conditions. Front. Energ. Res. 9, 788416. doi:10.3389/fenrg.2021.788416

CrossRef Full Text | Google Scholar

Li, Z., Li, W., Li, W., Wang, Q., Xiang, R., Cheng, J., et al. (2021b). Effects of Medium Fluid Cavitation on Fluctuation Characteristics of Magnetic Fluid Seal Interface in Agricultural Centrifugal Pump. Int. J. Agric. Biol. Eng. 14 (6), 85–92. doi:10.25165/j.ijabe.20211406.6718

CrossRef Full Text | Google Scholar

Liang, Z., Jiang, J., and Cheng, L-J. (1997). A Study on the Oscillation of the Cloud of Bubbles in a Dilute Solid-Liquid Two-Phase Flow. J. Huazhong Univ. Sci. Tech. 1997 (09), 45–48.

Google Scholar

Liao, T-T. (2012). Research on the Size of Sediment Passing through the Turbine Effects on Cavitation and Cavitation Erosion for the Blade of Three Gorges Hydropower Plant. China Rural Water and Hydropower 2012 (02), 121–123+126.

Google Scholar

Lu, L. (1991). Bubble Collapse in Solid-Liquid Two-Phase Fluid [J]. Acta Mechanica Sinica 1991 (01), 8–16.

Google Scholar

Shengyang, P. (2020). Application of Vortex Dynamics in Solid-Liquid Two Phase Flow of Tubular Turbine [D]. Chengdu: Xihua University.

Google Scholar

Shu-tang, T. (2000). Tubular Turbine Generator Set and its Selection Method [M]. Beijing: China Electric Power Press.

Google Scholar

Sun, J. (2022). “Study on the Influence of Operating Head on Cavitation Performance of an Ultra-low Head Two-Blade Tubular Turbine [J/OL],” in Proceedings of the CSEE, 1–12.

Google Scholar

Teran, L. A., Rodríguez, S. A., Lain, S., and Jung, S. (2018). Interaction of Particles with a Cavitation Bubble Near a Solid Wall. Phys. Fluids 30, 123304. doi:10.1063/1.5063472

CrossRef Full Text | Google Scholar

Wang, L., Li, B-Y., and Zhao, W-G. (2019). Dynamics and Wear Analysis of Hydraulic Turbines in Solid-Liquid Two-Phase Flow. Open Phys. 17 (1), 790–796. doi:10.1515/phys-2019-0082

CrossRef Full Text | Google Scholar

Wang, Z., Liu, H., Gao, Q., Wang, Z., Wang, Y., Wang, G., et al. (2021). Numerical Investigation of Ventilated Cavitating Flow in the Wake of a Circular Cylinder. Phys. Rev. Fluids 6 (6), 064303. doi:10.1103/physrevfluids.6.064303

CrossRef Full Text | Google Scholar

Wangxu, L., Zhenggui, L., Wanquan, D., Lei, J., Yilong, Q., and Huiyu, C. (2021). Particle Image Velocimetry Flowmeter for Natural Gas Applications. Flow Meas. Instrumentation 82, 102072. doi:10.1016/j.flowmeasinst.2021.102072

CrossRef Full Text | Google Scholar

Wu, L., and Zhu, Q. (2021). Impacts of the Carbon Emission Trading System on China's Carbon Emission Peak: A New Data-Driven Approach. Nat. Hazards 107 (3), 2487–2515. doi:10.1007/s11069-020-04469-9

CrossRef Full Text | Google Scholar

Xu-na, G., Yuan, J., Jiang, F., and Ma, X. (2019). Molecular Dynamics Simulation of Hydraulic Mechanical Cavitation. J. Eng. Therm. Energ. Power 34 (08), 43–49. doi:10.16146/j.cnki.rndlgc.2019.08.007

CrossRef Full Text | Google Scholar

Zeng, Q-F., and He, Z-B. (2020). “Numerical Simulation of the Interaction between Cavitation Bubbles and Sediment Particles in the Hydroturbine,” in Proceedings of the 31st National Symposium on Hydrodynamics (Volume II), Xiamen, Fujian, China, October 30–November 3, 2020, 65–73.

Google Scholar

Zhang, G., and Wei, X-Z. (2014). Numerical Analysis for Effects of Concentration and Diameter of Sediment on Solid-Liquid Two-Phase Flow in Hydraulic Turbine Runner. Trans. Chin. Soc. Agric. Eng. 30 (23), 94–100. doi:10.3969/j.issn.1002-6819.2014.23.013

CrossRef Full Text | Google Scholar