Metaheuristic Algorithm Based Maximum Power Point Tracking Technique Combined With One Cycle Control For Solar Photovoltaic Water Pumping Systems

Solar photovoltaic technology has become eminent in the world because of its clean and abundant nature and can be effectively used for water pumping applications. A maximum power point tracking method is indispensable to achieve the best benefit from photovoltaic systems. Conventional maximum power tracking methods become successful only under uniform irradiance conditions and fail to track the maximum power under partial shading conditions (PSC). Hence, nature-inspired metaheuristic algorithms were proposed to track the optimum power under varying environmental conditions. This study proposes a method for improving the performance of the nature-inspired maximum power point tracking algorithms by using a nonlinear control technique called one cycle control. Based on the duty cycle obtained from the tracking algorithm the one cycle control technique generates pulses for the DC–DC converter, which is connected to a brushless DC motor pump system through a voltage source inverter. The performance of the proposed system under various PSCs is validated using the Cuckoo search, particle swarm optimization, and grey wolf algorithms. Simulation results for various shading patterns prove the supremacy of the system with respect to convergence speed, tracking efficiency, robustness, steady-state oscillations at maximum power point, and initial exploration oscillations in comparison with systems without one cycle control. In addition, the introduction of a KY converter as a DC–DC converter reduces the output voltage ripple in the system. Thus, the proposed system with one cycle control overcomes the disadvantages of the existing methods and can be effectively utilized for water pumping applications.

1 Introduction

The need for energy resources for the social and economic development of society is growing day by day. However, the threats caused by the usage of nonreplenishable resources like coal, oil, and natural gas can extend from global warming to the loss of biodiversity. To overcome this catastrophic climate change and energy crisis, renewable energy resources (solar, wind, and hydel) have been introduced for energy production, which are viable, replenishable, and pollution free. Among these, solar energy is considered to be the most beneficial because it is clean, abundant, and pollution free and reduces the carbon footprint in the world and slows down climate change. Solar photovoltaic systems are used to supply electricity for a wide variety of applications like water pumping, livestock watering, and street lighting. Standalone solar water pumping systems (Kumar et al., 2018) are emerging to be among the prominent applications of photovoltaic technology in rural farming, fish farms, etc., because of an increase in fuel prices and the unavailability of a national grid in remote areas. A reliable and cost-effective water pumping can be guaranteed with an energy-efficient motor that has a long life, low maintenance, low radio frequency interference, and low noise (Kumar and Singh, 2016). Hence, a brushless DC (BLDC) motor with the above-mentioned benefits is identified as the appropriate motor for solar-fed water pumping applications (Kiran, 2018).

The photovoltaic (PV) output power is mainly fluctuating because of varying solar insolation and temperature. Hence, the PV system is embedded with maximum power point tracking (MPPT) algorithms like hill climbing, incremental conductance, and perturb and observe (P&O) to obtain the highest power generated. These algorithms ensure optimum power point tracking under normal irradiation conditions. Partial shading conditions (PSCs) (Kermadi et al., 2020a) occurring because of nonuniform irradiances received in PV panels because of buildings, telephone poles, trees, etc. also cause a reduction in output power of the panel. Multiple peaks in the power–voltage (P–V) characteristic curve occurring during partial shading cannot be differentiated via conventional MPPT algorithms, and these methods trap the local peak instead of the actual global peak. Hence, to mitigate the issue of obtaining a global power peak from the P–V curve, many solutions have been proposed in the literature.

Artificial intelligence-based techniques like fuzzy logic (FL) (Li et al., 2019) and artificial neural networks (ANNs)) (Rizzo and Scelba, 2015) have been introduced to track the global maximum power point (GMPP) under partial shading and variable irradiance conditions. However, complex hardware implementation requires greater computation time, and the requirement of large training data for both ANN and FL decreases its efficiency in calculating the maximum power point. Thus, metaheuristic algorithm-based MPPT techniques that mimic the behavior of fireflies, bees, ants, birds, etc. were developed to impart efficient, precise, and prompt response in GMPP tracking under PSCs. One of the significant bio-inspired algorithms was particle swarm optimization (PSO) (Liu et al., 2012) algorithm with greater tracking speed and better global convergence rate. Researchers have also proposed several other algorithms to track the GMPP under varying irradiance conditions like the Cuckoo search (CS) algorithm (ref), grey wolf optimization (GWO) (Mohanty et al., 2016), firefly algorithm (Sundareshwaran et al., 2014), and flower pollination algorithm (FPA) (Prasanth Ram and Rajasekar, 2017). All these algorithms raise their performance by improving population size and boosting the number of iterations, thereby increasing the computational complexity. In addition, all these optimization algorithms follow the same principles of exploration of search space and exploitation to find the best solution.

An intelligent monkey king algorithm was proposed (Kumar et al., 2017a) for GMPP detection under the partially shaded condition of PV arrays. This algorithm reduces the computational burden compared to existing GMPP tracking techniques but with increased oscillations during tracking. Moreover, a Boost converter is used as the DC–DC converter, and the battery is used as the load. Hence, the performance of the system when connected to AC has to be evaluated.

A mathematics-based hybrid Cauchy and Gaussian sine–cosine optimization algorithm was proposed (Kumar et al., 2017b) for lead acid battery charging using a single current sensor. Even though the cost and complexity of the system were reduced using this algorithm, tracking time and tracking efficiency have to be improved and the behavior of the algorithm when connected to an AC motor has to be evaluated (a normal harmony search algorithm-based MPPT) (Ikhlaq Hussain et al., 2018) with a reduced sensor proposed to improve the searching ability and increase the rate of convergence during GMPP tracking of solar PV systems. However, the validity of the system was checked for grid-connected mode only.

Another MPPT tracking algorithm called whale optimization with differential evolution (WODE) for dynamic and steady-state conditions of a partially shaded PV system was proposed (Kumar et al., 2017c) to reduce the steady-state oscillation and computational burden and hence reduce the power loss in the output. However, the reliability of the system is proved with the Boost converter as the DC–DC converter and battery as the load.

Some of the algorithms developed for GMPP tracking (Ahmed and Salam, 2014; Ram and Rajasekar, 2017; Kermadi et al., 2020b) are subjected to transient oscillations while searching for maximum power point, thereby decreasing the efficiency of the system. An MPPT algorithm based on a fractional chaotic ensemble particle swarm optimizer (Yousri et al., 2020) was tested only for uniform irradiation conditions, whereas the effectiveness of the technique under dynamic conditions was not illustrated. In Jamaludin et al. (2021), MPPT based on salp swarm optimization was presented. However, the tracking time taken by this algorithm is greater than the proposed one.

Hybridization between conventional and metaheuristic algorithms was developed to improve the performance of these algorithms. Some of the works presented in the literature are PSO with P&O (Mao et al., 2019), FPA with P&O (Ram et al., 2020), PSO with adaptive-network-based fuzzy inference system (Priyadarshi et al., 2019), fuzzy with PSO (Priyadarshi et al., 2018), and hybrid GWO-FL (Eltamaly and Farh, 2019). These techniques were combined to reduce the oscillations while reaching MPP. These methods provide improved performance but involve complex programming and high computational load in MPPT compared to existing systems.

Precise tracking, simple programming, and higher convergence rate are the prime concerns for the MPPT algorithms used in standalone photovoltaic applications. These advantages can be achieved by metaheuristic algorithms like PSO, CS, and GWO. In this study, a new strategy based on one cycle control (OCC) (Smedely and Cuk, 1995) is combined with MPPT algorithms for the efficient operation of water pumping systems. The MPPT algorithms are used to find the optimum value of the duty cycle corresponding to obtaining maximum power. Hence, based on the obtained duty cycle, the OCC-based technique generates pulses to be applied to the DC–DC converter.

OCC-based technique guarantees faster response and better source and load perturbation rejection (Binitha and Kumar, 2013) compared to systems using conventional PWM control and is proved through obtained results. Most studies in the area of OCC focused on power factor correction and DC Microgrid voltage regulation (de Carvalho Neto et al., 2018). Fewer works in literature dealt with the application of OCC with MPPT algorithms. Moreover, this work presents the KY converter (Hwu and Yau, 2009) as the DC–DC converter as it has low voltage ripple and nonpulsating output current compared to Boost or Buck–Boost converters.

Thus, this study proposes metaheuristic MPPT algorithms with OCC and KY converter for standalone PV-fed water pumping systems. The efficacy of the proposed method is validated through simulation results under normal and PSCs.

The major outcomes of this work are as follows:

A novel technique combining metaheuristic algorithm-based MPPT and OCC is introduced to obtain the GMPP.

The presented method is tested using three different types of metaheuristic algorithms, namely, CS, GWO, and PSO.

The effectiveness of the proposed system is established under various environmental conditions and verified using simulation results with the three different algorithms.

The proposed method has low oscillations around GMPP, higher convergence speed, and better tracking efficiency compared to existing systems without OCC.

2 Proposed System Description

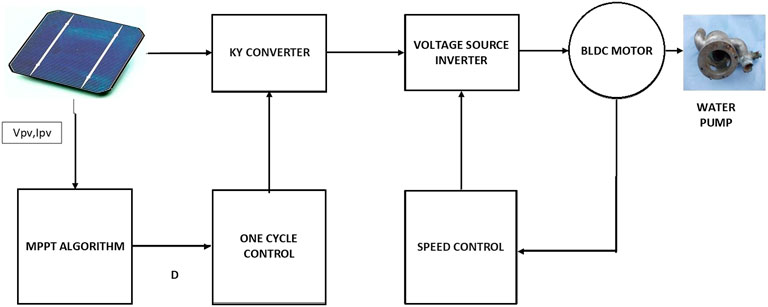
The block diagram of the system described in the current work is shown in Figure 1. The proposed system consists of a solar PV panel that through a KY converter and a voltage source inverter feeds the BLDC motor and water pump. Moreover, the system has no access to a grid or battery and operates with the energy powered by solar cells only. An 810 W PV panel under normal conditions (1000 W/m²) is taken to design the system. Metaheuristic MPPT algorithms along with OCC generate pulses for the KY converter, which assists in obtaining GMPP at various climatic conditions. Moreover, the BLDC motor pump with a voltage rating of 48 V and a rated speed of 3,000 rpm is selected for the system. Hysteresis current control technique is applied to BLDC motor for constant speed operation. KY converter is designed as the DC–DC converter in the proposed arrangement because of reduced voltage ripple and good load transient behavior. The various components in the system are explained as follows.

FIGURE 1

FIGURE 1. Block diagram of the proposed system.

2.1 Photovoltaic System

The photovoltaic plant of the system consists of 3 PV modules connected in series to obtain the required power. The PV parameters of the system are shown in Table 1.

TABLE 1

TABLE 1. Parameters of the photovoltaic system.

2.1.1 Partial Shading Effects of Photovoltaic Systems

In order to provide adequate power for a particular application, PV modules can be connected in series or parallel. However, some conditions like cloudy weather and shadows from birds and trees obstruct the PV modules from receiving the same irradiance as given in Figure 2A. This situation is termed partial shading. During this circumstance, the shaded cells carry a current higher than actual, thus making them reverse biased. As a result, shaded cells act as load, absorbing power from the series-connected unshaded cells. Moreover, the heat produced by this power can damage the cells by creating hotspots (Ahmed et al., 2019). This can be avoided by including bypass diodes in series with the PV modules, which protect the cells from hot spot effects by providing an additional path to the generated high current. However, the presence of bypass diodes can cause multiple peaks in the P–V characteristics of the solar module depending upon the irradiance levels. Hence, in the P–V curve, the GMPP is the point corresponding to maximum power while the remaining are treated as local maximum power points. The P–V characteristics of the PV module under partial shading and normal conditions are illustrated in Figure 2B.

FIGURE 2

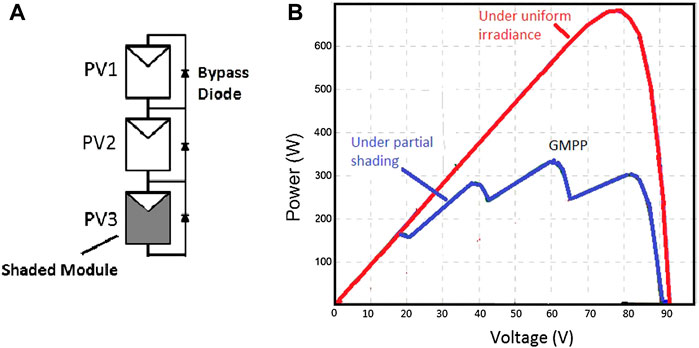
FIGURE 2. (A) partial shaded photo photovoltaic (PV) module and (B) PV characteristics under normal and partial shading

2.2 KY Converter

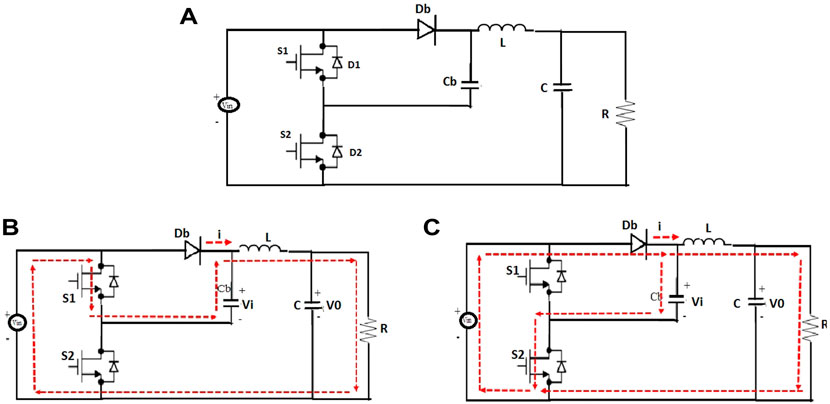
The output of the PV panel is given to a step-up DC converter called the KY converter. The proposed converter has low voltage ripple, nonpulsating output current, and higher voltage gain (Karthikeyan and Essaki, 2018) compared to Boost converter. The boosted output voltage is fed to the BLDC motor pump system through a voltage source inverter. Thus, an output voltage with low ripple and comparatively higher efficiency can be achieved, which can be implemented for the proposed system. As illustrated in Figure 3A, the KY converter has two MOSFET switches S1 and S2 with body diodes D1 and D2, output inductor L, output capacitor C, diode Db, and one energy transferring capacitor C_b for keeping the voltage constant. The switch S1 operates for a period of D and S2 for (1-D), where D is the duty cycle for S1. The two different modes of operation of the converter are as follows:

FIGURE 3

FIGURE 3. (A) KY converter. (B) Mode 1 operation and (C) Mode 2 operation.

Mode 1: In this mode, S1 is turned on and S2 is off as shown in Figure 3B, causing inductor L to be magnetized. Moreover, capacitor C_b is discharged in this mode.

The voltage across inductor L in this mode is given as follows:

$V_L=V_{in}+V_{Cb}-V_o(1)$

V_in—input voltage, V_Cb—voltage across capacitor C_b, and V_o—output voltage.

Mode 2: In this mode, S1 is turned off and S2 is on, as shown in Figure 3C, thereby causing L to be demagnetized. Capacitor C_b is charged to input voltage V_in within a short time.

The voltage across inductor L in this mode is given as follows:

$V_L=V_{in}-V_o(2)$

The voltage gain of the KY converter is given as follows:

$\frac{V_o}{V_{in}}=1+D(3)$

V_o—output voltage or DC link voltage, 135V.

V_in = Vpv − 96.3 V

D—duty cycle of switch S1

The duty cycle is obtained as follows:

$\frac{135}{96.3}=1+D(4)$

D = 0.4 switching frequency fsw-20 kHz

Based on the above parameters, the KY converter is designed and the obtained values for inductor and capacitors are shown in Table 2.

TABLE 2

TABLE 2. Design parameters of the KY converter.

2.3 Brushless DC Motor Pump System

A 48 V, 500 W, 3000 rpm (N) BLDC motor is chosen for the proposed system. The centrifugal pump is selected for the application by assessing the value of proportionality constant K with the equation

$K=\frac{P}{{\omega }_r^3}$

$K=\frac{500}{{\left(\frac{2\ast 3.14\ast 3000}{60}\right)}^3}=1.61\ast {10}^{-5}Watt/rad/\sec (5)$

P is the motor power, and W_r is the rated speed of the BLDC motor in rad/sec.

${\omega }_r=\frac{2\ast \prod \ast N}{60}$

3 Proposed Control Strategy

The main objective of this study is to obtain maximum possible power from PV arrays with the shortest possible time, lower steady-state oscillation, and higher tracking efficiency with reduced output voltage ripple thereby obtaining an efficient water pumping system. Hence, a novel technique combining metaheuristic algorithm-based MPPT and OCC is introduced to obtain the above-mentioned objective. MPPT algorithms, namely, PSO, CS, and GWO, applied to the system and OCC strategy are explained in detail in the subsequent sections.

3.1 Metaheuristic Algorithms

Many nature-inspired evolutionary algorithms have been developed for optimization in the past few years. Two crucial basic characteristics of these modern metaheuristic algorithms are intensification (exploitation) and diversification (exploration). These algorithms search, wisely for the best solution in a search space, thus providing the most suitable answer.

3.1.1 Particle Swarm Optimization

PSO is a swarm intelligence optimization algorithm developed based on the behavior of bird flocks. Simple implementation, fast convergence, and the ability to find the best solution in a multidimensional path make it suitable for finding GMPP. This algorithm uses several particles in an n-dimensional space, and each particle has its own position (P) and velocity (V). Duty cycle is assigned as the particle. To obtain the optimum point, the particle swarm moves toward the best position of its own (Pbest) or the best position in the neighborhood (Gbest) by continuously changing the position and velocity as required. The standard PSO algorithm can be defined by the following equations:

$v_i^{(k+1)}=\omega v_i^k+c1r1\ast (Pbest-p_i^k)+c2r2\ast (Gbest-p_i^k)(6)$

$p_i^{(k+1)}=p_i^k+v_i^{(k+1)}(7)$

i = 1,2,....N.

v_i and p_i are the velocity and position of particle i, respectively; k represents the iteration number; W is the inertia weight; r1 and r2 are random variables whose values are uniformly distributed in the range [0, 1]; and c1 and c2 represent the cognitive and social coefficients, respectively.

The flow chart of the PSO algorithm for MPPT is illustrated in Figure 4A.

FIGURE 4

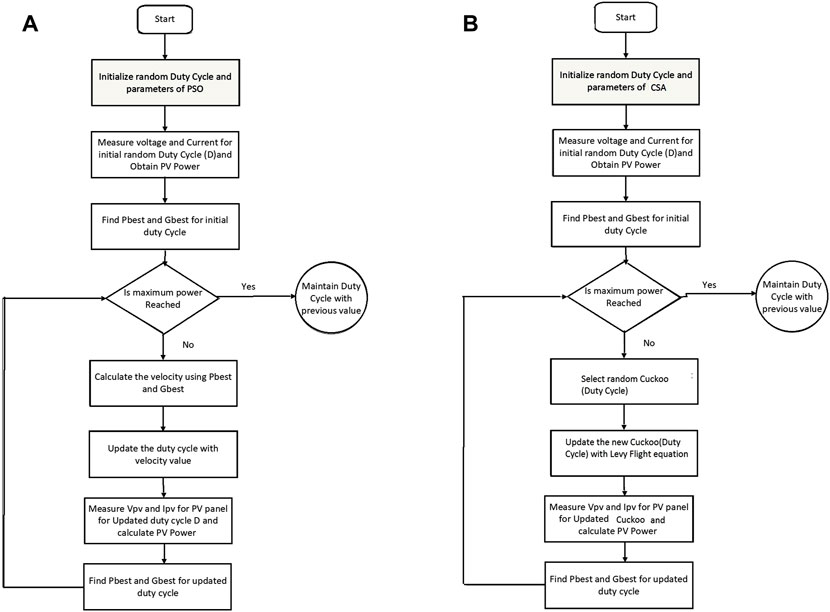
FIGURE 4. Flowchart. (A) particle swarm optimization (PSO) algorithm and (B) Cuckoo search algorithm.

3.1.2 Cuckoo Search Algorithm

CS algorithm is a metaheuristic method inspired by the behavior of cuckoo bird species in their reproduction process. Cuckoos are parasitic organisms that lay their eggs inside other birds’ nests instead of building their own nests. Cuckoo birds will fly randomly from one nest to another and choose the best nest so that their eggs have the best chance to hatch and generate a new generation of cuckoos. Based on this natural behavior, a CS optimization algorithm is developed.

The trajectories chosen by the birds while searching for nests can be modeled using mathematical functions. Levy flight model is most commonly used in CS algorithm for nest searching, where Levy flight can be thought of as a random walk with step size having Levy probability distribution. The objective function in maximization problems like MPPT is proportional to the fitness of a solution.

The equation for implementing a new solution to CS algorithm, using Levy flight, is expressed as follows:

$x_j^{i+1}=x_j^i+\alpha \oplus Levy(8)$

i is the sample number, and α is the step size.

In most cases, α = 1. The product ⊕ means entry-wise multiplications.

In this case, the samples are defined as the values of PV voltages Vi (i = 1, 2 … n). The fitness function is the value of power at MPP, which is obtained from the value of duty cycles. The maximum power provided by its corresponding voltage is considered to be the current best sample. New samples are generated based on the following equation:

$V_j^{i+1}=V_j^i+\alpha \ast Levy(9)$

Figure 4B indicates the flowchart of CS algorithm.

3.1.3 Grey Wolf Optimization Algorithm

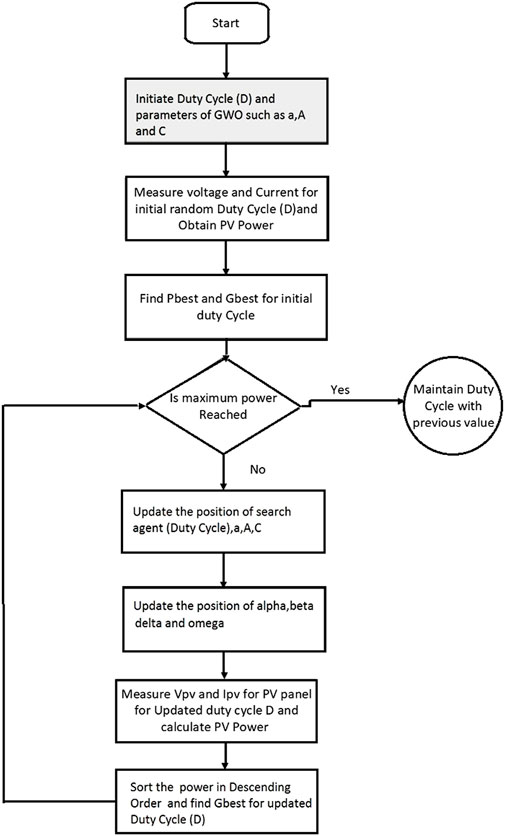
GWO is a metaheuristic algorithm that imitates the leadership and hunting method of grey wolves in nature. In GWO algorithm, four different types of grey wolves are used, namely, alpha (α), beta (β), delta (Δ), and omega (Ω). When developing GWO, alpha is taken as the leader giving the fittest solution to the optimization problem. The second and third options are beta and delta; omega wolves are dominated by delta, and they have to submit to alpha and beta. They use three main steps in hunting, namely, searching for the prey, encircling the prey, and attacking the prey. The encircling action is modeled by the following equations:

$\overrightarrow{D}=\overrightarrow{C}\ast \overrightarrow{Xp\left(t\right)}-\overrightarrow{Xp\left(t\right)}(10)$

$\overrightarrow{X(t+1)}=\overrightarrow{Xp\left(t\right)}-\overrightarrow{A\ast }\overrightarrow{D}(11)$

D, A, and C represent coefficient vectors, where t denotes the current iteration, Xp is the prey’s position vector, and X involves the grey wolf’s position vector. The A and C vectors are determined as follows:

$A=2\ast a\ast r1-a(12)$

$C=2\ast r2(13)$

where components of “a” are randomly decreased from 2 to 0 and r1 and r2 are random vectors in [0, 1]. This algorithm is simple, possesses faster convergence and good accuracy, and can be applied for obtaining global MPP. Figure 5 illustrates the flowchart of the GWO algorithm.

FIGURE 5

FIGURE 5. Flowchart of the grey wolf algorithm.

3.2 One cycle control

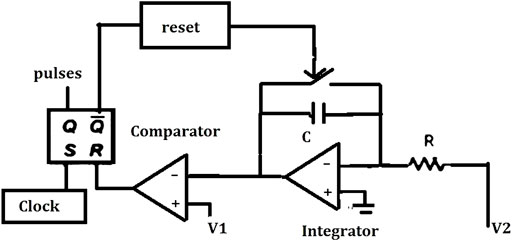
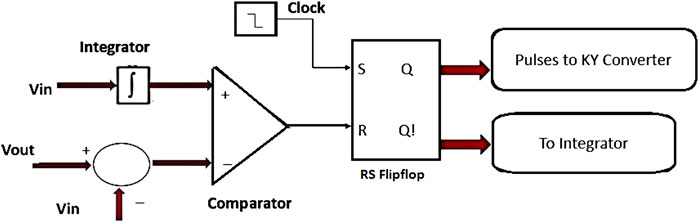
OCC is a nonlinear technique that controls the duty cycle of the switch in each cycle such that averaged value of the switching variable is proportional to control reference. In other words, using this technique, the amplitude of the carrier is controlled rather than the control variable. This method used in power converters outperforms the existing PWM switching techniques by providing key advantages like a fast dynamic response, good stability, excellent disturbance rejection, and robust performance. The block diagram of the OCC controller is shown in Figure 6.

FIGURE 6

FIGURE 6. One cycle control (OCC) controller block diagram.

The OCC controller is basically composed of a comparator, a resettable integrator, and an RS flip-flop connected to an oscillator in S input for generating the clock at a constant switching frequency. The output generated by the integrator, which is a ramp signal is compared with the reference value in the comparator. The ramp signal value increases till the reference, and then, the integrator gets resettled. Furthermore, the Qbar output of RS flip-flop becomes 0, till the beginning of the next switching cycle. Thus, in this method, the reference voltage in each cycle will be exactly equal to the average value of the output signal. OCC-based technique combined with PI control was applied in standalone applications but with increased complexity and increased transients. The proposed method has the ability to overcome the limitations of conventional techniques and provide efficient performance to the water pumping system. The one cycle-based controller applied in the proposed system is elaborated in the following section.

3.2.1 One Cycle Control applied to KY converter

In this system, a KY converter is used as the DC–DC converter. The output voltage equation of the KY converter is given as follows:

$\frac{Vout}{Vin}=1+D(14)$

Vout and Vin are the output and input voltages of the converter, respectively, and D is the duty cycle of the converter. Rearranging the above equation,

$Vout-Vin=DVin(15)$

$Vout-Vin=\frac{{\displaystyle {\int }_0^{Ton}Vindt}}{Ts}(16)$

The input voltage Vin is obtained from the duty cycle corresponding to maximum power point. In this type of OCC method, based on the above equations, the input voltage is integrated using the integrator. Likewise, the difference between output and input voltage is measured and compared with the integrator output (Vin) in the comparator as shown in Figure 7. As long as Vin is less than Vout–Vin, the comparator output remains 0, keeping the S–R flip flop in the ON condition. Since the Q output of the S–R flip flop is feeding the switch of the KY converter, it also remains in the ON state. Every time the difference between output and input voltages reaches Vin, the flip-flop resets and remains low until the next clock signal, thereby keeping the KY converter output pulses in low state.

FIGURE 7

FIGURE 7. OCC-based pulse generation of the KY converter.

4 Simulation Results

The proposed photovoltaic water pumping system model illustrated in Figure 1 is used for simulation and consists of three series PV modules, namely, KY converter, voltage source inverter, and BLDC motor pump system along with MPPT controller including OCC. Parameters of solar PV panels are detailed in Table 1.

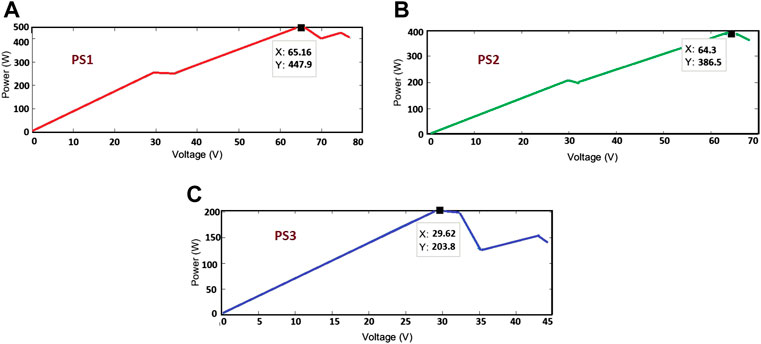
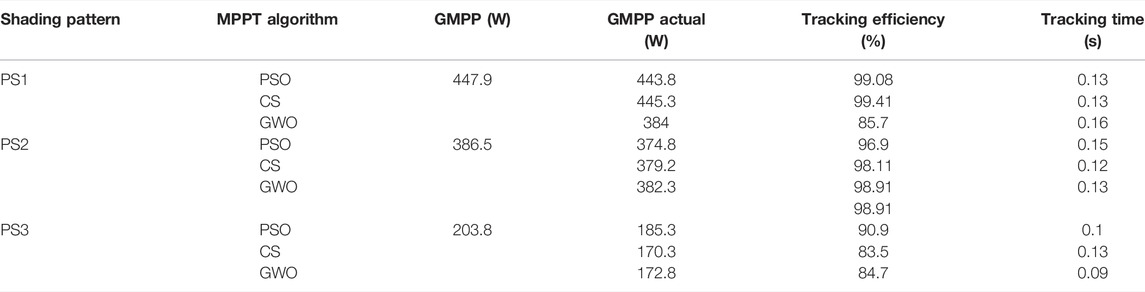
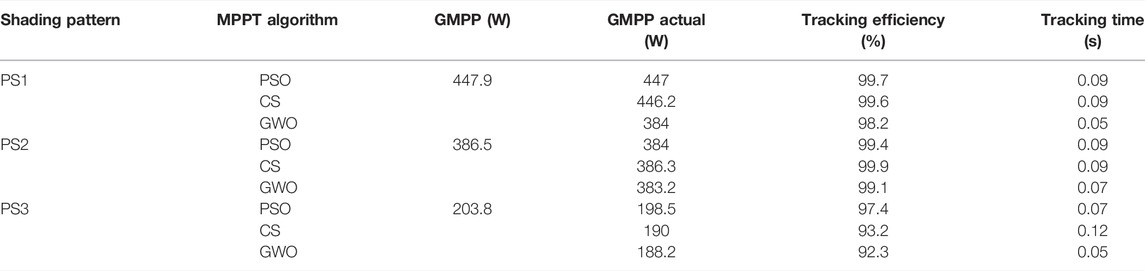
The partially shaded condition is obtained by making the irradiance of each model at different values. Three sets of PSCs are selected to test the performance of the system with OCC. The different PSCs indicate different GMPP positions in the P–V curve, which can be left, right, and middle GMPP. These are detailed in Table 3, and the corresponding P–V curves are represented in Figure 8. The three metaheuristic algorithms, namely, PSO, CS, and GWO, are used with OCC to test the performance of the system. Comparisons with systems without OCC prove the effectiveness of the proposed system in standalone applications.

TABLE 3

TABLE 3. Details of simulated shading patterns.

FIGURE 8

FIGURE 8. PV characteristics under partial shading. (A) PS1, (B) PS2, and (C) PS3.

4.1 Performance Analysis With Irradiation Patterns

4.1.1 Performance Analysis With PS1

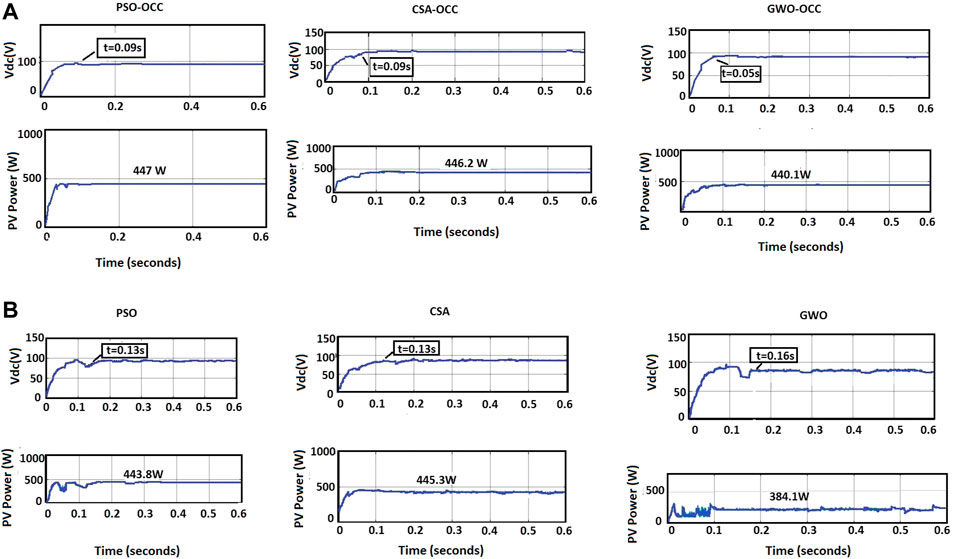
The obtained simulation results of PV power and DC link voltage with PSO, CS, and GWO with and without OCC for irradiation pattern 1 are presented in Figures 9A,B, respectively. This shading pattern has a GMPP of 447.9 W on the middle side of the P–V curve. The power values obtained from PSO, CS, and GWO algorithms are 447, 446.2, and 440.1 W, respectively. With OCC, the tracking time is 0.09 s for PSO, 0.09 s for CS, and 0.05 s for GWO. The results show that for systems without OCC, the tracking time is 0.13, 0.13, and 0.16 s for PSO, CS, and GWO, respectively. Moreover, the results show large power fluctuations during tracking time compared to OCC-based systems.

FIGURE 9

FIGURE 9. Performance with PS1. (A) with OCC and (B) without OCC.

4.1.2 Performance Analysis With PS2

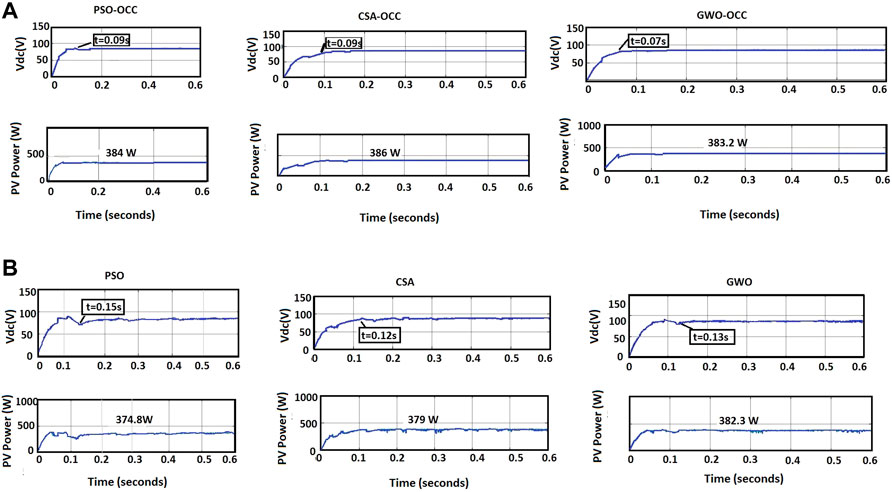
In irradiance pattern 2 (PS2), the GMPP is located on the right with 386.5 W. The obtained simulation results for GMPP and DC link voltage with and without OCC are presented in Figures 10A,B, respectively. The PSO, CS, and GWO achieved GMPP with 384, 386.3, and 383.2 W. The tracking time is 0.09 s with PSO, 0.09s with CS, and 0.07s with GWO. The same pattern without OCC had a tracking time of 0.15, 0.12, and 0.13 s for PSO, CS, and GWO, respectively. The graph proves that the MPPT tracking technique combined with OCC is more accurate with lower tracking time and less oscillation during tracking.

FIGURE 10

FIGURE 10. Performance with PS2 (A) with OCC and (B) without OCC.

4.1.3 Performance Analysis With PS3

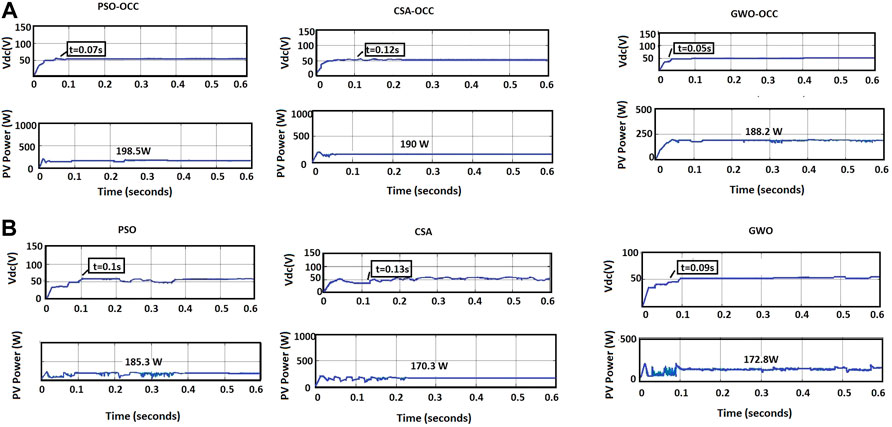
Irradiance Pattern3 (PS3) illustrates a GMPP of 203.8 W located on the left side of the P–V curve. The GMPP and DC link voltage obtained for the different MPPT algorithms with and without OCC are shown in Figures 11A,B, respectively. A GMPP of 198.5, 190, and 188.2 W was obtained. The tracking time was 0.07 s for PSO, 0.12 s for CS, and 0.05s for GWO. However, the results presented without OCC indicate that MPP is reached with higher oscillations and increased tracking time as in Figure 11B. A tracking time of 0.1, 0.13, and 0.09 s was obtained for PSO, CS, and GWO, respectively.

FIGURE 11

FIGURE 11. Performance with PS3 (A) with OCC and (B) without OCC.

4.2 Performance of the System

The OCC controller output waveforms (output pulses and integrator output) for irradiance pattern 1 are illustrated in Figures 12A,B, respectively. In a similar manner, BLDC motor speed and back emf obtained are shown in Figures 12C,D. Hysteresis current control makes the BLDC motor run at a constant speed of 3000 rpm except for very low irradiances.

FIGURE 12

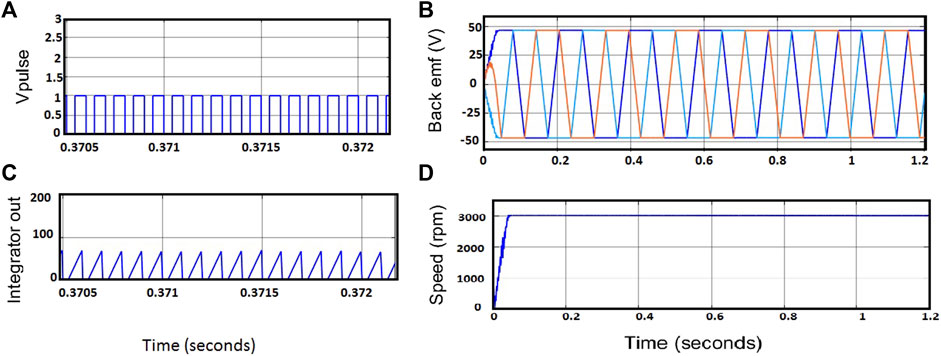
FIGURE 12. OCC waveforms. (A) Output pulses and (B) Integrator. Motor parameters (C) and Back emf (D) Speed.

5 Discussion

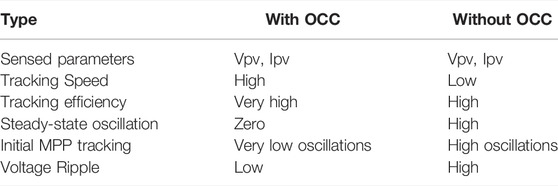
The simulation results for the system with and without OCC are listed in Tables 4, 5, respectively. The results show that systems using MPPT algorithms with OCC operate at a higher efficiency even under low irradiance conditions. Moreover, it has reduced oscillations, making reduced voltage ripple and lower tracking time compared to systems without OCC. The qualitative comparison in terms of tracking speed, tracking efficiency, sensed parameter, steady-state oscillation, initial MPP tracking, and output voltage ripple is presented in Table 6. Hence, the results prove that the proposed system operates with maximum power even under PSCs and has higher tracking efficiency, low steady-state oscillations, and reduced voltage ripple.

TABLE 4

TABLE 4. Results of shading patterns with OCC.

TABLE 5

TABLE 5. Results of shading patterns without OCC.

TABLE 6

TABLE 6. Qualitative comparison of systems with and without OCC.

6 Conclusion

This study presented a technique to track the GMPP of a brushless DC motor-driven PV-fed water pumping system under different environmental conditions. The proposed system combined metaheuristic MPPT algorithms like PSO, GWO, and CS algorithms with OCC to track the GMPP efficiently with higher tracking efficiency and lower oscillations during tracking and greater tracking speed. The performance of the system was compared with systems without OCC for three different PSCs through simulations. The results obtained revealed that the proposed system surpassed the existing technique without OCC in terms of tracking efficiency, tracking speed, and stability. Thus, this technique is expected to be a good choice for agriculturalists searching for efficient water pumping systems.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

ANN, artificial neural networks; BLDC, brushless dc; CS, cuckoo search; FL, fuzzy Logic; FPA, flower pollination algorithm; GMPP, global maximum power point; GWO, grey wolf optimization; MPPT, maximum power point tracking; P and O, perturb and observe; PSC, partial shading conditions; PSO, particle swarm optimization; PV, photo voltaic; P–V, power–voltage; OCC, one cycle control; WODE, whale optimization with differential evolution.

References

Ahmad, R., Murtaza, A. F., and Sher, H. A. (2019). Power Tracking Techniques for Efficient Operation of Photovoltaic Array in Solar Applications - A Review. Renew. Sustain. Energy Rev. 101, 82–102. doi:10.1016/j.rser.2018.10.015

CrossRef Full Text | Google Scholar

Ahmed, J., and Salam, Z. (2014). A Maximum Power Point Tracking (MPPT) for PV System Using Cuckoo Search with Partial Shading Capability. Appl. energy 119, 118–130. doi:10.1016/j.apenergy.2013.12.062

CrossRef Full Text | Google Scholar

Binitha, P. M., and Kumar, T. S. (2013). Comparison of PWM and One-Cycle Control for Switching Converters. Int. J. Emerg. Technol. Adv. Eng. 3 (4), 332–336.

Google Scholar

de Carvalho Neto, J. T., Salazar, A. O., Lock, A. S., and Fonseca, D. A. M. (2018). One Cycle Control for Battery Connected Standalone Photovoltaic Systems for DC Loads. IEEE Lat. Am. Trans. 16 (7), 1977–1983. doi:10.1109/tla.2018.8447365

CrossRef Full Text | Google Scholar

Eltamaly, A. M., and Farh, H. M. H. (2019). Dynamic Global Maximum Power Point Tracking of the PV Systems under Variant Partial Shading Using Hybrid GWO-FLC. Sol. Energy 177, 306–316. doi:10.1016/j.solener.2018.11.028

CrossRef Full Text | Google Scholar

Hwu, K. I., and Yau, Y. T. (2009). KY Converter and its Derivatives. IEEE Trans. Power Electron. 24 (1), 128–137. doi:10.1109/tpel.2008.2009178

CrossRef Full Text | Google Scholar

Jamaludin, M. N. I., Tajuddin, M. F. N., Ahmed, J., Azmi, A., Azmi, S. A., Ghazali, N. H., et al. (2021). An Effective Salp Swarm Based MPPT for Photovoltaic Systems under Dynamic and Partial Shading Conditions. IEEE Access 9, 34570–34589. doi:10.1109/access.2021.3060431

CrossRef Full Text | Google Scholar

Karthikeyan, G., and Essaki, R. (2018). KY Converter for Renewable Energy Systems. Int. J. Pure Appl. Math. 118.

Google Scholar

Kermadi, M., Chin, V. J., Mekhilef, S., and Salam, Z. (2020a). A Fast and Accurate Generalized Analytical Approach for PV Arrays Modeling under Partial Shading Conditions. Sol. Energy 208, 753–765. doi:10.1016/j.solener.2020.07.077

CrossRef Full Text | Google Scholar

Kermadi, M., Salam, Z., Ahmed, J., and Berkouk, E. M. (2020b). A High-Performance Global Maximum Power Point Tracker of PV System for Rapidly Changing Partial Shading Conditions. IEEE Trans. Industrial Electron. 68 (3), 2236–2245.

Google Scholar

Kiran, S. R. (2018). Analysis of Solar Photovoltaic Source Fed BLDC Motor Drive with Double Boost Converter for Water Pumping Application in Irrigation System. Int. J. Adv. Sci. Technol. 120, 73–84.

Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017a). Maximum Power Peak Detection of Partially Shaded PV Panel by Using Intelligent Monkey King Evolution Algorithm. IEEE Trans. Ind. Appl. 53 (6), 5734–5743. doi:10.1109/tia.2017.2725954

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017c). MPPT in Dynamic Condition of Partially Shaded PV System by Using WODE Technique. IEEE Trans. Sustain. Energy 8 (3), 1204–1214. doi:10.1109/tste.2017.2669525

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2018). Normal Harmonic Search Algorithm-Based MPPT for Solar PV System and Integrated with Grid Using Reduced Sensor Approach and PNKLMS Algorithm. IEEE Trans. Ind. Appl. 54 (6), 6343–6352. doi:10.1109/tia.2018.2853744

CrossRef Full Text | Google Scholar

Kumar, N., Hussain, I., Singh, B., and Panigrahi, B. K. (2017b). Single Sensor-Based MPPT of Partially Shaded PV System for Battery Charging by Using Cauchy and Gaussian Sine Cosine Optimization. IEEE Trans. Energy Convers. 32 (3), 983–992. doi:10.1109/tec.2017.2669518

CrossRef Full Text | Google Scholar

Kumar, R., and Singh, B. (2016). BLDC Motor-Driven Solar PV Array-Fed Water Pumping System Employing Zeta Converter. IEEE Trans. Ind. Appl. 52 (3), 2315–2322. doi:10.1109/tia.2016.2522943

CrossRef Full Text | Google Scholar

Li, X., Wen, H., Hu, Y., and Jiang, L. (2019). A Novel Beta Parameter Based Fuzzy-Logic Controller for Photovoltaic MPPT Application. Renew. energy 130, 416–427. doi:10.1016/j.renene.2018.06.071

CrossRef Full Text | Google Scholar

Liu, Y.-H., Huang, S.-C., Huang, J.-W., and Liang, W.-C. (2012). A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Energy Convers. 27 (4), 1027–1035. doi:10.1109/tec.2012.2219533

CrossRef Full Text | Google Scholar

Mao, M., Zhou, L., Yang, Z., Zhang, Q., Zheng, C., Xie, B., et al. (2019). A Hybrid Intelligent GMPPT Algorithm for Partial Shading PV System. Control Eng. Pract. 83, 108–115. doi:10.1016/j.conengprac.2018.10.013

CrossRef Full Text | Google Scholar

Mohanty, S., Subudhi, B., and Ray, P. K. (2016). A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System under Partial Shading Conditions. IEEE Trans. Sustain. Energy 7 (1), 181–188. doi:10.1109/tste.2015.2482120

CrossRef Full Text | Google Scholar

Prasanth Ram, J., and Rajasekar, N. (2017). A New Global Maximum Power Point Tracking Technique for Solar Photovoltaic (PV) System under Partial Shading Conditions (PSC). Energy 118, 512–525. doi:10.1016/j.energy.2016.10.084

CrossRef Full Text | Google Scholar

Prasanth Ram, J., and Rajasekar, N. (20172017). A Novel Flower Pollination Based Global Maximum Power Point Method for Solar Maximum Power Point Tracking. IEEE Trans. Power Electron. 32 (11), 8486–8499. doi:10.1109/tpel.2016.2645449

CrossRef Full Text | Google Scholar

Priyadarshi, N., Padmanaban, S., Holm-Nielsen, J. B., Blaabjerg, F., and Bhaskar, M. S. (2019). An Experimental Estimation of Hybrid ANFIS–PSO-Based MPPT for PV Grid Integration under Fluctuating Sun Irradiance. IEEE Syst. J. 14 (1), 1218–1229.

Google Scholar

Priyadarshi, N., Padmanaban, S., Maroti, P. K., and Sharma, A. (2018). An Extensive Practical Investigation of FPSO-Based MPPT for Grid Integrated PV System under Variable Operating Conditions with Anti-islanding Protection. IEEE Syst. J. 13 (2), 1861–1871.

Google Scholar

Ram, J. P., Pillai, D. S., Ghias, A. M. Y. M., and Rajasekar, N. (2020). Performance Enhancement of Solar PV Systems Applying P&O Assisted Flower Pollination Algorithm (FPA). Sol. Energy 199, 214–229. doi:10.1016/j.solener.2020.02.019

CrossRef Full Text | Google Scholar

Rizzo, S. A., and Scelba, G. (2015). ANN Based MPPT Method for Rapidly Variable Shading Conditions. Appl. Energy 145, 124–132. doi:10.1016/j.apenergy.2015.01.077

CrossRef Full Text | Google Scholar

Smedley, K. M., and Cuk, S. (1995). One-cycle Control of Switching Converters. IEEE Trans. Power Electron. 10 (6), 625–633. doi:10.1109/63.471281

CrossRef Full Text | Google Scholar

Sundareswaran, K., Peddapati, S., and Palani, S. (2014). MPPT of PV Systems under Partial Shaded Conditions through a Colony of Flashing Fireflies. IEEE Trans. Energy Convers. 29 (2), 463–472.

Google Scholar

Yousri, D., Thanikanti, S. B., Allam, D., Ramachandaramurthy, V. K., and Eteiba, M. B. (2020). Fractional Chaotic Ensemble Particle Swarm Optimizer for Identifying the Single, Double, and Three Diode Photovoltaic Models' Parameters. Energy 195, 116979. doi:10.1016/j.energy.2020.116979

CrossRef Full Text | Google Scholar