Optimal Transmission Switching Based on Analytical Target Cascading Algorithm

The penetration of a high proportion of renewable energy sources (RES) into the power grid intensifies the source–load imbalance, which greatly weakens the network transmission performance and power supply quality, and the effect of relying only on individual regulation within the region is negligible. To enhance the capacity of interconnection and coordination among different areas of power systems and improve the accommodation level of RES and low-carbon efficiency, an optimal transmission switching model based on the bus tearing method is proposed in this article. Firstly, the complex power system is decomposed based on the bus tearing method, and thus, the interconnected power grid structure of the multiarea system is constructed. Secondly, the optimal model of interconnected power grid decomposition and coordination structure considering renewable energy generation is constructed, based on exquisite modeling, to reduce the difficulty of unified analysis and decision-making of the multiarea interconnected power system, and the expression of the model is simplified in the form of the matrix. Then, the analytical target cascading (ATC) method is used to decouple the complex model from the main problem and subproblem and solve the distributed parallel problem, to understand the optimization of the decomposition and coordination structure of the interconnected power grid with source–load coordination. Finally, based on the case studies of the IEEE 14-bus system and IEEE 118-bus system, the effectiveness of the proposed model and method is verified, the coordinated operation of the interconnected power grid and the optimal allocation of network resources are achieved, and the economy of power system operation is improved.

Introduction

Recently, the world is at the intersection of a new scientific, technological, and industrial revolution. New technological breakthroughs accelerate industrial change and promote the emergence of new energy models and new industries. With the continuous expansion of the power grid scale, especially the introduction of the power market to maximize economic benefits, the utilization rate of renewable energy is gradually improved. Under the new situation, using reasonable and advanced methods to apply RES to the power grid is of great significance to the economic operation and low-carbon development of the power system. It also provides a reference for the flexible and efficient operation of a high proportion of new energy power systems under carbon neutral targets in the future.

The uncertainty of new energy and load will affect the safe operation of the power system. The correct establishment of an optimal power flow model is the key to solving the stable operation of the power system. The linearization and convex optimization methods are applied to the optimal power flow model to linearize the nonlinear power flow equation and improve the computational efficiency of the model (Yang et al., 2019). Then, Yang Z. et al. (2018) proposed that the hot start method should be applied to the optimal power flow model to solve the problem of certain deviation in the calculation of the linearization method. In addition, the use of the second-order cone relaxation optimal power flow model method to solve the optimal scheduling problem of power systems is also possible, but the error is large in large power systems (Torbaghan et al., 2020). Based on the analytic objective cascading method for multilevel hierarchical optimization of complex engineering systems (Mohammadi et al., 2019), the decentralized decision-making algorithm realized by TSO + DSO optimal power flow (OPF) model does not need a central coordinator, which greatly improves the computational efficiency of the algorithm.

On the whole, due to the reverse distribution of resources and loads in China, and the strong randomness and volatility of all kinds of renewable energy, with the large-scale grid connection of energy, there are limitations in the regulation of the power grid, and the imbalance between source and load is more prominent. Therefore, it is particularly necessary to strengthen the interconnection and coordination between regions of the power system. Power grid interconnection can make rational use of energy, facilitate the installation of large capacity and high-efficiency units, carry out long-distance power transmission, and realize the optimal allocation of resources in a wider range, which is of great significance to improve the low-carbon efficiency of the power system. At present, the power grid has the conditions of real-time topology control or even active splitting in normal operation. At present, some researchers have explored this problem. For example, Erseghe (2014) uses the ADMM algorithm to solve the distributed optimal power flow calculation of the AC system. The distributed interior point method is used to solve the distributed optimal power flow (Yang C. et al., 2018). To realize the synchronous iteration of each region, Ramanan et al. (2019) uses the synchronous alternating direction multiplier method to solve the parallel coordination optimization problem of multiple relatively independent subsystems, to obtain the global optimal solution of the system and then optimize the economic dispatch model of the interconnected power grid, and to solve the complex nonconvex nonlinear mixed integer programming problem. Feng et al. (2020) propose an innovative three-stage progressive solution method, and ingenious combination of integer factors and nonlinear factors can reduce the difficulty of solving the model. However, the ADMM algorithm is derived from the augmented Lagrange multiplier method and the adjacent point algorithm, which is easy to use due to the separable structure of the problem, and it does not eliminate the inherent shortcomings of the first-order algorithm (Jian et al., 2019). The objective cascade method can be used to accelerate the process of solving large-scale optimization problems which are difficult to solve in a centralized way and to manage systems with multiple independent control entities, which do not share their information. In Marvasti et al.’s study (2014), ATC is used to solve the problem of distributed OPF in an active distribution network with a microgrid. ATC is used to find the optimal generation scheduling with 1 day ahead scheduling (Zhang et al., 2017; Wu et al., 2022). In each iteration of ATC, only the voltage angle of the boundary bus needs to be shared between the master and slave coordination subproblems. Therefore, the data exchange volume of each iteration is low, and the communication structure is simple because each subproblem only communicates with the coordinator. The black start optimization model of transmission and distribution network is established by the objective cascade analysis method, which can effectively coordinate the recovery resources and process of transmission and distribution network and reduce the outage loss (Kargarian et al., 2018a). In addition, the objective cascade method is used to solve the subproblem, and the convergence speed of the algorithm can be accelerated by appropriately dividing the power system area (Mohammadi et al., 2018). A virtual function modeling method is proposed based on the objective cascade method to reduce the cost of the triangular grid (Li et al., 2019). A distributed algorithm based on an objective cascading method for power system optimal power flow problem was analyzed (Kargarian et al., 2018b). A two-layer framework was built by using the target cascade method, and a linear interactive scheduling model based on the active distribution network and virtual microgrid was proposed (Du et al., 2019), which solved the coupling problem caused by the interaction variables between the upper and lower layers and finally achieved the win–win cooperation between the distribution network and microgrid.

This article proposes an ATC-based economic dispatch method for optimal transmission switching which considers renewable energy for the first time. The method constructs a general economic dispatch model of optimal transmission switching considering wind photovoltaic renewable energy. In addition, the bus tearing method is used to segment the interconnected power grid, and more independent economic dispatching decision is made in each region of the segmentation. The decomposition coordination method is used between regions, to realize the coordination between interconnected regions by exchanging the boundary bus state quantity and finally realize the unified optimization of the interconnected power grid as a whole. Finally, through the test and analysis of IEEE 14-bus and IEEE 118-bus systems, the effectiveness of the proposed model is verified, and the effectiveness and feasibility of the ATC method are proved.

The main innovations of this article have two aspects.

(1) A network economic dispatch model considering renewable energy based on ATC is proposed for the first time. This method decomposes the interconnected power grid into regional optimization models, which can effectively improve the economy of the overall operation of the interconnected power grid, realize the optimal allocation of the overall system resources to a greater extent, and realize the source network collaborative optimization in a broader range.

(2) The combination of optimal transmission switching, renewable energy, and ATC can reduce the cost of power exchange between different regions, greatly increase the transmission capacity of the grid structure, and improve the universality of the model and method.

Decomposition of Interconnected Power Grid Based on Bus Tearing

Due to the large scale of the actual power grid, it is subjected to many factors such as regional management, information barriers, and many other factors. It is difficult to establish a unified interconnected power grid model. To improve the overall operation level of the interconnected power grid and speed up the calculation speed of the model, the bus tearing method (Yin and Sun, 2022) is used to split the interconnected grid.

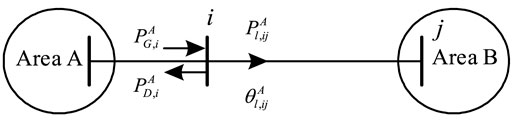
The system can be divided into multiple areas by the bus tearing method, and the tie lines between the two areas can be separated by variables to achieve regional decoupling. As illustrated in Figure 1, the interconnected power system is divided into two areas, area A and area B. This study only focuses on the distribution of active power, $P_{ij}$ signifies the transmission power, the two areas are connected by tie line $\left(i,j\right)$, and node i and node j belong to area A and area B, respectively. $P_{G,i}$ and $P_{D,i}$ denote the power generation and load of node i, respectively.

FIGURE 1

FIGURE 1. Interconnected power system with two areas.

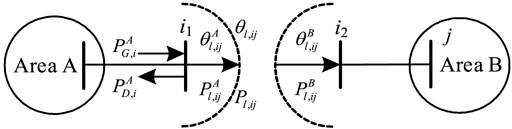
As illustrated in Figure 2, node i in area A is used as the boundary bus between two areas, which are split by the bus tearing method. So, node i is divided into two virtual boundary nodes i₁ and i₂, which are classified into area A and area B, respectively, and serve as the boundary nodes of the two areas.

FIGURE 2

FIGURE 2. Division of the interconnected power system with two areas.

To make the grid after the bus tearing method equivalent to the original grid, it is necessary to ensure that the voltage amplitude and phase angle of boundary nodes i₁ and i₂ are consistent and the input power of the nodes on both sides must be balanced to meet power balance conditions. The corresponding active power $P_{l,ij}$ on the original line $\left(i,j\right)$ is set as a global variable, and this variable is equivalent to two local variables $P_{l,ij}^A$ and $P_{l,ij}^B$, which, respectively, belong to area A and area B and satisfy the consistency constraint $P_{l,ij}^A=P_{l,ij}^B=P_{l,ij}$. Similarly, the phase angle difference ${\theta }_{l,ij}$ between the two ends of the connecting branch is equivalent, and ${\theta }_{l,ij}^A$ and ${\theta }_{l,ij}^B$ meet the constraint condition ${\theta }_{l,ij}^A={\theta }_{l,ij}^B={\theta }_{l,ij}$. As can be seen from Figure 2, after the split, the load of the original node i is assigned to area A, and the corresponding section is assigned to area B.

According to the above processing process, the interconnected power system can be decomposed by the bus tearing method, so there is no direct relationship between the areas; the factors that affect the optimization results of each area are only the global variables corresponding to the adjacent boundaries and their own local variables. Therefore, it can be solved independently for each area.

Mathematic Model

The optimal model of decomposition and coordination structure of interconnected power grid is an economic dispatching decision-making model based on RES and optimal transmission switching. Take area A as an example to describe the mathematical model, and then area B and area C are the same.

Objective Function

The objective function is to minimize the power generation cost of the conventional units of the system.

$\min {\displaystyle \sum _A{\displaystyle \sum _{g\in N_g^A}{C}_g\left(P_g^A\right)}}.(1)$

Constraints

(1) Generator output constraints:

${\underset{¯}{P}}_g^A\le P_g\le {\overline{P}}_g^A,\forall g\in N_g^A,(2)$

$-{\overline{P}}_l^A{z}_l^A\le P_{l,ij}^A\le {\overline{P}}_l^A{z}_l^A,\forall l\in N_L^A.(3)$

(2) Branch power flow constraints:

$b_l^A\left({\theta }_i^A-{\theta }_j^A\right)-P_{l,ij}^A+\left(1-z_l^A\right)M_l^A\ge 0,\forall l\in N_L^A,(4)$

$b_l^A\left({\theta }_i^A-{\theta }_j^A\right)-P_{l,ij}^A-\left(1-z_l^A\right)M_l^A\le 0,\forall l\in N_L^A,(5)$

$M_l^A\ge 2b_l^A{\overline{\theta }}_{ij}^A.(6)$

${\displaystyle \sum _{g\in N_g^A}{P}_g^A}+{\displaystyle \sum _{w\in N_W^A}{P}_{w,t}^A}+{\displaystyle \sum _{pv\in N_{PV}^A}{P}_{pv,t}^A}-{\displaystyle \sum _{d\in N_D^A}{P}_d^A}={\displaystyle \sum _{l\in N_L^A}{P}_{l,ij}^A}\_{\displaystyle \sum _{l\in N_L^A}{P}_{l,ji}^A}(7)$

(3) Regional power balance constraint:

(4) Consistency constraints between areas:

$P_{ij}^A=P_{ij},\forall A,\forall B\in {\text{Δ}}^A,\forall \left(i,j\right)\in {\text{Γ}}^{A,B},(8)$

${\theta }_{ij}^A={\theta }_{ij},\forall A,\forall B\in {\text{Δ}}^A,\forall \left(i,j\right)\in {\text{Γ}}^{A,B}.(9)$

(5) Branch breaking constraint:

${\displaystyle \sum _{l\in N_L^A}\left(1-z_l^A\right)}\le J^A.(10)$

(6) Photovoltaic output constraint:

$0\le P_{pv,t}^A\le P_{pv}^{A\max }.(11)$

(7) Wind power output constraint:

$0\le P_{w,t}^A\le P_w^{A\max }.(12)$

Model Simplification and Solution

The ATC algorithm is a multilevel ladder optimization design method, and each level is a target coordinated optimization design problem (Ahmadi-Khatir et al., 2014). The objective function of the coordination optimization problem is to coordinate the deviation function expression by setting the appropriate response, the weight coefficient of the coupling variable, and the corresponding target deviation weight (Huang et al., 2020). In this algorithm, there are multiple levels (at least 2), and each level includes at least one optimization problem. Optimization problems at different levels are hierarchically related, while problems within the same level are not related Mohammadi and Kargarian, 2020.

A two-level coordination algorithm based on the concept of analytical target cascading is proposed (Kargarian et al., 2015). The general concept of ATC is similar to ADMM and APP. In ADMM and APP, the concept of duality is applied, and a set of penalty functions are introduced, and then the original optimization problem is decomposed into several subproblems. But in ATC, the entire system is first decomposed into several lower-level systems, and then the concept of constraint relaxation (Biskas et al., 2005) is used to solve the problem. The optimization problems of different levels are connected by coupling variables, which are called target variables from the upper-level and response variables from the lower-level point of view. The upper-level optimization determines the values of the target variables and transfers them to the lower-level optimization problems, and the response from the lower-level optimization decision-making determines their distance from the target. In ATC, there are various forms of penalty function, such as quadratic function and exponential function, not just augmented Lagrangian function. Compared with the classic ADMM and APP, ATC is more flexible (Ji et al., 2021). More levels of ATC can be expressed by (13).

$\begin{array}{l}\min \varphi \left({\mathit{x}}_{sys},{\mathit{R}}^{sys}\right)+{\displaystyle {\sum }_{i=1}^N{\Vert w_{sub,i}^R\left({\mathit{R}}_{sub,i}^{sys}-{\mathit{R}}_{sub,i}^{sub}\right)\Vert }_2^2}+{\displaystyle {\sum }_{i=1}^N{\Vert w_{sub,i}^y\left({\mathit{y}}_{sub,i}^{sys}-{\mathit{y}}_{sub,i}^{sub}\right)\Vert }_2^2}\\ s.t.{\mathit{R}}^{sys}={\mathit{R}}^{sys}\left({\mathit{x}}^{sys},{\mathit{R}}_{sub}^{sys}\right),\\ g_{sys}\left({\mathit{x}}_{sys},{\mathit{R}}^{sys}\right)\le 0,\\ h_{sys}\left({\mathit{x}}_{sys},{\mathit{R}}^{sys}\right)=0.\end{array}(13)$

In (13), $x_{sys}$ indicates the upper system design variables, $R^{sys}$ denotes the upper system response (Lotfjou et al., 2010), and $\varphi (\cdot )$ shows the deviation between the system target and the response. $\Vert \cdot \Vert$ is the Euclidean norm, and ${\Vert \cdot \Vert }_2^2$ indicates that the deviation is calculated by using 2-norm. $g_{sys}(\cdot )$ and $h_{sys}(\cdot )$ manifest the vectors of the inequality and equality constraints, respectively. $w_i^R$ and $w_i^y$ represent the positive weight coefficients of response and coupling variables (Miyamoto et al., 2016), respectively. In the objective function (13), the second and third terms are deviations represented by lower-level system responses and coupling variables. The model of lower-level system can be expressed as (14)

$\begin{array}{l}\min {\Vert w_{sub,i}^R\left({\mathit{R}}_{sub,i}^{sys}-{\mathit{R}}_{sub,i}^{sub}\right)\Vert }_2^2+{\Vert w_{sub,i}^y\left({\mathit{y}}_{sub,i}^{sys}-{\mathit{y}}_{sub,i}^{sub}\right)\Vert }_2^2,\\ {\mathit{R}}_{sub,i}^{sub}={\mathit{R}}_{sub,i}^{sys}\left({\mathit{x}}_{sub,i},{\mathit{y}}_{sub,i}^{sub}\right),\\ s.t.g_{sub,i}\left({\mathit{x}}_{sub,i},{\mathit{y}}_{sub,i}^{sub},{\mathit{R}}_{sub,i}^{sub}\right)\le 0,\\ h_{sub,i}\left({\mathit{x}}_{sub,i},{\mathit{y}}_{sub,i}^{sub},{\mathit{R}}_{sub,i}^{sub}\right)\le 0.\end{array}(14)$

In (14), the response value $R_{sub,i}^{sys}$ and the coupling variable target are set as constants. In ATC, the response $R_{sub}^{sub}$ and the coupling variables $y_{sub,i}^{sub}$ of the lower-level system are fixed. Then, the response targets $R_{sub,i}^{sys}$ and coupling variables $y_{sub,i}^{sys}$ of the upper system level are solved and transferred to the lower-level system. Finally, the updated $R_{sub,i}^{sub}$ and $y_{sub,i}^{sub}$ are calculated and passed to the upper-level system. The above process is repeated until the problem converges.

Model Simplification

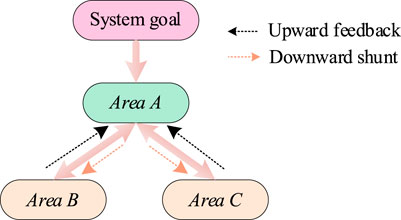
Due to the system facing difficulty in dealing with the coupling problem between areas A, B, and C, the ATC algorithm is used to solve it. Taking the bilevel system structure illustrated in Figure 3 as an example, the decision variables of the upper and lower levels of the system are iteratively optimized to minimize the total operating cost of the system. The upper level is constantly diverted from the top to the bottom, and the lower level responds constantly from the bottom to the top, to realize the unified decision-making and optimization of the whole system.

FIGURE 3

FIGURE 3. System structure of the upper and lower system.

To describe the solving process of the ATC algorithm, the matrix expression of the model is given.

$\min F^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)+{\displaystyle \sum _{n\in N}{F}_n^B\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)},(15)$

$s.t.\{\begin{array}{c}{g}^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)\le 0,\\ h^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)=0,\end{array}(16)$

$s.t.\{\begin{array}{c}{g}_n^D\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)\le 0,\\ h_n^D\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)=0,\end{array}(17)$

$c=\mathit{t}-\mathit{r}=0,(18)$

where $g^A$ and $h^A$ express the inequality and equality constraints of area A, respectively. $x$ represents the local decision variables of the upper system excluding the tie-line. $y$ shows the local decision variables of the lower system excluding the tie-line. $x,t_1,t_2,\dots t_n$ denote the regional variables of the upper system. $g_n^D$ and $h_n^D$ manifest the inequality and equality constraints of the nth lower system, respectively. $y,r_1,r_2\dots r_n,t_1^{\prime },t_2^{\prime },\dots t_m^{\prime }$ represents the upper system area coupling constraint between the variable and the nth lower system area variable.

As the model is a nonconvex mixed integer programming model, and the ATC method is essentially an augmented Lagrangian function method, its convergence is only guaranteed on the convex problem, so the convex optimization idea is used to give an approximate solution to the model.

In this study, the objective function of the model, that is, the power generation cost of conventional units is linearized, and the branch power balance constraint is treated as a quadratic constraint. The original nonconvex power system economic dispatching problem is transformed into a mixed integer quadratic programming problem; thus, a preliminary dispatching feasible solution can be obtained. Then, according to the feasible solution, through the unit output interval compression technology, the new mixed integer quadratic programming model is resolved, and the final economic scheduling result is obtained. The unit output interval compression technology is to find valuable singularities within the set range of conventional unit output and to set a reasonable linearized piecewise value of unit generation cost based on the first stage system dispatching. It can be used to find a better balance between the efficiency of the algorithm and the error caused by linearization. The updating process of the unit output interval can be expressed as follows.

$\{\begin{array}{l}{P}_g^{lb}=P_{g\min },\hfill \\ P_g^{ub}=P_{g,\min }+\xi \frac{\pi }{f_g}.\hfill \end{array}(19)$

Model Decoupling

Due to the existence of a coupling constraint (18), the matrix expression cannot be independently solved. To solve independently, the above bilevel optimization problems need to be decomposed. As demonstrated in Figure 4, the power system is divided into areas A, B, and C, and a bilevel interconnection structure is constructed, that is, the upper system (area A) and the lower system (areas B and C). Two different sets of variables are introduced to model the shared variable c, to establish the objective functions and constraints related to each area. The first variable is the target variable, which is a vector of shared variables sent from the upper system to the lower system. The second variable is the response variable, which is the vector of the shared variable transferred from the lower system to the upper system. In other words, the power transmission between the upper and lower systems is realized by introducing two different sets of variables.

FIGURE 4

FIGURE 4. Relationship between the confidence interval and sample size.

According to the introduced target variable and response variable, the coupling constraint (Equation 18) is solved in the optimization model of the upper system and the lower system, respectively. Here, the penalty function $\zeta$ is used to relax the coupling constraints.

$\mathit{\zeta }\left(\mathit{c}\right)=\mathit{\lambda }\odot \left(\mathit{t}-\mathit{r}\right)+{\Vert \mathit{\mu }\odot \left(\mathit{t}-\mathit{r}\right)\Vert }_2^2,(20)$

where $\odot$ represents the Hadamard product. $\lambda$ and $\mu$ are the primary and quadratic multipliers of the penalty function, respectively.

$\begin{array}{l}\min F^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)+{\displaystyle \sum _{n\in N}\zeta \left(c\right),}\\ s.\mathit{t}.\{\begin{array}{c}{g}^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)\le 0,\\ h^A\left(\mathit{x},{\mathit{t}}_1,{\mathit{t}}_2\dots {\mathit{t}}_n\right)=0.\end{array}\end{array}(21)$

$\begin{array}{l}\min F_n^B\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)+{\displaystyle \sum _{n\in N}\zeta \left(c\right),}\\ s.\mathit{t}.\{\begin{array}{c}{g}_n^B\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)\le 0,\\ h_n^B\left(\mathit{y},{\mathit{r}}_1,{\mathit{r}}_2\dots {\mathit{r}}_n,{\mathit{t}}_1^{\prime },{\mathit{t}}_2^{\prime }\dots {\mathit{t}}_m^{\prime }\right)=0.\end{array}\end{array}(22)$

After the coupling constraints between the upper and lower systems are relaxed by (20), the upper and lower systems only need to meet the local constraints, which constitute the optimization models of the upper system and the lower system, respectively, as revealed in (21) and (22). As a result, the decoupling of the upper level and lower level systems is achieved.

$F^A+{\displaystyle \sum _{n=1}^N{\mathit{\lambda }}_n\odot \left({\mathit{t}}_n-{\mathit{r}}_n^{\ast }\right)+}{\displaystyle \sum _{n=1}^N{\Vert {\mathit{\mu }}_n\odot \left({\mathit{t}}_n-{\mathit{r}}_n^{\ast }\right)\Vert }_2^2}.(23)$

When the upper system (area A) is solving its own model, the new value $t_n^{\ast }$ after the optimization of the virtual load $t_n$ is passed to the lower system, and it participates in the optimization of the lower system as a known quantity. Concurrently, the new value $r_n^{\ast }$ obtained after the optimization of the virtual generator $r_n$ is fed back to the upper system to participate in the optimization, which repeatedly constitutes the iterative optimization process of the upper and lower levels. The objective function of the lower level system is updated to (24) after the penalty function is added.

$F_n^{B\left(C\right)}+{\displaystyle \sum _{n=1}^N{\mathit{\lambda }}_n\odot \left({\mathit{t}}_n^{\ast }-{\mathit{r}}_n\right)+}{\displaystyle \sum _{n=1}^N{\Vert {\mathit{\mu }}_n\odot \left({\mathit{t}}_n^{\ast }-{\mathit{r}}_n\right)\Vert }_2^2}.(24)$

Therefore, in interconnected optimal transmission switching based on ATC, the decomposed upper system model is composed of (23) and (16) and the lower system is composed of (24) and (17). The upper–lower system has been decomposed and can be solved independently, through continuous iteration until the convergence condition is met.

Convergence Condition and Multiplier Updating Principles

The ATC algorithm is essentially an extension and improvement of the Lagrange multiplier method. The convergence criterion of the economic dispatch algorithm for the optimization of the interconnected power grid structure is as follows (Ramanan et al., 2019).

$\left|{\mathit{t}}_{nk}-{\mathit{r}}_{nk}\right|\le {\epsilon }_1,(25)$

$\left|\frac{F_k^A+{\displaystyle \sum _{n=1}^N{F}_{nk}^{B\left(C\right)}-\left(F_{k-1}^A+{\displaystyle \sum _{n=1}^N{F}_{n\left(k-1\right)}^{B\left(C\right)}}\right)}}{F_k^A+{\displaystyle \sum _{n=1}^N{F}_{nk}^{B\left(C\right)}}}\right|\le {\epsilon }_2.(26)$

Eq. 25 indicates that, in the kth iteration, the virtual generator $r_{nk}$ of the lower system and the virtual load $t_{nk}$ of the upper system are used as coupling variables, and the difference between them meets the required accuracy requirements ${\epsilon }_1$. Eq. 26 denotes whether the overall cost of the decomposed upper and lower system satisfies the accuracy in the adjacent iterations. That is, whether the difference between the two iterations is less than the given termination tolerance ${\epsilon }_2$.

If the convergence condition (25) and (26) cannot simultaneously be satisfied, the multiplier of the Lagrange penalty function is updated according to (27).

$\{\begin{array}{l}{\mathit{\lambda }}_{nk}={\mathit{\lambda }}_{n\left(k-1\right)}+2{\mathit{\mu }}_{\left(k-1\right)}\odot {\mathit{\mu }}_{\left(k-1\right)}\odot \left[{\mathit{t}}_{n\left(k-1\right)}-{\mathit{r}}_{n\left(k-1\right)}\right],\hfill \\ {\mathit{\mu }}_{nk}^2=\beta {\mathit{\mu }}_{n\left(k-1\right)}.\hfill \end{array}(27)$

To speed up the convergence speed, the value of $\beta$ is generally $2\le \beta \le 3$, and it takes $\beta$ = 2.3 in this study, the initial value of the multiplier is generally a small constant, which is set to 1.5 in this paper.

ATC Algorithm Flow

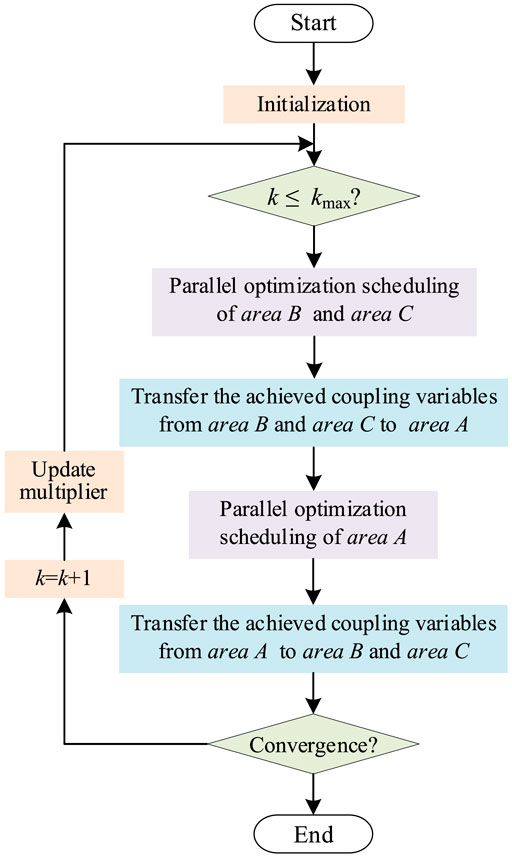
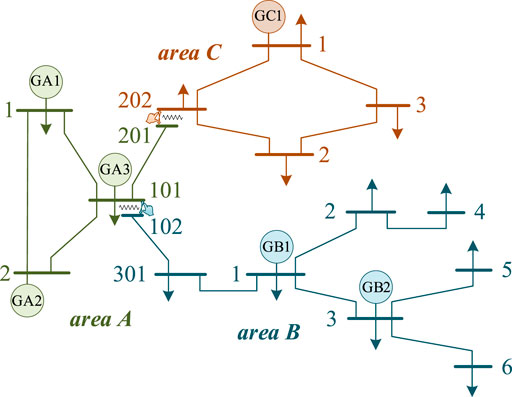
The flow of the economic dispatching algorithm for interconnected optimal transmission switching based on ATC is illustrated in Figure 5. The upper system is area A, the lower system is areas B and C, and area B is not connected to area C.

FIGURE 5

FIGURE 5. Solution flow based on ATC for interconnected power network structure.

The detailed solving steps are as follows.

(1) Set the maximum number of iterations, the initial value of the conventional unit parameters, Lagrangian penalty function primary term multiplier and quadratic term multiplier, etc., and set the number of iterations k = 1.

(2) Solving areas B and C optimization problems. According to (24) and (17) of the lower system model, areas B and C are optimized in parallel, and the results obtained by the solution are transferred to area A.

(3) Solving area A optimization problem. Optimization is performed according to (23) and (16), and the results obtained by the solution are transferred to areas B and C.

(4) Determine whether the iteration can be terminated. If conditions (25) and (26) are achieved, then terminate the iterative process and output the optimal results. If the conditions (25) and (26) are not satisfied concurrently, then update the multiplier according to (27) and proceed to the next iteration (k = k+1) and return to (2).

Example Analysis

The modified IEEE 14-bus (Jabarnejad, 2018) and the modified IEEE 118-bus test system (Ruiz et al., 2012) are selected to simulate and analyze the effectiveness of the proposed model. The test computer is configured with AMD R7-5800H Series CPU, the main frequency is 3.2GHz, and the memory is 16G. GAMS (General Algebraic Modeling System) software is used to program, and CPLEX solver is called for a solution.

IEEE 14-Bus System

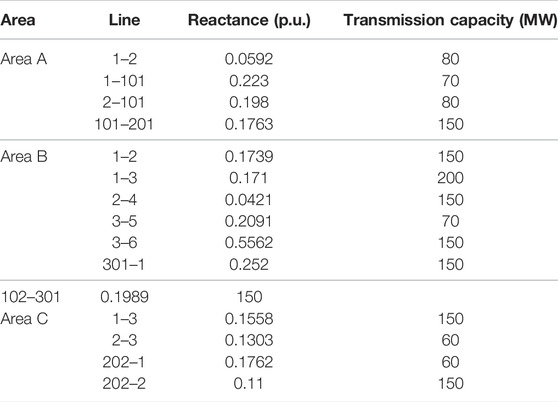
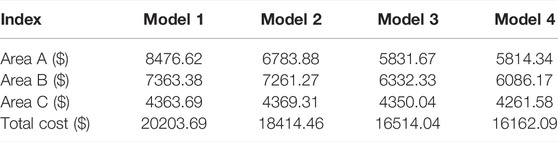
The IEEE 14-bus test system consists of six generators and 16 lines. The parameters of units and lines are displayed in Tables 1, 2. Area A is equipped with a 60 MW wind turbine and a 60 MW photovoltaic at bus 2 and bus 1, area B is equipped with a 50 MW wind turbine and a 50 MW photovoltaic at bus 2 and bus 4, area C is equipped with a 60 MW wind turbine and a 60 MW photovoltaic at bus 2 and bus 3, respectively. It is decomposed into three areas interconnected system by the bus tearing method, and the decomposed system is illustrated in Figure 6. Setting the number of cutting transmission lines in areas A and B to 1, the decision variable decides which line to cut off when the result is optimal.

TABLE 1

TABLE 1. Generator parameters.

TABLE 2

TABLE 2. IEEE 14-bus line parameters.

FIGURE 6

FIGURE 6. Three regional interconnection system.

Effectiveness Analysis of ATC Algorithm

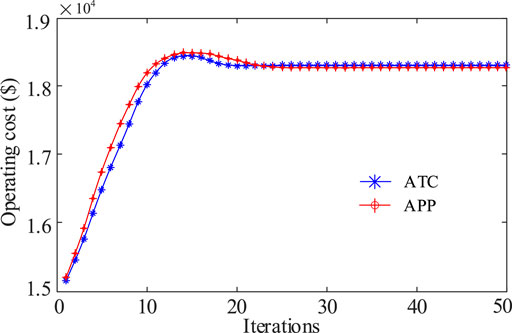
To demonstrate the effectiveness and convergence of the ATC algorithm used in this study, the results of the ATC algorithm used to solve the proposed model are compared with the APP algorithm. The comparison results are illustrated in Table 3 and Figure 7.

TABLE 3

TABLE 3. Results of different algorithms.

FIGURE 7

FIGURE 7. Comparison of ATC and APP operating costs.

As can be seen from Table 3, the operating cost of the APP algorithm is 18212.23$, while that of the ATC algorithm is 18394.46$. Due to the different penalty coefficients selected, the running cost of the ATC algorithm is slightly higher than that of the APP algorithm. In terms of convergence performance, the number of iterations of the ATC algorithm is 34 and that of the APP algorithm is 43, which shows that the convergence speed of the ATC algorithm used in this study is fast. The convergence performance of the APP algorithm depends on its parameters and regional division of the power grid. Due to the complexity of the optimal transmission switching, it is difficult to obtain a sufficient and effective solution. On the other hand, the ATC algorithm has strong expansibility and unlimited series, so it has good applicability to the optimal transmission switching of the system.

Comparison of Four Structural Optimization Models

To demonstrate the effectiveness of the model proposed in this article, the following four optimization models are tested and compared.

Model 1: the effects of optimal transmission switching and wind/photovoltaic system optimization are not considered.

Model 2: optimal transmission switching is not considered, but the influence of wind power and the photovoltaic system is considered.

Model 3: optimal transmission switching is considered, but the effects of wind power and photovoltaic systems are not taken into account.

Model 4: the optimal transmission switching in each area, as well as the influence of wind power and photovoltaic system, is considered.

The total system operation cost of Model 1 is 20203.69$, and the costs of areas A, B, and C are 8476.62$, 7363.18$, and 4363.69$, respectively. According to the operation status of the transmission line, the transmission capacity of the transmission line 101–201 of area A is 0, which means that area C can operate independently and can realize distributed autonomy without receiving relief from the upper system (area A).

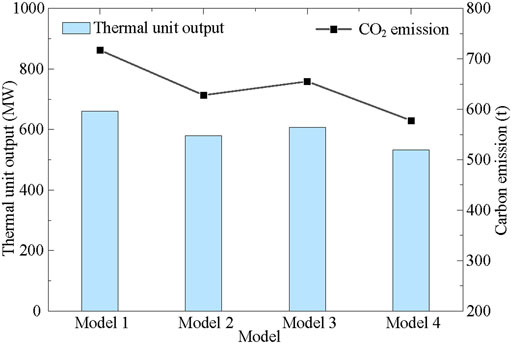
As can be seen from Figure 8, compared with Model 1, due to the consideration of wind power and photovoltaic power generation system in Model 2, the output of thermal units with higher power generation cost is significantly reduced, the pressure of thermal units is alleviated, and the consumption of fossil energy is reduced, thus improving the economy of the system; the detailed data are illustrated in Table 4. Besides, this conclusion can also be obtained from the comparison of Model 3 and Model 4. In addition, as can be seen from the line chart of Figure 8; because of the consideration of both new energy and optimal transmission switching in Model 4, the output of thermal units is significantly reduced compared with several other models, thus reducing the use of fossil fuels and reducing carbon dioxide emissions by 139.232, 50.153, and 77.27 tons, respectively, compared with Model 1, Model 2, and Model 3. The decision results demonstrate that the power grid economy is taken as the objective function, the output of generators and the operation status of transmission lines are taken as decision quantities to consider the optimal transmission switching, the output of thermal power units and the consumption of fossil fuels can be fully reduced, it provides more space for the acceptance of RES, so as to reduce carbon emissions.

FIGURE 8

FIGURE 8. Unit output and carbon emission of four models.

TABLE 4

TABLE 4. Operation status of transmission line in four models.

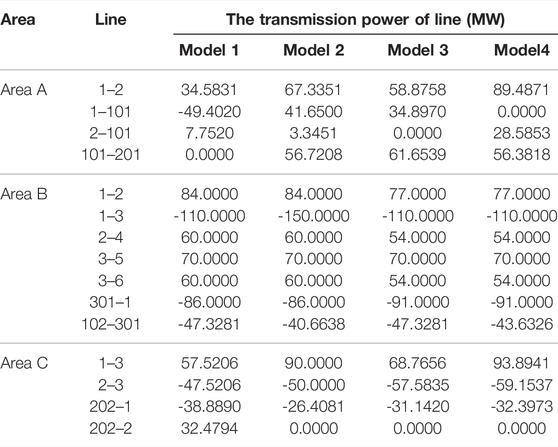
The transmission line operation of the four models is illustrated in Table 5. As can be seen from Figure 8 above, compared with Model 1, the output of the unit GA1 in Model 3 increased by 22.44%, and the output of the unit GA2 with the worst economy decreased by 29.57%. This is because the operation state of the transmission line can be adjusted according to the corresponding load mode, when branch 2–101 in area A and branch 202–2 in area C are cut off, the transmission congestion in the system is alleviated, so that the generating power of the more economical unit GA1 can be sent out. The operating costs of each area are 5831.67$, 6332.33$, and 4350.04$, respectively, which are 14.00 and 0.31% lower than that of Model 1, respectively, and the total cost of the system is 16514.04$, which is 18.26% lower than that of Model 1. It describes that the economic dispatching mode which regards the power grid structure as a dynamic change can achieve the purpose of alleviating network congestion and plays a positive role in the operation economy of the system.

TABLE 5

TABLE 5. Operation status of transmission line in four models.

The total system cost of Model 4 is 16062.09$, which is 20.00, 12.23, and 2.13% lower than that of Model 1 and Model 3, respectively. The results show that Model 4 is more economical than only connecting wind power and photovoltaic system or considering optimal transmission switching. The state of the transmission line can be optimized by the load mode, and branch 1–101 in area A is cut off in the process of regulation, thus reducing the degree of transmission congestion. Compared with Models 1–3, the output of unit GA1 is significantly increased, the output of unit GA2 is also greatly reduced, the generation power of other units with the general economy is also reduced to a certain extent, and the transmission power of some transmission lines is greatly increased (such as line 1-2, etc.), which further shows that the access of wind power and photovoltaic systems and the measures of interrupting transmission lines are applied to power grid dispatching at the same time. It will play a great role in improving the economy of the system operation, and then through the coordination and cooperation among different areas of the power system, the cooperative dispatching of the source network can be realized to a greater extent.

IEEE 118-Bus System Calculation

To test the effectiveness of the proposed model in a large-scale actual power grid, it takes the modified IEEE 118-bus system as an example to test the effectiveness of the proposed model. The system has 53 generators, 91 loads, and 186 lines, and the detailed system data can be found in Fernández-Blanco et al. (2017).

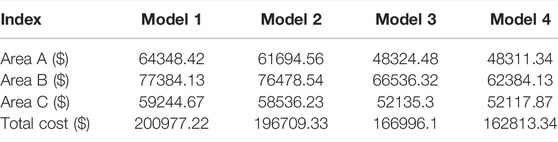
To verify the effectiveness of the proposed model, four models are simulated and tested based on the IEEE118-bus system, and the results are compared as illustrated in Table 6.

TABLE 6

TABLE 6. Comparison of the economy in four models.

As is perspicuously illustrated in Table 6, the total cost of Model 4 is 162813.34$, which is 17.23% lower than that of Model 2 without considering optimal transmission switching, and the operating costs of the three areas are reduced by 21.69%, 18.43%, and 10.96%, respectively. The total cost of Model 3 is 166996.10$, which is 16.91% lower than that of Model 1 without considering optimal transmission switching, and the operating costs of the three areas are 24.90%, 14.02%, and 12.00% lower than that of Model 1, respectively. This indicates that, under the premise of ensuring the safe operation of the system, through the optimal transmission switching, it fully excavates the potential of power generation resources, releases the transmission capacity of the grid structure, and tellingly improves the economy of the system operation.

It is apparent from Table 6 that the total cost of Model 2 is 196709.33$, which is 2.12% lower than that of Model 1 without considering renewable energy, and the operating costs of the three areas are reduced by 4.12%, 1.17%, and 1.20%, respectively. The total cost of Model 4 is 2.50% lower than that of Model 3 without considering renewable energy, and the operating costs of the three areas are 0.03%, 6.24%, and 0.03% lower than that of Model 3, respectively. It reveals that, without considering the optimal transmission switching, the grid-connected generation of renewable energy can be conducive and can reduce the cost of other power generation resources, thus slightly reducing the cost of system operation.

Compared with Models 1–3, the total cost of Model 4 decreased by 18.99%, 17.23%, and 2.50%, respectively, and the operating costs of areas A, B, and C were 48311.34$, 62384.13$, and 52117.87$, respectively, which are manifested in an uneven downward trend compared with Models 1–3, as is described in Figure 9. In addition, the decrease of the operating cost of area A and area B in Model 4 is higher than that in Models 1–3, which is due to the serious blocking between area A and area B, so the cost savings are more conspicuous.

FIGURE 9

FIGURE 9. Regional operating cost line chart of four models.

Hence, wind power, photovoltaic systems, and cut-off transmission lines are simultaneously applied to the power grid to achieve cooperation among system areas, which can efficaciously reduce power generation costs and improve energy efficiency, to achieve the flexibility and economy of the overall operation of the system.

Conclusion

In this study, the dispatching optimization problem of a multiarea power system is studied. Considering the optimal transmission switching and distributed energy grid-connected generation, an optimal economic dispatching model of interconnected power grid decomposition and coordination structure based on the bus tearing method is proposed. The analytical target cascading algorithm is used to solve the problem, and the conclusions based on the example test can be drawn as follows:

(1) The proposed model can effectively improve the economy of the overall operation of the interconnected power grid, significantly improve the capability of flexible operation of the power grid, make efficient use of power generation resources, and realize the unified optimization of the interconnected power grid as a whole.

(2) The proposed model adds discrete variables to indicate whether the transmission line is running or not, so that it can make a reasonable decision on the transmission network architecture needed by the system. The combination of optimal transmission switching, renewable energy, and interconnected power grid coordinated operation greatly enhances the transmission capacity of the grid structure and improves the accommodation capacity of RES and reduces fossil fuel consumption, thus reducing carbon emissions.

(3) The ATC algorithm has the preponderance of fast convergence, strong expansibility, and unlimited series, so it can realize the parallel optimization of multiarea power grids and has perfect applicability to the large-scale system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, Further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was funded by the Open Foundation of key Laboratory of Modern Power system Simulation Control and Green Electric Energy New Technology of the Ministry of Education (MPSS 2021–01).

Conflict of Interest

Author XqZ is employed by the company Yantai Power Supply Company, State Grid Shandong Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi-Khatir, A., Conejo, A. J., and Cherkaoui, R. (2014). Multi-Area Unit Scheduling and Reserve Allocation under Wind Power Uncertainty. IEEE Trans. Power Syst. 29, 1701–1710. doi:10.1109/TPWRS.2013.2293542

CrossRef Full Text | Google Scholar

Biskas, P. N., Bakirtzis, A. G., Macheras, N. I., and Pasialis, N. K. (2005). A Decentralized Implementation of DC Optimal Power Flow on a Network of Computers. IEEE Trans. Power Syst. 20, 25–33. doi:10.1109/TPWRS.2004.831283

CrossRef Full Text | Google Scholar

Du, P., Chen, Z., Chen, Y., Ma, Z., and Ding, H. (2019). A Bi-level Linearized Dispatching Model of Active Distribution Network with Multi-Stakeholder Participation Based on Analytical Target Cascading. IEEE Access 7, 154844–154858. doi:10.1109/ACCESS.2019.2949097

CrossRef Full Text | Google Scholar

Erseghe, T. (2014). Distributed Optimal Power Flow Using ADMM. IEEE Trans. Power Syst. 29, 2370–2380. doi:10.1109/TPWRS.2014.2306495

CrossRef Full Text | Google Scholar

Feng, Z.-k., Niu, W.-j., Cheng, X., Wang, J.-y., Wang, S., and Song, Z.-g. (2020). An Effective Three-Stage Hybrid Optimization Method for Source-Network-Load Power Generation of cascade Hydropower Reservoirs Serving Multiple Interconnected Power Grids. J. Clean. Prod. 246, 119035. doi:10.1016/j.jclepro.2019.119035

CrossRef Full Text | Google Scholar

Fernández-Blanco, R., Dvorkin, Y., and Ortega-Vazquez, M. A. (2017). Probabilistic Security-Constrained Unit Commitment with Generation and Transmission Contingencies. IEEE Trans. Power Syst. 32, 228–239. doi:10.1109/TPWRS.2016.2550585

CrossRef Full Text | Google Scholar

Huang, S., Wu, Q., Zhao, J., and Liao, W. (2020). Distributed Optimal Voltage Control for VSC-HVDC Connected Large-Scale Wind Farm Cluster Based on Analytical Target Cascading Method. IEEE Trans. Sustain. Energ. 11, 2152–2161. doi:10.1109/TSTE.2019.2952122

CrossRef Full Text | Google Scholar

Jabarnejad, M. (2018). Approximate Optimal Transmission Switching. Electric Power Syst. Res. 161, 1–7. doi:10.1016/j.epsr.2018.03.021

CrossRef Full Text | Google Scholar

Ji, X., Zhang, Y., Han, X., Ye, P., Xu, B., and Yu, Y. (2021). Multi-level Interactive Unit Commitment of Regional Power System. Int. J. Electr. Power Energ. Syst. 125, 106464. doi:10.1016/j.ijepes.2020.106464

CrossRef Full Text | Google Scholar

Jian, J., Zhang, C., Yang, L., and Meng, K. (2019). A Hierarchical Alternating Direction Method of Multipliers for Fully Distributed Unit Commitment. Int. J. Electr. Power Energ. Syst. 108, 204–217. doi:10.1016/j.ijepes.2018.12.043

CrossRef Full Text | Google Scholar

Kargarian, A., Fu, Y., and Li, Z. (2015). Distributed Security-Constrained Unit Commitment for Large-Scale Power Systems. IEEE Trans. Power Syst. 30, 1925–1936. doi:10.1109/TPWRS.2014.2360063

CrossRef Full Text | Google Scholar

Kargarian, A., Mehrtash, M., and Falahati, B. (2018a). Decentralized Implementation of Unit Commitment with Analytical Target Cascading: A Parallel Approach. IEEE Trans. Power Syst. 33, 3981–3993. doi:10.1109/TPWRS.2017.2787645

CrossRef Full Text | Google Scholar

Kargarian, A., Mohammadi, J., Guo, J., Chakrabarti, S., Barati, M., Hug, G., et al. (2018b). Toward Distributed/Decentralized DC Optimal Power Flow Implementation in Future Electric Power Systems. IEEE Trans. Smart Grid 9, 2574–2594. doi:10.1109/TSG.2016.2614904

CrossRef Full Text | Google Scholar

Kargarian Marvasti, A., Fu, Y., DorMohammadi, S., and Rais-Rohani, M. (2014). Optimal Operation of Active Distribution Grids: A System of Systems Framework. IEEE Trans. Smart Grid 5, 1228–1237. doi:10.1109/TSG.2013.2282867

CrossRef Full Text | Google Scholar

Li, W., Xiao, M., Yi, Y., and Gao, L. (2019). Maximum Variation Analysis Based Analytical Target Cascading for Multidisciplinary Robust Design Optimization under Interval Uncertainty. Adv. Eng. Inform. 40, 81–92. doi:10.1016/j.aei.2019.04.002

CrossRef Full Text | Google Scholar

Lotfjou, A., Shahidehpour, M., Yong Fu, Y., and Zuyi Li, Z. (2010). Security-Constrained Unit Commitment with AC/DC Transmission Systems. IEEE Trans. Power Syst. 25, 531–542. doi:10.1109/TPWRS.2009.2036486

CrossRef Full Text | Google Scholar

Miyamoto, T., Mori, K., Kitamura, S., and Izui, Y. (2016). Solving Distributed Unit Commitment Problem with Walrasian Auction. IEEE Trans. Syst. Man. Cybern, Syst. 46, 1088–1097. doi:10.1109/TSMC.2015.2468197

CrossRef Full Text | Google Scholar

Mohammadi, A., and Kargarian, A. (2020). Accelerated and Robust Analytical Target Cascading for Distributed Optimal Power Flow. IEEE Trans. Ind. Inf. 16, 7521–7531. doi:10.1109/TII.2020.2973213

CrossRef Full Text | Google Scholar

Mohammadi, A., Mehrtash, M., Kargarian, A., and Barati, M. (2018). “Tie-Line Characteristics Based Partitioning for Distributed Optimization of Power Systems,” in Proceeding of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5-10 Aug. 2018 (IEEE), 1–5. doi:10.1109/PESGM.2018.8586072

CrossRef Full Text | Google Scholar

Mohammadi, A., Mehrtash, M., and Kargarian, A. (2019). Diagonal Quadratic Approximation for Decentralized Collaborative TSO+DSO Optimal Power Flow. IEEE Trans. Smart Grid 10, 2358–2370. doi:10.1109/TSG.2018.2796034

CrossRef Full Text | Google Scholar

Ramanan, P., Yildirim, M., Chow, E., and Gebraeel, N. (2019). An Asynchronous, Decentralized Solution Framework for the Large Scale Unit Commitment Problem. IEEE Trans. Power Syst. 34, 3677–3686. doi:10.1109/TPWRS.2019.2909664

CrossRef Full Text | Google Scholar

Ruiz, P. A., Foster, J. M., Rudkevich, A., and Caramanis, M. C. (2012). Tractable Transmission Topology Control Using Sensitivity Analysis. IEEE Trans. Power Syst. 27, 1550–1559. doi:10.1109/TPWRS.2012.2184777

CrossRef Full Text | Google Scholar

Torbaghan, S. S., Suryanarayana, G., Hoschle, H., D'hulst, R., Geth, F., Caerts, C., et al. (2020). Optimal Flexibility Dispatch Problem Using Second-Order Cone Relaxation of AC Power Flows. IEEE Trans. Power Syst. 35, 98–108. doi:10.1109/TPWRS.2019.2929845

CrossRef Full Text | Google Scholar

Wu, H., Wang, J., Lu, J., Ding, M., Wang, L., Hu, B., et al. (2022). Bilevel Load-Agent-Based Distributed Coordination Decision Strategy for Aggregators. Energy 240, 122505. doi:10.1016/j.energy.2021.122505

CrossRef Full Text | Google Scholar

Yang, C., Liang, H., Liu, Y., Gu, X., Li, X., and Zang, E. (2018a). “Parameter Optimization of Hydropower Governor for Small System during Black Start,” in Proceeding of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5-10 Aug. 2018 (IEEE), 1–5. doi:10.1109/PESGM.2018.8586610

CrossRef Full Text | Google Scholar

Yang, Z., Xie, K., Yu, J., Zhong, H., Zhang, N., and Xia, Q. X. (2019). A General Formulation of Linear Power Flow Models: Basic Theory and Error Analysis. IEEE Trans. Power Syst. 34, 1315–1324. doi:10.1109/TPWRS.2018.2871182

CrossRef Full Text | Google Scholar

Yang, Z., Zhong, H., Bose, A., Zheng, T., Xia, Q., and Kang, C. (2018b). A Linearized OPF Model with Reactive Power and Voltage Magnitude: A Pathway to Improve the MW-Only DC OPF. IEEE Trans. Power Syst. 33, 1734–1745. doi:10.1109/TPWRS.2017.2718551

CrossRef Full Text | Google Scholar

Yin, L., and Sun, Z. (2022). Distributed Multi-Objective Grey Wolf Optimizer for Distributed Multi-Objective Economic Dispatch of Multi-Area Interconnected Power Systems. Appl. Soft Comput. 117, 108345. doi:10.1016/j.asoc.2021.108345

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, G., Qu, T., Liu, Y., and Zhong, R. Y. (2017). Analytical Target Cascading for Optimal Configuration of Cloud Manufacturing Services. J. Clean. Prod. 151, 330–343. doi:10.1016/j.jclepro.2017.03.027

CrossRef Full Text | Google Scholar

Nomenclature

Indices

A, B, C Set of areas.

$N_g^A$ Set of thermal units in area A. Set of conventional units in area A.

$N_D^A$ Set of load in area A.

$N_L^A$ Set of branches in area A.

$N_N^A$ Set of node in area A.

$N_g^A$ Set of thermal units in area A. Set of conventional units in area A.

$N_w^A$ Set of wind farms in area A.

$N_{pv}^A$ Set of photovoltaic systems in area A.

${\Delta }^A$ Set of areas adjacent to area A.

${\Gamma }^{A,B}$ Set of tie line connecting area A and area B.

${\Gamma }^{A,C}$ Set of tie line connecting area A and area C.

Parameters

$J^A$ Maximal number of line interruptions allowed in area A.

$M_l^A$ Large constants.

${\overline{P}}_g^A,{\underset{¯}{P}}_g^A$ Upper and lower limits of output active power of unit g in area A (MW).

${\overline{P}}_l^A$ The upper limit of the transmission capacity of branch l in area A (MW).

$P_{l,ij}^A$ The active power of each area in branch l, its first and end nodes are node i, j, respectively (MW). The active power flows through the original tie line $(i,j)$ in area A (MW).

$P_w^{A\max }$ Maximal active power output by doubly-fed units in area A (MW).

$b_l^A$ Susceptibility of branch l in area A (s).

${\overline{\theta }}_i^A,{\underset{¯}{\theta }}_i^A$ Upper and lower limits of the voltage phase angle of node i in area A (°).

${\theta }_i^A,{\theta }_j^A$ Voltage phase angle of nodes i and j in area A (°).

$z_l^A$ Status of branch l in area A (binary variable)

$P_{pv}^{A\max }$ Maximal active power output by photovoltaic power generation in area A (MW).

$\left(i,j\right)\in {\Gamma }^{A,B}$ The start and end nodes of the tie-line between area A and area B, node i and node j are in area A and area B, respectively.

$\left(i,j\right)\in {\Gamma }^{A,C}$ The start and end nodes of the tie-line between area A and area C, node i and node j are in area A and area C, respectively.

$\xi$ Linear piecewise value.

$f_g$ Power generation cost coefficient of unit g.

$P_g^{ub}$, $P_g^{lb}$ Upper/lower bound of updated unit e output (MW).

$\pi$ Constant.

Variables

$P_g$ The output of unit g (MW).

$P_g^A$ The output of unit g at period t in area A (MW).

$P_{pv,t}^A$ Output of photovoltaic power generation during period t in area A (MW).

$P_{w,t}^A$ The output of doubly fed units in area A (MW).

$P_l^A$ The transmission power of transmission line l in area A (MW).

$P_d^A$ The load is consumed by each regional system in area A (MW).

$P_{G,i}$ The power generation of node i in area A (MW).

$P_{l,ij}^A$ The active power of each area in branch l, its first and end nodes are node i, j, respectively (MW). The active power flows through the original tie line $(i,j)$ in area A (MW).

${\theta }_i^A$ The voltage phase angle at node i in area A (°).

${\theta }_j^A$ The voltage phase angle at node j in area A (°).

Functions

$C_g(\cdot )$ Generation cost characteristic function of unit g.