- 1School of Artificial Intelligence, Anhui University, Hefei, China
- 2State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun, China
- 3School of Mechanical Engineering, Tongji University, Shanghai, China
An accurate state of health and remaining useful life prediction is important to provide effective judgment for the lithium-ion battery and reduce the probability of battery effectiveness. This article proposes a hybrid model for the prediction by combining an improved decomposition algorithm, an improved parameterization algorithm, and a least squares support vector regression algorithm. The capacity signal is decomposed by the improved complete ensemble empirical mode decomposition with an adaptive noise algorithm to solve the backward problem. Then, the least squares support vector regression algorithm is used to predict each decomposition component separately. To obtain better parameters of the prediction model, a good point set principle and inertia weights are introduced to optimize a sparrow search algorithm. Experimental results confirm that the proposed hybrid prediction model has high accuracy, good stability, and strong robustness, which achieves a minimum 0.3% mean absolute error of the B0005 battery. The impact of prediction steps on accuracy is also discussed in this article. The results verified the capacity accuracy of the batteries predicted by eight steps.
Introduction
The lithium-ion battery has been widely used in pure electric or hybrid electric vehicles, satellites, and aircrafts due to its high energy density, long power endurance, satisfying nominal voltage, low self-discharge rate, long cycle, and rare memory effect (Lin et al., 1153; Li et al., 2021). With the increase in charging and discharging times, the chemical reaction inside the battery will become slow, which will eventually lead to the aging of the battery. The aging of the battery makes the actual capacity of the battery far lower than its rated capacity, resulting in a performance of degradation. An aging battery will directly lead to the failure of an automobile or satellite power system, affecting the regular use of the whole machine. In recent years, the prediction of battery state of health (SOH) and remaining useful life (RUL) has become a challenging problem in the field of prognostic and health management (PHM), to reduce some major disasters caused by battery aging. Extensive attention is attracted on the degradation of batteries. The estimation methods can be roughly divided into model-based methods and data-driven methods (Hannan et al., 2017; Kong et al., 2021).
The model-based method mainly uses the empirical degradation model such as the exponential model and polynomial model to describe the trend of battery capacity degradation, and then the method uses a particle filter (PF) to obtain and adjust the parameters of the model to track the aging trend of batteries (Wei et al., 2018). Li and Xu (2015) employed a mixture of Gaussian process (MGP) and a PF algorithm to predict battery SOH under uncertain conditions. Zhang et al. (2017a) developed an improved unscented particle filter (IUPF) method, using an algorithm called Markov chain Monte Carlo, to maintain the diversity of samples to solve the particle degeneracy phenomenon. Based on a double exponential mathematical model, Chen et al. (2020) applied a second-order central differential particle filter method to predict the SOH and RUL more accurately by optimizing the importance probability density function of the PF method. Hu et al. (2018) proposed an SOC and SOH co-estimation scheme based on the fractional-order calculus. The comparative studies show that it improves the modeling accuracy appreciably from its second- and third-order counterparts. The model-based method has succeeded in the PHM prediction of the battery. However, there is no general and accurate mathematical model to describe the degradation of different types of batteries, and the particle degeneracy phenomenon of the PF cannot be completely eliminated. In addition, the results are prone to large deviations due to the noise in the simulation process.
The data-driven approach obtains the battery degradation trend based on historical data without a definite mathematical model, and this approach is more suitable for different types of battery prediction. These methods include artificial neural network (ANN) (Li et al., 2019a; Gong et al., 2021; Yang, 2021), support vector regression (SVR) (Zhang et al., 2016; Feng et al., 2019; Wang et al., 2019; Li et al., 2020), relevance vector machine (RVM) (Cadini et al., 2019; Zhang et al., 2020), and Gaussian process regression (GPR) (Nagulapati et al., 2021; Pang et al., 2021). Deng et al. (2022) extracted the random capacity under different voltage segments from the partial charging process, and the average value and standard deviation of the random capacity were used as the input of the GPR model to estimate the battery SOH. Tang et al. (Tang et al., 2021) reconstructed the voltage curve from the measured data with the changing current and noise, and this article extracted the corresponding health indicators from the IC curve to estimate the SOH of the battery. To predict the SOH and RUL of batteries, Ma and Zhang et al. (Ma et al., 2019) employed a combination neural network composed of long short-term memory neural network (LSTM) and convolutional neural network (CNN) by using the false nearest neighbors method to calculate the size of the input window. The results showed that the proposed approach performs well in improving the accuracy and stability of the prediction. To optimize the extreme learning machine (ELM) model parameters, Zhu et al. (2019) developed an algorithm called the differential evolution gray wolf optimization (DE-GWO). The experiment results demonstrated that the DGWO-ELM method offers reduced errors. Although some deep learning networks such as LSTM and gated recurrent unit (GRU) usually perform well on a large number of datasets, they are weak in learning with small samples, and they consume a lot of computation (Zhao et al., 2018; Ungurean et al., 2020; Liu et al., 2021). SVR not only has the advantages of minimizing structural risks and being suitable for small sample predictions but also can improve the efficiency of regression convergence (Patil et al., 2015; Zhang et al., 2018). To find the optimal parameters of SVR algorithm, Qin et al. (2015) utilized particle swarm optimization (PSO) to find the best coefficient c and kernel radius g in SVR to improve the accuracy and the robustness of battery RUL prediction to a certain extent. However, the PSO algorithm is easy to fall into the local optimal value, and the problem of premature convergence exists. Li et al. (2019b) and Wang et al. (2019) designed an improved bird swarm algorithm (IBSA) and an artificial bee colony (ABC) algorithm to obtain the parameters of SVR models for life prediction. The aforementioned two hybrid algorithms can improve the accuracy of parameters and RUL prediction by using the historical capacity data. However, they also have a shortcoming of easily falling into the local optimum and then the global optimal value can hardly be found.
In the practical working process, batteries are easily affected by physical characteristics and the external working environment. There is a short-term capacity regeneration phenomenon of the batteries due to the accompanied noise (Li et al., 2019c; Sui et al., 2020). To reduce the disturbance of the random noise to battery SOH estimation, some signal processing methods have been proposed (Zhang et al., 2017b). Chang et al. (2017) directly used an improved empirical mode decomposition algorithm to decompose the original signal into several components and then employed the hybrid model of UKF and RVM to track the degradation trend of the batteries. On the basis of Ref. 36, Qu et al. (2019) developed the mode decomposition with adaptive noise and then utilized the PSO algorithm to optimize the mixed model for RUL prediction. The methods mentioned previously reduced the instability of time series which have strong nonlinearity, time-varying, and high complexity. However, they have the problems of some “spurious” modes in the early stages of the decomposition.
In order to solve the problems previously mentioned, a combination algorithm of improved CEEMDAN (ICEEMDAN), improved sparrow search algorithm (ISSA), and LSSVR model is proposed in this article. ICEEMDAN is utilized to decompose historical capacity data of batteries, and ISSA is introduced to obtain two important parameters of the LSSVR model to improve the performance of life prediction.
This article is organized as follows: related algorithms used in this work are presented in Section 2. Section 3 mainly describes the experimental data, model evaluation criteria, and prediction process. Experimental results are analyzed and discussed in detail from three aspects with two open source datasets in Section 4. Conclusions and future work are presented in Section 5.
Related Technology and Theory
Decomposition Methods in Data Processing
The EMD proposed in 1988 is a time-frequency focusing algorithm with a high signal-to-noise ratio. It is suitable for processing non-stationary and nonlinear signals. According to the data time scale characteristics, complex signals can be decomposed into various intrinsic mode functions (IMFs).
In order to solve the problem of noise residue, modal aliasing, and false modes that appeared early in the EMD method, the ICEEMDAN algorithm is proposed by adding the positive and negative Gaussian white noise and calculating the local mean.
The detailed ICEEMDAN algorithm steps are described as follows:
Step 1:By Eq. 1, add noise to the original signal ζ.
where ε0 is the reciprocal of the expected signal-to-noise ratio and ω(i) is a Gaussian white noise with zero mean and unit variance.
Step 2: Decompose the noisy signal to obtain the first IMF1 component and residual component R1 by EMD algorithm.
Step 3: The second residual component was calculated by the local mean of R1+β1E2 (ω(i)), and then the second IMF2 is calculated by:
Step 4: By Eq. 4, calculate the kth residue Rk in turn.
Step 5: Calculate the kth IMFk component
Step 6: Repeat steps 4 and 5 to obtain several IMFs and a residual component.
Sparrow Search Algorithm
The sparrow search algorithm (SSA) is a novel swarm intelligence optimization algorithm proposed in 2020, mainly inspired by the behavior of sparrows (Xue and Shen, 2020). Compared with other optimization algorithms such as GWO, DE, and PSO, it has achieved good results in engineering applications for its characteristics of fast convergence, high search accuracy, and strong robustness. The population of the sparrow is grouped into explorers and scroungers. Explorers are responsible for looking for food, and scroungers mainly obtain food following explorers. Each individual will monitor the behavior of other individuals and compete for food.
The sparrow search algorithm is represented as follows:
1) Position and fitness equation of sparrows
The position of sparrows can be described by the following matrix:
where n is the number of sparrows and d is the dimension of the variable.
The fitness values are defined by the following vectors:
2) Position update:
Explorers have better fitness and a larger range of foraging search than scroungers. Therefore, they can get the food in the search process first and provide the position and direction of food for the whole population.
Explorers’ position update is described by Eq. 8.
where t represents the number of current iterations, αssa represents a random number between 0 and 1, AR is the alarm value and AR∈[0,1], ST is the safety threshold and ST∈[0.5, 1], Qssa is the random number with Gaussian distribution, and L is a 1×d matrix in which each element has a value of 1.
3) Location update:
The location update of scroungers can be calculated by Eq. 9.
where XP is the best position occupied by the current explorer, Xworst is the worst position in the whole sparrow population, and Assa is a 1×d matrix in which each element is randomly assigned 1 or -1 and the condition Assa+ = AssaT (AssaAssaT)−1 is satisfied.
4) Anti-predation behavior:
The sparrow will make anti-predation behavior if they are aware of the danger, and can be calculated by:
where Xbest is the current global optimal position, βssa is the control parameter of the step with Gaussian distribution, which is a random number between 0 and 1, Kssa is the step control parameter with the random value between -1 and 1, fi is the current sparrow’s fitness, fbest is the best current global fitness, fworst is the worst current global fitness, and εssa is the minimum constant to avoid zero denominators.
In the SSA, the population initialization is random, which may cause the population distribution to be far from the actual solution, thus reducing its optimization ability and convergence speed. In order to guarantee the population diversity of SSA, the good point set principle is developed for initialization to make the initial solution evenly distributed in the area of search.
In the H-dimensional euclidean space, there is a unit cube:
Here, Pn (k) is the good point set if the deviation satisfies the relationship.
where r is the good point, ε is a positive integer, C (r, ε) is a constant, p is the smallest prime, and (p-H/2)≥H.
The inertia weight is an important parameter in population optimization which affects the ability and speed of the global and local search. In this article, new adaptive weights are introduced by using adaptive weight coefficients to improve the optimization ability.
The adaptive weight formulas of wssa and the position update are as follows:
Least Squares Support Vector Regression
The theory of SVM proposed in 1999 is not only efficient and simple but also has good robustness (Vapnik, 1999). It can be used to solve some classification regression problems with fewer samples. However, when dealing with large samples, the SVM algorithm will become complex with a long training time and low prediction accuracy. LSSVR converts the constraints of SVR into an equation, which has good nonlinear fitting ability and generalization ability. It significantly reduces the amount of calculation and improves the prediction accuracy.
The LSSVR model in a high-dimensional space can be described as:
where f(x) is the output, ϕ(x) is a nonlinear mapping function, w is the normal vector, and b is the displacement term.
According to the minimum structural risk theory, the optimization problem of the LSSVR problem can be described by Eq. 15:
where γ is the penalty constant, which affects the complexity of the model; the larger the value of γ is, the model will become more accurate but more complex. The smaller the value of γ is, the larger the deviation between f (xi) and yi can be tolerated. ξi is the regression error.
Transforming the optimization problem into a maximum value problem of α:
where α is the Lagrange multiplier.
The LSSVR regression model can be finally transformed into:
where K (xi,xj) is the Gaussian radial basis kernel function.
Complete Prediction Process of the Hybrid Model
In this article, a combination algorithm is proposed to improve the performance of life prediction, which is shown in Figure 1.
The detailed prediction process is divided into the following steps:
Step 1: Decompose the capacity of batteries into five IMFs and a residual by the ICEEMDAN algorithm.
Step 2: Predict the signal after mode decomposition by the LSSVR model, the parameters of which are optimized by ISSA. The prediction modes are divided into 1-step advance forecast, 4-step advance forecast, 6-step advance forecast, and 8-step advance forecast.
Step 3: After the prediction of each decomposed signal is completed, the prediction results are reconstructed as the final capacity prediction results.
Experimental Data and Detailed Prediction Process
Experimental Data
Two open source datasets are applied for battery life prediction: one is from the National Aeronautics and Space Administration (NASA), and the other is from the Center for Advanced Life Cycle Engineering (CALCE) at the University of Maryland (He et al., 2011). In total, six lithium-ion batteries (#5, #6, #7, CS-35, CS-37, and CS-38) are selected from the datasets for algorithm verification. The batteries of NASA are commercially available 18,650 cells with a standard rated capacity of 2Ah, while those of CALCE are square lithium cobalt oxide batteries with a rated capacity of 1.1Ah. The cycle test experiments of the four batteries are all carried out at room temperature, which mainly include three different operational profiles. For NASA batteries, during the charging phase, the three batteries are initially charged in the constant current (CC) mode under a current of 1.5 A until the voltage reaches 4.2V; then, the voltage is kept at 4.2 V until the current drops to 20 mA. In the discharging phase, three batteries are discharged in the CC mode under a suitable current until the respective cut-off voltages are reached. The battery capacity degradation of NASA does not gradually decrease in strict accordance with the increase in the number of cycles, but rises in a small range. The main reason is that the chemical reaction inside the battery is easily interfered by external factors in cyclic charging and discharging. The batteries of CALCE are CS2 with the rated capacity of 1.1Ah. During the charging process, the batteries are charged in the CC mode at a constant current of 0.5C until the charging cut-off voltage reaches 4.2V, and then charged in the constant voltage (CV) mode until the current dropped to 0.05 A. During the discharge process, the batteries are discharged in the CC mode at different constant current until the discharge cut-off voltage reaches 2.7 V.
Model Evaluation Criteria
Four popular metrics are utilized to measure and demonstrate the model which is defined by Eq. 18:
where MAE represents the mean absolute error, M is the total number of the predicted battery capacity value, yn* is the predicted battery capacity in the nth cycle, yn is the actual battery capacity in the nth cycle, RMSE represents the root mean square error, MAPE represents the mean absolute percentage error, R2 represents the decisive factor, and
The 95% confidence interval (CI) of the model is applied for the assessment of the uncertainty, which represents the interval of the prediction error. The equation is as follows:
A relative error (RE) is defined by Eq. 20 to evaluate the model accuracy of RUL prediction:
Experimental Results and Analysis
In this article, the prediction performance and generalization ability of the proposed combination model is conducted from three aspects to verify the effectiveness.
ISSA Verification
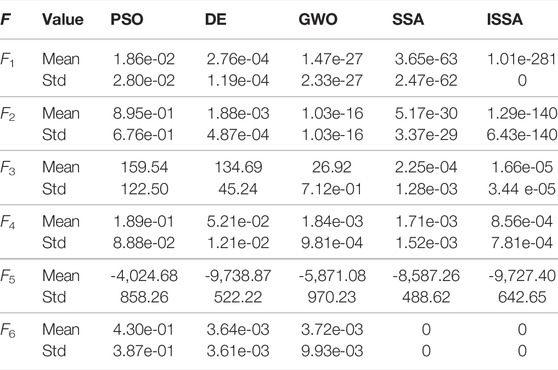
Six classical functions are used including four unimodal functions and two multimodal functions for ISSA verification. The benchmark function is shown in Table 1.
To compare the optimization performance with ISSA, PSO, DE, GWO, and SSA algorithms are chosen. The parameter settings of the five optimization algorithms are listed in Table 2.
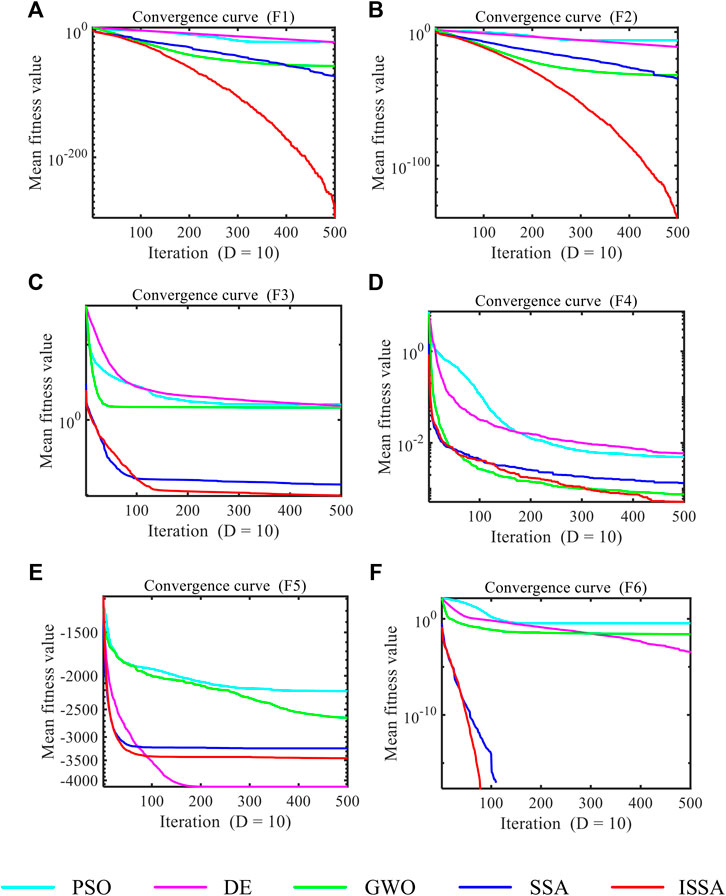
To ensure the robustness of the five algorithms, they are run 50 times for each test function independently, and then the average value (Mean) and the standard deviation (Std) are recorded and listed in Table 3. For functions F1 and F2, although the statistical index of ISSA has not been greatly improved, the stability of the algorithm is much higher than that of the other four algorithms. For the multimodal function F5, the ISSA achieves the best performance, and the result is much better than that of PSO, GWO, and SSA algorithms. For the multimodal function F6, the statistical results of ISSA and SSA are almost the same and are much better than the other optimization algorithms.
Figure 2 shows the average fitness curve of the five algorithms in each test function to better reflect the dynamic optimization results. It can be seen intuitively that the convergence speed and optimization ability of ISSA are higher than those of the other four algorithms.
Performance of the Hybrid Model
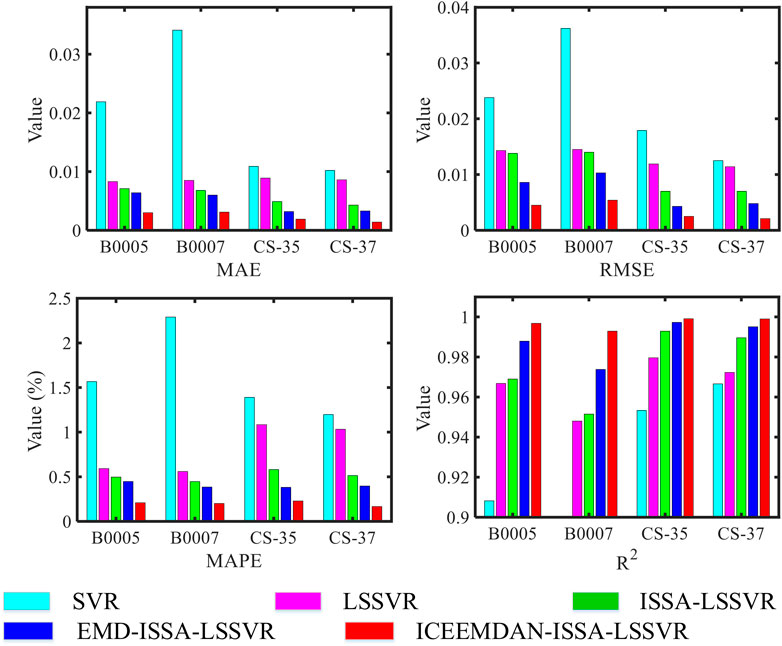
The superiority of the hybrid model is verified by comparison between SVR-LSSVR, ISSA-LSSVR, EMD-ISSA-LSSVR, and ICEEMDAN-ISSA-LSSVR algorithms on B0005, B0007, CS-35, and CS-37. The parameter settings of the hybrid model are listed in Table 4. The first 50% of each battery data is for training, while the left 50% is for test.
As shown in Figure 3, there is an obvious lag in the prediction results of SVR, LSSVR, and ISSA-LSSVR models on the four batteries. The prediction performance of LSSVR is better than that of SVR, confirming the superiority of LSSVR algorithm. The parameters of SVR and LSSVR prediction models are given randomly, while ISSA-LSSVR algorithm can automatically find the best parameters of LSSVR in the process of training. The proposed hybrid model achieves a better prediction effect and has a higher degree of fitting with the actual available capacity than EMD-ISSA-LSSVR, indicating that the effect of ICEEMDAN decomposition algorithm is better. Figure 4 shows the statistical intuitive chart of the prediction error on the four batteries. For the three indexes of MAE, RMSE, and MAPE, the algorithms of SVR, LSSVR, ISSA-LSSVR, EMD-ISSA-LSSVR, and the proposed hybrid model show a decreasing trend, while R2 shows an increasing trend, indicating that the proposed algorithm has the highest accuracy. Taking the B0007 battery as an example, the MAE, RMSE, and MAPE predicted by the proposed algorithm are 0.0031, 0.0054, and 0.2009, respectively. They are fewer than those of the other four algorithms. The R2 predicted by the proposed algorithm is 0.9929 which is the largest.
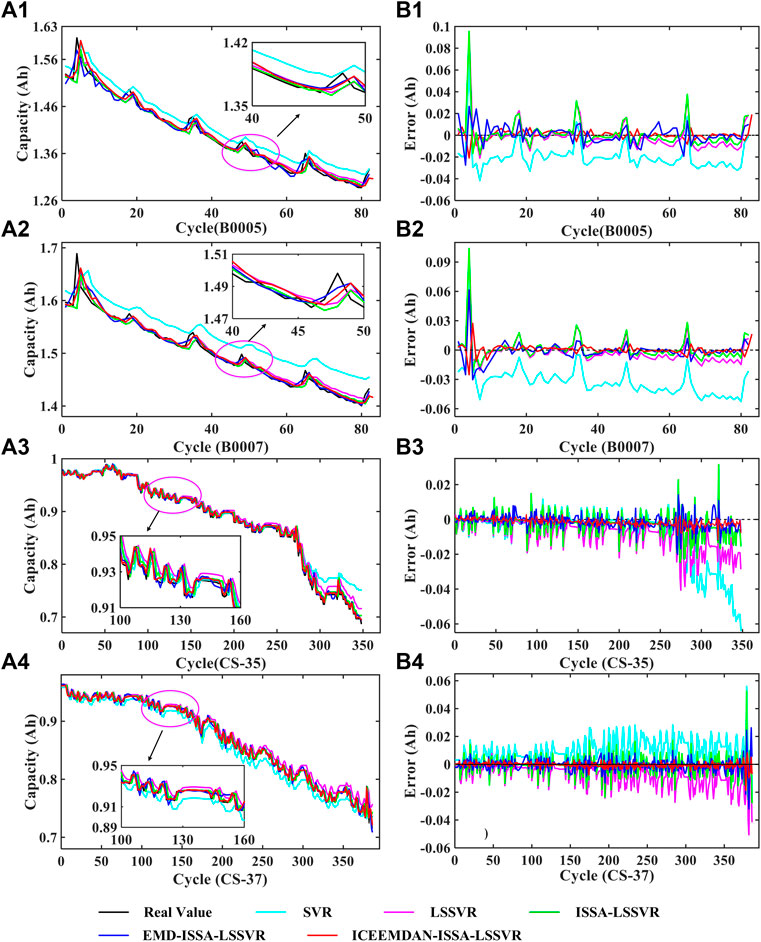
FIGURE 3. Prediction capacity results and errors of different algorithmss (a1–a4) is the prediction capacity. (b1–b4) is the prediction error.
To verify the stability of the algorithm, taking B0005 and CS-35 as examples, the capacity predictions including the confidence interval and the probability density curve are shown in Figure 5 and Figure 6. The narrower 95% ranges indicate the stronger robustness of the prediction models. It can be seen from the figure that 95% IC of the proposed method is the smallest, which confirms that the proposed algorithm can give better performance for capacity prediction.
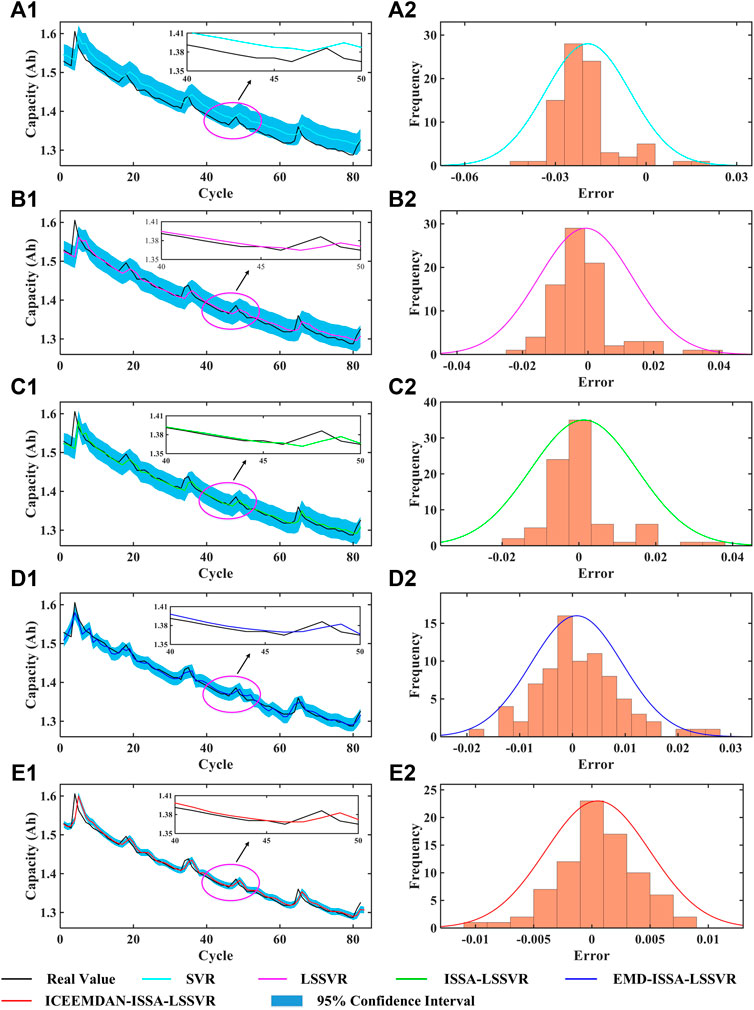
FIGURE 5. Prediction results of the five algorithms on the B0005 battery. (a1–e1) Prediction capacity. (a2–e2) Probability density curve of the prediction error.
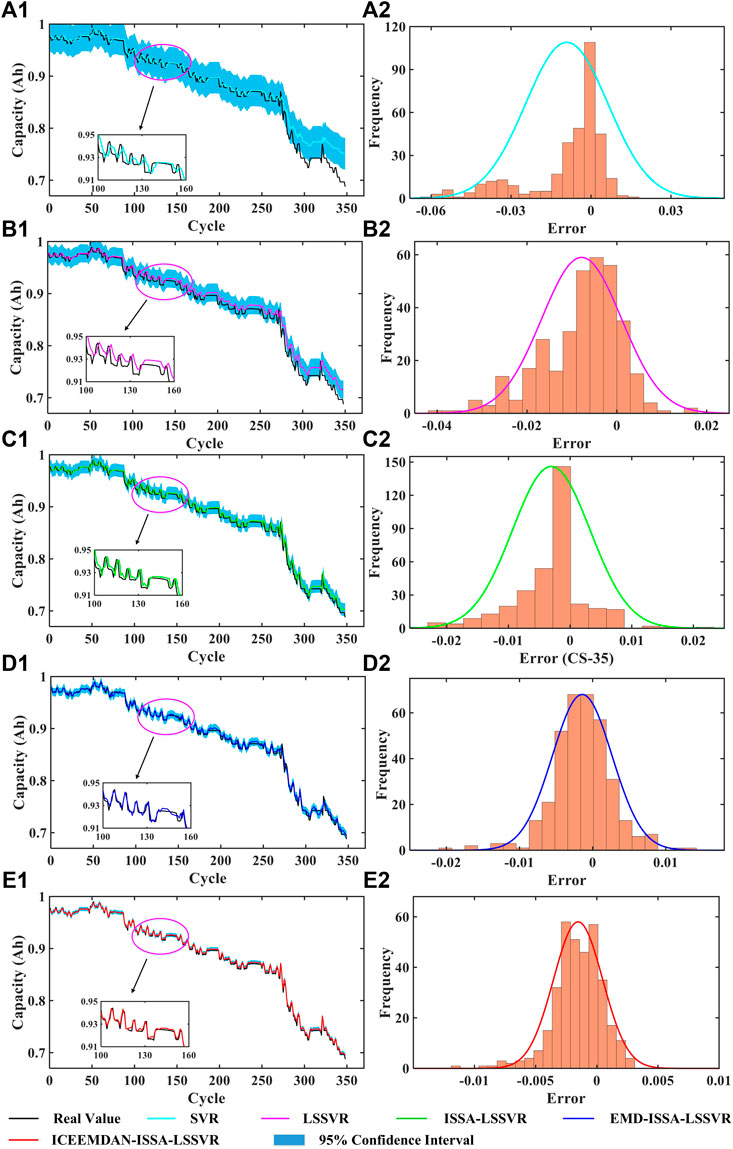
FIGURE 6. Prediction results of the five algorithms on the CS-35 battery. (a1–e1) Prediction capacity. (a2–e2) Probability density curve of the prediction error.
Performance on Multi-Step Prediction in Advance
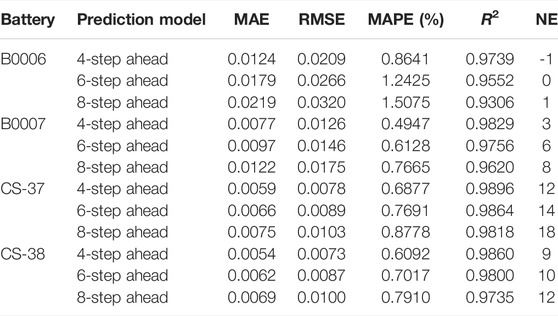
Step-by-step prediction is sometimes difficult to ensure the safety and stability of battery long-term operation. To verify the stability of the model, the capacity is predicted in many steps, that is, the actual capacity in the window d is used to predict the capacity in the future n + l secondary charge–discharge cycle, and l is the number of steps in advance. The ability of the proposed combination algorithm in multi-step prediction is tested by four steps in advance, six steps in advance, and eight steps in advance. B0006, B0007, CS-37, and CS-38 batteries are selected as experimental subjects.
The prediction results for the available capacity are shown in Figure 7. It is not difficult to see that with the increase of the number of cycles or prediction steps in advance, the error of the combined model will increase accordingly, and the corresponding life error will gradually increase.
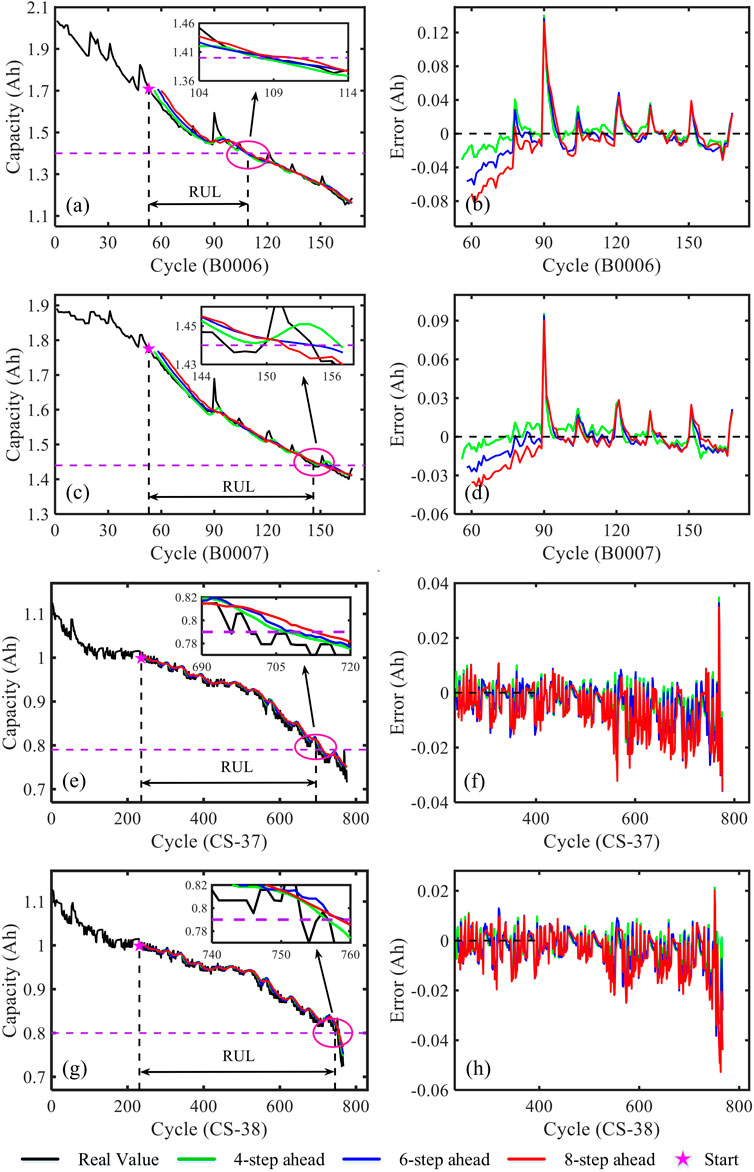
FIGURE 7. Prediction results on the multi-step prediction in advance. (A,B) Capacity and error on B0006. (C,D) Capacity and error on B0007. (E,F) Capacity and error on CS-37. (G,H) Capacity and error on CS-38 of the prediction error.
Table 5 shows the statistical results of the capacity error of multi-step prediction. The MAE of B0007 obtained by eight steps in advance prediction is 0.0122 Ah, RMSE is 0.0175 Ah, MAPE is 0.7665, R2 is 0.9620, and the battery life error is 8. The MAE of CS-37 obtained by eight steps prediction is 0.0075 Ah, RMSE is 0.0103 Ah, MAPE is 0.8778, R2 is 0.9818, and the battery life error is 18. This demonstrates that the proposed hybrid model also has a higher prediction level in the multi-step prediction, which can predict the capacity of the battery in a longer time step and provide a more reliable guarantee for the safety of the battery system.
Conclusion
A novel data-driven hybrid model is proposed for SOH and RUL prediction of batteries. The feasibility and superiority of the model are verified from different directions by battery aging datasets from NASA and CALCE. The ISSA plays a significant role in the parameter optimization of LSSVR, which dramatically improves the prediction accuracy of capacity. The ICEEMDAN decomposition algorithm can reduce the random noise interference and solve the backward problem of capacity data. The results of eight steps in advance show that the proposed model can still obtain the accurate capacity of the battery with a longer time step in the future. It can provide a more reliable guarantee for the safety of the battery system.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, Further inquiries can be directed to the corresponding author.
Author Contributions
WD, ZD, and YL: for critically reading the manuscript and helpful discussions; YC and WD: conceptualization; YC: methodology; YC and WD: software; YC and WD: validation; YC: formal analysis; YC: data curation; YC: writing–original draft preparation; YC and ZD: writing–review and editing; ZD and YL: supervision.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cadini, F., Sbarufatti, C., Cancelliere, F., and Giglio, M. (2019). State-of-life Prognosis and Diagnosis of Lithium-Ion Batteries by Data-Driven Particle Filters. Appl. Energ. 235, 661–672. doi:10.1016/j.apenergy.2018.10.095
Chang, Y., Fang, H., and Zhang, Y. (2017). A New Hybrid Method for the Prediction of the Remaining Useful Life of a Lithium-Ion Battery. Appl. Energ. 206, 1564–1578. doi:10.1016/j.apenergy.2017.09.106
Chen, Y., He, Y., Li, Z., Chen, L., and Zhang, C. (2020). Remaining Useful Life Prediction and State of Health Diagnosis of Lithium-Ion Battery Based on Second-Order Central Difference Particle Filter. IEEE Access 8, 37305–37313. doi:10.1109/access.2020.2974401
Deng, Z., Hu, X., Li, P., Lin, X., and Bian, X. (2022). Data-Driven Battery State of Health Estimation Based on Random Partial Charging Data. IEEE Trans. Power Electron. 37 (5), 5021–5031. doi:10.1109/tpel.2021.3134701
Feng, X., Weng, C., He, X., Han, X., Lu, L., Ren, D., et al. (2019). Online State-Of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 68 (9), 8583–8592. doi:10.1109/tvt.2019.2927120
Gong, C., Xwa, B., and Yha, B. (2021). Remaining Useful Life and State of Health Prediction for Lithium Batteries Based on Empirical Mode Decomposition and a Long and Short Memory Neural Network[J]. Energy 232, 116812.
Hannan, M. A., Lipu, M. S. H., Hussain, A., and Mohamed, A. (2017). A Review of Lithium-Ion Battery State of Charge Estimation and Management System in Electric Vehicle Applications: Challenges and Recommendations. Renew. Sust. Energ. Rev. 78, 834–854. doi:10.1016/j.rser.2017.05.001
He, W., Williard, N., Osterman, M., and Pecht, M. (2011). Prognostics of Lithium-Ion Batteries Based on Dempster-Shafer Theory and the Bayesian Monte Carlo Method. J. Power Sourc. 196 (23), 10314–10321. doi:10.1016/j.jpowsour.2011.08.040
Hu, X., Yuan, H., Zou, C., Li, Z., and Zhang, L. (2018). Co-Estimation of State of Charge and State of Health for Lithium-Ion Batteries Based on Fractional-Order Calculus. IEEE Trans. Veh. Technol. 67 (11), 10319–10329. doi:10.1109/tvt.2018.2865664
Kong, J.-z., Yang, F., Zhang, X., Pan, E., Peng, Z., and Wang, D. (2021). Voltage-temperature Health Feature Extraction to Improve Prognostics and Health Management of Lithium-Ion Batteries. Energy 223 (6), 120114. doi:10.1016/j.energy.2021.120114
Li, F., and Xu, J. (2015). A New Prognostics Method for State of Health Estimation of Lithium-Ion Batteries Based on a Mixture of Gaussian Process Models and Particle Filter. Microelectronics Reliability 55 (7), 1035–1045. doi:10.1016/j.microrel.2015.02.025
Li, L.-L., Liu, Z.-F., Tseng, M.-L., and Chiu, A. S. F. (2019). Enhancing the Lithium-Ion Battery Life Predictability Using a Hybrid Method. Appl. Soft Comput. 74, 110–121. doi:10.1016/j.asoc.2018.10.014
Li, W., Jiao, Z., Du, L., Fan, W., and Zhu, Y. (2019). An Indirect RUL Prognosis for Lithium-Ion Battery under Vibration Stress Using Elman Neural Network. Int. J. Hydrogen Energ. 44 (23), 12270–12276. doi:10.1016/j.ijhydene.2019.03.101
Li, X., Yuan, C., and Wang, Z. (2020). State of Health Estimation for Li-Ion Battery via Partial Incremental Capacity Analysis Based on Support Vector Regression. Energy 203, 117852. doi:10.1016/j.energy.2020.117852
Li, X., Zhang, L., Wang, Z., and Dong, P. (2019). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on a Hybrid Model Combining the Long Short-Term Memory and Elman Neural Networks. J. Energ. Storage 21, 510–518. doi:10.1016/j.est.2018.12.011
Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2021). A Distributed Double-Newton Descent Algorithm for Cooperative Energy Management of Multiple Energy Bodies in Energy Internet. IEEE Trans. Ind. Inf. 17 (9), 5993–6003. doi:10.1109/tii.2020.3029974
Lin, C. P., Cabrera, J., Yang, F., Ling, M. H., Tsui, K. L., and Bae, S. J. Battery State of Health Modeling and Remaining Useful Life Prediction through Time Series Model[J]. Appl. Energ. 275, 115338.
Liu, K., Shang, Y., Ouyang, Q., and Widanage, W. D. (2021). A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Ind. Electron. 68 (4), 3170–3180. doi:10.1109/tie.2020.2973876
Ma, G., Zhang, Y., Cheng, C., Zhou, B., Hu, P., and Yuan, Y. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on False Nearest Neighbors and a Hybrid Neural Network. Appl. Energ. 253, 113626. doi:10.1016/j.apenergy.2019.113626
Nagulapati, V. M., Lee, H., Jung, D., Brigljevic, B., Choi, Y., and Lim, H. (2021). Capacity Estimation of Batteries: Influence of Training Dataset Size and Diversity on Data Driven Prognostic Models, Reliability Eng. Syst. Saf. 216. 108048. doi:10.1016/j.ress.2021.108048
Pang, X., Liu, X., Jia, J., Wen, J., Shi, Y., Zeng, J., et al. (2021). A Lithium-Ion Battery Remaining Useful Life Prediction Method Based on the Incremental Capacity Analysis and Gaussian Process Regression. Microelectronics Reliability 127, 114405. doi:10.1016/j.microrel.2021.114405
Patil, M. A., Tagade, P., Hariharan, K. S., Kolake, S. M., Song, T., Yeo, T., et al. (2015). A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energ. 159, 285–297. doi:10.1016/j.apenergy.2015.08.119
Qin, T., Zeng, S., and Guo, J. (2015). Robust Prognostics for State of Health Estimation of Lithium-Ion Batteries Based on an Improved PSO–SVR Model[J]. Microelectronics and Reliability 55 (9-10), 1280–1284. doi:10.1016/j.microrel.2015.06.133
Qu, J., Liu, F., Ma, Y., and Fan, J. (2019). A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 7 (99), 87178–87191. doi:10.1109/access.2019.2925468
Sui, X., He, S., Stroe, D. I., and Teodorescu, R. (2020). in Lithium-ion Battery State of Health Estimation Using Empirical Mode Decomposition Sample Entropy and Support Vector machine[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC) (IEEE), 3424–3429.
Tang, X., Wang, Y., Liu, Q., and Gao, F., (2021). Reconstruction of the Incremental Capacity Trajectories from Current-Varying Profiles for Lithium-Ion Batteries[J]. ISCIENCE 24 (10), 103103. doi:10.1016/j.isci.2021.103103
Ungurean, L., Micea, M. V., and Cârstoiu, G. (2020). Online State of Health Prediction Method for Lithium‐ion Batteries, Based on Gated Recurrent Unit Neural Networks. Int. J. Energ. Res 44 (8), 6767–6777. doi:10.1002/er.5413
Vapnik, V. N. (1999). An Overview of Statistical Learning Theory. IEEE Trans. Neural Netw. 10 (5), 988–999. doi:10.1109/72.788640
Wang, Y., Ni, Y., Lu, S., Wang, J., and Zhang, X. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee colony. IEEE Trans. Veh. Technol. 68 (10), 9543–9553. doi:10.1109/tvt.2019.2932605
Wei, J., Dong, G., and Chen, Z. (2018). Remaining Useful Life Prediction and State of Health Diagnosis for Lithium-Ion Batteries Using Particle Filter and Support Vector Regression. IEEE Trans. Ind. Electron. 65 (7), 5634–5643. doi:10.1109/tie.2017.2782224
Xue, J., and Shen, B. (2020). A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 8 (1), 22–34. doi:10.1080/21642583.2019.1708830
Yang, Y. (2021). A Machine-Learning Prediction Method of Lithium-Ion Battery Life Based on Charge Process for Different Applications. Appl. Energ. 292 (5), 116897. doi:10.1016/j.apenergy.2021.116897
Zhang, C., He, Y., Du, B., Yuan, L., Li, B., and Jiang, S. (2020). Transformer Fault Diagnosis Method Using IoT Based Monitoring System and Ensemble Machine Learning. Future Generation Comp. Syst. 108, 533–545. doi:10.1016/j.future.2020.03.008
Zhang, C., He, Y., Yuan, L., He, W., Xiang, S., and Li, Z. (2016). A Novel Approach for Diagnosis of Analog Circuit Fault by Using GMKL-SVM and PSO. J. Electron. Test. 32 (5), 531–540. doi:10.1007/s10836-016-5616-y
Zhang, C., He, Y., Yuan, L., and Xiang, S. (2017). Capacity Prognostics of Lithium-Ion Batteries Using EMD Denoising and Multiple Kernel RVM. IEEE Access 5, 12061–12070. doi:10.1109/access.2017.2716353
Zhang, X., Miao, Q., and Liu, Z. (2017). Remaining Useful Life Prediction of Lithium-Ion Battery Using an Improved UPF Method Based on MCMC. Microelectronics Reliability 75, 288–295. doi:10.1016/j.microrel.2017.02.012
Zhang, Y., Xiong, R., He, H., and Pecht, M. G. (2018). Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 67 (7), 5695–5705. doi:10.1109/tvt.2018.2805189
Zhao, Q., Qin, X., Zhao, H., and Feng, W. (2018). A Novel Prediction Method Based on the Support Vector Regression for the Remaining Useful Life of Lithium-Ion Batteries. Microelectronics Reliability 85, 99–108. doi:10.1016/j.microrel.2018.04.007
Keywords: lithium-ion battery, life prediction, parameterization algorithm, mode decomposition, support vector regression
Citation: Chen Y, Duan W, Ding Z and Li Y (2022) Battery Life Prediction Based on a Hybrid Support Vector Regression Model. Front. Energy Res. 10:899804. doi: 10.3389/fenrg.2022.899804
Received: 19 March 2022; Accepted: 08 April 2022;
Published: 30 May 2022.
Edited by:
Xiao Wang, Wuhan University, ChinaReviewed by:
Jiaqiang Tian, Xi’an University of Technology, ChinaTongmao Zhang, The University of Manchester, United Kingdom
Yajian Zhang, Shanghai University, China
Copyright © 2022 Chen, Duan, Ding and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenxian Duan, ZHd4MzQyOTc3NTQyQDEyNi5jb20=
 Yuan Chen
Yuan Chen Wenxian Duan
Wenxian Duan Zhenhuan Ding
Zhenhuan Ding Yingli Li
Yingli Li