A Method for Directly Extracting the Jacobian Matrix of the Power Flow Equations of a Power System in Polar Coordinates

This paper presents a method to directly extract the Jacobian matrix of a power system’s power flow (PF) equations in polar coordinates (termed as DEJMP method). This method is designed to reduce the computational complexity of the extraction process and improve the computational efficiency of the relevant PF algorithm. Direct extraction of the Jacobian matrix from the complex power equation in polar coordinates precludes an increase in both the number of procedural steps and the computational expense, which is a problem associated with the conventional PF (C-PF) algorithm due to its requirement that the derivatives of the active and reactive bus power equations be taken in separate steps. The DEJMP method avoids the trigonometric calculations used in the conventional method for computing the Jacobian matrix, resulting in a significant increase in computational efficiency. In addition, simulation results obtained for IEEE-300, S-1047, S-2383, and S-9241 bus systems validate the efficiency of the DEJMP-based PF algorithm. The DEJMP-based PF algorithm requires more than 20% less time to calculate the PF than the C-PF algorithm. This decrease in computing time is more pronounced for large systems.

1 Introduction

Power flow (PF) calculations (Tinney and Hart, 1967; Pourbagher, 2016; Issicaba, 2019) are a basic tool used to determine the steady-state operating condition of a power system based on the given operating environment and network structure, with the goal of facilitating the formulation of power supply schemes and real-time monitoring of the power grid. Therefore, rapid and reliable PF algorithms are urgently needed for power grids (Tang et al., 2019; Tostado-Véliz et al., 2019; Tostado-Véliz et al., 2021; Wei and Zhao, 2021; Xiao et al., 2021).

From a mathematical perspective, the calculation of the PF is a problem of solving a system of multivariate nonlinear equations. The Newton method is widely used to calculate the PF, and its ncomputational load depends heavily on the formation of the Jacobian matrix. Reducing the complexity of this process is an essential means of improving the computational efficiency of the relevant algorithm and lowering the cost of the computation of the PF. To date, the most common way of acquiring the Jacobian matrix of the power flow equation is as follows:

In Semlyen and de Leon (2001) and Alves et al. (2003), algorithms for reducing the Jacobian matrix calculation time in PF are proposed, and their performance is reviewed. In Jegatheesan et al. (2008) the Jacobian matrix is generated by using the power fluxes in the network elements as the basic components. Network elements are added one by one, and the Jacobian matrix is updated thoroughly. In Filho et al. (2009), the generic formulation of the Jacobian matrix in polar coordinates is given, and the method to estimate this matrix is discussed. In Xu et al. (2009), the approximate expressions of the power flow Jacobian matrix are presented. Some indices are established to quantify the error between the power flow Jacobian matrix and these expressions. In Chen et al. (2016), a measurement-based method is suggested to compute the power flow Jacobian matrix. The technique proposed by Chen et al. (2016) is unique for its ability to adapt fast to system operating points and topology changes. In Chappa and Thakur (2018), a PMU measurement-based method proposed by Lim and DeMarco (2016) is used to generate a Jacobian matrix and identify weak nodes in power systems. A complete comparison study of existing power flow solution strategies and methods for obtaining Jacobian matrices in these solutions is described in Dutto et al. (2019). In Varwandkar (2019), the realification of PF is studied, and the disadvantages of the conventional PF method that needs to estimate the Jacobian matrix are investigated. The Jacobian matrix for Newton-Raphson power flow solutions is given in a concise form (Conlin et al., 2021). Moreover, a variety of Jacobian matrix calculating methods is also explored (Conlin et al., 2021).

In most of the above methods, the real and imaginary parts of the complex power are separated before extracting the Jacobian matrix. These methods are computationally complex and time-consuming since they rely on trigonometric computations.

To address this problem, this paper presents a novel solution. The main contributions of this paper are as follows:

1) A method to directly extract the Jacobian matrix of the PF equations in polar coordinates (termed as DEJMP method) from the complex power equation is presented. This method considerably reduces the computational complexity of extracting the Jacobian matrix of a power system’s power flow (PF) equations in polar coordinates.

2) A DEJMP-based PF algorithm is also suggested. The suggested PF algorithm takes significantly less time to compute than previous algorithms, thanks to the DEJMP approach.

Simulation results obtained for IEEE-300, S-1047, S-2383, and S-9241 bus systems validate the efficiency of the proposed method.

2 Conventional Method to Calculate the Jacobian Matrix of the PF

The complex PF equation can be expressed as:

$\text{Δ}\dot{\mathit{S}}=diag\left(\dot{\mathit{V}}\right)\widehat{\mathit{Y}}\widehat{\mathit{V}}-\dot{\mathit{S}}(1)$

where $\dot{\mathit{V}}$ and $\widehat{\mathit{V}}$ are the voltage vector and its conjugate, respectively; $\dot{\mathit{S}}={[\cdots ,S_a,\cdots ]}^T\in {ℂ}^n$, $S_a$ is the complex injection power at the bus $a$; $n$ is the number of buses.

To solve the above PF equation using the Newton-Raphson method, it is necessary to calculate the Jacobian matrix of the PF equation (Chappa and Thakur, 2017). This Jacobian matrix is calculated in most conventional PF algorithms via the following steps.

Step 1: separate the real and imaginary parts of the PF equation:

$\text{Δ}{P}_a=V_a{\displaystyle {\sum }_{b=1}^n{Y}_{ab}}{V}_b\cos {\theta }_{ab}-P_a(2)$

$\text{Δ}{Q}_a=V_a{\displaystyle {\sum }_{b=1}^n{Y}_{ab}}{V}_b\sin {\theta }_{ab}-Q_a(3)$

where $V_a$ is the voltage amplitude at the bus $a$; ${\theta }_{ab}=({\delta }_a-{\delta }_b-{\alpha }_{ab})$, ${\delta }_a$ and ${\delta }_b$ are the phase angle at bus $a$ and $b$, respectively; $P_a$ and $Q_a$ are active and reactive power at bus $a$, respectively; $Y_{ab}$ and ${\alpha }_{ab}$ are the amplitude and the angle of the element of the bus admittance matrix.

Step 2: calculate the partial derivatives of $\text{Δ}{P}_a$ and $\text{Δ}{Q}_a$ with respect to $V_a$ and ${\delta }_a$.

$\frac{\partial \text{Δ}{P}_a}{\partial V_a}=2V_a{Y}_{aa}\cos {\alpha }_{aa}+{\displaystyle {\sum }_{\begin{array}{l}b=1\\ b\ne a\end{array}}^{\text{n}}{Y}_{ab}}{V}_b\cos {\theta }_{ab}(4)$

$\frac{\partial \text{Δ}{P}_a}{\partial V_b}=V_a{Y}_{ab}\cos {\theta }_{ab}(5)$

$\frac{\partial \text{Δ}{P}_a}{\partial {\delta }_a}=-V_a{\displaystyle {\sum }_{\begin{array}{l}b=1\\ b\ne a\end{array}}^n{Y}_{ab}}{V}_b\sin {\theta }_{ab}(6)$

$\frac{\partial \text{Δ}{P}_a}{\partial {\delta }_b}=V_a{Y}_{ab}{V}_b\sin {\theta }_{ab}(7)$

$\frac{\partial \text{Δ}{Q}_a}{\partial V_a}={\displaystyle {\sum }_{\begin{array}{l}b=1\\ b\ne a\end{array}}^n{Y}_{ab}}{V}_b\sin {\theta }_{ab}-2V_a{Y}_{aa}\sin {\alpha }_{aa}(8)$

$\frac{\partial \text{Δ}{Q}_a}{\partial V_b}=V_a{Y}_{ab}\sin {\theta }_{ab}(9)$

$\frac{\partial \text{Δ}{Q}_a}{\partial {\delta }_a}=V_a{\displaystyle {\sum }_{\begin{array}{l}b=1\\ b\ne a\end{array}}^n{Y}_{ab}}{V}_b\cos {\theta }_{ab}(10)$

$\frac{\partial \text{Δ}{Q}_a}{\partial {\delta }_b}=-V_a{Y}_{ab}{V}_b\cos {\theta }_{ab}(11)$

Step 3: based on (4–11), Form the Jacobian matrix of the PF equation.

$\left[\begin{array}{cccccc}⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \frac{\partial \text{Δ}{P}_a}{\partial V_a}& \frac{\partial \text{Δ}{P}_a}{\partial V_b}& \cdots & \frac{\partial \text{Δ}{P}_a}{\partial {\delta }_a}& \frac{\partial \text{Δ}{P}_a}{\partial {\delta }_b}& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \frac{\partial \text{Δ}{Q}_a}{\partial V_a}& \frac{\partial \text{Δ}{Q}_a}{\partial V_b}& \cdots & \frac{\partial \text{Δ}{Q}_a}{\partial {\delta }_a}& \frac{\partial \text{Δ}{Q}_a}{\partial {\delta }_b}& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]\left[\begin{array}{c}⋮\\ \text{Δ}{V}_a\\ ⋮\\ ⋮\\ \text{Δ}{\delta }_a\\ ⋮\end{array}\right]=-\left[\begin{array}{c}⋮\\ \text{Δ}{P}_a\\ ⋮\\ ⋮\\ \text{Δ}{Q}_a\\ ⋮\end{array}\right](12)$

The extracted Jacobian matrix is a system (12) coefficient matrix derived after removing the rows and columns corresponding to the slack and power/voltage (PV) buses.

As shown in steps 1–3, trigonometric operations are required to obtain the Jacobian matrix elements. These techniques are time-consuming and computationally complex. To address the aforementioned difficulties, the following section proposes a method for directly extracting the Jacobian matrix of the PF equations in polar coordinates (dubbed the DEJMP method) from the complex power equation.

3 DEJMP Methods

Under the condition that the bus voltage $\dot{\mathit{V}}=\mathit{V}{e}^{i\delta }$, the following linear equation of $\mathrm{\Delta }\dot{\mathit{S}}$ from the complex bus power equation,:

$\left(\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{V}},\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{\delta }}\right)\left(\begin{array}{l}\text{Δ}\mathit{V}\\ \text{Δ}\mathit{\delta }\end{array}\right)=-\text{Δ}\dot{\mathit{S}}(13)$

where

$\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{V}}=diag\left(\widehat{\mathit{Y}}\widehat{\mathit{V}}\right)diag\left(e^{i\delta }\right)+diag\left(\dot{\mathit{V}}\right)\widehat{\mathit{Y}}diag\left(e^{-i\delta }\right)(14)$

$\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{\delta }}=j\left(diag\left(\widehat{\mathit{Y}}\widehat{\mathit{V}}\right)diag\left(\dot{\mathit{V}}\right)-diag\left(\dot{\mathit{V}}\right)\widehat{\mathit{Y}}diag\left(\widehat{\mathit{V}}\right)\right)(15)$

diag signifies the operation of taking the diagonal matrix of the corresponding vector, $\dot{\mathit{Y}}\in {ℂ}^{n\times n}$ and $\widehat{\mathit{Y}}\in {ℂ}^{n\times n}$ are the bus admittance matrix and its conjugate, respectively, $\dot{\mathit{V}}\in {ℂ}^n$ and $\widehat{\mathit{V}}\in {ℂ}^n$ are the voltage vector and its conjugate, respectively, $\mathit{V}\in {ℝ}^n$ and $\mathit{\delta }\in {ℝ}^n$ are the magnitude and phase angle of the voltage, respectively; $\text{Δ}\mathit{V}$ and $\text{Δ}\mathit{\delta }$ are the increments in the magnitude and phase angle of the voltage, respectively.

Let $\mathit{D}=diag\left(\widehat{\mathit{Y}}\widehat{\mathit{V}}\right)diag\left(\dot{\mathit{V}}\right)$ and $\mathit{J}=diag\left(\dot{\mathit{V}}\right)\widehat{\mathit{Y}}diag\left(\widehat{\mathit{V}}\right)$, Equations 14, 15 can be rewritten as:

$\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{V}}=\left(\mathit{D}+\mathit{J}\right)diag{\left(\mathit{V}\right)}^{-1}(16)$

$\frac{\partial \text{Δ}\dot{\mathit{S}}}{\partial \mathit{\delta }}=j\left(\mathit{D}-\mathit{J}\right)(17)$

Based on 16, 17, we can obtain:

$\left(\begin{array}{cc}\mathit{D}+\mathit{J}& j\left(\mathit{D}-\mathit{J}\right)\end{array}\right)\left(\begin{array}{c}diag{\left(\mathit{V}\right)}^{-1}\text{Δ}\mathit{V}\\ \text{Δ}\mathit{\delta }\end{array}\right)=-\text{Δ}\dot{\mathit{S}}(18)$

Extraction of the real and imaginary parts of the system (18) gives

$\left(\begin{array}{cc}{\mathit{D}}_{\mathit{R}}+{\mathit{J}}_{\mathit{R}}& -{\mathit{D}}_{\mathit{I}}+{\mathit{J}}_{\mathit{I}}\\ {\mathit{D}}_{\mathit{I}}+{\mathit{J}}_{\mathit{I}}& {\mathit{D}}_{\mathit{R}}-{\mathit{J}}_{\mathit{R}}\end{array}\right)\left(\begin{array}{c}diag{\left(\mathit{V}\right)}^{-1}\text{Δ}\mathit{V}\\ \text{Δ}\mathit{\delta }\end{array}\right)=-\left(\begin{array}{c}\text{Δ}\mathit{P}\\ \text{Δ}\mathit{Q}\end{array}\right)(19)$

where $\mathit{D}={\mathit{D}}_{\mathit{R}}+j{\mathit{D}}_{\mathit{I}}$, and $\mathit{J}={\mathit{J}}_{\mathit{R}}+j{\mathit{J}}_{\mathit{I}}$. The extracted Jacobian matrix is the coefficient matrix of system (19) produced after removing the rows and columns corresponding to the slack and power/voltage (PV) buses.

The DEJMP method is summarized below:

ALGORITHM 1

Algorithm 1. DEJMP.

The proposed method differs from the conventional method in three aspects: (1) the Jacobian matrix is directly extracted from the complex power equation; (2) the real and imaginary parts are separated after complex-number calculations; and (3) the process of taking the derivatives of the active and reactive power equations in separate steps is absent. Consequently, compared to the conventional method, using the DEJMP method to obtain the Jacobian matrix is much less computationally expensive.

4 DEJMP-Based PF Algorithm

A DEJMP-based PF algorithm is introduced to improve the efficiency of calculating the PF:

ALGORITHM 2

Algorithm 1. DEJMP-based PF.

The essential difference between the DEJMP-based PF algorithm and the conventional PF(C-PF) algorithm lies in step 3. See Section 4 for a more detailed discussion of the advantages of the DEJMP-based PF algorithm.

5 Simulation and Discussion

The effectiveness of the proposed DEJMP-based PF algorithm is examined by comparing it with the C-PF algorithm in polar coordinates. The two algorithms are implemented on the IEEE-300, S-1047, S-2383, and S-9241 bus systems in MATLAB 2020b on a computer with an Intel Core i5-8500 processor and 8 GB of memory and running on the 64-bit Windows 10 Operating System.

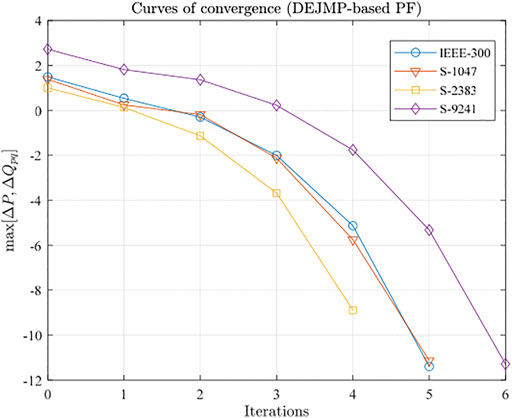
Figure 1 shows the curves of convergence of the DEJMP-based PF and C-PF algorithms.

FIGURE 1

FIGURE 1. Curves of convergence.

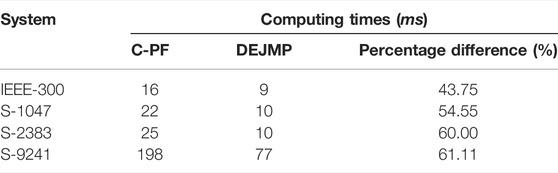
Table 1 compares the computing times of the two algorithms.

TABLE 1

TABLE 1. Computing times of PF.

An analysis of Table 1 reveals that the DEJMP-based PF algorithm is much more efficient at extracting the Jacobian matrix than the C-PF algorithm. This advantage is more pronounced for large systems. Simulation results obtained on the S-9241 system show that the computing time of the DEJMP-based PF algorithm is 23.97% less than that of the C-PF algorithm.

To further illustrate the effectiveness of the DEJMP-based PF algorithm, the times (obtained using the Run and Time functions in MATLAB) required by the two algorithms to calculate the Jacobian matrix of each system selected for simulation are compared, as shown in Table 2.

TABLE 2

TABLE 2. Computing times to obtain the Jacobian matrix.

Clearly, the DEJMP method avoids the trigonometric operations involved in the conventional method during the calculation of the Jacobian matrix and, therefore, considerably improves the computational efficiency of the relevant process. In particular, compared to the C-PF algorithm, the DEJMP-based PF algorithm requires 61.11% less time to calculate the Jacobian matrix of the S-9241 system.

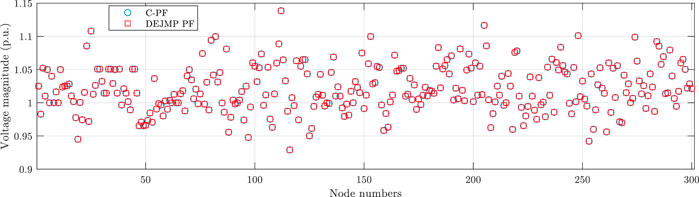
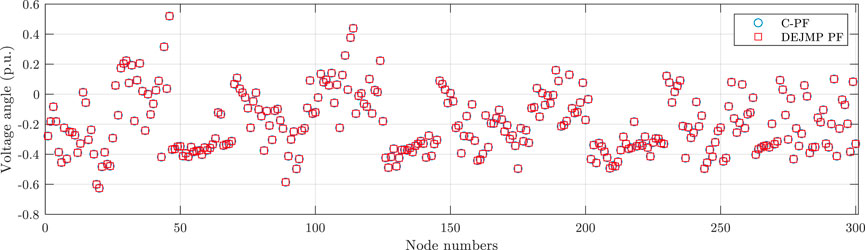
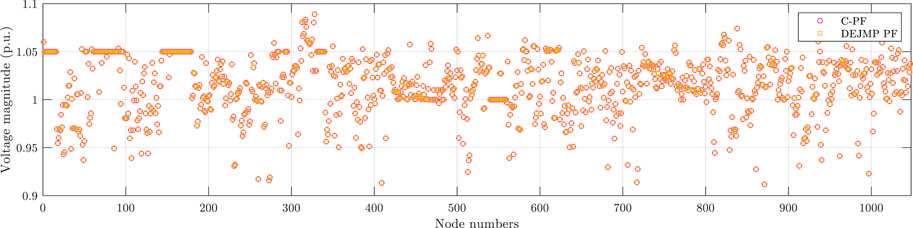
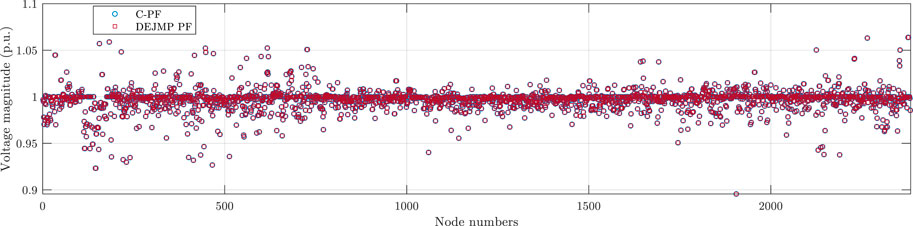
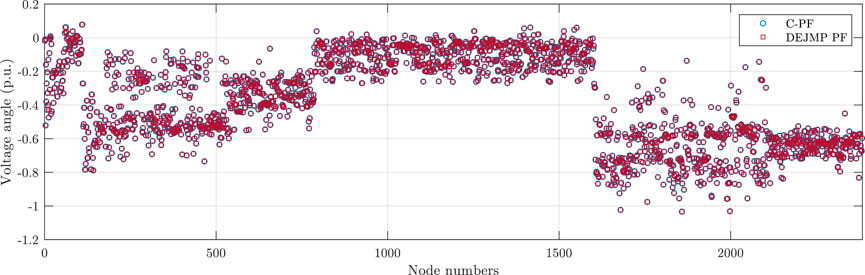
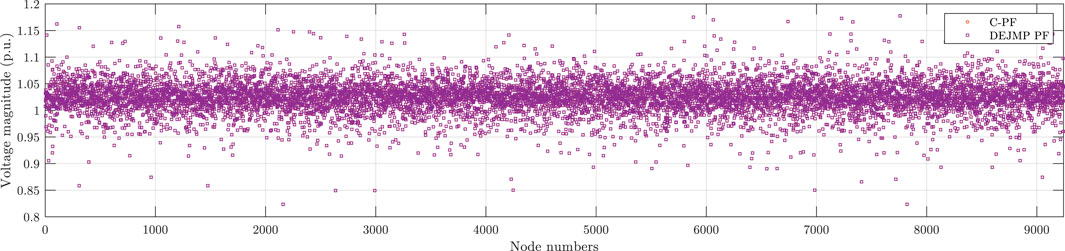
It is worth noting that the Jacobian matrix generated by DEJMP is identical to that obtained by traditional methods. As a result, the DEJMP-based method produces the same PF results as traditional PF algorithms. Figures 2–9 demonstrate the voltage magnitude and angle results of DEJMP-based PF and C-PF, respectively.

FIGURE 2

FIGURE 2. the voltage magnitude obtained by DEJMP-based PF and C-PF on IEEE-300 bus systems.

FIGURE 3

FIGURE 3. the voltage angle obtained by DEJMP-based PF and C-PF on IEEE-300 bus systems.

FIGURE 4

FIGURE 4. the voltage magnitude obtained by DEJMP-based PF and C-PF on S-1047 bus systems.

FIGURE 5

FIGURE 5. the voltage angle obtained by DEJMP-based PF and C-PF on S-1047 bus systems.

FIGURE 6

FIGURE 6. the voltage magnitude obtained by DEJMP-based PF and C-PF on S-2383 bus systems.

FIGURE 7

FIGURE 7. the voltage angle obtained by DEJMP-based PF and C-PF on S-2383 bus systems.

FIGURE 8

FIGURE 8. the voltage magnitude obtained by DEJMP-based PF and C-PF on S-9241 bus systems.

FIGURE 9

FIGURE 9. the voltage angle obtained by DEJMP-based PF and C-PF on S-9241 bus systems.

As shown in Figures 2–9, the PF results of the DEJMP-based algorithm are the same as the conventional PF algorithms.

6 Conclusion

This paper presents a method to directly extract the Jacobian matrix of the PF equations of a power system in polar coordinates from its complex power equation (termed the DEJMP method). The DEJMP method improves the computational efficiency of the relevant process because it avoids the complex trigonometric operations involved in the conventional method during the calculation of the Jacobian matrix. The simulation results show that the DEJMP-based PF algorithm requires more than 40% less time to calculate the Jacobian matrix than the C-PF algorithm. This decrease in computing time is more pronounced for large systems. In fact, the DEJMP approach can be used to increase the performance of any algorithm that includes the calculation of the Jacobian matrix, aside from the PF (e.g., those used to produce state and optimal PF estimates for power systems). In later publications, relevant discoveries will be provided.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, HW and ZL; methodology, HW and ZL; software, ZL and HW; validation, HW and Hobo Wei; formal analysis, ZL and HW; investigation, ZL and HW; resources, HW; data curation, ZL, HW, and Hobo Wei; writing—original draft preparation, ZL; writing—review and editing, HW; visualization, ZL; super-vision, HW; project administration, HW; funding acquisition, HW. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (NSFC), grant number 51967002.

Conflict of Interest

Author HW is employed by power dispatching control center of Guangxi power grid.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alves, D. A., da Silva, L. C. P., Castro, C. A., and da Costa, V. F. (2003). Continuation Fast Decoupled Power Flow with Secant Predictor. IEEE Trans. Power Syst. 18, 1078–1085. doi:10.1109/TPWRS.2003.814892

CrossRef Full Text | Google Scholar

Chappa, H. K., and Thakur, T. (2017). “Condition Number Monitoring of Power Flow Jacobian Matrix to Detect Impending Voltage Instability,” in 2017 14th IEEE India Council International Conference (INDICON), 1–5. doi:10.1109/INDICON.2017.8487475

CrossRef Full Text | Google Scholar

Chappa, H. K., and Thakur, T. (2018). “Identification of Weak Nodes in Power System Using Conditional Number of Power Flow Jacobian Matrix,” in 2018 International Conference and Utility Exhibition on Green Energy for Sustainable Development (ICUE), 1–6. doi:10.23919/ICUE-GESD.2018.8635676

CrossRef Full Text | Google Scholar

Chen, Y. C., Wang, J., Dominguez-Garcia, A. D., and Sauer, P. W. (2016). Measurement-Based Estimation of the Power Flow Jacobian Matrix. IEEE Trans. Smart Grid 7, 2507–2515. doi:10.1109/TSG.2015.2502484

CrossRef Full Text | Google Scholar

Conlin, E., Dahal, N., Rovnyak, S. M., and Rovnyak, J. L. (2021). “Introducing a Concise Formulation of the Jacobian Matrix for Newton-Raphson Power Flow Solution in the Engineering Curriculum,” in 2021 IEEE Power and Energy Conference at Illinois (PECI), 1–8. doi:10.1109/PECI51586.2021.9435220

CrossRef Full Text | Google Scholar

Derakhshandeh, S. Y., and Pourbagher, R. (2016). Application of High‐order Newton‐like Methods to Solve Power Flow Equations. IET Gener. Transm. & Distrib. 10 (6), 1853–1859. doi:10.1049/iet-gtd.2015.0998

CrossRef Full Text | Google Scholar

Dutto, S., Masetti, G., Chiaradonna, S., and Giandomenico, F. D. (2019). On Extending and Comparing Newton-Raphson Variants for Solving Power-Flow Equations. IEEE Trans. Power Syst. 34, 2577–2587. doi:10.1109/TPWRS.2019.2897640

CrossRef Full Text | Google Scholar

Filho, J. A. P., Martins, N., and Falcao, D. M. (2009). “Identifying Power Flow Control Infeasibilities in Large Scale Power System Models,” in 2009 IEEE Power Energy Society General Meeting, 1. doi:10.1109/PES.2009.5275664

CrossRef Full Text | Google Scholar

Jegatheesan, R., Mohd Nor, N., and Romlie, M. F. (2008). “Newton-raphson Power Flow Solution Employing Systematically Constructed Jacobian Matrix,” in 2008 IEEE 2nd International Power and Energy Conference, 180–185. doi:10.1109/PECON.2008.4762458

CrossRef Full Text | Google Scholar

Lim, J. M., and DeMarco, C. L. (2016). SVD-based Voltage Stability Assessment from Phasor Measurement Unit Data. IEEE Trans. Power Syst. 31, 2557–2565. doi:10.1109/TPWRS.2015.2487996

CrossRef Full Text | Google Scholar

Santos, E. P., Kobay, B., Rosa, M. A., Souza Salgado, R., and Issicaba, D. (2019). Modified Tensor Method to Power Flow Analysis. IET Gener. Transm. & Distrib. 13 (7), 3960–3967. doi:10.1049/iet-gtd.2018.6187

CrossRef Full Text | Google Scholar

Semlyen, A., and de Leon, F. (2001). Quasi-Newton Power Flow Using Partial Jacobian Updates. IEEE Trans. Power Syst. 16, 332–339. doi:10.1109/59.932265

CrossRef Full Text | Google Scholar

Tang, K., Dong, S., Shen, J., Zhu, C., and Song, Y. (2019). A Robust and Efficient Two-Stage Algorithm for Power Flow Calculation of Large-Scale Systems. IEEE Trans. Power Syst. 34, 5012–5022. doi:10.1109/TPWRS.2019.2914431

CrossRef Full Text | Google Scholar

Tinney, W., and Hart, C. (1967). Power Flow Solution by Newton's Method. IEEE Trans. Power Apparatus Syst. PAS-86, 1449–1460. doi:10.1109/TPAS.1967.291823

CrossRef Full Text | Google Scholar

Tostado-Veliz, M., Kamel, S., and Jurado, F. (2019). A Robust Power Flow Algorithm Based on Bulirsch-Stoer Method. IEEE Trans. Power Syst. 34, 3081–3089. doi:10.1109/TPWRS.2019.2900513

CrossRef Full Text | Google Scholar

Tostado-Veliz, M., Kamel, S., and Jurado, F. (2021). Two Efficient and Reliable Power-Flow Methods with Seventh Order of Convergence. IEEE Syst. J. 15, 1026–1035. doi:10.1109/JSYST.2020.3004667

CrossRef Full Text | Google Scholar

Varwandkar, S. D. (2019). Realification of Power Flow. IEEE Trans. Power Syst. 34, 2433–2440. doi:10.1109/TPWRS.2018.2889408

CrossRef Full Text | Google Scholar

Wei, C., and Zhao, Y, Z. Y. (2021). Analysis and Design of a Non-isolated High Step-Down Converter with Coupled Inductor and ZVS Operation. IEEE Trans. Ind. Electron. 69, 9007. doi:10.1109/TIE.2021.3114721

CrossRef Full Text | Google Scholar

Xiao, D., Chen, H., Wei, C., and Bai, X. (2021). Statistical Measure for Risk-Seeking Stochastic Wind Power Offering Strategies in Electricity Markets. J. Mod. Power Syst. Clean. Energy 2021, 1–6. doi:10.35833/MPCE.2021.000218

CrossRef Full Text | Google Scholar

Zhiyou Xu, Z., Qingquan Jia, Q., and Liu Li, L. (2009). “The Approximate Expression of Power Flow Jacobian Matrix and Analysis,” in 2009 International Conference on Sustainable Power Generation and Supply, 1–4. doi:10.1109/SUPERGEN.2009.5347967

CrossRef Full Text | Google Scholar