- 1School of Control and Computer Engineering, North China Electric Power University, Beijing, China
- 2Energy and Electricity Research Center, Jinan University, Guangzhou, China
To realize the lower carbon and more efficient operation of energy hubs in the joint electricity and carbon market, a day-ahead bidding strategy is proposed for the energy hub operator (EHO). Considering the uncertainties of prices, demands, and renewable energy sources, this strategy is formulated as a novel two-stage distributionally robust joint chance-constrained optimization problem. A total distance-based ambiguity set is proposed to preserve the mean value of uncertain factors. By introducing this indicator function, this problem is further reformulated as a mixed-integer linear programming (MILP) problem. Simulations are performed based on the electricity and carbon prices in Europe, and the relation between the carbon emission and operational cost is further investigated in the case studies.
1 Introduction
1.1 Motivation
Energy hubs (EHs) are recognized as a powerful platform to realize the efficient energy conversion and utilization for the future low carbon society, e.g., buildings and industry parks (Mohammadi et al., 2017). With the deregulation of the energy market and the emergence of the carbon market, the energy hub operator (EHO) can participate in both electricity and carbon markets (Ding et al., 2020). It brings significant flexibility to the EHO in reducing the carbon emission (Olsen et al., 2018), while introducing additional risks to the operational cost, e.g., uncertain carbon prices (Sun and Huang, 2020). These uncertainties should be properly modeled and incorporated into the risk management scheme of EHOs.
1.2 Literature Review
The bidding strategies of EHOs within the electricity market, including the day-ahead and real-time electricity market, can always be modeled as deterministic optimization problems to reduce the operational cost (Brahman et al., 2015), emissions (Brahman et al., 2015), and maximize the utility (Li et al., 2018). A time-series technique for predicting the power generation of the photovoltaic (PV) cell is applied in (Brahman et al., 2015), and it is assumed that there is no bias from the actual renewable output to the forecast value. A mathematical program with equilibrium constraints is proposed for studying the strategic behaviors of profit-driven EHs in both the electricity and thermal markets from a deregulated market point of view, and the uncertainties of electricity and heating demand are neglected in the bidding optimization process, considering the conciseness ofthe model. However, one significant feature of EHs is to cope with the fluctuation and intermittency of the distributed renewable generation with the flexibility provided by multicarrier energy systems (Jadidbonab et al., 2020).
Furthermore, according to the uncertainties of renewable energy sources, loads, prices, etc., the deterministic strategies can be further extended to stochastic optimization (Davatgaran et al., 2018; Zhao et al., 2020; Jadidbonab et al., 2020), robust optimization (Lu et al., 2020), distributionally robust optimization (Zhao et al., 2019), and hybridization (Liu et al., 2021). The hybrid alternating current/direct current (AC/DC) microgrid is embedded as an electrical hub for EHs to realize the high efficiency of energy conversion, and a two-stage stochastic programming problem is proposed, where uncertain day-ahead prices, loads, PV, and ambient temperatures are depicted by scenario trees. Making full use of the thermal demand flexibility, the quality of thermal service is modeled as a chance constraint (Zhao et al., 2020). In Oskouei et al. (2021), a large set of industrial EHs are integrated into virtual EHs to trade energy in various markets, and the robust approach is coordinated with a stochastic programming model to formulate a hybrid expression of uncertainties, considering the priority of day-ahead electricity prices. The ability of EHs to participate in the joint electricity and thermal markets in the form of virtual power plants (VPPs) is explored in Jadidbonab et al. (2020), and a self-scheduling program is proposed for virtual EHs to maximize the revenue.
When the carbon emission is considered, the bidding management should consider the carbon emissions as objective functions (Yang et al., 2019) or constraints (Cheng et al., 2018). For the given carbon permit prices, a price-taker bidding strategy is proposed for the VPP operator to bid in the energy, ancillary services, and carbon market in (Yang et al., 2019), where carbon emissions, greenhouse gases, and pollutants are effectively reduced by the carbon trading mechanism. In Cheng et al. (2018), an analytical model called carbon emission flow is proposed to quantify the allocation of carbon emission among different energy carriers in delivery and conversion processes including both primary and secondary energy. This work is further used to realize the coordination between transmission and distribution systems with locational marginal electricity and uniform carbon prices in Cheng et al. (2020). Though there have been few studies about carbon trading in the existing literature, the uncertainties of carbon prices have not been considered in existing works (Yang et al., 2019; Cheng et al., 2018, 2020). It introduces additional risks to EHOs involving carbon markets.
The prevalent works on the risk hedging strategies of EHOs in various markets are to manage specific uncertainties. These uncertainties are the aggregation of prices, renewable energy output, loads, etc. They can be further depicted by the stochastic model (Zhao et al., 2020), uncertain sets (Lu et al., 2020), and ambiguity sets (Zhao et al., 2019). The required scenarios for stochastic optimization rapidly increase with a growing number of uncertainties to sustain an acceptable confidence level, or uncertainties are assumed to obey exact probability distributions which are normally unrealistic. In robust optimization, uncertainties are always depicted as an uncertainty set, e.g., polyhedron, which ignores the distribution information, and the optimized result by considering the worst condition can be overconservative. To address these limitations, the ambiguity sets are proposed under different metrics, e.g., total distance (Liu et al., 2021) and moment-based distances (Zhao et al., 2019). However, when the carbon price uncertainties are considered, the ambiguity sets have not been modeled.
To address the uncertainties under joint electricity and carbon markets, the EHO should optimize the conversion, storage, and consumption processes within EHs. As the distributed energy resources are to be integrated into EHs, the conversion process, from renewable energy sources and gas to electricity and thermal energy, has been embedded into the bidding strategies of EHOs (Davatgaran et al., 2018; Dai et al., 2017). Using existing electrical and thermal energy storage systems (ESSs), the electricity and thermal energy can be charged and discharged efficiently. The demand response programs have been considered from the energy consumption perspective, and the quality of thermal services has been utilized to reduce the operational risk (Zhao et al., 2020). The flexibility of the thermal demand has not been explored to reduce the risks under joint electricity and carbon markets.
1.3 Contributions
To manage the uncertainties in joint electricity and carbon markets, a novel day-ahead bidding strategy is proposed for the EHO. This strategy is formulated as a two-stage distributionally robust chance-constrained programming problem, where the uncertainties of prices, loads, renewable energy sources, and ambient temperature are formulated as a novel ambiguity set. The quality of service for the thermal demand is relaxed and treated as a joint chance constraint. Based on duality, the problem is reformulated as a mixed-integer linear programming (MILP) problem. The main contribution of this article can be summarized as follows:
• A novel ambiguity set is proposed for electrical prices and carbon prices. The first-order information is preserved in this set.
• A novel two-stage distributionally robust joint chance-constrained programming problem is proposed to manage the uncertainties in the joint electricity and carbon markets.
The rest of this article is organized as follows. The day-ahead bidding scheme is proposed in Section 2. The two-stage distributionally robust joint chance-constrained programming problem is formulated in Section 3. The deterministic reformulation method is given in Section 4. Case studies are performed in Section 5. Conclusions are drawn in Section 6.
2 Day-Ahead Bidding of Energy Hubs in the Joint Electricity and Carbon Market
In this section, a typical EH model is introduced, together with its bidding scheme in the joint electricity and carbon market.
2.1 Energy Hub Models
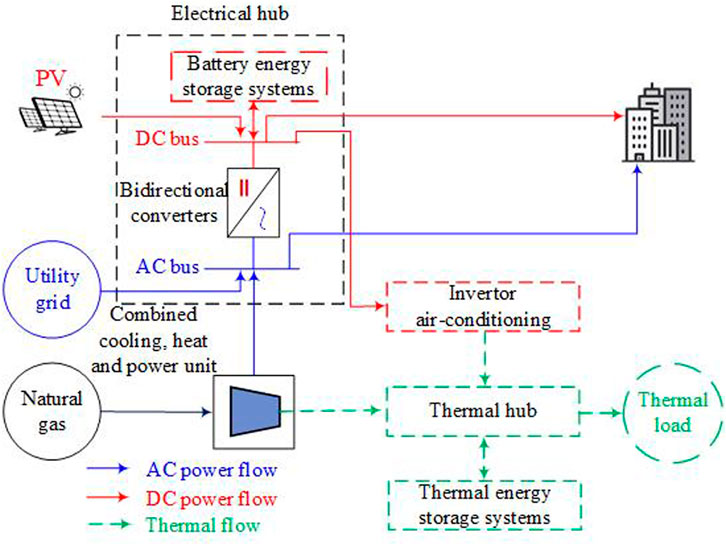
An EH is typically treated as a multiple-input and multiple-output energy conversion system, including the functions of conversion, storage, and consumption (Zhao et al., 2020). Considering the electrification of buildings, transportation, and industries in the coming decades, there exist electrical and thermal hubs in the system (Oskouei et al., 2021). The input of the EH is the utility grid (UG), PV generation, and natural gas. The energy conversion is realized by the combined heat and power (CHP) unit and air-conditioning. The AC/DC conversion in the electrical hub is realized by the bi-directional AC/DC converters. The battery and thermal ESSs are used to store electricity and thermal.
2.2 Day-Ahead Bidding Progress of Energy Hubs
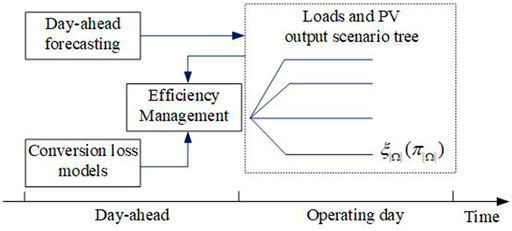
The EHO is to manage the conversion, storage, and utilization processes in the EHs while participating in both electricity and carbon markets. The EHO acts as the price taker in both markets. The bidding procedure for the EHO is shown in Figure 1.
As shown in Figure 1, the EHO can buy and sell electricity in the day-ahead and real-time markets. The carbon permit is purchased in the day-ahead and real-time carbon markets. In the day-ahead bidding, the electricity and carbon prices are given, while the real-time electricity and carbon prices, together with PV output, demand, and ambient temperature, are uncertain, which is depicted by a scenario tree with uncertain probability density functions (PDFs).
3 Distributionally Robust Bidding Problem Formulation
The optimal day-ahead bidding problem for EHs is formulated as a bi-objective two-stage distributionally robust optimization problem in this section, including the day-ahead operation and real-time operation recourse.
3.1 Two-Stage Distributionally Robust Chance-Constrained Programming Problem
A two-stage distributionally robust chance constrained optimization problem is shown as follows:
where x represents the day-ahead bidding strategy of EHO, including the electricity and carbon permit purchase plan, as shown in Eq. 6. X is the first-stage constraint set, including box constraints Eqs 7, 8. ρ is the weight factor between the expected value and conditional value at risk (CVaR), which is employed as a measure of the tail risk with the given confidence level α. The choice of ρ depends on the risk preference of the EHO. For instance, if the EHO is only concerned about the expected cost minimization, ignoring the potential trading risk in extreme conditions, ρ is set to be 0. The calculation of CVaR is shown as follows:
where η is the value at risk (VaR). For more details on VaR refer to Rockafellar and Uryasev (2000).
where πω and π0,ω are the real probability density and nominal probability density of scenario ω. As shown in Eq. 3, the ambiguity set only limits the density function on the given support set Ω. The mean value of prices and renewable energy outputs is preserved by the third line of Eq. 3 (Liu et al., 2021). This ambiguity set is further represented by the compact format Gω ≤ e.
where Dyω ≥hω − Tωx is the compact representation of Eqs 10–12, 14–33.
The following distributionally robust chance constraint is introduced to balance the feasibility of the recourse problem and uncertainties:
where β is the confidential level of the feasibility of the constraint (Eq. 13). The detailed formulation on the first stage and second stage optimization problems are given in the following subsections.
3.2 Day-Ahead Bidding Optimization
The first stage optimization is to minimize the total cost in the day-ahead market, including the electricity and carbon cost, as follows:
where λDA(t) and μDA(t) are the electricity and carbon prices in the day-ahead markets. The day-ahead bidding plan is limited by the following constraints:
where PUG, min, PUG, max, ΦC, min, and ΦC, max are the minimal and maximal electricity and carbon purchasing limits in the day-ahead and real-time markets.
3.3 Real-Time Operation Optimization
Real-time operation optimization is to minimize the real-time operational cost by optimal scheduling of the generation, conversion, and consumption processes within EHs. The objective function in the second stage optimization is depicted as follows:
where subscription ω represents for scenario ω. λRT,ω(t) and μRT,ω(t) are the real-time electricity and carbon prices in the electricity and carbon markets. pRT(t) and ϕRT(t) are the real-time power between the EH and UG and carbon permit purchased, respectively. cES,CH and cES,DC are the charging and discharging cost of battery energy systems (BESs), respectively. pES,CH,ω(t) and pES,DC,ω(t) are the charging and discharging rates of the BES, respectively. cGAS is the price of natural gas. vCHP,ω(t) and vGAS,ω(t) are the gas consumption of CHP and gas boiler, respectively.
The constraints for within the EHs include the thermal, electrical, conversion, storage, and carbon emission constraints, as shown in the following subsections.
3.3.1 Constraints for the Thermal Hub
The energy balance equations in the heating and cooling hubs of the EH are depicted as follows:
where qHVAC,TD,ω(t) and qHVAC,CD,ω(t) are the heating and cooling demand to control the indoor room temperature, respectively. qTD,ω(t) and qCD,ω(t) are the heating and cooling demand, respectively. qAC,ω(t) and qCE,ω(t) are the heating consumption and cooling output of the absorption chiller, respectively. qCHP,ω(t) and qGAS,ω(t) are the heating output of the CHP and gas boiler, respectively. qHS,CH,ω and qHS,DC,ω(t) are the charging and discharging rates of heating energy storage (HES), respectively. qCS,CH,ω and qCS,DC,ω(t) are the charging and discharging rates of cooling energy storage (CES), respectively. qIAC,ω(t) is the cooling output of the inverter air-conditioning system.
Eqs 10, 11 depict the energy balance on the heating hub and cooling hub, respectively.
The indoor room temperature of a cluster of buildings is managed via the consumption of heating and cooling from the EH, as shown in Figure 2. Based on Fourier’s law, the relationship between the heating/cooling loads and indoor room temperature can be approximated by the following linear equations (Zhang et al., 2018):
where Θin,ω(t) and Θam,ω(t) are the indoor temperature and ambient temperature, respectively. cair is the air heating capacity (kWh/°C), and RT is the thermal resistance of the building envelope (°C/kW). To guarantee the thermal service quality, the indoor room temperature should be guaranteed within the given range as follows:
where Θin, min and Θin, max are the minimal and maximal limitations for the indoor room temperature, respectively.
3.3.2 Constraints of the Electrical Hub
In the electrical systems, the power balance equations on the AC bus and DC bus of the electrical hub can be depicted as follows:
where pCHP,ω(t) is the electric output of CHP, pAC2DC,ω(t) and pDC2AC,ω(t) are the power transferred from the AC bus to DC bus and DC bus to AC bus, respectively. pAC,ω(t) and pDC,ω(t) are the AC load and DC load, respectively. pIAC,ω(t) is the electricity consumption of the inverter air-conditioning system. ηBIC is the efficiency of the bidirectional converter (BIC). Eqs 14, 15 depict the power balance on the AC bus and DC bus of the electrical hub, respectively.
The limitations for power exchange between the UG and EH and power transferring on the BIC are shown as follows:
where PBIC,max is the capacity of the BIC. IDC2AC,ω(t) is a binary variable, indicating the operating status of BICs, i.e., 1 if BIC is on the inverter mode and 0 on the rectifier mode.
Eqs 16, 17 represent the power range limitation on the day-ahead and real-time power exchange between the EH and utility grid. Eqs 18, 19 are the constraints for power conversion from the DC bus to AC bus and AC bus to DC bus, respectively. IDC2AC forces the unidirection of power conversion on the BIC.
3.3.3 Constraints of Energy Conversion
The energy conversion constraints are to depict the relationship among energy carriers within the EH, which can be depicted as the following linear functions (Zhao et al., 2020):
where ηCHPe and ηCHPh are the electricity and heat conversion efficiency of CHP, respectively. ηGAS, ηIAC, ηAC, and ηPCS are the conversion efficiencies of the gas boiler, absorption chiller, air conditioner, and ice storage air conditioner, respectively.
Eq. 20 shows the energy conversion from gas to electricity. The conversion from gas to heating is depicted by Eqs 21, 22, using the CHP and gas boiler, respectively. The conversion from electricity to cooling is depicted by Eqs 23, 24, using the air conditioner and ice storage air conditioner, respectively. The conversion from heating to cooling is shown in Eq. 25. It should be noted that these linear functions might be oversimplified, especially for the CHP. If heat recovery and other processes are considered, their equations can be replaced by more accurate convex or non-convex models, balancing the optimality and feasibility (Dai et al., 2017).
3.3.4 Constraints of Energy Storage Systems
Considering the self-discharge, charge, and discharge of processes, the constraints for the ESSs, including BES, CES, and HES, are represented as follows (Zhao et al., 2018):
where yDC(t), yCH(t), and yES(t) represent the discharging, charging, and energy status of BES, HES, and CES, respectively. ICH,k(t) is a binary variable, indicating the charging and discharging status, respectively. ηy,CH, ηy,DC, and ηy represent the charging, discharging, and self-discharging efficiency of ESSs, respectively. yDC,max, yCH,max, yES,min, and yES,max are the limitations for the discharging, charging, and energy status, respectively.
Eqs 26–28 are the limitations on the discharging, charging, and energy status of ESSs, respectively. The energy status dynamic is shown in Eq. 29. Eqs 30–32 enforce that the ESS can only be either charging or discharging within each period. After the operation, the energy status should be the same as the initial status, as depicted by Eq. 32.
3.3.5 Constraints of Carbon Emission
The carbon emissions are generated by the utilized electricity and gas, which should be less than the purchased carbon permit in the day-ahead market and real-time market, as follows:
where νele and νgas are the carbon emission co-efficients of electricity and natural gas, respectively.
4 Deterministic Reformulation
As shown in Eqs 1–5, the formulated problem is a two-stage distributionally robust jointed chance-constrained programming problem. This problem cannot be solved directly as the density function is uncertain. It is further reformulated as its deterministic counterpart, which is a mixed-integer linear programming problem.
4.1 Deterministic Reformulation of Jointed Chance Constraints
To reformulate the joint chance constraints (Eq. 5) as a deterministic constraint, an indicator function is introduced as follows, to show whether y is feasible or not under scenario ω:
Using the indicator function (Eq. 34), the joint chance constraint (Eq. 5) can be reformulated as the following constraints:
where M is a scalar big enough to guarantee the feasibility of problem (Eq. 4), when Iω is activated to 1. Based on the ambiguity set (3), constraint (Eq. 35) can be further reformulated as the following constraint:
where γ is the Lagrange multiplier of Gω ≤ e, that is, the ambiguity set (Eq. 3), and b (Iω) is the vector to represent the ∑ω∈ΩIωπω.
It can be seen that after the reformulation (Eq. 37), the jointed chance constraint can be solved by its deterministic counterpart.
4.2 Deterministic Reformulation of Second-Stage Optimization Problems
The expected CVaR value in Eq. 1, that is,
where
After the deterministic reformulation of the jointed chance constraints and the second-stage optimization problem, problems (1)–(5) can be treated as the following mixed-integer linear programming problem:
Problem (39) can be solved by offshore commercial solvers, e.g., Gurobi and Cplex.
5 Case Study
5.1 Case Description
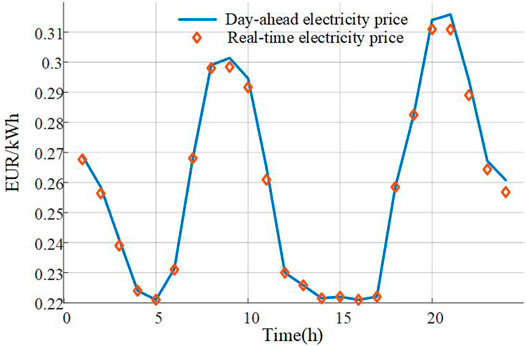
To verify the effectiveness of the proposed bidding strategy, an EH test system is proposed, as shown in Figure 2. The bidirectional AC/DC converter is used to realize the AC/DC conversion in the electrical hub. The electrical load, heat load, and cooling load profiles are obtained from Sadeghian et al. (2017). The day-ahead electricity price and expected real-time electricity price profiles are obtained from energy market prices in Omie (2022), as shown in Figure 3, and carbon prices are extracted from EU Carbon Permits (Tradingeconomics, 2022a). For the second stage optimization, 100 scenarios are generated, including the electrical prices, loads, PV output, and ambient temperature. α is set to 0.95. Other parameter settings are obtained from Zhao et al. (2020).
Numerical simulations were carried out on a desktop with an Intel Xeon Gold 6226R CPU and 128 GB of RAM. The MILP problem in Eq. 39 is solved by the commercial solver Gurobi with branch-and-cut and simplex methods.
To show the effectiveness of the proposed method, four different cases are performed as follows:
• Case I: The uncertainties have not been considered.
• Case II: τ = 0, β = 0, and ρ = 0.5.
• Case III: τ = 0.1, β = 0, and ρ = 0.5.
• Case IV: τ = 0.1, β = 0.1, and ρ = 0.5.
• Case V: τ = 0, β = 0, and ρ = 1.
5.2 Result Analysis
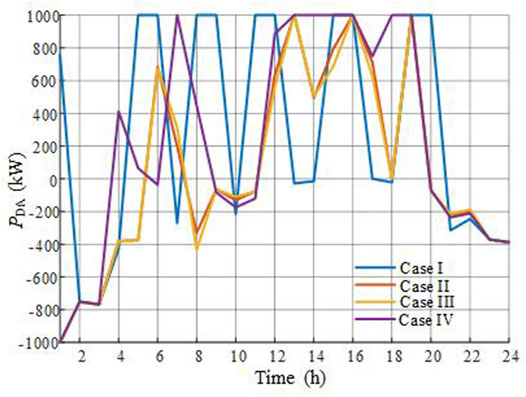
The simulation results under different cases are shown in Table 1, and the day-ahead bidding curves of the EHO in the day-ahead market are shown in Figure 4.
5.2.1 Impacts of Uncertainties
As shown in Table 1, an increase in the operational cost from 5027.94 $ to 5136.68 $ can be induced including uncertainties of PV output, demand, and ambient temperature. The day-ahead bidding curves of case I and case II vary, as shown in Figure 4, especially during the (0:00, 1:00). In case 1, the uncertainties have not been considered, which means forecast prices in the real-time market are accurate without bias, so it is specific for the EHO whether there is a need for arbitrage or not. In other words, the EHO tends to purchase as much electricity as possible, in the day-ahead market during time slots when the electricity price in the day-ahead market is lower than in the real-time market, e.g., (5:00, 6:00) and (8:00, 9:00). The purchased electricity during these time slots has reached the given upper limit, that is, 1000 kW.
To explore the effectiveness of the risk-averse, the risk factor ρ is set to be 1 in case V. In comparison with case II, the potential trading risk, which can be incurred in the extreme condition, is neglected by the EHO to search for a lower expected cost.
5.2.2 Impacts of Distributionally Robust Uncertainties
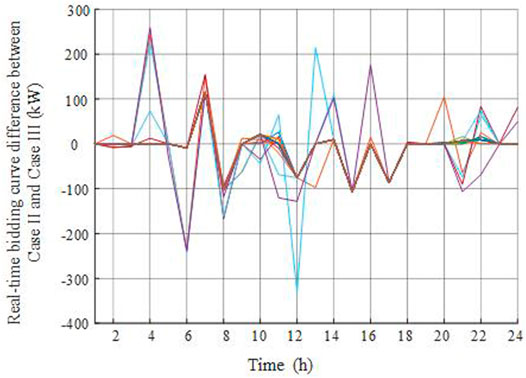
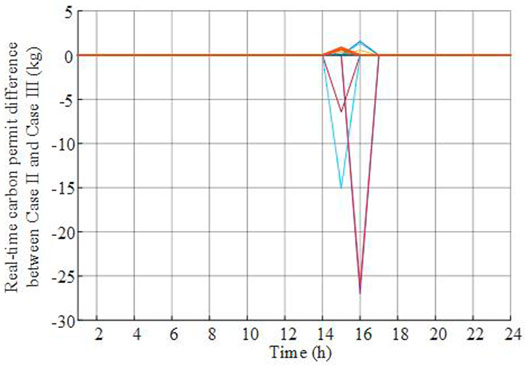
The real-time bidding and carbon permit trading difference curves between case II and case III are shown in Figures 5, 6. The uncertainties of the probability distribution are considered, and the worst condition is found by the optimization process. The variance from the nominal distribution of case II increases the operational cost, which seems slight due to limited differences among scenarios. The expected electricity purchased under nominal PDF in the real-time market increased by 220 kWh in case III. An interesting observation is that even if the electricity is increased, the carbon emission almost remains the same. It indicates that the proposed bidding strategy can always reduce carbon emissions, while the electricity bidding can be adjusted accordingly.
5.2.3 Impacts of Joint Chance Constrain Relaxation
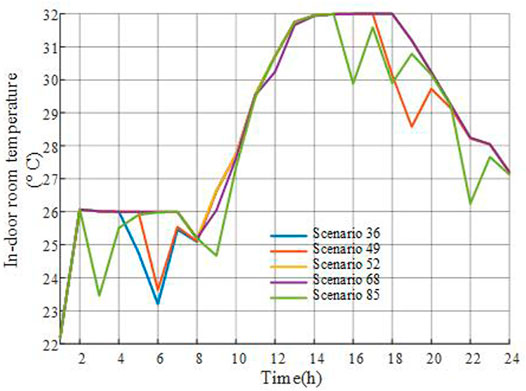
The indoor room temperature curve under scenarios 36, 49, 52, 68, and 85 are shown in Figure 7. In these five scenarios, the indoor room temperature has been relaxed as the highest temperature is more than 24°C, that is, the threshold temperature value. These relaxed scenarios can help reduce the carbon emission and operational cost. Furthermore, due to τ = 0.1, the number of total relaxed scenarios is 5, while it should be 10 when τ = 0.0, that is, the PDF is accurate.
6 Conclusion
In this study, a day-ahead bidding strategy is proposed for the EHO to manage its technical and economic behavior in the joint electricity and carbon market. To manage the ambiguity uncertainties of prices, loads, renewable energy output, and ambient temperature, this strategy is formulated as a two-stage distributionally robust joint chance-constrained programming problem and further been reformulated as a mixed-integer linear programming problem.
Simulations are performed on a test EH system, where the indoor room temperature can be relaxed in some scenarios. Results indicate that the proposed strategy can manage the uncertainties in the joint electricity and carbon market and reduce the operational cost and carbon emission by exploring the flexibility of the thermal demand.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
JL completed the technical writing, idea consultation, and supervision of this work, and other authors listed also made a direct contribution to the work.
Funding
The work was supported in part by the consulting research project of the Chinese Academy of Engineering (2021NXZD2) and in part by the National Natural Science Foundation of China (52061635102).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Brahman, F., Honarmand, M., and Jadid, S. (2015). Optimal Electrical and thermal Energy Management of a Residential Energy Hub, Integrating Demand Response and Energy Storage System. Energy and Buildings 90, 65–75. doi:10.1016/j.enbuild.2014.12.039
Cheng, Y., Zhang, N., Wang, Y., Yang, J., Kang, C., and Xia, Q. (2018). Modeling Carbon Emission Flow in Multiple Energy Systems. IEEE Trans. Smart Grid 10, 3562–3574.
Cheng, Y., Zhang, N., Zhang, B., Kang, C., Xi, W., and Feng, M. (2020). Low-carbon Operation of Multiple Energy Systems Based on Energy-Carbon Integrated Prices. IEEE Trans. Smart Grid 11, 1307–1318. doi:10.1109/tsg.2019.2935736
Dai, Y., Chen, L., Min, Y., Chen, Q., Hu, K., Hao, J., et al. (2017). Dispatch Model of Combined Heat and Power Plant Considering Heat Transfer Process. IEEE Trans. Sustain. Energ. 8, 1225–1236. doi:10.1109/tste.2017.2671744
Davatgaran, V., Saniei, M., and Mortazavi, S. S. (2018). Optimal Bidding Strategy for an Energy Hub in Energy Market. Energy 148, 482–493. doi:10.1016/j.energy.2018.01.174
Ding, T., Lu, R., Xu, Y., Yang, Q., Zhou, Y., Zhang, Y., et al. (2020). Joint Electricity and Carbon Market for Northeast Asia Energy Interconnection. Glob. Energ. Interconnection 3, 99–110. doi:10.1016/j.gloei.2020.05.002
Jadidbonab, M., Mohammadi-Ivatloo, B., Marzband, M., and Siano, P. (2020). Short-term Self-Scheduling of Virtual Energy Hub Plant within thermal Energy Market. IEEE Trans. Ind. Electron. 68, 3124–3136.
Li, R., Wei, W., Mei, S., Hu, Q., and Wu, Q. (2018). Participation of an Energy Hub in Electricity and Heat Distribution Markets: An Mpec Approach. IEEE Trans. Smart Grid 10, 3641–3653.
Liu, S., Zhao, T., and Wang, P. (2021). “Strategic Bidding for Energy Hubs Based on Hybrid Stochastic/distributionally Robust Optimization,” in 2021 IEEE Power & Energy Society General Meeting (PESGM) (IEEE), 1–5. doi:10.1109/pesgm46819.2021.9637912
Lu, X., Liu, Z., Ma, L., Wang, L., Zhou, K., and Feng, N. (2020). A Robust Optimization Approach for Optimal Load Dispatch of Community Energy Hub. Appl. Energ. 259, 114195. doi:10.1016/j.apenergy.2019.114195
Mohammadi, M., Noorollahi, Y., Mohammadi-Ivatloo, B., and Yousefi, H. (2017). Energy Hub: From a Model to a Concept - A Review. Renew. Sustainable Energ. Rev. 80, 1512–1527. doi:10.1016/j.rser.2017.07.030
Olsen, D. J., Zhang, N., Kang, C., Ortega-Vazquez, M. A., and Kirschen, D. S. (2018). Planning Low-Carbon Campus Energy Hubs. IEEE Trans. Power Syst. 34, 1895–1907.
Omie, (2022). Day-ahead Electricity price. Available at: https://www.omie.es/en/market-results/daily/daily-market/daily-hourly-price?scope=daily&date=2022-03-01.
Oskouei, M. Z., Mohammadi-Ivatloo, B., Abapour, M., Shafiee, M., and Anvari-Moghaddam, A. (2021). Strategic Operation of a Virtual Energy Hub with the Provision of Advanced Ancillary Services in Industrial parks. IEEE Trans. Sustain. Energ. 12, 2062–2073. doi:10.1109/tste.2021.3079256
Rockafellar, R. T., and Uryasev, S. (2000). Optimization of Conditional Value-At-Risk. Jor 2, 21–41. doi:10.21314/jor.2000.038
Sadeghian, H., Athari, M. H., and Wang, Z. (2017). “Optimized Solar Photovoltaic Generation in a Real Local Distribution Network,” in Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), 2017 IEEE (IEEE), 1–5. doi:10.1109/isgt.2017.8086067
Sun, W., and Huang, C. (2020). A Carbon price Prediction Model Based on Secondary Decomposition Algorithm and Optimized Back Propagation Neural Network. J. Clean. Prod. 243, 118671. doi:10.1016/j.jclepro.2019.118671
Tradingeconomics (2022). Carbonprice. Available at: https://tradingeconomics.com/commodity/carbon.
Yang, D., He, S., Chen, Q., Li, D., and Pandžić, H. (2019). Bidding Strategy of a Virtual Power Plant Considering Carbon-Electricity Trading. CSEE J. Power Energ. Syst. 5, 306–314.
Zhang, C., Xu, Y., Li, Z., and Dong, Z. Y. (2018). Robustly Coordinated Operation of a Multi-Energy Microgrid with Flexible Electric and thermal Loads. IEEE Trans. Smart Grid 10, 2765–2775.
Zhao, P., Gu, C., Huo, D., Shen, Y., and Hernando-Gil, I. (2019). Two-stage Distributionally Robust Optimization for Energy Hub Systems. IEEE Trans. Ind. Inform. 16, 3460–3469.
Zhao, T., Pan, X., Yao, S., Ju, C., and Li, L. (2020). Strategic Bidding of Hybrid Ac/dc Microgrid Embedded Energy Hubs: A Two-Stage Chance Constrained Stochastic Programming Approach. IEEE Trans. Sustain. Energ. 11, 116–125. doi:10.1109/tste.2018.2884997
Keywords: energy hubs, carbon, optimal bidding, uncertainties, distributionally robust
Citation: Ma L, Liu S and Liu J (2022) Distributionally Robust Optimal Bidding of Energy Hubs in the Joint Electricity and Carbon Market. Front. Energy Res. 10:898620. doi: 10.3389/fenrg.2022.898620
Received: 18 March 2022; Accepted: 11 April 2022;
Published: 26 May 2022.
Edited by:
Rui Wang, Northeastern University, ChinaReviewed by:
Xuewei Pan, Harbin Institute of Technology, ChinaYalong Li, China University of Mining and Technology, China
Copyright © 2022 Ma, Liu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:Shengwei Liu, MTU2MjI3Njc2NTFAMTYzLmNvbQ==
 Lifei Ma1
Lifei Ma1 Shengwei Liu
Shengwei Liu