A PANS Method Based on Rotation-Corrected Energy Spectrum for Efficient Simulation of Rotating Flow

Introduction

Rotating machinery, such as pumps and turbines, is widely used in engineering practice (Thangam et al., 1999), and their internal flow has large curvature and high rotation speed characteristics. These flow characteristics that play an important role in the performance need to be investigated in-depth (Huang X. et al., 2019), and the relationship between the external characteristics of the centrifugal pump and the internal flow state needs further study (Lin et al., 2022). For internal flow investigation, the computational fluid dynamics (CFD) method plays an efficient and reliable role in the simulation of complex flows (Zhang et al., 2020). In CFD, the Navier–Stokes equation is a mathematical expression that can adequately describe the motion of fluids. The direct numerical simulation (DNS) method concerns the direct application of this equation; thus, it can solve all turbulent flow fields. Nevertheless, according to Kolmogorov’s theory (Pope, 2000), when the DNS method is used, the length scale $\eta ={({\nu }^3/\epsilon )}^{1/4}$ and time scale ${\tau }_{\eta }={(\nu /\epsilon )}^{1/2}$ are very small, where $\nu$ is the kinematic viscosity and $\epsilon$ is the dispassion of turbulent kinetic energy. Consequently, the DNS method cannot be used to simulate the internal flow of rotating machinery with a high Reynolds number because of the unacceptable simulation cost. The large-eddy simulation (LES) method is used to resolve large vortices directly and model the small ones (Pope, 2000). Various studies have demonstrated that to simulate complex flows with multiple walls, LES requires meshes with an extremely high amount of elements, which leads to a very high number of calculations, making LES not suitable for engineering calculations. Currently, the Reynolds-averaged Navier–Stokes (RANS) method is widely used for its high performance-to-cost ratio (Pope, 2000). However, in the modeling process, the RANS method omits some key information, such as turbulence pulsation; thus, it is associated with some deficiencies when it comes to the simulation of flow with rotation and curvature characteristics. As a result, the balance between calculational accuracy and simulation cost is the main challenge for the turbulence models. In this aspect, hybrid models such as the partially averaged Navier–Stokes (PANS) model have shown their advantages.

Girimaji et al. (2003) proposed the PANS method, which is based on the ratio of the modeled to resolved turbulent kinetic energy, through which the conversion from DNS to RANS can be achieved. In the PANS method, the control parameters for bridging DNS and RANS are f_k and f_ε (Girimaji, 2006; Girimaji et al., 2006) which are the modeled-to-total ratio of the turbulent kinetic energy and its dissipation, respectively. At high Reynolds number flows, there is little dissipation in the resolved scales; thus, it is reasonable that f_ε is set to unity (Girimaji et al., 2006; Lakshmipathy and Girimaji, 2010). When f_k equals unity, the PANS model degrades to a RANS model, while when f_k equals 0, it indicates a DNS simulation. For flows with a high Reynolds number, a reasonable f_k distribution is a key factor for the PANS method. Based on different theories, several scholars have proposed different expressions of f_k. For example, Abdol-Hamid and Girimaji (2004) introduced an original two-stage procedure to calculate f_k, while Song and Park (2009) and Foroutan and Yavuzkurt (2014) deduced two different f_k formulations based on different energy spectra. Hu et al. (2014) proposed a modified f_k expression for unsteady cavitating flows, where f_k varies as a function of water density and mixture density. In a simulation of the flow around a Clark-Y hydrofoil, their modified model can accurately predict the cavity evolution, vortex shedding frequency, and lift force fluctuation. More recently, Wang et al. (2020) proposed a novel Omega-driven dynamic model, where control parameter f_k is automatically adjusted by the rigid vorticity ratio, and the results on three typical flows demonstrated that their model can improve the prediction accuracy.

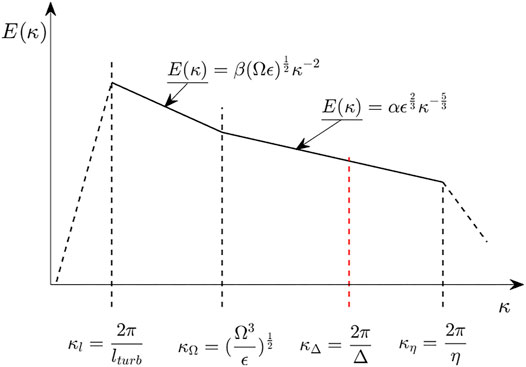
At present, there is no general expression of parameter f_k, and it is based on specific flow characteristics. According to the definition of f_k, its expression based on the energy spectrum is more reasonable, and studies have indicated that the expression of the energy spectrum in a rotating flow differs from that in an ordinary (non-rotating) flow. Zeman (1994) investigated the spectral energy transfer in rotating homogeneous turbulence and found that the wavenumber ${\kappa }_{\Omega }={({\Omega }^3/\epsilon )}^{1/2}$ determines the turbulence length scale and affects the spectral transfer and energy spectrum form in rotating flows, where ${\kappa }_{\Omega }$ is the Zeman number, and $\Omega$ denotes the rotation speed. Baroud et al. (2002) measured a rotating annulus and revealed that the energy cascade in rotating flow is $E\left(\kappa \right)\sim {\kappa }^{-2}$ rather than the expected one, which is $E\left(\kappa \right)\sim {\kappa }^{-5/3}$. By simulating a helical shell model, Rathor et al. (2020) confirmed that with the decreasing Rossby number, which corresponds to an increasing level of rotation, the compensated spectrum to the left of the Zeman scale (Zeman, 1994) departs from the plateau with an additional scaling factor that asymptotes to $E\left(\kappa \right)\sim {\kappa }^{-2}$. Canuto and Dubovikov (1997); Zhou (1995) obtained the same result through theoretical derivation. Thangam et al. (1999) proposed a model that combines an eddy viscosity model with the rotation-corrected energy spectrum. Their new model can reproduce the rotating effect of rotating homogeneous shear and rotating channel flows, which confirms the rationality of the rotation-corrected energy spectrum.

Since there is no f_k expression based on the rotation-corrected energy spectrum yet for the efficient simulation of the complex flow with rotation effect in the rotating machinery, in this paper, a new f_k expression based on the rotation-corrected energy spectrum is deduced and coupled with the PANS model. The PANS model with the new f_k expression is verified in the rotating channel flow. Then it is applied to flow simulation of a centrifugal pump impeller with complex flows of rotating stall and flow separation for further validation.

Governing Equations

The PANS model

In the following analysis, the SST PANS model (Luo et al., 2014; Ranjan and Dewan, 2015; Pereira et al., 2015; Ranjan and Dewan, 2016; Pereira et al., 2018; Qian et al., 2020) is used. The transport equations of the SST PANS model are as follows:

$\frac{\partial k_u}{\partial t}+u_j\frac{\partial k_u}{\partial x_j}=\stackrel{\sim }{P_{ku}}-{\beta }^{\ast }{k}_u{\omega }_u+\frac{\partial }{\partial x_j}\left(\left(\nu +{\sigma }_{ku}{\nu }_u\right)\frac{\partial k_u}{\partial x_j}\right),(1)$

$\frac{\partial {\omega }_u}{\partial t}+u_j\frac{\partial {\omega }_u}{\partial x_j}=\frac{\gamma }{{\nu }_u}\stackrel{\sim }{P_{ku}}-\frac{\gamma }{{\nu }_u}{\beta }^{\ast }(1-\frac{1}{f_{\omega }})k_u{\omega }_u-\frac{\beta {\omega }_u^2}{f_{\omega }}+2\left(1-F_{1u}\right){\sigma }_{\omega 2}\frac{1}{{\omega }_u}\frac{\partial k_u}{\partial x_j}\frac{\partial {\omega }_u}{\partial x_j}\frac{f_{\omega }}{f_k}+\frac{\partial }{\partial x_j}\left(\left(\nu +{\sigma }_{\omega u}{\nu }_u\right)\frac{\partial {\omega }_u}{\partial x_j}\right),(2)$

${\nu }_u=\frac{a_1{k}_u}{\max \left(a_1{\omega }_u,F_{2u}S\right)},(3)$

where u is the partially averaged velocity; partial averaging corresponds to filtering a portion of the fluctuating scales (Girimaji, 2006), and throughout the study, the words filtering and averaging will be used synonymously. k_u is the unresolved turbulent kinetic energy, ω_u is the unresolved specific dissipation rate, f_ω is the modeled-to-total ratio of the specific turbulence dissipation and $f_{\omega }=1/f_k$, υ is the kinematic viscosity, ${\nu }_u$ is the unresolved eddy viscosity, S is the invariant measure of the strain rate, ${\stackrel{\sim }{P}}_{ku}=\min \left(P_{ku},10{\beta }^{\ast }{k}_u{\omega }_u\right)$ is the production term, $P_{ku}={\nu }_u\frac{\partial u_i}{\partial x_j}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$, and $a_1$, β, β^*, σ_ω2, and γ are constant coefficients. Moreover, ${\sigma }_{ku}$ and ${\sigma }_{\omega u}$ are Prandtl numbers, and their specific forms are as follows:

${\sigma }_{ku}={\sigma }_k\frac{f_{\omega }}{f_k},{\sigma }_{\omega u}={\sigma }_{\omega }\frac{f_{\omega }}{f_k}.(4)$

In addition, F_1u and F_2u are two blending functions for the SST PANS model, which are defined as follows:

$F_{1u}=\tanh \left[{\left(\min [\max (\frac{\sqrt{k_u}}{{\beta }^{\ast }{\omega }_{u}y},\frac{500\nu }{y^2{\omega }_u}),\frac{4{\sigma }_{\omega 2u}{k}_u}{C{D}_{k\omega }{y}^2}]\right)}^4\right],(5)$

$F_{2u}=\tanh \left[{\left(\max \left(\frac{2\sqrt{k_u}}{{\beta }^{\text{*}}{\omega }_{u}y};\frac{500\nu }{y^2{\omega }_u}\right)\right)}^2\right],(6)$

$C{D}_{k\omega }=\max (\frac{2\rho {\sigma }_{\omega 2u}}{{\omega }_u}\frac{\partial k_u}{\partial x_i}\frac{\partial {\omega }_u}{\partial x_i},{10}^{-10}),(7)$

where y denotes the distance to the next surface.

f_k Expressions Based on the Energy Spectrum

According to the Kolmogorov hypothesis (Pope, 2000), the energy spectrum without rotation is $E\left(\kappa \right)=\alpha {\epsilon }^{2/3}{\kappa }^{-5/3}$, where $E\left(\kappa \right)$ is the energy spectrum, $\alpha$ is the Kolmogorov constant, $\epsilon$ is the dispassion of turbulent kinetic energy, and $\kappa$ is the wavenumber. Several researchers derived different f_k equations (Song and Park, 2009; Foroutan and Yavuzkurt, 2014; Qian et al., 2020) based on the Kolmogorov hypothesis. The f_k expression deduced by Song and Park (2009) can be seen as follows:

$f_k=\frac{k_u}{k_t}=\frac{{\displaystyle {\int }_{{\kappa }_{\Delta }}^{{\kappa }_{\eta }}E\left(\kappa \right)d\kappa }}{{\displaystyle {\int }_{{\kappa }_l}^{{\kappa }_{\eta }}E\left(\kappa \right)d\kappa }}=\frac{{\kappa }_{\eta }^{-2/3}-{\kappa }_{\Delta }^{-2/3}}{{\kappa }_{\eta }^{-2/3}-{\kappa }_l^{-2/3}}\approx {\left(\frac{\Delta }{\eta }\right)}^{2/3}\left(1-{\left(\frac{\Delta }{\eta }\right)}^{2/3}\right){\left(\frac{\Delta }{l_{turb}}\right)}^{2/3}.(8)$

Eq. 8 is named PANS-ES1. It is similar to that proposed by Song and Park (2009), and l_turb, η, and Δ denote the turbulent length scale for RANS, Kolmogorov length scale (length scale for DNS), and grid size, respectively. The corresponding coupled model with SST k-ω PANS is called SST k-ω PANS-ES1 hereafter.

$l_{turb}=\frac{k_T^{3/2}}{\epsilon },\eta ={\left(\frac{{\nu }^3}{\epsilon }\right)}^{1/4},\Delta ={\left(\Delta x\Delta y\Delta z\right)}^{1/3},(9)$

where k_T is the total turbulent kinetic energy, which is equal to k_r + k_u. In addition, k_r is the resolved turbulent kinetic energy, $k_r=0.5{(U_i-\stackrel{-}{U})}^2$, where $U_i$ is the instantaneous velocity and $\stackrel{-}{U}$ is the time-averaged velocity.

Different from Song et al., Foroutan and Yavuzkurt (2014) adopted a von Kármán-like spectrum (Schiestel and Dejoan, 2005) and derived another f_k formulation, (Eq. 10), which here is referred to as PANS-ES2, and the corresponding coupled model with SST k-ω PANS is called SST k-ω PANS-ES2 hereafter.

$f_k=1-{\left[\frac{{(l_{turb}/\Delta )}^{2/3}}{0.23+{(l_{turb}/\Delta )}^{2/3}}\right]}^{4.5}(10)$

For the rotation-corrected energy spectrum, the energy spectrum between κ_l and κ_η is divided into two parts by the Zeman number ${\kappa }_{\Omega }$ (Zeman, 1994), which is defined as ${({\Omega }^3/\epsilon )}^{1/2}$, where $\Omega$ denotes the rotation speed. More specifically, when ${\kappa }_c<{\kappa }_{\Omega }$, $E\left(\kappa \right)=\beta {\left(\Omega \epsilon \right)}^{1/2}{\kappa }^{-2}$, while when ${\kappa }_c>{\kappa }_{\Omega }$, $E\left(\kappa \right)=\alpha {\epsilon }^{2/3}{\kappa }^{-5/3}$ (Figure 1).

FIGURE 1

FIGURE 1. Rotation-corrected energy spectrum.

From the definition of f_k, $f_k=k_u/k_t$ (different from k_T in Eq. 9), it is assumed that for PANS simulation, the grid spacing is located between the turbulent length scale (l_turb) and the Kolmogorov length scale (η) (Song and Park, 2009). Therefore, the total turbulent kinetic energy k_t can be obtained as follows:

$\begin{array}{l}{k}_t={\displaystyle {\int }_0^{\infty }E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_l}^{{\kappa }_{\Omega }}E\left(\kappa \right)d\kappa }+{\displaystyle {\int }_{{\kappa }_{\Omega }}^{{\kappa }_{\eta }}E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_l}^{{\kappa }_{\Omega }}\beta {\epsilon }^{1/2}{\Omega }^{1/2}{\kappa }^{-2}d\kappa }+{\displaystyle {\int }_{{\kappa }_{\Omega }}^{{\kappa }_{\eta }}\alpha {\epsilon }^{2/3}{\kappa }^{-5/3}d\kappa }\\ =(\frac{3}{2}\alpha -\beta )\epsilon {\Omega }^{-1}+\frac{1}{2\pi }\beta {\epsilon }^{1/2}{\Omega }^{1/2}{l}_{turb}-{\left(\frac{1}{2\pi }\right)}^{\frac{2}{3}}\frac{3}{2}\alpha {\epsilon }^{2/3}{\eta }^{\frac{2}{3}}.\end{array}(11)$

For the small turbulent length scale (large wavenumber, κ_Δ∼κ_η), the turbulent kinetic energy cannot be resolved directly; thus, if ${\kappa }_{\Delta }<{\kappa }_{\Omega }$,

$\begin{array}{l}{k}_u={\displaystyle {\int }_{{\kappa }_{\Delta }}^{\infty }E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_{\Delta }}^{{\kappa }_{\Omega }}E\left(\kappa \right)d\kappa }+{\displaystyle {\int }_{{\kappa }_{\Omega }}^{{\kappa }_{\eta }}E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_{\Delta }}^{{\kappa }_{\Omega }}\beta {\epsilon }^{1/2}{\Omega }^{1/2}{\kappa }^{-2}d\kappa }+{\displaystyle {\int }_{{\kappa }_l}^{{\kappa }_{\eta }}\alpha {\epsilon }^{2/3}{\kappa }^{-5/3}d\kappa }\\ =(\frac{3}{2}\alpha -\beta )\epsilon {\Omega }^{-1}+\frac{1}{2\pi }\beta {\epsilon }^{1/2}{\Omega }^{1/2}\Delta -{\left(\frac{1}{2\pi }\right)}^{\frac{2}{3}}\frac{3}{2}\alpha {\epsilon }^{2/3}{\eta }^{\frac{2}{3}},\end{array}(12)$

and if ${\kappa }_{\Delta }>{\kappa }_{\Omega }$,

$\begin{array}{l}{k}_u={\displaystyle {\int }_{{\kappa }_{\Delta }}^{\infty }E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_{\Delta }}^{{\kappa }_{\eta }}E\left(\kappa \right)d\kappa }={\displaystyle {\int }_{{\kappa }_{\Delta }}^{{\kappa }_{\eta }}\alpha {\epsilon }^{2/3}{\kappa }^{-5/3}d\kappa }\\ ={\left(\frac{1}{2\pi }\right)}^{\frac{2}{3}}\frac{3}{2}\alpha {\epsilon }^{2/3}({\Delta }^{\frac{2}{3}}-{\eta }^{\frac{2}{3}}).\end{array}(13)$

Based on the study proposed by Thangam et al. (1999), it was assumed that $\alpha =\beta =1.8$. Consequently, the final f_k form for the rotation-corrected energy spectrum is as follows:

$f_k=\frac{k_u}{k_t}=\{\begin{array}{l}\frac{\text{0}\text{.}9\epsilon {\Omega }^{-1}+0.286{\left(\epsilon \Omega \right)}^{1/2}\Delta -0.793{\left(\epsilon \eta \right)}^{2/3}}{0.9\epsilon {\Omega }^{-1}+0.286{\left(\epsilon \Omega \right)}^{1/2}{l}_{turb}-0.793{\left(\epsilon \eta \right)}^{2/3}}({\kappa }_c\le {\kappa }_{\Omega })\\ \\ \frac{0.793{\epsilon }^{2/3}({\Delta }^{2/3}-{\eta }^{2/3})}{0.9\epsilon {\Omega }^{-1}+0.286{\left(\epsilon \Omega \right)}^{1/2}{l}_{turb}-0.793{\left(\epsilon \eta \right)}^{2/3}}({\kappa }_c>{\kappa }_{\Omega })\end{array}.(14)$

It should be noted that when ${\kappa }_{\Delta }={\kappa }_{\Omega }$, the above two equations are equivalent. Here, the f_k equation based on the rotation-corrected energy spectrum is referred to as PANS-RCES, and the corresponding coupled model with SST k-ω PANS is called SST k-ω PANS-RCES hereafter. In all PANS simulations, the dispassion of turbulent kinetic energy, $\epsilon$, is calculated by $\epsilon =\beta k\omega$, where $\beta$ is a constant coefficient.

Verification and Application

Verification in Rotating Channel Flow

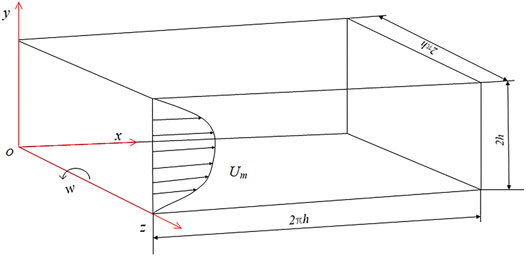
In rotating channel flows, the channel rotates in the spanwise direction with a constant angular velocity and is significantly affected by rotating flow characteristics, such as typical asymmetric distribution, streaks near the pressure side, and Taylor–Götler (TG) vortices (Grundestam et al., 2008), which is suitable for verifying the new f_k expression based on the rotation-corrected energy spectrum. In the present study, rotating channel flows with a Reynolds number of 7,000 and rotation numbers of 0.3 and 0.6 are simulated. The Reynolds number is defined as $\mathrm{Re}=U_{m}h/\nu$, where h is the half channel height and $\nu$ denotes the kinematic viscosity. In addition, rotation number Ro is defined as $Ro=2\omega h/U_m$, where ω denotes the angular velocity of the rotation and $U_m=1/2h{\displaystyle {\int }_0^{2h}U\left(y\right)}dy$ is the bulk velocity along the x coordinate. The simulation domain is exhibited in Figure 2, where $2\pi h\times 2h\times 2\pi h$ are the dimensions along with the x (streamwise), y (normal), and z (spanwise) directions, respectively. The positive x coordinate is the inflow direction.

FIGURE 2

FIGURE 2. Simulation domain of rotating channel flow.

Subsequently, the SST k-ω PANS-ES1, SST k-ω PANS-ES2, and SST k-ω PANS-RCES models are used to simulate the rotating channel flow. The new turbulence models are compiled in OpenFOAM, and the simulation results are compared with the DNS data (Yang et al., 2012). For all PANS simulations, the PISO algorithm is applied to pressure–velocity coupling. A “Gauss linear” scheme with second-order accuracy is chosen for both the gradient term and the divergence term. A second-order implicit backward scheme is used for the time scheme.

The simulation results of the velocity and Reynolds stress analyzed in this study were time-, spanwise-, and streamwise-averaged:

$\overline{\varphi }=\frac{1}{L_x{L}_{z}T}{\displaystyle {\int }_0^{L_x}{\displaystyle {\int }_0^{L_z}{\displaystyle {\int }_0^T\varphi }}}dxdzdt,(15)$

where $\varphi$ is a transient physical quantity, L_x and L_z are the streamwise and spanwise lengths, respectively, and T is the duration for time averaging. The half-height of the channel, h, is set as the reference scale for the length. Furthermore, the plane y/h = 0 is at the position of the pressure side, and y/h = 2 is at the position of the suction side.

Grid Convergence Study

A grid convergence study is performed for rotating channel flow to investigate grid dependence. The details of grid information and a part of the corresponding simulation results are shown in Table 1. The mesh elements vary in the y-direction (Kamble et al., 2019) as shown in Table 1. In the present grid convergence study, two rotation numbers of rotating channel flow are selected. Four meshes coupled with three different f_k expressions, 12 cases for each rotation number in total, are simulated. In Table 1, only the results of Ro = 0.6 calculated by SST k-ω PANS-RCES are shown, which are similar to results obtained by the other two f_k expressions. The same time step is used in all calculations, and the maximum Courant–Friedrichs–Lewy (CFL) number is all less than unity in the calculation process. For the y⁺ on the pressure surface (PS) and suction surface (SS) of the four meshes in the table, the y⁺ of the four meshes is all around unity, and the maximum is no more than 2, especially for the three grids except mesh1, the y⁺ is all below unity. By comparing the y⁺ of the PS and the SS (the first layer height of the PS and SS meshes are the same), it can be found that under the same grid, the y⁺ of the pressure surface is larger than that of the suction surface.

TABLE 1

TABLE 1. Parameters of grid convergence for rotating channel flow at Ro = 0.6.

The magnitude and distribution of f_k are key parameters that can determine the calculation accuracy of PANS models. Figure 3 plots the time-space-averaged results of the three f_k expressions in rotating channel flow. Four different meshes and two different rotation numbers are used in the simulation, and the legend is the same for both figures. For the same f_k expressions, the figures show that the magnitude of f_k decreases with the increase of grid points. By comparing the f_k distributions obtained using the three different expressions, the SST k-ω PANS-RCES result is much smaller than the results of SST k-ω PANS-ES1 and SST k-ω PANS-ES2, and the distribution pattern is also different. For all the three different f_k expressions, the f_k value is smaller in the region far from the wall than that in the region near the walls. However, the f_k profiles near the pressure and suction surface of the SST k-ω PANS-RCES are different from the ones of the other two f_k expressions. The f_k value based on the rotation-corrected energy spectrum near the walls is generally lower than those of the other two f_k expressions under both rotation numbers as shown in Figure 3, which may contribute to the better simulation performance near the walls.

FIGURE 3

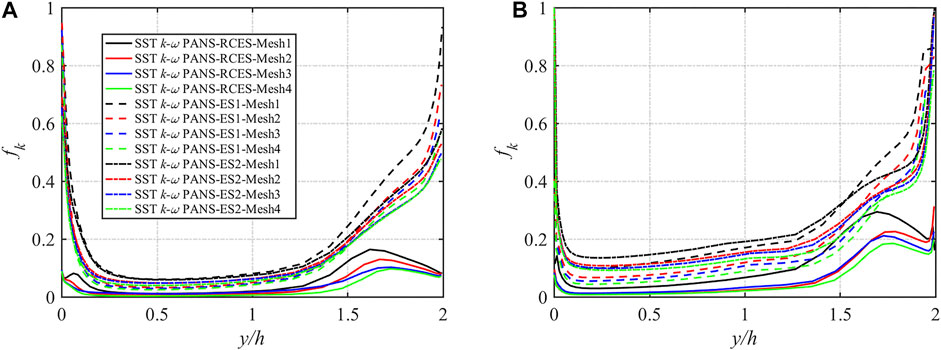
FIGURE 3. f_k distribution in rotating channel flow under different meshes: (A) Ro = 0.3 and (B) Ro = 0.6.

Due to the Coriolis effect, the mean streamwise velocity profiles are increasingly asymmetric with an increasing rotation rate, and their slope is equal to the rotation number at the main flow region of the channel (Kristoffersen and Andersson, 1993; Huang et al., 2017). The mean streamwise velocities obtained by the different f_k equations coupled with four meshes at Ro = 0.3 and 0.6 are presented in Figure 4, and the legend is the same as in Figure 3. It can be observed that reasonable results are obtained with different f_k expressions for all four meshes, and the slope of the mean streamwise velocity profiles is equal to the rotation number. For the same f_k expression, with the increase of mesh points, the numerical simulation results gradually approach the DNS results, and it converges when the number of mesh points increases to mesh3 at Ro = 0.3, and it happens at mesh2 when Ro = 0.6. For both two rotation numbers with four meshes, the results obtained by SST k-ω PANS-RCES are better than those obtained by SST k-ω PANS-ES1 and SST k-ω PANS-ES2. Especially, even with fewer meshes (mesh1, black solid lines), the SST k-ω PANS-RCES shows better performance than the other two PANS models with more mesh points (mesh2, red dotted, and dashed lines).

FIGURE 4

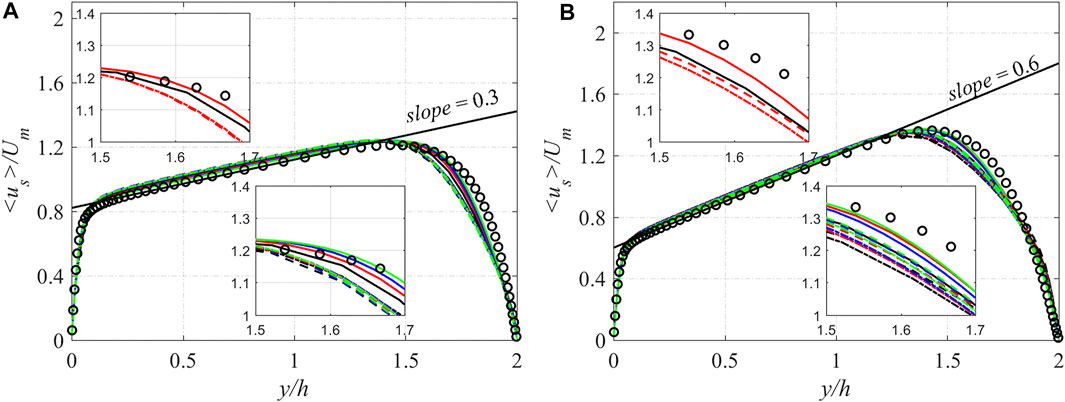
FIGURE 4. Mean streamwise velocity profiles in rotating channel flow: (A) Ro = 0.3 and (B) Ro = 0.6.

Near-Wall Velocity and Turbulence Statistics

The profiles of mean streamwise velocity in the near-wall area at both rotation numbers are shown in Figure 5 and Figure 6. According to the grid convergence study, results of Ro = 0.3 with mesh3 and results of Ro = 0.6 with mesh2 are discussed in this section. When Ro = 0.3, the results of SST k-ω PANS-RCES and SST k-ω PANS-ES1 are close to each other and consistent with DNS results, while the results of SST k-ω PANS-ES2 show some deviations. As for the velocity near the pressure side of Ro = 0.6, the results of the three models are relatively consistent. On the suction side, it can be observed more clearly that the SST k-ω PANS-RCES model has a more obvious advantage in predicting the near-wall velocity distribution under both rotation numbers, which is due to the more reasonable distribution of f_k near the suction side shown in Figure 3.

FIGURE 5

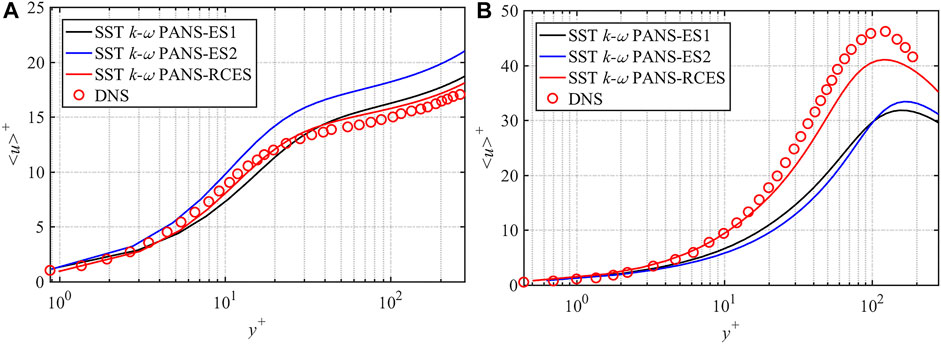
FIGURE 5. Comparison of mean streamwise velocity distribution in the near-wall area at Ro = 0.3: (A) pressure side and (B) suction side.

FIGURE 6

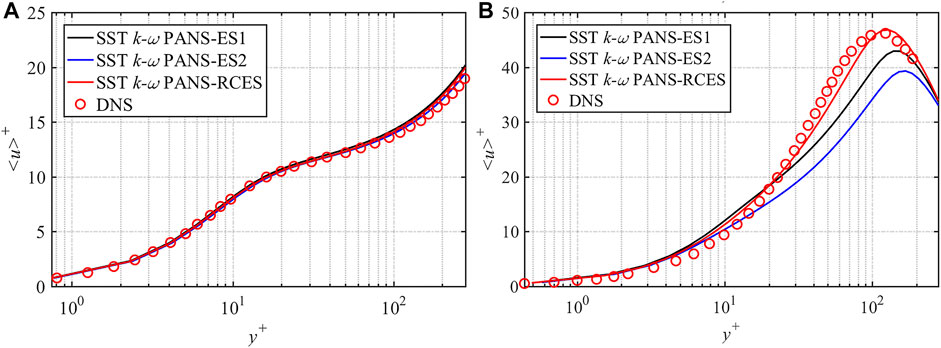
FIGURE 6. Comparison of mean streamwise velocity distribution in the near-wall area at Ro = 0.6: (A) pressure side and (B) suction side.

The profiles of root-mean-square (RMS) velocity and Reynolds shear stress under the two rotation numbers are exhibited in Figures 7, 8, respectively. v_rms is the RMS velocity in the normal direction. Since the results of the streamwise and the normal RMS velocity are similar, they are not presented here. The RMS velocity and Reynolds shear stress are normalized by $U_m$ and $U_m^2$, respectively. It was found that the RMS velocity and the Reynolds shear stress are higher on the pressure side and decrease from the pressure side toward the suction side. This suggests that the rotating effect strengthens the turbulence intensity at the pressure side and suppresses it at the suction side, which has also been confirmed by Kristoffersen and Andersson (1993). As for the normal RMS velocity at Ro = 0.3, at the near-wall area (y/h = 0–0.5 and y/h = 1.5–2), the result of the SST k-ω PANS-RCES model agrees well with the DNS results, while the other two models show some deviations in all regions. As for the Reynolds shear stress near the pressure surface (near y/h = 0–0.5) where the turbulence is enhanced, SST k-ω PANS-ES1 and SST k-ω PANS-RCES models show more convincible results than that of SST k-ω PANS-ES2 model. Near the suction side, only the SST k-ω PANS-RCES model can accurately predict the correct profile of Reynolds shear stress, which may be due to the decreased tendency of f_k at the near suction surface shown in Figure 3. Whether it is near the pressure side or the suction side, the SST k-ω PANS-ES2 model fails to predict the correct results.

FIGURE 7

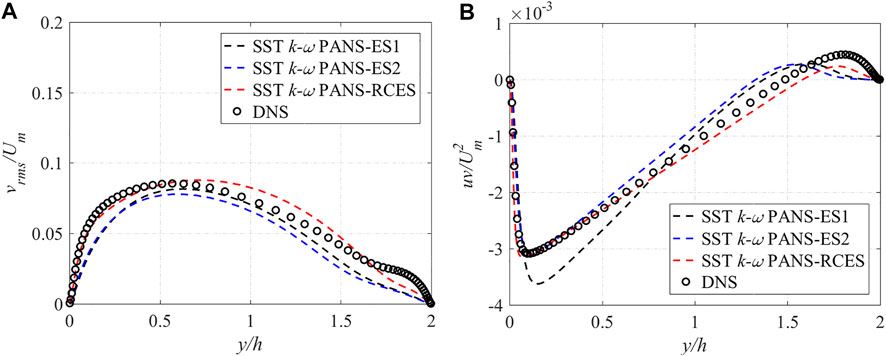
FIGURE 7. Comparison of turbulence statistics at Ro = 0.3 (A) normal RMS velocity (B) Reynolds shear stress.

FIGURE 8

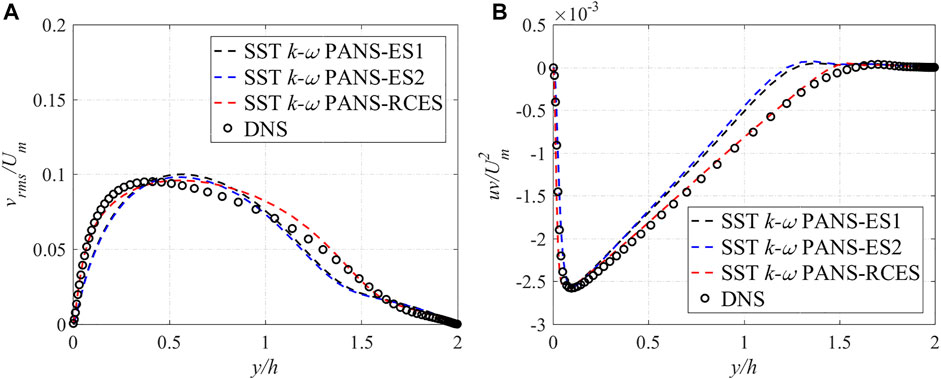
FIGURE 8. Comparison of turbulence statistics at Ro =0.6 (A) normal RMS velocity (B) Reynolds shear stress.

When Ro = 0.6, the v_rms results demonstrate that the SST k-ω PANS-RCES model performance is consistent with the DNS results. Especially in near-wall areas, the SST k-ω PANS-RCES model results agree well with the DNS data. As for the Reynolds shear stress, both the SST k-ω PANS-ES1 and SST k-ω PANS-ES2 model results exhibit some deviation at the mainstream region (y/h = 0.5–1.5), while the SST k-ω PANS-RCES model can accurately predict the correct profile in the whole area.

TG Vortices

Johnston et al. (1973) were the first to experimentally observe the TG vortices, and later, in a DNS study, Kristoffersen and Andersson (1993) observed the TG vortices as well. TG vortices are induced by the unstable flow near the pressure surface, and when the Reynolds number increases, their presence generates complex flow structures. Hence, the TG vortex is an important large-scale structure and a prominent physical phenomenon in rotating channel flows. To isolate the TG vortex, the fluctuation velocity is defined as follows:

$u_i\text{'}=u_i-\frac{1}{L_x{L}_{z}T}{\displaystyle {\int }_0^{L_x}{\displaystyle {\int }_0^{L_z}{\displaystyle {\int }_0^T{\stackrel{-}{u}}_{i}dxdzdt}}}.(16)$

That is, the fluctuation velocity is the difference between the instantaneous velocity and the time-, streamwise-, and spanwise-averaged velocities. The TG fluctuation is defined as the streamwise average of the fluctuation velocity:

$u_i^{TG}=\frac{1}{L_x}{\displaystyle {\int }_0^{L_x}{u}_i\prime dx}.(17)$

When the rotation number increases, the TG vortex becomes unstable. According to the DNS results of this example (Yang et al., 2010), the TG vortex becomes unstable and difficult to capture at Ro = 0.6; thus, in this section, the TG vortices at Ro = 0.3 with mesh3 are analyzed (Figure 9).

FIGURE 9

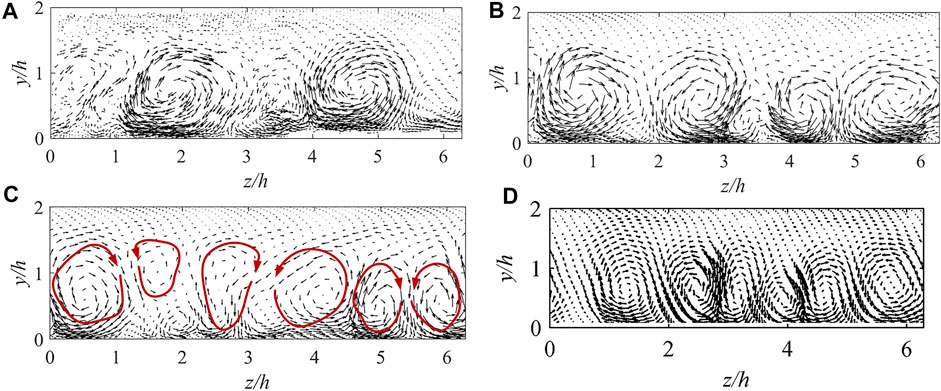
FIGURE 9. Comparison of Taylor–Götler vortices at Ro = 0.3: (A) SST k-ω PANS-ES1, (B) SST k-ω PANS-ES2, (C) SST k-ω PANS-RCES, and (D) DNS.

As can be observed in Figure 9, SST k-ω PANS-ES1 can predict only a pair of apparent vortices (z/h = 2 and z/h = 5), whereas SST k-ω PANS-ES2 predicts two pairs of vortices, and the vortex boundaries are very clear. Nevertheless, they are significantly different from the three pairs of TG vortices predicted by DNS. Only the SST k-ω PANS-RCES can capture all three pairs of vortices as DNS does. The vortex distribution on the right side of the flow channel is more apparent, while that on the left side is more ambiguous. By comparing the results, some discrepancies among the PANS results could be observed. Overall, the SST k-ω PANS-RCES results are better than those of SST k-ω PANS-ES1 and SST k-ω PANS-ES2, which further indicates that the SST k-ω PANS-RCES model based on the rotation-corrected energy spectrum is more suitable for predicting rotating flows.

Simulation Cost

For turbulence models, the balance of the simulation accuracy and cost is always the main target. According to the grid convergence study in Section 3.1.1, SST k-ω PANS-RCES with mesh1 can obtain similar results to the calculation accuracy of SST k-ω PANS-ES1 and SST k-ω PANS-ES2 with mesh2. For a better comparison of simulation cost, the time consumption (Tc) of four cases with two meshes at Ro = 0.6 is shown in Table 2. The statistical time consumption is 5,000 time steps after all calculations are stabilized. The Intel Xeon(R) Gold 5120 CPU with 2.2 GHz and 28 cores is installed in the simulation workstation. From Table 2, for the first three cases, it can be seen that the expression of RCES takes the shortest time to calculate the 5,000 time steps. In other words, for similar calculation accuracy, the newly developed f_k expression can save more calculation resources than the other expressions. For the last three cases with the same meshes, the time consumption is almost the same. Combined with the simulation performance, it can be found that the PANS model with the new f_k expression balances the simulation accuracy and the simulation cost commendably for rotating channel flow.

TABLE 2

TABLE 2. Time cost of different f_k expression for rotating channel flow at Ro = 0.6.

Application in a Centrifugal Pump

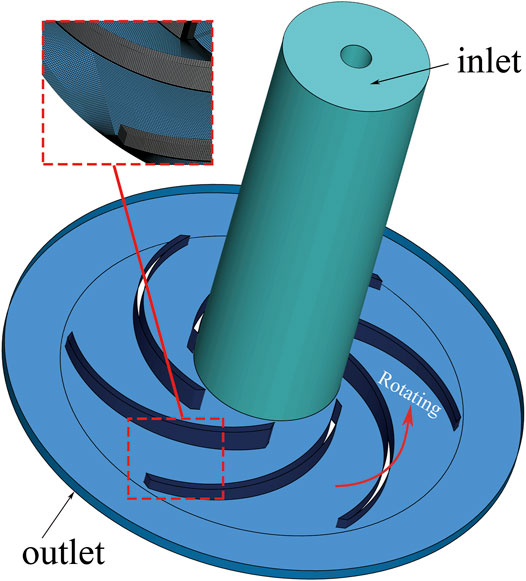
The flow in a centrifugal pump is another typical rotating flow type. The large curvature and multiwall characteristics of the pump structure make the accurate prediction of the internal flow very difficult. In this study, a low specific speed centrifugal pump is used to verify the applicability of the new f_k expression based on the rotation-corrected energy spectrum. The pump has a rotating speed of 725 r/min, inlet diameter of D₁ = 71 mm, and outlet radius of R₂ = 95 mm, and the Reynolds number based on the inlet diameter D₁ and the rated fiow rate Q₀ was approximately 5.5×10⁴. The calculation domain is illustrated in Figure 10, and the grid points are approximately 2.78 million, which is determined based on previous simulations of this flow case (Byskov et al., 2003; Huang et al., 2015). In addition, the flow rate at the design condition was 3.06 L/s, and at the stall condition, it was 0.76 L/s. The corresponding experimental and simulation results are found in the studies by Pedersen et al. (2003) and Byskov et al. (2003).

FIGURE 10

FIGURE 10. Computational domain of the centrifugal pump impeller.

Under the design conditions, the streamlines are smooth. Nevertheless, under part-load conditions, a stall happens in the impeller. More specifically, under stall conditions, a stall vortex is generated and blocks the channel. Therefore, the flow becomes more unstable, and the requirements for the turbulence model become higher (Pedersen et al., 2003; Zhou et al., 2014; Tao et al., 2014; Yao et al., 2016; Huang X.-b. et al., 2019). In this study, both the design-load condition, 1.0Q₀, and the part-load condition, 0.25Q₀, are used to verify the accuracy of the SST k-ω PANS-RCES (abbreviated as PANS hereafter) model. The mass flow rate is used as the inlet boundary condition, a pressure outlet boundary condition is used at the outlet, and a no-slip condition is set at the walls.

The Q = 1.0Q₀ flow condition results of the velocity vector distributions in the impeller mid-height at the different radial positions of r/R₂ = {0.65, 0.75, 0.90, 1.01} obtained by PANS and laser Doppler velocimetry (LDV) (Pedersen, 2000) are depicted in Figure 11. Under the design-load condition, the velocity vectors in the six flow channels are the same. The main feature is that the velocity at the suction surface (SS) of blades is large at 0.65 R₂ and 0.75 R₂, and the velocity at the pressure surface (PS) is small. The velocity distribution at 0.90 R₂ is more uniform. At 1.01 R₂, the velocity of the pressure surface is slightly greater than the velocity of the suction surface. This may be due to the secondary flow of the low specific speed centrifugal pump that causes the jet-wake flow at the exit to occur (Brun and Kurz, 2005; Zhang et al., 2019). The results of PANS and LDV show that PANS can capture the above phenomenon well. A more detailed comparison of the velocity distribution at 0.5 R₂ and 0.75 R₂ is shown in Figures 12, 13. From the figures, it is more obvious that the results of PANS are consistent with those of LES and PIV results, indicating that the velocity distribution can be well predicted in both near-wall and mainstream regions, and the newly developed f_k expression RCES can accurately predict the flow field in the design-load condition.

FIGURE 11

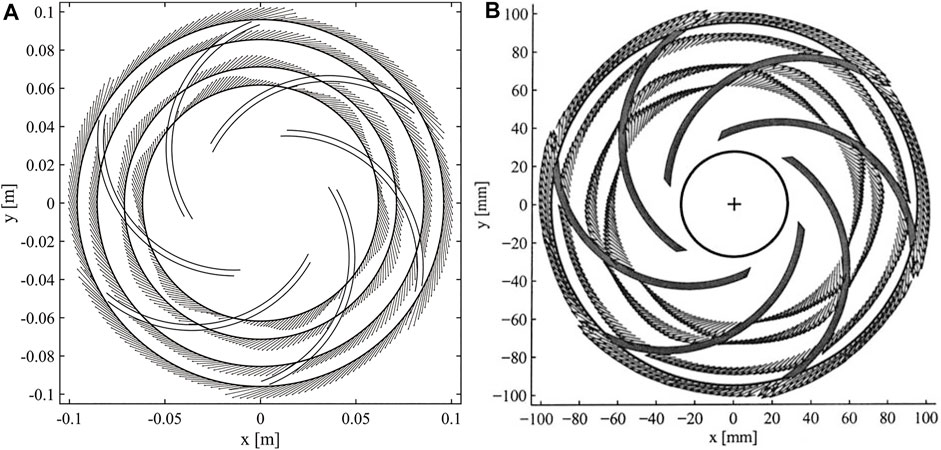
FIGURE 11. Velocity vector distributions at different radial positions under the design-load condition: (A) PANS and (B) LDV.

FIGURE 12

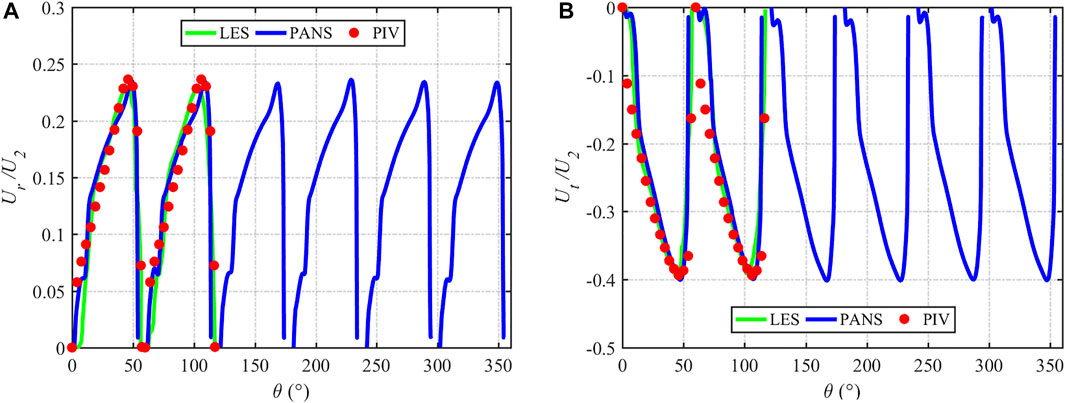
FIGURE 12. Comparison of time-averaged velocity at Q = 1.0Q₀ flow condition: (A) 0.5R₂ radial velocity and (B) 0.5R₂ tangential velocity.

FIGURE 13

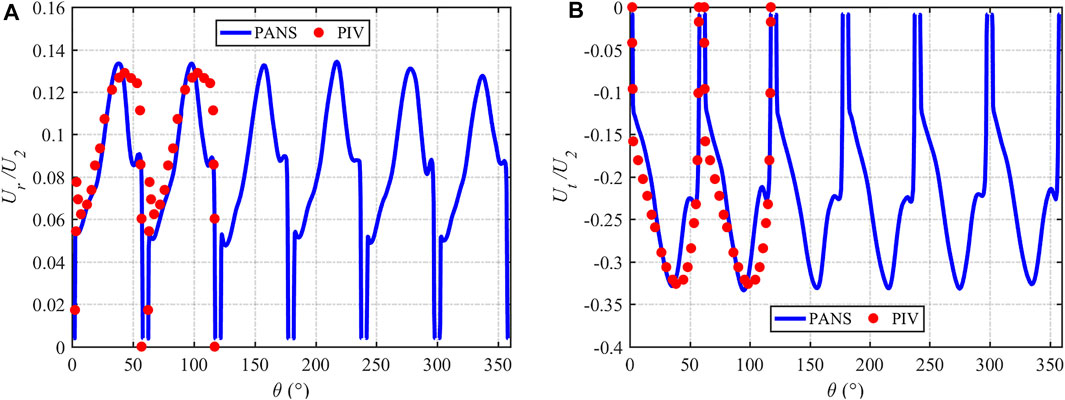
FIGURE 13. Comparison of time-averaged velocity at Q = 1.0Q₀ flow condition: (A) 0.75R₂ radial velocity and (B) 0.75R₂ tangential velocity.

The velocity vector in the impeller mid-height under the part-load condition is shown in Figure 14. Under this working condition, the velocity vector of adjacent flow passages is different, which can be marked as non-stall Passage A and stall Passage B, respectively. It can be seen from Figure 14 that only one vortex appears on the suction surface in the non-stall Passage A. A smaller vortex appears at the inlet of the stall passage, and a larger one appears near the exit of the passage. The results of PANS are consistent with those of LES. Figure 15 shows the velocity vector results of r/R₂ = {0.50, 0.65, 0.75, 0.90}. For stall passage, backflow occurs on the suction surface at the inlet, which is an important factor to generate stall vortices. The results of PANS and LES can accurately predict this result. For other flow direction positions, PANS also shows good prediction accuracy.

FIGURE 14

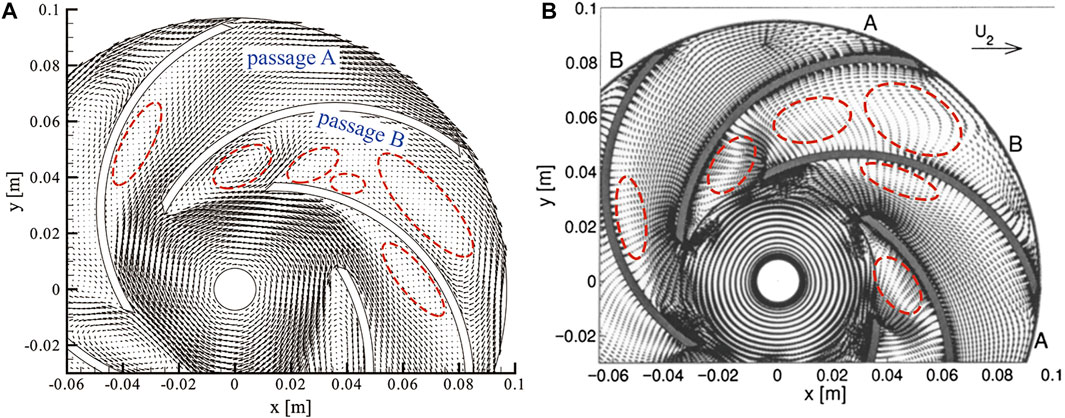
FIGURE 14. Velocity vector distributions in the impeller mid-height under 0.25Q₀ flow condition: (A) PANS and (B) LES.

FIGURE 15

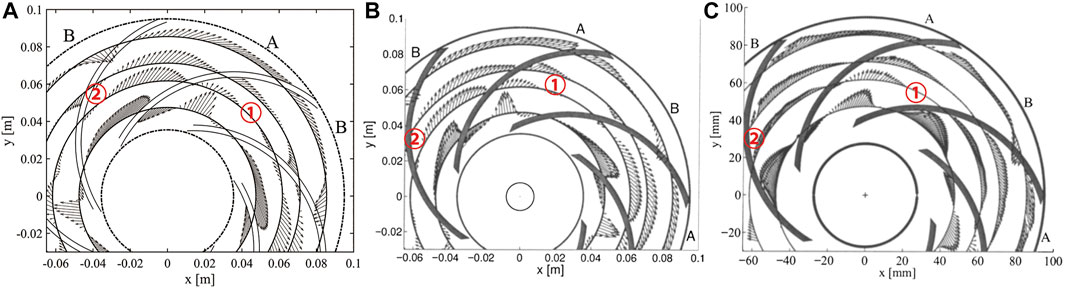
FIGURE 15. Velocity vector distributions in the impeller mid-height at different radial positions: (A) PANS, (B) LES, and (C) LDV.

Conclusion

1) An SST k-ω PANS model with a new expression of f_k based on the rotation-corrected energy spectrum is proposed in this study. The new model is verified in the rotating channel flow at two different rotation numbers, and then it is applied to a centrifugal pump impeller for further validation.

2) It was found that the f_k distribution of the new model is reasonably distributed in the rotating channel flow. In the near-wall area, the reasonable reduction of f_k allows the new model to have better performance in near-wall flow calculation. In the region near the pressure side with turbulence enhanced, the f_k value turns out to be small, and it increases toward the suction side since the turbulence is suppressed. The f_k distribution shows that it corresponds to the flow characteristics well, and the simulation results, including mean velocity, RMS velocities, and TG vortexes, agree well with the DNS data. From the calculation cost results, it was found that the new model shows a better performance than the other two PANS models with the same mesh points, and it shows comparable performance even with fewer mesh points.

3) The application of the new model in a centrifugal pump impeller shows that it can accurately capture the time-averaged flow fields including stall vortices under part-load conditions and velocity vector distributions under both design-load and part-load conditions. In addition, the new PANS model can predict the tangential and radial velocities well under both flow conditions, showing that the new model is appropriate for the simulation of flows with rotation effects.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

This is a joint work and the authors were in charge of their expertise and capability: BL worked on investigation, analysis, writing, and revision; WY and ZL worked on methodology and revision.

Funding

The authors would like to acknowledge the financial support received from the National Natural Science Foundation of China (grant number 52179093).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge ZL and Yaojun Li for their valuable advice to this study.

References

Abdol-Hamid, K., and Girimaji, S. S. (2004). A Two-Stage Procedure toward the Efficient Implementation of Pans and Other Hybrid Turbulence Models. Hampton, Virginia: Technical Memorandum NASA Langley Research Center.

Google Scholar

Baroud, C. N., Plapp, B. B., She, Z.-S., and Swinney, H. L. (2002). Anomalous Self-Similarity in a Turbulent Rapidly Rotating Fluid. Phys. Rev. Lett. 88 (11), 114501. doi:10.1103/PhysRevLett.88.114501

PubMed Abstract | CrossRef Full Text | Google Scholar

Brun, K., and Kurz, R. (2005). Analysis of Secondary Flows in Centrifugal Impellers. Int. J. Rotating Machinery 2005, 45–52. doi:10.1155/IJRM.2005.45

CrossRef Full Text | Google Scholar

Byskov, R. K., Jacobsen, C. B., and Pedersen, N. (2003). Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions-Part II: Large Eddy Simulations. J. Fluids Eng. 125 (1), 73–83. doi:10.1115/1.1524586

CrossRef Full Text | Google Scholar

Canuto, V. M., and Dubovikov, M. S. (1997). A Dynamical Model for Turbulence. V. The Effect of Rotation. Phys. Fluids 9 (7), 2132–2140. doi:10.1063/1.869332

CrossRef Full Text | Google Scholar

Foroutan, H., and Yavuzkurt, S. (2014). A Partially-Averaged Navier-Stokes Model for the Simulation of Turbulent Swirling Flow with Vortex Breakdown. Int. J. Heat Fluid Flow 50, 402–416. doi:10.1016/j.ijheatfluidflow.2014.10.005

CrossRef Full Text | Google Scholar

Girimaji, S. S., Jeong, E., and Srinivasan, R. (2006). Partially Averaged Navier-Stokes Method for Turbulence: Fixed Point Analysis and Comparison with Unsteady Partially Averaged Navier-Stokes. J. Appl. Mech. 73, 422–429. doi:10.1115/1.2173677

CrossRef Full Text | Google Scholar

Girimaji, S. S. (2006). Partially-Averaged Navier-Stokes Model for Turbulence: A Reynolds-Averaged Navier-Stokes to Direct Numerical Simulation Bridging Method. J. Appl. Mech. 73 (5), 413–421. doi:10.1115/1.2151207

CrossRef Full Text | Google Scholar

Girimaji, S. S., Srinivasan, R., and Jeong, E. (2003). “PANS Turbulence Model for Seamless Transition between RANS and LES Fixed-point Analysis and Preliminary Results,” in 4th ASME_JSME Joint Fluids Engineering Conference (Honolulu, Hawaii, USA. doi:10.1115/fedsm2003-45336

CrossRef Full Text | Google Scholar

Grundestam, O., Wallin, S., and Johansson, A. V. (2008). Direct Numerical Simulations of Rotating Turbulent Channel Flow. J. Fluid Mech. 598 (598), 177–199. doi:10.1017/s0022112007000122

CrossRef Full Text | Google Scholar

Hu, C., Wang, G., Chen, G., and Huang, B. (2014). A Modified PANS Model for Computations of Unsteady Turbulence Cavitating Flows. Sci. China Phys. Mech. Astron. 57 (10), 1967–1976. doi:10.1007/s11433-014-5538-6

CrossRef Full Text | Google Scholar

Huang, X.-b., Liu, Z.-q., Li, Y.-j., Yang, W., and Guo, Q. (2019). Study of the Internal Characteristics of the Stall in a Centrifugal Pump with a Cubic Non-linear SGS Model. J. Hydrodyn. 31 (4), 788–799. doi:10.1007/s42241-018-0170-y

CrossRef Full Text | Google Scholar

Huang, X., Liu, Z., and Yang, W. (2015). Comparative Study of SGS Models for Simulating the Flow in a Centrifugal-Pump Impeller Using Single Passage. Eng. Comput. 32 (7), 2120–2135. doi:10.1108/EC-09-2014-0193

CrossRef Full Text | Google Scholar

Huang, X., Yang, W., Li, Y., Qiu, B., Guo, Q., and Zhuqing, L. (2019). Review on the Sensitization of Turbulence Models to Rotation/curvature and the Application to Rotating Machinery. Appl. Maths. Comput. 341, 46–69. doi:10.1016/j.amc.2018.08.027

CrossRef Full Text | Google Scholar

Johnston, J. P., Halleen, R. M., and Lezius, D. K. (1973). Effects of Spanwise Rotation on the Structure of Two-Dimensional Fully Developed Turbulent Channel Flow. J. Fluid Mech. 56, 533–557. doi:10.1017/S0022112073002077

CrossRef Full Text | Google Scholar

Kamble, C., Girimaji, S. S., and Chen, H.-C. (2020). Partially Averaged Navier-Stokes Formulation of a Two-Layer Turbulence Model. AIAA J. 58 (1), 174–183. doi:10.2514/1.J058742

CrossRef Full Text | Google Scholar

Kristoffersen, R., and Andersson, H. I. (1993). Direct Simulations of low-Reynolds-number Turbulent Flow in a Rotating Channel. J. Fluid Mech. 256, 163–197. doi:10.1017/s0022112093002757

CrossRef Full Text | Google Scholar

Lakshmipathy, S., and Girimaji, S. S. (2010). Partially Averaged Navier-Stokes (PANS) Method for Turbulence Simulations: Flow Past a Circular Cylinder. J. Fluids Eng. 132 (12). doi:10.1115/1.4003154

CrossRef Full Text | Google Scholar

Lin, P., Yang, T., Xu, W., and Zhu, Z. (2022). Influence of Different Offset Angles of Inlet Guide Vanes on Flow Characteristics of Centrifugal Pump. Front. Energ. Res. 10, 818244. doi:10.3389/fenrg.2022.818244

CrossRef Full Text | Google Scholar

Luo, D., Yan, C., Liu, H., and Zhao, R. (2014). Comparative Assessment of PANS and DES for Simulation of Flow Past a Circular cylinder. J. Wind Eng. Ind. Aerodynamics 134, 65–77. doi:10.1016/j.jweia.2014.08.014

CrossRef Full Text | Google Scholar

Pedersen, N. (2000). Experimental Investigation of Flow Structures in a Centrifugal Pump Impeller Using Particle Image Velocimetry. USA: Technical University of Denmark. [Ph.D thesis]. dissertation.

Google Scholar

Pedersen, N., Larsen, P. S., and Jacobsen, C. B. (2003). Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions-Part I: Particle Image Velocimetry (PIV) and Laser Doppler Velocimetry (LDV) Measurements. J. Fluids Eng. 125 (1), 61–72. doi:10.1115/1.1524585

CrossRef Full Text | Google Scholar

Pereira, F. S., Vaz, G., Eça, L., and Girimaji, S. S. (2018). Simulation of the Flow Around a Circular cylinder at Re =3900 with Partially-Averaged Navier-Stokes Equations. Int. J. Heat Fluid Flow 69, 234–246. doi:10.1016/j.ijheatfluidflow.2017.11.001

CrossRef Full Text | Google Scholar

Pereira, S. F., Vaz, G., and Eca, L. (2015). “An Assessment of Scale-Resolving Simulation Models for the Flow Around a Circular cylinder,” in Turbulence, Heat and Mass Transfer (Sarajevo: Begell House), 8. doi:10.1615/ichmt.2015.thmt-15.540

CrossRef Full Text | Google Scholar

Pope, S. B. (2000). Turbulent Flows. Cambridge,UK: Cambridge University Press.

Google Scholar

Qian, Y., Wang, T., Yuan, Y., and Zhang, Y. (202011814). Comparative Study on Wind Turbine Wakes Using a Modified Partially-Averaged Navier-Stokes Method and Large Eddy Simulation. Energy 206, 118147. doi:10.1016/j.energy.2020.118147

CrossRef Full Text | Google Scholar

Ranjan, P., and Dewan, A. (2016). Effect of Side Ratio on Fluid Flow and Heat Transfer from Rectangular Cylinders Using the PANS Method. Int. J. Heat Fluid Flow 61 (B), 309–322. doi:10.1016/j.ijheatfluidflow.2016.05.004

CrossRef Full Text | Google Scholar

Ranjan, P., and Dewan, A. (2015). Partially Averaged Navier Stokes Simulation of Turbulent Heat Transfer from a Square cylinder. Int. J. Heat Mass Transfer 89, 251–266. doi:10.1016/j.ijheatmasstransfer.2015.05.029

CrossRef Full Text | Google Scholar

Rathor, S. K., Sharma, M. K., Ray, S. S., and Chakraborty, S. (2020). Bridging Inertial and Dissipation Range Statistics in Rotating Turbulence. Phys. Fluids 32 (9), 095104. doi:10.1063/5.0016495

CrossRef Full Text | Google Scholar

Schiestel, R., and Dejoan, A. (2005). Towards a New Partially Integrated Transport Model for Coarse Grid and Unsteady Turbulent Flow Simulations. Theoret. Comput. Fluid Dyn. 18 (6), 443–468. doi:10.1007/s00162-004-0155-z

CrossRef Full Text | Google Scholar

Song, C.-S., and Park, S.-O. (2009). Numerical Simulation of Flow Past a Square cylinder Using Partially-Averaged Navier-Stokes Model. J. Wind Eng. Ind. Aerodynamics 97, 37–47. doi:10.1016/j.jweia.2008.11.004

CrossRef Full Text | Google Scholar

Tao, R., Xiao, R., Yang, W., and Wang, F. (2014). A Comparative Assessment of Spalart-Shur Rotation/Curvature Correction in RANS Simulations in a Centrifugal Pump Impeller. Math. Probl. Eng. 2014, 1–9. doi:10.1155/2014/342905

CrossRef Full Text | Google Scholar

Thangam, S., Wang, X.-H., and Zhou, Y. (1999). Development of a Turbulence Model Based on the Energy Spectrum for Flows Involving Rotation. Phys. Fluids 11 (8), 2225–2234. doi:10.1063/1.870084

CrossRef Full Text | Google Scholar

Wang, C.-y., Wang, F.-j., Wang, B.-h., Tang, Y., and Zhao, H.-r. (2020). A Novel Omega-driven Dynamic PANS Model. J. Hydrodyn. 32, 710–716. doi:10.1007/s42241-020-0052-y

CrossRef Full Text | Google Scholar

Xianbei, H., Zhuqing, L., Wei, Y., Yaojun, L., and Zixuan, Y. (2017). A Cubic Nonlinear Subgrid-Scale Model for Large Eddy Simulation. J. Fluids Eng. 139 (4), 41101. doi:10.1115/1.4035217

CrossRef Full Text | Google Scholar

Yang, Z., Cui, G., Xu, C., Shao, L., and Zhang, Z. (2010). The Effect of the Taylor-Görtler Vortex on Reynolds Stress Transport in the Rotating Turbulent Channel Flow. Sci. China Phys. Mech. Astron. 53 (4), 725–734. doi:10.1007/s11433-010-0168-0

CrossRef Full Text | Google Scholar

Yang, Z., Cui, G., Xu, C., and Zhang, Z. (2012). Large Eddy Simulation of Rotating Turbulent Channel Flow with a New Dynamic Global-Coefficient Nonlinear Subgrid Stress Model. J. Turbulence 13 (48), N48–N20. doi:10.1080/14685248.2012.726996

CrossRef Full Text | Google Scholar

Yao, Z.-F., Yang, Z.-J., and Wang, F.-J. (2016). Evaluation of Near-wall Solution Approaches for Large-Eddy Simulations of Flow in a Centrifugal Pump Impeller. Eng. Appl. Comput. Fluid Mech. 10 (1), 452–465. doi:10.1080/19942060.2016.1189362

CrossRef Full Text | Google Scholar

Zeman, O. (1994). A Note on the Spectra and Decay of Rotating Homogeneous Turbulence. Phys. Fluids 6 (10), 3221–3223. doi:10.1063/1.868053

CrossRef Full Text | Google Scholar

Zhang, N., Liu, X., Gao, B., and Xia, B. (2019). DDES Analysis of the Unsteady Wake Flow and its Evolution of a Centrifugal Pump. Renew. Energ. 141, 570–582. doi:10.1016/j.renene.2019.04.023

CrossRef Full Text | Google Scholar

Zhang, X., Xia, G., Cong, T., Peng, M., and Wang, Z. (2020). Uncertainty Analysis on K-ε Turbulence Model in the Prediction of Subcooled Boiling in Vertical Pipes. Front. Energ. Res. 8, 584531. doi:10.3389/fenrg.2020.584531

CrossRef Full Text | Google Scholar

Zhou, P. J., Wang, F. J., Yang, Z. J., and Mou, J. G. (2014). Investigation of Rotating Stall for a Centrifugal Pump Impeller Using Various SGS Models. J. Hydrodyn. 29 (2), 235–242. doi:10.1016/S1001-6058(16)60733-3

CrossRef Full Text | Google Scholar

Zhou, Y. (1995). A Phenomenological Treatment of Rotating Turbulence. Phys. Fluids 7 (8), 2092–2094. doi:10.1063/1.868457

CrossRef Full Text | Google Scholar