
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 19 May 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.888585
This article is part of the Research TopicIntelligent Operation and Control in Next Generation Urban Power GridView all 14 articles
This article is concerned with the set-membership state estimation problem for power distribution networks (PDNs) over a resource-constrained communication network under the influence of unknown but bounded (UBB) noises. Firstly, in order to alleviate the pressure of information communication network (ICN) while meeting the state estimation requirements, the event-triggered mechanism is adopted to send data containing more valid information to estimation center, reasonably reducing the signal transmission frequency. Secondly, an event-triggered dual set-membership filter (ET-DSMF) is designed to improve the performance of state estimation. The proposed filter performs a discrete approximation for a semi-infinite programming problem by the random sampling technique, and a compact linearization error bounding ellipsoid is obtained by solving the dual problem of the nonlinear programming. Subsequently, a sufficient condition for the existence of the estimated ellipsoid is derived depending on the mathematical induction method. The key time-varying filter gain matrix and optimal estimated ellipsoid are determined recursively by solving a convex optimization problem, according to the minimum trace criterion. Finally, the effectiveness of the proposed filtering algorithm is demonstrated by performing simulation experiments on the IEEE 13 distribution test system.
In recent years, the operation and control of power distribution networks (PDNs) are facing severe challenges with the large access of flexible loads and renewable energy (Dehghanpour et al., 2018; Fang et al., 2020; Zhang and Wang, 2020). In order to improve the power quality, the distribution management system (DMS) is required to achieve a higher level of control and management for the PDNs. As the basis of the smart grid situation perception, the state estimation module is the core part of the DMS. By using real-time measurement data, the operation state of the system can be estimated, and its accuracy directly determines the dispatching and control ability of the DMS to PDNs.
The traditional static state estimation completely depends on the measurement set at a certain time to obtain the operation state of the system at that time, ignoring the change process of thesystem state in continuous time (Jin et al., 2020). By contrast, dynamic state estimation is to track the changes of system states by recursive update estimation, and another advantage is that it can predict the state of the next time. Therefore, it is more conducive to improve the management level of DMS and has attracted the extensive attention of researchers (Wang et al., 2020; Ji et al., 2021). So far, the estimation methods based on the Kalman filtering framework have been widely applied in the dynamic state estimation of PDNs, such as extended Kalman filter (EKF), unscented Kalman filter (UKF), and robust recursive Kalman filter (RKF). Specifically, aiming at the state estimation problem of nonlinear systems, the EKF linearizes the nonlinear equation by the Taylor series and truncates it to the first order. Nevertheless, large errors will be produced for some strongly nonlinear systems due to the ignoring of higher-order remainder terms (Zhao et al., 2016; Ćetenović et al., 2021). Differently, the UKF directly obtains the approximate probability distribution of nonlinear function with the help of unscented transform technique (Zhao and Mili, 2017; Bai et al., 2021b), which avoids the linearization process and fully considers the influence of the higher-order terms. The RKF can deduce the filter gain by solving the upper bound of the error covariance matrix, and the higher-order remainder is expressed by a combination of uncertain linear matrices. It has been proved that the estimation accuracy is significantly improved by considering the influence of linearization error (Bai et al., 2018; Tan et al., 2021).
It is worth noting that the abovementioned filtering algorithms are all designed based on the assumption that the system noises obey Gaussian distribution. Actually, in the engineering practice, the statistical characteristics of the PDNs noises are unknown, which will inevitably bring errors to the estimation results (Wang et al., 2017). Fortunately, although the statistical characteristics of the PDNs noises are unknown, their boundaries are usually easy to obtain. For example, the dynamic modeling error of the state space model can be restricted by a known interval, and the measurement errors of phasor measurement units (PMUs) are described as less than one percent of the total vector errors according to the IEEE standards (Martin et al., 2008; Qing et al., 2013). To deal with such unknown but bounded (UBB) noises, the set-membership filtering algorithm has been proposed by Schweppe (1968), and its main idea is to provide a set of state estimation that always contains the real states of the system (Cerone et al., 2014). In order to facilitate the description, the state estimation set is usually outsourced using regular geometry, such as ellipsoid (Calafiore, 2005; Ding et al., 2019), zonotope (Kühn, 1998; Alamo et al., 2005), and box (Ping et al., 2020). And the ellipsoid set becomes the geometric representation tool selected in this article due to its simple representation and smooth derivable boundary. After years of development, the results of the set-membership filtering algorithm in linear systems have been widely published (Becis-Aubry et al., 2008; Gubarev and Melnichuk, 2015; Liu et al., 2016). To realize the application of the set-membership theory in nonlinear systems, the nonlinear set-membership filtering algorithm has been developed (Scholte and Campbell, 2003; Calafiore, 2005) and widely applied in various fields, such as target tracking (Yu et al., 2016; Bai et al., 2021a), generator state estimation (Cheng et al., 2018), and power system state estimation (Qing et al., 2013; Zhang et al., 2020). In addition, what should be concerning is how to obtain the compact bound of the linearization error for strongly nonlinear systems. In this regard, the extended set-membership filter (ESMF) has been developed in Scholte and Campbell (2003), in which the interval analysis method is used to determine the uncertain boundary of linearization error. However, this method will increase the conservatism of boundary estimation. Here, we try to solve the tighter linearized error boundary by the semi-infinite programming approach (Vandenberghe and Boyd, 1996). Specifically, firstly, the dual form of semi-infinite programming is derived by the known lemma. Then, the continuous measure is discretized and approximated by random sampling technology (Wang et al., 2018) (e.g., the Monte Carlo sampling method), such that the discrete expressions of the compact linearized error boundary ellipsoid center and shape matrix can be obtained recursively.
From another perspective, the measurement and communication technologies have been developed rapidly in recent years. In comparison with the conventional distribution remote terminal units (DRTUs), the PMUs can accurately measure the phasor of voltage and current, and high-frequency sampling provides a lot of real-time system information for dynamic state estimation, which is more conducive to the implementation of dynamic state estimation (Zhang et al., 2020; Mohammadrezaee et al., 2021; Qu et al., 2021). However, due to the limited bandwidth of the information communication network (ICN), the transmission of large amounts of data inevitably leads to certain network-induced phenomena such as channel congestion and communication delay (Wei et al., 2015; Hu et al., 2020). In order to alleviate the transmission pressure of the ICN, the researchers have proposed many effective solutions (Ge et al., 2017; Peng and Li, 2018; Liu et al., 2019; Zou et al., 2021). Among them, the event-triggered mechanism has recently attracted increasing research interest in the field of power systems (Liu et al., 2017; Bai et al., 2021b; Cheng and Bai, 2021).
Different from the traditional time-based periodic transmission mechanism, event-triggered transmission mechanism refers to using the constructed trigger function to judge whether the measurement at the current time meets the trigger requirements, and only the data that meet the specific conditions are transmitted to the estimator for processing. It can effectively reduce the communication frequency and improve the communication efficiency while ensuring the PDNs state estimation performance. Nonetheless, so far, the problem of dynamic state estimation for the PDNs based on the event-triggered mechanism has not been fully studied considering nonlinear and unknown but bounded noises, which is the main motivation of our research.
In view of the above discussion, we aim to design a dual set-membership filtering algorithm for the PDNs state estimation under the event-triggered mechanism to achieve a balance of network resource utilization and system filtering performance. The main technical contributions for this article can be summarized as follows:
1) An event-triggered mechanism suitable for PDNs data transmission is proposed, which can reasonably reduce the data transmission frequency on the premise of ensuring the accuracy of state estimation, so as to provide a feasible method to alleviate the communication pressure and save network resources;
2) With the help of random sampling technique, the compact linearized error ellipsoid is obtained by solving the dual problem of nonlinear programming to reduce the conservatism of the set-membership filtering algorithm;
3) Based on recurrent linear matrix inequality (RLMI) and convex optimization theories, sufficient conditions for the existence of the estimated ellipsoid are derived, and the time-varying gain matrix is solved. Then, an event-triggered dual set-membership filter (ET-DSMF) is developed to realize the online state monitoring of the system and further improve the perception ability of the PDNs.
The contents of the article are organized as follows: Section 2 establishes the dynamic state model of the PDNs. Section 3 proposes the event-triggered mechanism. Section 4 mainly introduces the calculation method of the compact boundary of the linearization errors, and a dual set-membership filter based on the event-triggered mechanism is designed. In Section 5, The IEEE 13 PDN test system serves as an example to verify the effectiveness of the filtering algorithm proposed in this article. Finally, we summarize this article in Section 6.
In the dynamic state estimation of the PDNs, the system model is utilized to estimate the operation states at the current and predict the state changes at the next. In abstract, the system model of the PDNs includes the state model and measurement model, and its general model can be expressed by Eq. 1:
where
Assumption 1. The noise sequence ωk and vk satisfy the following ellipsoid constraints:
where
Assumption 2. The initial state x0 belongs to the initial state ellipsoid ϕ0 and defined as
where
In this article, the system is assumed in a quasi-steady state operation, and a widely used dynamic model is adopted to represent the equation of state:
where Ak is the state transfer matrix, which represents the speed of the state transfer; Bk is the input matrix, reflecting the changing trend in the state trajectory. The Holt-Winters two-parameter exponential smoothing method is employed to compute Ak and Bk online.
subject to
in which, α and β indicate smoothing parameters, taking the values between 0 and 1;
At present, hybrid measurements with DRTUs and PMUs are adopted in the PDNs to coordinate the economy of power network construction and the accuracy of state estimation. The use of various measurement devices increases the measurement redundancy and then provides reasonable measurement data for the PDNs state estimation. The DRTU measurements are expressed as
where
Besides, the PMU measurements are expressed as
where
Figure 1 shows the three phase unbalanced line model of the PDNs, where the missing phase line model is similar to the three-phase model and is not fully shown here.
The basic working architecture of the PDN based on an event-triggered mechanism is shown in Figure 2. To be specific, the measurement at the current moment collected using the PMU and DRTU measurement devices are compared with the measurement of the latest transmission by the event-triggered mechanism. When the triggering condition is satisfied, the current measurement will be transmitted to the remote estimation center via the ICN, otherwise the measurement will not be transmitted. According to the zero-order hold strategy, the last transmitted measurement will participate in the state estimation process in the estimation center. Since the event-triggered mechanism is adopted, the measurement devices only provide useful information to the estimation center, and the data transmitted by the ICN will greatly decrease, which reasonably alleviates the burden on the channel. Thus, the probability of network-induced phenomenon is effectively reduced.
The triggering condition is as follows:
The specific expression of Sk is
where ψ is the weight matrix of the opposite and positive definite and is assumed to be a unit matrix in this article. σi,k is the difference between the current measurement yi,k and the last transmitted value
and the following expression is given by:
When increasing the value of ɛi, the transmission frequency would decrease correspondingly. In engineering practice, the selection of ɛi should consider not only the network communication resources but also the system filtering performance. As such, the appropriate parameter selected can achieve a trade-off between energy conservation and the estimation performance of the distribution system. Then, the event-triggering function can be defined as follows:
The parameters μi,k are constructed to indicate whether the measurement is transmitted or not, and triggering logic variable is expressed as
If μi,k = 1, the event triggering is executed. Otherwise, by the zero-order hold strategy, the latest triggered one would be used to the filtering process instead of yi,k, so as to realize the measurement synchronization and the integrity of the measurement information. By Equations 17, 18, the non-triggering error can be described as
The current measurement information received by the estimation center is
where
Let
The above results will be fully reflected in the design process of the filter.
Remark 1. The different measurement devices such as the PMUs and DRTUs are equipped at the buses of the PDNs. The diversity of measurements will bring great challenges to the setting of event-triggering threshold. Based on this challenge, we develop the event-triggered mechanism described above. This is a relative event-triggered mechanism, which is different from the absolute one in Bai et al. (2021b).
Actually, the linearization error boundary determined by the interval analysis method is too conservative, and its cumulative effect will also affect the accuracy and even lead to filter divergence. In addition, the Lagrange remainder of the linearized nonlinear function can be used to represent the linearization error, but the process of optimizing the Hessian matrix is more complex. In this article, the linearization error is limited by solving the dual form of semi-infinite programming, which not only avoids the solution of Hessian matrix but also overcomes the defects of the interval analysis method, and a more compact linearization error boundary can be obtained.
A lemma will first be introduced for the formula derivation in this section.
Lemma 1. Wang et al. (2021) The optimization problem of the ellipsoid can be expressed as
with
Then, the optimal solution of Eq. 22 is
where
with
Next, we introduce the specific application of this lemma in this article. First, the Taylor expansion of the measurement equation is performed around
According to the properties of the ellipsoid, Eq. 26 is equivalent to:
where
As shown in Figure 3, we try to find a compact ellipsoid to cover the higher-order remainder term, assuming that the outsourced ellipsoid of the higher-order remainder term is expressed as ϕg,k+1. This article uses the nonlinear programming method to optimize the boundary of linearization error, which can get a tight boundary estimate. In general, it can be obtained from Lemma 1 that the linear programming Eq. 25 is the dual form of the nonlinear programming Eq. 22. Therefore, in order to achieve a balance between the estimation accuracy and the calculation amount, the continuous system is discretized by the Monte Carlo sampling method. In this regard, the nonlinear programming is converted into a linear programming problem. The following expression is established:
where
A nonlinear programming method can be used to optimize the linearized error boundary, so the following nonlinear programming problem can be constructed:
where
in which, h(⋅) is an arbitrary nonlinear continuous function, expressed here as a higher-order remainder term function.
The minimal volume of the linear error outsourcing ellipsoid can be obtained by solving the nonlinear programming problem. In order to make it more convenient, the continuous system is discretized by the Monte Carlo sampling method, and the discrete expression of the center and shape matrix of the ellipsoid are obtained by Eqs. 32, 33, which corresponds to Eq. 24 under continuous form. Moreover, the approximate expression of Eq. 25 is obtained, as shown in Eq. 34. Thus, an outsourcing compact ellipsoid with the linearization error is developed. The results obtained in this section will be used in the design of the dual set-membership filter. The specific process will be shown in detail in Section 4.2.
with
where coefficients τi(i = 1, … , m) are obtained by solving the linear programming shown in the solution Eq. 34
By Lemma 1, we obtain the dual form of nonlinear programming and the continuous expressions of the center and shape matrix of the linearized error ellipsoid. Then, the continuous system is discretized by the Monte Carlo sampling method, and the semi-infinite programming problem is transformed into a finite programming problem, so the discrete expressions of the ellipsoid center and shape matrix are obtained.
Remark 2. Different from the UKF, the approximate probability distribution of the nonlinear function cannot be obtained directly, since we assume that the true state is restricted to the ellipsoid, rather than obeying a particular Gaussian distribution. Wang et al. (2021) avoids the process of Taylor expansion by directly solving the approximate distribution of the nonlinear measurement function values. But this will still inevitably produce large errors for strong nonlinear systems. Therefore, the method in this article strikes a balance between the computational quantity and the estimation accuracy.
In this section, a set-membership filtering algorithm based on the event-triggered mechanism is proposed to solve the state estimation problem of the PDNs. And the real state is always confined to the set of state estimation. In order to deal with quadratic constraints such as event-triggered mechanism and external noises, RLMI technology is used to transform the externally bounded ellipsoid filtering problem into a convex optimization problem with linear matrix inequality constraints. The sufficient conditions for the existence of the estimated state set are strictly derived, and the filter gain parameters are easily obtained by solving the convex optimization problem(Boyd et al., 1994).
We begin by introducing two lemmas, which will be used in the proof of this section.
Lemma 2. (S-Procedure) (Bai et al., 2021a): Let ℏ0(⋅), ℏ1(⋅), …, ℏp(⋅) be the quadratic function of the variable
Lemma 3. (Schur Complement Equivalence) (Bai et al., 2021a): For matrices H1, H2, H3, where
One-step state prediction value
where Pk+1|k is the desired optimization variable.
It should be noted that calculating the volume of the ellipsoidal set is more difficult than the trace of the matrix Pk+1. The trace of Pk+1 is the sum of the semi-axes of the ellipsoid, by which the size of the ellipsoidal set can be reflected effectively. Therefore, the objective function Eq. 36 is the trace function.
where
Proof 1. In view of Equation 4, we can get one-step prediction state error
Let,
The following unequal conditions exist naturally:
Eq. 41 is equivalent to
By means of Lemma 1,
Equation 43 can be rewritten as
where
By Lemma 2, Equation 45 can be converted to the following formula:
The proof is completed.
On the other hand, based on the proposed event-triggered mechanism, the estimates can be expressed by:
where Kk+1 is the filter gain matrix to be solved. In addition, the estimated ellipsoid ϕk+1 is obtained by solving the semi-definite programming problem, based on the one-step state prediction value at k.
The optimal variable Pk+1 and the gain matrixes Kk+1 can be obtained by solving the following optimization problem:
where
Proof 2. According to Eq. 47,
with
Thus, xk+1 ∈ ϕk+1 is equivalent to
which can be rewritten as follows:
It can be seen from Lemma 1 that Eq. 48 is established if positive scalar λ3, λ4, λ5, λ6, λ7 exists to make the following inequality hold:
Equation 45 is equivalent to
where
Using Lemma 2, the following inequality relationship holds:
The proof is completed.
In order to more clearly show the filtering algorithm in this article, the ET-DSMF algorithm is summarized as in Algorithm 1.
Remark 3. It is worth mentioning that the filtering algorithms under the Kalman framework are studied based on the assumption that the noises obey Gaussian distribution (Yang and Li, 2009). However, because the distribution network is located at the end of the power system and there is serious electromagnetic interference, the above assumption is not in line with the actual project. In fact, compared with the statistical characteristics of noises, it is easier for us to know its boundaries. Fortunately, set-membership filtering can effectively deal with this unknown but bounded noises and provide an estimation set that always surrounds the real states.
Remark 4. In order to alleviate communication pressure and improve the induction phenomenon of measurement data in the transmission process, the event-triggered mechanism is integrated into the design of the set-membership filter. To tackle the effects of σk, we employ the prescribed triggering condition which can be rewritten as a quadratic constraint. Subsequently, by using S-procedure, this quadratic constraint can be easily dealt with and reflected in the obtained RLMIs. And the gain matrix and the filter of the optimal estimated ellipsoid are obtained by solving the convex optimization problem.
In this section, The IEEE 13 PDN test system is employed for simulation to verify the effectiveness of the ET-DSMF algorithm. The algorithm is implemented in MATLAB R2018b. The topology and the nominal data of the network are obtained from Kersting (1991). The measurement configuration is shown in Figure 4, where the PMUs are deployed at buses 1, 4, 6, 8, and 11. At the beginning, the power flow calculation result is taken as the real value of the state, and the measurement is obtained by superimposing the corresponding UBB noise on the power flow calculation result of the online test system. Moreover, the process equation is obtained by the Holt-Winters two-parameter exponential smoothing method with α = 0.9, β = 0.1. Let the shape matrix of the initial state be P0 = 4 × 10−3I. The process noise is set as Qk = 6 × 10–3, and measurement noise parameters are set as
Figures 5–7 show the performance of the DSMF and ESMF algorithms, taking the simulation results of a-phase at bus 4 as an example. It can be seen that both algorithms can achieve good estimation results. However, the MSE generated by the method proposed in this article is smaller. As shown in Figure 7, although the estimated boundaries obtained by the two algorithms can contain the real state, the proposed algorithm is less conservative owing to considering the compact linearization error ellipsoid. It is obvious that the boundary obtained by the DSMF algorithm is more compact than that obtained by the ESMF.
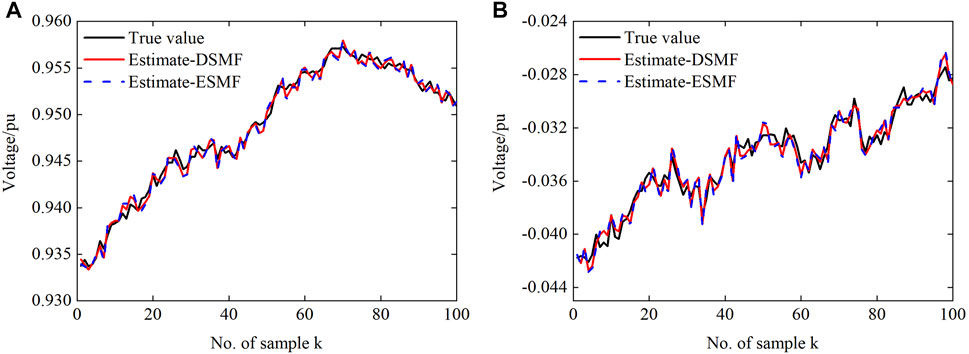
FIGURE 5. The true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.
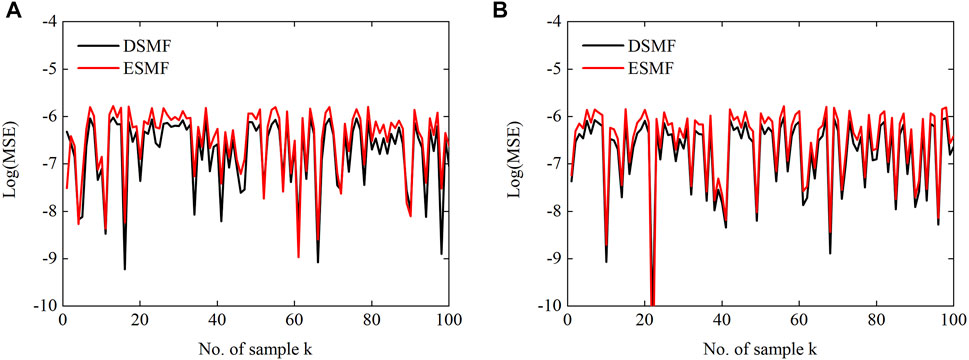
FIGURE 6. Log(MSE) between the true and estimated values of a-phase at bus 4 for the DSMF and ESMF algorithms: (A) the real part of the voltage and (B) the imaginary part of the voltage.
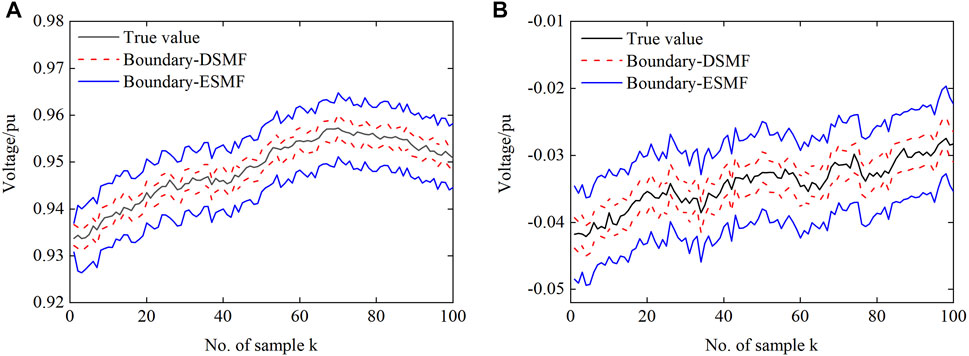
FIGURE 7. Boundaries between the true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.
Firstly, the event-triggering threshold is set as ɛi = 5 × 10–6. Figure 8 shows the state estimation ellipsoid center and boundary of the ET-DSMF algorithm, where κ = 83%. Although the estimation performance of the proposed algorithm degrades at a lower transmission rate, it ensures that the real state always resides in the estimation ellipsoid because the effective information is transmitted to the estimation center. In order to show the filtering results more clearly, Figure 9 shows the MSEs generated by the proposed algorithm. It can be seen that the estimation error is always below the minimum upper bound and close to the upper bound, which further shows the low conservatism of the proposed algorithm.
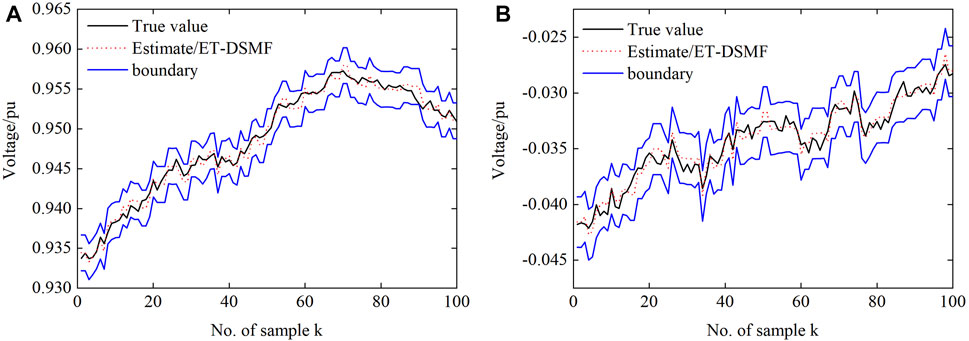
FIGURE 8. The true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.
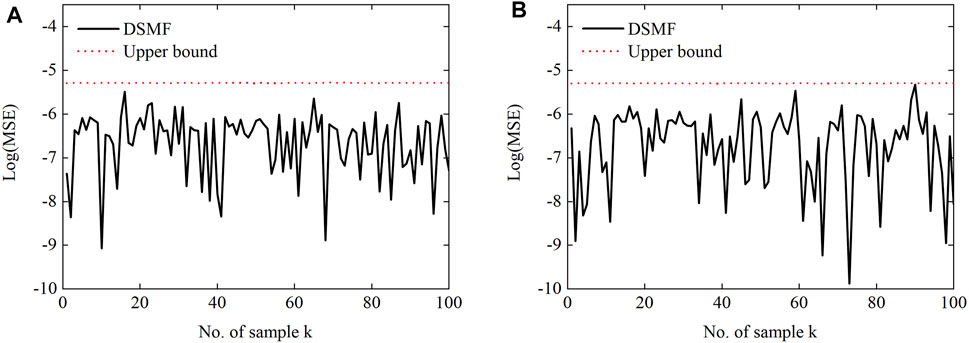
FIGURE 9. Log(MSE) between the true and estimated values of a-phase at bus 4 for the ET-DSMF algorithm: (A) the real part of the voltage and (B) the imaginary part of the voltage.
In order to verify the influence of the different triggering thresholds on the performance of the ET-DSMF algorithm, different triggering threshold parameters are selected, i.e., ET-DSMF1 with ɛi = 4 × 10–6, ET-DSMF2 with ɛi = 6 × 10–6, and ET-DSMF3 with ɛi = 8 × 10–6. Figure 10 and Figure 11 show the filtering curves and MSEs of c-phase at bus 4 under three different threshold parameters. In addition, to more clearly show the triggering time, the triggering sequences is shown in Figure 12. With the increase of the triggering threshold, the MSE of the ET-DSMF algorithm increases and the data transmission data decreases accordingly. Therefore, selecting the appropriate triggering threshold parameters can effectively alleviate the pressure of network communication and reduce the probability of network-induced phenomenon.
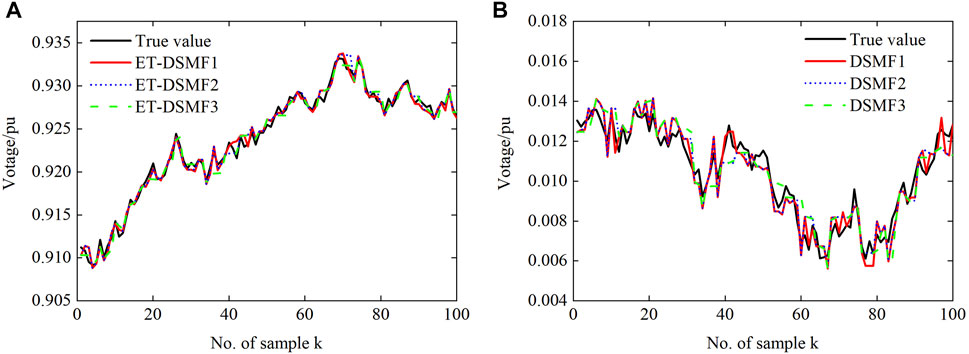
FIGURE 10. The true and estimated values of c-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.
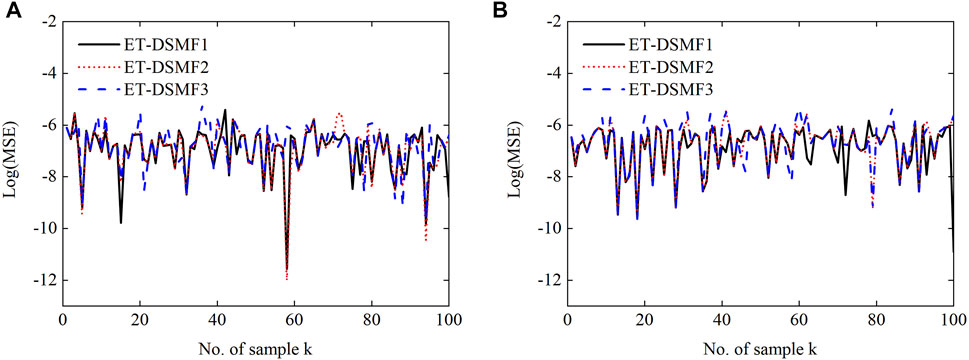
FIGURE 11. Log(MSE) between the true and estimated values of c-phase at bus 4 for the ET-DSMF algorithm: (A) the real part of the voltage and (B) the imaginary part of the voltage.
In this article, an event-triggered dual set-membership filtering algorithm is proposed. Firstly, considering the uncertainty caused by the linearization error, the approximate distribution range of linearization error is determined by the random sampling method, and the compact ellipsoid boundary of the linearization error is obtained by solving the dual problem of the semi-infinite programming, so as to reduce the conservatism of error boundary. Then, an event-triggered mechanism is introduced to reduce the communication burden. Finally, sufficient conditions for the existence of filter parameters are derived by lemmas, and the optimal state feasible set with ellipsoid as boundary is obtained by the semi-definite programming method. The simulation results show that the proposed method can still ensure good filtering performance even at a low transmission rate. In the future research, in order to further improve information transmission efficiency, we will integrate the dynamic event-triggered mechanism into the algorithm design of the PDNs set-membership state estimation. Moreover, in view of the extensive research on new energy grid connection, including wind and photovoltaic power generation, we will carry out distributed state estimation for the active PDNs combined with the algorithm proposed in this article.
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
XB and XJ contributed to the conception and design of the study. MD performed the method analysis. GL wrote the first draft of the manuscript. XB, JL, and XZ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alamo, T., Bravo, J. M., and Camacho, E. F. (2005). Guaranteed State Estimation by Zonotopes. Automatica 41, 1035–1043. doi:10.1016/j.automatica.2004.12.008
Bai, X., Wang, Z., Zou, L., and Cheng, C. (2018). Target Tracking for Wireless Localization Systems with Degraded Measurements and Quantization Effects. IEEE Trans. Ind. Electron. 65, 9687–9697. doi:10.1109/tie.2018.2813982
Bai, X., Wang, Z., Zou, L., and Zhang, Z. (2021a). Target Tracking for Wireless Localization Systems Using Set-Membership Filtering: A Component-Based Event-Triggered Mechanism. Automatica 132, 109795. doi:10.1016/j.automatica.2021.109795
Bai, X., Zheng, X., Ge, L., Qin, F., and Li, Y. (2021b). Event-triggered Forecasting-Aided State Estimation for Active Distribution System with Distributed Generations. Front. Energ. Res. 9, 327. doi:10.3389/fenrg.2021.707183
Becis-Aubry, Y., Boutayeb, M., and Darouach, M. (2008). State Estimation in the Presence of Bounded Disturbances. Automatica 44, 1867–1873. doi:10.1016/j.automatica.2007.10.033
Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan, V. (1994). Linear Matrix Inequalities in System and Control Theory. Philadelphia, PA: SIAM, Studies in Applied Mathematics.
Calafiore, G. (2005). Reliable Localization Using Set-Valued Nonlinear Filters. IEEE Trans. Syst. Man. Cybern. A. 35, 189–197. doi:10.1109/tsmca.2005.843383
Cerone, V., Lasserre, J.-B., Piga, D., and Regruto, D. (2014). A Unified Framework for Solving a General Class of Conditional and Robust Set-Membership Estimation Problems. IEEE Trans. Automat. Contr. 59, 2897–2909. doi:10.1109/TAC.2014.2351695
Ćetenović, D., Ranković, A., Zhao, J., Jin, Z., Wu, J., and Terzija, V. (2021). An Adaptive Method for Tuning Process Noise Covariance Matrix in Ekf-Based Three-phase Distribution System State Estimation. Int. J. Electr. Power Energ. Syst. 132, 107192. doi:10.1016/j.ijepes.2021.107192
Cheng, C., and Bai, X. (2021). Robust Forecasting-Aided State Estimation in Power Distribution Systems with Event-Triggered Transmission and Reduced Mixed Measurements. IEEE Trans. Power Syst. 36, 4343–4354. doi:10.1109/TPWRS.2021.3062386
Cheng, C., Bai, X., Zhang, Q., and Huang, C. (2018). Set-membership Filtering for Generator Dynamic State Estimation with Delayed Measurements. Syst. Sci. Control. Eng. 6, 35–43. doi:10.1080/21642583.2018.1531794
Dehghanpour, K., Wang, Z., Wang, J., Yuan, Y., and Bu, F. (2019). A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems. IEEE Trans. Smart Grid 10, 2312–2322. doi:10.1109/TSG.2018.2870600
Ding, D., Wang, Z., and Han, Q.-L. (2020). A Set-Membership Approach to Event-Triggered Filtering for General Nonlinear Systems over Sensor Networks. IEEE Trans. Automat. Contr. 65, 1792–1799. doi:10.1109/TAC.2019.2934389
Fang, Z., Lin, Y., Song, S., Song, C., Lin, X., and Cheng, G. (2020). Active Distribution System State Estimation Incorporating Photovoltaic Generation System Model. Electric Power Syst. Res. 182, 106247. doi:10.1016/j.epsr.2020.106247
Ge, X., Han, Q.-L., and Wang, Z. (2019). A Dynamic Event-Triggered Transmission Scheme for Distributed Set-Membership Estimation over Wireless Sensor Networks. IEEE Trans. Cybern. 49, 171–183. doi:10.1109/TCYB.2017.2769722
Gubarev, V. F., and Melnichuk, S. V. (2015). Guaranteed State Estimation Algorithms for Linear Systems in the Presence of Bounded Noise. J. Automat Inf. Scien 47, 1–10. doi:10.1615/JAutomatInfScien.v47.i3.10
Hu, J., Wang, Z., Liu, G.-P., Zhang, H., and Navaratne, R. (2021). A Prediction-Based Approach to Distributed Filtering with Missing Measurements and Communication Delays through Sensor Networks. IEEE Trans. Syst. Man. Cybern, Syst. 51, 7063–7074. doi:10.1109/TSMC.2020.2966977
Ji, X., Yin, Z., Zhang, Y., Wang, M., Zhang, X., Zhang, C., et al. (2021). Real-time Robust Forecasting-Aided State Estimation of Power System Based on Data-Driven Models. Int. J. Electr. Power Energ. Syst. 125, 106412. doi:10.1016/j.ijepes.2020.106412
Jin, Z., Zhao, J., Chakrabarti, S., Ding, L., and Terzija, V. (2020). A Hybrid Robust Forecasting-Aided State Estimator Considering Bimodal Gaussian Mixture Measurement Errors. Int. J. Electr. Power Energ. Syst. 120, 105962. doi:10.1016/j.ijepes.2020.105962
Kersting, W. H. (1991). Radial Distribution Test Feeders. IEEE Trans. Power Syst. 6, 975–985. doi:10.1109/59.11923710.1109/59.119237
Kühn, W. (1998). Rigorously Computed Orbits of Dynamical Systems without the Wrapping Effect. Computing 61, 47–67. doi:10.1109/TAC.2019.2934389
Liu, S., Wang, Z., Wei, G., and Li, M. (2020). Distributed Set-Membership Filtering for Multirate Systems under the Round-Robin Scheduling over Sensor Networks. IEEE Trans. Cybern. 50, 1910–1920. doi:10.1109/TCYB.2018.2885653
Liu, X., Li, L., Li, Z., Chen, X., Fernando, T., Iu, H. H.-C., et al. (2017). Event-trigger Particle Filter for Smart Grids with Limited Communication Bandwidth Infrastructure. IEEE Trans. Smart Grid 9, 6918–6928. doi:10.1109/TSG.2017.2728687
Liu, Y., Zhao, Y., and Wu, F. (2016). Ellipsoidal State‐bounding‐based Set‐membership Estimation for Linear System with Unknown‐but‐bounded Disturbances. IET Control. Theor. Appl. 10, 431–442. doi:10.1049/iet-cta.2015.0654
Martin, K. E., Hamai, D., Adamiak, M. G., Anderson, S., Begovic, M., Benmouyal, G., et al. (2008). Exploring the IEEE Standard C37.118-2005 Synchrophasors for Power Systems. IEEE Trans. Power Deliv. 23, 1805–1811. doi:10.1109/tpwrd.2007.916092
Mohammadrezaee, R., Ghaisari, J., Yousefi, G., and Kamali, M. (2021). Dynamic State Estimation of Smart Distribution Grids Using Compressed Measurements. IEEE Trans. Smart Grid 12, 4535–4542. doi:10.1109/TSG.2021.3071514
Peng, C., and Li, F. (2018). A Survey on Recent Advances in Event-Triggered Communication and Control. Inf. Sci. 457-458, 113–125. doi:10.1016/j.ins.2018.04.055
Ping, X., Yang, S., Ding, B., Raïssi, T., and Li, Z. (2020). Observer-based Output Feedback Robust Mpc via Zonotopic Set-Membership State Estimation for Lpv Systems with Bounded Disturbances and Noises. J. Franklin Inst. 357, 7368–7398. doi:10.1016/j.jfranklin.2020.05.014
Qing, X., Yang, F., and Wang, X. (2013). Extended Set-Membership Filter for Power System Dynamic State Estimation. Electric Power Syst. Res. 99, 56–63. doi:10.1016/j.epsr.2013.02.002
Qu, B., Wang, Z., and Shen, B. (2021). Fusion Estimation for a Class of Multi-Rate Power Systems with Randomly Occurring Scada Measurement Delays. Automatica 125, 109408. doi:10.1016/j.automatica.2020.109408
Scholte, E., and Campbell, M. E. (2003). A Nonlinear Set-Membership Filter for On-Line Applications. Int. J. Robust Nonlinear Control. 13, 1337–1358. doi:10.1002/rnc.856
Schweppe, F. (1968). Recursive State Estimation: Unknown but Bounded Errors and System Inputs. IEEE Trans. Automat. Contr. 13, 22–28. doi:10.1109/tac.1968.1098790
Tan, H., Shen, B., and Shu, H. (2021). Robust Recursive Filtering for Stochastic Systems with Time-Correlated Fading Channels. IEEE Trans. Syst. Man. Cybern, Syst. 1, 1. doi:10.1109/TSMC.2021.3062848
Vandenberghe, L., and Boyd, S. (1996). Semidefinite Programming. SIAM Rev. 38, 49–95. doi:10.1137/1038003
Wang, S., Zhao, J., Huang, Z., and Diao, R. (2018). Assessing Gaussian assumption of Pmu Measurement Error Using Field Data. IEEE Trans. Power Deliv. 33, 3233–3236. doi:10.1109/TPWRD.2017.2762927
Wang, X., Zhao, J., Terzija, V., and Wang, S. (2020). Fast Robust Power System Dynamic State Estimation Using Model Transformation. Int. J. Electr. Power Energ. Syst. 114, 105390. doi:10.1016/j.ijepes.2019.105390
Wang, Z., Shen, X., Liu, H., Meng, F., and Zhu, Y. (2021). Dual Set Membership Filter with Minimizing Nonlinear Transformation of Ellipsoid. IEEE Trans. Automat. Contr., 1. doi:10.1109/TAC.2021.3081078
Wang, Z., Shen, X., Zhu, Y., and Pan, J. (2018). A Tighter Set-Membership Filter for Some Nonlinear Dynamic Systems. IEEE Access 6, 25351–25362. doi:10.1109/ACCESS.2018.2830350
Wei, G., Liu, S., Song, Y., and Liu, Y. (2015). Probability-guaranteed Set-Membership Filtering for Systems with Incomplete Measurements. Automatica 60, 12–16. doi:10.1016/j.automatica.2015.06.037
Yang, F., and Li, Y. (2009). Set-membership Filtering for Systems with Sensor Saturation. Automatica 45, 1896–1902. doi:10.1016/j.automatica.2009.04.011
Yu, W., Zamora, E., and Soria, A. (2016). Ellipsoid Slam: a Novel Set Membership Method for Simultaneous Localization and Mapping. Auton. Robot 40, 125–137. doi:10.1007/s10514-015-9447-y
Zhang, J., Bai, X., Zheng, X., Li, M., Qin, F., and Shi, Y. (2020a). Event-trigger Extended Set-Membership Filter for Power Distribution Network Dynamic State Estimation. 2020 Chinese Automation Congress, 369–374. doi:10.1109/CAC51589.2020.9327219
Zhang, S., Liu, L.-G., and Li, H. (2020b). Gic Influence on Uhv Power Grids Based on Kalman Filter and Wams Data. IEEE Access 8, 202379–202386. doi:10.1109/ACCESS.2020.3036009
Zhang, Y., and Wang, J. (2020). Towards Highly Efficient State Estimation with Nonlinear Measurements in Distribution Systems. IEEE Trans. Power Syst. 35, 2471–2474. doi:10.1109/TPWRS.2020.2967173
Zhao, J., and Mili, L. (2017). Robust Unscented Kalman Filter for Power System Dynamic State Estimation with Unknown Noise Statistics. IEEE Trans. Smart Grid 10, 1215–1224. doi:10.1049/iet-gtd.2019.0031
Zhao, J., Netto, M., and Mili, L. (2017). A Robust Iterated Extended Kalman Filter for Power System Dynamic State Estimation. IEEE Trans. Power Syst. 32, 3205–3216. doi:10.1109/TPWRS.2016.2628344
Keywords: power distribution network, state estimation, set-membership filter, event-triggered mechanism, convex optimization
Citation: Bai X, Li G, Ding M, Ji X, Li J and Zheng X (2022) Dual Set-Membership State Estimation for Power Distribution Networks Under Event-Triggered Mechanism. Front. Energy Res. 10:888585. doi: 10.3389/fenrg.2022.888585
Received: 03 March 2022; Accepted: 24 March 2022;
Published: 19 May 2022.
Edited by:
Ke-Jun Li, Shandong University, ChinaReviewed by:
Wei Qiu, The University of Tennessee, United StatesCopyright © 2022 Bai, Li, Ding, Ji, Li and Zheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Li, cGVpbGlhbmdsakAxNjMuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.