- 1Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin, China
- 2Global Energy Interconnction Group Co., Ltd., Beijing, China
The heat storage property of building envelopes is usually modeled into virtual energy storage (VES) and regarded as a flexibility resource to support the energy scheduling of building energy systems (BESs). However, the adjustable potential of VES is uncertain, incurred by several ambient random variables with/without specific probability distributions, posing challenges in determining the operational planning schemes of the BES. This article is intended to study a day-ahead optimal scheduling method for a PV-integrated BES (known as PV-BES) with the consideration of VES using interval optimization methods. First, an interval number is used to characterize the uncertainties of outdoor temperature, light irradiance, and the occupant’s behavior reflected by the uncontrollable household load. Second, an interval VES model is developed by modeling VES’s virtual charge–discharge power (VCDP) with an interval number. Finally, a day-ahead optimal interval scheduling model for the PV-BES considering VES is formulated, aiming to minimize the electricity energy purchase cost of the PV-BES from the external grid. Numerical simulation is conduced, and the results validated the effectiveness of the proposed method.
1 Introduction
With the rapid development of the global economy and the continuous growth of the population, the energy consumption of building heating continues to increase (International Energy Agency, 2020; Pokhrela et al., 2021). In order to reduce carbon emissions in buildings, the introduction of renewable and clean energy in building energy systems (BESs) is being vigorously driven. Due to the advantages of photovoltaic (PV) power generation with easy installation, a short installation period, and no noise, PV has developed rapidly in the BES (Solar Power Europe 2020). Rooftop PV can be combined with buildings and has become a common form for supplying electrical energy (Hong et al., 2014). However, the PV output power has great uncertainty and is difficult to predict. At the same time, the peak-to-valley time of electrical loads of the PV-BES and PV power generation may not be synchronized, which may lead to the problem of the PV local consumption (Rifkin, 2012; Wang et al., 2020).
Some scholars propose to equip the PV-BES with a battery energy storage system (BESS) to realize the reliable local utilization of solar PV generation (Tyagi et al., 2021). However, at present, the installation and maintenance of the BESS is still expensive [e.g., the cost of the BESS is about US$209/kWh in 2020, meaning that the total cost of its installation by considering a BESS with 12 kWh and 2 h duration could reach $5,448 (Deng et al., 2022)], which limits the widespread deployment of the BESS in the end user side (Poonpun and Jewell, 2008; Deng et al., 2021). Due to the thermal inertia of the building envelope, compared with the speed of using electric heating equipment such as air conditioners to increase the indoor temperature, the reduction of the indoor temperature is slower, which makes the building envelope have a certain amount of heat storage capability. To utilize the heat storage capability more efficiently to flexibility for the energy scheduling of the PV-BES, the heat storage capability of the building envelope is usually modeled as a VES model. Without increasing additional investment and space occupation, VES can charge by increasing the electrical power consumption of the air conditioner and the indoor temperature when the PV output power is high or the electricity price is low; VES can discharge by reducing the electrical power consumption of the air conditioner and the indoor temperature when the PV output power is low or the electricity price is high (Oladokun and Odesola, 2015; Ramos et al., 2019; Jin et al., 2020). Therefore, VES can be used as an alternative to the BESS to reduce the electricity energy purchase cost while improving the PV local consumption rate.
In recent years, increasing attention has been drawn on the application of VES for serving the energy scheduling of the BES (Klein et al., 2019; Ji et al., 2020). Considering the relationship between electrical power and heating power of the air conditioner, Zhu et al. (2019) developed a load model of the air conditioner, which regards the variability of air conditioner temperature set points as VES to provide flexibility to the optimal scheduling of the PV-BES. An internal thermal balance model of a building considering the upper and lower boundaries of the indoor temperature comfort range is established by Jin et al. (2017) to introduce VES into the optimal scheduling of the PV-BES. Although the aforementioned studies introduce the concept of VES into the optimal scheduling of the PV-BES, specific parameters (e.g., charge–discharge power and heat storage capacity) are not proposed to quantify the adjustable potential from VES, which will lead to underutilization of VES in the process of serving the energy scheduling for the PV-BES. Nezhad et al. (2020) proposed two quantitative parameters (i.e., the baseline of heating power and the electrical power reduction) to represent the adjustable potential from VES by considering the electrical power used for heating.
Based on the two parameters proposed by Nezhad et al. (2020), Chen et al. (2018) and Liu (2021) proposed a charge–discharge power parameter to quantify the adjustable potential from VES. In addition, Chen et al. (2019), Reynders et al. (2017), and Yang et al. (2019) defined a heat storage capacity parameter of VES by considering the indoor temperature comfort range. Furthermore, with the heat storage capacity parameter, a state of charge parameter is defined by Song et al. (2017) to describe the ratio of the stored electrical energy to the heat storage capacity of VES. However, the influence of the uncertainty of some building energy resource parameters (e.g., outdoor temperature and light irradiance) on VES is ignored in the aforementioned studies, which would cause inaccurate performance quantification of VES and therefore could make the cost-effective operational planning schemes infeasible with the realization of real-time information.
With the consideration of parameter uncertainty, the optimal energy scheduling for the PV-BES essentially becomes an uncertainty optimization problem. Due to the complexity of occupant individual behavior in the building, it is difficult to represent some uncertain parameters with their probability distribution, posing difficulty on the optimal energy scheduling for the PV-BES by using probability distribution-based programming methods, such as stochastic optimization. As one of the main methods for solving uncertainty optimization problems, the interval optimization method can be used to characterize the uncertain factors by an interval number without the known probability distribution (Muncey, 1979; Huang et al., 1995; Stefan and Dorota, 1996). Based on this, the interval optimization method has been applied in many power system uncertainty optimization problems (Wang et al., 2014; Bai et al., 2017; Su et al., 2020). Su et al. (2020) and Bai et al. (2017) used the interval number to characterize the uncertainty of the PV output power and proposed an interval optimization strategy of the PV-BES based on the PV output power interval number. Wang et al. (2014) introduced the interval number of electrical loads, and based on the interval number of electrical loads, Wang et al. (2014) developed a day-ahead optimal scheduling method for the PV-BES.
Based on the earlier discussion, with the aid of the interval optimization method, this study is intended to propose a day-ahead optimal interval scheduling method for the PV-BES by considering the VES uncertainties incurred by several uncertain building energy resource parameters such as indoor/outdoor temperature. The contributions of this study are summarized as follows:
1) Based on the outdoor temperature and light irradiance interval numbers, an interval VES model is developed by modeling its virtual charge–discharge power (VCDP) interval variable, virtual state of charge (VSOC) interval number, and virtual heat storage capacity (VHSC). The proposed interval VES model can quantify the adjustable potential provided by the building envelope while considering the influence of the uncertainties of outdoor temperature and light irradiance.
2) With the aid of the interval optimization theory, an optimal interval scheduling method for the PV-BES with VES utilization is proposed to minimize the electricity energy purchase cost of the PV-BES. The proposed method can realize effective energy cost reduction while improving the local PV consumption in an uncertain ambient environment.
The rest of this article is organized as follows: Section 2 gives an overview of the system; Section 3 presents the modeling of building energy resources by using the interval number; Section 4 presents the proposed day-ahead optimal interval scheduling method for the PV-BES and the solving approach of the proposed model; Section 5 reports and discusses the simulation study; Section 6 draws the conclusion and future work.
2 Overview of the PV-BES
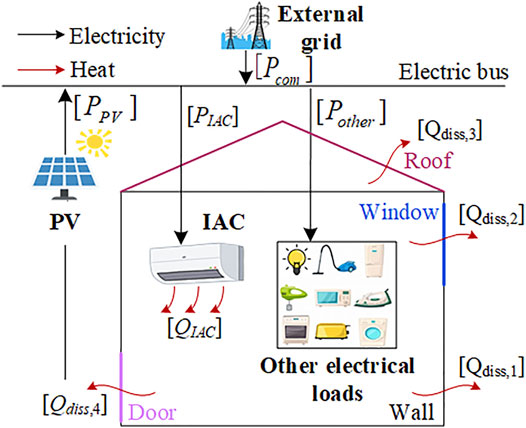
A typical grid-connected PV-BES framework is shown in Figure 1, mainly consisting of rooftop PV, an inverter air conditioner (IAC), and other electrical loads (OELs), where the OELs are regarded as an uncontrollable household load as a whole. The external grid and rooftop PV provide electrical power to the PV-BES, and the IAC and OELs consume electrical power in the PV-BES, which constitute the electrical power balance of the PV-BES. As an electrothermal conversion device, the IAC can consume electrical power to provide heating power to the PV-BES. The building envelope of the PV-BES dissipates heat. The heat dissipation power of the building envelope and the heating power of the IAC constitute the heating power balance of the PV-BES.
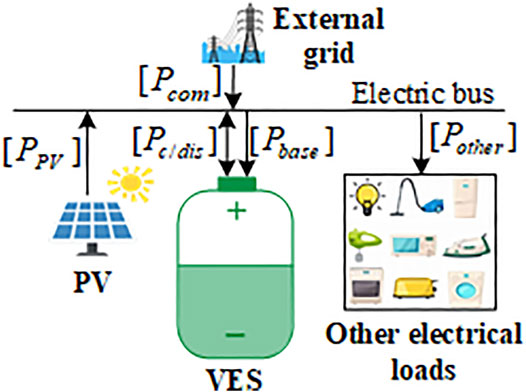
The building envelope and IAC can be modeled as VES shown in Figure 2 by considering the influence of the uncertainty of outdoor temperature and light irradiance on the adjustable potential that the building envelope can provide to the PV-BES. VES is used to quantify the uncertain adjustable potential provided by the building envelope for optimal scheduling of the PV-BES. When the indoor temperature rises, the building envelope stores heat energy, the VSOC of VES increases, and VES is in a charged state; when the indoor temperature drops, the building envelope releases heat energy, the VSOC of VES decreases, and the VES is in a discharge state. (The definitions of the VSOC and the VCDP are proposed in Section 3.1.3.)
3 Interval Modeling for Building Energy Resources
The interval VES model which is proposed to quantify the adjustable potential of the building envelope, the rooftop PV model based on the interval number, and the OEL model based on the interval number are interval-modeled in this section. For the simplicity and clarification of the modeling expression, the interval numbers that characterize uncertainty are defined as follows:
The symbol “ []” is uniformly used to represent interval numbers or interval variables in this article.
[PPV] shown in Figure 1 is used to describe the PV output power influenced by the uncertainty of light irradiance.
[PPV] = [PPV−, PPV+]. In the superscript, “-” indicates the lower limit of the interval number and “+” indicates the upper limit of the interval number.
[PIAC] and [QIAC] shown in Figure 1 describe the electrical power PIAC and the heating power QIAC of IAC. PIAC and QIAC are uncertain because PIAC and QIAC are related to the building heating power, which is influenced by outdoor temperature and light irradiance.
[Pother] shown in Figure 1 is defined to describe the OELs influenced by the occupant’s behavior.
[Qdiss,1]∼[Qdiss,4] shown in Figure 1 are used to describe the heat dissipation powers corresponding to different building envelopes influenced by the uncertainties of outdoor temperature and light irradiance.
[Pcom] shown in Figure 1 represents the commercial power from the external grid and is influenced by [PPV], [PIAC], and [Pother]. According to the interval number operation rules, [Pcom] should be defined as an interval number.
[Pc/dis] and [Pbase] shown in Figure 2 represent the VCDP interval variable and the baseline of the electrical power interval number of the VES, respectively.
3.1 Interval Virtual Energy Storage Model of the Building Envelope
The VES model based on the interval number is developed in this section. First, according to the heat exchange principle of the building envelope, considering the influence of outdoor temperature and light irradiance interval numbers on the heat exchange between the building envelope and indoor air, the interval number of building heat dissipation power is defined. Then, the IAC model is developed to describe the relationship between PIAC(t) and QIAC(t). Based on the heat dissipation power and IAC model, a VES model including the VCDP interval variable is developed to realize the interval characterization of the VES.
3.1.1 Building Heat Dissipation Power Based on the Interval Number
As shown in Figure 1, when the IAC works at the heating mode, the indoor temperature is higher than the inner surface temperature of the building envelope, which will lead to a heat exchange between the building indoor air and the building envelope (Muncey, 1979). This heat exchange is defined as the heat dissipation power of the building envelope Qdiss(t), as shown in Eq. 1. Qdiss(t) is influenced by outdoor temperature and light irradiance and is defined as the interval number
It should be noted that since Tin is influenced by the interval variable of the VCDP and Tin(t) is also described by the interval number.
Qsolar(t) depicted in Eq. 2 is the heating power contributed by the light radiation through the window to the room at time t, which is related to light irradiance (Muncey, 1979). Therefore, Qsolar(t) is defined as the interval number
where
Tisur(t) is influenced by indoor temperature and outdoor temperature and is defined as the interval number shown in Eq.(3)
where
3.1.2 Inverter Air Conditioner Model Based on the Interval Number
According to Kim et al. (2015), the relationship between PIAC(t) and QIAC(t) can be simplified to the linear relationship depicted in Eq. 7. It should be noted that to ensure the occupant’s thermal comfort, PIAC(t) and QIAC(t) are influenced by outdoor temperature and light radiance. Then, PIAC(t) and QIAC(t) are defined as the interval number.
where the adjustable range of PIAC(t) is shown in Eq.(8)
3.1.3 Virtual Energy Storage Model Based on the Interval Number
VES can be regarded as one of the energy storage devices. By analogy to the parameters of energy storage devices (charge–discharge power, capacity, and the state of charge) used in optimal scheduling models (Deng et al., 2021; Deng et al., 2022), the VES model depicted in Eq. 9 including the VCDP interval variable, VHSC parameter, and VSOC interval number is developed by considering the influence of the uncertainty of outdoor temperature and light irradiance
The VCDP is the charge–discharge power of VES, which describes the power variation before and after VES participates in the PV-BES scheduling. The optimal scheduling of the PV-BES is realized by controlling the VCDP. At the same time, because the VCDP is related to the heat dissipation power, the VCDP is defined as an interval variable. The VHSC is the heat capacity of the VES, which describes the maximum heat capacity that VES can provide for the optimal scheduling of the PV-BES. The VSOC is the ratio of the stored electric energy of VES to the VHSC. Since the stored electric energy of VES is related to the VCDP, the VSOC is defined as the interval number.
1) Virtual Charge–Discharge Power
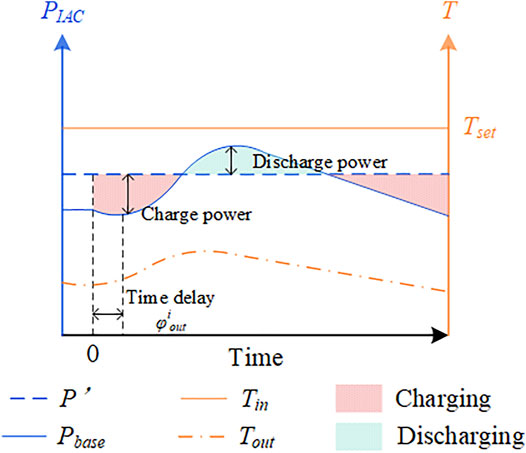
According to Song et al. (2017) and Huang et al. (1995), when QIAC(t) = Qdiss(t), Tin = Tset. Define the heating power that maintains Tin = Tset as the baseline of the heating power Qbase(t). According to Eq. 1, Qbase(t) is related to the interval numbers [Tisur(t)] and [Qsolar(t)]; then, Qbase(t) needs to be defined as the interval number, as shown in Eq. 10
It should be noted that during a specific scheduling period k (
Substituting Eq. 11 into Eq. 7, the baseline of the electrical power corresponding to the baseline of the heating power Qbase(k) can be obtained, as shown in Eq. 12
As shown in Figure 3, when PIAC = Pbase, Tin = Tset. If PIAC≠Pbase, such as P’ shown in Figure 3, a power deviation occurs between PIAC and Pbase, which is defined as the VCDP, as shown in Eq. 13. When the VCDP is greater than 0, VES is charged; otherwise, VES is discharged
Suppose that Pcom(k), PPV(k), and Pother(k) maintain. Considering the electrical power balance of the PV-BES shown in Figure 1, PIAC(k) during the k-th scheduling period is shown in Eq. 14
Substitute Eq. 14 into Eq. 13 to obtain Eq. 15
The VCDP is limited by the electrical power range of the IAC as shown in Eq. 13, and the maximum discharge power and maximum charge power of VES are shown in Eqs 16, 17. The maximum discharge power Pdismax(k) and the maximum charge power Pcmax(k) of VES are both influenced by the interval number [Pbase(k)]. According to the operation rule of the interval number, Pdismax(k) and Pcmax(k) should be defined as the number of intervals (Huang et al., 1995)
Virtual Heat Storage Capacity
The VHSC is related to the building equivalent heat capacity parameter and the indoor temperature comfort range [Tmin, Tmax] and is not influenced by outdoor temperature and light radiance. Therefore, the VHSC is defined as a parameter rather than an interval number. According to Song et al. (2017), the VHSC as shown in Eq. 18
Virtual State of Charge
VSOC is defined as the ratio of the stored heat energy of VES to the VHSC, which is used to describe the energy storage state of VES, as shown in Eq. 19, and its range is 0–1. When Tin = Tmin, VSOC takes 0, and when Tin = Tmax, VSOC takes 1
E(k) depicted in Eq. 20 is influenced by Tin, and Tin will be influenced by the VCDP interval variable. Then, E(k) needs to be defined as the interval number
3.2 Rooftop PV Model Based on the Interval Number
Since the PV output power will be influenced by the uncertainty of light irradiance, the rooftop PV model based on the interval number of light irradiance depicted in Eq. 21 is developed
It is assumed that the PV output power in the PV-BES is only used to meet the power demands of the PV-BES. When the power demand of the PV-BES is smaller than that of the maximum PV output power, the actual PV output power is less than that of the maximum PV output power, which will lead to the problem of the PV local consumption. Therefore, the PV local consumption rate η shown in Eq. 22 is introduced to describe the PV local consumption of the PV-BES. The larger the η is, the larger the PV local consumption is
3.3 Other Electrical Load Models Based on the Interval Number
OELs are generally predicted by the load simultaneous rate (Wang et al., 2014). Due to the uncertainty of the load simultaneous rate, the OEL model depicted in Eq. 23 is developed by using the interval number of the load simultaneous rate
where
4 Day-Ahead Optimal Interval Scheduling for the PV-BES
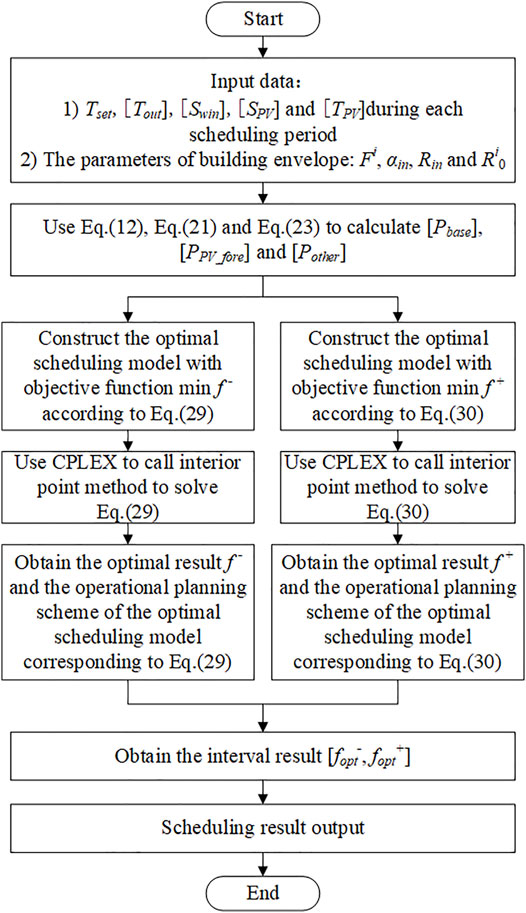
Based on the interval optimization theory, a day-ahead optimal interval scheduling method for the PV-BES based on VES is proposed. The method framework is shown in Figure 4. Taking the minimum electricity energy purchase cost as the interval objective function and considering the constraints of VES, PV, and the electrical power balance, a day-ahead optimal interval scheduling model considering VES is developed.
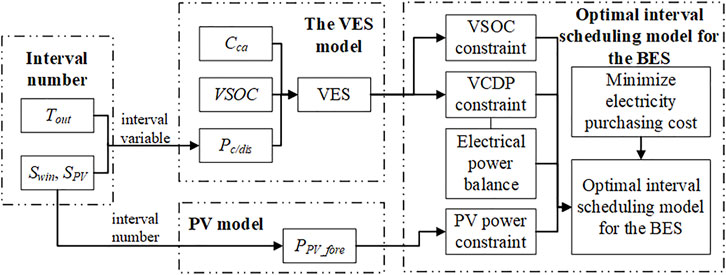
FIGURE 4. Framework of the day-ahead optimal interval scheduling method based on the interval number.
4.1 Interval Objective Function
The interval objective function depicted in Eq. 24 is proposed to minimize the electricity energy purchase cost of the BES. Due to the fact that VES participating in the optimal scheduling of the BES is uncertain, the electricity energy purchase cost is also an interval number (i.e., the objective function is in the form of [f])
4.2 Constraints
The optimal interval scheduling model proposed in this article includes VES constraints, the PV output power range constraint, and the electrical power balance constraint, as follows:
1) VES Constraints
(1) VSOC Constraint
The VSOC constraint is used to ensure the occupant’s thermal comfort, as shown in Eq. 25. When VSOC is 1, Tin is equal to Tmax; when VSOC is 0, Tin is equal to Tmin
(2) VCDP Constraint
The VCDP constraint is affected by the maximum charge power and the maximum discharge power of VES, as shown in Eq. 26
2) PV Output Power Range Constraint
The PV output power is constrained by the maximum PV output power, as shown in Eq. 27
3) Electrical Power Balance Constraint of the PV-BES
The electrical power balance in the process of PV-BES energy scheduling must be ensured (see Figure 2), as shown in constraint Eq. 28
4.3 Model Solving Method
According to the interval optimization theory (Huang et al., 1995), the electricity energy purchase cost interval result of the optimal interval scheduling model shown in Eqs 24–28 can be obtained by solving the optimal scheduling models corresponding to the objective function min f -and min f +, respectively. The interval result is expressed as [fopt-, fopt+]. At the same time, the operational planning scheme corresponding to the upper and lower boundaries of the interval result can provide a reference for the formulation of the PV-BES operational planning scheme.
The objective function min f - and its corresponding constraints are shown in Eq. 29
The objective function min f + and its corresponding constraints are shown in Eq.(30)
Using the CPLEX toolbox and calling the interior point method to solve the two functions shown in Eqs 29, 30, the interval result [fopt-, fopt+] of the PV-BES day-ahead optimal interval scheduling model proposed in this article can be obtained. The solution flowchart is shown in Figure 5.
5 Case Study
5.1 Input Data and Scenario Setting
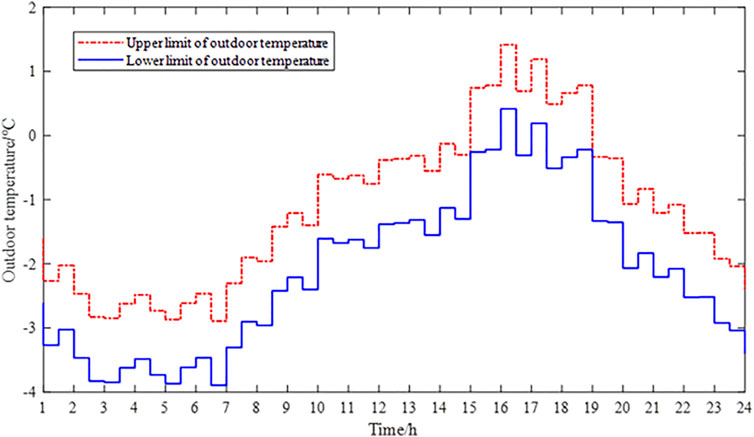
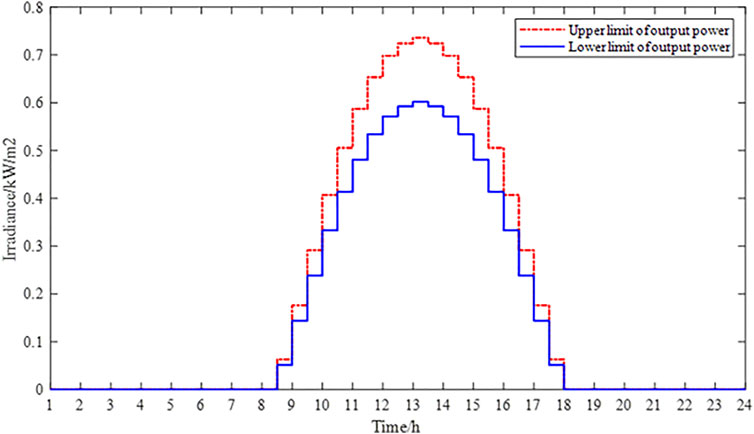
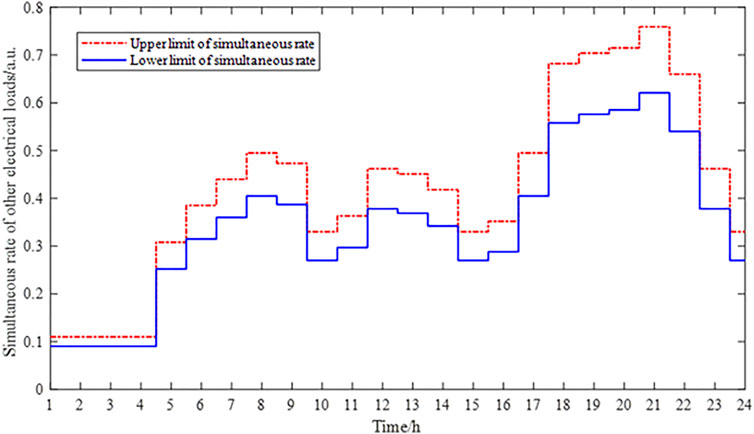
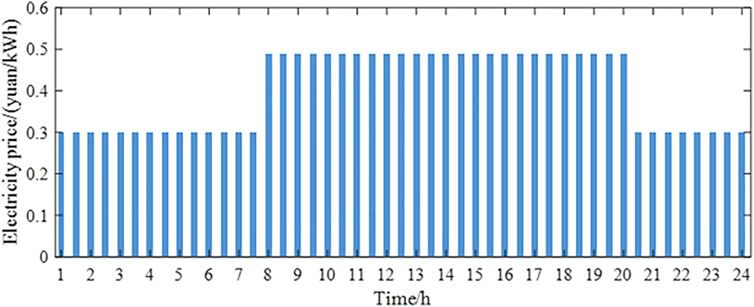
A six-story apartment building was used to verify the effectiveness of the day-ahead optimal interval scheduling method based on VES in this study. The effects of four building envelopes, including the wall, window, roof, and door, are considered in this study. Assume that the fluctuation range of the outdoor temperature is ±0.2°C and the fluctuation range of light irradiance and the simultaneous rate of OELs is ±10%. Then, the day-ahead outdoor temperature prediction interval, the light irradiance prediction interval, and the simultaneous rate prediction interval of OELs are shown in Figures 6–8 (Dong et al., 2020). The electricity price during each scheduling period is shown in Figure 9 (Tianjin Municipal People’s Government, 2020).
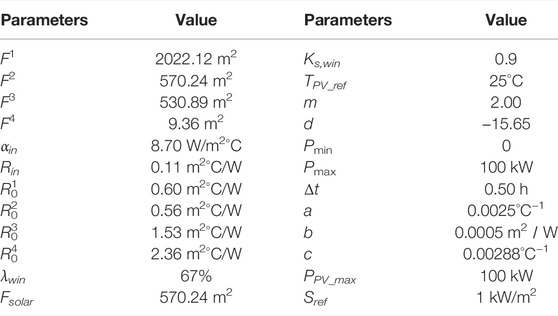
Considering the common occupied hours of the building, the indoor temperature scheme is set as follows: during the scheduling period of 4:00–9:00, 11:00–13:00, and 16:00–24:00, the indoor temperature setting value is set to 18°C, and the indoor temperature comfort range is set to 18°C and 20°C; in the remaining time, the indoor temperature setting value is set to 16°C, and the indoor temperature comfort range is set to 16°C and 20°C. The parameters related to the VES and PV are shown in Table 1.
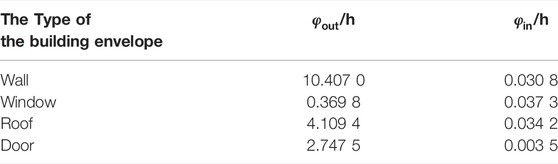
According to Eq. A1 and Eq. A2 in Appendix A, the heat lags of various building envelopes can be obtained, as shown in Table 2. Compared with the heat lags when the outdoor temperature is transmitted to the inner surface of the building envelope (φout), the heat lags when the indoor temperature is transmitted to the inner surface of the building envelope (φin) are relatively small. Therefore, φin is ignored to simplify the calculation. The minimum value of φout in various building envelopes is 0.3698 h, which is about 22 min. Considering that the temperature changes relatively slowly compared with the speed of power energy scheduling and to reduce the solution time of the day-ahead optimal interval scheduling model, the proposed optimal interval scheduling method schedules the PV-BES shown in Figure 2 over a 24 h time period with a 30 min interval (
To analyze the effectiveness of the day-ahead optimal interval scheduling method based on the VES proposed in this article, two typical scenarios are set.
Scenario I: Optimal interval scheduling for the PV-BES with the proposed method.
Scenario II: Optimal interval scheduling for the PV-BES without considering VES [following Wang et al. (2014)] (i.e., Tin varies with Tset).
5.2 Scheduling Results
When the optimal scheduling results are fopt- and fopt+, then, the interval results [fopt-, fopt+] and the corresponding operational planning schemes for Scenario I and Scenario II are given in this section.
5.2.1 Economic Analysis of Scheduling Results
The interval results (i.e., electricity energy purchase costs) for Scenario I and Scenario II are [365.15, 382.53] and [377.71, 389.88], respectively. When the optimal scheduling results are fopt- and fopt+, the corresponding PV local consumption rate, amounts of purchasing electricity, and electricity energy purchase costs for Scenario I and Scenario II are shown in Table 3. The variations of indoor temperature, the PV output power, commercial power from the external grid, and the total power consumption of the PV-BES are shown in Figures 10–13, respectively.
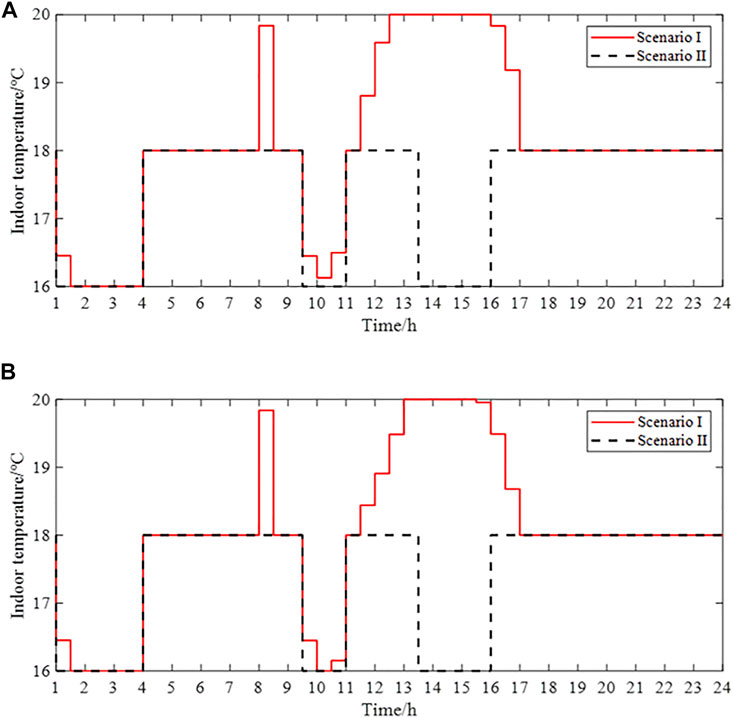
FIGURE 10. Corresponding indoor temperature when the optimal scheduling results are fopt- and fopt+. (A) Indoor temperature when the optimal scheduling result is fopt-. (B) Indoor temperature when the optimal scheduling result is fopt+.
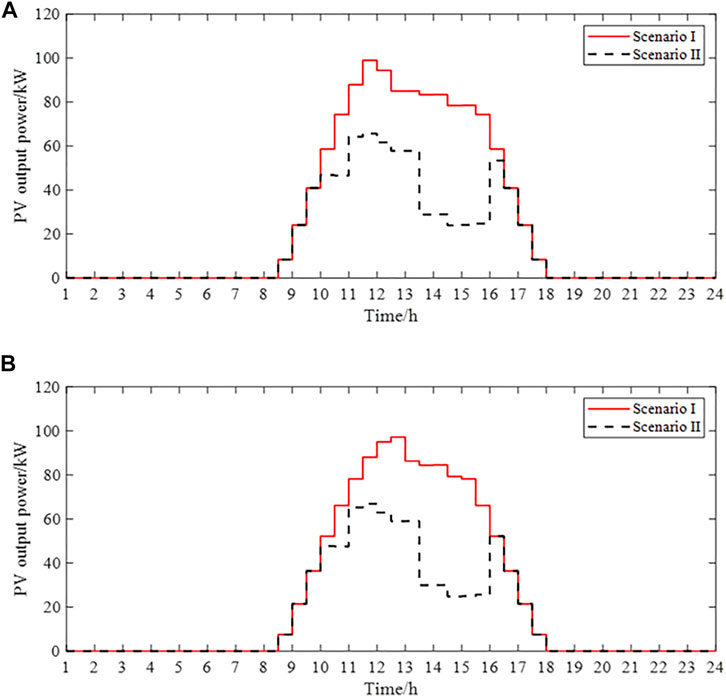
FIGURE 11. Corresponding PV output power when the optimal scheduling results are fopt- and fopt+. (A) PV output power when the optimal scheduling result is fopt-. (B) PV output power when the optimal scheduling result is fopt+.
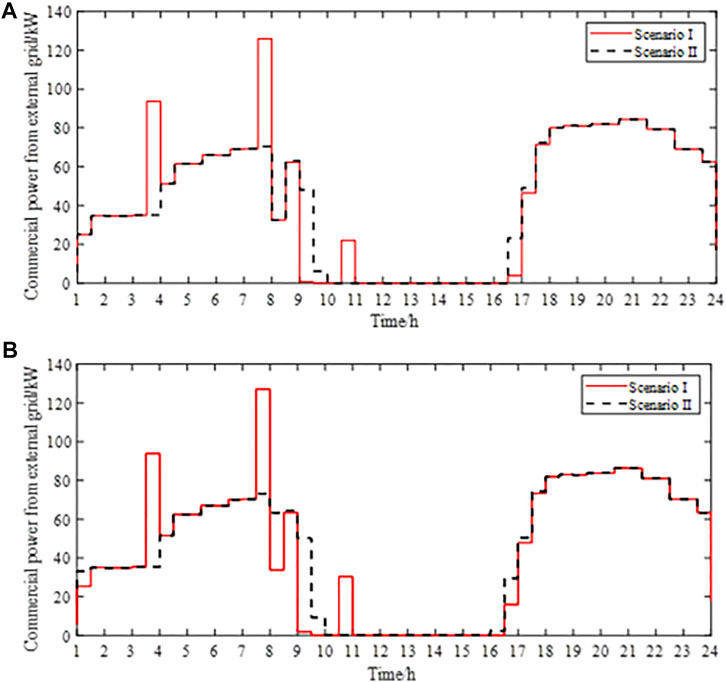
FIGURE 12. Corresponding commercial power from the external grid when the optimal scheduling results are fopt- and fopt+. (A) Commercial power from the external grid when the optimal scheduling result is fopt-. (B) Commercial power from the external grid when the optimal scheduling result is fopt+.
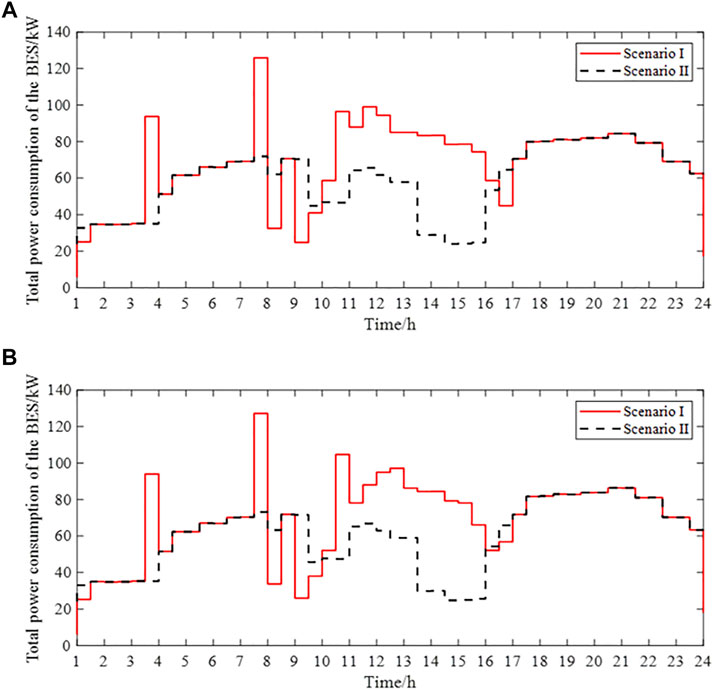
FIGURE 13. Corresponding total power consumption from the grid when the optimal scheduling results are fopt- and fopt+. (A) Total power consumption of the BES when the optimal scheduling result is fopt-. (B) Total power consumption of the BES when the optimal scheduling result is fopt+.
As shown in Table 3, on the basis of ensuring the occupant’s thermal comfort (as shown in Figure 10), the electricity energy purchase cost is reduced from 377.71 yuan and 389.88 yuan for Scenario II to 365.15 yuan and 382.53 yuan for Scenario I, respectively, a decrease of 3.33 and 1.89%, respectively, and the PV local consumption rate is improved from 54.71 to 61.11% for Scenario II to 88.89 and 95.78% for Scenario I. These data indicate that the day-ahead optimal interval scheduling method based on VES proposed in this article can reduce the electricity energy purchase cost and improve the PV local consumption rate. The reasons are analyzed as follows:
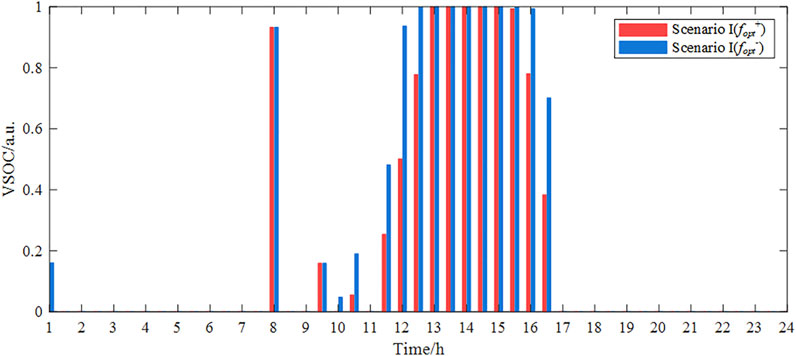
In terms of the economics of the PV-BES: as shown in Figure 9, during the scheduling period from 7:30 to 8:00, the electricity price is lower than that in the scheduling periods from 8:00 to 9:30. During the scheduling period from 7:30 to 8:00, compared with the scheduling result without considering VES for Scenario II, the commercial power from the external grid for Scenario I is higher (Figure 12). At this time, the VCDP for Scenario I is greater than 0 and the building VES is charged (as shown in Figures 14, 15). During the scheduling periods from 8:00 to 9:30, the electricity price is higher, and the commercial power from the external grid for Scenario I is lower than that for Scenario II, which means that the VCDP for Scenario I is less than 0 and VES releases the charged capacity during the scheduling period from 7:30 to 8:00 (as shown in Figures 14, 15). When the electricity price is high, VES is discharged, and when the electricity price is low, VES is charged, which reduces the electricity energy purchase cost of the PV-BES.
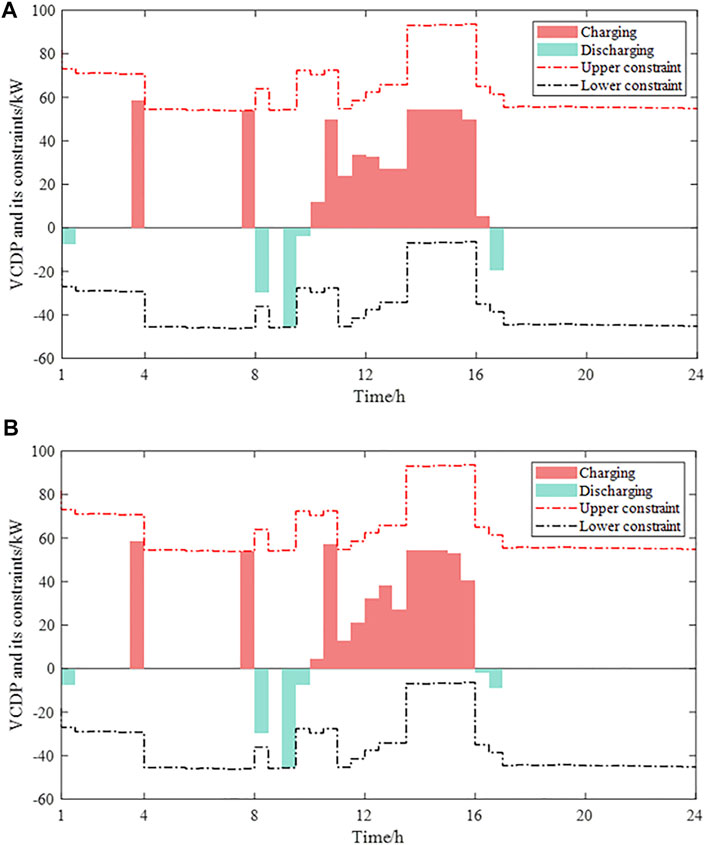
FIGURE 14. VCDP and its constraints when the optimal scheduling results are fopt- and fopt+ for Scenario I. (A) VCDP and its constraints when the optimal scheduling result is fopt- for Scenario I. (B) VCDP and its constraints when the optimal scheduling result is fopt+ for Scenario I.
In terms of PV local consumption: VES provided by the building envelope is ignored for Scenario II. The PV local consumption is only achieved by maintaining Tin = Tset (Figure 10) and meeting OELs of the PV-BES (Pother). VES is considered for Scenario I, which can provide more flexibility to meet building power demands. During the scheduling periods from 10:00 to 15:30, the maximum PV output power is greater than that in other scheduling periods, and VES for Scenario I is charged (Figures 10, 11). Then, the PV local consumption rate is improved.
In summary, the operational planning scheme with VES based on interval optimization can use VES to reduce the electricity energy purchase cost and improve the PV local consumption rate while considering the uncertainty of outdoor temperature and light irradiance.
5.2.2 Influence of the Uncertainty Degree on the Economics of the PV-BES
To analyze the influence of the uncertainty of outdoor temperature on the economics of the PV-BES, the fluctuation range of outdoor temperature is considered to be ±0.2°C, ±0.5°C, and ±1.0°C. The fluctuation range of light irradiance and the simultaneous rate of OELs is maintained at ±10%. The interval results [fopt-, fopt+] corresponding to different fluctuation ranges of outdoor temperature are shown in Table 4.
As shown in Table 4, with the increase of the uncertainty degree of outdoor temperature, the fluctuation range of the electricity energy purchase cost also increases, which indicates that the uncertainty degree of outdoor temperature has a direct influence on the electricity energy purchase cost. When the fluctuation range of outdoor temperature is ±0.2°C, the fluctuation range of the electricity energy purchase cost is 17.38 yuan. When the fluctuation range of outdoor temperature increases to ±0.5°C, the fluctuation range of the electricity energy purchase cost increases to 33.55 yuan, and the fluctuation range of the electricity energy purchase cost increases by 93%. When the fluctuation range of outdoor temperature increases to ±1.0°C, the fluctuation range of the electricity energy purchase cost increases to 50.44 yuan. Compared with the outdoor temperature fluctuation range of ±0.2°C, the fluctuation range of the electricity energy purchase cost increases by 190.22%.
To analyze the influence of the uncertainty of light irradiance on the economics of the PV-BES, the fluctuation range of light irradiance is considered to be ±10%, ±15%, and ±20%. The fluctuation range of outdoor temperature is maintained at ±0.2°C, and the simultaneous rate of OELs is maintained at ±10%. The interval results [fopt-, fopt+] corresponding to different fluctuation ranges of light irradiance are shown in Table 5.
As shown in Table 5, with the increase of the uncertainty degree of light irradiance, the fluctuation range of the electricity energy purchase cost also increases, which indicates that the uncertainty degree of light irradiance has a direct influence on the electricity energy purchase cost. When the fluctuation range of light irradiance is ±10%, the fluctuation range of electricity energy purchase cost is 17.38 yuan. When the fluctuation range of light irradiance increases to ±15%, the fluctuation range of the electricity energy purchase cost increases to 43.49 yuan, and the fluctuation range of the electricity energy purchase cost increases by 150.23%. When the fluctuation range of light irradiance increases to ±20%, the fluctuation range of the electricity energy purchase cost increases to 75.24 yuan. Compared with the light irradiance fluctuation range of ±10%, the fluctuation range of the electricity energy purchase cost increases by 332.91%.
6 Conclusion
In this study, an interval optimization-based day-ahead optimal interval scheduling method for the PV-BES with the consideration of the VES uncertainties is proposed. Particularly, the interval number is used to characterize the uncertain outdoor temperature, light irradiance, and OELs, and then, an interval VES model with VCDP interval variables is proposed. Based on the developed VES model, a cost-effective day-ahead optimal interval scheduling model for the PV-BES is proposed. The conclusions are as follows:
1) The VCDP interval variable and the VSOC interval number are proposed to quantify VES, and a day-ahead optimal interval scheduling method for the PV-BES is proposed by considering the constraints of the adjustable range of the VCDP interval variable and the VSOC interval number. This method can use the VES to participate in the optimal scheduling of the PV-BES while considering the influences of the uncertain outdoor temperature and light irradiance and then reduce the electricity energy purchase cost and improve the PV local consumption rate.
2) The uncertainty of the outdoor temperature and the light irradiance will influence the uncertainty of the PV-BES electricity energy purchase cost. When the fluctuation range of outdoor temperature increases from ±0.2°C to ±1.0°C, the fluctuation range of the PV-BES electricity energy purchase cost increases by 190.22%. When the fluctuation range of light irradiance increases from ±10% to ±20%, the fluctuation range of the PV-BES electricity energy purchase cost increases by 332.91%.
3) In order to further improve the matching degree between the PV-BES operational planning scheme and the actual operating conditions of the PV-BES and improve the operating economics of the PV-BES, future work will focus on developing a multi-time-scale optimal interval scheduling method.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
YM, YZ, and JZ conceptualized the study. YZ and YD performed the methodology and were responsible for software. HJ, ZL, and YG validated the results. YZ prepared the original draft. YM, YD, XJ, and JZ reviewed and edited the draft. YM and HJ supervised the study. ZL and YG completed the revised paper.
Funding
This paper was funded by the Science and Technology Foundation of Global Energy Interconnection Group Co., Ltd. (No. SGGEIG00JYJS2100033).
Conflict of Interest
Authors ZL and YG were employed by Global Energy Interconnction Group Co.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bai, M., Wang, Y., Tang, W., Wu, C., and Zhang, B. (2017). Day-ahead Optimal Dispatching of Regional Integrated Energy System Based on Interval Linear Programming. Power Syst. Tech. 41 (12), 3963–3970. doi:10.13335/j.1000-3673.pst.2017.0390
Chen, X., Wang, J., Xie, J., Xu, S., Yu, K., and Gan, L. (2018). Demand Response Potential Evaluation for Residential Air Conditioning Loads. IET Generation, Transm. Distribution 12 (19), 4260–4268. doi:10.1049/iet-gtd.2018.5299
Chen, Y., Chen, Z., Xu, P., Li, W., Sha, H., Yang, Z., et al. (2019). Quantification of Electricity Flexibility in Demand Response: Office Building Case Study. Energy 188, 116054. doi:10.1016/j.energy.2019.116054
Deng, Y., Zhang, Y., Luo, F., and Mu, Y. (2021). Operational Planning of Centralized Charging Stations Utilizing Second-Life Battery Energy Storage Systems. IEEE Trans. Sustain. Energ. 12 (1), 387–399. doi:10.1109/TSTE.2020.3001015
Deng, Y., Zhang, Y., Luo, F., and Ranzi, G. (2022). Many-Objective HEMS Based on Multi-Scale Occupant Satisfaction Modelling and Second-Life BESS Utilization. IEEE Trans. Sustain. Energ. 13, 934–947. doi:10.1109/TSTE.2022.3140765
Dong, J., Li, Y., Zhang, W., Zhang, L., and Lin, Y. (2020). Impact of Residential Building Heating on Natural Gas Consumption in the South of China: Taking Wuhan City as Example. Energ. Built Environ. 1 (4), 376–384. doi:10.1016/j.enbenv.2020.04.002
Esmaeel Nezhad, A., Rahimnejad, A., and Gadsden, S. A. (2021). Home Energy Management System for Smart Buildings with Inverter-Based Air Conditioning System. Int. J. Electr. Power Energ. Syst. 133, 107230. doi:10.1016/j.ijepes.2021.107230
Hong, T., Koo, C., Park, J., and Park, H. S. (2014). A GIS (Geographic Information System)-Based Optimization Model for Estimating the Electricity Generation of the Rooftop PV (Photovoltaic) System. Energy 65, 190–199. doi:10.1016/j.energy.2013.11.082
Huang, G. H., Baetz, B. W., and Patry, G. G. (1995). Grey Fuzzy Integer Programming: An Application to Regional Waste Management Planning under Uncertainty. Socio-Economic Plann. Sci. 29 (1), 17–38. doi:10.1016/0377-2217(94)00093-R10.1016/0038-0121(95)98604-t
International Energy Agency (2020). Renewables 2020. AvaliableAt: https://www.iea.org/reports/renewables-2020 (Accessed December 15, 2021).
Ji, Y., Xu, Q., Luan, K., and Yang, B. (2020). Virtual Energy Storage Model of Air Conditioning Loads for Providing Regulation Service. Energ. Rep. 6, 627–632. doi:10.1016/j.egyr.2019.11.130
Jin, X., Mu, Y., Jia, H., Wu, J., Jiang, T., and Yu, X. (2017). Dynamic Economic Dispatch of a Hybrid Energy Microgrid Considering Building Based Virtual Energy Storage System. Appl. Energ. 194, 386–398. doi:10.1016/j.apenergy.2016.07.080
Jin, X., Qi, F., Wu, Q., Mu, Y., Jia, H., Yu, X., et al. (2020). Integrated Optimal Scheduling and Predictive Control for Energy Management of an Urban Complex Considering Building thermal Dynamics. Int. J. Electr. Power Energ. Syst. 123, 106273. doi:10.1016/j.ijepes.2020.106273
Kim, Y.-J., Norford, L. K., and Kirtley, J. L. (2015). Modeling and Analysis of a Variable Speed Heat Pump for Frequency Regulation through Direct Load Control. IEEE Trans. Power Syst. 30 (1), 397–408. doi:10.1109/TPWRS.2014.2319310
Klein, K., Herkel, S., Henning, H.-M., and Felsmann, C. (2017). Load Shifting Using the Heating and Cooling System of an Office Building: Quantitative Potential Evaluation for Different Flexibility and Storage Options. Appl. Energ. 203, 917–937. doi:10.1016/j.apenergy.2017.06.073
Liu, X. (2021). Multiple Time‐scale Economic Dispatching Strategy for Commercial Building with Virtual Energy Storage under Demand Response Mechanism. Int. J. Energ. Res 45 (11), 16204–16227. doi:10.1002/er.6853
Oladokun, M. G., and Odesola, I. A. (2015). Household Energy Consumption and Carbon Emissions for Sustainable Cities - A Critical Review of Modelling Approaches. Int. J. Sust. Built Environ. 4 (2), 231–247. doi:10.1016/j.ijsbe.2015.07.005
Pokhrel, S. R., Hewage, K., Chhipi-Shrestha, G., Karunathilake, H., Li, E., and Sadiq, R. (2021). Carbon Capturing for Emissions Reduction at Building Level: A Market Assessment from a Building Management Perspective. J. Clean. Prod. 294, 126323. doi:10.1016/j.jclepro.2021.126323
Poonpun, P., and Jewell, W. T. (2008). Analysis of the Cost Per Kilowatt Hour to Store Electricity. IEEE Trans. Energ. Convers. 23 (2), 529–534. doi:10.1109/TEC.2007.914157
Reynders, G., Diriken, J., and Saelens, D. (2017). Generic Characterization Method for Energy Flexibility: Applied to Structural thermal Storage in Residential Buildings. Appl. Energ. 198, 192–202. doi:10.1016/j.apenergy.2017.04.061
Rifkin, J. (2012). The Third Industrial Revolution: How Lateral Power is Transforming Energy, the Economy, and the World. New York, NY: St. Martin’s Griffin.
Sánchez Ramos, J., Pavón Moreno, M., Guerrero Delgado, M., Álvarez Domínguez, S., and F. Cabeza, L. (2019). Potential of Energy Flexible Buildings: Evaluation of DSM Strategies Using Building thermal Mass. Energy and Buildings 203, 109442. doi:10.1016/j.enbuild.2019.109442
Solar Power Europe (2020). Global Market Outlook 2020-2024. AvaliableAt: https://www.solarpowereurope.org/global-market-outlook-2020-2024/ (Accessed December 15, 2021).
Song, M., Gao, C., Yan, H., and Yang, J. (2018). Thermal Battery Modeling of Inverter Air Conditioning for Demand Response. IEEE Trans. Smart Grid 9 (6), 5522–5534. doi:10.1109/TSG.2017.2689820
Stefan, C., and Dorota, K. (1996). Multiobjective Programming in Optimization of Interval Objective Functions - A Generalized Approach. Eur. J. Oper. Res. 94 (3), 594–598. doi:10.1016/0377-2217(95)00055-0
Su, Y., Zhou, Y., and Tan, M. (2020). An Interval Optimization Strategy of Household Multi-Energy System Considering Tolerance Degree and Integrated Demand Response. Appl. Energ. 260, 114144. doi:10.1016/j.apenergy.2019.114144
Tianjin Municipal People’s Government (2020). Subsidies for Clean Heating. AvaliableAt: http://www.tj.gov.cn/ zmhd/hygqx/202006/t20200612_2666059.html (Accessed December 15, 2021).
Tyagi, V. V., Chopra, K., Kalidasan, B., Chauhan, A., Stritih, U., Anand, S., et al. (2021). Phase Change Material Based advance Solar thermal Energy Storage Systems for Building Heating and Cooling Applications: A Prospective Research Approach. Sustainable Energ. Tech. Assessments 47, 101318. doi:10.1016/j.seta.2021.101318
Wang, D., Qi, T., Liu, Y., Wang, Y., Fan, J., Wang, Y., et al. (2020). A Method for Evaluating Both Shading and Power Generation Effects of Rooftop Solar PV Panels for Different Climate Zones of China. Solar Energy 205, 432–445. doi:10.1016/j.solener.2020.05.009
Wang, S., Wang, D., and Han, L. (2014). Interval Linear Programming Method for Day-Ahead Optimal Economic Dispatching of Microgrid Considering Uncertainty. Automation Electric Power Syst. 38 (24), 5–1147. doi:10.7500/AEPS20131212010
Yang, L., Guo, H., Huang, K., and Yang, J. (2019). Optimal Dispatch for a Combined Cooling, Heating and Power Microgrid Considering Building Virtual Energy Storage. J. Electr. Eng. Technol. 14 (2), 581–594. doi:10.1007/s42835-018-00055-z
Zhu, X., Yang, J., Liu, Y., Liu, C., Miao, B., and Chen, L. (2019). Optimal Scheduling Method for a Regional Integrated Energy System Considering Joint Virtual Energy Storage. IEEE Access 7, 138260–138272. doi:10.1109/ACCESS.2019.2942198
APPENDIX A
where mi is the number of material layers corresponding to the i-th building envelope; Di is the corresponding thermal inertia index of the i-th type of the building envelope;
NOMENCLATURE
VES Virtual energy storage
BES Building energy system
PV Photovoltaic
PV-BES PV-integrated BES
VCDP Virtual charge–discharge power
VHSC Virtual heat storage capacity
VSOC Virtual state of charge
IAC Inverter air conditioner
OELs Other electrical loads
BESS Battery energy storage system
Sets and indices
t Time t (h).
k The k-th scheduling period for a typical day, 1
[] Interval number.
Parameters and constants
Tmax Maximum room temperature (°C).
Tmin Minimum room temperature (°C).
Tin Indoor temperature (°C).
Tout Outdoor temperature (°C).
Tset Indoor temperature set point determined by the occupant (°C).
Tisur(t) Inner surface temperature of the i-th type building envelope at time t (°C).
Pmin Minimum input power of IAC (kW).
Pmax Maximum input power of IAC (kW).
Pcmax Maximum charge power of the VES (kW).
Pdismax Maximum discharge power of the VES (kW).
C Building equivalent heat capacity parameter (kJ/°C).
Fi Inner surface area of i-th type building envelope (m2).
Fsolar Window area that can project sunlight (m2).
αin Heat-transfer coefficient of the inner surface [W/(m2·°C)].
Rin Thermal resistance of the inner surface [(m2·°C)/W].
Ri0 Heat-transfer resistance of the building envelope of the i-th type building envelope [(m2·°C)/W].
Ks,win Window light irradiance correction factor.
Cca The VHSC of VES (kWh).
Sref Standard light irradiance of PV (kW/m2).
Swin(t) Window light irradiance at time t (kW/m2).
TPV_ref Standard temperature of PV (kW/m2).
m, d Constant coefficients of the IAC.
a, b, c Compensation coefficients of PV
p(k) Electricity price during the k-th scheduling period (yuan/kWh).
PPV_max Maximum PV power under the standard condition (kW).
Variables
E(k) Stored heat energy of VES during the k-th scheduling period (kWh).
PIAC(t) Electrical power of the IAC at time t (kW).
Pbase(k) Baseline of the electrical power during the k-th scheduling period (kW).
Pcom(k) Commercial power from the external grid during the k-th scheduling period (kW).
Pdiss(t) Self-discharge power at time t (kW).
PPV(k) Actual PV power during the k-th scheduling period (kW).
PPv_fore(k) Maximum PV power during the k-th scheduling period in a typical day (kW).
Pc/dis(k) The VCDP of VES during the k-th scheduling period (kW).
Pdismax(k) Maximum discharge power of VES during the k-th scheduling period (kW).
Pcmax(k) Maximum charge power of VES during the k-th scheduling period (kW).
Qbase(k) Baseline of the heating power during the k-th scheduling period (kW).
Qdiss(t) Heat dissipation power at time t (kW).
Qdiss,i(t) Heat dissipation power of the i-th type building envelope at time t (kW).
QIAC(t) Heating power of the IAC at time t (kW).
Keywords: interval optimization, virtual energy storage, building energy system, optimal scheduling, uncertainty
Citation: Mu Y, Zhang Y, Liu Z, Gao Y, Deng Y, Jin X, Jia H and Zhang J (2022) Day-Ahead Optimal Interval Scheduling for Building Energy System Considering Building Envelope Virtual Energy Storage Uncertainties. Front. Energy Res. 10:888107. doi: 10.3389/fenrg.2022.888107
Received: 02 March 2022; Accepted: 11 March 2022;
Published: 27 April 2022.
Edited by:
Shenxi Zhang, Shanghai Jiao Tong University, ChinaCopyright © 2022 Mu, Zhang, Liu, Gao, Deng, Jin, Jia and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yunfei Mu, eXVuZmVpbXVAdGp1LmVkdS5jbg==
 Yunfei Mu
Yunfei Mu Yaqing Zhang
Yaqing Zhang Zhe Liu2
Zhe Liu2 Youjun Deng
Youjun Deng Xiaolong Jin
Xiaolong Jin