- 1Army Academy of Armored Forces, Changchun, China
- 2School of Control Science and Engineering, Dalian University of Technology, Dalian, China
In this article, we study the global exponential stability of the equilibrium point for a class of memristor-based recurrent neural networks (MRNNs). The MRNNs are based on a realistic memristor model and can be implemented by a very large scale of integration circuits. By introducing a proper Lyapunov functional, it is proved that the equilibrium point of the MRNN is globally exponentially stable under two less conservative assumptions. Furthermore, an algorithm is proposed for the design of MRNN-based circuits with stable voltages. Finally, an illustration example is performed to show the validation of the proposed theoretical results; an MRNN-based circuit with stable voltages is designed according to the proposed algorithm.
1 Introduction
Recurrent networks have been one of the necessary tools to character system states since their wide applications in optimization (Li et al., 2021; Ma and Bian, 2021), games (Wu et al., 2019, 2021; Cheng et al., 2021), control (Yang et al., 2015; Jianmin et al., 2021; Toyoda and Wu, 2021), and so on (Wang et al., 2007; Shen et al., 2020; Shen and Raksincharoensak, 2021). In recent years, a new type of recurrent network was proposed based on a new two-terminal circuit element called the memristor (Chua, 1971; Strukov et al., 2008). Note that a memristor works like a biological synapse (Anthes, 2011; Qin et al., 2015) and has the ability of automatic information storage. Thus, memristors replaced resistors as synapses in recurrent neural networks, that is, memristor-based recurrent neural networks (MRNNs) (Anthes, 2011; Wen et al., 2013; Zhang et al., 2013). In recent years, the stability and stabilization of Boolean networks have been extensively investigated (Chen et al., 2018; Guo et al., 2019, 2021).
MRNNs have been a promising architecture in neuromorphic systems by virtue of their non-volatility, high-density, and physical storable feature. According to the realistic structure of MRNNs, several different mathematical models for MRNNs were proposed (Hu and Wang, 2010; Wu et al., 2011; Li et al., 2014; Chen et al., 2015; Jianmin et al., 2019). Meanwhile, notice that the MRNN, a special recurrent network, depends on the stability of its equilibrium points in application scenarios. Therefore, many interesting works were addressed to analyze the stability for the MRNNs (Hu and Wang, 2010; Wu et al., 2011; Li et al., 2014; Chen et al., 2015; Jianmin et al., 2019). A mathematical model of MRNN was proposed, and its global uniform asymptotic stability was investigated in a Lyapunov sense (Hu and Wang, 2010). A simple model of MRNN was introduced by Wu et al. (2011) by means of the typical current–voltage characteristics of memristors. A stochastic MRNN was proposed by Li et al. (2014) based on the work by Wang et al. (2007), in which therewas some unavoidable noise in real networks. Furthermore, the global exponential stability for the stochastic MRNN was studied under the framework of Filppov’s solution; three sufficient conditions with the form of linear inequalities were provided to determine the global exponential stability of the stochastic MRNN. The global asymptotic stability and synchronization of a class of fractional-order memristor-based delayed neural networks were investigated by Chen et al. (2015). The existence and global exponential stability were discussed by Jianmin et al. (2019) for an uncertain MRNN with mixed time delay under two assumptions.
Motivated by the aforementioned works, the global exponential stability of the equilibrium point is investigated for a class of MRNNs with time-varying delay, and its application to stabilize the voltage in a circuit network is carried out in this study. A sufficient condition is obtained for the global exponential stability of MRNNs. Based on this condition, an algorithm is proposed to stabilize the voltage of the MRNN-based circuit. The time-varying delay was considered in the activation functions of MRNN in this study. In addition, the activation functions in the MRNN are not necessarily non-decreasing, while the activation functions are non-decreasing in the works by Hu and Wang (2010); Wu et al. (2011); Li et al. (2014); Chen et al. (2015); Jianmin et al. (2019). Thus, the MRNN considered in this study is the extension from the view of activation functions compared with those in the works by Hu and Wang (2010); Wu et al. (2011); Li et al. (2014); Chen et al. (2015); Jianmin et al. (2019). Meanwhile, the stable voltage is a necessary prerequisite for obtaining high-quality electric energy in power systems, such as wind power converters (Kobravi et al., 2007). Consequently, the obtained theretical results are successfully applied to design the MRNN-based circuit system with global exponential stability, which makes it possible to apply the MRNN to power converters.
The structure of this article is given as follows: an MRNN with time-varying delay and some notations is introduced in Section 2. In Section 3, the global exponential stability of the equilibrium point for the MRNN is obtained, and an example is given to show the effectiveness of the obtained results. Then, an algorithm to design the MRNN-based circuit with stable voltage is proposed, and a simple application is carried out in Section 4. Finally, the main conclusions are given in Section 5.
2 Memristor-Based Recurrent Neural Network
In this section, some notations are introduced, and an MRNN is described under two assumptions based on the mathematical models by Wen et al. (2013); Jianmin et al. (2019).
Notation:
Consider the following MRNN, which was originated from Wen et al. (2013),
Here, fj (⋅) is the activation function, τj (⋅) is the time-varying delay, Ci is the capacitance of the capacitor, and xi(t) is the voltage of the capacitor.
Wi[xi(t)] is the memductance of the i − th memristor satisfying
Ii is an external input or bias and i, j = 1, 2, …, n. Let
From Jianmin et al. (2019), the MRNN (Eq. 1) is transformed into:
Here,
Next, let D = diag{d1, d2, …, dn},
In addition, there are two assumptions and one lemma, which will be needed in the sequel, for the MRNN (Eq. 7). The first assumption about the activation function fi is from Wen et al. (2013). The second assumption about the time-varying delay τj is from Wen et al. (2013).
S1. For i ∈ {1, 2, …, n}, the activation function fi is bounded continuous, and
Here, we set Lf = diag{l1, l2, …, ln}.
For i ∈ {1, 2, …, n}, the activation function gi is bounded continuous, gi (0) = 0, and
Here, we set
S2. For i ∈ {1, 2, …, n}, τi(t) satisfies
Here, we let
Remark 1. From Eq. 9, the activation functions gi [xi(t)] are non-monotonic in this study. On the other hand, we notice that the activation functions of MRNNs in the works by Hu and Wang (2010; Wu et al. (2011); Li et al. (2014); Chen et al. (2015); Jianmin et al. (2019) are non-decreasing. Thus, Eq. 1 is the extension from the view of activation functions compared with those references.
3 Globally Exponential Stability
In this section, we will prove that the MRNN (Eq. 1) is globally exponentially stable under the assumptions S1 and S2. A sufficient condition with the form of linear matrix inequalities can be obtained for globally exponential stability of MRNN by constructing a suitable Lyapunov functional.
Theorem 1. Assume that S1 and S2 hold. If there exist a matrix P = diag{p1, p2, …, pn} > 0, a constant k > 0, and small enough constants ξ > 0 and ϑ > 0 such that
Then, the equilibrium point of the MRNN (Eq. 1) is globally exponentially stable.
Proof. To simplify the proof, we make the following transformation:
where
where
We define a Lyapunov functional as follows:
where
Here, ξ, ϑ are small positive constants, and η is a positive constant to be determined.First, calculating the time derivative of
In addition,
Here, the parameter k is a positive constant. Substituting Eqs 18–20 into Eq. 17, we obtain
Second, by calculating the time derivative of
By Eq. 14, we have
Notice that
Substituting Eqs 23–25 into Eq. 22, we have
Third, calculating the time derivative of
Hence, by Eqs 21, 26, 27, we have
Let
Since Φ < 0, Ψ < 0, and by Eq. 29, we have
which means that
where
Next, by the aforementioned parameters and Eqs 2–6, it follows that D,
and the time-varying delays
for i = 1, 2, 3, 4. It is obvious that the assumptions S1 and S2 are satisfied. Then, by assumptions S1 and S2, we have
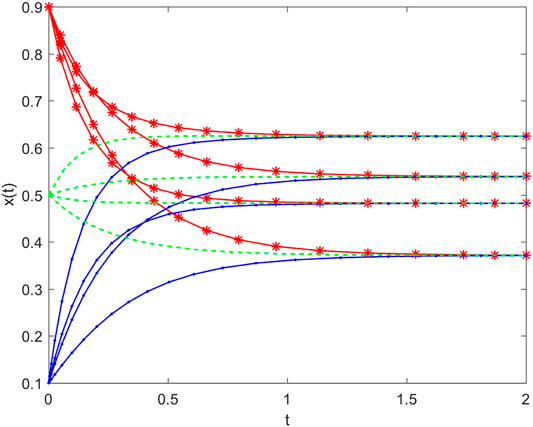
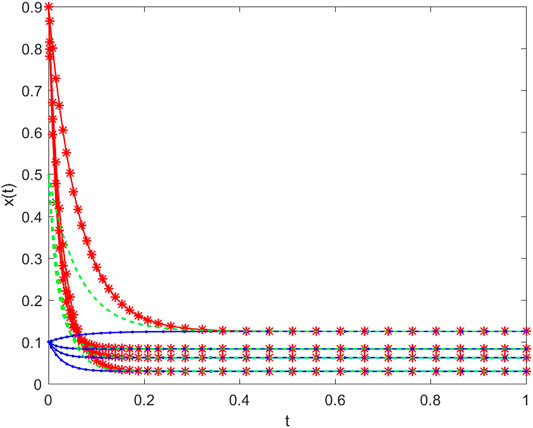
namely, by Theorem 1, the equilibrium point of the MRNN (Eq. 1) is globally exponentially stable.The initial values of the neural network (Eq. 1) are set at (0.1,0.1,0.1,0.1)T, (0.5,0.5,0.5,0.5)T, and (0.9,0.9,0.9,0.9)T. The solution trajectories of Eq. 1 are illustrated in Figure 1. From Figure 1, we see that the equilibrium point of the MRNN is globally exponentially stable, which shows the validation of the obtained result from Theorem 1.
4 An Algorithm to Design the MRNN-Based Circuit With Stable Voltages
Note that the stable voltage is a necessary prerequisite for obtaining high-quality electric energy in power systems. In this section, the two linear inequalities in Theorem 1 are used to design the MRNN-based circuit with globally exponentially stable voltages, which make it possible to apply the MRNN to power converters. The design process is described by the following four steps:
Step 1. Fix the values of capacitor Ci, external input Ii, and the resistors
Step 2. For the given time-varying delay τi(t) and the activation functions fi, gi, calculate the matrices Lf, Lg in the assumption S1 and the parameters
Step 3. Determine the parameters
• Fix a matrix P > 0 and the parameters k, ξ, and ϑ in Theorem 1.
• Substitute Ci, Ii,
• Substitute the matrices P, D, A, B, and U into the linear matrix inequalities (11).
• Solve Eq. 11 to obtain the matrix
• Calculate
Step 4. By substituting Ci, Ii,
Remark 3. From Step 3, the parameters
• Fix the values of parameters k = 1000, ξ = 0.001, and ϑ = 0.001 in Theorem 1 and a matrix P = diag{5, 5, 5, 5} > 0 and D = diag{30, 20, 25, 10}. Substitute the matrices P, D, B, and U into the linear matrix inequalities (11). Then, solve Eq. 11 to obtain the matrix
• Calculate
5 Conclusion
In this study, the global exponential stability of the equilibrium point of the MRNN is investigated for a class of general activation functions. A sufficient condition with the form of linear matrix inequalities is obtained for the global exponential stability. Furthermore, the proposed results are applied to design the MRNN-based circuits with stable voltages. From the view of the MRNN-based circuit, some elements of the MRNN-based circuit with stable voltages can be determined by the proposed algorithm. Note that the earth’s environmental pollution and the lack of energy restrict the survival and development of the human society. Wind energy, an environment-friendly renewable resource, has become one of the effective ways to solve these two difficulties. The conversion of wind energy into electric energy can rely on wind power converters. The mathematical model of the power system of new wind turbines was described by a recurrent network. Thus, further research will focus on transforming the output voltage of the wind power converter to ensure the stable amplitude of its output voltage based on MRNN with stability.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
ZY contributed to the globally exponential stability of MRNN by considering the proper assumptions and constructing a suitable Lyapunov functional. YL drafted the manuscript and contributed to the algorithm of design of the MRNN-based circuit with stable voltages, experiments, and conclusions. All authors agree to be accountable for the content of the work.
Funding
This work was financially supported by the China Postdoctoral Science Foundation (Grant No. 2020M670785).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, L., Wu, R., Cao, J., and Liu, J.-B. (2015). Stability and Synchronization of Memristor-Based Fractional-Order Delayed Neural Networks. Neural Networks 71, 37–44. doi:10.1016/j.neunet.2015.07.012
Chen, S., Wu, Y., Macauley, M., and Sun, X.-M. (2018). Monostability and Bistability of Boolean Networks Using Semitensor Products. IEEE Trans. Control. Netw. Syst. 6, 1379.
Cheng, D., Wu, Y., Zhao, G., and Fu, S. (2021). A Comprehensive Survey on STP Approach to Finite Games. J. Syst. Sci. Complex 34, 1666–1680. doi:10.1007/s11424-021-1232-8
Chua, L. (1971). Memristor-the Missing Circuit Element. IEEE Trans. Circuit Theor. 18, 507–519. doi:10.1109/tct.1971.1083337
Guo, Y., Wu, Y., and Gui, W. (2021). Stability of Discrete-Time Systems under Restricted Switching via Logic Dynamical Generator and Stp-Based Mergence of Hybrid States. IEEE Trans. Automatic Control. doi:10.1109/tac.2021.3105319
Guo, Y., Zhou, R., Wu, Y., Gui, W., and Yang, C. (2019). Stability and Set Stability in Distribution of Probabilistic Boolean Networks. IEEE Trans. Automatic Control. 64, 736–742. doi:10.1109/TAC.2018.2833170
Hu, J., and Wang, J. (2010). “Global Uniform Asymptotic Stability of Memristor-Based Recurrent Neural Networks with Time Delays,” in IEEE Congress on Cumputational Intelligence (Spain): Barcelona), 2127–2134. doi:10.1109/ijcnn.2010.5596359
Jianmin, W., Fengqiu, L., and Sitian, Q. (2021). Exponential Stabilization of Memristor-Based Recurrent Neural Networks with Disturbance and Mixed Time Delays via Periodically Intermittent Control. Int. J. Control Automation Syst. 19, 2284–2296. doi:10.1007/s12555-020-0083-8
Jianmin, W., Fengqiu, L., and Sitian, Q. (2019). Global Exponential Stability of Uncertain Memristor-Based Recurrent Neural Networks with Mixed Time Delays. Int. J. Machine Learn. Cybernetics 10, 743–755. doi:10.1007/s13042-017-0759-4
Kobravi, K., Kinsner, W., and Filizadeh, S. (2007). Analysis of Bifurcation and Stability in a Simple Power System Using Matcont. Can. Conf. Electr. Comput. Eng., 1150–1154. doi:10.1109/ccece.2007.292
Li, H., Shao, S., Qin, S., and Yang, Y. (2021). Neural Networks with Finite-Time Convergence for Solving Time-Varying Linear Complementarity Problem. Neurocomputing 439, 146–158. doi:10.1016/j.neucom.2021.01.015
Li, J., Hu, M., and Guo, L. (2014). Exponential Stability of Stochastic Memristor-Based Recurrent Neural Networks with Time-Varying Delays. Neurocomputing 138, 92–98. doi:10.1016/j.neucom.2014.02.042
Ma, L., and Bian, W. (2021). A Novel Multiagent Neurodynamic Approach to Constrained Distributed Convex Optimization. IEEE Trans. Cybern. 51, 1322–1333. doi:10.1109/TCYB.2019.2895885
Qin, S., Wang, J., and Xue, X. (2015). Convergence and Attractivity of Memristor-Based Cellular Neural Networks with Time Delays. Neural Networks 63, 223–233. doi:10.1016/j.neunet.2014.12.002
Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/TITS.2021.3074522
Shen, X., Zhang, X., and Raksincharoensak, P. (2020). Probabilistic Bounds on Vehicle Trajectory Prediction Using Scenario Approach. IFAC-PapersOnLine 53, 2385–2390. doi:10.1016/j.ifacol.2020.12.038
Strukov, D. B., Snider, G. S., Stewart, D. R., and Williams, R. S. (2008). The Missing Memristor Found. Nature 453, 80–83. doi:10.1038/nature06932
Toyoda, M., and Wu, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. doi:10.1109/tcyb.2019.2954849
Wang, Z., Lauria, S., Fang, J. a., and Liu, X. (2007). Exponential Stability of Uncertain Stochastic Neural Networks with Mixed Time-Delays. Chaos, Solitons & Fractals 32, 62–72. doi:10.1016/j.chaos.2005.10.061
Wen, S., Bao, G., Zeng, Z., Chen, Y., and Huang, T. (2013). Global Exponential Synchronization of Memristor-Based Recurrent Neural Networks with Time-Varying Delays. Neural Networks 48, 195–203. doi:10.1016/j.neunet.2013.10.001
Wu, A., Zeng, Z., Zhu, X., and Zhang, J. (2011). Exponential Synchronization of Memristor-Based Recurrent Neural Networks with Time Delays. Neurocomputing 74, 3043–3050. doi:10.1016/j.neucom.2011.04.016
Wu, Y., Cheng, D., Ghosh, B. K., and Shen, T. (2019). Recent Advances in Optimization and Game Theoretic Control for Networked Systems. Asian J. Control. 21, 2493–2512. doi:10.1002/asjc.2303
Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn. Syst. 32, 2910–2924. doi:10.1109/tnnls.2020.3008960
Yang, S., Guo, Z., and Wang, J. (2015). Robust Synchronization of Multiple Memristive Neural Networks with Uncertain Parameters via Nonlinear Coupling. IEEE Trans. Syst. Man. Cybern, Syst. 45, 1077–1086. doi:10.1109/tsmc.2014.2388199
Keywords: memristor, voltage, circuit, recurrent neural network, stability
Citation: Yao Z and Li Y (2022) Global Exponential Stability of a Class of Memristor-Based RNN and Its Application to Design Stable Voltage Circuits. Front. Energy Res. 10:887769. doi: 10.3389/fenrg.2022.887769
Received: 02 March 2022; Accepted: 17 March 2022;
Published: 27 April 2022.
Edited by:
Xun Shen, Tokyo Institute of Technology, JapanCopyright © 2022 Yao and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yingshun Li, bGVleXNAZGx1dC5lZHUuY24=
 Zhao Yao1,2
Zhao Yao1,2 Yingshun Li
Yingshun Li