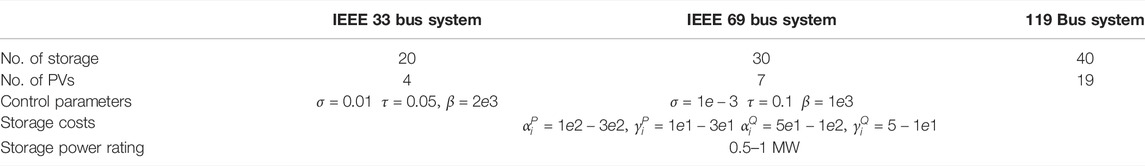Optimal Dispatch of a Virtual Storage Plant Using Inexact ADMM

A virtual storage plant (VSP) is identified as an effective approach to aggregating distributed storage devices participating in power network supports with similar capability as bulk storage systems. In this study, we develop a distributed control framework for cost-effective storage coordination in the distribution networks, in which the energy storage units are coordinated to contribute to a given power reference at the aggregated level while regulating the local network voltages in the presence of renewable generations. The salient features of the proposed VSP control roots from the successful employment of an inexact alternating direction method of multiplier (ADMM) algorithm, in which the primal updates have analytical solutions in closed form using proximal operators, which significantly reduces the computation efforts of individual storage agents, and renders fast storage dispatch. The proposed control is favorable for near real-time storage dispatch in an optimal manner, and its effectiveness is demonstrated using realistic distributed networks in the simulations.

Introduction

Distributed energy resources (DERs) transform the conventional role of passive distribution networks in modern power grids. These DERs include dispatchable units, such as diesel generators, energy storage systems, and nondispatchable units, for example, rooftop PV and small wind turbine systems. Although the deployment of renewable energy significantly helps with reduced carbon emissions, with their increased penetration, new network regulation issues appear. Distributed energy storage devices, located closed to the end-users and covering wide geographical areas, are identified as an effective measure to accommodate the intermittency of renewables without compromising the quality of power delivery (Morstyn et al., 2016).

Energy storage systems are widely available at different levels of a power system. As utility-scale storage systems, pumped-hydro storage, compressed-air energy storage, etc., have a long history of participating in energy markets and providing ancillary services to the transmission levels. In the near decades, distributed storage devices are integrated with smaller capacities but larger unit numbers. By the end of 2019, the residential energy storage systems coupled with rooftop PVs reached 2GW, representing a 57% annual increase in Europe; electrical vehicles, whose batteries can potentially contribute to grid supports, attained a 184% annual increase by September 2020 in the United Kingdom (Energy Storage News, 2019). The aggregation of distributed storage devices has a competitive capacity and presents more benefits over bulk storage. Such aggregated storage system is designed as a virtual storage plant (VSP), which seeks to use available storage resources providing flexibility to the large network interconnections.

The coordination of storage devices in a VSP relies on the cyber network for storage communications. This coincides with the concept of virtual power plants (VPPs) for the integration of general DERs (Kim et al., 2019; Cheng et al., 2017). The typical centralized control, in which a control center has access to every storage unit, will soon become inadequate regarding the expansions of the scales of storage in future distribution levels. On the other hand, distributed control collaborates individual agents to settle a given target based on neighboring communication, not only reducing the required bandwidth of the cyber layers but also enhancing robustness against failures and noises of the integrated systems (Olfati-Saber et al., 2007). Existing literature studies on distributed controls of power networks can be categorized into consensus-based controls (Wang et al., 2018,2019; Li et al., 2017) and optimization-based distributed controls (Yang et al., 2013a; Dall’Anese et al., 2018; Sulc et al., 2014; Tang et al., 2019; Li et al., 2019). Compared to the consensus controls, distributed optimization can generally achieve more sophisticated objectives, although deriving distributed solutions are not straightforward as that in a centralized setup. Yang et al. (2013b) and Xu et al. (2015) exploited the summation invariant of agent states under special cyber topologies, such that all agents are aggregated to provide a fixed amount of power and meanwhile minimize the overall cost; a similar method is employed for optimal VPP dispatch considering cyber attack in Li et al. (2018). Although these consensus controls are simple and effective in synchronizing agent states, system constraints cannot be easily handled by purely consensus-based methods. The power limits of DERs are enforced in Yang et al. (2013b), and then the algorithm stability is established by generalizing the unconstrained consensus cases. In addition, the optimal VSP operation should account for local voltage variations due to storage dispatch and load variations in the distribution level, but most of the studies (Yang et al., 2013a; Wang et al., 2019; Li et al., 2018; Zheng et al., 2018) were only concerned with the cyber layer and ignored the physical grid that holds the controllable units.

Distributed optimization, on the counterpart, can realize optimal storage dispatch and respect device and network constraints in a systematic manner Zhao and Ding, (2021). Primal-dual algorithms are usually used to derive distributed solutions for a centralized optimization problem by exploring the sparsity in the problem setup. For example, Mallada et al. (2017) developed the optimal frequency control in multi-area power networks in which the proposed control keeps the distributed structure of the typical automatic generation control (AGC) and incorporates frequency dynamics as part of the primal updates. For voltage control in distribution networks, Zhu and Liu (2016) modified the primal updates by a positive definite matrix, which maintains the direction of primal descent and leads to decentralized computation in radial networks. Tang et al. (2019) further employed the dual ascent by minimizing primal variables in each iteration for accelerated convergence but assumptions are made for homogeneous line parameters and 2-hop neighboring communications. A more relevant study by Dall’Anese et al. (2018) investigated optimal operations of a distribution network feeder as a VPP; the local voltage variations are considered, and the primal-dual algorithm is derived for the regularized Lagrangian showing better convergence. Dall’Anese et al. (2018), Zhu and Liu (2016), and Tang et al. (2019) used gradient-based methods for variable updates, whose slow converging rates are undesirable in time-critical and real-time applications. Combining the features of dual decomposition and the method of the multiplier, the alternating direction method of multiplier (ADMM) improves algorithm robustness and significantly reduces the needed number of iterations for convergence (Boyd et al., 2010; Feijer and Paganini, 1974). Distributed voltage regulation using ADMM is investigated in Sulc et al. (2014), in which the optimization is formulated in a consensus form with copied variables for fully distributed implementation. Similar concepts are employed for area voltage regulations of a partitioned distribution network (Xu and Wu, 2020), in which the dual update is accelerated to outperform the convergence of the original ADMM.

In Sulc et al. (2014), Xu and Wu (2020), and Zheng et al. (2018), the primal updates of ADMM were to find the minimizer of a constrained optimization problem. This process can be computational-intensive for high-dimensional problems. This disadvantage is first tackled for the linear regression issues in Mateos et al. (2010) using a consensus ADMM, which is further extended in Chang et al. (2015) and Chang (2016) considering coupled constraints by optimizing the dual problems based on inexact ADMM. In this investigation, a VSP is controlled to deliver the requested amount of power at the aggregated level by cost-effective storage coordination. This aggregated power reference can either follow an AGC signal or sustain for a specified amount and duration, for example, in the fast frequency reserve (FFR) defined by the National Grid in the United Kingdom (Zhao et al., 2020). In this study, the concerned VSP dispatch is formulated as an optimization problem considering both storage charging and discharging. We use voltage feedback and represent the formulation in an incremental form that accounts for voltage variations against storage dispatch and renewable generations. A proximal dual-consensus ADMM algorithm (PDC-ADMM) (Chang et al., 2015; Chang, 2016) is employed to solve the problem in a distributed manner, whose benefit is that the minimizer of the primal variables can be represented in a closed-form under coupled affine constraints. This results in a low-complexity algorithm that reduces the overall computation cost of ADMM. A similar problem setup appears in Chen and Li (2018), in which the primal update still depends on effective solvers to minimize a constrained optimization problem, and the impact of undispatchable units on network operation is ignored. The contribution of this study is that we develop a distributed control framework for optimal storage cooperation through VSP, considering local voltage regulations during storage dispatch based on the inexact PDC-ADMM, in which the variable update is accomplished by per-agent estimates and enjoy analytical forms that reduce the overall computation efforts.

The rest of the study is organized as follows: the System Modeling and Problem Formulation section describes the modeling of the cyber-physical systems involving the communication and distribution networks and formulates the optimization problem for VSP dispatch; the Inexact ADMM section illustrates the classical ADMM and the inexact variant of the ADMM algorithms using the proximal operators; Case Study discusses simulation results showing promising performance of the proposed approach in realistic distribution networks with real PV generation data; Conclusions are given in Data Availability Statement at the end.

System Modeling and Problem Formulation

In this section, models of the considered cyber-physical system are presented. We assume that the distribution network has a radial topology as for most real-world distribution networks. The consequent DistFlow model is linear with small approximation errors from the nonlinear power flow models (Zhu and Liu, 2016). If more general networks with meshed topologies are considered, linear approximations can be obtained as well (Dall’Anese et al., 2018).

DistFlow Model for Radial Distribution Networks

A radial distribution network is represented by a directed graph ${\mathcal{G}}_p$. Except for the substation node having a constant voltage, buses in the distribution networks are denoted by the set $\mathcal{N}$, among which the buses with storage are collected in the set $\mathcal{S}$, while all the other buses are collected in the set $\mathrm{ℒ}=\mathcal{N}\backslash \mathcal{S}$. Note that the buses in $\mathrm{ℒ}$ involve loads and renewables. The set of line segments connecting buses in $\mathcal{N}$ are denoted by the edge set ${{\rm E}}_p=\left\{\left(i,j\right)\subset \mathcal{N}\times \mathcal{N}\right\}$. For every line segment $\left(i,j\right)\in {{\rm E}}_p$, the DistFlow model is established as follows:

$P_{ij}-{\displaystyle \sum _{k\in {\mathcal{N}}_j}{P}_{jk}=-P_j^n},(\mathrm{1a})$

$Q_{ij}-{\displaystyle \sum }_{k\in {\mathcal{N}}_j}{Q}_{jk}=-Q_j^n,(\mathrm{1b})$

$V_i-V_j=r_{ij}^l{P}_{ij}+x_{ij}^l{Q}_{ij},(\mathrm{1c})$

where $P_{ij},Q_{ij}$ denote the active and reactive power flows on line $\left(i,j\right)$; the net injections of the bus $j$ are $P_j^n=P_j^g-P_j^l, Q_j^n=Q_j^g-Q_j^l,$ where $P_j^g,Q_j^g$ denote active/reactive powers from DERs and $P_j^l,Q_j^l$ denote the powers of load consumptions. The power flows from the substation to the end buses lead to voltage drops as $V_i-V_j$ described in (1c), where $r_{ij}^l$, $x_{ij}^l$ are resistance and reactance of the distribution lines, ${\mathcal{N}}_j$ denotes the set of neighbors of note $j$. The DistFlow model in (1) can be represented in a more compact form as (Zhu and Liu, 2016) follows:

$V=R^l{P}^n+X^l{Q}^n+V_0,(\mathrm{2a})$

$R^l=M^{-T}{D}_r{M}^{-1}, X^l=M^{-T}{D}_x{M}^{-1}.(\mathrm{2b})$

In Equation 2, $V$ is the vector of bus voltages and denoted as $V={\left(V_j\right)}_{j\in \mathcal{N}}$; similarly, $P^n={\left(P_j\right)}_{j\in \mathcal{N}}, Q^n={\left(Q_j\right)}_{j\in \mathcal{N}}$ are vectors of net bus injections, and $V_0=v_0{1}_{\left|\mathcal{N}\right|}$ where $v_0$ is the voltage magnitude of node 0 and $1_{\left|\mathcal{N}\right|}$ denotes a vector of all one with dimension $\left|\mathcal{N}\right|$, where $\left|\mathcal{N}\right|$ is the cardinality of $\mathcal{N}$. The matrix $M$ is the incidence matrix of the graph $\left(\mathcal{N},{\mathrm{ℰ}}_p\right)$, and $D_r=\text{diag}{\left(r_{ij}^l\right)}_{ij\in {\mathrm{ℰ}}_p},$ $D_x=\text{diag}{\left(x_{ij}^l\right)}_{ij\in {\mathrm{ℰ}}_p}$ are diagonal matrices of the line parameters.

Cyber Network

The cyber network communicating distributed storage devices are represented as a graph ${\mathcal{G}}_c=\left\{\mathcal{S},{\mathrm{ℰ}}_c\right\}$ in this study, where the graph edges in ${\mathrm{ℰ}}_c$ represent the communication lines among storage agents in $\mathcal{S}$. The connectivity of the graph is described by the adjacency matrix ${\mathcal{A}}_c={\left(a_{ij}\right)}_{i,j\in \mathcal{S}}$ where $a_{ij}=1$ for all $j\in {\mathcal{S}}_i$ and 0 otherwise, where ${\mathcal{S}}_i$ is the neighboring set of node $i$. We assume that the cyber graph is undirected and connected.

Problem Formulation

The optimization problem is formulated for the optimal storage coordination of a VSP located in a radial distribution network. The VSP is controlled to deliver a given amount of active power while regulating the local network voltage using its reactive power control capability. Considering every time slot $t$ in a time horizon $\mathcal{T}$ and $\forall i\in \mathcal{S}$, we have

$\underset{\left(P_{i,t}^b,Q_{i,t}^b\right)}{\min .}{\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}\left\{{\alpha }_{i,t}^P{\left(P_i^b\right)}^2+{\gamma }_{i,t}^P\left|P_i^b\right|+{\alpha }_{i,t}^Q{\left(Q_i^b\right)}^2+{\gamma }_{i,t}^Q\left|Q_i^b\right|\right\},(\mathrm{3a})$

$V_{\mathit{min}}{1}_{\left|\mathcal{S}\right|}\le {\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}\left\{R_i^l\left(P_{i,t}^b+P_{i,t}^l\right)+X_i^l\left(Q_{i,t}^b+Q_{i,t}^l\right)\right\}+{\displaystyle \sum }_{j=1}^{\left|\mathrm{ℒ}\right|}\left\{R_j^l{P}_{j,t}^n+X_j^l{Q}_{j,t}^n\right\}+V_0\le V_{\mathit{max}}{1}_{\left|\mathcal{S}\right|},(\mathrm{3b})$

${\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}{P}_{i,t}^b=P_t^A,(\mathrm{3c})$

${\left(P_{i,t}^b\right)}^2+{\left(Q_{i,t}^b\right)}^2\le {\left(S_i^b\right)}^2,(\mathrm{3d})$

$P_i^{b,min}\le P_{i,t}^b\le P_i^{b,max},(3e)$

$So{C}_{min}\le So{C}_{i,t}^b=So{C}_{i,t-1}^b+\frac{\eta P_{i,t}^b}{C{A}_i^b}\le So{C}_{max}, \forall i\in \mathcal{S}\text{.}(\mathrm{3f})$

In the optimization problem (3), $P_{i,t}^b,Q_{i,t}^b$ are active and reactive power outputs of the $i$th storage unit at the current time step. We assign a quadratic cost for every storage unit that is described by the parameters ${\alpha }_{i,t}^P, {\gamma }_{i,t}^P, {\alpha }_{i,t}^Q, {\gamma }_{i,t}^Q$ as in (Eq. 3a), and the absolute values indicate that both charging and discharging yield costs are related to storage usage. In (Eq. 3b), $R_i^l={\left(R_{ij}^l\right)}_{j\in \mathcal{S}}, X_i^l={\left(X_{ij}^l\right)}_{j\in \mathcal{S}}\in R^{\left|\mathcal{S}\right|}$ are column vectors of $R^l, X^l$ corresponding to the $i$th storage response on other storage buses, which can be understood as the bus voltage sensitivities with respect to the power injections at the $i$th buses. Here, we separately represent the power injections on the storage buses and load buses in $\mathrm{ℒ}$, whose net powers $P_{j,t}^n, Q_{j,t}^n$ combine the effects of renewables and loads as in (Eq. 3b); $V_{min}, V_{max}$ are the bus voltage limits. The VSP is optimized to provide the aggregated power $P_t^A$ as in (Eq. 3c). We mainly focus on inverter-based storage technologies, and the local constraints (3d)—(3e) characterize the limits of storage power capacity where $S_i^b$ is the apparent power limit of the power converter. Eq. 3f imposes the limits on storage energy capacity based on a general storage model, in which $\eta$ is the coefficient for charging/discharging, and $C{A}_i^b$ is the storage energy capacity. Note that (Eq. 3f) can be incorporated into (Eq. 3e) with time-varying power limits depending on the storage SoC (Dall’Anese et al., 2018); for example, storage with a full charge has $P_{i,t}^{b,max}=0$ and $P_{i,t}^{b,min}=-S_i^b$. To facilitate the algorithm implementation, the quadratic constraint (3d) is further linearized as follows:

$-S_i^b\le \cos \left(\tau \frac{\pi }{\kappa }\right)P_{i,t}^b+\sin \left(\tau \frac{\pi }{\kappa }\right)Q_{i,t}^b\le S_i^b, \tau =1,\dots ,\kappa ,(4)$

where the accuracy loss is 1.5% when $\kappa =8$ (Jabr, 2017). Moreover, considering that only the power injections on storage buses are known by agents, the network voltage constraint (3b) is rewritten in an increment form of storage power, as follows:

$V_{min}{1}_{\left|\mathcal{S}\right|}\le {\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}\left\{R_i^l\left(P_{i,t-1}^b+\mathrm{\Delta }{P}_{i,t}^b+P_{i,t}^l\right)+X_i^l\left(Q_{i,t-1}^b+\mathrm{\Delta }{Q}_{i,t}^b+Q_{i,t}^l\right)\right\}+{\displaystyle \sum }_{j=1}^{\left|\mathrm{ℒ}\right|}\left\{R_j^l{P}_{j,t}^n+X_j^l{Q}_{j,t}^n\right\}+V_0\le V_{max}{1}_{\left|\mathcal{S}\right|}.(5)$

It is assumed that the algorithm is fast enough such that the powers of loads and renewables are nearly constant within each time slot. From (Eq. 5) we denote

${\tilde{V}}_t={\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}\left\{R_i^l\left(P_{i,t-1}^b+P_{i,t}^l\right)+X_i^l\left(Q_{i,t-1}^b+Q_{i,t}^l\right)\right\}+{\displaystyle \sum }_{j=1}^{\left|\mathrm{ℒ}\right|}\left\{R_j^l{P}_{j,t}^n+X_j^l{Q}_{j,t}^n\right\}+V_0,(6)$

which is the vector of voltage magnitudes of storage buses before the agent actions and can be measured at the beginning of the current time step $t$. We denote $x_{i,t}={\left(P_{i,t}^b,Q_{i,t}^b\right)}^T=x_{i,t-1}+x_{i,t}$, and then the optimization problem (3) is arranged in the canonical form with the incremental variables $x_{i,t}$, considering storage outputs at $t-1$ are known by each agent.

$\underset{\begin{array}{c}\mathrm{\Delta }{x}_{i,t},\mathrm{\Delta }{r}_{i,t}\ge 0\\ \forall i\in S\end{array}}{\min }{\displaystyle \sum }_{i=1}^{\left|S\right|}\left\{\mathrm{\Delta }{x}_{i,t}^T{\mathrm{\Omega }}_{i,0}\mathrm{\Delta }{x}_{i,t}+{\mathrm{\Omega }}_{i,t-1}\mathrm{\Delta }{x}_{i,t}+\Vert {\mathrm{\Gamma }}_i\mathrm{\Delta }{x}_{i,t}+{\mathrm{\Gamma }}_i{x}_{i,t-1}\Vert \right\},(\mathrm{7a})$

${\displaystyle \sum }_{i=1}^{\left|\mathcal{S}\right|}\left(\left[\begin{array}{c}{A}_i\\ E\end{array}\right]\mathrm{\Delta }{x}_{i,t}+\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\le 0,(\mathrm{7b})$

$C\mathrm{\Delta }{x}_{i,t}+\mathrm{\Delta }{r}_{i,t}-d_i=0, \forall i\in \mathcal{S}\text{,}(\mathrm{7c})$

where

${\mathrm{\Omega }}_{i,0}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\alpha }_{i,t}^P,{\alpha }_{i,t}^Q\right), {\mathrm{\Omega }}_{i,t-1}=2x_{i,t-1}^T{\mathrm{\Omega }}_{i,0}, {\mathrm{\Gamma }}_i=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\gamma }_{i,t}^P,{\gamma }_{i,t}^Q\right),$

$A_i=\left[\begin{array}{c}{R}_i^l,X_i^l\\ -R_i^l,-X_i^l\end{array}\right], b_{i,t-1}=\left[\begin{array}{c}{\tilde{V}}_{i,t}{1}_i\\ -{\tilde{V}}_{i,t}{1}_i\end{array}\right], b_0=\left[\begin{array}{c}{V}_{\mathit{max}}{1}_{\left|\mathcal{S}\right|}\\ -V_{\mathit{min}}{1}_{\left|\mathcal{S}\right|}\end{array}\right],$

$E=\left[\begin{array}{cc}1& 0\\ -1& 0\end{array}\right], e_{i,t-1}=\left[\begin{array}{c}E{x}_{i,t-1}\\ -E{x}_{i,t-1}\end{array}\right], e_0=\left[\begin{array}{c}{P}_t^A\\ -P_t^A\end{array}\right],$

$C^s=\left[\begin{array}{cc}\cos \left(1\frac{\pi }{\kappa }\right)& \sin \left(1\frac{\pi }{\kappa }\right)\\ \cos \left(2\frac{\pi }{\kappa }\right)& \sin \left(2\frac{\pi }{\kappa }\right)\\ ⋮& ⋮\\ \cos \left(\kappa \frac{\pi }{\kappa }\right)& \sin \left(\kappa \frac{\pi }{\kappa }\right)\end{array}\right],C^p=\left[\mathrm{1,0}\right],C=\left[\begin{array}{c}\begin{array}{c}{C}^s\\ -C^s\end{array}\\ \begin{array}{c}{C}^p\\ -C^p\end{array}\end{array}\right],d_i=\left[\begin{array}{c}{S}_i^b{1}_{\kappa }-C^s{x}_{i,t-1}\\ S_i^b{1}_{\kappa }+C^s{x}_{i,t-1}\\ P_{i,t}^{\max }-C^p{x}_{i,t-1}\\ -P_{i,t}^{\min }+C^p{x}_{i,t-1}\end{array}\right].$

The vector $1_i$ has the $i$th entity equal to 1 and 0 for the others. The 1-norm ${\Vert \mathrm{■}\Vert }_1$ in the objective function (7a) accounts for storage costs in both charging and discharging modes; the coupled equality constraints 3(c) are represented in inequality, which with (Eq. 3b) is incorporated into (7b); (7c) are local constraints for storage capacity limits while $\mathrm{\Delta }{r}_{i,t}\ge 0$ is a slake variable.

Inexact ADMM

In this section, we introduce the basic principle of ADMM, based on which a proximal dual consensus ADMM is presented to solve convex optimization problem with coupled constraints. The inexact ADMM has the closed form for primal updates and thus reduces computational overheads of individual agents (Chang et al., 2015).

Alternating Direction Method of Multiplier

Consider the following optimization problem:

$\underset{x,r}{\min .}h\left(x\right)+g\left(r\right),(\mathrm{8a})$

$Ax+Br=c.(\mathrm{8b})$

For the augmented Lagrangian of (8), as $L_{\rho }\left(x,r,y\right)=h\left(x\right)+g\left(r\right)+y^T\left(Ax+Br-c\right)+\left(\rho /2\right)\mathrm{||}Ax+Br-c_2^2$, ADMM consists of the following iterations:

$x^{k+1}=\text{arg}\underset{x}{\min .}{L}_{\rho }\left(x,r^k,y^k\right),(\mathrm{9a})$

$r^{k+1}=\text{arg}\underset{r}{\min .}{L}_{\rho }\left(x^{k+1},r,y^k\right),(\mathrm{9b})$

$y^{k+1}=y^k+\rho \left(A{x}^{k+1}+B{r}^{k+1}-c\right).(\mathrm{9c})$

The updates of the primal variables are carried out jointly with respect to the augmented Lagrangian in a sequential fashion, while the dual update takes on a gradient step with coefficient $\rho .$ ADMM brings robustness and yields convergence without the restrictive assumptions for primal-dual and dual ascent algorithms (Boyd et al., 2010).

Inexact ADMM

In the classical ADMM, a central coordinator is usually needed to collect the primal variables in (Eq. 9c), and then the updated dual variable is broadcasted to every agent. To make the ADMM completely distributed, a consensus ADMM is proposed by Mateos et al. (2010), which is further developed to solve the problem with coupled constraints via its Lagrange dual problem (Chang et al., 2015;Chang, 2016). For an optimization problem in the form of (7), in which we make the generalization that $\mathrm{\Delta }{x}_{i,t}\in R^n, \mathrm{\Delta }{r}_{i,t}\in R^m$ and the other matrices have compatible sizes. The objection function of (7) can be separated for individual agents and denoted as $f_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)=g_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)+h_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)$, where $g_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)$ and $h_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)$ are the smooth and non-smooth parts, respectively. The Lagrange dual problem of (7) is considered and arranged in a consensus form, as follows:

$\underset{y_{i,t}\ge 0,z_{i,t}}{\min .} \underset{\begin{array}{c}\mathrm{\Delta }{x}_{i,t},\mathrm{\Delta }{r}_i\ge 0\\ i\in S\end{array}}{\max .}{\displaystyle \sum }_{i=1}^{\mathcal{S}}\left\{-f_i\left(\mathrm{\Delta }{x}_{i,t}\right)-y_{i,t}^T\left(\left[\begin{array}{c}{A}_i\\ E\end{array}\right]\mathrm{\Delta }{x}_{i,t}+\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)-z_{i,t}^T\left(C\mathrm{\Delta }{x}_{i,t}+\mathrm{\Delta }{r}_{i,t}-d_i\right)\right\},(\mathrm{10a})$

$y_{i,t}=t_{ij},y_{j,t}=t_{ij},\forall j\in {\mathcal{S}}_i,(\mathrm{10b})$

$z_{i,t}=l_i,i\epsilon \mathcal{S}\text{.}(\mathrm{10c})$

where $y_{i,t}, z_{i,t}$ are dual variables associated with the coupled constraints and local constraints. Since the dual variables of the coupled constraints are kept by individual agents, constraint (10b) imposes their consensus, in which $t_{ij}$ is an auxiliary variable. Constraint (10c) is a dummy constraint to make a strongly convex subproblem facilitating the following derivation (Chang, 2016). The augmented Lagrangian of (10) is as follows:

$\begin{array}{cc}\hfill L_c\left(y_i,z_i,{\lambda }_{+,ij},{\lambda }_{-,ij},{\nu }_i\right)& ={\displaystyle \sum }_{i=1}^{\mathcal{S}}\{{\phi }_i\left(y_i,z_i\right)+\frac{1}{\left|\mathcal{S}\right|}{y}_i^T(\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]\hfill \\ \hfill & -\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right])+z_i^T{d}_i\hfill \\ \hfill & +{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left[{\lambda }_{+,ij}^T\left(y_i-t_{ij}\right)+{\lambda }_{-,ij}^T\left(y_j-t_{ij}\right)\right]\hfill \\ \hfill & +{\nu }_i^T\left(z_i-l_i\right)+\frac{\tau }{2}{\Vert z_i-l_i\Vert }_2^2\hfill \\ \hfill & +\frac{\sigma }{2}{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left({\Vert y_i-t_{ij}\Vert }_2^2+{\Vert y_j-t_{ij}\Vert }_2^2\right)\}.\hfill \end{array}(11)$

where we drop the time stamp $t$ to simplify notions, and ${\phi }_i\left(y_i,z_i\right)=\underset{\mathrm{\Delta }{x}_i,\mathrm{\Delta }{r}_i\ge 0}{\max .}\left\{-f_i\left(\mathrm{\Delta }{x}_i\right)-y_i^T\left[\begin{array}{c}{A}_i\\ E\end{array}\right]x_{i,t}-z_i^T\left(C_i\mathrm{\Delta }{x}_i+\mathrm{\Delta }{r}_i\right)\right\}$, and ${\lambda }_{+,ij}^T, {\lambda }_{-,ij}^T,{\nu }_i$ are dual variables associated with the consensus and dummy constraints, $\tau , \sigma$ are positive coefficients of the Lagrange multipliers. Applying the ADMM procedure for (11), we have

$\begin{array}{cc}\hfill \left(y_i,z_i\right)& =\underset{y_i\ge 0,z_i}{\arg \min .}\{{\phi }_i\left(y_i,z_i\right)+\frac{1}{\left|\mathcal{S}\right|}{y}_i^T\left(\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\hfill \\ \hfill & +z_i^T{d}_i+{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left[{\lambda }_{+,ij}^T\left(y_i-t_{ij}\right)+{\lambda }_{-,ij}^T\left(y_j-t_{ij}\right)\right]\hfill \\ \hfill & +\frac{\sigma }{2}{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left({\Vert y_i-t_{ij}\Vert }_2^2+{\Vert y_j-t_{ij}\Vert }_2^2\right)\hfill \\ \hfill & +\frac{\tau }{2}{\Vert z_i-l_i^{k-1}+\frac{{\nu }_i^{k-1}}{\tau }\Vert }_2^2\},\hfill \end{array}(\mathrm{12a})$

$t_{ij}^k=\underset{t_{ij}}{\arg \min .}\left\{{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left({\Vert y_i^k-t_{ij}+\frac{{\lambda }_{+,ij}^{k-1}}{{\sigma }_1}\Vert }_2^2+{\Vert y_j^k-t_{ij}+\frac{{\lambda }_{-,ij}^{k-1}}{{\sigma }_1}\Vert }_2^2\right)\right\},(\mathrm{12b})$

$l_i^k=\underset{l_i}{\text{arg min}.}\left\{{\Vert z_i^k-l_i+\frac{{\nu }_i^{k-1}}{\tau }\Vert }_2^2\right\},(\mathrm{12c})$

${\nu }_i^k={\nu }_i^{k-1}+\tau \left(z_i^k-l_i^k\right),(\mathrm{12d})$

${\lambda }_{+,ij}^k={\lambda }_{+,ij}^{k-1}+{\sigma }_1\left(y_i^k-t_{ij}^k\right), {\lambda }_{-,ji}^k={\lambda }_{-,ji}^{k-1}+{\sigma }_1\left(y_i^k-t_{ji}^k\right).(12e)$

Deriving solutions of (12a)–(12c) and combining with (12d)–(12e) gives $t_{ij}^k=t_{ji}^k=\left(y_i^k+y_j^k\right)/2,$ $z_i^k=l_i^k, {\nu }_i^k=0$. So, (12) can be simplified as follows:

$\begin{array}{cc}\hfill \left(y_i,z_i\right)& =\underset{y_i\ge 0,z_i}{\text{arg min}.}\{{\phi }_i\left(y_i,z_i\right)+\frac{1}{\left|\mathcal{S}\right|}{y}_i^T\left(\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\hfill \\ \hfill & +z_i^T{d}_i+y_i^T{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left({\lambda }_{+,ij}^{k-1}+{\lambda }_{-,ij}^{k-1}\right)\hfill \\ \hfill & +{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left({\sigma \Vert y_i-\frac{y_i^{k-1}+y_j^{k-1}}{2}\Vert }_2^2\right)+{\frac{\tau }{2}\Vert z_i-z_i^{k-1}\Vert }_2^2\},\hfill \end{array}(\mathrm{13a})$

${\lambda }_{+,ij}^k={\lambda }_{+,ij}^{k-1}+\sigma \left(y_i^k-\frac{y_i^k+y_j^k}{2}\right), {\lambda }_{-,ji}^k={\lambda }_{-,ji}^{k-1}+\sigma \left(y_i^k-\frac{y_i^k+y_j^k}{2}\right).(\mathrm{13b})$

Using the minmax theorem and the strong convexity of (13a) (Chang, 2016), $y_i,z_i$ can be conveniently obtained by expanding ${\phi }_i$ and combining the linear and quadratic terms, which gives

$\begin{array}{c}\left(\mathrm{\Delta }{x}_{i,t}^k,\mathrm{\Delta }{r}_{i,t}^k\right)=\arg \underset{\mathrm{\Delta }{x}_{i,t},\mathrm{\Delta }{r}_{i,t}\ge 0}{\min .}\hfill \\ \{f_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)+\frac{\sigma }{4\left|{\mathcal{S}}_i\right|}\Vert \frac{1}{\sigma }\left(\left[\begin{array}{c}{A}_i\\ E\end{array}\right]\mathrm{\Delta }{x}_{i,t}+\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\hfill \\ -\frac{p_{i,t}^{k-1}}{\sigma }+{{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left(y_{i,t}^{k-1}+y_{j,t}^{k-1}\right)\Vert }_2^2+\frac{1}{2\tau }{\Vert C\mathrm{\Delta }{x}_{i,t}+\mathrm{\Delta }{r}_{i,t}-d_i+\tau z_{i,t}^{k-1}\Vert }_2^2\},\hfill \end{array}(\mathrm{14a})$

$y_{i,t}^k=\frac{1}{2\left|{\mathcal{S}}_i\right|}{\left[{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left(y_i^{k-1}+y_j^{k-1}\right)-\frac{1}{\sigma }{p}_{i,t}^{k-1}+\frac{1}{\sigma }\left(\left[\begin{array}{c}{A}_i\\ E\end{array}\right]\mathrm{\Delta }{x}_{i,t}+\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\right]}^{+},(\mathrm{14b})$

$z_{i,t}^k=z_{i,t}^{k-1}+\frac{1}{\tau }\left(C\mathrm{\Delta }{x}_{i,t}^k+\mathrm{\Delta }{r}_{i,t}^k-d_i\right),(\mathrm{14c})$

$p_{i,t}^k=p_{i,t}^{k-1}+c{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left(y_{i,t}^k+y_{j,t}^k\right),(\mathrm{14d})$

where $p_i^k={\displaystyle \sum }_{j\in {\mathrm{S}}_i}\left({\lambda }_{+,ij}^k+{\lambda }_{-,ji}^k\right)$ and ${\left[\mathrm{■}\right]}^{+}=\text{max}\left(0,\mathrm{■}\right)$. The iterative minimization of primal variables in (14a) does not need to be very accurate since it is an intermediate step in ADMM procedures (Mateos et al., 2010). In this regard, the inexact ADMM approximates (14a) by its first-order Taylor expansion at $\left(\mathrm{\Delta }{x}_{i,t}^{k-1},\mathrm{\Delta }{r}_{i,t}^{k-1}\right)$ (Chang, 2016). Denote the smooth part of (14a) as follows:

$\begin{array}{c}{\tilde{g}}_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)=\mathrm{\Delta }{x}_{i,t}^T{\mathrm{\Omega }}_{i,0}\mathrm{\Delta }{x}_{i,t}+{\mathrm{\Omega }}_{i,t-1}\mathrm{\Delta }{x}_{i,t}\hfill \\ +\frac{\sigma }{4\left|{\mathcal{S}}_i\right|}\Vert \frac{1}{\sigma }\left(\left[\begin{array}{c}{A}_i\\ E\end{array}\right]\mathrm{\Delta }{x}_{i,t}+\left[\begin{array}{c}{b}_{i,t-1}\\ e_{i,t-1}\end{array}\right]-\left[\begin{array}{c}{b}_0/\left|\mathcal{S}\right|\\ e_0/\left|\mathcal{S}\right|\end{array}\right]\right)\hfill \\ -\frac{1}{\sigma }{p}_{i,t}^{k-1}+{{\displaystyle \sum }_{j\in {\mathcal{S}}_i}\left(y_{i,t}^{k-1}+y_{j,t}^{k-1}\right)\Vert }_2^2+\frac{1}{2\tau }{\Vert C\mathrm{\Delta }{x}_{i,t}+\mathrm{\Delta }{r}_{i,t}-d_i+\tau z_{i,t}^{k-1}\Vert }_2^2.\hfill \end{array}(15)$

To derive an analytical solution, (14a) is simplified as follows:

$\begin{array}{c}\hfill \left(\mathrm{\Delta }{x}_{i,t}^k,\mathrm{\Delta }{r}_{i,t}^k\right)=\arg \underset{\mathrm{\Delta }{x}_{i,t},\mathrm{\Delta }{r}_{i,t}\ge 0}{\min .}\{h_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)+{\left({\nabla }_x{\tilde{g}}_{i,t}^{k-1}\right)}^T(\mathrm{\Delta }{x}_{i,t}\\ \hfill & -\mathrm{\Delta }{x}_{i,t}^{k-1})+{\left({\nabla }_r{\tilde{g}}_{i,t}^{k-1}\right)}^T\left(\mathrm{\Delta }{r}_{i,t}-\mathrm{\Delta }{r}_{i,t}^{k-1}\right)\hfill \\ \hfill & +\frac{{\beta }_i}{2}{\Vert \mathrm{\Delta }{x}_{i,t}-\mathrm{\Delta }{x}_{i,t}^{k-1}\Vert }_2^2+\frac{{\beta }_i}{2}{\Vert \mathrm{\Delta }{r}_{i,t}-\mathrm{\Delta }{r}_{i,t}^{k-1}\Vert }_2^2\},\hfill \end{array}(16)$

where ${\beta }_i>0$ is some penalty coefficient. Expanding the gradients ${\nabla }_x{\tilde{g}}_{i,t}^{k-1}$ and ${\nabla }_r{\tilde{g}}_{i,t}^{k-1}$ gives

$\mathrm{\Delta }{x}_{i,t}^k=\arg \underset{\mathrm{\Delta }{x}_{i,t}}{\min .}\left\{{\Vert {\mathrm{\Gamma }}_i\mathrm{\Delta }{x}_{i,t}+{\mathrm{\Gamma }}_i{x}_{i,t-1}\Vert }_1+\frac{{\beta }_i}{2}{\Vert \mathrm{\Delta }{x}_{i,t}-\left(\mathrm{\Delta }{x}_{i,t}^{k-1}-\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\right)\Vert }_2^2\right\},(\mathrm{17a})$

$\mathrm{\Delta }{r}_{i,t}^k={\left[\left(1-\frac{1}{{\beta }_i\tau }\right)\mathrm{\Delta }{r}_{i,t}^{k-1}+\frac{1}{{\beta }_i\tau }\left(d_i-C\mathrm{\Delta }{x}_{i,t}^{k-1}-\tau z_{i,t}^{k-1}\right)\right]}^{+}.(\mathrm{17b})$

To solve (17a) with non-smooth 1-norm terms, we employ the proximal operator for each coordinate of $\mathrm{\Delta }{x}_{i,t}$. Denoting the $j$th component of $\mathrm{\Delta }{x}_{i,t}^k$ as $\mathrm{\Delta }{x}_{i,t}^k\left(j\right)$, we have

$\mathrm{\Delta }{x}_{i,t}^k\left(j\right)=\arg \underset{\mathrm{\Delta }{x}_{i,t}\left(j\right)}{\min .}\left\{\left|{\mathrm{\Gamma }}_i\left(j\right)\mathrm{\Delta }{x}_{i,t}\left(j\right)+{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)\right|+\frac{{\beta }_i}{2}{\left[\mathrm{\Delta }{x}_{i,t}\left(j\right)-\left(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)-\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)\right)\right]}^2\right\},(18)$

where ${\text{Γ}}_i\left(j\right)$ is the $j$th diagonal element of ${\text{Γ}}_i$ and${\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)$ is the $j$th component of the gradient vector. Since $h_{i,t}\left(\mathrm{\Delta }{x}_{i,t}\right)={\displaystyle \sum }_{j=1}^n{h}_{i,t}^j\left(\mathrm{\Delta }{x}_{i,t}\left(j\right)\right)={\displaystyle \sum }_{j=1}^n\left|{\Gamma }_i\left(j\right)\mathrm{\Delta }{x}_{i,t}\left(j\right)+{\Gamma }_i\left(j\right)x_{i,t-1}\left(j\right)\right|$ is separatable, and notice that (Eq. 18) is a proximal operator for a scaler function $h_{i,t}^j\left(\mathrm{\Delta }{x}_{i,t}\left(j\right)\right)$, which is precomposed by an affined form. Thus, we rearrange (18) as follows:

$\begin{array}{cc}\hfill \mathrm{\Delta }{x}_{i,t}^k\left(j\right)& =\arg \underset{\mathrm{\Delta }{x}_{i,t}\left(j\right)}{\min .}\{h_{i,t}^j\left(\mathrm{\Delta }{x}_{i,t}\left(j\right)\right)\hfill \\ \hfill & +{\left[\mathrm{\Delta }{x}_{i,t}\left(j\right)-\left(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)-\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)\right)\right]}^2\}\hfill \\ \hfill & =\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}{.}_{h_{i,t}^j/{\beta }_i}\left(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)-\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)\right)\hfill \\ \hfill & =\frac{1}{{\mathrm{\Gamma }}_i\left(j\right)}\{\mathrm{p}\mathrm{r}\mathrm{o}{\mathrm{x}}_{{\mathrm{\Gamma }}_i^2\left(j\right)\left|\mathrm{■}\right|/{\beta }_i}[{\mathrm{\Gamma }}_i\left(j\right)(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)\hfill \\ \hfill & -\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right))+{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)]-{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)\},\hfill \end{array}(19)$

where the last equation uses the scaling and translation property of the proximal operator (denoted as prox.) for scalar functions (Beck, 2017). The proximal operator of the absolute value is called soft thresholding (Boyd et al., 2010), and thus, (19) can be computed analytically as follows:

$\begin{array}{c}\hfill \mathrm{\Delta }{x}_{i,t}^k\left(j\right)=\frac{1}{{\mathrm{\Gamma }}_i\left(j\right)}\{[{\mathrm{\Gamma }}_i\left(j\right)\left(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)-\frac{{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)}{{\beta }_i}\right)\hfill \\ \hfill {+{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)-\frac{{\mathrm{\Gamma }}_i^2\left(j\right)}{{\beta }_i}]}^{+}-[-{\mathrm{\Gamma }}_i\left(j\right)\left(\mathrm{\Delta }{x}_{i,t}^{k-1}\left(j\right)-\frac{1}{{\beta }_i}{\nabla }_x{\tilde{g}}_{i,t}^{k-1}\left(j\right)\right)\hfill \\ \hfill {-{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)-\frac{{\mathrm{\Gamma }}_i^2\left(j\right)}{{\beta }_i}]}^{+}-{\mathrm{\Gamma }}_i\left(j\right)x_{i,t-1}\left(j\right)\}.\hfill \end{array}(20)$

From (Eq. 20), we recover the optimal VSP control as defined in the System Modeling and Problem Formulation section. This gives the control commands for storage agents:

$\mathrm{\Delta }{P}_{i,t}^k=\frac{1}{{\gamma }_{i,t}^P}\left\{{\left[{\gamma }_{i,t}^P\left(\mathrm{\Delta }{P}_{i,t}^{k-1}-\frac{1}{{\beta }_i}{\nabla }_P{\tilde{g}}_{i,t}^{k-1}\right)+{\gamma }_{i,t}^P{P}_{i,t-1}-\frac{{\gamma }_{i,t}^{P 2}}{{\beta }_i}\right]}^{+}-{\left[-{\gamma }_{i,t}^P\left(\mathrm{\Delta }{P}_{i,t}^{k-1}-\frac{1}{{\beta }_i}{\nabla }_P{\tilde{g}}_{i,t}^{k-1}\right)-{\gamma }_{i,t}^P{P}_{i,t-1}-\frac{{\gamma }_{i,t}^{P 2}}{{\beta }_i}\right]}^{+}-{\gamma }_{i,t}^P{P}_{i,t-1}\right\},(\mathrm{21a})$

$\mathrm{\Delta }{Q}_{i,t}^k=\frac{1}{{\gamma }_{i,t}^Q}\left\{{\left[{\gamma }_{i,t}^Q\left(\mathrm{\Delta }{Q}_{i,t}^{k-1}-\frac{1}{{\beta }_i}{\nabla }_Q{\tilde{g}}_{i,t}^{k-1}\right)+{\gamma }_{i,t}^Q{Q}_{i,t-1}-\frac{{\gamma }_{i,t}^{Q 2}}{{\beta }_i}\right]}^{+}-{\left[-{\gamma }_{i,t}^Q\left(\mathrm{\Delta }{Q}_{i,t}^{k-1}-\frac{1}{{\beta }_i}{\nabla }_Q{\tilde{g}}_{i,t}^{k-1}\right)-{\gamma }_{i,t}^Q{Q}_{i,t-1}-\frac{{\gamma }_{i,t}^{Q 2}}{{\beta }_i}\right]}^{+}-{\gamma }_{i,t}^Q{Q}_{i,t-1}\right\}.(\mathrm{21b})$

Combining (21) with the primal and dual updates in (17b), (14b)–(14d) makes up the control law of storage devices in a VSP. Assuming a zero-duality gap, and the primal and dual optimal is attainable, the only requirement for the algorithm convergence is that the penalty coefficient ${\beta }_i$ should be larger than some constant determined by the modulus and Lipschitz constant of the smooth part of the objection function $g_{i,t}$ (Chang, 2016).

Case Study

The performance of the proposed method in optimal storage dispatch is demonstrated in this section. A VSP has an aggregator which receives high-level power reference for participating in transmission-level operations. Note that individual storage agents need to know this VSP power reference $P_t^A$, which can be either estimated by a first-order consensus algorithm or broadcasted by the VSP aggregator with low communication costs. We consider three study cases in the simulations, i.e., the IEEE 33-bus system, IEEE-68 bus system (Schneider et al., 2017), and a 199-bus system originally presented in Zhang et al. (2007). All the three distribution networks have radial topology, but the proposed algorithm can be employed for general network scenarios using linear approximation or voltage sensitivity matrix derived in fast-decoupled power flow. The diagram of the IEEE 33-bus system is shown in Figure 1 with an illustration of the VSP concept.

FIGURE 1

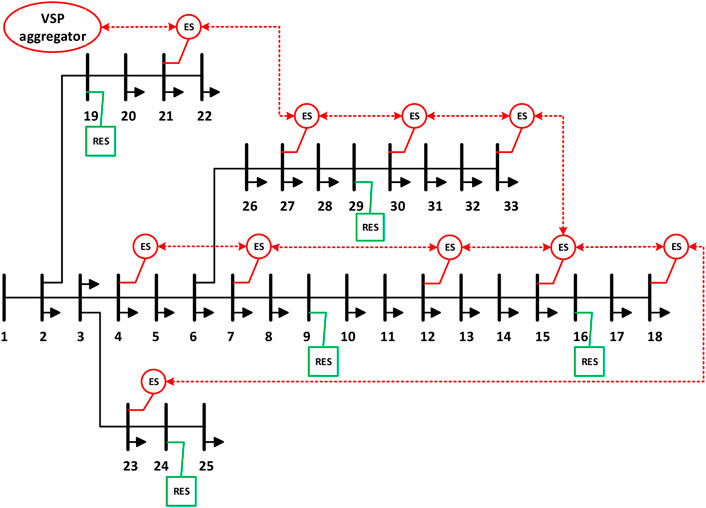
FIGURE 1. Diagram of the IEEE 33-bus system with distributed energy storage systems aggregated as a VSP (black solid line: distribution lines; red dashed line: communication lines).

Simulation Setup

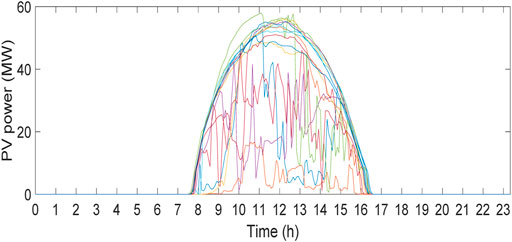
The simulations use real PV generation data sampled at 5 min, which are collected from a 75 MW solar power plant in Colorado, United States (Solar Power Data for Integration). The PV generation data from different days are used (Solar Power Data for Integration Studies, 2006) for 25 PV systems covering 24 h, and their profiles are shown in Figure 2. The PV powers are scaled-down by 150 times to suit the capacities of the distribution networks. The buses where the storage and PVs are located are randomly selected, while the loads are assumed to be constant in the simulations. The VSP dispatch commands are each randomly generated in 10 min. The voltage limits for cases 1 and 2 are 0.95–1.05 p.u., and 0.99–1.01 p.u. for case 3. Figure 3 shows the voltage profile of the IEEE 33 and IEEE 69 bus systems with integrated PV systems. This indicates that without storage response, a significant voltage increase is observed during peak PV generation hours.

FIGURE 2

FIGURE 2. Realistic generation profiles for 25 PV systems in 24 h.

FIGURE 3

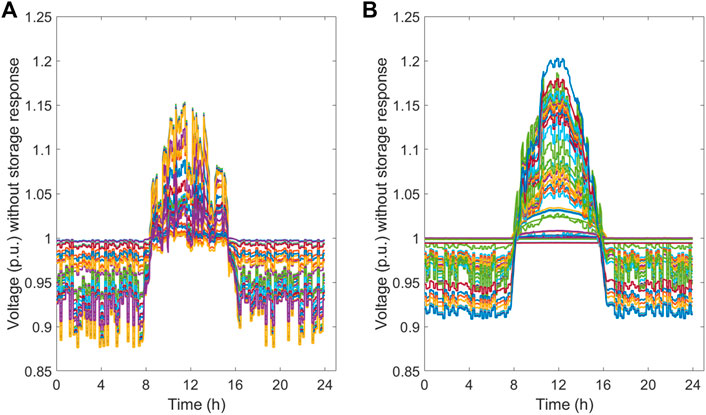
FIGURE 3. System voltage profiles under no storage response: (A) IEEE 33-bus system and (B) IEEE 69-bus system.

Table 1 gives the storage and control parameters in the simulations. The storage agents are labeled by the same bus number where they are located. We assume a ring topology for storage communication in the VSP cyber network, that id each storage agent communicates to its 2 most adjacent neighbors in the undirect graph. The sampling time of the algorithm is set to 1 min, which gives enough time for algorithm convergence at each time step. The storage power capacities and costs are randomly selected from the ranges provided in Table 1. We assume that all the storages have enough energy in the considered duration. The condition for algorithm termination is the accuracy of the objection function $\left({\text{obj}}^k-{\text{obj}}^{\ast }\right)/{\text{obj}}^{\ast }\le 1e^{-5}$, where ${\text{obj}}^{\ast }$ is the cost of a centralized optimization for the same problem.

TABLE 1

TABLE 1. Parameters of the storage assets in the VSP.

Simulation Results

Case I: The IEEE 33-bus system is rated at 12.7 kV with 3.75 MW/2.3MVar loads in total. The PV generations are selected from the data profile and integrated into the network at random buses. Figures 4A, B compares the VSP aggregated powers and costs under the proposed distributed control and a centralized optimization using YALMIP. This illustrates that the proposed VSP control can track the given power reference in a timely fashion and yield almost identical storage costs with respect to a centralized optimization result. The voltage profiles of the system are given in Figures 4C,D. Again, the proposed distributed control, i.e., Figure 4D generates similar results as the centralized scenario in Figure 4C, both of which successfully restrict the voltage within 0.95–1.01p.u., compared to the significant voltage variation observed in Figure 2A. Generally, the computational time of the distributed approach scales linearly with respect to the dimension of the decision variables, while the centralized approach has a high-order polynomial relation between the computational time and the dimension.

FIGURE 4

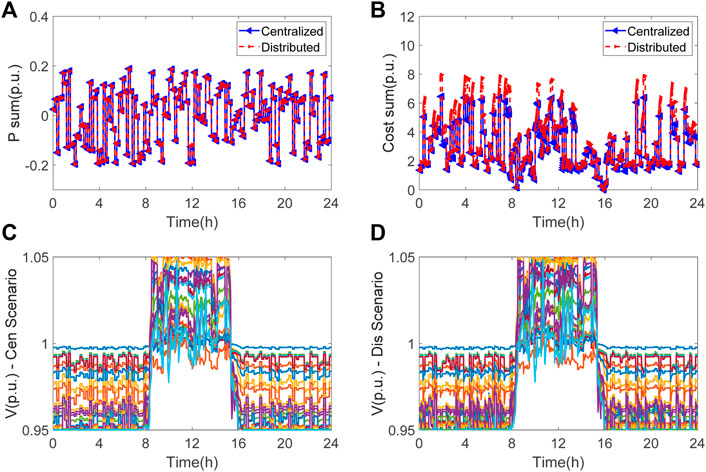
FIGURE 4. Case I: comparative results of VSP dispatch using a centralized optimization and the proposed distributed control: (A) VSP power outputs; (B) storage costs in the VSP; (C) voltage profile under the centralized control scenario; and (D) voltage profile under the distributed control scenario.

Case II: The IEEE 69 bus system is used in this study case. The radial distribution network is rated at 12.7 kV. The total loads are 3.8 MW and 2.7 MVar. Again, the simulation results in Figure 5 indicate that the proposed distributed control accomplishes nearly identical results as a centralized optimization in VSP dispatch and voltage regulations, while the distributed control has fewer requirements on the communication capability of the cyber network.

FIGURE 5

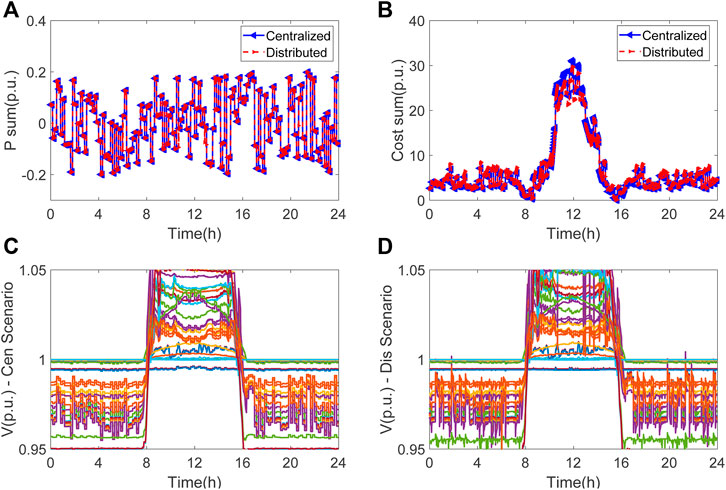
FIGURE 5. Case II: comparative results of VSP dispatch using a centralized optimization and the proposed distributed control: (A) VSP power outputs; (B) storage costs in the VSP; (C) voltage profile under the centralized control scenario; (D) voltage profile under the distributed control scenario.

Case III: The data of the 119-bus system is obtained from Zhang et al. (2007) and the diagram is shown in Figure 6. The nominal voltage of the system is 11 kV, and all the initial tie switches are open to making a radial distribution network. The total power loads are 22.7 MW and 17.0 MVar. In Figure 7, we present the active powers and reactive powers of the total 40 storage units in the VSP. The first column gives the results from a centralized optimization using CPLEX, while the second column is the result using the proposed PDC-ADMM method. It can be observed that the centralized control maintains the storage power references in each dispatch duration, while the proposed distributed control can gradually approach the optimal dispatch using feedback from the previous time step. Figure 8 validates the performance of the proposed VSP control in terms of the power reference tracking and voltage regulations similar to the results in IEEE 33-bus and IEEE 69-bus systems. Note that the proposed control framework generalizes the functionalities of storage solely by providing voltage supports in distribution networks.

FIGURE 6

FIGURE 6. Diagram of the 69 and 119-bus systems.

FIGURE 7

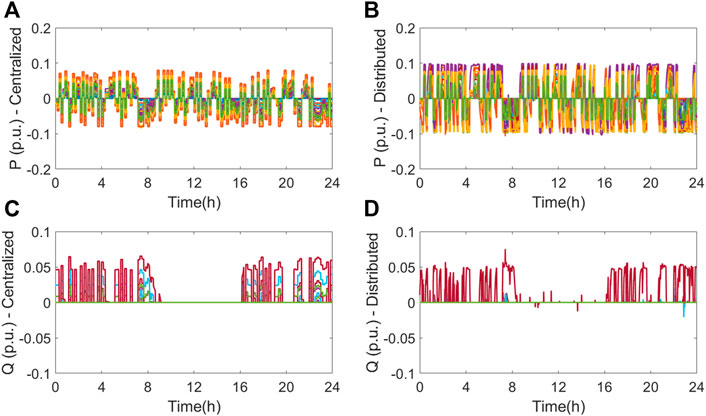
FIGURE 7. Case III: comparative results of VSP dispatch using a centralized optimization and the proposed distributed control: (A,B) active power outputs of individual storage devices; and (C,D) reactive power outputs of individual storage devices.

FIGURE 8

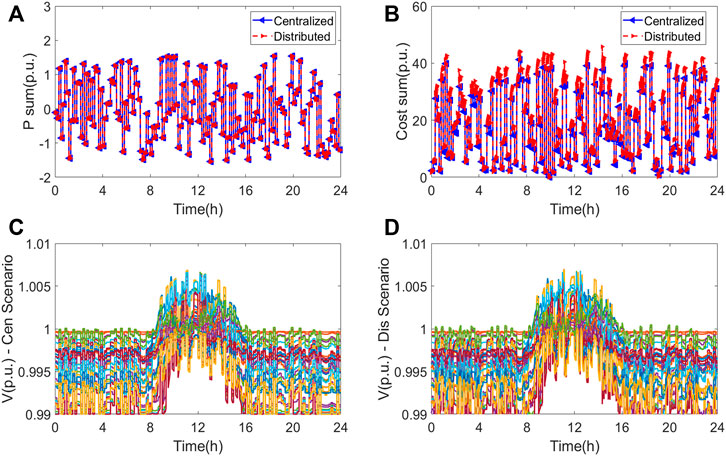
FIGURE 8. Case III: comparative results of VSP dispatch using a centralized optimization and the proposed distributed control: (A,B) active power outputs of individual storage devices; and (C,D) reactive power outputs of individual storage devices.

The centralized optimization can provide the global optimal regarding the storage dispatch in the convexified optimization problem. It provides a lower bound on the cost of storage coordination. The proposed distributed control framework uses an inexact approach to reduce the computational efforts of each storage agent. So, the accuracy of the optimization is compromised in exchange for the speed of storage dispatch. In addition, for the sake of practical implementation, we set a fixed value for the maximum number of iterations. So, the distributed control approach might output the calculated storage setpoints even when a suboptimal solution is obtained. These are the reasons that cause slight differences in the cost and storage dispatch between the centralized and distributed approach, but the control performance regarding the reference tracking and voltage regulation is almost in the two control scenarios.

Conclusion

This study presents a distributed control framework for the optimal coordination of distributed energy storage devices providing active power at the aggregated level in response to the request from system operators. The proposed control also covers the functionality of local voltage regulation that is widely defined by grid codes in the distribution networks. An improved ADMM algorithm is employed to solve the formulated optimization problem considering storage charging/discharging and its active/reactive power control capabilities. This leads to a fully distributed storage dispatch with analytical control laws based on the inexactness of intermediate ADMM calculations. The closed-form solution significantly reduces the computation overhead in algorithm iterations. The simulation results using MATLAB validate that the proposed VSP control can track the given power reference in a cost-effective manner while maintaining a flat voltage profile against renewable variations. In future work, the proposed control framework will be extended to a robust optimization framework that can handle uncertainties from the renewables and loads.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

DC: algorithm, mathematical formulation, draft preparation; ZW: algorithm and modeling; XW: idea and supervision; YW: manuscript writing and proofreading; WW: review and editing; KZ: data provision and figure plot; DY: proofreading.

Conflict of Interest

DY is employed by the State Grid Hubei Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer TZ is currently organizing a Research Topic with the author(s) XW.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beck, A. (2017). First-order Methods in Optimization. Society for Industrial and Applied Mathematics.

Google Scholar

Boyd, S., Parikh, N., and Chu, E. (2010). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. FNT Mach. Learn. 3 (1), 1–122. doi:10.1561/2200000016

CrossRef Full Text | Google Scholar

Chang, T.-H., Hong, M., and Wang, X. (2015). Multi-Agent Distributed Optimization via Inexact Consensus ADMM. IEEE Trans. Signal Process. 63 (2), 482–497. Jan.15. doi:10.1109/tsp.2014.2367458

CrossRef Full Text | Google Scholar

Chang, T. (2016). A Proximal Dual Consensus ADMM Method for Multi-Agent Constrained Optimization. IEEE Trans. Signal Process. 64 (14), 3719. doi:10.1109/TSP.2016.2544743

CrossRef Full Text | Google Scholar

Chen, G., and Li, J. (2018). A Fully Distributed ADMM-Based Dispatch Approach for Virtual Power Plant Problems. Appl. Math. Model. 58, 300–312. doi:10.1016/j.apm.2017.06.010

CrossRef Full Text | Google Scholar

Cheng, M., Sami, S., and Wu, J. (2017). Benefits of Using Virtual Energy Storage System for Power System Frequency Response. Appl. Energy 194, 378–385. doi:10.1016/j.apenergy.2016.06.113

CrossRef Full Text | Google Scholar

Dall’Anese, E., Guggilam, S. S., Simonetto, A., Chen, Y. C., and Dhople, S. V. (2018). Optimal Regulation of Virtual Power Plants. IEEE Trans. Power Syst. 33 (2), 1868. doi:10.1109/TPWRS.2017.2741920

CrossRef Full Text | Google Scholar

Energy Storage News (2019). Europe’s Residential Market Installed 745MWh of Battery Storage in 2019: SolarPower Europe. Available: https://www.energy-storage.news/news/europes-residential-market-installed-745mwh-of-battery-storage-in-2019-sola.

Google Scholar

Feijer, D., and Paganini, F. (1974). Stability of Primal–Dual Gradient Dynamics and Applications to Network Optimization. Automatica 46 (12).

Google Scholar

Jabr, R. A. (2017). Linear Decision Rules for Control of Reactive Power by Distributed Photovoltaic Generators. IEEE Trans. Power Syst. 33 (2), 2165. doi:10.1109/TPWRS.2017.2734694

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., Mohanpurkar, M., Luo, Y., Hovsapian, R., et al. (2019). Capability‐coordinated Frequency Control Scheme of a Virtual Power Plant with Renewable Energy Sources. IET Gener. Transm. Distrib 13, 3642–3648. doi:10.1049/iet-gtd.2018.5828

CrossRef Full Text | Google Scholar

Li, C., Coelho, E. A. A., Dragicevic, T., Guerrero, J. M., and Vasquez, J. C. (2017). Multiagent-Based Distributed State of Charge Balancing Control for Distributed Energy Storage Units in AC Microgrids. IEEE Trans. Ind. Appl. 53 (3), 2369–2381. doi:10.1109/tia.2016.2645888

CrossRef Full Text | Google Scholar

Li, P., Liu, Y., Xin, H., and Jiang, X. (2018). A Robust Distributed Economic Dispatch Strategy of Virtual Power Plant under Cyber-Attacks. IEEE Trans. Ind. Inf. 14 (10), 4343–4352. doi:10.1109/tii.2017.2788868

CrossRef Full Text | Google Scholar

Li, Q., Gao, D. W., Zhang, H., Wu, Z., and Wang, F.-y. (2019). Consensus-Based Distributed Economic Dispatch Control Method in Power Systems. IEEE Trans. Smart Grid 10 (1), 941–954. doi:10.1109/tsg.2017.2756041

CrossRef Full Text | Google Scholar

Mallada, E., Zhao, C., and Low, S. (2017). Optimal Load-Side Control for Frequency Regulation in Smart Grids. IEEE Trans. Autom. Contr. 62 (12), 6294–6309. doi:10.1109/tac.2017.2713529

CrossRef Full Text | Google Scholar

Mateos, G., Bazerque, J. A., and Giannakis, G. B. (2010). Distributed Sparse Linear Regression. IEEE Trans. Signal Process. 58 (10), 5262–5276. doi:10.1109/tsp.2010.2055862

CrossRef Full Text | Google Scholar

Morstyn, T., Hredzak, B., and Agelidis, V. G. (2016). Control Strategies for Microgrids with Distributed Energy Storage Systems: An Overview. IEEE Trans. Smart Grid 9 (4), 3652. doi:10.1109/TSG.2016.2637958

CrossRef Full Text | Google Scholar

Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 95 (1), 215–233. doi:10.1109/jproc.2006.887293

CrossRef Full Text | Google Scholar

Schneider, K. P., Mather, B. A., and Pal, B. C. (2017). Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 99, 1. doi:10.1109/TPWRS.2017.2760011

CrossRef Full Text | Google Scholar

Solar Power Data for Integration Studies (2006). NREL. Available at: https://www.nrel.gov/grid/solar-power-data.html.

Google Scholar

Sulc, P., Backhaus, S., and Chertkov, M. (2014). Optimal Distributed Control of Reactive Power via the Alternating Direction Method of Multipliers. IEEE Trans. Energy Convers. 29 (4), 968–977. doi:10.1109/tec.2014.2363196

CrossRef Full Text | Google Scholar

Tang, Z., Hill, D. J., and Liu, T. (2019). Fast Distributed Reactive Power Control for Voltage Regulation in Distribution Networks. IEEE Trans. Power Syst. 34 (1), 802–805. doi:10.1109/tpwrd.2018.2868158

CrossRef Full Text | Google Scholar

Wang, D., Meng, K., Gao, X., Qiu, J., Lai, L. L., and Dong, Z. Y. (2018). Coordinated Dispatch of Virtual Energy Storage Systems in LV Grids for Voltage Regulation. IEEE Trans. Ind. Inf. 14 (6), 2452–2462. doi:10.1109/tii.2017.2769452

CrossRef Full Text | Google Scholar

Wang, Y., Xu, Y., Tang, Y., Liao, K., Syed, M. H., Guillo-Sansano, E., et al. (2019). Aggregated Energy Storage for Power System Frequency Control: A Finite-Time Consensus Approach. IEEE Trans. Smart Grid 10 (4), 3675–3686. doi:10.1109/tsg.2018.2833877

CrossRef Full Text | Google Scholar

Xu, T., and Wu, W. (2020). Accelerated ADMM-Based Fully Distributed Inverter-Based Volt/Var Control Strategy for Active Distribution Networks. IEEE Trans. Ind. Inf. 16 (12), 7532–7543. doi:10.1109/tii.2020.2966713

CrossRef Full Text | Google Scholar

Xu, Y., Zhang, W., Hug, G., Kar, S., and Li, Z. (2015). Cooperative Control of Distributed Energy Storage Systems in a Microgrid. IEEE Trans. Smart Grid 6 (1), 238–248. doi:10.1109/tsg.2014.2354033

CrossRef Full Text | Google Scholar

Yang, H., Yi, D., Zhao, J., and Dong, Z. (2013). Distributed Optimal Dispatch of Virtual Power Plant via Limited Communication. IEEE Trans. Power Syst. 28 (3), 3511–3512. doi:10.1109/tpwrs.2013.2242702

CrossRef Full Text | Google Scholar

Yang, S., Tan, S., and Xu, J.-X. (2013). Consensus Based Approach for Economic Dispatch Problem in a Smart Grid. IEEE Trans. Power Syst. 28 (4), 4416–4426. doi:10.1109/tpwrs.2013.2271640

CrossRef Full Text | Google Scholar

Zhang, D., Fu, Z., and Zhang, L. (2007). An Improved TS Algorithm for Loss-Minimum Reconfiguration in Large-Scale Distribution Systems. Electr. Power Syst. Res. 77, 685–694. doi:10.1016/j.epsr.2006.06.005

CrossRef Full Text | Google Scholar

Zhao, T., and Ding, Z. (2021). Cooperative Optimal Control of Battery Energy Storage System under Wind Uncertainties in a Microgrid. IEEE Trans. Power Syst. 33 (2), 2292. doi:10.1109/TPWRS.2017.2741672

CrossRef Full Text | Google Scholar

Zhao, T., Parisio, A., and Milanovic, J. V. (2020). Distributed Control of Battery Energy Storage Systems for Improved Frequency Regulation. IEEE Trans. Power Syst. 35 (5), 3729–3738. doi:10.1109/tpwrs.2020.2974026

CrossRef Full Text | Google Scholar

Zheng, Y., Song, Y., Hill, D. J., and Zhang, Y. (2018). Multiagent System Based Microgrid Energy Management via Asynchronous Consensus ADMM. IEEE Trans. Energy Convers. 33 (2), 886–888. doi:10.1109/tec.2018.2799482

CrossRef Full Text | Google Scholar

Zhu, H., and Liu, H. J. (2016). Fast Local Voltage Control under Limited Reactive Power: Optimality and Stability Analysis. IEEE Trans. Power Syst. 31 (5), 3794–3803. doi:10.1109/tpwrs.2015.2504419

CrossRef Full Text | Google Scholar