A Detailed Review Investigating the Mathematical Modeling of Solar Stills

In recent years providing potable water for humans has become a major problem, especially in rural and remote regions. In the last few decades, methods of providing potable water using solar radiation have proved that there are methods without negative impacts. Solar is a solution and attractive alternative to still non-potable water without adverse consequences on ecosystems. Researchers have presented the results of their investigations in journals, using experimental, numerical, and analytical forms through the study of solar still performance in native climatic conditions. This paper undertakes an extensive review of recent modeling processes in solar stills and the thermal models proposed and derived for different types of solar stills and the modifications recommended to enhance efficiency and performance. During the selection of appropriate geometry and belonging components, this evaluation demonstrates that numerous designs and characteristics are useful in terms of productivity and efficiency. According to the reviewed results, the definition of concentration ratio is a fundamental concept for evaluating the evaporative heat transfer coefficient in relation to the convective heat transfer coefficient. Employing phase change materials, the results reveal that a large mass of PCM produces less solar still productivity, whereas increasing the PCM to water mass ratio from 10 to 100 reduces productivity by up to 30%. Using a parabolic concentrator, results show that productivity can be increased by 56 and 38.5% in the winter and summer, respectively.

Introduction

Water is the most significant and essential matter for advancing the lives of humans. It is a valuable natural endowment and a significant renewable supply with inherent benefits for human communities. Today, access to potable, clean, and healthful water is the most essential requirement for people in many countries. In some situations, extraordinarily pure water is needed, such as in laboratories, hospitals, and the chemical and medical industries, etc. Contamination it transforms potable water into polluted water with potentially dangerous consequences for humans and our planet, as it could destroy people and other creatures. In the villages of many countries, people have begun to use underground water during droughts since freshwater resources have dwindled or ended. The groundwater supply in developing countries is being reduced at a more accelerated rate compared with developed countries. One of the human and significant reasons for contaminating underground water is applying extreme amounts of chemical fertilizers and pesticides in agriculture. To reuse contaminated and dirty water or desalinate saline and seawater, scientists and researchers are exploring innovative methods and technologies. They have developed methods and technologies to produce potable and pure water from resources that must be ecosystem-friendly with the least cost to nature and humans to not repeatedly pollute the environment. Recent technologies for desalination processes generally utilize high energy to provide potable water from seawater by separating impurity and solid particles from seawater. These technologies operate based on state change or filtering with membrane processes such as vapor compression, multiple effect distillation, multi-stage flash distillation, reverse osmosis, and electro-dialysis to treat saline water. These technologies are often not efficient and cost-effective due to the complexity of environmental pollution, the need for highly skilled services, and maintenance.

Employing solar radiation to supply freshwater for human utilization and industry from brackish water as an ecosystem-friendly energy source is a hopeful and intelligent choice instead of fossil fuels. Compared with other desalination processes, it has the advantages of free-cost resources and low-cost maintenance and service. Numerous styles and types of designs, fabrication substances, geometries, and configurations are used in solar stills all over the world by researchers. For rural, remote, and desert regions, the most efficient and suitable solar still is a unit that is small, uncomplicated, and self-governing. These units can help rural and remote communities to provide pure and healthy water at remarkably lower costs. Compared with other solar desalination units and systems, solar is more simplistic, portable, convenient development, scalable, easy to build that can produces distilled water for human consumption. The only problem with solar still technology is the daily productivity requirements of covering human demands, although researchers are working on it. In this regard, various solar still arrangements have been designed and constructed in recent years. Their performance, in the form of experimental and theoretical methods of improving and modifying them have been explored in a number of published articles. However, to change, modify, or redesign the experimental setup and enhance performance or study the influence parameters, experimental investigations require higher costs and time compared with theoretical studies; hence, theoretical investigations have general flexibility to examine changes. Theoretical research can analyze the significant parameters and details of solar stills, more quickly and simply to find the best performance and efficiency.

Thermal modeling is one of the most cost-effective and established theoretical methods used to assess the performance of a thermal system. In a solar still, the energy balance of the employed ingredients is utilized for thermal modeling. Thermal modeling precisely exhibits the performance of the solar still under real climatic conditions. Based on this, different thermal models have been proposed and implemented for solar still research. However, due to operational difficulties and less productivity than the prognosticated amount, the proposed models are not fit for real situations. Furthermore, during the study and design of the solar still, a distinct platform is not utilized. Hence, to recognize and propose this technology to market for use in remote regions, a basic and comprehensive study needs to consider different theories, modeling, and designs of solar stills. Usually, researchers try to investigate the meaningful topic, detail, and parameters from their point of view. There is a serious lack of reviews collecting all of points of view, bringing together effective details and information about appropriate configurations and conditions for each issue. This comparison would provide guidance and suggestions to others for improvement. Thereby, this work summarizes significant and effective theoretical papers, examining the methodologies, approaches to solving problems, and substantial improvements in theoretical studies on solar stills. It accurately analyses various thermal models and theoretical studies to present a detailed review of solar stills. The meaningful parameters and corrections on the technology of solar stills regarding thermal modeling development are analyzed precisely, and new outlines are suggested for subsequent investigations. As an introduction, the next section explores solar still systems and the basic rules used to produce potable water from a contaminated source.

The goal of this review is to provide a novel, significant, and original way to mathematically describe a solar still. This study shows genuine breakthroughs and advancements in solar stills in a theoretical form. It also offers remarkable, advanced modeling of a solar still with accurate relationships.

Solar Still System

Renewable energy is now widely advocated and popular, with countless research (Alayi et al., 2021a; Assad et al., 2021; Assad and Rosen, 2021; Alayi et al., 2021b; Alayi et al., 2021c; Pishkariahmadabad et al., 2021; Sadeghi et al., 2022) devoted to the subject. This research is mostly concerned with the application of energy and exergy analysis (Chen et al., 2021; Alayi et al., 2021d; Mohtaram et al., 2021). Solar stills, which may involve phase change materials (Alhuyi Nazari et al., 2021), are a technology for purifying water using renewable energies. A solar still utilizes the Sun’s radiation rather than other sources of energy, such as fossil fuels, to convert brackish water to potable water. Solar still systems can provide potable water for rural communities where no other sources are accessible and are ecosystem-friendly.

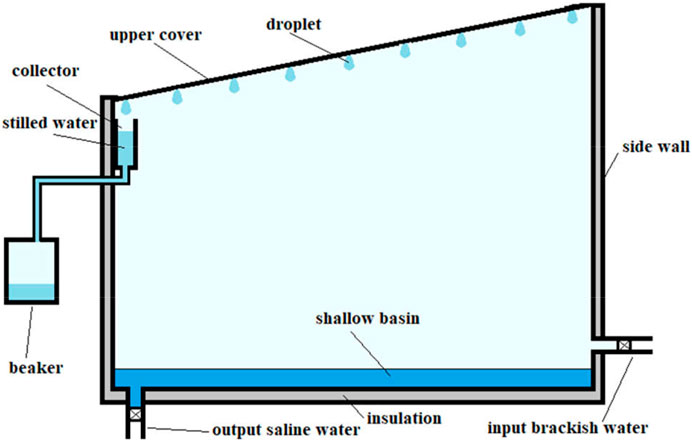
A solar still is a closed enclosure in which brackish water enters and potable water is created. In the solar stills, there is a shallow basin to hold brackish water, in which the brackish water temperature rises and evaporates eventually by the Sun’s radiation. Commonly, the basin interior is painted a black color to absorb the maximum amount of solar radiation. The structure of a solar still is usually constructed with substances such as masonry bricks, concrete, aluminum, galvanized iron, etc. The upper cover of solar stills is commonly made up of materials with a good ability to transmit the Sun radiation such as glass or plastic, and additionally, it is a place to condense water vapor and flow droplets over its surface. One of the essential aspects of the solar still is insulation, which must be perfectly executed to reduce energy loss from the solar still structure such as four walls and a shallow basin. The materials used extensively for insulation can be sawdust, rock wool, polyurethane foam, and glass wool.

The simplest type of solar still is a single basin single slope which can be constructed with effortlessly accessible substance and at the least cost. The single basin single slope solar still works based on the natural hydrological cycle of evaporation and condensation water. Water evaporation takes place in the basin, which contains brackish water, and the condensation process occurs on the upper cover of the solar still, which is cooler than water vapor. Energy, in the form of the Sun’s radiation, enters the solar still, which increases the temperature of the brackish water in the basin. Due to this increase in brackish water temperature, the water evaporates, and vapor leaves the basin. The freed water vapor from the brackish water surface moves toward the upper cover of solar still because its density is less than air and its temperature is higher than air. Air vapor flows from the brackish water surface in the basin to the upper cover of solar still. When it encounters the upper cover, water vapor condenses because of the different temperatures between them, and eventually, droplets are formed. Finally, the droplets move gradually down because of the slope of the upper cover and are collected in a beaker as pure and potable water. The solar still structure is placed in such a way toward sunlight to achieve the highest energy for the solar radiation. A simple solar still is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic of a simple solar still.

Solar stills are categorized into two main groups: active solar stills and passive solar stills. When a solar still works without any external devices or components, it is called a passive solar still. In the active solar still, it is possible to use other equipment to increase productivity and performance, such as flat plate collectors, photovoltaic systems, and sun-tracking systems, etc.

Energy Cascade for Solar Still

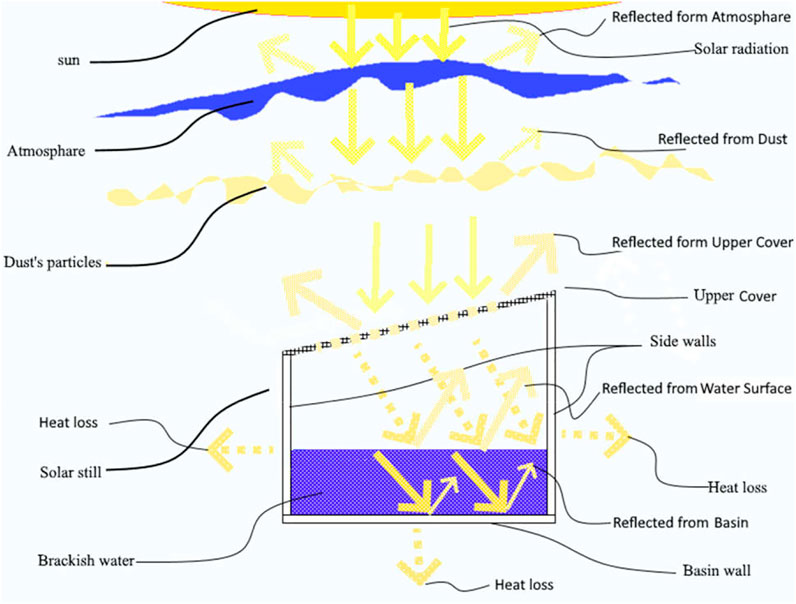
To enhance understanding and awareness it is necessary to track and take into account the energy from the Sun to the Earth sequentially into the solar still. This enables us to calculate and count the amount of energy. Furthermore, other details may need to be accurately considered and their influence on the main objectives analyzed.

The Sun’s radiation or solar energy is the source of energy input to the solar still. Before entering the Earth’s surface, some of this energy is taken and reflected in the Earth’s atmosphere and dust particles in the air, respectively. Therefore, the amount of energy that arrives on the Earth’s surface is diminished. The rest of the Sun’s radiation reaches the solar still’s upper cover. The upper cover must be essentially transparent to pass the Sun’s energy into the solar still. However, it reflects and absorbs a limited quantity of the given energy. In the end, the remaining energy reaches the brackish water and the lower side, which is painted black. A small quantity of the solar radiation reflects from the brackish water surface, and most of the solar radiation warms the brackish water, and the lower side absorbs the remaining energy. The warmed brackish water begins to evaporate slightly, and it needs energy to change the phase from liquid to gas, which is known as latent energy. During the change phase, the water vapor goes up and makes contact with the upper cover. Over the upper cover, other latent energy from the water vapor goes to the atmosphere, and another phase change happens. The Sun radiation that enters the solar still causes the four side walls and lower side of the basin to warm, and an amount of energy goes to the atmosphere again as energy loss. Figure 2 demonstrates the energy cascade of a solar still.

FIGURE 2

FIGURE 2. Schematic representation of energy cascade for conventional solar still.

Solar Still Heat Transfer

The heat transfer is divided into two main groups: steady and transient, although frequently, the heat transfer is transient in nature. In the steady-state, the heat transfer does not change with time. In contrast, it changes with time and is time-dependent in the transient state. Working with the steady-state heat transfer is easier than with transient because of some complexities regarding time’s derivative. Therefore, taking some assumptions, the transient heat transfer could be presumed to be a steady-state.

The heat transfer in a solar still can be divided into two categories: inside the solar still and outside the solar still. The heat transfer inside the solar still regards the conversion of solar energy to the rising temperature of the brackish water, solar still walls, and the change phase. However, the heat transfer outside of the solar still is from the energy losses from the walls and cooling outside the upper cover.

Inside the solar still, the significant part of the heat transfer is convective heat transfer between brackish water and the inner side of the upper cover. It follows Newton’s law of cooling, which depends on the convective heat transfer coefficient, brackish water temperature, an area exposed to heat transfer, and the inner side of the upper cover that can be written as (Sahota and Tiwari, 2017):

$q_{conv.}=h_{c}A\left(T_{bw}-T_{upi}\right)(1)$

The heat transfer coefficient is ordinarily accompanied by the Nusselt number, which is characterized by the type of flow. It follows from Eq. 2 for the free convention type (Sahota and Tiwari, 2017):

$Nu= C {\left(GrPr\right)}^n K^{\prime }(2)$

Where C and n are utilized as the constants that depend on the body’s geometry and can be achieved by correlation of empirical data. In the above correlation, the factor of $K^{\text{'}}$ is about the problem and implies entire physical behavior. where Grashof number (Gr), Nusselt number (Nu), and Prandtl number (Pr) are written as follows (Sahota and Tiwari, 2017):

$Gr=\frac{cg{l}^3{\rho }^2 \mathrm{\Delta }T}{\mu } (3)$

$Nu=\frac{h_{c}l}{k}(4)$

$Pr=\frac{\mu C_p}{k}(5)$

The internal convection heat transfer coefficient from the free surface of the fluid to the condensing cover surface is also calculated using Dunkle’s relation [86]:

$h_c=0.844{\left[\left(T_{bw}-T_{uc}\right)+\frac{\left(P_{bw}-P_{uci}\right)\left(T_{bw}\right)}{268\times {10}^3-P_{bw}}\right]}^{\frac{1}{3}} (6)$

The following expressions are used to determine the saturation vapor pressures at water surface temperature and the inner surface temperature of the upper cover (Sahota and Tiwari, 2017):

$P\left(T\right)=\exp \left[25.317-\left(\frac{5144}{T}\right)\right] (7)$

However, Dunkle’s relation has some restrictions, including 1) it is reasonable for the ordinary working temperature to be 50°C, with 17°C identical temperature difference. 2) The mean distance between condensing and evaporating surfaces has no bearing. 3) It is solely acceptable for there to be upward heat exchange inside a horizontal sealed air space or parallel condensation and evaporation surfaces.

The heat transfer from inside the solar still to the ambient succeeds with the conduction method through the sides (walls). In the steady-state heat condition through a plane wall, Fourier’s law of heat is utilized in the following form (Bergman et al., 2011):

$q_{cond.}=-kA\frac{\mathrm{\Delta }T}{L} (8)$

Where K is the heat conductivity coefficient depending on materials, A is an area normal to heat transfer direction, L is the wall thickness, and $\Delta T$ is the temperature difference between two surfaces of the wall.

Another heat transfer mechanism in a solar still is the radiative heat transfer. Generally, this mechanism is between two bodies with different surface temperatures, in which heat is transferred with electromagnetic waves, and no need for a medium at all. An incident of radiative energy on a body is divided into three parts: a fraction of it is absorbed, another fraction is reflected, and the others are transmitted through the body. It can be shown with the following relation (Sahota and Tiwari, 2017):

$I_{total}=I_a+I_r+I_t(9)$

$\epsilon +\beta +\alpha =1(10)$

The heat transfer between the sky and a body is conducted according to the Stefan–Boltzmann law as follows (Bergman et al., 2011):

$q_{rad.}=\mathit{ϵ}\sigma A\left(T_b^4-T_{sky}^4\right)(11)$

Where $T_{sky}$ is the sky temperature, with a few relations introduced for it as follows (Sahota and Tiwari, 2017):

$T_{sky}=0.0552T_a^{1.5} (12)$

$T_{sky}=T_a-6(13)$

$T_{sky}=T_a-12(14)$

The radiation heat transfer exhibits similar to the style of convection heat transfer relationship (Bergman et al., 2011):

$q_{rad.}=h_{r}A\left(T_b-T_{sky}\right)(15)$

Where $h_r$ is defined as the radiative heat transfer coefficient with the following parameters (Bergman et al., 2011):

$h_r=\mathit{ϵ}\sigma \left(T_b+T_{sky}\right)\left(T_b^2+T_{sky}^2\right)(16)$

Finally, evaporation is the last method of consuming energy in a solar still. Changing the phase from liquid to vapor is called evaporation. Evaporation heat transfer is between liquid bulk and the inner surface of the upper cover.

The evaporative heat transfer coefficient between brackish water and the inner surface of the upper cover can be defined with Eq. 17 or proposed by Bowen (Bowen, 1926) and Dunkle (Dunkle, 1961) with Eq. 18 which has been investigated that the value $16.273\times {10}^{-3}$ is the most depiction of the evaporative phenomena and considering the terms of $P_{bw}$ and $P_{uci}$ (Sahota and Tiwari, 2017):

$h_{ew}=0.013h_{cw}(17)$

$h_{ew}=16.273\times {10}^{-3}\times h_{bw-uci}\left[\frac{P_{bw}-P_{uci}}{T_{bw}-T_{uci}}\right](18)$

The evaporative heat transfer rate between water bulk and upper cover inner surface is given by (Sahota and Tiwari, 2017):

$q_{e,bw-uci}=h_{ew}\left(T_{bw}-T_{uci}\right)(19)$

The upper cover temperature rises more than the atmosphere temperature due to absorbing a fraction of solar radiation and water vapor inside the solar still. Therefore, two heat transfer mechanisms, including convective and radiation, are established between the upper cover surface and the atmosphere. Their relations are the same as driven and presented mentioned relations for inside the solar still with the exception that the convective heat transfer coefficient between the upper cover outer surface and the atmosphere is related to wind speed. McAdams (Hawkins, 1954) presented an equation that varies with wind speed to 5 m/s by the following relation (Sahota and Tiwari, 2017):

$h_c=5.7+3.8V,0<V<5\text{m}/\text{s}(20)$

Where $V$ is the wind speed. Considering the effect of free convection and radiation, Watmuff et al. (Watmuff et al., 1977) modified that relation, which varies with wind speed to 7 m/s as follows (Sahota and Tiwari, 2017):

$h_c=2.8+3V,0<V<7\text{m}/\text{s}(21)$

The concept of electrical resistance can be useful in the diffusion of heat, which is an accepted analogy in heat transfer science and modeling. Thermal resistance is defined as a driving potential to the corresponding transfer rate ratio, which is temperature difference and heat transfer rate, respectively. It is possible to assume a thermal circuit from basin water inside the solar still to the atmosphere using the overall heat transfer coefficient, which is defined with an expression analogous to Newton’s law of cooling as follows:

$U_{o,uc}=\frac{1}{\frac{1}{h_{c, bw-uc}}+\frac{l_{uc}}{K_{uc}}+\frac{1}{h_{r,uc-a}+h_{c,uc-a}}}(22)$

The above relation is the heat transfer coefficient from the upper cover of solar still that can be called overall heat loss from water mass to the atmosphere from the upper cover.

Heat loss from water mass occurs through the basin to the atmosphere by way of the basin liner and insulation with the mechanism of convection, conduction, convection, and radiation, respectively. It is useful to employ the definition of the overall heat transfer coefficient for heat loss from the basin to the atmosphere in case of being mounted on the stand as follows:

$U_{o,b}=\frac{1}{\frac{1}{h_{c,bw-b}}+\frac{l_{in}}{K_{in}}+\frac{1}{h_{r,b-a}+h_{c,b-a}}}(23)$

Heat loss from side walls to the atmosphere is defined with a fraction of the wet area as follows (Sahota and Tiwari, 2017):

$U_{o,sw}=\left(\frac{A_{sw}}{A_b}\right)U_{o,b}(24)$

Identical relations between productivity (distilled water) and efficiency have been used by researchers. The productivity of a solar still is defined as the water mass obtained in an hour as follows (Sahota and Tiwari, 2017):

$m_w=\frac{h_{c,bw-up}\left(T_{bw}-T_{uci}\right)}{h_l}\times 3600(25)$

Where $h_l$ is the latent heat of vaporization. The daily productivity can be computed as follows (Sahota and Tiwari, 2017):

$M_w={\displaystyle \sum _{i=1}^{24}{m}_{w_i}}(26)$

The thermal efficiency of a solar still may be expressed as the ratio of the quantity of thermal energy utilized to take a determined quantity of distilled water to the incident solar energy in a provided time interval. Therefore, the definition of instantaneous efficiency can be represented as follows (Sahota and Tiwari, 2017):

${\eta }_i=\frac{m_w{h}_l}{I\left(t\right)A_b}={\left(\alpha \tau \right)}_{bw}-\frac{U_t\left(T_{bw}-T_a\right)}{I\left(t\right)}(27)$

Where $U_t$ is the overall heat-transfer coefficient from the brackish water to the atmosphere through the top, bottom, and side walls of a solar still. Furthermore, the overall thermal efficiency for passive and active solar stills can be expressed as follows (Sahota and Tiwari, 2017):

${\eta }_{passive}=\frac{{\displaystyle \int m_w{h}_{l}dt}}{A_b{\displaystyle \int I\left(t\right)dt}}(28)$

${\eta }_{active}=\frac{{\displaystyle \int m_w{h}_{l}dt}}{A_b{\displaystyle \int I\left(t\right)dt}+A_c{\displaystyle \int I_c\left(t\right)dt}}(29)$

The latent heat of vaporization $\left(h_l\right)$ depends on the temperature, which is expressed as follows (Toyama and Kagakuv, 1972; Fernández and Chargoy, 1990):

$h_l=3.1615\times {10}^6\left[1-\left(7.616\times {10}^{-4}\right)T\right]T>343 K(30)$

$h_l=2.4935\times {10}^6\left[1-\left(9.477\times {10}^{-4}\right)T+\left(1.313\times {10}^{-7}\right)T^2-\left(4.497\times {10}^{-9}\right)T^3\right]T<343 K(31)$

Basic Methodology Analysis of Solar Still Components

In this section, the simplest design of solar stills, namely the single basin single slope, is considered in comparison to other solar still systems to create thermal concepts and drive relevant equations. This work provides a thorough view of thermal modeling, as well as quick recognition of numerous theoretical solar still modeling and basic solar still relationships. The thermal model is obtained using the energy balance equation for the single basin single slope solar still components, including the basin, upper cover, and brackish water. To make working with equations easier, the energy balance for each component is written based on the average temperature of that component. To summarize, the area of each solar still component is equaled and included in the other units of that component. Furthermore, the following suitable assumptions are taken into account for the most exact modeling:

• All processes in the solar still are considered to be in a quasi-steady state.

• The brackish water layers in the basin have no temperature gradient.

• The brackish water’s evaporative loss, heat capacity, and absorption of the upper cover and insulation materials are so low that they can be overlooked.

• The solar still is impervious to leakage of vapor and brackish water mass.

The following is how the energy balance is applied to the main components (Tiwari et al., 2007; Sampathkumar et al., 2010; Elango et al., 2015; Sahota and Tiwari, 2017).

Basin Liner

The steady-state form of energy balance can be used in the simplest form for the component of the basin liner. The summation of the given rate of energy to brackish water through convection and the delivered rate of energy to the atmosphere through conduction and convection mechanisms equals the absorption rate of energy from solar radiation. It can be written as follows, in the mathematical form (Sahota and Tiwari, 2017):

$E_{b-bw}+E_{b-a}={\alpha }_b^{\prime }I{\left(t\right)}_s(32)$

By writing equivalent relations, it becomes (Sahota and Tiwari, 2017):

$h_{b-bw}\left(T_b-T_{bw}\right)+h_{b-a}\left(T_b-T_a\right)={\alpha }_b^{\prime }I{\left(t\right)}_s(33)$

Where (Sahota and Tiwari, 2017),

${\alpha }_b^{\prime }={\alpha }_b\left(1-{\alpha }_{uc}\right)\left(1-{\beta }_{uc}\right)\left(1-{\beta }_{bw}\right)\left(1-{\alpha }_{bw}\right)(34)$

Brackish Water

The energy balance for brackish water can be written similarly to the basin liner. The sum of the absorbed rate of energy from solar radiation, the received rate of the energy from the basin liner through convection, and the received rate of energy from external devices equals the stored rate of energy and the loss rate of the energy to the upper cover inner surface through convection, evaporation, and radiation. It can be expressed mathematically as follows (Sahota and Tiwari, 2017):

${\alpha }_{bw}^{\prime }I{\left(t\right)}_s+E_b+E_{exd}=m_{bw}{C}_{bw}\frac{d{T}_{bw}}{dt}+E_c+E_e+E_r (35)$

By writing equivalent relations, it becomes (Sahota and Tiwari, 2017):

${\alpha }_{bw}^{\prime }I{\left(t\right)}_s+h_{b-bw}\left(T_b-T_{bw}\right)+E_{exd}=m_{bw}{C}_{bw}\frac{d{T}_{bw}}{dt}+h_{t_{bw-uci}}\left(T_{bw}-T_{uci}\right) (36)$

Where (Sahota and Tiwari, 2017),

${\alpha }_{bw}^{\prime }={\alpha }_{bw}^{\prime }\left(1-{\alpha }_{uc}^{\prime }\right)\left(1-{\beta }_{uc}\right)\left(1-{\beta }_{bw}\right)(37)$

The term $E_{exd}$ can only be used with active solar stills.

Upper Cover Inner Surface

The energy balance for the inner surface of the upper cover is similar to that of the basin liner. The sum of the absorbed rate of solar radiation and the received rate of energy of brackish water through convection, evaporation, and radiation equals the rate of energy lost to the upper cover outer surface through conduction (Sahota and Tiwari, 2017).

${\alpha }_{uc}^{\prime }I{\left(t\right)}_s+E_{conv.}+E_{evap.}+E_{rad.}=E_{cond.} (38)$

Which, in analogous form, can be written as follows (Sahota and Tiwari, 2017):

${\alpha }_{uc}^{\prime }I{\left(t\right)}_s+h_{t_{uci}}\left(T_{bw}-T_{uci}\right)=\frac{K_{uc}}{L_{uc}}\left(T_{uci}-T_{uco}\right)(39)$

Where (Sahota and Tiwari, 2017),

${\alpha }_{uc}^{\prime }={\alpha }_{uc}\left(1-{\beta }_{uc}\right)(40)$

Upper Cover Outer Surface

Similarly, the energy balance for the upper cover’s outer surface is achieved. The received energy from the upper cover inner surface through conduction equals the loss energy rate to the atmosphere through convection and radiation (Sahota and Tiwari, 2017).

$E_{cond.}=E_{conv.}+E_{rad.} (41)$

By writing them down, it becomes easier to find related relations.

$\frac{K_{uc}}{L_{uc}}\left(T_{uci}-T_{uco}\right) =h_{t_{uco}}\left(T_{uco}+T_a\right)(42)$

Components’ Temperature

The temperature of each component, including the basin liner, brackish water, upper cover inner surface, and upper cover outer surface, may be determined by rearranging the derived prior expressions as shown below.

The temperature of the upper cover outer surface may be computed using the following equation:

$T_{uco}=\frac{\left(\frac{K_{uc}}{L_{uc}}\right)T_{uci}+h_{t_{uco}}{T}_a}{\left(\frac{K_{uc}}{L_{uc}}\right)+h_{t_{uco}}} (43)$

The temperature of the upper cover inner surface may be determined using the preceding relation:

$T_{uci}=\frac{{\alpha }_{uc}^{\prime }I{\left(t\right)}_s+h_{t_{uci}}{T}_{bw}+\frac{\frac{K_{uc}}{L_{uc}}{h}_{t_{uco}}}{\frac{K_{uc}}{L_{uc}}+h_{t_{uco}}}{T}_a}{\left(\frac{K_{uc}}{L_{uc}}\right)+h_{t_{uci}}-\frac{{\left(\frac{K_{uc}}{L_{uc}}\right)}^2}{ \frac{K_{uc}}{L_{uc}}+h_{t_{uco}}}} (44)$

The following equation may be used to compute the temperature of the basin liner (Sahota and Tiwari, 2017):

$T_b=\frac{{\alpha }_b^{\prime }I{\left(t\right)}_s+h_{bw} T_{bw}+h_b{T}_a}{h_{bw}+h_b}(45)$

Finally, based on the needed temperature from other components such as the basin liner, upper cover inner surface, and upper cover outer surface, the temperature of brackish water may be estimated. To simplify Eq. 36, the relevant relations of the basin liner and top cover inner surface temperatures are used (Sahota and Tiwari, 2017):

${\alpha }_{eff}I{\left(t\right)}_s+U_a{T}_a=m_{bw}{C}_{bw}\frac{d{T}_{bw}}{dt}+U_{bw}{T}_{bw} (46)$

Where (Sahota and Tiwari, 2017),

${\alpha }_{eff}={\alpha }_{bw}^{\prime }+\frac{h_{b-bw }}{h_{bw}+h_b}{\alpha }_b^{\prime }+\frac{h_{t_{bw-uci}}}{\frac{k_{uc}}{L_{uc}}+h_{t_{uci}}-\frac{{\left(\frac{k_{uc}}{L_{uc}}\right)}^2}{\frac{k_{uc}}{L_{uc}}+h_{t_{uco}}}}{\alpha }_{uci}^{\prime }(47)$

And

$U_a=\frac{h_{b-bw}{h}_b}{h_{bw}+h_b}+\frac{h_{t_{bw-uci}}{h}_{t_{uco}}\left(\frac{k_{uc}}{L_{uc}}\right)}{\frac{k_{uc}}{L_{uc}}+h_{t_{uci}}-\frac{{\left(\frac{k_{uc}}{L_{uc}}\right)}^2}{\frac{k_{uc}}{L_{uc}}+h_{t_{uco}}}} (48)$

$U_{bw}=h_{b-bw}\left(1+\frac{h_b}{h_{bw}+h_b}\right)+h_{t_{bw-uci}}\left(1-\frac{h_{t_{uci}}}{\frac{k_{uc}}{L_{uc}}+h_{t_{uci}}-\frac{{\left(\frac{k_{uc}}{L_{uc}}\right)}^2}{\frac{k_{uc}}{L_{uc}}+h_{t_{uco}}}}\right) (49)$

Equation 46 can be rearranged in the following way (Sahota and Tiwari, 2017):

$\frac{d{T}_{bw}}{dt}+C{T}_{bw}=f\left(t\right)(\mathrm{46a})$

Where (Sahota and Tiwari, 2017),

$C=\frac{U_{bw}}{m_{bw}{C}_{bw}}(\mathrm{47a})$

$f\left(t\right)=\frac{{\alpha }_{eff}I{\left(t\right)}_s+U_a{T}_a}{m_{bw}{C}_{bw}}(\mathrm{48a})$

To find the analytical solution, a few assumptions have been made, including the values of “C” and “f(t)” being constant and a short time period during the time period analyzed. The solution to the preceding first-order differential equation is obtained by applying the initial condition, $T_{bw}\left(0\right)=T_0$ (Sahota and Tiwari, 2017),

$T_{bw}\left(t\right)=\frac{f\left(t\right)}{a}\left[1-\exp \left(-at\right)\right]+T_0\text{exp}\left(-at\right)(\mathrm{49a})$

Mathematical Models of Solar Still

Ali et al. (2015) report theoretical and practical work on a solar still with a pin-fin absorber plate. The distillation of brackish water by the solar still with a regular absorber plate and a pin-fin absorber plate was examined. The energy balance was used for the main parts of the active solar still as follows (Ali et al., 2015):

${\alpha }_{uc}I+Q_{c,bw-uc}+Q_{e,bw-uc}+Q_{r,bw-uc}-Q_{c,uc-a}+Q_{r,uc-a}={\left(m{C}_p\right)}_{uc}\frac{d{T}_{uc}}{dt}(50)$

${\alpha }_{bw}{\text{ε}}_{\text{uc}}I+Q_{c,b-bw}-Q_{c,bw-uc}-Q_{e,bw-uc}-Q_{r,bw-uc}-Q_{fw}-Q_{loss,sw-a}={\left(m{C}_p\right)}_{bw}\frac{d{T}_{bw}}{dt}(51)$

${\alpha }_b{\text{ε}}_{\text{uc}}\left(1-{\alpha }_{bw}-{\beta }_{bw}\right)I+Q_{c,b-bw}-Q_{loss,b-a}={\left(m{C}_p\right)}_b\frac{d{T}_b}{dt}(52)$

They used the convective and evaporative heat transfer coefficients proposed by Dunkle (Eqs 6, 18). However, the heat loss coefficient was calculated using the following equations (Anderson, 1983) for wind speeds (V) greater than 5 m/s (Ali et al., 2015):

$h_{c,uc-a}=6.15V^{0.8}(53)$

Furthermore, the convective heat transfer coefficient between the basin liner and brackish water was considered to be 120 and 150 $W/m^{2}K$ for the regular and modified absorber plates, respectively. They also utilized Eq. 12 to estimate the temperature of the sky. There is reasonable concordance between experimental and theoretical results. Experimental and theoretical investigations demonstrate that a still with pin-fin absorber plate outperforms a regular one. However, the difference in performance between regular and modified solar still is marginal. This is owing to the little variation in their surface areas available for exchange. Compared to a regular solar still, the daily productivity of the modified example with a pin-fin absorber plate is enhanced by 12%.

Alaudeen et al. (2015) studied theoretically and experimentally a single-slope solar still with a glass basin including two compartments, the upper and lower compartments as evaporating and heating zones, respectively. The lower compartment consists of glass strips for heat storage materials to increase performance. In addition, aluminum cubes and sponges were designed to float in the upper compartment. Their results showed that the unit with the corrugated sheet has higher efficiency. They modeled the unit by using simulation software. In the theoretical modeling section, the transient form of energy balance was used for the basin as follows (Alaudeen et al., 2015):

$I{\alpha }_b-Q_{c,b-bw}-Q_{loss}=m_b{C}_{p,b}\frac{d{T}_b}{dt}(54)$

The convective heat transfer coefficient between the basin and brackish water and the heat loss from the basin to the atmosphere was assumed to be 135 and 14 $W/m^{2}K$, respectively. Equation 6 (Dunkle’s relation) was used as a convective heat transfer between brackish water and the upper cover, and Eq. 18 as an evaporative heat transfer from the basin to the upper cover. The following correlation gives the latent heat of evaporation for water at a specified basin water temperature (°C) (Alaudeen et al., 2015).

$h_{fg}=1000\left(2503.3-2.398T\right)(55)$

In addition, at a specific temperature, the partial pressure of water vapor in the air was determined as follows (Alaudeen et al., 2015):

$p=7235-431.43+10.76T^2(56)$

The air specific heat capacity between the upper cover and the basin was estimated using the following correlation in terms of average temperature (Tav in °C) (Alaudeen et al., 2015)

$C_p=999.2+0.14339T_{av}+0.0001101T_{av}^2-6.7581e\left(-8\right)T_{av}^3(57)$

The immediate water output was offered by (Alaudeen et al., 2015),

$m_e=\frac{h_{e,bw-uc}\left(T_{bw}-T_{uc}\right)}{h_{fg}}(58)$

The time interval was initially set to 5 s, and the temperature of the water, glass, and plate is considered to be the atmosphere. The parameter change for the subsequent time step is rewritten as follows (Alaudeen et al., 2015):

$T_{uc}=T_{uc}+d{T}_{uc}(59)$

$T_{bw}=T_{bw}+d{T}_{bw}(60)$

$T_b=T_b+d{T}_b(61)$

Their results showed that corrugated sheets yielded the highest distilled water at 2.64 kg/m2, which is almost 43% higher than the conventional unit. The cost of producing each liter of drinkable water, including mineral additives, was about $0.2. Furthermore, the cost of material and manufacturing for a 1 m² galvanized iron basin was about $83, but the cost of utilizing a glass basin was about $25.

Rajaseenivasan et al. (2016) investigated theoretically and experimentally a glass basin, which was divided into two sections, including preheater (lower) and evaporator (upper) sections by a glass plate. They applied energy storing materials in five rectangular hollow glasses as fins in the preheater section. The effects of preheater depth and energy storage materials on solar still performance were investigated. Their results showed that increasing water depth causes productivity to decrease and enhances nocturnal productivity. Charcoal as an energy storage material augments the total distillate output by up to 3.61 kg in a day. In the preheater and middle glass, they employed the energy balance as follows (Rajaseenivasan et al., 2016):

$I{A}_{wp,eff}{\alpha }_{wp}{\epsilon }_{uc}{\epsilon }_{we}{\epsilon }_{mg}+Q_{c,b-wp}-Q_{c,wp-mg}-Q_{f,wp}=m_{wp}{C}_{wp}\frac{d{T}_{wp}}{dt}(62)$

Where $A_{wp,eff}=A_w-A_{sh}$ and $A_{sh}=n_{fin}[H_{fin}{l}_{sh}\sin \theta +H_{fin}{l}_{sh}\cos \theta -l_{sh}^2\sin \theta \cos \theta$ (Rajaseenivasan et al., 2016)].

$I{A}_{mg}{\alpha }_{mg}{\epsilon }_{uc}{\epsilon }_{we}+Q_{c,wp-mg}-Q_{c,wp-we}=m_{mg}{C}_{mg}\frac{d{T}_{mg}}{dt}(63)$

$I{A}_{we}{\alpha }_{we}{\epsilon }_{uc}+Q_{c,mg-we}+Q_{f,we}-Q_{c,we-uc}-Q_{e,we-uc}-Q_{r,we-uc}=m_{we}{C}_{we}\frac{d{T}_{we}}{dt}(64)$

They used Dunkle’s relations for convective and evaporative heat transfer coefficients. The time interval in this study was set to 10 s, and all of the parameters were evaluated on the day of the experiment. For the next step, Eqs 59–61 were employed. They observed that reducing the water depth from 8 to 2 cm increases the system’s daily production from 3.12 to 3.25 kg/day. The highest night distillate is 1.27 kg/m² for the glass basin solar still with charcoal and 0.46 kg/m² for the conventional solar still. The highest output improvement was 26.74, 29.3, and 33.7% in the glass basin solar still utilizing river sand, metal trash, and charcoal, respectively.

Karimi Estahbanati et al. (2016) conducted both experimental and theoretical studies on the issue of using an internal reflector (IR) on the productivity of a single-slope solar still. The effect of all of the solar still’s walls, including those to the north, south, west, and east of the still, on the amount of gotten solar radiation to brine is modeled in their model. They proposed the following energy balances for the main components of solar still (Karimi Estahbanati et al., 2016):

$Q_{sun,uc}+Q_{c,bw-uc}+Q_{e,bw-uc}+Q_{r,bw-uc}-Q_{c,uc-a}+Q_{r,uc-a}={\left(m{C}_p\right)}_{uc}\frac{d{T}_{uc}}{dt}(65)$

$Q_{sun,bw}+Q_{b-bw}-Q_{c,bw-uc}+Q_{e,bw-uc}-Q_{r,bw-uc}={\left(m{C}_p\right)}_{bw}\frac{d{T}_{bw}}{dt}(66)$

$Q_{sun,b}-Q_{b-bw}-Q_{b-a}={\left(m{C}_p\right)}_b\frac{d{T}_b}{dt}(67)$

Based on the amount of shape factors between the wall-brine surface and cover-brine surface, the received diffuse solar radiation reaches brackish water and walls. As a result, the solar energy received by the solar still components can be stated as follows:

Upper cover (Karimi Estahbanati et al., 2016):

$\begin{array}{c}{Q}_{sun,uc}=\left(I_B+I_D\right)A_{uc}{\alpha }_{uc}+I_B\left(S_2{F}_{euc}+S_1{F}_{kuc}\right){\epsilon }_{uc}{\beta }_{dl}{\alpha }_{uc}\\ +\left(I_B\left(A_{uc}-\left(S_1+S_2\right)\right)+I_D{A}_{uc}{F}_{ucbw}\right){\epsilon }_{uc}{\alpha }_{uc}{F}_{bwuc}\\ \left({\beta }_w+{\epsilon }_{uc}^2{\beta }_b\right)+I_D{A}_{uc}{\epsilon }_{uc}{\alpha }_{uc}{\beta }_{tl}\left(F_{uck}{F}_{kuc}+2\times F_{uce}{F}_{euc}+F_{ucf}{F}_{fuc}\right)\end{array}(68)$

Basin liner (Karimi Estahbanati et al., 2016):

$\begin{array}{c}{Q}_{sun,b}=I_B\left(A_{uc}-\left(S_1+S_2\right)\right){\epsilon }_{uc}{\epsilon }_{bw}{\alpha }_b\\ +I_B\left(S_1\left({\beta }_{sl}+{\beta }_{dl}{F}_{ebw}\right){\epsilon }_{uc}{\epsilon }_{bw}{\alpha }_b\right)\\ +S_2\left({\beta }_{sl}+{\beta }_{dl}{F}_{kbw}\right)+I_D{A}_{uc}{\epsilon }_{uc}{\epsilon }_{bw}{\alpha }_b\\ (F_{ucba}+{\rho }_{tl}\left(F_{uck}{F}_{kbw}+2\times F_{uce}{F}_{ebw}+F_{ucf}{F}_{fbw}\right))\end{array}(69)$

East wall (Karimi Estahbanati et al., 2016):

$Q_{sun,e}=I_B{S}_2{\epsilon }_{uc}{\alpha }_e+I_D{A}_{uc}{\epsilon }_{uc}{\alpha }_e\left(F_{uce}+{\beta }_{tl}\left(F_{uct}{F}_{te}+F_{uck}{F}_{ke}+F_{ucf}{F}_{fe}\right)+F_{ucbw}{F}_{bwe}\right)(70)$

Back wall (Karimi Estahbanati et al., 2016):

$Q_{sun,k}=I_B{S}_1{\epsilon }_{uc}{\alpha }_k+I_D{A}_{uc}{\epsilon }_{uc}{\alpha }_k\left(F_{uck}+{\beta }_{tl}\left(2\times F_{uce}{F}_{ek}+F_{ucf}{F}_{fbw}\right)+F_{ucbw}{F}_{bwk}\right)(71)$

West wall (Karimi Estahbanati et al., 2016):

$Q_{sun,t}=I_B{S}_2{\epsilon }_{uc}{\alpha }_t+I_D{A}_{uc}{\epsilon }_{uc}{\alpha }_t\left(F_{uct}+{\beta }_{tl}\left(F_{uce}{F}_{et}+F_{uck}{F}_{kt}+F_{ucf}{F}_{ft}\right)+F_{ucbw}{F}_{bwt}\right)(72)$

Brackish water (Karimi Estahbanati et al., 2016):

$Q_{sun,bw}={\alpha }_{bw}\times \frac{Q_{sun,b}}{{\tau }_{uc}{\alpha }_b}(73)$

Their mathematical approach determines incident irradiance, calculates the productivity of solar stills with IRs installed on various walls, and takes into account the influence of all basin walls. Their model can accurately anticipate the trend of experimental data by comparing theoretical data with current experimental results. Their findings reveal that placing IR on the front, side, and rear walls boosts solar still efficiency by 18, 18, and 22% on all days of the year, respectively. Furthermore, installing IR on all walls increases productivity by 65, 22, and 34% during the winter, summer, and full year, respectively.

Panchal and Thakkar (2016) theoretically and experimentally studied a solar still coupled with evacuated tubes. They used fourteen double-walled hard borosilicate glass tubes inclined at an angle of 45° from the horizontal. They managed to make the outer tubes transparent and coated the inner tubes to absorb solar radiation as much as possible. They wrote the energy balance of brackish water in solar still coupled with evacuated tubes as follows (Panchal and Thakkar, 2016):

${\alpha }_{bw}\left(1-{\alpha }_{uc}\right)I+h_{total,uc-bw}\left(T_{uc}-T_{bw}\right)+Q_u-h_{total}\left(T_{bw}-T_{uci}\right)=m_{bw}{C}_{bw}\frac{d{T}_{bw}}{dt}(\mathrm{74a})$

When the heat acquired by evacuated tubes $\left(Q_u\right)$ was calculated, it was found to be (Panchal and Thakkar, 2016):

$Q_u=F_R\left[{\left(\alpha \epsilon \right)}_{et}{I}_{et}-U_{Let}\frac{A_{ss}}{A_{et}}\left(T_{bw}-T_a\right)\right](\mathrm{74b})$

Where ${\left(\alpha \epsilon \right)}_{et}$ was intended to be 0.87. They discovered that actual and theoretical outcomes of an evacuated tube coupled with solar still were quite comparable in both summer and winter climate conditions. In the solar still, polyurethane foam type (5 cm) was utilized as insulation with better thermal resistance. The evacuated tubes coupled with solar still generated distilled water not only during the day but also at night.

El-Naggar et al. (2016) investigated experimentally and theoretically conventional single-basin solar still with a finned-basin liner. They used appropriate programs to optimize and predict the thermal performance of the systems under consideration. The daily distilled water of conventional and modified units was seen to be 4.235 and 4.802 kg/m²d, respectively, with daily efficiency of 42.36 and 55.37%. Their findings revealed that the convective heat transfer coefficient of the finned one was 3.6 times higher than the conventional one. The findings revealed that there is a reasonable agreement between measured and calculated daily productivity. The fee for 1 L of distilled water was determined to be 0.018 $.

When analyzing the energy balance for the basin, the fin shadow area affects the solar radiation intensity acquired by the still basin. They estimated the shadow area of the fins using the method described by Jaefarzadeh (Jaefarzadeh, 2004). The following equation was used for the shadow area caused by one fin (El-Naggar et al., 2016):

$A_{sh}=H_f{l}_{sh}\left(\sin \phi +\cos \phi \right)-l_{sh}^2\sin \phi \cos \phi (75)$

Where (El-Naggar et al., 2016),

$\phi ={\sin }^{-1}\cos {\theta }_v/\sin {\theta }_i(76)$

For the basin with fin shadow effect, the energy balance equation is as follows (El-Naggar et al., 2016):

${\epsilon }_{uc}{\alpha }_{bw}I{A}_{bw,eff}+h_{cb}\left(T_{p,f}-T_{bw,f}\right)-h_c{A}_{bw}\left(T_{bw,f}-T_{uci,f}\right)={\left(mC\right)}_{bw}\frac{d{T}_{bw}}{dt}(77)$

Where the convective heat transfer coefficient is as (El-Naggar et al., 2016):

$h_{cb}=\left(0.54\frac{K_{bw}}{ds}{\left(Gr.\text{Pr}\right)}^{0.25}\right)A_{p,eff}+\left(0.8\frac{K_{bw}}{d_{bw}}{\left(Gr.\text{Pr}\right)}^{0.25}{\left[1+{\left(1+\frac{1}{p{r}^{0.5}}\right)}^2\right]}^{-0.25}\right)A_f{\eta }_f(78)$

The finned basin liner’s energy balance equation is as follows (El-Naggar et al., 2016):

${\epsilon }_{uc}{\alpha }_{bw}{\alpha }_p{I}_{pf}+h_{cb}\left(T_{p,f}-T_{bw,f}\right)-U_b{A}_b\left(T_{pf}-T_a\right)={\left(mC\right)}_{pf}\frac{d{T}_{pf}}{dt}(79)$

Where the total solar radiation incident on the finned basin liner and the total mass of the basin liner and fins are as (El-Naggar et al., 2016):

$I_{pf}=\left(I_{f,bw}\frac{A_f}{2}\right)+\left(I_{f,e}\frac{A_f}{2}\right)+\left(I_t{A}_{p,eff,sh}\right)(80)$

$m_p={\rho }_p\left(A_p{x}_p+n_{f}l{H}_f{x}_f\right)(81)$

Compared to a conventional unit, the unified fins with the basin produced 11.8% more distilled water and had 23.5% higher daily efficiency.

Tanaka( 2016) combined vertical multiple-effect diffusion solar still and tilted wick still to analyze solar still unit theoretically. He designed vertical multiple-effect diffusion solar still to have a series of vertical and parallel partitions and a double glass cover in contact with saline-soaked wicks with narrow air gaps between the partitions. The moisture-rich layers of air in the tilted wick still and the multiple-effect still were considered to be connected. As a result, water vaporized from the wick of the tilted wick still can gradually move to the humid air layer between the inner glass cover and the first partition of the multiple-effect still. They considered adding heat to the multiple-effect solar still by using the latent heat of condensation on the front surface of the first partition.

The energy balance for the tilted wick section’s wick and the first partition of the multiple-effect section (p1) may be stated as (Tanaka, 2016):

$Q_{dr,w}+Q_{df,w}-Q_{\left(c+m\right)w-ha}-Q_{r,w-gti}-Q_{d,w-a}=Q_{f,w}(82)$

$Q_{dr,p1}+Q_{df,p1}+Q_{\left(c+m\right),ha-p1}-Q_{r,p1-gmi}-Q_{\left(r+d+e\right),p1-p2}=Q_{f,p1}+{\left(m{C}_p\right)}_{p1}\frac{d{T}_{p1}}{dt}(83)$

Except for the first (p1) and last (pn) partitions, the energy balance for ith partition pi may be represented as (Tanaka, 2016):

$Q_{\left(r+d+e\right),p\left(i-1\right)-pi}-Q_{\left(r+d+e\right),pi-p\left(i+1\right)}=Q_{f,pi}+{\left(m{C}_p\right)}_{pi}\frac{d{T}_{pi}}{dt}(84)$

Radiation and convection mechanisms are used to release energy to the environment from the last partition (pn). This may be phrased in the following way (Tanaka, 2016):

$Q_{\left(r+d+e\right),p\left(n-1\right)-pn}-Q_{\left(r+c\right),pn-a}={\left(m{C}_p\right)}_{pn}\frac{d{T}_{pn}}{dt}(85)$

The heat transfer coefficient of forced convection from the outer plates to the ambient air in this study was determined using Eq. 20. The following relations were applied to estimate the convective heat and mass transfer between the humid air layer and the enclosing inner surfaces of both sections and the heat and mass transfer coefficients on the surfaces (Aihara, 1986):

$Nu=0.022R{a}^{2/5}(86)$

$Sh=0.022{\left(Ra.Le\right)}^{2/5}(87)$

$Ra=\frac{g{l}^3\text{Pr}}{{\text{ν}}^2}\left(\frac{T_1}{T_2}-1\right) (88)$

The following is an expression of the heat transfer rate of mass transfer between the partitions (Bird et al., 1966):

$Q_{e,pi-p\left(i+1\right)}=\frac{h_{l}D{P}_{total}}{R{\delta }_{gp}{T}_{mean}}\ln \left(\frac{p_{total}-p_s\left(T_{p\left(i+1\right)}\right)}{p_{total}-p_s\left(T_{pi}\right)} \right)(89)$

The temperature differential between the humid air layer and each condensing surface determines the condensation ratio on the three internal condensing surfaces of the humid air layer. On three typical days including the spring, summer, and winter, and considering 5 mm as the diffusion gap between partitions and using 10 partitions, total daily distillate production was indicated to be approximately 19.2, 16.0, and 15.9 kg/m2d, respectively.

Sivakumar et al. (2016) developed a mathematical model that took into account the influence of the basin’s heat capacity and the glass cover on the performance and exergy destruction of typical solar still. The energy balance for the glass cover and the basin is then outlined below, taking into account their heat capacity (Sivakumar et al., 2016).

$I\left(t\right)\left(1-\beta \right){\text{α}}_{\text{uc}}+\left(h_{c,bw-uc}+h_{e,bw-uc}+h_{r,bw-uc}\right)\left(T_{bw}-T_{uc}\right)-\left(h_{c,uc-a}+h_{r,uc-a}\right)\left(T_{uc}-T_a\right)={\left(mc\right)}_{uc}\frac{d{T}_{uc}}{dt}(90)$

$I\left(t\right)\left(1-\beta \right)\left(1-{\text{α}}_{\text{uc}}\right)\left(1-{\text{α}}_{\text{bw}}\right){\text{α}}_b-h_{c,b-bw}\left(T_b-T_{bw}\right)-\frac{K_{ins}}{L_{ins}}+\frac{K_{wood}}{L_{wood}}+h_{c,wood-a}\left(T_b-T_a\right)={\left(mc\right)}_{uc}\frac{d{T}_{uc}}{dt}(91)$

It was discovered that the cumulative yield when heat capacity is taken into account (2.02 kg/d) is higher than the obtained yield when heat capacity is not taken into account (1.8 kg/d). The increased cumulative production when heat capacity is taken into account may be attributed to the heat storage capacity of the basin, which raises the yield. When heat capacity is factored in, the total yield of solar energy increases by 10.38%.

Sherif et al.( 2016) used an unsaturated porous medium (sand) that was initially saturated by saline water, as well as the use of a focusing reflector to increase the productivity of solar stills. They concentrated on the porous media mathematical model and its solution through a finite volume technique. They utilized the terms absorbed/scattered solar energy and water vapor source/sink. The porous media was added to the double slope solar still (DSSS) system (sand). The porous medium, humid air region, and glass coverings are the three systems that make up the physical model. Each system has its own set of subsystems, such as scattering and absorbing models, evaporation models, capillary models, and crystallization models in the case of porous media. The gas absorption model is part of the humid air region system. As a sub-system, the glass cover system using the absorption model is used. Solar flux and ambient temperature are calculated throughout the day using solar radiation and ambient temperature models, respectively. Solar radiation on the horizontal and inclined surfaces was calculated using Ashrae clear sky model (Elsayed et al., 1994). In this study, the porous medium is thought to be a semitransparent medium for solar energy, which results in diffuse radiation. Internal reflection and scattering are also taken into account. The size of local intensity has been determined experimentally to vary with the variation in intensity at any point (Rababa’h, 2003). Absorption and scattering in sand layers are used to calculate the energy absorbed by every element inside the porous medium. The J-function (Leveret-function) (Kaviany, 2012) was employed in the capillary pressure equation. The energy balance in the porous medium mathematical model was written as follows (Sherif et al., 2016):

$-\frac{\partial }{\partial z}\left(-K_{eff}\frac{\partial T}{\partial z}\right)-\left({\dot{m}}_l^{″}{C}_{pl}+{\dot{m}}_v^{″}{C}_{pv}+{\dot{m}}_a^{″}{C}_{pa}\right)\frac{\partial T}{\partial z}-{\dot{m}}_{evp}^{″}{h}_{fg}-{\dot{m}}_{crs}^{″}{h}_{cr}+q_{solo1}^{″}{\gamma }_{eff}\exp \left(-{\gamma }_{eff}\left(L-z\right)\right)={\left(\rho C_p\right)}_{eff}\frac{\partial T}{\partial t}(92)$

The following is the energy balancing equation for east or west upper cover sides, taking each side orientation into account (Sherif et al., 2016):

$\frac{\partial }{\partial z}\left(-K_{uc}\frac{\partial T_{uc}}{\partial z}\right)+\frac{\partial }{\partial z}\left(q_{solo}^{″}{e}^{-{\gamma }_{uc}\frac{L_1-Z_1}{\cos {\theta }_2}}\right)-\frac{\partial }{\partial z}\left(q_{reflec}^{″}{e}^{-{\gamma }_{uc}{Z}_1}\right)={\left(\rho C_p\right)}_{uc}\frac{\partial T_{uc}}{\partial t}(93)$

The second and third terms in the above equation are the solar radiation absorbed in the upper cover thickness through both sides of the upper cover, and the solar radiation absorbed in the upper cover thickness that is transferred from the humid air region, respectively. The thickness of the sand has been discovered to have a considerable impact on solar still production. When the solar flux was high, the porous medium of a large size produced more distillate, while the porous medium of a small size produced more distillate when the solar flux was low. The solar still productivity improved when a compound parabolic concentrator was added to the porous medium; the increase was 56 and 38.5% in the winter and summer, respectively.

In their evaluation, Al-Sulttani et al. (Al-Sulttani et al., 2017) compared a double-slope solar still hybrid with rubber scrapers (DSSSHS) to a conventional double-slope solar still. The suggested DSSSHS design takes advantage of employing a slight slope in the solar still’s condensing cover, which enables more solar radiation to enter the still. The rubber scrapers are used to overcome the drawbacks of utilizing a small slope. The theoretical values of convective and evaporative heat transfer coefficients, as well as theoretical values of the yields, were determined considering experimental measurements. They calculated convective heat transfer from water to glass cover using the temperature-dependent physical characteristics of humid air provided by (Jain and Tiwari, 2003) as follows:

$K=0.0244\times 0.7673\times {10}^{-4}{T}_v(94)$

$\beta =\frac{1}{T_v}(95)$

${\rho }_v=\frac{353.44}{T_v}(96)$

$\mu =1.718\times {10}^{-5}+4.62\times {10}^{-8}{T}_v(97)$

$C_v=999.2+0.1434T_v+1.101\times {10}^{-4}{T}_v^2-6.7581\times {10}^{-8}{T}_v^3(98)$

The following is the energy balance equation for brackish water that exchanges energy as heat with the basin liner, upper cover, and the atmosphere (Al-Sulttani et al., 2017).

$H_{bw}\left(t\right)+q_{c,b-bw}-q_{cbw}-q_{ebw}-q_{rbw}={\left(m{C}_p\right)}_{bw}\frac{d{T}_{bw}}{dt}(99)$

Where $H_{bw}\left(t\right)$ is the amount of solar energy absorbed by brackish water as a proportion of total solar radiation. The following equations [56] were used to calculate the convective heat transfer coefficient from the basin liner to brackish water:

$h_{c,b-bw}=0.54\times \frac{K_{bw}R{a}_{bw}^{0.25}}{L_{bw}}{10}^4<Ra<{10}^7(100)$

$h_{c,b-bw}=0.15\times \frac{K_{bw}R{a}_{bw}^{0.25}}{L_{bw}}{10}^4<Ra<{10}^7(101)$

They used the following form of the energy balance equation for the basin (Al-Sulttani et al., 2017):

$H_b\left(t\right)-q_{c,b-bw}-q_{b-a}={\left(m{C}_p\right)}_b\frac{\partial T_b}{\partial t}(102)$

Where $H_b\left(t\right)$ is the amount of solar energy absorbed by the basin as a proportion of total solar radiation. Rubber scrapers improved the total internal heat transfer coefficient and productivity in the DSSSHS model. For the situation when the slope of the upper cover is relatively small (approximately 3.0°), the maximum measured value of the total internal heat transfer coefficient for the DSSSHS is 38.754 W/m2 °C, and the daily productivity is 4.24 L/m2d with a productivity improvement of 63%. Rubber scrapers also prevented re-evaporation and the condensate accumulated and left for a longer time period on the inner surface of the upper cover from falling.

Madhlopa (2017) explored different evaporative heat transfer coefficients using view factors from radiative heat exchange. The first model employed the concentration ratio, which is dependent on various thermodynamic factors within solar still (Tsilingiris, 2009). Equations 103, 104 (Madhlopa, 2017) shows convective and evaporative heat transfer coefficients, which are used to compute the concentration ratio in the first model. The concentration ratio, as shown in Eq. 105 (Madhlopa, 2017), is a ratio of the evaporative heat transfer coefficient to the convective heat transfer coefficient. In the first model, the concentration ratio is determined by the temperature-dependent specific heat capacity of air, specific latent heat of vaporization, and partial vaper pressure.

$h_{c, bw-uc}=b{K}_a{Z}^{3d-1}\left(\frac{g{\rho }_a{\beta }_a}{{\mu }_a{\alpha }_a}\right){\left[\left(T_{bw}-T_{uc}\right)\frac{T_{bw}\left(P_{bw}-P_g\right)\left(M_a-M_v\right)}{M_a{P}_{to}-P_w\left(M_a-M_v\right)}\right]}^d (103)$

$h_{e,bw-uc}=\frac{1000H{h}_{c, bw-uc}{R}_a{P}_{to}}{C_{p,a}{R}_v\left(P_{to}-P_{bw}\right)\left(P_{to}-P_{uc}\right)}(104)$

$C_r=\frac{h_{e,bw-uc}}{h_{c, bw-uc}}(105)$

The study relied on the thermophysical parameters of a binary mixture. For realistic solar still applications, they discovered that d = 1/3 may be utilized in a wide range of operating temperatures, and b = 0.075 when the rate of distilled is less than ${10}^{-4} kg/m^{2}s$, and b = 0.05 for greater distillate yields.

The concentration ratio in the second model is a function of the third-order polynomial of the solar still’s operating temperature (Rahbar and Esfahani, 2013). The following is a suggested polynomial function for the concentration ratio:

$C_r=0.035+0.058T_i+2.5 \times {10}^{-4}{T}_i+4.23\times {10}^{-5}{T}_{i}308.15<T_i<358.15(106)$

Results revealed that in the first model, the concentration ratio has a critical value whereas, in the second model, it does not have a turning point in the temperature range under consideration. The concentration ratio of both models is the same at the stated operating temperature. In constrained situations, his results demonstrated that the quantity of evaporative heat transfer coefficient employed by the first model is higher than that of the second model. Furthermore, the root mean square error obtained with the first model was smaller than that produced with the second model.

Abu-Arabi et al. (2018) presented a model to study the solar still, which is connected to an external solar collector and consists of Sodium Thiosulfate Pentahydrate as a phase change material (PCM). They found that a high mass of PCM causes less productivity as the productivity decreases by up to 30% by increasing the PCM to water mass ratio from 10 to 100. While the basin water temperature was higher for a higher prolonged time by comprising considerable PCM mass in the system. They showed that over the outer side of solar still, decreasing the overall heat transfer coefficient from 10.4 to 2.6 W/m²·K can enhance productivity higher than 100%. They observed that as the cooling water flow rate increases from 0.01 to 0.1 kg/s over the upper cover, the productivity increases considerably. When an overall energy balance is performed in the brackish water, the following results are obtained (Abu-Arabi et al., 2018):

${\dot{m}}_F{H}_F+A_p{Q}_r+A_p{Q}_{ext}+{\dot{m}}_c{H}_{c,in}-\left(A_p{Q}_L^{top}+m_c{H}_{c,out}+{\dot{m}}_f{H}_f+A_p{Q}_{pcm}\right)=m_{bw}\frac{d{H}_{bw}}{dt}(107)$

The following equation was used to determine the relationship between $Q_{ext}$ and $Q_r$, as stated by Duffie and Beckman (Panchal and Thakkar, 2016):

$A{Q}_{ext}=F^{\prime }({\alpha }_p{\text{ε}}_g{Q}_r-U_L\left(T_{h,in}-T_a\right))(108)$

They used the values of 0.83, 0.95, and 0.88 for the collector efficiency factor $\left(F^{\prime }\right)$, the absorptivity of the solar collector plate $\left({\alpha }_p\right)$ and transmissivity of the solar collector glass $\left({\text{ε}}_g\right)$. To calculate the radiation heat transfer coefficient, Eq. 13 was used to estimate the sky’s temperature. In addition, Eq. 21 was used to compute the convection heat transfer coefficient. A Nusselt number of four was used to estimate the convection heat transfer coefficient from the upper cover to the cooling water film since the flow is laminar. The stored or released energy of PCM was calculated as follows (Abu-Arabi et al., 2018):

$\begin{array}{l}{Q}_{PCM}=\left(\frac{M_{equ}}{A_p}\frac{d{T}_{PCM}}{dt}\right)for T_{PCM}\ne T_m\\ Q_{PCM}=\frac{m_{PCM}}{A_P}\frac{L}{\mathrm{\Delta }t} for T_{PCM}=T_m\end{array}(109)$

The following are the energy balance equations for the system at night (discharging mode) (Abu-Arabi et al., 2018):

${\dot{m}}_F{H}_F+Q_{PCM}-\left(Q_L^{top}+{\dot{m}}_f{H}_f\right)=M_{bw}\frac{d{H}_{bw}}{dt}(110)$

Comparing theoretical and experimental results showed reasonable agreement for the productivity and water temperature. The chosen PCM conducted admirably in terms of providing energy during the night for steady water production and also increased total productivity.

Scope for Future Research

Solar stills are an uncomplicated, economical, and vital apparatus, especially in rural and remote regions. Due to various factors such as the material, climatic conditions, water quality, and so on, serious work on using long-term processes has not yet been completed. Due to the complexity of such studies, many areas of solar still research have not yet been explored. Some researchers have investigated the intensity of water salinity, total dissolved solids, turbidity, presence of minerals, and pH value on solar still output. It is important to develop appropriate software to investigate solar stills, as simulation studies have not yet been performed, compared with other powerful simulations in thermal and fluid flow simulating. The following are suggestions for future research directions:

1) One of the important components in increasing the productivity of a solar still is the upper cover, which functions as a transmittance medium for entering solar energy and transferring the heat as the latent heat from water vapor inside the solar still to the atmosphere outside of the solar still. The second duty of the upper cover means transferring the latent heat to the atmosphere is weak due to the low thermal conductivity of the upper cover materials and high temperature of the sides because it is in front of the solar radiation and absorbs some quantity of solar energy. Therefore, absorbing a portion of solar radiation decreases the level of temperature difference required for heat transfer from the inside solar still to the outside. The solar still could be redesigned in such a way that the transmittance medium (upper cover) and condensing plate are separate from each other. According to this idea, the upper cover duty is only a medium across solar radiation, and the condensation cover is only for transferring latent heat to the atmosphere. Of course, using this idea, the solar still becomes complicated and with more details, costs, and components.

2) Losing energy from the solar still sides to the atmosphere should be taken seriously. Researchers attempt to increase productivity using many components, redesign, geometries, etc. and sometimes ignore energy loss results as a factor that reduces or undermines efforts. It is evident that research on insulating all sides of the solar still to date is not satisfactory, and there is good potential for research and study of materials and multi-layer sides (walls), among other areas.

3) Solar energy has been considered only to vaporize the water in the basin, which can be thought of as other available forms of energy in the absence or weak solar radiation similar to wind energy, sea wave energy, Earth thermal energy, waste energy of homes, industries, and factories, etc. For example, using wind energy to evaporate the basin water and resume the distillation process might be explored during the night or when solar radiation is poor. In reality, water distillation may be carried out using a combination of solar and alternative energy sources.

4) Thermal models accurately investigate the physical phenomena of a solar still using the correct formula and energy balance. The next step toward becoming better and more precise might be to reduce assumptions and get closer to reality. The influence of thermal and velocity boundary layers, contact resistance between components, leaks, and other factors should also be addressed.

Conclusion

Potable water is critical for human and societal development, particularly in rural and remote regions. Solar stills were developed to produce distilled water in places with abundant solar radiation, such as the south and east. The single basin single slope solar still is the most basic form, and it is simple to design that anyone could build. Due to limited production, however, researchers have been working on a variety of alternate solar still models. This research analyzes theoretical principles and presents various thermal models of solar stills in the form of a variety of designs. All the studied thermal models have benefits and constraints due to the assumptions used to simulate the climate conditions of the region. Theoretical modeling of a solar still is a simple and quick way to study crucial factors such as efficiency, distilled water output, basin water temperature, and so on. The use of theoretical modeling aids in the selection of a suitable model as well as the evaluation of economic and technological obstacles. Accurate modeling allows for simulations that are close to real conditions, allowing for precise component selection and cost-to-productivity analysis. Before manufacturing and implementation, thermal modeling allows for an examination and comparison of alternative designs, fabrication costs, distilled water costs, climatic conditions, and numerous components. According to a review of several solar thermal models for passive and active units, further research is needed on energy loss, alternate energy use in the absence and weakness of solar radiation, and waste energy from other sources.

Due to the inexpensive cost of distilled water produced by solar stills, these devices are gaining popularity in comparison to fossil fuels. Although solar still units have poor productivity compared to current desalination systems, when fossil fuel resources grow scarcer, solar still units will become a dominant technology. On three typical days, covering the spring, summer, and winter, daily distillation production was estimated to be roughly 19.2, 16.0, and 15.9 kg/m²d, respectively, utilizing a 5 mm diffusion gap between partitions and ten partitions. Rubber scrapers enhanced the DSSSHS model’s overall internal heat transfer coefficient and productivity. The maximum observed value of the total internal heat transfer coefficient for the DSSSHS is 38.754 W/m²°C, and the daily productivity is 4.24 L/m²d, with a productivity improvement of 63% when the slope of the upper cover is relatively short (approximately 3.0°).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu-Arabi, M., Al-harahsheh, M., Mousa, H., and Alzghoul, Z. (2018). Theoretical Investigation of Solar Desalination with Solar Still Having Phase Change Material and Connected to a Solar Collector. Desalination 448, 60–68. doi:10.1016/j.desal.2018.09.020

CrossRef Full Text | Google Scholar

Aihara, T. (1986). JSME Data Book: Heat Transfer. Maruzen, Tokyo: The Japan Society of Mechanical Engineering.

Google Scholar

Al-Sulttani, A. O., Ahsan, A., Rahman, A., Nik Daud, N. N., and Idrus, S. (2017). Heat Transfer Coefficients and Yield Analysis of a Double-Slope Solar Still Hybrid with Rubber Scrapers: an Experimental and Theoretical Study. Desalination 407, 61–74. doi:10.1016/j.desal.2016.12.017

CrossRef Full Text | Google Scholar

Alaudeen, A., Thahir, A. S. A., Vasanth, K., Tom, A. M. I., and Srithar, K. (2015). Experimental and Theoretical Analysis of Solar Still with Glass basin. Desalination Water Treat. 54 (6), 1489–1498.

Google Scholar

Alayi, R., Jahangiri, M., Guerrero, J. W. G., Akhmadeev, R., Shichiyakh, R. A., and Zanghaneh, S. A. (2021). Modelling and Reviewing the Reliability and Multi-Objective Optimization of Wind-Turbine System and Photovoltaic Panel with Intelligent Algorithms. Clean. Energ. 5 (4), 713–730. doi:10.1093/ce/zkab041

CrossRef Full Text | Google Scholar

Alayi, R., Mohkam, M., Seyednouri, S. R., Ahmadi, M. H., and Sharifpur, M. (2021). Energy/economic Analysis and Optimization of On-Grid Photovoltaic System Using CPSO Algorithm. Sustainability 13 (22), 12420. doi:10.3390/su132212420

CrossRef Full Text | Google Scholar

Alayi, R., Zishan, F., Mohkam, M., Hoseinzadeh, S., Memon, S., and Garcia, D. A. (2021). A Sustainable Energy Distribution Configuration for Microgrids Integrated to the National Grid Using Back-To-Back Converters in a Renewable Power System. Electronics 10 (15), 1826. doi:10.3390/electronics10151826

CrossRef Full Text | Google Scholar

Alayi, R., Zishan, F., Seyednouri, S. R., Kumar, R., Ahmadi, M. H., and Sharifpur, M. (2021). Optimal Load Frequency Control of Island Microgrids via a PID Controller in the Presence of Wind Turbine and PV. Sustainability 13 (19), 10728. doi:10.3390/su131910728

CrossRef Full Text | Google Scholar

Alhuyi Nazari, M., Maleki, A., Assad, M. E. H., Rosen, M. A., Haghighi, A., Sharabaty, H., et al. (2021). A Review of Nanomaterial Incorporated Phase Change Materials for Solar thermal Energy Storage. Solar Energy 228, 725–743. doi:10.1016/j.solener.2021.08.051

CrossRef Full Text | Google Scholar

Ali, C., Rabhi, K., Nciri, R., Nasri, F., and Attyaoui, S. (2015). Theoretical and Experimental Analysis of Pin Fins Absorber Solar Still. Desalination Water Treat. 56 (7), 1705–1711. doi:10.1080/19443994.2014.956344

CrossRef Full Text | Google Scholar

Anderson, E. E. (1983). Fundamentals of Solar Energy Conversion. Reading.

Google Scholar

Assad, M. E. H., Aryanfar, Y., Radman, S., Yousef, B., and Pakatchian, M. (2021). Energy and Exergy Analyses of Single Flash Geothermal Power Plant at Optimum Separator Temperature. Int. J. Low-Carbon Tech. 16 (3), 873–881. doi:10.1093/ijlct/ctab014

CrossRef Full Text | Google Scholar

Assad, M., and Rosen, M. A. (2021). Design and Performance Optimization of Renewable Energy Systems. Cambridge, MA, USA: Academic Press.

Google Scholar

Bergman, T. L., Lavine, A. S., Incropera, F. P., and DeWitt, D. P. (2011). Introduction to Heat Transfer. Hoboken, NJ, USA: John Wiley & Sons.

Google Scholar

Bird, R. B., Lightfoot, E. N., and Stewart, W. E. (1966). Transport Phenomena: 7. Pr. Hoboken, NJ, USA: Wiley.

Google Scholar

Bowen, I. S. (1926). The Ratio of Heat Losses by Conduction and by Evaporation from Any Water Surface. Phys. Rev. 27 (6), 779–787. doi:10.1103/physrev.27.779

CrossRef Full Text | Google Scholar

Chen, L., Wang, Y., Xie, M., Ye, K., and Mohtaram, S. (2021). Energy and Exergy Analysis of Two Modified Adiabatic Compressed Air Energy Storage (A-CAES) System for Cogeneration of Power and Cooling on the Base of Volatile Fluid. J. Energ. Storage 42, 103009. doi:10.1016/j.est.2021.103009

CrossRef Full Text | Google Scholar

Dunkle, R. (1961). “Solar Water Distillation: the Roof Type Still and a Multiple Effect Diffusion Still,” in Proc. International Heat Transfer Conference (Boulder, Colorado, USA: University of Colorado).

Google Scholar

El-Naggar, M., El-Sebaii, A. A., Ramadan, M. R. I., and Aboul-Enein, S. (2016). Experimental and Theoretical Performance of Finned-Single Effect Solar Still. Desalination Water Treat. 57 (37), 17151–17166. doi:10.1080/19443994.2015.1085451

CrossRef Full Text | Google Scholar

Elango, C., Gunasekaran, N., and Sampathkumar, K. (2015). Thermal Models of Solar Still-A Comprehensive Review. Renew. Sustain. Energ. Rev. 47, 856–911. doi:10.1016/j.rser.2015.03.054

CrossRef Full Text | Google Scholar

Elsayed, M. M., Taha, I. S., and Sabbagh, J. A. (1994). Design of Solar thermal Systems. Jeddah, Saudi Arabia: Scientific Publishing Center, King Abdulaziz University Jeddah.

Google Scholar

Fernández, J., and Chargoy, N. (1990). Multi-stage, Indirectly Heated Solar Still. Solar energy 44 (4), 215–223. doi:10.1016/0038-092x(90)90150-b

CrossRef Full Text | Google Scholar

Hawkins, G. A. (1954). Heat Transmission. William H. McAdams. McGraw-Hill, New York-London, Ed. 3, 1954. Xiv + 532 Pp. Illus. $8.50. Science 120 (3128), 984. doi:10.1126/science.120.3128.984

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaefarzadeh, M. R. (2004). Thermal Behavior of a Small Salinity-Gradient Solar Pond with wall Shading Effect. Solar Energy 77 (3), 281–290. doi:10.1016/j.solener.2004.05.013

CrossRef Full Text | Google Scholar

Jain, D., and Tiwari, G. N. (2003). Thermal Aspects of Open Sun Drying of Various Crops. Energy 28 (1), 37–54. doi:10.1016/s0360-5442(02)00084-1

CrossRef Full Text | Google Scholar

Karimi Estahbanati, M. R., Ahsan, A., Feilizadeh, M., Jafarpur, K., Ashrafmansouri, S.-S., and Feilizadeh, M. (2016). Theoretical and Experimental Investigation on Internal Reflectors in a Single-Slope Solar Still. Appl. Energ. 165, 537–547. doi:10.1016/j.apenergy.2015.12.047

CrossRef Full Text | Google Scholar

Kaviany, M. (2012). Principles of Heat Transfer in Porous media. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Madhlopa, A. (2017). Theoretical and Empirical Study of Heat and Mass Transfer inside a basin Type Solar Still. Energy 136, 45–51. doi:10.1016/j.energy.2016.09.126

CrossRef Full Text | Google Scholar

Mohtaram, S., Sun, Y., Omidi, M., and Lin, J. (2021). Energy-exergy Efficiencies Analyses of a Waste-To-Power Generation System Combined with an Ammonia-Water Dilution Rankine Cycle. Case Stud. Therm. Eng. 25, 100909. doi:10.1016/j.csite.2021.100909

CrossRef Full Text | Google Scholar

Panchal, H. N., and Thakkar, H. (2016). Theoretical and Experimental Validation of Evacuated Tubes Directly Coupled with Solar Still. Therm. Eng. 63 (11), 825–831. doi:10.1134/s0040601516110045

CrossRef Full Text | Google Scholar

Pishkariahmadabad, M., Ayed, H., Xia, W.-F., Aryanfar, Y., Almutlaq, A. M., and Bouallegue, B. (2021). Thermo-economic Analysis of Working Fluids for a Ground Source Heat Pump for Domestic Uses. Case Stud. Therm. Eng. 27, 101330. doi:10.1016/j.csite.2021.101330

CrossRef Full Text | Google Scholar

Rababa’h, H. M. (2003). Experimental Study of a Solar Still with Sponge Cubes in basin. Energ. Convers. Manage. 44 (9), 1411–1418.

Google Scholar

Rahbar, N., and Esfahani, J. A. (2013). Productivity Estimation of a Single-Slope Solar Still: Theoretical and Numerical Analysis. Energy 49, 289–297. doi:10.1016/j.energy.2012.10.023

CrossRef Full Text | Google Scholar

Rajaseenivasan, T., Tinnokesh, A. P., Kumar, G. R., and Srithar, K. (2016). Glass basin Solar Still with Integrated Preheated Water Supply - Theoretical and Experimental Investigation. Desalination 398, 214–221. doi:10.1016/j.desal.2016.07.041

CrossRef Full Text | Google Scholar

Sadeghi, B., Shafaghatian, N., Alayi, R., El Haj Assad, M., Zishan, F., and Hosseinzadeh, H. (2022). Optimization of Synchronized Frequency and Voltage Control for a Distributed Generation System Using the Black Widow Optimization Algorithm. Clean. Energ. 6 (1), 869–882. doi:10.1093/ce/zkab062

CrossRef Full Text | Google Scholar

Sahota, L., and Tiwari, G. (2017). Advanced Solar-Distillation Systems. Green. Energ. Technol 10, 978–981.

Google Scholar

Sampathkumar, K., Arjunan, T. V., Pitchandi, P., and Senthilkumar, P. (2010). Active Solar Distillation-A Detailed Review. Renew. Sustain. Energ. Rev. 14 (6), 1503–1526. doi:10.1016/j.rser.2010.01.023

CrossRef Full Text | Google Scholar

Sherif, A. M., Taha, I. S., Morsy, M., Elbeblawy, H., and Salem, M. (2016). “Theoretical Study of Enhancement of Solar Still Using Porous Medium and Compound Parabolic Concentrator,” in Proceedings of ICFD12: Twelfth International Conference of Fluid Dynamics, 19-20 December, 2016 (Cairo, Egypt: Le Méridien Pyramids Hotel, Cairo, EGYPTAt).

Google Scholar

Sivakumar, V., Sundaram, E. G., and Sakthivel, M. (2016). Investigation on the Effects of Heat Capacity on the Theoretical Analysis of Single Slope Passive Solar Still. Desalination Water Treat. 57 (20), 9190–9202. doi:10.1080/19443994.2015.1026284

CrossRef Full Text | Google Scholar

Tanaka, H. (2016). Theoretical Analysis of a Vertical Multiple-Effect Diffusion Solar Still Coupled with a Tilted Wick Still. Desalination 377, 65–72. doi:10.1016/j.desal.2015.09.013

CrossRef Full Text | Google Scholar

Tiwari, G. N., Dimri, V., Singh, U., Chel, A., and Sarkar, B. (2007). Comparative thermal Performance Evaluation of an Active Solar Distillation System. Int. J. Energ. Res. 31 (15), 1465–1482. doi:10.1002/er.1314

CrossRef Full Text | Google Scholar

Toyama, S., and Kagakuv, K. (1972). Gijitsu, 24, 159. Tokyo, Japan: Maruzen.

Google Scholar

Tsilingiris, P. T. (2009). Analysis of the Heat and Mass Transfer Processes in Solar Stills - the Validation of a Model. Solar Energy 83 (3), 420–431. doi:10.1016/j.solener.2008.09.007

CrossRef Full Text | Google Scholar

Watmuff, J., Charters, W., and Proctor, D. (1977). “Solar and Wind Induced External Coefficients-Solar Collectors,” in Cooperation Mediterraneenne Pour l'Energie Solaire, 56.

Google Scholar

Glossary

$A_{bw,eff}$ Unshaded area of basin surface in the presence of fins $\left(m^2\right)$

$A_p$ Bottom area of basin $\left(m^2\right)$

$A_{p,eff}$ Effective area of the finned-plate $\left(m^2\right)$

$A_f$ Total surface area $\left(m^2\right)$

$A_{et}$ Area of evacuated tube $\left(m^2\right)$

$A_{ss}$ Area of solar still $\left(m^2\right)$

$A_c$ Collector surface area $\left(m^2\right)$

$A_b$ Basin’s area $\left(m^2\right)$

$A_{sw}$ Wetted side wall area $\left(m^2\right)$

A Area normal to heat transfer direction $\left(m^2\right)$

C Constant

$C_p$ Specific heat coefficient (kj/kgK)

D Diffusivity of water vapor

$ds$ Standard length of the absorber plate (m)

$d_{bw}$ Basin water depth (m)

$E_b$ Received rate of the energy from the basin liner $\left(\text{W}/m^2\right)$

$E_{exd}$ Received rate of energy from external devices $\left(\text{W}/m^2\right)$

$E_{b-bw}$ Energy transfer between basin liner and brackish $\left(\text{W}/m^2\right)$

$E_{b-a}$ Energy transfer between basin liner and atmosphere $\left(\text{W}/m^2\right)$

$F_R$ Collector heat removal factor

$F_{ij}$ Shape factor of surface j to surface j

$Gr$ Grashof number

$g$ Earth’s gravity acceleration $\left(m/s^2\right)$

$h_{bw-uc}$ Convective heat transfer coefficient between brackish water and upper cover inner surface $\left(W/m^{2}K\right)$

$h_{cw}$ Water convective heat transfer coefficient $\left(W/m^{2}K\right)$

$h_{r,uc-a}$ Radiative heat transfer coefficient between upper cover and atmosphere $\left(W/m^{2}K\right)$

$h_{c,up-a}$ Convective heat transfer coefficient between upper cover and atmosphere $\left(W/m^{2}K\right)$

$h_{c, bw-uc}$ Convective heat transfer coefficient between brackish water and upper cover $\left(W/m^{2}K\right)$

$h_{c,bw-b}$ Convective heat transfer coefficient between brackish water and basin liner $\left(W/m^{2}K\right)$

$h_{r,b-a}$ Radiative heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$

$h_{c,b-a}$ Convective heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$

$h_l$ Latent heat of vaporization (W/kg)

$h_{b-bw}$ Heat $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$

$h_{b-bw}$ Heat $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$

$h_{b-a}$ Heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$

$h_{t_{bw-uci}}$ Total heat transfer coefficient between brackish water and upper cover inner surface $\left(W/m^{2}K\right)$

$h_{t_{uco}}$ Total heat transfer coefficient of upper cover outer surface $\left(W/m^{2}K\right)$

$h_{t_{uci}}$ Total heat transfer coefficient of upper cover inner surface $\left(W/m^{2}K\right)$

$H_f$ height of the fin (m) Enthalpy of fresh water produced $\left(j/kg\right)$

$H$ Specific latent heat of vaporization (J/kg) Heigh, (m)

$H_F$ Enthalpy of feed $\left(j/kg\right)$

$H_{c,in}$ Enthalpy of inlet cooling water $\left(j/kg\right)$

$H_{c,out}$ Enthalpy of outlet cooling water $\left(j/kg\right)$

$H_f$ height of the fin (m) Enthalpy of fresh water produced $\left(j/kg\right)$

H Specific latent heat of vaporization (J/kg) Heigh, (m)

$h_{cr}$ Enthalpy of crystallization (kj/kg)

$h_{b-a}$ Heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and atmosphere $\left(W/m^{2}K\right)$

$h_{b-bw}$ Heat $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$ Heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$

$h_{fg}$ Vaporization enthalpy (kJ/kg)

$H_{bw}$ Enthalpy of brackish water $\left(j/kg\right)$

$h_{bw}$ heat transfer coefficient between basin liner and brackish water $\left(W/m^{2}K\right)$

$h_{ew}$ Evaporative-Water heat transfer coefficient $\left(W/m^{2}K\right)$

$h_r$ Radiative heat transfer coefficient $\left(W/m^{2}K\right)$

$h_c$ Convective heat transfer coefficient $\left(W/m^{2}K\right)$

$I_{f,e}$ The total solar radiation intensities incident on east surfaces of the fin $\left(W/m^2\right)$

$I_{f,bw}$ The total solar radiation intensities incident on west $\left(W/m^2\right)$

$I_c\left(t\right)$ Solar radiation intensity on collector or concentrator panel $\left(W/m^2\right)$

$I{\left(t\right)}_s$ Intensity of the Sun’s radiation on the sloped upper cover surface

$I\left(t\right)$ Solar radiation intensity $\left(W/m^2\right)$

$I_{total}$ Total incident radiation energy $\left(W/m^2\right)$

$I_a$ Absorbed radiation energy $\left(W/m^2\right)$

$I_r$ Reflected radiation energy $\left(W/m^2\right)$

$I_t$ Transmitted radiation energy $\left(W/m^2\right)$

$l_{uc}$ Upper cover length (m)

$I_D$ Diffuse solar radiation $\left(W/m^2\right)$

$I_B$ Beam solar radiation $\left(W/m^2\right)$

L Wall thickness (m) Length, (m)

$k$ Thermal conductivity $\left(W/mk\right)$ Back wall

$K_{bw}$ Thermal conductivity of brackish water $\left(W/mk\right)$ Brackish water thermal conductivity (W/mK)

$K_{eff}$ Effective thermal conductivity $\left(kW/mK\right)$

$K_{ins}$ Thermal conductivity of insulation material (W/mK)

$K_{wood}$ Thermal conductivity of wood (W/mK)

$K_{bw}$ Thermal conductivity of brackish water $\left(W/mk\right)$ Brackish water thermal conductivity (W/mK)

$K_{uc}$ Upper cover conductivity coefficient (W/mK) Thermal conductivity coefficient of upper cover (W/mK)

$K_{uc}$ Upper cover conductivity coefficient (W/mK) Thermal conductivity coefficient of upper cover (W/mK)

l Characteristic length (m)

$l_{sh}$ Shadow length of the fin (m)

$L_{ins}$ Hickness of insulation (m)

$L_1$ Upper cover thickness (m)

$L_{PCM}$ Latent heat of PCM (kj/kg)

Le Lewis number

$L_{wood}$ Thickness of wood material (m)

L Wall thickness (m) Length, (m)

$L_{uc}$ Thickness of upper cover (m)

$M_w$ Daily productivity (kg/s)

$m_w$ Water mass (kg/s)

$M_a$ Air molecular mass (kg/kmole)

$M_{equ}$ Equivalent heat capacity of PCM (kj/kgK)

$m_{bw}$ Brackish water mass $\left(kg\right)$

${\dot{m}}_f$ Flow rate of distilled water $\left(kg/s\right)$

${\dot{m}}_c$ Flow rate of cooling water $\left(kg/s\right)$

${\dot{m}}_F$ Flow rate of feed water $\left(kg/s\right)$

$M_v$ Vapor molecular mass (kg/kmole)

${\dot{m}}_{crs}^{\text{'}\text{'}}$ Crystallization salt mass rate $\left(kg/s\right)$

${\dot{m}}_l^{\text{'}\text{'}}$ Liquid mass rate $\left(kg/s\right)$

${\dot{m}}_v^{\text{'}\text{'}}$ Vapor mass rate $\left(kg/s\right)$

${\dot{m}}_a^{\text{'}\text{'}}$ Dry air mass rate $\left(kg/s\right)$

${\dot{m}}_{evp}^{\text{'}\text{'}}$ Volumetric evaporation rate $\left(kg/m^{3}s\right)$

n Constant Number of fin

$n_f$ Number of fins

Nu Nusselt number

$Pr$ Prandtl number Prandtl number

$P_{bw}$ The partial vapor pressure at water surface temperature (Pa)

$P_{uci}$ The partial vapor pressure at the upper cover inner surface temperature (Pa)

$P$ Partial pressure (Pa)

Pr Prandtl number Prandtl number

$p_s$ Saturated water vapor pressure (Pa)

$P_{uc}$ Upper cover pressure (Pa)

$P_{to}$ Total pressure (Pa)

$Q_{pcm}$ Phase change material energy stored or released $\left(W/m^2\right)$

$Q_L^{top}$ Top and edge sides heat losses $\left(W/m^2\right)$

$Q_r$ Solar irradiation $\left(W/m^2\right)$

$Q_{ext}$ External energy coming from the solar collector $\left(W/m^2\right)$

$q_{solo}^{\text{'}\text{'}}$ Incident solar flux on glass cover

surface (W/m 2)

$q_{solo1}^{\text{'}\text{'}}$ Incident solar flux on porous medium surface (W/m 2)

$Q_{f,w}$ enthalpy increase of feeding saline water in the wick (kj/kg)

$Q_{d,w-a}$ Conduction heat transfer from the wick (w) to the surroundings (a) $\left(W/m^2\right)$

$Q_{r,w-gti}$ Radiation heat transfer from the wick (w) to the inner glass cover of the tilted wick section $\left(W/m^2\right)$

$Q_{\left(c+m\right)w-ha}$ Convection heat transfer and mass transfer from the wick (w) to the humid air layer (ha) $\left(W/m^2\right)$

$Q_{df,w}$ absorption of diffuse solar radiation on the wick $\left(W/m^2\right)$

$Q_{dr,w}$ Absorption of direct solar radiation on the wick $\left(W/m^2\right)$

$q_{conv.}$ Convective heat transfer (W)

$q_{cond.}$ Conductive heat transfer (W)

$q_{rad.}$ Radiative heat transfer (W)

$q_{e,bw-uci}$ Evaporative heat transfer rate between brackish water and upper cover inner surface $\left(W/m^2\right)$

Ra Rayleigh number Air gas constant (J/kgK)

$R$ Gas constant of the water

$R_a$ Rayleigh number Air gas constant (J/kgK)

$R_v$ Vapor gas constant (j/kgk)

Sh Sherwood number

$T$ Temperature (K)

$T_a$ atmosphere temperature (K) Local air temperature (K)

$T_{bw}$ brackish water temperature (K) Brackish water water surface temperature (K) Water temperature (K)

$T_b$ Basin liner temperature (K) Absolute temperature of the body (K)

$T_{uco}$ Upper cover outer surface temperature (K)

$T_{uci}$ Upper cover inner surface temperature (K) The inner surface of the upper cover temperature (K)

$T_{uci,f}$ Temperature of upper cover inner surface with finned-basin liner (K)

$T_{bw,f}$ Temperature of brackish water with finned-basin liner (K)

$T_{p,f}$ Temperature of finned-basin liner (K)

$T_{mean}$ Mean temperature of the evaporating and condensing surfaces (K)

$T_i$ Operating temperature (k)

$T_{bw}$ brackish water temperature (K) Brackish water water surface temperature (K) Water temperature (K)

$T_{uci}$ Upper cover inner surface temperature (K) The inner surface of the upper cover temperature (K)

$T_{bw}$ brackish water temperature (K) Brackish water water surface temperature (K) Water temperature (K)

$T_a$ atmosphere temperature (K) Local air temperature (K)

$T_b$ Basin liner temperature (K) Absolute temperature of the body (K)

$T_{sky}$ Sky temperature (K)

$U_{o,b}$ Basin overall heat transfer coefficient $\left(W/m^{2}K\right)$

$U_{o,sw}$ Side wall overall heat transfer coefficient $\left(W/m^{2}K\right)$

$U_{o,uc}$ Upper cover overall heat transfer coefficient $\left(W/m^{2}K\right)$

$U_t$ overall heat transfer coefficient $\left(W/m^{2}K\right)$ Overall heat-transfer coefficient $\left(W/m^{2}K\right)$

$U_t$ overall heat transfer coefficient $\left(W/m^{2}K\right)$ Overall heat-transfer coefficient $\left(W/m^{2}K\right)$

$U_{bw}$ Overall heat transfer coefficient to brackish water $\left(W/m^{2}K\right)$

$U_a$ Overall heat loss coefficient to atmosphere $\left(W/m^{2}K\right)$

$U_{let}$ Total heat transfer loss coefficient of evacuated tube $\left(W/m^{2}K\right)$

$U_L$ Overall heat transfer coefficient of loss $\left(W/m^{2}K\right)$

$V$ Wind speed (m/s)

$x_f$ Thickness of fin (m)

$x_p$ Thickness of absorber plate (m)

$Z$ Height/depth (m)

Greek letters

α Absorptivity

${\alpha }_p$ Solar collector plate

${\alpha }_a$ Air absorptivity

${\alpha }_{uc}^{\text{'}}$ Upper cover’s absorbed fraction of solar radiation

${\alpha }_{bw}^{\text{'}}$ Brackish water’s absorbed fraction of solar radiation

${\alpha }_b^{\text{'}}$ Basin liner’s absorbed fraction of solar radiation

${\alpha }_{eff}$ Effective solar radiation

${\alpha }_{bw}$ Brackish water absorptivity

${\alpha }_b$ Basin liner absorptivity

${\alpha }_{uc}$ Upper cover absorptivity

$\alpha \tau$ Product of absorptance and transmittance

${\beta }_a$ Air thermal expansion coefficient (1/k)

${\beta }_{uc}$ Upper cover reflectivity

${\beta }_{bw}$ Brackish water reflectivity

${\gamma }_{eff}$ Effective Absorption coefficient (1/m)

${\gamma }_{uc}$ Upper cover absorption coefficient (1/m)

$\delta$ thermal expansion coefficient

${\delta }_{gp}$ Diffusion gap between partitions

ε Transmissivity/

${\text{ε}}_g$ Transmissivity of the solar collector glass

${\eta }_{passive}$ Passive overall thermal efficiency

${\eta }_{active}$ Active overall thermal efficiency

${\eta }_i$ Instantaneous efficiency

${\eta }_f$ fin efficiency

${\theta }_2$ Upper cover angle of solar incident (degree)

${\theta }_i$ Incidence angle of direct solar radiation to a horizontal plane with normal (degree)

${\theta }_v$ Angle of refraction (degree)

$\mu$ Dynamic viscosity.

${\mu }_a$ Air dynamic viscosity (kg/ms)

$\text{ν}$ Kinematic viscosity $\left(m^2/s\right)$

$\rho$ Density $\left(kg/m^3\right)$

${\rho }_a$ Air density (kg m3)

$\sigma$ Stefan–Boltzmann constant $\left(=5.67\times {10}^{-8} W/\left(m^2 K^4\right)\right)$

Subscripts

m Mass transfer

dr The absorption of direct solar radiation

df The absorption of diffuse solar radiation

ha Humid air

P2 The second partition of the multiple-effect section

gmi Inner glass cover of the multiple-effect section

P1 The first partition of the multiple-effect section

pf Finned-basin liner

p Absorber plate (basin liner)

b Basin liner

uc Upper cover

bw Brackish water

t West wall

e East wall

f Front wall

k Thermal conductivity $\left(W/mk\right)$ Back wall

sw Side wall

fw Feed water

we Water in evaporator

wp Water in preheater

eff Effective

mg Middle glass

sh Shadow

n Constant Number of fin

et Evacuated tube