Neural Network Acceleration of Genetic Algorithms for the Optimization of a Coupled Fast/Thermal Nuclear Experiment

Genetic algorithms (GA) are used to optimize the Fast Neutron Source (FNS) core fuel loading to maximize a multiobjective function. The FNS has 150 material locations that can be loaded with one of three different materials resulting in over 3E+71 combinations. The individual designs are evaluated with computationally intensive calls to MCNP. To speed up the optimization, convolutional neural networks (CNN) are trained as surrogate models and used to produce better performing candidates that will meet the design constraints before they are sent to the costly MCNP evaluations. A major hurdle in training neural networks of all kinds is the availability of robust training data. In this application, we use the data produced by the GA as training data for the surrogate models which combine geometric features of the system to predict the objectives and constraint objectives. Utilizing the surrogate models, the accelerated algorithm produced more viable designs that significantly improved the objective function utilizing the same computational resources.

1 Introduction

The optimization of nuclear problems can be a complex task often with multiple competing objectives and constraints. There is much research into the optimization of various aspects of nuclear reactors such as the initial design (Gougar, et al., 2010), fuel shuffling (Zhao, et al., 1998; Chapot, Da Silva and Schirru 1999), and shielding (Kim and Moon 2010; Tunes, De Oliveira and Schön 2017) optimizations. Due to the non-linear nature of these problems, optimization algorithms such as evolutionary and simulated annealing algorithms are often used. These methods do not guarantee that the optimal solution is found but can, with sufficient computational resources, clever heuristics, and the application of expert knowledge, often find solutions which are near-optimal.

When an optimization is of a function that is prohibitively expensive (such as solving the neutron transport equation), a surrogate model (Sobester, Forrester and Keane 2008) is produced and optimized instead. Surrogate models generally trade the computation expense of the original function for less accurate, but less expensive functions. The surrogate model is optimized instead of the original function. These can be as simple as linear functions or as complex as deep neural networks. In nuclear optimizations, surrogate models have been built to approximate expensive functions such as finite-element structural analysis (Prabhu, et al., 2020), computational fluid dynamics (Hanna, et al., 2020), and neutron transport (Faria and Pereira, 2003; Hogle 2012; El-Sefy et al., 2021; Sobes, et al., 2021) related objectives.

In this paper, an optimization of the Fast Neutron Source at the University of Tennessee was performed using objectives calculated by solving the neutron transport equation. A surrogate model for these objectives is presented, and a genetic algorithm with and without acceleration using that surrogate model are compared. The following sections include overviews of both the Fast Neutron Source and of the neural network architecture used as the surrogate models. Two genetic algorithm optimizations are presented, the first uses the Non-dominated Sorting Algorithm-II and Monte Carlo N-Particle transport code (MCNP) (Goorley, et al., 2012) to solve the objective and constraint functions. The second optimization uses surrogate models with the NSGA-II algorithm, after which the individuals in the Pareto Front are evaluated with MCNP.

1.1 Fast Neutron Source

The Fast Neutron Source (FNS) (Pevey, et al., 2020) will be a platform for sub-critical integral cross section experiments at the University of Tennessee. It will be driven by 2.5 MeV neutrons produced by a deuterium-deuterium (DD) neutron generator and feature a flexible construction which will produce sub-critical benchmark experiments targeting specific nuclear data needs of next generation reactors.

The reduction of the uncertainty on next-generation reactor designs is a need for the expected rapid deployment of next generation reactors. Nuclear data uncertainty is propagated to all nuclear-related figures of merit of reactors such as k-eff, void, temperature and power reactivity coefficients and reactivity worth’s. In a recent assessment of the nuclear data needed for advanced reactors, it was found that for several next-generation reactors need better resolved nuclear data (Bostelmann, et al., 2021). For example, in a sensitivity analysis of the Advanced Burner Reactor 1000 MWth Reference Concept, it was shown that the uncertainty in important nuclear characteristics is driven by uncertainties in uranium, plutonium, iron and sodium. In this concept, the uncertainty on k-eff, temperature coefficients of reactivity and Na void worth were 0.900%, 8.397% and 13.483%, respectively. These uncertainties require added margin in designs and can lead to less-than-optimal designs to account for these uncertainties.

Systematic integral data assimilation can be done to decrease these uncertainties. In this type of analysis, a suite of known benchmark models is collected, and a sensitivity analysis is completed for each. The known experimental values (and associated biases in the computational models) are then used to further decrease the uncertainty in the relevant quantities of interest. The FNS will be a source of these types of benchmarks which targets the reduction of uncertainties in neutronics calculation due to nuclear data uncertainty. The goal of a given configuration of the FNS then is to maximize the relevance of the experiment to some target advanced reactor concept and to maximize the total flux produced by the configuration to reduce the required FNS run-times.

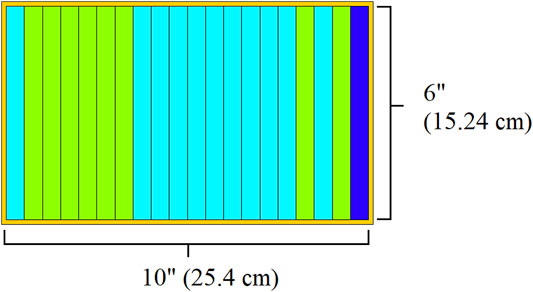
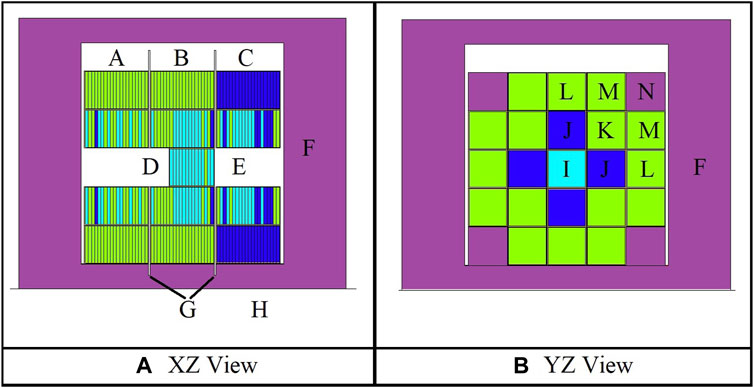
The most basic geometry unit of the FNS are six″ x six″ x 0.5″ plates which can be one of three different materials in this study. Up to 20 of these plates are combined into aluminum cassettes (See Figure 1). Twenty-five of these cassettes are then combined into a 5 × 5 array called a zone (See Figure 2). There are three zones in the FNS, as seen in Figure 2A. In each zone, due to rotational symmetry, there are up to six unique cassette patterns (labeled I-N in Figure 2B). Note that in the work in this paper only the interior three cassette patterns (I, J, K) in each zone are optimized. The corner cassettes (N) are filled with stainless steel in this optimization and the cassettes labelled L and M are either the target coolants material (Zone A, B) or the thermal moderator (Zone C). The center cassette pattern, labeled I, is a variable sized that can be between 0-30 plates (up to an interior length 15″). The length of this cassette is a function of the number of plates within the cassette, with the experiment volume moving along with the cassette’s changing length. The DD neutron source is in Zone C in a fixed location and is modelled as an isotropic 2.5 MeV neutron source. Other features of the FNS in the MCNP model are the stainless-steel reflector (F), the concrete pedestal (H), and the B₄C plates (G) which ensure subcriticality when inserted.

FIGURE 1

FIGURE 1. Fast neutron source single cassette MCNP geometry.

FIGURE 2

FIGURE 2. Fast Neutron Source MCNP Geometry (A) XZ and (B) YZ View.

2 Materials and Methods

2.1 Non-Dominated Sorting Algorithm-II

Genetic algorithms are a class of optimization algorithms which implement natural selection to optimize what may otherwise be intractable optimization problems. In simplest terms, a genetic algorithm takes an initial generation of individuals which are evaluated with respect to one or more objectives, and a subset of these individuals is selected and then combined to produce a unique individual and/or mutated randomly. How exactly each of the steps is accomplished is part of the art of a well-designed genetic algorithm. Genetic algorithms can also be augmented by using user-defined heuristics in each step to further increase the effectiveness of the algorithm to produce a suite of individuals required by the analyst.

The Non-Dominated Sorting Algorithm-II (Deb et al., 2002) is a well-known variation on the standard genetic algorithm which incorporates the heuristics of elitism, non-dominated sorting and crowding distance to select the parents of the next generation. Elitism is simply the idea that parents are compared to the children of the current generation. This ensures that no progress made during the optimization is lost from one generation to the next. Non-dominated sorting is a heuristic for selecting which individuals are selected as parents of the next generation, which ranks individuals by the number of other individuals which dominate it (i.e.: have a better evaluation of an objective function). If no other individual has at least one objective which is better than a given individual, then that individual is non-dominated and is assigned rank 1. Subsequent individuals are assigned a non-dominated rank based on how many and which individuals dominate it. Rank 2 individuals are only dominated by rank 1 individuals, etc. Parents of the next generation are selected based on their non-dominated rank. If there are more individuals in each rank than there are available slots for parents, then the crowding distance metric is applied. Crowding distance is a heuristic which calculates the volume around each individual in the objective space. Individuals are selected as parents first based on the minimum and maximum for each objective function, and then by which occupy the largest volume in the objective space until the parent population is full. This heuristic is meant to both preserve the maximum and minimum individuals for each objective function and to preferentially select individuals which are in a less populated section of the objective space as parents with the goal of increasing the genetic diversity of the population.

The NSGA-II Algorithm is presented in Figure 3. It is adapted from the original paper describing the algorithm, A Fast and Elitist Multiobjective Genetic Algorithm NSGA-II (Deb et al., 2002):

FIGURE 3

FIGURE 3. The Non-Dominated Sorting Genetic Algorithm-II (Deb et al., 2002).

2.2 Convolutional Neural Networks

A convolutional neural network (CNN) is a type of artificial neural network which can approximate a function in which not just the input values are important, but the relative positional information of the inputs is also important. CNNs are used primarily in machine vision tasks (Krizhevsky, Sutskever and Hinton 2012) and language processing tasks (Kalchbrenner, Grefenstette and Blunsom 2014). In machine vision tasks, the magnitude, relative position, and combinations of pixels are important for predicting what the pixels represent. In machine language tasks the relative positions of words are an important aspect to producing accurate translations.

CNN architectures include several layer types such as convolutional layers, pooling layers, non-linearity layers and fully connected layers (Albawi et al., 2017). In the convolutional layer, the namesake of the neural network architecture, is the convolution operation performed on the input to the layer and one or more learned kernels to produce a feature map. The convolution operation is a mathematical function that describes how one function modifies another as it is shifted over it. In practical terms, with a 2D input and kernel, the dot product between both functions is calculated and stored in the feature map. The kernel is then shifted by some number of columns and the dot product is calculated again. A non-linear function, such as a Rectified Linear Unit, is applied to the outputs of the convolutional layers.

The next layer type is the pooling layers. In these layers, a fixed filter is applied to the input to the layer. Commonly used filters are averaging and maximum pooling filters which return the average of a subset of the feature map or the maximum value within a subset. Unlike the convolutional layer, the stride of this operation is generally equal to the width of the filter. Commonly in machine-vision tasks a 2 × 2 filter is used. A 2 × 2 max pooling layer would reduce the size of the feature map by producing a new feature map which is composed of the maximum values in each 2 × 2 grid in the input feature map.

The last layer type commonly used in convolutional neural networks are fully connected layers. These final layers take as input the flattened final feature maps from the previous layers and non-linearly combine them into a prediction. The weights and biases in these layers, along with the kernels of the convolutional layers, are trained by backpropagation algorithm used to train other neural networks.

In nuclear applications, the relative position of materials to each other is important information when predicting nuclear quantities of interest such as k-eff. The k-eff of a given configuration of fissile, moderating, and absorbing materials is a function of where these materials are in 3-D space relative to each other, along with their respective nuclear data. CNNs produce predictions based on combinations of features which incorporate this 3-D data. There are other deep neural network architectures, such as recurrent (Liang and Hu, 2015) and transformer networks (Han et al., 2022), that have similarly been applied to machine vision tasks and therefore may also be able to predict nuclear related figures of merit such as k-eff, representativity, etc.

3 Results and Discussion

This section discusses the initial optimization of the FNS using the NSGA-II algorithm and the subsequent optimization using the CNN-based surrogate models for the objective and constraint functions.

3.1 Optimization of the FNS by NSGA-II

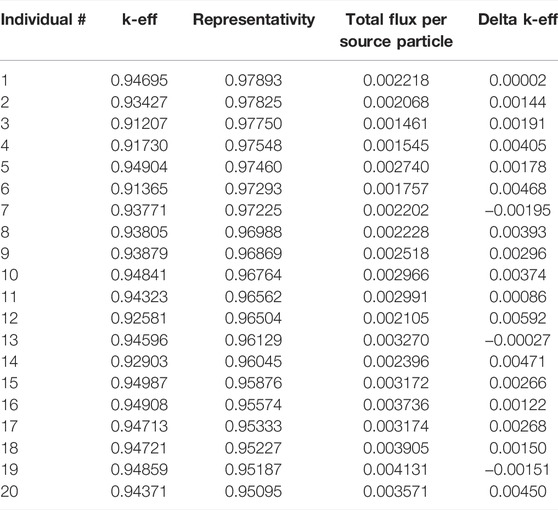
The target of this FNS optimization is a generic sodium cooled fast reactor spectra. The objectives of this optimization are the maximization of the neutron flux per source particle in the experiment volume, the maximization of the representativity of the flux spectra in the experiment volume and the maximization of the change in k-eff when placing the target material in the experiment volume. These objectives are used as heuristics in place of the true objective of the FNS, which is to produce configurations which minimize the uncertainty on a target reactor concept propagated from nuclear data. Maximizing the total flux per source particle would mean reducing the total time required to complete a FNS experiment to sufficient statistical certainty. Representativity, or the E similarity coefficient in the SCALE manual (Rearden and Jessee 2018), is the angle between two n-length vectors in n-dimensional space. A value of 0 means that the two vectors are perpendicular to each other, a value of 1.0 would correspond to the two vectors pointing in the same direction and are therefore proportional to each other. The integral k-eff objective seeks to maximize the delta between the FNS experiment and an integral experiment where the entire experiment volume is filled with the material of interest. This last objective approximates a potential use-case of the FNS to perform integral experiment where the reactivity worth of the target moderator in the system is being measured before and after insertion. Maximizing the Δk-eff of that experiment would make the practical matter of measuring the reactivity difference easier.

These objectives were calculated by an MCNP source calculation with a total uncertainty on the experimental volume flux tally converged to <0.005% standard error. In addition, a constraint on k-eff was enforced which required all parents to have a k-eff below 0.95. This constraint was calculated using MCNP and to a standard uncertainty of at least 0.00150 dk-eff. An increasingly strict constraint on representativity based on the idea of simulated annealing was also enforced. This constraint increased linearly over the first 50 generations of the optimization to E > 0.95. This constraint was enforced such that if there were not enough individuals in the parent population which met it, then it would be relaxed until at least 20 individuals met the constraint. Enforcing the constraint on representativity later in the optimization allows the algorithm to explore areas on the design space that would not be allowed by a strict constraint.

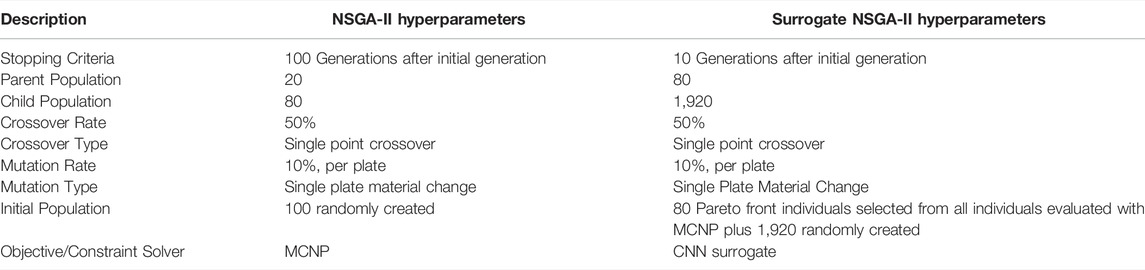
This optimization used three plate types: 9.75% enriched uranium metal, polyethylene, and sodium metal. The initial optimization of the FNS was run on the NECLUSTER at the University of Tennessee. This NSGA-II algorithm was implemented with the parameters described in Table 1. A total of 8,100 potential patterns of the FNS were evaluated in this optimization. Of these, 3,145 individual patterns met the k-eff criteria and were evaluated for the neutron flux-based objectives. The stopping criteria used for this optimization was number of generations, which was selected due to taking approximately 3 days (wall time) to complete. The MCNP calculations of the objective functions required the most computational time.

TABLE 1

TABLE 1. Description of NSGA-II and surrogate NSGA-II hyperparameters.

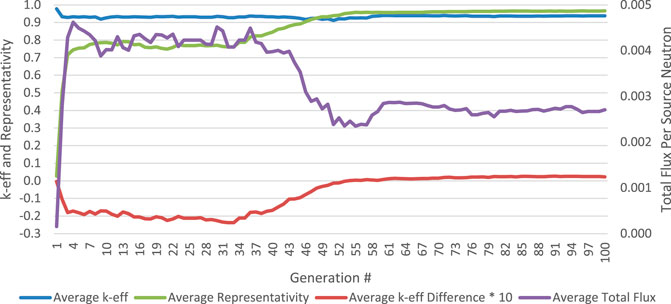
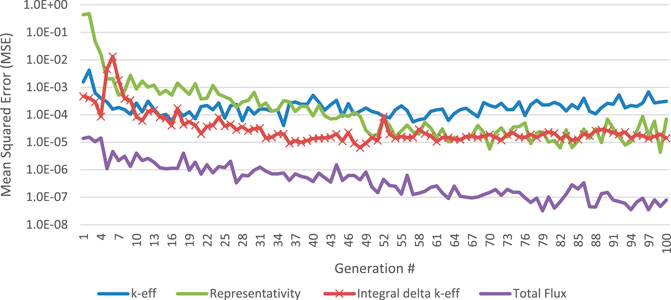
Figure 4 shows the average k-eff, representativity, total flux, and the integral k-eff value (times 10). The integral value is multiplied by 10 to show more detail in the data. Some features of this figure are that the linearly increasing constraint on representativity is obvious from both the linearly increasing average representativity and the decreasing average total flux over generations 34 to 53. Thereafter, the average total flux of the parents increases slightly but plateaus at generation 61.

FIGURE 4

FIGURE 4. Average parent objective function and constraint evaluation during NSGA-II optimization.

This optimization produced a Pareto front of FNS designs which can be seen in Table 2. This set of individuals represent the trade-off between the objective functions of representativity, total flux and integral k-eff as found by the optimization algorithm. The representativity of these individuals ranges from 0.9510 to 0.9789. The total flux in the experiment volume ranges from 0.00146 to 0.0041, and the $\Delta k$ of the integral experiment ranges from -0.00592 to +0.00195. Like previous analysis of a simplified approximation of the FNS, the representativity of the flux in the experiment volume and the total of that flux are negatively correlated (-0.858) while the flux and $\Delta k$-eff are positively correlated (0.810). An increase in $\Delta k$-eff will increase the total flux in the experimental volume but at the expense of the ability of the flux spectra to match the primarily fast target spectra as measured by representativity.

TABLE 2

TABLE 2. Final 20 individuals NSGA-II optimization.

3.2 Surrogate Model Optimization of the FNS

The surrogate model optimization of the FNS used the same objectives and constraint as the optimization described in Section 3.1, but with the CNN-based surrogate models as solvers for the MCNP k-eff and source calculations required to evaluate the objectives. The architectures of these networks were found by the application of the Keras Tuner Python library (O'Malley, et al., 2019) using the data produced by the NSGA-II optimization. The hyper parameters found by this optimization can be found in Table 3. Further discussion of the method of optimizing the surrogate models will be presented in a forthcoming PhD dissertation at the University of Tennessee by the lead author.

TABLE 3

TABLE 3. FNS CNN surrogate model hyperparameters.

The surrogate-based optimization algorithm is as follows:

1. Initialize population of 100 individuals and evaluate for objectives and constraint with MCNP.

2. Train surrogate models if more than 100 individuals have been evaluated.

3. Run NSGA-II algorithm (Deb et al., 2002) with the parameters described in Table 1, using the CNN-based surrogate models as the objective and constraint solvers.

4. Evaluate the final Pareto front (80 individuals) from the surrogate-based optimization with MCNP

5. If the total number of generations equals the stopping criteria, exit.

6. Return to Step #2

The data produced by the outer loop of the optimization, where MCNP is used to calculate the objectives and the constraint functions for every individual, was used for the training of the surrogate models used to evaluate the objectives of the inner loop of the optimization. A minimum of 100 valid individuals are required for training to occur, so after the first generation only the k-eff surrogate model was trained. The objective functions were trained after generation 2. The surrogate models were trained for 500 epochs using 90% of the available training data with 10% used for validation. The weights and biases of the epoch which minimized the validation error were used as the surrogate model for that generation. The models were initialized with random weights at the beginning of the optimization.

The ability of the surrogate models to predict their respective values can be quantified by calculating the mean squared error (MSE) of the predictions to the true values as defined by,

$MeanSquaredError=\frac{1}{n}{\displaystyle \sum _{n=1}^n{\left(x_i-{\widehat{x}}_i\right)}^2}.$

Where, $x_i$ and ${\widehat{x}}_i$ are the true and predicted values.

The MSE of each of the surrogate models initially are relatively large and decrease as the number of training examples increases. The surrogate model predicting k-eff is the first to stabilize at a value of approximately 1.0E-01 at generation 10. During the optimization the training data for this model increases by 80 in each step. If an individual does not have a k-eff below 0.95, then the three objective functions are not calculated for it. Figure 5 shows the MSE of the prediction of the objective and constraints versus the true, MCNP-calculated, values for all individuals produced in each generation. The MSE of the surrogate models of the objective functions plateau at approximately generation 36 for the experimental k-eff value surrogate, generation 65 for the representativity surrogate and generation 80 for the total flux surrogate.

FIGURE 5

FIGURE 5. MSE of surrogate models during optimization.

During this optimization, a total of 8,100 individuals were evaluated with MCNP and 2,120,000 individuals were evaluated with the surrogate models. Of the 8,100 patterns evaluated with MCNP a total of 5,868 individuals met the k-eff constraint and therefore evaluated with a MCNP source calculation. The average objective function and k-eff of all the individuals in the parent population is plotted in Figure 6. Like the NSGA-II algorithm before, the constraint on representativity that is maximally applied at generation 50 has a visible effect on the parent population.

FIGURE 6

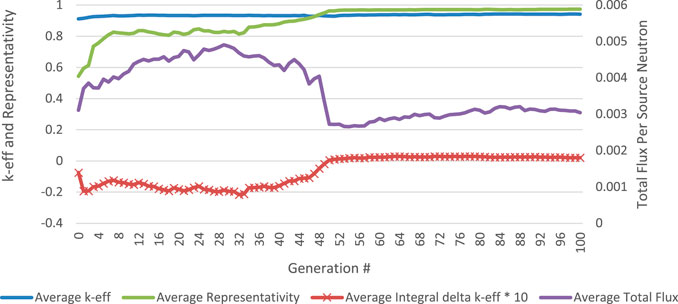
FIGURE 6. Average objective and constraint evaluation during surrogate NSGA-II optimization for all parents in each generation.

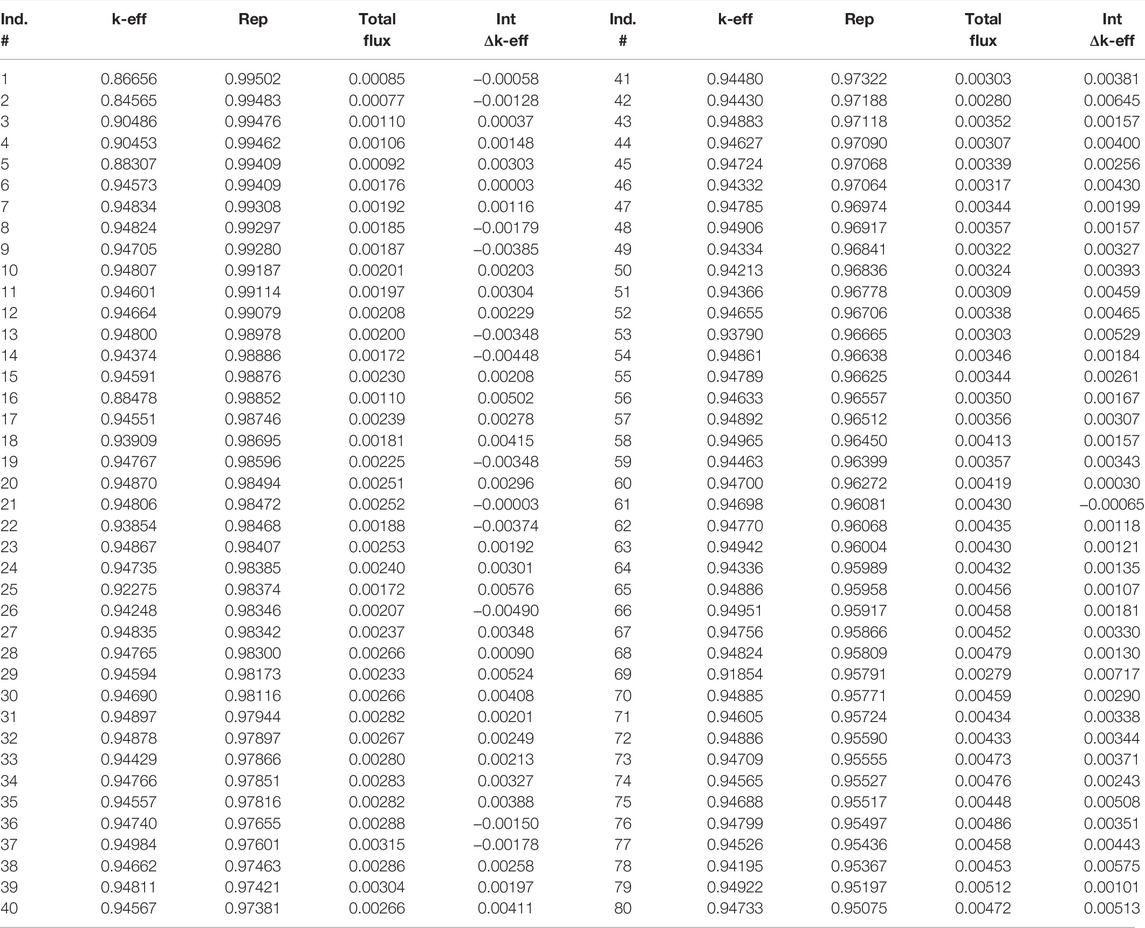
The objective and constraint evaluations of the Pareto front individuals are provided in Table 4. The representativity of these individuals ranged between 0.95075 and 0.99502, the total flux per source neutron between 0.00077 and 0.00512 and the maximum and minimum integral Δk-eff values were +0.00717 and -0.00490, respectively. Like in the NSGA-II calculation, representativity and total flux per source neutron had a strong negative correlation (-0.95096).

TABLE 4

TABLE 4. Final 100 individuals CNN-surrogate NSGA-II optimization.

3.3 Comparison of the Optimizations

The surrogate-based NSGA-II optimization of the FNS produced a Pareto front of potential FNS designs which outperformed those produced by the standard NSGA-II algorithm. Table 5 presents the average, maximum and minimum of the objectives and constraint functions of the final Pareto front of each calculation. The surrogate-based optimization produced individuals with higher representativity, total flux per source particle and both a larger positive and negative integral Δk-eff. The final Pareto front of both calculations plotted by representativity vs. total flux per source particle and integral experimental k-eff vs. representativity is presented in Figure 7 and Figure 8. These figures show that the surrogate-model based optimization produced a suite of individuals which better optimize the objectives.

TABLE 5

TABLE 5. Average, Minimum and Maximum Constraint and Objective Functions of Final Pareto Front of NSGA-II and NSGA-II Surrogate Calculations. Mean values are italicized with the minimum and maximum values given in brackets below.

FIGURE 7

FIGURE 7. Comparison of Pareto Front Individuals from Both Optimizations, Total Flux vs. Representativity.

FIGURE 8

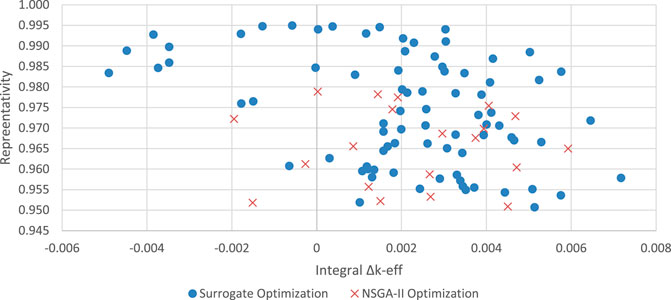
FIGURE 8. Comparison of Pareto Front Individuals from Both Optimizations, Representativity vs. Integral Experiment Δk-eff.

A total of 8,100 potential FNS patterns were evaluated in during the both the NSGA-II and NSGA-II surrogate optimizations. In the standard NSGA-II calculation a total of 3,145 potential patterns met the k-eff constraint of 0.95. During the NSGA-II with surrogate model, a total of 5,845 potential patterns met the k-eff constraint. This is an increase of over 85% more viable FNS configurations evaluated in the surrogate accelerated calculation.

The trade-off of this increase in both calculational efficiency and in the more optimized Pareto Front is computational time for both the increased number of MCNP calculations and for the training and utilizing of the surrogate models. The increased number of MCNP calculations is a by-product of more effectively producing potential FNS designs and could be resolved by decreasing the number of the parent population. In the first time step the training of the surrogate models required an average of 2.3 min. By the final time step this increased to a maximum of 33 min. This increase in time requirement could be offset by capping the total number of examples used for surrogate model training or by reducing the size and complexity of the surrogate models themselves. Once trained, the surrogate models required on average a total of approximately 7.5 s to evaluate the 1,920 unique children in each interior GA step.

4 Conclusion

The work in this paper presents the benefit of accelerating a genetic algorithm used for a multi-objective optimization of a nuclear experiment using convolutional neural network surrogate models comparing to a standard benchmark genetic algorithm. These surrogate models are trained in-line during the genetic algorithm and allow the evaluation of an increased number of potential designs, which leads to an increase in all objective functions. The architectures for the k-eff, representativity, neutron flux and integral k-eff experiment surrogate models are presented along with the methodology for producing them. Future work includes further expanding the use of the surrogate models for other useful objectives relevant for selecting FNS designs and producing more surrogates for other FNS designs targeting uncertainties in next-generation reactor designs.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JP: Student research lead and lead author. VS: Committee member and primary research advisor. WH: Graduate committee chair and research lead.

Funding

This work is funded by the University of Tennessee, Knoxville Department of Nuclear Engineering.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This is a short text to acknowledge the contributions of specific colleagues, institutions, or agencies that aided the efforts of the authors.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.874194/full#supplementary-material

References

Albawi, S., Tareq, A. M., and Al-Zawi, S. (2017). “Understanding of a Convolutional Neural Network,” in 2017 International Conference on Engineering and Technology (ICET), 1–6. doi:10.1109/icengtechnol.2017.8308186

CrossRef Full Text | Google Scholar

Bostelmann, R., Ilas, G., Celik, C., Holcomb, A. M., and Wieselquist, W. (2021). Nuclear Data Assessment for Advanced Reactors. Oak Ridge, TN (United States): Tech. Rep., Oak Ridge National Lab. doi:10.2172/1840202

CrossRef Full Text | Google Scholar

Chapot, J. L. C., Carvalho Da Silva, F., and Schirru, R. (1999). A New Approach to the Use of Genetic Algorithms to Solve the Pressurized Water Reactor's Fuel Management Optimization Problem. Ann. Nucl. Energy 26, 641–655. doi:10.1016/s0306-4549(98)00078-4

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

El-Sefy, M., Yosri, A., El-Dakhakhni, W., Nagasaki, S., and Wiebe, L. (2021). Artificial Neural Network for Predicting Nuclear Power Plant Dynamic Behaviors. Nucl. Eng. Technol. 53, 3275–3285. doi:10.1016/j.net.2021.05.003

CrossRef Full Text | Google Scholar

Faria, E. F., and Pereira, C. (2003). Nuclear Fuel Loading Pattern Optimisation Using a Neural Network. Ann. Nucl. Energy 30, 603–613. doi:10.1016/s0306-4549(02)00092-0

CrossRef Full Text | Google Scholar

Goorley, T., James, M., Booth, T., Brown, F., Cox, L. J., Durkee, J., et al. (2012). Initial MCNP6 Release Overview. Nucl. Technol. 180, 298–315. doi:10.13182/nt11-135

CrossRef Full Text | Google Scholar

Gougar, H. D., Ougouag, A. M., Terry, W. K., and Ivanov, K. N. (2010). Automated Design and Optimization of Pebble-Bed Reactor Cores. Nucl. Sci. Eng. 165, 245–269. doi:10.13182/nse08-89

CrossRef Full Text | Google Scholar

Han, K., Yunhe, W., Hanting, C., Xinghao, C., Jianyuan, G., Zhenhua, L., et al. (2022). “A Survey on Vision Transformer,” in IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE).

CrossRef Full Text | Google Scholar

Hanna, B. N., Dinh, N. T., Youngblood, R. W., and Bolotnov, I. A. (2020). Machine-Learning Based Error Prediction Approach for Coarse-Grid Computational Fluid Dynamics (CG-CFD). Prog. Nucl. Energy 118, 103140. doi:10.1016/j.pnucene.2019.103140

CrossRef Full Text | Google Scholar

Hogle, S. (2012). Optimization of Transcurium Isotope Production in the High Flux Isotope Reactor. PhD Thesis. University of Tennessee.

Google Scholar

Kalchbrenner, Nal., Grefenstette, Edward., and Blunsom, Phil. (2014). “A Convolutional Neural Network for Modelling Sentences,” in Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) (Baltimore, Maryland: Association for Computational Linguistics), 655–665. doi:10.3115/v1/p14-1062

CrossRef Full Text | Google Scholar

Kim, B. S., and Moon, J. H. (2010). Use of a Genetic Algorithm in the Search for a Near-Optimal Shielding Design. Ann. Nucl. Energy 37, 120–129. doi:10.1016/j.anucene.2009.11.014

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 25. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

Liang, M., and Xiaolin, H. (2015). “Recurrent Convolutional Neural Network for Object Recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 3367–3375.

Google Scholar

O'Malley, T., Elie, B., Long, J., Franccios, C., Haifeng, J., and Luca, I. (2019). Keras Tuner. https://github.com/keras-team/keras-tuner.

Google Scholar

Pevey, J., Chvála, O., Davis, S., Sobes, V., and Hines, J. W. (2020). Genetic Algorithm Design of a Coupled Fast and Thermal Subcritical Assembly. Nucl. Technol. 206, 609–619. doi:10.1080/00295450.2019.1664198

CrossRef Full Text | Google Scholar

Prabhu, S. R., Pandey, M. D., Christodoulou, N., and Leitch, B. W. (2020). A Surrogate Model for the 3D Prediction of In-Service Deformation in CANDU Fuel Channels. Nucl. Eng. Des. 369, 110871. doi:10.1016/j.nucengdes.2020.110871

CrossRef Full Text | Google Scholar

Rearden, B. T., and Jessee., M. A. (2018). SCALE Code System. Oak Ridge, TN (United States): Tech. Rep., Oak Ridge National Lab. doi:10.2172/1426571

CrossRef Full Text | Google Scholar

Sobes, V., Hiscox, B., Popov, E., Archibald, R., Hauck, C., Betzler, B., et al. (2021). AI-Based Design of a Nuclear Reactor Core. Sci. Rep. 11, 19646–19649. doi:10.1038/s41598-021-98037-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sobester, A., Forrester, A., and Keane, A. (2008). Engineering Design via Surrogate Modelling: A Practical Guide. John Wiley & Sons.

Google Scholar

Tunes, M. A., De Oliveira, C. R. E., and Schön, C. G. (2017). Multi-Objective Optimization of a Compact Pressurized Water Nuclear Reactor Computational Model for Biological Shielding Design Using Innovative Materials. Nucl. Eng. Des. 313, 20–28. doi:10.1016/j.nucengdes.2016.11.009

CrossRef Full Text | Google Scholar

Zhao, J., Knight, B., Nissan, E., and Soper, A. (1998). FUELGEN: A Genetic Algorithm-Based System for Fuel Loading Pattern Design in Nuclear Power Reactors. Expert Syst. Appl. 14, 461–470. doi:10.1016/s0957-4174(98)00005-0

CrossRef Full Text | Google Scholar