Impact of Electrical Connection Distance on the Open Loop Modal Resonance of Grid Connected Photovoltaic Farms

The grid connection of photovoltaic (PV) farms may cause power system oscillations under the condition of open-loop modal resonance (OLMR). This study elucidated the origin of the induced low-frequency oscillations and examined the impact of the electrical distance between grid-connected PV farms on OLMR intensity by using a simplified real power network. A linearized state-space model of the real power system comprising grid-connected PV farms was derived. Based on this, an OLMR analysis was performed to examine the impact of the electrical distance between the grid-connected PV farms as well as between each grid-connected PV farm and the main grid. The OLMR analysis results indicate that the strength of the OLMR increases with the electrical distance between the PV farms, thereby leading to growing power oscillations. Moreover, the increase of electrical distance between each of the grid-connected PV farms and the main grid has a greater effect on OLMR intensity. Additionally, the non-linear simulations were performed to confirm the correctness of the OLMR analysis. Finally, by re-tuning the parameters of the control system of the grid-connected PV farms to reduce the phase-locked loop bandwidth, the OLMR can be effectively eliminated to avoid power oscillations.

1 Introduction

In recent years, as environmental pollution and energy crisis problems have become increasingly severe, several countries are actively transforming to green and sustainable energy systems. The proposal of the “carbon peak and neutrality” goal implies that the development of new alternative and clean energy is an inevitable trend in the current era (Wang et al., 2021). Among various alternative energy sources, solar energy has recently received remarkable attention, and its application technology has developed considerably (Donaldson et al., 2021). At present, solar power generation technologies mainly include concentrated solar power (CSP) and photovoltaic (PV) power generation (Abubakr et al., 2022). Owing to the high costs of the CSP technology, the PV power generation technology is widely worldwide. The fast-paced development in PV power generation technology has led to a notable increase in its installed capacity. Nonetheless, the PV power generation principle and control methods are considerably different from those of conventional power generation (Kou et al., 2020; Quan et al., 2020). In 2017, a regional power network in the western areas of China experienced power oscillations of approximately 1 Hz caused by PV grid connections, which led to the disassembly of some power stations and affected the safety and stable operation of the power systems.

At present, researchers worldwide have been focusing on inverter structure and control, maximum power point tracking (MPPT) strategy, operation optimization, and stability analysis aspects of PV power generation. Khasim (Khasim et al., 2021) proposed a novel asymmetric multilevel inverter topology, which uses an asymmetric DC power supply to achieve a 21-level output voltage without an H-bridge. Mahmoud (Mahmoud and Lehtonen, 2020) proposed a three-level control strategy with different time resolutions to minimize voltage deviation and voltage flicker in high PV penetrated distribution systems. Further, an adaptive discrete proportional–integral–differential controller was used to control the dynamic microgrid inverter voltage (Kumar and Tyagi, 2021), and DC–DC and DC–AC converters were coordinated and controlled (Emara et al., 2021), both of which improved voltage stability. Based on the adaptive neural fuzzy reasoning system (ANFIS), Priyadarshi and Ibrahim (Priyadarshi et al., 2020; Ibrahim et al., 2021) studied the MPPT algorithm to quickly achieve the maximum power. In addition, ANFIS has been applied to the areas of detection, identification, and defect/fault elimination in PV systems (Bendary et al., 2021; Mansouri et al., 2021). Further, on the premise of ensuring the reliability of photovoltaic microgrids and renewable energy source integration system, the corresponding highest penetration was determined (Ali et al., 2021; Harasis et al., 2021). Mahmoud (Mahmoud and Lehtonen, 2021) proposed comprehensive analytical expressions to solve the problem of optimal allocation of multiple PV units in distribution systems, which has high performance in accuracy, flexibility and computational speed.

The influence of the power grid strength and control loop interactions on the system stability were previously demonstrated (Huang et al., 2015; Xia et al., 2018; Malik et al., 2019) by using the state-space model and eigenvalue method. The stability of the system degrades whenever the power grid strength lowers or the interactions intensify. Moreover, Eftekharnejad (Eftekharnejad et al., 2013) reported that a high penetration of PV generation would reduce the damping of certain critical modes, which in turn causes the system to oscillate, compromising the system’s stability. Furthermore, it was shown that a high penetration of the PV generation can affect the voltage stability of the system (Yan and Saha, 2012). Moradi-Shahrbabak (Moradi-Shahrbabak and Tabesh, 2018) conducted stability analysis based on the state-space model and suggested that the damping of the oscillation mode would change with the change of parameters (i.e., capacitance and reactance) corresponding to the DC-link and front-end converter. They also showed that the increase of capacitance and reactance can lead to the risk of instability. Using a theoretical analysis, Du (Du et al., 2020) proposed an index to assess the impact of an increase in the number of PV power generation units on the stability of the system. Based on the aforementioned studies, it is evident that the connection of PV power systems to a grid would affect the stability of the system in many aspects.

Previously (Du et al., 2017; Du et al., 2018; Chen et al., 2019), a new concept of open-loop modal resonance (OLMR) for the grid-connected wind power generation was proposed to induce power system oscillations. The novel OLMR theory provides an alternative perspective to understand the mechanism of the oscillatory instability caused by a grid-connected wind power generation system. It also constitutes a tool to examine the risk of oscillations caused by the grid-connected wind power generation system in practical power systems. The OLMR theory was based on the state-space model of the open-loop subsystem, and evaluated the instability risk of the system with the OMLR condition, which makes up for the deficiency of the traditional modal analysis method in revealing the stability mechanism. In this study, the OLMR theory was applied to investigate the occurrence of low-frequency oscillations caused by a grid-connected PV power generation in the regional power system in western China. The investigation aimed to understand why the grid-connected PV power generation system induces low-frequency oscillations in the regional power system. This is the first aspect of the contributions made by the present study.

According to relevant prior studies (Du et al., 2017; Du et al., 2018; Chen et al., 2019), the stronger the OLMR, the more at risk would be the grid-connected wind power generation system. However, the key elements, which may affect the intensity of the OLMR were not studied. Therefore, in the present study, the electrical distance between multiple grid-connected PV farms (under OLMR) and that between each of the grid-connected PV farms and main grid are examined. This study sought to understand why the low-frequency oscillations caused by the grid-connected PV power generation system occurred in a particular regional power system in western China. Subsequently, this examination could serve as a practical guidance for the planning of grid connections of PV generators in the future to avoid the aforementioned challenges. This forms the second potential contribution of this study.

Herein, the theory of OLMR is introduced first in Section 2. In Section 3, the mathematical model of a PV farm is built using the model (Tan et al., 2004; Du et al., 2020). In Section 4, a linearized state-space model of the simplified regional power system in western China with two grid-connected PV farms (where the low-frequency oscillations were observed) is established. Section 5 details the application of the theory of OLMR to examine the impact of the electrical distance between the two grid-connected PV farms and the intensity of the OLMR between each of the grid-connected PV farms. Furthermore, the results of the non-linear simulation are presented to demonstrate the correctness of the OLMR analysis. Finally, conclusions and future work are presented in Section 6.

This study made several notable contributions. First, based on the OLMR theory, the origin of the induced low-frequency oscillations in the regional power system was elucidated. Second, the influence of the electrical distance on the OLMR was examined using several numerical examples. This paper showed that re-tuning parameters is beneficial in eliminating OLMR and improving the closed-loop mode damping (−0.015→0.119). In addition, we revealed that a constant electrical distance between each of the grid-connected PV farms and the main grid would not affect the oscillation stability of the PV power generation system. This feature is applicable in the design and planning of large-scale grid-connected PV farms.

2 Open-Loop Modal Analysis

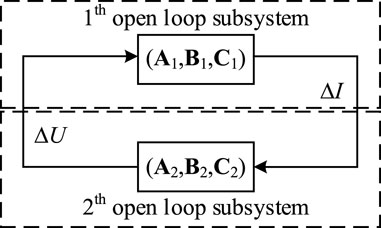
A closed-loop interconnection model can be divided into two open-loop subsystems interconnected by current and voltage, as shown in Figure 1.

FIGURE 1

FIGURE 1. Closed-loop interconnection model.

$\left({\mathbf{A}}_1,{\mathbf{B}}_1,{\mathbf{C}}_1\right)$ and $\left({\mathbf{A}}_2,{\mathbf{B}}_2,{\mathbf{C}}_2\right)$ are the state-space models of two open-loop subsystems, respectively. Their linearized state-space equations are given by

$\{\begin{array}{l}\frac{d}{dt}\text{Δ}{\mathbf{X}}_1={\mathbf{A}}_1\text{Δ}{\mathbf{X}}_1+{\mathbf{B}}_1\text{Δ}{\mathbf{V}}_1\\ \text{Δ}{\mathbf{I}}_1={\mathbf{C}}_1\text{Δ}{\mathbf{X}}_1\end{array}(1)$

$\{\begin{array}{l}\frac{d}{dt}\text{Δ}{\mathbf{X}}_2={\mathbf{A}}_2\text{Δ}{\mathbf{X}}_2+{\mathbf{B}}_2\text{Δ}{\mathbf{V}}_2\\ \text{Δ}{\mathbf{I}}_2={\mathbf{C}}_2\text{Δ}{\mathbf{X}}_2\end{array}(2)$

the prefix $\text{Δ}$ denotes the small increment of a variable; the subscript is the serial number of the open-loop subsystem; $\text{Δ}\mathbf{X}$ is the state variable column matrix of the open-loop subsystem; $\text{Δ}\mathbf{A}$, $\text{Δ}\mathbf{B}$, and $\text{Δ}\mathbf{C}$ are the state matrix, input matrix, and output matrix of the open-loop subsystem, respectively.

The two open-loop subsystems are represented by two transfer functions, $G_1\left(s\right)$ and $G_2\left(s\right)$, given by

$\{\begin{array}{l}{G}_1\left(s\right)={\displaystyle \sum _{h=1}^n\frac{R_{1h}}{(s-{\lambda }_{1h})}}+K_1\\ G_2\left(s\right)={\displaystyle \sum _{h=1}^m\frac{R_{2h}}{(s-{\lambda }_{2h})}}+K_2\end{array}(3)$

where ${\lambda }_{1h},h=\mathrm{1,2},\cdots ,n$ are the eigenvalues of the open-loop state matrix A₁, $R_{1h},h=\mathrm{1,2},\cdots ,n$ are the residues corresponding to ${\lambda }_{1h},h=\mathrm{1,2},\cdots ,n$, K₁ is the constant term of $G_1\left(s\right)$, ${\lambda }_{2h},h=\mathrm{1,2},\cdots ,m$ are the eigenvalues of the open-loop state matrix A₂, $R_{2h},h=\mathrm{1,2},\cdots ,m$ are the residues corresponding to ${\lambda }_{2h},h=\mathrm{1,2},\cdots ,m$, and K₂ is the constant term of $G_2\left(s\right)$.

The characteristic equation of the closed-loop interconnected system can be obtained as follows:

$1=G_1\left(s\right)G_2\left(s\right)(4)$

Substituting Eq. 3 in Eq. 4, replacing s by ${\tilde{\lambda }}_{1i}$, which is a solution of Eq. 4, and then multiplying both sides by ${({\tilde{\lambda }}_{1i}-{\lambda }_{1i})}^2$ considering ${\lambda }_{2i}\approx {\lambda }_{1i}$ (OLMR condition), the following is obtained:

$\begin{array}{l}{({\tilde{\lambda }}_{1i}-{\lambda }_{1i})}^2\approx \left\{R_{1i}+({\tilde{\lambda }}_{1i}-{\lambda }_{1i})\left[{\displaystyle \sum _{\begin{array}{l}h=1\\ h\ne i\end{array}}^n\frac{R_{1h}}{({\tilde{\lambda }}_{1i}-{\lambda }_{1h})}+K_1}\right]\right\}\\ \begin{array}{ccc}& & \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}\end{array}\times \left\{R_{2i}+({\tilde{\lambda }}_{1i}-{\lambda }_{1i})\left[{\displaystyle \sum _{\begin{array}{l}h=1\\ h\ne i\end{array}}^m\frac{R_{2h}}{({\tilde{\lambda }}_{1i}-{\lambda }_{2h})}+K_2}\right]\right\}\end{array}(5)$

where R_1i and R_2i are the residues corresponding to ${\lambda }_{1i}$ and ${\lambda }_{2i}$, respectively. Hence, in the neighborhood of ${\lambda }_{1i}$,

$\text{Δ}{\lambda }_{1i}^2={({\tilde{\lambda }}_{1i}-{\lambda }_{1i})}^2\approx \underset{{\tilde{\lambda }}_{1i}\to {\lambda }_{1i}}{\mathbf{lim}}{({\tilde{\lambda }}_{1i}-{\lambda }_{1i})}^2\approx R_{1i}{R}_{2i}(6)$

Similarly, replacing s by ${\tilde{\lambda }}_{2i}$, which is also a solution of Eq. 4, the following is obtained:

$\text{Δ}{\lambda }_{2i}^2={({\tilde{\lambda }}_{2i}-{\lambda }_{2i})}^2\approx \underset{{\tilde{\lambda }}_{2i}\to {\lambda }_{2i}}{\mathbf{lim}}{({\tilde{\lambda }}_{2i}-{\lambda }_{2i})}^2\approx R_{1i}{R}_{2i}(7)$

From Eqs. 6 and 7,

$\{\begin{array}{l}{\tilde{\lambda }}_{1i}\approx {\lambda }_{1i}\pm \sqrt{R_{1i}{R}_{2i}}\\ {\tilde{\lambda }}_{2i}\approx {\lambda }_{2i}\pm \sqrt{R_{1i}{R}_{2i}}\end{array}(8)$

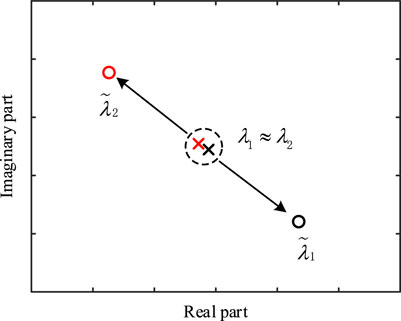
According to (8), when the OLMR condition is satisfied, the corresponding closed-loop mode (${\tilde{\lambda }}_{1i}$ and ${\tilde{\lambda }}_{2i}$) would be located in the opposite position around the modal resonance point (${\lambda }_{2i}\approx {\lambda }_{1i}$) on the complex plane, as shown in Figure 2. Evidently, one of the closed-loop modes (${\tilde{\lambda }}_{1i}$) would move to the right on the complex plane. If the closed-loop mode moves to the right half plane on the complex plane, the system would become unstable.

FIGURE 2

FIGURE 2. The phenomenon of OLMR.

3 Mathematical Model OF PV Farm

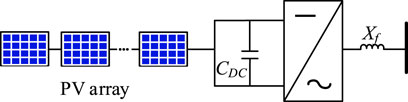
PV power generation is a technology that converts solar energy into electrical energy via the photovoltaic effect. A PV farm mainly comprises a PV array, an inverter and its control system, and filter reactance. Its basic structure is shown in Figure 3, where $X_f$ denotes the filter reactance and $C_{DC}$ is the capacitance of the DC capacitor.

FIGURE 3

FIGURE 3. Schematic of a PV farm.

3.1 PV Array Model

Tan (Tan et al., 2004) proposed a mathematical model for PV arrays, assuming that its operation is under standard temperature (25 °C) and illumination (1000 W/m²) conditions.

$I_{PV}=n_p{I}_{sc}\left[1-C_1\left(\exp \left(\frac{U_{PV}}{n_s{C}_2{U}_{oc}}\right)-1\right)\right](9)$

where $C_1=\left(1-I_m/I_{sc}\right)\exp \left(-U_m/\left(C_2{U}_{oc}\right)\right)$ and $C_2=\left(U_m/U_{oc}-1\right)\cdot {\left[\ln \left(1-I_m/I_{sc}\right)\right]}^{-1}$. $I_{PV}$ is the output current of the PV array, $U_{PV}$ is the positive and negative voltage of the PV array, $n_p$ and $n_s$ are the parallel number and series number of PV cells, respectively, $I_m$, $I_{sc}$, $U_m$ and $U_{oc}$ are the maximum power point current, short-circuit current, maximum power point voltage, and open-circuit voltage of the PV array, respectively.

3.2 Model of the Inverter Inner and Outer Loop Control System

The dynamic model of the capacitor voltage is given as

$C_{DC}{U}_{DC}\frac{d{U}_{DC}}{dt}=P_1-P_2(10)$

where $C_{DC}$ is the capacitance of the DC capacitor, $U_{DC}$ is the voltage across the DC capacitor, $P_1$ is the output active power of the PV array, and $P_2$ is the active power flowing into the inverter from the capacitor.

The control system of the inverter is divided into outer loop control and inner loop control. The block diagram of the inverter control system is shown in Figure 4.

FIGURE 4

FIGURE 4. Block diagram of the inverter control system.

The outer loop control model is designed using Eq. 11 as:

$\{\begin{array}{l}\frac{d{x}_1}{dt}=K_{i1}\left(U_{DC}^{ref}-U_{DC}\right)\\ I_d^{ref}=x_1+K_{p1}\left(U_{DC}^{ref}-U_{DC}\right)\end{array}(11)$

where $x_1$ is the state variable of the output of the integral link of the voltage control outer loop, the superscript ref is the reference value of the corresponding quantity, $K_{p1}$ and $K_{i1}$ are the proportional and integral coefficients of the voltage control outer loop, respectively.

The current inner loop control model is shown in Eq. 12 as:

$\{\begin{array}{l}\frac{d{x}_2}{dt}=K_{i2}(I_d^{ref}-I_d)\\ \frac{d{x}_3}{dt}=K_{i3}(I_q^{ref}-I_q)\\ U_d^{ref}=x_2+K_{p2}(I_d^{ref}-I_d)-X_f{I}_q+U_{td}\\ U_q^{ref}=x_3+K_{p3}(I_q^{ref}-I_q)-X_f{I}_d+U_{tq}\end{array}(12)$

where $x_2$ and $x_3$ are the state variables of the output of the integral link of the inner loop for the current control of d-axis and q-axis, respectively. $X_f$ is the filter reactance. $I_d$ and $I_q$ are the d-axis and q-axis components of the inverter output current, respectively. $U_d$ and $U_q$ are the d-axis and q-axis components of the AC side port voltage of the inverter, $U_{td}$ and $U_{tq}$ are the d-axis and q-axis components of the voltage of the junction point of PV farm, respectively. $K_{p2}$, $K_{i2}$, $K_{p3}$, and $K_{i3}$ are proportional–integral (PI) control parameters of the d-axis and q-axis current inner loop, respectively.

3.3 Filter Model

The mathematical model of the filter is shown in Eq. 13 as follows:

$\{\begin{array}{l}{X}_f\frac{d{I}_d}{dt}=X_f{\omega }_0{I}_q+{\omega }_0{U}_d-{\omega }_0{U}_{\text{t}d}\\ X_f\frac{d{I}_q}{dt}=-X_f{\omega }_0{I}_d+{\omega }_0{U}_q-{\omega }_0{U}_{tq}\end{array}(13)$

where ${\omega }_0$ is the power frequency.

3.4 Phase-Locked Loop Model

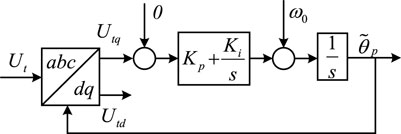
The control structure of the phase-locked loop (PLL) model is shown in Figure 5.

FIGURE 5

FIGURE 5. Control structure of the PLL model.

The dynamic model of the PLL can be obtained using Eq. 14.

$\{\begin{array}{l}\frac{d{\tilde{\theta }}_p}{dt}=K_p{U}_{tq}+x_{pll}+{\omega }_0\\ \frac{d{x}_{pll}}{dt}=K_i{U}_{tq}\end{array}(14)$

where, $K_p$ and $K_i$ are the control parameters of the PLL, $U_{tq}$ is the q-axis component of the voltage at the junction point, and $x_{pll}$ is the state variable of the output of the integral link of the PLL.

Thus, Eqs. 9–14 constitute the mathematical model of the PV farm.

4 Linearized State-Space Model of the Photovoltaic Power Generation System

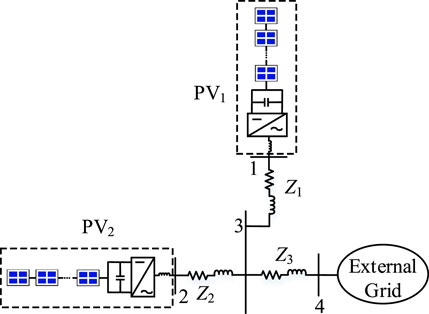
A PV power generation system with two PV farms is illustrated in Figure 6. The system’s structure is simplified based on a regional power network in the western area of China, and the main grid is replaced by an infinite system. To study the impact of the electrical distance between grid-connected PV farms on the stability of the system oscillation, a linearized state-space model of the PV power generation system is established. The linearized model of the PV farm is based on the mathematical model proposed in Section 3.

FIGURE 6

FIGURE 6. Schematic of the PV power generation system.

Assuming that the mathematical model, operating state and control parameters of PV₁ and PV₂ are consistent, the linearized state-space model of the kth (k = 1,2) PV farm can be expressed as follows:

$\{\begin{array}{l}\frac{d}{dt}\text{Δ}{\mathit{X}}_k={\mathit{A}}_p\text{Δ}{\mathit{X}}_k+{\mathit{B}}_p\text{Δ}{\mathit{V}}_k\\ \text{Δ}{\mathit{I}}_k={\mathit{C}}_p\text{Δ}{\mathit{X}}_k,\begin{array}{cc}& k=\mathrm{1,2}\end{array}\end{array}(15)$

where $\text{Δ}{\mathit{X}}_k$ is the state variable vector of the kth PV farm (i.e., the kth PV). $\text{Δ}{\mathit{A}}_k$, $\text{Δ}{\mathit{B}}_k$, and $\text{Δ}{\mathbf{C}}_k$ are the linearized state matrix, input matrix, and output matrix of the kth PV, respectively. $\text{Δ}{\mathbf{V}}_k={\left[\begin{array}{cc}\text{Δ}{V}_{kx}& \text{Δ}{V}_{ky}\end{array}\right]}^T$ and $\text{Δ}{\mathbf{I}}_k={\left[\begin{array}{cc}\text{Δ}{I}_{kx}& \text{Δ}{I}_{ky}\end{array}\right]}^T$, where $V_{kx}+j{V}_{ky}$ and $I_{kx}+j{I}_{ky}$ are the terminal voltage and output current of the kth PV in the common x-y coordinate, respectively.

The node admittance matrix of the power system can be written as

$\left[\begin{array}{c}\text{Δ}{\mathit{I}}_1\\ \text{Δ}{\mathit{I}}_2\\ \mathit{0}\\ \mathit{0}\end{array}\right]=\left[\begin{array}{cccc}{\mathit{Y}}_{11}& {\mathit{Y}}_{12}& {\mathit{Y}}_{13}& {\mathit{Y}}_{14}\\ {\mathit{Y}}_{21}& {\mathit{Y}}_{22}& {\mathit{Y}}_{23}& {\mathit{Y}}_{24}\\ {\mathit{Y}}_{31}& {\mathit{Y}}_{32}& {\mathit{Y}}_{33}& {\mathit{Y}}_{34}\\ {\mathit{Y}}_{41}& {\mathit{Y}}_{42}& {\mathit{Y}}_{43}& {\mathit{Y}}_{44}\end{array}\right]\left[\begin{array}{c}\text{Δ}{\mathit{V}}_1\\ \text{Δ}{\mathit{V}}_2\\ \text{Δ}{\mathit{V}}_3\\ \text{Δ}{\mathit{V}}_4\end{array}\right](16)$

where ${\mathit{Y}}_{ij}=\left[\begin{array}{cc}{\mathit{Y}}_{ijxx}& {\mathit{Y}}_{ijxy}\\ {\mathit{Y}}_{ijyx}& {\mathit{Y}}_{ijyy}\end{array}\right](i,j=\mathrm{1,2,3,4})$.

$\left[\begin{array}{c}\text{Δ}{\mathit{V}}_1\\ \text{Δ}{\mathit{V}}_2\end{array}\right]\mathrm{=}{\mathit{Y}}^{-1}\left[\begin{array}{c}\text{Δ}{\mathit{I}}_1\\ \text{Δ}{\mathit{I}}_2\end{array}\right](17)$

where $\mathit{Y}\mathrm{=}\left[\begin{array}{cc}{\mathit{Y}}_{11}& {\mathit{Y}}_{12}\\ {\mathit{Y}}_{21}& {\mathit{Y}}_{22}\end{array}\right]\mathrm{-}\left[\begin{array}{cc}{\mathit{Y}}_{13}& {\mathit{Y}}_{14}\\ {\mathit{Y}}_{23}& {\mathit{Y}}_{24}\end{array}\right]{\left[\begin{array}{cc}{\mathit{Y}}_{33}& {\mathit{Y}}_{34}\\ {\mathit{Y}}_{43}& {\mathit{Y}}_{44}\end{array}\right]}^{\mathrm{-}1}\left[\begin{array}{cc}{\mathit{Y}}_{31}& {\mathit{Y}}_{32}\\ {\mathit{Y}}_{41}& {\mathit{Y}}_{42}\end{array}\right]$, and ${\mathit{Y}}^{-1}=\left[\begin{array}{cc}{\mathit{Z}}_{11}& {\mathit{Z}}_{12}\\ {\mathit{Z}}_{21}& {\mathit{Z}}_{22}\end{array}\right]$.

According to Eqs. 15, 17, the following full-order linearized model of the PV power generation system depicted in Figure 6 is obtained by

$\left[\begin{array}{c}\frac{d}{dt}\text{Δ}{\mathit{X}}_1\\ \frac{d}{dt}\text{Δ}{\mathit{X}}_2\end{array}\right]={\mathit{A}}_s\left[\begin{array}{c}\text{Δ}{\mathit{X}}_1\\ \Delta {\mathit{X}}_2\end{array}\right](18)$

where ${\mathit{A}}_s\mathrm{=}\left[\begin{array}{cc}{\mathit{A}}_p+{\mathit{B}}_p{\mathit{Z}}_{\mathrm{11}}{\mathit{C}}_p& {\mathit{B}}_p{\mathit{Z}}_{12}{\mathit{C}}_p\\ {\mathit{B}}_p{\mathit{Z}}_{21}{\mathit{C}}_p& {\mathit{A}}_p+{\mathit{B}}_p{\mathit{Z}}_{22}{\mathit{C}}_p\end{array}\right]$.

5 Sample Analysis

This section presents an analysis of the impact of the electrical distance between grid-connected PV farms and the control parameters on the OLMR by using the results of the calculation examples. The electrical distance between nodes represents the closeness of the connection between them, which is jointly determined by the physical distance and the connection mode between nodes. The system structure is shown in Figure 6. The system parameters and PV farm parameters are provided in the Appendix. In this study, the model building and non-linear simulation are completed by code programming in M-file of MATLAB, and the non-linear simulation is obtained using the improved Euler method.

5.1 Influence of OLMR on Oscillation Stability

The open-loop modes of the subsystems of the two PV farms can be calculated using Eq. 15. As their mathematical models, control parameters, and operating states are essentially the same, the oscillation modes of the open-loop subsystems are also the same. Under the current situation, two groups of oscillation modes were mainly examined. The specific values and damping are shown in Table 1, which shows that the damping of the oscillation mode dominated by the PLL is smaller than that dominated by the DC voltage outer loop and the real part is closer to the virtual axis. As this study was focused on the stability of grid-connected PV farms, only the oscillation mode dominated by the PLL with weaker damping was considered.

TABLE 1

TABLE 1. Open-loop oscillation modes of the PV farm.

Considering the main grid as an infinite system, the PV power generation system shown in Figure 6 can be regarded as a closed-loop interconnected system composed of two PV farm subsystems. The dominant modes $({\lambda }_1,{\lambda }_2)$ of the PLL of the two open-loop subsystems are essentially the same, thus satisfying the conditions for the occurrence of OLMR. Therefore, the closed-loop modes corresponding to the open-loop modes are distributed on both sides of the open-loop mode. The closed-loop oscillation modes $({\tilde{\lambda }}_1,{\tilde{\lambda }}_2)$ are calculated using Eq. 18, as shown in Figure 7.

FIGURE 7

FIGURE 7. OLMR phenomenon of ${\lambda }_1$ and ${\lambda }_2$.

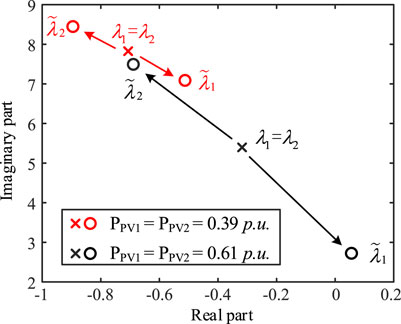
As can be observed in Figure 7, when OLMR occurs, a closed-loop mode would appear on the right side of the open-loop mode, and the damping decreases, that is, the oscillation stability of the closed-loop system decreases as compared with that in the open-loop system.

In order to study the influence of PV power generation variation on the OLMR, low-power generation (P_PV1 = P_PV2 = 0.39 p. u.) and high-power generation (P_PV1 = P_PV2 = 0.61 p. u.) are considered. The PLL dominant modes $({\lambda }_1,{\lambda }_2,{\tilde{\lambda }}_1,{\tilde{\lambda }}_2)$ are also calculated, as shown in Figure 8. Evidently, as long as the OLMR condition is satisfied, there would be closed-loop mode damping reduction, even negative damping. Figures 7, 8 indicate that the increase of power generation decreases the stability of the system.

FIGURE 8

FIGURE 8. OLMR phenomenon of ${\lambda }_1$ and ${\lambda }_2$ when PV power generation varies.

5.2 Impact of Electrical Distance Between Grid-Connected PV Farms on System Stability

For a PV power generation system with two PV farms, the electrical distance between the grid-connected PV farms is an important factor affecting the system’s oscillation stability.

To study the impact of different electrical distances on the system stability, the distance between two PV farms is gradually increased, that is, the values of $Z_1$ and $Z_2$ are gradually increased by $\mathrm{\Delta }{Z}_{\mathrm{1,2}}=0.002+j0.02$ at each step. Eqs. 15 and 18 are used to calculate the open-loop oscillation modes and closed-loop oscillation modes, respectively. Table 2 lists the calculation results of the open-loop oscillation modes and open-closed-loop oscillation mode offsets ($\mathrm{\Delta }\lambda =\tilde{\lambda }-\lambda$). The trajectories of the open-loop oscillation mode and closed-loop oscillation mode on the complex plane are shown in Figure 9.

TABLE 2

TABLE 2. Calculation results for increasing electrical distance between PV farms.

FIGURE 9

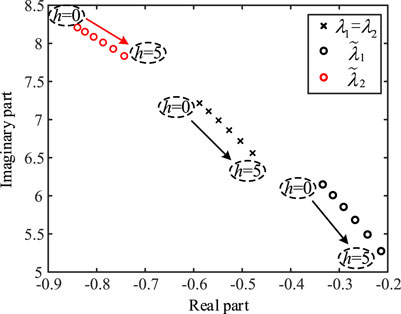
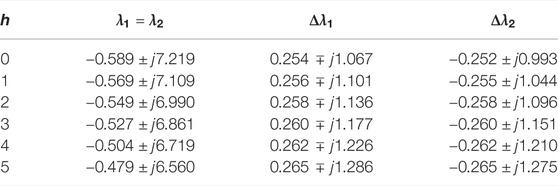
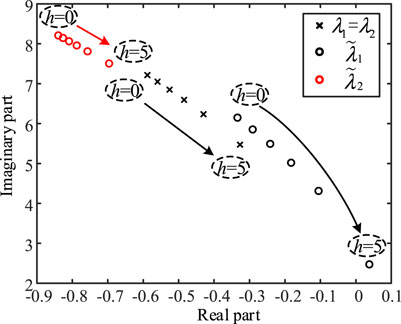
FIGURE 9. Trajectories of open and closed-loop mode with increasing electrical distance between the PV farms.

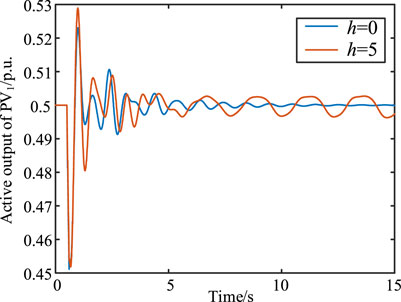
According to the results shown in Table 2 and Figure 9, as the electrical distance between grid-connected PV farms increases, the open-loop oscillation mode damping, dominated by the PLL, decreases. The offset ($\mathrm{\Delta }\lambda$) of the open-loop and closed-loop oscillation modes also increases. This implies that the resonance intensity increases, so that the damping of the weakly damped closed-loop oscillation mode gradually decreases, and the oscillation stability of the system decreases. When h = 0 and h = 5, the damping coefficients of the closed-loop mode are −0.05 and −0.04 respectively; the damping decreases, but the decrease is not evident. To verify the correctness of the eigenvalue analysis, a non-linear simulation of the system was performed. The fault setting was that the active power output of PV₁ decreases by 15% at 0.5 s and returns to normal after 0.1 s. Figure 10 shows the non-linear simulation results of the active power output of PV₁. Evidently, compared with the non-linear simulation result of h = 5, the oscillation frequency is higher, and the oscillation attenuation speed is faster when h = 0. The stability can be recovered faster, that is, the oscillation stability of the system is better. The non-linear simulation results agree well with the eigenvalue analysis results.

FIGURE 10

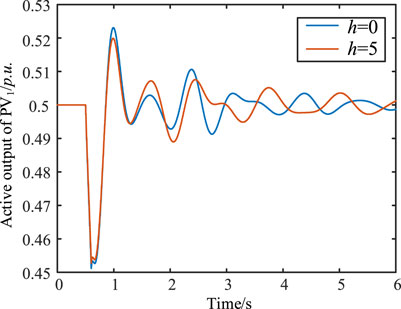
FIGURE 10. Non-linear simulation results of the active power output of PV₁ when the electrical distance between PV farms increases.

5.3 Impact of Electrical Distance Between Each PV Farm and Main Grid on System Stability

The electrical distance between each of the PV farms and the main grid was adjusted, without changing the electrical distance between the PV farms, and its stability was then studied. $Z_1$ and $Z_2$ remained the same while the value of $Z_3$ was increased successively. Additionally, $\mathrm{\Delta }{Z}_3=0.002+j0.02$ for each step. Eqs. 15 and 18 were used to calculate the open-loop and closed-loop oscillation modes, respectively. Table 3 lists the calculation results of the offset of the open-loop oscillation mode and the open-loop oscillation mode. The trajectories of the open-loop oscillation mode and the closed-loop oscillation mode on the complex plane are shown in Figure 11.

TABLE 3

TABLE 3. Calculation results when $Z_3$ increases.

FIGURE 11

FIGURE 11. Trajectories of the open and closed-loop mode when $Z_3$ increases.

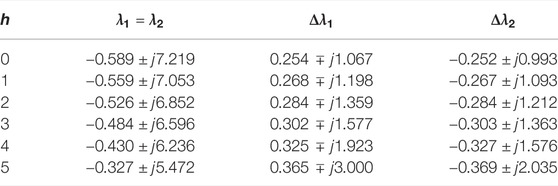
As indicated by the results shown in Table 3 and Figure 11, when $Z_3$ increases, the open-loop oscillation mode damping, dominated by the PLL, decreases significantly. The resonance intensity significantly increases, such that the offset ($\mathrm{\Delta }\mathrm{\lambda }$) of the open and closed-loop oscillation modes increases significantly, and the damping of the weakly damped closed-loop oscillation mode decreases. When $Z_3$ is excessively increased (h = 5), the negatively damped closed-loop oscillation mode appears, that is, the current system is unstable. Further, the non-linear simulation of the system was performed. The fault setting is that the active power output of PV₁ decreases by 15% at 0.5 s and returns to normal after 0.1 s. Figure 12 shows the non-linear simulation results of PV₁ active power output. When h = 0, the oscillation gradually attenuates and tends to be stable, and the system is stable. When h = 5, the oscillation frequency of the system decreases and begins to diverge. At this point, the system is unstable, which is consistent with the result of eigenvalue analysis.

FIGURE 12

FIGURE 12. Non-linear simulation results of the active power output of PV₁ when $Z_3$ increases.

The obtained results indicate that the increasing electrical distance between the PV farms and $Z_3$ would lead to a decrease in the open-loop oscillation mode damping led by the PLL and an increase in the resonance intensity. Additionally, it can lead to a decrease in the system stability. When the increase is excessively large, negative damping of the closed-loop mode may appear, which makes the system unstable. Therefore, increasing the electrical distance between PV farms and $Z_3$ is essentially increasing the electrical distance between each of the PV farms and the main grid. In other words, increasing the electrical distance between each of the PV farms and the main grid increases the OLMR intensity and thus reduces the system stability. If the electrical distance increases excessively, the system may become unstable.

5.4 Impact of Re-Tuning Parameters Using Participation Factor

To improve the phenomenon of system instability caused by an increase in $Z_3$, the participation factor of the closed-loop mode ${\tilde{\lambda }}_1$ is calculated for h = 0 and h = 5, and the calculation results are shown in Figure 13. For h = 0 and h = 5, the difference in ${\tilde{\lambda }}_1$ value is negligible. ${\tilde{\lambda }}_1$ is mainly related to $\mathrm{\Delta }{U}_{DC}$, $\mathrm{\Delta }{x}_1$, $\mathrm{\Delta }{\tilde{\theta }}_p$, and $\Delta x_{pll}$ of PV₁ and PV₂; the effects of $\mathrm{\Delta }{\tilde{\theta }}_p$ and $\mathrm{\Delta }{x}_{pll}$ are relatively more prominent.

FIGURE 13

FIGURE 13. (A) Participation factor of ${\tilde{\lambda }}_1$, (B) Participation of the state variables in ${\tilde{\lambda }}_1$.

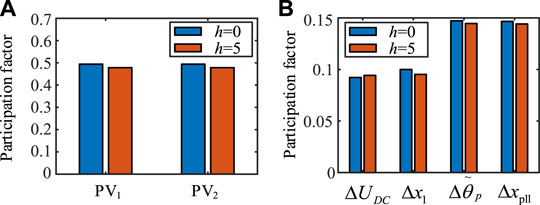
Control parameters are also important factors that affect the resonant intensity of the open-loop mode. To improve the stability of the system when h = 5, the OLMR intensity needs to be reduced. As shown in Figure 13, the ${\tilde{\lambda }}_1$ value is mainly related to the PLL control parameters. In this study, the control parameters of the PLL of PV₂ (K_p: 0.005→0.03, K_i: 0.2→0.1) were adjusted to reduce the PLL bandwidth. The open-loop and closed-loop oscillation modes were calculated using Eqs. 15 and 18. Table 4 lists the calculation results of the open-loop oscillation mode, the closed-loop oscillation mode, and the offset of the open-loop and closed-loop oscillation modes. According to the results shown in Table 4, the open-loop oscillation modes ${\lambda }_1$ and ${\lambda }_2$ exhibit a large difference when the parameters are re-tuned, which makes the real part of $\mathrm{\Delta }{\lambda }_1$ smaller. This implies that the OLMR intensity is reduced. At this time, there is no negative damping closed-loop mode in the PV power generation system; this implies that the system is stable.

TABLE 4

TABLE 4. Calculation results before and after parameter adjustments.

The same system disturbance was set for the nonlinear simulation of the system. Figure 14 shows the simulation result of the PV₁ active power output. Thus, after parameter adjustment, the system can remain stable after a disturbance, and the system stability is improved; this is consistent with the model analysis result. Evidently, the reduction of the PLL bandwidth can compensate for greater electrical distance.

FIGURE 14

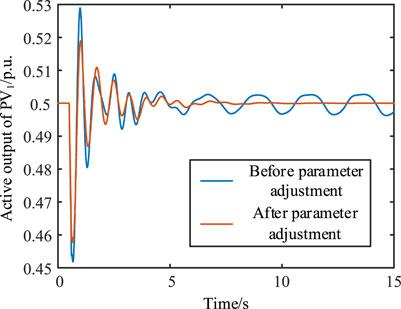
FIGURE 14. Non-linear simulation results of the active power output of PV₁ before and after parameter adjustments.

5.5 Electrical Distance between Each PV Farm and Main Grid Kept Unchanged

To further determine the impact of the electrical distance between grid-connected PV farms, as well as between each of the PV farms and the main grid, the electrical distance between each PV farm and the main grid was kept unchanged while increasing the electrical distance between PV farms. The specific adjustment scheme is as follows. The PV power generation system in this example can be considered as composed of two PV farms in parallel. According to the relevant knowledge of circuit principles, $\mathrm{\Delta }{Z}_{\mathrm{1,2}}=0.002+j0.02$ and $\mathrm{\Delta }{Z}_3=-0.001-j0.01$ were adjusted each time, so that the electrical distance between each of PV farms and the main grid remained unchanged. Open-loop and closed-loop oscillation modes were calculated using the same method. Table 5 lists the calculation results of the open-loop oscillation mode and the offset of the open-loop oscillation mode dominated by the PLL. The trajectories of the open-loop oscillation mode and the closed-loop oscillation mode on the complex plane are shown in Figure 15.

TABLE 5

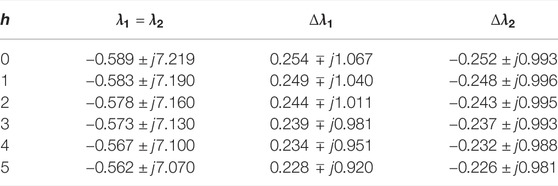
TABLE 5. Calculation results when the electrical distance between each of PV farms and the main grid remains unchanged.

FIGURE 15

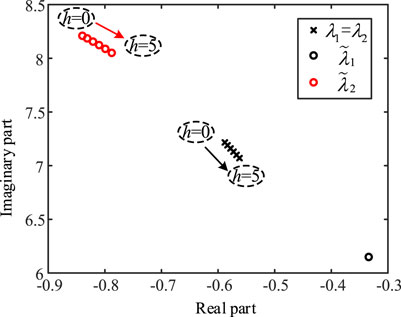
FIGURE 15. Trajectories of the open and closed-loop mode when the electrical distance between each of the PV farms and the main grid remains unchanged.

Table 5 and Figure 15 indicate that the damping of the open-loop oscillation mode dominated by the PLL changes slightly, and the resonant intensity is weakened when the electrical distance between each of the PV farms and the main grid is constant with increasing electrical distance between the PV farms. Additionally, increasing the electrical distance between each of the grid-connected PV farms and the main grid has a greater effect on the OLMR intensity as compared with that between individual grid-connected PV farms. In addition, the closed-loop oscillation mode near the virtual axis led by the PLL is essentially stationary in the complex plane when the electrical distance between each of PV farms and the main grid is constant; this implies that the risk of instability of PV power generation system would not increase.

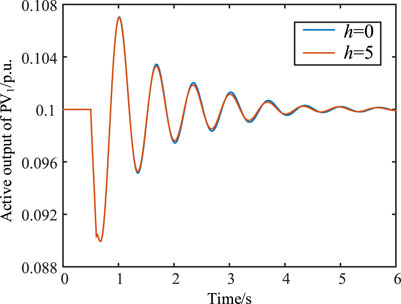
A non-linear simulation of the system was performed with the fault setting such that the active power output of PV₁ decreases by 15% at 0.5 s and returns to normal after 0.1 s. Figure 16 shows the non-linear simulation results of the PV₁ active power output. When h = 0 and 5, its response characteristics are essentially consistent. This is in agreement with the results of the eigenvalue analysis.

FIGURE 16

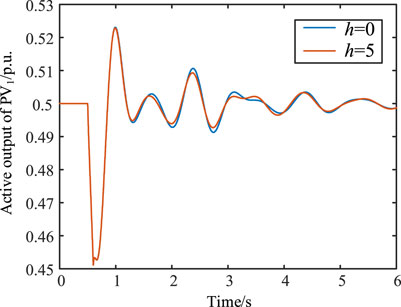
FIGURE 16. Non-linear simulation results of the active power output of PV₁ when the electrical distance between each of the PV farms and the main grid remains unchanged.

To verify that the oscillation stability of the system is affected when the electrical distance between each of the PV farms and the main grid is constant, the PV power generation system shown in Figure 6 was adjusted. The number of PV farms was increased to 9 in parallel, and a centralized external transmission was also adopted. The active power output of each PV farm was adjusted to 0.1 p. u. In the new system, the electrical distance between each PV farm and the main grid remained unchanged, that is, $\mathrm{\Delta }{Z}_{1,\cdots ,9}=0.009+j0.09$, and $\mathrm{\Delta }{Z}_{10}=-0.001-j0.01$ ($Z_{10}$ is the external transmission line parameter) are adjusted each time. Eq. 13 is not applicable to the current system; therefore, the perturbation method was adopted to calculate the closed-loop oscillation mode. Table 6 lists the calculation results of the least damped closed-loop oscillation mode (${\lambda }_{\min }$) dominated by the PLL. The non-linear simulation of the system was performed, and the fault setting was the same as above. Figure 17 shows the non-linear simulation results of the active power output of PV₁.

TABLE 6

TABLE 6. Calculation results of.${\lambda }_{\min }$.

FIGURE 17

FIGURE 17. Non-linear simulation results of the active power output of PV₁ in the new system.

The results shown in Table 6 and Figure 17 verify that under the conditions of changing the number and operating level of grid-connected PV farms, as long as the electrical distance between each of PV farms and the main grid remains unchanged, the PV power generation system would not increase the risk of instability. This finding can be applied to the planning and design of PV farms. In the practical situation, the number and location of PV farms planned according to the PV power generation system are combined with the electrical distance to design the location of the connection point, thus potentially improving the oscillation stability of the system.

5.6 Discussion

As indicated by the afore described results, when OLMR occurs in the PV power generation system, there is a corresponding closed-loop mode with reduced damping, which reduces the system stability. It is determined that increasing PV power generation reduces system stability, which is consistent with the conclusion of Eftekharnejad (Eftekharnejad et al., 2013). Increasing the electrical distance between grid-connected PV farms and between each of grid-connected PV farms and the main grid reduces the strength of the power grid, which will increase the OLMR intensity and thus reduces the stability of the PV generation system. Evidently, the findings herein confirm the relevant conclusions by prior studies (Huang et al., 2015; Xia et al., 2018; Malik et al., 2019). It has been proposed that increased PLL bandwidth would decrease stability (Céspedes and Sun, 2011; Liu et al., 2021). In this study, PLL parameters were re-tuned to reduce PLL bandwidth and improve system stability. The electrical distance between each of the PV farms and the main grid remained unchanged by adjusting the external transmission distance of the PV system when the distance between PV farms increases, so that the stability of the system will not be affected.

6 Conclusion

On the basis of the OLMR theory of the mode analysis method, this study examined the impact of the electrical distance between grid-connected PV farms in an actual PV power generation system. The main conclusions of this study are summarized as follows.

When the OLMR occurs in a PV power generation system, there may be a weakly damped or negatively damped closed-loop mode, which implies that the stability of the system would decrease.

With the increase in the electrical distance between the grid-connected PV farms as well as between each of the grid-connected PV farms and the main grid, the intensity of the OLMR would increase, which may lead to the appearance of negative damping mode $\left({\tilde{\lambda }}_1=0.038\pm j2.473\right)$ and make the system unstable. Moreover, the increase in the electrical distance between each of the grid-connected PV farms and the main grid has a greater effect on the OLMR than that between individual grid-connected PV farms.

By re-tuning the control parameters (K_p: 0.005→0.03, K_i: 0.2→0.1) of the PLL, the open-loop modal resonant condition is not satisfied; this can effectively improve the closed-loop mode damping (−0.015→0.119). A constant electrical distance between each of the grid-connected PV farms and the main grid would not affect the oscillation stability of the PV power generation system.

The aforedescribed research findings can guide the grid-connected planning of large-scale PV power generation. In practice, the number and location of PV farms planned according to the PV power generation system can be combined with the consideration of electrical distance to design the location of the connection point, thus improving the oscillation stability of the system.

This study focused only on the influence of electrical distance on the OLMR when the PV power generation system adopts a parallel structure. There is no systematic study on the more complex chain structure; however, it is evidently a greater challenge because the electrical distance between each of PV farms and the main grid in the chain case is different.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BZ proposed this research direction and assigned the work. PS determined the research method and completed the main work. The rest of the work is done by YX and ZZ.

Funding

“This work is supported by the Science and Technology Project of State Grid Sichuan Electric Power Company (No.52199720002S)”.

Conflict of Interest

BZ, PS, YX and ZZ were employed by State Grid Sichuan Electric Power Company.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix

The system parameters shown in Figure 6 were as follows. The system base value was S_b = 100 MW. The power generation of PV₁ and PV₂ were 0.5 p. u. and 0.5 p. u., respectively. The transmission line impedances were Z_1,2 = 0.01 + j0.1 p. u. and Z₃ = 0.04 + j0.4 p. u., respectively.

The filter reactance of PV farms was $X_f$ = 0.05 p. u., DC capacitance and PI gains of inverter control system (see Figure 4) were C_DC = 50 mF, K_p1 = 0.2, K_i1 = 15, K_p2 = 1, K_i2 = 30, K_p3 = 1, K_i3 = 30. PI gains of PLL (see Figure 5) were K_p = 0.005, K_i = 0.2. The parameters of PV array were I_m = 5.68 A, I_sc = 6.75 A, U_m = 26.2 V, U_oc = 36.4 V, n_s = 3,000, and n_p = 10.

In order to relate PI controller parameters to physical implementation, the bandwidth of each controller is given. The corresponding controller bandwidths for DC-link voltage, current control and PLL were 0.758, 45.212 and 0.696 Hz. The results obtained are calculated on the basis of a prior study (Teodorescu et al., 2011).

References

Abubakr, H., Vasquez, J. C., Mahmoud, K., Darwish, M. M. F., and Guerrero, J. M. (2022). Comprehensive Review on Renewable Energy Sources in Egypt-Current Status, Grid Codes and Future Vision. IEEE Access 10, 4081–4101. doi:10.1109/ACCESS.2022.3140385

CrossRef Full Text | Google Scholar

Ali, E. S., El-Sehiemy, R. A., Abou El-Ela, A. A., Mahmoud, K., Lehtonen, M., Darwish, M. M. F., et al. (2021). An Effective Bi-stage Method for Renewable Energy Sources Integration into Unbalanced Distribution Systems Considering Uncertainty. Processes 9, 471. doi:10.3390/pr9030471

CrossRef Full Text | Google Scholar

Bendary, A. F., Abdelaziz, A. Y., Ismail, M. M., Mahmoud, K., Lehtonen, M., and Darwish, M. M. F. (2021). Proposed ANFIS Based Approach for Fault Tracking, Detection, Clearing and Rearrangement for Photovoltaic System. Sensors 21, 2269. doi:10.3390/s21072269

PubMed Abstract | CrossRef Full Text | Google Scholar

Céspedes, M., and Sun, J. (2011). “Modeling and Mitigation of Harmonic Resonance between Wind Turbines and the Grid,” in 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17-22 Sept. 2011, 2109–2116. doi:10.1109/ECCE.2011.6064047

CrossRef Full Text | Google Scholar

Chen, C., Du, W., Wang, L. A., and Wang, H. (2019). Mechanism Investigation of Sub-synchronous Oscillations in Power Systems as Caused by Multi-Modal Resonance within DFIG-Based Wind Farm. Proc. CSEE 39, 642–651. doi:10.13334/j.0258-8013.pcsee.181319

CrossRef Full Text | Google Scholar

Donaldson, D. L., Piper, D. M., and Jayaweera, D. (2021). Temporal Solar Photovoltaic Generation Capacity Reduction from Wildfire Smoke. IEEE Access 9, 79841–79852. doi:10.1109/ACCESS.2021.3084528

CrossRef Full Text | Google Scholar

Du, W., Bi, J., and Wang, H. (2018). Damping Degradation of Power System Low-Frequency Electromechanical Oscillations Caused by Open-Loop Modal Resonance. IEEE Trans. Power Syst. 33, 5072–5081. doi:10.1109/TPWRS.2018.2805187

CrossRef Full Text | Google Scholar

Du, W., Chen, X., and Wang, H. F. (2017). Power System Electromechanical Oscillation Modes as Affected by Dynamic Interactions from Grid-Connected PMSGs for Wind Power Generation. IEEE Trans. Sustain. Energy 8, 1301–1312. doi:10.1109/TSTE.2017.2677094

CrossRef Full Text | Google Scholar

Du, W., Ma, Z., Wang, Y., and Wang, H. F. (2020). Harmonic Oscillations in a Grid-Connected PV Generation Farm Caused by Increased Number of Parallel-Connected PV Generating Units and Damping Control. CSEE JPES. doi:10.17775/CSEEJPES.2020.02790

CrossRef Full Text | Google Scholar

Eftekharnejad, S., Vittal, V., Heydt, G. T., Keel, B., and Loehr, J. (2013). Small Signal Stability Assessment of Power Systems with Increased Penetration of Photovoltaic Generation: A Case Study. IEEE Trans. Sustain. Energy 4, 960–967. doi:10.1109/TSTE.2013.2259602

CrossRef Full Text | Google Scholar

Emara, D., Ezzat, M., Abdelaziz, A. Y., Mahmoud, K., Lehtonen, M., and Darwish, M. M. F. (2021). Novel Control Strategy for Enhancing Microgrid Operation Connected to Photovoltaic Generation and Energy Storage Systems. Electronics 10, 1261. doi:10.3390/electronics10111261

CrossRef Full Text | Google Scholar

Harasis, S., Sozer, Y., and Elbuluk, M. (2021). Reliable Islanded Microgrid Operation Using Dynamic Optimal Power Management. IEEE Trans. Ind. Appl. 57, 1755–1766. doi:10.1109/TIA.2020.3047587

CrossRef Full Text | Google Scholar

Huang, Y., Yuan, X., Hu, J., and Zhou, P. (2015). Modeling of VSC Connected to Weak Grid for Stability Analysis of DC-Link Voltage Control. IEEE J. Emerg. Sel. Top. Power Electron. 3, 1193–1204. doi:10.1109/JESTPE.2015.2423494

CrossRef Full Text | Google Scholar

Ibrahim, S. A., Nasr, A., and Enany, M. A. (2021). Maximum Power Point Tracking Using ANFIS for a Reconfigurable PV-Based Battery Charger under Non-uniform Operating Conditions. IEEE Access 9, 114457–114467. doi:10.1109/ACCESS.2021.3103039

CrossRef Full Text | Google Scholar

Khasim, S. R., C, D., Padmanaban, S., Holm-Nielsen, J. B., and Mitolo, M. (2021). A Novel Asymmetrical 21-Level Inverter for Solar PV Energy System with Reduced Switch Count. IEEE Access 9, 11761–11775. doi:10.1109/ACCESS.2021.3051039

CrossRef Full Text | Google Scholar

Kou, G., Chen, L., VanSant, P., Velez-Cedeno, F., and Liu, Y. (2020). Fault Characteristics of Distributed Solar Generation. IEEE Trans. Power Deliv. 35, 1062–1064. doi:10.1109/TPWRD.2019.2907462

CrossRef Full Text | Google Scholar

Kumar, M., and Tyagi, B. (2021). A Robust Adaptive Decentralized Inverter Voltage Control Approach for Solar PV and Storage-Based Islanded Microgrid. IEEE Trans. Ind. Appl. 57, 5356–5371. doi:10.1109/TIA.2021.3094453

CrossRef Full Text | Google Scholar

Liu, J., Du, X., Liu, Y., Li, D., Zhang, B., and Tong, C. (2021). “A New Control Strategy Based on PLL to Enhance System Stability under Varying Output Power in Weak Grids,” in 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10-14 Oct. 2021, 335–339. doi:10.1109/ECCE47101.2021.9595914

CrossRef Full Text | Google Scholar

Mahmoud, K., and Lehtonen, M. (2021). Comprehensive Analytical Expressions for Assessing and Maximizing Technical Benefits of Photovoltaics to Distribution Systems. IEEE Trans. Smart Grid 12, 4938–4949. doi:10.1109/TSG.2021.3097508

CrossRef Full Text | Google Scholar

Mahmoud, K., and Lehtonen, M. (2020). Three-Level Control Strategy for Minimizing Voltage Deviation and Flicker in PV-Rich Distribution Systems. Int. J. Electr. Power & Energy Syst. 120, 105997. doi:10.1016/j.ijepes.2020.105997

CrossRef Full Text | Google Scholar

Malik, S. M., Sun, Y., Ai, X., Chen, Z., and Wang, K. (2019). Small-Signal Analysis of a Hybrid Microgrid with High PV Penetration. IEEE Access 7, 119631–119643. doi:10.1109/ACCESS.2019.2937123

CrossRef Full Text | Google Scholar

Mansouri, M. M., Hadjeri, S., and Brahami, M. (2021). New Method of Detection, Identification, and Elimination of Photovoltaic System Faults in Real Time Based on the Adaptive Neuro-Fuzzy System. IEEE J. Photovoltaics 11, 797–805. doi:10.1109/JPHOTOV.2021.3051145

CrossRef Full Text | Google Scholar

Moradi-Shahrbabak, Z., and Tabesh, A. (2018). Effects of Front-End Converter and DC-Link of a Utility-Scale PV Energy System on Dynamic Stability of a Power System. IEEE Trans. Ind. Electron. 65, 403–411. doi:10.1109/TIE.2017.2721902

CrossRef Full Text | Google Scholar

Priyadarshi, N., Padmanaban, S., Holm-Nielsen, J. B., Blaabjerg, F., and Bhaskar, M. S. (2020). An Experimental Estimation of Hybrid ANFIS-PSO-Based MPPT for PV Grid Integration under Fluctuating Sun Irradiance. IEEE Syst. J. 14, 1218–1229. doi:10.1109/JSYST.2019.2949083

CrossRef Full Text | Google Scholar

Quan, X., Yu, R., Zhao, X., Lei, Y., Chen, T., Li, C., et al. (2020). Photovoltaic Synchronous Generator: Architecture and Control Strategy for a Grid-Forming PV Energy System. IEEE J. Emerg. Sel. Top. Power Electron. 8, 936–948. doi:10.1109/JESTPE.2019.2953178

CrossRef Full Text | Google Scholar

Tan, Y. T., Kirschen, D. S., and Jenkins, N. (2004). A Model of PV Generation Suitable for Stability Analysis. IEEE Trans. Energy Convers. 19, 748–755. doi:10.1109/TEC.2004.827707

CrossRef Full Text | Google Scholar

Teodorescu, R., Liserre, M., and Rodriguez, P. (2011). Grid Converters for Photovoltaic and Wind Power Systems. Hoboken, NJ, United States: John Wiley & Sons.

Google Scholar

Wang, B., Xie, X., Ding, W., Yang, D., Ying, L., and Zhu, G. (2021). “Optimization of Retail Packages Adapted to the Electricity Spot Market with the Goal of Carbon Peak and Carbon Neutrality,” in 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 9-11 Oct. 2021, 311–317. doi:10.1109/REPE52765.2021.9617090

CrossRef Full Text | Google Scholar

Xia, Y., Yu, M., Wang, X., and Wei, W. (2019). Describing Function Method Based Power Oscillation Analysis of LCL-Filtered Single-Stage PV Generators Connected to Weak Grid. IEEE Trans. Power Electron. 34, 8724–8738. doi:10.1109/TPEL.2018.2887295

CrossRef Full Text | Google Scholar

Yan, R., and Saha, T. K. (2012). Investigation of Voltage Stability for Residential Customers Due to High Photovoltaic Penetrations. IEEE Trans. Power Syst. 27, 651–662. doi:10.1109/TPWRS.2011.2180741

CrossRef Full Text | Google Scholar