Influence of Geometric Parameters of Tiny Blades on the Shroud of a Centrifugal Pump on the Cavitation Suppression Effect

In this paper, the effect of adding non-connected forms of tiny blades with different parameters of radial position, width, and length to the shroud of the impeller on the cavitation performance of a centrifugal pump is researched. A modified SST k-ω turbulence model combined with the Zwart–Gerber–Belamri cavitation model is used for numerical simulation of the model pump. The results show that the numerical prediction of the original pump agrees well with the experimental results. Adding tiny blades with different radial positions, widths, and lengths has a small effect on the pump head and efficiency under each working condition. Adding tiny blades near the impeller inlet has better suppression of cavitation in the initial stage, and adding tiny blades in the middle and backward positions has a better suppression effect on all stages of cavitation. There is an optimal tiny blade width to make the cavitation suppression effect optimal, and the optimal width of the model in this study is 3/4 of that of the main blade. The effect of a tiny blade length on cavitation performance is small. The existence of tiny blades slightly increases the turbulent kinetic energy in the low-turbulent kinetic energy region near the impeller inlet, significantly reduces the turbulent kinetic energy in the high-turbulent kinetic energy region near the outlet, and reduces the overall pressure pulsation main frequency amplitude during pump operation, making its operation more stable.

1 Introduction

As fluid-transfer power equipment, centrifugal pumps are widely used in the national life and economic production and play an important role. Cavitation is a flow phenomenon that is difficult to avoid during the operation of centrifugal pumps. Its generation is due to the process of cavitation generation, development, and collapse when the local pressure in the liquid medium decreases to the critical pressure. Cavitation can interfere with the normal flow of the flow field. In serious cases, it will reduce the normal energy conversion inside the impeller (Brennen, 1994), accompanied by noise and vibration (Chudina, 2003; Li et al., 2018), which will reduce the hydraulic performance of the pump. Moreover, the bubble collapse process will produce an extremely high local pressure and temperature and high-speed microjets, which can cause erosion of the overflow components (Brujan and Matsumoto, 2012; Wijngaarden, 2016; Dular et al., 2019) and greatly reduce the service life of the pump. Therefore, the research of cavitation suppression in centrifugal pumps is a popular field.

Many scholars have done a lot of research work on centrifugal pump cavitation suppression. Luo et al. and Pei et al. (Luo et al., 2008; Pei et al., 2017) improved the hydraulic and cavitation performance of the pump by optimizing the geometric parameters of the impeller. Adding inducers to the impeller inlet (Acosta, 1958), inducing partial high-pressure fluid injection into the inlet from the pump outlet (Wong et al., 1965; Cui et al., 2019), etc., are methods to suppress cavitation by increasing the impeller inlet pressure. Zhao and Zhao, (2017) placed obstacles at suitable locations on the pressure surface of the blade to inhibit cavitation development. Wei et al. (Wei et al., 2021) improved the fluid dynamics at the inlet of centrifugal pumps by adding a deflector plate, which contributed to the suppression of cavitation instability in high-speed centrifugal pumps. Kurokawa, (2011) designed J-slots in the inlet section wall of centrifugal pumps with inducers to suppress various anomalous flow phenomena such as cavitation by controlling the angular momentum of the main flow. Zhao et al., (2020) studied the method of opening slits on the blade of a centrifugal pump, leading the fluid from the high-pressure region to the low-pressure region and effectively restraining the development of cavitation. (Zhu and Chen, 2012) added a small vice blade to the leading edge of the blade and improved the cavitation performance and hydraulic efficiency by taking advantage of the inflow characteristics and the automatic pressure balancing effect of the clearance channel. Slotting on the pressure side of the leading edge of the blades induces a relatively high pressure, which suppresses the growth of the bubble volume within the impeller (Zhao et al., 2018). A proper inlet diameter of the splitter blade can effectively avoid flow obstruction at the impeller inlet and vortex cavitation in the blade channel (Zhang et al., 2014).

Cavitation occurs at the location of the lowest pressure, usually slightly behind the suction surface of the blade inlet and close to the hub of the impeller (Guan, 2011). Therefore, in this paper, different schemes were designed successively and the effect of adding non-connected forms of tiny blades on the shroud of the impeller with different radial positions, widths, and length parameters on the cavitation performance of a centrifugal pump was investigated. Moreover, by the numerical simulation method, the changes of the bubble volume, flow field structure, turbulent kinetic energy distribution, pressure distribution, and the pressure pulsation amplitude of the main frequency in the impeller under different cavitation margins were compared and analyzed.

2 Numerical Methods

2.1 Governing Equations

The governing equations for fluid motion are the Reynolds averaged Navier–Stokes equations.

Continuity equation:

$\frac{\partial {\rho }_m}{\partial t}+\frac{\partial \left({\rho }_m{u}_i\right)}{\partial x_i}=0(1)$

Momentum equation:

$\frac{\partial \left({\rho }_m{u}_i\right)}{\partial t}+\frac{\partial \left({\rho }_m{u}_i{u}_j\right)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\left(\mu +{\mu }_t\right)\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial u_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k}{\delta }_{ij}\right)\right](2)$

where ρ_m is the mixture density; t is the time; u_i, u_j, and u_k are the velocity components; p is the local pressure; μ is the viscosity; μ_t is the turbulence viscosity; and δ_ij is the Kronecker symbol.

Here, the mixture density ρ_m is defined as

${\rho }_{\mathit{m}}={\alpha }_{\mathit{v}}{\rho }_{\mathit{v}}+{\rho }_{\mathit{l}}\left(1-{\alpha }_{\mathit{v}}\right)(3)$

where α is the volume fraction of one component. The subscripts v and l refer to the vapor and liquid components, respectively.

2.2 Turbulence Model

The SST k-ω turbulence model (Menter, 1994) was used to close the Reynolds-averaged Navier–Stokes equations. The SST k-ω turbulence model takes the k-ω model in the boundary layer region of the wall and the k-ε model in the region away from the boundary layer, which combines the advantages of both models and can predict flow separation on smooth surfaces more accurately

$\frac{\partial \left({\rho }_{m}k\right)}{\partial t}+\frac{\partial \left({\rho }_{m}k{u}_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_k\frac{\partial k}{\partial x_j}\right)+G_k-Y_k+S_k(4)$

$\frac{\partial \left({\rho }_m\omega \right)}{\partial t}+\frac{\partial \left({\rho }_m\omega u_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_{\omega }\frac{\partial \omega }{\partial x_j}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }(5)$

${\mu }_t={\rho }_m\frac{k}{\omega }(6)$

where G_k and G_ω are the generating terms of turbulent kinetic energy k and dissipation rate ω, respectively; Γ_k and Γ_ω are the effective diffusion coefficients of k and ω, respectively; Y_k and Y_ω are the dissipations of k and ω, respectively; S_k and S_ω are user-defined source phases; and D_ω is the cross-diffusion term.

However, the uncorrected SST k-ω turbulence model will overpredict the viscosity of the two-phase mixture of vapor and liquid phases during cavitation, resulting in inaccurate prediction of bullbe shedding (Reboud and Dellanoy, 1994; Zheng et al., 2018). In this paper, a modified SST k-ω turbulence model is adopted to reduce the turbulent viscosity in order to capture the flow state of the cavitation flow more accurately. The turbulent viscosity in the region where cavitation occurs is reduced by modifying the density function f (ρ_m) as follows:

${\mu }_{\mathit{t}}=\mathit{f}\left({\rho }_{\mathit{m}}\right)\frac{\mathit{k}}{\omega }(7)$

$\mathit{f}\left({\rho }_{\mathit{m}}\right)={\rho }_{\mathit{v}}+\frac{{\left({\rho }_{\mathit{m}}-{\rho }_{\mathit{v}}\right)}^{\mathit{n}}}{{\left({\rho }_{\mathit{l}}-{\rho }_{\mathit{v}}\right)}^{\mathit{n}\mathrm{-1}}};n\ge \mathrm{1}(8)$

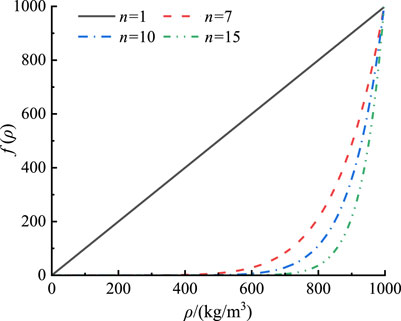
where n is taken as 10 (Coutier-Delgosha et al., 2003; Ji et al., 2014).

The variation curve of the f(ρ_m) function is shown in Figure 1. It can be seen from the figure that the corrected density is significantly reduced in the mixing region of the two-phase flow, thereby reducing the turbulent viscosity.

FIGURE 1

FIGURE 1. Modified function of turbulent viscosity.

2.3 Cavitation Model

The Zwart–Gerber–Belamri cavitation model (Zwart et al., 2004) based on the Rayleigh–Plesset equation was used, neglecting the surface tension term and the second-order time derivative term, assuming a constant gas nucleus density in the fluid domain, and focusing on the effect of the change in the radius of the bubble during the initial generation and development of cavitation. It is suitable for calculating the transient characteristics of cloud cavitation within a centrifugal pump, and the equation is

$\frac{\partial \left({\rho }_{\mathit{m}}{f}_{\mathit{v}}\right)}{\partial t}+\frac{\partial \left({\rho }_{\mathit{m}}{u}_i{f}_{\mathit{v}}\right)}{\partial x_i}=m^{+}-m^{-}(9)$

$m^{+}=F_{\mathit{vap}}\frac{3{\alpha }_{\mathit{nuc}}\left(1-{\alpha }_{\mathit{v}}\right){\rho }_{\mathit{v}}}{R_{\mathit{b}}}\sqrt{\frac{2}{3}\frac{p_{\mathit{v}}-p}{{\rho }_{\mathit{l}}}};p\le p_v(10)$

$m^{-}=F_{\mathit{cond}}\frac{3{\alpha }_{\mathit{v}}{\rho }_{\mathit{v}}}{R_{\mathit{b}}}\sqrt{\frac{2}{3}\frac{p-p_{\mathit{v}}}{{\rho }_{\mathit{l}}}};p\mathrm{>}{p}_v(11)$

where f_v is the vapor-phase mass fraction, m⁺ is the evaporating phase, m⁻ is the condensing phase, F_vap is the evaporation coefficient, F_cond is the condensation coefficient, R_b is the vacuole radius, α_nuc is the volume fraction of cavitation nuclei, p is the flow field pressure, and p_v is the saturated vapor pressure. Based on the experience of previous research (Zwart et al., 2004; Ji et al., 2013), F_vap = 50, F_cond = 0.01, R_b = 1 × 10⁻⁶ m, α_nuc = 5 × 10⁻⁴, and saturated vapor pressure p_v = 3169 Pa at 25°C.

3 Research Model and Preliminary Location Scheme Design

3.1 Research Model

In this paper, a low-specific speed centrifugal pump with a specific speed of ns = 32 was adopted as the research object, which mainly consists of five parts, such as the inlet section, impeller, volute, shroud, and hub. The rated head H₀ = 4.2 m, the rated flow rate Q₀ = 8.6 m3/h, and the rated speed n = 500 rpm. The main geometric parameters of the model pump are as follows: the inlet section diameter D_j = 107 mm, the impeller inlet diameter D_i = 90 mm, the impeller outlet diameter D₂ = 310 mm, the impeller outlet width b₂ = 12 mm, the blade inlet diameter D_b = 80 mm, the blade inlet angle β₁ = 37°, the blade outlet angle β₂ = 37°, blades are cylindrical blades, the blade number Z = 6, and the blade thickness δ = 4 mm, as shown in Figure 2A, where D_X, L, W, and δ₁ are the inlet diameter, length, width, and thickness of the tiny blades, respectively.

FIGURE 2

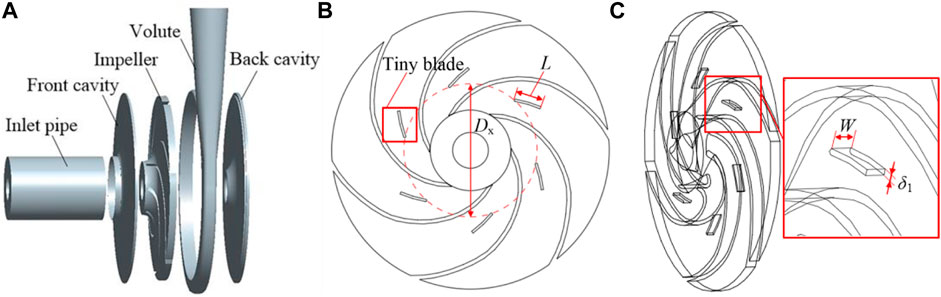
FIGURE 2. (A) Geometric model of the centrifugal pump. (B,C) Schematic diagram of geometric parameters such as length, inlet diameter, width, and thickness of tiny blades.

3.2 Preliminary Location Scheme Design

According to previous studies (Zhang et al., 2015), the design of splitting blades in the impeller of a centrifugal pump will have a certain suppression and optimization effect on cavitation but will have a greater impact on the hydraulic performance of the centrifugal pump. In order to minimize the influence on the external characteristics of the centrifugal pump and to reduce the disturbance of the flow in the impeller, the effect of arranging tiny blades of a non-connected form with different radial positions, widths, and length parameters on the inner surface of the shroud of the impeller on the cavitation performance is investigated. When the splitting blades are located in the middle of the flow channel, the pressure distribution of the flow channel of the impeller conforms to the general principle of the pressure distribution of the centrifugal pump, and the inlet diameter of the splitter blade has the greatest impact on the performance. Therefore, the middle position of the tiny blade should be determined first (He et al., 2006; Yuan et al., 2008). The shape of the tiny blade is the same as that of the corresponding position of the main blade. The length L of the tiny blade is 1/8 of the length of the main blade, and the width W and thickness δ₁ of the tiny blade are 1/2 of the main blade. The number of the tiny blades is the same as the quantity of the main blade, and the inlet diameter of the tiny blade is D_x. First, five location schemes are designed, as shown in Table 1.

TABLE 1

TABLE 1. Radial position scheme of tiny blades.

4 Grid Generation

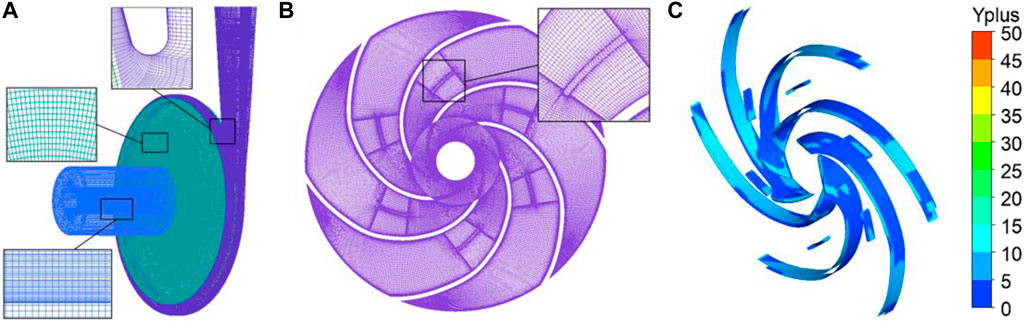
ICEM CFD software was used to discretize the hexahedral structured mesh of the inlet section, impeller, front and rear cavities, and volute of the centrifugal pump model, as shown in Figure 3A, B. In order to improve the calculation accuracy, the grid was locally densified on the walls of each part of the model. The calculation domain of the Scheme A1 model was divided into four groups of grids with different numbers to verify the grid independence, which was used to exclude the influence of the number of grids on the error of the calculation results, as shown in Table 2. From the calculated results, it can be seen that the relative error of the head is within 1% as the number of meshes increases, and finally, the number of meshes of all calculated models is discrete into a number of meshes comparable to Mesh4 for simulation.

FIGURE 3

FIGURE 3. (A,B) Grid of calculation domains. (C) Y⁺ distribution of blades.

TABLE 2

TABLE 2. Mesh independence analysis.

Since different turbulence models have different requirements on the grid density near the wall, in order to ensure that the grid density near the wall can accurately capture the flow in the boundary layer, it is necessary to analyze the Y⁺ value of the near wall. Y⁺ is defined as

${\mathit{Y}}^{+}=\frac{\mathrm{\Delta }\mathit{n}\sqrt{{\tau }_{\omega }/\rho }}{\mathit{v}}(12)$

where Δn is the distance between the two mesh nodes closest to the wall and τ_ω is the wall shear stress.

In this study, the modified SST k-ω turbulence model is selected. The requirements of the k-ω model for the mesh quality of the near-wall region can be satisfied when Y⁺ is less than 100 (Li et al., 2012). The maximum Y⁺ value of the impeller models with small blades arranged is 15, as shown in Figure 3C.

5 Boundary Condition Setting

ANSYS CFX software was used for numerical simulation. The main boundary conditions are set as follows: pressure inlet and mass flow outlet. The impeller domain was set as the rotating domain, and the others were the static domains. The two outer surfaces of the hub and shroud were set as rotating wall surfaces, and the rest were isothermal and non-slip wall surfaces. In the steady calculation, the dynamic static interface was set to the frozen rotor. In the unsteady calculation, the dynamic static interface was set as the transient rotor stator. In the process of solving, the advection scheme adopted the high-resolution format, and the transient scheme adopted the second-order backward Euler difference format. The two-phase medium calculated by the simulation was water and water vapor at 25°C. The volume fractions of the liquid and vapor phases at the inlet were set to 1 and 0, respectively. The reference pressure of the calculation domain was 0 Pa, the saturated vapor pressure was 3,169 Pa, and the convergence accuracy was set to 1 × 10⁻⁵. In the simulation, cavitation occurs in the centrifugal pump by continuously reducing the inlet pressure. First, the steady calculation is carried out, and then, the steady calculation result is taken as the initial value for unsteady calculations. For unsteady calculations, the time step was taken as Δt = 0.001 s; that is, every 3° rotation of the impeller is a time step. Then, each time step was iteratively calculated 20 times, and finally, a convergence result was saved every 15° rotation. The total number of calculation steps was 600 steps, and the last calculation stable rotation period was selected for unsteady characteristic analysis.

6 Simulation Algorithm Verification and Preliminary Result Analysis

6.1 Simulation Algorithm Verification

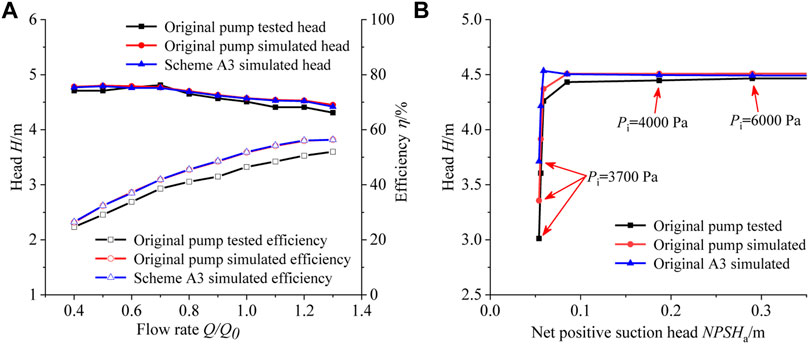
The external characteristics and cavitation performance tests of the original model centrifugal pump were completed on the visualized closed centrifugal pump test platform in the Key Laboratory of Fluid Machinery and Systems of Gansu Province, and the test system is shown in Figure 4. The medium of test is clear water at room temperature (25°C). The test is conducted in accordance with the national standard GB/T 3216-2016 “Hydraulic Performance Acceptance Test for Rotary Power Pumps Level 1, Level 2, and Level 3”. The tested curves of external characteristics and cavitation characteristics of the centrifugal pump are shown in Figure 5A,B, respectively. From Figure 5A, it can be seen that the simulated values of head and efficiency of the original pump under each flow rate condition are basically consistent with the trend of the experimental values. The maximum error between the simulated value of the original pump head and the experimental value occurs when Q/Q₀ is 1.3, and the error is 3.25%. Also, the original pump efficiency simulation value is higher than the experimental value, and the maximum efficiency error is 5.68%. These errors are caused by measurement errors, manufacturing errors of the test pump, and insufficient consideration of wear-ring clearance and surface roughness in the simulation calculation model. It can be seen from Figure 5B that the simulated value of the original pump is slightly larger than the experimental value under different cavitation margins, and the simulated value is in close agreement with the experimental value. Therefore, the reasonableness and accuracy of the simulation algorithm for the hydraulic performance and cavitation performance of the centrifugal pump were verified.

FIGURE 4

FIGURE 4. Sketch map of the centrifugal pump closed test bench (1, electric motor; 2, torque meter; 3, visual centrifugal pump; 4, outlet pressure sensor; 5, electromagnetic flow meter; 6, outlet valve; 7, vacuum gauge; 8, cavitation tank; 9, liquid ring vacuum pump; 10, inlet valve; 11, inlet pressure sensor).

FIGURE 5

FIGURE 5. (A) Hydraulic performance and (B) cavitation performance curves of the centrifugal pump.

6.2 Preliminary Location Scheme Results and Analysis

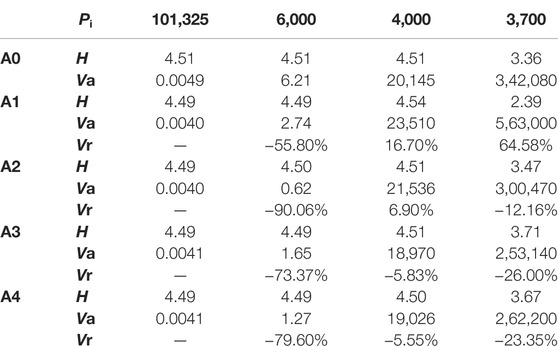
Numerical simulations of external characteristics and cavitation performance were carried out for the original pump model and four radial position scheme models at the design flow rate Q₀, respectively, and the calculation results are shown in Table 3, where P_i is the centrifugal pump inlet pressure, Pa; H is the head, m; V_a is the volume of cavitation in the impeller, mm³; and V_r is the percentage change in cavitation volume compared with the original impeller at the same inlet pressure. When the centrifugal pump inlet pressure P_i = 6,000 Pa (NPSH_a = 0.290 m), it is the initial stage of cavitation; when P_i = 4,000 Pa (NPSH_a = 0.085 m), it is the development stage of cavitation; and when P_i = 3,700 Pa (NPSH_a = 0.054 m), it is the serious stage of cavitation.

TABLE 3

TABLE 3. Simulation results.

From the data in Table 3, it can be seen that when the pump inlet pressure P_i = 101,325 Pa, the head H of schemes A1–A4 is slightly reduced compared with that of the original pump A0; when P_i = 6,000 Pa, the head H of schemes A1–A4 is slightly reduced compared with that of the original pump A0, but the bubble volume V_a of schemes A1–A4 becomes smaller compared with that of A0, indicating that schemes A1–A4 all have the effect of cavitation suppression, the suppression effect is obvious, and the maximum reduction of cavitation volume of the A2 scheme was 90.06%; when P_i = 4,000 Pa, the H of schemes A1–A4 do not change much, but V_a of schemes A1 and A2 increase slightly compared with that of A0, indicating that the cavitation development is promoted. V_a of schemes A3 and A4 decreased compared with that of A0, indicating that the cavitation development is suppressed; when P_i = 3,700 Pa, H of scheme A1 decreased more compared with that of A0, and H the other three schemes were higher than that of A0. The bubble volume of scheme A1 was larger than that of scheme A0, and those of the other three schemes were all lower than that of scheme A0, indicating that A1 promotes cavitation at this time, while A2, A3, and A4 all inhibited the development of cavitation.

After comprehensive analysis, the cavitation volume in the impeller of scheme A3 was reduced at each selected inlet pressure point (cavitation incipient to cavitation severe stage), with a maximum reduction of 73.37%, and the head was the highest at the lowest inlet pressure point P_i = 3,700 Pa, which was 10.4% higher than that of the original pump. Compared with the simulated value of the external characteristics of the original pump, the hydraulic performance of scheme A3 at different operating points changes less, as shown in Figure 5A, and reduces the critical cavitation allowance point, as shown in Figure 5B. After comprehensive comparison, it can be concluded that A3 has the best comprehensive effect on cavitation suppression.

7 Further Width Scheme Design and Result Analysis

7.1 Width Scheme Design

The preliminary scheme studied the influence of the radial position parameters of the tiny blades on the cavitation performance and hydraulic performance, and numerical simulations were carried out at the design flow rate of Q₀. The results showed that the radial position of the tiny blades of scheme A3 has the best comprehensive suppression effect on the cavitation of the centrifugal pump, and the influence on the hydraulic performance of the centrifugal pump is small. Next, based on the location of this scheme, the effect of the width parameter of the tiny blade on the cavitation performance and hydraulic performance of the centrifugal pump was studied. Five additional schemes with tiny blade widths are designed, in which the tiny blade thickness remains unchanged. W represents the tiny blade width, and b is the main blade width at the scheme A3 radial position. The design scheme is shown in Table 4.

TABLE 4

TABLE 4. Scheme of tiny blade width.

7.2 Effect of Width Parameters on Performance

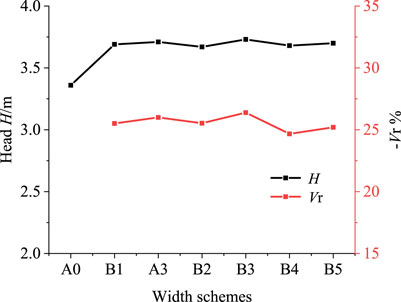
Figure 6 depicts the percentage reduction in head and bubble volume for different tiny blade width schemes at NPSH_a = 0.054 m. It can be seen that compared with the original pump, the addition of different widths of tiny blades increased the head after breakage and reduced the volume of bubbles, and all schemes improved the cavitation performance of the centrifugal pump. With the gradual increase in the width of the tiny blade, the change trend of the percentage reduction in the volume of the bubble is consistent with the change trend of the head, showing a trend of first increase and then decrease. It can be seen that there is an optimal width parameter for the cavitation suppression effect. As far as scheme B3 (the tiny blade width is 3/4 of the width of the same radial position of the main blade) is concerned, its head is the highest, 3.73 m, 11% higher than that of the original pump, and the smallest volume of the bubble is 26.39% less than that of the original pump. Next, the optimal width of scheme B3 will be selected for analysis of the internal flow field.

FIGURE 6

FIGURE 6. Head and percentage reduction of bubble volume, NPSH_a = 0.054 m.

7.3 Analysis of The Internal Flow Field of The Width Scheme

7.3.1 Vapor Volume Fraction Contour

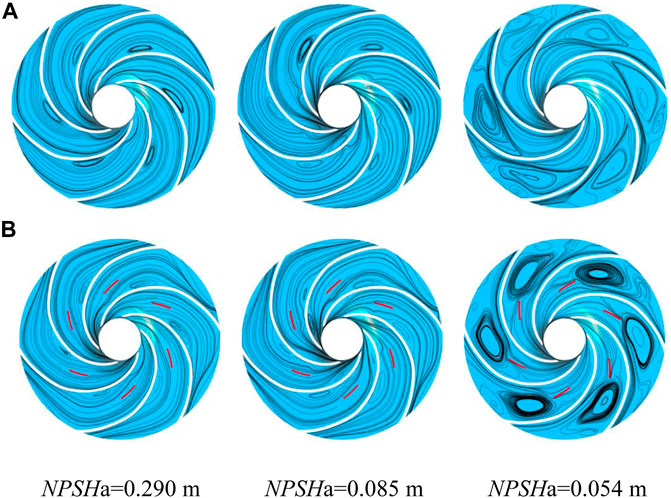
Figure 7 shows the contour of the isosurface of the steam volume fraction (α_v = 10%) in the impeller at different cavitation margins. Analysis of the figure shows that the bubbles first appear near the inlet of the impeller blades, and as the cavitation margin decreases, the volume of the bubbles gradually increases and spreads toward the outlet of the flow channel. The existence of bubbles seriously obstructs the normal flow in the flow channel. Compared with the original impeller, after adding tiny blades, when NPSH_a = 0.290 m, the bubble volume in the impeller of scheme B3 decreased by 84.42%. When NPSH_a = 0.085 m, the bubble volume in the B3 impeller decreased by 5.73%. When NPSH_a = 0.054 m, the bubble volume in the B3 impeller was reduced by 26.39%. After adding the tiny blade, the bubble volume in the impeller under different cavitation margins is significantly reduced, which effectively suppresses the occurrence and development of cavitation and improves the cavitation performance of the centrifugal pump.

FIGURE 7

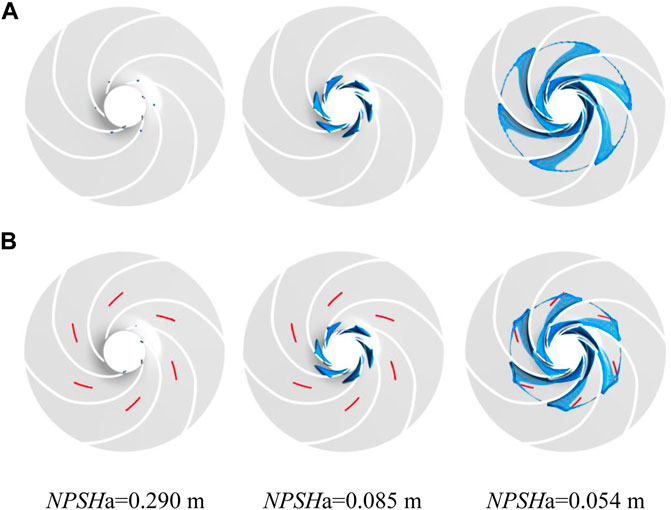
FIGURE 7. Vapor volume fraction distribution of the impeller: (A) original impeller and (B) B3 impeller.

7.3.2 Flow Field Structure

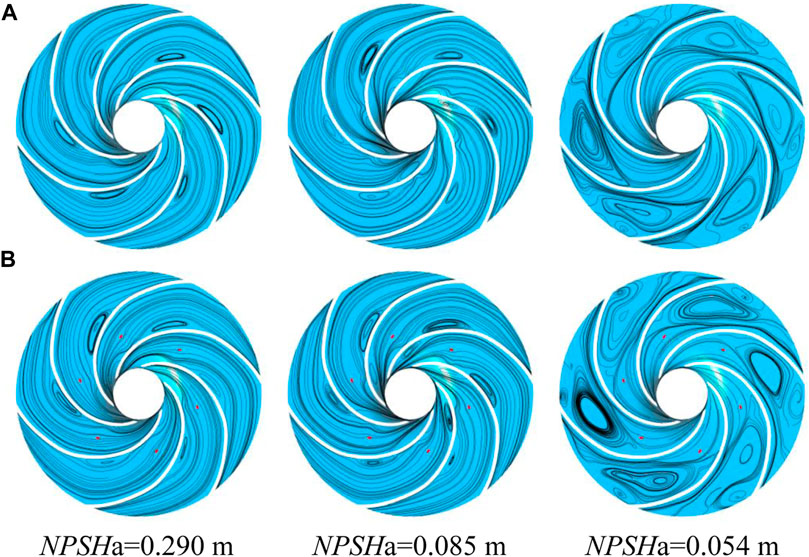
Figure 8 shows the flow distribution in the middle section of the impeller at different cavitation margins. Analysis of the figure shows that at each stage of cavitation, vortices are generated in each flow channel of the impeller, and the existence of vortices hinders the normal flow of the fluid, and as the cavitation margin decreases, the vortices move toward the outlet direction, the intensity and the scale of vortices increase, and the flow becomes more turbulent. After the shroud of the impeller increases the tiny blades, in the initial and development stages of cavitation, the vortex intensity is significantly reduced, the flow loss is reduced, and the existence of tiny blades plays a role in combing the flow field structure. However, in the cavitation severe stage, the tiny blades make the vortex intensity enhanced. This is because in the serious cavitation stage, there are many bubbles in the impeller, the two-phase flow is extremely complex, and the vortex is behind the tiny blade. The tiny blade does work on the fluid flowing through it, the fluid kinetic energy increases, the fluid with increased kinetic energy accelerates the rotation speed of the vortex when flowing through the edge of the vortex, and there is sudden diffusion of the channel after flowing through the small blade.

FIGURE 8

FIGURE 8. Distribution of Streamlines: (A) original impeller and (B) B3 impeller.

8 Final Length Parameter Scheme Design and Result Analysis

8.1 Length Parameter Scheme Design

The previous group of schemes studied the effect of the tiny blade width parameter on the cavitation performance and hydraulic performance of the centrifugal pump, and it was found that the tiny blades width of scheme B3 has the best effect on cavitation suppression and less effect on the hydraulic performance of the centrifugal pump. Next, with the tiny blade width (W = 3/4 b) of scheme B3 as the basis, we continued to control the tiny blade inlet diameter constant for a deeper study and to study the influence of tiny blade length parameters on the performance of centrifugal pumps and design as shown in Table 5, with three groups of length schemes for research, where L represents the length of the tiny blades and l represents the length of the main blade.

TABLE 5

TABLE 5. Tiny blade length schemes.

8.2 Effect of Length Parameters on Performance

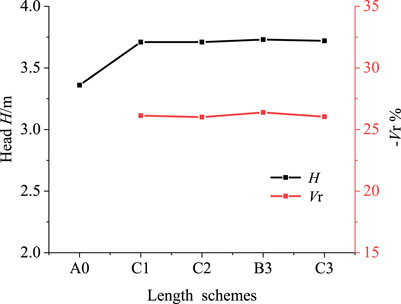
Figure 9 depicts the head and cavitation volume reduction percentages for different tiny blade length schemes at NPSH_a = 0.054 m. From the figure, it can be seen that under different cavitation margins, compared with the original pump A0 scheme, with the length change of the tiny blades, their hydraulic performance changes less and the cavitation suppression effect is similar to that of scheme B3, indicating that the length parameter of the tiny blades has less influence on the cavitation performance. Since scheme C1 has the shortest length of 5 mm but the hydraulic performance and cavitation performance are also better in all stages of cavitation, scheme C1 is chosen next for impeller internal flow field analysis.

FIGURE 9

FIGURE 9. Head and percentage reduction of vacuole volume, NPSH_a = 0.054 m.

8.3 Analysis of the Internal Flow Field of the Width Scheme

8.3.1 Bubble Volume Analysis

The bubble volume, V_cav, is defined as

${\mathit{V}}_{\mathrm{c}\mathrm{a}\mathrm{v}}={\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\alpha }_{\mathrm{v}\mathit{,i}}}{\mathit{V}}_{\mathit{i}}(13)$

where N is the total number of control units in the impeller; α_v,i is the volume fraction of the vapor phase in control unit i; and V_i is the volume of control unit i.

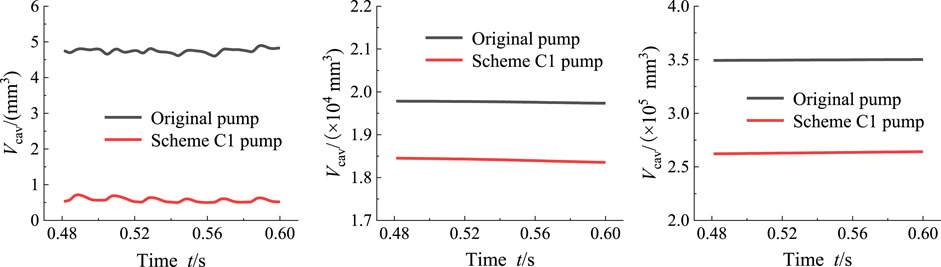
Figure 10 shows the variation of the bubble volume inside the impeller at the last rotation cycle at different cavitation margins. The results show that at the initial stage of cavitation, the bubble volume curve fluctuates up and down with time, showing a clear unsteady characteristic. However, as the cavitation margin decreases, the bubble volume in the impeller increases, and the bubble volume continues to fluctuate with the rotation of the impeller, but the fluctuation is relatively small. Scheme C1 shows a significant decrease in the volume of the bubble in the impeller compared with the original impeller at the same cavitation margins. At the initial stage of cavitation with a cavitation margin of NPSH_a = 0.290 m, the average volume of bubbles in the original impeller and scheme C1 impeller during the rotation cycle was 6.21 and 0.98 mm³, respectively, and the volume of bubbles in the C1 impeller was reduced by 84.15%; at the stage of cavitation development with a cavitation margin of NPSH_a = 0.085 m, the volume of bubbles in the original impeller and C1 impeller during the rotation cycle was 20,145 mm³ and 18,791 mm³, respectively, and the C1 bubble volume was reduced by 6.72%; at the cavitation severe stage NPSH_a = 0.054 m, the bubble volumes of the original impeller and C1 impeller during the rotation cycle were 3,42,080 and 2,52,360 mm³, respectively, and the C1 bubble volume was reduced by 26.23%. It can be found that the tiny-blade scheme is particularly effective in suppressing cavitation during the initial and severe stages of cavitation.

FIGURE 10

FIGURE 10. Cavitation volume under different NPSH_a.

8.3.2 Turbulent Kinetic Energy Distribution

Figure 11 shows the distribution of turbulent kinetic energy in the middle section of the impeller. The magnitude of the turbulent kinetic energy represents the turbulent intensity. As shown in Figures 7, 11, at the initial and developing stages of cavitation, cavitation is mainly generated near the inlet of the impeller. The arrangement of tiny blades can increase the turbulent energy near the inlet, and in the low-turbulent kinetic energy region, which also increases its turbulent intensity, the increased turbulent energy is still small. Moreover, the turbulent flow has the characteristics of pressure and velocity pulsation as well as the characteristics of high momentum and fast transfer, thus suppressing the initial and developmental stages of cavitation. When the cavitation develops to the severe stage, the turbulent kinetic energy on the pressure surface of the main blade in front of the tiny blade increases slightly, and the high-turbulent kinetic energy area behind the tiny blade near the outlet position decreases significantly. The turbulent dissipation loss decreases, and the hydraulic performance improves, as shown in Figure 10, when NPSH_a = 0.054 m.

FIGURE 11

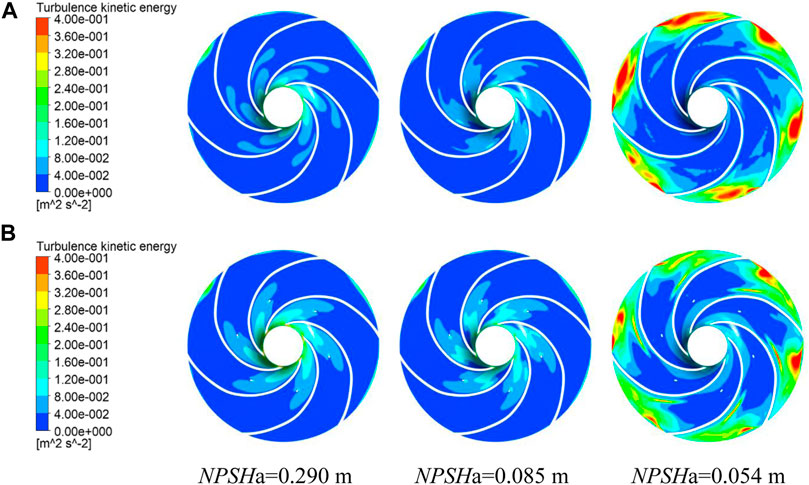
FIGURE 11. Turbulent kinetic energy distribution in the middle section of the impeller: (A) original impeller and (B) B3 impeller.

8.3.3 Flow Field Structure

Figure 12 depicts the streamline distribution in the middle section of the impeller at different cavitation margins. It can be seen from Figures 8, 12 that the longer tiny blades of scheme B3 weaken the strength and scale of the vortices in the flow channel during the cavitation initial and development stages. However, after the shortening of the tiny blade, compared with the original impeller, the length of the tiny blade of scheme C1 is only 5 mm, and its ability to confine and comb the fluid is weakened, so the intensity and scale of the vortex in the impeller of scheme C1 have less change compared with the original impeller but have a slight tendency to enhance, indicating that the shorter tiny blade has a certain disturbing effect on the flow field structure, especially near the blade inlet. However, it can be seen from Figure 10 that the shorter, tiny blade scheme C1 still significantly reduces the volume of cavitation in the impeller. In the severe cavitation stage, the vortex intensity in the impeller is significantly weaker in scheme C1 compared to the flow field structure of scheme B3 but slightly enhanced compared to the original impeller flow field structure. This is due to the reduced work capacity of the flowing fluid after the shortening of the small blades; the kinetic energy obtained by the flowing fluid is reduced, and the vortex promotion effect is relatively weaker.

FIGURE 12

FIGURE 12. Distribution of streamline: (A) original impeller and (B) B3 impeller.

8.3.4 Pressure Distribution

Figure 13 shows the absolute pressure contour distribution in the middle section of the impeller. The cavitation in the impeller is caused by the pressure at the location of the cavitation falling below the saturated vapor pressure. With the development of cavitation, the low-pressure area in the impeller first appears at the inlet of the impeller, so the bubble also first appears at the inlet of the blade. With the cavitation margin reduced, the low-pressure area spreads from the inlet of the blade to the outlet, and the cavitation also spreads from the inlet to the outlet. The distribution change of the bubble volume fraction is consistent with the distribution change of the low-pressure area, as shown in Figures 7, 13. After cavitation occurs, with the gradual reduction of the cavitation margin, the existence of tiny blades induces the relative high pressure near the impeller inlet. The pressure change is an important factor in inhibiting the diffusion of low-pressure areas in the impeller to the outlet, which in turn suppresses the expansion of the volume of the bubble. As shown in Figure 13, when NPSHa = 0.054 m, it can also be seen that the pressure gradient near the impeller outlet is larger, and the head after breaking is also higher, which improves the hydraulic performance during cavitation.

FIGURE 13

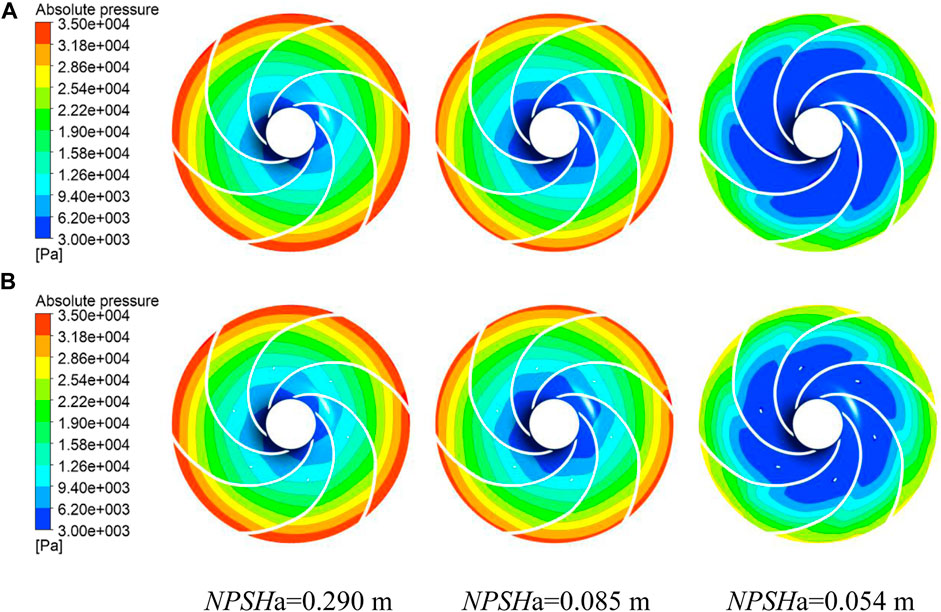
FIGURE 13. Pressure distribution in the middle section of the impeller: (A) original impeller and (B) B3 impeller.

8.3.5 Pulsation Amplitude Analysis

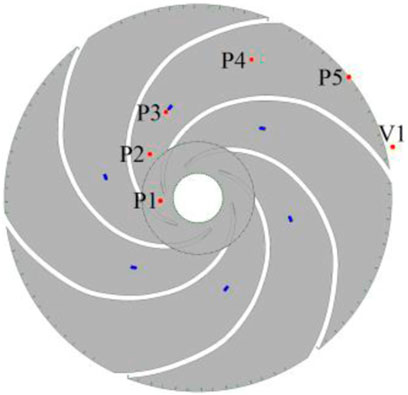
In order to better analyze the transient frequency characteristics of the flow field, six absolute pressure-monitoring points, such as P1-P5 and V1, are set in the middle of the impeller flow channel and at the position of the volute, as shown in Figure 14.

FIGURE14

FIGURE14. Monitoring points in the impeller middle plane.

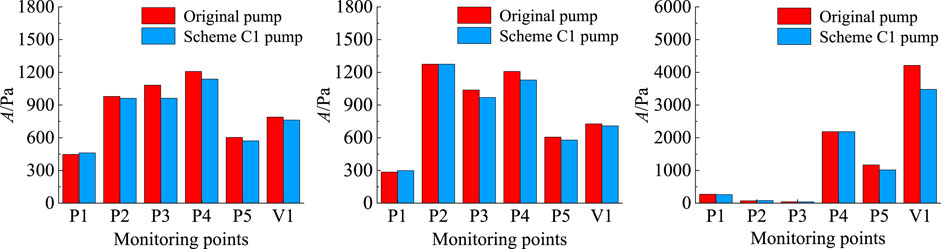
Figure 15 depicts the main frequency amplitude of pressure pulsation obtained by a fast Fourier transform (FFT) of the absolute pressure at each monitoring point, and A is the main frequency amplitude. From Figure 15, it can be obtained that at each stage of cavitation, compared with the original impeller, the C1 impeller has a decreasing trend in the amplitude of pressure pulsation at all monitoring points, except for a slight increase in pressure pulsation at two points, P1 and P2, near the inlet, which is consistent with the results of the turbulence energy analysis in Figure 11. This indicates that the existence of the tiny blades will indeed produce a small disturbance to its front impeller inlet position and produce an optimization effect on the flow field behind it. In general, the addition of tiny blades can reduce the overall pressure pulsation in the pump, which then also reduces the noise and vibration generated by the operation of the centrifugal pump.

FIGURE15

FIGURE15. Amplitude of main frequency of pressure.

9 Conclusion

In this study, the effects of adding non-connected tiny blades with different radial positions, widths, and length parameters to the shroud of a low-specific speed centrifugal pump impeller on the cavitation performance were investigated by combining numerical simulation and experiments, and the cavitation volume, flow field structure, turbulence energy, pressure distribution, and pressure pulsation amplitude were comparatively analyzed. On the basis of comparison and analysis, the conclusions are as follows:

1) Compared with the original pump, after adding tiny blades with different radial positions, widths, and lengths to the shroud of the impeller, the effect on the head and efficiency of the centrifugal pump under each working condition is small, and the relative change rate is within ±1.0%. Adding tiny blades near the inlet of the shroud of the impeller has a suppressive effect on the initial stage of cavitation and a facilitating effect on the development and severe stages of cavitation. The addition of tiny blades in the middle and backward positions of the impeller radius produced inhibitory effects in all stages of cavitation, especially in the initial and severe stages of cavitation.

2) There is an optimal width of the tiny blade to achieve the best cavitation suppression effect, and when the width of the tiny blade is equal to 3/4 of the width of the main blade, the cavitation performance of the centrifugal pump is optimal. The tiny blade length parameter has little effect on the cavitation performance.

3) The tiny blades slightly increase the turbulent energy near the blade inlet, inducing a relatively high pressure near the inlet and reducing the turbulent energy in the high-turbulent energy region near the impeller outlet. At the same time, it reduces the overall pressure pulsation in the pump, which in turn reduces noise and vibration and makes its cavitation operation more stable.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ZZ completed the writing, the experiment part and the data processing. WZ provided theoretical guidance and shared in writing, and revising the paper.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52169018) and the Industrial Support Plan Project of Gansu Provincial Education Department (2021CYZC-27).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Acosta, A. J. (1958). “An Experimental Study of Cavitating Inducers,” in Second Symposium on Naval Hydrodynamics: Hydrodynamic Noise Cavity Flow (Washington, D.C.: Office of Naval Research - Department of the Navy), 533–557.

Google Scholar

Brennen, C. E. (1994). Hydrodynamics of Pumps. Norwich, VT, USA: Concepts ETI Inc.

Google Scholar

Brujan, E.-A., and Matsumoto, Y. (2012). Collapse of Micrometer-Sized Cavitation Bubbles Near a Rigid Boundary. Microfluid Nanofluid 13, 957–966. doi:10.1007/s10404-012-1015-6

CrossRef Full Text | Google Scholar

Chudina, M. (2003). Noise as an Indicator of Cavitation in a Centrifugal Pump. Acoust. Phys. 49 (4), 463–474. doi:10.1134/1.1591303

CrossRef Full Text | Google Scholar

Coutier-Delgosha, O., Fortes-Patella, R., and Reboud, J. L. (2003). Evaluation of the Turbulence Model Influence on the Numerical Simulations of Unsteady Cavitation. J. Fluids Eng. 125 (1), 38–45. doi:10.1115/1.1524584

CrossRef Full Text | Google Scholar

Cui, B., Zhu, K., Zhang, Y., and Lin, P. (2019). Experimental and Numerical Study of the Performance and Cavitation Flow of Centrifugal Pump with Jetting Device. J. Mech. Sci. Technol. 33 (10), 4843–4853. doi:10.1007/s12206-019-0925-6

CrossRef Full Text | Google Scholar

Dular, M., Požar, T., Zevnik, J., and Petkovšek, R. (2019). High Speed Observation of Damage Created by a Collapse of a Single Cavitation Bubble. Wear 418-419, 13–23. doi:10.1016/j.wear.2018.11.004

CrossRef Full Text | Google Scholar

Guan, X. F. (2011). Modern Pumps Theory and Design. Beijing, CHN: China Space Navigation Press.

Google Scholar

He, Y., Yuan, S., Guo, X., Yuan, J., Chong, X., and Huang, L. (2006). Numerical Simulation for 3-D Incompressible Turbulent Flow in the Impeller with Splitting Vanes of Centrifugal Pump. Chin. J. Mech. Eng. 40 (11), 153–157. doi:10.3901/JME.2004.11.153

CrossRef Full Text | Google Scholar

Ji, B., Luo, X., Arndt, R. E. A., and Wu, Y. (2014). Numerical Simulation of Three Dimensional Cavitation Shedding Dynamics with Special Emphasis on Cavitation-Vortex Interaction. Ocean Eng. 87, 64–77. doi:10.1016/j.oceaneng.2014.05.005

CrossRef Full Text | Google Scholar

Ji, B., Luo, X., Wu, Y., Peng, X., and Duan, Y. (2013). Numerical Analysis of Unsteady Cavitating Turbulent Flow and Shedding Horse-Shoe Vortex Structure Around a Twisted Hydrofoil. Int. J. Multiphase Flow 51, 33–43. doi:10.1016/j.ijmultiphaseflow.2012.11.008

CrossRef Full Text | Google Scholar

Kurokawa, J. (2011). J-Groove Technique for Suppressing Various Anomalous Flow Phenomena in Turbomachines. Int. J. Fluid Machinery Syst. 4 (1), 1–13. doi:10.5293/ijfms.2011.4.1.001

CrossRef Full Text | Google Scholar

Li, X., Yuan, S., Pan, Z., Li, Y., and Yang, J. (2012). Realization and Application Evaluation of Near-Wall Mesh in Centrifugal Pumps. Trans. Chin. Soc. Agric. Eng. 28 (20), 67–72. doi:10.3969/j.issn.1002-6819.2012.20.009

CrossRef Full Text | Google Scholar

Li, Y., Feng, G., Li, X., Si, Q., and Zhu, Z. (2018). An Experimental Study on the Cavitation Vibration Characteristics of a Centrifugal Pump at normal Flow Rate. J. Mech. Sci. Technol. 32 (10), 4711–4720. doi:10.1007/s12206-018-0918-x

CrossRef Full Text | Google Scholar

Luo, X., Zhang, Y., Peng, J., Xu, H., and Yu, W. (2008). Impeller Inlet Geometry Effect on Performance Improvement for Centrifugal Pumps. J. Mech. Sci. Technol. 22 (10), 1971–1976. doi:10.1007/s12206-008-0741-x

CrossRef Full Text | Google Scholar

Menter, F. R. (1994). Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 32 (8), 1598–1605. doi:10.2514/3.12149

CrossRef Full Text | Google Scholar

Pei, J., Yin, T., Yuan, S., Wang, W., and Wang, J. (2017). Cavitation Optimization for a Centrifugal Pump Impeller by Using Orthogonal Design of experiment. Chin. J. Mech. Eng. 30 (1), 103–109. doi:10.3901/CJME.2016.1024.125

CrossRef Full Text | Google Scholar

Reboud, J. L., and Dellanoy, Y. (1994). “Two-Phase Flow Modelling of Unsteady Cavitation,” in Proc. Second Intl Symp. on Cavitation, Tokyo, Japan, 39–44.

Google Scholar

Wei, Z., Tao, R., Xiao, R., and Hu, H. (2021). Hydrodynamic Improvement by Adding Inlet Baffles on Centrifugal Pump for Reducing Cavitation Instabilities. J. Vibration Control., 1–12. doi:10.1177/10775463211047401

CrossRef Full Text | Google Scholar

Wijngaarden, L. (2016). Mechanics of Collapsing Cavitation Bubbles. Ultrason. Sonochem. 29, 524–527. doi:10.1016/j.ultsonch.2015.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Wong, G. S., Macgregor, C. A., and Hoshide, R. K. (1965). Suppression of Cavitation and Unstable Flow in Throttled Turbopumps. J. Spacecraft Rockets 2 (1), 73–80. doi:10.2514/3.28124

CrossRef Full Text | Google Scholar

Yuan, S. Q., Zhang, J. F., Yuan, J. P., and Fu, Y. D. (2008). Orthogonal Experimental Study Effect of Main Geometry Factors of Splitter Blades on Pump Performance. J. Drainage Irrigation Machinery 26 (2), 1–5. doi:10.3969/j.issn.1674-8530.2008.02.001

CrossRef Full Text | Google Scholar

Zhang, Y. L., Yuan, S. Q., Zhang, J. F., Feng, Y. N., and Lu, J. X. (2014). Numerical Investigation of the Effects of Splitter Blades on the Cavitation Performance of a Centrifugal Pump. IOP Conf. Ser. Earth Environ. Sci. 22 (5), 052003. doi:10.1088/1755-1315/22/5/052003

CrossRef Full Text | Google Scholar

Zhang, Y., Yuan, S., Zhang, J. F., Peng, Y., and Mao, J. (2015). Numerical Analysis on Effects of Splitter Blades on Cavitation Performance in a Centrifugal Pump. J. Drainage Irrigation Machinery Eng. 33 (10), 846–852. doi:10.3969/j.issn.1674-8530.14.0142

CrossRef Full Text | Google Scholar

Zhao, W. G., Lu, J. J., and Zhao, F. R. (2020). Cavitation Control of Centrifugal Pump Based on gap Jet Principle. J. ZheJiang Univ. (Engineering Science) 54 (9), 1785–1794. doi:10.3785/j.issn.1008-973X.2020.09.015

CrossRef Full Text | Google Scholar

Zhao, W. G., Zhai, L. J., Xia, T., and Li, S. S. (2018). Numerical Simulation of Slotted Blade in Centrifugal Pump on Cavitation Suppression. Trans. Chin. Soc. Agric. Mach 49, 157–164. doi:10.6041/j.issn.1000-1298.2018.12.019

CrossRef Full Text | Google Scholar

Zhao, W., and Zhao, G. (2017). An Active Method to Control Cavitation in a Centrifugal Pump by Obstacles. Adv. Mech. Eng. 9 (11), 168781401773294. doi:10.1177/1687814017732940

CrossRef Full Text | Google Scholar

Zheng, X. B., Liu, L. L., Guo, P. C., and Hong, F. (2018). Numerical Investigation of Three-Dimensional Cavitating Performance of NACA66 Hydrofoil Base on Different Cavitation Models. Chin. J. Hydrodynamics 33 (2), 199–206. doi:10.16076/j.cnki.cjhd.2018.02.008

CrossRef Full Text | Google Scholar

Zhu, B., and Chen, H.-x. (2012). Cavitating Suppression of Low Specific Speed Centrifugal Pump with gap Drainage Blades. J. Hydrodyn 24 (5), 729–736. doi:10.1016/S1001-6058(11)60297-7

CrossRef Full Text | Google Scholar

Zwart, P. J., Gerber, A. G., and Belamri, T. (2004). “A Two-Phase Flow Model for Predicting Cavitation Dynamics,” in Fifth international conference on multiphase flow, Yokohama, Japan, May 30-June 3, 2004, 152.

Google Scholar