Integrated Optimal Planning of Distribution Network With Geographical-Zone-Restricted Renewable Energy Sources

Recently, a lot of renewable energy sources have been integrated into the distribution network. In consideration of economy and construction feasibility, some renewable energy sources are required to be installed in specific areas. In this paper, a bi-layer distribution network planning optimization model that considers the geographical restrictions of the installation locations of the substation, pumped storage plant, photovoltaic (PV) and wind power, as well as the impact of operation on planning, is proposed. In the planning optimization layer, the optimal distribution network topology with minimal total cost is obtained. The locations of the renewable energy sources and the substation are determined by the particle swarm optimization (PSO), and then all the components are interconnected using the dynamic minimum spanning tree (DMST) method. In the operation optimization layer, the economic operation strategy of the hybrid energy system with uncertainty is obtained by the scenario-based stochastic optimal power flow (OPF). The forecast error of the uncertain variable is represented by the probability distribution function, and the roulette wheel mechanism (RWM) is used to generate the stochastic scenarios. A modified 103-bus system is used to test the effectiveness of the proposed method, and the simulation results show that the proposed method can effectively reduce the total cost of the distribution network.

1 Introduction

With the shortage of fossil energy and the increasingly serious environmental pollution problems, renewable energy sources such as photovoltaic (PV) and wind power have been developed rapidly in recent years (Chen et al., 2021; Hu et al., 2021; Mohandes et al., 2021). The installation location of the renewable energy is affected by geographical conditions. In order to achieve maximum economic benefits, PV power stations are usually installed in areas with high illumination intensity, and wind farms are built in places with sufficient wind energy (Hou et al., 2016; Li et al., 2020; Marcochi de Melo et al., 2021). To easily obtain water sources and build upstream reservoirs, pumped storage plants are generally built near rivers in mountainous areas. However, there lacks effective methods to handle such cases at present. It is necessary to find a cost-effective approach for distribution network planning that takes into account geographical constraints.

The optimization of distribution network planning and operation is an intensively studied topic in power engineering (Baringo et al., 2020; MohammadiFathabad et al., 2020; Ugranlı, 2020). The traditional distribution network contains transmission, substation, distribution and power equipment (Khator and Leung, 1997). In reference (Carrano et al., 2006), there is only traditional power equipment and no distributed generation devices in the distribution network. The planning of this distribution system is to optimize the connection of cables with the highest economic benefits and system reliability. With the integration of a large number of distributed energy equipment such as wind power, PV, energy storage equipment, new planning approaches need to be explored for the modern distribution network to improve the economic efficiency and determine the scheduling of newly connected renewable power generation equipment (Ding et al., 2012; (Wang et al., 2014). With the knowledge of the pumped storage capacity and wind speed, the generating/pumping power of the pumped storage and output power of wind farm are optimized in (Ding et al., 2012) to minimize the operation cost of distribution network. In the work of (Wang et al., 2014), a robust optimization problem is formulated to optimize the location and the size of the distribution generation to minimize microgrid costs.

Traditionally, the planning optimization and operation optimization of the distribution network are independently executed, and the operation optimization is carried out after the planning optimization. When renewable energy sources or energy storage equipment are connected to the distribution network, the operation mode of these equipment will affect the transmission losses of the grid and operation mode of the equipment (Ashoornezhad et al., 2021; Koutsoukis and Georgilakis, 2022; Mejia et al., 2022). Therefore, the traditional separated planning method cannot guarantee optimal results. It is imperative to combine the planning optimization and operation optimization together for better performance (Carpinelli et al., 2013; Sedghi et al., 2016; Tang and Low, 2017; Celli et al., 2018; Lazzeroni and Repetto, 2019). In (Lazzeroni and Repetto, 2019), the size and location of the battery are optimized to reduce the power loss. A battery planning optimization framework to improve wind power penetration, in which the optimal placement and daily scheduling of energy storage strategies are optimized, is proposed in (Ghofrani et al., 2013). To improve the voltage profile, reliability and economic benefits of the distribution network, a comprehensive strategic model is proposed to plan the location and size of photovoltaic, battery storage and distributed static compensator (Roy Ghatak et al., 2018). The authors in (Arasteh et al., 2016) presented a bi-level optimization model for distribution network. This model considered the distribution network reconfiguration and the demand response. However, the location and capacity of distributed devices are not optimized in this article. In (Zhang et al., 2013), the optimal pumped storage capacity is found by a multi-scenario approach aiming to reduce the operation cost of the distribution network and wind power curtailments. However, the network loss is not considered. There are also many researches on the expansion planning of distribution networks (Ouyang et al., 2010; Ganguly et al., 2013; Ziari et al., 2013; Koutsoukis et al., 20142014; Muñoz-Delgado et al., 2016), including the planning of new cables, substations, distributed generation equipment and energy storage equipment, etc. In (Tarôco et al., 2016), the allocation of the substations, distributed generation units, and the topology of distribution network are formulated as a multi-objective optimization to reduce the cost and improve the system reliability. A multi-stage expansion planning problem considering the load growth is formulated in (Sedghi et al., 2013), and is solved by a modified particle swarm optimization (PSO) algorithm. This expansion planning problem is divided into four stages. At each stage, new substations, main and reserve feeders, energy storage units and distribution generators will be installed into the existing distribution network. However, the geographical constraints of storage units and distributed generation equipment are not considered, i.e., those components can be installed on any existing node. The work in (Xing et al., 2016) presented an expansion planning model of the distribution network considering the allocation of the new cable, substation and distributed generator. The optimization model is formulated as a mixed integer non-linear programming problem, which is solve by a second-order cone programming method. However, the locations of the substation and distributed generation are limited to a few pre-selected nodes.

This paper proposes a bi-layer integrated planning approach for the distribution network. Geographical location constraints are considered in the distribution network optimization model. The proposed optimization model combines the planning and operation optimization of distribution network to reduce the total cost of the distribution network. The uncertainty of the load, illumination intensity, wind speed and electricity price is modeled by the probability distribution function, and the roulette wheel mechanism (RWM) is adopted to generate the stochastic scenarios. In the planning layer, an effective PSO-based method is adopted to determine the locations of the substation, pumped storage plant, PV and WT, then a DMST method is used to connect all the components with minimal cable cost. In the operation layer, the optimal operation strategy is obtained based on the topology determined in the planning layer.

The rest of this paper is organized as follows. The problem formulation is presented in Section 2. The solution approach of the optimization problem is given in Section 3. The case study and conclusions are presented in Section 4 and Section 5, respectively.

2 Problem Formulation

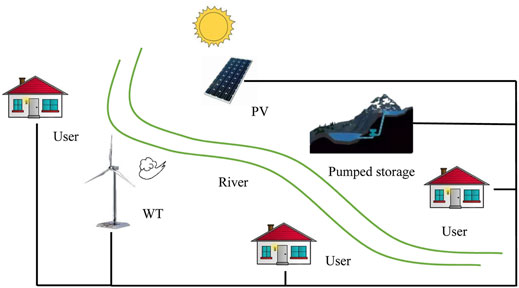
A diagram of a modern distribution network with renewable energy sources, such as wind turbine (WT), PV and pumped storage plant, is shown in Figure 1. Unlike traditional power generation equipment, these renewable energy sources are environmentally friendly, but they have strict requirements on the location of the construction.

FIGURE 1

FIGURE 1. Diagram of distribution network integrated planning problem.

In this study, an integrated optimal planning model of distribution network with geographical location constraints is formulated. The objective of distribution network planning optimization is to find the most cost-effective layout and dispatch strategy of the distribution network. The optimization problem is divided into two layers, i.e., integrated planning optimization and embedded operation optimization layer. In the integrated planning optimization layer, the locations of substation, pumped storage plant, PV, WT, pumped storage plant and the connection layout of all components are optimized to obtain the optimal distribution network topology. The embedded operation optimization is to schedule the pumped storage plant power to minimize the operation cost of the distribution system under the topology obtained from the integrated planning optimization layer.

2.1 Integrated planning optimization layer: minimize the total cost of the distribution network

The net present value (NPV) (Huang et al., 2020) of the total cost of distribution network operators in the planning years, that is, the sum of the cable cost and the distribution network operation cost, is taken as the objective function:

$F\left(L_{xy}\right)=min(NP{V}_{CC}+ NP{V}_{OC}) (1)$

where

$L_{xy}=(L_x,L_y)\in A(2)$

$\text{Here}$ $F$ represents the objective function value. $NP{V}_{CC}$ is the total NPV of the cable cost. $NP{V}_{OC}$ is the total NPV of the distribution network operation cost. $L_{xy}$ is a vector which represents the locations of the substation, pumped storage plant, PV and WT. $L_x$ and $L_y$ represent the abscissa and ordinate coordinates of $L_{xy}$, respectively. $A$ represents a restriction zone where components can be installed. In this study, two types of restriction zones are considered, i.e., rectangle and parallelogram. Based on the actual situation, the construction locations of the substation, PV and WT are set as a rectangular area. According to the shape of the river, the construction location of the pumped storage is set as a parallelogram area. For rectangular areas, the construction locations can be expressed as the limitations of x coordinate and y coordinate, respectively. The geographical constraints for rectangular areas are presented as

$L_x^{min}\le L_x\le L_x^{max}(3)$

$L_y^{min}\le L_y\le L_y^{max}(4)$

where $L_x^{min}$ and $L_x^{max}$ indicate the lower and upper limits of the $L_x$, respectively. $L_y^{min}$ and $L_y^{max}$ indicate the lower and upper limits of the $L_y$, respectively. For parallelogram areas, the construction locations can be expressed as the limitations of x coordinate and y coordinate, respectively, and a limitation between the x coordinate and the y coordinate. It can be presented as a combination of Eqs 3, 4, 5.

$k_1{L}_x-b_1\le L_y\le k_2{L}_x-b_2(5)$

where $k_1$, $b_1$, $k_2$, $b_2$ are the parameters of the parallelogram areas.

The cost of the cable includes the initial investment cost, maintenance cost and replacement cost. It depends on the length and type of the cable, so it is closely related to the connection layout of the distribution network. Different installation locations of the components will correspond to different distribution network connection layouts. The NPV of the cable cost within the planning years is expressed as

$NP{V}_{CC}={\displaystyle \sum }_{y=1}^{N_{Plan}}{C}_{CCost,y}\ast {\left(1+r\right)}^{-y}(6)$

where

$C_{CCost,y}={\displaystyle \sum }_{l=1}^{N_l}(L_l\ast C_{I,m,y}+L_l\ast C_{R,m,y}+L_l\ast C_{M,m,y})(7)$

where $C_{CCost,y}$ is the total cost of the cable at year $y$. $N_{Plan}$ is the planning horizon. $C_{I,m,y}$, $C_{R,m,y}$ and $C_{M,m,y}$ represent the unit initial investment cost, replacement cost and maintenance cost of type $m$ cable at year $y$, respectively. $L_l$ is the length of cable $l.$ $N_l$ is the total number of cables.

2.2 Embedded operation optimization layer: minimize the operation cost of the distribution network.

The locations of the substation, pumped storage plant, PV and WT will affect the connection layout of cables. Meanwhile, the locations of these equipment and the connection mode of the cables will affect the operation mode of the distribution network, especially the power losses. In order to improve the economic benefits of distribution network operator, the objective function of operation optimization is to minimize the NPV of the distribution network operation cost in the planning years. It is expressed as

$NP{V}_{OC}\left(P_{PS}\right)=\min {\displaystyle \sum }_{y=1}^{N_{Plan}}{C}_{OC,y}\ast {\left(1+r\right)}^{-y}(8)$

where

$C_{OC,y}={\displaystyle \sum }_{t=1}^{T_y}{P}_{PG}\left(t\right)\ast C_P\left(t\right)(9)$

$\text{Here }{C}_{OC,y}$ is the operation cost of the distribution network at year $y$. $r$ is the interest rate. $P_{PG}\left(t\right)$ is the active power purchased from the power grid at time $t$. $C_P\left(t\right)$ is the electricity price at time $t$. $T_y$ is the number of simulation hours per year. $P_{PS}$ is the control variables in the embedded optimization layer, which represents the operating power of pumped storage plant. The positive value represents that the pumped storage plant absorbs electricity from the power grid for water storage, while the negative value represents that the pumped storage plant generates electricity and delivers electricity to the distribution network.

The main constraints of the optimization including the power flow constraints and pumped storage plant constraints. The power flow constraints are described as

$P_{PV,i}+P_{WT,i}-P_{Load,i}-P_{PS,i}=V_i{\displaystyle \sum }_{j=1}^{N_{Bus}}{V}_j\left(G_{i,j}\text{cos}{\theta }_{i,j}+B_{i,j}\text{sin}{\theta }_{i,j}\right)(10)$

$Q_{Load,i}=-V_i{\displaystyle \sum }_{j=1}^{N_{Bus}}{V}_j(G_{i,j}\text{sin}{\theta }_{i,j}-B_{i,j}\text{cos}{\theta }_{i,j})(11)$

$V_i^{min}\le V_i\left(t\right)\le V_i^{max}(12)$

$I_{i,j}\left(t\right)\le I_{i,j}^{max}(13)$

where $P_{\text{PV}.i}$ is active power generated by PV. $P_{\text{Load}.i}$ and $Q_{\text{Load}.i}$ are the active power and reactive power of load, respectively. $V_i$ and $V_j$ are the voltage of node $i$ and $j$, respectively. $V_i^{min}$ and $V_i^{max}$ are the minimum and maximum allowable voltage of the node $i$, respectively. $G_{i,j}$ and $B_{i,j}$ are the real and imaginary elements of the admittance matrix. ${\theta }_{i,j}$ is the phase angle difference between node $i$ to node $j$. $N_{\text{Bus}}$ is the total number of buses in the distribution network. $I_{i,j}\left(t\right)$ is the current from bus $i$ to bus $j$ at time $t$. $I_{i,j}^{\text{max}}$ is the upper limit of current from bus $i$ to bus $j$.

Pumped storage plants have two operation modes: pumping and generating electricity (Ma et al., 2015). The generating mode and pumping mode are described as Eqs 14, 15, respectively.

$P_{PS}\left(t\right)=e_T\rho gh{q}_g\left(t\right)(14)$

$P_{PS}\left(t\right)=\frac{\rho gh{q}_p\left(t\right)}{e_p}(15)$

where $e_T$ and $e_p$ are the efficiency of the turbine generator and pump motor, respectively. $\rho$ is the density of water. $g$ is the acceleration of gravity. $h$ is the elevating head. $q_g\left(t\right)$ and $q_p\left(t\right)$ are the water volumetric flow rate of the turbine generator and pump motor at time, respectively.

The amount of water in the upper reservoir is calculated by

$Q_{UR}\left(t+1\right)=Q_{UR}\left(t\right)+\underset{t}{\overset{t+1}{{\displaystyle \int }}}{q}_p\left(t\right)dt-\underset{t}{\overset{t+1}{{\displaystyle \int }}}{q}_g\left(t\right)dt(16)$

where $Q_{UR}\left(t\right)$ is the water quantity in the upper reservoir at time $t$.

In order to represent the storage state of a pumped storage plant, the state of charge (SOC) is introduced. The SOC of a pumped storage plant is expressed as

$SO{C}_{PS}\left(t\right)=\frac{Q_{UR}\left(t\right)}{Q_{UR}^{max}}(17)$

where $Q_{UR}^{max}$ is the maximum limit of upper reservoir water quantity. $SO{C}_{PS}\left(t\right)$ is the SOC of the pumped storage plant at time $t$.

The amount of the water in the upper reservoir should be between the maximum allowable reservoir capacity and the minimum allowable reservoir capacity. It also requires that the amount of water in the upstream reservoir remain unchanged for 1 day. These constraints of the pumped storage plant are presented as follows.

$Q_{UR}^{min}\le Q_{UR}\left(t\right)\le Q_{UR}^{max}(18)$

$SO{C}_{PS}\left(T_{Start}\right)=SO{C}_{PS}\left(T_{End}\right)(19)$

where $Q_{UR}^{min}$ is the minimum limit of upper reservoir water quantity. $T_{Start}$ and $T_{End}$ are the start and end time of the day, respectively.

3 Solution Approach

From the previous section, it can be seen that the formulated distributed network planning optimization model is a non-linear problem. There are many methods to solve such problem, such as dynamic programming (Ganguly et al., 2013), differential algorithm (Zhang et al., 2016), and genetic algorithm (Ghofrani et al., 2013), (Awad et al., 2014). Considering the complexity of this optimization model, a method based on the particle swarm optimization and dynamic minimum spanning tree (PSO-DMST) is proposed to solve the corresponding bi-layer planning problem. The details of the problem solving are given below.

3.1 Particle Swarm Optimization-Dynamic Minimum Spanning Tree Method in Planning Optimization Layer

The locations of the PV, WT, substation and pumped storage plant are determined by the PSO method (Kennedy and Eberhart, 1995). Each particle represents a potential coordinate (x, y) of the component. The update formulas of the particles are as follows.

$v_{id}^{k+1}=\omega v_{id}^k+r_1{c}_1\left(p_{id}^k-x_{id}^k\right)+r_2{c}_2\left(g_{id}^k-x_{id}^k\right)(20)$

$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}(21)$

where $v_{id}^k$ and $x_{id}^k$ denote the position and velocity of the particle in the $k$ th iteration, respectively. $p_{id}^k$ and $g_{id}^k$ denote the personal best and the global best of $k$ th iteration of dimension $d$, respectively. $\omega$ is the inertia weight. $c_1$ and $c_2$ are learning coefficients. $r_1$ and $r_2$ are two random numbers in the range [0,1]. In order to improve the performance of the algorithm, the linearly decreasing inertia weight is used in this study (Fei and He, 2015), which is presented as

$\omega ={\omega }_{\text{max}}-\left({\omega }_{\text{max}}-{\omega }_{\text{min}}\right)\frac{k}{k_{\text{max}}}(22)$

where ${\omega }_{max}$ and ${\omega }_{min}$ are the maximum and minimum inertia weights, respectively. $k$ and $k_{max}$ are the iteration number and maximum number of iterations, respectively.

Once the locations of the PV, WT, substation and pumped storage plant are determined, it is necessary to find an effective way to connect all the components in the distribution network. This problem is similar to the minimum spanning tree (MST) problem in graph theory (Bondy and Murty, 1976). In MST, each PV, WT, substation and pumped storage plant and load corresponds to a vertex in the graph, and these vertices are connected with minimum total weight. In the traditional MST, the weight is the distance between two vertices, that is, the cable length between two components. This method can finally connect all components with the shortest cable. After the distribution network topology is determined, the cable type is selected according to the peak load, and then the total cable cost can be calculated according to the length and type of the cable. However, MST can only guarantee that the length of the cable is the shortest but does not guarantee that the cost of the cable is the smallest.

Since one of the optimization goals is to minimize the cost of the cable, on the basis of the MST, the DMST that takes into account the influence of the load size on the cable selection is adopted for the cable connection. In DMST, the weight of two vertices is the cost of the cable that connecting two vertices. Thus, the minimum cost of cable can be guaranteed over the planning horizon. Figure 2 is presented as an example to show the difference between the MST and DMST for cable connection. Figure 2A is the undirected graph that gives all possible connecting cables and the corresponding length of each cable. Figure 2B and Figure 2C show the cable connection result obtained by MST method. Figure 2D is the cable connection result obtained by DMST. Here, two types of cables distinguished by color and the number in parentheses are adopted. The numbers in parentheses indicate the type of the cable. When the number of connected loads is less than or equal to 2, a cable with a smaller capacity (black solid line, type 1) can be selected, and when the number of connected loads exceeds 2, a cable with a larger capacity (red solid line, type 2) should be selected. And it assumes that the unit cost of black cable is 1 and that of red cable is 2. It can be seen that the cable cost of MST is 7.3, and that the cable cost of DMST is 6.8. Therefore, it demonstrated that the DMST method can obtain lower cable cost than the MST method.

FIGURE 2

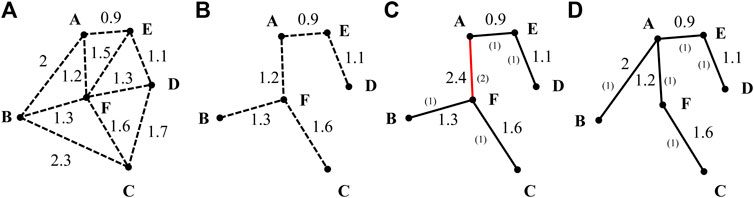
FIGURE 2. Layout by MST and DMST (A) Undirected graph (B) MST before cable selection (C) MST after cable selection (D) DMST.

3.2 Scenario-Based Stochastic Optimal Power Flow in Operation Optimization Layer

In the distribution network, there are many uncertain variables, such as load, renewable energy generation and electricity price. Taking into account these uncertainties, a scenario-based stochastic model is adopted to optimize the operation of distribution network.

The process of the scenario-based stochastic modeling is mainly divided into three steps: scenario generation, scenario reduction and scenario aggregation. Firstly, the RWM is used to generate the original scenarios based on the probability density function of the forecast error. In this paper, it is considered that the forecast errors of load, PV output, wind power generation and electricity price obey normal distribution. Secondly, similar scenarios and the scenarios with low probability are omitted. Thirdly, the optimization problem is solved under the remaining scenarios in a deterministic model, and the expected solution results are obtained by the scenario aggregation. More details on the modeling of the required scenarios can be found in reference (Mohammadi et al., 2014).

The final value of the uncertain variable can be calculated by

$P_{n,m,t}^{\text{s}}=P_{n,m,t}^{\text{forecast}}+\Delta P_{n,m,t}^{\text{s}}(23)$

where $n$ is the index of the uncertain variables, i.e., PV output, WT output, load, and electricity price. $m$ is the number of uncertain variables with index $n$. $P_{n,m,t}^{\text{forecast}}$ is the initial forecast value and $\Delta P_{n,m,t}^{\text{s}}$ is the estimated forecast error.

The length of each scenario is equal to the number of uncertain variables multiplied by the time dimension. The structure of each scenario can be expressed as follows.

$\left[P_{PV,1}^{\text{s}},\dots ,P_{PV,t}^s,\dots ,P_{PV,T}^{\text{s}},P_{WT,1}^s,\dots ,P_{WT,t}^s,\dots ,P_{WT,T}^{\text{s}},P_{L,1}^{\text{s}},\dots ,P_{L,t}^{\text{s}},\dots ,P_{L,T}^s,C_{P,1}^{\text{s}},\dots ,C_{P,t}^{\text{s}},\dots ,C_{P,T}^{\text{s}}\right](24)$

where $P_{PV,t}^s$ is the PV output at hour $t$ in the $s$ th scenario. $P_{WT,t}^s$ is the WT generation at hour $t$ in the $s$ th scenario. $P_{L,t}^s$ is the value of the load at hour $t$ in the $s$ th scenario. $C_{P,t}^s$ is the electricity price at hour $t$ in the $s$ th scenario. $N_L$ is the total number of the loads. $T$ is the scheduling horizon of 1 day.

Based on the generated scenarios, the optimal power flow is carried out in MATPOWER 6.0 toolbox (Zimmerman et al., 2011) to find the optimal operation strategy of the distribution network, check the power flow constraints, and calculate the operation cost of the distribution network.

3.3 Proposed Optimization Framework

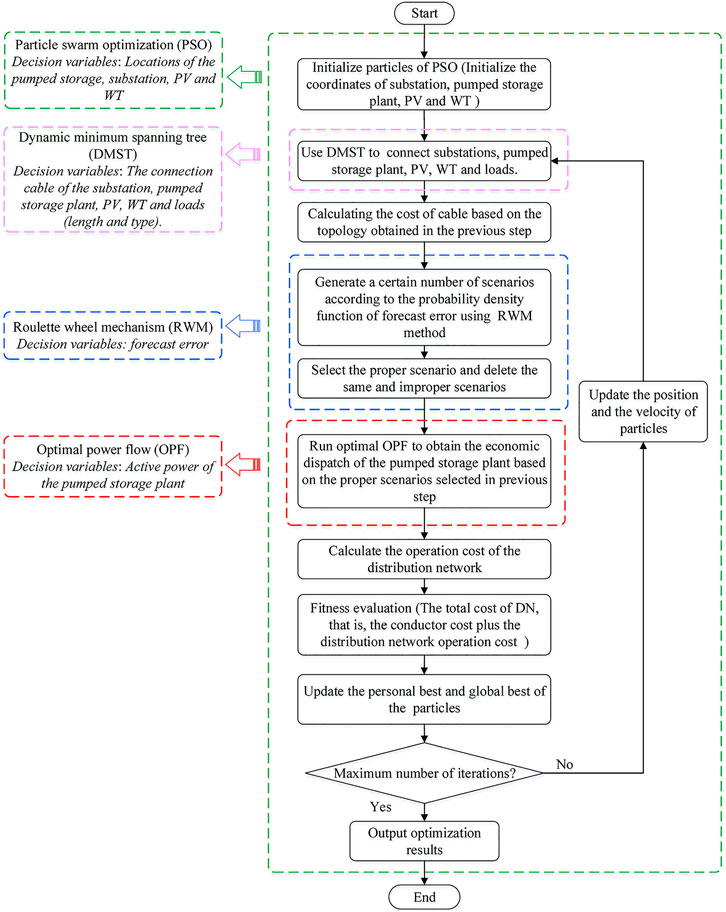
Combining the two optimization layers, the whole flow chart of the optimization problem is shown in Figure 3. The main steps are presented as follows.

FIGURE 3

FIGURE 3. Flowchart of the proposed bi-layer planning model.

Step 1. : Initialize the position and velocity of PSO particles, that is, the potential construction location of substation, pumped storage plant, PV and WT.

Step 2. : Use the DMST to connect the substation, pumped storage plant, PV, WT and loads.

Step 3. : Calculate the cost of cables based on the topology obtained in the previous step.

Step 4. : Generate a certain number of scenarios based on the probability density function of the forecast error using the roulette wheel mechanism.

Step 5. : Select the proper scenarios and delete the same and improper scenarios.

Step 6. : According to the cable connection mode obtained in the previous step, run OPF of the selected scenario to find the optimal operation strategy that minimizes the operation cost of the distribution network.

Step 7. : Calculate the total operating cost of the distribution network based on the operation mode of the pumped storage plant obtained in the previous step.

Step 8. : Fitness evaluation, that is, calculate the total cost of the distribution network (cable cost plus operation cost).

Step 9. : According to fitness value, update the personal best and the global best of the particles.

Step 10. : Determine whether the maximum number of iterations has been reached. If it is achieved, terminate the algorithm and output the result; if not, update the position and velocity of the particle and go to step 2.

4 Case Study

4.1 System Description

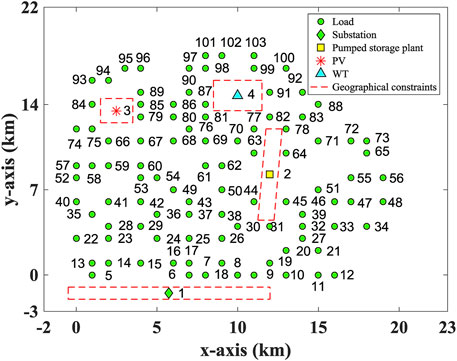
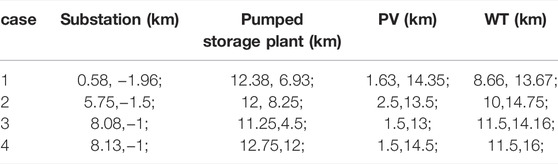
The proposed distribution planning method is tested on a modified 103-bus distribution system with a base voltage of 34.5 kV. The original coordinates of the loads are referred to (Carrano et al., 2005), and some modifications were made to them for this study. In the modified 103-bus distribution system, there are 99 loads with fixed position coordinates, as well as one substation, one pumped storage plant, one PV and one WT whose position coordinates need to be optimized. It is assumed that the distribution network is connected to the transmission network at coordinates (10, −5) km. Geographical constraints are expressed in Table 1. The modified system with the geographical location limitations is shown in Figure 4. Seven types of cables are selected to connect all components. Details of each cable are shown in Table 2 (Carrano et al., 2005).

TABLE 1

TABLE 1. Geographical constraints of each component.

FIGURE 4

FIGURE 4. 103-bus distribution network under study.

TABLE 2

TABLE 2. Cable parameters.

The load, photovoltaic power generation, wind power and electricity price data are obtained from Denmark power grid. The base load values for each load are obtained from (Carrano et al., 2005). The rated active power of the photovoltaic is 1 MW. The maximum water quantity of the upper reservoir is 50,000 ${\text{m}}^3$. The total efficiency of pumped storage is 0.75, and the maximum generating power is 1 MW. In this study, the pumping head is 60 m high. It is assumed that the total planning period is 15 years. The total number of particle swarm is 25 and the maximum iteration number is 100. The learning coefficients of PSO are 2. The minimum and maximum values of inertia weight are 0.4 and 0.9, respectively.

According to the geographical constraints and optimization procedure, the studies are categorized into 4 cases, as shown in Table 3. Case 1 is the base case, in which the locations of the components are random selected in the constrained zone, and the planning and operation procedure are separated. In case 2, the locations of the components are determined by experience of the staff, i.e., the center of the constrained zone. In case 3 and case 4, the locations of the components are determined by the proposed method. The difference between case 3 and case 4 is the sequence of planning optimization and operation optimization.

TABLE 3

TABLE 3. Case description.

4.2 Experimental Results

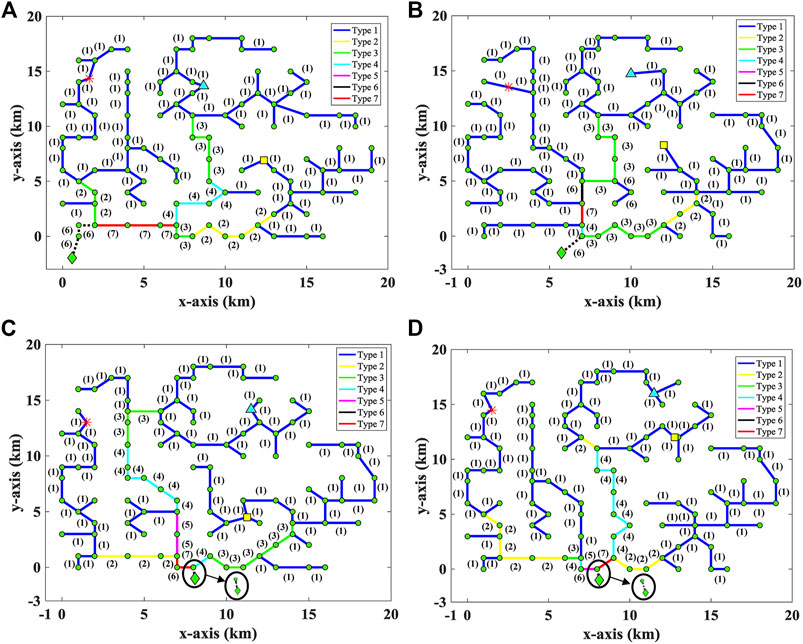
The topologies of the distribution network planning problem in four cases are shown in Figure 5. In Figures 5A,B,C,D are the topologies of the distribution network in case 1, case 2, case 3 and case 4, respectively. The coordinates of the substation, pumped storage plant, PV and WT in the four cases are shown in Table 4. In these figures, the solid line represents one cable, and the dotted line represents two cables of the same type. Different types of cables are distinguished by color and the number in parentheses is the type of the cable.

FIGURE 5

FIGURE 5. Distribution network topology (A) Case 1 (B) Case 2 (C) Case 3 (D) Case 4.

TABLE 4

TABLE 4. The Coordinates of the 103-bus distribution network in four cases.

From these topologies, it can be seen that all the loads, substation, pumped storage plant, PV and WT in the studied distribution network are connected without crossover. Meanwhile, the locations of the substation, pumped storage plant, PV and WT are also in the constrained zones. Details of the optimization results, including the NPV of cable cost, the NPV of operation cost and the NPV of total cost, are presented in Table 5.

TABLE 5

TABLE 5. The results of the 103-bus distribution network in four cases.

Comparing the NPV of cable cost in the four cases, it can be seen that the values of case 3 and case 4 are smaller than those of case 1 and case 2. The results of case 3 and case 4 are similar. It demonstrated that, compared with experience oriented or random selected locations, the proposed method helps to reduce the total cost of the cable. Comparing the NPV of operation cost in four cases, the lowest operation cost is obtained by case 4. This indicates that the location and connection mode of the components have an important influence on the operation of the distribution network. It can be found that although the cable cost of case 4 is higher than case 3, the operating cost of case 4 is much smaller than case 3, so the minimum total cost is obtained from case 4. This shows that when the topology optimization and operation optimization of the distribution network are separated, although the distribution network topology with smaller equipment investment cost can be obtained, the corresponding operating cost may not be minimal. Because the operation cost accounts for a large proportion of the total cost, the result of combining topology optimization and operation optimization is better than that of separating them. In order to improve the economic benefits, it is necessary to combine the planning optimization and operation optimization of the distribution network.

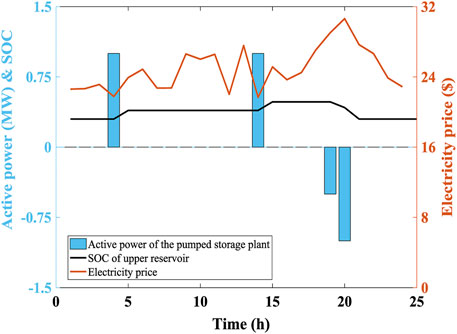
To prove the effectiveness of the proposed method, the economic dispatch of pumped storage plant in a selected scenario is presented in Figure 6. From Figure 6, it can be seen that pumped storage pumps water when the electricity price is low, and generates electricity when the electricity price is high, which can increase the profit of the distribution network operator.

FIGURE 6

FIGURE 6. Active power of the pumped storage plant.

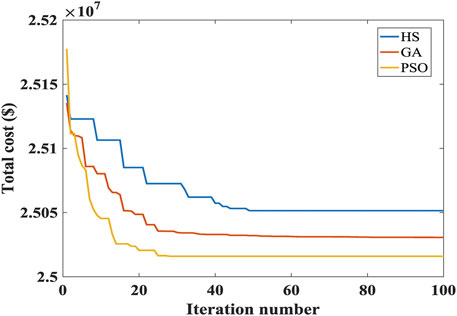
To further verify the effectiveness of the proposed PSO-based method, the performance of the PSO-based method is compared with genetic algorithm (GA) and harmony search (HS) in case 4. The comparison results are shown in Figure 7. It shows that the PSO-based method converges quickly and its optimization result is better than two other methods under the same experimental environment.

FIGURE 7

FIGURE 7. Convergence process.

5 Conclusion

In this paper, an integrated planning optimization model for the distribution network with geographical restrictions is established. The integrated planning optimization model is divided into two layers. In the planning optimization layer, the PSO method is used to optimize the locations of the substation, pumped storage plant, PV and WT, and then the DMST method is used to connect all the components without crossover. In the embedded operation optimization layer, considering the uncertainty of load, illumination intensity, wind speed and electricity price, a scenario-based stochastic OPF is carried out and the dispatch of the pumped storage plant is determined. The dispatch results show that the operating state of the pumped storage is closely related to the electricity price. It charges when the electricity price is low and discharges when the electricity price is high. By using the proposed method, both the total cost of the cable and the operation cost of the distribution network are reduced. In addition, the PSO-based optimization method is compared with the GA and the HS. The comparison results show that the PSO-based method converges faster and obtains better experimental results than the other two methods. In summary, the proposed method can provide cost-effective guidance for the planning and operation of distribution network with the consideration of geographical constraints.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KQ contributed to the conception and design of the proposed strategy. All authors wrote and edited the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant 52107073.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arasteh, H., Sepasian, M. S., and Vahidinasab, V. (2016). An Aggregated Model for Coordinated Planning and Reconfiguration of Electric Distribution Networks. Energy 94, 786–798. doi:10.1016/j.energy.2015.11.053

CrossRef Full Text | Google Scholar

Ashoornezhad, A., Falaghi, H., Hajizadeh, A., and Ramezani, M. (2021). A Two-Stage Multi-Period Distribution Network Expansion Planning Considering the Integration of Private Investors. Int. Trans. Electr. Energ. Syst. 31 (12), e13226. doi:10.1002/2050-7038.13226

CrossRef Full Text | Google Scholar

Awad, A. S. A., el-Fouly, T. H. M., and Salama, M. M. A. (2014). Optimal ESS Allocation and Load Shedding for Improving Distribution System Reliability. IEEE Trans. Smart Grid 5 (5), 2339–2349. doi:10.1109/tsg.2014.2316197

CrossRef Full Text | Google Scholar

Baringo, L., Boffino, L., and Oggioni, G. (2020). Robust Expansion Planning of a Distribution System with Electric Vehicles, Storage and Renewable Units. Appl. Energ. 265, 114679. doi:10.1016/j.apenergy.2020.114679

CrossRef Full Text | Google Scholar

Bondy, J. A., and Murty, U. S. R. (1976). Graph Theory with Applications. London: The Macmillan Press Ltd.

Google Scholar

Carpinelli, G., Celli, G., Mocci, S., Mottola, F., Pilo, F., and Proto, D. (2013). Optimal Integration of Distributed Energy Storage Devices in Smart Grids. IEEE Trans. Smart Grid 4 (2), 985–995. doi:10.1109/tsg.2012.2231100

CrossRef Full Text | Google Scholar

Carrano, E. G., Soares, L. A. E., Takahashi, R. H. C., Saldanha, R. R., and Neto, O. M. (2006). Electric Distribution Network Multiobjective Design Using a Problem-specific Genetic Algorithm. IEEE Trans. Power Deliv. 21 (2), 995–1005. doi:10.1109/tpwrd.2005.858779

CrossRef Full Text | Google Scholar

Carrano, E. G., Takahashi, R. H. C., Cardoso, E. P., Neto, O. M., and Saldanha, R. R. (2005). Multiobjective Genetic Algorithm in the Design of Electric Distribution Networks: Simulation Data. Orlando, FL: Tech. Rep. Univ. Fed. Minas Gerais, available at: http://www.mat.ufmg.br/∼taka/techrep/agnet01.pdf.

Google Scholar

Celli, G., Pilo, F., Pisano, G., and Soma, G. G. (2018). Distribution Energy Storage Investment Prioritization with a Real Coded Multi-Objective Genetic Algorithm. Electric Power Syst. Res. 163, 154–163. doi:10.1016/j.epsr.2018.06.008

CrossRef Full Text | Google Scholar

Chen, H., Gao, L., and Zhang, Z. (2021). Multi-objective Optimal Scheduling of a Microgrid with Uncertainties of Renewable Power Generation Considering User Satisfaction. Int. J. Electr. Power Energ. Syst. 131, 107142. doi:10.1016/j.ijepes.2021.107142

CrossRef Full Text | Google Scholar

Ding, H., Hu, Z., and Song, Y. (2012). Stochastic Optimization of the Daily Operation of Wind Farm and Pumped-Hydro-Storage Plant. Renew. Energ. 48, 571–578. doi:10.1016/j.renene.2012.06.008

CrossRef Full Text | Google Scholar

Fei, S.-w., and He, Y. (2015). A Multiple-Kernel Relevance Vector Machine with Nonlinear Decreasing Inertia Weight PSO for State Prediction of Bearing. Shock and Vibration 2015, 1–6. doi:10.1155/2015/685979

CrossRef Full Text | Google Scholar

Ganguly, S., Sahoo, N. C., and Das, D. (2013). Multi-objective Planning of Electrical Distribution Systems Using Dynamic Programming. Int. J. Electr. Power Energ. Syst. 46, 65–78. doi:10.1016/j.ijepes.2012.10.030

CrossRef Full Text | Google Scholar

Ghofrani, M., Arabali, A., Etezadi-Amoli, M., and Fadali, M. S. (2013). A Framework for Optimal Placement of Energy Storage Units within a Power System with High Wind Penetration. IEEE Trans. Sustain. Energ. 4 (2), 434–442. doi:10.1109/tste.2012.2227343

CrossRef Full Text | Google Scholar

Hou, P., Hu, W., Chen, C., and Chen, Z. (2016). Optimisation of Offshore Wind Farm cable Connection Layout Considering Levelised Production Cost Using Dynamic Minimum Spanning Tree Algorithm. IET Renew. Power Generation 10 (2), 175–183. doi:10.1049/iet-rpg.2015.0052

CrossRef Full Text | Google Scholar

Hu, J., Liu, X., Shahidehpour, M., and Xia, S. (2021). Optimal Operation of Energy Hubs with Large-Scale Distributed Energy Resources for Distribution Network Congestion Management. IEEE Trans. Sustain. Energ. 12 (3), 1755–1765. doi:10.1109/tste.2021.3064375

CrossRef Full Text | Google Scholar

Huang, C., Hou, H., Yu, G., Zhang, L., and Hu, E. (2020). Energy Solutions for Producing Shale Oil: Characteristics of Energy Demand and Economic Analysis of Energy Supply Options. Energy 192, 116603. doi:10.1016/j.energy.2019.116603

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). Particle Swarm Optimization.” in Proceedings of ICNN'95 - International Conference on Neural Networks. Perth, WA, Australia, 1942–1948.

Google Scholar

Khator, S. K., and Leung, L. C. (1997). Power Distribution Planning: A Review of Models and Issues. IEEE Trans. Power Syst. 12 (3), 1151–1159. doi:10.1109/59.630455

CrossRef Full Text | Google Scholar

Koutsoukis, N. C., and Georgilakis, P. S. (2022). A Multistage Distribution Network Planning Method Considering Distributed Generation Active Management and Demand Response. IET Renew. Power Gen 16 (1), 65–76. doi:10.1049/rpg2.12325

CrossRef Full Text | Google Scholar

Koutsoukis, N. C., Georgilakis, P. S., and Hatziargyriou, N. D. (2014). A Tabu Search Method for Distribution Network Planning Considering Distributed Generation and UncertaintiesInternational Conference on Probabilistic Methods Applied to Power Systems. Durham: PMAPS, 1–6.

Google Scholar

Lazzeroni, P., and Repetto, M. (2019). Optimal Planning of Battery Systems for Power Losses Reduction in Distribution Grids. Electric Power Syst. Res. 167, 94–112. doi:10.1016/j.epsr.2018.10.027

CrossRef Full Text | Google Scholar

Li, J., Hu, W., Wu, X., Huang, Q., Liu, Z., Chen, C., et al. (2020). Cable Connection Optimization for Onshore Wind Farms Considering Restricted Area and Topography. IEEE Syst. J. 14 (3), 3082–3092. doi:10.1109/jsyst.2020.2982843

CrossRef Full Text | Google Scholar

Ma, T., Yang, H., Lu, L., and Peng, J. (2015). Pumped Storage-Based Standalone Photovoltaic Power Generation System: Modeling and Techno-Economic Optimization. Appl. Energ. 137, 649–659. doi:10.1016/j.apenergy.2014.06.005

CrossRef Full Text | Google Scholar

Marcochi de Melo, D., Lopes, E. C., Motta, J. G., Asano, R., Valverde, M., Suyama, R., et al. (2021). Integrated Intelligent Geoprocessing Tool for Screening Candidate Locations Suitable for Distributed Generation Deployment. Renew. Energ. 177, 797–806. doi:10.1016/j.renene.2021.05.100

CrossRef Full Text | Google Scholar

Mejia, M. A., Macedo, L. H., Muñoz-Delgado, G., Contreras, J., and Padilha-Feltrin, A. (2022). Medium-term Planning of Active Distribution Systems Considering Voltage-dependent Loads, Network Reconfiguration, and CO2 Emissions. Int. J. Electr. Power Energ. Syst. 135, 107541. doi:10.1016/j.ijepes.2021.107541

CrossRef Full Text | Google Scholar

Mohammadi Fathabad, A., Cheng, J., Pan, K., and Qiu, F. (2020). Data-driven Planning for Renewable Distributed Generation in Distribution Systems. IEEE Trans. Power Syst. (99), 1

Google Scholar

Mohammadi, S., Soleymani, S., and Mozafari, B. (2014). Scenario-Based Stochastic Operation Management of Microgrid Including Wind, Photovoltaic, Micro-turbine, Fuel Cell and Energy Storage Devices. Int. J. Electr. Power Energ. Syst. 54, 525–535. doi:10.1016/j.ijepes.2013.08.004

CrossRef Full Text | Google Scholar

Mohandes, B., Wahbah, M., Moursi, M. S. E., and El-Fouly, T. H. M. (2021). Renewable Energy Management System: Optimum Design and Hourly Dispatch. IEEE Trans. Sustain. Energ. 12 (3), 1615–1628. doi:10.1109/tste.2021.3058252

CrossRef Full Text | Google Scholar

Muñoz-Delgado, G., Contreras, J., and Arroyo, J. M. (2016). Multistage Generation and Network Expansion Planning in Distribution Systems Considering Uncertainty and Reliability. IEEE Trans. Power Syst. 31 (5), 3715–3728. doi:10.1109/TPWRS.2015.2503604

CrossRef Full Text | Google Scholar

Ouyang, W., Cheng, H., Zhang, X., and Yao, L. (2010). Distribution Network Planning Method Considering Distributed Generation for Peak Cutting. Energ. Convers. Manag. 51 (12), 2394–2401. doi:10.1016/j.enconman.2010.05.003

CrossRef Full Text | Google Scholar

Roy Ghatak, S., Sannigrahi, S., and Acharjee, P. (2018). Optimised Planning of Distribution Network with Photovoltaic System, Battery Storage, and DSTATCOM. IET Renew. Power Generation 12 (15), 1823–1832. doi:10.1049/iet-rpg.2018.5088

CrossRef Full Text | Google Scholar

Sedghi, M., Ahmadian, A., and Aliakbar-Golkar, M. (2016). Optimal Storage Planning in Active Distribution Network Considering Uncertainty of Wind Power Distributed Generation. IEEE Trans. Power Syst. 31 (1), 304–316. doi:10.1109/tpwrs.2015.2404533

CrossRef Full Text | Google Scholar

Sedghi, M., Aliakbar-Golkar, M., and Haghifam, M.-R. (2013). Distribution Network Expansion Considering Distributed Generation and Storage Units Using Modified PSO Algorithm. Int. J. Electr. Power Energ. Syst. 52, 221–230. doi:10.1016/j.ijepes.2013.03.041

CrossRef Full Text | Google Scholar

Tang, Y., and Low, S. H. (2017). Optimal Placement of Energy Storage in Distribution Networks. IEEE Trans. Smart Grid 8 (6), 3094–3103. doi:10.1109/tsg.2017.2711921

CrossRef Full Text | Google Scholar

Tarôco, C. G., Takahashi, R. H. C., and Carrano, E. G. (2016). Multiobjective Planning of Power Distribution Networks with Facility Location for Distributed Generation. Elect. Power Syst. Res. 141, 562

Google Scholar

Ugranlı, F. (2020). Probabilistic Distribution Planning: Including the Interactions between Chance Constraints and Renewable Energy. Sustain. Energ. Grids Netw. 23, 100372.

Google Scholar

Wang, Z., Chen, B., Wang, J., Kim, J., and Begovic, M. M. (2014). Robust Optimization Based Optimal DG Placement in Microgrids. IEEE Trans. Smart Grid 5 (5), 2173–2182. doi:10.1109/tsg.2014.2321748

CrossRef Full Text | Google Scholar

Xing, H., Cheng, H., Zhang, Y., and Zeng, P. (2016). Active Distribution Network Expansion Planning Integrating Dispersed Energy Storage Systems. IET Generation, Transm. Distribution 10 (3), 638–644. doi:10.1049/iet-gtd.2015.0411

CrossRef Full Text | Google Scholar

Zhang, N., Kang, C., Kirschen, D. S., Xia, Q., Xi, W., Huang, J., et al. (2013). Planning Pumped Storage Capacity for Wind Power Integration. IEEE Trans. Sustain. Energ. 4 (2), 393–401. doi:10.1109/tste.2012.2226067

CrossRef Full Text | Google Scholar

Zhang, Y., Dong, Z. Y., Luo, F., Zheng, Y., Meng, K., and Wong, K. P. (2016). Optimal Allocation of Battery Energy Storage Systems in Distribution Networks with High Wind Power Penetration. IET Renew. Power Generation 10 (8), 1105–1113. doi:10.1049/iet-rpg.2015.0542

CrossRef Full Text | Google Scholar

Ziari, I., Ledwich, G., Ghosh, A., and Platt, G. (2013). Optimal Distribution Network Reinforcement Considering Load Growth, Line Loss, and Reliability. IEEE Trans. Power Syst. 28 (2), 587–597. doi:10.1109/tpwrs.2012.2211626

CrossRef Full Text | Google Scholar

Zimmerman, R. D., Murillo-Sánchez, C. E., and Thomas, R. J. (2011). MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 26, 12.

CrossRef Full Text | Google Scholar