Scalability of Nek5000 on High-Performance Computing Clusters Toward Direct Numerical Simulation of Molten Pool Convection

In a postulated severe accident, a molten pool with decay heat can form in the lower head of a reactor pressure vessel, threatening the vessel’s structural integrity. Natural convection in molten pools with extremely high Rayleigh (Ra) number is not yet fully understood as accurate simulation of the intense turbulence remains an outstanding challenge. Various models have been implemented in many studies, such as RANS (Reynolds-averaged Navier–Stokes), LES (large-eddy simulation), and DNS (direct numerical simulation). DNS can provide the most accurate results but at the expense of large computational resources. As the significant development of the HPC (high-performance computing) technology emerges, DNS becomes a more feasible method in molten pool simulations. Nek5000 is an open-source code for the simulation of incompressible flows, which is based on a high-order SEM (spectral element method) discretization strategy. Nek5000 has been performed on many supercomputing clusters, and the parallel performance of benchmarks can be useful for the estimation of computation budgets. In this work, we conducted scalability tests of Nek5000 on four different HPC clusters, namely, JUWELS (Atos Bullsquana X1000), Hawk (HPE Apollo 9000), ARCHER2 (HPE Cray EX), and Beskow (Cray XC40). The reference case is a DNS of molten pool convection in a hemispherical configuration with Ra = 10¹¹, where the computational domain consisted of 391 million grid points. The objectives are (i) to determine if there is strong scalability of Nek5000 for the specific problem on the currently available systems and (ii) to explore the feasibility of obtaining DNS data for much higher Ra. We found super-linear speed-up up to 65536 MPI-rank on Hawk and ARCHER2 systems and around 8000 MPI-rank on JUWELS and Beskow systems. We achieved the best performance with the Hawk system with reasonably good results up to 131072 MPI-rank, which is attributed to the hypercube technique on its interconnection. Given the current HPC technology, it is feasible to obtain DNS data for Ra = 10¹², but for cases higher than this, significant improvement in hardware and software HPC technology is necessary.

Introduction

In a postulated severe accident scenario of a light water reactor, the reactor core can melt down and relocate to the lower head of the reactor pressure vessel. Due to the decay heat and oxidation, the debris, also called corium, can form a molten pool with heat fluxes that can threaten the integrity of the pressure vessel. One of the strategies to keep the corium inside the pressure vessel by maintaining the vessel’s structural integrity is called in-vessel retention (IVR), which is performed by cooling the external surface of the lower head. To ensure the success of the IVR strategy (Fichot et al., 2018; Villanueva et al., 2020; Wang et al., 2021), it is crucial to analyze the heat flux distribution imposed by the corium on the vessel. First, the heat fluxes must not exceed the given critical heat flux (CHF) of the vessel. Second, such heat flux distributions can be used to assess the structural response of the vessel.

Numerous studies have been conducted on the molten pool simulation, both experimentally (Asfia and Dhir, 1996; Bernaz et al., 1998; Sehgal et al., 1998; Helle et al., 1999; Fluhrer et al., 2005) and numerically (Shams, 2018; Whang et al., 2019; Dovizio et al., 2022). However, many challenges remain in the numerical simulation of molten pool convection. One of them is to properly reproduce the intensive turbulence caused by the strong heat source inside the molten pool. Figure 1 shows the observation of thermo-fluid behavior of the BALI molten pool experiment (Bernaz et al., 1998). It is shown that the flow domain can be divided into three regions. Turbulent Rayleigh–Bénard convection (RBC) cells are observed in the upper part of the fluid domain. The second region is the damped flow in the lower part of the domain, where the flow is mainly propelled by shear forces. The third is the flow that descends along the curved wall, which is known as the ν-phenomenon (Nourgaliev et al., 1997).

FIGURE 1

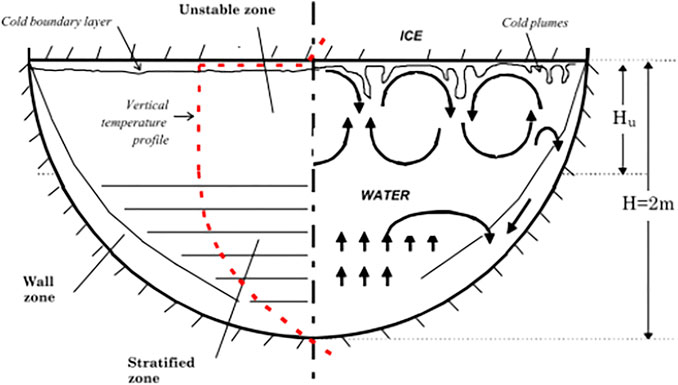
FIGURE 1. General flow observations in BALI experiments (Bernaz et al., 1998).

The Reynolds-averaged Navier–Stokes (RANS) models are commonly utilized to model turbulent flows (Chakraborty, 2009). However, Dinh and Nourgaliev pointed out that RANS models such as the $k-\epsilon$ model are not suitable for modeling the turbulent natural convection flow (Dinh and Nourgaliev, 1997) because the thermo-fluid behavior in the molten pool is characterized as internally heated (IH) natural convection, which is different from the force convection flow. Large-eddy simulation (LES) has also been implemented to simulate molten pool convection, but more qualification and quantification are needed (Zhang et al., 2018). On the other hand, direct numerical simulation (DNS) can provide the most accurate simulation results because it does not have assumption models on the turbulence flows (Grötzbach and Wörner, 1999; Yildiz et al., 2020). But, it requires much more computational results than those of the RANS and LES models. Recently Bian et al. (2022a), Bian et al. (2022b) conducted a DNS of molten pool convection with Rayleigh number Ra = 10¹¹ in a hemispherical configuration using an open-source code Nek5000 (Fischer et al., 2016). The results of the thermo-fluid behavior, shown in Figures 2 and 3, are consistent with the observations in the BALI experiment, which are the RBC flow in the upper region, the damped flow in the lower region that facilitates thermal stratification, and the descending flow on the curved region that effectively transfer heat to the bottom. Although the Rayleigh number in this case (which is already the highest Ra value to date in a hemispherical geometry) is significantly less than the prototypic value of 10¹⁶–10¹⁷, the DNS data can offer valuable information on the thermo-fluid behavior of internally heated molten pools. In addition, it can serve as reference data for the assessment of RANS and LES models, such as the turbulent quantities that cannot be obtained from experiments. However, if DNS data can be generated for even higher Rayleigh numbers, better insights and understanding can be attained relevant to the prototypic case. It is important to note, though, that the higher the Rayleigh number, the required computational resources for a DNS calculation rise exponentially. Hence, such calculations must use high-performance computing (HPC) systems, which can also support the computational tool of choice. In this study, we explore the feasibility of obtaining DNS data for higher Ra numbers using Nek5000.

FIGURE 2

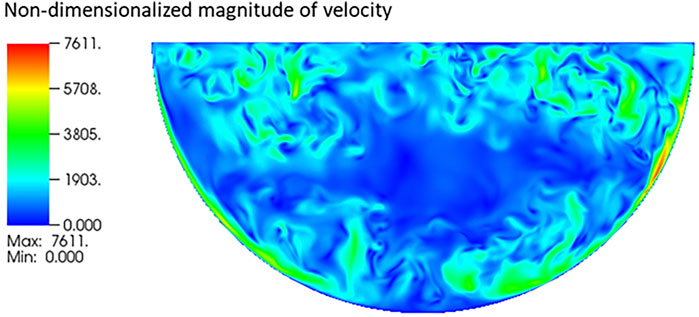
FIGURE 2. Instantaneous distribution of the magnitude of the velocity of an internally heated natural convection with Ra = 10¹¹ (Bian et al., 2022).

FIGURE 3

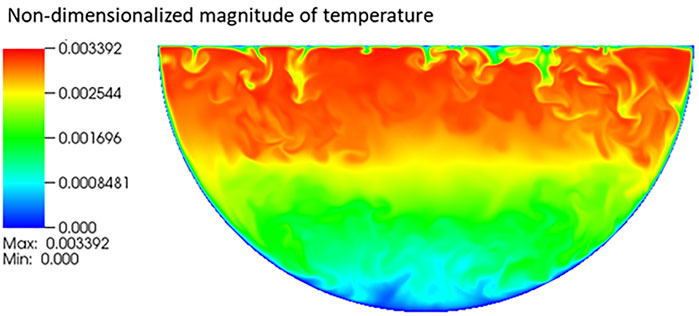
FIGURE 3. Instantaneous temperature distribution of an internally heated natural convection with Ra = 10¹¹ (Bian et al., 2022).

Nek5000 is an open-source computational fluid dynamics (CFD) code with spatial discretization based on the spectral element method (SEM), which features scalable algorithms to be faster and more efficient. Goluskin et al. (2016) conducted a series of DNS simulations of internally heated natural convection with different Rayleigh numbers in a box geometry using Nek5000. We also used Nek5000 to analyze molten pool convection in different geometries (Bian et al., 2022). Since the DNS works usually demand large computational resources, it is necessary to compute the budget based on the scalability performance of the code. Recently, few scalability tests of Nek5000 have been performed by Fischer et al., (2015); Fischer et al., (2015); Offermans et al., (2016); Merzari et al., (2016); Merzari et al., (2020) analyzing the algorithms for performance characteristics on large-scale parallel computers. Offermans et al. (2016) discussed in detail the scalability of pipe flow simulations on Petascale systems with CPUs. Furthermore, Merzari et al. (2016) compared the LES with RANS calculations for a wire-wrapped rod bundle. In addition, Merzari et al. (2020) studied the weak scaling performances for Taylor–Green vortex simulation on a heterogenous system (Summit at Oak Ridge National Laboratory).

In this study, we perform scalability tests of Nek5000 based on the molten pool simulation using four different high-performance computing (HPC) clusters, namely, JUWELS¹, ARCHER2², Hawk³, and Beskow⁴. The objective of this work is two-fold. The first is to determine if there is strong scalability of Nek5000 for molten pool natural convection on the available HPC systems. This is carried out by running the benchmark case having a specific Ra number with different MPI ranks. The second is to explore the feasibility of obtaining DNS data for much higher Ra number. In the following, Section 2 gives a description of the benchmark case and the governing equations. Section 3 briefly introduces the discretization scheme in Nek5000 and presents the mesh used in the simulations. Section 4 illustrates the scalability result of the benchmark tests on the four different HPC clusters and estimates the feasibility of performing DNS of molten pool convection at extremely high Rayleigh numbers. Finally, the concluding remarks are given in Section 5.

Benchmark Case

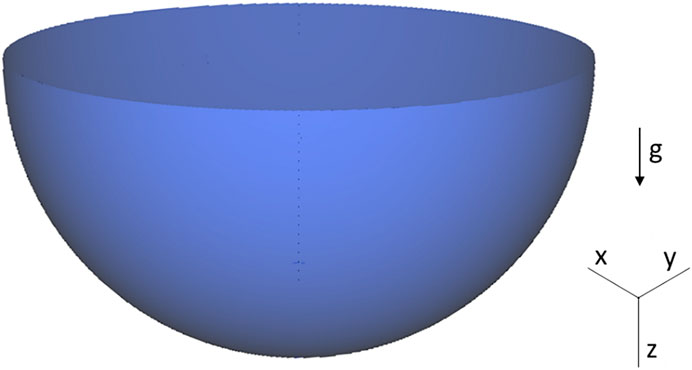
In this work, a DNS simulation of the internally heated molten pool in the hemispherical domain is selected as the benchmark case for the scalability test. The 3D hemispherical cavity is shown in Figure 4, which represents the lower head of the reactor pressurized vessel. The cavity contains two no-slip boundaries, the top wall and the curved wall. The isothermal condition is specified on the boundaries. To simulate the decay heat effect in the corium, a homogenous volumetric heat source is arranged inside the domain. The gravity field is parallel with the vertical z-direction, as shown in Figure 4. The thermo-fluid behavior in the molten pool is characterized as an internally heated natural convection where the flow motion is propelled by buoyancy force induced by the density difference of the fluid due to the internal heat source.

FIGURE 4

FIGURE 4. Computational domain.

The Oberbeck–Boussinesq approximation (Oberbeck, 1879; Rajagopala et al., 2009) is commonly used to model the natural convection, which is mainly propelled by the buoyancy force. With this approximation, the density variation of the fluid is assumed to only depend on the change of temperature such that

$\frac{\rho -{\rho }_{\ast }}{{\rho }_{\ast }}=-\beta \left(T-T_{\ast }\right),$

where $\rho$ is the density, ${\rho }_{\ast }$ is the reference density at the reference temperature $T_{\ast }$, and $\beta$ is the expansion coefficient. Incorporating this assumption, the governing equations of the thermo-fluid behavior are given below (Goluskin, 2016)

$\nabla \cdot \mathit{u}=0,$

$\frac{\partial \mathit{u}}{\partial t}+\mathit{u}\cdot \nabla \mathit{u}=-\frac{1}{{\rho }_{\ast }}\nabla p+\nu {\nabla }^2\mathit{u}+g\beta T\overrightarrow{z},$

$\frac{\partial T}{\partial t}+\mathit{u}\cdot \nabla T=k{\nabla }^{2}T+\frac{Q}{{\rho }_{\ast }{c}_p},$

where $\mathit{u}$, $p$, and $T$ are the velocity, pressure, and temperature field, respectively. The parameters $\nu$, $g$, $k$, and $c_p$ are the kinematic viscosity, gravity acceleration, thermal diffusivity, and thermal capacity, respectively. The first one is the mass equation which controls the divergence free of the incompressible flow. The second equation is the momentum equation which solves the flow motion within the molten pool. On the right hand, the terms represent the pressure, shear and buoyancy effect, respectively. The last equation is the energy equation which solves the temperature field, and the terms on the right hand are the diffusive term and heat source term. To generalize the problem, the equations can be normalized using a characteristic length $l \left[m\right]$, time scale $\frac{l^2}{\alpha } \left[s\right]$, and temperature scale $\Delta =\frac{l^{2}Q}{\alpha {\rho }_{\ast }{c}_p} \left[K\right]$. The normalized equations of the molten pool convection are shown below

$\nabla \cdot {\mathit{u}}^{\ast }=0.$

$\frac{\partial {\mathit{u}}^{\ast }}{\partial t^{\ast }}+{\mathit{u}}^{\ast }\cdot \nabla {\mathit{u}}^{\ast }=-\nabla p\ast +\mathrm{Pr}{\nabla }^2{\mathit{u}}^{\ast }+Ra\mathrm{Pr}{T}^{\ast }\overrightarrow{z}.$

$\frac{\partial T^{\ast }}{\partial t^{\ast }}+{\mathit{u}}^{\ast }\cdot \nabla T^{\ast }={\nabla }^2{T}^{\ast }+1.$

In the equations, the variables with the star notation are the corresponding nondimensional fields. There are two nondimensional numbers in the normalized equation, namely, the Rayleigh number $Ra=\frac{g\beta l^3\Delta }{\alpha v}$ and the Prandtl number $\mathrm{Pr}=\frac{\nu }{\alpha }$ . The Rayleigh number indicates the ratio of the fluid inertial force to the viscous force, which can be treated as the primary control number of the IH natural convection. When the Rayleigh number increases, the natural convection will first change from laminar flow to turbulent flow and the intensity of the turbulence will become stronger. Therefore, with the larger Rayleigh number, more detail of the flow need to be solved in the DNS simulations, and correspondingly larger resources are required. The Prandtl number is a material-dependent parameter, representing the ratio of momentum diffusion to heat diffusion.

Numerical Settings

The equations are solved using Nek5000, which is based on the SEM discretization method. The SEM can be treated as the combination of the finite element method (FEM) and spectral method (SM), which absorbs both the generality of the former and the accuracy of the latter. When using the SEM, the computational domain will be divided into elements, similar to the FEM. Within each element, the SEM is implemented in such a manner that unknown in each element can be represented by using a chosen function space and the weights on the collocation points in the element. In Nek5000, for the convenience of numerical integration, the Gauss–Legendre–Lobatto (GLL) points are used as the collocation points. In this study, the Pn–Pn method (Tomboulides et al., 1997; Guermond et al., 2006) is selected as the solver for the governing Navier–Stokes equations in Nek5000, and the time discretization method is an implicit–explicit BDFk-EXTk (backward difference formula and EXTrapolation of order k). The Helmholtz solver is used for the passive scalar equation. Details about the discretization of the governing equations can be found in the theory guide of Nek5000 (Deville et al., 2002).

When generating the DNS mesh of the IH natural convection in the molten pool, the smallest dissipation length scale of both the bulk flow and boundary layer should be considered, which puts the highest restriction on the computational effort. In a turbulence natural convection, the mesh requirement depends on the Rayleigh number and the Prandtl number (Shishkina et al., 2010). A Rayleigh number of 10¹¹ is set in this study. If the Rayleigh number increases by 10, the mesh resolution should also practically increase by 10. It should be mentioned that the computational domain comprises elements in Nek5000, and the elements are divided by the GLL grid points on the element edges according to the polynomial order. In this case, it is the distance between adjusting grid points that satisfy the mesh size.

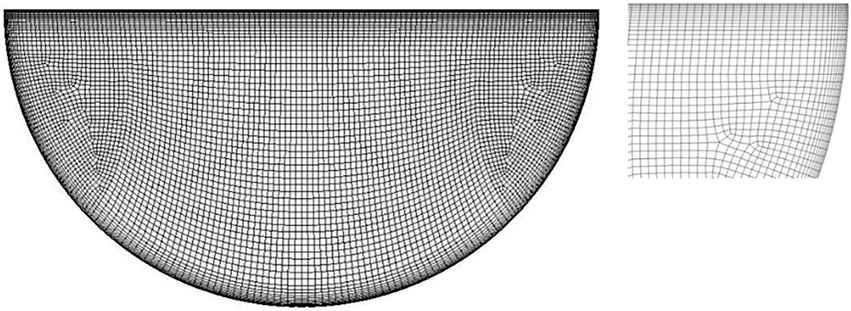
After the pre-estimation of the DNS mesh, the total element number in the computational domain is about 764K. The mesh on a sample middle plane is shown in Figure 5, and it is shown that the boundary layers have been refined. In this approach, the polynomial order or the order of the function space used is 7, which yields a total of 391M GLL grid points in the whole domain. The overall settings of the simulation are listed in Table 1. A quasi-steady state is first established, which means that an energy balance of the system has been attained. After that, we conduct the scalability tests starting from the steady-state simulations on the four different HPC clusters.

FIGURE 5

FIGURE 5. Mesh on a middle slice of the computational domain.

TABLE 1

TABLE 1. Summary of key simulation parameters.

Benchmark Tests

We performed the benchmark tests on three different European Petascale systems, namely, JUWELS at Julich Supercomputing Centre, ARCHER2 at EPCC, the University of Edinburgh, and Hawk at HLRS High-Performance Computing Center Stuttgart, as shown in Table 2. JUWELS is an Intel Xeon–based system and has a total of 2,271 compute nodes with Intel processors. The interconnect used is a Mellanox InfiniBand EDR fat-tree network. ARCHER2 is an HPE Cray EX system and has 5,860 compute nodes with AMD processors. The HPE Cray slingshot with 2x100 Gbps bi-directional per node is used as the interconnection. Hawk is an HPE Apollo 9000 system and has 5,632 AMD EPYC compute nodes. The interconnect is InfiniBand HDR200 with a bandwidth of 200 Gbit/s and an MPI latency of ∼1.3us per link. In addition to the EU Petascale systems, the Beskow cluster at KTH PDC is also used. It is a Cray XC40 system based on Intel Haswell and Broadwell processors and Cray Aries interconnect technology. The cluster has a total of 2,060 compute nodes.

TABLE 2

TABLE 2. HPC systems overview.

The corresponding software, including compilers and MPI libraries on these systems, is presented in Table 3. On ARCHER2, the compiler flags for AMD CPU architectures have been loaded by default using the module “craype-x86-rome”. The default compiler flags “-march = znver2 –mtune = znver2 –O3” for GCC has been adapted to AMD CPU architectures on Hawk. Only pure MPI runs are performed on fully occupied nodes for all systems, and even using few cores per node used can accelerate the performances for general CFD applications, that is, one MPI process is used per core on the node.

TABLE 3

TABLE 3. Overview of the software environment of the HPC systems.

One linear interprocessor communication model has been developed by Fischer et al. (2015),

$T_c\left(m\right)=\left(\alpha +\beta m\right)T_a,$

where $T_c$ is the communication time, α and β are two dimensionless parameters, $m$ is the message length, and $T_a$ is the inverse of the observed flop rate. We used the model to measure the latencies and bandwidths on these systems. The latencies and bandwidths for a word with 64-bit length for these systems using 512 MPI-rank are presented in Table 4.

TABLE 4

TABLE 4. Overview of latencies and bandwidths on the systems used.

The benchmark case consists of 763,904 elements with the 7^th polynomial order. The total number of grid points is around 391 million. We run the case with different MPI-ranks up to 1,000 steps. The speed-up for the strong scalability tests is measured following the same method used by Offermans et al. (2016). In addition, we only consider the execution times during the time-integration phase without I/O operations.

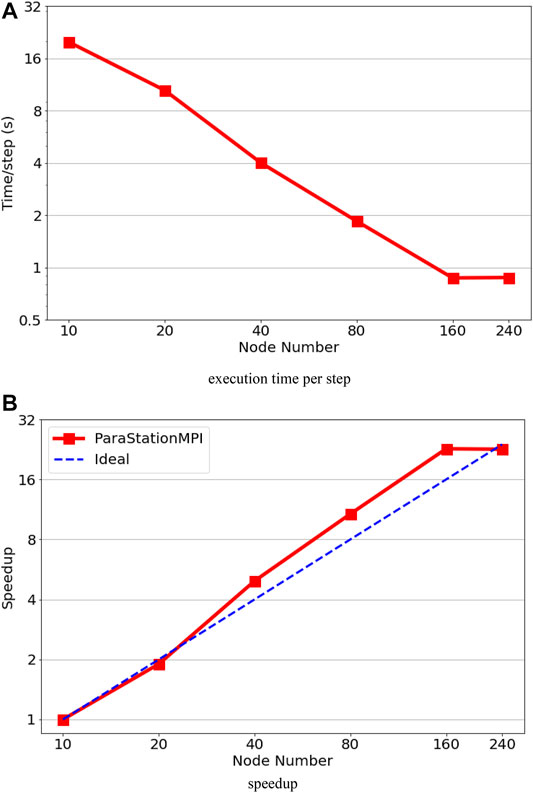
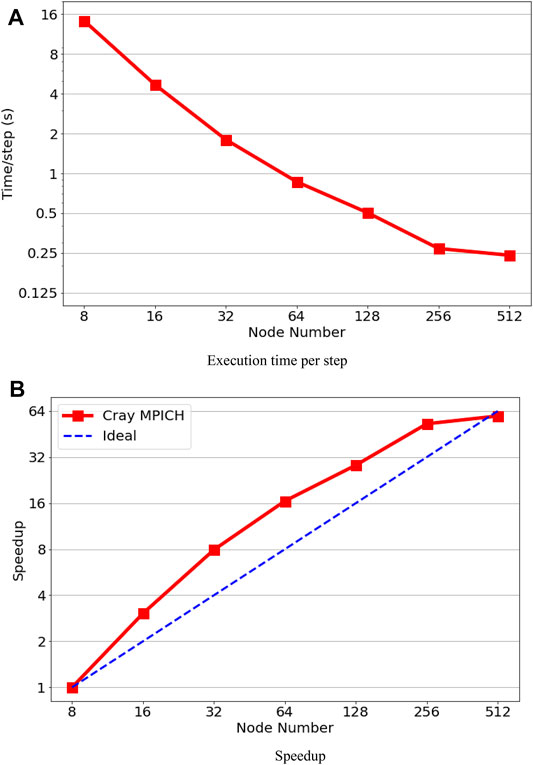
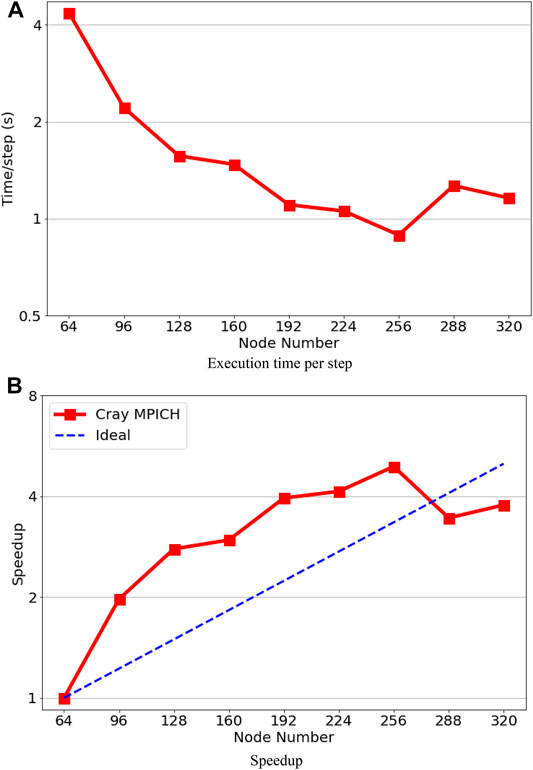
Figures 6A,B shows the execution time in second per step and speedup on the JUWELS cluster. The test was performed from 480 MPI-rank (i.e., fully occupied 10 nodes) to 11520 MPI-rank (i.e., fully occupied 240 nodes). The maximum speed-up of 20.5 can be achieved with 160 nodes (7680 MPI-rank), and then the performance becomes worse with increase in the number of node number. We observe super-linear speedup with increasing number of MPI-rank until 7680 MPI-rank. The super-linear speedup is not surprising for Nek5000’s strong scalability test due to cache memory usage and SIMD (simple instruction multiple data); for a more detailed analysis, see Offermans et al. (2016).

FIGURE 6

FIGURE 6. Performance results on the JUWELS system. (A) Execution time per step. (B) Speedup.

The performance results on ARCHER2 are presented in Figures 7A,B. We also observed a super-linear speedup on the AMD CPU based system. The execution time per step continually reduces from 8 nodes (1024 MPI-rank) to 256 nodes (32768 MPI-rank), and then the performance improves slightly with doubted MPI-rank to 65536. The performances are limited to around 8,000–16000 grid points. By comparing with MPI-rank on JUWELS, which is an Intel CPU–based system, the performance on the JUWELS system is better. However, we obtain better node-to-node performances and strong scaling on the ARCHER system.

FIGURE 7

FIGURE 7. Performance results on the ARCHER2 system. (A) Execution time per step. (B) Speedup.

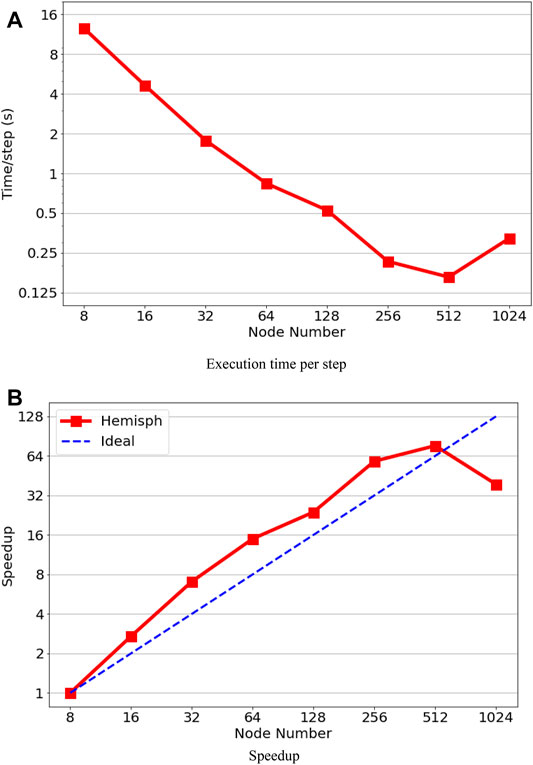
The performance results on Hawk are shown in Figures 8A,B. By comparing with ARCHER2, we observe that the execution times per step are very similar to those on ARCHER2 using 8 nodes (1024 MPI-rank) to 256 nodes (32768 MPI-rank), mostly due to the factor that both systems have the same AMD CPUs. On the other hand, the performance can be sped up from 32768 to 65536 MPI-rank on Hawk, that is, the execution time per step reduces from 0.22 to 0.16 s. From the log files, we found that the main difference between the two systems is the communication time. A 9-dimensional enhanced hypercube topology is used for the interconnecting on Hawk, which means that less bandwidth is available if the dimension of the hypercube is higher (Dick et al., 2020). With 16 computer nodes connected to a common switch as one hypercube node, the case of 65536 MPI-rank with 512 nodes corresponds to 2˄5 hypercube nodes (i.e., 5-dimensional binary cube topology). In addition, the gather–scatter operation in the Nek5000’s crystal router for MPI global communication supports to exchange messages of arbitrary length between any nodes within a hypercube network (Fox et al., 1988; Schliephake and Larue, 2015). As a result, the required communication time can be reduced, especially for irregular applications.

FIGURE 8

FIGURE 8. Performance results on the Hawk system. (A) Execution time per step. (B) Speedup.

The performance results on the Beskow cluster are shown in Figure 9. The test started from 64 nodes (2048 MPI-rank) due to the memory limitation (64GB RAM/node) on the compute nodes. Then the MPI-rank increases by 1024, and it is found that the execution time per time step achieves the minimum at 256 nodes (8192 MPI-rank), and the maximum speed-up here is 4.9. After 8192 MPI-rank, the performance becomes worse when the MPI-rank continually increases. Like in previous systems, a super-linear performance has been observed on the Beskow cluster before the maximum speedup point.

FIGURE 9

FIGURE 9. Performance results on the Beskow system. (A) Execution time per step. (B) Speedup.

In general, the benchmark case simulated using Nek5000 can achieve super-linear speed-up in all the tested HPC systems, although within certain MPI-rank ranges due to communication requirements (Offermans et al., 2016). The ARCHER2 and Hawk systems have the highest speed-up upper bound (65536 MPI rank), while Hawk has relatively smaller execution time per timestep than ARCHER2. The super-linear scalability means that one can save calculation time by increasing the MPI rank within the linear speed-up range. However, after the speedup limitation, the performance of the code would become worse and inefficient.

The case with Ra = 10¹¹ in reaching a quasi-steady state took about 2M core-hour computational resources. This includes ramping up the Ra from 10¹⁰ to the target 10¹¹. Since the Rayleigh number of the prototypic corium or the prototypic molten pool experiments is higher than the benchmark case in this study, we need to consider the available computational resources of DNS simulations of the molten pool with higher Rayleigh numbers in the future. From the numerical aspect, when the Rayleigh number increases 10 times to 10¹², the mesh size of the computational domain is supposed to be 10 times. In addition, the velocity magnitude of the flow is expected to be ${10}^{1/2}$ times larger. If the CFL condition number is kept the same, the time step is then reduced to about 3% of the case with Rayleigh number 10¹¹. From the computed aspect, the required minimum MPI ranks for a certain simulation are limited by the maximum element number capacity on each core. By taking the ARCHER2 system as an example, the minimum MPI rank of the simulation with Ra = 10¹¹ is 1024. When the Rayleigh number increases to 10¹², the minimum MPI rank should be 10240 because the total element number of the simulation becomes 10 times larger. Therefore, if the Rayleigh becomes 10¹², the whole simulation will require about 300 times core-hours than the original case, which is about 600M core-hours.

Practically, given the highest allocation that can be made available to any research group, which is in the order of 200M core-hours per year, the amount of time needed to reach a quasi-steady state at Ra = 10¹² is estimated to be about 3 years. If this is again projected for an order of magnitude higher Rayleigh number, 10¹³, with the required mesh, the amount of time needed is about 900 years. Hence, for the ultimate case of 10¹⁷, such DNS is rendered unfeasible given the current technology. In the meantime, before the needed development of both hardware and software technology happens, we need to rely on less accurate models such as LES or RANS. However, these models need to be modified and verified with the help of available reference DNS data with the highest Ra.

To aim for DNS for Ra = 10¹² to 10¹³, exascale supercomputer systems with a capacity of more than 1 exaflops (10¹⁸ flops) will be required. However, all exascale supercomputers will be heterogenous systems with emerging architecture⁵. In this case, the GPU-based Nek5000 code, namely, NekRS (Fischer et al., 2021) must be utilized.

Conclusion

We have presented the scalability of Nek5000 on four HPC systems toward the DNS of molten pool convection. As low latencies of MPI communication and memory bandwidth are essential for CFD applications, the linear communication models for the four systems have been addressed. The case can be scaled up to 65536 MPI-rank on the Hawk and ARCHER2 systems. But, the best performance can be achieved on the Hawk system in comparison with the others. This is attributed to its lower latency in global communication and the hypercube technique that was used for the interconnection, which both accelerates the embedded crystal algorithm in Nek5000 for global MPI communication. Furthermore, we also observed that super-linear speed-up can be achieved using fewer MPI-ranks on both Intel and AMD CPUs.

For the reference case Ra = 10¹¹, current CPU-based Petascale systems are sufficient for obtaining DNS data using Nek5000. Depending on the resources available, the choice of MPI-rank to obtain the data as efficiently as possible can be guided by the scalability of the specific system, as shown in this article. For an order of magnitude higher Ra, that is, 10¹², the required resources can readily increase two orders of magnitude. To obtain better efficiency, the relatively new GPU-based NekRS can also be used, but further development is needed, and sufficient GPU resources must be made available. For the prototypic Ra, about 10¹⁶ to 10¹⁷, current HPC technology is not up to task in obtaining DNS data. In this case, less accurate LES or RANS should be used. However, such models must be verified with the help of available reference DNS data with the highest Ra, and possible modifications might be necessary.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BB: methodology, calculation, data processing, writing and review; JG: methodology, calculation, data processing, writing and review; WV: supervision, methodology, writing and review, funding and computer resources acquisition.

Funding

The funding support is partially from EU-IVMR Project No. 662157, Boshen Bian’s PhD scholarship from China Scholarship Centre (CSC), the EuroCC project, which has received funding from the European Union’s Horizon 2020 research and innovation program under Grant 951732, and the Swedish e-Science Research Center (SeRC) through the SESSI program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the funding support from EU-IVMR. Boshen Bian appreciates the PhD scholarship from China Scholarship Centre (CSC). We also acknowledge DECI and PRACE projects for granting us access to the ARCHER2 system at EPCC, JUWELS system at JSC, and Hawk system at HLRS. Part of the computations was enabled on Beskow at PDC provided by the Swedish National Infrastructure for Computing (SNIC).

Footnotes

¹https://www.fz-juelich.de/ias/jsc/EN/Expertise/Supercomputers/JUWELS/JUWELS_news.html

²https://www.archer2.ac.uk/

³https://kb.hlrs.de/platforms/index.php/HPE_Hawk

⁴https://www.pdc.kth.se/hpc-services/computing-systems/beskow-1.737436

⁵https://eurohpc-ju.europa.eu

References

Asfia, F. J., and Dhir, V. K. (1996). An Experimental Study of Natural Convection in a Volumetrically Heated Spherical Pool Bounded on Top with a Rigid wall. Nucl. Eng. Des. 163 (3), 333–348. doi:10.1016/0029-5493(96)01215-0

CrossRef Full Text | Google Scholar

Bernaz, L., Bonnet, J. M., Spindler, B., and Villermaux, C. (1998). “Thermal Hydraulic Phenomena in Cerium Pools: Numerical Simulation with TOLBIAC and Experimental Validation with BALI,” in OECD/CSNI Workshop on In-vessel Core Debris Retention and Coolability, Garching, Germany, March 3-6.

Google Scholar

Bian, B., Villanueva, W., and Dovizio, D. (2022a). Direct Numerical Simulation of Molten Pool Convection in a 3D Semicircular Slice at Different Prandtl Numbers. Nucl. Eng. Des..

Google Scholar

Bian, B., Villanueva, W., and Dovizio, D. (2022b). Direct Numerical Simulation of Molten Pool Natural Convection in A Hemispherical Configuration. in Proceedings of the Ninth International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, NURETH-19, Brussels, Belgium, March 6-11, 2022

Google Scholar

Chakraborty, N. (2009). The Effects of Turbulence on Molten Pool Transport during Melting and Solidification Processes in Continuous Conduction Mode Laser Welding of Copper-Nickel Dissimilar Couple. Appl. Therm. Eng. 29, 3618–3631. doi:10.1016/j.applthermaleng.2009.06.018

CrossRef Full Text | Google Scholar

Deville, M. O., Fischer, P. F., and Mund, E. H. (2002). High-Order Methods for Incompressible Fluid Flow. Cambridge: Cambridge University Press.

Google Scholar

Dick, B., Bonisch, T., and Krischok, B. (2020). Hawk Interconnect Network. Available at: https://kb.hlrs.de/platforms/upload/Interconnect.pdf (Accessed January 20, 2022).

Google Scholar

Dinh, T. N., and Nourgaliev, R. R. (1997). Turbulence Modelling for Large Volumetrically Heated Liquid Pools. Nucl. Eng. Des. 169, 131–150. doi:10.1016/s0029-5493(96)01281-2

CrossRef Full Text | Google Scholar

Dovizio, D., Komen, E. M. J., Bian, B., and Villanueva, W. (2022). “RANS Validation of a Corium Pool in a Hemispherical,” in Proceedings of the Ninth International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, NURETH-19, Brussels, Belgium, March 6-11, 2022.

Google Scholar

Fichot, F., Carénini, L., Villanueva, W., and Bechta, S. (2018). “A Revised Methodology to Assess In-Vessel Retention Strategy for High-Power Reactors,” in Proceedings of the 26th International Conference on Nuclear Engineering (ICONE-26), London, UK, July 22-26. doi:10.1115/icone26-82248

CrossRef Full Text | Google Scholar

Fischer, P., Heisey, K., and Min, M. (2015). “Scaling Limits for PDE-Based Simulation,” in 22nd AIAA Computational Fluid Dynamics Conference, 22-26 June 2015, Dallas, TX (Du Page County: American Institute of Aeronautics and Astronautics).

Google Scholar

Fischer, P., Kerkemeier, S., Min, M., Lan, Y., Phillips, M. T., Rathnayake, E. M., et al. (2021). NekRS, a GPU-Accelerated Spectral Element Navier-Stokes Solver. CoRR abs/2104.05829.

Google Scholar

Fischer, P., Lottes, J., Kerkemeier, S., Marin, O., Heisey, K., Obabko, A., et al. (2016). Nek5000: User’s Manual. Argonne National Laboratory.

Google Scholar

Fluhrer, B., Alsmeyer, H., Cron, T., Messemer, G., Miassoedov, A., and Wenz, T. (2005). “The Experimental Programme LIVE to Investigate In-Vessel Core Melt Behaviour in the Late Phase,” in Proceedings of Jahrestagung Kerntechnik 2005, Nürnberg, German, May 10 (INFORUM GmbH).

Google Scholar

Fox, G. (1988). Solving Problems on Concurrent Processors: General Techniques and Regular Problems 1. Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Goluskin, D. (2016). Internally Heated Convection and Rayleigh-Bénard Convection. Cham: Springer Briefs in Thermal Engineering and Applied Science.

Google Scholar

Goluskin, D., Van der Poel, , and Erwin, P. (2016). Penetrative Internally Heated Convection in Two and Three Dimensions. J. Fluid Mech. 791, R6. doi:10.1017/jfm.2016.69

CrossRef Full Text | Google Scholar

Grötzbach, G., and Wörner, M. (1999). Direct Numerical and Large Eddy Simulations in Nuclear Applications. Int. J. Heat Fluid Flow 20 (3), 222–240. doi:10.1016/S0142-727X(99)00012-0

CrossRef Full Text | Google Scholar

Guermond, J. L., Minev, P., and Shen, J. (2006). An Overview of Projection Methods for Incompressible Flows. Comp. Methods Appl. Mech. Eng. 195, 6011–6045. doi:10.1016/j.cma.2005.10.010

CrossRef Full Text | Google Scholar

Helle, M., Kymäläinen, O., and Tuomisto, H. (1999). “Experimental COPO II Data on Natural Convection in Homogenous and Stratified Pools,” in Proceedings of the Ninth International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, NURETH-9, San Francisc, USA, October 3-8.

Google Scholar

Merzari, E., Fischer, P., Min, M., Kerkemeier, S., Obabko, A., Shaver, D., et al. (2020). Toward Exascale: Overview of Large Eddy Simulations and Direct Numerical Simulations of Nuclear Reactor Flows with the Spectral Element Method in Nek5000. Nucl. Tech. 206, 1308–1324. doi:10.1080/00295450.2020.1748557

CrossRef Full Text | Google Scholar

Merzari, E., Fischer, P., Yuan, H., Van Tichelen, K., Keijers, S., De Ridder, J., et al. (2016). Benchmark Exercise for Fluid Flow Simulations in a Liquid Metal Fast Reactor Fuel Assembly. Nucl. Eng. Des. 298, 218–228. doi:10.1016/j.nucengdes.2015.11.002

CrossRef Full Text | Google Scholar

Nourgaliev, R. R., Dinh, T. N., Sehgal, B. R., Nourgaliev, R. R., Dinh, T. N., and Sehgal, B. R. (1997). Effect of Fluid Prandtl Number on Heat Transfer Characteristics in Internally Heated Liquid Pools with Rayleigh Numbers up to 1012. Nucl. Eng. Des. 169 (1-3), 165–184. doi:10.1016/s0029-5493(96)01282-4

CrossRef Full Text | Google Scholar

Oberbeck, A. (1879). Ueber die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 243, 271–292. doi:10.1002/andp.18792430606

CrossRef Full Text | Google Scholar

Offermans, N., Marin, O., Schanen, M., Gong, J., Fischer, P., and Schlatter, P. (2016). “On the strong Scaling of the Spectral Elements Solver Nek5000 on Petascale Systems,” in Exascale Applications and Software Conference, EASC 2016, Stockholm, Sweden, April 25-29, 2016. article id a5.

Google Scholar

Rajagopal, K. R., Saccomandi, G., and Vergori, L. (2009). On the Oberbeck-Boussinesq Approximation for Fluids with Pressure Dependent Viscosities. Nonlinear Anal. Real World Appl. 10, 1139–1150. doi:10.1016/j.nonrwa.2007.12.003

CrossRef Full Text | Google Scholar

Schliephake, M., and Laure, E. (2015). “Performance Analysis of Irregular Collective Communication with the Crystal Router Algorithm,” in Proceedings of the 2014 Exascale Applications and Software Conference, Cham: (Springer), 130–140. doi:10.1007/978-3-319-15976-8_10

CrossRef Full Text | Google Scholar

Sehgal, B. R., Bui, V. A., Dinh, T. N., Green, J. A., and Kolb, G. (1998). “SIMECO Experiments on In-Vessel Melt Pool Formation and Heat Transfer with and without a Metallic Layer,” in Proceedings of the OECD/CSNI Workshop, Garching, Germany, March 3-6.

Google Scholar

Shams, A. (2018). Towards the Accurate Numerical Prediction of thermal Hydraulic Phenomena in Corium Pools. Annals Nucl. Energ. 117117, 234234–246246. doi:10.1016/j.anucene.2018.03.031

CrossRef Full Text | Google Scholar

Shishkina, O., Stevens, R. J. A. M., Grossmann, S., and Lohse, D. (2010). Boundary Layer Structure in Turbulent thermal Convection and its Consequences for the Required Numerical Resolution. New J. Phys. 12 (7), p.075022. doi:10.1088/1367-2630/12/7/075022

CrossRef Full Text | Google Scholar

Tomboulides, A. G., Lee, J. C. Y., and Orszag, S. A. (1997). Numerical Simulation of Low Mach Number Reactive Flows. J. Scientific Comput. 12, 139–167.

Google Scholar

Villanueva, W., Filippov, A., Jules, S., Lim, K., Jobst, M., Bouydo, A., et al. (2020). “Thermo-mechanical Modelling of Reactor Pressure Vessel during Core Melt In-Vessel Retention,” in Proceedings of the International Seminar on In-vessel retention: outcomes of the IVMR project, Juan-les-Pins, France, January 21-22.

Google Scholar

Wang, H., Villanueva, W., Chen, Y., Kulachenko, A., and Bechta, S. (2021). Thermo-mechanical Behavior of an Ablated Reactor Pressure Vessel wall in a Nordic BWR under In-Vessel Core Melt Retention. Nucl. Eng. Des. 351, 72–79. doi:10.1016/j.nucengdes.2021.111196

CrossRef Full Text | Google Scholar

Whang, S., Park, H. S., Lim, K., and Cho, Y. J. (2019). Prandtl Number Effect on thermal Behavior in Volumetrically Heated Pool in the High Rayleigh Number Region. Nucl. Eng. Des. 351, 72–79. doi:10.1016/j.nucengdes.2019.05.007

CrossRef Full Text | Google Scholar

Yildiz, M. A., Botha, G., Yuan, H., Merzari, E., Kurwitz, R. C., and Hassan, Y. A. (2020). Direct Numerical Simulation of the Flow through a Randomly Packed Pebble Bed. J. Fluids Eng. 142 (4), 041405. doi:10.1115/1.4045439

CrossRef Full Text | Google Scholar

Zhang, L., Luo, S., Zhang, Y., Tian, W., Su, G. H., and Qiu, S. (2018). Large Eddy Simulation on Turbulent Heat Transfer in Reactor Vessel Lower Head Corium Pools. Ann. Nucl. Energ. 111, 293–302. doi:10.1016/j.anucene.2017.08.055

CrossRef Full Text | Google Scholar