Improved Electrogeometric Model of UHV Transmission Line Based on Long Gap Discharge and Its Application

Based on long air gap discharge test data and lightning return stroke observation data, an improved electrogeometric model (EGM) considering terrain conditions is established and verified to analyze the lightning shielding performance of UHV transmission lines. The striking distance formula is modified as r_s = 0.13 (I² + 40I)^0.814. In this paper, the lightning shielding failure rate of three-phase conductors of EHV and UHV transmission lines calculated by the improved EGM model is consistent with the lightning observation data of actual transmission lines in Japan and the scaled lightning discharge simulation experimental results of UHV transmission lines in plains and mountainous areas of China, which verifies the applicability of the improved EGM model to evaluate the lightning shielding performance of large-scale UHV transmission lines. The improved EGM model is applied to evaluate the influence of tower type and slope steepness on the shielding failure tripping rate of UHV transmission lines. The shielding failure tripping rate of the SZ322 tower is higher than that of the SZT1 tower, and the shielding failure tripping rate of UHV transmission lines is greatly affected by slope gradient and increases with the increase of slope gradient.

1 Introduction

In the context of achieving the goal of carbon peaking and carbon neutralization, China is accelerating the construction of UHV to meet the needs of large-scale development and consumption of clean energy such as wind and solar energy. Large-scale transmission lines are exposed to the natural environment and are vulnerable to lightning strike during thunderstorm season (Hengxin et al., 2016). The lightning shielding failure of Durong line of the 1,000 kV transmission line in China occurred in 2015 and 2017. In addition, the lightning shielding failure of Binjin line, Fufeng line, and Jinsu line of the ±800 kV transmission line in China has occurred more than 10 times since 2010 (Chongyu et al., 2015). The UHV transmission line has large transmission capacity and low loss, but it is more prone to lightning shielding failure than 220 kV and below transmission lines, and the harm and loss caused by the accident are even greater. The operation experience of relevant industries has also shown that the current lightning tripping fault of UHV transmission lines is mainly caused by lightning shielding failure (Shen et al., 2021; Shen and Raksincharoensak, 2021). One of the reasons is that the current design of the lightning shielding system of UHV transmission lines draws on the calculation model of low-voltage transmission lines, resulting in large calculation errors. Therefore, it is necessary to study the lightning shielding performance evaluation model for large-scale UHV transmission lines.

The electrogeometric model (EGM) method is mainly used to study the shielding failure performance of transmission lines, which is widely used by power enterprises IEC and IEEE. Since Wagner proposed the concept of lightning return stroke model in 1961 (Wagner and Hileman, 1961), many scholars have tried to improve the striking distance formula in various ways. In 1968, Whitehead and Armstrong firstly proposed the typical EGM model by using the 1–3 m gap discharge test (Armstrong and Whitehead, 1968). Since then, many scholars have further improved the typical EGM model on this basis to make the evaluation of lightning shielding performance of transmission lines more applicable. In 1985, the IEEE working group proposed the general striking distance formula and the striking distance coefficient based on various factors (Grant et al., 1985). These improved striking distance formulas based on the discharge test data of 1–4 m gap distance played an important guiding role in the lightning shielding performance of low-voltage transmission lines. With the improvement of the voltage level of transmission lines, especially the rapid development of UHV AC and DC transmission technology, the air gap is further lengthened, and the shielding failure of UHV transmission lines is too high and some fully shielded lines in the theoretical model cannot be well explained by the typical EGM model method.

In recent years, scholars have begun to try to combine the practical operation experience of transmission lines with the experimental data of longer gap discharge to improve the striking distance formula and striking distance coefficient in the EGM model (Wang et al., 2014; Yu et al., 2017). The striking distance formula of the EGM model is derived from the gap discharge test results and lightning observation empirical formula. Thus, the accuracy of the lightning empirical formula also affects the accuracy of the model. Taniguchi et al. conducted the gap discharge test with the maximum gap distance of 6 m in 2008, and improved the EGM model combined with the probability formula of return stroke velocity (Taniguchi et al., 2010). In 2014, Wang et al. carried out negative impulse discharge tests on 1–10 m long air gaps with two kinds of voltage waveforms of −20/2,500 μs and −80/2,500 μs (Wang et al., 2014; Yu et al., 2014). Then, they conducted lightning shielding simulation tests of UHV AC transmission lines with a scale of 1:12.5, and obtained the lightning shielding performance of scaled UHV transmission lines (Yunzhu, 2015). The above large-scale discharge test provides basic data for the correction of the striking distance formula and the striking distance coefficient in the EGM model suitable for UHV transmission lines. In addition, the relationship between the primary lightning stroke current I and the primary lightning discharge speed v₁ is the empirical formula I = 2,400v₁³ estimated by a large number of theoretical analysis (Shen et al., 2021). In 1984, Idone et al. found that the speed of subsequent return strokes had a good nonlinear correlation with the peak lightning current through an artificial lightning experiment (Idone et al., 1984). Yu et al. (2017) combined the large-scale long air gap discharge data with the probability distribution of the return stroke velocity of the artificial lightning pilot channel of Idone, and proposed an improved stroke distance formula related to the lightning return stroke velocity. Since the striking distance formula is related to the dispersion probability of the return stroke velocity, the striking distance formula is a dispersion form related to the return stroke velocity. However, the actual lightning process is random, and the lightning return stroke speed does not only consist the limited lightning return stroke speed considered in its dispersion form. The relevant research by Idone et al. (1984) shows that the probability distribution law of Idone’s return stroke velocity in the pilot channel of an artificially induced mine conforms to the relationship between return stroke velocity and current peak recommended by Lundholm (1957). Since the relationship between return stroke velocity and lightning current peak value proposed by Lundholm can be verified with the experimental data of artificial lightning induction in laboratory, the formula of striking distance in the EGM model can be modified to a formula only related to the amplitude of return stroke current (Yang et al., 2021a; Yang et al., 2021b).

In this paper, the data of large-scale long air gap negative discharge characteristics with the relationship between return stroke velocity and lightning current peak proposed by Lundholm (1957) modify the striking distance formula and the striking distance coefficient in the EGM model and use a calculation method to consider the incidence angle of lightning leader. The lightning shielding failure rate of ultra-high-voltage transmission lines in Japan is calculated by the improved EGM model in this paper, and the results are compared with the lightning observation data to verify the adaptability of the improved EGM model to the evaluation of lightning shielding failure rate of large-scale transmission lines. Combined with the simulation test of lightning shielding performance of UHV transmission lines, the influence of terrain conditions on the lightning shielding performance of UHV transmission lines is analyzed and compared with the calculation results of the improved EGM model in this paper. Finally, considering that the tower structure of 1,000 kV transmission lines in China is diverse, and the lightning shielding performance of transmission lines is greatly affected by terrain conditions, the improved EGM model is used to calculate and analyze the influence of tower structure and slope gradient on the lightning shielding performance of UHV transmission lines.

2 Improved Electrogeometric Model Based on Long Gap Discharge Results and Natural Lightning Data

2.1 Relationship Between Natural Lightning Return Stroke Current and Return Stroke Velocity

At the beginning of the 1950s, some researchers found that the lightning return stroke speed was not stable (Lundholm, 1957). When the lightning leader falls, the leader head potential V_s is proportional to the primary lightning current I, and inversely proportional to the primary lightning speed v₁. In 1963, Wagner established the relationship between lightning current amplitude I and lightning leader head potential V_s as shown in Eq. 1 (Wagner, 1963):

$V_s=60\left(I/v_1\right)\times \ln \left(2r\prime /d\prime \right)(1)$

where I is the primary lightning current, kA; v₁ is the lightning discharge speed with the speed of light as the unit value, p.u.; r′ is the distance between the lightning leader head and the ground at the last jump, m; d′ is the corona radius of the leader head, m. The long-term observation results show that r′ and d′ increase with lightning current I, while the variation of logarithm ln(2r′/d′) is small. Taking ln(2r′/d′) as 4.6, Eq. 2 can be obtained.

$V_s=276\left(I/v_1\right)(2)$

Idone et al. (1984) found that there is a good nonlinear correlation between the speed of the subsequent return stroke and the peak lightning current through the artificial lightning experiment. Their research results basically verify the relationship between the return stroke speed recommended by Lundholm and the peak current as shown in Eq. 3 (Lundholm, 1957):

$v_{rs}=c{\left(1+W/I_p\right)}^{-0.5}(3)$

where v_rs is the pilot return stroke speed, km/s. c is the speed of light, km/s. I_p is the peak return stroke current, kA. W is a constant. Idone et al. used the least square method to fit the experimental data and got W = 40.

2.2 Striking Distance Formula Based on Long Gap Discharge Results

The relationship between 50% negative switching impulse breakdown voltage (U50%) of the 1–10 m rod–rod gap and gap distance d is shown in Eq. 4.

$U_{50\%}=0.9667d^{0.614}(4)$

where U_50% is 50% negative switching impulse breakdown voltage, kV; d is gap distance, m.

By substituting Eq. 3 into Eq. 2, the relationship between lightning current I and lightning leader tip potential V_s can be obtained as Eq. 5.

$V_s=276I{\left(1+40/I\right)}^{0.5}(5)$

Assuming that the U_50% of the rod–rod gap is equal to the tip potential of the lightning leader, the striking distance formula can be derived as Eq. 6.

$r_s=0.13{\left(I^2+40I\right)}^{0.814}(6)$

Comparison of different striking distance is shown in Figure 1. As the peak lightning current is less than 40 kA, the present striking distance in this paper is less than that of most scholars. When the peak lightning current exceeds 80 kA, the present striking distance is larger.

FIGURE 1

FIGURE 1. Comparison of different striking distance formulas.

2.3 Striking Distance Coefficient

In the typical EGM model, the striking distances between lightning leader tip and the lightning conductor, each phase conductor, and the earth are the same (Anderson et al., 1993). However, factors such as terrain condition, operation voltage, and the upward leader process of the earth surface object will affect the striking distance. Subsequent scholars introduced the concept of striking distance coefficient to distinguish the striking distance difference between lightning leader tip and phase conductors, lightning conductor, and earth (Golde, 1977), as shown in Eqs 7, 8.

$r_g=K_g{r}_c(7)$

$r_{gw}=K_{gw}{r}_c(8)$

where r_c, r_gw, and r_g are the striking distances of lead to conductor, ground line, and earth, respectively. K_g and K_gw are respectively the striking distance coefficient against ground and the striking distance coefficient against ground line.

Since the U_50% of the 1–4 m rod–plane gap is slightly higher than that of the rod–rod gap, previous scholars believe that the ground striking distance coefficient K_g should be less than 1 (Qian et al., 2010; Wenxia et al., 2015). Experimental results of longer air gap negative switching impulse discharge show that the U_50% of the rod‐plane gap is lower than that of the rod–rod gap as gap distance exceeds 4 m (Grant et al., 1985). Thus, the coefficient K_gw was revised to 1.1. However, optical observation results of the physical discharge process (Wang et al., 2014) show that the downward streamer-leader discharge process of rod‐plane gap is more obvious than that of rod–rod gaps under the negative switching impulse as the gap distance exceeds 4 m. It indicates that the final discharge length of rod–plane gaps is smaller than that of rod–rod gaps. Hence, taking the coefficient K_gw as 1.1 may overestimate the lightning attractive ability of the earth. In the present study, the striking distance coefficient K_g = 1.05 and K_gw = 1.

2.4 Calculation Method of the Improved Electrogeometric Model

In the EGM model, it is considered that the development of the lightning downward leader is stochastic before reaching the critical striking distance of the stroke object. Hence, the probability distribution of lightning leader incidence in the range of −π/2 to π/2 angle has been considered as Eq. 9.

$p\left(\psi \right)=0.75{\cos }^3\psi (9)$

A schematic diagram of the EGM model under plains and mountainous terrain conditions is shown in Figure 2.

FIGURE 2

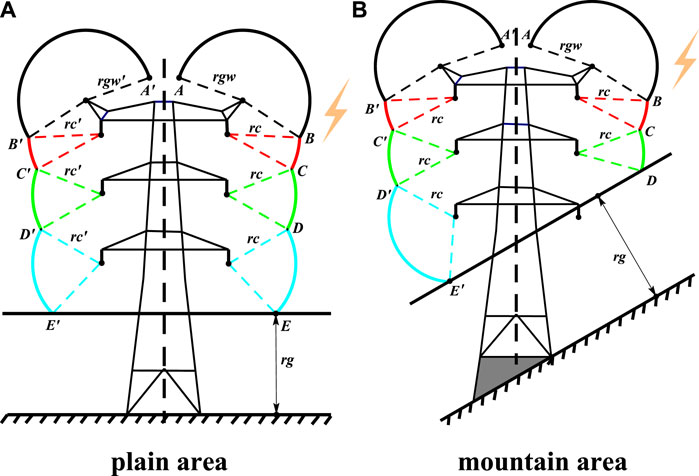
FIGURE 2. Diagram of the EGM model for transmission lines in plains and mountainous areas. (A) Plains area. (B) Mountain area.

As shown in Figure 2A, arcs are made with the center of the lightning conductor and the three-phase conductor, respectively, and the radius of their respective striking distances. At this point, a curved surface is formed by arc AB, arc BC, arc CD, arc DE, and line EE′ along the direction of the transmission line. Only when the lightning downward leader falls into the positioning surface of the corresponding object is it believed that the lightning will strike the object. Thus, the arc BC, arc CD, and arc DE are also called the shielding arc. As the lightning return stroke current varies, the grounding conductors, phase conductors, and earth will be changed. For transmission lines in mountainous areas, as shown in Figure 2B, the shielding arc of the lines on both sides of the tower is not symmetrical due to the angle of the hillside. This is due to the inclination of the striking distances of earth line DE, which makes the shielding arc of the line facing the slope side decrease, while the other side increases. Besides, only when the lightning return stroke leader current exceeds the lightning current withstand level of transmission line I_min can insulation flashover occur on the transmission line.

The detailed calculation method of the EGM model used in this paper is shown in Figure 3. At a certain angle θ and ψ, the unit area of the shielding arc per unit length of the line perpendicular to the leading incident direction dA is

$dA=r_{s}d\theta \cos {\theta }_3=r_{s}d\theta \sin \left(\theta +\psi \right)(10)$

FIGURE 3

FIGURE 3. Diagram of the EGM model calculation method.

The corresponding exposure area of a lightning leader with a certain amplitude and incident angle perpendicular to the incident direction of the leader is

$X={\displaystyle {\int }_{-{\theta }_2}^{{\theta }_1}{\displaystyle {\int }_{-{\psi }_2}^{{\psi }_1}{r}_s\sin \left(\theta +\psi \right)}}g\left(\psi \right)d\psi d\theta (11)$

where g(ψ) is the probability density function of the incident direction of the lightning leader, −π/2< $\psi$ <π/2.

The number of unit length line shielding strike fault is

$n=N{\displaystyle {\int }_{r_{\min }}^{r_{\max }}Xp\left(r_s\right)}d{r}_s=N{\displaystyle {\int }_{I_{\min }}^{I_{\max }}Xp\left(I\right)}dI(12)$

where N is the number of falling thunders per year per unit area, strokes/km²/a; p(r_s) and p(I) are the probability distribution density function of r_s and I, respectively; r_max is the maximum striking distance that can cause shielding failure; r_min is the minimum striking distance that can cause shielding failure tripping, m; I_max is the maximum shielding current; I_min is the minimum shielding trip lightning current, namely, line lightning withstand level, kA. The calculation process of the present EGM model is shown in Figure 4. It is mainly used to calculate the maximum and minimum shielding trip lightning current of the line, and then according to Eqs 11, 12, concurrency points in turn, the angle of lightning incident and lightning incident position and amplitude of lightning current are circulated. Finally, the total projection width is calculated and the shielding tripping rate is obtained.

FIGURE 4

FIGURE 4. Improved EGM model calculation flow chart.

3 Verification and Analysis of the Improved EGM Model With Observation and Experimental Results

3.1 Comparison With Observation Data of 500 kV and UHV Transmission Lines in Japan

In order to verify the applicability of the present EGM model, the present EGM model in this paper is applied to calculate the lightning stroke rate to power lines of 500 kV and UHV transmission lines in Japan. The specific parameters of 500 kV and UHV double-circuit transmission lines on the same tower in Japan are shown in Table 1.

TABLE 1

TABLE 1. Size parameters of double-circuit AC transmission lines on the same tower in Japan.

For the lightning density N_g, the typical EGM model is 3.0 strokes/km²/a, the 500 kV line area in Japan is 4.9 strokes/km²/a, and the UHV line area is 5.2 strokes/km²/a (Taniguchi et al., 2010).

The probability density of lightning current amplitude is

$P\left(i\right)=0.0475e^{-\frac{i}{20}}+0.001e^{-\frac{i}{50}}(13)$

In this paper, the improved EGM model results are compared with the typical EGM model results, Taniguchi et al. (2010) and Yu et al. (2017) improved EGM model results, and long-term lightning observation results in Japan (Taniguchi et al., 2009) are shown in Figure 5.

FIGURE 5

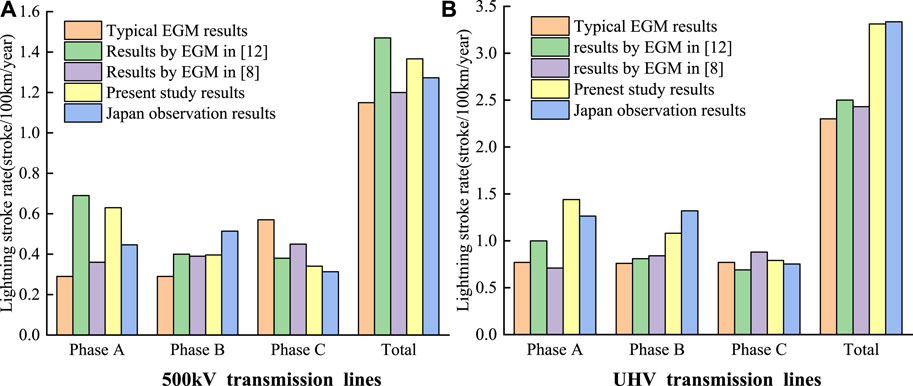
FIGURE 5. Comparison of different lightning stroke rate calculation methods with actual observation data. (A) 500 kV transmission lines. (B) UHV transmission lines.

In order to facilitate accurate comparison, the lightning stroke rate of each phase p_A, p_B, p_C in each model is divided by their total P to obtain the proportion of each phase P_A, P_B, P_C in each model as shown in Eq. 14.

$P_A=\frac{p_A}{P},P_B=\frac{p_B}{P},P_C=\frac{p_C}{P},(14)$

As shown in Figure 5A, for 500 kV transmission lines, the total lightning stroke rate of the improved EGM model in this paper and the improved EGM model in Taniguchi et al. (2010) is slightly different from the actual observation data, which is 7% larger and 6% smaller, respectively, and the lightning stroke rate of each phase calculated by the two models is 45%:30%:25% and 30%:32%:38%, respectively. Compared with the typical EGM model and the improved EGM model in Yu et al. (2017), the two models are closer to the 36%:40%:24% of the actual operation observation results in Japan (Taniguchi et al., 2009).

As shown in Figure 5B, for UHV transmission lines, the lightning stroke rate calculated by the present EGM model is closer to the observation results in Japan with a deviation of −0.73%. The calculated shielding failure ratio of each phase is 43:33:24, which is closest to the 38:39:23 observed in Japan (Taniguchi et al., 2009) compared to the other three models. This also reflects that the improved EGM model in this paper is more suitable for the calculation of lightning shielding performance of large-scale UHV transmission lines.

3.2 Comparison With Lightning Discharge Simulation Test Results With Scaled UHV Transmission Line

In the past few years, a series of lightning discharge tests of scaled UHV transmission line have been carried out under different terrain conditions in China (Yu, 2012; Wang et al., 2014; Yu et al., 2014; Yunzhu et al., 2014; Yunzhu, 2015; Zongxi et al., 2016; Yu et al., 2017). In these tests, a 10-m-long steel rod with a spherical tip was applied to simulate the downward leader. The scaled ratio of UHV transmission line was 1:12.5. In Yunzhu (2015), Yu et al. (2017), Yunzhu et al. (2014), and Zongxi et al. (2016), the gap distance between the high voltage rod tip and the scaled line was 5 m. According to the ratio of 1:12.5, the striking distance of the actual line can be calculated to be 62.5 m. According to the improved striking distance formula as Eq. 6, the lightning return stoke current can be deduced as 28.7 kA.

To compare calculation results of the present EGM model with lightning discharge simulation test results, the ratio of each phase line effective shielding arcs la, lb, lc to total effective shielding arc L under a lightning current of 28.7 kA is calculated by the present EGM model as shown in Eq. 15.

$P_a=\frac{l_a}{L},P_b=\frac{l_b}{L},P_c=\frac{l_c}{L}(15)$

In the calculation, the tower type is SZ322, which is the same as that in simulation tests in Yunzhu (2015), Yu et al. (2017), Yunzhu et al. (2014), and Zongxi et al. (2016). The protection angle of UHV transmission line is 1.5°. The slope angle of mountain ground is 30°. The ratio of each phase line shielding failure calculated by the improved EGM model is compared with the lightning discharge test results of UHV transmission lines (Yunzhu, 2015), as shown in Figure 6.

FIGURE 6

FIGURE 6. Comparison chart of shielding failure proportion of each phase line.

As shown in Figure 6, in a plains area, the ratio of the ABC three-phase line shielding failure rate calculated by the improved EGM model in this paper is 63%:37%:0, and the probability of the ABC three-phase conductor being attacked in the test is 52%:35%:12%. Both show that the shielding failure probability of phase A is the highest, followed by phase B and phase C. Considering the dispersion of the discharge direction in the lightning discharge simulation experiment, there is a certain deviation between the improved EGM model and the test data. In mountainous areas, the ratio of the ABC three-phase line shielding failure calculated by the improved EGM model is 28%:38%:34%, which is in good agreement with those results in lightning discharge tests of the scaled UHV transmission line of 25%:44%:31%.

According to the comparison results in Section 2.1 and Section 2.2, the calculation results of shielding failure ratio of three-phase lines of large-scale transmission lines by the present improved EGM model in this paper are consistent with observation results of lightning shielding failure of EHV and UHV transmission lines in Japan and the lightning discharge tests of scaled UHV transmission lines in plains and mountainous areas in China. The above results indicate that the present EGM model proposed in this paper is more appropriate for lightning shielding performance evaluation of large-scale transmission lines.

4 The Effect of Terrain and Tower Structure on Lightning Shielding Performance of UHV Transmission Lines

To study the effect of terrain and tower structure on lightning shielding performance of UHV transmission lines, two tower structures, SZT1 and SZ322, are applied to calculate the lightning shielding failure tripping out rate of UHV transmission lines in plains and mountainous areas. The terrain slope angle is set between 0° and 70° to simulate different terrains. The two tower structures, SZT1 and SZ322, are shown in Figure 7. The detailed transmission line parameters are shown in Table 2.

FIGURE 7

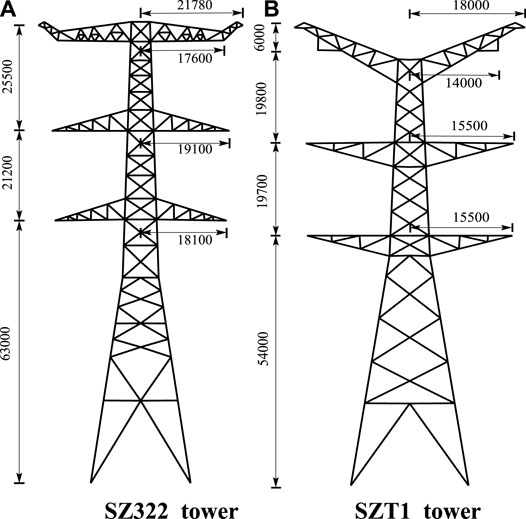
FIGURE 7. Structure diagram of SZT1 and SZ322 double-circuit tower on the same tower. (A) SZ322 tower, (B) SZT1 tower.

TABLE 2

TABLE 2. Practical size parameters of SZT1 and SZ322 tower lines.

The calculation lightning shielding failure tripping out rate by the present EGM model is shown in Figure 8. The lightning shielding failure tripping out rate of UHV transmission lines increases with the terrain slope angle. Because the terrain slope angle is 0°, the shielding failure tripping out rate of the line is close to 0. Because the terrain slope angle is 30°, the shielding failure tripping out rates of the SZT1-type tower line and the SZ322-type tower line are 0.12 strokes/(100 km·a) and 0.13 strokes/(100 km·a), respectively. When the terrain slope reaches 70°, the shielding failure trip rates of the two tower lines reach 0.38 strokes/(100 km·a) and 0.41 strokes/(100 km·a), respectively. Besides, under the same terrain condition, the shielding failure tripping out rate of the SZ322 tower line is higher than that of the SZT1 tower line. It is due to the fact that the height of the SZ322 tower line is significantly higher than that of the SZT1 tower line. The grounding line of the SZ322 tower line is much higher than that of the SZT1 tower line, but the height of the C phase conductor is not much different. The lightning protection effect of grounding line in the SZ322 tower line on the conductor is weaker than that of the SZT1 tower line. Therefore, the probability of lightning shielding failure tripping out rate of the SZ322 tower line is higher than that of SZT1 in a mountainous area.

FIGURE 8

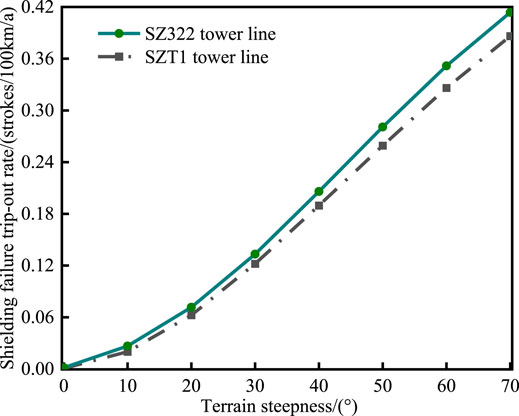
FIGURE 8. Influence of slope steepness under different tower models on shielding failure tripping out rate of 1,000 kV lines in China.

5 Conclusion

In order to analyze the lightning shielding performance of UHV transmission line more accurately, based on the long gap discharge test data and the lightning current return stroke current formula verified by researchers, this paper modifies the existing striking distance formula and uses the improved EGM model and the lightning simulation test of UHV transmission lines to analyze the influence of topography on the lightning tripping out rate of large-scale transmission lines.

(1) Based on the long air gap discharge test data of rod–rod gaps and lightning current return stroke velocity formula, the proposed striking distance formula is r_c = 0.13 (I² + 40I)^0.814, the earth striking distance coefficient is 1.05, and the ground wire striking distance correction coefficient is 1.0.

(2) The calculation results of lightning shielding failure rate of UHV transmission lines by the present EGM model consist of the lightning observation data of the UHV transmission line in Japan and the lightning discharge simulation test results of scaled UHV transmission lines in plains and mountainous areas in China. which verifies the applicability of the improved EGM model in large-scale transmission lines.

(3) The tower configuration and terrain steepness have a significant impact on the shielding failure tripping out rate of 1,000 kV lines in China. The shielding failure tripping rate of the SZ322 tower UHV line is higher than that of the SZT1 tower line. With the increase of terrain steepness, line shielding failure trip rate is also increasing rapidly.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YH: Conceptualization and writing—original draft preparation; MY: software and analysis; LQ: project administration; YA: software; JW: funding acquisition and validation; YC: Drawing; XS: supervision; QW: revision; CM: figures; BA: supervision; DC: figures.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 51807113 and in part by the Natural Science Foundation of Shandong Province under Grant ZR202103040796.

Conflict of Interest

Authors CM, BA, and DC are employed by Jining Huayuan Thermal Power Plant.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, J. G., Clayton, R., and Elahi, H. (1993). Estimating Lightning Performance of Transmission Lines. II. Updates to Analytical Models[J]. IEEE Trans. Power Deliv. 8 (3), 1254–1267. doi:10.1109/61.252647

CrossRef Full Text | Google Scholar

Armstrong, H., and Whitehead, E. (1968). Field and Analytical Studies of Transmission Line Shielding. IEEE Trans. Power Apparatus Syst. PAS-87 (1), 270–281. doi:10.1109/tpas.1968.291999

CrossRef Full Text | Google Scholar

Chongyu, X., Haiyue, W., and Feifei, D. (2015). Typical Cases Analysis of ±800kV UHV DC Transmission Line. Hunan Electr. Power 36 (1), 55–59. doi:10.3969/j.issn.1008-0198.2016.01.016

CrossRef Full Text | Google Scholar

Golde, R. H. (1977). Lightning, (Vol. 1). London: Academic Press.

Google Scholar

Grant, I. S., Anderson, J. G., and Hileman, A. R. (1985). A Simplified Method for Estimating Lightning Performance of Transmission Lines[J]. IEEE Trans. Power Apparatus Syst. PAS-104 (4), 918–932. doi:10.1109/TPAS.1985.319093

CrossRef Full Text | Google Scholar

Hengxin, H., Weijiang, C., and Yu, Y. N. (2016). Lightning Shielding Failure protection of the Strained Angled tower of Double Circuit UHV AC Transmission Lines[J]. High Voltage Eng. 42 (11), 3448–3455. doi:10.13336/j.1003-6520.hve.20161031011

CrossRef Full Text | Google Scholar

Idone, V. P., Orville, R. E., Hubert, P., Barret, L., and Eybert-Berard, A. (1984). Correlated Observations of Three Triggered Lightning Flashes. J. Geophys. Res. 89 (D1), 1385–1394. doi:10.1029/jd089id01p01385

CrossRef Full Text | Google Scholar

Lundholm, R. (1957). Calculation of Transmission Line Lightning Voltages by Field Concepts. Trans. Am. Inst. Electr. Eng. Part III Power App. Syst. 76 (3), 1271–1281. doi:10.1109/AIEEPAS.1957.4499772

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2021). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty, Electric Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Qian, P., Jun, L., and Peng, B. (2010). Application of Improved Electrical Geometry Model Method in Calculation of Lightning Tripping Rate of 1000kv Transmission Line[J]. Power Syst. Technology 34 (9), 155–159. doi:10.1109/CCECE.2010.5575154

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Li, Y., Khajorntraidet, C., Li, S., and Zhuang, J. (2021). Mixture Density Networks-Based Knock Simulator. IEEE/ASME Trans. Mechatronics 27, 159–168. Early Access. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transportation Syst. Early Access. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Taniguchi, S., Tsuboi, T., Okabe, S., Nagaraki, Y., Takami, J., and Ota, H. (2010). Improved Method of Calculating Lightning Stroke Rate to Large-Sized Transmission Lines Based on Electric Geometry Model. IEEE Trans. Dielect. Electr. Insul. 17 (1), 53–62. doi:10.1109/tdei.2010.5412002

CrossRef Full Text | Google Scholar

Taniguchi, S., Tsuboi, T., and Okabe, S. (2009). Observation Results of Lightning Shielding for Large-Scale Transmission Lines. IEEE Trans. Dielect. Electr. Insul. 16 (2), 552–559. doi:10.1109/tdei.2009.4815191

CrossRef Full Text | Google Scholar

Wagner, C. F., and Hileman, A. R. (1961). The Lightning Stroke-II. Trans. Aiee, Part. Power Appar. Syst. 80 (3), 622–636. doi:10.1109/aieepas.1961.4501104

CrossRef Full Text | Google Scholar

Wagner, C. (1963). The Relation between Stroke Current and the Velocity or the Return Stroke. IEEE Trans. Power Apparatus Syst. 82 (68), 609–617. doi:10.1109/tpas.1963.291375

CrossRef Full Text | Google Scholar

Wang, Y., Zhijun, L., and Min, D. (2014). Research on Typical Long Air Gaps with Negative Switching impulses(I)—Experiments[J]. Proc. CSEE 34 (21), 3534–3540. doi:10.13334/j.0258-8013.pcsee.2014.36.020

CrossRef Full Text | Google Scholar

Wenxia, S., Qing, Y., Yongfu, L., and Fan, S. (2015). Analysis and prospect of Lightning Shielding Failure Evaluation Methods of Transmission Lines[J]. High Voltage Eng. 41 (8), 2500–2513. doi:10.13336/j.1003-6520.hve.2015.08.004

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., et al. (2021). Deep Learning-Based SCUC Decision-Making: An Intelligent Data-Driven Approach with Self-Learning Capabilities. IET Gener. Transm. Distrib 16, 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yu, W. (2012). Experimental Study of Breakdown Characteristics of Long Air Gaps and Their Applications in Lightning Protection[D]. Wuhan Univ.

Google Scholar

Yu, W., Xishan, W., and Lei, L. (2014). Breakdown Characteristics of Long Air gap with Negative Polarity Switching Impulse[J]. IEEE Trans. Dielectrics Electr. Insul. 21 (2), 603–611. doi:10.1109/TDEI.2013.003627

CrossRef Full Text | Google Scholar

Yu, W., Yeqiang, D., Xishan, W., and Ma, Y. (2017). An Improved Electric Geometry Model Based on Breakdown Test of Long Air Gaps and Suited for Large-Sized Transmission Lines[J]. Proc. Csee 37 (12), 3654–3661. doi:10.13334/j.0258-8013.pcsee.161081

CrossRef Full Text | Google Scholar

Yunzhu, A., Lei, L., and Xishan, W. (2014). Impacting Factors of Large-Sized Model Test for Lightning Shielding Performance of UHV Transmission Lines [J]. Power Syst. Technology 38 (05), 1385–1389. doi:10.13335/j.1000-3673.pst.2014.05.040

CrossRef Full Text | Google Scholar

Yunzhu, A. (2015). Study on Lightning Stroke Characteristics Based on Negative Impulse Discharge Characteristics of Long Air Gap[D]. Wuhan Univ.

Google Scholar

Zongxi, L., Lei, L., Yu, W., et al. (2016). Effect of Terrains on Lightning Shielding Performance of UHV Common-tower Double-Transmission Lines [J]. High Voltage Eng. 42 (9), 2950–2955. doi:10.13336/j.1003-6520.hve.20160907034

CrossRef Full Text | Google Scholar