
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 11 April 2022
Sec. Nuclear Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.860480
This article is part of the Research Topic Radiation Protection and Measurement in Nuclear Reactors View all 9 articles
The production and release of fission products in fuel rods and the primary coolant have been simulated by the kinetic model during the normal operation of a pressurized water reactor. The typical ratio of I-131/I-133 in the primary coolant has been theoretically estimated at the equilibrium conditions for intact fuels and fuel failure with small or large defects, respectively. The radiochemical data in the primary loops have been gathered and compiled from thirty-six cycles in the operating CPR1000 PWR units. The statistical results show that the predictions made by the model and the statistical results in the operating CPR1000 PWR units are qualitatively in agreement for both intact fuel and fuel failure. It also indicates that the conventional threshold I-131/I-133 ≥ 0.1 for fuel failure may cause misjudgment due to the overlap of distributions, and I-131/I-133 ≥ 0.15 can distinguish 98% operation date for intact fuel rods and 94% operation data for fuel failure.
Very stringent requirements are set on the nuclear fuel design to ensure the fuel rods’ mechanical integrity during normal operation of a nuclear power plant. However, it is not possible to avoid the failure of a small number of fuel rods loaded in the core during the entire lifetime of a nuclear power plant. Once fuel rods fail, the noble gases and the volatile fission products accumulated in the fuel gap between pellets and cladding can be released to the primary coolant, resulting in an increase of the radiation dose and radioactive waste. The actinides disseminated in the fuel rods can also be released to the primary loops when secondary hydriding occurs. When the fission products’ activity level in the coolant reaches a given value, the plant should be placed into a safe shutdown within a few hours to notably prevent further deterioration of the fuel rods, which could notably lead to radiological protection and radioactive waste-related difficulties/issues.
During the operation of the nuclear power plant, the primary coolant is regularly sampled from the primary circuit to conduct radiochemical analysis and assess the activity concentration of radionuclides such as noble gases and radioiodines. This information is notably used to assess the integrity of the fuel loaded in the core. The half-life of I-131 and I-133 is 8.02 days and 20.8 h, respectively. The ratio of the activity concentration of these two radioiodines, 131/I-133, is one of the most commonly used indicators to preliminarily determine the status of fuel rods in NPPs (Alvarez et al., 2010). According to the experience in European and American PWRs, the typical values of I-131/I-133 are 0.1, 1.0, and 0.6 in the case of intact fuels, small failure, and large failure, respectively. Based on operating radiochemical data of a French pressurized water reactors, A. Tigeras et al. (2009) proposed that I-131/I-133>0.08 should be used as a fuel failure criterion. It is suggested to determine the size of fuel failure in PWR by a tight defect with I-131/I-133>1.0 and a large defect with I-131/I-133 < 0.4 (Cheng et al., 2003). Westinghouse suggested the following criteria: possibly no defect with I-131/I-133≤0.1, a large crack with 0.1≤I-131/I-133≤0.3, a small hole with 0.3≤I-131/I-133≤0.5, and a tight crack with I-131/I-133≥0.5 (Eicheldinger, 1975; Lin, 2013). I-131/I-133<0.1 is used as the criterion of no leaking fuel rods in VVER in Finland (L. Kekkonen, 2015). I-131/I-133<0.6 and I-131<15 MBq/t are used to determine no fuel failure in VVER in the Krško reactor in Slovenian (M Chambers et al., 2013). These thresholds to judge fuel failure are highly dependent on the specific operating parameters of the PWRs. Thus, it is necessary to determine the thresholds for fuel failure in Chinese PWRs.
In this study, the range of I-131/I-133 values was theoretically derived for typical fuel status based on the kinetic model of the generation and migration of I-131 and I-133 in the primary coolant of pressurized water reactors. The analytical results have also been verified by comparing them with measured radiochemical data in the operating 1000MWe CPR1000 PWRs of China General Nuclear Power Group (CGN).
The heavy nuclei of uranium, plutonium, and other heavy atoms in the fuel pellets undergo fission reactions under neutron irradiation to produce fission fragments (or fission products) with different mass numbers. These fission fragments accumulate in the fuel pellet and can be released through recoil and knockout into the fuel gap between the pellet and the cladding. The surface of the fuel pellet and the inner surface of the cladding have a certain adsorption effect on iodine isotopes. Some iodine isotopes are deposited on the outer surface of the pellet or the inner surface of the cladding, while the others are free in the air gap (Olander, 1985; Lewis, 1987; Lewis, 1988).
During fuel manufacture, a small quantity of uranium particles can adhere to the outer surface of the cladding called tramp uranium. When the fuel rod made with zirconium alloy is intact, the fission products inside the cladding cannot penetrate into the primary coolant, but the fission products generated from any tramp uranium on the external cladding surface will be released into the primary circuit. In addition, small amount of fuel particles can be present into the coolant from previous cycles if a large fuel failure occurred in these previous cycles. This part of the actinide nuclides may affect the radioactivity level of the fuel surface and the primary circuit in the considered cycle. Taking account of similar physical and chemical behaviors, tramp uranium and the disseminated actinides are classified into one category, tramp uranium, in this study. Figure 1 illustrates the release and migration of fission products in the primary loops from a failed fuel rod.
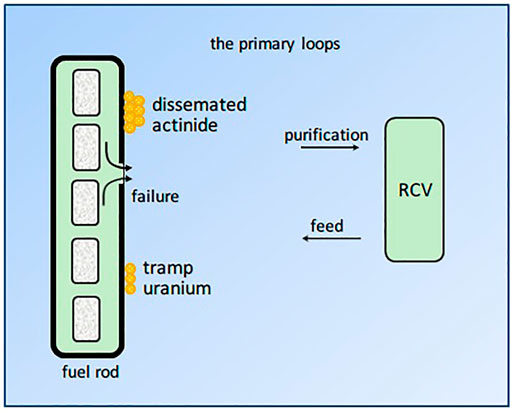
FIGURE 1. Schematic diagram of fission product migration in the primary loops from the failed fuel rod.
The general relation between the fission product activity and the atom inventory can be represented by Eq. 1, as follows:
where
To facilitate the following analysis the tramp uranium and the disseminated actinide are collectively referred to as uranium contamination in this study. With respect to release through recoil, 50% of the fission products generated by neutron irradiation of uranium contamination are released into the primary coolant (Genin et al., 2018). It can be described by the following kinetic equation (Chun et al., 1998; Kim, 2012):
where
For most of the iodine isotopes, the term
Therefore, the specific activity of fission product release can be calculated using the following formula:
The fission yields of I-131 and I-133 depend on the uranium and plutonium composition in the fuel pellet. Although there are several fissionable actinides in the fuel pellet, U-235 and Pu-239 contribute to almost all nuclear power according to core physics calculation. The equivalent cumulative yields of fission products can be estimated from the respective fission yields of U-235 and Pu-239 by weighting their fission fraction (Chun et al., 1998),as follows:
where
Based on the core isotopic depletion analysis, U-235 fission fraction in the fuel rods will gradually decrease, but the Pu-239 fission fraction in the fuel will correspondingly increase by transmutation of U-238 (Dan Gabriel, 2010). According to fuel management design of 18 months refueling cycles in CPR1000 reactors, almost all core power is due to U-235 and Pu-239 fission. The initial U-235 enrichment in fuel assemblies is 4.45 wt% in equilibrium cycles in these cycles. Table 1 lists the equivalent cumulative yields for I-131, I-133, and I-134 at the beginning of a cycle (BOC), the median of a cycle (MOC), and the end of a cycle (EOC).
According to the operating parameters of the CPR1000 reactor, it can be concluded that I-131/I-133 in one fuel cycle without fuel failure is in the range of 0.06–0.08.
In order to explicitly recognize the origin of high iodine activity in primary loops in cycles without fuel failure, I-134 has also been introduced in the study because it is one indicator of the uranium contamination outside the fuel rods and is proportional to the contaminated actinides in the primary (Zeh et al., 2008). The relations of I-131, I-133, and I-134 are derived and summarized in Table 2. If the relative relationship among the volume activities of these radioiodine isotopes measured in the primary coolant deviates significantly, indicating that there may be defective fuel rods in the core.
When the fuel rods fail, some of the primary coolant enters the fuel gap through the failure due to the pressure difference between the fuel gap and the primary loops and vaporizes rapidly, and the radioiodines are released to the primary circuit by the steam. The measured iodine activity
The following kinetic equations are used to describe the release of fission products from the fuel pellet to the primary circuit:
where
When the equilibrium is reached, the atoms inventory in the primary loop can be calculated as follows:
For the large failure in a fuel rod,
For the same nuclide, it can be considered that the escape rate for isotopes with similar half-life is not remarkably different. Allison and Robertson (1961) proposed that the escape rate coefficient of fission products released from the fuel to the primary circuit is proportional to the square root of the decay constant.
The ratio of I-131/I-133 for large failure and small failure can be calculated as follows:
In the operating CPR1000 PWR units, the activities of I-131 and I-133 have been recognized by the respective characteristic gamma rays. The uncertainties of the measured activities of I-131 and I-133 are considered uncorrelated in the study. So the uncertainty of the I-131/I-133 ratio can be obtained as follows.
where
In order to verify the aforementioned model, the measured radiochemical data in the primary coolant and operation conditions in thirty-six fuel cycles of fourteen operating pressurized water reactors were collected. These reactors are CPR1000 types with an electrical power of about 1089 MWe, and the cores are loaded with 157 AFA 3G AA fuel assemblies with an active height of 3656 mm (cold). Each fuel assembly is arranged in a 17 × 17 square array and contains 264 fuel rods. The nominal letdown rate is 13.6 t/h if fuel failure does not happen, and the maximum letdown rate is 27.2 t/h if there are defective fuel rods in the core. These reactors are identical or similar in the core design, fuel design, fuel management, purification capabilities, and operating modes. According to the sipping inspection results after shutdown, the radiochemical data are divided into two types: data with intact fuel and data with fuel failure; the distribution of I-131/I-133 in the two data sets is analyzed.
The activity concentration of iodine isotopes in the primary coolant may fluctuate to a certain extent due to the extent of fuel damage, the power level, etc. When the specific activities of iodine isotopes are so low and close to the lower detection limit, the relative error is too large that it is not suitable to evaluate the fuel reliability by the I-131/I-133 ratio. In this case, the ratio of radioactive noble gas may be more suitable as an indicator for judging fuel failure because noble gas can migrates more easily than iodine.
The raw data for I-131 and I-133 in the primary coolant for the fuel cycles with intact fuel are provided in Figure 2A. It shows the proportionality between the activity concentration of I-131 and I-133. The relationship between the I-131/I-133 ratio and I-131 has been analyzed, which is illustrated in Figure 2B. I-131 activity concentrations are distributed within a wide range, 1 MB/t to 800 MB/t, while the I-131/I-133 ratios are distributed in a narrower range of 0.06–0.15. It shows that the I-131/I-133 ratio is a more reliable indicator to assess the fuel integrity than the absolute activity concentration values of iodine isotopes in the primary loops. This is mainly because the high iodine activity concentration in the primary loops may result from the disseminated actinides from previous cycles with fuel failures due to secondary hydriding.
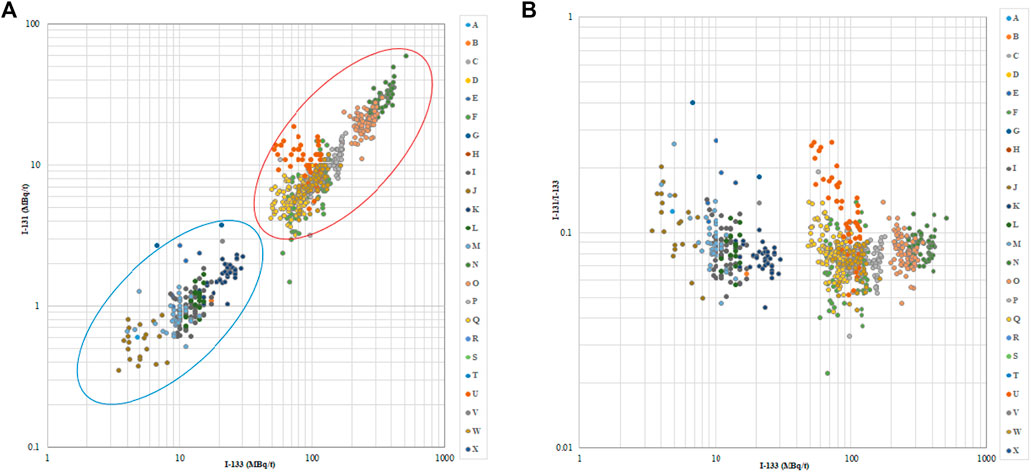
FIGURE 2. Distribution of I-131, I-133, and I-131/I-133 in primary loops in cycles with intact fuel: (A) Distribution between I-131 and I-133, and (B) Distribution between I-131/I-133 and I-133.
As shown in Figure 3, the statistic shows two frequency peaks of I-131, I-133, and I-134 activity concentration for all the cycles with intact fuel rods. The frequency at the first peak is high, but the corresponding activity is low, showing that the level of contamination on the fuel surface of AFA 3G fuel is low and most of the cycles are not contaminated. The frequency at the second peak is relatively low, but the corresponding activity concentration is very high, indicating that these cycles were significantly affected by disseminated actinides and this happens less often. As shown in Figure 3, I-131/I-133 ratios are 0.11 and 0.09 for the first and second peak, respectively. The I-131/I-134 ratios are 0.04 and 0.03 for the first and second peak, respectively. The measured I-131/I-133 ratios are in good agreement with the theoretical values in Table 2.
The raw data for I-131 and I-133 in the primary coolant for fuel cycles with fuel failures are provided in Figure 4A. The distribution of the I-131/I-133 ratio and I-131 is presented in Figure 4B. Both figures show that I-131 activity concentrations, I-133 activity concentrations, and I-131/I-133 ratios are distributed within a wide range. Most of the I-131/I-133 ratio values are distributed within the range of 0.06–3.0. The measured I-131/I-133 ratio values range covers the typical I-131/I-133 ratio values with small failures and large failures. A proportion of I-131/I-133 ratios in cycles G and K overlaps with the values for cycles without fuel failure in Figure 2B. Although fuel failure has happened at beginning of the two cycles, a further analysis shows that the reasons are different: the low release rate of iodine to the coolant for small failure that make the activity concentration increase difficult to observe in the primary loops in cycle G (failed fuel rods with this behavior have been identified as “weak leakers”), and a large amount of disseminated actinides due to significant secondary hydridring that generates more I-131 activity than I-131 activity in cycle K.
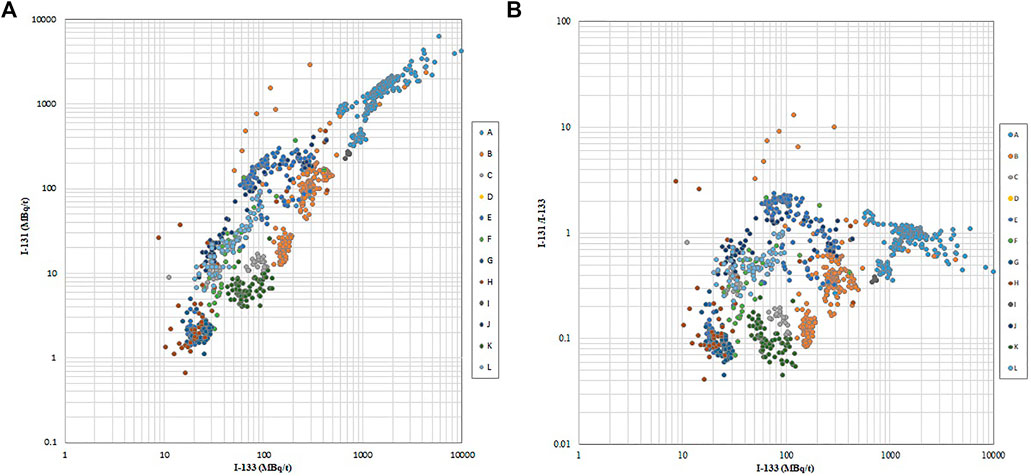
FIGURE 4. Distribution of I-131, I-133, and I-131/I-133 in primary loops in cycles with fuel failure: (A) Distribution between I-131 and I-133, and (B) Distribution between I-131/I-133 and I-133.
Figure 5 shows the distribution of I-131/I-133 ratio values in the CPR1000 cycles in which there is only one failed fuel rod. It shows two obvious distribution peaks: the lower peak is located at around 1.7 when the reactor operated from 40 to 70 days and the higher peak is near 0.72 when the reactor operated from 80 days to shutdown. According to the results in section 1.3, the former peak corresponds to a small fuel failure, and the latter corresponds to a larger fuel failure. This variation indicates the qualitative evolution of the fuel failure size from the middle of cycle to the end of the cycle during the operation.
The cumulative frequency distributions of I-131/I-133 ratio values of 24 cycles without fuel failure and 10 cycles with fuel failure (not including cycles G and K) in CPR1000 PWRs are shown in Figure 6. The continuous cumulative frequency distribution curves for intact fuel and for fuel failure overlap for ratios of around 0.10. It shows that using 0.1 as the I-131/I-133 ratio threshold for fuel failure identification may cause misjudgments. If the I-131/I-133 ratio threshold is increased to 0.15, 98% of the measured data in cycles without fuel failure and 94% measured data in cycles with fuel failure can be distinguished readily. It will help identify the fuel failure more effectively even though the measurement uncertainty has been considered. For one specific gamma spectroscopy, the uncertainty of the measured radioactivity is related to the detection time. According to operation experience in CPR1000 units, both relative uncertainties of measured activities of I-131 and I-133 are less than 10%. According to formula (14), the uncertainty of the I-131/I-133 ratio is less than 0.1414 times of I-131/I-133 and is slight in the overlap region.
Based on the generation and migration mechanisms of radioiodines in the coolant during the operation of a pressurized water reactor, a kinetic model of the radioiodine volume activity and the I-131/I-133 ratio for intact fuel rods and defective fuel rods is established theoretically. The results of the theoretical model are in good alignment with the statistical results of measured radiochemical data from cycles with intact fuel qualitatively and that from cycles with fuel failure quantitatively, for CPR1000 reactors. It is however noted based on analysis of measured data that the release of radioiodine isotopes from the defective fuel rods is complex notably due to the dynamical evolution of the failure size in one cycle and may be so slow especially when the size of fuel failure is very small that it becomes not easy to interpret. Therefore, it is suggested to consider a value of 0.15 as the I-131/I-133 ratio threshold for fuel failure in order to identify the fuel failure more effectively in CPR1000 units.
The raw/processed data required to reproduce these findings cannot be shared at this time due to legal and confidential reasons. Further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The financial support from the Project of Research on Key Technologies for Zero Failure of Nuclear Fuel Assemblies in Pressurized Water Reactor Operation (No. 3100121513) in China General Nuclear Power Group is highly appreciated.
PF and SH were employed by China Nuclear Power Technology Research Institute Co., Ltd. SL was employed by Yangjiang Nuclear Power Co., Ltd. XY was employed by Liaoning Hongyanhe Nuclear Power Co., Ltd. JX was employed by Fujian Ningde Nuclear Power Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors are thankful to Sofia Bouhrizi of EDF; Zhijun Li, Kewa Cui, and Juan Li of China Nuclear Power Technology Research Institute Co. Ltd; and Xiaodong Yang of CGNPC Uranium Resources Co. Ltd. for their help and discussion in this study.
Allison, G. M., and Robertson, R. F. (1961). The Behaviour of Fission Products in Pressurized-Water Systems- (A Review of Defect Tests on UO2 Fuel Elements at Chalk River). Ontario (Canada), Atomic Energy of Canada Ltd.
Alvarez, L., Daniels, T., and Dangoulème, D. (2010). Review of Fuel Failures in Water Cooled Reactors (No. NF-T-2.1). Vienna (Austria). International Atomic Energy Agency.
Chambers, M., Kadivnik, D., and Kurinčič, B. (2013). “Evaluation of Reactor Coolant System Specific Activity to Determine Fuel Integrity at NPP Krško” in Proceeding of 22nd international conference nuclear energy for new Europe. Ljubljana (Slovenia), Nuclear Society of Slovenia.
Cheng, B., Lin, C. C., Watkins, K., and Hemholz, H. (2003). Fuel Integrity Monitoring and Failure Evaluation Handbook: Revision 1. Palo Alto, CA: EPRI.
Chun, M.-H., Tak, N.-I., and Lee, S.-K. (1998). Development of a Computer Code to Estimate the Fuel Rod Failure Using Primary Coolant Activities of Operating PWRs. Ann. Nucl. Energ. 25 (10), 753–763. doi:10.1016/s0306-4549(97)00126-6
Eicheldinger, C. (1975). Source Term Data for Westinghouse Pressurized Water Reactors (WCAP-8253). Pittsburgh, Pa. (United States): Westinghouse Electric Corp.
Gabriel, D. C. (2010). Handbook of Nuclear Engineering - Reactor Design. Karlsruhe (Germany), Springer Science & Business Media, 1247–1249.
Genin, J., Jobert, T., and Engler, N. (2018). “The OSCAR-FP V1. 4 Code Simulation of Fission Product and Alpha Emitter Contamination in PWR Circuits” in Proc. 21st Int. Conf. on Water Chemistry in Nuclear Reactor Systems (NPC 2018), San Francisco(USA), Electric Power Research Institute (EPRI).
Kekkonen, L. (2015). “Fuel Reliability Experience in Finland,” in Proceedings of 11th International conferences on WWER fuel performance, modelling and experimental support. Varna (Bulgaria), Institute for Nuclear Research and Nuclear Energy (INRNE) of the Bulgarian Academy of Sciences and International Atomic Energy Agency (IAEA).
Kim, K.-T. (2012). Relation between a Fuel Rod Failure Cause and a Reactor Coolant Radioactivity Variation. Nucl. Eng. Des. 248, 156–168. doi:10.1016/j.nucengdes.2012.03.051
Lewis, B. J. (1987). Fission Product Release from Nuclear Fuel by Recoil and Knockout. J. Nucl. Mater. 148 (1), 28–42. doi:10.1016/0022-3115(87)90515-0
Lewis, B. J. (1988). Fundamental Aspects of Defective Nuclear Fuel Behaviour and Fission Product Release. J. Nucl. Mater. 160 (2-3), 201–217. doi:10.1016/0022-3115(88)90049-9
Lin, C. C. (2013). Radiochemical Technology in Nuclear Power Plants. La Grange Park, Illinois (USA), American Nuclear Society.
Olander, D. R. (1985). Fundamental aspects of nuclear reactor fuel elements: solutions to problems (No. TID-26711-P2). California Univ., Berkeley (USA). Dept. of Nuclear Engineering.
Tigeras, A., Bachet, M., Catalette, H., and Simoni, E. (2009).Fuel Failure Detection, Characterization and Modelling: Effect on Radionuclide Behaviour in PWR Primary Coolant. Doctoral dissertation. Paris XI University.
Keywords: fuel failure, I-131/I-133, fission product release, CPR1000, failure size
Citation: Fu P, Liang S, Lu S, Zhou W, Yang X, Xu J and Han S (2022) Relationship Between Fuel Reliability and I-131/I-133 in the Primary Coolant of CPR1000 PWRs. Front. Energy Res. 10:860480. doi: 10.3389/fenrg.2022.860480
Received: 23 January 2022; Accepted: 28 February 2022;
Published: 11 April 2022.
Edited by:
Guang Hu, Xi’an Jiaotong University, ChinaReviewed by:
Shanfang Huang, Tsinghua University, ChinaCopyright © 2022 Fu, Liang, Lu, Zhou, Yang, Xu and Han. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pengtao Fu, ZnVwZW5ndGFvQGNnbnBjLmNvbS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.