Influence Factors of the Bottom Hole Flow Pressure in a High-Pressure and High-Temperature Condensate Gas Reservoir: Applicability Analysis

Introduction

In China, high-pressure and ultra-high-pressure gas reservoirs account for more than one-third of the total gas reservoirs, and their current proven reserves account for about one-ninth of the total proved reserves of natural gas (Wang, et al., 2011; Hong et al., 2018). In recent years, large gas fields such as Kela 2, Dina, Dabei, and Keshen discovered in Tarim area, as well as Heba, Qingxichang, and Shuangmiao gas fields discovered in northeastern Sichuan, are all ultra-high-pressure gas reservoirs. Bottom hole flow pressure is a key parameter to calculate single-well energy storage and dynamic reserves, especially during the production testing. For conventional gas wells, the bottom hole flow pressure can be measured by placing a pressure gauge at the bottom hole. However, for high-pressure and high-temperature gas reservoirs, this conventional method is no longer applicable due to the high bottom hole pressure and temperature.

Thus, analytical and numerical methods have been applied to calculate the bottom hole flow pressure for high-pressure and high-temperature condensate gas reservoirs. Meanwhile, many essential parameters should be considered in the calculating process, such as the deviation factor of natural gas (Li et al., 2001; Zhang et al., 2005), the gas viscosity (John et al., 1964; Dempesey, 1965; Lee, 1966), friction coefficient (Colebrook 1938; Swamee and Jain, 1976), and even the change in the diameter of the tubes. This report reviews the models and methods of calculating the bottom hole flow pressure for single-phase flow in high-pressure and high-temperature gas reservoirs. And the models are calculated to discuss the influence factors of the bottom hole pressure in Figure 1. Then, the relatively reasonable method in gas reservoir engineering can be summarized for the development of high-pressure and high-temperature condensate gas reservoirs.

FIGURE 1

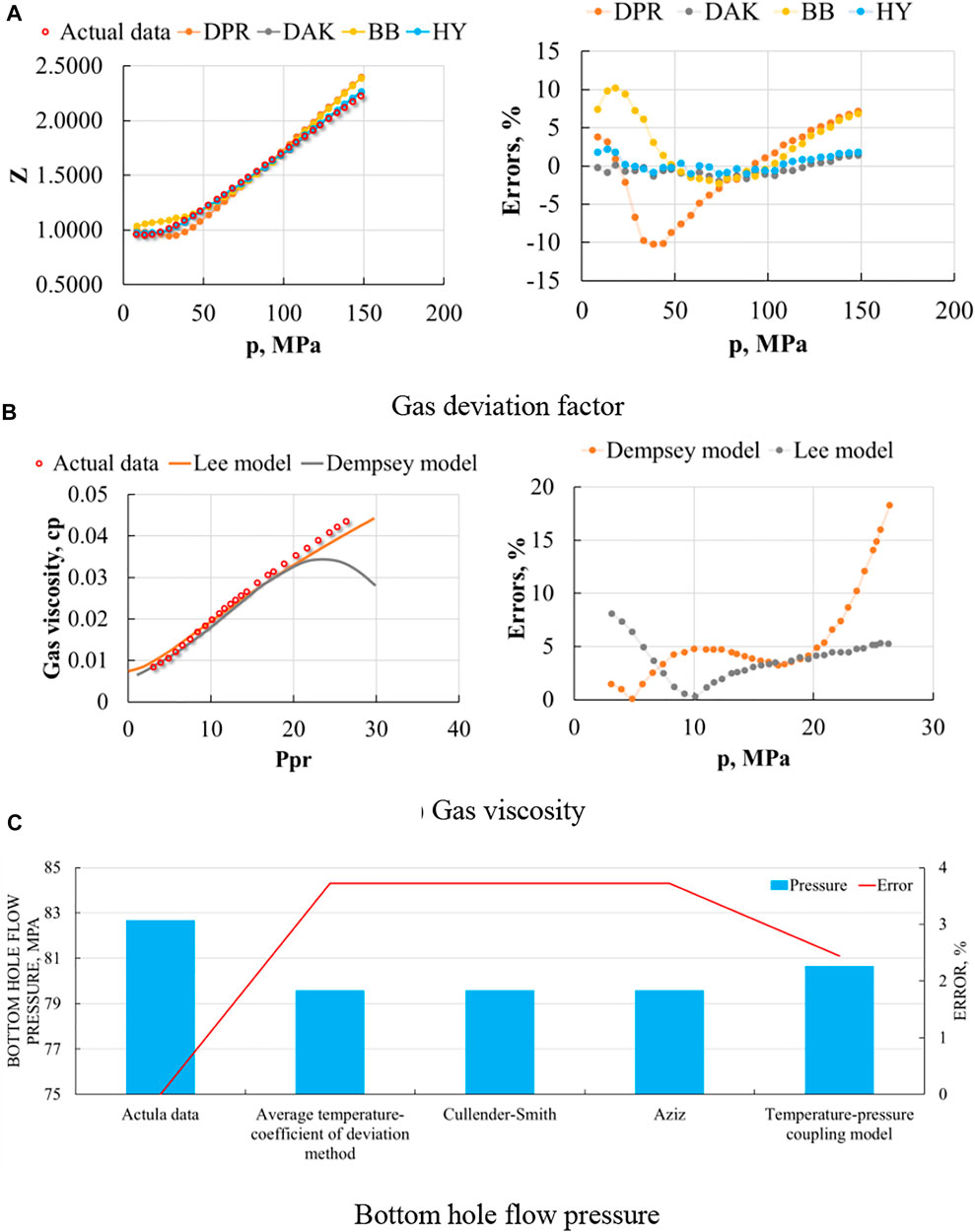
FIGURE 1. The influences of fluid and engineering properties on calculating results and errors for high-pressure and high-temperature condensate gas reservoirs (data from Yang et al., 2019; Peng et al., 2017). (A) Gas deviation factor. (B) Gas viscosity. (C) Bottom hole flow pressure.

Influences of Fluid Property

• Gas deviation factor. It is one of the extremely important physical parameters of natural gas, which directly affects the original geological reserves of the gas reservoir. The deviation factor of natural gas is also known as the deviation coefficient; it is the ratio of the actual gas volume to the ideal gas volume of the same mole number at the same temperature and pressure under a given pressure and temperature. The gas deviation factor is related to the characteristics, temperature, and pressure of the gas. At low pressure, natural gas can be regarded as an ideal gas following the ideal gas law. However, when the gas pressure rises, and when the gas temperature approaches the critical temperature, the deviation of the real gas from the ideal gas can be large. At present, there are many calculation models of gas deviation factor, which are mainly divided into two categories: one is the experimental method, and the other is the calculation method. Although the data measured by the experimental method is more accurate, the error is low, and the reliability is high, the cost of the experiment is high, the cycle is long, and the operation is difficult, so the calculation method is generally used to determine the deviation factor. The calculation methods can be divided into three categories: the plate method, the plate fitting method, and the equation of state method. The plate method (deviation coefficient plate) has no specific equation, which is inconvenient for the realization of computer programming, so its application is greatly restricted, and hence the latter two calculation methods are often used. The plate fitting method is the empirical formula method and uses the equation of state to regress the plate to obtain the expression of the deviation factor on the quasi-critical pressure and quasi-critical temperature. At present, the more commonly used empirical formula methods are BB method (Brill and Begges, 1974), HY method (Yarborough and Hall, 1974), DPR method (Dranchuk et al., 1973), DAK method (Dranchuk et al., 1975), Li method (Li et al., 2001), Zhang method (Zhang et al., 2005), etc. As shown in Figure 1A, the maximum deviation values and average deviation values of HY model and DAK model are the lowest; the maximum deviation is about 2.3%, and the average deviation is between 0.32% and 0.51%, which can meet the project required. The calculation deviation of DAK method is the lowest. In practical application, DAK method is preferred for the calculation.

• Gas viscosity. It refers to the measurement of fluid resistance to shear action; generally speaking, the greater the viscosity, the more difficult it is for the fluid to flow. The viscosity of natural gas under high pressure is quite different from that under low pressure. When at low pressure condition, the viscosity of natural gas is little affected by pressure and only increases with the increase of temperature. However, under the condition of high temperature and high pressure, the viscosity of natural gas will also change accordingly. The procedure for determining the value of its viscosity is also very important in the process of calculating the bottom hole flow pressure. The methods for calculating natural gas viscosity are the Dempesey model (Dempesey, 1965), Lee model (Lee, 1966), Lucas model, LBC model (John et al., 1964), etc. As shown in Figure 1B, a comparison between the calculated results and the experimental data shows that the relative error of high pressure reaches 4.8–18.3%, which indicates that the two models cannot be applied to the calculation of gas viscosity in high pressure gas reservoirs. Peng et al. (2017) used the nonlinear method to improve these two models, and the results were in good agreement with the actual data.

• Friction coefficient. It plays a key role in the process of calculating the converted bottom hole flow pressure. The coefficient of friction can be determined from the Moody plate introduced in fluid mechanics. In order to realize the programming of its calculation method, three empirical analytical formulas, Colebrook method (Colebrook 1938), Jain method (Swamee and Jain, 1976), and Chen method, are usually used to calculate the friction coefficient. For abnormally high-pressure gas reservoirs, the above three empirical analytical formulas cannot completely cover the entire flow interval. Therefore, it is necessary to first determine the flow region where the fluid is located and then select the corresponding formula to calculate the friction coefficient.

Influence of Engineering Property

Usually, corresponding analytical models are used to calculate the bottom hole flow pressure according to wellhead test pressure and gas well characteristics. However, there is little research on the influence of the change in the diameter of tubes on the bottom hole flow pressure. At present, the commonly used methods for calculating the bottom hole flow pressure mainly include the following: average temperature-deviation coefficient method, Cullender–Smith method, Aziz method, and temperature–pressure coupled model.

In the average temperature-deviation coefficient method, the natural gas deviation factor is not applied for correction, and the variation of temperature with wellbore depth is not considered (Wang, 1999). Some scholars did not consider the correction of acid gas in natural gas components when calculating the bottom hole pressure (He and Wang, 2014). In some research in the literature, the effect of friction coefficient on bottom hole flow pressure has not been considered (Li et al., 2001; Zhang et al., 2019).

Different conversion methods can be used to calculate the bottom hole flow pressure. One set of actual data from a typical high-pressure and high-temperature condensate gas reservoir in Northwest China has been used to calculate the bottom hole flow pressure. The effect of change in the tube diameters on the bottom hole pressure is mainly reflected in the friction coefficient. A comparison of different calculated results with different tube diameters shows that the relative errors of different tube diameters are small and have less influence on the bottom hole flow pressure, which are between 0.5% and 1%. Therefore, the change in the tube diameter can be ignored when calculating the bottom hole flow pressure. Meanwhile, a comparison of methods of calculating the bottom hole flow pressure is shown in Figure 1C; the results of average temperature-deviation coefficient method, Cullender–Smith method, and Aziz method are the same, and the errors are about 3.73%. The temperature–pressure coupled model method is more reasonable for the high-pressure and high-temperature condensate gas reservoirs.

Conclusion

1) For high-pressure and high-temperature condensate gas reservoirs, the gas deviation factor can be obtained by the HY method and DAK method. The BB method and DPR method are not appropriate.

2) For gas viscosity calculation, the Lee model has a lower error than the Dempesey model under high-pressure and high-temperature conditions. However, some modification for Lee model is needed to make the error lower than 1%.

3) Under high-pressure and high-temperature conditions, in order to obtain more accurate bottom hole flow pressure, the temperature–pressure coupling model can be applied. The average temperature-coefficient of deviation method and Cullender–Smith method are not suitable.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

RC, WH, BX, XS, DY, and CW were employed by No.1 Gas Production Plant of XinJiang Oilfield Company, CNPC.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brill, J. P., and Beggs, D. H. (1974). Two-phase Flow in Pipes. Tulsa, Oklahoma: University of Tulsa.

Google Scholar

Colebrook, C. (1938). Turbulent Flow in Pipes, with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. J. Inst. Civil Eng. 11, 133–156.

Google Scholar

Dempesey, P. M. (1965). The Effect of Sulfur Deposition on Gaswell Inflow Performance. SPE Reservoir Eng. 12 (02), 118–123.

Google Scholar

Dranchuk, P., and Abou-Kassem, H. (1975). Calculation of Z Factors for Natural Gases Using Equations of State. J. Can. Pet. Technol. 14 (03), 34–36. doi:10.2118/75-03-03

CrossRef Full Text | Google Scholar

Dranchuk, P., Purvis, R., and Robinson, D. (1973). Computer Calculation of Natural Gas Compressibility Factors Using the Standing and Katz Correlation. Edmonton: Annual Technical Meeting.

Google Scholar

He, Z., and Wang, Y. (2014). A New Method for Calculation of Gas Well Bottom-Hole Pressure. Liaoning Chem. Industry 43 (02), 218–219.

Google Scholar

Hong, F., Jiang, L., Zhuo, Q., Zhang, F., Lu, X., Ma, X., et al. (2018). Types of Abnormal High-Pressure Gas Reservoir in Foreland Basins of China. Nat. Gas Geosci. 29 (03), 317–327. doi:10.1016/j.jnggs.2018.10.001

CrossRef Full Text | Google Scholar

John, L., Bruce, G. B., and Charies, R. C. (1964). Calculating Viscosities of Reservoir Fluids from Their Compositions. J. Can. Pet. Technol. 16(10), 1171–1176.

Google Scholar

Lee, A. L., Gonzalez, M. H., and Eakin, B. E. (1996). The Viscosity of Natural Gases. Trans. AIME. 237, 9997–1000.

Google Scholar

Li, X., Zhuang, X., Tao, G., Sui, X., and Xie, L. (2001). Comprehensive Appraisal and Selection for Gas Compressibility Factor Calculation Model. Oil Drilling Process 02, 42–85.

Google Scholar

Peng, D., Yang, J., Liu, Z., Wang, T., Zhang, S., Zhou, Y., et al. (2017). The Calculation Method and Improvement for Viscosity of Ultra High Pressure Natural Gas. Chengdu: International Field Exploration and Development Conference.

Google Scholar

Swamee, P. K., and Jain, A. K. (1976). Explicit Equations for Pipe-Flow Problems. J. Hydr. Div. 102, 657–664. doi:10.1061/jyceaj.0004542

CrossRef Full Text | Google Scholar

Wang, C. (1999). An Improved Method of Average Temperature and Average Compressibility Factor for Calculating Bottom Hole Pressure of Gas Well. Pet. Exploration Develop. 02, 102–105.

Google Scholar

Wang, W., Guo, Y., and Liu, H. (2011). A New Method for Evaluation of Single Well-Controlled Dynamic Reserves in Overpressured Gas Reservoir. Xinjiang Pet. Geology. 32 (3), 291.

Google Scholar

Yang, G., Qian, L., Li, L., Hu, D., She, J., Ruan, M., et al. (2019). Calculation of Deviation Factor and Bottom Hole Flowing Pressure: Examples from Gas Reservoirs of Maokou Formation, Shuangyushi Block, Sichuan Basin. Nat. Gas Exploration Develop. 01, 79–85.

Google Scholar

Yarborough, L., and Hall, K. R. (1974). How to Solve Equation of State for Z-Factors. Oil Gas J. 72 (7), 86–88.

Google Scholar

Zhang, G., Li, M., and Bo, D. (2005). Practical Calculation Model of Gas Deviation Factor with High and Super-high Pressure. Nat. Gas Industry 08, 79–93.

Google Scholar

Zhang, J., Xia, J., Luo, K., and Li, Y. (2019). Productivity Evaluation Method and Application of Abnormally High Pressure Gas Reservoir. Beijing: Petroleum Industry Press.

Google Scholar