UKF-Based Parameter Estimation and Identification for Permanent Magnet Synchronous Motor

The accuracy of rotor position estimation determines the performance of the sensorless control system of a permanent magnet synchronous motor. In order to realize the accurate control of rotor position and speed, it is necessary to identify the motor parameters. Modeling and simulation of the state estimation are investigated for a permanent magnet synchronous motor with parameter identification based on the unscented Kalman filter (UKF) in this article. Based on the mathematical model of the motor, the unscented Kalman filter is used to identify the rotor flux and quadrature axis inductance simultaneously, and the identified parameters are used to update the motor model in the sensorless vector control algorithm. The simulation results show that the unscented Kalman filter can converge to the real value in a short time with small errors. It can follow the changes of motor parameters well and achieve high-precision speed and position estimation.

Introduction

Permanent magnet synchronous motor (PMSM) has been widely used in the fields of new energy vehicles, power generation, and servo drive due to its advantages of large starting torque, high operation efficiency, high power density, and low failure rate (Chen et al., 2014; Chen et al., 2019; Cui et al., 2020; Wang et al., 2021). In the traditional vector control system, sensors are usually used to obtain rotor speed and position information; but in practical application, the existence of sensors increases the motor volume and system cost, and it is difficult to install and maintain in some harsh environments, which reduces the reliability of the system (Pan and Gao, 2018). Therefore, the research of new control strategy to improve the performance of the PMSM control system and ensure the reliable and safe operation of PMSM has become a research hotspot in the field of motor control (Zhu et al., 2014; Cheng et al., 2015; Deng et al., 2019; He and Wu, 2019). With the development of sensorless drive technology of permanent magnet synchronous motor, many methods have been proposed to estimate the speed and position of the rotor, such as the model reference adaptive control method (Zhong and Lin, 2017; Zhong et al., 2018; Wang et al., 2020a), sliding mode observer method (Liu et al., 2016; Liang et al., 2017; Lu et al., 2021), Kalman filter algorithm (Moon and Kwon, 2016; Yang et al., 2016; Luo et al., 2019), and artificial intelligence algorithm (Fadil et al., 2015). It is worth mentioning that the UKF can be applied to a nonlinear model and has been widely used in the estimation of the rotor position and speed of the PMSM drive system (An and Hameyer, 2014; Zhou et al., 2018; Tao and Guo, 2019; Yin et al., 2019).

The accuracy of rotor position estimation determines the performance of the PMSM sensorless control system. Accurate position estimation relies on accurate motor parameters. In some cases, the parameters displayed on the motor nameplate and data manual may change due to high temperature, demagnetization, and other operating conditions in long-term operation, which will affect the control precision (Nahid-Mobarakeh et al., 2004; Wang et al., 2019; Wang et al., 2020b). Therefore, accurate parameter identification is of great significance for motor control. In the vector control system, good operation of the system depends on whether the controller design of the speed ring and current ring is reasonable (He et al., 2019), while the parameter setting of the controller of the speed ring needs to obtain the value of the permanent magnet flux chain (Cao et al., 2015), and the current loop needs to call the stator resistance and inductance value. In order to ensure the control effect as much as possible, in recent years, the parameter identification method combined with the control of sensorless has been widely concerned and studied.

At present, PMSM parameter identification technology can be divided into three categories: 1) frequency-domain identification; 2) time-domain identification, such as the recursive least square method (RLS), unscented Kalman filter (UKF), and model reference adaptive method; and 3) artificial intelligence methods, such as neural network identification and genetic algorithm,. Comparing the abovementioned methods, it is found that although the frequency-domain identification is relatively mature, it requires strict input signal and cannot reflect the nonlinearity in the dynamic process. The recursive least square method needs to use the derivative of the objective function to the motor parameters in the optimization process, which is sensitive to the measurement noise and speed fluctuation. The model reference adaptive method can effectively estimate the rotor position, but the premise is to establish an accurate mathematical model (Kyoon, 2017). The research on the identification method based on artificial neural network is not mature in theory and needs the support of special hardware. Therefore, it is difficult to achieve satisfactory results in the actual system with these methods.

The UKF is one of the effective methods to estimate the parameters of PMSM, which is widely used in sensorless PMSM systems. The UKF is based on unscented transformation (UT). For the nonlinear model, the conventional processing method is EKF, and many scholars have used EKF to estimate the motor state. EKF is the Taylor expansion of the model function of a highly complex nonlinear system and the first-order linear truncation of the expansion. In this way, the model can be transformed into a linear problem processed by using a computer and then the Kalman filter. Compared with the approximation of nonlinear function, the approximation of Gaussian distribution is much simpler. The UKF carries out UT transformation near the estimation point, so that the mean and covariance of the obtained sampling point set match the original statistical characteristics (Moon and Kwon, 2016). Then, the nonlinear mapping of these sampling point sets is directly carried out to eliminate the error caused by the linearization of extended Kalman filter (EKF) algorithm, which not only realizes the accurate estimation of rotor speed and position but also accurately estimates the parameters of the motor. It has the characteristics of simple method and good system stability and can effectively improve the control accuracy of the motor. The UKF overcomes the noise sensitivity of the least square method to some extent, which can jointly estimate the states and parameters of PMSM.

In this article, considering the influence of motor parameters on the rotor position, a parameter identification method of permanent magnet synchronous motor is proposed based on the UKF. The main contributions of this article can be outlined as follows.

(1) Based on the analysis of the mathematical model of PMSM in a static coordinate system, this article investigates a state observer with the unscented Kalman filter in the sensorless control of PMSM. It not only estimates the speed and position of the motor but also realizes the identification of motor inductance L_d and L_q and flux linkage ψ_f.

(2) The resistance R_s changes under the influence of temperature, which will affect the identification results. In this article, we treat the influence of temperature and other factors as the state noise of the motor. The inductance and flux linkage are identified to ensure that the steady-state error is smaller than that obtained in the study of Moon and Kwon, 2016, and Zhou et al., 2018.

(3) The parameter identification results can be used for parameter configuration of the PMSM control system. This article provides a solution to improve the performance of the PMSM control system via the UKF and verifies the superiority of this method in state estimation.

The rest of this article is organized as follows. In Mathematical Model of PMSM, we present the mathematical model of PMSM. In Main Results, we analyze the principle of the UKF control scheme and present the main results. A simulation result is used to verify the proposed method in The Simulation Case. Finally, Conclusion concludes this article.

Mathematical Model of PMSM

PMSM is a nonlinear and strong coupled complex system. It is very difficult to study and control the motor by using the mathematical model in a three-phase coordinate system. However, if we use the mathematical model of a two-phase coordinate system to study it, it will be much simpler. The stator current of the motor can be divided into two components in the two-phase coordinate system. The control of the two components can achieve the effect of controlling the motor. During the research and analysis of the PMSM control system, the first step is to build the mathematical model of the system. In different coordinate systems, there are different mathematical models. It is very important to select the appropriate model for different operating environments.

PMSM has the characteristics of being multivariable, strong coupling, and nonlinearity. In order to achieve good speed regulation performance, it is necessary to realize the approximate decoupling of the control object. Therefore, the mathematical model is established in the αβ-axis rotating coordinate system to analyze the performance of PMSM. The voltage equation of PMSM in the αβ-axis rotating coordinate system is as follows:

$\left\{\begin{array}{c}{u}_{\alpha }=R_s{i}_{\alpha }+\frac{d{\psi }_{\alpha }}{dt};\hfill \\ u_{\beta }=R_s{i}_{\beta }+\frac{d{\psi }_{\beta }}{dt}.\hfill \end{array}\right.(1)$

The flux linkage equation is

$\left\{\begin{array}{c}{\psi }_{\alpha }=L{i}_{\alpha }+{\psi }_f\cos \theta ;\hfill \\ {\psi }_{\beta }=L{i}_{\beta }+{\psi }_f\sin \theta .\hfill \end{array}\right.(2)$

The electromagnetic torque equation is

$T_e=p_n[{\psi }_{\alpha }{i}_{\beta }-{\psi }_{\beta }{i}_{\alpha }].(3)$

The mechanical motion equation is

$\frac{d{\omega }_e}{dt}=\frac{p_n}{J}(T_e-T_l-B{\omega }_e).(4)$

Here, u_α and u_β are the voltage of α and β axes, respectively, i_α and i_β are the current of α and β axes, respectively, ψ_α and ψ_β are the flux of α and β axes, respectively, L_α and L_β are the inductance of α and β axes respectively, R_s is the stator resistance, ω_e is the rotor angular speed, ψ_f is the rotor flux, p_n is the pole number of the motor, T_e is the electromagnetic torque, T_l is the load torque, J is the moment of inertia, and B is the friction coefficient. According to Eqs. 1–4, the state equation of PMSM can be written as

$\left\{\begin{array}{c}\frac{d{i}_{\alpha }}{dt}=-\frac{R_s}{L}{i}_{\alpha }+{\omega }_e\frac{{\psi }_f}{L}\sin \theta +\frac{u_{\alpha }}{L};\hfill \\ \frac{d{i}_{\beta }}{dt}=-\frac{R_s}{L}{i}_{\beta }-{\omega }_e\frac{{\psi }_f}{L}\cos \theta +\frac{u_{\beta }}{L};\hfill \\ \frac{d{\omega }_e}{dt}=\frac{p_n^2}{J}{\psi }_f(i_{\beta }\cos \theta -i_{\alpha }\sin \theta )-\frac{B}{J}{\omega }_e-p_n\frac{T_l}{J};\hfill \\ \frac{d\theta }{dt}={\omega }_e.\hfill \end{array}\right.(5)$

From the model, permanent magnet motor is a 4-order, nonlinear, and coupling model, and we set the stator current i_α and i_β, rotor angular speed ω_e, and rotor position angle θ as state variables and stator voltage u_α and u_β as control variables.

We define state vector $x={\left[\begin{array}{cccc}\hfill i_{\alpha }\hfill & \hfill i_{\beta }\hfill & \hfill {\omega }_e\hfill & \hfill \theta \hfill \end{array}\right]}^{\text{T\hspace{0.17em}}}$ and input vector $u={\left[\begin{array}{cc}\hfill u_{\alpha }\hfill & \hfill u_{\beta }\hfill \end{array}\right]}^{\text{T\hspace{0.17em}}}$. Rotor angular speed and rotor position angle state components are estimators, and only current state components are measurable, which is detected by the system current sensor.

The nonlinear model of permanent magnet linear synchronous motor given by Eq. 5 is deterministic. Due to non-ideal factors such as asymmetry of motor parameters and current detection error, the stochastic state space model may be more accurate. Therefore, we consider the state equation as follows:

$\dot{x}=f(x,u)+w.(6)$

In Eq. 5, speed and position state components are estimators, and only current state components are measurable. The phase current of PMSM is detected by the system current sensor, and the output phase current of the two-phase motor is obtained through the Clarke transformation from abc three-phase to αβ static two-phase. Therefore, the measurement equation of the sensorless driving system is linear, and it can be written as

$z=hx+v,(7)$

where $h=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$.

In Eqs. 6, 7, the system produces process noise w and observation noise v due to non-ideal factors such as asymmetry of motor parameters and current detection error. The process noise w is assumed to be a Gaussian white noise with zero mean and covariance Q and is independent of state variables x. The observation noise v is a Gaussian white noise with zero mean and covariance R, which is independent of w and v.

Therefore, we consider the state space model as follows:

$\left\{\begin{array}{c}\dot{x}=f(x,u)+w;\hfill \\ z=hx+v.\hfill \end{array}\right.(8)$

where x, u, and z are the state variables, control variables, and measurement variables, respectively. f (⋅) is the nonlinear function of the motor, and h (⋅) is the measurement matrix.

Main Results

We divide this section into two parts. First, we introduce the principle of UKF and estimate the rotor speed and position. Second, the parameter identification algorithm based on the UKF is given.

Brief Introduction of the UKF and State Estimation of PMSM Based on the UKF

Unscented Kalman filter (UKF) algorithm is another extended algorithm of Kalman filter algorithm. It carries out parameter identification by estimating the state matrix at each time. By giving an initial state quantity and then performing traceless transformation on the mean and covariance, the state quantity at the next time interval is obtained. When the parameter in the state matrix is stable, it is the identification value of the parameter.

The state space expression of the sensorless system of permanent magnet synchronous motor is

$\left\{\begin{array}{c}{x}_{k+1}=f(x_k,u_k)+w_k;\hfill \\ z_k=h(x_k)+v_k.\hfill \end{array}\right.(9)$

where x_k+1 and x_k are the system state vectors of the current time and the previous time, respectively; u_k is the system input vector; w_k is the system process noise vector; v_k is the measurement noise vector of the system; and z_k is the output vector of the system. In the recursive calculation of UKF, the noise vectors w_k and v_k are not used directly, but the covariance matrix Q of w_k and the covariance matrix R of v_k are used.

The state vector estimation process of the nonlinear system shown in Eq. 9 based on UKF algorithm is divided into four stages: state vector initialization, sigma point calculation, time update, and measurement update.

Step 1: initialization.

$\left\{\begin{array}{c}{\widehat{x}}_0=\mathbb{E}\{x_0\}\hfill \\ P_0=\mathbb{E}\left\{(x_0-{\widehat{x}}_0){(x_0-{\widehat{x}}_0)}^{\text{T}}\right\}\hfill \end{array}\right.(10)$

Step 2: we select proportional symmetric sampling to determine the sigma point set and introduce UT transform to approximate the nonlinearity, and 2n + 1 sigma points can be obtained.

UT transformation uses a fixed number of parameters to approximate a Gaussian distribution. Its implementation principle is some points in the original distribution are selected according to a certain rule; the mean and covariance of the state distribution of these points are equal to the mean and covariance of the original state distribution. These points are substituted into the nonlinear function to obtain the set of nonlinear function value points. Through these point sets, the transformed mean and covariance can be obtained. For any nonlinear system, a posterior mean and covariance accurate to the third moment can be obtained by using this set of sampling points.

$\begin{array}{ll}\hfill & \left\{\begin{array}{c}{\chi }_{i,k|k}={\widehat{x}}_{k|k},i=0\hfill \\ {\chi }_{i,k|k}={\widehat{x}}_{k|k}+{(\sqrt{(n+\lambda )P_{k|k}})}_i,i=\mathrm{1,2},\dots ,n\hfill \\ {\chi }_{i,k|k}={\widehat{x}}_{k|k}-{(\sqrt{(n+\lambda )P_{k|k}})}_i,i=n+1,\dots ,2n\hfill \end{array}\right.\hfill \end{array}(11)$

$\begin{array}{ll}\hfill & \left\{\begin{array}{c}{\omega }_i^{(m)}=\frac{\lambda }{n+\lambda },i=0\hfill \\ {\omega }_i^{(c)}=\frac{\lambda }{n+\lambda }+(1-{\alpha }^2+\beta ),i=0\hfill \\ {\omega }_i^{(m)}={\omega }_i^{(c)}=\frac{1}{2(n+\lambda )},i=\mathrm{1,2},\dots ,2n\hfill \end{array}\right.\hfill \end{array}(12)$

where λ = α² (n + k) − n, α ∈ [0.000 1, 1] is the proportion factor, and the distribution distance of particles can be adjusted by changing the value of α to reduce the error. k is the redundancy, which is generally 0 and is optimal at β = 2. ${(\sqrt{(n+\lambda )P_{k|k}})}_i$ is the i-th column of the square root of the matrix, ${\omega }_i^{(m)}$ is the weighted mean, and ${\omega }_i^{(c)}$ is the weighted covariance.

Step 3: time update: the sigma point transfer is realized according to the discrete system state, Eq. 9:

${\chi }_{i,k+1|k}=f\left({\chi }_{i,k|k}\right).(13)$

The predicted mean and covariance of the state vector are obtained according to the transmission results.

$\begin{array}{l}\hfill {\widehat{x}}_{k+1|k}=\sum _{i=0}^{2n}{\omega }_i^{(m)}{\chi }_{i,k+1|k}\end{array}(14)$

$\begin{array}{l}\hfill P_{k+1|k}=\sum _{i=0}^{2n}{\omega }_i^{(c)}[{\chi }_{i,k+1|k}-{\widehat{x}}_{k+1|k}]{[{\chi }_{i,k+1|k}-{\widehat{x}}_{k+1|k}]}^{\text{T}}+Q.\end{array}(15)$

Step 4: measurement update.

The sampling point prediction equation of observation is given as follows:

$z_{i,k|k-1}=h(x_{k|k-1}).(16)$

The transformation value z_i,k|k−1 obtained by Eq. 10 is weighted and summed to obtain the measurement prediction value ${\widehat{z}}_{k|k-1}$ of the system and the variance P_z,k|k−1 and cross covariance P_xz,k|k−1 of the system measurement variables.

${\widehat{z}}_{k|k-1}=\sum _{i=0}^{2n}{\omega }_i^{(m)}{z}_{i,k|k-1}.(17)$

The time update equation is established as follows:

${\widehat{x}}_{k+1}={\widehat{x}}_{k+1|k}+K_{k+1}(z_{k+1}-h({\widehat{x}}_{k+1|k})),(18)$

where ${\widehat{x}}_{k+1}$ is the posterior estimation of the state vector at time k + 1 and ${\widehat{x}}_{k+1|k}$ is the prior estimation of the state vector at time k + 1. The difference $z_{k+1}-h({\widehat{x}}_{k+1|k})$ between the measured variable and its prediction is called the innovation or residue of the measurement process, which reflects the inconsistency between the predicted value and the real value. The matrix K_k+1 is called the residual gain.

The posteriori error is

$e_{k+1}=x_{k+1}-{\widehat{x}}_{k+1}=x_{k+1}-{\widehat{x}}_{k+1|k}-K_{k+1}(z_{k+1}-{\widehat{z}}_{k+1}).(19)$

The posteriori error covariance is

$P_{k+1}=\mathbb{E}(e_{k+1}{e}_{k+1}^{\text{T}}).(20)$

Let$\frac{\partial P_{k+1}}{\partial K_{k+1}}=0$, and the Kalman gain is found.

$K_{k+1}=P_{xz,k+1|k}{P}_{z,k+1|k}^{-1}.(21)$

Then,

$\begin{array}{l}\hfill P_{z,k+1|k}=\sum _{i=0}^{2n}{\omega }_i^{(c)}[z_{i,k+1|k}-{\widehat{z}}_{k+1|k}]{[z_{i,k+1|k}-{\widehat{z}}_{k+1|k}]}^{\text{T}}+R\\ \hfill P_{xz,k+1|k}=\sum _{i=0}^{2n}{\omega }_i^{(m)}[{\chi }_{i,k+1|k}-{\widehat{x}}_{k+1|k}]{[z_{i,k+1|k}-{\widehat{z}}_{k+1|k}]}^{\text{T}}.\end{array}(22)$

From Eq. 9, we can use Eqs. 11–21 to carry out the iterative operation of the unscented Kalman filter. Thus, the rotor speed and position of the permanent magnet synchronous motor are estimated.

Parameter Identification of PMSM Based on the UKF

Considering the short control period of the discrete-time system, it can be considered that the rotor flux linkage ψ_f and the quadrature axis inductance L do not change in each control cycle. The motor parameters are regarded as a state of slow change concering time, so as to form an extended nonlinear system with the current equation according to the voltage equation of Eq. 1 and the flux linkage Eq. 2.

$\left\{\begin{array}{c}\frac{d{i}_{\alpha }}{dt}=-\frac{R_s}{L}{i}_{\alpha }+{\omega }_e\frac{{\psi }_f}{L}\sin \theta +\frac{u_{\alpha }}{L};\hfill \\ \frac{d{i}_{\beta }}{dt}=-\frac{R_s}{L}{i}_{\beta }-{\omega }_e\frac{{\psi }_f}{L}\cos \theta +\frac{u_{\beta }}{L};\hfill \\ \frac{d}{dt}{\psi }_f=0;\hfill \\ \frac{d}{dt}L=0.\hfill \end{array}\right.(23)$

It can be seen from Eq. 24 that the rank of the identification equation is 2 and can only realize the full rank identification of two parameters. Therefore, we regard R_s as a constant and only apply it to synchronous identification of two parameters of rotor flux ψ_f and inductor L.

We define state vector $x={\left[\begin{array}{cccc}\hfill i_{\alpha }\hfill & \hfill i_{\beta }\hfill & \hfill {\psi }_f\hfill & \hfill L\hfill \end{array}\right]}^{\text{T\hspace{0.17em}}}$, input vector $u={\left[\begin{array}{cc}\hfill u_{\alpha }\hfill & \hfill u_{\beta }\hfill \end{array}\right]}^{\text{T\hspace{0.17em}}}$, and output vector $z={\left[\begin{array}{cc}\hfill i_{\alpha }\hfill & \hfill i_{\beta }\hfill \end{array}\right]}^{\text{T\hspace{0.17em}}}$. The system and output measurements are

$\frac{d}{dt}\left[\begin{array}{c}\hfill i_{\alpha }\hfill \\ \hfill i_{\beta }\hfill \\ \hfill {\psi }_f\hfill \\ \hfill L\hfill \end{array}\right]=\left[\begin{array}{c}\hfill -\frac{R_s}{L}{i}_{\alpha }+{\widehat{\omega }}_e\frac{{\psi }_f}{L}\sin \widehat{\theta }\hfill \\ \hfill -\frac{R_s}{L}{i}_{\beta }-{\widehat{\omega }}_e\frac{{\psi }_f}{L}\cos \widehat{\theta }\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill \frac{1}{L}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{L}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill u_{\alpha }\hfill \\ \hfill u_{\beta }\hfill \end{array}\right].(24)$

$z=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]x.(25)$

The results show that the rotor flux observer is a 4-order nonlinear system. After calculating the Jacobian matrix of the nonlinear equation, the linear system is obtained as follows:

$\dot{x}=\left[\begin{array}{cccc}\hfill -\frac{R_s}{L}\hfill & \hfill 0\hfill & \hfill {\widehat{\omega }}_e\frac{1}{L}\sin \widehat{\theta }\hfill & \hfill -{\widehat{\omega }}_e{\psi }_f\frac{1}{L^2}\sin \widehat{\theta }\hfill \\ \hfill 0\hfill & \hfill -\frac{R_s}{L}\hfill & \hfill -\widehat{{\omega }_e}\frac{1}{L}\cos \widehat{\theta }\hfill & \hfill \widehat{{\omega }_e}{\psi }_f\frac{1}{L^2}\cos \widehat{\theta }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]x+\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]u.(26)$

Discretizing Eqs. 25, 26, we can get

$\left\{\begin{array}{c}{x}_{k+1}=F_{k}x+M_{k}u+w_k;\hfill \\ z_k=C_{k}x+v_k.\hfill \end{array}\right.,(27)$

where

$\begin{array}{ccc}\hfill F_k=\left[\begin{array}{cccc}\hfill 1-\frac{R_s}{L}{T}_s\hfill & \hfill 0\hfill & \hfill {\widehat{\omega }}_e\frac{1}{L}\sin \widehat{\theta }{T}_s\hfill & \hfill -{\widehat{\omega }}_e{\psi }_f\frac{1}{L^2}\sin \widehat{\theta }{T}_s\hfill \\ \hfill 0\hfill & \hfill 1-\frac{R_s}{L}{T}_s\hfill & \hfill -\widehat{{\omega }_e}\frac{1}{L}\cos \widehat{\theta }{T}_s\hfill & \hfill \widehat{{\omega }_e}{\psi }_f\frac{1}{L^2}\cos \widehat{\theta }{T}_s\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],& \hfill & \hfill \end{array}$

$M_k=\left[\begin{array}{cc}\hfill \frac{1}{L}{T}_s\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{L}{T}_s\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],C_k=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],(28)$

where T_s represents the time interval from time k to time k + 1.

After the system equation is obtained, the parameter identification algorithm is obtained by step 2 to step 4 for iteration.

The Simulation Case

In order to verify the correctness of speed and motor parameter identification based on UKF algorithm, it is applied to the PMSM vector control system, and the system simulation model based on Figure 1 structure is established in the Matlab/Simulink environment.

FIGURE 1

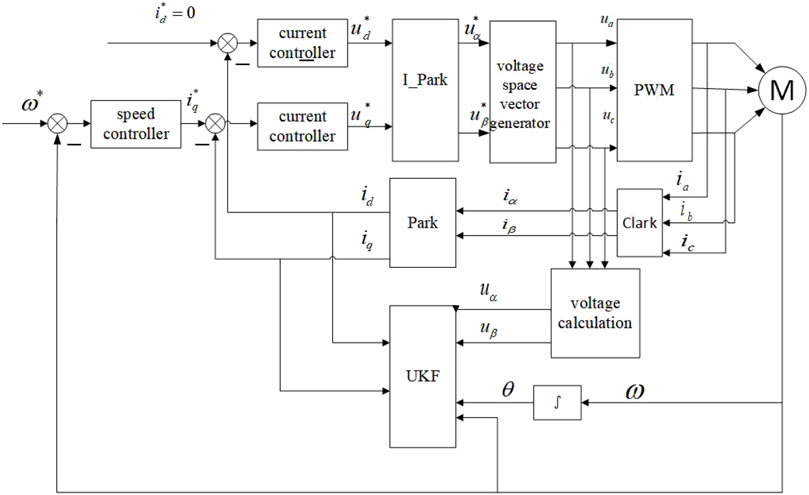
FIGURE 1. Block diagram of the vector control scheme for PMSM without a position sensor with parameter identification.

The control strategy of the motor and the structure block diagram of the control system are shown in Figure 1. Three-phase current i_a, i_b, i_c is transformed into two-phase current i_α, i_β after Clark transformation; after Park transformation, the AC flow is equivalent to two DC components d and q for operation, and through the calculation of i_d and i_q, the given voltage value $u_d^{*}$ and $u_q^{*}$ is obtained. They are converted into a PWM pulse to drive the high-power IGBT through the voltage space vector generation module, which generates the rotating voltage vector and makes the motor run. Clark and Park transformation need position information of motor rotor, and position angle θ is still used here.

The control system adopts the speed and current double closed-loop control strategy. The sampling value of stator current is obtained by a sampling circuit, and then, the current is decomposed into mutually perpendicular current components i_d and i_q by coordinate transformation. The voltage of the motor cannot be measured, so the given value of the voltage is used instead of the actual value. In the sensorless part, UKF algorithm is used to estimate the motor speed. According to the abovementioned analysis, the accuracy of identification is easily affected by the changes of motor parameters, so this article estimates the speed and identifies the motor parameters and uses the identified parameters to update the reference model. Since the parameters to be identified include motor speed ω, position θ, inductance L, and flux ψ_f, this article adopts a step-by-step identification algorithm. First, we fix inductance L and flux ψ_f and use UKF algorithm to identify speed ω and position θ on line. Then, we fix speed ω and position θ and use UKF algorithm to identify inductance L and flux ψ_f on line.

In order to verify the effectiveness of the parameter identification scheme of PMSM under sensorless control, the UKF estimation module uses Matlab/Simulink for simulation. The parameters of the simulation motor are shown in Table 1.

TABLE 1

TABLE 1. Parameters of PMSM.

In general, the random interference in the system and part of the measurement noise are unknown. Therefore, the covariance matrix of system noise and measurement noise will be determined by experience and simulation. Appropriate initial value selection can make the algorithm have high-precision prediction results under the premise of convergence. In this article, the following covariance matrix and initial value are used on the premise of a large number of research and experiments.

$Q=\left[\begin{array}{cccc}\hfill 0.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.01\hfill \end{array}\right],R=\left[\begin{array}{cc}\hfill 0.2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.2\hfill \end{array}\right].$

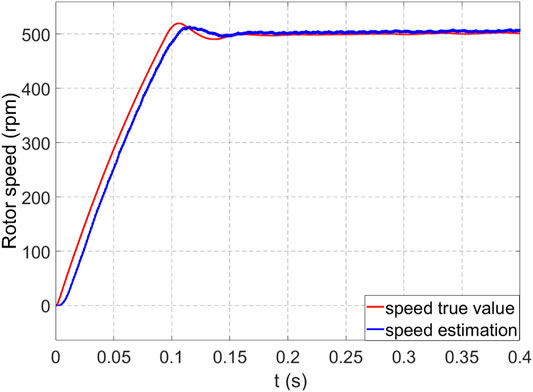
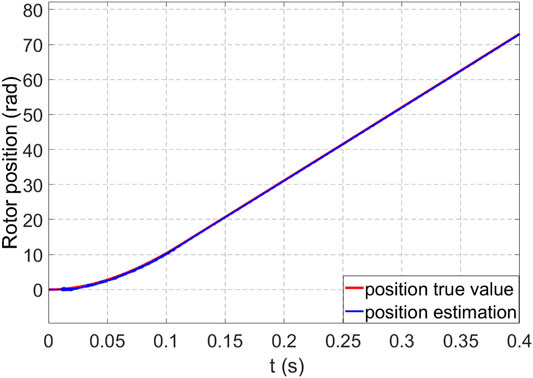
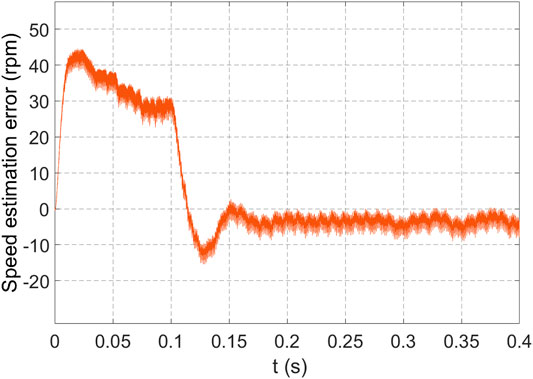
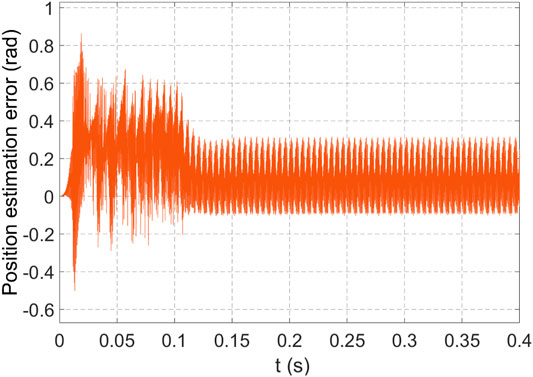
The simulation results are shown in Figures 2–5. First, the control system with a position sensor is simulated, and the motor voltage, current, speed, and position signals are recorded. The UKF is used to estimate the speed and position of the PMSM and compare with the simulated speed and position signals. Figure 2 and Figure 3 are the speed and position diagrams of PMSM estimated by the UKF, respectively, and Figure 4 and Figure 5 are the estimation errors of speed and position, respectively. It can be seen from the simulation results that the estimated value obtained by UKF algorithm can better track the actual value.

FIGURE 2

FIGURE 2. Rotor speed.

FIGURE 3

FIGURE 3. Rotor position.

FIGURE 4

FIGURE 4. Speed estimation error.

FIGURE 5

FIGURE 5. Position estimation error.

Figure 4 and Figure 5 show that there is a deviation between the estimation value and the actual value, but after iterative correction for 0.15 s, the speed regulation is stable.

Motor parameters play an important role in the mathematical model of motor. It has an impact on the state equation of motor and the stability, accuracy, and rapidity of the whole system. In the motor mathematical model and equation discussed above, there are mainly the following parameters: resistance R_s, inductance L, and flux ψ_f. Through the simulation, it is found that the motor resistance has little influence on the speed and position estimation results, while the rotor flux and inductance deviation have great influence on the estimation results.

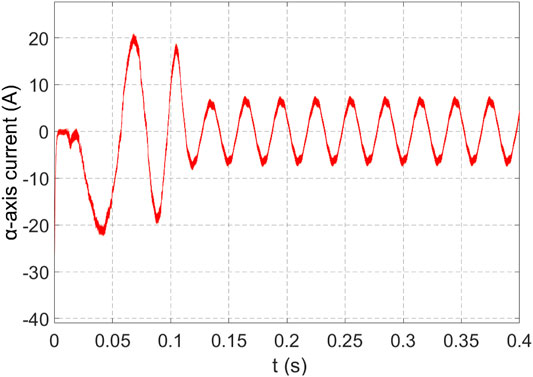
After UKF algorithm, the estimated values of each state variable are obtained, as shown in Figures 6–11. It can be seen from Figures 6, 7 that the UKF can not only accurately identify the stator flux but also accurately identify the stator current.

FIGURE 6

FIGURE 6. Identification value of α-axis current.

FIGURE 7

FIGURE 7. Identification value of β-axis current.

FIGURE 8

FIGURE 8. Flux identification value.

FIGURE 9

FIGURE 9. Inductance identification value.

FIGURE 10

FIGURE 10. Speed estimation with parameter identification.

FIGURE 11

FIGURE 11. Position estimation with parameter identification.

Figures 6, 7 of αβ-axis currents tend to be stable after 0.15 s. This is consistent with the change of speed in Figure 2. The speed is controlled by the current loop. After one and a half cycles, currents reach the rated current value of 5A. After coordinate transformation, the αβ two-phase current has a phase difference of 90 under the shaft system.

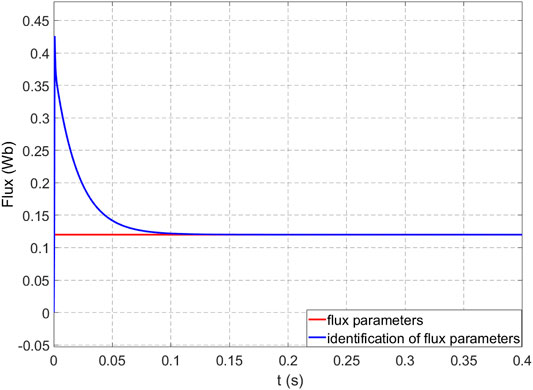
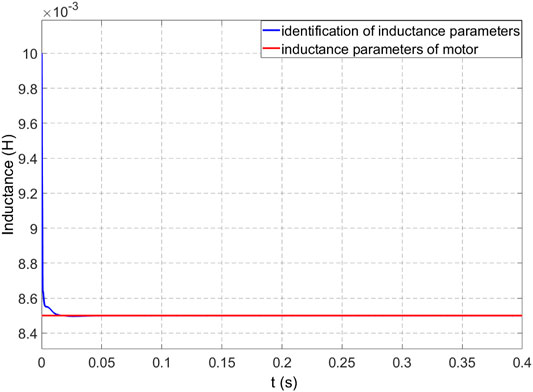
This reflects the effectiveness of the observer. Figure 8 is the result of motor flux identification. The identified flux is 0.12 wb, which has good stability and is close to the actual value of 0.12 wb, and the error is close to zero, which verifies the effectiveness of the identification method. Figure 9 is the result of inductance identification, and the identification value tends to 8.5 mH quickly, which is basically the same as the actual value. Both the inductance L and the flux linkage ψ_f can converge to the true value, and the error is almost zero.

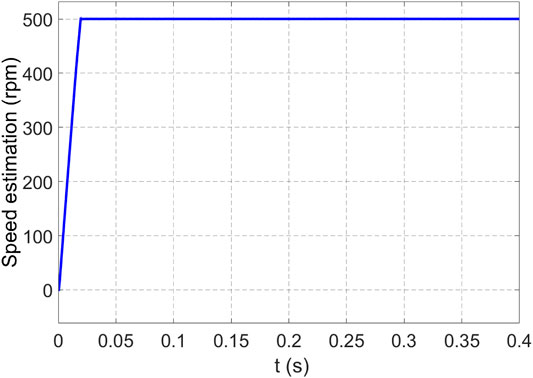
The flux linkage parameters and inductance parameters identified by the UKF are applied to the UKF system in real time to estimate the motor speed and position, and good control effect is obtained, as shown in Figures 10, 11.

The identified parameters are fed back to the system, and the UKF can update the motor parameters in the mathematical model in time, which greatly reduces the estimation error. After the identified parameters are fed back to the sensorless vector control scheme, the control performance and parameter identification results of the whole scheme remain stable in dynamic and steady state.

Conclusion

In this article, UKF-based parameter identification was considered for permanent magnet synchronous motor. The rotor flux and inductance parameters based on the UKF model have been modified in real time, and the estimation effect of the UKF has been compensated effectively. UKF algorithm requires less computation, but the accuracy of identification results is high. It is a very advantageous online motor parameter identification method, which is suitable for state estimation and model identification of nonlinear systems. The performance of a PMSM sensorless control system can be guaranteed even if the motor parameters have some errors. The simulation results have shown that the parameter identification algorithm can effectively identify the rotor flux linkage and inductance in real time and can effectively estimate the speed and position with high estimation accuracy, which can meet the real-time requirements of motor control.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, and further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

ZW, XL, WW, BY, WL, QL, SW, and QC were employed by the Northwest Branch of State Grid Corporation of China. YZ was employed by the Nari Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, L., and Hameyer, K. (2014). Rotor Position and Speed Estimation of Interior Permanent Magnet Synchronous Motor Using Unscented Kalman Filter. In 17th International Conference on Electrical Machines and Systems (ICEMS). Hangzhou, 727–732. doi:10.1109/icems.2014.7013577

CrossRef Full Text | Google Scholar

Cao, R., Cheng, M., and Zhang, B. (2015). Speed Control of Complementary and Modular Linear Flux-Switching Permanent-Magnet Motor. IEEE Trans. Ind. Electron. 62 (7), 4056–4064. doi:10.1109/tie.2015.2390194

CrossRef Full Text | Google Scholar

Chen, L., Sun, X., Jiang, H., and Xu, X. (2014). High Performance Control of a Permanent Magnet Synchronous Motor for Electric Vehicle Applications. Jnl Comp. Theo Nano. 11 (3), 706–710. doi:10.1166/jctn.2014.3415

CrossRef Full Text | Google Scholar

Chen, Z., Zhang, H., Tu, W., Luo, G., Manoharan, D., and Kennel, R. (2019). Sensorless Control for Permanent Magnet Synchronous Motor in Rail Transit Application Using Segmented Synchronous Modulation. IEEE Access. 7, 76669–76679. doi:10.1109/access.2019.2921916

CrossRef Full Text | Google Scholar

Cheng, S., Luo, D., Huang, S., Chen, Z., and Huang, K. (2015). Control Strategy for Permanent Magnet Synchronous Motor with Contra‐rotating Rotors under Unbalanced Loads Condition. IET Electric Power Appl. 9 (1), 71–79. doi:10.1049/iet-epa.2014.0130

CrossRef Full Text | Google Scholar

Cui, F., Sun, Z., Xu, W., Zhou, W., and Liu, Y. (2020). Comparative Analysis of Bilateral Permanent Magnet Linear Synchronous Motors with Different Structures. Trans. Electr. Mach. Syst. 4 (2), 142–150. doi:10.30941/cestems.2020.00019

CrossRef Full Text | Google Scholar

Deng, T., Su, Z., Li, J., Tang, P., Chen, X., and Liu, P. (2019). Advanced Angle Field Weakening Control Strategy of Permanent Magnet Synchronous Motor. IEEE Trans. Veh. Technol. 68 (4), 3424–3435. doi:10.1109/tvt.2019.2901275

CrossRef Full Text | Google Scholar

Fadil, H., Driss, Y., and Aite, Y. (2015). Sliding-mode Speed Control of PMSM With Fuzzy-Logic Chattering Minimization-Design and Implementation. Information. 6 (3), 432–442. doi:10.3390/info6030432

CrossRef Full Text | Google Scholar

He, B., Deng, Y., He, D., Tian, H., and Liu, Y. (2019). Vector Control Strategy of Permanent Magnet Synchronous Motor with Motor Driven Actuator. Micromotors. 52 (3), 62–68.

Google Scholar

He, C., and Wu, T. (2019). Analysis and Design of Surface Permanent Magnet Synchronous Motor and Generator. Trans. Electr. Mach. Syst. 3 (1), 94–100. doi:10.30941/cestems.2019.00013

CrossRef Full Text | Google Scholar

Kyoon, K. (2017). Robust Adaptive Speed Regulator With Self-Tuning Law for Surfaced-Mounted Permanent Magnet Synchronous Motor. Control. Eng. Pract. 11, 55–71. doi:10.1016/j.conengprac.2017.01.014

CrossRef Full Text | Google Scholar

Liang, D., Li, J., and Qu, R. (2017). Sensorless Control of Permanent Magnet Synchronous Machine Based on Second-Order Sliding-Mode Observer with Online Resistance Estimation. IEEE Trans. Ind. Applicat. 53 (4), 3672–3682. doi:10.1109/tia.2017.2690218

CrossRef Full Text | Google Scholar

Liu, X., Yu, X., Ma, G., and Xi, H. (2016). On Sliding Mode Control for Networked Control Systems with Semi-Markovian Switching and Random Sensor Delays. Inf. Sci. 337-338, 44–58. doi:10.1016/j.ins.2015.12.023

CrossRef Full Text | Google Scholar

Lu, W., Tang, B., Ji, K., Lu, K., Wang, D., and Yu, Z. (2021). A New Load Adaptive Identification Method Based on an Improved Sliding Mode Observer for PMSM Position Servo System. IEEE Trans. Power Electron. 36 (3), 3211–3223. doi:10.1109/tpel.2020.3016713

CrossRef Full Text | Google Scholar

Luo, S., Chen, X., Song, Y., Guo, C., and Shu, H. (2019). Design of Model Predictive Controllers for PMSM Drive System Based on the Extended Kalman Filter Observer. Ijehv. 11 (4), 378–394. doi:10.1504/ijehv.2019.10024319

CrossRef Full Text | Google Scholar

Moon, C., and Kwon, Y. A. (2016). Sensorless Speed Control of Permanent Magnet Synchronous Motor by Unscented Kalman Filter Using Various Scaling Parameters. J. Electr. Eng. Technology. 11 (2), 347–352. doi:10.5370/jeet.2016.11.2.347

CrossRef Full Text | Google Scholar

Nahid-Mobarakeh, B., Meibody-Tabar, F., and Sargos, F.-M. (2004). Mechanical Sensorless Control of PMSM with Online Estimation of Stator Resistance. IEEE Trans. Ind. Applicat. 40 (2), 457–471. doi:10.1109/tia.2004.824490

CrossRef Full Text | Google Scholar

Pan, S., and Gao, J. (2018). Summarization of Sensorless Control Technology for Permanent Magnet Synchronous Motor. Micromotors. 51 (3), 62–69.

Google Scholar

Tao, C., and Guo, Z. (2019). The Identification for Rotor Flux Linkage of Permanent Magnet Synchronous Motor Base on Dual Unscented Kalman Filter Algorithm. Sci. Technology Eng. 19 (6), 122–128.

Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems With Constant Power Loads. IEEE Trans. Power Electron. 36 (7), 7866–7879. doi:10.1109/tpel.2021.3049241

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Ma, D., and Liu, Z. (2019). The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energ. 10 (3), 1459–1469. doi:10.1109/tste.2019.2894633

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Ma, D., and Hu, X. (2020a). Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid. 11 (4), 2856–2866. doi:10.1109/TSG.2020.2970174

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Zhang, P., Gui, Y., Qin, D., and Wang, P. (2020b). Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energ. Convers. 35 (3), 1585–1595. doi:10.1109/TEC.2020.2980033

CrossRef Full Text | Google Scholar

Yang, S., Wang, J., Zhang, G., Yang, X., and Wang, S. (2016). A Review on Induction Motor Control Based on the Kalman Filter. Control Eng. China. 23 (1), 30–37.

Google Scholar

Yin, Z., Tang, R., Du, C., and Wang, Y. (2019). Moment of Inertia Identification Based on Unscented Kalman Filter for Permanent Magnet Synchronous Motors. In 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), 1141–1145. doi:10.1109/iciea.2019.8834168

CrossRef Full Text | Google Scholar

Zhong, C., and Lin, Y. (2017). Model Reference Adaptive Control (MRAC)-based Parameter Identification Applied to Surface-Mounted Permanent Magnet Synchronous Motor. Int. J. Electronics. 104 (11), 1854–1873. doi:10.1080/00207217.2017.1329946

CrossRef Full Text | Google Scholar

Zhong, Z., Jin, M., and Shen, J. (2018). Full Speed Range Sensorless Control of Permanent Magnet Synchronous Motor with Phased PI Regulator-Based Model Reference Adaptive System. Proc. CSEE 38 (4), 1203–1211. doi:10.13334/j.0258-8013.pcsee.162121

CrossRef Full Text | Google Scholar

Zhou, H., Liu, Z., and Yang, X. (2018). Motor Torque Fault Diagnosis for Four Wheel Independent Motor-Drive Vehicle Based on Unscented Kalman Filter. IEEE Trans. Veh. Technol. 67 (3), 1969–1976. doi:10.1109/tvt.2017.2751750

CrossRef Full Text | Google Scholar

Zhu, Q., Zhang, Z., Yang, H., and Zhu, Y. (2014). Research on Sensorless PMSM Current Control Strategies. Control. Eng. China 21 (4), 547–553.

Google Scholar