Modeling Study on Oil Particle Filtration Performance of a Composite Coalescing Filter

The traditional theoretical model is not suitable for the simulation of the oil particle filtration process of a composite filter due to its huge difference in fiber diameter. In this paper, the concept of fiber dispersion σ was introduced into a mathematical model for describing the dynamic filtration process of a composite filter. The results show that the model is in good agreement with the experimental data. As the packing density is constant, the higher the fiber dispersion, the better performance is. In addition, the effect of different factors on the efficiency of different mechanisms was discussed. For fine particles (<0.1 μm), diffusion is the dominant mechanism. For coarse particles (>1 μm), the inertia impaction mechanism dominates the filtration efficiency. The fiber diameter has a significant effect on the inertia impaction mechanism. The single-fiber efficiency by inertia impaction mechanism is obviously affected by filtration velocity. The packing density has an effect on all mechanisms except for the diffusion mechanism. Moreover, such a model would contribute to an accurate prediction of the dynamic filtration performance of composite filters with polydisperse fiber diameter and improve performance by adjusting parameters reasonably.

Introduction

Oil particles are a common particulate pollutant, mainly arising from human activities such as cooking, smoking (Sun et al., 2011; Huang et al., 2010), and industrial processes such as natural gas transportation, mechanical atomization, metal cutting, condensation, and evaporation (Gonfa et al., 2015). These oil particles released into the air harm human health and cause environmental pollution. In addition, oil particles cause corrosion, damage, and other harm to the system and equipment used in the industrial process. Fiber filtration is widely used in many fields such as air purification (Luengas et al., 2015), dust removal (Bullock and Driver, 1967), and oil mist purification (Brahm, 2012) due to low cost and high efficiency. Different from solid particles, oil particles are liquid. Due to the fluidity of liquids, particles will undergo wetting, coalescence, evolution, and draining in a filter (Chen et al., 2017).

As early as 1999, Walsh et al. (1996) divided the filtration process into multiple stages according to the change of pressure drop. Subsequently, Contal et al. (2004) and Frising et al. (2005) studied the filtration phenomenon of liquid particles on a high-efficiency particulate air (HEPA) filter, and they divided the liquid filtration process into four stages. In the first stage, oil droplets were intercepted, wetting and spreading on the fibers. In the second stage, with the accumulation of droplets, a liquid bridge was formed. In the third stage, the liquid bridge evolved into a liquid film. The filter reaches steady drainage in the fourth stage. Previous reports mainly focus on experimental study, with a few theoretical studies on liquid particle filtration.

Pressure drop and filtration efficiency are important parameters of filtration. For pressure drop, Hinds (2012) proposed the expression to obtain the pressure drop of clean filters in classical filtration theory. Davies (1973) also developed a semi-empirical formula to calculate the pressure drop according to Darcy’s law. Those expressions were widely used to predict the pressure drop of a filter. For filtration efficiency, there are five main mechanisms for capturing particles: diffusion, interception, inertia impaction, electrostatic, and gravity (Li et al., 2014a). Based on the Kuwabara-Happel model (Happel, 1959; Kuwabara, 1959), Some researchers (Wang et al., 2007; Hubbard et al., 2012; Chen et al., 2017; Choi et al., 2017) developed most theoretical models of filtration under different mechanisms to determine the filtration of solid particles. However, these models also apply to describe the filtration of liquid particles. In addition, the saturation of the filter is also an important parameter for liquid particle filtration. The saturation directly affects the airflow channel of the filter and is related to the pressure drop and efficiency. Liew and Conder (1985) proposed an expression of saturation based on the capillary number. Meanwhile, Liew suggested the empirical expression of wet pressure drop at saturation state. However, the formulas mentioned above are suitable for describing the static parameter of filtration.

There are only a few reports on model studies of dynamic filtration of liquid particles. Some researchers (Frising et al., 2005; Tekasakul et al., 2008; Charvet et al., 2010) divided the filter into layers for describing the dynamic filtration process. Those models adopted the “wet diameter” and “wet packing density” proposed by Davies to describe the characteristics of filtration. With the development of filtration materials, many composite filters consisting of micrometer and nanometer fibers have been fabricated (Xu et al., 2018; Li et al., 2014b; Zhao et al., 2015) for particles filtration. But, the models are not suitable to describe the dynamic filtration of composite filters due to the great differences in fiber diameter.

In this paper, the fiber diameter dispersion σ was introduced to depict the inhomogeneity of fiber diameter in a composite filter. We set up a model based on the idea of “wet diameter” and “wet packing density” for a composite filter. The accuracy of the model was verified by the experiment data in our published paper. The change of drainage rate was predicted and the effect of dispersion σ on filtration performance was analyzed. In addition, the effect of different factors on total efficiency and single-fiber efficiency of the filter under different mechanisms were discussed on the basis of the model.

Physical Model

When particles are captured onto the fiber, a barrel or clam-shell morphology is formed. Oil particles accumulate continuously with loading. Due to Plateau-Rayleigh instability, the liquid forms a string of barrel droplets on the fiber (Roe, 1975). However, the barrel shape is hardly described by mathematical methods. For convenience of calculation, we assumed that a virtual “liquid tube” is formed on the fiber, as shown in Figure 1. With the accumulation of liquid particles on fiber, the diameter of the “liquid tube” gradually increases.

FIGURE 1

FIGURE 1. Schematic diagram of “liquid tube.”

Simulation and Experimental Method

Mathematical Model

Governing Equation

During the filtration process, the mass change of the droplets on the filter is described as:

$\frac{\mathrm{d}{\mathrm{m}}_{\mathrm{i}}}{\mathrm{d}\mathrm{t}}\mathrm{=}{\displaystyle \mathrm{\sum }_{\mathrm{j}}{\mathrm{F}}_{\mathrm{j},\mathrm{i}}-{\mathrm{D}}_{\mathrm{i}}}(1)$

where, $\frac{d{m}_i}{dt}$ is the change rate of mass of droplets loaded on the filter at time i; $F_{j,i}$ is the collection rate of particle size j at time i; $D_i$ is the drainage rate of the filter at time i.

In the dynamic filtration process, the droplet mass on filters varied with loading, which caused the change of wet diameter of the fiber and wet packing density.

Wet Diameter and Wet Packing Density

Wet diameter $d_{fwet}$ and wet packing density ${\mathrm{\alpha }}_{wet}$ are calculated by the following equations (Frising et al., 2005):

$d_{fwet,i}={\mathrm{d}}_{\mathrm{f},0}\sqrt{1+\frac{{\mathrm{m}}_{\mathrm{i}}}{{\mathrm{\rho }}_{\mathrm{l}}\mathrm{\Omega }\mathrm{z}\mathrm{\alpha }}}(2)$

${\mathrm{\alpha }}_{wet,i}={\mathrm{\alpha }}_{\mathrm{0}}+\frac{{\mathrm{m}}_{\mathrm{i}}}{{\mathrm{\rho }}_{\mathrm{l}}\mathrm{\Omega }\mathrm{z}}(3)$

Where, $d_{fwet,i}$ and ${\mathrm{\alpha }}_{wet,i}$ are the wet diameter and wet packing density of composite filter at time i respectively. $d_{f,0}$ and ${\mathrm{\alpha }}_0$ are the diameter and packing density of the clean filter. $m_i$ is the droplets mass on the filter at time i. ${\rho }_l$ is the density of the liquid. $\mathrm{\Omega }$ is the area of the composite filter. $z$ is the thickness of the composite filter.

Fiber Diameter Modification by Dispersion $\mathrm{\sigma }$

It was mentioned above that the fibers in the composite filter have different sizes. Thus, the valid value of fiber diameter affects the calculation. We suggested the expression of a valid diameter of fiber by introducing the dispersion σ, which is described as:

${\mathrm{d}}_{\mathrm{f}}={\mathrm{d}}_{\mathrm{f},\mathrm{D}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{e}\mathrm{s}}\sqrt{1+\mathrm{\sigma }}(4)$

where, $d_{f,Davies}$ is the fiber diameter calculated by the Davies pressure drop equations (Davies, 1973).

Filtration Efficiency

In our case, the filtration mechanisms include diffusion, inertia impaction, interception, and the interaction between diffusion and interception. The electrostatic mechanism is ignored since the oil droplet is a poor conductor.

First, the efficiency due to diffusion mechanism at time i (Happel, 1959):

${\mathrm{\eta }}_{D,i}=2\mathrm{P}{\mathrm{e}}_i^{-2/3}(5)$

where $P{e}_{\text{i}}$, is Pelect number at time i, defined as;

$P{e}_i=\frac{{\mathrm{d}}_{\mathrm{f}\mathrm{w}\mathrm{e}\mathrm{t},\mathrm{i}}\mathrm{U}}{\mathrm{D}}(6)$

Second, the efficiency by inertia impaction mechanism at time i is suggested as follows (Stechkina and Kirsch, 1969):

${\mathrm{\eta }}_{I,i}=\frac{\mathrm{S}{\mathrm{t}}_{\mathrm{i}}}{4\mathrm{K}{\mathrm{u}}_{\mathrm{i}}^2}\left(29.6-28{\mathrm{\alpha }}_{wet,i}^{0.62}\right){\mathrm{N}}_{R,i}^2-27.5{\mathrm{N}}_{R,i}^{2.8}(7)$

where $N_{R,i}$ is the ratio of particle diameter to fiber diameter, $d_p/d_{fwet,i}$; $K{u}_i$ is Kuwabara constant; $S{t}_i$ is Stokes number.

Third, the capture efficiency by interception mechanism at time i (Lee and Liu, 1982):

${\mathrm{\eta }}_{R,i}=\frac{\left(1-{\mathrm{\alpha }}_{wet,i}\right){\mathrm{N}}_{R,i}^2}{\mathrm{K}{\mathrm{u}}_i\left(1+{\mathrm{N}}_{R,i}\right)}(8)$

Finally, the efficiency by the interaction mechanism of diffusion mechanism and interception at time i (Hinds, 2012):

${\mathrm{\eta }}_{DR,i}=\frac{1.24N_{R,i}^{2/3}}{{\left(K{u}_{i}P{e}_i\right)}^{1/2}}(9)$

The single-fiber efficiency at time i ${\mathrm{\eta }}_{F,i}$ is determined from:

${\mathrm{\eta }}_{\mathrm{F},\mathrm{i}}={\mathrm{\eta }}_{\mathrm{D},\mathrm{i}}+{\mathrm{\eta }}_{\mathrm{I},\mathrm{i}}+{\mathrm{\eta }}_{\mathrm{R},\mathrm{i}}+{\mathrm{\eta }}_{\mathrm{D}\mathrm{R},\mathrm{i}}(10)$

The total efficiency of the composite filter is obtained:

${\mathrm{\eta }}_{T,i}=1-\exp \left[\frac{-4{\mathrm{\alpha }}_{\mathrm{w}et,i}{\mathrm{\eta }}_{F,i}z}{\mathrm{\pi }{d}_{\mathrm{f}\mathrm{w}\mathrm{e}\mathrm{t},\mathrm{i}}}\right](11)$

Pressure Drop

According to classical filtration theory (Hinds, 2012), the pressure drop is calculated as follows:

$\mathrm{\Delta }{P}_i=\frac{{\mathrm{F}}_{\mathrm{i}}\mathrm{\mu }\mathrm{U}{\mathrm{l}}_{\mathrm{i}}}{1-{\alpha }_{\mathrm{w}\mathrm{e}\mathrm{t},i}}(12)$

where $F$ is dimensionless drag factor; $\mathrm{\mu }$ is gas viscosity; $U$ is the face velocity; $l$ is the fiber length of per unit area;

$\mathrm{l}=\frac{4{\alpha }_{\mathrm{\text{we}}\mathrm{t},i}z}{\pi d_{fwet,i}^2}(13)$

Drainage Rate

There is no drainage in the initial stage of coalescence filtration. The saturation of the filter gradually increases with loading. The drainage phenomenon was observed when the saturation reached the minimum saturation $S_0$. The minimum saturation $S_0$ was defined as follows (Raynor and Leith, 2000):

$S_0=0.96\frac{{\alpha }^{0.39}}{\mathrm{B}{\mathrm{o}}^{\left[0.47+0.24\ln \left(Bo\right)\right]}\mathrm{C}{\mathrm{a}}^{0.11}}(14)$

where $Bo$ is the Bond number and $Ca$ is the capillary number:

$\mathrm{B}\mathrm{o}=\left(\frac{{\rho }_{l}g{d}_f^2}{{\gamma }_l}\right)\mathrm{\times }{10}^5(15)$

$\mathrm{C}\mathrm{a}=\left(\frac{\mathrm{\mu }U}{{\gamma }_l}\right)\times {10}^5(16)$

where ${\gamma }_l$ is the surface tension of liquid; $g$ is gravitational constant.

In the dynamic filtration process, the real-time saturation $S_i$ of the filter is calculated as follows:

$S_i=\frac{{\mathrm{m}}_{\mathrm{i}}}{{\mathrm{\rho }}_{\mathrm{l}}{\mathrm{V}}_{\mathrm{v}\mathrm{o}\mathrm{i}\mathrm{d}}}(17)$

where, $S_i$ is the saturation of filter at time i; $V_{void}$ is the void space in filter, $m_i$ is the mass of liquid on the filter at time i. When the filter reach to equilibrium stage, $S_i=S_e$, $S_e$ is the saturation when the filter is in saturation state.

The dimensionless drainage rate $D_r$ is defined as (Raynor and Leith, 2000):

${\mathrm{D}}_r=\{\begin{array}{cc}\text{0}& \left(S_i\le S_0\right)\\ \mathrm{A}\ast \ln \left(\frac{S_i}{S_0}\right)& \left(S_i\mathrm{>}{S}_0\right)\end{array}(18)$

The drainage rate $D$ is calculated as:

$\mathrm{D}=\frac{{\gamma }_{l}z\mathrm{W}{\mathrm{D}}_r}{{\mathrm{\mu }}_l}(19)$

where $A$ is the dimensionless drainage coefficient; ${\mathrm{\mu }}_l$ is the dynamic viscosity of liquid; $W$ is the width of filter in the direction perpendicular to airflow and to gravity.

In summary, the pressure drop and filtration efficiency of a composite filter at time i can be calculated by Equations 11, 12.

Experimental

The filtration experiments used for composite filters were conducted on the special apparatus shown in Figure 2. Oleic acid was applied in the filtration experiments, which generated oil aerosol mists by a simple atomizer manufactured in-house. The oil mist from the aerosol generator was mixed with the dried compressed air in the mixing chamber. The concentration of oil mist at the filter upstream and downstream was measured by an Electrical Low-Pressure Impactor (ELPI, DEKATI). The pressure drop of the composite filter was measured continuously by a differential pressure transmitter and recorder (Asmik, MIK-9600D). A High-Efficiency Particulate Air (HEPA) filter was employed to purify the waste gas before entering the flowmeter and pump. A vacuum pump was used to pump the gas and allowed to change speed for different filtration velocities.

FIGURE 2

FIGURE 2. Experimental apparatus.

The composite filter was placed into a filter holder. The composite filter was fabricated through the chemical vapor deposition (CVD) method to grow carbon nanotube (CNT) fibers on the porous nickel foam filter. The characterizations of the composite filter have been reported in our previously published work (Xu et al., 2018). Briefly, the CNT content of the composite filter is 15.51%. The packing density of the filter is 0.045. The thickness of the filter is 4 mm. The pore size of the filter is in the range of 0.314–1.02 μm. The Davies fiber diameter of the composite filter is 4.63 μm. Obviously, the value of Davies diameter is inconsistent with the actual fiber diameter. It is because the composite filter mainly consists of carbon nanotube fibers. The diameter of a single carbon nanotube is about 60 nm. However, many carbon nanotube bundles were formed in the preparation process due to coalescence, which results in the inhomogeneity of fiber diameter. Thus, it is necessary to introduce the dispersion σ for computing the performance parameters of the composite filter.

Results and Discussions

Model Validation

The accuracy of the model was verified by the data obtained from the experimental apparatus in our published work (Xu et al., 2018). Figure 3 shows the comparison of the model and experimental data. It can be seen that the error is less than 7.5%, and the pressure drop profile of the model is near to that of data from Figure 3A. In addition, the hypothesis of the liquid tube represents that the model does not take into account the formation of liquid films, which is a common phenomenon occurring in coalescence filtration. The experimental results from the literature indicated that the composite filter could restrain the formation of a liquid film. The model proves this conclusion. Figure 3B shows the efficiency curve of the composite filter. It demonstrates that the model curve shows exponential increase until it reaches the saturation state. Nevertheless, the experimental curve decreases at the beginning of filtration then increases exponentially. This can be attributed to the partial wetting of droplets on fibers at the beginning of filtration. The application condition of the hypothesis of liquid tube involves perfect wetted fiber. In addition, the total wetting area of the droplet on fiber overtakes the surface area of the filter within a few minutes according to the literature (Xu et al., 2020). Therefore, the curve of experimental data presents hysteresis compared with the model.

FIGURE 3

FIGURE 3. Verification results of dynamic filtration model: (A) Dynamic pressure drop; Efficiency.

As shown in Figure 3, incomplete wetting has a little effect on the change of pressure drop, but an obvious effect on the filtration efficiency. The reason is that the pressure drop and efficiency in the model are only related to fiber diameter and packing density without considering the fiber surface area. In practice, the fiber surface area is an important factor affecting efficiency. The surface area undergoes great change until perfectly wetting.

The comparison indicated that the model is in good agreement with the experimental data. The model is suitable for describing and predicting the dynamic filtration of the composite filter.

Drainage Rate

Drainage is an important phenomenon for liquid particle filtration. The start time and the amount of drainage affect the performance of the filter. Figure 4 shows the change of drainage rate over filtration time. It can be seen that the drainage rate is zero within the first 80 min. When reaching the minimum saturation S₀, the filter starts to drain out the liquid. The drainage rate increases exponentially and finally reaches constant. In addition, the curves of pressure drop and efficiency have no fluctuation after drainage.

FIGURE 4

FIGURE 4. Change of drainage rate in dynamic filtration.

Influence of Fiber Dispersion

The dispersion $\sigma$ reflects the dispersion degree of fibers in the filter. The higher the dispersion, the more obvious fiber diameter discretization is. When the dispersion σ is zero, all fibers in the filter have the same diameter. Fiber diameter is closely related to the flow field around fiber and the specific surface area of the filter.

Figure 5 shows the effect of fiber dispersion on pressure drop, filtration efficiency, and drainage rate. When the dispersion increases, the value of the pressure drop of the filter decreases gradually at saturation. The specific surface area of the filter decreases with the increase of fiber dispersion, which results in the decrease of the amount of liquid loaded on the filter at saturation state. Therefore, the saturation decreases at a steady state. The pressure drop of the filter decreases. In addition, the decrease in the specific surface area of the filter causes the decrease of the beginning time of drainage, shown in Figure 5C. Figure 5B shows the change of filtration efficiency under different dispersions. With the increase of fiber dispersion, the efficiency shows great improvement. When the dispersion increases from 0.5 to 20, the efficiency of the clean filter increases from 66% to 100%. In addition, when the dispersion is less than 2, the efficiency of the filter at the saturation stage decreases with the decrease of the dispersion.

FIGURE 5

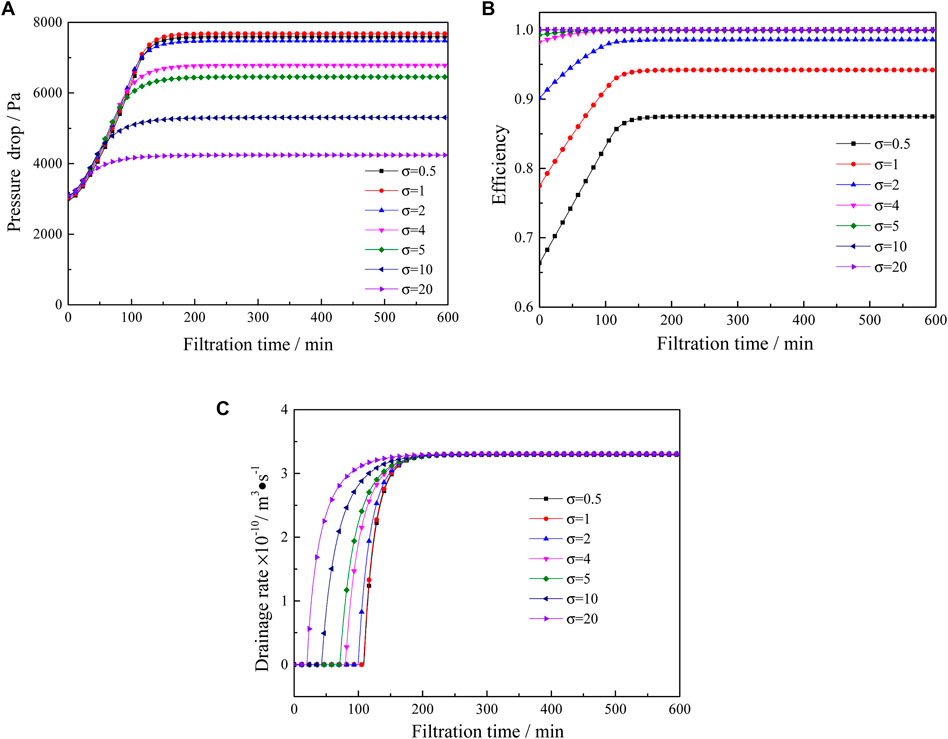
FIGURE 5. Diagram of variation of fiber dispersion on filter performance of filter: (A) Dynamic pressure drop; (B) Filtration efficiency; (C) Drainage rate.

Therefore, it is reasonable to conclude that the composite filter with high fiber dispersion has better performance for liquid particles as the packing density is constant.

Mechanisms Discussion of Different Factors

In the classical filtration theory, the fiber materials possess the most penetrating particle size (MPPS). The most penetrating particle size is caused by the different mechanisms for capturing particles of different sizes. The dominance of these mechanisms on serial sizes particles is the essence affecting the filtration performance. Next, the effect of different factors on the total efficiency and single-fiber efficiency of the filter under different mechanisms are discussed.

Fiber Diameter

Figure 6A shows the total efficiency of the filter under four mechanisms. The result demonstrates that the total efficiency of diffusion mechanism and interaction mechanism between diffusion and interception decreases exponentially with the increase of fiber diameter when the fiber diameter is greater than 0.4 μm. The inertia impaction and interception mechanisms begin to decrease when the fiber diameter reaches 1.5 μm. The total efficiency of all mechanisms decreases exponentially when the fiber diameter reaches 3 μm. The fiber diameter is an important parameter used to characterize the flow regime around the fibers. For diameter <528 nm, the gas around fiber is in the transition or free molecular flow regime. In transition or free molecular flow regime, the disturbances by fiber to the airflow field are reduced or even ignored. Thus, the streamlines have only a little deviation from a straight line near fiber. The decrease of deviation enhances the contact probability between particles and fibers. This is beneficial to filtration efficiency.

FIGURE 6

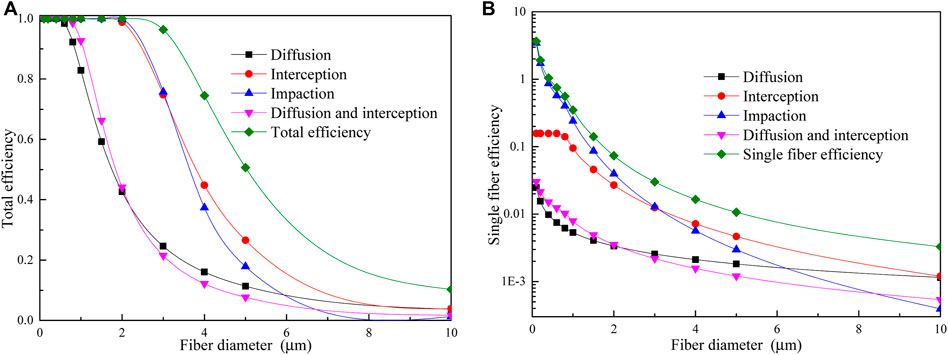
FIGURE 6. Effect of fiber diameter on filtration efficiency: (A) Total filter efficiency; (B) Single-fiber efficiency.

The single-fiber efficiency decreases with the increase of fiber diameter, rather than as the total efficiency begins to decrease until a certain diameter, as shown in Figure 6B. It can be seen that the inertia impaction differs by one order of magnitude from the interception mechanism at smaller fiber diameter. The action of the diffusion mechanism is close to the interaction mechanism between diffusion and interception. With the increase of fiber diameter, all curves in Figure 6B show a reduction tendency. In addition, the fiber diameter has little effect on the diffusion mechanism. The inertia impaction mechanism is significantly affected by the fiber diameter, showing a decline of five orders of magnitude. The results show that the flow regime around fiber has an obvious effect on each mechanism.

Particle Diameter

Figure 7 shows the effect of particle size change on the total efficiency and single-fiber efficiency of the filter. Firstly, the total efficiency under all mechanisms has no obvious change with particle size, as shown in Figure 7A. The interception mechanism and inertia impaction mechanism increase sharply with the increase of particle size, then to stable. The diffusion mechanism decreases sharply when the particle size reaches 0.15 μm. The interaction mechanism of diffusion and interception decreases greatly after the particle size reaches 0.4 μm. The results indicate that particle size has a significant effect on different mechanisms.

FIGURE 7

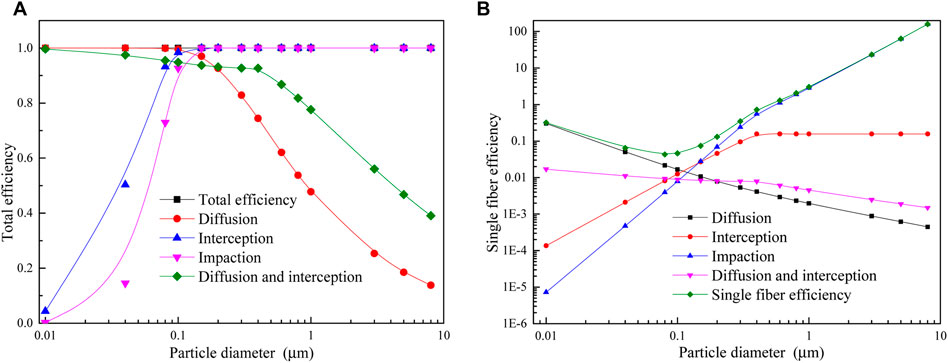
FIGURE 7. Effect of particle diameter on filtration efficiency: (A) Total filter efficiency; (B) Single-fiber efficiency.

Figure 7B shows the effect of particle size on single-fiber efficiency. When the particle size is 0.01 μm, the main action mechanism is the diffusion mechanism. The action from the inertia impaction mechanism is the least for fine particles. The difference between the diffusion and inertia impaction mechanisms is on five orders of magnitude. With the increase of particle size, the efficiency of the diffusion mechanism decreases gradually, and the interception and inertia impaction mechanism increases sharply. The diffusion mechanism has a dominant action for filtering particles less than 0.1 μm. Four mechanisms are in the same order of magnitude at 0.1 μm. With the further increase of particle size, the interception and inertia impaction mechanism gradually dominate. When the particle size is greater than 1 μm, the inertia impaction mechanism dominates the single-fiber efficiency. The interception mechanism has no change as the particle size is larger than 1 μm. In addition, the single-fiber efficiency firstly decreases and then increases with the increase of particle size.

Filtration Velocity

The effect of filtration velocity on filtration efficiency is shown in Figure 8. The filtration velocity has an obvious effect on the total of the diffusion mechanism and the interaction mechanism between diffusion and interception, presented in Figure 8A. After the filtration velocity reaches 0.2 m/s, the diffusion mechanism and the interaction mechanism between diffusion and interception decrease obviously. In addition, filtration velocity has no effect on the total efficiency. This is because the diffusion mechanism contributes greater than 80% to capture efficiency for droplets less than 0.1 μm (Yang, 2012). The mass proportion of fine particles to the total mass of particles is small. Thus, the decrease of efficiency by diffusion mechanism has no obvious effect on total efficiency.

FIGURE 8

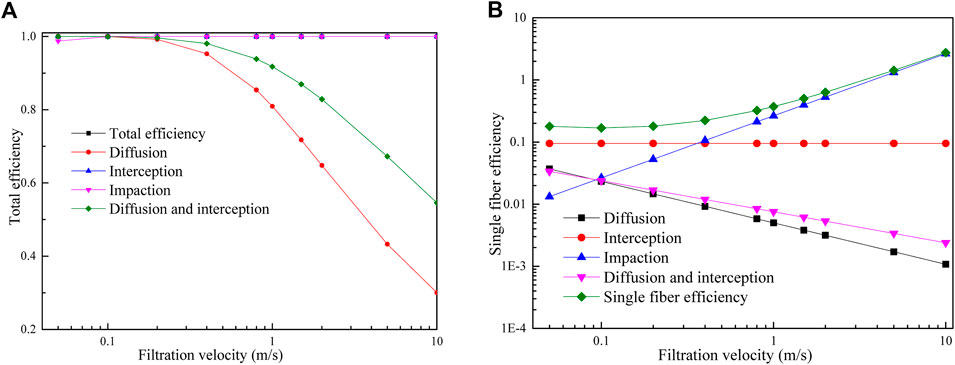
FIGURE 8. Effect of filtration velocity on filtration efficiency: (A) Total filter efficiency; (B) Single-fiber efficiency.

With the increase of filtration velocity, the single-fiber efficiency of the interception mechanism shows no change. However, the single-fiber efficiency under the inertia impaction mechanism increases by two orders of magnitude. The single-fiber efficiency under the diffusion mechanism and the interaction mechanism between diffusion and interception decrease by one order of magnitude. This can be attributed to the increase of the Stokes number as filtration time increases. Stokes number is the governing parameter for inertial impaction.

Packing Density

Figure 9 shows the effect of packing density on filtration efficiency. As the packing density increases, the total efficiency under the diffusion mechanism and the interaction mechanism between diffusion and interception increase sharply, as shown in Figure 9A. The interception mechanism and inertia impaction mechanism increase slightly when the packing density increases from 0.01 to 0.02, and then to stable. The packing density has no effect on the total efficiency of the filter.

FIGURE 9

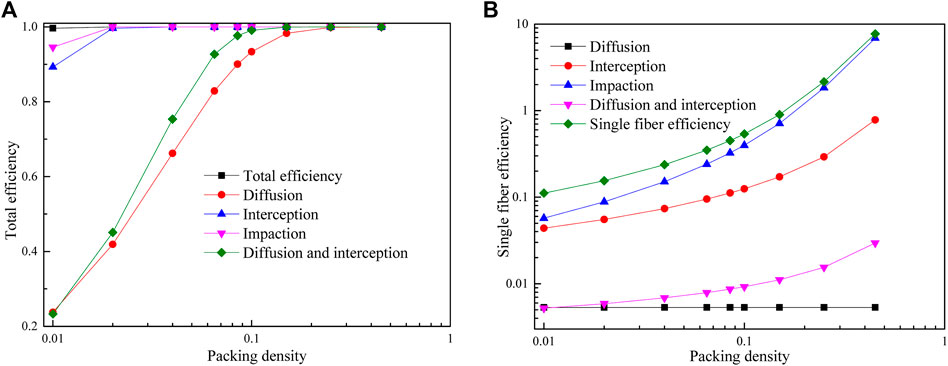
FIGURE 9. Effect of packing density on filtration efficiency: (A) Total filter efficiency; (B) Single-fiber efficiency.

The effect of packing density on single-fiber efficiency is presented in Figure 9B. Apart from the diffusion mechanism, other mechanisms show an increasing tendency with the increase of packing density. The increase of inertia impaction mechanism is largest, reach to two orders of magnitude.

Conclusion

In this paper, due to the inhomogeneity of fiber diameter in the composite filter, we introduced the fiber dispersion σ into the dynamic filtration model to describe the filtration process of a composite filter. Firstly, the accuracy of the model was verified. Compared with the experiment data, the model can predict the pressure drop and filtration efficiency. The change of drainage rate in filtration process was determined through the model. After reaching minimum saturation S₀, the filter begins to drain out, the drainage rate increase exponentially and finally becomes constant. The results show that the model can predict accurately the dynamic filtration process of a composite filter. Secondly, the influence of fiber dispersion on filtration performance was analyzed. When the dispersion increases, the pressure drop at saturation of decreases gradually and the initial filtration efficiency increases. The increase of dispersion causes the decrease of the beginning time of drainage. Thirdly, the effect of different factors on total efficiency and single-fiber efficiency of the filter under different mechanisms were discussed. The fiber diameter has a significant effect on the inertia impaction mechanism. The diffusion mechanism is dominant for capturing fine particles. When the particle size is greater than 1 μm, the inertia impaction mechanism dominates the filtration efficiency. Filtration velocity has a positive influence on the inertia impaction mechanism and a negative impact on other mechanisms. Packing density has an obvious effect on the diffusion mechanism as packing density less than 0.1.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CX and LL conducted the simulations and prepared the article. CX and JZ contributed to analysis of simulation data. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52100131) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 20KJB470007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brahm, J. (2012). Manufacturing: Eliminating Oil Mists in the Manufacturing Environment. Filtration + Separat. 49, 39–41. doi:10.1016/S0015-1882(12)70059-9

CrossRef Full Text | Google Scholar

Bullock, E. W., and Driver, W. E. (1967). Bag Type Dust Collector. U.S. Patent 3 (345), 806. 1967-10-10.

Google Scholar

Charvet, A., Gonthier, Y., Gonze, E., and Bernis, A. (2010). Experimental and Modelled Efficiencies during the Filtration of a Liquid Aerosol with a Fibrous Medium. Chem. Eng. Sci. 65, 1875–1886. doi:10.1016/j.ces.2009.11.037

CrossRef Full Text | Google Scholar

Chen, L., Ding, S., Liang, Z., Zhou, L., Zhang, H., and Zhang, C. (2017). Filtration Efficiency Analysis of Fibrous Filters: Experimental and Theoretical Study on the Sampling of Agglomerate Particles Emitted from a GDI Engine. Aerosol Sci. Tech. 51, 1082–1092. doi:10.1080/02786826.2017.1331293

CrossRef Full Text | Google Scholar

Choi, H.-J., Kumita, M., Seto, T., Inui, Y., Bao, L., Fujimoto, T., et al. (2017). Effect of Slip Flow on Pressure Drop of Nanofiber Filters. J. Aerosol Sci. 114, 244–249. doi:10.1016/j.jaerosci.2017.09.020

CrossRef Full Text | Google Scholar

Contal, P., Simao, J., Thomas, D., Frising, T., Callé, S., Appert-Collin, J. C., et al. (2004). Clogging of Fibre Filters by Submicron Droplets. Phenomena and Influence of Operating Conditions. J. Aerosol Sci. 35, 263–278. doi:10.1016/j.jaerosci.2003.07.003

CrossRef Full Text | Google Scholar

Davies, C. (1973). Air Filtration. London: Academic Press.

Google Scholar

Frising, T., Thomas, D., Bémer, D., and Contal, P. (2005). Clogging of Fibrous Filters by Liquid Aerosol Particles: Experimental and Phenomenological Modelling Study. Chem. Eng. Sci. 60, 2751–2762. doi:10.1016/j.ces.2004.12.026

CrossRef Full Text | Google Scholar

Gonfa, G., Bustam, M. A., Sharif, A. M., Mohamad, N., and Ullah, S. (2015). Tuning Ionic Liquids for Natural Gas Dehydration Using COSMO-RS Methodology. J. Nat. Gas Sci. Eng. 27, 1141–1148. doi:10.1016/j.jngse.2015.09.062

CrossRef Full Text | Google Scholar

Happel, J. (1959). Viscous Flow Relative to Arrays of Cylinders. Aiche J. 5, 174–177. doi:10.1002/aic.690050211

CrossRef Full Text | Google Scholar

Hinds, W. C. (2012). Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles. John Wiley and Sons.

Huang, X.-F., He, L.-Y., Hu, M., Canagaratna, M. R., Sun, Y., Zhang, Q., et al. (2010). Highly Time-Resolved Chemical Characterization of Atmospheric Submicron Particles during 2008 Beijing Olympic Games Using an Aerodyne High-Resolution Aerosol Mass Spectrometer. Atmos. Chem. Phys. 10, 8933–8945. doi:10.5194/acp-10-8933-2010

CrossRef Full Text | Google Scholar

Hubbard, J. A., Brockmann, J. E., Dellinger, J., Lucero, D. A., Sanchez, A. L., and Servantes, B. L. (2012). Fibrous Filter Efficiency and Pressure Drop in the Viscous-Inertial Transition Flow Regime. Aerosol Sci. Tech. 46, 138–147. doi:10.1080/02786826.2011.616555

CrossRef Full Text | Google Scholar

Kuwabara, S. (1959). The Forces Experienced by Randomly Distributed Parallel Circular Cylinders or Spheres in a Viscous Flow at Small Reynolds Numbers. J. Phys. Soc. Jpn. 14, 527–532. doi:10.1143/jpsj.14.527

CrossRef Full Text | Google Scholar

Lee, K. W., and Liu, B. Y. H. (1982). Theoretical Study of Aerosol Filtration by Fibrous Filters. Aerosol Sci. Tech. 1, 147–161. doi:10.1080/02786828208958584

CrossRef Full Text | Google Scholar

Li, P., Wang, C., Zhang, Y., and Wei, F. (2014a). Air Filtration in the Free Molecular Flow Regime: A Review of High-Efficiency Particulate Air Filters Based on Carbon Nanotubes. Small 10, 4543–4561. doi:10.1002/smll.201401553

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P., Wang, C., Li, Z., Zong, Y., Zhang, Y., Yang, X., et al. (2014b). Hierarchical Carbon-Nanotube/quartz-Fiber Films with Gradient Nanostructures for High Efficiency and Long Service Life Air Filters. RSC Adv. 4, 54115–54121. doi:10.1039/c4ra08746a

CrossRef Full Text | Google Scholar

Liew, T. P., and Conder, J. R. (1985). Fine Mist Filtration by Wet Filters-I. Liquid Saturation and Flow Resistance of Fibrous Filters. J. Aerosol Sci. 16, 497–509. doi:10.1016/0021-8502(85)90002-3

CrossRef Full Text | Google Scholar

Luengas, A., Barona, A., Hort, C., Gallastegui, G., Platel, V., and Elias, A. (2015). A Review of Indoor Air Treatment Technologies. Rev. Environ. Sci. Biotechnol. 14, 499–522. doi:10.1007/s11157-015-9363-9

CrossRef Full Text | Google Scholar

Raynor, P. C., and Leith, D. (2000). The Influence of Accumulated Liquid on Fibrous Filter Performance. J. Aerosol Sci. 31, 19–34. doi:10.1016/S0021-8502(99)00029-4

CrossRef Full Text | Google Scholar

Roe, R.-J. (1975). Wetting of fine Wires and Fibers by a Liquid Film. J. Colloid Interf. Sci. 50, 70–79. doi:10.1016/0021-9797(75)90255-6

CrossRef Full Text | Google Scholar

Stechkina, I. B., and Kirsch, A. A. (1969). Studies on Fibrous Aerosol Filters-IV Calculation of Aerosol Deposition in Model Filters in the Range of Maximum Penetration. Ann. Occup. Hyg. 12, 1–8. doi:10.1093/annhyg/12.1.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Y.-L., Zhang, Q., Schwab, J. J., Demerjian, K. L., Chen, W.-N., Bae, M.-S., et al. (2011). Characterization of the Sources and Processes of Organic and Inorganic Aerosols in New York City with a High-Resolution Time-Of-Flight Aerosol Mass Apectrometer. Atmos. Chem. Phys. 11, 1581–1602. doi:10.5194/acp-11-1581-2011

CrossRef Full Text | Google Scholar

Tekasakul, S., Suwanwong, P., Otani, Y., and Tekasakul, P. (2008). Pressure Drop Evolution of a Medium-Performance Fibrous Filter during Loading of Mist Aerosol Particles. Aerosol Air Qual. Res. 8, 348–365. doi:10.1007/s10453-008-9091-510.4209/aaqr.2008.06.0023

CrossRef Full Text | Google Scholar

Walsh, D. C., Stenhouse, J. I. T., Scurrah, K. L., and Graef, A. (1996). The Effect of Solid and Liquid Aerosol Particle Loading on Fibrous Filter Material Performance. J. Aerosol Sci. 26, 617–618. doi:10.1016/0021-8502(96)00381-3

CrossRef Full Text | Google Scholar

Wang, J., Chen, D. R., and Pui, D. Y. H. (2006). Modeling of Filtration Efficiency of Nanoparticles in Standard Filter media. J. Nanopart. Res. 9, 109–115. doi:10.1007/s11051-006-9155-9

CrossRef Full Text | Google Scholar

Xu, C., Xie, W., Yu, Y., Zhang, J., and Yang, J. (2018). A Carbon Nanotubes Composite Filter for Removal of Oil Particles. Mater. Res. Express 6, 025024. doi:10.1088/2053-1591/aaed80

CrossRef Full Text | Google Scholar

Xu, C. W., Yu, Y., Xie, W. X., Zhang, J., and Yang, J. G. (2020). Analysis on Shape Characteristic of Oil Droplet on Fiber without Gravity. J. Southeast Univ. 50, 516–521. doi:10.3969/j.issn.1001-0505.2020.03.014

CrossRef Full Text | Google Scholar

Yang, C. (2012). Aerosol Filtration Application Using Fibrous Media-An Industrial Perspective. Chin. J. Chem. Eng. 20, 1–9. doi:10.1016/S1004-9541(12)60356-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Zhong, Z., Low, Z.-X., and Yao, Z. (2015). A Multifunctional Multi-Walled Carbon Nanotubes/ceramic Membrane Composite Filter for Air Purification. RSC Adv. 5, 91951–91959. doi:10.1039/c5ra18200j

CrossRef Full Text | Google Scholar