Unsteady Motion of Shock Wave for a Supersonic Compression Ramp Flow Based on Large Eddy Simulation

A large eddy simulation (LES) is conducted to investigate shock wave/turbulent boundary layer interaction in a 24° compression ramp at a high inlet Mach number of $Ma=2.9$. The recycling/rescaling Method is used as the inflow turbulence generation technique. The shock wave structure and boundary layer flow in the interaction region are studied by flow visualization methods, such as vortex recognition and numerical schlieren. The distributions of turbulent kinetic energy and Reynolds normal stresses at different streamwise locations are analyzed. The results show that a strong anisotropy turbulent flow appears in the reattached boundary layer after the interaction of the shock wave. The large-scale unsteady motion of the separation shock wave is analyzed by using the intermittent factor and power spectrum. It is found that the shock moves around the averaged separation position, and the length scale is equal to 72% of the inlet boundary layer thickness. The power spectrum analysis reveals the existence of low-frequency instability in the separation region.

1 Introduction

The shock wave/turbulent boundary layer interaction (SWBLI) is one of the important physical phenomena in the supersonic flow, which contains complex aerodynamic and thermodynamic problems. The interaction can significantly alter the heat conduction characteristics and produce a strong pressure fluctuation. Although the 2D compression ramp is a simple geometric model in the SWBLI, however the flow phenomena contain boundary layer unsteady flow, separation, reattached flow, and turbulent fluctuation enhancement caused by a strong adverse pressure gradient. The transient flow field presents a highly three-dimensional state (Lee and Wang 1995), and the multiscale interaction produces complex flow structures (Wang 2015). Thus, the simple 2D model is the best model for the validation of the computational fluid dynamics (CFD) method.

In the past, extensive research studies have been conducted on the SWBLI by experimental and numerical methods, but there are still some issues to be explored further. Dolling (Dolling 2001) considered that the low-frequency unsteady flow should be studied for the future in detail. Settles et al. (Settles et al., 1979) conducted a surface oil flow experiment on a compression ramp with an angle of 24°. It was found that the pattern of the “node-saddle point” is alternately arranged near the reattachment line downstream of the ramp, which proves the existence of the streamwise vortex. Smits and Muck (Smits and Muck 1987) used a hot wire anemometer to measure the compression ramp flow and studied the effects of turbulent fluctuation enhancement with three different angles of the ramp. It was found that when the intensity of the shock wave is sufficiently strong, the unsteady motion of the shock wave will become important due to turbulent fluctuation enhancement. Ganapathisubramani et al. (Ganapathisubramani et al., 2007) used high-speed particle image velocimetry (PIV) technology to measure the compression ramp flow. It was found that the strip-like structures with different momentum exist in the upstream boundary layer, and these strip structures cause a low-frequency pulsation of the separation bubble. Wu et al. (Wu et al., 2013) used nano-tracer planar laser scattering (NPLS) technology to study the laminar/turbulent SWBLI on the supersonic compression ramp; the overall flow field was analyzed and local fine structures were identified.

Yi Zhuang et al. (Zhuang et al., 2018a) have performed an experimental investigation on a compression ramp shock wave/turbulent boundary layer interaction at $Ma=2.83$. The ice cluster–based planar laser scattering technique was applied to acquire high spatiotemporal resolution images at the center plane. Two-dimensional slices of the coherent vertical structure (CVS) were acquired and extracted from these images with a machine learning–based method. By comparing the features CVS acquired before and after the interaction, the evolution of CVSs in the SWBLI flow was analyzed.

In fact, a large number of experimental studies were carried out at higher Reynolds numbers. But Bookey et al. (Bookey et al., 2005) selected a low-density gas as the working medium to reduce the Reynolds number in the experiment and achieve the numerical simulation (DNS, LES) comparison with experiments. Adams et al. (Adams 2000) used the DNS method to study the supersonic compression ramp flow and found that the Reynolds shear stress after the SWBLI increases more greatly than the Reynolds normal stress. Loginov et al. (Loginov et al., 2006) used the LES method to study the statistical parameter distributions and fluctuation characteristics of the turbulent boundary layer in the compression ramp and compared numerical results with the experimental data. The flow field analysis showed that the large-scale three-dimensional flow structure downstream of the ramp is the principal reason for the spanwise unevenness of the flow field. Wu et al. (Wu and Martin 2008) used the DNS method to study the SWBLI in the compression ramp, with the inlet flow parameters consistent with the experimental conditions given by Bookey et al. (Bookey et al., 2005). By observing the spatiotemporal evolution and using the correlation analysis of the flow field, it was found that the shock wave motion always lags behind the pulsation of the separation bubble. Therefore, a “feedback loop” model consisting of the separation bubble, shear layer, and shock wave system is proposed to explain the mechanism of the low-frequency unsteady motion of the shock wave.

Kenzo S.et al. (Sasaki et al., 2021) have investigated the mechanisms of low-frequency unsteadiness in an impinging shock wave/turbulent boundary layer interaction at a Mach number of $Ma=2$. The Strouhal number $St=fL/U_{\infty }$ was used for the space-time spectral analysis to identify the key features of the shock motion, where L is defined as the interaction length and f is the frequency of fluctuation. The dominant frequency in the vicinity of the shock was exhibited by the streamwise evolution of the pre-multiplied spectrum of pressure fluctuations. In the upstream boundary layer, the spectrum presents mainly high-frequency content ($St>1$) linked to the incoming turbulent eddies. However, in the vicinity of the shock position, a low-frequency broadband range emerges and is centered approximately at $St=0.03$. As the author pointed out, the large gap between these frequency scales has been reported in previous investigations by Touber and Sandham (Touber and Sandham 2011) and Dupont et al. (Dupont et al., 2006).

In this study, a large eddy simulation is used to study the SWBLI phenomenon of the 24° compression ramp; detailed analysis and discussion are carried out to understand the unsteady features of the shock wave in the SWBLI. The remainder of this manuscript is organized as follows. Section 2 gives a description of the numerical methods and techniques used in this study, including the generation of the inlet turbulent boundary layer, geometric model, and mesh distribution. Section 3 compares the simulation results with experiments and numerical results in the literature to verify the reliability of the program, and the details of the flow field are discussed and analyzed. The last section gives some conclusions of this study.

2 Compression Ramp and Numerical Method

The work in this study is based on the NUAA-Turbo CFD solver developed by our research group. In the large eddy simulation (LES), the finite volume method is used and the ROE scheme is used for the evaluation of convective fluxes, the WENO_ZQ scheme (Zhu and Qiu 2017) with fifth-order precision for the interface reconstruction, and the sixth-order central difference scheme for the spatial discretization of viscous fluxes. Time discretization uses the Runge–Kutta method with a total variation reduction property of third-order accuracy (Shu and Osher 1989). The dynamic sub-grid scale model is considered, and the sub-grid scale viscosity coefficient is determined with the two consecutive filtering by the method of Germano et al. (Germano 1991).

The inlet boundary layer thickness $\delta$ of the compression ramp is used to make the length scale dimensionless. The computation domain consists of two parts: the flat plane computation domain (auxiliary computation domain) and the 24° compression ramp computation domain (primary computation domain). The “recycling/rescaling” method was used to generate the turbulent boundary layer in the auxiliary computation domain and the computed turbulence information as the inlet boundary condition of the primary computation domain. In the auxiliary computation, the distance from the inlet plane “$7.3\delta$” is set as the recycled plane. The schematic of the computation domain is shown in Figure 1. The coordinate system origin is located at the ramp, and the coordinate axes “x, y, and z” indicate the streamwise, spanwise, and normal directions respectively. The upstream and downstream lengths of the ramp are both $7.73\delta$, the spanwise width is $2.15\delta$, and the normal height along the wall is $5.23\delta$. The number of grid points in the three directions is “505 × 89 × 112”. The grid is evenly distributed in the spanwise and refined along the streamwise direction at the ramp and in the normal direction to guarantee $z^{+}\approx 1$ in the first layer of the grid near the wall. The flow field of the recycled plane in the auxiliary computation domain is extracted as the inlet boundary condition for the primary computation. It is specially noted that when the primary/auxiliary computation domain uses grids of different resolutions, the process of flow field extraction needs to interpolate the variables. For details, this method can refer to Zhong et al., (2021).

FIGURE 1

FIGURE 1. Computational domain for the LES.

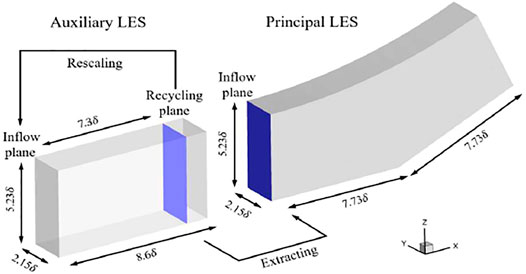
For the primary computation domain, the upper boundary of the computational domain and the outlet are set to the subsonic outlet boundary condition. The wall condition of the non-slip isothermal is adopted to the wall, and the wall isothermal temperature is 307 K. The spanwise boundary adopts periodic boundary condition, and the inlet turbulent boundary conditions are dynamically given by the auxiliary computation. For the auxiliary computation, the boundary layer conditions are consistent with the main computation, and the flow Mach number is $\text{M}a=2.9$, the flow static temperature is 108.1 K, and the flow density is $0.074kg/m^3$.

In order to verify the reliability of the LES software, the numerical results of the compression ramp will be compared with the experimental results under the same inlet flow conditions.

3 Result Analysis and Discussion

Figure 2 shows the distribution of the averaged wall pressure and skin friction coefficient along the streamwise direction in the primary computation domain, where the DNS results of Wu et al. (Wu and Martin 2008) and Tong et al. (Tong et al., 2017) and the experimental data of Bookey et al. (Bookey et al., 2005) are also presented for the purpose of comparison. By solving the position where the averaged skin friction coefficient $C_f$ is zero, the averaged separation point $x_{sep}=-2.7\delta$ and the re-attachment point $x_{rea}=0.8\delta$ in the ramp flow are obtained. Overall, the computed pressure distribution and friction coefficient distribution are in good agreement with the experimental values. At upstream of the ramp, it agrees well with the experimental values and DNS results. But it is slightly higher downstream of the ramp. The reason is that the predicted separation region size is slightly smaller and the separated shear layer completes the reattachment process in advance downstream of the ramp; thus, the wall pressure increases rapidly and the range of the pressure platform is shortened.

FIGURE 2

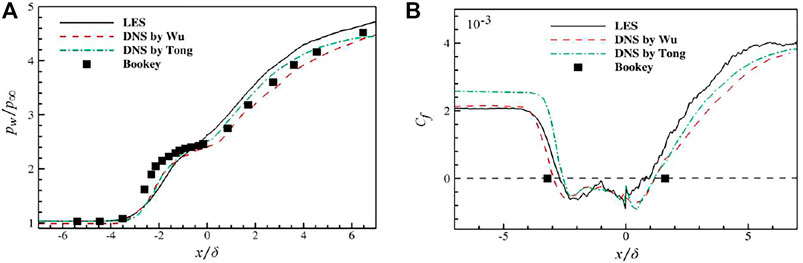
FIGURE 2. Distribution of averaged wall pressure and skin friction coefficient. (A) Averaged wall pressure. (B) Averaged skin friction coefficient.

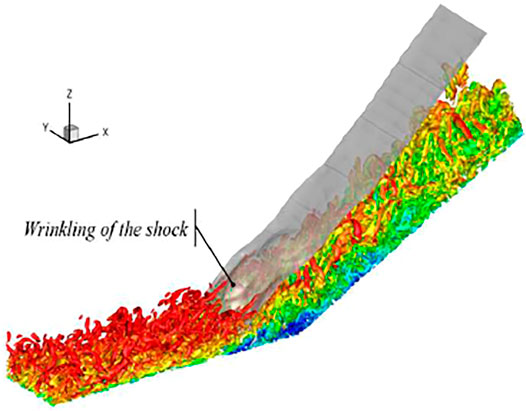
Figure 3 illustrates the instantaneous flow structure in the compression ramp computation domain. Among them, the quasi-order vortex structure of the turbulent boundary layer is displayed using the Q criterion, and the streamwise direction velocity is used for coloring. The translucent gray surface in the figure is the dimensionless pressure isosurface $\text{p}/\left({\rho }_{\infty }{U}_{\infty }^2\right)=1.7$, which is used to represent the three-dimensional structure of the separation shock wave. As can be seen in the figure, the flow field in the interaction region has significant three-dimensional characteristics. When a large vortex structure passes through the root of the shock wave, it breaks under the effect of turbulent fluctuation enhancement at the ramp. At the same time, the shock wave deforms at the root, and the shock surface wrinkles along the spanwise direction. While away from the interaction region, the shock wave keeps still the typical two-dimensional structure characteristic.

FIGURE 3

FIGURE 3. Shock surface wrinkling.

In order to further illustrate the interaction process between the shock wave and turbulent boundary layer, a slice contour in three directions is used to show the flow field details inside the interaction region, as shown in Figure 4. The streamwise and spanwise directions show the numerical schlieren diagram, which is used to show the shock wave, turbulent boundary layer, and flow structure in the separation bubble. It can be seen that the large-scale structure in the interaction region breaks into small-scale structures, which is well agreed with Zhuang Y.et al. (Zhuang et al., 2018b) experimental observation. But, on the slope downstream of the ramp, a large-scale quasi-order structure in the boundary layer is re-established. The instantaneous streamwise direction velocity contour ($y/\delta =0.02$, approach laminar sublayer) is shown on the slice parallel to the wall. It can be seen that a velocity strip structure alternately arranged along the spanwise direction is observed both upstream and downstream of the ramp in this region. In addition, the flow scale in the separation bubble along the spanwise direction is very different, indicating that the separation bubble is a multiscale flow structure.

FIGURE 4

FIGURE 4. Vortex structure in the interaction region.

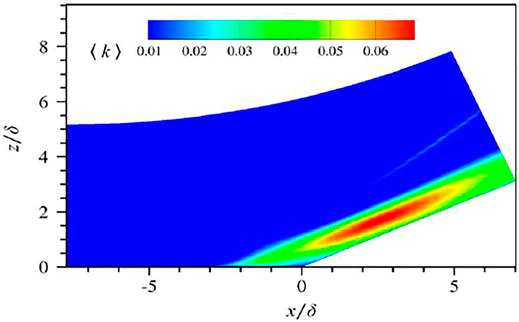
3.1 Turbulent Fluctuation

When the flow passes through the interaction region, the turbulent fluctuation is significantly enhanced due to the strong inverse gradient pressure in this region. Figure 5 is a contour of the time-space averaged turbulent kinetic energy. The definition of turbulent kinetic energy is as follows: $k=\left(\overline{\rho u^{\prime }{u}^{\prime }}+\overline{\rho v^{\prime }{v}^{\prime }}+\overline{\rho w^{\prime }{w}^{\prime }}\right)/2{\rho }_{\infty }{U}_{\infty }^2$). It can be seen from the figure that the intensity of the turbulent kinetic energy after the interaction region rapidly increases and reaches its peak value downstream of the ramp. The increase of the turbulent kinetic energy means significantly that a large number of small-scale structures are generated after the SWBLI.

FIGURE 5

FIGURE 5. Contour of time-spanwise averaged turbulent kinetic energy.

Figure 6 presents the variation of Reynolds normal stress $R_{ii}$ at different locations in the interaction region. It can be seen that near the ramp ($x=0.66\delta$), the three Reynolds stress components produce a sharp peak value. As the separated boundary layer reattaches, the Reynolds stress continues to decrease and tends to return to the pre-interaction state at $(x=2.68\delta )$. It is noted that the distribution of Reynolds stress $R_{22}$ in the boundary layer is relatively smooth and appears as a bimodal distribution near the ramp.

FIGURE 6

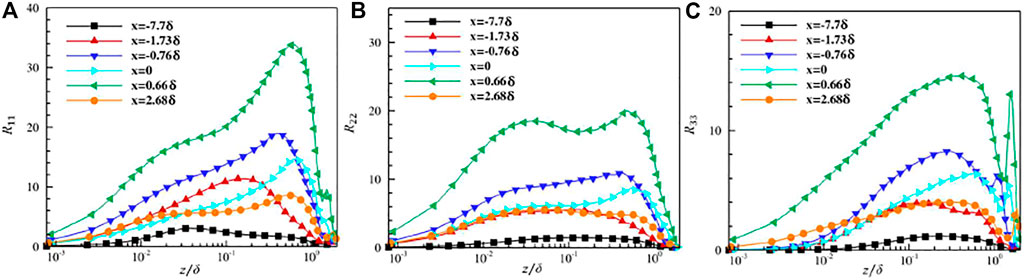
FIGURE 6. Distribution of Reynolds normal stresses at different streamwise locations. (A) Streamwise component. (B) Spanwise component. (C) Wall-normal component.

3.2 Unsteady Motion of Shock Waves

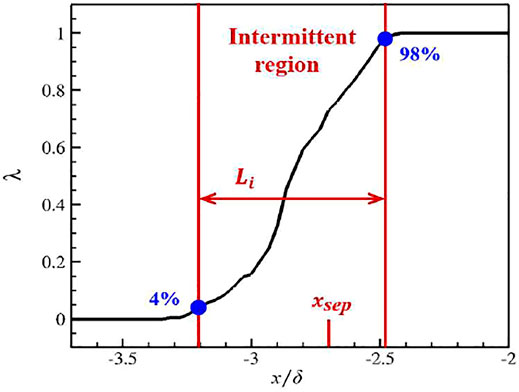
In order to study the shock wave unsteady motion, intermittent factors are usually used to measure the range of shock wave motion along the streamwise direction. The intermittent factor is defined as the time when the instantaneous wall pressure somewhere in the streamwise direction is greater than the given threshold takes up the proportion of the total flow field time. The computation formula is as follows (Dolling and Or 1985):

$\mathit{\lambda }=\frac{\mathit{T}\mathit{i}\mathit{m}\mathit{e}\left[{\mathit{p}}_{\mathit{w}}>\left({\overline{\mathit{p}}}_{\mathit{w}}+3\mathit{\sigma }\left({\mathit{p}}_{\mathit{w}}\right)\right)\right]}{\mathit{T}\mathit{o}\mathit{t}\mathit{a}\mathit{l}\mathit{t}\mathit{i}\mathit{m}\mathit{e}},$

where $p_w$ represents the instantaneous wall pressure; ${\overline{p}}_w$ and $\sigma \left(p_w\right)$ represent the average wall pressure of the inlet boundary layer and the standard deviation of the wall pressure, respectively, and the sum of the two is set as the threshold for the computation of the intermittent factor.

Figure 7 exhibits the local distribution of the intermittent factor in the compression ramp. It is known from the definition of the intermittent factor that in the undisturbed upstream boundary layer and downstream region of the ramp, the intermittent factor is always equal to 0 (or 1). However, in the vicinity of the average separation point, the separation shock wave shows a strong unsteady flow characteristic, which is represented by the intermittent factor: $0<\lambda <1$. Wu et al. (Wu and Martin 2008) considered that the motion of the shock wave is closely related to the pulsation of the separation bubble. For comparison, the upper and lower limitations of the given intermittent factor are 98 and 4%, respectively, to estimate the streamwise direction range of the shock wave motion as follows: $-3.2\delta \le x\le -2.48\delta$ . It can be seen that the flow movement of the separation shock wave in the intermittent region is carried out around the average separation point$(x=-2.7\delta )$. By computation, the length of the intermittent region in this simulation is $L_i=0.72\delta$ which is slightly smaller than that in the DNS result of the study by Tong et al. (Tong et al., 2017$L_i=0.72\delta$) ($L_i=0.72\delta$)

FIGURE 7

FIGURE 7. Intermittency factor of the separation shock.

3.3 Görtler Flow Vortex

From the abovementioned analysis, the supersonic compression ramp flow has significant three-dimensional characteristics. Especially on the slope downstream of the ramp, the flow field shows a strong unevenness in the spanwise direction. This phenomenon is closely related to the presence of Görtler flow vortex (Dolling and Or 1985; Grilli et al., 2013).

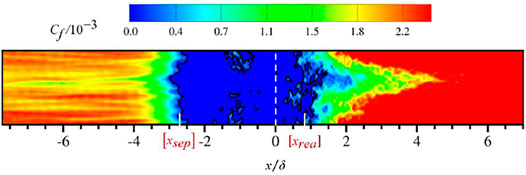
Figure 8 shows a time-averaged skin friction coefficient contour. The white dashed line represents the location of the ramp. The solid black line in the figure is used to show the separation and reattachment positions of the boundary layer near the ramp defined by the time-averaged friction coefficient equal to 0. It can be observed that the skin friction coefficient of the inlet boundary layer represents a strip pattern alternately arranged which is consistent with the spanwise distribution of the time-averaged separation line. This indicates that the distribution of the separation line is, in a great measure, determined by the skin friction coefficient of the inlet boundary layer. Due to the low-frequency pulsation of the separation bubble, the average reattachment still exhibits strong transient flow characteristics. When the separated boundary layer reattaches, the skin friction coefficient distribution appears as an obvious “V” structure, which is caused by the presence of Görtler vortex pairs. The existence of this “V” structure was also confirmed by Fu-Lin et al., (2016).

FIGURE 8

FIGURE 8. Contour of the time-averaged skin friction coefficient.

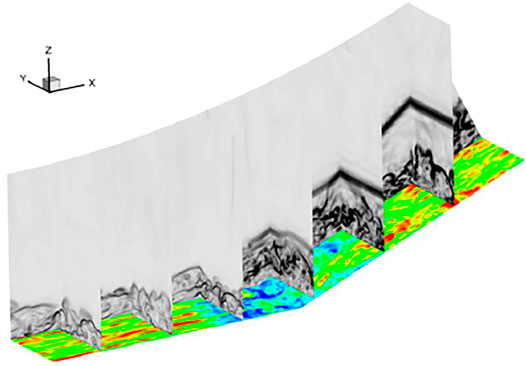
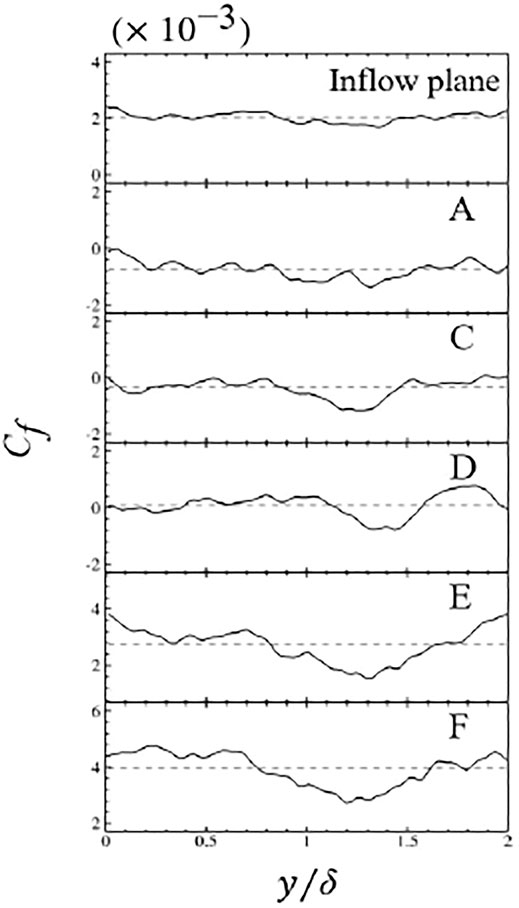
The formation of Görtler vortices is related to the curvature of the concave surface. In order to describe the spatial development of the Görtler vortex in detail, Figure 9 shows the flow field details on six different sections downstream of the average separation point. These six sections are named A ∼ F, corresponding to the streamwise direction positions: $-1.7\delta$, $-1.4\delta$, $-0.6\delta$, $0.7\delta$, $3.3\delta$, and $5.5\delta$, respectively. A schematic diagram of six positions is given in Figure 9A, in which the background is space-time–averaged numerical schlieren. Figure 9B shows the streamwise direction vorticity ${\omega }_x$ contour, and streamline distribution on six sections, where the vorticity contour has a range $-0.5\le {\omega }_x\le 0.5$. In sections A and B, the streamlines in the near wall region are gradually bent, and a smaller streamwise vortex is formed. When the flow develops to section C, it can be clearly seen in this figure that there is a large pair of vortexes in the streamwise direction (B) and a small pair of vortexes in the streamwise direction (A), and the entire boundary layer has a large amount of vortexes in this direction. With the separated boundary layer reattach in the sections D, E and F, the larger pair of the streamwise vortexes gradually occupies almost the entire span width (about $2\delta$) and appears as a classical kidney eddy structure.

FIGURE 9

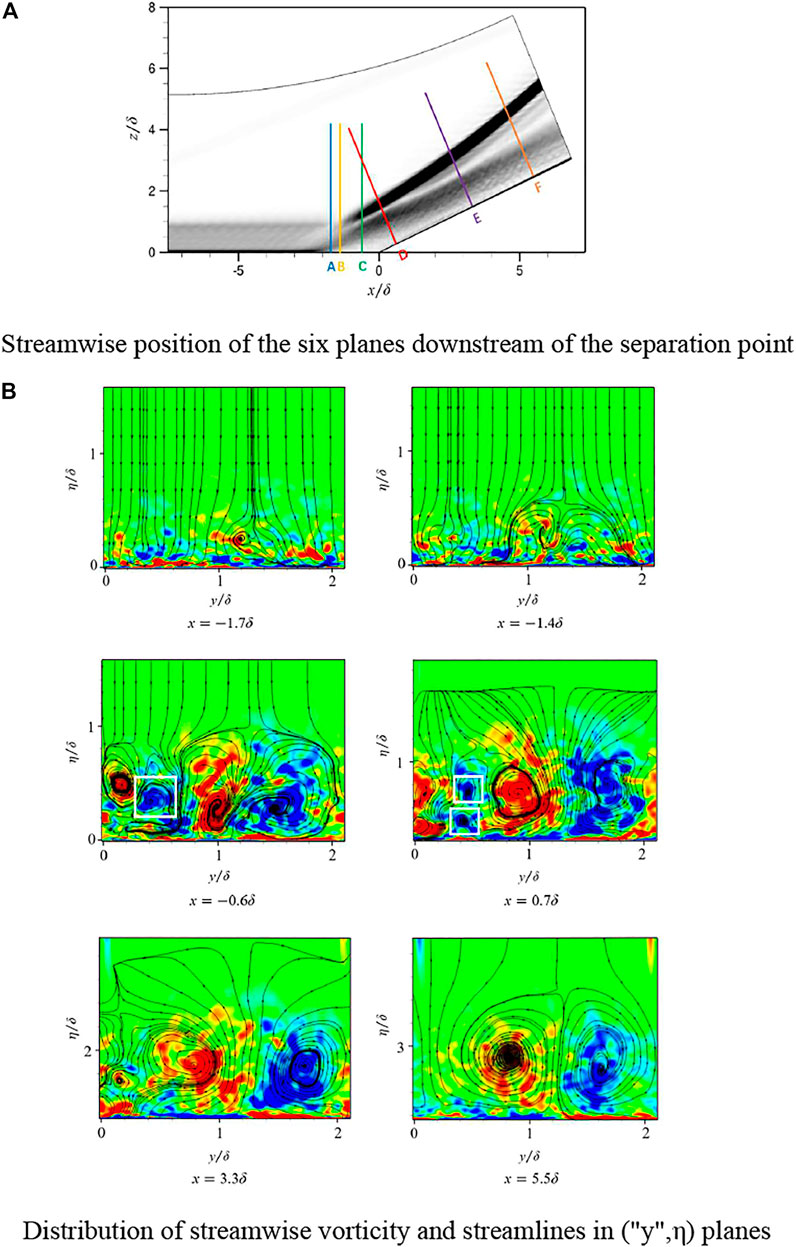
FIGURE 9. Spatial evolution of Görtler-like vortices in the compression ramp. (A) Streamwise position of the six planes downstream of the separation point. (B)Distribution of streamwise vorticity and streamlines in (“y”,η) planes.

Figure 9B illustrates that it can be estimated that the center of the Görtler vortex pair is located at $y=1.2\delta$. In general, the position of the Görtler vortex in the spanwise direction changes constantly with time due to the turbulent flow (Floryan 1991), but Figure 10 shows the time-averaged skin friction coefficient along the span in different sections, including the inlet section of the ramp computation domain and the A, C, D, E, and F sections in Figure 9 so that the variation of the spanwise distribution of the skin friction coefficient with the development of the flow field can be presented. The dotted line in the figure indicates the time-span–averaged result at this section. At the inlet section, it can be found that the skin friction coefficient along the spanwise direction is not evenly distributed, and a low skin friction coefficient region appears near the spanwise center. Sections A, C, and D are all located in the separation region, so the friction coefficients of these three locations are close to 0. In addition, due to the shock wave/boundary layer interaction and Görtler instability, the skin friction coefficient of these three sections along the spanwise direction shows strong fluctuation. Especially, an obvious low friction coefficient region is formed between $y/\delta =1\sim 1.5$. In sections E and F, the amplitude of this low-friction coefficient region is further increased, and a V-shaped distribution is formed. The fluid near the wall converges between the pair of Görtler vortexes and moves toward the outer layer of the boundary layer, locally resulting in a lower friction coefficient. In section F, the skin friction coefficient at the spanwise position $y=1.2\delta$ reaches a minimum, which is exactly the same as the center position of the Görtler vortex pair. In fact, by observing the friction coefficient distribution at the six different sections, it can be found that the low-friction coefficient region of the inlet section has a high degree of coincidence with the downstream section in the spanwise position. This phenomenon indicates that the spanwise position of the Görtler vortex downstream of the ramp is likely to be affected by the spanwise friction coefficient distribution at the inlet section.

FIGURE 10

FIGURE 10. Distribution of the averaged skin friction coefficient in the spanwise direction.

3.4 Low-Frequency Instability

In order to study the low-frequency motion of the separated shock wave, it is necessary to collect the signal of numerical pressure for spectrum analysis. Therefore, 528 wall pressure probes are arranged along the flow direction in the middle section of the calculation domain. The arrangement of these probes is consistent with the grid distribution, that is, one probe is arranged in the center of each wall grid cell. It is worth noting that the signal acquisition process is carried out after the SWBLI flow field is fully established. In order to ensure sufficient time resolution, data recording is carried out every ten time steps in the large eddy simulation, and the physical time interval between two adjacent recording points is $\Delta t=0.01\delta /U_{\infty }$. According to the Nyquist sampling theorem, the highest physical frequency that can be captured is $f_s=1/\left(2\Delta t\right)=50U_{\infty }/\delta$, which is far greater than the characteristic frequency $U_{\infty }/\delta$ of the turbulent boundary layer. Because the low-frequency instability of the SWBLI has a wide frequency range, in order to accurately capture the low-frequency characteristics, the signal acquisition time should cover at least one low-frequency instability period. Table 1 shows the relevant information of pressure signal acquisition in this large eddy simulation.

TABLE 1

TABLE 1. Relevant information of pressure signal acquisition.

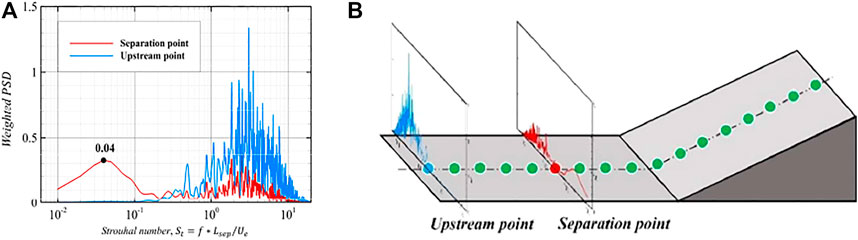
Figure 11 presents the variation of wall pressure with time at two different positions upstream of the corner (the corner position is $\text{x}=0$ ) in the center plane, and the wall pressure is nondimensionlized by using the inlet pressure $P_{\infty }$. The blue solid line represents the pressure signal graph collected at the inlet turbulent boundary layer, where the pressure fluctuation is not disturbed by the downstream interference area flow. It can be seen that the pressure signal around $P_w/P_{\infty }$ presents a random fluctuation, and the amplitude of fluctuation is very small. The red solid line indicates the pressure fluctuation with time at the average separation point ($x_{sep}=-2.7\delta$). Compared with the inlet, the pressure signal at the average separation point has larger amplitude of fluctuation due to the interaction between the shock wave and turbulent boundary layer. In addition, from the red solid line, the pressure signal at the separation point not only includes the high-frequency fluctuation but also has the low-frequency fluctuation component as shown in Figure 11.

FIGURE 11

FIGURE 11. Wall pressure signal (A) and power spectrum (B).

Next, we will make a strict quantitative analysis of the wall pressure fluctuation signal from the perspective of spectral analysis. The Welch method (Barbe et al., 2010) is used to segment the discrete pressure signal, aiming to obtain a smoother and less variance power spectrum density (PSD) curve. In this study, the collected pressure signals are divided into three segments, and the coincidence rate between the segments is 50%. The Hanning window is used to add windows for each segment to improve the variance performance. It should be noted that in the Welch method, the more segmented the data, the smoother the power spectrum curve and the smaller the noise, but at the same time, the resolution of the power spectrum will be affected. Therefore, in the process of data segmentation, we must consider the balance of noise and resolution in the power spectrum curve. Figure 11B shows the PSD distribution curve corresponding to the abovementioned two wall pressure signals, where the abscissa is the dimensionless frequency proposed by Dussauge et al. (Dussauge et al., 2006), which is defined as $St=f{L}_{sep}/U_e$. It can be seen from the figure that the peak value of pressure fluctuation energy in the upstream boundary layer is located in the high-frequency region, while the peak value of pressure fluctuation energy at the average separation point is located in the low-frequency region. Figure 12 shows the weighted power spectrum density (WPSD) expressed as $WPSD\left(f\right)=f\ast PSD\left(f\right)df$. From this figure, we can see more clearly the frequency components of pressure signals at different flow direction positions. For the upstream boundary layer, the fluctuating energy is mainly distributed between ${10}^0\sim {10}^1$, and the peak frequency is about $St=3$, which is consistent with the characteristic frequency of the fully developed turbulent boundary layer. For the signal at the average separation point, there is also a wide small peak area in the high-frequency region, which is similar to the WPSD curve obtained in the upstream turbulent boundary layer. At the same time, the red curve shows a more obvious energy peak appearing in the low-frequency region, and the corresponding characteristic frequency is $St=0.04$, which is completely consistent with the result (0.02–0.05) summarized by Dussauge et al. (Dussauge et al., 2006). In addition, Wang Bo et al. (Wang 2015), Kenzo S. et al. (Sasaki et al., 2021), Tong et al. (Tong et al., 2017), Touber and Sanham (Touber and Sandham 2009), and Pasquariello et al. (Pasquariello et al., 2017) obtained similar results in their respective numerical simulations.

FIGURE 12

FIGURE 12. (A) Frequency weighted power spectrum distribution and (B) collected positions.

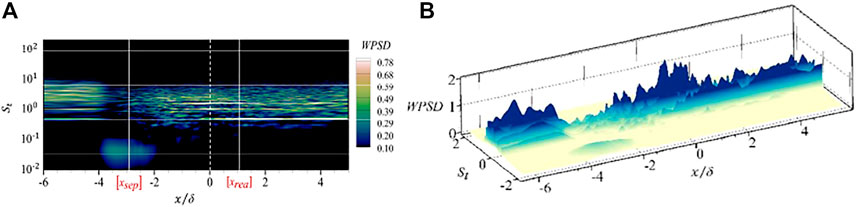
In order to study the distribution of low-frequency instability characteristics in the whole field of the compression corner, Figure 13 shows the distribution of WPSD on all pressure probes. The white solid line is used to represent the position of the average separation point $x_{sep}$ and the average reattachment point $x_{rea}$ and the white dotted line is used to represent the position of the corner. Once again, it can be clearly seen that the turbulence generation technology in this study does not introduce any low-frequency energy at the inlet. By observing the whole flow field, it is found that this low-frequency instability mainly exists near the average separation point, while in other locations of the flow field, the energy of pressure fluctuation almost exists in the high-frequency range. Especially when the boundary layer is reattached in the downstream, its power spectrum distribution is almost the same as that in the upstream, and the reattached boundary layer shows a process of flow recovery. This study considers that this low-frequency motion is caused by the unsteady motion of large-scale separation bubbles. Obviously, the scale of the separation bubble is larger than that of any flow in the boundary layer.

FIGURE 13

FIGURE 13. (A) WPSD contour map of the wall pressure signal (B) peak map of wall pressure signal.

4 Conclusion

In this study, a large eddy simulation (LES) is conducted to investigate the shock wave and turbulent boundary layer interaction in a 24° compression ramp with an inflow Mach number of $Ma=2.9$ and compared with experimental and numerical simulation results in the literature. The shock wave/turbulent boundary layer interaction (SWBLI) was analyzed from two aspects: time domain and frequency domain. The main conclusions are as follows:

The shock wave/turbulent boundary layer interaction represents some flow structure characteristics. When the large scale vortex passes the root of the shock wave, the shock wave surface wrinkles due to the intermittence of the large-scale vortex in the spanwise direction. Under the strong inverse gradient pressure of the compression ramp, the large-scale vortex breaks into a small-scale vortex, the turbulent boundary layer manifests a strong anisotropy characteristic, and the turbulent kinetic energy rapidly increases in the outer layer of the boundary layer downstream of the ramp.

In the region of interaction, the separated shock wave represents an unsteady motion along the streamwise direction. This phenomenon is successfully captured by the intermittent factor. The range of the shock wave motion is $-3.2\delta \le x\le -2.48\delta$, indicating that the unsteady shock wave motion is around the average separation point.

The LES simulation represents a pair of streamwise vortices, called Görtler vortex, occupying almost the entire span width about $2\delta$ on the compression ramp. It is found that the spanwise skin friction coefficient distribution at the inlet of the turbulent boundary layer not only determines the spanwise separation location of the turbulent boundary but also makes the downstream Görtler vortex to be fixed at a certain spanwise position, thus forming a time stable flow structure.

The low-frequency instability in the SWBLI is successfully captured by using the power spectrum analysis method. The corresponding characteristic frequency is $St=0.04$ near the average separation point. The spectrum analysis indicates that the shock wave motion is related to the pulsation of the separation bubble, while in other locations of flow field, the energy of pressure fluctuation represents almost exclusively the high-frequency characteristics of the fully developed turbulent boundary layer.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XH, L-XW, and D-DZ contributed to the conception and design of the study. XH provided an idea scheme; XH, L-XW, and D-DZ coded; XH analyzed; and NG and l wrote the first draft. All authors contributed to manuscript revision and read and approved the submitted version.

Conflict of Interest

Author XH was employed by the company AECC HUNAN Aviation Powerplant Research Institute.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adams, N. A. (2000). Direct Simulation of the Turbulent Boundary Layer along a Compression Ramp at M = 3 and Re=1685. J. J. Fluid Mech. 420 (1), 47–83. doi:10.1017/S0022112000001257

CrossRef Full Text | Google Scholar

Barbe, K., Pintelon, R., and Schoukens, J. (2010). Welch Method Revisited: Nonparametric Power Spectrum Estimation via Circular Overlap. J. IEEE Trans. Signal Process. 58 (2), 553–565. doi:10.1109/TSP.2009.2031724

CrossRef Full Text | Google Scholar

Bookey, P., Wyckham, C., and Smits, A. (2005). New Experimental Data of STBLI at DNS/LES Accessible Reynolds Numbers. Reno: 43rd AIAA Aerospace Sciences Meeting and Exhibit. doi:10.2514/6.2005-309

CrossRef Full Text | Google Scholar

Dolling, D. S. (2001). Fifty Years of Shock-Wave/boundary-Layer Interaction Research - what Next? AIAA J. 39 (8), 1517–1531. doi:10.2514/3.14896

CrossRef Full Text | Google Scholar

Dolling, D. S., and Or, C. T. (1985). Unsteadiness of the Shock Wave Structure in Attached and Separated Compression Ramp Flows. J. Experiments Fluids 3 (1), 24–32. doi:10.1007/BF00285267

CrossRef Full Text | Google Scholar

Dupont, P., Haddad, C., and Debieve, J. F. (2006). Space and Time Organization in a Shock-Induced Separated Boundary Layer. J. Fluid Mech. 559, 255. doi:10.1017/S0022112006000267

CrossRef Full Text | Google Scholar

Dussauge, J. P., Dupont, P., and Debiève, J. F. (2006). Unsteadiness in Shock Wave Boundary Layer Interactions with Separation. J. Aerospace Sci. Tech. 10 (2), 85–91. doi:10.1016/j.ast.2005.09.006

CrossRef Full Text | Google Scholar

Floryan, J. M. (1991). On the Görtler Instability of Boundary Layers. J. Prog. Aerospace Sci. 28 (3), 235–271. doi:10.1016/0376-0421(91)90006-P

CrossRef Full Text | Google Scholar

Fu-Lin, Ton., Tang, Zhi-Gong., and Xin-Liang, Li. (2016). Direct Numerical Simulation of Shock-Wave and Transitional Boundary Layer Interaction in a Supersonic Compression Ramp. J. Chin. J. Aeronautics 37 (12), 3588–3604. doi:10.7527/S1000-6893.2016.0096

CrossRef Full Text | Google Scholar

Ganapathisubramani, B., Clemens, N., and Dolling, D. (2007). Effects of Upstream Coherent Structures on Low-Frequency Motion of Shock-Induced Turbulent Separation. Reno: 45th AIAA Aerospace Sciences Meeting and Exhibit. doi:10.2514/6.2007-1141

CrossRef Full Text | Google Scholar

Germano, M. (1991). A Dynamic Subgrid-Scale Eddy Viscosity Model. Phys. Fluids A 3, 1760–1765. doi:10.1063/1.857955

CrossRef Full Text | Google Scholar

Grilli, M., Hickel, S., and Adams, N. A. (2013). Large-Eddy Simulation of a Supersonic Turbulent Boundary Layer over a Compression–Expansion Ramp. J. Int. J. Heat Fluid Flow 42 (8), 79–93. doi:10.1016/j.ijheatfluidflow.2012.12.006

CrossRef Full Text | Google Scholar

Lee, C. B., and Wang, S. (1995). Study of the Shock Motion in a Hypersonic Shock System/turbulent Boundary Layer Interaction. Experiments in Fluids 19 (3), 143–149. doi:10.1007/BF00189702

CrossRef Full Text | Google Scholar

Loginov, M. S., Adams, N. A., and Zheltovodov, A. A. (2006). Large-eddy Simulation of Shock-Wave/turbulent-Boundary-Layer Interaction. J. J. Fluid Mech. 565 (1), 135–169. doi:10.1017/S0022112006000930

CrossRef Full Text | Google Scholar

Pasquariello, V., Hickel, S., and Adams, N. A. (2017). Unsteady Effects of Strong Shock-Wave/Boundary-Layer Interaction at High Reynolds Number. J. J. Fluid Mech. 823 (1), 617–657. doi:10.1017/jfm.2017.308

CrossRef Full Text | Google Scholar

Sasaki, K., Barros, D. C., Andre, V., and Cavalieri, G. (2021). Causality in the Shock Wave/turbulent Boundary Layer Interaction. J. Phys. Rev. Fluids 6 (6), 064609. doi:10.1103/PhysRevFluids.6.064609

CrossRef Full Text | Google Scholar

Settles, G. S., Fitzpatrick, T. J., and Bogdonoff, S. M. (1979). Detailed Study of Attached and Separated Compression Corner Flowfields in High Reynolds Number Supersonic Flow. AIAA J. 17 (6), 579–585. doi:10.2514/3.61180

CrossRef Full Text | Google Scholar

Shu, C. W., and Osher, S. (1989). Efficient Implementation of Essentially Non-oscillatory Shock-Capturing Schemes. J. J. Comput. Phys. 77 (2), 439–471. doi:10.1016/0021-9991(88)90177-5

CrossRef Full Text | Google Scholar

Smits, A. J., and Muck, K.-C. (1987). Experimental Study of Three Shock Wave/Turbulent Boundary Layer Interactions. J. Fluid Mech. 182 (182), 291. doi:10.1017/S0022112087002349

CrossRef Full Text | Google Scholar

Tong, F., Yu, C., and Tang, Z. (2017). Numerical Studies of Shock Wave Interactions with a Supersonic Turbulent Boundary Layer in Compression Corner: Turning Angle Effects. J. Comput. Fluids 149, 56–69. doi:10.1016/j.compfluid.2017.03.009

CrossRef Full Text | Google Scholar

Touber, E., and Sandham, N. D. (2009). Large-Eddy Simulation of Low-Frequency Unsteadiness in a Turbulent Shock-Induced Separation Bubble. J. Theor. Comput. Fluid Dyn. 23 (2), 79–107. doi:10.1007/s00162-009-0103-z

CrossRef Full Text | Google Scholar

Touber, E., and Sandham, N. D. (2011). Low-order Stochastic Modelling of Low-Frequency Motions in Reflected Shockwave/boundary-Layer Interactions. J. Fluid Mech. 671, 417. doi:10.1017/S0022112010005811

CrossRef Full Text | Google Scholar

Wang, Bo. (2015). The Investigation into the Shock Wave/boundary-Layer Interaction Flow Field Organization. Changsha: Graduate School of National University of Defense Technology.

Google Scholar

Wu, M., and Martin, M. P. (2008). Analysis of Shock Motion in Shockwave and Turbulent Boundary Layer Interaction Using Direct Numerical Simulation Data. J. J. Fluid Mech. 594 (594), 71–83. doi:10.1017/S0022112007009044

CrossRef Full Text | Google Scholar

Wu, Yu., Shi-He, Yi., and Chen, Zhi. (2013). Experimental Investigations on Structures of Supersonic Laminar/turbulent Flow over a Compression Ramp. J. Acta Phys. 62 (18), 308–319. doi:10.7498/aps.62.184702

CrossRef Full Text | Google Scholar

Zhong, Dong-Dong., WangXu, Li., and Ge, Ning. (2021). Reflected Shock/Boundary Layer Interaction Structure Analysis Based on Large Eddy Simulation. Chin. J. aeronautics 34 (5), 364–372. doi:10.1016/j.cja.2020.12.009

CrossRef Full Text | Google Scholar

Zhu, J., and Qiu, J. (2017). A New Type of Finite Volume WENO Schemes for Hyperbolic Conservation Laws. J. Sci. Comput. 73 (2-3), 1338–1359. doi:10.1007/s10915-017-0486-8

CrossRef Full Text | Google Scholar

Zhuang, Yi., Tan, Hui-Jun., Li, Xin., Guo, Yun-Jie., and Sheng, Fa-Jia. (2018). Evolution of Coherent Vertical Structures in a Shock Wave/turbulent Boundary-Layer Interaction Flow, Phys. Fluids 30, 111702. doi:10.1063/1.5058278

CrossRef Full Text | Google Scholar

Zhuang, Yi., Tan, Hui-Jun., Li, Xin., Sheng, Fa-Jia., and Zhang, Yu-chao. (2018). Görtler-like Vortices in an Impingingshock Wave/turbulent Boundary Layerinteraction Flow. Phys. Fluids 30, 061702. doi:10.1063/1.5034242

CrossRef Full Text | Google Scholar