Development and Application of an Aerosol Model Under a Severe Nuclear Accident

Radioactive aerosol will transport in the containment and also will leak into the environment under a severe nuclear accident. Thus, it is of great significance for predicting the behavior of aerosol under a severe nuclear accident. In order to analyze the aerosol behavior, an improved multi-component sectional model is developed, which improves section numbers and updates the aerosol particle density at each time step. The model’s dependability is confirmed to use benchmark and experimental values. An excellent agreement can be observed between simulation and benchmark. On this premise, the LBLOCA accident is chosen to explore the behavior of radioactive aerosol in the containment. The finding shows that the aerosol is mostly deposited on the structure’s surface due to gravity in the LBLOCA accident. According to a comparison of the influence of aerosol natural deposition mechanisms on the distribution of diameter particles, Brownian diffusion, thermophoresis, diffusiophoresis, and gravity all have an effect on aerosol in the range of 0.01 $\mu m$–0.03 $\mu m$ particles, and the deposition of 2 $\mu m$–20 $\mu m$ particles is mainly due to gravity. After comparing and evaluating the influence of aerosol density in the containment, it can be inferred that changed aerosol particle density leads aerosol particles coagulate into larger particles.

Introduction

After the Fukushima accident, the study of severe accidents (SA) has gained more international attention (Wittneben, 2012). In a hypothetical nuclear power plant severe accident, the release of radioactive fission products can occur from the core fuel, the fuel-cladding gap, and the material in the cavity. The fission product released by core melting will leak into the containment through the primary system break, and if the accident deteriorates further, it will lead to containment failure, resulting in radioactive fission products being released into the environment (Allelein et al., 2009; Lin, W. et al., 2014). Radioactive fission products exist as gases, aerosols, or deposited onto heat structure, and the most radioactive fission products within the containment are transported with the movement of the aerosol (Soffer et al., 1995). Aerosol particles released into the containment will change due to collisions between particles, and some of the aerosol particles will deposit onto the containment heat structure because of temperature, density, diffusion, and gravity (Raj Sehgal, 2012). Otherwise, the detailed aerosol property is necessary to calculate the radioactive aerosol removal efficiency of engineered safeguards, such as the spray system and the filtration system (Porcheron et al., 2008; Rýdl et al., 2019; Wang et al., 2021). Therefore, it is significant to study the radioactive aerosol distribution and the radioactive aerosol behavior under a severe nuclear accident.

In the past research studies, many researchers have developed codes to study the behavior of the radioactive aerosol. For instance, Klinik et al. (2010) used the integrated program ASTEC to perform transient simulations of thermal-hydraulic phenomena and aerosol behavior in tests on containment systems of different sizes, such as the Phebus. The FP containment bench, the KAEVER containment bench, and the Battelle containment bench obtained good simulation results. For the deposition and coagulation behavior of aerosols in a nuclear reactor, Alipchenkov et al. (2009) have developed a code for calculating the behavior of aerosol-shaped fission products in the primary circuit of a nuclear reactor, which focuses on the development of models for predicting the deposition and coagulation rate of aerosols. There are also many numerical studies to solve the aerosol general dynamic equation, such as the sectional method (Gelbard and Seinfeld, 1980), the moment method (Wang et al., 2019), the discrete-sectional method (Li and Cai, 2020), and the Monte Carlo method (Bird, 1994; Liu and Chan, 2018). The sectional method is commonly used to describe the multicomponent aerosol dynamic behavior in the nuclear power plant. Because the sectional method requires the number of sections and the boundary of the section is fixed, this model also is called the fixed section model. MAEROS code developed based on the sectional method is widely used in the accident analysis program (Gelbard, 1982), such as MELCOR (Humphries et al., 2017) and CONTAIN (Murata et al., 1997). MAEROS is a multi-sectional, multi-component aerosol dynamic code that evaluates the size distribution of each type of aerosol mass, or component, as a function of time. MAEROS code also will deal with deposition processes of the radioactive aerosol. In the MAEROS code, the radioactive aerosol particles are allocated into fixed sections by particle volume, and the composition of the aerosol particles in the same section is considered uniform.

This sectional method discussed previously has fixed a section boundary and constant section number, and the aerosol particle density is constant by the input data. As known, when the reactor core begins melting in a severe accident, the radioactive aerosol source will continuously change along with the development of the accident, and the radioactive aerosol components released from the reactor core are also different. Moreover, the radioactive aerosol coagulation behavior and deposition behavior will change the components of radioactive aerosol. Thus, the radioactive aerosol density is closely associated with the deposition behavior and coagulation behavior. In the MAEROS code, in order to simplify the coefficients, it restricts the maximum section number. The geometric constraint is $v_{l+1}/v_l>2$, where $v_l$ is the radioactive aerosol particle volume at the lower boundary of section $l$. $v_{l+1}$ is the radioactive aerosol particle volume at the upper boundary of section $l+1$. The fixed section model cannot improve the calculation accuracy and get more detailed radioactive aerosol distribution by increasing the section number. In a word, the traditional sectional method has some drawbacks which need to increase the section number and update the radioactive aerosol density to simulate multi-component radioactive aerosol behavior during severe accidents.

The objective of this research first proposes an improved multi-component sectional method to simulate aerosols under severe accident. Then, the improved model is verified and validated by the benchmark and experiment. Furthermore, this research investigates the distribution of CsI aerosol under the LBLOCA accident and the effect of the natural deposition mechanism and aerosol density on the aerosol distribution.

Mathematical Method

Aerosol Dynamic Models

The spatial and chemical composition of the particles are represented by the size distribution function $n\left(v,t\right)$, where $n\left(v,t\right)dv$ is the number of particles in the particle range $\left[v,v+dv\right]$ and the number of particles in the volume range $v$ to $v+dv$. The collide and coagulate are described by the general particulate conservation (Gelbard and Seinfeld, 1978).

$\begin{array}{c}\begin{array}{c}\frac{\partial n\left(v,t\right)}{\partial t}=-\frac{\partial }{\partial v}\left[I\left(v,t\right)n\left(v,t\right)\right]+\frac{1}{2}\underset{0}{\overset{v}{{\displaystyle \int }}}\beta \left(u,v-u\right)n\left(u,t\right)n\left(v-u,t\right)du\\ -n\left(v,t\right)\underset{0}{\overset{\infty }{{\displaystyle \int }}}\beta \left(v,u\right)n\left(u,t\right)du+S\left(v,t\right)\end{array}\end{array}(1)$

where $I\left(v,t\right)$ is the rate of change of the particle volume due to mass exchange with the liquid phase. $\beta \left(v,u\right)$ is the coagulation coefficient for particles of volumes $v$ and $u$. $S$ is the net increase rate of particles flowing into the system.

By discretizing the aerosol particles into $m$ sections and $s$ components, the mass of the section $l$ at a given time is defined as $Q_l$:

$Q_l\left(t\right)={{\displaystyle \sum }}_{k=1}^s{Q}_{l,k}\left(t\right)=\underset{v_{l-1}}{\overset{v_l}{{\displaystyle \int }}}vn\left(v,t\right)dv(2)$

where $Q_{l,k}\left(t\right)$ is the mass of the component $k$ in the section $l$. $v_l$ and $v_{l-1}$ are the upper and lower boundaries of the section $l$, respectively. $n\left(v,t\right)$ is the distribution function of the section $l$; the mass concentration change rate for the component $k$ of the aerosol particle in the section $l$ can be written as the following equation (Gelbard and Seinfeld, 1980).

$\begin{array}{c}\begin{array}{c}\frac{d{Q}_{l,k}\left(t\right)}{dt}=\frac{1}{2}{\displaystyle \sum }_{i=1}^{l-1}{\displaystyle \sum }_{j=1}^{l-1}\left[{{\displaystyle {}^{1a}\overline{\beta }}}_{i,j,l}{Q}_{j,k}{Q}_i+{{\displaystyle {}^{1b}\overline{\beta }}}_{i,j,l}{Q}_{i,k}{Q}_j\right]\\ -{\displaystyle \sum }_{i=1}^{l-1}\left[{{\displaystyle {}^{2a}\overline{\beta }}}_{i,l}{Q}_i{Q}_{l,k}-{{\displaystyle {}^{2b}\overline{\beta }}}_{i,l}{Q}_l{Q}_{i,k}\right]-\frac{1}{2}{{\displaystyle {}^3\overline{\beta }}}_{l,l}{Q}_l{Q}_{l,k}\\ -Q_{l,k}{\displaystyle \sum }_{i=l+1}^m{{\displaystyle {}^4\overline{\beta }}}_{i,l}{Q}_i+{\overline{S}}_{l,k}-{\overline{\text{Ψ}}}_{l,k}{Q}_{l,k}\end{array}\end{array}(3)$

where $d{Q}_{l,k}\left(t\right)/dt$ is the aerosol mass change rate of the component $k$ in the section $l$ at a time $t$, ${{\displaystyle {}^{1a}\overline{\beta }}}_{i,j,l}$, ${{\displaystyle {}^{1b}\overline{\beta }}}_{i,j,l}$ is agglomeration rata of particles in section $i$ and section $j$ to form a particles in section $l$, ${{\displaystyle {}^{2a}\overline{\beta }}}_{i,l}$ is agglomeration rata of particles in section $i$ and section $l$ to form a particle larger than section $l$, ${{\displaystyle {}^{2b}\overline{\beta }}}_{i,l}$ is agglomeration rata of particles in section $i$ and section $l$ to form a particle in section $l$, ${{\displaystyle {}^3\overline{\beta }}}_{l,l}$ is agglomeration rata of particles both in section $l$ to form a particle in section $l$, ${{\displaystyle {}^4\overline{\beta }}}_{i,l}$ is agglomeration rata of particles in section $l$ and section $i$ ($i>l$). The coagulation coefficient of the traditional sectional method is shown in Table 1. ${\overline{S}}_{l,k}$ is the source of the component $k$ of the aerosol particle in section $l$. ${\overline{\text{Ψ}}}_{l,k}$ is the aerosol removal rate of component $k$ of the aerosol particle in section $l$.

TABLE 1

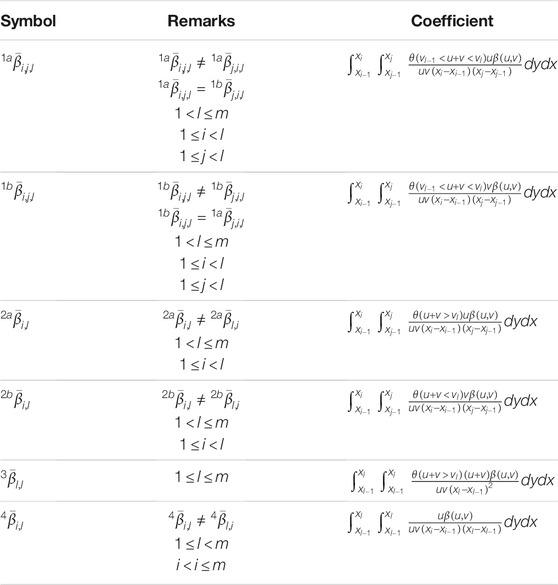
TABLE 1. Coagulation coefficients (Gelbard and Seinfeld, 1980).

Moreover, the first and second terms in the right of Eq. 3 indicate the flux of the radioactive aerosol component $k$ into the size section $l$ from the lower size sections by coagulating with each section. The third term represents the flux of the component $k$ out of the section $l$ due to the coagulation of particles within the section $l$. For $l<m$ in the fourth term, the flux of the component $k$ leaves section $l$ by coagulation of particles within the section $l$ and those of higher sections. The fifth term represents the source term of the component $k$ in the section $l$ entering the containment. The sixth term is the removal flux of the component $k$ in the section $l$ by a natural settlement mechanism. The detailed theory of the natural settlement mechanism is as follows.

Aerosol Removal Models

For the calculation of the deposition term in this study, gravity, Brownian diffusion, thermophoresis, and diffusiophoresis are considered for each heat structure surface of the containment, and the removal rate of all heat structure surfaces is added up to the total removal rate (Murata et al., 1997; Humphries et al., 2017).

${\overline{\text{Ψ}}}_{l,k}={\displaystyle \sum }_{j=1}^{N_{str}}{\lambda }_{j,l}{Q}_{l,k}(4)$

where $N_{str}$ is the total number of heat structure surfaces for aerosol deposition in the control volume, and ${\lambda }_{j,l}$ is the deposition rate for the heat structure $j$ for the aerosol section $l$. The natural deposition coefficients can be calculated by using the deposition velocity.

${\lambda }_{j,l}=\frac{A_j}{V}\left(v_s+v_{diff}+v_{therm}+v_{diffusio}\right)(5)$

where $A_j$ is the area of the heat structure surface $j$, and $V$ is the control volume atmosphere volume. The velocity of aerosol deposition on a heat structure surface is defined as follows.

Gravitational Deposition

$v_s=\frac{d_p^2{\rho }_{p}g{C}_m}{18\mu \chi }(6)$

where $v_s$ is the gravitational deposition velocity, $d_p$ is the particle diameter, ${\rho }_p$ is the particle density, $C_m$ is the Cunningham slip correction factor, $\mu$ is the viscosity of air, $\chi$ is the dynamic shape factor, and $g$ is the acceleration of gravity.

The Cunningham slip correction factor in Eq. 6 is expressed as follows.

$C_m=1+N_{Kn}\left[1.257+0.4\exp \left(-\frac{1.1}{N_{Kn}}\right)\right](7)$

Here, $N_{Kn}$ is the Knudsen number $2\lambda /d_p$, and $\lambda$ is the mean-free path of gas.

The gravitational deposition is effective for upward surfaces, such as the floor and pool. As for the downward surface, this mechanism will not act on it. Also, one basic hypothetical condition of this model is that the aerosol particle Reynolds number must be less than 1, which means that inertial effects of the flow may be neglected.

Brownian Diffusion

Brownian diffusion of aerosols refers to the deposition of aerosols due to mutual collision between the aerosol and the heat structure surface. The deposition velocity because of Brownian diffusion is defined as follows.

$v_{diff}=\frac{\sigma T{C}_m}{3\pi \mu \chi d_p\Delta }(8)$

where $v_{diff}$ is the diffusion deposition velocity, $\sigma$ is Boltzmann constant, $T$ is atmosphere temperature, and $\Delta$ is the diffusion boundary layer thickness.

Thermophoresis

Thermophoresis is caused by the temperature gradient between the aerosol particles and heat structure surface, and the aerosol particles will deposit on the object surface at a lower temperature. The thermophoretic deposition velocity is defined as follows.

$v_{therm}=\frac{3\mu C_m\left(c_t{N}_{Kn}+\frac{k_{gas}}{k_p}\right)}{2\mu {\rho }_{gas}T\left(1+3F_{slip}{N}_{Kn}\right)\left(1+2c_t{N}_{Kn}+\frac{k_{gas}}{k_p}\right)}\nabla T(9)$

where $k_{gas}/k_p$ is the ratio of the air thermal conductivity to aerosol thermal conductivity, $\nabla T$ is the structure surface temperature gradient, ${\rho }_{gas}$ is the gas density, $T$ is the wall temperature, $F_{slip}$ is the slip factor, and ${\text{c}}_{\text{t}}$ is the constant associated with the thermal accommodation coefficients.

Diffusiophoresis

The diffusiophoresis process is also as known as a vapor condensation process. When the vapor condenses on the surface of the heat structure surface, composition gradients will exist in the adjacent gas, which will affect aerosol deposition behavior on the surface. The aerosol particles will remove along with the concentration gradient, which is caused by vapor condensation on the heat structure surface.

$\begin{array}{c}{v}_{diffusio}=\left(\frac{\sqrt{M_s}}{X_s\sqrt{M_s}+X_{NC}\sqrt{M_{NC}}}\right)\left(\frac{W_{cond}}{{\rho }_s}\right)\end{array}(10)$

where $M_s$ is the molecular weight of water, $M_{NC}$ is the molecular weight of non-condensable gases, $W_{cond}$ is the condensation mass flux to the surface, ${\rho }_s$ is the density of bulk gas, $X_s$ is the mole fraction of water vapor in the bulk gas, and $X_{NC}$ is the mole fraction of non-condensable gases in the bulk gas.

Improvement of the Multi-Component Sectional Method

The agglomeration kernels of the four mechanisms are proposed in the study by Humphries et al. (2017).

$\begin{array}{c}{\beta }_B=\frac{2\pi \left(D_i+D_j\right)\left({\gamma }_i{d}_i+{\gamma }_j{d}_j\right)}{F}\end{array}(11)$

$\begin{array}{c}{\beta }_S={\epsilon }_g\frac{\pi }{4}{C}_s{\left({\gamma }_i{d}_i+{\gamma }_j{d}_j\right)}^2\left|v_{s,i}-v_{s,j}\right|\end{array}(12)$

$\begin{array}{c} {\beta }_{T1}=\sqrt{\frac{{\pi }^2{\epsilon }_t}{120v_g}}{C}_s{\left({\gamma }_i{d}_i+{\gamma }_j{d}_j\right)}^3\end{array}(13)$

$\begin{array}{c}{\beta }_{T2}=\frac{0.04029{\rho }_g^{1/4}{\epsilon }_t^{3/4}}{{\mu }_g^{5/4}}{C}_s{\left({\gamma }_i{d}_i+{\gamma }_j{d}_j\right)}^2\left|\frac{{\rho }_i{C}_i{d}_i^2}{{\chi }_i}-\frac{{\rho }_j{C}_j{d}_j^2}{{\chi }_j}\right|\end{array}(14)$

where $d$ is the aerosol particle diameter, $\gamma$ is the agglomeration shape factor, $F$ is the correction coefficient, $C_s$ is the aerosol particle sticking coefficient, and ${\epsilon }_g$ is the collision efficiency, which is defined below.

$\begin{array}{c}{\epsilon }_g=1.5{\left[\frac{\min \left(d_i,d_j\right)}{\left(d_i+d_j\right)}\right]}^2\end{array}(15)$

where $v_s$ is the settling velocity of the gravitational mechanism, which is defined as

$\begin{array}{c}{v}_s=\frac{{\rho }_{i}g{d}_i^2{C}_i}{18{\mu }_g{\chi }_i}\end{array}(16)$

where $\rho$ is the particle density, $g$ is the acceleration of gravity, ${\mu }_g$ is the gas viscosity, ${\chi }_i$ is the dynamic shape factor, and $C$ is the Cunningham slip correction factor in Eq. 7. $D$ is the particle diffusivity, which is defined as

$\begin{array}{c}D=\frac{k{T}_g}{3\pi d{\mu }_g\chi }C\end{array}(17)$

According to the traditional section method, if the coagulation coefficient is resolved at each time step, it will waste the computation time. Therefore, it is necessary to simplify the calculation process of the coagulation coefficient.

Such as ${{\displaystyle {}^{1a}\overline{\beta }}}_{i,j,l}$ in Table 1, it can be written as

$\begin{array}{c}{{\displaystyle {}^{1a}\overline{\beta }}}_{i,j,l}={\displaystyle \sum }_n\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_n\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\end{array}(18)$

where the subscript $n$ represents the agglomeration mechanisms. According to Eq. 11, the variable related to the aerosol particle density is separated from the double integral sign in Eq. 18. The Brownian agglomeration can be further written as

$\begin{array}{c}\begin{array}{c}{{\displaystyle {}^{1a}\overline{\beta }}}_{B,i,j,l}=\frac{{\rho }_j^{\ast }}{{\rho }_j}\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_B^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ =k_B\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_B^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\end{array}\end{array}(19)$

where the superscript ∗ represents the standard agglomeration coefficients and density. By analogy, the gravitational agglomeration can be written as

$\begin{array}{c}\begin{array}{c}{{\displaystyle {}^{1a}\overline{\beta }}}_{S,i,j,l}=|\frac{{\rho }_i{\rho }_j^{\ast }}{{\rho }_i^{\ast }{\rho }_j}\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ +\frac{{\rho }_j{\rho }_j^{\ast }}{{\rho }_j^{\ast }{\rho }_j}\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(2\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx|\\ =|k_{s1}\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ +k_{s2}\underset{x_{i-1}}{\overset{x_j}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx|\end{array}\end{array}(20)$

The turbulent agglomeration can be written as

$\begin{array}{c}\begin{array}{c}{{\displaystyle {}^{1a}\overline{\beta }}}_{T1,i,j,l}={\left(\frac{{\rho }_g}{{\rho }_g^{\ast }}\right)}^{0.5}\frac{{\rho }_j^{\ast }}{{\rho }_j}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{T1\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ =k_{t1}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\end{array}\end{array}(21)$

$\begin{array}{c}\begin{array}{c}{{\displaystyle {}^{1a}\overline{\beta }}}_{T2,i,j,l}=|{\left(\frac{{\rho }_g}{{\rho }_g^{\ast }}\right)}^{0.25}\frac{{\rho }_i{\rho }_j^{\ast }}{{\rho }_i^{\ast }{\rho }_j}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{T2\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ +{\left(\frac{{\rho }_g}{{\rho }_g^{\ast }}\right)}^{0.25}\frac{{\rho }_j{\rho }_j^{\ast }}{{\rho }_j^{\ast }{\rho }_j}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{T2\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx|\\ =|k_{t2\left(1\right)}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx\\ +k_{t2\left(2\right)}\underset{x_{i-1}}{\overset{x_i}{{\displaystyle \int }}}\underset{x_{j-1}}{\overset{x_j}{{\displaystyle \int }}}\frac{\theta \left(v_{l-1}<u+v<v_l\right)u{\beta }_{S\left(1\right)}^{\ast }\left(u,v\right)}{uv\left(x_i-x_{i-1}\right)\left(x_j-x_{j-1}\right)}dydx|\end{array}\end{array}(22)$

According to the above equation, the standard agglomeration coefficients are only calculated before the iterative process. The coefficients of $k_B$, $k_{s1}$, $k_{s2}$, $k_{t1}$, $k_{t2\left(1\right)}$, and $k_{t2\left(2\right)}$ need an update at every time step. Therefore, the aerosol model is developed based on the aforementioned work. The flow chart of the radioactive aerosol analysis is shown in Figure 1, where $t$ is time, $\Delta t$ is the time step, $l$ is the section number, $m$ is the total section number, ${\rho }_p$ is the radioactive aerosol particle density, $v_l$ is the lower boundary of the section $l$, and $v_{l+1}$ is the upper boundary of the section $l$. Detailed information for calculating the coagulation coefficient is discussed in the study by Gelbard (1982). The radioactive aerosol density is updated at each time step. The Runge–Kutta integration methods are adopted to numerically solve the equation and update the radioactive aerosol conditions.

FIGURE 1

FIGURE 1. Flow chart of the model.

Verification and Validation of the Model

The aerosol model is validated by comparison with the benchmark, including two different coagulation problems and two different coagulation problems combined with deposition problems (Shaker et al., 2012). The aerosol model next is verified with the STORM experiment (Castelo et al., 1999), in which the main objective is to ensure the aerosol behaviors.

Validation With the Benchmark

Benchmark 1: Constant coagulation rate [$\text{β}\left(\text{u},\text{v}\right)=\text{constant}$, $\overline{\text{Ψ}}=0$]

It is assumed that the coagulation rate is constant, and the deposition rate and source term are zero. The exact solution is as follows.

$n\left(v,t\right)=\frac{4N_0}{v_{m0}\left(2+N_0\beta t\right)}exp-\frac{2}{v_{m0}\left(2+N_0\beta t\right)}v(23)$

where $N_0$ is the total initial number of particles per unit volume, and $v_{m0}$ is the initial mean volume of particles present in the distribution.

Benchmark 2: Linear coagulation rate [$\beta \left(u,v\right)={\beta }_1(u+v)$, $\overline{\text{Ψ}}=0$]

$\begin{array}{c}n\left(v,t\right)=\frac{N_0\left(1-T_1\right)}{v\sqrt{T_1}}\exp \left(-\left(1+T_1\right)\left(\frac{v}{v_{m0}}\right)\right)I_1\left(2\left(\frac{v}{v_0}\right)\sqrt{T_1}\right)\end{array}(24)$

$\begin{array}{c}{T}_1=1-\exp \left(-{\tau }_2\right)\end{array}(25)$

$\begin{array}{c}{\tau }_2=N_0\beta v_{0}t\end{array}(26)$

Benchmark 3: Constant coagulation rate and a constant deposition rata [$\text{β}\left(\text{u},\text{v}\right)=\text{constant}$ and $\overline{\text{Ψ}}=\text{constant}$]

$\begin{array}{c}n\left(v,t\right)=\frac{G{N}_0}{v_{m0}}\exp \left(-G\frac{v}{v_{m0}}\right)\end{array}(27)$

$\begin{array}{c}G=\frac{N+\frac{2{\lambda }_0}{\beta }}{N_0+\frac{2{\lambda }_0}{\beta }}\end{array}(28)$

$\begin{array}{c}N=\frac{2{\lambda }_0}{\beta }\frac{\exp \left(-{\lambda }_{0}t\right)}{\left(1+\frac{2{\lambda }_0}{\beta N_0}\right)-\exp \left(-{\lambda }_{0}t\right)}\end{array}(29)$

Benchmark 4: Linear coagulation rate and a constant deposition rata [$\beta \left(u,v\right)={\beta }_1(u+v)$ and $\overline{\text{Ψ}}=\text{constant}$]

$\begin{array}{c}n\left(v,t\right)=\frac{N_{0}Texp\left(\frac{T-1}{\theta }\right)}{v_0\left(\frac{v}{v_0}\right)\sqrt{g}}\exp \left(-\left(1+g\right)\left(\frac{v}{v_0}\right)\right)I_1\left(2\left(\frac{v}{v_0}\right)\sqrt{g}\right)\end{array}(30)$

$\begin{array}{c}T=\exp \left(-\theta \tau \right)\end{array}(31)$

$\begin{array}{c}g=1-\exp \left(\frac{T-1}{\theta }\right)\end{array}(32)$

$\begin{array}{c}\theta =\frac{{\lambda }_0}{N_0{v}_0\beta }\end{array}(33)$

The error value for the radioactive aerosol number of different section numbers between numerical and exact solutions to the equation GED is less than 10⁻³, as shown in Figure 2. The number of sections is selected as 20, 50, 100, and 300. The initial number of the radioactive aerosol number is 1 × 10¹⁰. By calculating the error value for chosen sections, the errors in the four selected sections gradually decreased. The error value is the least one when dividing the radioactive aerosol particle into 300 sections, as shown in Figure 2. It is mainly due to the effective reduction of the assumed initial distribution function when the number of sections increases. Therefore, the appropriate number of sections can be selected in the numerical simulation to reduce the error between the simulation values and the exact solution.

FIGURE 2

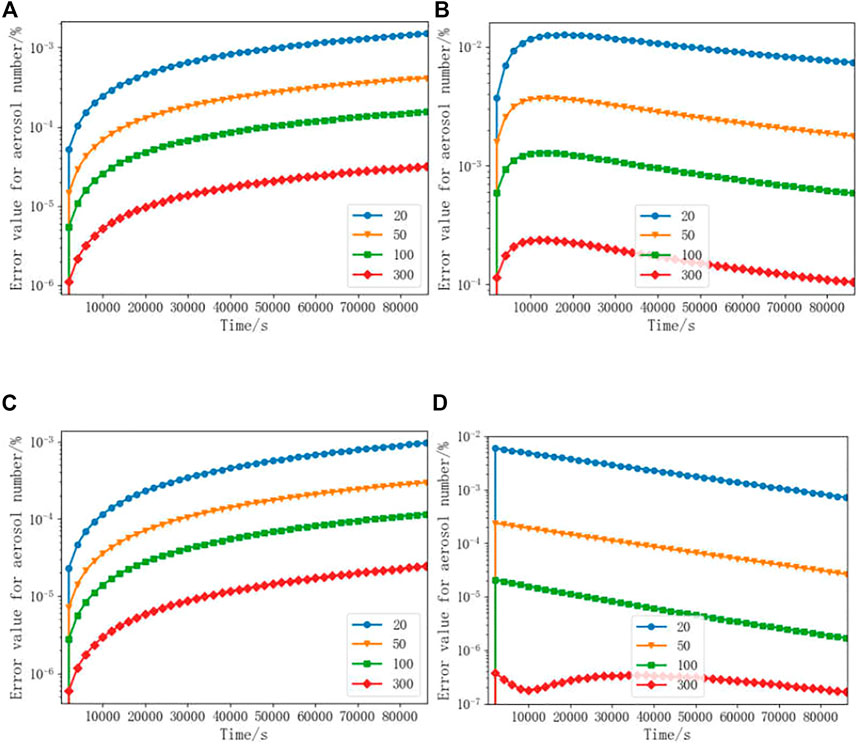
FIGURE 2. Error value for the number of radioactive aerosols for the different sections. [(A), Constant coagulation kernel; (B), linear coagulation kernel; (C), constant coagulation kernel and the constant deposition rate of particles; and (D), linear coagulation kernel and the constant deposition rate of particles].

The error value for the radioactive aerosol number of different initial particles between the numerical and exact solutions to the equation GDE is less than 10⁻³, as shown in Figure 3. The initial radioactive aerosol particle concentration is selected as ${10}^{10}/m^3$, ${10}^{11}/m^3$, and ${10}^{12}/m^3$. The section number of radioactive aerosol is 200 sections. By comparing the influence of different initial particles on the error, it appears that the error increases with the increasing initial radioactive aerosol particles, as shown in Figure 3.

FIGURE 3

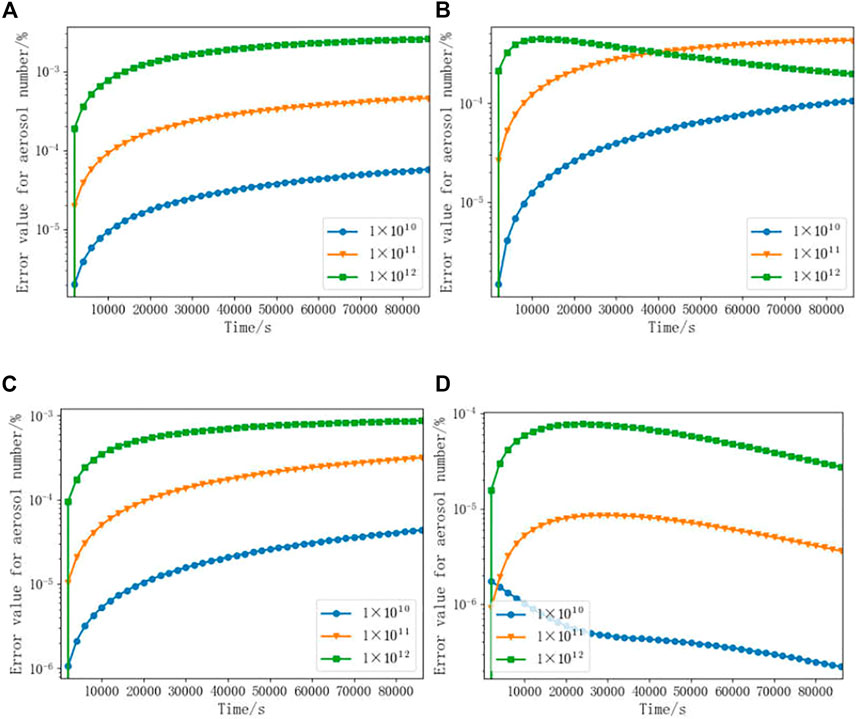
FIGURE 3. Error value for the number of radioactive aerosols for different initial particle numbers. [(A), Constant coagulation kernel; (B), linear coagulation kernel; (C), constant coagulation kernel and the constant deposition rate of particles; (D), linear coagulation kernel and the constant deposition rate of particles].

The distribution of the radioactive aerosol particle number is presented in Figure 4. The initial radioactive aerosol particle number is ${10}^{10}/m^3$. The radioactive aerosol particles are divided into 200 sections. Figures 4A,B depict the radioactive aerosol particles distribution of different coagulation kernels at 0 and 24 h, respectively. This is because a smaller radioactive aerosol particle when coagulated with a larger radioactive aerosol particle will form a new bigger radioactive aerosol particle. This leads radioactive aerosol particles to move from a less section to a larger section. The radioactive aerosol particles move to the larger section obviously in benchmark 1. Figures 4C,D show the radioactive aerosol particle distribution with deposition at 0 and 24 h, respectively. It shows that radioactive aerosol particle deposition has a significant impact on the behavior of radioactive aerosol in nuclear power plants.

FIGURE 4

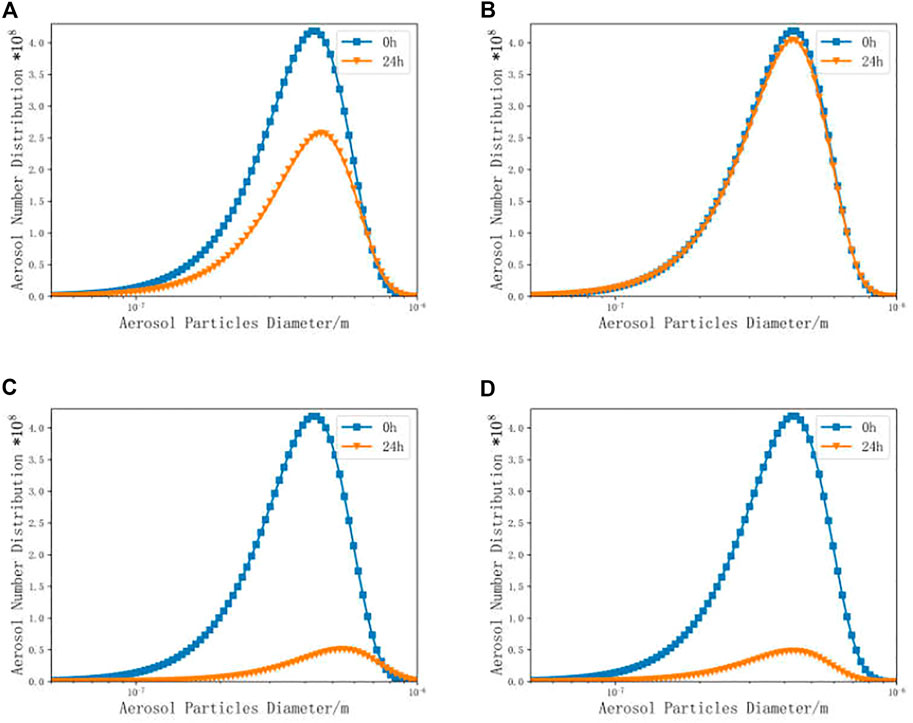
FIGURE 4. Distribution of radioactive aerosol particles. [(A), constant coagulation kernel; (B), linear coagulation kernel; (C), constant coagulation kernel and the constant deposition rate of particles; (D), linear coagulation kernel and the constant deposition rate of particles].

Verification With the Experiment

The STORM-SR11 test from the International Standard Problem 40 (ISP-40) is selected for aerosol model validation. The experiment consisted of two phases: the first focusing on deposition due to natural deposition mechanisms and the second on the resuspension process of aerosols under conditions of increased airflow. This study focuses on the first phase for validation.

Figure 5 shows a schematic diagram of the STORM test facility. The test section is a 5.0055 m long straight tube with an internal diameter of 63 mm made of stainless steel. In the deposition test, the supplied carrier gas and aerosol are mixed in a mixing tank and flow into the test section, where the exhaust from the test section is connected to a cleaning and filtration system. The aerosol used is tin oxide (SnO₂), and the carrier gas is a mixture of nitrogen, steam, argon, helium, and air.

FIGURE 5

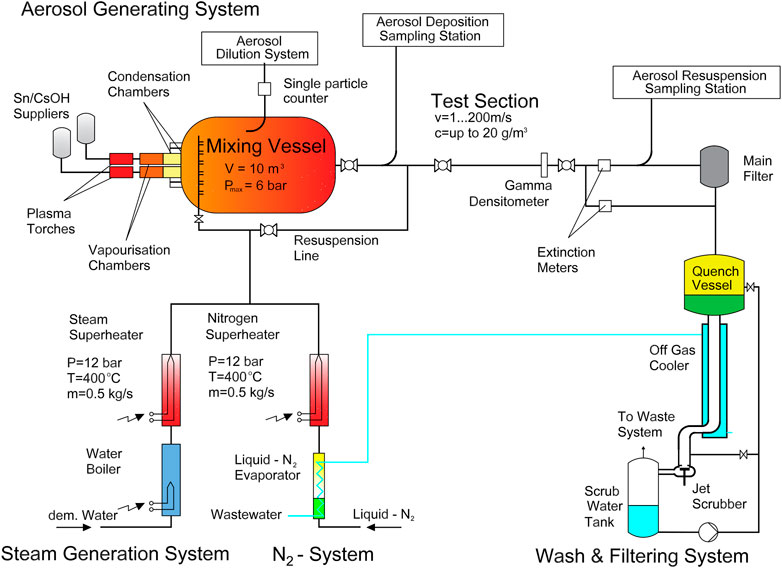
FIGURE 5. STORM experimental facility (Castelo et al., 1999).

The constant mass flow rate of the aerosol in the test is 3.83 × 10–4 kg/s. Assuming that its initial distribution follows a log-normal distribution, the number distribution particle size f(d) is defined as follows.

$\begin{array}{c}f\left(d\right)=\frac{1}{d\ln {\sigma }_g\sqrt{2\pi }}exp\left[-\frac{1}{2}{\left(\frac{\ln d-\ln d_g}{\ln {\sigma }_g}\right)}^2\right]\end{array}(34)$

where $d_g=\overline{\ln d}$ is the geometric mean diameter. $\ln {\sigma }_g={\left[\overline{{[\ln d-\ln d_g]}^2}\right]}^{1/2}$ is the standard geometric deviation. $d$ is the particle diameter. The aerosol distribution in the initial state is shown in Figure 6.

FIGURE 6

FIGURE 6. Initial aerosol distribution.

The time of the numerical simulation is the same as the experiment time of 9,000 s. Figure 7 shows the comparison between the simulated results and the experiment values. There are three distinct peaks, which are located at 1.02, 3.27, and 4.36 m. The maximum measured peak value is 0.292 kg/m². The peak of the measured values in the experiment is caused by the uneven surface of the test pipe joints. The simulated results and the measured values of the smooth pipes agree very well, and they all show a constant decrease in the aerosol mass along the pipe. Table 2 depicts the deposition mass of the simulated and measured values. The deposition mass changes with the number of nodes. As the number of nodes increases, the error between the simulated value and the measured value also decreases, which gave the minimum error 6.19%.

FIGURE 7

FIGURE 7. Aerosol deposition along with the test pipe.

TABLE 2

TABLE 2. The deposited mass.

Application of the Aerosol Model Under Severe Accident

Accident Sequences

In this research, an LBLOCA accident is selected to study the particle distribution and behavior of aerosols, with a breach diameter of 50 cm and a breach location in the hot leg. To maximize the release rate of aerosols under accident conditions, all safe injection systems in the primary system are shut down. The sequence of events is shown in Table 3, the pressure vessel failing at 5,489 s.

TABLE 3

TABLE 3. Sequence of events.

According to the source term evaluation results after the Fukushima accident, when a serious accident occurs, the monitoring data for I¹³¹, Cs¹³⁴, and Cs¹³⁷ are the most nuclides, and they are also the widely important nuclides in the radiation evaluation. The air source term of I¹³¹ is 60–390 PBq, the air source term of Cs¹³⁴ is 15–20 PBq, and the air source term of Cs¹³⁷ is 5–50 PBq, after the accident (Bois et al., 2014; Cervone and Franzese, 2014; Koo et al., 2014). Therefore, this study focuses on the fission product CsI. Figure 8 shows the variation of the mass of CsI aerosols with time for the accident sequence. The aerosol starts to increase at 8 s due to core exposure; when the temperature exceeds the melting temperature at 1,664 s, the core starts to melt and the aerosol release rate starts to increase dramatically and reaches a peak, with a small increase at 5,489 s due to pressure vessel failure.

FIGURE 8

FIGURE 8. Change of the CsI aerosol mass with time.

As the accident proceeds, the aerosol mass will peak at 2,000 and 6,710 s. Figure 9 shows the distribution of the aerosol mass at 2,000, 6,710, and 10,000 s. According to the mass distribution, the CsI aerosol particles mainly concentrated at 0.41 um. The mass of the CsI aerosol mass at 2,000 s is maximum in the containment, as shown in Figure 8, and the max aerosol mass in Figure 9 is 2 kg. When the pressure vessel failure is at 5,489 s, the CsI aerosol mass rises again and reaches a maximum at 6,710 s, in which the max aerosol particle mass is 1.43 kg. At the end of the calculation, the CsI aerosol mass drops to 1.22 kg. It can also be seen that according to Figure 9, the distribution of the CsI aerosol mass is declining with the accident process.

FIGURE 9

FIGURE 9. Distribution of the CsI aerosol mass.

Effect of the Natural Deposition on Aerosols

The natural deposition is the primary removal mechanism of aerosols. Thus, the effect of different natural deposition on aerosols is important. As shown in Figure 10, at the end of the simulation, gravity accounts for 54% of the total deposition mass, thermophoresis 28%, diffusion 3%, and Brownian diffusion 15%. Comparing the natural deposition mass of aerosols under the accident conditions, gravitational effect is more than the other three deposition mechanisms.

FIGURE 10

FIGURE 10. Natural deposition of the CsI aerosol within the containment.

Different deposition mechanisms can also have an impact on aerosol particle distribution. Figure 11 shows the effect of the different mechanisms on the aerosol particle. As can be seen from the figure, the natural deposition mechanism has a certain impact on the particles between 0.01 $\mu m$ and 0.03 $\mu m$ and has an obvious effect on the particle gravity between 2 $\mu m$ and 20 $\mu m$, especially because the excessive gravity will increase, leading to the removal of large-diameter particles.

FIGURE 11

FIGURE 11. Effect of the deposition mechanism on the distribution of aerosol diameter particles.

Influence of the Aerosol Particle Density

In this section, the influence of the radioactive aerosol particle density of a seven-component problem is discussed. The detailed density of the seven components is listed in Table 4. The initial components’ mass concentration and the initial radioactive aerosol particle numbers are shown in Figure 12. The different line types represent different component mass distribution and the radioactive aerosol particle number distribution. CsI is defined as component 1, UO₂ as component 2, H₂O as component 3, Te as component 4, B₂O₃ as component 5, Cd as component 6, and Pb as component 7. Number distribution is the axis on the left. Other curves are the axis on the right.

TABLE 4

TABLE 4. Component densities.

FIGURE 12

FIGURE 12. Initial aerosol distribution.

The particle number and component mass distribution in the presence of the aerosol coagulation process have been tabulated in Figures 13, 14. The difference in the radioactive aerosol particle number distribution can be seen in Figure 13. The aerosol particle number of the fixed density peaks at 0.45 $\mu m$, but the aerosol particle number of the changed density peaks at 0.65 $\mu m$. Therefore, the distribution of the changed density moves to larger particles, where the aerosol particle number decreases 16% relative to the fixed density. Figure 14 depicts the effect of different densities on the seven components’^, mass distribution. The mass distribution of seven components increases as the radioactive aerosol particles coagulate into bigger aerosol particles. The aerosol particle mass of the fixed density peaks at 0.63 $\mu m$, and the aerosol particle mass of the changed density peaks at 0.80 $\mu m$. So we can conclude that the density has a great influence on the multicomponent aerosol particle distribution.

FIGURE 13

FIGURE 13. Effect of different densities on the aerosol particle number distribution.

FIGURE 14

FIGURE 14. Effect of different densities on the component mass distribution.

Conclusion

This research adopts the improved multi-component aerosol sectional model to analyze the behavior of radioactive aerosol under severe accidents, which considers coagulation, deposition, and source term. The development model has demonstrated encouraging accuracy throughout the validation with the benchmark and experiment. The simulation result has a good agreement with the benchmark, where the error is less than 10⁻³. The comparison with the STORM experiment also has a satisfied result. The sensitivity analysis of the section number shows that the appropriate number can effectively improve the simulation error.

Furthermore, according to the analysis under the LBLOCA accident, gravity deposition is the main deposition method in the aerosol deposition mechanism, accounting for 54% of the total deposition. The natural deposition mechanism affects the particles in the 0.01 $\mu m$–0.03 $\mu m$, and for the aerosol particles in the 2 $\mu m$–20 $\mu m$, gravity has a significant influence on it. Otherwise, compared to the influence of different densities on the aerosol distribution at the end of the study, it shows that the fixed density is significantly different from the changed density. The changed density will lead aerosol particles to move to bigger sections. The results of this study can be used to predict the behavior of radioactive aerosols in the containment under severe nuclear accidents and provide a basis for emergency measures. Further optimization and improvement will be made for the problems existing in this model, containing the influence of the temperature on the aerosol behavior.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JW conceived and planned this work, wrote, and finalized the manuscript. XY and BZ provided constructive discussions. YG, QS, PG, SY, and CT contributed to review and revision.

Funding

This study is financially supported by the National Natural Science Foundation of China (Grant Nos. 12175116 and 11805112).

Conflict of Interest

Authors SY and CT were employed by the China Nuclear Power Operation Technology Corporation, Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipchenkov, V. M., Kiselev, A. E., Strizhov, V. F., Tsaun, S. V., and Zaichik, L. I. (2009). Advancement of Modeling Deposition and Coagulation of Aerosols in a Nuclear Reactor. Nucl. Eng. Des. 239 (4), 641–647. doi:10.1016/j.nucengdes.2008.12.025

CrossRef Full Text | Google Scholar

Allelein, H. J., Auvinen, A., Ball, J. S. G., and Weber, G. (2009). State of the Art Report on Nuclear Aerosols. OECD Report NEA/CSNI/R(2009)5.

Google Scholar

Bailly du Bois, P., Garreau, P., Laguionie, P., and Korsakissok, I. (2014). Comparison between Modelling and Measurement of marine Dispersion, Environmental Half-Time and 137cs Inventories after the Fukushima Daiichi Accident. Ocean Dyn. 64 (3), 361–383. doi:10.1007/s10236-013-0682-5

CrossRef Full Text | Google Scholar

Bird, G. A. (1994). Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Oxford Engineering Science Series. Oxford, New York: Clarendon Press, Oxford University Press.

Google Scholar

Castelo, A. R., Capitao, J. A., and Santi, G. D. (1999). International Standard Problem 40 Aerosol Deposition and Resuspension. Magn. Reson. Med. 21 (2), 302–307.

Google Scholar

Cervone, G., and Franzese, P. (2014). “Source Term Estimation for the 2011 Fukushima Nuclear Accident,” in Data Mining for Geoinformatics Methods and Applications. Editors G. Cervone, J. Lin, and N. Waters (New York: Springer), 49–64. doi:10.1007/978-1-4614-7669-6_3

CrossRef Full Text | Google Scholar

Gelbard, F. (1982). MAEROS User Manual. Sandia National Laboratories Report SAND80-0822, U. S. Nuclear Regulatory Commission Report NUREG/CR-1391. doi:10.2172/6459120

CrossRef Full Text | Google Scholar

Gelbard, F., and Seinfeld, J. H. (1978). Numerical Solution of the Dynamic Equation for Particulate Systems. J. Comput. Phys. 28 (3), 357–375. doi:10.1016/0021-9991(78)90058-X

CrossRef Full Text | Google Scholar

Gelbard, F., and Seinfeld, J. H. (1980). Simulation of Multicomponent Aerosol Dynamics. J. Colloid Interf. Sci. 78 (2), 485–501. doi:10.1016/0021-9797(80)90587-1

CrossRef Full Text | Google Scholar

Humphries, L. L., Beeny, B. A., Gelbard, F., Louie, D. L., and Phillips, J. (2017). MELCOR Computer Code Manuals. In Reference Manual (Vol. 2). Sandia National Laboratories Report SAND2017-0876 O. doi:10.2172/1433918

CrossRef Full Text | Google Scholar

Kljenak, I., Dapper, M., Dienstbier, J., Herranz, L. E., Koch, M. K., and Fontanet, J. (2010). Thermal-hydraulic and Aerosol Containment Phenomena Modelling in ASTEC Severe Accident Computer Code. Nucl. Eng. Des. 240 (3), 656–667. doi:10.1016/j.nucengdes.2009.12.002

CrossRef Full Text | Google Scholar

Koo, Y.-H., Yang, Y.-S., and Song, K.-W. (2014). Radioactivity Release from the Fukushima Accident and its Consequences: a Review. Prog. Nucl. Energ. 74 (3), 61–70. doi:10.1016/j.pnucene.2014.02.013

CrossRef Full Text | Google Scholar

Li, C., and Cai, R. (2020). Tutorial: the Discrete-Sectional Method to Simulate an Evolving Aerosol. J. Aerosol Sci. 150, 105615. doi:10.1016/j.jaerosci.2020.105615

CrossRef Full Text | Google Scholar

Lin, W., Chen, L., Yu, W., Ma, H., Zeng, Z., Lin, J., et al. (2014). Radioactivity Impacts of the Fukushima Nuclear Accident on the Atmosphere. Atmos. Environ. 102, 311–322. doi:10.1016/j.atmosenv.2014.11.047

CrossRef Full Text | Google Scholar

Liu, H. M., and Chan, T. L. (2018). Two-component Aerosol Dynamic Simulation Using Differentially Weighted Operator Splitting Monte Carlo Method. Appl. Math. Model. 62 (OCT), 237–253. doi:10.1016/j.apm.2018.05.033

CrossRef Full Text | Google Scholar

Murata, K. K., Williams, D. C., Tills, J., Griffith, R. O., Gido, R. G., Tadios, E. L., et al. (1997). Code Manual for Contain 2.0: A Computer Code for Nuclear Reactor Containment Analysis. Nuclear React. Tech.7. doi:10.2172/569132

CrossRef Full Text | Google Scholar

Porcheron, E., Lemaitre, P., Nuboer, A., and Vendel, J. (2008). Heat, Mass and Aerosol Transfers in spray Conditions for Containment Application. Jpes 2 (2), 633–647. doi:10.1299/jpes.2.633

CrossRef Full Text | Google Scholar

Raj Sehgal, B. (2012). Nuclear Safety in Light Water Reactors, 426–509. doi:10.1016/C2010-0-67817-5

CrossRef Full Text | Google Scholar

Rýdl, A., Fernandez-Moguel, L., and Lind, T. (2019). Modeling of Aerosol Fission Product Scrubbing in Experiments and in Integral Severe Accident Scenarios. Nucl. Tech. 205 (5), 655–670. doi:10.1080/00295450.2018.1511213

CrossRef Full Text | Google Scholar

Shaker, M. O., Aziz, M., Ali, R., Sirwah, M., and Slama, M. (2012). Numerical and Analytical Solutions of the Aerosol Dynamic Equation in Reactor Containment. Arab J. Nucl. Sci. Appl. 45 (4), 96–108. http://www.esnsaeg.com/download/researchFiles/10_96-108.pdf.

Google Scholar

Soffer, L., Burson, S. B., Ferrell, C. M., Lee, R. Y., and Ridgely, J. N. (1995). Accident Source Terms for Light-Water Nuclear Power Plants. Final Report. U.S. Nuclear Regulatory Commission. Washington, DC(United States): Division of Systems Technology. doi:10.2172/29438

CrossRef Full Text | Google Scholar

Wang, F., Cheng, X., and Gupta, S. (2021). Cocosys Analysis on Aerosol Wash-Down of Thai-AW3 experiment and Generic Containment. Ann. Nucl. Energ. 153, 108076. doi:10.1016/j.anucene.2020.108076

CrossRef Full Text | Google Scholar

Wang, K., Yu, S., and Peng, W. (2019). A Novel Moment Method Using the Log Skew normal Distribution for Particle Coagulation. J. Aerosol Sci. 134, 95–108. doi:10.1016/j.jaerosci.2019.04.013

CrossRef Full Text | Google Scholar

Wittneben, B. B. F. (2012). The Impact of the Fukushima Nuclear Accident on European Energy Policy. Environ. Sci. Pol. 15 (1), 1–3. doi:10.1016/j.envsci.2011.09.002

CrossRef Full Text | Google Scholar