Research on Thermal-Hydraulic Parameter Prediction Method of the Small Lead–Bismuth Fast Reactor Core Based on Adaptive RBF Neural Network

In this study, a cladding surface temperature prediction method based on an adaptive RBF neural network was proposed. This method can significantly improve the accuracy and efficiency of the thermal safety evaluation of the lead–bismuth fast reactor. First, based on the sub-channel analysis program SUBCHANFLOW, the core sub-channel model of the small lead–bismuth fast reactor SPALLER-100 was established. Second, the calculated 2000 groups of core power distribution and coolant flow distribution data were used as training samples. The adaptive RBF neural network model was trained to predict the surface temperature of fuel elements in the lead–bismuth fast reactor. Finally, by comparison, the effectiveness and superiority of the adaptive RBF neural network method were proved. The results indicate that the relative error of the maximum temperature of the fuel cladding predicted using the adaptive RBF neural network method was less than 0.5%, which can be used for the rapid prediction of the thermal and hydraulic parameters of the lead–bismuth fast reactor.

Introduction

As one of the six originally selected GEN IV nuclear energy systems of the Generation IV International Forum, the lead-cooled fast reactor (LFR) has attracted continuous and widespread research upsurge worldwide (Pioro 2016; Alemberti 2017; Forum 2014). The distinctive configurations and features offer the LFR distinctive advantages in the aspects of long-term fuel sustainability, safety, economics, proliferation resistance, and physical protection.

So far, major nuclear powerhouses have proposed their own LFR development road map and relevant conceptual designs. In terms of technology maturity, Russia’s BREST–300 takes the considerably leading position, which is expected to operate in 2026 (Forum 2014; Zabudko et al., 2021). In parallel, activities are also carried out on SVBR-100, which is based on the previous naval propulsion systems. Meanwhile, Japan has developed a small LFR (LSPR) and a direct-contact PBWFR (Takahashi et al., 2008; Alemberti et al., 2014). Europe proposed the industrial-size plant ELFR design along with its demonstrator called ALFRED (Alemberti et al., 2020). In the United States, only limited development of the SSTAR has been implemented (Smith et al., 2008). Moreover, a number of innovative LFR conceptual designs that are in various stages have been carried out for different purposes worldwide (Forum 2014). It is worth noting that the research on LFR systems in China has received great emphasis from research institutes to universities (Wu et al., 2016). One of the representative LFR activities in China is the CLEAR series carried out by the Institute of Nuclear Energy Safety Technology (INEST) within the Chinese Academy of Sciences (CAS), which adopts a pool-type configuration and use lead–bismuth eutectic (LBE) as the primary coolant. Other research institutes including the China Institute of Atomic Energy (CIAE) and Nuclear Power Institute of China (NPIC) also carried out their own LFR system concepts (Pioro 2016; Ma et al., 2019).

Actually, in the past decade, a large number of the major LFR design and engineering problems have been tackled, and improvements have been implemented in the practices. Issues such as system integration, component design, performance assessment, lead technology, and safety analysis (including accident mitigation) have got remarkable achievements. However, some technological problems still exist that needed to be resolved, for example, material corrosion, fuel development, and further safety validation. Among these problems, a common problem is the detection and prediction of the cladding maximum temperature, since the cladding maximum temperature is a key parameter of the LFR’s thermal safety criteria. It is well known that the high boiling temperature of lead allows the LFR to require neither pressurization nor concerning the overheating of the primary coolant. However, the cladding maximum temperature still needs to be considered in the LFR thermal safety analysis due to its higher coolant operating temperature. The chemical reaction between the LBE and the cladding material, and the failure of the cladding are closely related to the cladding temperature.

In recent years, the neural network has been proven that it is qualified to provide accurate and fast thermal parameter prediction. The representative application is reported in Cong et al. (2013), which uses an artificial neural network and wavelet analysis to carry out the nonlinear research of reactor thermal-hydraulic analysis. Cong’s work proves that the neural network method is feasible in thermal-hydraulic analysis. Subsequently, much research has been carried out to verify the feasibility and accuracy of the neural network method in different aspects of reactor thermal-hydraulic analysis. Wang used the BP artificial neural network method to predict the three key parameters of core fuel refueling of Qinshan phase II PWR (Wang et al., 2020). Based on the regularized radial basis function (RBF) neural network model, Peng studied the power distribution of the ACP-100 modular reactor. It is not only concluded that the method can accurately reconstruct the axial power distribution of the reactor core but also proved that the method has good robustness and can overcome the inherent uncertainty in the power distribution reconstruction (Peng et al., 2014). Furthermore, Xia constructed a real-time three-dimensional distribution monitoring system of core power by using the nuclear measurement system and RBF neural network, which improved the accuracy and real-time performance of monitoring (Xia et al., 2014). Chen established a feature fusion neural network with seven layers to predict the key safety parameters of the Qinshan reactor. The prediction results show great agreement with the simulation data conducted using the COSMO code (Chen et al., 2022). Although the neural network method has been widely used in the prediction of thermal-hydraulic parameters of reactors and shows great agreement beyond expectation, the relevant research on lead–bismuth fast reactors is still insufficient.

In the present study, the adaptive RBF neural network method is selected to predict the cladding surface temperature of the SPALLER-100 reactor after comparing the performance of several neural network methods. (At present, the BP neural network and RBF neural network are often used to study, so this study takes the BP neural network as a typical comparison.) The training data samples used as a training set and prediction set are obtained by SUBCHANFLOW program. The performance and generalization ability of the adaptive RBF neural network were also verified.

Mathematical Model and Method

A Brief Introduction of the RBF Neural Network

The radial basis function (RBF) neural network is a feedforward neural network with a three-layer structure, namely, the input layer, the output layer, and the hidden layer as is shown in Figure 1 (Hartman, Keeler, and Kowalski 1990; Park and Sandberg 1991). The basic mathematical model of the RBF neural network is a locally distributed non-negative nonlinear function with central radial symmetric decay. It can approach any nonlinear function with arbitrary precision and has the ability to approximate the error of global, which fundamentally solves the local optimization problem of the BP neural network. Moreover, it has a compact topology so that the structural parameters can realize separation learning and achieves quick convergence. This characteristic is quite suitable for the real-time control.

FIGURE 1

FIGURE 1. The structure of the RBF neural network.

The output of hidden layer neurons is as follows:

${\text{h}}_{\text{j}}=\text{e}\text{x}\text{p}\left(-\frac{\Vert \text{x}-{\text{c}}_{\text{j}}{\Vert }^2}{2{\text{b}}_{\text{j}}^2}\right),(1)$

where $x$ = ${\left[x_i\right]}^T$ represents the input of the network, the hidden layer output of the network is expressed as $h$ = ${\left[h_j\right]}^T$, $h_j$ is the output of the jth neuron in the hidden layer, $c$ = $\left[c_{ij}\right]$ = $\left[\begin{array}{ccc}{c}_{11}& \cdots & c_{1m}\\ ⋮& \ddots & ⋮\\ c_{n1}& \cdots & c_{nm}\end{array}\right]$ is the coordinate vector of the center point of the Gaussian basis function of the jth neuron in the hidden layer, $i=\mathrm{1,2,3},\dots ,n$, $j=\mathrm{1,2,3},\dots ,m$; $b={[b_1,b_2,\dots ,b_m]}^T$, and $b_j$ is the width of the Gaussian basis function of the jth neuron in the hidden layer. The implied number of layers in this article is 20, and the transfer function is tanh.RBF network weights are as follows:

$\text{ω}={[{\text{ω}}_1,\dots ,{\text{ω}}_{\text{m}}]}^{\text{T}},(2)$

The output of RBF network is as follows:

${\text{y}}_{\text{m}}\text{t}={\text{ω}}_1{\text{h}}_1+\dots +{\text{ω}}_{\text{m}}{\text{h}}_{\text{m}},(3)$

The error index of the RBF neural network can be written as follows:

$\text{E}\left(\text{t}\right)=\frac{1}{2}{(\text{y}\left(\text{t}\right)-{\text{y}}_{\text{m}}\left(\text{t}\right))}^2,(4)$

In addition, the RBF neural network has the characteristics of self-learning, self-organizing, and self-adaptive functions. Meanwhile, the RBF neural network has the uniform approximation to nonlinear continuous functions and high learning efficiency. The advantages expressed before offers the RBF neural network the capability of large-scale data fusion and data high-speed parallel processing. Presently, the RBF neural network has been successfully applied to the aspects of nonlinear function approximation, time series analysis, data classification, pattern recognition, information processing, image processing, system modeling, control, fault diagnosis, etc. (Seshagiri and Khalil 2000; Li et al., 2004; Wang and Yu 2008).

Adaptive RBF Neural Network

An adaptive algorithm is a process aimed at approaching the target continuously, which is based on a gradient algorithm. By introducing the adaptive algorithm into the conventional neural network, the “over-fitting” phenomenon can be effectively eliminated. Thus, it can significantly reduce the dependence on the accuracy of the neural network identifier and dramatically improve the weakness of the conventional neural network.

According to mature literature, compared with the adaptive BP neural network, the adaptive RBF neural network can effectively improve the performance of the controller when the system has large uncertainty and has a better prediction effect (Zhu et al., 2008). In view of this, the adaptive gradient descent (Adam) algorithm is adopted to overcome the drawbacks of falling into local minimum and slow convergence that the traditional BP neural network has. The flowchart of the adaptive RBF neural network algorithm is demonstrated in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of adaptive RBF neural network algorithm.

The Adam algorithm updates the parameters as follows:

${\text{θ}}_{\text{t}+1}={\text{θ}}_{\text{t}}-\frac{\text{η}}{\sqrt{{\widehat{\text{ν}}}_{\text{t}}}+\text{ϵ}}{\widehat{\text{m}}}_{\text{t}},(5)$

where $\eta$ is the learning rate, which controls the update ratio of weights and takes a smaller value, which will make the training converge to better performance, $t$ is the iteration time, ${\widehat{m}}_t$ is the weighted average of the gradient, and ${\widehat{\nu }}_t$ is the weighted deviation. During training, $\beta$ represents the error signal between the output layer and the hidden layer, ${\beta }_1$ is the exponential decay rate of the first moment estimation, and ${\beta }_2$ is the exponential decay rate of the second moment estimation. In this article, $\eta =0.001$, ${\beta }_1=0.9$, ${\beta }_2=0.999$, and $\mathrm{ϵ}={10}^{-8}$. The detailed process is shown in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of Adam algorithm.

SPALLER-100 Introduction

SPALLER-100 is a small lead–bismuth fast reactor with a thermal power of 100 MW (Liu et al., 2020). The schematic diagram of the small lead–bismuth fast reactor SPALLER-100 core is shown in Figure 4 (cross-section view) and the main parameters of the SPALLER-100 is listed in Table 1. The core of the SPALLER-100 is hexagonal and consists of 48 fuel assembly, 13 control rod components, 66 reflector components, and 126 shielding components. The coolant and reflector were 208 Pb–Bi, and the shielding material was B₄C. In this study, the SPALLER-100 is chosen as the research target.

FIGURE 4

FIGURE 4. Cross-section view and the nodalizaiton scheme of SPALLER-100 core.

TABLE 1

TABLE 1. Main parameters of the SPALLER-100.

SUBCHANFLOW Code Description

The data used for training the RBF neural network is conducted using the SUBCHANFLOW code. SUBCHANFLOW is a sub-channel flow code to analyze thermal-hydraulic phenomena in the core of pressurized water reactors, boiling water reactors, and innovative reactors operated with gas or liquid metal as coolant, which is developed by the Karlsruhe Institute of Technology (Imke and Sanchez. 2012).

The SUBCHANFLOW code can handle rectangular and hexagonal geometry fuel rod types. The total flow or each channel flow can be selected as the boundary conditions. According to the friction force at the inlet of the tube bundle, the flow can be automatically allocated to the parallel channel. In addition, the given inlet and outlet pressure difference boundary can be used for steady-state calculation. The inlet fluid temperature and outlet pressure are always given as boundary conditions. In this study, the SPALLR-100 core channel is divided and numbered first. The nodalization scheme of the SPALLER-100 core is shown in Figure 4A. The nodalization scheme of the SPALLER-100 core is shown in Figure 4B. The heat conduction of fuel rod (heating part) in the SUBCHANFLOW is solved using the standard finite volume method. The convective heat transfer coefficient between the fuel rod and coolant is calculated according to the empirical relationship between the heat transfer form and coolant flow pattern. The constitutive relation used in the SUBCHANFLOW code is listed as follows:

(1) Physical properties model: the thermophysical properties data of lead–bismuth alloy are from the HLMC handbook.

(2) Thermal conductivity model: SUBCHANFLOW uses the full implicit finite difference method to calculate the heat conduction process in fuel core and cladding materials.

(3) Heat convection model: the general heat transfer equation of liquid metal heat transfer:

$\text{N}\text{u}=\text{A}+\text{B}\cdot \text{P}{\text{e}}^{\text{C}},(6)$

(4) Pressure loss model: the Novendstern model and Rehme model are used for the pressure drop calculation.

Performance Analysis of the Adaptive RBF Neural Network

The feasibility, accuracy, and efficiency of the RBF neural network are verified based on the steady-state data in this section. First, the hottest assembly in the core is found according to the SUBCHANFLOW calculation results. This searching process repeats 100 times to guarantee the result’s reliability. Second, focusing on the hottest assembly, several groups of data were randomly selected with the power ranging from 0 to 1,200 kW and the mass flow ranging from 1,200 to 2,200 kg/s. Third, these data are calculated using the SUBCHANFLOW code as an input. Finally, 2000 groups of effective data samples are obtained. Among these 2000 groups of data samples, 1900 groups are selected as the training set, and the remaining 100 groups are selected as the prediction set. Then, the prediction model is evaluated by comparing the error between the prediction results and the calculation result.

Figure 5A and Figure 6A demonstrate the error band between the prediction result and the calculation result of the adaptive BP neural network and adaptive RBF neural network separately. It can be observed that the prediction results conducted using the adaptive RBF neural network show a good agreement with the calculation results in the cladding maximum temperature, since the error bound is within 5%. Meanwhile, Figure 5B and Figure 6B show the comparison results between the predicted and experimental values of the two methods. By comparing the two figures, it can be seen that the fitting results of the two lines in Figure 6B are better, that is, the adaptive RBF neural network shows a better performance in predicting cladding maximum temperature than the adaptive BP neural network.

FIGURE 5

FIGURE 5. The error comparison diagram and the error bound of adaptive BP neural network.

FIGURE 6

FIGURE 6. The error comparison diagram and the error bound of adaptive RBF neural network.

Table 2 illustrates the efficiency and accuracy of different methods after 50 times prediction. The adaptive RBF neural network reaches the average relative error of 0.10 within 6 s and 160 iteration times, which is fully superior to the adaptive BP neural network. Therefore, the adaptive RBF neural network prediction model has better accuracy and feasibility in predicting cladding maximum temperature.

TABLE 2

TABLE 2. Comparison of calculation efficiency.

The Transient Prediction Performance Analysis

In the transient response analysis part, the axial and radial power of each fuel rod in the fuel assembly is assumed and uniformly distributed for simplification, since the power distribution has a little influence on the transients. All the coolant channels in a single assembly can be merged into a large channel centered on the fuel rod with the equivalent heating perimeter and wetted perimeter. The initial power is set to 30 MW. Figure 7 shows the variation of the coolant mass flow and the variation of the maximum cladding temperature conducted using the SUBCHANFLOW code.

FIGURE 7

FIGURE 7. Variation of coolant mass flow and cladding maximum temperature within 80s.

Among these calculation data, 800 groups were randomly selected in the 80s data sample, 750 groups were used as the training set, and the remaining 50 groups were used as the prediction set. Similar to Performance Analysis of the Adaptive RBF Neural Network, the mass flow and the heating power is considered as the input and the cladding maximum temperature is considered as the output. The neural network is operated to predict the cladding maximum temperature in the following 5s, that is, 80–85s. Thus, the error bound between the prediction results and the calculation results is used to evaluate the transient performance of different prediction methods, which is shown in Figures 8A,B, Figures 9A,B.

FIGURE 8

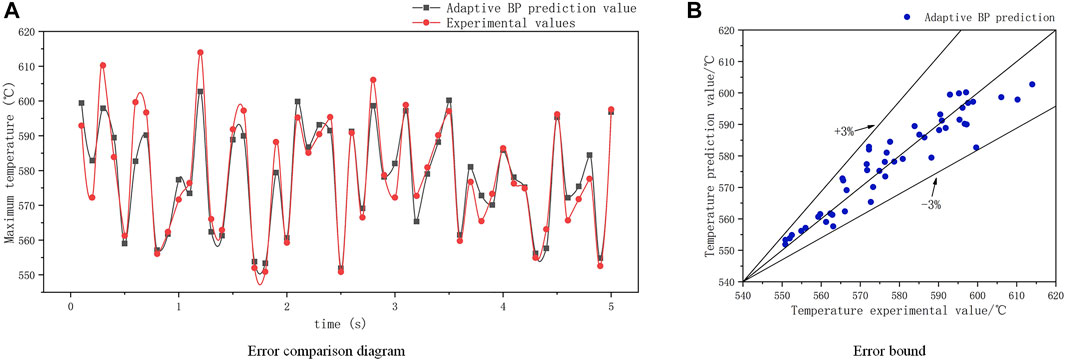
FIGURE 8. The error comparison diagram and the error bound of adaptive BP neural network under coolant mass flow variation condition.

FIGURE 9

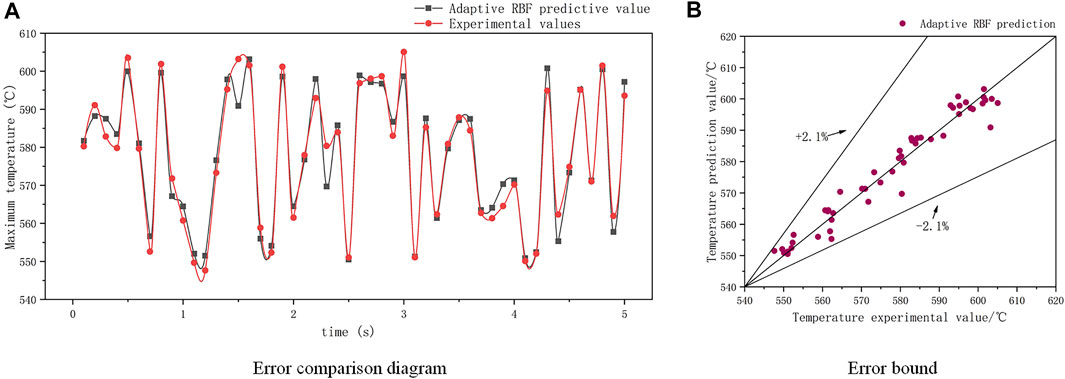
FIGURE 9. The error comparison diagram and the error bound of adaptive RBF neural network under coolant mass flow variation condition.

Both the adaptive BP neural network and adaptive RBF neural network show remarkable transient prediction ability to the mass flow variation with the error bound being within 3%. It can be concluded from Figures 8B, 9B that the difference between the two prediction results is not large. However, in the error point diagram given by Figures 8A, 9A, it can be clearly seen that the results of adaptive RBF are compared with adaptive BP, and most of the data are close to the center line, indicating that its stability is better. The average errors are shown in Table 3. The maximum relative error of adaptive RBF neural network is 2.1%, and the average absolute error is 2.94°C, which proves the adaptive RBF neural network is able to deal with transient conditions as well. Also, it is reasonable to infer that the adaptive RBF neural network will have a better accuracy when extending the prediction time, since the preorder prediction result will influence the following prediction result.

TABLE 3

TABLE 3. Comparison of average error under mass flow variation condition.

Prediction Performance to the Power Variation

Similarly, transient responses to the power variation are verified by setting the initial coolant mass flow to 4,000 kg/s, and assuming the core power changes. Figure 10 shows the change of core power and the cladding maximum temperature calculated using the SUBCANFLOW code within 80s. The effectiveness of the adaptive RBF neural network under power variation conditions is analyzed.

FIGURE 10

FIGURE 10. Variation of reactor power and cladding maximum temperature within 80s.

Figure 11 gives the predicting error bound of the adaptive BP neural network and adaptive RBF neural network during power variation condition separately. The average error data are shown in Table 4. It can be seen that compared with the adaptive BP results, the adaptive RBF has more error points close to the center line, and its accuracy is better. In addition, the correctness of the aforementioned results can be verified from the point-line diagrams of the predicted and experimental values given in Figure 11A and Figure 11B. As shown in Table 4, the error of adaptive RBF neural network is less than 1%, which is slightly better than the adaptive BP neural network prediction method.

FIGURE 11

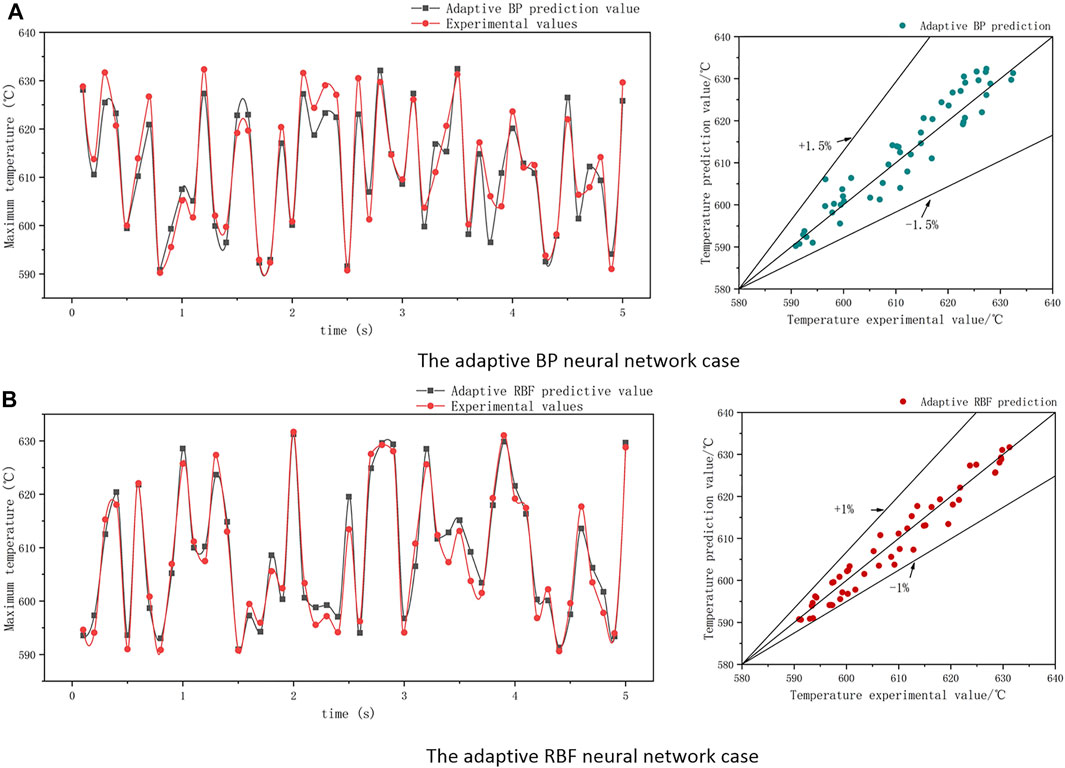
FIGURE 11. The accuracy comparation between adaptive BP neural network and adaptive RBF neural network.

TABLE 4

TABLE 4. Average error results calculated by different methods.

Combined with the conclusion conducted in Prediction Performance to the Power Variation, it can be concluded that the adaptive RBF neural network shows good effectiveness and superiority in predicting cladding maximum temperature under power variation and coolant mass flow variation conditions. Thus, the adaptive RBF neural network can be used to real-time predict the dynamic value of LFR cladding maximum temperature, which is obviously beneficial for the reactor’s safety under both transient conditions and accident.

Conclusion

This study analyzes the performance of the adaptive RBF neural network in predicting the cladding maximum temperature for the typical LFR. The feasibility, accuracy, and efficiency of the adaptive RBF neural network under both steady-state and transient conditions are evaluated. The conclusions drawn from the study are summarized as follows:

(1) A cladding maximum temperature prediction method based on the adaptive RBF neural network for the LFR is proposed. The SUBCHANFLOW program is used to generate data for the RBF neural network training.

(2) By comparing the adaptive RBF neural network and the adaptive BP neural network, the adaptive RBF neural network shows full superiority. The adaptive RBF neural network has good feasibility, accuracy, and efficiency in predicting the cladding maximum temperature of the lead–bismuth fast reactor.

(3) The adaptive RBF neural network can accurately predict the trend of the cladding maximum temperature in short time under the transient conditions of power variation and coolant mass flow variation.

(4) The real-time thermal-hydraulic parameter prediction capability of the adaptive RBF neural network is of great significance for the LFR’s thermal safety.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

RL contributes to the nodalizaiton scheme and debugging of the SUBCHANFLOW code.

Funding

This study is funded by the Research Foundation of Education Bureau of Hunan Province, China (Grant No. 20B490) and Hunan Science and Technology Innovation Team Project (Grant No. 2020RC4053).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alemberti, A., Caramello, M., Frignani, M., Grasso, G., Merli, F., Morresi, G., et al. (2020). ALFRED Reactor Coolant System Design. Nucl. Eng. Des. 370, 110884. doi:10.1016/j.nucengdes.2020.110884

CrossRef Full Text | Google Scholar

Alemberti, A., Smirnov, V., Smith, C. F., and Takahashi, M. (2014). Overview of lead-cooled Fast Reactor Activities. Prog. Nucl. Energ. 77, 300–307. doi:10.1016/j.pnucene.2013.11.011

CrossRef Full Text | Google Scholar

Alemberti, A. (2017). The lead Fast Reactor: an Opportunity for the Future?

Google Scholar

Chen, Y., Wang, D., Kai, C., Pan, C., Yu, Y., and Hou, M. (2022). Prediction of Safety Parameters of Pressurized Water Reactor Based on Feature Fusion Neural Network. Ann. Nucl. Energ. 166, 108803. doi:10.1016/j.anucene.2021.108803

CrossRef Full Text | Google Scholar

Cong, T., Su, G., Qiu, S., and Tian, W. (2013). Applications of ANNs in Flow and Heat Transfer Problems in Nuclear Engineering: a Review Work. Prog. Nucl. Energ. 62, 54–71. doi:10.1016/j.pnucene.2012.09.003

CrossRef Full Text | Google Scholar

Houssin, D., Dujardin, T., Cameron, R., Tam, C., Paillere, H., Baroni, M., and Vance, R. (2015). Technology Road-Map-Nuclear Energy (No. NEA-IEA--2015). Organisation for Economic Co-operation and Development. Hartman, Eric J, James D Keeler, and Jacek M %J Neural Computation Kowalski. Layered neural networks with Gaussian hidden units as universal approximations 2, 210–215.

Google Scholar

Imke, U., and Sanchez, V. H. (2012). Validation of the Subchannel Code SUBCHANFLOW Using the NUPEC PWR Tests (PSBT). Science and Technology of Nuclear Installations.

Google Scholar

Li, Y., Qiang, S., Zhuang, X., and Kaynak, O. (2004). Robust and Adaptive Backstepping Control for Nonlinear Systems Using RBF Neural Networks. IEEE Trans. Neural Netw. 15 (3), 693–701. doi:10.1109/tnn.2004.826215

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Zhao, P., Zhang, B., Yu, T., Xie, J., Chen, Z., et al. (2020). Study on Core Conceptual Design of Ultra-long Life Small Naturally Circulating Pb - Bi Fast Reactor. At. Energ. Sci. Tech. 54 (7), 1254–1265.

Google Scholar

Ma, Z., Ma, Z., Wu, Y., Gao, F., Hei, B., and Su, G. H. (2019). Design and R&D Progress of Core Assembly Deformation Test Facility for China Demonstration Fast Reactor. Nucl. Eng. Des. 348, 65–77. doi:10.1016/j.nucengdes.2019.04.002

CrossRef Full Text | Google Scholar

Park, J., and Sandberg, I. W. (1991). Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 3 (2), 246–257. doi:10.1162/neco.1991.3.2.246

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, X., Ying, D., Li, Q., and Wang, K. (2014). Application of Regularized Radial Basis Function Neural Network in Axial Power Distribution Reconstruction of Reactor Core. Nucl. Power Eng. 35 (S2), 12–15.

Google Scholar

Pioro, I. (2016). Handbook of Generation IV Nuclear Reactors. Woodhead Publishing.

Google Scholar

Seshagiri, S., and Khalil, H. K. (2000). Output Feedback Control of Nonlinear Systems Using RBF Neural Networks. IEEE Trans. Neural Netw. 11 (1), 69–79. doi:10.1109/72.822511

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, C. F., Halsey, W. G., Brown, N. W., Sienicki, J. J., Moisseytsev, A., and Wade, D. C. (2008). SSTAR: The US lead-cooled Fast Reactor (LFR). J. Nucl. Mater. 376 (3), 255–259. doi:10.1016/j.jnucmat.2008.02.049

CrossRef Full Text | Google Scholar

Takahashi, M., Uchida, S., Yamada, Y., and Koyama, K. (2008). Safety Design of Pb–Bi-Cooled Direct Contact Boiling Water Fast Reactor (PBWFR). Prog. Nucl. Energ. 50 (2-6), 269–275. doi:10.1016/j.pnucene.2007.11.082

CrossRef Full Text | Google Scholar

Wang, Duan., Wang, Weice., and Pan, Cuijie. (2020). Key Parameters of Core Refueling for Pressurized Water Reactors Based on Adaptive BP Neural Network. At. Energ. Sci. Tech. 54, 112–118.

Google Scholar

Wang, S., and Yu, D. L. (2008). Adaptive RBF Network for Parameter Estimation and Stable Air-Fuel Ratio Control. Neural Networks 21 (1), 102–112. doi:10.1016/j.neunet.2007.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Bai, Y., Song, Y., Huang, Q., Zhao, Z., and Hu, L. (2016). Development Strategy and Conceptual Design of China lead-based Research Reactor. Ann. Nucl. Energ. 87, 511–516. doi:10.1016/j.anucene.2015.08.015

CrossRef Full Text | Google Scholar

Xia, Hong., Li, Bin., and Liu, Jianxin. (2014). Research on Three-Dimensional Power Distribution Method of Pressurized Water Reactor Core Based on RBF Neural Network. At. Energ. Sci. Tech. 4, 48.

Google Scholar

Zabudko, L. M., Grachev, A. F., Zherebtsov, A. A., Lachkanov, E. V., Mochalov, Y. S., Skupov, M. V., et al. (2021). Status on Performance Study of Mixed Nitride Fuel Pins of BREST Reactor Type. Nucl. Eng. Des. 384, 111430. doi:10.1016/j.nucengdes.2021.111430

CrossRef Full Text | Google Scholar

Zhu, Q., Fei, S., Zhang, T., and Li, T. (2008). Adaptive RBF Neural-Networks Control for a Class of Time-Delay Nonlinear Systems. Neurocomputing 71 (16-18), 3617–3624. doi:10.1016/j.neucom.2008.04.012

CrossRef Full Text | Google Scholar