Analysis of Current Differential Protection Considering Rated Capacity of Inverter-Interfaced Renewable Plant

With the increasing capacity of grid-connected renewable energy power plants (REPPs), the fault current characteristics are remarkably altered. The limited amplitude and controlled initial phase angle of REPPs’ short-circuit current become highlighted. As a result, the differential current is no longer greater than restraint current on both sides of the protected devices when a fault occurs. It may lead to mal-operation of the current differential protection, which is used widely. It is necessary to demonstrate the cause-and-effect relationship between REPPs’ rated capacity and the protection adaptability. To solve this problem, the relationship between the rated capacity of inverter-interfaced REPP (IIREPP) and fault current amplitude, as well as its initial phase angle, is deduced first based on the IIREPPs’ fault behaviors. Further, by analyzing the influence of different rated capacity of REPPs on the ratio of operate to restraint current, the analytical expression of the IIREPP’s maximum rated capacity is deduced, which is suitable for analyzing the adaptability of differential protection. Finally, the simulation tests were carried out based on PSCAD/EMTDC. The test results show that the aforementioned expression is effective for evaluating the adaptability of current differential protection.

Introduction

In order to reduce the carbon emission, the inverter-interfaced renewable energy power plant (IIREPP) proportion becomes higher and higher (Li et al., 2021). The IIREPPs often refer to the photovoltaic power stations or direct-drive wind farms. Different from traditional synchronous generators, the fault characteristics of IIREPPs are influenced by the control strategies of inverters that have low overcurrent ability and rapid transient response (Li et al., 2021; Liu et al., 2022; Li et al., 2022a; Li et al., 2022b; Li et al., 2022c). As a result, the fault currents provided by the power grid connected with a large number of IIREPPs are remarkably altered. The existing protection principles are no longer available (Zhou et al., 2022).

The percentage restrained differential protection is widely applied to the outgoing transmission line connected with the IIREPPs (Telukunta et al., 2017). The protection can provide high sensitivity when the IIREPPs’ proportion is small. However, once the IIREPPs’ capacity is near one of the connected power grids, the sensitivity becomes lower. It is because fault current contributions from the IIREPPs have a great impact on the differential- and restraint-current in the protection zone (Jia et al., 2018). In order to evaluate the adaptability of current differential protection for outgoing lines, it is essential to reveal the relationship between the IIREPPs’ rated capacity and their fault current.

In order to reveal the IIREPPs’ fault current characteristics, the fundamental amplitude of short-circuit current was first deduced, considering the influence of fault-ride-through (FRT) control strategy (Liu et al., 2018). However, the initial phase angle of fault current cannot be developed. The angle is not only affected by FRT control strategy, but also related to the faulty voltage dip, the rated capacity of IIREPP, and so on. Recently, the studies on the angle are less. Only in the literature (Li et al., 2018), the relationship between the initial phase angle and the positive-to-negative sequence current reference is deduced, taking the impact of the FRT control strategy into consideration. However, the impact of IIREPPs’ rated capacity on the angle was ignored.

For analyzing the adaptability of current differential protection, it was revealed that the sensitivity of percentage restrained differential protection would be reduced because of the IIREPPs’ reactive power compensation (Wang et al., 2017), but the result was from the simulation analysis. Further, the protection sensitivity was analyzed theoretically (Han et al., 2018), but this study focused only on the impact of the limited amplitude of fault current from the IIREPPs. Actually, it was pointed that the tripping failures of differential protection relays installed in a weak grid with large-scale IIREPPs are caused by angular difference of the two terminals’ fault current (Li et al., 2018). However, the IIREPPs’ maximum capacity was not deduced for ensuring the current differential protection is perfectly selective. Thus, the maximum allowable capacity of the IIREPPs connected with T-connection lines was theoretically studied, considering the influence of two-terminal current differential protection (Liu and Li, 2016). However, the ratio of operate to restraint current was not considered. Moreover, the maximum capacity was not represented by a mathematical expression.

In these previous studies, the relationship between the IIREPPs’ capacity and the ratio of operate to restraint current is not taken into account. As a result, the existing studies on the IIREPPs’ allowable maximum capacity cannot be used for estimating the adaptability of the percentage restrained differential protection. Main contributions of this article are as follows: (1) to reveal the relationship between the ratio of operate to restraint current and IIREPPs’ rated capacity based on the IIREPPs’ fault current characteristics and (2) to deduce the maximum capacity expression of the IIREPPs privately connected with the outgoing line that differential protection is applied to.

In this article, considering the IIREPPs’ rated capacity, the fundamental amplitude and initial phase angle expression of short-circuit current are first derived. Further, the influence of the rated capacity on the two-terminal restraint- and differential-current of an outgoing line with the IIREPPs is analyzed. The IIREPPs’ maximum rated capacity is expressed theoretically. Finally, the capacity expression is verified by means of MATLAB calculation and PSCAD/EMTDC simulation analysis.

Fault Current Expression Considering IIREPPS’ Capacity

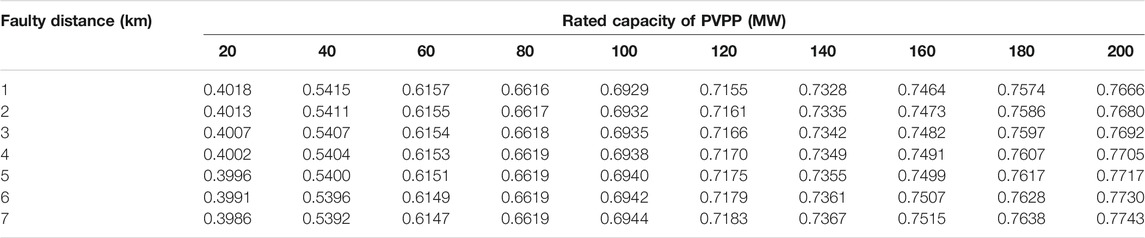
As shown in Figure 1A, each inverter-interfaced generation unit (IIGU) is connected to the box transformers through DC/AC inverter in the IIREPPs. The inverters can isolate IIGU from the connected grid. Thus, the fault currents provided by the IIGUs included in an IIREPP are mainly determined by the fault responses of inverters’ control and protection system.

FIGURE 1

FIGURE 1. (A) IIGU’s topology. (B) Grid connected topology of PVPP. (C) Operation characteristics of percentage restrained differential protection. (D) Equivalent circuit diagram.

Because of a grid fault, three-phase voltages U_g-abc are altered, but the voltages U_i-abc at the inverter’s AC side cannot immediately vary. As a result, the currents flowing through the inverter i_abc rapidly increase. The inverter’ dual closed-control loop undergoes a transient response process. If the amplitudes of i_abc reach the inverters’ maximum allowable current, the current limiter is activated. Meanwhile, the DC-link voltage U_dc increases. If the positive-sequence component of U_g-abc is less than 0.9 p.u. and U_dc is greater than U_dc-1^*, the chopper circuit is triggered. The mentioned transient response process is approximately one to two cycles. In this stage, the fault current characteristics fed by IIGUs are too complex to represent. After the stage, the fault current can be derived based on the inverters’ FRT goal.

The typical FRT goal is to restrain negative sequence current through the inverters (Kabiri et al., 2016; Jia et al., 2019). Therefore, the fault currents of the IIGUs are expressed as follows:

$\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]=\frac{2}{3{\gamma }^2{U}_{\mathrm{g}\text{N}}^2}\left[\begin{array}{cc}{u}_{\text{g}d}& u_{\text{g}q}\\ u_{\text{g}q}& -u_{\text{g}d}\end{array}\right]\left[\begin{array}{c}{P}_0\\ Q_0\end{array}\right](1)$

where i_d and i_q denote d- and q-axis current components through the inverters. γ = U_g^p/U_gN is the positive-sequence voltage dip of U_g-abc; U_gN is the rated phase-voltage amplitude. u_gd and u_gq are the d- and q-axis positive-sequence voltage. Q₀ is the reactive power provided by the IIGUs and determined by the FRT requirements (Fortmann et al., 2015). P₀ is the active power output, which is mainly determined by solar intensity (or wind speed) and the activation state of current limiter. If the active-power loss of the inverters is ignored, P₀ can be calculated as follows:

$P_0=\{\begin{array}{cc}{P}_{\text{dc}}& \alpha =\text{0}\\ \sqrt{{\left(I_{\lim }{S}_{\text{N}}/I_{\text{N}}\right)}^2-Q_0^2}& \alpha =1\end{array}(2)$

where P_dc is the active power supplied by an IIGU; α represents the activation state of current limiter. The current limiter is activated if α = 0; the limiter is deactivated if α = 1. I_lim is the inverter’s maximum allowable current. S_N is the IIGU’s rated capacity, and I_N is the rated phase-current amplitude.

Combining with Equations 1 and 2, the fault current amplitude fed by the IIGUs is as follows:

$I_{\text{f}}^{\text{m}}=\{\begin{array}{cc}\frac{2\sqrt{P_{\text{dc}}^2+Q_0^2}}{3\gamma U_{\text{gN}}}& \alpha =\text{0}\\ I_{\lim }=\left(1.5\sim 2\right)\frac{2S_{\text{N}}}{3U_{\text{gN}}}& \alpha =1\end{array}(3)$

As shown in Equation 3, the fault current amplitude is related as follows: (1) rated capacity S_N, rated phase-voltage U_gN, and the DC-side active power P_dc; and (2) the positive-sequence voltage dip γ and the required reactive power Q₀. Because the current limiter is easily activated, the fault current amplitude is limited and equal to 1.5 to 2 times rated current. In this case, the amplitude is proportional to the IIGU’s capacity.

Assuming that initial phase angle of the voltage U_g-abc is θ₀ at the occurrence time of a grid fault, based on Equation 1, the initial phase angle of fault current provided by the IIGUs can be obtained as follows:

${\theta }_{\phi }={\theta }_0+\arctan \frac{u_{\text{g}q}{P}_0-u_{\text{g}d}{Q}_0}{u_{\text{g}d}{P}_0+u_{\text{g}q}{Q}_0}+{\delta }_{\phi }(4)$

where the subscript φ = a, b, c represents a-, b-, and c-phase. δ_a = 0, δ_b = −2π/3, δ_c = 2π/3.

Grid-voltage–oriented vector control strategy is usually adopted for the grid-connected inverter, so u_gq = 0 in Equation 4. The initial phase angle of fault current can also be expressed as follows:

${\theta }_{\phi }=\{\begin{array}{cc}{\theta }_0+\arctan \left(\left|Q_0\right|/P_{\text{dc}}\right)+{\delta }_{\phi }& \alpha =0\\ {\theta }_0+\arctan \left(\left|Q_0\right|/\sqrt{{\left(I_{\lim }{S}_{\text{N}}/I_{\text{N}}\right)}^2-Q_0^2}\right)+{\delta }_{\phi }& \alpha =1\end{array}(5)$

In Equation 5, the angle is decided by the ratio of required reactive power to DC-side active power when the current limiter is deactivated. The angle is affected by the rated capacity, the ratio of maximum allowable current to rated current, and the reactive power once the limiter is activated. The ratio is normally equal to 1.5 to 2. Moreover, the reactive power is mainly determined by the voltage dip and the IIGUs’ rated capacity. With the increasing rated capacity, the voltage dip would be smaller. Therefore, the angle is related to the rated capacity.

Relationship Between the Ratio of Operate-to-Restraint Current and IIREPPS’ Rated Capacity

Taking an actual photovoltaic power plant (PVPP), for example, the impact of rated capacity on the current differential protection of outgoing line is developed theoretically in this section. The topology of the PVPP is shown in Figure 1B. In a PVPP, a large number of photovoltaic generation units (PVGUs) are included and connected to the 35-kV/110-kV main transformer through a collecting line. Then they are integrated into the equivalent power grid through a 110-kV outgoing line. The algorithm of two-terminal current differential protection widely used for outgoing line is as follows:

$\left|{\dot{I}}_{\text{p}}+{\dot{I}}_{\text{s}}\right|/\left|{\dot{I}}_{\text{p}}-{\dot{I}}_{\text{s}}\right|>k(6)$

where İ_p is the fundamental phase-current provided by the PVPP, and İ_s is the current of the equivalent power grid. k is the restraint coefficient that is usually 0.5 to 0.8. ∣İ_p + İ_s∣denotes the differential current, and ∣İ_p-İ_s∣is the restraint current. ∣İ_p + İ_s∣/∣İ_p-İ_s∣represents the ratio of operate to restraint current.

An equivalent circuit diagram is described as Figure 1D when a bolted fault occurs in the outgoing line as shown in Figure 1B. In Figure 1D, Z_p represents the equivalent positive-sequence impedance of box transformers, collecting lines and main transformer; Z_L1 is the equivalent positive-sequence impedance of outgoing line at PVPP side; Z_L2 represents the impedance at grid side; Z_s denotes the positive-sequence impedance of the equivalent power grid; Z_f is additional impedance under different faults and calculated as follows:

$Z_{\text{f}}=\{\begin{array}{l}{Z}_{\text{f}}^{\left(3\right)}=0\\ Z_{\text{f}}^{\left(2\right)}=\left(Z_{\text{p}}+Z_{\text{L}1}\right)//\left(Z_{\text{s}}+Z_{\text{L}2}\right)\\ Z_{\text{f}}^{\left(\mathrm{1,1}\right)}=\left[\left(Z_{\text{p}}+Z_{\text{L}1}\right)//\left(Z_{\text{s}}+Z_{\text{L}2}\right)\right]//\to \\ \leftarrow \left[\left(Z_{\text{p0}}+Z_{\text{L}10}\right)//\left(Z_{s0}+Z_{\text{L}20}\right)\right]\\ Z_{\text{f}}^{\left(1\right)}=\left[\left(Z_{\text{p}}+Z_{\text{L}1}\right)//\left(Z_{\text{s}}+Z_{\text{L}2}\right)\right]+\to \\ \leftarrow \left[\left(Z_{\text{p0}}+Z_{\text{L}10}\right)//\left(Z_{\text{s}0}+Z_{\text{L}20}\right)\right]\end{array}(7)$

where the superscripts (3), (2), (1,1), and (1), respectively, represent three-line fault, line-to-line fault, two line-to-ground faults, and a single line-to-ground fault. Z_p0 represents zero-sequence impedance of main transformer, Z_L10 and Z_L20 are zero-sequence impedance of outgoing line at PVPP- and grid-side, and Z_s0 is zero-sequence impedance of equivalent power grid.

In Figure 1D, I_p^p and I_s^p denote the positive-sequence current through outgoing line at PVPP and grid sides. They can be expressed as follows:

$\{\begin{array}{l}{\dot{I}}_{\text{p}}^{\text{p}}\left(Z_{\text{p}}+Z_{\text{L}1}\right)+\left({\dot{I}}_{\text{p}}^{\text{p}}+{\dot{I}}_{\text{s}}^{\text{p}}\right)Z_{\text{f}}-{\dot{U}}_{\text{g}}^{\text{p}}=0\\ {\dot{I}}_s^{\text{p}}\left(Z_{\text{s}}+Z_{\text{L}2}\right)+\left({\dot{I}}_{\text{p}}^{\text{p}}+{\dot{I}}_{\text{s}}^{\text{p}}\right)Z_{\text{f}}-{\dot{E}}_{\text{s}}=0\end{array}(8)$

According to Equation 8, the differential and restraint currents can be deduced as follows:

$\{\begin{array}{l}\left|{\dot{I}}_{\text{p}}^{\text{p}}+{\dot{I}}_{\text{s}}^{\text{p}}\right|=\left|\frac{{\dot{U}}_g^{\text{p}}-{\dot{I}}_{\text{p}}^{\text{p}}\left(Z_{\text{p}}+Z_{\text{L}1}\right)}{Z_{\text{f}}}\right|\\ \left|{\dot{I}}_{\text{p}}^{\text{p}}-{\dot{I}}_s^{\text{p}}\right|=\left|\frac{-{\dot{U}}_{\text{g}}^{\text{p}}+{\dot{I}}_{\text{p}}^{\text{p}}\left(Z_{\text{p}}+Z_{\text{L}1}+2Z_{\text{f}}\right)}{Z_{\text{f}}}\right|\end{array}(9)$

Because the relationship between positive-sequence current and its corresponding phase current is decided only by the fault types, Equation 6 can also be rewritten as follows:

$\left|{\dot{I}}_{\text{p}}+{\dot{I}}_{\text{s}}\right|/\left|{\dot{I}}_{\text{p}}-{\dot{I}}_{\text{s}}\right|=\left|{\dot{I}}_{\text{p}}^{\text{p}}+{\dot{I}}_{\text{s}}^{\text{p}}\right|/\left|{\dot{I}}_{\text{p}}^{\text{p}}-{\dot{I}}_{\text{s}}^{\text{p}}\right|>k(10)$

Substituting Equation 9 into Equation 10, the algorithm of differential protection is derived as follows:

$\{\begin{array}{l}\frac{\left|{\dot{I}}_{\text{p}}-{\dot{I}}_{\text{s}}\right|}{\left|{\dot{I}}_{\text{p}}+{\dot{I}}_{\text{s}}\right|}=\left|1-Z_{\text{op}}\right|<\frac{1}{k}\\ Z_{\text{op}}=\frac{2Z_{\text{f}}}{{\dot{U}}_{\text{g}}^{\text{p}}/{\dot{I}}_{\text{p}}^{\text{p}}-\left(Z_{\text{p}}+Z_{\text{L}1}\right)}\end{array}(11)$

where Z_op is the operate impedance and can be used for evaluating the percentage restraint differential protection. If Z_op is located only inside the dotted circle in Figure 1C, the differential protection can trip for internal faults. Figure 1C shows the operation characteristics of differential protection as the IIREPPs’ rated capacity increases. Because the fault current amplitude İ_p^p provided by a PVPP is closely related to its rated capacity, Z_op that is influenced by the quantity U˙_g^p/İ_p^p can be altered with the increasing rated capacity. Combining with Equations 3 and 5, the quantity U˙_g^p/İ_p^p can be expressed as follows:

$\frac{{\dot{U}}_{\text{g}}^{\text{p}}}{{\dot{I}}_{\text{p}}^{\text{p}}}=\frac{\gamma U_{\text{gN}}}{I_{\lim }}\angle -\arctan \left(\left|Q_0\right|/\sqrt{{\left(I_{\lim }{S}_{\text{N}}/I_{\text{N}}\right)}^2-Q_0^2}\right)(12)$

According to Equations 3 and 12, the amplitude of U˙_g^p/İ_p^p becomes smaller with the increasing rated capacity. As a result, the operate impedance Z_op becomes larger and falls outside the dotted circle as shown in Figure 1C. The differential protection may malfunction in the protection zone.

Maximum Rated Capacity Estimation for Adapting Current Differential Protection

In this section, the main concern is to estimate maximum rated capacity of IIREPPs with the effective sensitivity and reliability of differential protection. As the aforementioned analysis, the operate impedance Z_op can reflect the operation characteristics of differential protection and is affected by the quantity U˙_g^p/İ_p^p. Thus, it is necessary to analyze the amplitude of U˙_g^p. According to Equation 8, U˙_g^p can be expressed as follows:

$\frac{{\dot{U}}_{\text{g}}^{\text{p}}\left(Z_{\text{s}}+Z_{\text{L}2}+Z_{\text{f}}\right)-E_{\text{s}}{Z}_{\text{f}}}{\left(Z_{\text{p}}+Z_{\text{L}1}\right)\left(Z_{\text{s}}+Z_{\text{L}2}\right)+\left(Z_{\text{p}}+Z_{\text{L}1}+Z_{\text{s}}+Z_{\text{L}2}\right)Z_{\text{f}}}=\frac{{\dot{U}}_g^{\text{p}}\left(Z_{\text{s}}+Z_{\text{L}2}+Z_{\text{f}}\right)-E_{\text{s}}{Z}_{\text{f}}}{Z_{\text{m}}}=I_{\text{p}}^{\text{p}}(13)$

Further, by substituting Equations 3 and 5 into Equation 13, the amplitude of U˙_g^p can be calculated as follows:

$\{\begin{array}{l}\left|\frac{\gamma U_{\text{gN}}\left(Z_{\text{s}}+Z_{\text{L}2}+Z_{\text{f}}\right)-I_{\text{f}}^{\text{m}}{Z}_{\text{m}}{\text{e}}^{\text{j}\left({\theta }_{\phi }-{\theta }_{\text{0}}\right)}}{E_{\text{s}}{\dot{Z}}_{\text{f}}}\right|=1\\ {\text{e}}^{\text{j}\left({\theta }_{\phi }-{\theta }_{\text{0}}\right)}=\sqrt{1-{\left(Q_0/1.5S_{\text{N}}\right)}^2}+\text{j}\frac{Q_0}{1.5S_{\text{N}}}\end{array}(14)$

Based on Equations 14 and 11, the relationship between IIREPPs’ maximum rated capacity S_N(max) and percentage restraint coefficient k can be expressed as follows:

$\{\begin{array}{l}\left|S_{\text{N}\left(\text{max}\right)}A-\sqrt{{\left(1.5S_{N\left(\text{max}\right)}\right)}^2-Q_0^2}B-\text{j}\frac{4Q_0}{9}\right|=\frac{1}{S_{N\left(\text{max}\right)}k}\left|\frac{2\gamma U_{\text{gN}}^2\sqrt{{\left(1.5S_{N\left(\text{max}\right)}\right)}^2-Q_0^2}}{3}+C-\frac{S_{N\left(\text{max}\right)}^2{Z}_1}{U_{\text{gN}}}\right|\\ Z_1=Z_{\text{p}}+Z_{\text{L}1};Z_2=Z_{\text{s}}+Z_{\text{L}2}+Z_{\text{f}}\\ A=\left(2\gamma Z_2+Z_1\right)-\text{j}\frac{8{\dot{Z}}_{\text{m}}{Q}_0}{27U_{\text{gN}}^2}\\ B=\frac{8Z_{\text{m}}}{27U_{\text{gN}}^2}+\frac{4}{9}\\ C=\text{j}2\gamma U_{\text{gN}}^2{Q}_0/3\end{array}(15)$

As shown in Equation 15, the IIREPPs’ maximum rated capacity that is accepted for current differential protection is mainly affected as follows: (1) the factors determined by fault scenarios include Z₁, Z₂, Z_m, γ; (2) the rated voltage U_gN; and (3) the required reactive power Q₀. For analyzing protection adaptability, the aforementioned factors can be known as the constant quantities. Therefore, using (15), the maximum rated capacity can be calculated for evaluating the adaptability of current differential protection of outgoing line connected with large-scale IIREPP.

Theoretical Analysis and Simulation Verification

In order to evaluate the adaptability of differential protection and verify the availability of maximum capacity expression, the actual power grid with a PVPP shown as Figure 1B is studied based on MATLAB and PSCAD/EMTDC.

The PVGUs in the PVPP are connected into 35-kV collecting line through 0.38-kV/35-kV box transformers. The PVPP’s rated capacity is 10–200 MVA, and the short-circuit capacity of equivalent power grid is 100 MVA. The percent impedance of box transformer is 6.05%, and the short-circuit loss is 105 kW. The length of collecting line is 3.3 km; the positive- and negative-sequence impedance are 0.111 + j0.377 Ω/km. The zero-sequence impedance is 0.343 + j1.152 Ω/km. The percent impedance of 35-kV/110-kV main transformer is 5%, and the short-circuit loss is 90 kW. The length of 110-kV outgoing line is 8.943 km, the positive- and negative-sequence impedance are 0.106 + j0.38 Ω/km. The zero-sequence impedance is 0.328 + j1.28 Ω/km. The impedance of equivalent power grid is 8.162 + j93.337Ω, and the electromotive force Ė_s is equal to 15 kV∠0°. Moreover, the restraint coefficient k applied for current differential protection of the outgoing line is equal to 0.8.

Evaluation for the Operation Characteristics of Differential Protection With Different Rated Capacities

Assuming that a grid fault occurs at different locations of the 110-kV outgoing line, the faulty distance seen from the PVPP side varies from 0 to 8.943 km. Table 1 shows the calculated amplitude results of the operate impedance Z_op with different rated capacity and various fault locations under the phase A and B faults. Moreover, the ratio of restraint to differential current is shown in Figure 2 under different fault types based on MATLAB.

TABLE 1

TABLE 1. The operate impedance amplitude with different rated capacity and various fault locations.

FIGURE 2

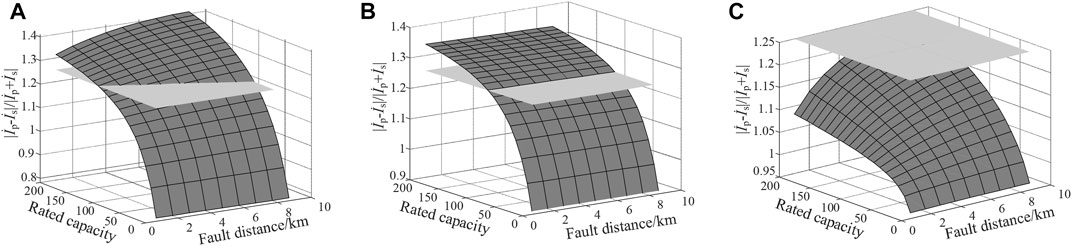
FIGURE 2. The relationship between ratio of restraint-to differential-current, rated capacity, and fault locations: (A) phase A-GND fault, (B) phase A-B fault, and (C) phase A-B-GND fault.

From Table 1, the operate impedance increases from 0.4018 to 0.7666 when the rated capacity increases from 10 to 200 MW, and the faulty distance is 1 km. In the same fault scenarios, the ratio of restraint to differential-current increases from 0.882 to 1.336 in Figure 2B. Once the ratio is greater than 1.25 (1/k = 1.25), the current differential protection of the outgoing line malfunctions.

In the other cases, because of the increasing rated capacity, the operate impedance amplitude is also deduced as shown in Table 1. Moreover, when the fault location is the same with the aforementioned case, under a phase A-GND fault, the ratio increases from 0.785 to 1.315 in Figure 2A with the increasing rated capacity. Under a phase A-B-GND fault, the ratio increases from 0.955 to 1.083 in Figure 2C. It means that under different fault types the ratios are various. The maximum rated capacities for adapting current differential protection are different under different fault types. From Figures 2A,B, the maximum rated capacities are 108.059 and 87.586 MW when the faulty distance is 4.47 km. According to Equation 15, the corresponding calculated capacities are 108.059 and 87.586 MW. These results are consistent.

Verification for Maximum Rated Capacity of the IIREPPs

In order to verify Equation 15, an electromagnetic transient simulation model as shown in Figure 1B is established based on PSCAD/EMTDC. It is assumed that at t = 1 s, the same fault as described in Section 5.1 occurs and the cleared time is t = 1.5 s. As the mentioned discussion, the calculated maximum rated capacity is 87.586 MW when a phase A-B fault is placed in the outgoing line, and the faulty distance is 4.47 km. Thus, the PVPP’s capacities are set with 80 and 90 MW in the simulation tests. The calculated capacity is 108.059 MW under the phase A-GND faults, so the simulation capacities are 100 and 110 MW. The simulation capacities are 150 and 200 MW under the phase A-B-GND faults. Figure 3 shows the simulated results of the ratio of restraint to differential current under different faults.

FIGURE 3

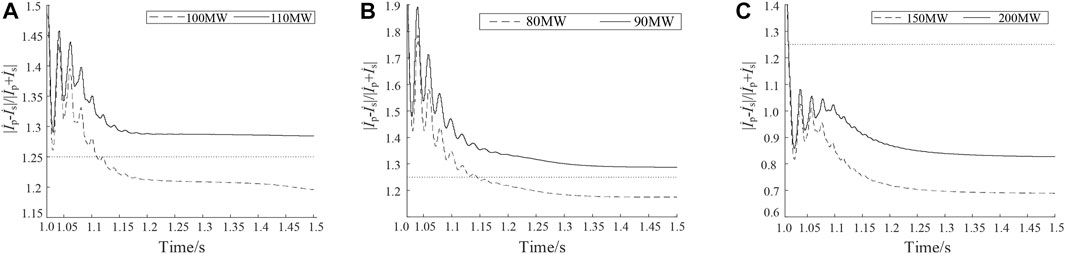
FIGURE 3. Ratio of restraint- and differential-current under various fault: (A) phase A-GND fault, (B) phase A-B fault, and (C) phase A-B-GND fault.

From Figure 3, with the increasing rate capacity, the ratio varies from 1.175 to 1.289 under the phase A-B faults. The ratio is from 1.207 to 1.286 under the phase A-GND faults and from 0.693 to 0.833 under the phase A-B-GND faults. In Figure 3B, when the rated capacity is 90 MW and greater than 87.586 MW, the ratio is 1.289 and greater than 1.25. In Figure 3A, when the rated capacity is 110 MW and greater than 108.059 MW, the ratio is 1.286. These results show that if the simulated capacity is greater than the calculated maximum capacity, the simulated ratio is greater than 1.25. It means that the expression of the IIREPP’s maximum rated capacity is correct and can be used for evaluating the adaptability of current differential protection.

Conclusion

In this article, the fundamental amplitude and initial phase angle of the short-circuit current provided by the IIREPPs are expressed by the corresponding rated capacities. Further, the relationship between the ratio of the operate-to-restraint current and IIREPPs’ rated capacity is developed. It is found that the ratio becomes larger and larger with the increasing rated capacity. As a result, the existing current differential protection may malfunction. In order to ensure that the existing protection has high selectivity and reliability, the IIREPP’s maximum rated capacity expression is derived. The maximum capacity is related to the fault types, the fault locations, the required reactive power, and so on. By the theoretical calculation and simulation analysis, the proposed expression is effective for evaluating the adaptability of current differential protection. However, an improved principle is not taken into account for solving the mal-operation problems of the traditional protection. In further works, some novel protection algorithms should be done.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

SL led analysis and wrote the manuscript. DW performed the experiment. HZ and ZL carried out the study and collect important background information. XD helped perform the analysis with constructive discussions. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by Open Fund of State Key Laboratory of Power Grid Safety and Energy Conservation (China Electric Power Research Institute) (No. JBB51202001892).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fortmann, J., Pfeiffer, R., Haesen, E., Hulle, F., Martin, F., Urdal, H., et al. (2015). Fault‐Ride‐Through Requirements for Wind Power Plants in the ENTSO‐E Network Code on Requirements for Generators. IET Renew. Power Generation 9, 18–24. doi:10.1049/iet-rpg.2014.0105

CrossRef Full Text | Google Scholar

Han, B., Li, H., Wang, G., Zeng, D., and Liang, Y. (2018). A Virtual Multi-Terminal Current Differential Protection Scheme for Distribution Networks with Inverter-Interfaced Distributed Generators. IEEE Trans. Smart Grid 9, 5418–5431. doi:10.1109/TSG.2017.2749450

CrossRef Full Text | Google Scholar

Jia, K., Li, Y., Fang, Y., Zheng, L., Bi, T., and Yang, Q. (2018). Transient Current Similarity Based protection for Wind Farm Transmission Lines. Appl. Energ. 225, 42–51. doi:10.1016/j.apenergy.2018.05.012

CrossRef Full Text | Google Scholar

Jia, J., Yang, G., Nielsen, A. H., and Ronne-Hansen, P. (2019). Impact of VSC Control Strategies and Incorporation of Synchronous Condensers on Distance protection under Unbalanced Faults. IEEE Trans. Ind. Electron. 66, 1108–1118. doi:10.1109/TIE.2018.2835389

CrossRef Full Text | Google Scholar

Kabiri, R., Holmes, D. G., and McGrath, B. P. (2016). Control of Active and Reactive Power Ripple to Mitigate Unbalanced Grid Voltages. IEEE Trans. Ind. Applicat. 52, 1660–1668. doi:10.1109/TIA.2015.2508425

CrossRef Full Text | Google Scholar

Li, Y., Jia, K., Bi, T., Yan, R., Li, W., and Liu, B. (2018). “Analysis of Line Current Differential protection Considering Inverter-Interfaced Renewable Energy Power Plants,” in 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe, ISGT-Europe 2017 - Proceedings, Turin, Italy, 26-29 Sept. 2017, 1–6. doi:10.1109/ISGTEurope.2017.8260157

CrossRef Full Text | Google Scholar

Li, Y., Han, M., Yang, Z., and Li, G. (2021). Coordinating Flexible Demand Response and Renewable Uncertainties for Scheduling of Community Integrated Energy Systems with an Electric Vehicle Charging Station: A Bi-Level Approach. IEEE Trans. Sustain. Energ. 12, 2321–2331. doi:10.1109/TSTE.2021.3090463

CrossRef Full Text | Google Scholar

Li, Y., Wang, B., Yang, Z., Li, J., and Chen, C. (2022a). Hierarchical Stochastic Scheduling of Multi-Community Integrated Energy Systems in Uncertain Environments via Stackelberg Game. Appl. Energ. 308, 118392. doi:10.1016/j.apenergy.2021.118392

CrossRef Full Text | Google Scholar

Li, Y., Li, K., Yang, Z., Yu, Y., Xu, R., and Yang, M. (2022b). Stochastic Optimal Scheduling of Demand Response-Enabled Microgrids with Renewable Generations: An Analytical-Heuristic Approach. J. Clean. Prod. 330, 129840. doi:10.1016/j.jclepro.2021.129840

CrossRef Full Text | Google Scholar

Li, Y., Wang, R., and Yang, Z. (2022c). Optimal Scheduling of Isolated Microgrids Using Automated Reinforcement Learning-Based Multi-Period Forecasting. IEEE Trans. Sustain. Energ. 13, 159–169. doi:10.1109/TSTE.2021.3105529

CrossRef Full Text | Google Scholar

Liu, X., and Li, Y. (2016). Effect of IIDG Connected to Grid as a Teed Line on Longitudinal Differential protection and Maximum Penetration Capacity. Power Syst. Technol. 40, 1595–1600. doi:10.13335/j.1000-3673.pst.2016.05.045

CrossRef Full Text | Google Scholar

Liu, S. M., Bi, T. S., Xue, A. C., and Liu, J. Z. (2018). Equivalent Model for Calculating Fault Current from Inverter-Interfaced Renewable Energy Generators. J. Env Inform. 32, 36–44. doi:10.3808/jei.201800392

CrossRef Full Text | Google Scholar

Liu, S., Zhang, H., Zhang, P., Li, Z., and Wang, Z. (2022). Equivalent Model of Photovoltaic Power Station Considering Different Generation Units' Fault Current Contributions. Energies 15, 229. doi:10.3390/en15010229

CrossRef Full Text | Google Scholar

Telukunta, V., Pradhan, J., Pradhan, J., Agrawal, A., Singh, M., and Srivani, S. G. (2017). Protection Challenges under Bulk Penetration of Renewable Energy Resources in Power Systems: A Review. CSEE J. Power Energ. Syst 3, 365–379. doi:10.17775/CSEEJPES.2017.00030

CrossRef Full Text | Google Scholar

Wang, X., Cui, Y., and Hu, G. (2017). Sensitivity Studies on Differential protection during the Output Line of Grid-Connected Photovoltaic Systems Occur Asymmetrical Faults. Power Syst. Prot. Control. 41, 100–105. doi:10.7667/PSPC161757

CrossRef Full Text | Google Scholar

Zhou, C., Zou, G., Zang, L., and Du, X. (2022). Current Differential Protection for Active Distribution Networks Based on Improved Fault Data Self-Synchronization Method. IEEE Trans. Smart Grid 13, 166–178. doi:10.1109/TSG.2021.3116608

CrossRef Full Text | Google Scholar