Acoustic-Electrical Joint Localization Method of Partial Discharge in Power Transformer Considering Multi-Path Propagation Impact

Efficient and accurate localization of partial discharge (PD) is of paramount importance to ensure the safe operation of power transformers. However, the multi-path propagation effect introduced by the reflection, refraction and diffraction of the ultrasonic signal may add significant computational complexity to the localization process and degrade the localization accuracy. This paper proposes an acoustic- electrical joint method for partial discharge location in the power transformer with the full consideration of the multi-path propagation impact. Unlike the conventional error analysis methods, a partial discharge localization model is proposed for characterizing the multipath propagation impact without the prior knowledge of the transcendental error probability. Based on the matrix inequality transformation and relaxation, the high-dimensional nonlinear localization equations are transformed into a set of second-order convex optimization equations that can be solved using the convex second-order cone program (SOCP). The proposed solution can significantly reduce the computational complexity and improve the localization accuracy as well as avoid the local optimum and slow convergence. The solution is assessed through extensive experiments based on simulations, testbed and trial deployment in comparison with the existing solutions with the localization error of about 0.1 m.

Introduction

It is well known that the insulation of large transformers is one of the fundamental and stringent requirements to ensure the safe and reliable operation of electric power substations. In the past decades, the timely detection and analysis of partial discharge (PD) have been widely investigated for fault detection and diagnosis of the internal insulation deterioration of power transformers (e.g., Tarimoradi and Gharehpetian, 2017; Wang et al., 2017; Chen, 2019; Ganguly et al., 2020; Karami et al., 2020). This enables the determination of fault type and location at the early stage, and hence the field maintenance can be timely carried out to prevent the power transformers from failures or outages.

In general, the partial discharge can make the insulation being destroyed and gradually expand due to the direct bombardment of the discharge particles, resulting in insulation breakdown; In addition, the chemical action of the active gases (e.g., heat, ozone and nitrogen oxide) produced by the discharge can lead to corrosion of the partial insulation, which increases the dielectric loss and finally leads to thermal breakdown (Kallberg, 1980; Naderi et al., 2007). More specifically, the partial discharge can introduce the following impacts:

1) Partial discharge can lead to the separation and cleavage of chemical bonds and the destruction of the insulating material’s molecular structure. This may introduce discharge at the concentration of the electric field and leads to dendritic discharge traces and insulation breakdown.

2) The thermal effect of discharge point leads to the thermal cracking of insulation or promotes oxidative cracking. This may increase the conductivity and dielectric loss that accelerates the aging process.

3) The generated ozone and nitrogen oxides during the discharge can lead to a nitric acid chemical reaction. Such a reaction can corrode the insulator when meet with the water, resulting in the deterioration of insulation performance.

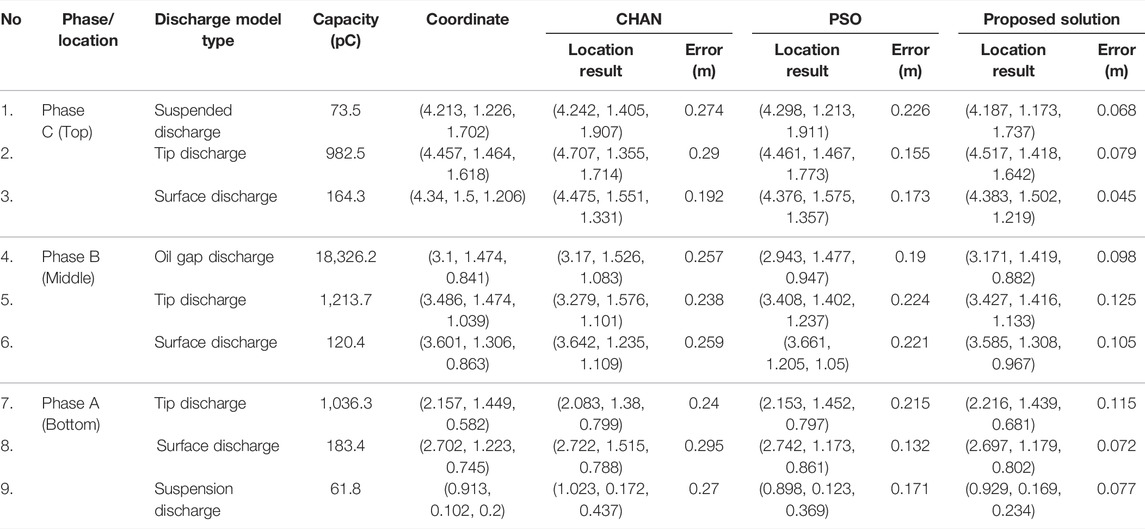
In addition, the high-energy radiation phenomenon during partial discharge can potentially degrade the insulating materials. The X wax (a waxy substance produced by overheating) deposited on the solid insulation makes it difficult to dissipate heat, resulting in overheating and damages to the solid insulation. The examples of insulation discharge phenomena in the transformers are illustrated in Figure 1.

FIGURE 1

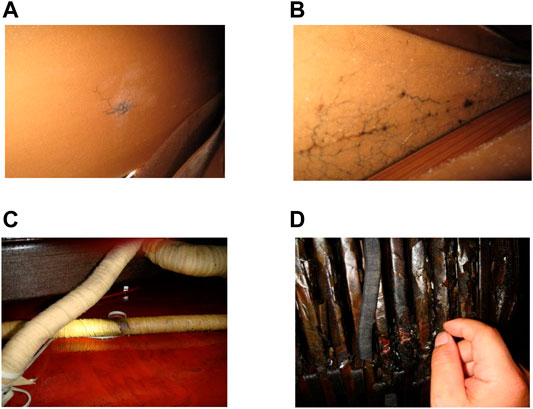
FIGURE 1. Insulation discharge phenomena of transformers. (A) Insulation paperboard at the outer enclosure of transformer (B) Insulation paperboard at the lower end of the winding (C) Winding cable discharge (D) Internal discharge of winding.

At present, the partial discharge localization of power transformers is mainly based on electrical (mainly in ultra-high frequency) and ultrasonic detection methods (e.g., (Luo Yongfen et al., 2006; Moore et al., 2006; Markalous et al., 2008; Coenen and Tenbohlen, 2012; Tarimoradi and Gharehpetian, 2017)). The electrical method mainly detects the UHF (Ultra High Frequency) electromagnetic wave generated by partial discharge sources. Considering that the propagation speed of the electrical signal is the speed of light, the electrical method requires a high sampling frequency reaching the nanosecond level or even sub-nanosecond level. Moreover, the electrical wave signal is shielded and attenuated by the power trans-former borne (Kweon et al., 2005).

The ultrasonic detection method detects and analyses the arrival time of the PD pulse signal to determine the location of partial discharge sources. Due to the advantages of non-destructive, robust and high precision, the ultrasonic detection method is one of the most widely used location technologies of power transformers (Howells and Norton, 1978; Han-Lee Song, 1994; Cakir et al., 2013; Hekmati and Hekmati, 2017; Wang et al., 2017; Chen, 2019). The location solutions can be classified into the pure acoustic-based method, the pure electrical-based method and the acoustic electrical joint method (e.g., Markalous et al., 2008; Coenen and Tenbohlen, 2012; Rubio-serrano et al., 2012). The pure acoustic localization method and the pure electrical-based localization method select the arrival time of one ultrasonic sensor or UHF sensor signal as the reference time and then measure the time delay of other signals relative to the reference time for partial discharge localization. The acoustic electrical joint method is considered as the arrival time of the electric pulse signal of the partial discharge as the reference time since the electric signal delay is very tiny and can be ignored compared with the ultrasonic signals. Through using a set of ultrasonic synchronized sensors to measure the ultrasonic time delay and multiplying the equivalent sound velocity, the distance of discharge source to individual sensors can be calculated, as suggested in (Meka et al., 2018). The ultrasonic wave propagation speed within the transformer is close to that of sound wave speed, and the electromagnetic wave speed is about two-thirds of that of lightwave speed. Therefore, the time error of the pure electrical-based localization method is much larger than other methods. The existing study (Coenen and Tenbohlen, 2012) confirmed that the positioning accuracy of the electric acoustic joint method is higher than that of the pure acoustic method. Since the time arrival time of the acoustic signal is not easy to be accurately measured, a larger error can be introduced between the acoustic and acoustic signals. Moreover, for multiple PD sources, the acoustic-electrical joint method is expected to provide improved performance in terms of distinguishing the signals from different PD sources in practical deployment compared with the acoustic-based method.

The main factors affecting the accuracy of the partial dis-charge localization are the nonlinear localization equation solving method and the elimination method of various errors in the localization process. In the existing studies, many optimization algorithmic solutions, e.g., the particle swarm optimization and its extensions (Hooshmand et al., 2013; Wang et al., 2017; Meka et al., 2018), genetic algorithm (Chang et al., 2014; Li and Luan, 2018), fuzzy clustering (Contin et al., 2002; Homaei et al., 2014), have been adopted attempting to obtain the optimal solution of the nonlinear localization problem. However, there are many problems in the practical application, e.g., falling into local optimum, slow convergence speed, and premature nature. It is difficult to ensure the robustness and accuracy of the solved results. Also, the existing literature mainly focuses on the influence of sensor measurement error rather than the error caused by multi-path propagation.

Unlike our previous work (Jia et al., 2021) that presented an acoustic-based method for PD location, this paper proposes an acoustic-electrical joint method for locating the partial discharge sources in a power transformer considering the influence of the multi-path propagation effect. In this paper, the following contributions are made:

1) The proposed acoustic-electrical joint localization method fully considered the impact of multipath propagation errors to accurately describe the phenomenon of PD signal propagation in the power transformer.

2) The acoustic-electrical joint localization is formulated as a second-order cone program (SOCP) that can efficiently obtain the accurate PD source locations whilst avoiding the local optimum and slow convergence.

3) The proposed algorithmic solution of PD localization is extensively assessed and validated by a range of experiments based on simulations, experimental testbed and field test against a set of existing solutions.

The remainder of this work is as follows: the analysis of the partial discharge propagation path in the transformer is presented in Analysis of Partial Discharge Propagation Path in Transformer. SOCP Localization Model formulates the PD location problem and adopts the SOCP to solve the localization model. Performance Evaluation and Numerical Result carries out a range of experiments to validate the proposed method. Finally, the conclusions and future work are discussed in Conclusive Remarks.

Analysis of Partial Discharge Propagation Path in Transformer

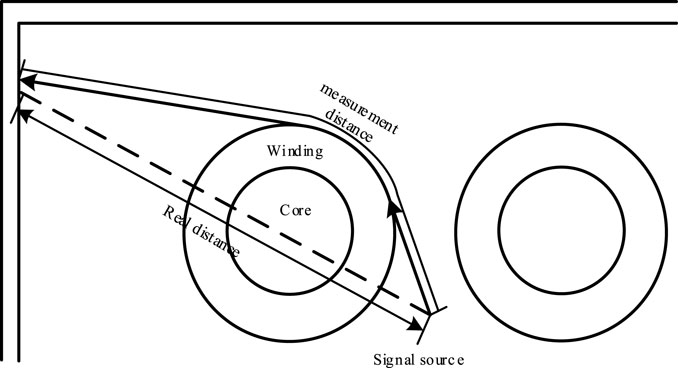
When the internal medium of the power transformer is affected by dampness, aging, breakdown, or other reasons, the power transformer may cause insulation weakness points. When the applied voltage exceeds the weakness point thresh-old voltage, it will emit electric and ultrasonic signals. Due to the complexity of the internal structure of the power transformer, the propagation process of electric and ultrasonic signals can be divided into four categories, as shown in Figure 2.

1) Internal reflection process of power transformer: when the ultrasonic wave touches the winding or borne, it will be reflected, thus prolonging the time delay to reach the sensor;

2) The internal refraction process of power transformer: when the ultrasonic wave travels through the winding or borne, it will be refracted, thus also prolonging the time delay to reach the sensor;

3) The diffraction process in power transformer: under the condition that the ultrasonic wave wavelength is close to the shelter width, the direction of the ultrasonic wave may change when it touches the winding;

4) Refraction process of power transformer borne: when the ultrasonic wave touches the power transformer borne, it will continue to spread in the borne. However, the wave propagating in the border decays very fast, it can be filtered by the threshold method.

FIGURE 2

FIGURE 2. Diagram of the relationship between measurement distance and real distance.

SOCP Localization Model

Suppose synchronized one electric PD sensor and $n$ ultrasonic PD sensors are arranged around the power transformer. The time delay between the measurement sensor and the PD source can be formulated as Eq. 1:

$t_i=\frac{r_i}{v}=\frac{1}{v}(d_i+n_i+e_i)(1)$

In Eq. 1, $r_i$ is the measured distance from the PD to the $i$ th sensor $(i=\mathrm{1,2},\cdots ,n)$. $v$ is the ultrasonic wave propagation velocity within the transformer. $d_i$ is the real distance between the $i$ th sensor and the PD source (all variables units in this paper are in meters). $n_i$ denotes the sensor measurement error that follows the normal distribution $N(0,{\sigma }^2)$ (Chan and Ho, 1994) with the mean value of 0 and variance of ${\sigma }^2$, and $\left|n_i\right|\ll d_i$. $e_i$ is the error caused by the velocity affected by the composite path in the process of signal propagation.

$r_i=t_{i}v(2)$

$d_i=\Vert x-s_i\Vert (3)$

In Eq. 3, $x$ and $s_i$ denotes the three-dimensional coordinates of the PD source and the $i$ th sensor, i.e. $(x_x,y_x,z_x)$ and $(x_{s_i},y_{s_i},z_{s_i})$, respectively. Here, Figure 2 illustrates the relationship between measurement distance and real distance.

By square the two sides of Eq. 1 and substituting formulas Eqs 2, 3,

$r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2=2n_i\Vert x-s_i\Vert +n_i^2(4)$

Considering $\left|n_i\right|\ll d_i$, $n_i^2$ can be omitted as a high-order small quantity,

$n_i\approx \frac{r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }(5)$

So, the localization model can be formulated as

$\underset{x}{\min }\underset{e_i}{\max }{{\displaystyle \sum _{i=1}^N\left(\frac{r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)}}^2(6)$

Eq. 6 can be reformed as:

$\underset{x}{\min }{\displaystyle \sum _{i=1}^N{\left[\underset{e_i}{\max }\left(\frac{r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)\right]}^2}(7)$

Considering $0\le e_i\le {\rho }_i$, which ${\rho }_i$ is the upper bound of $e_i$.

$\begin{array}{l}\underset{e_i}{\max }\left(\frac{r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)\\ =\max \left(\frac{r_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert },\frac{r_i^2-2r_i{\rho }_i+{\rho }_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)\end{array}(8)$

Define ${\xi }_i$:

${\xi }_i=\frac{r_i^2-2r_i{e}_i+e_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }(9)$

So, according to SCOP, Eq. 7 can be rewritten as

$\begin{array}{l}\underset{x,\xi }{\min }{\displaystyle \sum _{i=1}^N{\xi }_i}\hfill \\ {\left(\frac{r_i^2-2r_i{\rho }_i+{\rho }_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)}^2\le {\xi }_i\hfill \\ {\left(\frac{r_i^2-{\Vert x-s_i\Vert }^2}{2\Vert x-s_i\Vert }\right)}^2\le {\xi }_i\hfill \end{array}(10)$

Considering ${\Vert x\Vert }^2$ is a non-convex parameter, the second-order relaxing parameter is defined as ${\Vert x\Vert }^2\le y$. So ${\Vert x-s_i\Vert }^2$ can be converted to $y-2s_{i}x+{\Vert s_i\Vert }^2$ and the following can be obtained:

$\begin{array}{l}\underset{x,\xi }{\min }{\displaystyle \sum _{i=1}^N{\xi }_i}\hfill \\ \frac{{\left(r_i^2-2r_i{\rho }_i+{\rho }_i^2-y+2s_{i}x-{\Vert s_i\Vert }^2\right)}^2}{4\left(y-2s_{i}x+{\Vert s_i\Vert }^2\right)}\le {\xi }_i\hfill \\ \frac{{\left(r_i^2-y+2s_{i}x-{\Vert s_i\Vert }^2\right)}^2}{4\left(y-2s_{i}x+{\Vert s_i\Vert }^2\right)}\le {\xi }_i\hfill \\ {\Vert x\Vert }^2\le y\hfill \end{array}(11)$

Here, Eq. 11 is a convex second-order cone program (SOCP)and the PD source localization can be implemented through solving Eq. 11 using the toolbox (CVX toolbox) in MATLAB (ver. R2019b).

Performance Evaluation and Numerical Result

Simulation Experiment

This section firstly carries out the performance evaluation of the proposed PD location solution through simulations. The simulated ODFS-334MVA/500kV transformer (8.6 m × 6.7 m × 7.6 m) in Figure 3. The propagation process of the ultrasonic wave within the studied transformer is simulated using the Edge-diffraction-toolbox (MATLAB ver. R2019b). In simulations, the ultrasonic wave propagation speed in the core, winding and oil are set as 5200 m/s, 3750 m/s and 1450 m/s, respectively, as suggested in (Harrold, 1979; Yang et al., 2021; Yang et al., 2022b). In this work, the errors of individual sensors follow the normal distribution described as $\mu =0$, $\sigma =3\times {10}^{-5}$.

FIGURE 3

FIGURE 3. Simulated power transformer.

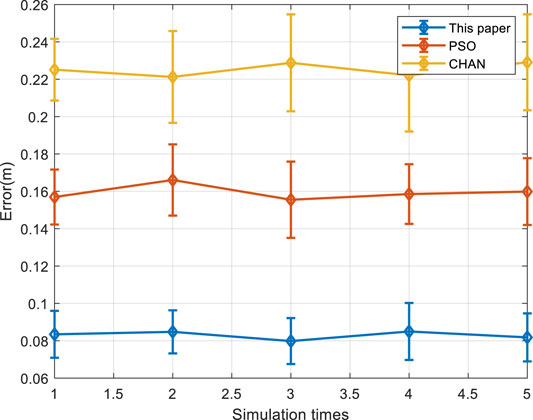
Through MATLAB, randomly select the position of discharge source in different media of core, winding and oil, repeat the above simulation experiment for 10,000 times, and get the positioning error statistics of different positioning methods, as shown in Figure 4.

FIGURE 4

FIGURE 4. Performance comparison of the proposed solution against the CHAN and PSO algorithms.

Figure 4 gives the simulation results of the proposed PD localization method against the existing CHAN and PSO algorithmic solutions (Yang et al., 2022a; Shen and Raksincharoensak, 2021; Xun et al., 2021; Yang, 2021). Since the refraction and diffraction errors are not considered in the CHAN algorithm, a significant PD source localization error can be produced. On the other hand, the PSO algorithm may fall into the local optimum in the iterative search process. As a result, the proposed method provides better performance compared with the comparison benchmarks with the overall positioning error within the range of 0.05–0.1 M.

Testbed Validation

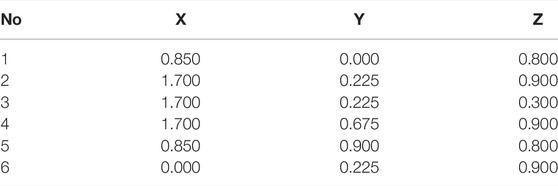
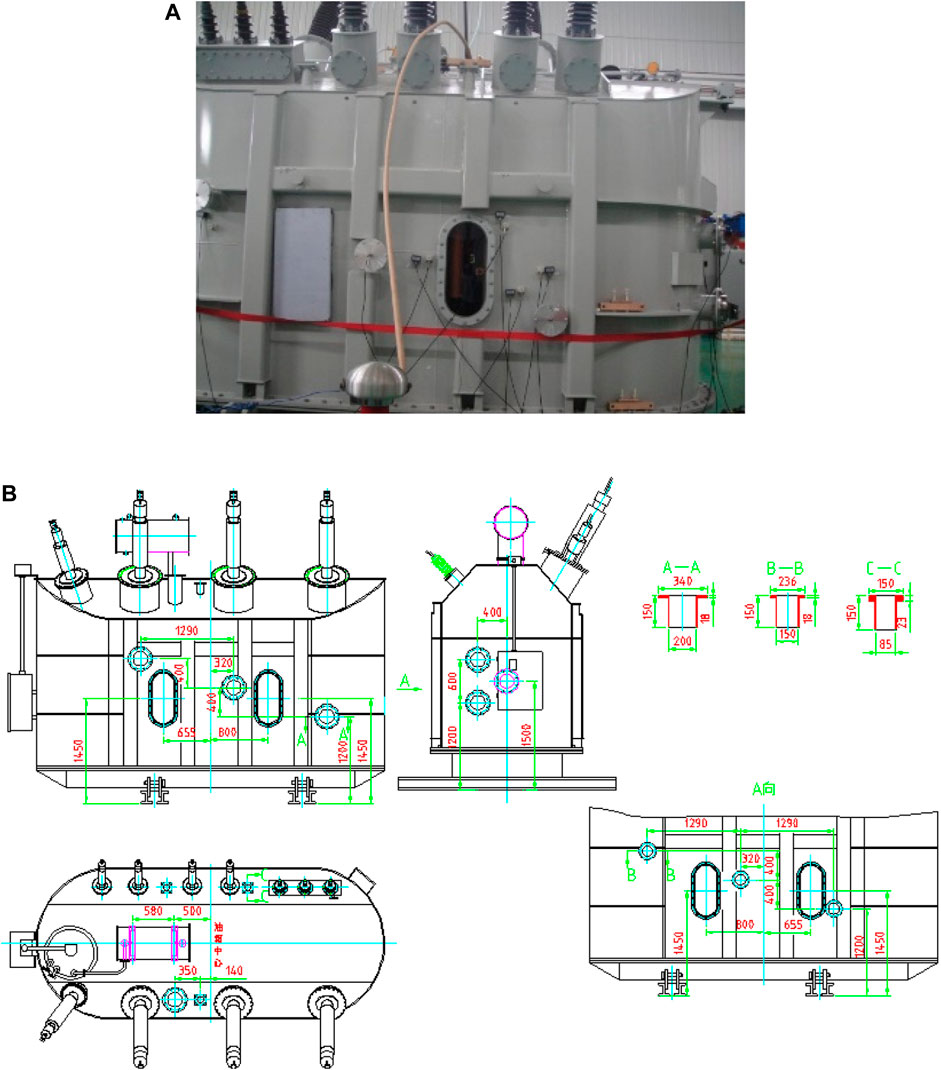
The TWCP-0.5/50 transformer testbed is used for further validation (Wu et al., 2017; Han, 2019; Le et al., 2021). In the testbed, different forms of discharge models, e.g., oil gap discharge and tip discharge, are implemented. Figure 5 illustrates the TWCP-0.5/50 transformer testbed from both the front and back view with the deployed ultrasonic partial discharge sensors as well as the fault setting devices. Table 1 gives the locations of the deployed ultrasonic sensors in terms of spatial coordinates in the testbed.

FIGURE 5

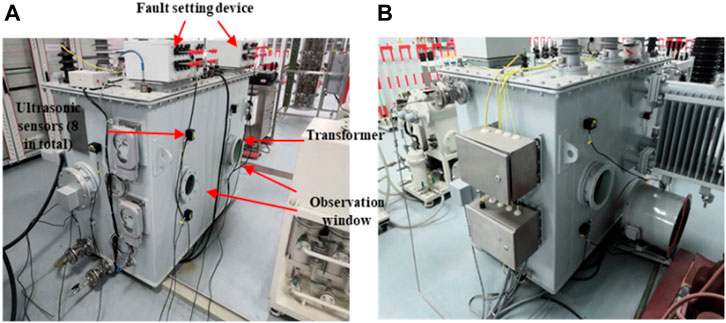
FIGURE 5. TWCP-0.5/50 transformer and deployment of the installed ultrasonic partial discharge sensors. (A) Front view (B) Back view.

TABLE 1

TABLE 1. Spatial coordinate of ultrasonic sensor of TWCP-0.5/50.

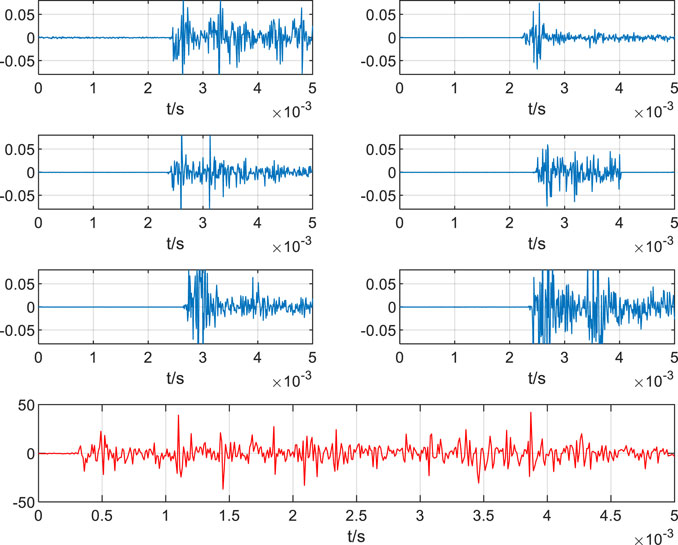
In the testbed, the transformer is operated with the rated voltage. Here, the ultrasonic testing equipment bandwidth is 100 kHz with a sampling frequency of 20 MHz. The ultrasonic localization result based on the TWCP-0.5/50 transformer testbed is presented in Figure 6. In addition, the developed PD localization method is assessed against the existing solutions in the TWCP-0.5/50 testbed. Table 2 presents the numerical results.

FIGURE 6

FIGURE 6. The ultrasonic localization result using TWCP-0.5/50 transformer testbed

TABLE 2

TABLE 2. Performance comparison of Pd location algorithm in power transformer of twcp-0.5/50.

Table 2 presents the numerical results of the proposed solution against the CHAN and PSO algorithms.

The numerical results demonstrate that the proposed solution outperforms the comparison benchmarks, i.e., Chan and PSO algorithm, in terms of localization accuracy.

Field Test

The specifications and technical parameters of the 110kV transformer are as follows (Toyoda and Wu, 2021; Wu et al., 2021):

1) Type: S10-6300/110

2) Capacity: 6300/6300KVA

3) Rated voltage ratio: 110/35 kV/10.5 kV

4) Insulation level: LI480AC200/LI200AC95-LI75AC25

5) Connection group: YNd11

6) Short circuit impedance: 9%

7) Cooling mode: ONAN

The size of the transformer is 5.8 × 2.300 × 2 m, and the drawing is shown in Figure 7.

FIGURE 7

FIGURE 7. Field experiment transformer. (A) Photos of transformer (B) Size and structure.

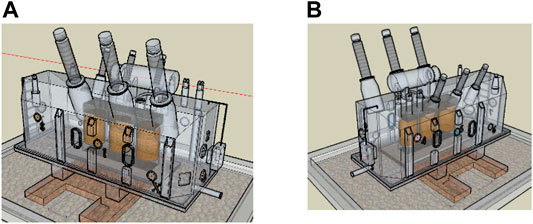
Eight ultrasonic sensors (No. 1–8) and one UHF sensor (No. x) are arranged around the transformer to form a three-dimensional sensor array, as shown in Figure 8.

FIGURE 8

FIGURE 8. Schematic diagram of transformer sensor location. (A) Front view (B) Back view.

In this work, the suspension discharge, tip discharge, surface discharge, and oil gap discharge models are developed. The electrodes at both ends of the model are made of brass, and the insulating material in the middle is polytetrafluoroethylene. The corresponding finite element models are established for analysis, and the electric fields of the discharge models are simulated, respectively, as illustrated in Figure 9.

FIGURE 9

FIGURE 9. Discharge models. (A) Suspension discharge model (B) Analysis simulation of suspension discharge model (C) Tip discharge model (D) Analysis simulation of tip discharge model (E) Surface discharge model (F) Analysis simulation of surface discharge model (G) Oil gap discharge model (H) Analysis simulation of oil gap discharge model.

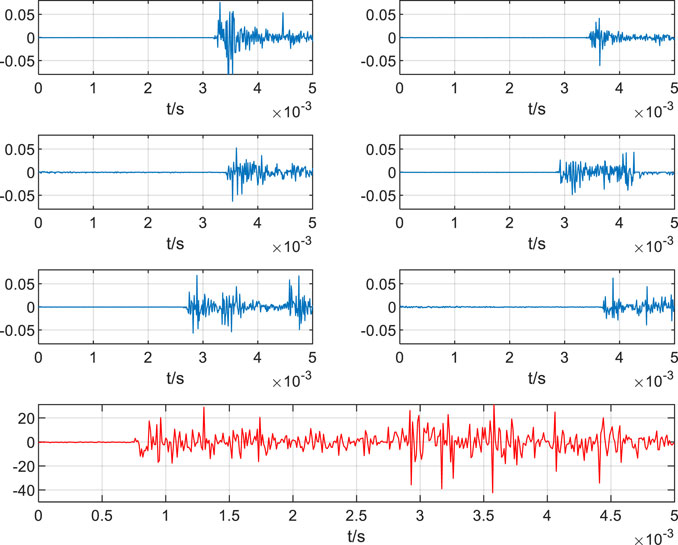
The discharge defects in Figure 9 relate to the electrical glue stick and put into the transformer, and the high voltage line that is corona free (red wire) and ground wire are appropriately tied to the electrical glue stick. This can pressurize the two poles of the discharge point defects to ensure the occurrence of partial discharge, as illustrated in Figure 10.The acoustic-electrical joint localization results are presented in Figure 11.

FIGURE 10

FIGURE 10. Discharge model in transformer.

FIGURE 11

FIGURE 11. Recording results of ultrasonic localization experiment of Field experiment transformer.

The proposed solution is further assessed in the field transformer that is operated at the rated voltage. The same sampling frequency is adopted in this experiment as in the testbed validation. The performance of the solution is evaluated against the CHAN algorithm and PSO-based algorithm. The numerical results are presented in detail in Table 3.

TABLE 3

TABLE 3. Performance Comparison of PD localization algorithm in power transformer.

Conclusive Remarks

This work presented an acoustic-electrical joint PD source localization solution that fully considered the multi-path propagation effect within the transformers. The SOCP algorithm is exploited and designed for PD source localization. The developed method has been extensively assessed and validated through simulations, testbed and field deployment. The obtained experimental results clearly demonstrated the effectiveness of the developed method and its benefit over the existing CHAN algorithm and PSO-based localization solution with the localization error of about 0.1 m.

For future work, a set of directions are considered worth further research exploitation. The proposed method needs to be evaluated through extensive experiments considering the cases of multiple partial discharge sources. Also, the advanced modeling techniques need to be further investigated for accurate characterization of multi-media refraction and diffraction.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JJ, HF and BW contributed to conception and design of the study. YL and YY organized the database. YC and DJ performed the statistical analysis.

Conflict of Interest

Author JJ was employed by the company State Grid Jiangsu Electric Power Co., Ltd. Author HF was employed by the company State Grid Jiangsu Electric Power Co., Ltd. Author YL was employed by the company State Grid Taizhou Power Supply Company. Author YY was employed by the company State Grid Lianyungang Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cakir, O., Kaya, I., Yazgan, A., and Cakir, Ö. (2013). Dynamic Orientation of Receiver Arrays Using Particle Swarm Optimisation. Electron. Lett. 49, 1313–1315. doi:10.1049/el.2013.2165

CrossRef Full Text | Google Scholar

Chan, Y. T., and Ho, K. C. (1994). A Simple and Efficient Estimator for Hyperbolic Location. IEEE Trans. Signal. Process. 42, 1905–1915. doi:10.1109/78.301830

CrossRef Full Text | Google Scholar

Chang, Y.-T., Wu, C.-L., and Cheng, H.-C. (2014). The Enhanced Locating Performance of an Integrated Cross-Correlation and Genetic Algorithm for Radio Monitoring Systems. Sensors 14, 7541–7562. doi:10.3390/s140407541

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z. (2019). Review of Direction of Arrival Estimation Algorithms for Partial Discharge Localisation in Transformers. IET Sci. Meas. Tech. 13, 529–535. doi:10.1049/iet-smt.2018.5297

CrossRef Full Text | Google Scholar

Coenen, S., and Tenbohlen, S. (2012). Location of PD Sources in Power Transformers by UHF and Acoustic Measurements. IEEE Trans. Dielect. Electr. Insul. 19, 1934–1940. doi:10.1109/TDEI.2012.6396950

CrossRef Full Text | Google Scholar

Contin, A., Cavallini, A., Montanari, G. C., Pasini, G., and Puletti, F. (2002). Digital Detection and Fuzzy Classification of Partial Discharge Signals. IEEE Trans. Dielect. Electr. Insul. 9, 335–348. doi:10.1109/TDEI.2002.1007695

CrossRef Full Text | Google Scholar

Ganguly, B., Chaudhury, S., Biswas, S., Dey, D., Munshi, S., Chatterjee, B., et al. (2020). Wavelet Kernel Based Convolutional Neural Network for Localization of Partial Discharge Sources within a Power Apparatus. IEEE Trans. Ind. Inf. 17, 1. doi:10.1109/TII.2020.2991686

CrossRef Full Text | Google Scholar

Han, J. (2019). A Novel Low Voltage Ride through Strategy for Cascaded Power Electronic Transformer. Prot. Control. Mod. Power Syst. 4, 1. doi:10.1186/s41601-019-0137-1

CrossRef Full Text | Google Scholar

Han-Lee Song, S. (1994). Automatic Vehicle Location in Cellular Communications Systems. IEEE Trans. Veh. Technol. 43, 902–908. doi:10.1109/25.330153

CrossRef Full Text | Google Scholar

Harrold, R. (1979). Acoustic Waveguides for Sensing and Locating Electrical Discharges in High Voltage Power Transformers and Other Apparatus. IEEE Trans. Power Apparatus Syst. 98, 449–457. doi:10.1109/TPAS.1979.319381

CrossRef Full Text | Google Scholar

Hekmati, A., and Hekmati, R. (2017). Optimum Acoustic Sensor Placement for Partial Discharge Allocation in Transformers. IET Sci. Meas. Tech. 11, 581–589. doi:10.1049/iet-smt.2016.0417

CrossRef Full Text | Google Scholar

Homaei, M., Moosavian, S. M., and Illias, H. A. (2014). Partial Discharge Localization in Power Transformers Using Neuro-Fuzzy Technique. IEEE Trans. Power Deliv. 29, 2066–2076. doi:10.1109/TPWRD.2014.2339274

CrossRef Full Text | Google Scholar

Hooshmand, R. A., Parastegari, M., and Yazdanpanah, M. (2013). Simultaneous Location of Two Partial Discharge Sources in Power Transformers Based on Acoustic Emission Using the Modified Binary Partial Swarm Optimisation Algorithm. IET Sci. Meas. Tech. 7, 119–127. doi:10.1049/iet-smt.2012.0029

CrossRef Full Text | Google Scholar

Howells, E., and Norton, E. T. (1978). Detection of Partial Discharges in Transformers Using Acoustic Emission Techniques. IEEE Trans. Power Apparatus Syst. 97, 1538–1549. doi:10.1109/TPAS.1978.354646

CrossRef Full Text | Google Scholar

Jia, J., Hu, C., Yang, Q., Lu, Y., Wang, B., and Zhao, H. (2021). Localization of Partial Discharge in Electrical Transformer Considering Multimedia Refraction and Diffraction. IEEE Trans. Ind. Inf. 17, 5260–5269. doi:10.1109/TII.2020.3023883

CrossRef Full Text | Google Scholar

Kallberg, B. (1980). Location of Partial Discharges in Power Transformers by Computation and Measurement of Capacitively Transmitted Voltage Pulses. IEEE Trans. Power Apparatus Syst. PAS-99, 589–596. doi:10.1109/TPAS.1980.319705

CrossRef Full Text | Google Scholar

Karami, H., Tabarsa, H., Gharehpetian, G. B., Norouzi, Y., and Hejazi, M. A. (2020). Feasibility Study on Simultaneous Detection of Partial Discharge and Axial Displacement of HV Transformer Winding Using Electromagnetic Waves. IEEE Trans. Ind. Inf. 16, 67–76. doi:10.1109/TII.2019.2915685

CrossRef Full Text | Google Scholar

Kweon, D.-J., Chin, S.-B., Kwak, H.-R., Kim, J.-C., and Song, K.-B. (2005). The Analysis of Ultrasonic Signals by Partial Discharge and Noise from the Transformer. IEEE Trans. Power Deliv. 20, 1976–1983. doi:10.1109/TPWRD.2004.833923

CrossRef Full Text | Google Scholar

Le, Shuting., Wu, Yuhu., Guo, Yuqian., and Del Vecchio, Carmen. (2021). Game Theoretic Approach for a Service Function Chain Routing in NFV with Coupled Constraints. IEEE Trans. Circuits Syst. 68, 3557. doi:10.1109/tcsii.2021.3070025

CrossRef Full Text | Google Scholar

Li, A., and Luan, F. (2018).An Improved Localization Algorithm Based on CHAN with High Positioning Accuracy in NLOS-WGN Environment. in 10th International Conference on Intelligent Human-Machine Systems and Cybernetics, 332–335.

CrossRef Full Text | Google Scholar

Luo Yongfen, Y., Ji Shengchang, S., and Li Yanming, Y. (2006). Phased-ultrasonic Receiving-Planar Array Transducer for Partial Discharge Location in Transformer. IEEE Trans. Ultrason. Ferroelect., Freq. Contr. 53, 614–622. doi:10.1109/TUFFC.2006.1610570

PubMed Abstract | CrossRef Full Text | Google Scholar

Markalous, S., Tenbohlen, S., and Feser, K. (2008). Detection and Location of Partial Discharges in Power Transformers Using Acoustic and Electromagnetic Signals. IEEE Trans. Dielect. Electr. Insul. 15, 1576–1583. doi:10.1109/TDEI.2008.4712660

CrossRef Full Text | Google Scholar

Meka, K., Giridhar, A. V., and Siva Sarma, D. V. S. S. (2018). PD Source Location Utilizing Acoustic TDOA Signals in Power Transformer by Fuzzy Adaptive Particle Swarm Optimization. Radioengineering 27, 1119–1127. doi:10.13164/re.2018.1119

CrossRef Full Text | Google Scholar

Moore, P. J., Portugues, I. E., and Glover, I. A. (2006). Partial Discharge Investigation of a Power Transformer Using Wireless Wideband Radio-Frequency Measurements. IEEE Trans. Power Deliv. 21, 528–530. doi:10.1109/TPWRD.2005.848438

CrossRef Full Text | Google Scholar

Naderi, M., Vakilian, M., Blackburn, T. R., Phung, B. T., Naderi, M., and Nasiri, A. (2007). A Hybrid Transformer Model for Determination of Partial Discharge Location in Transformer Winding. IEEE Trans. Dielect. Electr. Insul. 14, 436–443. doi:10.1109/TDEI.2007.344625

CrossRef Full Text | Google Scholar

Rubio-serrano, J., Rojas-moreno, M. V., Posada, J., Martínez-tarifa, J. M., Robles, G., and Garcia-souto, J. A. (2012). Electro-acoustic Detection, Identification and Location of Partial Discharge Sources in Oil-Paper Insulation Systems. IEEE Trans. Dielect. Electr. Insul. 19, 1569–1578. doi:10.1109/TDEI.2012.6311502

CrossRef Full Text | Google Scholar

Shen, Xun., and Raksincharoensak, Pongsathorn. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Tarimoradi, H., and Gharehpetian, G. B. (2017). Novel Calculation Method of Indices to Improve Classification of Transformer Winding Fault Type, Location, and Extent. IEEE Trans. Ind. Inf. 13, 1531–1540. doi:10.1109/TII.2017.2651954

CrossRef Full Text | Google Scholar

Toyoda, M., and Wu, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. doi:10.1109/tcyb.2019.2954849

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y.-B., Chang, D.-G., Fan, Y.-H., Zhang, G.-J., Zhan, J.-Y., Shao, X.-J., et al. (2017). Acoustic Localization of Partial Discharge Sources in Power Transformers Using a Particle-Swarm-Optimization-Route-Searching Algorithm. IEEE Trans. Dielect. Electr. Insul. 24, 3647–3656. doi:10.1109/TDEI.2017.006857

CrossRef Full Text | Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn. Syst. 32 (6), 2910–2924. doi:10.1109/TNNLS.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y. H., Dong, X. Z., and Mirsaeidi, S. (2017). Modeling and Simulation of Air-Gapped Current Transformer Based on Preisach Theory. Prot. Control. Mod. Power Syst. 2, 11. doi:10.1186/s41601-017-0046-0

CrossRef Full Text | Google Scholar

Xun, S., Tinghui, O., Nan, Y., and Jiancang, Z. (2021). Sample-based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Networks Learn. Syst., 1–8. doi:10.1109/tnnls.2021.3102323

CrossRef Full Text | Google Scholar

Yang, N. (2021). “A Comprehensive Review of Security-Constrained Unit Commitment,” in Journal of Modern Power Systems and Clean Energy. doi:10.35833/MPCE.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022a). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty. Electr. Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022b). Intelligent Data-Driven Decision-Making Method for Dynamic Multisequence: An E-Seq2Seq-Based SCUC Expert System. IEEE Trans. Ind. Inf. 18, 3126–3137. doi:10.1109/TII.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Dong, Z., Wu, L., Zhang, L., Shen, X., Chen, D., et al. (2021). A Comprehensive Review of Security-Constrained Unit Commitment. J. Mod. Power Syst. Clean Energy, 1–14. doi:10.35833/MPCE.2021.000255

CrossRef Full Text | Google Scholar