Heat Transfer Characteristics and Pressure Drop of U-type Channel in Vacuum Distillation Process for Titanium Sponge

Blockage of the U-type channel exacerbates the intermittency of production, and clarifying the channel heat transfer characteristics and pressure drop is an effective way to address this problem. The channel heat transfer and flow characteristics of the fluid in the channel are experimentally investigated in this study. According to the experiments, the heat transfer coefficient is between 59.95 and 200.29 W/m²⋅K and increases with the flow velocity and fluid temperature. Because the pressure drop is usually accompanied by a change in the energy loss of the fluid, the energy loss is evaluated experimentally. The results demonstrate that the friction loss in the straight tube section accounts for 80% of the energy loss. A bent tube of 90° is recommended instead of a right-angle tube to reduce the pressure drop. A dimensionless relation regarding the Nusselt number is presented to predict the heat transfer characteristics. We provided proposals to address the problem of blockage of the U-type channel, this is helpful to reduce production energy consumption and improve the quality of titanium sponge.

Introduction

The Kroll process is a unique existing industrial process for titanium sponge, the primary industrial choice in titanium chains, and this process has played a significant role in the titanium industry over the past decades (Nagesh et al., 2008; Zhang et al., 2011; Wang and Wu., 2021). The Kroll process is costly, energy-intensive, and intermittent (Wang et al., 2017; Takeda and Okabe, 2019). After the reduction process, the remaining magnesium and magnesium chloride were separated via vacuum distillation to obtain a titanium sponge (Nagesh et al., 2004; Cui et al., 2011). The fluid was distilled from the reduction reactor to the condenser, and the channel was easily blocked in the production process because of the unreasonable heating system of the heater and the energy loss of the fluid. This further exacerbated the intermittency of production, leading to a long production period. Titanium sponge pores were easy to sinter and other problems (Li et al., 2015; Liang et al., 2018) affected the distillation period, further increasing the energy consumption. However, this difficulty has not yet been effectively addressed. To address this blockage, it is necessary to clarify the channel heat transfer characteristics and pressure drop.

Currently, there is no research on the heat transfer characteristics and pressure drop of U-type channels in the vacuum distillation processes for titanium sponges. Therefore, this experiment referred to the literature on the heat transfer of fluids in a tube (Gorman et al., 2015; Moghadam et al., 2020; Qi et al., 2019; Baik et al., 2019). Hekmatipour et al. (2017) experimentally studied the convective heat transfer of nanofluids in a tube. In this study, we present a correlation relation for the nanofluid to predict the Nusselt number. Wen et al. (2019) experimentally investigated the air flowing through helical tube bundles and obtained the flow and convective heat transfer characteristics. We propose two empirical relations to describe the convective heat transfer coefficient and friction factor. Sarmadian et al. (2020) investigated the heat transfer characteristics in a heat exchanger and discussed the heat transfer improved by twisted tapes. The channel heat transfer performance and pressure drop improved with the installation of the twisted tapes. The friction and heat transfer characteristics of a fluid influenced by a circular ring turbulator in a tube were experimentally studied (Kongkaitpaiboon et al., 2010), and the heat transfer rates increased from approximately 57–195% when the CRTs were installed. Baba et al. (2018) studied the convective heat transfer of an Fe₃O₄-water nanofluid in a heat exchanger. The heat transfer and pressure drop of different heat exchangers are also discussed. We propose a correlation for the Nusselt number. Similarly, the aforementioned studies provide theoretical support for this experiment.

The heat transfer and flow characteristics of a mixed system of nitrogen, gaseous magnesium, and gaseous magnesium chloride in the channel were investigated experimentally. The Nusselt number dimensionless correlation relation was obtained based on experimental data.

Methods

Experimental Apparatus

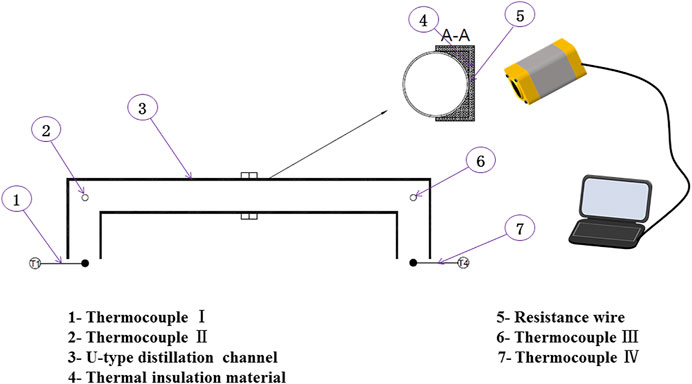
Figure 1 shows the apparatus used in this experiment. The distillation channel is 1Cr18Ni9Ti stainless steel tube, length of the horizontal section is 3.62 m, vertical section is 0.40 m, inner diameter is 0.129 m, and outer diameter is 0.159 m. A heater with constant power was used to heat the distillation tube to maintain the fluid temperature, and the parameters are listed in Table 1.

FIGURE 1

FIGURE 1. Schematic of the experimental apparatus.

TABLE 1

TABLE 1. Detailed parameters of heater.

To measure the temperature of the outer wall of the heater, an RSE300 infrared thermal imager was used. Two K-type thermocouples were installed on the tube to obtain the temperature of its outer wall. In addition, the fluid temperature was measured using two other K-type thermocouples at the inlet and outlet. By pumping a vacuum with nitrogen, the pressure drop can be obtained based on the vacuum degree.

In this study, the fluid consisted of a mixed system of nitrogen, gaseous magnesium, and gaseous magnesium chloride (listed in Table 2). As the temperature increased from 913.00 to 1023.00 K.

TABLE 2

TABLE 2. Components of the typical industrial vacuum distillation mixture.

Theoretical Background

Pressure Drop

Clearly, as the fluid is distilled from the reduction reactor to the condenser in the straight tube section, the energy loss is caused by the viscous force of the fluid. There was a local loss because the flow direction changed dramatically at the right angle of the channel.

Taking the horizontal line of the channel inlet and outlet as a benchmark, the inlet velocity was considered as zero. The Bernoulli equation of the fluid is as follows:

$\frac{\mathrm{\Delta }p}{\rho g}=\frac{\alpha v^2}{2g}+L(1)$

Furthermore, the energy loss of the fluid is as follows:

$\text{L}=\text{γ}\frac{l}{d}\frac{v^2}{2g}+\xi \frac{v^2}{2g}(2)$

Clearly, the local loss coefficient is 1.97. The coefficient of frictional loss was calculated using formula (3) to (5) (Demirkir and Erturk, 2021) and verified according to the range of the Reynolds number.

$\text{γ}=\frac{64}{Re}\left(Re<2320\right)(3)$

$\text{γ}=\frac{0.3164}{R{e}^{0.25}}\left(4\times {10}^3<Re<{10}^5\right)(4)$

$\text{γ}=0.0032+0.221R{e}^{-0.237}\left({10}^5<Re<3\times {10}^6\right)(5)$

Hence, the flow velocity can be solved by Eq. (1)–(5).

Heat Conduction

In the distillation process, the channel is isothermal, and the axial heat transfer can be ignored and regarded as a one-dimensional heat conduction with an internal heat source.

The resistance wire conducts heat through the channel and insulation layer, and the power is obtained as follows:

$\text{P}=P_{\text{lo}}+P_{ef}(6)$

Mathematical formulation of heat conduction in thermal insulation layer is expressed as follows:

$\frac{d^{2}t}{d{x}^2}+\frac{\mathrm{\Phi }}{{\lambda }_a}=0(7)$

$\text{x}=0,\frac{dt}{dx}=0(8)$

$\text{x}=\text{δ},\text{t}=t_h(9)$

Heat transfer process with the channel is analyzed as follows:

$t_o-t_i=\frac{{\Phi }_{ef}}{2\pi l{\lambda }_t}ln\frac{d_i}{d_o}(10)$

$t_i-t_f=\frac{{\Phi }_{ef}}{h\pi l{d}_i}(11)$

The heat transfer coefficient is complex heat transfer coefficient, and the heat transfer coefficient is obtained as follows:

$\text{h}=\frac{2{\lambda }_t{\Phi }_{ef}}{2\pi l{d}_i{\lambda }_t\left(t_o-t_f\right)-d_i{\Phi }_{ef}ln\frac{d_i}{d_o}}(12)$

Furthermore, the Nusselt, Reynolds, and Prandtl numbers are obtained as follows, respectively:

$\text{Nu}=\frac{h{d}_i}{{\lambda }_f}(13)$

$\text{Re}=\frac{\rho v{d}_i}{\mu }(14)$

$\text{Pr}=\frac{\mu Cp}{{\lambda }_f}(15)$

Results and Discussions

Energy Loss

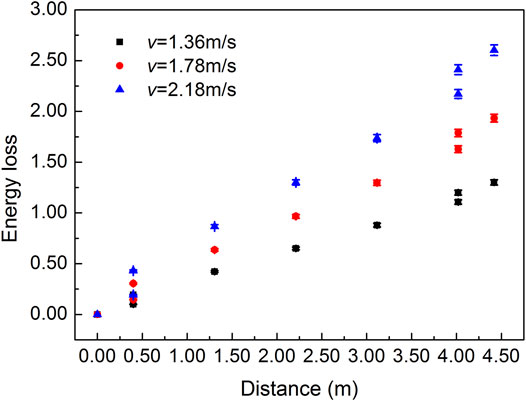
The pressure drop is usually accompanied with change in the energy loss of the fluid. Figure 2 shows the energy loss of the fluid inside the channel under various flow velocities. It is observed that the energy loss increases with distance and reaches a maximum as the fluid reaches the condenser. The energy loss doubled when the flow velocity increased from 1.36 to 2.18 m/s. Furthermore, the friction loss in the straight tube section accounted for 80% of the energy loss, which was proportional to the square of the flow velocity. Therefore, the pressure drop can be controlled at a reasonable level by pumping the vacuum in the production process to reduce energy loss.

FIGURE 2

FIGURE 2. Variation in energy loss for different fluid velocities.

As shown in Figure 2, the energy loss increases suddenly owing to the local loss at the right angle of the channel. As observed in the theoretical background sections, the pressure drop increases because of the increase in fluid energy loss to a great extent. Improving the channel structure to reduce the local loss coefficient may be an effective way to reduce pressure drop. The local loss coefficient of the bent tube with 90° was several times smaller than that of the right-angle tube, and under similar conditions, the fluid energy loss in the bent tube with 90° decreased by 13% compared with that in the right-angle tube. Therefore, a bent tube of 90° is recommended instead of a right-angle tube.

Heat Transfer Coefficient

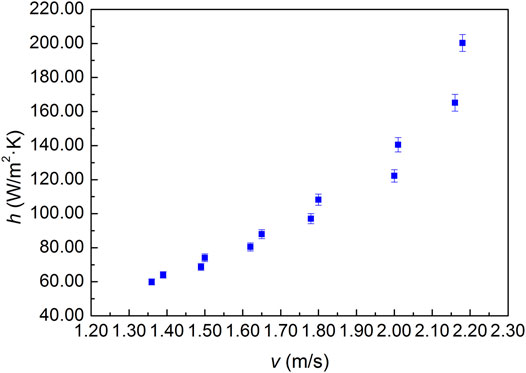
The heat transfer coefficient inside the whole channel is not constant, and the heat transfer coefficient in this study is mean heat transfer coefficient. Figure 3 shows the variation in the heat transfer coefficient with fluid velocity. The heat transfer coefficient increased as the Reynolds number increased because the flow velocity increased, resulting in an increase in the intensity of convective heat transfer. The extent of the increase in the heat-transfer coefficient also increased with a further increase in the flow velocity. Furthermore, as observed in Figure 3, the heat transfer coefficient is between 59.95 and 200.29 W/m²⋅K.

FIGURE 3

FIGURE 3. Effects of fluid velocity on the heat transfer.

In addition, the effect of the fluid temperature on heat transfer was investigated. The temperature difference decreases as the fluid temperature increases. An increase in the fluid temperature increases the thermal conductivity and reduces the dynamic viscosity of the fluid. Therefore, the heat transfer coefficient increases and boosts the intensity of the convective heat transfer.

Heat Transfer Characteristics

The temperature ranges from 913.00 to 1023.00 K, fluid thermo-physical properties have no significant change, and the Prandtl number is between 0.0204 and 0.0208, which is approximately 0.0205 in this study. Therefore, the dimensionless relation is determined by the Nusselt and Reynolds numbers, as expressed in Eq. 16 as follows:

$\text{Nu}=\text{C}R{e}^n(16)$

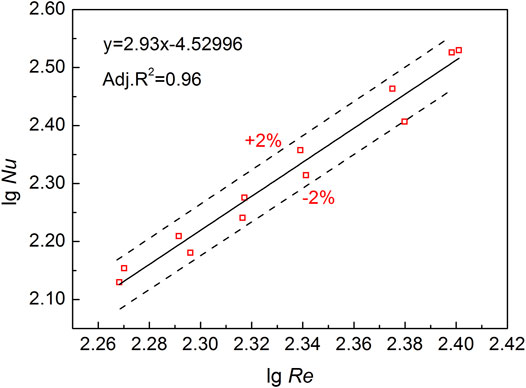
Constants C and n were determined from the experimental data. Figure 4 shows the Reynolds and Nusselt numbers logarithmic fitting relation, and the relational formula is expressed as follows:

$\text{Nu}=2.95\times {10}^{-5}R{e}^{2.93}\left(Adj.R^2=0.96\right)(17)$

FIGURE 4

FIGURE 4. Reynolds and Nusselt numbers logarithmic fitting relation.

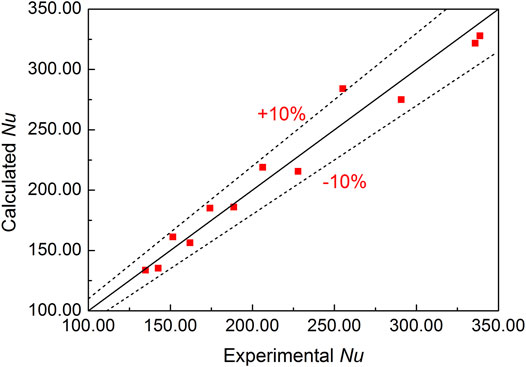
Furthermore, Figure 5 shows a comparison of the Nusselt numbers calculated from Eq. 17 using the experimental Nusselt number, that is, the convective heat transfer characteristics for 185.45 < Re < 250.18, Pr = 0.0205 could be predicted using Eq. 17 and with no significant errors.

FIGURE 5

FIGURE 5. Calculated Nusselt and experimental Nusselt numbers.

Conclusion

The channel heat transfer and flow characteristics of the fluid in the channel were investigated experimentally. The energy loss of the fluid was also analyzed. The impact of the flow velocity and temperature on the heat transfer coefficient was discussed. The conclusions are as follows:

1) The pressure drop increased with the energy loss. The energy loss of the fluid in the channel consists of the friction loss in the straight tube section and local loss at the right angle of the channel. The friction loss in the straight-tube section accounted for 80% of the energy loss. A bent tube of 90° is recommended to minimize the local loss to lower the pressure drop.

2) The heat transfer coefficient is between 59.95 and 200.29 W/m²⋅K. Moreover, the heat transfer coefficient increases with fluid velocity and fluid temperature.

3) A dimensionless relation regarding the Nusselt number is presented to predict the heat transfer characteristics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KY, CZ, HY, and FW conceived and designed the study. KY, CZ, and HY were responsible for the experimental operation, and KY analyzed the experimental data. KY wrote the manuscript, and FW revised it.

Funding

The author acknowledges the financial support received from the National Natural Science Foundation of China (grant number 51874108), the Science and Technology Foundation of Guizhou Province (grant number QKHJC 2019-1406, and QKHJC-ZK 2021-YB261), and the Talent Projects of Guizhou University and the Education Department of Guizhou Province (grant number GDPY 2019-20, and QJHKYZ 2021-097).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Qiang Liang and Lvguo Zhang of Zunyi Titanium Co., Ltd. for providing experimental batches in this work.

References

Baba, M. S., Raju, A. V. S. R., and Rao, M. B. (2018). Heat Transfer Enhancement and Pressure Drop of Fe3O4 -water Nanofluid in a Double Tube Counter Flow Heat Exchanger with Internal Longitudinal Fins. Case Stud. Therm. Eng. 12, 600–607. doi:10.1016/j.csite.2018.08.001

CrossRef Full Text | Google Scholar

Baik, W., Lee, W., and Yun, R. (2019). Heat Transfer and Pressure Drop Characteristics of CO2 Mixtures in a Pipeline under the Seawater Condition. Int. J. Heat Mass Transfer 136, 627–634. doi:10.1016/j.ijheatmasstransfer.2019.03.026

CrossRef Full Text | Google Scholar

Bera, T. K., Biswas, S. K., Rajan, K., and Nagaraju, J. (2014). Projection Error Propagation-Based Regularization (PEPR) Method for Resistivity Reconstruction in Electrical Impedance Tomography (EIT). Measurement 49, 329–350. doi:10.1016/j.measurement.2013.11.003

CrossRef Full Text | Google Scholar

Cui, C., Hu, B., Zhao, L., and Liu, S. (2011). Titanium alloy Production Technology, Market Prospects and Industry Development. Mater. Des. 32, 1684–1691. doi:10.1016/j.matdes.2010.09.011

CrossRef Full Text | Google Scholar

Demirkır, Ç., and Ertürk, H. (2021). Convective Heat Transfer and Pressure Drop Characteristics of Graphene-Water Nanofluids in Transitional Flow. Int. Commun. Heat Mass Transfer 121, 105092. doi:10.1016/j.icheatmasstransfer.2020.105092

CrossRef Full Text | Google Scholar

Gorman, J. M., Carideo, M., Sparrow, E. M., and Abraham, J. P. (2015). Heat Transfer and Pressure Drop Comparison of Louver- and plain-finned Heat Exchangers where One Fluid Passes through Flattened Tubes. Case Stud. Therm. Eng. 5, 122–126. doi:10.1016/j.csite.2015.03.002

CrossRef Full Text | Google Scholar

Hekmatipour, F., Akhavan-Behabadi, M. A., Sajadi, B., and Fakoor-Pakdaman, M. (2017). Mixed Convection Heat Transfer and Pressure Drop Characteristics of the Copper Oxide-Heat Transfer Oil (CuO-HTO) Nanofluid in Vertical Tube. Case Stud. Therm. Eng. 10, 532–540. doi:10.1016/j.csite.2017.09.009

CrossRef Full Text | Google Scholar

Kongkaitpaiboon, V., Nanan, K., and Eiamsa-ard, S. (2010). Experimental Investigation of Convective Heat Transfer and Pressure Loss in a Round Tube Fitted with Circular-Ring Turbulators. Int. Commun. Heat Mass Transfer 37, 568–574. doi:10.1016/j.icheatmasstransfer.2009.12.016

CrossRef Full Text | Google Scholar

Liang, L., Dachun, L., Heli, W., Kaihua, L., Juhai, D., and Wenlong, J. (2018). Removal of Chloride Impurities from Titanium Sponge by Vacuum Distillation. Vacuum 152, 166–172. doi:10.1016/j.vacuum.2018.02.030

CrossRef Full Text | Google Scholar

Liang, L., Kaihua, L., Qingdong, M., and Cong, W. (2015). “Research on Quality Improvement of Titanium Sponge by Process Optimization,” in Rare Metal Technology 2015. Editors N. R. Neelameggham, S. Alam, H. Oosterhof, A. Jha, D. Dreisinger, and S. Wang (Switzerland, FL: Springer, Cham Press), 231–237. doi:10.1007/978-3-319-48188-3_26

CrossRef Full Text | Google Scholar

Moghadam, M. T., Behabadi, M. A. A., Sajadi, B., Razi, P., and Zakaria, M. I. (2020). Experimental Study of Heat Transfer Coefficient, Pressure Drop and Flow Pattern of R1234yf Condensing Flow in Inclined plain Tubes. Int. J. Heat Mass Transfer 160, 120199. doi:10.1016/j.ijheatmasstransfer.2020.120199

CrossRef Full Text | Google Scholar

Nagesh, C. R. V. S., Ramachandran, C. S., and Subramanyam, R. B. (2008). Methods of Titanium Sponge Production. Trans. Indian Inst. Met. 61, 341–348. doi:10.1007/s12666-008-0065-7

CrossRef Full Text | Google Scholar

Nagesh, C. R. V. S., Rao, C. S., Ballal, N. B., and Rao, P. K. (2004). Mechanism of Titanium Sponge Formation in the Kroll Reduction Reactor. Metall. Materi Trans. B 35, 65–74. doi:10.1007/s11663-004-0097-2

CrossRef Full Text | Google Scholar

Qi, C., Chen, X., Wang, W., Miao, J., and Zhang, H. (2019). Experimental Investigation on Flow Condensation Heat Transfer and Pressure Drop of Nitrogen in Horizontal Tubes. Int. J. Heat Mass Transfer 132, 985–996. doi:10.1016/j.ijheatmasstransfer.2018.11.092

CrossRef Full Text | Google Scholar

Sarmadian, A., Moghaddam, H. A., Asnaashari, A., Joushani, H. A. N., Moosavi, M., Islam, M. S., et al. (2020). Flow Boiling Heat Transfer and Pressure Drop Characteristics of Isobutane in Horizontal Channels with Twisted tapes. Int. J. Heat Mass Transfer 162, 120345. doi:10.1016/j.ijheatmasstransfer.2020.120345

CrossRef Full Text | Google Scholar

Takeda, O., and Okabe, T. H. (2019). Current Status of Titanium Recycling and Related Technologies. JOM 71, 1981–1990. doi:10.1007/s11837-018-3278-1

CrossRef Full Text | Google Scholar

Wang, W., Wu, F., and Jin, H. (2017). Enhancement and Performance Evaluation for Heat Transfer of Air Cooling Zone for Reduction System of Sponge Titanium. Heat Mass. Transfer 53, 465–473. doi:10.1007/s00231-016-1836-z

CrossRef Full Text | Google Scholar

Wang, W., and Wu, F. (2021). Quantifying Heat Transfer Characteristics of the Kroll Reactor in Titanium Sponge Production. Front. Energ. Res. 9, 759781. doi:10.3389/fenrg.2021.759781

CrossRef Full Text | Google Scholar

Wen, J., Fu, Y., Bao, X., Liu, Y., and Xu, G. (2019). Flow Resistance and Convective Heat Transfer Performances of Airflow through Helical-Tube Bundles. Int. J. Heat Mass Transfer 130, 778–786. doi:10.1016/j.ijheatmasstransfer.2018.10.129

CrossRef Full Text | Google Scholar

Zhang, W., Zhu, Z., and Cheng, C. Y. (2011). A Literature Review of Titanium Metallurgical Processes. Hydrometallurgy 108, 177–188. doi:10.1016/j.hydromet.2011.04.005

CrossRef Full Text | Google Scholar

Nomenclature

c_p Specific heat capacity of the fluid, J/mol⋅K

d Diameter, m

g Acceleration of gravity (9.81 m/s²)

h Heat transfer coefficient, W/m²⋅K

L Energy losses

l Tube length, m

M Relative molecular mass

Nu Nusselt number

Pr Prandtl number

P Power

Re Reynolds number

t Temperature , K

U Uncertainty

v Fluid velocity, m/s

▵p Pressure drop, kPa

α Kinetic energy correction factor

γ Frictional loss coefficient

δ Thickness, m

λ Thermal conductivity, W/m⋅K

ξ Local loss coefficient

ω Molar fraction

ρ Density, Kg/m³

μ Dynamic viscosity, Pa⋅s

Φ˙ Inner heat source, W/m3

Φ Heat flux, W

Subscripts

a Aluminum silicate fiber

ef Effective

h Outer wall of heater

lo Loss

i Inner

o Outer

t Tube

x Component