
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 21 March 2022
Sec. Nuclear Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.849229
This article is part of the Research Topic Artificial Intelligence Applications in Nuclear Energy View all 13 articles
To meet the numerous application demands of lead-bismuth reactors, different design optimization tasks need to be conducted on these reactors based on the existing reactor core solutions. However, the design optimization of lead-bismuth reactors is a challenging task because it is a complex, multi-dimensional, and nonlinear constrained problem. To resolve these issues and improve the efficiency of design optimization, a new method, called the KSM-OLHS-SEUMRE method, based on the Kriging surrogate model (KSM), orthogonal Latin hypercube sampling (OLHS), and space exploration and unimodal region elimination (SEUMRE) algorithm is proposed in this study. Based on this method, a design optimization program of lead-bismuth reactors (DOPPLER-K) is developed, which realizes functions like sample point generation, optimization analysis, pre-post processing of reactor calculation, coupling of the Reactor Monte Carlo (RMC) calculation code and the Steady-state Thermal-hydraulic Analysis Code (STAC). Further, taking lead-bismuth reactors SPALLER-4 and URANUS as prototypes, the proposed intelligent optimization method for preliminary design of lead-bismuth reactor core is verified. The results show that this method can rapidly and accurately find the target scheme satisfying the optimization conditions, and it is three orders of magnitude faster than pure Monte Carlo calculation. Compared with the initial core scheme of URANUS, the optimization rates of fuel loading, total core mass, active zone volume, and total core volume are reduced by 10.8, 11.5, 18.1, and 17.1%, respectively. These results validate the feasibility and efficacy of the proposed method for design optimization of lead-bismuth reactor core.
Over the recent years, lead-bismuth reactors have received considerable attention from the major nuclear energy countries owing to their unique characteristics such as long-life, miniaturization ability, high flux, and natural circulation, which lead to outstanding advantages in the utilization of nuclear energy (Wu, 2018). However, it may be noted that different technical indicators and reactor core design schemes are required in various application scenarios and missions, thus numerous design optimization tasks need to be conducted based on the existing lead-bismuth reactor core schemes. It is well known that since it involves coupled calculation and analysis of physical/thermal-hydraulic characteristics and strength of structural materials, the design optimization of lead-bismuth reactor core is a complex, multi-dimensional, and nonlinear constrained problem, and a large uncertainty exists in the calculation results, which is caused by the nuclear reaction cross section, approximation of calculation model, etc. The existing traditional semi-empirical design methods that rely on the designer experience cannot find the optimal solution efficiently under the influence of multi-factor coupling. On the other hand, the single heuristic optimization algorithms, such as genetic algorithm, simulated annealing algorithm, particle swarm algorithm, etc., need a large number of stochastic samples and Monte Carlo calculations to support the design optimization and suffer from the problems of slow convergence and a trend of falling into local optimum (Meneses et al., 2009; Khoshahval et al., 2011; Zameer et al., 2014). Therefore, it is necessary to develop an intelligent optimization method for preliminary design of lead-bismuth reactor core with random effects, low computational cost, high convergence speed, and strong optimization ability.
To solve these problems such as excessive calculation, slow convergence, and large uncertainty in traditional Monte Carlo computation and single heuristic optimization algorithm, the surrogate modeling technique in which an approximate model is constructed based on the experimental points to replace the complex original model has been considered. The commonly used surrogate models include the response surface method, radial basis function interpolation, Kriging model, and so on (Zhang, 2014). Among them, the Kriging surrogate model (KSM) can not only fit a smooth curve closer to the original objective function but also can be easily adapted to different variation trends, and it covers the inherent uncertainty of objective functions by selecting different regression models and related functions (Kempf et al., 2012). Therefore, although the accuracy of the KSM will decrease when solving the prediction of the objective function with more than 8 design parameters, the KSM is still used in this study due to its overall strong fitting effect and the modeling method that can cover the inherent uncertainty in the reactor calculation. To date, KSM has been widely used in the design optimization of aerospace, machinery, automobiles, and other fields, and it is now being used in the reactor field as well. Zeng et al. (2020) used KSM to provide a generalized framework for the core optimization of sodium-cooled fast reactor, and Kempf et al. (2012) used it to obtain the optimal geometric parameters for a high-flux research reactor. Kim et al. used the KSM for shape optimization of the inlet plenum and rising channels in the pebble-bed modular reactor (Kim and Lee, 2009). Li et al. studied the effects of flow and heat transfer factors in the rod bundle of fast reactor assemblies on the thermal-hydraulic characteristics through the Kriging technology (Song and Yang, 2018). All the above studies verified the good prediction accuracy and high computational efficiency of the KSM. Thus, the optimization method combined with KSM can be a feasible and effective approach for the design optimization of a lead-bismuth reactor core.
In this study, an intelligent optimization method is proposed for preliminary design of lead-bismuth reactor core, which is based on the combination of KSM, orthogonal Latin hypercube sampling (OLHS), and space exploration and unimodal region elimination (SEUMRE) algorithm. This method is called the KSM-OLHS-SEUMRE method. By coupling the reactor Monte Carlo (RMC) code, a Monte Carlo code for reactor core analysis, and the steady-state thermal-hydraulic analysis code (STAC), a design optimization program of lead-bismuth reactors based on KSM-OLHS-SEUMRE (DOPPLER-K) has been developed. Taking lead-bismuth reactors SPALLER-4 and URANUS as prototypes, the proposed optimization method is verified through a rapid search for target design schemes and core parameter optimization.
The rest of this paper is organized as follows. Section 2 provides a brief introduction to the KSM-OLHS-SEUMRE method and the DOPPLER-K software. The construction principles of KSM, OLHS, and SEUMRE algorithm are described in Section 3. The optimization verification results for SPALLER-4 and URANUS are discussed in Section 4. Finally, the study is concluded in Section 5.
The intelligent optimization method constructed in this study includes the KSM-OLHS-SEUMRE method (introduced in Section 2.1) and DOPPLER-K software (introduced in Section 2.2). The construction principles of KSM, OLHS and SEUMRE involved in KSM-OLHS-SEUMRE method are described in Section 3.
Different from traditional or single heuristic optimization method, the optimization method adopted in this research firstly uses KSM technology to replace the original Monte Carlo code with slow calculation speed to predict the core characteristic parameters, which not only greatly improves the calculation efficiency, but also realizes the target prediction under the simultaneous coupling of multiple core design parameters. Secondly, when multiple design parameters influence at the same time and the design range is wide, this method makes the optimization avoid the problem of local optimum and difficult convergence in the traditional optimization algorithm as far as possible through sequence iteration, preferential addition point selection and SEUMRE space search technology to improve the optimization search efficiency. Finally, through the developed DOPPLER-K software, the automatic execution of sampling, Monte-Carlo program calling calculation and target optimization analysis can be carried out, which provides great convenience to optimization designers.
The design optimization of lead-bismuth reactor core generally involves the establishment of a mathematical model, selection of design variables, calculation of physical/thermal characteristic parameters, and determination of the optimal scheme. Based on this strategy and the construction principles in Section 3, the optimization method KSM-OLHS-SEUMRE is developed. Its flow chart is shown in Figure 1A, and the basic implementation steps are as follows:
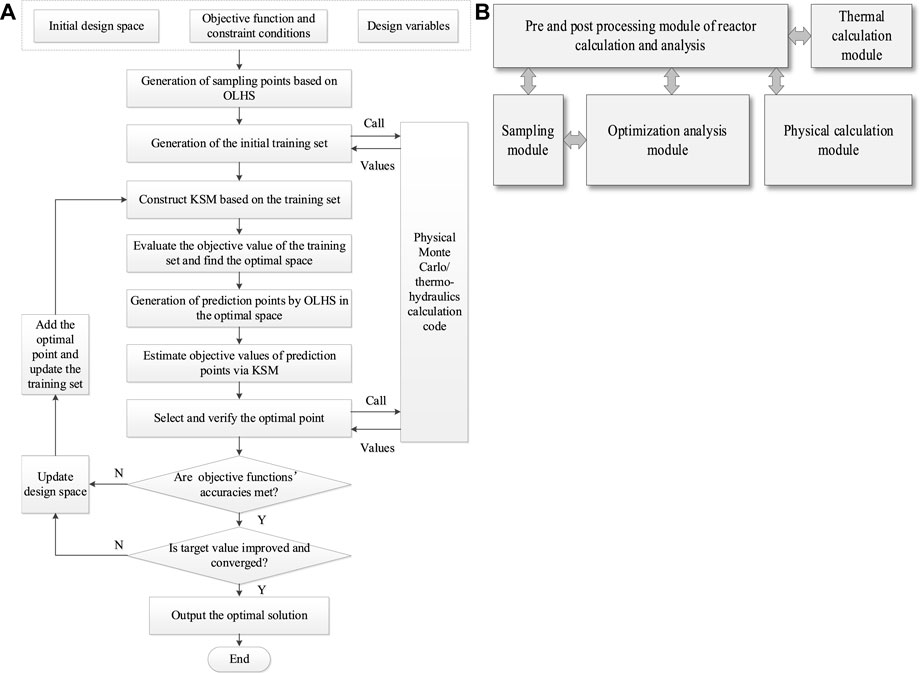
FIGURE 1. Intelligent optimization method. (A) Flow chart of KSM-OLHS-SEUMRE method, (B) Functional modules of DOPPLER-K.
Step 1. Establish the mathematical model of the lead-bismuth reactor core to be optimized, including design space and variables, objective functions, and constraint conditions.
Step 2. Generate sample points of the mathematical model by the OLHS technique.
Step 3. Calculate sample points to generate the training set based on the physical Monte-Carlo/thermal-hydraulics calculation code.
Step 4. Construct KSM based on the training set and evaluate the objective values of the training set to find the optimal space.
Step 5. Predict the points of target/constraint functions and assess them to select the optimal point verified by physical Monte Carlo/thermal-hydraulics calculation code.
Step 6. Update the design space and KSM continuously based on the principle of optimal point selection and SEUMRE algorithm to improve the prediction accuracy and overall optimization efficiency of the model.
Step 7. Perform iterative optimization to quickly approximate the objective function and obtain the optimal convergence solution.
Based on the KSM-OLHS-SEUMRE method, the design optimization program of lead-bismuth reactors, called DOPPLER-K software, which couples RMC and STAC and realizes functions, such as sampling, modeling, and optimization, has been developed in MATLAB. The functional modules of DOPPLER-K software are shown in Figure 1B.
In the sampling module, all the design variables are sampled and saved in the initial training set using OLHS after the user defines the variables and initial design space.
In the physical calculation module, some characteristic parameters of sample points are calculated by RMC (Kan et al., 2015), a three-dimensional Monte Carlo neutron transport code developed by the Reactor Engineering Analysis Laboratory (REAL), Department of Engineering Physics, Tsinghua University. These characteristic parameters, such as effective multiplication factor (Keff), flux, power, and burnup, can be used as objective functions or constraint conditions for design optimization of the lead-bismuth reactor core.
In the thermal calculation module, thermal-hydraulic characteristic parameters, such as the maximum fuel cladding and pellet temperature, coolant velocity, based on the sample points and reactor core power distribution are used as the constraint conditions for the design optimization of lead-bismuth reactor core. These parameters are calculated by STAC (Zhao et al., 2020), which was developed by one of the authors and includes the physical model of liquid lead/lead-bismuth, calculation model of wall heat transfer and pressure drop, and some models built for lead-bismuth reactor like single channel, closed parallel multichannel, and hottest channel model.
As the coupling interface of sampling, physical/thermal-hydraulic calculation, and optimization analysis, the pre and post processing module automatically matches the reactor core parameter values of sampling points to generate the input file, reads the physical/thermal characteristic parameters of output files after carrying out parallel calculations by calling RMC and STAC automatically, and finally generates the training set or accuracy verification conditions.
In the optimization analysis module, firstly, the KSM is constructed by analyzing the structural characteristics of known objective function values and quantifying their spatial correlation. Secondly, the objective function values of new valuation points are predicted based on the surrogate models after determining the neighborhood range and searching for neighborhood points. Finally, according to the principle of optimal point selection and SEUMRE algorithm, the sample points are updated to revise the surrogate model and the design space to approximate the target function iteratively until the optimal solution is obtained.
Kriging is a regression algorithm for spatial modeling and prediction of random fields based on the theory of correlation functions and structural analysis. In contrast to other interpolation algorithms, the KSM is an optimal unbiased estimation technique, which is composed of a global trend function
Here,
In other words, the mathematical expectation of random distribution bias is zero, and the variance
Where
To select the best combination of regression model and correlation function to construct KSM, the selection of regression model was first carried out. As shown in Figure 2A, the comparison of the fitting effects of KSM constructed by the combination of zero-order, first-order and second-order regression models with Gaussian correlation functions shows that the fitting effects of KSM constructed by the second-order regression model are more smooth and consistent. Then, the second-order regression model is combined with the exponential, Gaussian, linear and cubic spline correlation functions to construct the model for comparison of fitting effect. As shown in Figure 2B, it can be seen that the fitting effect of Gaussian and exponential function is the best. Since the fitting effects of Gaussian and exponential correlation functions are consistent, the mean square error (MSE) is used for experimental comparison. As shown in Figure 2C, the MSE of KSM constructed by Gaussian function is slightly smaller than that of exponential function, which is relatively better. Consequently, the second-order regression and Gaussian correlation function are used to construct the KSM in this study.
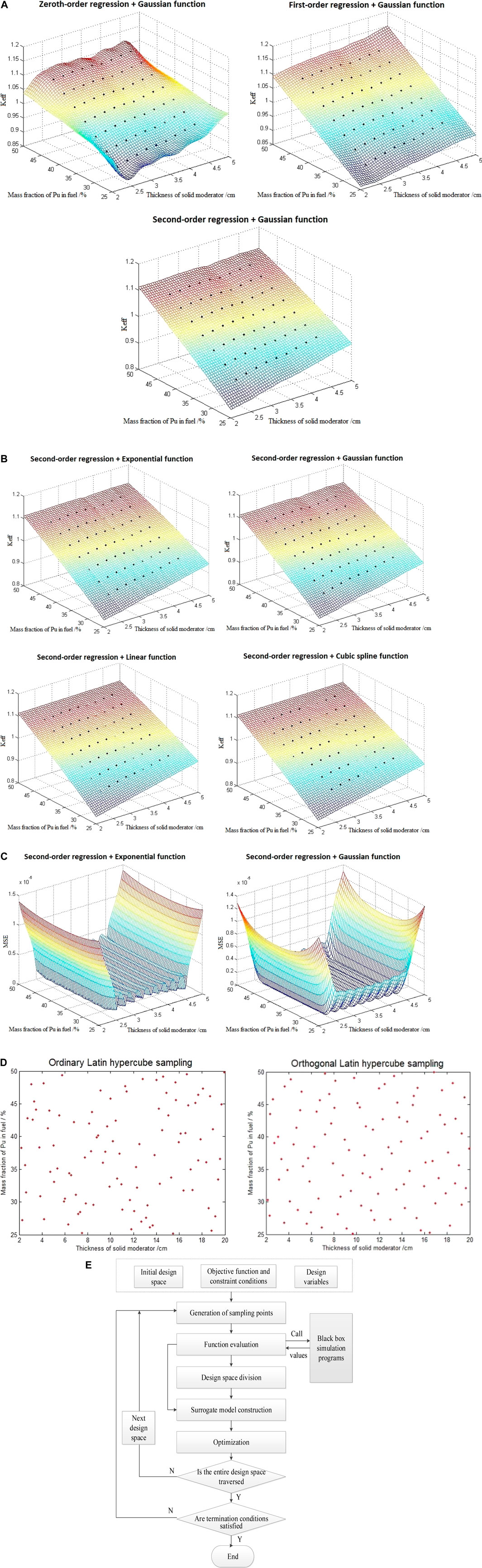
FIGURE 2. Construction records of KSM, OLHS, and SEUMRE. (A) Fitting effect of KSM constructed by different regression models with Gaussian function, (B) Fitting effect of KSM constructed by different correlation function with second-order regression model, (C) MSE of KSM constructed by exponential/Gaussian correlation function with second-order regression model, (D) Comparison between ordinary LHS and OLHS distribution, (E) Flow diagram of SEUMRE algorithm.
The selection of sampling points is vital for evaluating the target objects and constructing the surrogate model. Since the sampling points should be selected to represent almost the entire design space and their number should be as less as possible to avoid redundant calculation, it is particularly significant to pick a sampling method with both orthogonality and uniformity.
Based on the ordinary Latin hypercube sampling (LHS) (Pebesma and Heuvelink, 1999), OLHS evenly divides the sampling space into N grids to ensure that there is at least one sample point in each grid, which effectively avoids the uneven distribution of sampling results when sampling fewer points by LHS and facilitates spatially balanced sampling. A comparison between LHS and OLHS distribution is given in Figure 2D.
A large number of statistical sampling and calculations are required to ensure the accuracy of KSM when the object to be optimized has a strong degree of non-linearity and a wide range of design variables. Thus, to improve the efficiency of optimized search, the SEUMRE algorithm is introduced to rapidly find the global optimum solution by updating the optimal region repeatedly and iteratively.
The flow diagram of SEUMRE algorithm is shown in Figure 2E. First, the design space is divided into different spaces after generating the training data in the initial design space and assessing the objects/constraints, and the most promising space is determined. Next, the surrogate model is constructed to predict the points and select the local optimal point to obtain the next promising space. Finally, the above steps are repeated for iterative search until all the spaces are traversed and the global optimal solution is acquired (Younis and Dong, 2010).
The critical reactor core usually requires thousands of kilograms of fuel because of the small fuel fission cross section under fast-spectrum conditions. The fast-spectrum lead-bismuth reactor is generally heavy and expensive due to a large amount of fuel loading and high-density of lead-bismuth. Therefore, the minimum fuel loading of reactor core is considered as the optimization goal, and lead-bismuth reactors SPALLER-4 (independently developed by one of the authors) and URANUS (Lee, 2017; Kwak and Kim, 2018; designed by Seoul National University, South Korea) are taken as prototypes. The design parameters of the two reactors are listed in Table 2. Two optimization models are established after a certain simplification process. Different design variables and constraints are set for the two models to find the optimal reactor core scheme and optimal parameters through the intelligent optimization method (introduced in Section 2), and they are verified by the RMC code.
The original structure of SPALLER-4 is shown in Figure 3. Considering the limited reactivity adjustment capability of the control rod system and the corrosive effect of lead-bismuth on materials, the SPALLER-4 optimization model can be described as follows:
where
Considering that the increase in the initial reactivity and breeding ability and the decrease in the neutron leakage and parasitic absorption can effectively reduce the fuel loading, and the size of core and lattice affects the fuel loading by changing the neutron energy spectrum and neutron leakage (Michael and Pavel, 2005; Zhang et al., 2020). And basing on the prototype value of the core and the design parameters’ values of the classic liquid metal cooled reactor core such as ALFRED (Grasso et al., 2014), ELECTRA (Suvdantsetseg, 2012) and CEFR (Yang and Guo, 2020), the design variables and their ranges are set as shown in Table 3. 480 initial sample points are randomly sampled by OLHS in these ranges and calculated by physical and thermal calculation modules of DOPPLER-K.
To ensure the prediction accuracy of KSM, the accuracy of surrogate model is verified in each iterative optimization step. Five groups are randomly selected from the training set as the contrast group and are compared with the values calculated by RMC code, and the remaining groups are used as the training set to fit and construct the KSM.
Table 4 and Figure 4A show the accuracy verification results of KSM for predicting third year Keff and burnup at full power operating conditions in the optimal design space, which contains 155 groups in the final training set. It can be seen that the relative errors between the predicted Keff and burnup by KSM and the calculated values by RMC are within ±0.1% and ±1%, respectively. This indicates that when a certain amount of training data is ensured, KSM has a high accuracy for linear or nonlinear, directly or indirectly correlated target prediction, which is affected by multiple parameters at the same time. Compared with the RMC code, the calculation time is greatly reduced.
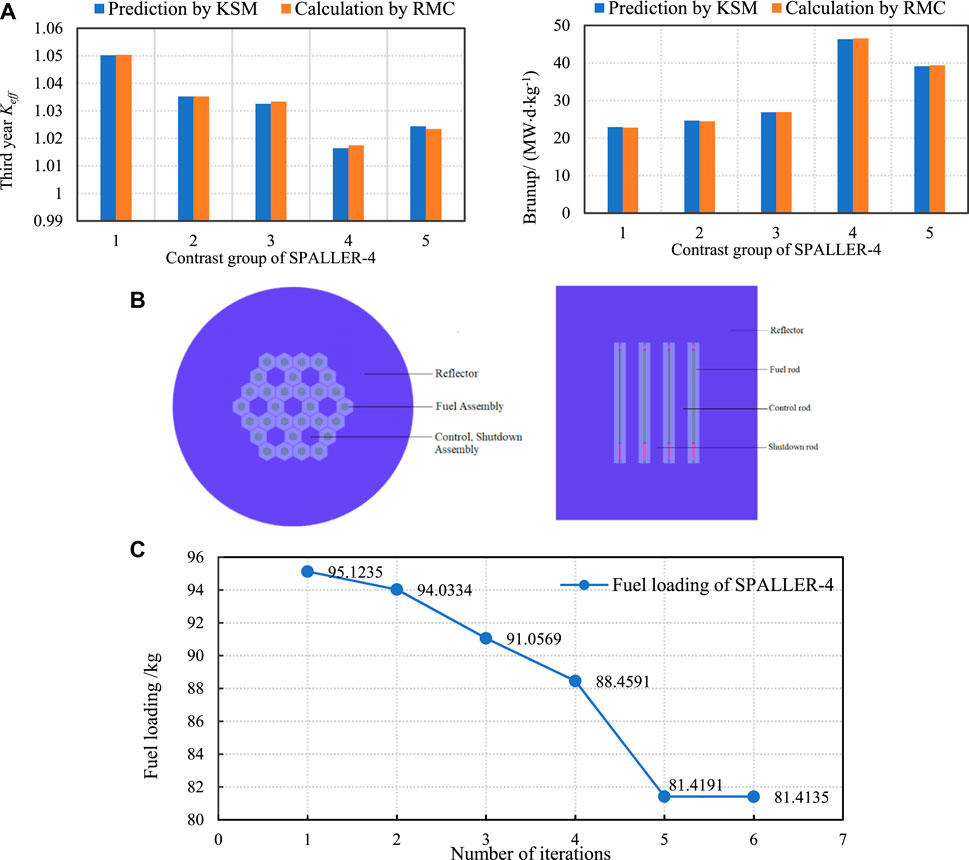
FIGURE 4. Optimization verification results of SPALLER-4. (A)Comparison of Keff and burnup obtained based on KSM and RMC, (B) Core structure of SPALLER-4 to be optimized, (C) Iterative graph of fuel loading optimization for SPALLER-4.
According to the original design parameters, the core structure of SPALLER-4 (shown in Figure 4B) to be optimized is constructed after some simplification. After calculating 480 groups of initial training sets by the RMC code, the intelligent optimization method is used for iterative optimization. 1,060,000 groups of schemes are predicted by KSM in each iteration, and a total of 175 iterations are carried out. After verification by RMC, six groups of solutions meet the optimization constraints, and the final two iterative schemes meet the convergence conditions (shown in Figure 4C). In the entire optimization process, 655 groups of training data are calculated.
Table 5 shows the final optimal design scheme, which is verified by RMC. This scheme meets all the constraint limits of initial Keff, refueling interval, steady-state thermal safety conditions, etc. The minimum fuel loading is 81.4135 kg, which is significantly lower than the original fuel loading. At the same time, the relative error between the predicted value by KSM and the calculated value by RMC is within the accuracy range, and the search speed of the target scheme is much higher than that of the traditional Monte Carlo calculation and the single heuristic optimization algorithm.
To verify the feasibility of the proposed intelligent optimization method in practical engineering, a core optimization model is established based on the lead-bismuth reactor URANUS (shown in Figure 5). In this section, a three-dimensional and six-constraint optimization problem is solved with Ubiquitous, Robust, Accident-forgiving, Nonproliferating and Ultra-lasting Sustainer (URANUS) model for demonstrating the validity of the proposed model in parameter optimization. The optimization model can be described as follows:
where
Similar to the optimization steps of SPALLER-4 model, the optimization variables of URANUS and their range are listed in Table 6. Further, 216 groups of initial sample points are randomly sampled by OLHS in these ranges and calculated by physical and thermal calculation modules of DOPPLER-K.
The accuracy verification results of KSM for predicting 20th year Keff and burnup at full power operating conditions in the optimal design area, which contains 45 groups of training sets, are shown in Table 7 and Figure 6A. It is clear that the relative errors between the predicted Keff and burnup by KSM and the calculated values by RMC are within ±0.1% and ±1%, respectively.
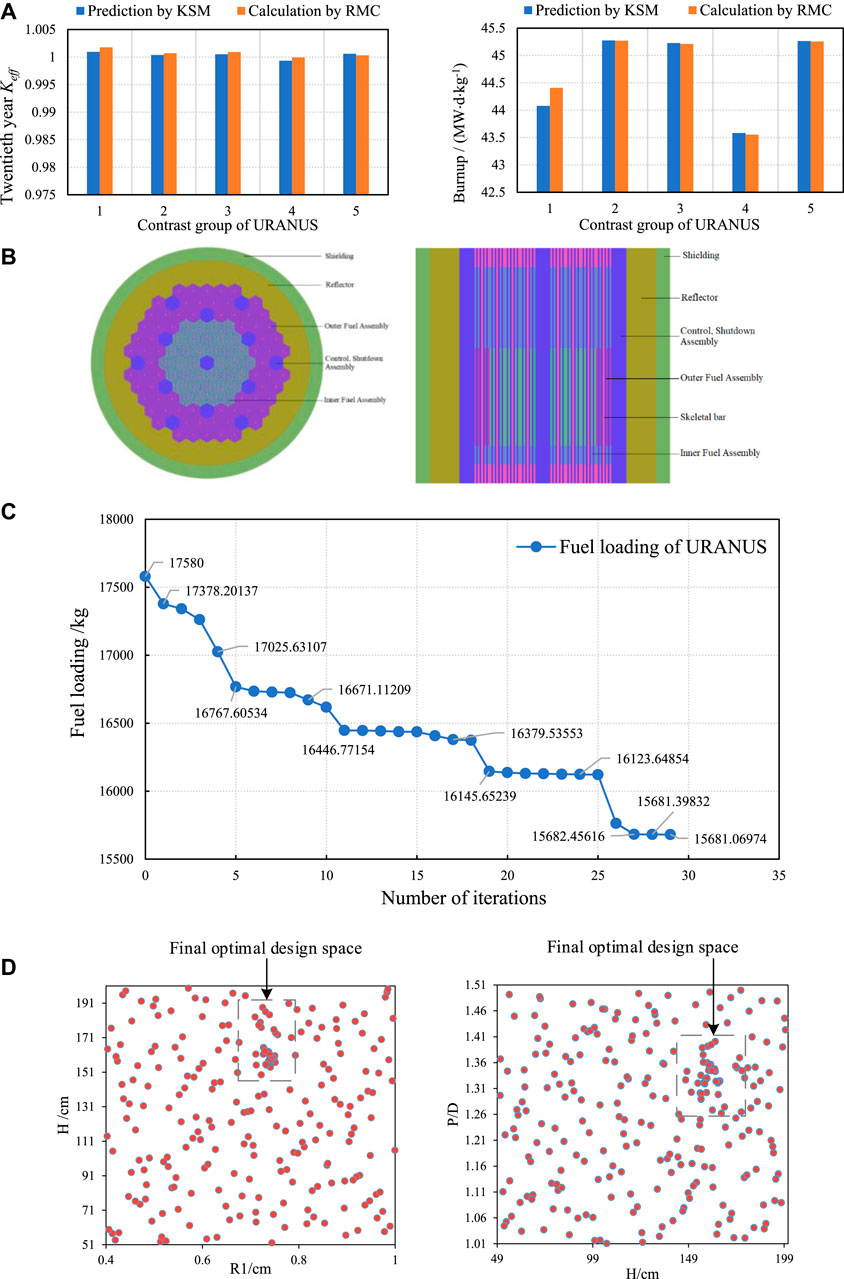
FIGURE 6. Optimization verification results of URANUS. (A) Comparison of Keff and burnup obtained using KSM and RMC code, (B) Core structure of URANUS for optimization verification, (C). Iterative graph of fuel loading optimization for URANUS, (D) Final optimal design space for URANUS.
According to the original design parameters, the core structure of URANUS (shown in Figure 6B) to be optimized is constructed after some simplification. After calculating 216 groups of initial training sets by the RMC code, the intelligent optimization method is used for iterative optimization. Further, 1060000 groups of schemes are predicted by KSM in each iteration, and a total of 37 iterations have been carried out. After verification calculation by RMC, 29 groups of solutions meet the optimization constraints, and the final two iterative schemes meet the convergence conditions (shown in Figure 6C). At this time, the final optimal range of design parameters is shown in Figure 6D and Table 8. Compared to initial design space, the range of optimal space is reduced. In the entire optimization process, 253 groups of training data are calculated.
Table 9 presents a comparison between the initial and optimized schemes. Compared with the initial model under the same constraint limits, the optimized core fuel loading, total mass, volume of active zone, and total volume are reduced by 1,899 kg, 20,149 kg, 0.944,047 m3, and 1.467,536 m3, respectively, and the reduction rates are 10.8, 11.5, 18.1, and 17.1%. This verifies the efficacy of the proposed intelligent optimization method for preliminary design and optimization of lead-bismuth reactor core.
In this study, an intelligent optimization method, which included KSM-OLHS-SEUMRE method and DOPPLER-K software, was developed for addressing the problems of multiple physical parameters, multiple variables, multiple constraints, a large amount of calculation, and low speed in the design optimization of lead-bismuth reactors. Lead-bismuth reactors: SPALLER-4 and URANUS, were used as verification examples to find the optimal scheme and optimal parameters. The entire calculation process could be automatically completed by the developed software. The main results of the study are summarized as follows:
1) KSM has a high prediction accuracy. According to the KSM prediction results for the two optimization examples, it can be concluded that when a certain amount of training data is given, the KSM has a high accuracy for the prediction of multi-constrained, linear or nonlinear, directly or indirectly related objective functions. Meanwhile, compared with the RMC code, which needed approximately 6.5 h to calculate a group of schemes, the KSM only needed more than 2 min to predict 1,060,000 groups of data under the same computer hardware conditions. Therefore, the KSM-based intelligent optimization method can greatly shorten the calculation time and improve the efficiency of preliminary design scheme search and optimization.
2) The proposed method is feasible, efficient, and effective for preliminary design and optimization of lead-bismuth reactor core. The optimal design scheme of SPALLER-4 was obtained using the five-variable and six-constraint model, which indicated that the intelligent optimization method is fast and efficient for the optimal scheme search under the influence of multi-factor coupling. The optimization of URANUS was conducted using a three-variable and six-constraint model, and the optimization rates of fuel loading, total core mass, active zone volume, and total core volume were found to be 10.8, 11.5, 18.1, and 17.1%, respectively, which suggested that the proposed method is effective for parameter optimization of the lead-bismuth reactor core.
3) Comparing the optimization results of SPALLER-4 model and URANUS model, it can be seen that the dimension of design variables will affect the training amount required to ensure the accuracy of Kriging surrogate model. The more design variables there are, the more training volume is required. While the number of objective/constraint functions does not affect the training number. In addition, to a certain extent, the search efficiency and optimization effect of the target scheme are also affected by the initial design variables, the initial optimal range and constraints. Therefore, the intelligent optimization method constructed in this study can better improve the optimization effect after reasonably and comprehensively selecting design variables and setting design scope.
Overall, to achieve different reactor design objectives, the proposed intelligent optimization method can rapidly identify the key design parameters and influence laws. Furthermore, through the rapid estimation of the reactor by this method, the optimal design space and preliminary design scheme of parameters matching the objectives can be obtained to provide reference for the detailed reactor scheme. Thus, the proposed method opens a new route for the design optimization of miniaturized and lightweight lead-bismuth reactors in remote areas or marine environment in the future.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
QL: Methodology, Software, Data curation, Verification, and Writing—original draft and revising. ZL: Conceptualization, Project administration, and Writing—reviewing and editing. YX: Verification. PZ: Writing—reviewing and Supervision. YZ: Writing—reviewing. TY: Resources. TY: Supervision.
This study is supported by the National Natural Science Foundation of China (Grant No. 12005097), Ministry of Equipment Development of Central Military Commission (Grant No. 6142A07190106), Natural Science Fund of Hunan Province (Grant No. 2020JJ5465), Department of Education of Hunan Province (Grant No. 9B494), and Science and Technology Innovation Team Project Fund of Hunan Province (Grant No. 2020RC4053).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors would like to thank the Reactor Engineering Calculation and Analysis Laboratory (REAL team) of Tsinghua University which has independently developed the reactor Monte Carlo (RMC) analysis code, all the technology and fund supporters in this study and MJEditor (www.mjeditor.com) for its linguistic assistance during the preparation of this manuscript.
Grasso, G., Petrovich, C., Mattioli, D., Artioli, C., Sciora, P., Gugiu, D., et al. (2014). The Core Design of ALFRED, a Demonstrator for the European lead-cooled Reactors. Nucl. Eng. Des. 278, 287–301. doi:10.1016/j.nucengdes.2014.07.032
Jin, R., Chen, W., and Simpson, T. (2000). Comparative Studies of Metamodeling Techniques under Multiple Modeling Criteria. Struct. Multidisciplinary Optimization 23 (1), 1–13. doi:10.2514/6.2000-4801
Kempf, S., Forget, B., and Hu, L.-W. (2012). Kriging-based Algorithm for Nuclear Reactor Neutronic Design Optimization. Nucl. Eng. Des. 247 (Jun), 248–253. doi:10.1016/j.nucengdes.2012.03.001
Khoshahval, F., Minuchehr, H., and Zolfaghari, A. (2011). Performance Evaluation of Pso and ga in Pwr Core Loading Pattern Optimization. Nucl. Eng. Des. 241 (3), 799–808. doi:10.1016/j.nucengdes.2010.12.023
Kim, K.-Y., and Lee, S.-M. (2009). Shape Optimization of Inlet Plenum in a PBMR-type Gas-Cooled Nuclear Reactor. J. Nucl. Sci. Technol. 46 (7), 649–652. doi:10.1080/18811248.2007.9711571
Kwak, J., and Kim, H. R. (2018). Development of Innovative Reactor-Integrated Coolant System Design Concept for a Small Modular lead Fast Reactor. Int. J. Energ. Res 42 (13), 4197–4205. doi:10.1002/er.4177
Lee, J. (2017). Conceptual Neutronic Design of Inverted Core for Lead-Bismuth Cooled Small Modular Reactor. Graduate School of Seoul National University. Available at: : https://s-space.snu.ac.kr/handle/10371/123541.
Meneses, A. A. d. M., Machado, M. D., and Schirru, R. (20092009). Particle Swarm Optimization Applied to the Nuclear Reload Problem of a Pressurized Water Reactor. Prog. Nucl. Energ. 51, 319–326. doi:10.1016/j.pnucene.2008.07.002
Michael, J. D., and Pavel, H. (2005). Reactor Physics Challenges in Gen-Iv Reactor Design. Nucl. Eng. Techn. 37 (1), 1–10. Available at: https://www.researchgate.net/publication/229009639.
Pebesma, E. J., and Heuvelink, G. B. M. (1999). Latin Hypercube Sampling of Gaussian Random Fields. Technometrics 41 (4), 303–312. doi:10.1080/00401706.1999.10485930
Song, L., Yang, H., and Zhiwei, Z. (2018). Fast Reactor Fuel Assembly Design Based on the Kriging Method. At. Energ. Sci. Techn. 052 (007), 1288–1293. doi:10.7538/yzk.2017.youxian.0650
Suvdantsetseg, E. (2012). Design Studies of ELECTRA: European Lead-Cooled Training Reactor. Other Phys. Top. 177 (3), 303–313. doi:10.3109/09553002.2012.638357
Wang, K., Li, Z., She, D., Liang, J. g., Xu, Q., Qiu, Y., et al. (2015). RMC - A Monte Carlo Code for Reactor Core Analysis. Ann. Nucl. Energ. 82 (10), 121–129. doi:10.1016/j.anucene.2014.08.048
Wu., Y. (2018). Research Progress and Application Prospects of lead-based Reactors. Mod. Phys. knowledge 30 (04), 37–41.
Yang, H., and Guo, M. (2020). Design Innovation and Realization of Experimental Fast Reactors in China. At. Energ. Sci. Techn. 54 (S01), 199–206. doi:10.7538/yzk.2020.zhuankan.0432
Younis, A., and Dong, Z. (2010). Metamodelling and Search Using Space Exploration and Unimodal Region Elimination for Design Optimization. Eng. Optimization 42 (6), 517–533. doi:10.1080/03052150903325540
Zameer, A., Mirza, S. M., and Mirza, N. M. (2014). Core Loading Pattern Optimization of a Typical Two-Loop 300MWe PWR Using Simulated Annealing (SA), Novel Crossover Genetic Algorithms (GA) and Hybrid GA(SA) Schemes. Ann. Nucl. Energ. 65 (mar), 122–131. doi:10.1016/j.anucene.2013.10.024
Zeng, K., Stauff, N. E., Hou, J., and Kim, T. K. (2020). Development of Multi-Objective Core Optimization Framework and Application to Sodium-Cooled Fast Test Reactors. Prog. Nucl. Energ. 120 (2020), 103184–184. doi:10.1016/j.pnucene.2019.103184
Zhang, Y. (2014). Global Sensitivity Analysis of Multi-Parameter Nonlinear System and Research on Dynamic Surrogate Model. Hunan University.
Zhang, Y., Wang, C., Lan, Z., Wei, S., Chen, R., Tian, W., et al. (2020). Review of Thermal-Hydraulic Issues and Studies of Lead-based Fast Reactors. Renew. Sust. Energ. Rev. 120 (C), 109625. doi:10.1016/j.rser.2019.109625
Keywords: lead-bismuth reactor, intelligent optimization, Kriging surrogate model, SEUMRE algorithm, orthogonal Latin hypercube sampling
Citation: Li Q, Liu Z, Xiao Y, Zhao P, Zhao Y, Yang T and Yu T (2022) An Intelligent Optimization Method for Preliminary Design of Lead-Bismuth Reactor Core Based on Kriging Surrogate Model. Front. Energy Res. 10:849229. doi: 10.3389/fenrg.2022.849229
Received: 05 January 2022; Accepted: 10 February 2022;
Published: 21 March 2022.
Edited by:
Jun Wang, University of Wisconsin-Madison, United StatesReviewed by:
Fenglei Niu, North China Electric Power University, ChinaCopyright © 2022 Li, Liu, Xiao, Zhao, Zhao, Yang and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zijing Liu, bGl1emlqaW5nMTEyM0AxNjMuY29t; Tao Yu, dGFveXUwNjI2QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.