Stochastic and Iterative Based Optimization for Enhancing Dynamic Performance of Interconnected Power System With Hybrid Energy Storage

With the growing dominance of inverter-based resources (IBRs), the synchronous inertia of the interconnected power systems (IPSs) is affected. The increase in IBRs results in a decrease in the system inertia. The decrease in inertia impacts the initial rate of decline of the frequency. Thus, there is a need for faster frequency response requirements to enhance the dynamic performance of the IPS. With the massive penetration of the plug-in hybrid electric vehicles (PHEVs) into expanding smart cities, PHEVs can act as controllable loads which support the inertial response of the system in a rapid manner. This gives a scope to monitor a large amount of EV operational data to ensure reliable operation considering extensive penetration of EVs. This study proposes a stochastic and iterative based optimization for a two-area interconnected power system (IPS) coupled with a hybrid energy storage system (HESS). The HESS uses 10,000 plug-in hybrid electric vehicles (PHEVs) in each area and a superconducting magnetic energy storage (SMES) device to aid load frequency control (LFC). The 10,000 PHEVs would contribute to massive operational data, which needs to be considered while studying the IPS dynamic performance. Here, we investigated two discrete tie lines: HVDC links parallel to the alternating current (AC) tie line and a virtual synchronous power-based (VSP)-HVDC link parallel to the AC tie line. The controller’s optimal parameters are recorded using two meta-heuristic algorithms, that is, particle swarm optimization (PSO) and biogeography-based optimization (BBO) along with simultaneous coordinated tuning of secondary controller and storage units. Results are taken both in the presence and absence of a HESS with two types of tie links. The analysis is performed with typical load changes and sensitivity analysis scenarios for an accurate record of variations in the outcomes. Thus, the proposed BBO-based LFC tracks the supply and demand variations, ensuring precision and accuracy, indicating improved IPS dynamic performance in smart cities.

Introduction

The decarbonization of the transport and the energy sectors is no longer a choice (1). With emerging technologies, the countries in the world are trying to reach ambitious goals owing to sustainable challenges and objectives. The increasing electric mobility market for the existing interconnected power systems represents a key factor for more sustainable transport and in the energy sector in terms of energy storage and generation profile. Besides that, with the integration of sensors, information and communication technologies, and Internet of things (IoT) devices, the traditional cities are transforming to smart cities (2). The smart electric network in a smart city gives a flexibility in the interconnected power system.

The present-day power system is complex and widely interconnected, with energy demand escalating continuously. The traditional power system needs enormous capital for electricity generation and harms the environment. With the focus on improving the earth’s climate, the conventional power system is being transformed into a decentralized, distributed generation. The distributed generation uses environment-sustainable sources such as solar, wind, geothermal, biomass, and small hydro to meet the growing demand. However, due to these sources’ intermittent nature, the electric grid faces operational challenges like reliability, power quality, grid stability, and, in particular, frequency control.

The interconnected power system’s successful operation requires matching the total generation to the total load demand and losses associated with the system. The instantaneous balance between the total generation and the total load reflects on the interconnected power system’s frequency. With time, the operating point of the power system changes. Large penetration of electric vehicles (EVs) into the smart city’s existing power pool raises electric grid (EG) reliability concerns, disrupting smart city transportation service. This gives a scope to monitor a large amount of EV operational data and provide inertial support for the EG to ensure reliable operation considering extensive penetration of EVs. Therefore, the system can notice the irregularities in the nominal frequency and power exchange schedules, producing undesirable effects. The two variables of interest are frequency and power exchanges between tie-links. Frequency stability is a rather important issue in a large interconnected power system. The load frequency control problem has been supplemented with significant research contributions from time to time, like controller designs incorporating parameter uncertainties, excitation control, load changes and characteristics, and AC/DC transmission links (Ibraheem and Kothari, 2005). Also, with the grid’s multi-unit nature, including various conventional and renewable units, the grid frequency deviates rigorously in terms of which conventional load frequency control cannot satisfy the requirements up to the mark. Any small disturbance in one area may lead to instability in the entire grid system. The variation in system parameters is indicated by area control error (ACE) in the interconnected system due to its dependence on frequency and tie-line power. Usually, the AC tie line serves the purpose, but it is economical to use the HVDC link parallel to the AC tie line for long-distance benefits. HVDC line also improves stability due to fewer losses and the absence of reactive power. HVDC lines are also useful in avoiding loop flows in the interconnected system. In the study by Elyas et al. (2014), conventional AGC is modified for the deregulated power market and the system with renewable sources, and the system performance is analyzed with both AC and DC tie lines. In the study by Pham et al. (2016), LFC of a four-area power system with thermal units is investigated with HVDC links, and functional observers are designed for feedback control. In the study by (Kachhwaha et al., 2016), LFC of a multi-unit power system is modeled with EV and fractional order PID (FOPID), and the simulation is carried out for the cases with and without EV in which the dynamic performance of the system is enhanced with EV. In the study by Anil et al. (2016), various controllers are designed for LFC of a multi-unit power system in which HVDC with the H-infinity controller stands better than the HVDC optimal sliding mode controller and HVDC-PI controller. In the study by Johnson and Shubhanga. (2016), a 14-bus AC IEEE system is modified with an HVDC link to eliminate loop flow in the interconnected power system. Sivadanam et al. (2020) discussed the inertial response of different types of power systems which impacts the frequency control of different types of systems.

Even though load frequency control has been dealt with for more than 3 decades, the introduction of renewable energy sources, energy storage, and electric vehicles poses new challenges in power systems’ operation. With massive penetration of renewable units with less or no inertia, the system’s inertia gets disturbed. Usually, voltage source converters (VSCs) are used to improve transient stability in HVDC transmission. A VSC-HVDC system contains energy stored in DC link capacitors utilized for emulating inertia, and this strategy is named inertia emulation control (INEC). This is well illustrated in the study by Zhu et al. (2013) with various load changes and faults. In the study by Elyas et al. (2014), a two-area system is considered, and a derivative-based virtual inertia controller is designed in which the dynamic performance like peak overshoots is improved compared to HVDC transmission lines. In the study by Elyas et al. (2014), the concept of virtual synchronous power (VSP)-based virtual inertia emulation is proposed for AGC of the multi-unit interconnected power system. The inertia emulation process needs some energy, which can be provided by any energy storage devices. In general, SMES is preferable due to its fast-responding nature with which it can supply rapid power in a short duration of time. In the study by Praghnesh and Sinha. (2018), SMES is incorporated with thyristor-controlled phase shifters for the interconnected system, and craziness-based PSO is implemented to optimize the parameters Bhatt et al., 2010. On the other hand, PHEV can act as a distributed storage system, an effective solution for LFC in interconnected systems. In the study by Musio and Damiano (2012), the effect of PHEV on the cost of a virtual power plant is well analyzed.

Swarm intelligence techniques can be used to optimize the controller parameters for better system performance. In the study by Rupali and Chaphekar, (2015), PSO is implemented on a two-area interconnected power system. BBO is the upcoming latest and effective technique in optimization. In the study by Pham et al. (2016), the travelling salesman problem is solved effectively using BBO. In the study by Rahman et al. (2015), three degrees of freedom PI controller is optimized using BBO. In the study by Hari Kumar and Ushakumari. (2014) conventional PID controller for a multi-unit system is replaced with a BBO optimized controller to enhance the system performance. In the study by Roy et al. (2014), BBO and oppositional BBO (OBBO) optimized controllers for the interconnected system are compared with PSO in which BBO improves system transients and settling time. Barisal and Mishra. (2018) presented automatic generation control of interconnected power systems with diverse generation sources. The work by Oshnoei et al. (2019) considered electric vehicles as a part of each area and proposed a TID controller for different load changes. Surya & Sinha. (2018) discussed the impact of ultracapacitor and thyristor control phase shifters on load frequency control using the ANFIS technique. Yang et al. (2017) proposed a two-level control using the multi-agent method for load frequency control. In the study by llias et al. (2016), the authors proposed optimization of PID controllers utilizing the evolutionary particle swarm optimization technique for a two-area interconnected power system. Abd-Elazim and Ali. (2016) proposed a BAT optimization technique for the design of optimum load frequency controllers for non-linear interconnected power systems. From the literature, the authors noticed the use of the following algorithms, namely, back tracking search algorithm (Madasu et al., 2017), Artificial Bee Colony (Kouba et al., 2015), Particle Swarm Optimization (Kouba et al., 2015), differential search algorithm (Guha et al., 2017), fractal search algorithm (Sivalingam et al., 2017), flower pollination algorithm (Madasu et al., 2018), harmony search algorithm (Shankar and Mukherjee, 2016), and JAYA algorithm (Annamraju and Nandiraju., 2019), for optimization of different types of controllers in the interconnected power systems. Sivadanam et al. (2020) proposed Particle Swarm Optimization and Biogeography Based Optimization algorithm (Sivadanam et al., 2021) for improving the dynamic performance of the interconnected power system.

Most of the works in the literature are implemented on the conventional power systems but with the rising growth of smart cities and introduction of IBRs, power electronic converters, energy storage systems, electric vehicles etc., the frequency control needs to be studied in different scenarios for interconnected power systems for successful operation and control of the modern electric grid. To the best of the author’s knowledge, this is the first study which utilizes smart city transportation service as a variable for the frequency control of the IPS. This study uses the PHEVs as a part of the hybrid energy storage system (HESS) and utilizes aggregated PHEV demand to enable the frequency control. The main contributions and key features of the article are as follows:

i. The study includes the aggregated PHEV demand as a signal controlled by the transmission system operator as a part of smart city service.

ii. The controller parameters are tuned using optimization techniques for a large interconnected system. The robustness of the controller is analyzed with different parameters.

iii. The frequency deviations and tie-line deviations are observed for HVDC and VSP-HVDC tie-links in large, interconnected power systems.

In this study, a two-area interconnected power system with two reheat thermal units with a PID controller for secondary control is considered, and PHEV and SMES units are incorporated in each area. An HVDC link and a VSP-HVDC link are added parallel to the AC tie line in two different case studies. The system is simulated at various load changes. Simultaneous coordinated tuning of the secondary controller and storage unit parameters with PSO and BBO is carried out at different load changes, and sensitivity analysis is carried out with and without the PID controller. The steady-state and transient state analysis is carried out, and variation in frequency and tie-line power is plotted for every typical case study. Simulation is carried out in a MATLAB/SIMULINK environment.

The remaining section of the article is organized into five sections. In Modeling of the Proposed System, the mathematical modeling of the system will be introduced. Biogeography Based Optimization Algorithm deals with the optimization approach used to tune the controller parameters. The results and discussion are presented in Results and Discussion. Sensitivity Analysis With HVDC and VSP- HVDC Links deals with sensitivity analysis to verify the robustness of the proposed controller. Finally, Conclusion provides conclusions drawn based on case studies.

Modeling of the Proposed System

The proposed system model consists of a two-area interconnected power system with thermal units incorporated with a hybrid energy storage system in each unit, which is modeled in two different scenarios, that is, with an HVDC link and a VSP-HVDC link.

Two-Area Interconnected System With Thermal Units

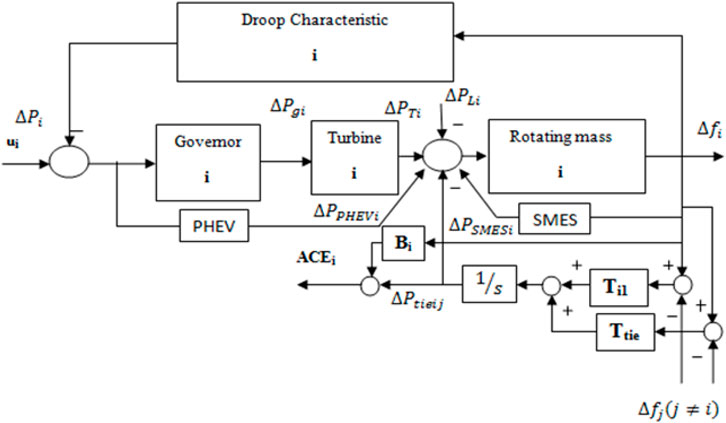
The primary regulation of AGC is required to curb the oscillations under load changes. The secondary regulation is needed to bring back the distorted value to the nominal range value, that is, to make the steady-state error zero. The PID controller is used as a secondary controller in this study, which increases the type of the system to make the steady-state error zero. A generalized multi-area interconnected system is modeled in Figure 1, as shown below. In Figure 1, B_i = bias coefficient of area-i; ∆f_i, ∆f_j = change in area-i and area-j frequency, respectively; ∆P_gi = governor output in area-i; ∆P_Ti = turbine output in area-i; ∆P_SMESi = output of SMES unit in area-i; ∆P_tieij = tie-line power; ∆P_PHEVi = output of PHEV in area-i; ∆P_i, = input power of area-i.

FIGURE 1

FIGURE 1. LFC of the interconnected power system with PHEV and SMES incorporation.

Hybrid Energy Storage System

The hybrid energy storage system constitutes plug-in hybrid electric vehicles which are used in the transportation sector and a superconducting magnetic energy storage, an electrical storage device.

Plug-In Hybrid Electric Vehicles

The carbonization of the transport sector in a city is one of the main reasons for pollution. With the use of plug-in hybrid electric vehicles (PHEVs) in the transport sector, a revolution in the world transport sector has begun to mitigate the rising global climatic changes. The technological advancements of battery systems and power electronic devices make the PHEVs a more viable option for all the common people in coming years. The adoption of PHEVs in large numbers into the interconnected power system can be used to help the electric grid in emergency situations. It will be economical if the PHEV data in an area are gathered together and then aggregated as the total PHEV demand and made available as a correction signal for the operator to meet the grid requirements, particularly active power injections. The battery state-of-charge (SOC) determines the participation factor of each PHEV.

Superconducting Magnetic Energy Storage

The superconducting magnetic energy storage (SMES) is an electrical energy storage device which has fast response time, high power capability in short time, flexible control of real power, high storage efficiency, and high-power density. The SMES uses the direct current passing through a superconducting coil which is cooled by bringing the temperature below a critical value. This produces a magnetic field, and the energy can be stored in it. To obtain the superior, several subsystems need to be designed carefully. A SMES unit consists of a sizeable superconducting coil with a cryogenic cooling system. The equivalent circuit of the SMES uses a lumped parameter model represented through a six-segment design comprising self-inductances (L_i), mutual couplings among sections (i and j, M_ij), AC loss resistances (R_si), skin effect related resistances (R_pi), turn-ground (shunt-C_Shi), and turn-turn capacitances (series-C_Si). This model is suitable for a frequency range from DC to a few thousand Hertz. The addition of spike capacitors (C_Sg1 and C_Sg2) along with a filter capacitor C_F in parallel with grounding balance resistors (R_g1 and R_g2) allows for diminishing the effect of resonances. A metal-oxide-semiconductor (MOV) protection for passing voltage surge suppression is included between your SMES product and the DC/DC converter (Molina and Mercado, 2011). The equivalent circuit of the SMES coil is shown in Supplementary Figure S1.

HVDC Link in Parallel With AC Tie Line

The high voltage alternating current (HVAC) which is used for transferring bulk power to long distances suffers from stability issues, reactive power control problems, etc. With the development of high voltage direct current (HVDC), there are advantages like no reactive power consumption, low losses, and possible asynchronous connections like solar, wind, etc. The growth of the alternate fuel sources led to increasing HVDC interconnections into the interconnected power system. By this interconnection of the AC tie-line parallel with the HVDC link, the frequency deviation is very low, leading to improved quality and continuity of power supply to the customers.

The variation in tie-line power now depends on both AC and DC power change, which is modeled in the following equation.

$\mathrm{\Delta }{P}_{tie}=\mathrm{\Delta }{P}_{AC}+\mathrm{\Delta }{P}_{DC}(1)$

The area control error (ACE) is responsible for considering the local impact on other areas in the interconnected areas. The area control error (ACE) is a function of total tie-link power and the power obtained from the hybrid energy storage system. The total tie-link power includes both the AC and DC tie-link power. The beta (β) is the frequency bias coefficient of each area. The ACE helps in achieving the load frequency control (LFC). The modified area control errors of both the areas with the inclusion of HVDC links are as follows:

$AC{E}_1=\mathrm{\Delta }{P}_{tie,11}+\mathrm{\Delta }{P}_{tie,12}+B_1\mathrm{\Delta }{f}_1+\mathrm{\Delta }{P}_{SMES1}+\mathrm{\Delta }{P}_{PHEV1}+\mathrm{\Delta }{P}_{DC1}(2)$

$AC{E}_2=a_{12}\left(\mathrm{\Delta }{P}_{tie,22}+\mathrm{\Delta }{P}_{tie,12}\right)+B_2\mathrm{\Delta }{f}_2+\mathrm{\Delta }{P}_{SMES2}+\mathrm{\Delta }{P}_{PHEV2}+\mathrm{\Delta }{P}_{DC2}(3)$

The schematic diagram of the interconnected system with HVDC is as shown in Supplementary Figure S2A.

VSP-HVDC Line in Parallel With AC Tie Line

Usually, conventional generators with the droop capability are responsible for providing sufficient inertia against frequency deviations in the system. However, the penetration of renewables in the modern power system imposes very low or no inertia, disturbing the system inertia. Inertia plays a significant role in damping oscillations due to sudden changes. Hence, there is a need to emulate the inertia into the system so that the system’s transient stability can be improved. The inertia emulation control (INEC) strategy is proposed recently, which supports the AC network during and following disturbances, with minimal impact on the systems connected beyond the HVDC system’s terminals (Rakhshani et al., 2017).

Configuration of the System With VSP-HVDC Line

The configuration of the two-area system with the VSP-HVDC line in parallel with the AC tie line is shown in Supplementary Figure S2B.

Derivative Control-Based Virtual Inertia Emulation

With the change in active power, the grid frequency varies. The derivative of frequency is used to adjust active power, emulating the inertia into the system by the following control law (Elyas et al., 2014) in power electronic converters.

$P_{EM}=g{\omega }_0\frac{d\left(\mathrm{\Delta }{\omega }_0\right)}{dt} (4)$

where g is the gain of conversion and ω₀ is the scheduled grid frequency. This conversion process generally requires energy which can be gained by other areas or any available storage units. In this study, SMES is installed to serve the purpose. The block diagram of the control scheme for inertia emulation is in Supplementary Figure S3. Under various disturbances, the frequency may alter due to the change in active power. The derivative of frequency is used in the control law of the power electronic converter to regulate the active power such that system stability is retained (Rakhshani et al., 2016). A low pass filter is used due to the sensitivity of the system to the noise. The emulated power in both areas is given by the following:

$\mathrm{\Delta }{P}_{ESS1}\left(s\right)=\frac{J_1}{s{T}_{ESS}+1}\left(s\mathrm{\Delta }{f}_1\left(s\right)\right)(5)$

$\mathrm{\Delta }{P}_{ESS2}\left(s\right)=\frac{J_1}{s{T}_{ESS}+1}\left(s\mathrm{\Delta }{f}_2\left(s\right)\right)(6)$

The frequency deviation of the two-area interconnected system, including SMES and PHEV with VSP-HVDC line in parallel to the AC tie link, is given as follows:

$\mathrm{\Delta }{f}_1=\frac{1}{2H_{1}s+D_1}\left(\mathrm{\Delta }{P}_1+\mathrm{\Delta }{P}_{PHEV1}-\mathrm{\Delta }{P}_{SMES1}-\mathrm{\Delta }{P}_{dc1}-\mathrm{\Delta }{P}_{tie12}+\mathrm{\Delta }{P}_{ESS1}-\mathrm{\Delta }{P}_{L1}\right)(7)$

$\mathrm{\Delta }{f}_2=\frac{1}{2H_{2}s+D_2}\left(\mathrm{\Delta }{P}_2+\mathrm{\Delta }{P}_{PHEV2}-\mathrm{\Delta }{P}_{SMES2}-\mathrm{\Delta }{P}_{dc2}+\mathrm{\Delta }{P}_{tie12}+\mathrm{\Delta }{P}_{ESS2}-\mathrm{\Delta }{P}_{L2}\right)(8)$

Biogeography Based Optimization Algorithm

Simon has introduced the BBO algorithm motivated by the migration of biological species between islands. It is constructed based on biogeography, which is the study of biological groups over time and space. It belongs to the class of metaheuristic algorithms. The effectiveness of the algorithm lies in its iterative and stochastic nature to optimize the given fitness function subjected to constraints even in a complex environment. The evolution of new species, migration of existing species, and extinction of species form the development of the algorithm. The islands which support the life are known to have high suitability indices (HSIs), and the islands which do not have favorable conditions for the growth of species are known to have low sustainability indices (LSIs). The HSI and LSI depend on the suitability index values (SIVs). The SIVs are characterized by the geography, rainfall, temperature, vegetation, etc. Based on the immigration and emigration rates, the algorithm achieves optimum solution based on SIV and HSI. The migration and mutation are the most important steps in the determination of the optimum solution.

The process of migration is based on immigration and emigration that occur among geographical regions. The parameters that control the migration process are immigration rate (λ) and emigration rate (µ).

$\mathrm{\lambda }=\left(1-\mathrm{N}/{\mathrm{N}}_{\max }\right)I(9)$

$\mathrm{\mu }=\mathrm{E}\mathrm{N}/{\mathrm{N}}_{\max }(10)$

where N, E, Nmax, and I represent the number of species, maximum emigration rate, maximum species number, and maximum immigration rate.

Results and Discussion

The suggested algorithm’s efficacy and effectiveness can be verified by considering a two-area interconnected power system that consists of two thermal units with a hybrid energy storage system (PHEV and SMES) in each area. The test system’s transfer function model is developed in MATLAB/SIMULINK, and the algorithm is created in m-file. The system’s dynamic performance can be realized with two step load patterns: 0.01 pu and 0.05 pu under different scenarios. In scenario-1, the HVDC link is parallel with the AC tie link, and in scenario-2, the VSP-HVDC link is in parallel with the AC tie link. The PID controller’s optimal parameters are achieved by applying a technique known as Simultaneous Coordinated Control (SCC) using PSO and BBO. The objective function minimizes frequency deviation in both the areas along with stable tie-line power exchange.

Scenario-1: With HVDC Link

In this scenario, the two-area interconnected power system has an HVDC link parallel to the AC tie link. The performance of the system is analyzed at load changes of 0.01 and 0.05 pu, respectively. The plots of frequency variation and tie-line power variation are shown in the following content for typical case studies with the presence and absence of the hybrid energy storage system. Figures 2A,D represent variations of frequency in area-1 for 0.01 and 0.05 pu change in load. The results show that the BBO algorithm has a minimum first peak with minimum steady-state oscillations and takes less time to reach a steady-state than PSO. The magnitude of frequency deviation is more in the 0.05-pu step load pattern. Figures 2B,E represent the tie-line power variation, which explains that the net power schedules between area 1 and area 2 are more stable with BBO.

FIGURE 2

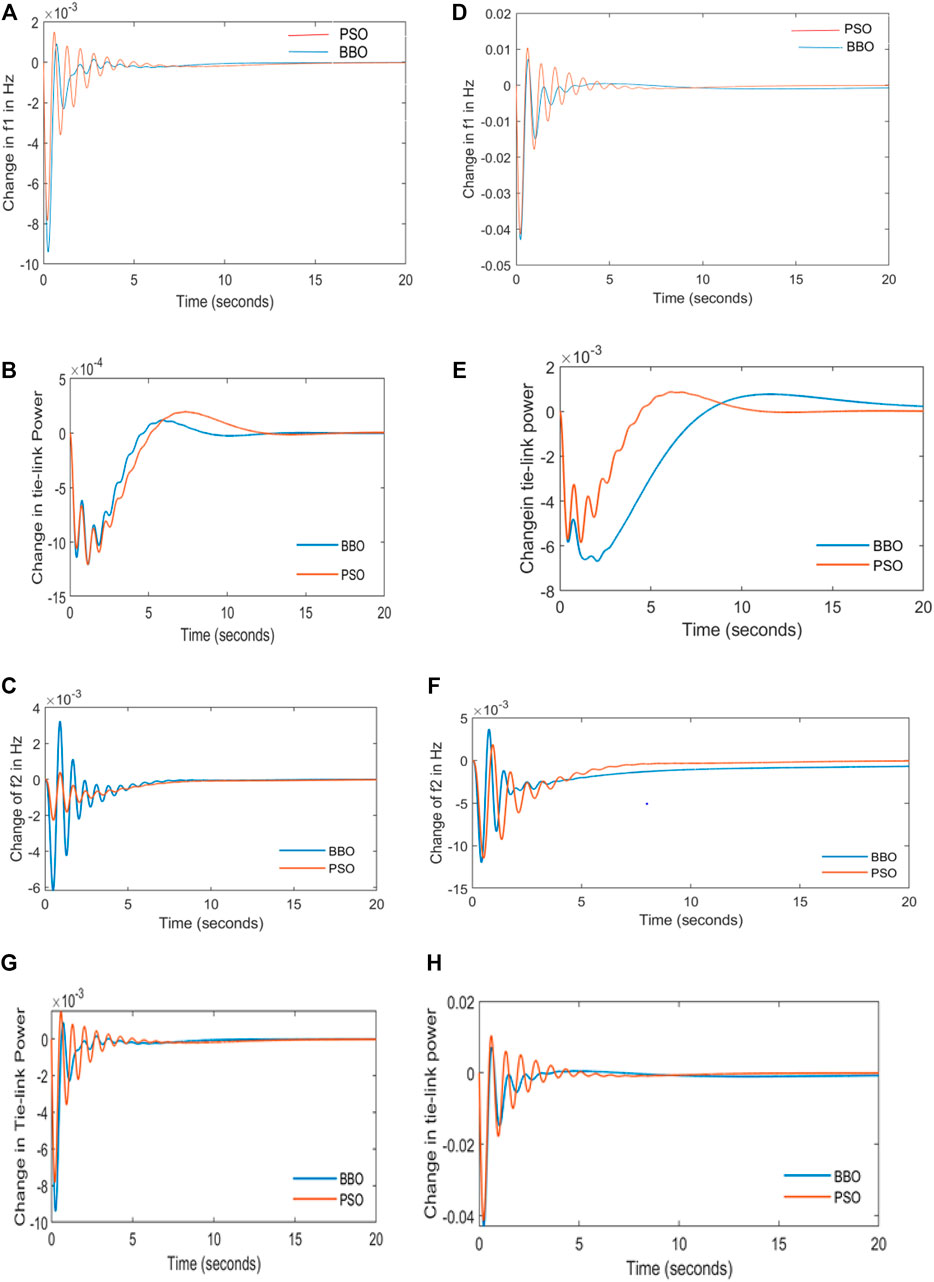
FIGURE 2. Dynamics of Area-1 and Area-2 with and without HESS for 1% and 5% change in load with HVDC link. (A) Dynamics of f1 at 1% Load Change with HESS. (B) Dynamics of Ptie at 1% Load Change with HESS. (C) Dynamics of f2 at 1% Load Change with HESS. (D) Dynamics of f1 at 5% Load Change with HESS. (E) Dynamics of Ptie at 5% Load Change with HESS. (F) Dynamics of f2 at 5% Load Change with HESS (G) Dynamics of Ptie at 1% Load Change without HESS. (H) Dynamics of Ptie at 5% Load Change without HESS.

Figures 2C,F represent variations of frequency in area-2 for 0.01 and 0.05 pu change in load. The results show that the BBO algorithm has a minimum first peak with minimum steady-state oscillations and takes less time to reach a steady-state than PSO. The magnitude of frequency deviation is more in the 0.05-pu step load pattern. Figures 2G,H represent the tie-line power variation in the absence of HESS at 0.01 and 0.05 pu load disturbances. The oscillations in tie-line power in the absence of HESS are more than those of the system in HESS’s presence.

Scenario-2: With VSP-HVDC Link

The two-area system is modeled with the VSP-HVDC link parallel to the AC tie line, enhancing the system inertia, thereby improving the system stability. Figures 3A,B represent the deviation of frequency in area-1 at 0.01 and 0.05 pu step load patterns. The results show that the BBO algorithm has a minimum first peak with minimum steady-state oscillations and takes less time to reach a steady-state than PSO.

FIGURE 3

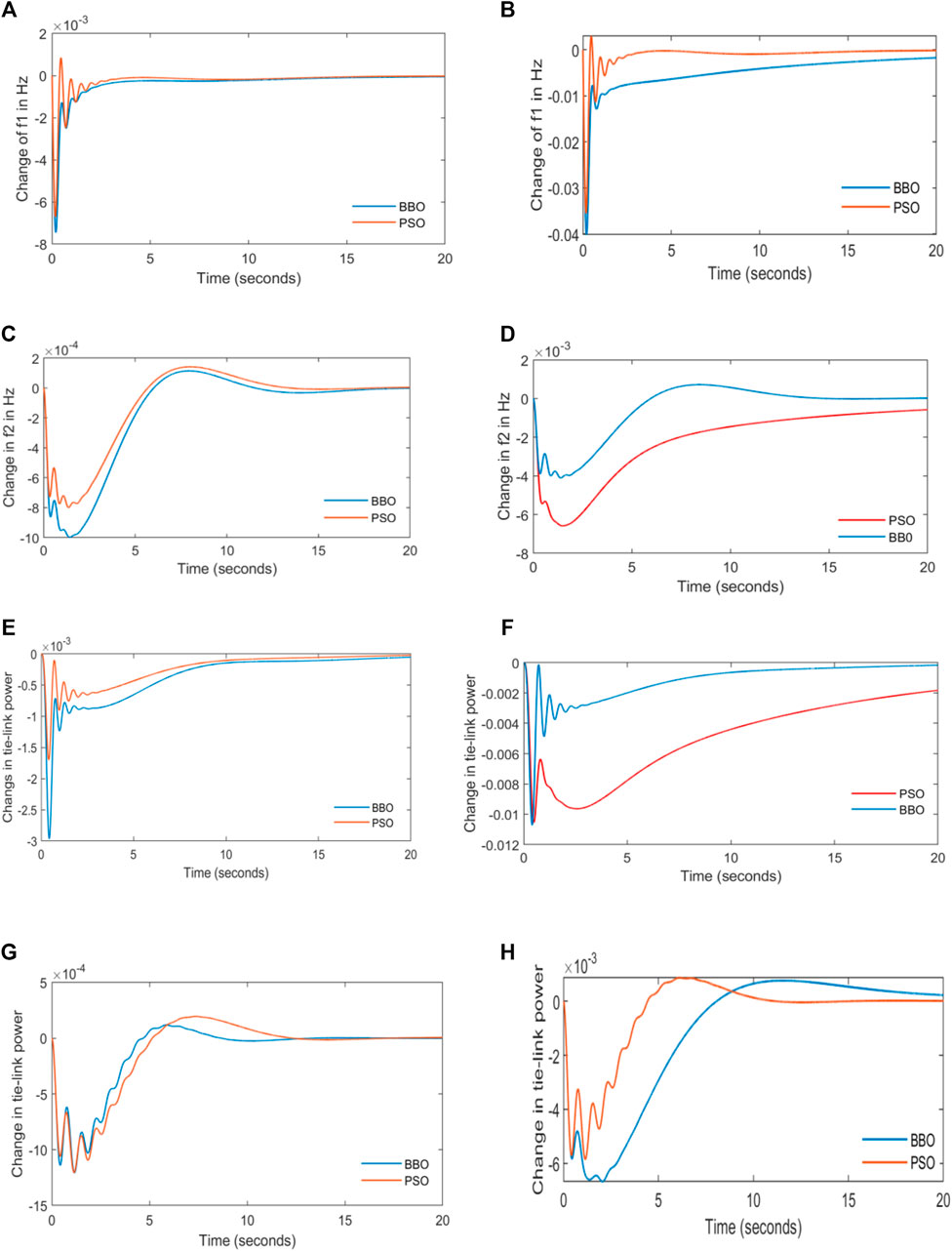
FIGURE 3. Dynamics of Area-1 and Area-2 with and without HESS for 1% and 5% change in load with VSP-HVDC link. (A) Dynamics of f₁ at 1% Load Change with HESS. (B) Dynamics of P_tie at 1% Load Change with HESS. (C) Dynamics of f₂ at 1% Load Change with HESS. (D) Dynamics of f₁ at 5% Load Change with HESS. (E) Dynamics of P_tie at 5% Load Change with HESS. (F) Dynamics of f₂ at 5% Load Change with HESS. (G) Dynamics of P_tie at 1% Load Change without HESS. (H) Dynamics of P_tie at 5% Load Change without HESS.

Figures 3C,D represent variations of frequency in area-2 for 0.01 and 0.05 pu change in load. The results show that the BBO algorithm has a minimum first peak with minimum steady-state oscillations and takes less time to reach a steady-state than PSO. The magnitude of frequency deviation is more in the 0.05-pu step load pattern. Figures 3E,F represent the tie-line power variation at 0.01 and 0.05 pu load change, respectively, which explains that the net power schedules between area 1 and area 2 are more stable with BBO. Figures 3G,H represent the tie-line power variation of the system in the absence of the HESS unit in which oscillations are more than those of the system with HESS.

Sensitivity Analysis With HVDC and VSP- HVDC Links

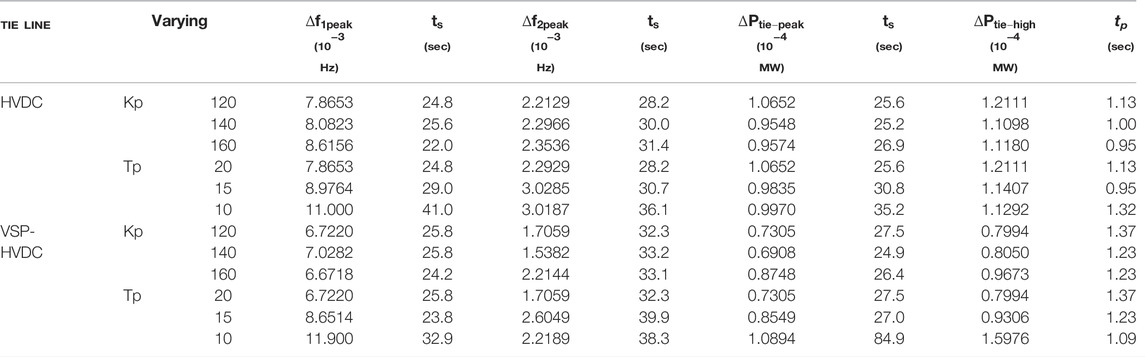
Sensitivity analysis is performed for the two-area interconnected system with the HVDC link in parallel with the AC tie line, including PHEV and SMES units to demonstrate the robustness of the proposed algorithm by varying the system parameters such as gain (K_P) and time constant (T_P) of the transfer function block of the power system at 0.01 pu load change condition. The value of K_P is set to 120, 140, and 160 and T_P as 10, 15, and 20 in each case, and the system is tuned with the BBO algorithm for the optimal values of the PID controller in the presence and absence of the HESS unit. The variation in frequency and tie-line power for different K_P values are plotted in Figures 4A–C.

FIGURE 4

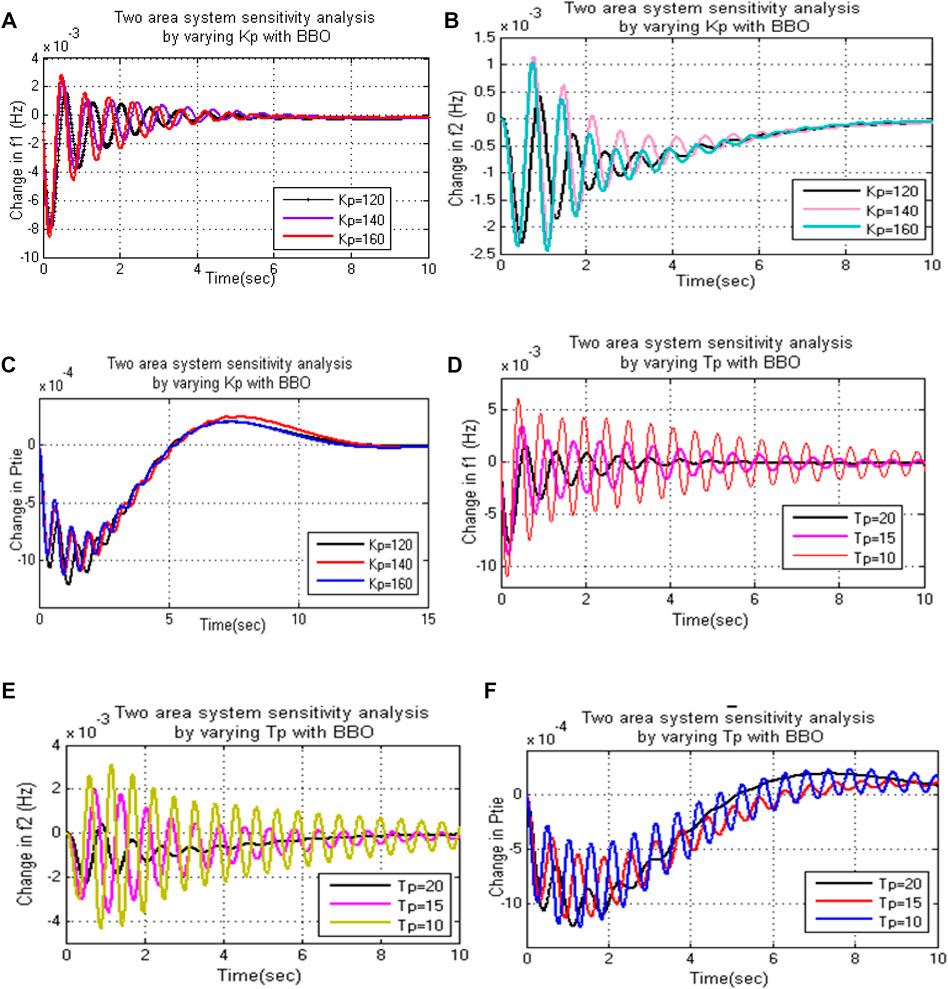
FIGURE 4. Sensitivity analysis in the presence of HVDC link. (A) Effect of variation of Kp on f₁. (B) Effect of variation of Kp on f₂. (C) Effect of variation of Kp on P_tie. (D) Effect of variation of Tp on f₁. (E) Effect of variation of Tp on f₂. (F) Effect of variation of Tp on P_tie.

Figures 4D–F represent the variation of frequency in area-1, area-2, and tie-line power with various values of T_P. From the above plots, it is clear that with the increase in K_P and the decrease in T_P, the oscillations increased enormously, and the settling time also increased, which is undesirable.

Figures 5A–C represent the plots with the variation of K_P. Figures 5D–F represent the plots with the variation of T_P. It is observed that the settling time is much improved, and oscillations decreased with virtual inertia emulation when compared to the standard HVDC line. It is also observed that the change in T_P affects the system parameters compared to the change in K_P.

FIGURE 5

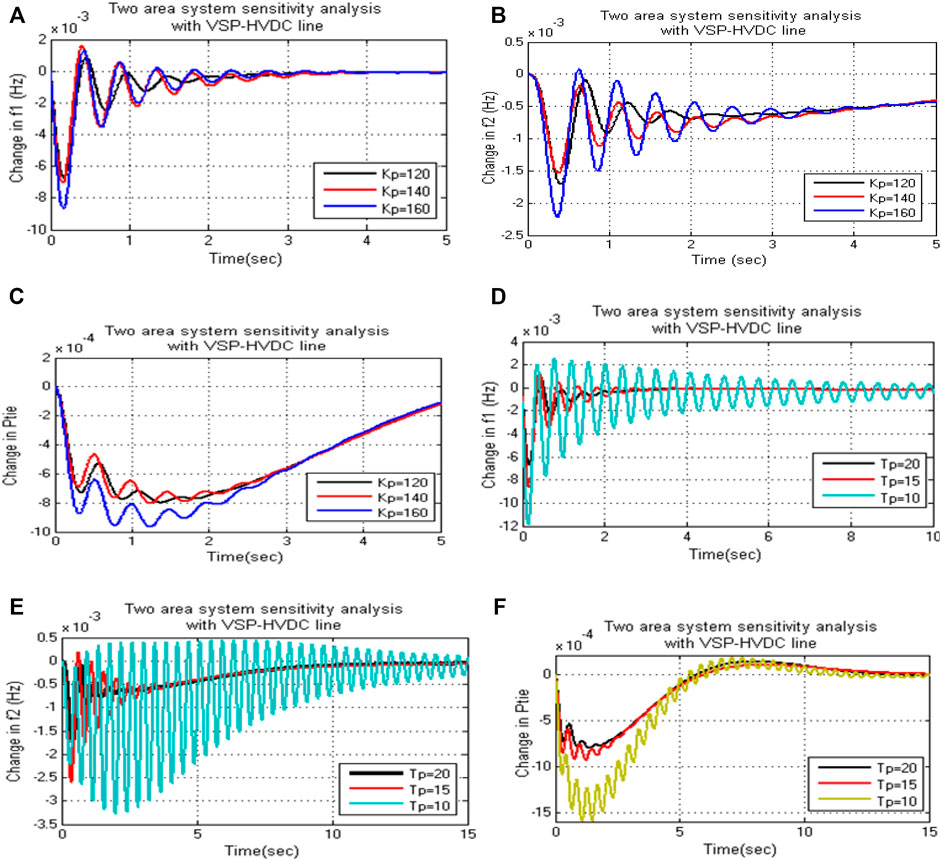
FIGURE 5. Sensitivity analysis in the presence of VSP-HVDC link. (A) Effect of variation of Kp on f₁. (B) Effect of variation of Kp on f₂. (C) Effect of variation of Kp on P_tie. (D) Effect of variation of Tp on f₁. (E) Effect of variation of Tp on f₂. (F) Effect of variation of Tp on P_tie.

The performance of the system is determined by the first peak overshoot value of area-1 and area-2 frequencies (∆f_1peak,∆f_2peak), first peak overshoot of change in tie-line power (∆P_(tie-peak)), settling time (t_s), the highest possible peak value in tie-line power variation (∆P_(tie-high)) and its corresponding time (t_p), steady-state error (e_ss), and oscillations, which are enlisted in the following tables.

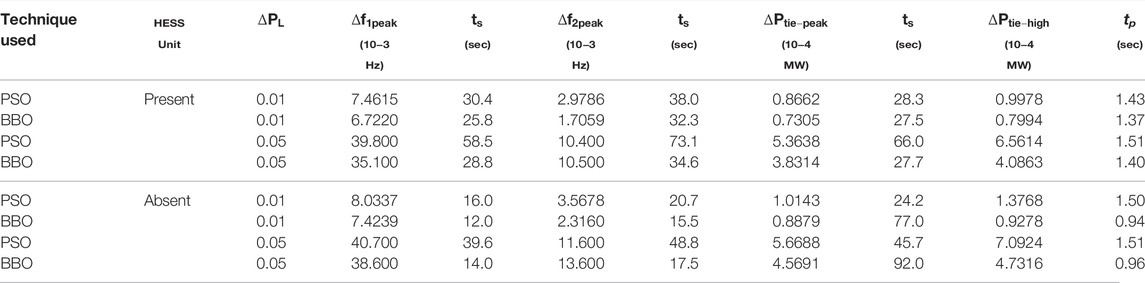
Tables 1, 2 represent the variation of system parameters under 0.01 and 0.05 pu load changes when the system is optimized with PSO and BBO for HVDC and VSP-HVDC interconnected lines. From Table 1, the change in peak frequency of area-1 of the system with PSO is 7.46*10–3 Hz and improved with BBO optimization up to 6.7*10–3 Hz for 1% load change. The settling time of the area-1 proposed model when optimized with BBO is 19.70 s for 5% load change, whereas it is 68 s with PSO optimization. It can be noted that the system optimized with BBO gives better results with low peak overshoot and less settling time, indicating the fast recovery of the system to its stable operating point. The maximum peak overshoot in the tie-line power is reduced with BBO optimization.

TABLE 1

TABLE 1. Performance analysis of the two-area interconnected system with HVDC link.

TABLE 2

TABLE 2. Performance analysis of the two-area interconnected system with VSP-HVDC line.

VSP-HVDC line inclusion in the system improves the transient stability compared to the HVDC line, evident from the decrease in peak overshoot and settling time. The role of SMES is pivotal in damping oscillations, which is evident from the above analysis. The steady-state error is zero due to the presence of a PID controller in both areas. From Table 2, it is observed that the peak value of change in frequency of area-2 of the proposed interconnected system incorporated with HESS is 2.97*10–3 Hz with PSO, and it is decreased to 1.70*10–3 Hz with BBO optimization for 1% load change case. Also ∆P_(tie-peak) for 5% load change is 5.36*10–4 MW with the HESS unit, and it is increased to 5.66*10–4 MW when the HESS unit is disconnected, which demonstrates the role of the storage element in the system.

Table 3 represents the sensitivity analysis of the two-area interconnected system, including SMES and PHEV for both HVDC and VSP-HVDC line cases and their respective performance at a 1% load change condition with K_p’s variation and T_p optimized with BBO technique.

TABLE 3

TABLE 3. Sensitivity analysis of the presented two-area system.

With an increase in K_P and decrease in T_P, the peak overshoot of frequency and tie-line power increased, indicating the decrease in transient stability. For the case of T_p = 15, the peak change in tie-line power is recorded as 0.98*10–4 MW for the HVDC tie line, whereas it is decreased to 0.85*10–4 MW with the VSP-HVDC line, which demonstrates the effect of virtual inertia emulation into the system.

Conclusion

The penetration of a large number of renewable units with low inertia in the present-day power systems is the severe cause for disturbing the system inertia. This criterion may lead to system frequency and tie-line power to move out of limits leading to transient instability, which is undesirable. This explains the need for virtual inertia emulation to build a secure and stable power system. This study presents a novel model of AGC of an interconnected system incorporated with the SMES and PHEV units in each area. PHEV aids in the LFC problem and SMES serve to supply energy for the virtual inertia emulation process and damp oscillations. On the other hand, PHEVs are pollution-free, which is very desirable in the present-day situation.

The performance of the two-area interconnected system is investigated with two discrete transmission lines since the transmission line plays a pivotal role in power exchange between different areas in an interconnected model. HVDC line in parallel with the AC line and VSP-HVDC line in parallel with the AC line are placed separately, and the system is optimized in each case with PSO and BBO techniques by simultaneous coordinated tuning of the secondary controller and SMES unit. Sensitivity analysis is also performed for each scenario. Results indicate that with virtual inertia emulation, the system’s transient stability is improved when the system, including PHEV and SMES, is optimized with BBO. The high penetration levels of electric vehicles can lead to stability issues in the interconnected power systems. The EV charging demand needs to be carefully monitored for optimal operation of interconnected power systems. The authors would like to extend the work by increasing different penetration levels of the plug-in hybrid electric vehicles and evaluate the various combinations of hybrid energy storage systems by integrating communication delays, analyzing the filter requirements, and demanding response services offered by the load. The authors would like to add that if the total generation demanded by the load is met by renewable energy sources, the system would be sustainable (Nallapaneni and Chopra, 2021).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

NS: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing—original draft, and visualization. NB: resources, supervision, and writing—review and editing. SM: resources, supervision, and writing—review and editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.845686/full#supplementary-material

Abbreviations

ACE, Area control error; AGC, Automatic generation control; BBO, Biogeography based optimization; EG, Electric grid; HESS, Hybrid energy storage system; HSI, High suitability index; HVAC, High voltage alternating current; HVDC, High voltage direct current; IPS, Interconnected power system; IBR, Inverter based resources; LFC, Load frequency control; LSI, Low suitability index; PHEV, Plug-in hybrid electric vehicles; PSO, Particle swarm optimization; SIV, Suitability index variable; SMES, Superconducting magnetic energy storage; VSP, Virtual synchronous power.

References

Abd-Elazim, S. M., and Ali, E. S. (2016). Load Frequency Controller Design via BAT Algorithm for Nonlinear Interconnected Power System. Int. J. Electr. Power Energ. Syst. 77, 166–177. doi:10.1016/j.ijepes.2015.11.029

CrossRef Full Text | Google Scholar

Anil Kumar, T., Venu, G., and Venkata Ramana, N. (2016). “Load Frequency Control of Multi Area Power System in Deregulated Environment with Robust Controllers in Coordination with Frequency Controllable HVDC Link,” in International Conference on Energy Efficient Technologies for Sustainability, 473–478. doi:10.1109/iceets.2016.7583801

CrossRef Full Text | Google Scholar

Annamraju, A., and Nandiraju, S. (2019). Coordinated Control of Conventional Power Sources and PHEVs Using Jaya Algorithm Optimized PID Controller for Frequency Control of a Renewable Penetrated Power System. Prot. Control. Mod. Power Syst. 4, 28. doi:10.1186/s41601-019-0144-2

CrossRef Full Text | Google Scholar

Barisal, A. K., and Mishra, S. (2018). Improved PSO Based Automatic Generation Control of Multi-Source Nonlinear Power Systems Interconnected by AC/DC Links. Cogent Eng. 5, 1422228. doi:10.1080/23311916.2017.1422228

CrossRef Full Text | Google Scholar

Bhatt, P., Roy, R., and Ghoshal, S. P. (2010). “GA/Particle Swarm Intelligence Based Optimization of Two Specific Varieties of Controller Devices Applied to Two-Area Multi-Units Automatic Generation Control. Int. J. Electr. Power Energy Syst. 32 (4), 299–310. doi:10.1016/j.ijepes.2009.09.004

CrossRef Full Text | Google Scholar

Elyas, R., Remon, D., Cantarellas, A. M., Rouzbehi, K., and Rodriguez, P. (2014). “Integration of Renewable Generation for Frequency Support of HVDC/AC Interconnected Systems under Power Market Scenario,” in IEEE PES General Meeting Conference & Exposition, 1–5.

Google Scholar

Guha, D., Roy, P. K., and Banerjee, S. (2017). Study of Differential Search Algorithm Based Automatic Generation Control of an Interconnected thermal-thermal System with Governor Dead-Band. Appl. Soft Comput. 52, 160–175. doi:10.1016/j.asoc.2016.12.012

CrossRef Full Text | Google Scholar

Hari Kumar, R., and Ushakumari, S. (2014). “Biogeography Based Tuning of PID Controllers forLoad Frequency Control in Microgrid,” in International Conference on Circuits, Power and Computing Technologies [ICCPCT-2014], 797–802. doi:10.1109/iccpct.2014.7054992

CrossRef Full Text | Google Scholar

Ibraheem, P. K., and Kothari, D. P. (2005). Recent Philosophies of Automatic Generation Control Strategies in Power Systems. IEEE Trans. Power Syst. 20 (No. 1), 346–357.

CrossRef Full Text | Google Scholar

Johnson, Teena., and Shubhanga, K. N. (2016). “Loop Flow Performance of Interconnected Power Systems with HVDC Links,” in IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems, 1–6. doi:10.1109/icpeices.2016.7853342

CrossRef Full Text | Google Scholar

Kachhwaha, A., Pandey, S. K., Dubey, A. K., and Gupta, S. (2016). “Interconnected Multi-Unit Two-area Automatic Generation Control Usingoptimal Tuning of Fractional Order PID Controller along with Electrical Vehicle Loading,” in IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems, 1–5. doi:10.1109/icpeices.2016.7853167

CrossRef Full Text | Google Scholar

Kouba, N. E. Y., Menaa, M., Hasni, M., and Boudour, M. (2015). “Optimal Control of Frequency and Voltage Variations Using PID Controller Based on Particle Swarm Optimization,” in 2015 4th international conference on systems and control (Sousse, Tunisia: ICSC), 424–429. doi:10.1109/icosc.2015.7152777

CrossRef Full Text | Google Scholar

llias, H., Fikri, A., and Zahari, M. (2016). Optimisation of PID Controller for Load Frequency Controller in Two-Area Power System Using Evolutionary Particle Swarm Optimisation. Int. J. Elect. Syst. 12 (2), 315–324.

Google Scholar

Madasu, S. D., Kumar, M. L. S. S., and Singh, A. K. (2017). Comparable Investigation of Backtracking Search Algorithm in Automatic Generation Control for Two Area Reheat Interconnected thermal Power System. Appl. Soft Comput. 55, 197–210. doi:10.1016/j.asoc.2017.01.018

CrossRef Full Text | Google Scholar

Madasu, S. D., Sai Kumar, M. L. S., and Singh, A. K. (2018). A Flower Pollination Algorithm Based Automatic Generation Control of Interconnected Power System. Ain Shams Eng. J. 9, 1215–1224. doi:10.1016/j.asej.2016.06.003

CrossRef Full Text | Google Scholar

Molina, M. G., and Mercado, P. E. (2011). Power Flow Stabilization and Control of Microgrid with Wind Generation by Superconducting Magnetic Energy Storage. IEEE Trans. Power Electron. 26 (3), 910–922. doi:10.1109/tpel.2010.2097609

CrossRef Full Text | Google Scholar

Musio, M., and Damiano, A. (2012). A Virtual Power Plant Management Model Based on Electric Vehicle Charging Infrastructure Distribution. 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), 1–7. doi:10.1109/ISGTEurope.2012.6465684

CrossRef Full Text | Google Scholar

Nallapaneni, M. K., and Chopra, S. S. (2021). “Electric Vehicles Participation in Load Frequency Control of an Interconnected Power System Is Not Sustainable,” in 6th AIEE Energy Symposium Current and Future Challenges to Energy Security: the energy transition, a pathway from low carbon to decarbonization.

Google Scholar

Oshnoei, A., Khezri, R., Muyeen, S. M., Oshnoei, S., and Blaabjerg, F. (2019). Automatic Generation Control Incorporating Electric Vehicles. Electric Power Components Syst. 47, 720–732. doi:10.1080/15325008.2019.1579270

CrossRef Full Text | Google Scholar

Pham, D. T., Huynh, T. T. B., and Dang, M. C. (2016). “An Improving of Migration Operator in Biogeography-Based Optimization for Solving Traveling Salesman Problem,” in International Conference on Computational Intelligence and Cybernetics, 33–40.

CrossRef Full Text | Google Scholar

Pham, T. N., Trinh, H., and Hien, L. V. (2016). Load Frequency Control of Power Systems with Electric Vehicles and Diverse Transmission Links Using Distributed Functional Observers. IEEE Trans. Smart Grid (7), 238–252. doi:10.1109/tsg.2015.2449877

CrossRef Full Text | Google Scholar

Prakash, S., and Sinha, S. K. (2018). ALFC of Hybrid Multi-Generation Power System Using UC and TCPS by ANFIS Control Technique. Int. J. Elect. 106, 174–211. doi:10.1080/00207217.2018.1519857

CrossRef Full Text | Google Scholar

Rahman, A., Chandra Saikia, L., and Sinha, N. (2015). Load Frequency Control of a Hydro-thermal System under Deregulated Environment Using Biogeography-Based Optimized Three Degree-Of-freedom Integral-Derivative Controller. IET Generation, Transmission & Distribution, 2284–2293. doi:10.1049/iet-gtd.2015.0317

CrossRef Full Text | Google Scholar

Rakhshani, E., Remon, D., Mir Cantarellas, A., Martinez Garcia, J., and Rodriguez, P. (2017). Virtual Synchronous Power Strategy for Multiple HVDC Interconnections of Multi-Area AGC Power Systems. IEEE Trans. Power Syst. 32 (3), 1665–1677. doi:10.1109/tpwrs.2016.2592971

CrossRef Full Text | Google Scholar

Rakhshani, E., Remon, D., Mir Cantarellas, A., and Rodriguez, P. (2016). Analysis of Derivative Control Based Virtual Inertia in Multi-Area High-Voltage Direct Current Interconnected Power Systems”. IET Gener. Transm. Distrib. 10 (6), 1458–1469. doi:10.1049/iet-gtd.2015.1110

CrossRef Full Text | Google Scholar

Roy, A., Dutta, S., and Roy, P. K. (2014). “Automatic Generation Control by SMES-SMES Controllers of Two-Area Hydro-Hydro System,” in 1st International Conference on Non-Conventional Energy (ICONCE 2014), 302–307. doi:10.1109/ICONCE.2014.6808731

CrossRef Full Text | Google Scholar

Rupali, R. K., and Chaphekar, S. N. (2015). “Particle Swarm Optimization Based PI Controller for Two Area Interconnected Power System,” in International Conference on Energy Systems and Applications, 496–500.

Google Scholar

Shankar, G., and Mukherjee, V. (2016). Load Frequency Control of an Autonomous Hybrid Power System by Quasi-Oppositional harmony Search Algorithm. Int. J. Electr. Power Energ. Syst. 78, 715–734. doi:10.1016/j.ijepes.2015.11.091

CrossRef Full Text | Google Scholar

Sivadanam, N., Nagu, B., and Sydulu, M. (2020). Inertial Response and Frequency Control in Electric Vehicles Integrated Renewable and Non-renewable Power System. J. Green Eng. 10 (11), 10981–10993.

Google Scholar

Sivadanam, N., Nagu, B., and Sydulu, M. (2020). Performance Optimization of an Interconnected Power System in the Presence of Plug-In Hybrid Electric Vehicles. J. Green Eng. 10 (9), 4910–4925.

Google Scholar

Sivadanam, N., Bhookya, N., and Maheswarapu, S. (2021). Dynamic Performance Enhancement of Interconnected Hybrid Thermal Power System in the Presence of Electric Vehicles. Case Stud. Therm. Eng. 26, 101045. doi:10.1016/j.csite.2021.101045

CrossRef Full Text | Google Scholar

Sivalingam, R., Chinnamuthu, S., and Dash, S. S. (2017). A Hybrid Stochastic Fractal Search and Local Unimodal Sampling Based Multistage PDF Plus (1 + PI) Controller for Automatic Generation Control of Power Systems. J. Franklin Inst. 354, 4762–4783. doi:10.1016/j.jfranklin.2017.05.038

CrossRef Full Text | Google Scholar

Yang, S., Huang, C., Yu, Y., Yue, D., and Xie, J. (2017). Load Frequency Control of Interconnected Power System via Multi-Agent System Method, 45, 839–851. doi:10.1080/15325008.2015.1131764Load Frequency Control of Interconnected Power System via Multi-Agent System MethodElectric Power Components Syst.

CrossRef Full Text | Google Scholar

Zhu, J., Campbell, D. B., Grain, P. A., and AndrewChris, J. R. G. B. (2013). Inertia Emulation Control Strategy for VSC-HVDC Transmission Systems. IEEE Trans. Power Syst. (28), 1277–1287. doi:10.1109/tpwrs.2012.2213101

CrossRef Full Text | Google Scholar