Denoising Method of Nuclear Signal Based on Sparse Representation

Nuclear signals are sensitive to noise which may affect final monitoring results significantly. In order to suppress the nuclear signal noise, a sparse representation method, which is based on the sparse representation of signals and a matching pursuit algorithm, has been proposed for denoising. Time–frequency matching “atoms” have been selected for building an over-complete library by training atoms matching with the characteristics of nuclear signals regardless of the noise. The best time–frequency matching atoms have been extracted by sparsely representing the noisy signals with an Orthogonal Matching Pursuit (OMP) algorithm and the library. The residual ratio threshold has been chosen as a stopping criterion in the OMP algorithm for avoiding the influence of improper selection of iterations on denoising results. At the end, the pulse matching the atom extracted by each iteration has been optimized by performing effective sparse representation on the original noiseless nuclear signal component in noisy nuclear signals. The proposed method has been used to denoise the simulated and measured signals and has been compared with the nuclear denoising result using traditional wavelet theory. The results show that the proposed method can accurately suppress the noise interference of nuclear signals, and the denoising effect is better than that of the traditional wavelet method.

Introduction

Nuclear radiation detection is one of the key technologies in nuclear analysis and also the fundamental of nuclear science and technology and has been widely applied in the operation of nuclear power and its safety, uranium mining and metallurgy, environmental monitoring and radiation protection, homeland security and nuclear non-proliferation, industrial buildings and radiation imaging, and other fields. The nuclear information, such as energy, time, and position, is usually converted into voltage in visual and thus can be expediently analyzed and used for obtaining valuable information (KNOLL, 2000). As the nuclear signals are usually very weak and there is large electromagnetic noise in a practical environment, therefore, noise suppression has become a problem that must be solved in the analysis and processing of nuclear signals in nuclear measurement systems (Williams, 2005; Hashemian and Bean, 2011; To-Po Wang and Zong-Wei Li, 2014; Min et al., 2015).

Sparse representation of signals is a method to represent the original signal as accurately as possible by less specific information, first proposed by Mallet and Zhang in 1993 (Mallat and Zhifeng Zhang, 1993), in which the signal can be represented by a linear superposition of different basis signals, and the set of these basis signals is called a dictionary, and the basis signals are called atoms. The sparse representation of signals is based on the adaptive selection of a small number of atoms to represent the signal with full consideration of the signal characteristics, and because the method does not require the atoms to have orthogonality, the selection of atoms in the dictionary is flexible and can better characterize the signal and retain the frequency- and time-domain information of the original signal to the maximum extent, and it has many advantages such as a wide range of signal representation, concise representation method, and strong representation capability (Mallat and Zhifeng Zhang, 1993; Zhang et al., 2017; Othmen et al., 2021; Shi et al., 2021), which has been more often applied in the fields of image restoration, image denoising, and signal recognition (Deeba et al., 2020; Maqsood and Javed, 2020; Alotaibi, 2021; Balnarsaiah and Rajitha, 2021). Sparse representation methods include both sparse decomposition algorithms and construction of over-complete atomic dictionaries, and the main sparse decomposition algorithms are convex optimization algorithms and greedy algorithms. Typical convex optimization algorithms include Basis Pursuit (BP) (Ekanadham et al., 2011), and in 2015, Selesnick et al. constructed convex sparse representation models based on parametric non-convex functions and proposed corresponding sparse decomposition algorithms, which achieved superior performance in signal denoising and other aspects (Selesnick et al., 2014; Parekh and Selesnick, 2015). Convex optimization algorithms have a more rigorous mathematical optimization solution process, and compared with greedy algorithms, convex optimization algorithms can find sparser or more accurate solutions, but the computational complexity is high and will take a lot of time. Typical greedy algorithms include Matching Pursuit (MP) (Mallat and Zhifeng Zhang, 1993), Orthogonal Matching Pursuit (OMP) (Yi and Song, 2015), which is developed on the basis of MP, Regularized Orthogonal Matching Pursuit (ROMP) (Sajjad et al., 2015), Sparsity Adaptive Matching Pursuit (SAMP) (Wang et al., 2020), Compressive Sampling Matching Pursuit (CoSaMP) (Huang et al., 2017), Subspace Pursuit (SP) (Li et al., 2015), and other methods, and all of them can achieve sparse signal reconstruction very well. Matching Pursuit class algorithms are commonly used for image sparse representation, and Rubinstein’s team (Rubinstein et al., 2008) used Batch Orthogonal Matching Pursuit (Batch-OMP) to achieve fast noise reduction and sparse representation processing of image signals. Greedy class algorithms with mature theory, low complexity, and fast running speed are widely used for signal sparse decomposition. The construction of over-complete dictionaries mainly includes conformal dictionaries and learning dictionaries. Constructed dictionaries are constructed by analyzing the signal feature structure, using parametric wavelets as atoms, and obtaining a large number of different atoms by changing parameters, such as the Gabor time–frequency atom dictionary (Mallat and Zhifeng Zhang, 1993) and the chirplet time–frequency atom dictionary (Mann and Haykin, 1995). The learned dictionaries are mainly learned from training samples and have good adaptability, but in application scenarios where the signal interference noise is relatively strong, the learned dictionaries may not be optimal and do not perform well for sparse representations of other signals of the same type; moreover, dictionary learning algorithms are generally high in complexity and are not suitable for dealing with large-scale datasets. The current typical dictionary learning methods include the method of optimal directions (MOD) (Engan et al., 2000), K-SVD (Aharon et al., 2005), and online dictionary learning (ODL) (Celik and Bilge, 2017). At the moment, sparse decomposition’s application and research in nuclear signal processing is still in its infancy. In 2011, Trigano T et al. (Trigano et al., 2011) conducted a study on activity estimation of radioactive source based on the sparse representation of signals method and investigated the efficiency of this approach on simulation and real datasets. And also in 2018, Zhang (Zhang et al., 2018) investigated the rapid and effective extraction method of nuclear pulse signals based on the sparse representation method.

In this paper, a sparse representation method has been applied for denoising nuclear signals. As nuclear signal matching atoms, Gabor time–frequency atoms and chirplet time–frequency atoms, which can accurately correlate with the characteristics of the original nuclear signal, were first produced. Gabor and chirplet atoms exhibit good time–frequency aggregation, according to the uncertainty principle, and the nuclear signal is a type of uncertain signal with unpredictable time and amplitude. The time–frequency features of the nuclear signal can be completely revealed utilizing the sparse representation of the signal generated using the Gabor dictionary and chirplet dictionary. Then, the Orthogonal Matching Pursuit (OMP) algorithm was applied for searching the best matched atom in the noisy nuclear signals from the over-complete library composed of time–frequency atoms, and the threshold of residual ratio was taken as the stopping criterion of OMP algorithm. Because the matched atoms obtained from each iteration can only effectively sparse represent the original nuclear signals without noise components, the aim of nuclear signal denoising can be achieved. In this work, the above methods have been used to denoise the simulated and measured nuclear signals, respectively (Chen et al., 2009; Zhou et al., 2011). The results prove that the method proposed in this paper is more effective and superior compared with the traditional wavelet denoising method.

Original Research Article

Sparse Representation Theory of Signals

Any signal $f\in R^N$ can be represented as a linear combination of atoms ${\left({\varphi }_{\gamma }\left(t\right)\right)}_{\gamma \in \Gamma }$ in the dictionary D:

$f={\displaystyle \sum }_{\gamma \in \Gamma }{\alpha }_{\gamma }{\varphi }_{\gamma } ,(1)$

where ${\alpha }_{\gamma }$ is the expansion coefficient. Since the dictionary D is non-orthogonal and over-complete, a signal f has various possible representations in the dictionary D. Solving the sparse signal representation coefficient in a certain atomic dictionary D is equivalent to solving the following optimization problem:

$\left(P_0\right)\mathrm{:}\min \Vert x_0\Vert s.t. y=Dx,(2)$

where $\mathrm{\Vert }x{\mathrm{\Vert }}_0=\left|\{\text{i}:x\left(\text{i}\right)\ne 0\}\right|$ is the number of non-zero terms in the coefficient vector x.

The denoising of the nuclear signals infected by noise can be composed of two parts, namely, the original nuclear signals without noise and the noise signal, and its mathematical model can be expressed as (SARKAR et al., 2012)

$f=f_p+f_n,(3)$

where $f$ is the nuclear signal infected by noise, $f_p$ is the original nuclear signal without noise, and $f_n$ is the noise signal.

Basically, $f_p$ has a particular structure, but $f_n$ does not, or $f_p$ and $f_n$ have different structures. If there is some kind of atom $P_{\gamma }$, and its atomic structure is related to $f_p$ and unrelated or has weak correlation to $f_n$, when sparse representation based on the decomposition algorithm is done to $f_p$ in an over-complete dictionary of atoms composed of $P_{\gamma }$ atoms, the inner product of atoms and $f_p$ must be greater than that of atoms and $f_n$. Based on the rational of MP algorithm, the first extracted nuclear signal must be the original nuclear signal without noise and can be formulized as

$f={\displaystyle \sum }_{k=1}^k<R^{k}f,p_{\gamma }^k>p_{\gamma }^k+R^{k+1}f,(4)$

where ${\displaystyle \sum }_{k=1}^k<R^{k}f,p_{\gamma }^k>p_{\gamma }^k$ is the original nuclear signal without noise, $R^{k+1}f$ represents the noise signal, and $p_{\gamma }^k$ denotes matched atoms for nuclear signals.

Sparse Representation and Decomposition Algorithm

Orthogonal Matching Pursuit Signal Sparse Decomposition Algorithm

The process of Matching Pursuit algorithm (Mallat and Zhifeng Zhang, 1993) is presented as follows: Firstly, the atom $x_{r_0}$ that best matches the signal y to be decomposed is selected from the over-perfect dictionary to satisfy the following conditions:

$|<y,x_{r_0}>|=sup|<y,x_{r_i}>|.(5)$

The signal can be decomposed into components and residuals on the optimal atom:

$y=<y,x_{r_0}>x_{r_0}+R_1,(6)$

where R₁ is the residue after the optimal matching of the original signal with the optimal atom. The same decomposition process above can be carried out for the residue after the best matching:

$R_t=<R_t,x_{r_t}>x_{r_t}+R_{t+1}.(7)$

After the T step decomposition, the signal is decomposed into

$y={\displaystyle \sum }_{t=0}^{T-1} <R_t,g_{r_t}>g_{r_t }+R_T.(8)$

And a small number of atoms can represent the main component of the signal, namely,

$y\approx {\displaystyle \sum }_{t=0}^{T-1}<R_t,g_{r_t}>g_{r_t}.(9)$

From Equation 6, it can be seen that the sparse decomposition of signals by the matching tracking algorithm is a continuous iterative process. Without limiting the residual energy threshold and decomposition iteration times, signals can be decomposed indefinitely on a fixed atomic dictionary.

The OMP algorithm uses the Gram–Schmidt orthogonalization method to normalize the matched atoms $x_{r_t}$ at each step of MP decomposition (Yi and Song, 2015), which can not only accelerate the convergence rate but also avoid introducing unnecessary components when residual errors are projected on the atoms $x_{r_t}$. The specific process assumes $u_0=x_{r_0}$, the most matching atom $x_{r_t}$ is selected according to Equation 7, and then $x_{r_t}$ is normalized:

$u_t=x_{rt}-{\displaystyle \sum }_{t=0}^{N-1}\frac{<x_{rt},u_{t-1}>}{u_{t-1}^2}{u}_{t-1}.(10)$

After N iterations, the system output signal y is decomposed:

$y={\displaystyle \sum }_{t=0}^{N-1}\frac{<x_{rt},u_{t-1}>}{u_{t-1}^2}{u}_{t-1}+R_N.(11)$

The Nuclear Signal Over-Complete Atomic Dictionary

The Gabor Atomic Over-Complete Dictionary

According to the principle of sparse representation, the sparse representation of a signal can be achieved in any over-complete atomic dictionary (Mallat and Zhifeng Zhang, 1993). From the point of view of obtaining a better sparse representation of the signal, the over-complete dictionary of atoms chosen or constructed should match as closely as possible the intrinsic structure and properties of the signal, so that as few atoms as possible can be used for the representation, and the representation results will be more sparse. In addition, in order to better describe the time-varying characteristics of non-stationary nuclear signals from the perspective of time–frequency analysis, the atoms in the dictionary should have good resolution in both the time domain and the frequency domain. In this study, a Gabor atom is firstly used to construct an over-complete dictionary due to the best time–frequency aggregation. It is expressed as follows:

$g_{\gamma }\left(t\right)=\frac{1}{\sqrt{s}}g\left(\frac{t-u}{s}\right)cos\left(vt+w\right),(12)$

where $g\left(t\right)=e^{-\pi t^2}$ represents a Gaussian window function, $\gamma =(s, u, v, w)$ is the atomic time–frequency parameter, $s$ is the scaling factor, u is the shift factor, $v$ is the frequency factor, and $w$ is the phase factor. Signal sparse representation requires high redundancy and enough diversity of atomic dictionary. To meet the design requirements, we discretize the atomic time–frequency parameters into

$\gamma =(a^j, p{a}^j \Delta u, k{a}^{-j} \Delta v, i\Delta w).(13)$

Here, a = 2, ∆u = 1/2, ∆v = π, ∆w = π/6, $0<j\ll lo{g}_{2}N$, $0\ll P\ll N{2}^{-j+1}$, $0\ll k\ll 2^{j+1}$, $0\ll i\ll 12$, and N represents the number of sampling points of a frame signal processed.

The Chirplet Atomic Over-Complete Dictionary

The chirplet atom (Mann and Haykin, 1995) is the most widely used atom after the Gabor atom. On the principle of Gabor atom, and then the chirplet atom, a one-dimensional frequency modulation parameter is added, which makes the chirplet atom have a good matching effect on the linear frequency modulation signal. It can be expressed as follows:

$g_{\gamma }\left(t\right)=\frac{1}{\sqrt{s}}g\left(\frac{t-u}{s}\right)exp\left(j(\xi \left(t-u\right)+\frac{1}{2}c{(t-u)}^2)\right),(14)$

where $g\left(t\right)=e^{-\pi t^2}$ represents a Gaussian window function, $\gamma =(s, u, \xi , c)$ is the atomic time–frequency parameter, $s$ is the telescopic scale, u is the shift factor, $\xi$ is the modulation factor, namely, frequency center, and c is the linear frequency modulation factor responding signal frequency over time. The real part of the time–frequency atom can be expressed as

$g_{\gamma }\left(t\right)=\frac{1}{\sqrt{s}}g\left(\frac{t-u}{s}\right)cos(\xi \left(t-u\right)+\frac{1}{2}c{(t-u)}^2).(15)$

According to the optimal discretization method, the atomic parameter set γ is discretized:

$\gamma ==(s, u, \xi , c, \omega )=(a^j, p{a}^j \Delta u, k{a}^{-j} \Delta \xi , l{a}^{-2j} \Delta c, i\Delta w),(16)$

in which a = 2, ∆u = 1/2, ∆$\xi$ = π, ∆w = π/6, $0<j\ll lo{g}_{2}N$, $0\ll P\ll N{2}^{-j+1}$, $0\ll k<2^{j+1}$, $0\ll l<2^{j+1}$, $0\ll i\ll 12$, and N represents the number of sampling points of a frame signal processed.

The Termination Conditions of Residual Threshold

The iterative termination conditions of the OMP algorithm are mainly composed by the hard and soft threshold methods. The former refers to the fixed iteration termination number K, and the original signal was replaced with the linear combination of K original signals. This method is simple but has the flaw that the K value is difficult to determine accurately. When K is too small, the original noiseless signal component will be lost, while the noise component will be introduced in reverse with a very large K. On the contrary, the soft threshold method holds that the iteration is terminated when the residual signal is less than a certain threshold. Its denoising effect is fine when the signal-to-noise ratio is high, whereas at low signal-to-noise ratios, a larger noise component will impact on the judgment of the residual error threshold. Thus, no matter how many times iteration was done, the residual all cannot reach the specified threshold. In addition, when the number of iterations is too much, a noise component will further be introduced, which also will influence the denoising effect. A termination condition of the residual ratio threshold of the signal denoising was introduced in the study of Liang and Que (2010) based on the MP theory, which avoids the influence on the judgment of the threshold of the residual ratio when the noise energy is large; as a consequence, the noise disturbance was reduced, and the robustness of the sparse representation was improved. Taking $R^{k}f$ and $R^{k+1}f$, respectively, as the k-th and k+1-th residuals, the residual error ratio is

$q\left(R^{K}f\right)=\frac{\Vert R^{K+1}f-\xi R^{K}f\Vert }{\xi R^{K}f},(17)$

where $\xi =\sqrt{E\left[{\left(R^{k+1}f\right)}^2\right]/E\left[{\left(R^{k}f\right)}^2\right]}$ and E(·) denotes the expectation value.

Steps of Nuclear Signal Denoising Method Based on Sparse Representation

The steps of the nuclear signal denoising method based on sparse representation are presented as follows:

1) The number of dictionary contents will be huge, when the length of the signal to be processed is large enough for the size of the over-complete dictionary used in sparse decomposition which depends on the length of the signal to be processed. To solve this problem, the collected data sequence is divided into blocks. A Block is a segment of an entire data sequence (Rubinstein et al., 2008).

2) The corresponding time–frequency atoms are constructed according to the characteristics of the nuclear signal, and the over-complete atomic dictionary is generated according to the length of the Block.

3) For each Block, OMP decomposition is performed separately. Set the cumulative number of stopping iterations N = 1, and set the maximum allowed number of stopping iterations to K.

4) According to the threshold condition of residual ratio, do determination when the OMP calculation iteration termination condition is satisfied. If not, return to step 3); if so, a Block denoising ends.

5) Each Block is processed separately and then spliced.

Flow chart of the sparse decomposition algorithm based on block processing is shown in Figure 1, and the detailed algorithm is shown in Table 1.

FIGURE 1

FIGURE 1. Flow chart of the sparse decomposition algorithm based on block processing.

TABLE 1

TABLE 1. Nuclear signal sparse decomposition algorithm based on block processing.

Simulation Verification and Analysis

Nuclear Signal Simulation

The simulation experiment is designed to verify the effectiveness of the method based on sparse representation. According to the random statistical law of nuclear event (Bertuccio and Pullia, 1993; Georgiev and Gast, 1993), the waveform shape, amplitude, adjacent pulse time interval, and system interference noise characteristics of the nuclear signal are statistically described, and then the simulated nuclear signal is generated on this basis.

1) The mathematical model of pulse waveform

To select an appropriate signal mathematical model according to the type of preamplifier after the detector, in this paper, a resistance–capacitance feedback preamplifier is employed to simulate the output pulse waveform. It is approximated by a double exponential function:

$s_n\left(t\right)=A_n\times (e^{-(t-t_n)/{\tau }_1}-e^{-(t-t_n)/{\tau }_2})\times u(t-t_n),(18)$

where $A_n$ represents the amplitude of the nth pulse waveform, t_n stands for the formation time of the pulse waveform, ${\tau }_1$ and ${\tau }_2$ show the corresponding slow time constant and fast time constant, respectively, and the function $u(t-t_n)$ is the first step function$.$.

2) The pulse time interval satisfies the exponential distribution rule

$dI\left(t\right)=m{e}^{-mt}dt,(19)$

where m represents the average counting rate of pulses.

3) The pulse amplitude is proportional to the energy loss of the incident particle in the detector, which has random fluctuation characteristics. Generally, the pulse amplitude distribution of the nuclear signal meets the conditions of normal distribution:

$H\left(\mathit{A}\right)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-(A-\overline{A}{)}^2/2{\sigma }^2},(20)$

where $\overline{A}$ is the average pulse amplitude and $\sigma$ is the amplitude standard deviation determined by the intrinsic energy R of the detector and the average pulse amplitude, $\sigma =R\times (\overline{A}/2.355 )$.

4) The statistical characteristics of noise interference

The interference noise will be introduced in the measurement of the nuclear signal due to the influence of electronic devices and environment. The white noise distribution satisfies the normal distribution rule and is superposed linearly with the nuclear signal to form an observation signal. The slow and fast time constants in the dual exponential function are set to 20 and 0.5 µs, respectively, based on the pulse waveform of the nuclear signal. For the pulse amplitude, the natural resolution of the detector is set to 20%, and the average pulse amplitude is set to 1 V, which obeys the normal distribution. The generation time of the pulse waveform is obtained randomly through exponential distribution according to the pulse time interval and the setting of the average count rate of nuclear signal pulse of 6,000 cps. For the interference noise, the mean value and standard deviation of the noise signal are set as 0 and 0.2 V, respectively, which obeys the additive superposition rule. Figure 2 shows the original nuclear signal obtained by sampling frequency 1 MHz and sampling time 1 ms.

FIGURE 2

FIGURE 2. Simulation GUI interface of the nuclear signal.

Analysis of Denoising Effect of Nuclear Signal

The wavelet analysis method is selected to denoise the simulated signal to compare and illustrate the denoising effect of this method. Wavelet packets, respectively, choose wavelet Db4 and wavelet Db8, which are currently widely applied in the nuclear signal denoising area, and the denoising results are shown in Figure 3: straight from the top, in turn, plots present the original nuclear signal without noise, the nuclear signal with noise, the result of the sparse decomposition based on the Gabor dictionary, the result of the sparse decomposition based on the chirplet dictionary, the result processed by Db8, and the result processed by Db4.

FIGURE 3

FIGURE 3. Denoising results of the nuclear pulse simulation signal.

In this work, three parameters were introduced, which formed the evaluation index of denoising effect, that is, signal-to-noise ratio (SNR), root mean square error (RMSE), and normalized correlation coefficient (NCC). The SNR was used to evaluate the noise energy; the smaller the value of SNR, the lower the noise energy in the signal. The RMSE was used to evaluate the overall error between the recovered signal after denoising and the original noise bureau broadcast signal. The smaller the value of RMSE is, the lower the error is. The NCC reflects the degree of similarity between the recovered signal and the original ideal signal waveform without noise after denoising, and the closer it is to 1, the more similar the two waveforms are.

Based on the results in Figure 3 and Table 2, the following conclusions can be drawn by comparing the denoising results and denoising evaluation indexes of the four methods:

1) The denoising effect of the nuclear signal based on sparse representation introduced in this paper is better than that of wavelet analysis. The waveform of each pulse recovery signal remains consistent, the pulse trend remains the same, and the error based on sparse representation is the smallest compared with the original pulse signal after denoising.

2) The denoising results obtained by denoising the nuclear signal based on sparse representation are related to the selection of over-complete dictionaries, and the results vary obviously by different over-complete dictionaries.

3) The selection of wavelet basis has great influence on the denoising effect of the nuclear signal based on wavelet analysis. Compared with that of the original signal, the amplitude of the denoised signal has big error, and its waveform was distorted.

TABLE 2

TABLE 2. Calculation results of denoising effect evaluation indexes.

The Verification of Measured Signals

In the laboratory, a γ pulse nuclear signal was obtained through the nuclear measurement system composed of an NaI detector and γ radiation source ⁶⁰Co. Figure 4 shows the waveform measured by the above measurement system in the laboratory by the sampling frequency of 100 M Hz. Due to the weak interference in the laboratory, the nuclear signal can be easily differentiated. In this paper, background noise of the laboratory is measured and amplified and then superimposed into the measured signal to simulate the noisy nuclear signal. Its waveform is shown in Figure 5.

FIGURE 4

FIGURE 4. Measured nuclear pulse signals in the laboratory.

FIGURE 5

FIGURE 5. Measured nuclear pulse signals with noise superimposed in the laboratory.

The method introduced in this paper is adopted to carry out denoising processing for the above nuclear signal with noise, and the result is shown in Figure 6A. Meanwhile, the denoising results by wavelet morphology–wavelet method were also measured and are shown in Figures 6B,C.

FIGURE 6

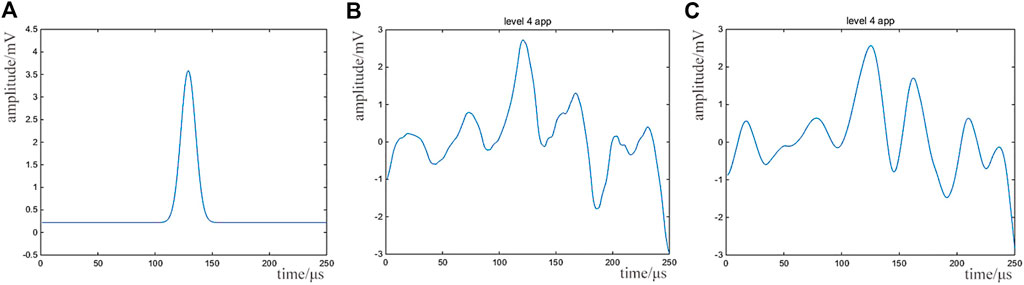
FIGURE 6. Denoising result of nuclear pulse signals measured in the laboratory: (A) denoising result based on sparse representation; (B) denoising result by wavelet morphology–wavelet method (Db4); (C) denoising result by wavelet morphology–wavelet method (Db8).

Due to the small noise interference of the original measured nuclear signal, it can be approximately equivalent to the ideal noise-free waveform, and the evaluation index of denoising effect of each method is calculated. The results are shown in Table 3.

TABLE 3

TABLE 3. Evaluation indexes of denoising effect of measured nuclear signals in the laboratory.

Based on the results in Figure 6 and Table 3, the method in this paper can still restore the measured nuclear pulse signal in the laboratory under high noise, whereas the denoising effect of wavelet method is poor with large energy loss and large distortion. In general, the method of denoising the nuclear signal introduced in this paper has high accuracy, small waveform distortion, and good retention of the time characteristics and amplitude of the original nuclear pulse signal. So, its denoising effect is obviously better than that of the wavelet method.

To validate the denoising effect of the method in this paper for a weak signal under a long cable transmission nuclear measurement system, a set of neutron detection systems was built in the laboratory, which modeled the measurement system in the core pool of a sodium-cooled fast reactor. In the system, the Am–Be neutron source and LB-125 fission ionization chamber were applied, and the output signal of the fission ionization chamber was transported through a 10 m long cable to the preamplifier for amplification to improve the SNR of the detector and then sent to the linear amplifier through a long shielded cable. The structural block diagram of the neutron measurement system is shown in Figure 7.

FIGURE 7

FIGURE 7. Structural block diagram of the neutron measurement system.

The nuclear pulse signal shown in Figure 8 was read out by the neutron detection system built in this paper after the main amplifier. Due to the long distance between the preamplifier and the fission ionization chamber, interference noise can easily be mixed into the measurement process through the transmission cable, so large noise has been superimposed in the nuclear pulse signal measured by the experiment.

FIGURE 8

FIGURE 8. Nuclear pulse signal output by the neutron detection system built in the laboratory.

The nuclear pulse signal denoising method adopted in this paper was used for sparse decomposition and reconstruction of the nuclear pulse signal output by the neutron detection system built in the laboratory. Figure 9 shows the result obtained through adjusting the iteration threshold parameters.

FIGURE 9

FIGURE 9. Nuclear pulse signal obtained by sparse decomposing and reconstruction.

RMSE, NCC, SNR, and other parameters cannot be used for evaluation, as there is no way to obtain the nuclear pulse without noise through the neutron detection system. However, from the reconstructed pulse image, we can obviously find the method can effectively extract the nuclear signal from the system with a random noise signal and maintain the time information of the original pulse.

Conclusion

In this paper, a sparse representation–based nuclear signal denoising method is proposed for nuclear signal extraction in a strong noise interference environment. Firstly, the Gabor time–frequency atoms and chirplet time–frequency atoms are constructed, and then the sparse decomposition and reconstruction of the signal are performed by the Batch Orthogonal Matching Pursuit (Batch-OMP) algorithm, and the residual ratio threshold is used as the termination condition of the iteration of the algorithm. The simulation results show that this method outperforms the traditional wavelet method in all indexes, with high accuracy and low error, and retains the kernel signal characteristics. The experiments prove that the method can effectively extract the kernel signal in the noisy environment and retain the original pulse information well.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

S-H and NS completed the algorithm and simulation and wrote the manuscript. L-S, S-H, NS, BC, and X-Z completed the experimental research. L-S, BC, and X-Z revised the article.

Funding

This work was supported by the National Natural Science Foundation of China for Youth (12005098), the Research Foundation of Education Bureau of Hunan Province, China (Grant No. 18C0472), and the Open Fund Project of Nuclear Fuel Cycle Technology and Equipment Collaborative Innovation Center of Hunan Province (2019KFY14).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aharon, M., Elad, M., and Bruckstein, A. (2005). K-svd:design Dictionaries Sparse Representation. SPARS 5, 9–12.

Google Scholar

Alotaibi, N. (2021). A Novel Method to Denoise Images Based on a Meta-Heuristic Algorithm and Pre-learned Dictionary. Ijies 14 (1), 203–211. doi:10.22266/ijies2021.0228.20

CrossRef Full Text | Google Scholar

Balnarsaiah, B., and Rajitha, G. (2021). Denoising and Optical and Sar Image Classifications Based on Feature Extraction and Sparse Representation. arXiv preprint arXiv:2106.01896.

Google Scholar

Bertuccio, G., and Pullia, A. (1993). A Method for the Determination of the Noise Parameters in Preamplifying Systems for Semiconductor Radiation Detectors. Rev. Scientific Instr. 64 (11), 3294–3298. doi:10.1063/1.1144293

CrossRef Full Text | Google Scholar

Celik, C., and Bilge, H. S. (2017). Content Based Image Retrieval with Sparse Representations and Local Feature Descriptors : A Comparative Study. Pattern Recognition 68, 1–13. doi:10.1016/j.patcog.2017.03.006

CrossRef Full Text | Google Scholar

Chen, G. Y., Bui, T. D., and Krzyżak, A. (2009). Invariant Pattern Recognition Using Radon, Dual-Tree Complex Wavelet and Fourier Transforms. Pattern Recognition 42 (9), 2013–2019. doi:10.1016/j.patcog.2008.10.008

CrossRef Full Text | Google Scholar

Deeba, F., Kun, S., Ali Dharejo, F., and Zhou, Y. (2020). Sparse Representation Based Computed Tomography Images Reconstruction by Coupled Dictionary Learning Algorithm. IET image process 14 (11), 2365–2375. doi:10.1049/iet-ipr.2019.1312

CrossRef Full Text | Google Scholar

Ekanadham, C., Tranchina, D., and Simoncelli, E. P. (2011). Recovery of Sparse Translation-Invariant Signals with Continuous Basis Pursuit. IEEE Trans. Signal. Process. 59 (10), 4735–4744. doi:10.1109/tsp.2011.2160058

PubMed Abstract | CrossRef Full Text | Google Scholar

Engan, K., Aase, S. O., and Husøy, J. H. (2000). Multi-frame Compression: Theory and Design. Signal. Process. 80 (10), 2121–2140. doi:10.1016/s0165-1684(00)00072-4

CrossRef Full Text | Google Scholar

Georgiev, A., and Gast, W. (1993). Digital Pulse Processing in High Resolution, High Throughput, Gamma-ray Spectroscopy. IEEE Trans. Nucl. Sci. 40 (4), 770–779. doi:10.1109/23.256659

CrossRef Full Text | Google Scholar

Hashemian, H. M., and Bean, W. C. (2011). Sensors for Next-Generation Nuclear Plants: Fiber-Optic and Wireless. Nucl. Sci. Eng. Eng. J. Am. Nucl. Soc. 169, 262–278. doi:10.13182/nse10-48

CrossRef Full Text | Google Scholar

Huang, F., Tao, J., Xiang, Y., Liu, P., Dong, L., and Wang, L. (2017). Parallel Compressive Sampling Matching Pursuit Algorithm for Compressed Sensing Signal Reconstruction with OpenCL. J. Syst. Architecture 72 (C), 51–60. doi:10.1016/j.sysarc.2016.07.002

CrossRef Full Text | Google Scholar

Knoll, G. F. (2000). Radiation Detection and Measurement. 3rd ed. New Jersey: John Wiley and Sons.

Google Scholar

Li, H., Wimalajeewa, T., and Varshney, P. K. (2015). On the Detection of Sparse Signals with Sensor Networks Based on Subspace Pursuit. IEEE.

Google Scholar

Liang, Wei., and Que, Pei-Wen. (2010). Residual Rat Io Iteration Termination Condition for MP Method. JOURNAL SH ANGHAI JIAOTONG UNIVERSIT Y 44 (02), 171–176. doi:10.1007/BF00961363

CrossRef Full Text | Google Scholar

Mallat, S. G., and Zhifeng Zhang, Z. (1993). Matching Pursuits with Time-Frequency Dictionaries. IEEE Trans. Signal. Process. 41, 3397–3415. doi:10.1109/78.258082

CrossRef Full Text | Google Scholar

Mann, S., and Haykin, S. (1995). The Chirplet Transform: Physical Considerations. IEEE Trans. Signal. Process. 43 (11), 2745–2761. doi:10.1109/78.482123

CrossRef Full Text | Google Scholar

Maqsood, S., and Javed, U. (2020). Multi-modal Medical Image Fusion Based on Two-Scale Image Decomposition and Sparse Representation. Biomed. Signal Process. Control. 57, 101810. doi:10.1016/j.bspc.2019.101810

CrossRef Full Text | Google Scholar

Min, M.-G., Lee, J.-K., Ji, Y.-H., Jo, S.-H., and Kim, H.-J. (2015). Evaluation of Electromagnetic Interference Environment of the Instrumentation and Control Systems in Nuclear Power Units. Nucl. Eng. Des. 285 (apr), 15–22. doi:10.1016/j.nucengdes.2014.12.038

CrossRef Full Text | Google Scholar

Othmen, F., Lazzaretti, A., and Baklouti, M. (2021). A Sparse Representation Classification for Noise Robust Wrist-Based Fall Detection. 14th Int. Conf. Health Inform., 409–416. doi:10.5220/0010238804090416

CrossRef Full Text | Google Scholar

Parekh, A., and Selesnick, I. W. (2015). Convex Denoising Using Non-convex Tight Frame Regularization. IEEE Signal. Process. Lett. 22 (10), 1786–1790. doi:10.1109/lsp.2015.2432095

CrossRef Full Text | Google Scholar

Rubinstein, R., Zibulevsky, M., and Elad, M. (2008). Efficien T Implementation of the K-SVD Algorithm and the Batch-OMP Method. Technical report. Israel: Department of Computer Science, Technion, Technical CS–08.

Google Scholar

Sajjad, M., Mehmood, I., and Ba Ik, S. W. (2015). Sparse Coded Image Super-resolution Using K-Svd Trained Dictionary Based on Regularized Orthogonal Matching Pursuit. Bio-medical Mater. Eng. 26 (Suppl. 1s1), S1399. doi:10.3233/bme-151438

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, P., Chakraborty, C., and Ghosh, M. (2012). Content Based Leukocyte Image Retrieval Ensembling Quaternion Fourier Transform and Gabor-Wavelet Features[C]//2012. 12th Int. Conf. Intell. Syst. Des. Appl., 345–350. doi:10.1109/ISDA.2012.6416562

CrossRef Full Text | Google Scholar

Selesnick, I. W., Parekh, A., and Bayram, I. (2014). Convex 1-d Total Variation Denoising with Non-convex Regularization. IEEE Signal. Process. Lett. 22 (2), 141–144. doi:10.1109/LSP.2014.2349356

CrossRef Full Text | Google Scholar

Shi, M., Zhang, F., Wang, S., Zhang, C., and Li, X. (2021). Detail Preserving Image Denoising with Patch-Based Structure Similarity via Sparse Representation and SVD. Computer Vis. Image Understanding 206, 103173. doi:10.1016/j.cviu.2021.103173

CrossRef Full Text | Google Scholar

To-Po Wang, T. P., and Zong-Wei Li, Z. W. (2014). Significant Reduction of Electromagnetic Interference for Fine-Motion Control Rod Drive in a Nuclear Reactor. IEEE Trans. Ind. Electron. 61 (10), 5582–5589. doi:10.1109/tie.2013.2297352

CrossRef Full Text | Google Scholar

Trigano, T., Sepulcre, Y., and Roitman, M. (2011). On Nonhomogeneous Activity Estimation in Gamma Spectrometry Using Sparse Signal Representation. IEEE.

Google Scholar

Wang, Y., Peng, Y., Liu, S., Li, J., and Wang, X. (2020). Sparsity Adaptive Matching Pursuit for Face Recognition. J. Vis. Commun. Image Representation 67 (7), 102764. doi:10.1016/j.jvcir.2020.102764

CrossRef Full Text | Google Scholar

Williams, T. (2005). Chapter 8-Electromagnetic Compatibility. Circuit Designers Companion. Amsterdam: Elsevier.

Google Scholar

Yi, S., and Song, L. (2015). Sparse Signals Recovery from Noisy Measurements by Orthogonal Matching Pursuit. Inverse Probl. Imaging 9 (1), 231–238. doi:10.3934/ipi.2015.9.231

CrossRef Full Text | Google Scholar

Zhang, Jiangmei, Zhu, Qingping, and Ji, Haibo (2018). A Pulse Signal Recovery Method Based on Sparse Representation. J. Beijing Inst. Tech. 27 (96), 5–12.

Google Scholar

Zhang, Z., Xu, Y., and Yang, J. (2017). A Survey of Sparse Representation: Algorithms and Applications. IEEE Access 3, 490–530. doi:10.1109/ACCESS.2015.2430359

CrossRef Full Text | Google Scholar

Zhou, B., An, Y. L., and Chen, C. Z. (2011). Fault Diagnosis for Low-Speed Rolling Bearing Using Stress Wave and Wavelet Analysis. Amr 199-200, 1031–1035. doi:10.4028/www.scientific.net/amr.199-200.1031

CrossRef Full Text | Google Scholar