Day-Ahead Economic Dispatch of AC/DC Hybrid Distribution Network Based on Cell-Distributed Management Mode

Current development trends suggest that future networks will be AC/DC hybrid distribution networks (AC/DC HDNs) operating under the Cell-distributed management mode (CDMM). Cross-Cell transaction in the economic dispatch of CDMM-based distribution networks is necessary to ensure Cell demand, improve the level of renewable energy generation outpower consumption, and enhance the economic efficiency of the whole system. To realize adjacent Cell and cross-Cell transactions in this management mode, this paper proposes a day-ahead economic dispatch model of AC/DC HDNs based on CDMM. The proposed model includes a power transaction stage and a security check stage. In the power transaction stage, a Cell-to-Cell transaction model based on the alternating direction method of multipliers is established. This model forms a consistent transaction plan between different Cells on the basis of information exchange between the Cell operator and the Cell system operator. In the security check phase, a security check model based on data-driven distributionally robust optimization is developed to reduce the transfer power according to various security considerations. Alternate iteration of these two stages enables the day-ahead economic dispatch of AC/DC HDNs based on CDMM for adjacent Cell and cross-Cell transactions. Finally, the effectiveness of the proposed model is verified through a numerical example. The differences among four dispatch models are analyzed to illustrate the need for cross-Cell transactions, and the impact of the confidence level on the dispatch results is discussed.

1 Introduction

According to the International Energy Agency, solar and wind power are predicted to account for 36% of electricity generation by 2050, when it is hoped that the world will have achieved net zero emissions (IEA, 2021). To achieve this goal, the physical form and management model of future distribution networks must fundamentally change. The ELECTRA proposal states that generation will shift from central transmission system connected generation to decentralized distribution system connected generation (D’hulst et al., 2015). With the emergence of renewable energy generations (REGs), DC loads, energy storages (ESs), and electric vehicles, the disadvantages of traditional AC distribution networks for operation and dispatch are becoming increasingly conspicuous (Liu et al., 2019). Future development trends indicate that AC/DC hybrid distribution networks (AC/DC HDNs), which provide flexible power control, will become one of the main physical forms of distribution networks. At the same time, the number of controllable units inside the distribution network is expected to increase sharply as high numbers of REGs and flexible loads are connected to the distribution network. Thus, it will become more difficult for the distribution system operator (DSO) to organize all controllable units centrally inside the distribution network. Dividing the distribution network into multiple Cells with REGs and loads would enable the orderly management of the whole distribution network by means of internal self-governance of Cells and coordination and mutual assistance between Cells (D’hulst et al., 2015; Yu et al., 2015). This represents an important development in the management of future distribution networks. Therefore, it is important to research the economic dispatch of AC/DC HDNs based on the Cell-distributed management mode (CDMM).

There have been few studies on the distributed dispatch and control of distribution networks based on CDMM. The existing literature mostly focuses on aspects such as the operation control system and the power market mechanism, with no further research on the specific dispatch model. In terms of the operation control system, a two-level voltage and four-level frequency control scheme that is applicable to CDMM has been proposed (D’hulst et al., 2015). Regarding the power market mechanism, CDMM requires a new design scheme that allows the resources within each Cell to participate flexibly in power transactions (Martini et al., 2015; Cabiati et al., 2018). Viktorija et al. (Bobinaite et al., 2018) combined several objectives, elements, designs, and evaluation criteria into an economically effective electricity market for CDMM.

The introduction of controllable power electronics such as soft open points (SOPs) and voltage source converters (VSCs) means that the operational control of AC/DC HDNs is significantly different from that of conventional AC distribution networks. As a result, existing AC distribution network scheduling models (Yang and Wu, 2019; Zhang et al., 2019) cannot be directly applied. In terms of the optimal dispatch of AC/DC HDNs, previous studies can be divided into two categories: centralized optimal dispatch (Zhu et al., 2018; Kang et al., 2020) and distributed optimal dispatch (Qi et al., 2018; Gao et al., 2021). For the centralized optimal dispatch model, a two-stage optimal dispatch model for DSOs has been established based on stochastic optimization (SO) theory (Kang et al., 2020), allowing the uncertainty of REG output to be handled by adjusting the transmission power of VSCs and the charging and discharging power of ESs in the second-stage model. The DSO regulates the demand response power, the charging and discharging power of ESs, the transmission power of SOPs, and the output power of controllable distributed generations to achieve the lowest operating cost and the maximum consumption rate of REG output for the whole AC/DC HDN (Zhu et al., 2018). As centralized optimal dispatch requires the DSO to integrate network-wide information (which is contrary to the independent operation of Cells in CDMM), models and methods related to centralized optimal dispatch cannot be applied to CDMM.

For distributed optimal dispatch models, the current research mainly focuses on analytical target cascading (ATC) or the alternating direction method of multipliers (ADMM). ATC divides the whole system into multiple levels of connected subsystems with links between parent- and sub-level subsystems, and no links between subsystems at the same level (Kim et al., 2003). Based on ATC, a three-level structure consisting of a DC subsystem, VSCs, and AC subsystems has been established to achieve distributed dispatch in an AC/DC HDN by adjusting the transmission power between subsystems at different levels (Qi et al., 2018). However, the limitations of the ATC principle mean that power transmission can only be realized between adjacent subsystems, and cross-Cell power transactions are not supported. Based on the decomposition-coordination process, ADMM decomposes a large-scale optimization problem into several small-scale subproblems and achieves global convergence by coordinating the solution process of each subproblem (Boyd et al., 2010). The centralized optimal dispatch model for AC/DC HDNs has been decomposed into optimal dispatch models for the DC and AC subsystems, enabling distributed dispatch between neighboring subsystems by coordinating the VSC transmission power (Gao et al., 2021). Once again, however, this model does not consider cross-Cell transactions. When electricity transaction is only allowed between adjacent Cells, electricity cannot be traded flexibly across the system, which may result in the electricity demand of some Cells not being met and the excess REG of some Cells cannot be fully consumed. The overall system revenue and renewable energy utilization is affected.

The uncertainty of REG output is a key concern in the distribution network dispatch problem, leading to models based on SO and robust optimization (RO) (Fu et al., 2020; Kang et al., 2020). In recent years, distributionally RO (DRO) (Wang et al., 2016), which obtains the optimal decision solution by finding the worst probability distribution under the associated uncertainties, has been increasingly used. DRO offers relatively easy parameter acquisition and does not require the dual problem to be formulated. Data-driven DRO (DDRO) relies only on historical data, and has been widely applied in unit commitment (Ding et al., 2019), expansion planning for transmission systems (Bagheri et al., 2017), reactive power optimization for distribution networks (Ding et al., 2018), and distributed optimal dispatch for AC/DC HDNs (Gao et al., 2021). DDRO forms the basis of the model proposed in this paper.

CDMM can solve the many problems of DSO or CSO directly controlling the controllable units of the whole network by means of intra-Cell autonomy and inter-Cell coordination and mutual assistance. This study considers an AC/DC HDN with high-ratio REG access, and establishes a day-ahead economic dispatch model of the AC/DC HDN based on CDMM (hereafter referred to as the “distributed economic dispatch model”). This model achieves the optimal dispatch of adjacent Cells and cross-Cells. The main contributions of this study are as follows.

1) First, the basic structure of CDMM is explained based on a typical AC/DC HDN, and the rights and obligations of the Cell operator (CO) and the Cell system operator (CSO) are clarified. Definitions of the transaction power and price are then introduced, and inter-relationships between different powers and between different prices are analyzed.

2) The day-ahead economic dispatch model of the AC/DC HDN based on CDMM is proposed. This model contains two parts: the power transaction stage and the security check stage. The power transaction stage consists of an ADMM-based Cell-to-Cell (C2C) transaction model, while the security check phase is formulated upon a DDRO-based security check model for cross-Cell transactions. Through alternate iterations of the two stages, the day-ahead economic dispatch for the AC/DC HDN based on CDMM (hereafter referred to as the “distributed economic dispatch”) supporting adjacent Cell and cross-Cell power transactions is realized.

3) The effectiveness of the proposed model is verified by numerical examples. The differences between the different distributed dispatch model and the centralized dispatch model are analyzed to demonstrate the necessity of cross-Cell transactions, and the impact of the confidence level on the dispatch results is discussed.

2 CDMM for AC/DC HDNs

With the sudden increase in the number of controllable units inside the distribution network, the centralized control of all controllable units inside the distribution network by the DSO faces the following problems (Zheng et al., 2015): 1) the large amount of data from the sudden increase of controllable units inside the distribution network may lead to communication bottlenecks; 2) the large scale of the optimization problem of the DSO leads to expensive computation. To solve these challenges, some research institutions have proposed CDMM.

A Cell is defined as a group of interconnected loads, distributed energy resources, and storage units within well-defined grid boundaries, corresponding to a physical portion of the grid and corresponding to a confined geographical area (D’hulst et al., 2015). Each Cell is autonomous and reciprocates control. The CO is only responsible for the operation and dispatch of the Cell under its jurisdiction. The CSO serves several Cells and is responsible for coordinating the transaction plans between them, as well as the transactions between each Cell and the superior grid. The CSO may be a DSO. During the formation of the day-ahead dispatch plan for the AC/DC HDN, COs make transaction plans with other COs or the superior grid based on their own dispatch models. Based on the transaction plans uploaded by COs, the CSO updates the transaction prices, guidance powers, and other information, and then sends these data to each CO to allow the individual transaction plan to be adjusted, and finally assists each CO in reaching a consistent transaction plan. The CDMM for AC/DC HDNs is shown in Supplementary Figure S1, where the AC and DC Cells are connected through the VSC or SOP.

Compared with the centralized management model, CDMM has the following advantages by means of intra-Cell autonomy and inter-Cell coordination and mutual assistance (Li Jiayong et al., 2021): 1) the control unit inside the Cell only has communication connections with the COs, and only a small amount of information needs to be exchanged between the COs and the CSO, so the communication burden will be greatly relieved; 2) the large-scale optimization problem of the CSO is decomposed into small-scale optimization problems of multiple COs, which reduces the difficulty of centralized processing of large amount of data by the CSO; 3) each CO can make decisions independently according to its own operation rules.

2.1 Cell Operator

The CO has access to all information inside the Cell, and can give control instructions to each underlying regulatory object inside the Cell to ensure the safe operation of the whole Cell. The CO is rational and honest (Day, 1971) and non-strategic (Crespo-Vazquez et al., 2021), and is only aware of information that is relevant to itself.

Based on the supply and demand ratio (SDR) (Liu et al., 2017) of each Cell, the threshold “SDR = 1”is used to distinguish the Cell’s identity as a seller or buyer. The formula for calculating the SDR of Cell-m ($\mathit{SD}{\mathit{R}}_{\mathit{m}}$) is shown in Eq. 1. The notation related to time t is omitted from all equations in this paper to simplify the expressions.

$\mathit{SD}{\mathit{R}}_{\mathit{m}}=\frac{{\displaystyle {\sum }_{\mathit{i}\in {\mathbf{\Omega }}_{\text{m}}^{\text{node}}}{\mathit{P}}_{\mathit{R},\mathit{i}}}}{{\displaystyle {\sum }_{\mathit{i}\mathrm{\in }{\mathbf{\Omega }}_{\mathrm{m}}^{\mathrm{node}}}{\mathit{P}}_{\mathit{L},\mathit{i}}}}(1)$

where ${\mathbf{\Omega }}_{\text{m}}^{\text{node}}$ is the set of nodes inside Cell-m; ${\mathit{P}}_{\mathit{R},\mathit{i}}$ and ${\mathit{P}}_{\mathit{L},\mathit{i}}$ are the REG active output and active load at node-i, respectively.

If the Cell’s SDR ≤1, the Cell is a buyer Cell (BC) whose CO is a buyer Cell operator (BCO). If the Cell’s SDR >1, the Cell is a seller Cell (SC) whose CO is a seller Cell operator (SCO). A Cell may change from BC to SC, or vice versa, at any moment. At any one time, the CO can only make one kind of transaction for buying or selling electricity, and cannot make arbitrage transactions (Baroche et al., 2019). In addition, when there is no direct electrical connection between the BC and the SC involved in a transaction, several third-party Cells (TPCs) are needed to transfer the power; their operators are called TPC operators (TPCOs), and may also be BCOs or SCOs.

2.2 Transaction Powers

The transaction powers involved in the proposed model are the project power, wheeling power, and sanction power. The project power is the power purchased or sold by COs to achieve the Cell’s own supply and demand balance, which should be clearly defined and agreed by both transaction parties. Some project power must be transferred through TPCs, and this is defined as the wheeling power. Considering the power loss during transmission, it is stipulated that the value of the wheeling power for determining the wheeling cost is the average value at the inflow and outflow interface of the TPC. The wheeling power may pose a threat to the operational security of the TPC through which it flows, so the TPCO needs to confirm or reduce the wheeling power flowing through itself and submit the results to the CSO for confirmation. The power confirmed by the CSO is called the sanction power. When the wheeling power is reduced by multiple TPCs, the CSO selects the smallest transaction power after reduction as the sanction power according to the security principle. In the next model iteration, if the wheeling power has been reduced by the TPCO, the newly formed project power should remain the same as the sanction power; otherwise, it should be no less than the sanction power.

As the actual loss of the cross-Cell transaction power transmitted through TPCs is not known when the CO declares the transaction power, in this paper, that transmission loss is estimated in advance based on the predicted loss factor (${\mathit{\beta }}_{\mathit{TPC}}^{\mathit{loss}}$) and is allocated between the BCO and SCO. Let ${\mathit{P}}_{\mathit{mn}-\mathit{r}}$ be the project power of Cell-m trading with Cell-n via route-r. If Cell-m is a SC, then ${\mathit{P}}_{\mathit{mn}-\mathit{r}}$ is positive; otherwise, ${\mathit{P}}_{\mathit{mn}-\mathit{r}}$ is negative. Assuming that Cell-m is a SC and Cell-n is a BC, the transmission power flowing from SC-m (${\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\mathit{T},\mathit{m}}$), the transmission power flowing into BC-n (${\mathit{P}}_{\mathit{nm}-\mathit{r}}^{\mathit{T},\mathit{n}}$), and the estimated wheeling power flowing from TPC-o located along route-r (${\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\mathit{W},\mathit{o}}$) as shown in Eqs 2–4.

${\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\mathit{T},\mathit{m}}={\mathit{P}}_{\mathit{mn}-\mathit{r}}\left(1+{\mathit{N}}_{\mathit{r},\mathit{mn}}^{\mathit{TPC}}{\mathit{\beta }}_{\mathit{TPC}}^{\mathit{loss}}\right)(2)$

${\mathit{P}}_{\mathit{nm}-\mathit{r}}^{\mathit{T},\mathit{n}}=-{\mathit{P}}_{\mathit{nm}-\mathit{r}}(3)$

${\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\mathit{W},\mathit{o}}={\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\mathit{T},\mathit{m}}\left[1-\left({\mathit{N}}_{\mathit{r},\mathit{mo}}^{\mathit{TPC}}+1\right){\mathit{\beta }}_{\mathit{TPC}}^{\mathit{loss}}\right](4)$

where ${\mathit{N}}_{\mathit{r},\mathit{mn}}^{\mathit{TPC}}$ and $N_{\mathit{r},\mathit{mo}}^{\mathit{TPC}}$ are the number of TPCs between Cell-m and Cell-n and between Cell-m and TPC-o on route-r, respectively.

To ensure the power demand within the BC, when the transaction plan is formulated, the transmission power received by the BC is used as the transaction power and all transmission losses are borne entirely by the SC. In Eq. 2, the power provided by SC consists of transaction power and predicted losses. In Eq. 3, the transmission power received by BC does not take into account the transmission loss of the cross-Cell transaction power. When the transaction is concluded for settlement, the BCO and SCO share the power loss according to a certain percentage. That is, the BCO is also required to bear a certain percentage of the transaction loss according to the transaction price agreed by both parties. In the case of a Cell-to-Grid (C2G) transaction, Cells are responsible for the full estimated loss.

2.3 Transaction Prices

The transaction prices involved in the proposed model include the base price, transfer price, and contract price.

The base price is either the C2G base price or the C2C base price, depending on the transaction object. The C2G base price is the purchase price (${\lambda }_{\mathit{G}}^{\mathit{B}}$) and sale price (${\lambda }_{\mathit{G}}^{\mathit{S}}$) of the superior grid. The C2C base price is the purchase price of a BCO. For different SCOs, the base price for both parties varies depending on the supply and demand relationship. Assuming Cell-n is a BC, the initial base price for Cell-n (${\lambda }_{\mathit{mn}-\mathit{r}}^{\mathit{base}}$) to purchase electricity from Cell-m via route-r is

${\lambda }_{\mathit{mn}-\mathit{r}}^{\mathit{base}}=\frac{{\lambda }_{\mathit{G}}^{\mathit{B}}{\lambda }_{\mathit{G}}^{\mathit{S}}}{\left({\lambda }_{\mathit{G}}^{\mathit{S}}-{\lambda }_{\mathit{G}}^{\mathit{B}}\right)\mathit{SD}{\mathit{R}}_{\mathit{n}}+{\lambda }_{\mathit{G}}^{\mathit{B}}}(5)$

where $SD{R}_n$ is the SDR of Cell-n.

During the iterative process of information interaction between the CO and CSO, the CSO updates the base price according to the transaction wishes of both parties in order to reach an agreement. The specific update formula is described in Section 3.2.2.

The transfer price is the price at which TPCs transfer the wheeling power. The formula for calculating the transfer price (${\lambda }_{\mathit{TPC}}$) is

${\lambda }_{TPC}={\beta }_{TPC}^{cost}\left({\lambda }_G^S-{\lambda }_G^B\right)(6)$

where ${\mathit{\beta }}_{\mathit{TPC}}^{\mathit{cost}}$ is the ratio of the transfer price to the difference between ${\lambda }_{\mathit{G}}^{\mathit{S}}$ and ${\lambda }_{\mathit{G}}^{\mathit{B}}$.

The contract price is the final transaction price of the power purchased and sold by COs, and consists of the base price and the transfer price. The contract price of Cell-m trading with Cell-n via route-r (${\lambda }_{mn-r}$) is

${\lambda }_{mn-r}=\{\begin{array}{cc}{\lambda }_{\mathit{mn}-\mathit{r}}^{\mathit{base}}-{\alpha }_{cost}^S{\lambda }_{\mathit{TPC}}{\displaystyle {\sum }_{o=1}^{{\mathit{N}}_{\mathit{r},\mathit{mn}}^{\mathit{TPC}}}{\beta }_{mn-r}^o}& if\mathit{Cell}-\mathit{m}\mathrm{is}\mathrm{a}\mathrm{SC}\\ {\lambda }_{nm-r}^{\mathit{base}}+{\alpha }_{\mathit{cost}}^{\mathit{B}}{\lambda }_{\mathit{TPC}}{\displaystyle {\sum }_{o=1}^{N_{r,mn}^{TPC}}{\beta }_{\mathit{mn}-\mathit{r}}^o}& \mathit{if}\mathit{Cell}-\mathit{m}\mathrm{is}\mathrm{a}\mathrm{BC}\end{array}(7)$

where ${\alpha }_{\mathit{cost}}^{\mathit{S}}$ and ${\alpha }_{\mathit{cost}}^{\mathit{B}}$ are the C2C wheeling cost allocation coefficients of the SC and BC; ${\beta }_{\mathit{mn}-\mathit{r}}^o$ is the absolute value of the ratio of the wheeling power transferred by TPC-o located on route-r to $P_{\mathit{mn}-\mathit{r}}$.

The C2C contract price should be between ${\lambda }_{\mathit{G}}^{\mathit{S}}$ and ${\lambda }_{\mathit{G}}^{\mathit{B}}$ (Jadhav et al., 2019) and be required to ensure the financial balance within the AC/DC HDN (Liu et al., 2017). When ${\lambda }_{\mathit{mn}-\mathit{r}}$ is lower than ${\lambda }_{\mathit{G}}^{\mathit{B}}$ or higher than ${\lambda }_{\mathit{G}}^{\mathit{S}}$, adjusted values of ${\lambda }_{\mathit{mn}-\mathit{r}}$ and ${\lambda }_{\mathit{nm}-\mathit{r}}$ are given by Eqs 8, 9.

${\lambda }_{\mathit{mn}-\mathit{r}}=\{\begin{array}{c}{\lambda }_{\mathit{G}}^{\mathit{S}} \\ {\lambda }_{\mathit{mn}-\mathit{r}}\\ {\lambda }_{\mathit{G}}^{\mathit{B}} \end{array}\begin{array}{c}i\mathit{f}{\lambda }_{\mathit{mn}-\mathit{r}}>{\lambda }_{\mathit{G}}^{\mathit{S}}\\ if{\lambda }_{\mathit{G}}^{\mathit{B}}\le {\lambda }_{\mathit{mn}-\mathit{r}}\le {\lambda }_{\mathit{G}}^{\mathit{S}}\\ \mathit{if}{\lambda }_{\mathit{mn}-\mathit{r}}<{\lambda }_{\mathit{G}}^{\mathit{B}}\end{array}(8)$

${\lambda }_{nm-r}=\{\begin{array}{cc}{\lambda }_{mn-r}+{\lambda }_{TPC}{\displaystyle {\sum }_{o=1}^{N_{r,mn}^{TPC}}{\beta }_{mn-r}^o}& ifCell-m\text{is}\text{a}\text{SC}\\ {\lambda }_{mn-r}-{\lambda }_{TPC}{\displaystyle {\sum }_{o=1}^{N_{r,mn}^{TPC}}{\beta }_{mn-r}^o}& ifCell-m\text{is}\text{a}\text{BC}\end{array}(9)$

The C2G contract price for Cell-m via route-r (${\lambda }_{mG-r}$) is

${\lambda }_{mG-r}=\{\begin{array}{c}\begin{array}{cc}{\lambda }_G^B-{\lambda }_{TPC}{\displaystyle {\sum }_{p=1}^{N_{r,mG}^{TPC}}{\beta }_{mG-r}^p}& ifCell-m\text{is}\text{a}\text{SC}\end{array}\\ \begin{array}{cc}{\lambda }_G^S+{\lambda }_{TPC}{\displaystyle {\sum }_{p=1}^{N_{r,mG}^{TPC}}{\beta }_{mG-r}^p}& ifCell-m\text{is}\text{a}\text{BC}\end{array}\end{array}(10)$

where $N_{r,mG}^{TPC}$ is the number of TPCs between Cell-m and the superior grid on route-r; ${\beta }_{mG-r}^p$ is the absolute value of the ratio of the wheeling power transferred by TPC-p located on route-r to the value of the project power of cell-m transacting with the superior grid via route-r.

3 Day-Ahead Economic Dispatch Model of AC/DC HDN Based on CDMM

The distributed economic dispatch consists of two phases: a power transaction and a security check. The iterative process is shown in Figure 1, whereby the adjacent Cell and cross-Cell transaction plan that satisfies consistency and security is obtained through alternate iterations of the two phases.

FIGURE 1

FIGURE 1. Iterative process of distributed economic dispatch.

In the power transaction phase, the COs formulate their own transaction plans according to the ADMM-based C2C transaction model and submit them to the CSO. The CSO aggregates the transaction plans, and then formulates the guidance power for each trade and sends it to each CO. Finally, a consistent transaction plan is formed through the exchange of information between COs and the CSO. The unmet trading demand is subsequently balanced by trading with the superior grid.

In the security check phase, each TPCO conducts a security check of the transmission power plan through the DDRO-based security check model and reduces any trading that may undermine its own security. The CSO compiles and processes information regarding the transaction plan and sanction power, and sends it to the relevant COs for the next round of power transactions.

3.1 DDRO-Based Cell Optimal Dispatch Model

The DDRO-based Cell optimal dispatch model is established under various operational constraints within the Cell and the uncertainty of REG output. Based on DDRO, several uncertain scenarios are constrained using the L₁-norm and the L_∞-norm (Gao et al., 2021) to obtain the optimal dispatch scheme and the transaction plan with other Cells and the superior grid in the worst probability distribution.

3.1.1 Objective Function

The objective function of the DDRO-based Cell optimal dispatch model is the profit considering the uncertainty of REG output, as shown in Eqs 11–17. According to the two-stage DDRO theory (Gao et al., 2021), in the first stage, the CO forms a dispatch plan so as to achieve the maximum income based on the power transaction revenue, power supply revenue, and demand response cost, without considering the uncertainty of REG output. In the second stage, the REG output and load demand within the Cell are regulated to ensure the safe operation of the Cell based on the REG output in each uncertainty scenario.

$\begin{array}{l}\underset{{\mathit{x}}_{\mathit{m}},{\mathit{y}}_{\mathit{m}}^{\mathrm{0}}}{\mathit{min}}-{\mathit{f}}_{\mathit{m}}^{1-1}-{\mathit{f}}_{\mathit{m}}^{1-2}-{\mathit{f}}_{\mathit{m}}^{1-3}+{\mathit{f}}_{\mathit{m}}^{1-4}+\underset{\mathit{p}{\mathit{r}}_{\mathit{s}}}{\mathit{max}}\underset{{\mathit{y}}_{\mathit{m}}^{\mathit{s}}}{\mathit{min}}{\displaystyle {\sum }_{\mathit{s}\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\mathit{p}{\mathit{r}}_{\mathit{s}}}\left(-{\mathit{f}}_{\mathit{m},\mathit{s}}^{2-1}+{\mathit{f}}_{\mathit{m},\mathit{s}}^{2-2}\right)\hfill \\ over x_m=\left\{x_m^{C2C},x_m^{C2G}\right\}=\left\{{\left({\mathit{P}}_{mn-r}\right)}_{n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}\backslash m,r\mathrm{\in }{\mathbf{\Omega }}_{\mathrm{mG}}^{\mathrm{Rou}}},{\left({\mathit{P}}_{\mathit{mG}-\mathit{r}}\right)}_{\mathit{r}\mathrm{\in }{\mathbf{\Omega }}_{\mathrm{mG}}^{\mathrm{Rou}}}\right\},\hfill \\ {\mathit{y}}_{\mathit{m}}^0={\left\{\Delta {\mathit{P}}_{\mathit{L},\mathit{i}}^0,\Delta {\mathit{P}}_{\mathit{R},\mathit{i}}^0\right\}}_{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}}},y_m^s={\left\{\Delta P_{L,i}^s,\Delta {\mathit{P}}_{\mathit{R},\mathit{i}}^{\mathit{s}}\right\}}_{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}},s\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\hfill \end{array}(11)$

$f_m^{1-1}={\displaystyle \sum _{n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}\backslash m}{\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mG}}^{\text{Rou}}}{\lambda }_{mn-r}}}{P}_{mn-r}(12)$

$f_m^{1-2}={\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mG}}^{\text{Rou}}}{\lambda }_{mG-r}}{P}_{mG-r}(13)$

$f_m^{1-3}={\displaystyle \sum _{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}}}{\lambda }_L}\left(P_{L,i}-\Delta P_{L,i}^0\right)(14)$

$f_m^{1-4}={\displaystyle \sum _{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}}}K1}{\left(\Delta P_{L,i}^0\right)}^2+K2\Delta P_{L,i}^0(15)$

$f_{m,s}^{2-1}={\displaystyle \sum _{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}}}{\lambda }_L}\left(P_{L,i}-\Delta P_{L,i}^s\right)(16)$

$f_{m,s}^{2-2}={\displaystyle \sum _{i\mathrm{\in }{\mathbf{\Omega }}_{\text{m}}^{\text{node}}}K1}{\left(\Delta P_{L,i}^s\right)}^2+K2\Delta P_{L,i}^s(17)$

where ${\mathit{f}}_{\mathit{m}}^{1-1}$ and $f_m^{1-2}$ are the C2C transaction revenue and C2G transaction revenue, respectively; ${\mathit{f}}_{\mathit{m}}^{1-3}$ and $f_m^{1-4}$ are the power supply revenue and demand response cost in the forecast scenario, respectively; ${\mathit{f}}_{\mathit{m},\mathit{s}}^{2-1}$ and ${\mathit{f}}_{\mathit{m},\mathit{s}}^{2-2}$ are the power supply revenue and demand response cost in uncertain scenario-s, respectively; $\mathit{p}{\mathit{r}}_{\mathit{s}}$ is the probability of uncertainty scenario-s; ${\mathbf{\Omega }}_{\text{Sce}}$ is the set of all uncertainty scenarios; ${\mathbf{\Omega }}_{\text{cell}}$ is the set of all Cells; ${\mathbf{\Omega }}_{\mathrm{mn}}^{\mathrm{Rou}}$ and ${\mathbf{\Omega }}_{\mathrm{mG}}^{\mathrm{Rou}}$ are the sets of transmission routes between Cell-m and Cell-n, and between Cell-m and the superior grid, respectively; $\Delta P_{L,i}^0$ and $\Delta {\mathit{P}}_{\mathit{L},\mathit{i}}^{\mathit{s}}$ are the demand response powers of node-i in the forecast scenario and in uncertain scenario-s, respectively; $\Delta {\mathit{P}}_{\mathit{R},\mathit{i}}^0$ and $\mathrm{\Delta }{\mathit{P}}_{\mathit{R},\mathit{i}}^{\mathit{s}}$ are the discarded REG outputs of node-i in the forecast scenario and in uncertain scenario-s, respectively; ${\lambda }_L$ is the customer tariff; and $K1$ and $K2$ are the demand response rates of the users.

3.1.2 Constraints

(1) Transaction power constraints

Because of the uncertainty of REG output, the SDRs of Cell in different scenarios are different. In order to ensure that the electricity demand of the Cell can be satisfied in each scenario, this paper distinguish the identity of seller or buyer of the Cell based on the SDR of the Cell in the scenario with the least uncertain REG output (the worst scenario). If the SDR of the Cell in the worst case scenario is ≤1, the Cell is BC, otherwise the Cell is SC, and the Cell has only one power purchase and sale identity in different scenarios at the same time.

1) Transaction power constraints of the SCO

$\{\begin{array}{c}{\displaystyle \sum _{\mathit{r}\mathrm{\in }{\mathbf{\Omega }}_{\mathrm{mG}}^{\mathrm{Rou}}}{\mathit{P}}_{\mathit{mn}-\mathit{r}}}\le \mathit{N}{\mathit{P}}_{\mathit{n}}^{\mathit{Wor}}\mathit{if}\mathit{SD}{\mathit{R}}_{\mathit{n}}^{\mathit{Wor}}\le 1\\ {\displaystyle \sum _{\mathit{r}\mathrm{\in }{\mathbf{\Omega }}_{\mathrm{mG}}^{\mathrm{Rou}}}{\mathit{P}}_{\mathit{mn}-\mathit{r}}}=0\mathit{else}\end{array}(18)$

where $N{P}_n^{Wor}$ and $SD{R}_n^{Wor}$ are the net load and SDR of Cell-n in the worst-case scenario, respectively.

2) Transaction power constraints of the BCO

$\{\begin{array}{c}{\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mG}}^{\text{Rou}}}{P}_{mn-r}}\ge N{P}_n^{Wor}ifSD{R}_n^{Wor}\mathrm{>}1\\ {\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mG}}^{\text{Rou}}}{P}_{mn-r}}=0else\end{array}(19)$

3) Relationship between the project power and sanction power

$\{\begin{array}{c}\begin{array}{cc}\left|P_{mn-r}\right|\ge \left|P_{mn-r}^{San}\right|& if{I}_{mn-r}=1\end{array}\\ \begin{array}{cc}{P}_{mn-r}=P_{mn-r}^{San}& if{I}_{mn-r}=0\end{array}\end{array}(20)$

$\{\begin{array}{c}\begin{array}{cc}\left|P_{mG-r}\right|\ge \left|P_{mG-r}^{San}\right|& if{I}_{mG-r}=1\end{array}\\ \begin{array}{cc}{P}_{mG-r}=P_{mG-r}^{San}& if{I}_{mG-r}=0\end{array}\end{array}(21)$

where $P_{mn-r}^{San}$ and $P_{mG-r}^{San}$ are the sanction powers of $P_{mn-r}$ and $P_{mG-r}$, respectively; and $I_{mn-r}$ and $I_{mG-r}$ are flag bits to allow changes to $P_{mn-r}$ and $P_{mG-r}$, respectively.

(2) Uncertainty scenario probability constraints

$p{r}_s$ should satisfy the L₁-norm constraint and the L_∞-norm constraint. Let $\mathbf{p}{\mathbf{r}}_{\mathbf{s}}=\left[\begin{array}{cc}\mathit{p}{\mathit{r}}_1,& \mathrm{...}\end{array}\right]$ and $\mathbf{p}{\mathbf{r}}_{\mathbf{s}}^{\mathbf{exp}}=\left[\begin{array}{cc}\mathit{p}{\mathit{r}}_1^{\mathit{exp}},& \mathrm{...}\end{array}\right]$ be the true distribution and the experience distribution of uncertainty scenarios, respectively, where $p{r}_1^{exp}$ is the experience probability of uncertain scenario-1. The feasible domain ($\mathrm{\mathbb{P}}$) of $p{r}_s$ is

$\mathrm{\mathbb{P}}=\left\{\begin{array}{cc}\left\{\mathit{p}{\mathit{r}}_{\mathit{s}}\right\}& |\begin{array}{c}0\mathrm{\le }\mathit{p}{\mathit{r}}_{\mathit{s}}\mathrm{\le }1\mathit{s}\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}\\ {\displaystyle \sum }_{\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\mathit{p}{\mathit{r}}_{\mathit{s}}=1\\ {||\mathbf{p}{\mathbf{r}}_{\mathbf{s}}\mathrm{-}\mathbf{p}{\mathbf{r}}_{\mathbf{s}}^{\mathbf{exp}}||}_1\mathrm{\le }{\mathit{\theta }}_{\mathrm{1}}\\ {||\mathbf{p}{\mathbf{r}}_{\mathbf{s}}\mathrm{-}\mathbf{p}{\mathbf{r}}_{\mathbf{s}}^{\mathbf{exp}}||}_{\mathrm{\infty }}\mathrm{\le }{\mathit{\theta }}_{\mathrm{\infty }}\end{array}\end{array}\right\}(22)$

where ${\theta }_1$ and ${\theta }_{\infty }$ are the allowable deviation limits of $p{r}_s$ when the L₁-norm constraint and the L_∞-norm constraint are satisfied, respectively.

In addition, $\mathbf{p}{\mathbf{r}}_{\mathbf{s}}$ should satisfy the confidence constraints

$\mathrm{Pr}\left\{{||\mathbf{p}{\mathbf{r}}_{\mathbf{s}}\mathrm{-}\mathbf{p}{\mathbf{r}}_{\mathbf{s}}^{\mathbf{exp}}||}_1\mathrm{\le }{\mathit{\theta }}_{\mathrm{1}}\right\}\mathrm{\ge }1\mathrm{-}2{\mathit{N}}_{\mathit{Sce}}{\mathit{e}}^{-\frac{2\mathit{M}{\mathit{\theta }}_1}{{\mathit{N}}_{\mathit{Sce}}}}(23)$

$\mathrm{Pr}\left\{{||\mathbf{p}{\mathbf{r}}_{\mathbf{s}}\mathrm{-}\mathbf{p}{\mathbf{r}}_{\mathbf{s}}^{\mathbf{exp}}||}_{\mathrm{\infty }}\mathrm{\le }{\mathit{\theta }}_{\mathrm{\infty }}\right\}\mathrm{\ge 1-2}{\mathit{N}}_{\mathit{Sce}}{\mathit{e}}^{\mathrm{-2}\mathit{M}{\mathit{\theta }}_{\mathrm{\infty }}}(24)$

where $M$ is the number of original data and $N_{Sce}$ is the number of uncertainty scenarios. Let the right half of the above two equations be ${\gamma }_1$ and ${\gamma }_{\infty }$. By adjusting ${\gamma }_1$ and ${\gamma }_{\infty }$, the fluctuation range of $\mathbf{p}{\mathbf{r}}_{\mathbf{s}}$ can be limited.

(3) Interface transmission power constraint

${\left(P_i^{VSC}\right)}^2+{\left(Q_i^{VSC}\right)}^2\le 2\cdot \frac{S_i^{VSC}}{\sqrt{2}}\cdot \frac{S_i^{VSC}}{\sqrt{2}}(25)$

$P_i^{VSC,DC}=-\left(P_i^{VSC}+\mu \left|P_i^{VSC}\right|\right)(26)$

$P_i^{grid}\le P_{i,max}^{grid}(27)$

where $P_i^{VSC}$ and $Q_i^{VSC}$ are the active and reactive powers injected into the distribution network by the VSC at node-I, respectively; $S_i^{VSC}$ is the capacity of the VSC at node-i; $P_i^{VSC,DC}$ is the DC active power injected into the distribution network by the VSC at node-i; $\mu$ is the transmission loss coefficient of the VSC; and $P_i^{grid}$ and $P_{i,max}^{grid}$ are the active powers injected into the distribution network by the superior grid at node-i and its upper limit value, respectively. Note that both $P_i^{VSC}$ and $P_i^{grid}$ are composed of the transmission power of the sanction power and the project power.

(4) Branch flow constraints subject to cone relaxation

$\begin{array}{cc}{\displaystyle \sum _{h\mathrm{\in }{\mathbf{\Omega }}_{\text{i}}^{\text{FN}}}{P}_{hi}^s}-r_{hi}{i}_{hi}^s=N{P}_i^s+{\displaystyle \sum _{j\mathrm{\in }{\mathbf{\Omega }}_{\text{i}}^{\text{CN}}}{P}_{ij}^s}& 0\le s\le N_{Sce}\end{array}(28)$

${\displaystyle \sum _{h\mathrm{\in }{\mathbf{\Omega }}_{\text{i}}^{\text{FN}}}{Q}_{hi}^s}\begin{array}{cc}-x_{hi}{i}_{hi}^s=N{Q}_i^s+{\displaystyle \sum }_{j\mathrm{\in }{\mathbf{\Omega }}_{\text{i}}^{\text{CN}}}{Q}_{ij}^s& 0\le s\le N_{Sce}\end{array}(29)$

$\begin{array}{cc}{u}_h^s-u_i^s+\left(r_{hi}+x_{hi}\right)i_{hi}^s=2\left(r_{hi}{P}_{hi}^s+x_{hi}{Q}_{hi}^s\right)& 0\le s\le N_{Sce}\end{array}(30)$

$\begin{array}{cc}{||\begin{array}{c}2P_{hi}^s\\ 2Q_{hi}^s\\ i_{hi}^s-u_{hi}^s\end{array}||}_2\le i_{hi}^s+u_h^s& 0\le s\le N_{Sce}\end{array}(31)$

$\begin{array}{cc}N{P}_i^s={\mathit{P}}_{L,i}-\Delta {\mathit{P}}_{L,i}^s-{\mathit{P}}_{R,i}^s+\Delta {\mathit{P}}_{R,i}^s-{\mathit{P}}_i^{VSC}-{\mathit{P}}_i^{grid}& 0\le \mathit{s}\le N_{Sce}\end{array}(32)$

$\begin{array}{cc}N{\mathit{Q}}_i^s={\mathit{Q}}_{L,i}-\Delta {\mathit{Q}}_{L,i}^s-{\mathit{Q}}_{R,i}^s+\Delta {\mathit{Q}}_{R,i}^s-{\mathit{Q}}_i^{VSC}-{\mathit{Q}}_i^{grid}& 0\le s\le N_{Sce}\end{array}(33)$

where ${\mathbf{\Omega }}_{\text{i}}^{\text{FN}}$ and ${\mathbf{\Omega }}_{\text{i}}^{\text{CN}}$ are the sets of parent nodes and child nodes of node-i, respectively; $P_{hi}^s$ , $Q_{hi}^s$ , and $i_{hi}^s$ are the active power, reactive power, and the square of the current of line-hi in scenario-s, respectively, where s = 0 for the forecast scenario; $P_{ij}^s$ and $Q_{ij}^s$ are the active power and reactive power of line-ij in scenario-s, respectively; $r_{hi}$ and $x_{hi}$ are the resistance and reactance of line-hi, respectively; $N{P}_i^s$ and $N{Q}_i^s$ are the net active load and net reactive load at node-i in scenario-s, respectively; $u_h^s$ and $u_i^s$ are the square of the voltage at node-h and node-i in scenario-s, respectively; $Q_{L,i}$ is the reactive active load at node-i; $\Delta Q_{L,i}^s$ is the reactive demand response power at node-i in scenario-s; $P_{R,i}^s$ and $Q_{R,i}^s$ are the REG active and reactive power outputs at node-i in scenario-s, respectively; and $\Delta P_{R,i}^s$ and $\Delta Q_{R,i}^s$ are the discarded REG active and reactive power outputs at node-i in scenario-s, respectively.

For the DC distribution network, the branch flow model under cone relaxation is still applicable when the reactive power inside the network is not considered (Wu et al., 2020). Hence, the branch flow model for the DC distribution network is not repeated here.

(5) Security constraints

$\begin{array}{cc}{\left(U_{min}\right)}^2\le u_i^s\le {\left(U_{max}\right)}^2& 0\le s\le N_{Sce}\end{array}(34)$

$\begin{array}{cc}0\le i_{hi}^s\le {\left(I_{max}\right)}^2& 0\le s\le N_{Sce}\end{array}(35)$

where $U_{min}$ and $U_{max}$ are the upper and lower limits of the bus voltage, respectively; and $I_{max}$ is the upper limit of the line current.

(6) Demand response power constraints and REG outpower constraints

$\begin{array}{cc}\Delta P_{L,i}^s\le P_{L,i}^s& 0\le s\le N_{Sce}\end{array}(36)$

$\begin{array}{cc}\Delta Q_{L,i}^s=\Delta P_{L,i}^s\mathit{tan}{\phi }_{L.i}& 0\le s\le N_{Sce}\end{array}(37)$

$\begin{array}{cc}\Delta P_{R,i}^s\le P_{R,i}^s& 0\le s\le N_{Sce}\end{array}(38)$

$\begin{array}{cc}\Delta Q_{R,i}^s=\Delta P_{R,i}^s\mathit{tan}{\phi }_{R.i}& 0\le s\le N_{Sce}\end{array}(39)$

where ${\phi }_{L.i}$ and ${\phi }_{R.i}$ are the power factor angles of the load and REG at node-i, respectively.

3.2 ADMM-Based C2C Transaction Model

In the DDRO-based Cell optimal dispatch model described in Section 3.1, none of the COs considers the transaction willingness of other COs, making it difficult for both parties involved in the transaction to reach agreement. Thus, based on the DDRO-based Cell optimal dispatch model, we propose an ADMM-based C2C transaction model according to CDMM.

In this section, we first establish a multi-Cell centralized economic dispatch model according to the DDRO-based Cell optimal dispatch model. This is then decoupled into an ADMM-based C2C transaction model based on the C2C transaction coupling constraint, enabling a consistent transaction plan to be reached between Cells in CDMM.

3.2.1 Multi-Cell Centralized Economic Dispatch Model

The objective function of the multi-Cell centralized economic dispatch model is shown in Eq. 40. The CSO maximizes the network-wide benefit by adjusting the controllable devices inside the Cell, such as the transmission power of VSCs, the demand response load power, and the discarded REG output in different scenarios.

$\begin{array}{l}\underset{P^{VSC},y^0}{min}{\displaystyle \sum _{m\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}}{\displaystyle \sum _{n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}\backslash m}{\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mn}}^{\text{Rou}}}-f_m^{1-1}-f_m^{1-3}+f_m^{1-4}}}}\hfill \\ +\underset{p{r}_s}{max}\underset{y^s}{min}{\displaystyle \sum _{s\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}p{r}_s}\left(-f_{m,s}^{2-1}+f_{m,s}^{2-2}\right)\hfill \end{array}(40)$

The multi-Cell centralized economic dispatch model satisfies the constraints in Eqs 2, 3, Eqs 7–10, Eqs 18–20, Eqs 22–39.

In the multi-Cell centralized economic dispatch model, the CSO directly controls the regulation units within each Cell. However, this does not meet the requirements of CDMM.

3.2.2 ADMM-Based C2C Transaction Model

In order to build the ADMM-based C2C transaction model, this paper decouples the multi-Cell centralized economic scheduling model with the C2C transaction power of Cells ($x_m^{C2C}$) as the decoupling parameter. The C2C transaction coupling constraint is introduced as shown in Eq. 41. Note that the base price of C2C transactions is the Lagrange multiplier of Eq. 41.

$\begin{array}{cc}{P}_{mn-r}+P_{nm-r}=0& \forall m,n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}} \forall r\mathrm{\in }{\mathbf{\Omega }}_{\text{mn}}^{\text{Rou}}\end{array}(41)$

The optimization variables of decoupled economic scheduling model are $x_m^{C2C}$, $y_m^0$, and $y_m^s$ of each Cell. The decoupled economic scheduling model has a multi-block structure. However, multi-block ADMM is not guaranteed to converge when solving convex problems. Thus, the guidance power ($z={\left\{{\left(P_{mn-r}^{\ast }\right)}_{n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}\backslash m,r\mathrm{\in }{\mathbf{\Omega }}_{\text{mn}}^{\text{Rou}}}\right\}}_{m\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}}$) is introduced to transform the decoupled economic scheduling model into a two-block structure, the convergence of which has been proved (Boyd et al., 2010). The first block of variables is $x_m^{C2C}$, $y_m^0$, and $y_m^s$ of each Cell, and the second block of variables is the guidance power. By alternately updating the two blocks of variables, the transaction plans between Cells finally reach agreement.

At the kth C2C transaction iteration, the formula for $P_{\mathit{mn}-\mathit{r}}^{\ast ,\left(k\right)}$ is as shown in Eq. 42 (Li Peng et al., 2021). With the introduction of ${\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\ast ,\left(\mathit{k}\right)}$, Eq. 41 is transformed into Eq. 43.

${\mathit{P}}_{mn-r}^{\ast ,\left(k\right)}=\frac{{\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\left(k\right)}-{\mathit{P}}_{\mathit{nm}-\mathit{r}}^{\left(k\right)}}{2}(42)$

$\begin{array}{cc}\{\begin{array}{c}{\mathit{P}}_{mn-r}^{\ast ,\left(k\right)}+{\mathit{P}}_{nm-r}^{\ast ,\left(k\right)}=0\\ {\mathit{P}}_{mn-r}^{\left(k\right)}={\mathit{P}}_{mn-r}^{\ast ,\left(k\right)}\end{array}& \forall \mathit{m},\mathit{n}\mathrm{\in }{\mathit{\Omega }}_{\mathit{Cell}}\forall \mathit{r}\mathrm{\in }{\mathit{\Omega }}_{\mathit{mn}}^{\mathit{rou}}\end{array}(43)$

Through the above transformations, the ADMM-based C2C transaction model is formed as follows. In which, the objective function is shown in Eq. 44 and the constraints are the same as the multi-Cell centralized economic dispatch model.

$\begin{array}{l}\underset{x_m^{C2C,(k)},y_m^{0,(k)}}{min}-{\mathit{f}}_{\mathit{m}}^{1-1,(k)}-{\mathit{f}}_{\mathit{m}}^{1-3,(k)}+{\mathit{f}}_{\mathit{m}}^{1-4,(\mathit{k})}\hfill \\ +{\displaystyle \sum _{n\mathrm{\in }{\mathbf{\Omega }}_{\text{cell}}\backslash m}{\displaystyle \sum _{r\mathrm{\in }{\mathbf{\Omega }}_{\text{mn}}^{\text{Rou}}}\left[{\lambda }_{\mathit{mn}\mathrm{-}\mathit{r}}^{base,\left(k-1\right)}\left({\mathit{P}}_{\mathit{mn}\mathrm{-}\mathit{r}}^{\ast ,\left(k-1\right)}-{\mathit{P}}_{\mathit{mn}\mathrm{-}\mathit{r}}^{\left(k\right)}\right)+\frac{{\mathit{\rho }}^{\left(k-1\right)}}{2}||{\mathit{P}}_{\mathit{mn}\mathrm{-}\mathit{r}}^{\ast ,\left(k-1\right)}-{\mathit{P}}_{\mathit{mn}\mathrm{-}\mathit{r}}^{\left(k\right)}||\begin{array}{c}2\\ 2\end{array}\right]}}\hfill \\ +\underset{p{r}_s^{\left(k\right)}}{max}\underset{y_m^{s,(k)}}{min}{\displaystyle \sum _{s\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\mathit{P}{r}_s^{\left(k\right)}}\left(-{\mathit{f}}_{m,s}^{2-1,(k)}+f_{\mathit{m},\mathit{s}}^{2-2,(k)}\right)\hfill \end{array}(44)$

where ${\rho }^{(k-1)}$ is the penalty parameter.

Because Eq. 44 has a min-max-min structure, the column-and-constraint generation algorithm is used to determine the solution. Due to space limitations, we do not expand the description here and details can be found in literature (Ding et al., 2018).

After receiving the transaction plans uploaded by the COs, the CSO calculates $P_{mn-r}^{\ast ,\left(k\right)}$ based on Eq. 43, and determines whether the transaction plans between Cells are consistent. Let ${\mathbf{r}}^{\left(\mathit{k}\right)}=\left[\begin{array}{cc}{\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\left(\mathit{k}\right)}-{\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\ast ,\left(\mathit{k}\right)},& \cdots \end{array}\right]$ and ${\mathbf{s}}^{\left(k\right)}=\left[\begin{array}{cc}{\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\ast ,\left(k\right)}-{\mathit{P}}_{\mathit{mn}-\mathit{r}}^{\ast ,\left(\mathit{k}-1\right)},& \cdots \end{array}\right]$ be the primal and dual residuals, respectively. The judgment criterion for reaching agreement on the transaction power between Cells is

$\mathit{max}(||{\mathbf{r}}^{\left(\mathit{k}\right)}{||}_{\mathrm{2}},||{\mathbf{s}}^{\left(\mathit{k}\right)}{||}_{\mathrm{2}})\mathrm{<}{\mathit{\epsilon }}_{\mathit{ADMM}}(45)$

If the residuals satisfy this criterion, the C2C transaction is closed; otherwise, the CSO needs to update the base price, contract price, and penalty parameters. The update formulas for the base price and penalty parameters are given by Eqs 46, 47.

${\lambda }_{mn-r}^{base,\left(k\right)}={\lambda }_{mn-r}^{base,\left(k-1\right)}+\varphi \left(P_{mn-r}^{\ast ,(k)}-P_{mn-r}^{\left(k\right)}\right)={\lambda }_{mn-r}^{base,\left(k-1\right)}-\frac{\varphi }{2}\left(P_{mn-r}^{\left(k\right)}+P_{nm-r}^{\left(k\right)}\right)(46)$

${\rho }^{\left(k\right)}=\{\begin{array}{c}{\rho }^{\left(k-1\right)}{\kappa }_{2}if {\kappa }_1{||{\mathit{s}}^{\left(k\right)}||}_2<{||{\mathit{r}}^{\left(k\right)}||}_{2}andk<k_{max}\\ \frac{{\rho }^{\left(k-1\right)}}{{\kappa }_2}if {\kappa }_1{||{\mathit{r}}^{\left(k\right)}||}_2<{||{\mathit{s}}^{\left(k\right)}||}_{2}andk<k_{max}\\ {\rho }^{\left(k-1\right)}otherwise\end{array}(47)$

where $\varphi$ is the price update coefficient; ${\kappa }_1$ is the ratio coefficient of ${\mathit{s}}^{\left(k\right)}$ to ${\mathit{r}}^{\left(k\right)}$ ; ${\kappa }_2$ is the change multiplier of the penalty parameter; and $k_{max}$ is the maximum number of iterations of C2C transactions.

The COs and the CSO eventually reach a consistent transaction plan through the iteration of information exchange. Each CO develops an initial transaction plan without considering the Lagrange penalty term in the objective function of the C2C transaction model.

3.3 DDRO-Based Security Check Model

As the transmission of cross-Cell transaction power can compromise the internal security of the TPC, this paper proposes a DDRO-based security check model that considers various operational constraints within the TPC and the uncertainty of REG power output. The TPCO determines the reduction plan for the transfer power by considering the wheeling revenue, power supply revenue, and demand response cost.

The objective of the DDRO-based security check is to achieve the maximum profit considering the uncertainty of REG output. The TPCO determines the reduction of wheeling powers based on the wheeling revenue, power supply revenue, and demand response cost in the first stage. The safe operation of the Cell is then achieved in the second stage by the TPCO adjusting the REG output and load demand within the Cell according to the REG output in each uncertain scenario. The objective function is given by Eqs 48–53.

$\begin{array}{l}\underset{x_u,y_u^0}{min}-f_u^{1-1}-f_u^{1-2}+f_u^{1-3}+\underset{p{r}_s}{max}\underset{y_u^s}{min}{\displaystyle \sum _{\mathit{s}\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\mathit{p}{\mathit{r}}_{\mathit{s}}}\left(-{\mathit{f}}_{\mathit{u},\mathit{s}}^{2-1}+{\mathit{f}}_{\mathit{u},\mathit{s}}^{2-2}\right)\hfill \\ over x_u={\left\{\Delta P_v^{W,u}\right\}}_{v\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{W}}},y_u^0={\left\{\Delta P_{L,l}^0,\Delta P_{R,l}^0\right\}}_{l\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}}},y_u^s={\left\{\Delta P_{\mathit{L},\mathit{l}}^{\mathit{s}},\Delta {\mathit{P}}_{\mathit{R},\mathit{l}}^{\mathit{s}}\right\}}_{l\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}},s\mathrm{\in }{\mathbf{\Omega }}_{\text{Sce}}}\hfill \end{array}(48)$

${\mathit{f}}_{\mathit{u}}^{1-1}={\displaystyle \sum _{\mathit{v}\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{W}}}{\mathit{\lambda }}_{\mathit{TPC}}}\left({\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}-\mathrm{\Delta }{\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}\right)(49)$

$f_u^{1-2}={\displaystyle \sum _{l\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}}}{\lambda }_L}\left(P_{L,l}-\mathrm{\Delta }{P}_{L,l}^0\right)(50)$

$f_u^{1-3}={\displaystyle \sum _{l\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}}}K1}{\left(\mathrm{\Delta }{\mathit{P}}_{L,l}^0\right)}^2+K2\mathrm{\Delta }{\mathit{P}}_{L,l}^0(51)$

$f_{u,s}^{2-1}={\displaystyle \sum _{\mathit{l}\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}}}{\mathit{\lambda }}_{\mathit{L}}}\left({\mathit{P}}_{\mathit{L},\mathit{l}}-\mathrm{\Delta }{\mathit{P}}_{\mathit{L},\mathit{l}}^{\mathit{s}}\right)(52)$

$f_{u,s}^{2-2}={\displaystyle \sum _{l\mathrm{\in }{\mathbf{\Omega }}_{\text{u}}^{\text{node}}}\mathit{K}1}{\left(\mathrm{\Delta }{P}_{\mathit{L},\mathit{l}}^{\mathit{s}}\right)}^2+\mathit{K}2\mathrm{\Delta }{\mathit{P}}_{\mathit{L},\mathit{l}}^{\mathit{s}}(53)$

where $f_u^{1-1}$ is the wheeling revenue; $f_u^{1-2}$ and $f_u^{1-3}$ are the power supply revenue and demand response cost in the forecast scenario, respectively; $f_{u,s}^{2-1}$ and $f_{u,s}^{2-2}$ are the power supply revenue and demand response cost in uncertain scenario-s, respectively; ${\mathbf{\Omega }}_{\text{u}}^{\text{W}}$ is the set of wheeling powers flowing through TPC-u; ${\mathbf{\Omega }}_{\text{u}}^{\text{node}}$ is the set of nodes of TPC-u; ${\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}$ and $\Delta {\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}$ are wheeling power-v and its reduced power, respectively; $P_{L,l}$ is the active load at node-l; and $\mathrm{\Delta }{\mathit{P}}_{\mathit{L},\mathit{l}}^0$ and $\mathrm{\Delta }{\mathit{P}}_{\mathit{L},\mathit{l}}^{\mathit{s}}$ are the demand response power of node-l in the forecast scenario and in uncertain scenario-s, respectively.

In addition to the constraints shown in Eqs 22–39, the transaction power of each TPCO in the safety calibration phase is kept constant, the wheeling power constraints specific to the DDRO-based security check model are as follows:

$\{\begin{array}{cc}\begin{array}{c}{\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}-\Delta {\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}\ge {\mathit{P}}_{\mathit{v}}^{\mathit{s},\mathit{u}}\\ \Delta {\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}=0 \end{array}& \begin{array}{c}\mathit{if}{\mathit{I}}_{\mathit{v}}^{\mathit{W},\mathit{u}}=1\\ \mathit{if}{\mathit{I}}_{\mathit{v}}^{\mathit{W},\mathit{u}}=0\end{array}\end{array}(54)$

where $P_v^{S,u}$ is the sanction power of $P_v^{W,u}$ and $I_v^{W,u}$ is a flag bit permitting changes to ${\mathit{P}}_{\mathit{v}}^{\mathit{W},\mathit{u}}$ .

After completing the security check, the TPCO uploads the reduction plan to the CSO. If all cross-Cell transaction plans are not reduced, the whole distributed economic dispatch ends. Otherwise, the CSO updates the sanction power and tradable route information and sends it to each CO, and the distributed economic dispatch enters the next round of the power transaction stage.

3.4 Process of Day-Ahead Economic Dispatch Model of AC/DC HDN Based on CDMM

The specific steps of the whole economic dispatch model are described below. The process is illustrated in Supplementary Figure S2.

Step 1: COs upload the transaction identity and demands to the CSO, and BCOs send base price to the CSO.

Step 2: The CSO informs each CO of the tradable route, transaction price, sanction power, saleable power of each SCO, and shortage power of each BCO.

Step 3: Each CO develops one transaction plan according to the ADMM-based C2C transaction model and uploads it to the CSO.

Step 4: The CSO updates the guidance power and determines whether the transaction plans between Cells are in agreement. If there is agreement, skip to step 6; otherwise, proceed to step 5.

Step 5: The CSO updates the transaction prices and penalty parameters, and sends auxiliary information to each CO. Return to step 3.

Step 6: COs that still have transaction demand make the C2G transaction and upload the transaction plan to the CSO.

Step 7: The CSO informs each TPCO of the wheeling power flowing at each interface of the TPC under its jurisdiction and the corresponding sanction power.

Step 8: The TPCO performs a security check based on the DDRO-based security check model and uploads the reduction plan to the CSO.

Step 9: If all CO’s cross-Cell transaction powers are not being cut, i.e., there is no reduced transaction plan, end economic dispatch; otherwise, proceed to step 10.

Step 10: The CSO updates the sanction power and the tradable route information. Return to step 2.

4 Case Study

The numerical example considered in this section has been modified from the IEEE-123 node system (Li et al., 2017). The system topology is shown in Supplementary Figure S3. The voltage level of the AC Cells is 10 kV and that of the DC Cells is ±10 kV. The line parameters have been reported in the literature (Li et al., 2017). The capacity and $\mu$ value of each VSC are 3 MW and 2% (Ahmed et al., 2018), respectively. The control mode of VSC-1, VSC-5, and VSC-6 is U_dcQ control, and the control mode of the remaining VSCs is PQ control. The maximum predicted load of the system is 19 MW, and load prediction curves of the Cells are shown in Supplementary Figure S4A (Dang et al., 2018). The total installed REG capacity is 18 MW, and the distribution ratio of REG capacity in each Cell is 25%:15%:15%:15%:20%:10%. The predicted wind turbine (WT) and photovoltaic (PV) outputs are shown in Supplementary Figure S4B. ${\lambda }_L$ , ${\lambda }_G^S$ , and ${\lambda }_G^B$ are shown in Supplementary Figure S5 (Dang et al., 2018).

According to DDRO, a normal distribution model with predicted WT and PV output values as the expected values and a variance of 0.2 times the expected value is established to generate 1,000 sets of REG output data. Four uncertainty scenarios are then obtained using K-means clustering. Supplementary Figures S6A,B show the net power (load minus generation) and SDR of each cell under the worst-case scenario, respectively. Other numerical parameters are listed in Table 1, where $N_B$ is the number of nodes in the entire AC/DC HDN.

TABLE 1

TABLE 1. Results of distributed economic dispatch.

4.1 Analysis of Distributed Economic Dispatch Results

The benefits of each Cell are presented in Table 1. The net electricity consumption in Table 1 is the difference between the forecast electricity consumption of the load for the whole day and the forecast REG for the whole day.

The following conclusions can be drawn from Table 1.

1) The total revenue of the Cell is mainly determined by the load supply revenue and transaction revenue. Because ${\lambda }_L$ , $K1$ , and $K2$ are the same for all Cells, the load supply revenue subtracted from the demand response cost of each Cell is proportional to the Cell’s load electricity consumption. The transaction revenue of each Cell is inversely proportional to the Cell’s net electricity consumption. A larger net electricity consumption means that more electricity needs to be purchased from SCs or the superior grid, which translates to higher transaction fees being paid by the Cell. Conversely, if the net electricity consumption is positive, a transaction revenue can be gained by the Cell.

2) Except for Cell-6, remaining Cells have multiple connections to different Cells or the superior grid. Therefore, the remaining Cells act as TPCs to obtain the wheeling revenue by transferring wheeling power. Because ${\beta }_{TPC}^{cost}$ is 5%, the transfer price is low, and the wheeling revenue of each Cell is small and has no significant impact on the Cell’s total revenue.

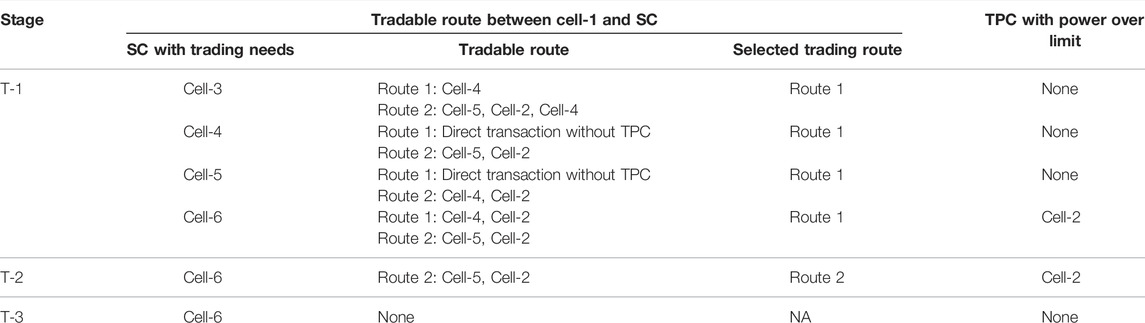
The results of the all-day economic dispatch are influenced by various factors such as the load consumption and REG situation at different moments, the transmission capacity limitation of the trading route, and so on. Without loss of generality, we first take the transaction plan of Cell-1 at 12:00 as an example to illustrate the whole process of distributed economic dispatch. The stages of distributed economic dispatch are referenced as “X-n,” such as “T-1” and “S-1” for the first set of power transaction and security check stages, respectively. To facilitate comparison between the initial transaction plan and the adjusted transaction plan, “T-0” is used to indicate the initial transaction plan.

The absolute values of the transaction power of Cell-1 and the primal residual of the transaction power at the end of each stage of distributed economic dispatch at 12:00 are given in Figure 2; Table 2, respectively. Table 3 presents the trading route information of Cell-1 at each stage of distributed economic dispatch. The following conclusions can be drawn from Figure 2; Tables 2, 3.

1) When each CO makes a transaction plan based on its own economic optimum in stage T-0, it is difficult for both trading parties to agree on the transaction plan, resulting in a large primal residual.

2) In stage T-1, according to the ADMM-based C2C transaction model, the primal residual meets the agreement criterion for the C2C transaction, and both trading parties agree on the transaction power. The specific C2C transaction adjustment process is described later in this paper.

3) During stage S-1, the CSO informs the TPCO of the wheeling power at each interface of the TPC under its jurisdiction and the security check is performed. After the security check, the transaction power between Cell-1 and Cell-6 causes the line current in Cell-2 to cross the limit. Thus, transaction powers $P_{16-1}$ and $P_{61-1}$ are slashed to zero by cell-2.

4) In stage T-2, although more power can be transmitted by the trading route between Cell-1, Cell-3, Cell-4, and Cell-5, there is no trading demand from Cell-3, Cell-4, or Cell-5. Thus, Cell-1 is unable to purchase more power from them and can only trade through a secondary route between Cell-1 and Cell-6. This transaction plan also fails the security check in stage S-2 and is cancelled due to the impact on the security of cell-2.

5) In stage T-3, Cell-1 and the other Cells cannot trade with each other, meaning that Cell-1 can only purchase power from the superior grid to meet its own load demand.

FIGURE 2

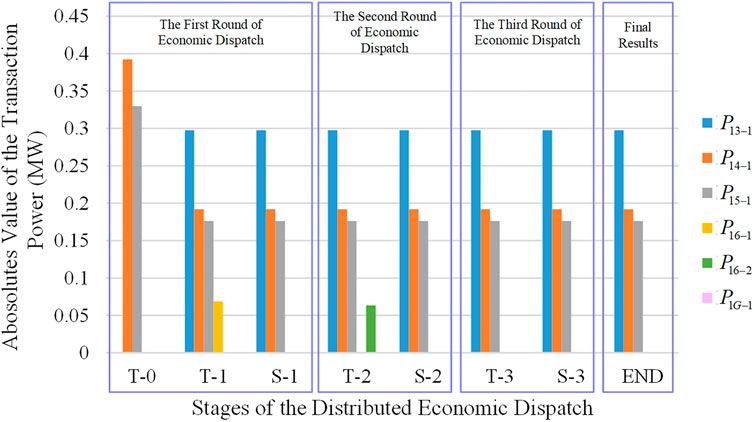
FIGURE 2. Absolute values of the transaction power of Cell-1 at the end of each stage of distributed economic dispatch.

TABLE 2

TABLE 2. Primal residuals of transaction power at the end of each stage of distributed economic dispatch.

TABLE 3

TABLE 3. Trading route information of cell-1 at each stage of distributed economic dispatch.

The following is an example of the first round of the C2C transaction and the security check at 12:00. This example illustrates the process of transaction plan adjustment and power reduction in detail.

(1) Analysis of C2C transaction

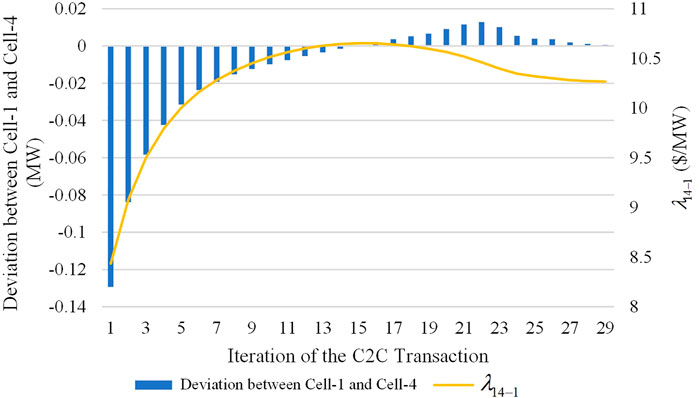
The iterative processes of the transaction plan between Cell-1 and Cell-4 are taken as examples. Figures 3A,B show the variation process of the transaction powers and guidance powers of Cell-1 and Cell-4. Figure 4 illustrate the variation process in the deviation of the transaction plan between Cell-1 and Cell-4, where a positive deviation indicates that the trading willingness of the SC is higher than that of the BC, and vice versa; ${\lambda }_{14-1}$ is also shown in these figures. As can be seen from Figures 3, 4:

1) When there is a deviation between the BC and the SC, the CSO first adjusts the guidance power based on the transaction power of the BC and the SC, and then each CO adjusts its own transaction power to gradually approach the guidance power. Finally, when the residuals meet the agreement criterion, the transaction plans of the BC and SC are in agreement.

2) In the early stages of the C2C process, $\left|P_{14-1}\right|$ > $\left|P_{41-1}\right|$ indicates that the willingness of Cell-1 to purchase power is greater than the willingness of Cell-4 to sell power, leading to a gradual increase in ${\lambda }_{14-1}$ . After 16 iterations, $\left|P_{14-1}\right|$ < $\left|P_{41-1}\right|$ and ${\lambda }_{14-1}$ starts to decrease.

(2) Analysis of security check

FIGURE 3

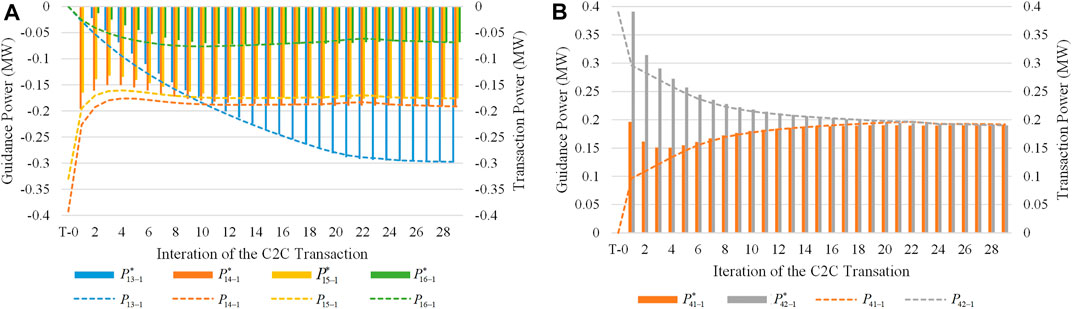
FIGURE 3. (A) Variation process of transaction power and guidance power of Cell-1. (B) Variation process of transaction power and guidance power of Cell-4.

FIGURE 4

FIGURE 4. Variation process of the deviation of the transaction plan and ${\lambda }_{14-1}$ .

After stage T-1, Cell-2 validates the transaction power between Cell-1 and Cell-6 for transfer by Cell-2 in various uncertainty scenarios, and finally determines that this transaction plan should be cut based on the worst-case scenario. Figure 5 shows the demand response and abandonment output of REG for Cell-2 under the original wheeling power and reduced wheeling power conditions.

FIGURE 5

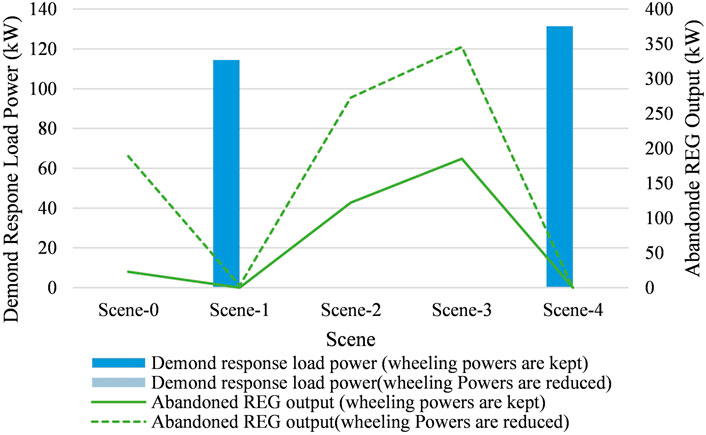
FIGURE 5. Demand response and abandonment output of REG for Cell-2 under original wheeling power and reduced wheeling power conditions.

Cell-2 undertakes the power transfer plan for transactions between Cell-1 and Cell-6, but the actual transmission loss of Cell-2 is higher than the predicted transmission loss of the wheeling power. Thus, as can be seen from Figure 5, Cell-2 needs to reduce its load by 131 kW through demand response if the wheeling power is to remain constant in the worst-case scenario. According to the DDRO-based security check model, Cell-2 slashes the transaction plan between Cell-1 and Cell-6 to zero. As can be seen from Figure 2, after the power reduction, the transmission of $P_{16-1}$ will no longer pose a threat to the security of Cell-2.

4.2 Comparison of Centralized Economic Dispatch and Distributed Economic Dispatch

In this section, the following four dispatch models are set up to illustrate the characteristics of distributed economic dispatch and the necessity of cross-Cell transaction by analyzing each revenue and transaction plan under different scheduling models.

Case-1: centralized economic dispatch model

Case-2: distributed economic dispatch model only supporting transactions between adjacent Cells and not allowing arbitrage

Case-3: distributed economic dispatch model supporting transactions between adjacent Cells and arbitrage

Case-4: distributed economic dispatch model proposed in this paper

According to the arithmetic structure shown in Figure 3 in Supplementary Material, in Case-2, DC Cell (Cell-4, Cell-5, Cell-6) can only trade with adjacent AC Cell, and AC Cell can only trade with adjacent DC Cell and superior grid, and the rest conditions are kept the same as Case-4.

In Case-3, a distributed dispatch model that allows arbitrage is constructed based on the literature (Gao et al., 2021), and the specific dispatch model is shown in Appendix. Because arbitrage transactions are allowed, the identity of seller or buyer of each Cell is no longer distinguished, and each Cell can carry out purchase and sale behaviors simultaneously.

For comparison, this paper assumes that in Case-1, the transaction revenue of each Cell is accounted for based on the load ratio of each Cell. the total all-day revenue of AC/DC HDN of the four dispatch models is shown in Table 4. The breakdown of all-day revenue for each Cell is shown in Figure 6, where the LSRMDRC is load supply revenue minus demand response cost. Since the wheeling revenue exists only in Case-4 and the value is small, it is not shown in Figure 6.

TABLE 4

TABLE 4. All-day revenue of AC/DC HDN under the four dispatch models

FIGURE 6

FIGURE 6. The breakdown of all-day revenue for each Cell.

As can be seen from Table 4, the difference between the all-day revenue of Case-1, Case-3, and Case-4 is smaller, with Case-4’s revenue being closer to Case-1. Case-2’s all-day revenue decrease significantly compared to the three dispatch models mentioned above. As can be seen from Figure 6, the all-day revenue gap of Case-1, Case-3, and Case-4 is mainly caused by the difference in transaction revenue; the plunge in revenue of Case-2 is mainly due to the reduction in LSMRDC of Cell-4, Cell-5, and Cell-6.

The following is a comparative analysis of the causes of revenue differences of different dispatch models.

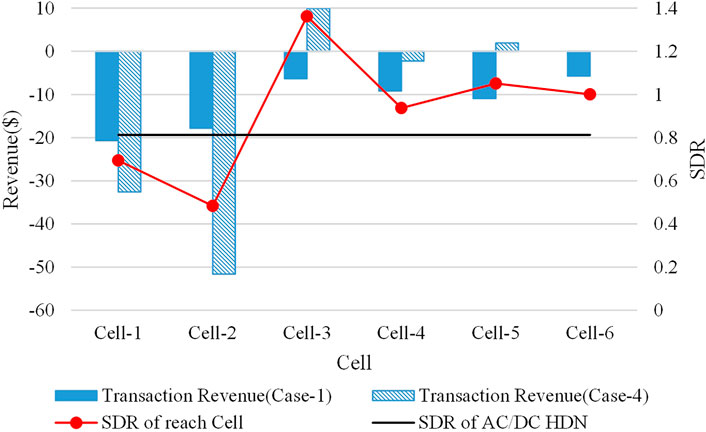
(1) Comparative analysis of dispatch results of Case-1 and Case-4.

Through further analysis, the difference in revenue of the two dispatch models is mainly affected by the SDR of each Cell.

If the SDR of a Cell is higher than the average SDR of the whole AC/DC HDN at a certain moment, that Cell will obtain more revenue in Case-4. In contrast, the revenue of that Cell will decrease in Case-4 if its SDR is lower than the average. Without loss of generality, the following is an example of the transaction revenue of each Cell at the 10:00 moment. Figure 7 shows the transaction revenue of each Cell at 10:00 in Case-1and Case-4.

1) In Case-1, because the average SDR of the whole AC/DC HDN is less than 1, the CSO needs to purchase power from the superior grid to ensure the power supply for the load of the whole system. The purchase fee is apportioned to each Cell, causing each Cell have negative transaction revenues.

2) In Case-4, because Cell-3, Cell-5 have SDRs greater than 1, positive transaction revenues can be obtained through C2C or C2G transactions. Cell-6’s SDR is approximated at 1 and the transaction revenue is approximated at 0. Because the SDR of Cell-4 is higher than the average SDR of the AC/DC HDN at that moment, the purchase fee in Case-4 is lower than in Case-4. The SDRs of Cell-1 and Cell-2 are lower than the average SDR of the AC/DC HDN at that time, so the purchase fee is higher than in Case-4.

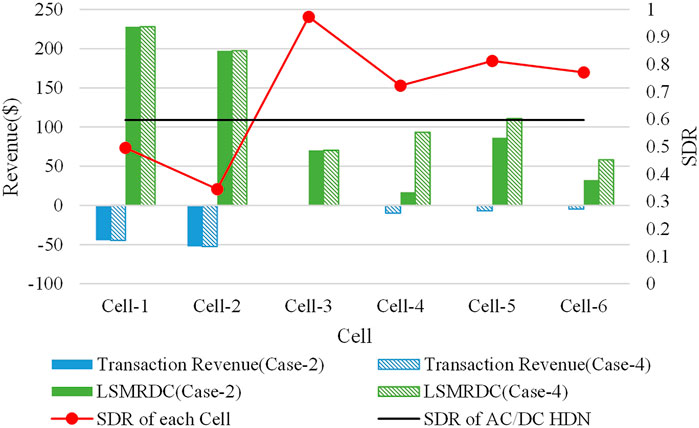
(2) Comparative analysis of dispatch results of Case-2 and Case-4

FIGURE 7

FIGURE 7. Transaction revenue of each Cell at 10:00 in Case-1and Case-4.

In Case-2, each Cell can only trade with adjacent Cells, and arbitrage transaction by Cells is not allowed. At this time, the Cell without direct physical connection to the superior grid may have insufficient power to be sold by adjacent Cells, resulting in internal load shedding, and causing a decrease in revenue of the whole system.

In the following, the LSMRDCs for each Cell at the 15:00 moment is illustrated as an example. Figure 8 gives the SDR, transaction revenue, and LSMRDC for each Cell at the 15:00 moment.

FIGURE 8

FIGURE 8. SDR, transaction revenue, and LSMRDC for each Cell at the 15:00.

As can be seen from Figure 8, at 15:00, the SDR of all Cells are less than 1, and all Cells need to purchase power to ensure internal power demand. Cell-4, Cell-5, and Cell-6, which are not directly connected to the superior grid, cannot purchase power through the adjacent Cells and can only shed part of the load to ensure the safe operation of the Cells, resulting in a sudden reduction of their revenue.

(3) Comparative analysis of dispatch results of Case-3 and Case-4

In Case-3, although each Cell can only trade with adjacent Cells, cross-Cell transaction is also objectively possible because arbitrage transaction is allowed. Considering the existence of arbitrage transactions, the purchase and sale prices of each Cell are not restricted in Case-3.

As can be seen in Table 4, the revenue of Case-3 and Case-4 are relatively close. However, due to the different implementation mechanisms of the two dispatch models, there may be significant differences in the resulting transaction plans. The 15:00 moment is still used as an example for the following illustration. As can be seen from Figure 8, the SDR of all the Cells at 15:00 are less than 1. In Case-3, Cell-4, Cell-5, and Cell-6, which have no direct physical connection with the superior grid, need to purchase power from Cell-1, Cell-2, and Cell-3 to meet the internal power demand of the Cells. In Case-4, each Cell can trade directly with the superior grid to ensure the electricity demand within the Cell. Table 5 gives the transaction revenues for each Cell in Case-3 and Case-4 at that moment.

1) In Case-3, the revenue of each Cell is influenced by its location in AC/DC HDN in addition to its internal source load profile.

TABLE 5

TABLE 5. Transaction revenues for each Cell in Case-3 and Case-4 at that moment.

• For example, to meet the power purchase demand of Cell-4, Cell-5, and Cell-6, Cell-1, Cell-2, and Cell-3 need to purchase an additional portion of power from the superior grid, and their power purchase costs increase. But limited by the ADMM transaction model, the new additional power purchase cost of Cell-1, Cell-2, and Cell-3 is greater than their C2C transaction revenue, resulting in a decrease in the total transaction revenue of these three Cells. Correspondingly, the C2C purchase cost of Cell-4, Cell-5, and Cell-6 in Case-3 is lower than their C2G purchase cost in Case-4, so the total transaction revenue of these three Cells rises.

2) In Case-4, the revenue of each Cell is mainly influenced by the internal source load situation, which is beneficial to incentivize each Cell to develop distributed REG.

In the following, the reasons for the decrease in transaction revenue at the 15:00 moment for Cell-1, Cell-2, and Cell-3 in Case-3 are further elaborated.

The transaction between Cell-2 and Cell-4 is illustrated as an example. Figure 9A gives the iterative change process of the power sold (P₂₄) from Cell-2 to Cell-4, the power purchased (P₄₂) from Cell-4 to Cell-2, and the transaction price (λ₂₄). Figure 9B gives the total revenue, penalty cost and arbitrage revenue of P₂₄ at different levels (compared with the guidance power (P^* ₂₄) in the 4th iteration) in the 4th transaction iteration where the price is basically stable. Figure 9C gives the change in the total revenue of P₄₂ at different levels (compared to the guidance power P^* ₄₂ in the 4th iteration) at the 4th transaction iteration.

1) As seen in Figure 9A, P₂₄ is greater than P₄₂ in both the 2nd and 3rd iterations, i.e., the supply of traded power exceeds the demand, causing λ₂₄ to drop significantly and finally stabilize at $11.07/MW, which is lower than the selling price of the superior grid ($22.3/MW). The arbitrage revenue of Cell-2 is negative, resulting in a lower revenue for Cell-2 in Case-3 than its revenue in Case-4.

2) From Figure 9B, if Cell-2 reduces the power sold to Cell-4 in the 4th iteration because of the negative arbitrage revenue, Cell-2 has to pay more penalty cost according to the ADMM model. Therefore, even if the arbitrage revenue is negative, Cell-2 is still forced to sell power to Cell-4 according to the guide power P^* ₂₄.

3) From Figure 9C, it can be seen that if P₄₂ deviates from P^* ₄₂ by a large amount, it will likewise lead to a decrease in Cell-4’s total revenue. Therefore, Cell-4 will also purchase power from Cell-2 at the same guidance power P^* ₂₄.

FIGURE 9

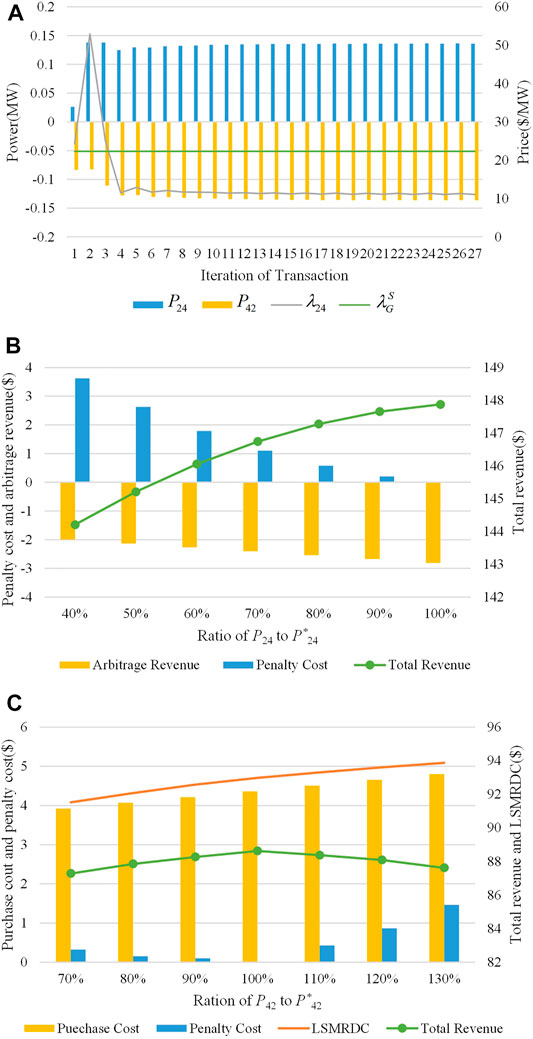
FIGURE 9. (A) Transaction power and price of Cell-2 and Cell-4. (B) Total revenue of Cell-2 selling different level power in the 4th iteration. (C) Total revenue of Cell-4 purchasing different level power in the 4^th iteration.

From the above analysis, it can be seen that although there is an unreasonable situation in Case-3 where some of the Cells have negative arbitrage revenues due to their location, a consistent transaction plan is eventually formed by the ADMM model.

4.3 Effect of Confidence on Dispatch Results

Finally, we analyze the impact of confidence levels on the dispatch results. Without loss of generality, Cell-1, and Cell-4 at 12:00 are chosen as representative Cells for analyzing the impact of changes in confidence level on revenues. If ${\gamma }_1$ = ${\gamma }_{\infty }$ , the values of ${\theta }_1$ and ${\theta }_{\infty }$ when ${\gamma }_1$ is 0.1, 0.3, 0.5, 0.7, and 0.9 are shown in Figure 10A. The final transaction power P and contract price λ between Cell-1 and Cell-4 are shown in Figure 10B.

FIGURE 10

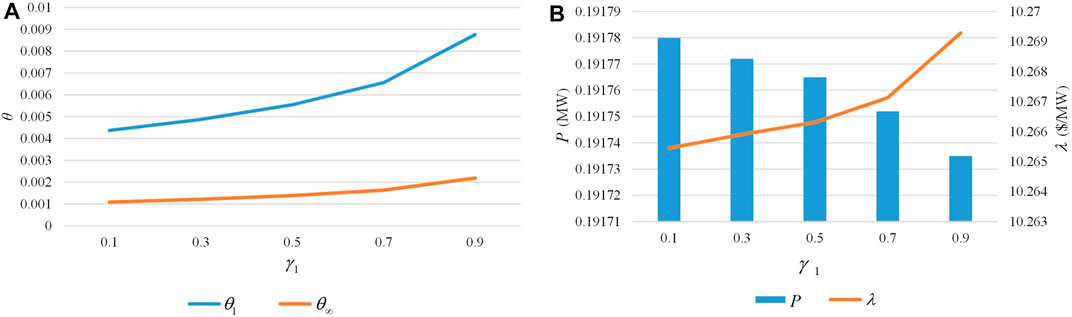
FIGURE 10. (A) Impact of confidence on $\theta$ . (B) Impact of confidence on the final transaction power and contract price.

As can be seen from Figure 10A, a higher confidence level results in a larger uncertainty set, which leads to a higher probability of uncertain scenarios with lower REG output and a more conservative DDRO model. In turn, this leads to an increase in the willingness of BCs to purchase power and a decrease in the willingness of SCs to sell power. The increase in transaction plan disagreement makes Cell-1(BC) tend to increase the purchase price to buy more power, but Cell-4(SO) tends to reduce the transaction power to cope with the possible risks, resulting in the final traded power P decreasing with increasing confidence and the contract price λ increasing with increasing confidence, as shown in Figure 10B.

5 Conclusion

To realize flexible transactions among Cells in CDMM, this paper has proposed a day-ahead economic dispatch model for AC/DC HDNs based on CDMM. The distributed economic dispatch of adjacent Cell and cross-Cell power transactions was realized through the alternate iterations of power transactions and security checks. The following conclusions have been obtained in this study.

1) The day-ahead economic dispatch model of AC/DC HDNs proposed in this paper decouples the large-scale operational dispatch model into low-interaction information internal dispatch models for each Cell. This protects the information privacy of each Cell and realizes flexible transactions among Cells.

2) The distributed economic dispatch model allowing cross-Cell transaction proposed in this paper can effectively motivate the Cell to increase its own REG installed capacity, promote the low-carbon transformation of the distribution network, and avoid certain Cells from being unable to supply electricity normally or causing unreasonable losses due to their own connection with the superior grid.

3) As the confidence level increases, the conservativeness of each Cell’s transaction plan increases. As a result, the willingness of BCs to purchase power increases and the willingness of SCs to sell power decreases, resulting in less transaction power and higher transaction prices.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

WW: Conceptualization, Methodology, Validation, Formal analysis, Writing-review and editing. TH: Conceptualization, Methodology, Software, Formal analysis, Writing-review and editing. TX: Conceptualization, Writing-review and editing, Data curation.

Funding

This paper is supported by the National Key Research and Development Program of China (2020YFB2104500): Research and application demonstration project of the urban integrated energy system with intelligent IoT control technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer YM declared a shared affiliation, with no collaboration, with the authors to the handling editor at the time of the review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.832243/full#supplementary-material

References

Ahmed, H. M. A., Eltantawy, A. B., and Salama, M. M. A. (2018). A Generalized Approach to the Load Flow Analysis of AC-DC Hybrid Distribution Systems. IEEE Trans. Power Syst. 33 (2), 2117–2127. doi:10.1109/TPWRS.2017.2720666

CrossRef Full Text | Google Scholar

Bagheri, A., Wang, J., and Zhao, C. (2017). Data-Driven Stochastic Transmission Expansion Planning. IEEE Trans. Power Syst. 32 (5), 3461–3470. doi:10.1109/TPWRS.2016.2635098

CrossRef Full Text | Google Scholar

Baroche, T., Pinson, P., Latimier, R. L. G., and Ahmed, H. B. (2019). Exogenous Cost Allocation in Peer-To-Peer Electricity Markets. IEEE Trans. Power Syst. 34 (4), 2553–2564. doi:10.1109/TPWRS.2019.2896654

CrossRef Full Text | Google Scholar

Bobinaite, V., Obushevs, A., Oleinikova, I., and Morch, A. (2018). Economically Efficient Design of Market for System Services under the Web-Of-Cells Architecture. Energies 11 (4), 729. doi:10.3390/en11040729

CrossRef Full Text | Google Scholar

Boyd, S., Parikh, N., Chu, E., Peleato, B., and Eckstein, J. (2010). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. FNT Machine Learn. 3 (1), 1–122. doi:10.1561/2200000016

CrossRef Full Text | Google Scholar

Cabiati, M., Tornelli, C., and Martini, L. (2018). “The ELECTRA Web-Of-Cells Control Architecture Concept for the Future Power System Operation,” in AEIT International Annual Conference, Bari, Italy, 1–6. doi:10.23919/AEIT.2018.8577221

CrossRef Full Text | Google Scholar

Crespo-Vazquez, J. L., AlSkaif, T., Gonzalez-Rueda, A. M., and Gibescu, M. (2021). A Community-Based Energy Market Design Using Decentralized Decision-Making under Uncertainty. IEEE Trans. Smart Grid 12 (2), 1782–1793. doi:10.1109/TSG.2020.3036915

CrossRef Full Text | Google Scholar

D'hulst, R., Fernandez, J. M., Rikos, E., Kolodziej, D., Heussen, K., Geibelk, D., et al. (2015). “Voltage and Frequency Control for Future Power Systems: the ELECTRA IRP Proposal,” in Proceedings of 2015 International Symposium on Smart Electric Distribution Systems and Technologies (EDST) (Vienna, Austria, 245–250. doi:10.1109/SEDST.2015.7315215

CrossRef Full Text | Google Scholar

Dang, C., Wang, X., Wang, X., Li, F., and Zhou, B. (2018). DG Planning Incorporating Demand Flexibility to Promote Renewable Integration. IET Generation, Transm. Distribution 12 (20), 4419–4425. doi:10.1049/iet-gtd.2018.5648

CrossRef Full Text | Google Scholar

Day, R. H. (1971). Rational Choice and Economic Behavior. Theor. Decis. 1, 229–251. doi:10.1007/BF00139569

CrossRef Full Text | Google Scholar

Ding, T., Yang, Q., Liu, X., Huang, C., Yang, Y., Wang, M., et al. (2019). Duality-Free Decomposition Based Data-Driven Stochastic Security-Constrained Unit Commitment. IEEE Trans. Sustain. Energ. 10 (1), 82–93. doi:10.1109/TSTE.2018.2825361

CrossRef Full Text | Google Scholar

Ding, T., Yang, Q., Yang, Y., Li, C., Bie, Z., and Blaabjerg, F. (2018). A Data-Driven Stochastic Reactive Power Optimization Considering Uncertainties in Active Distribution Networks and Decomposition Method. IEEE Trans. Smart Grid 9 (5), 4994–5004. doi:10.1109/TSG.2017.2677481

CrossRef Full Text | Google Scholar

Fu, Y., Zhang, Z., Li, Z., and Mi, Y. (2020). Energy Management for Hybrid AC/DC Distribution System with Microgrid Clusters Using Non-cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 11 (2), 1510–1525. doi:10.1109/TSG.2019.2939586

CrossRef Full Text | Google Scholar

Gao, H., Wang, J., Liu, Y., Wang, L., and Liu, J. (2021). An Improved ADMM-Based Distributed Optimal Operation Model of AC/DC Hybrid Distribution Network Considering Wind Power Uncertainties. IEEE Syst. J. 15 (2), 2201–2211. doi:10.1109/JSYST.2020.2994336

CrossRef Full Text | Google Scholar

International Energy Agency (2021). World Energy Outlook 2021. Paris: IEA. Available at: https://www.iea.org/reports/world-energy-outlook-2021.

Google Scholar

Jadhav, A. M., Patne, N. R., and Guerrero, J. M. (2019). A Novel Approach to Neighborhood Fair Energy Trading in a Distribution Network of Multiple Microgrid Clusters. IEEE Trans. Ind. Electron. 66 (2), 1520–1531. doi:10.1109/TIE.2018.2815945

CrossRef Full Text | Google Scholar

Kang, P., Guo, W., Huang, W., Qiu, Z., Yu, M., Zheng, F., et al. (2020). Two-Stage Stochastic Programming Scheduling Model for Hybrid AC/DC Distribution Network Considering Converters and Energy Storage System. Appl. Sci. 10, 181. doi:10.3390/app10010181

CrossRef Full Text | Google Scholar

Kim, H. M., Michelena, N. F., Papalambros, P. Y., and Jiang, T. (2003). Target Cascading in Optimal System Design. J. Mech. Des. 125 (3), 474–480. doi:10.1115/1.1582501

CrossRef Full Text | Google Scholar

Li, J., Khodayar, M. E., Wang, J., and Zhou, B. (2021). Data-Driven Distributionally Robust Co-optimization of P2P Energy Trading and Network Operation for Interconnected Microgrids. IEEE Trans. Smart Grid 12 (6), 5172–5184. doi:10.1109/TSG.2021.3095509

CrossRef Full Text | Google Scholar

Li, P., Ji, H., Wang, C., Zhao, J., Song, G., Ding, F., et al. (2017). Coordinated Control Method of Voltage and Reactive Power for Active Distribution Networks Based on Soft Open Point. IEEE Trans. Sustain. Energ. 8 (4), 1430–1442. doi:10.1109/TSTE.2017.2686009

CrossRef Full Text | Google Scholar

Li, P., Yang, M., Yu, Y., Hao, G., and Li, M. (2021). Decentralized Distributionally Robust Coordinated Dispatch of Multiarea Power Systems Considering Voltage Security. IEEE Trans. Ind. Applicat. 57 (4), 3441–3450. doi:10.1109/TIA.2021.3079365

CrossRef Full Text | Google Scholar

Liu, N., Yu, X., Wang, C., Li, C., Ma, L., and Lei, J. (2017). Energy-Sharing Model with Price-Based Demand Response for Microgrids of Peer-To-Peer Prosumers. IEEE Trans. Power Syst. 32 (05), 3569–3583. doi:10.1109/TPWRS.2017.2649558

CrossRef Full Text | Google Scholar

Liu, X., Liu, Y., Liu, Y., Xiang, Y., and Yuan, X. (2019). Optimal Planning of AC-DC Hybrid Transmission and Distributed Energy Resource System: Review and Prospects. Csee Jpes 5 (3), 409–422. doi:10.17775/CSEEJPES.2019.00540

CrossRef Full Text | Google Scholar

Martini, L., Radaelli, L., Brunner, H., Caerts, C., Morch, A., Hanninen, S., et al. (2015). “ELECTRA IRP Approach to Voltage and Frequency Control for Future Power Systems with High DER Penetration,” in 23rd International Conference on Electricity Distribution, Lyon, France, 1357.

Google Scholar

Peng, Q., and Low, S. H. (2018). Distributed Optimal Power Flow Algorithm for Radial Networks, I: Balanced Single Phase Case. IEEE Trans. Smart Grid 9 (1), 111–121. doi:10.1109/TSG.2016.2546305

CrossRef Full Text | Google Scholar

Qi, C., Wang, K., Fu, Y., Li, G., Han, B., Huang, R., et al. (2018). A Decentralized Optimal Operation of AC/DC Hybrid Distribution Grids. IEEE Trans. Smart Grid 9 (6), 6095–6105. doi:10.1109/TSG.2017.2703582

CrossRef Full Text | Google Scholar

Wang, Z., Bian, Q., Xin, H., and Gan, D. (2016). A Distributionally Robust Co-ordinated Reserve Scheduling Model Considering CVaR-Based Wind Power Reserve Requirements. IEEE Trans. Sustain. Energ. 7 (2), 625–636. doi:10.1109/TSTE.2015.2498202

CrossRef Full Text | Google Scholar

Wu, Z., Sun, Q., Gu, W., Chen, Y., Xu, H., and Zhang, J. (2020). AC/DC Hybrid Distribution System Expansion Planning under Long-Term Uncertainty Considering Flexible Investment. IEEE Access 8, 94956–94967. doi:10.1109/ACCESS.2020.2990697

CrossRef Full Text | Google Scholar

Yang, Y., and Wu, W. (2019). A Distributionally Robust Optimization Model for Real-Time Power Dispatch in Distribution Networks. IEEE Trans. Smart Grid 10 (4), 3743–3752. doi:10.1109/TSG.2018.2834564

CrossRef Full Text | Google Scholar

Yu, Y., Liu, Y., and Qin, C. (2015). Basic Ideas of the Smart Grid. Engineering 1 (4), 405–408. doi:10.15302/J-ENG-2015120

CrossRef Full Text | Google Scholar

Zhang, Y., Ai, X., Wen, J., Fang, J., and He, H. (2019). Data-Adaptive Robust Optimization Method for the Economic Dispatch of Active Distribution Networks. IEEE Trans. Smart Grid 10 (4), 3791–3800. doi:10.1109/TSG.2018.2834952

CrossRef Full Text | Google Scholar

Zheng, W., Wu, W., Zhang, B., Li, Z., and Liu, Y. (2015). Fully Distributed Multi‐area Economic Dispatch Method for Active Distribution Networks. IET Generation, Transm. Distribution 9 (12), 1341–1351. doi:10.1049/iet-gtd.2014.0904

CrossRef Full Text | Google Scholar

Zhu, Z., Liu, D., Liao, Q., Tang, F., Zhang, J., and Jiang, H. (2018). Optimal Power Scheduling for a Medium Voltage AC/DC Hybrid Distribution Network. Sustainability 10 (2), 318. doi:10.3390/su10020318

CrossRef Full Text | Google Scholar