Direct Numerical Simulation of Heat Transfer of Lead–Bismuth Eutectic Flow Over a Circular Cylinder at Re = 500

The flow and heat transfer characteristics of the lead–bismuth eutectic (LBE) (Prandtl number Pr = 0.025) passing over a circular cylinder at Re = 500 are studied by direct numerical simulation and compared with the case of the air (Pr = 0.71). This article makes two major contributions: (1) heat transfer characteristics for the LBE flowing past a circular cylinder. For the case of air, the results show that a similarity exists among the wake structure of instantaneous temperature, fluctuating temperature, and velocity. However, these fields differ severely for the case of LBE. The local time-averaged Nusselt number ($\overline{Nu}$) and circumferentially averaged $\overline{Nu}$ are smaller in the LBE than that in the air. The circumferential and spanwise distributions of $\overline{Nu}$ in the LBE show a greater uniformity. The regions with larger circumferential or spanwise inhomogeneity appear in the flow separation zone. Besides, a resemblance between the distribution of the root mean square of fluctuation temperature and the turbulence kinetic energy can be recognized in the air; however, the similarity disappears for the case of LBE and in which the temperature fluctuation is smaller than that in the air. (2) Study on the temperature and velocity defect laws in the wake. By introducing the defect scales, it is concluded that the velocity field has not entered the self-preserving state yet, while the self-preserving state starts at the location of five times the diameter of the cylinder downstream of the cylinder for the temperature in the LBE and that of 21 times for the temperature in the air. In summary, even if without taking the buoyancy force into consideration, this article provides a fruitful description of the flow and heat transfer characteristics when the LBE flows past a cylinder, which is a typical flow in a helical coil steam generator of lead–bismuth alloy-cooled fast reactors. These highly resolved data on velocity and temperature are valuable for turbulence and heat fluxes modeling in the future and may facilitate the in-depth understanding of such flow and heat transfer characteristics within a limited variation range of operating temperature.

1 Introduction

As single-phase coolants with good performance, liquid metals are widely used in advanced nuclear reactor systems (Todreas and Kazim, 2011), chip cooling (Khalaj and Halgamuge, 2017; Muhammad et al., 2020), spallation particle sources (Batta et al., 2015), and other applications with extremely high heat loads. The larger thermal conductivity of liquid metals, resulting in a lower molecular Prandtl number (Pr ∼10⁻²), guarantees higher heat exchange efficiency. Unlike ordinary fluids (Pr ∼1), the temperature field in a flow of fluids with a low Pr differs significantly from its velocity field (Zhang et al., 2019), leading to many open problems in the understanding of the underlying physical mechanism and characteristics of its heat transfer.

Molten lead–bismuth eutectic (LBE), a typical kind of liquid metals, is the coolant in lead–bismuth alloy-cooled fast reactors, that is, LFRs, one of Gen IV reactors (Abram and Ion, 2008). In a helical coil steam generator of an LFR system, LBE in the shell side transfers the heat taken from the nuclear reactor core to the cooling water in the tube side, which makes it of great importance to analyze the flow and heat transfer behavior when LBE sweeps the tube bundle of the steam generator. The Pr of LBE under the operating conditions of LFRs is within the range of 0.01–0.03 (Greenspan et al., 2008; Concetta, 2015; Guo et al., 2015). Experimental researches on thermohydraulic characteristics of LBE have been widely carried out, and many heat transfer correlations have been derived (Knebel et al., 2002; Ma et al., 2006; Shen et al., 2021). However, data obtained by experimental techniques are yet insufficient. Limited by the opaque and strong corrosiveness of LBE and the current experimental measurement techniques, these experiments mainly focus on the pressure drop, temperature difference, and heat transfer coefficient, while the details of the temperature and velocity fields are difficult to measure (Marocco et al., 2012; Zhang et al., 2020). In addition, most experimental studies on the characteristics of flow and heat exchange focus on the pipes, annular cavities, or longitudinally flow through fuel rods (Lefhalm et al., 2004; Tarantino et al., 2008; Cho et al., 2011). Few researches on external flows such as LBE sweeping the tube bundle in a helical coil steam generator have been reported yet.

Computational fluid dynamics (CFD) (Versteeg and Malalasekera, 2007) can be divided into three categories, including the direct numerical simulation (DNS) method, the large eddy simulation method, and the Reynolds-averaged Navier–Stokes (RANS) method, which provides another research approach. As the most practical option of industrial relevance, the RANS method needs the least computational costs. The key issue in the RANS simulation of liquid metals such as LBE is the closure of the turbulent heat flux term. Simple gradient diffusion hypothesis (Weigand et al., 1997), generalized gradient diffusion hypothesis (Ince and Launder, 1989), second-moment closures (Roelofs, 2019), and Algebraic Heat Flux Model (AHFM) series models (Shams et al., 2019) have been put forward to solve this issue. Nevertheless, models based on gradient diffusion hypothesis provide reliable results only for fluids with a Pr in the order of unity. Second-moment closures and AHFM series models give reasonable results for fluids with a low Pr under simple configuration conditions. The performance of these models needs to be improved under complex configuration conditions such as flows with separations (De Santis and Shams, 2018).

In recent years, DNS has been used to study the fluids with a very low Pr due to the high-fidelity data it can provide (Roelofs et al., 2015). For example, Kawamura et al. (1998) and Kawamura et al. (1999) investigated the influence of Pr and Reynolds number (Re) on the turbulent heat transfer in a channel by means of DNS, the Pr of which varies from 0.025 to 5.0. Redjem-Saad et al. (2007) used DNS to analyze the flow and turbulent heat transfer characteristics of fluids with the Pr within the range of 0.026 to 1.0 in a pipe. DNS is also used in the simulation of forced and mixed convention in a backward-facing step under a uniform heat flux boundary condition for fluids with different Pr to study the influence of Pr on turbulent Pr (Pr_t) (Zhao et al., 2018). These studies have confirmed that the heat transfer characteristics of fluids with a low Pr are significantly different from those of fluids with Pr ∼1. Particular patterns of Pr_t and time constant ratio occur for fluids with a low Pr, especially when flow separation happens, thus bringing a necessity to look into it more deeply.

So far, researches on the flow and heat transfer characteristics of fluids with a low Pr by DNS focus on simple configurations such as a channel, backward-facing step, annular cavity, and pipes. Investigations on the characteristics of external flow and heat transfer such as the phenomenon when LBE sweeps the tube bundle have been rarely reported. High-fidelity data of temperature and velocity fields under these conditions are insufficient. In this article, the flow and heat transfer characteristics of LBE passing a circular cylinder, the basic unit of a tube bundle, are studied by DNS as the beginning of a series of research. In addition, the case of air is also simulated for comparison.

The rest of this article is organized as follows. In Section 2, the problem definition and the methodology are described. The detailed results and discussion about the Nusselt number (Nu), the temperature field, the further analysis of velocity and temperature defect laws in the wake, and so on, are presented in Section 3. The conclusions are given in Section 4.

2 Problem Description and Methodology

2.1 Problem Description

This article is focused on the heat transfer when high-temperature fluid passes a circular cylinder at a constant low temperature. Three-dimensional incompressible flows without buoyancy are investigated at Pr = 0.025 (LBE) and Pr = 0.71 (air), simulating the situation within a limited temperature variation range. The governing equations are nondimensionalized by such characteristics: the diameter of the cylinder (D), the velocity of inflow (U_∞), the temperature difference between inflow and cylinder (T_∞ − T_wall), the characteristic time (D/U_∞), the density of inflow (ρ_∞), and the characteristic pressure (ρ_∞U_∞²). Dimensionless governing equations are written as follows:

$\nabla \cdot \mathit{u}\mathit{=0}.(1)$

$\frac{\partial \mathit{u}}{\partial \mathit{t}}+\mathit{u\cdot }\nabla \mathit{u=-}\nabla \mathit{p+}\frac{\mathit{1}}{\mathrm{Re}}{\nabla }^{\mathit{2}}\mathit{u},(2)$

$\frac{\partial \mathit{T}}{\partial \mathit{t}}+\mathit{u}\cdot \nabla \mathit{T=}\frac{\mathit{1}}{\mathrm{RePr}}{\nabla }^{\mathit{2}}\mathit{T},(3)$

where u is the velocity; t is the time; p is the pressure; and T is the temperature difference between local fluid temperature and the cylinder. All data and physical quantities in this article are nondimensionalized, if not particularly illustrated.

The computational domain is a cuboid (50D × 40D × 6D), and the origin of which is placed at the center of the cylinder, as shown in Figure 1. The outlet is set as a constant boundary condition with zero reference pressure. Periodic boundary condition is imposed in the spanwise direction of the domain.

FIGURE 1

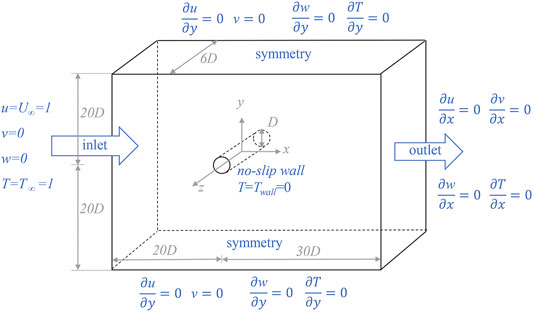
FIGURE 1. Schematic diagram of the computational domain and corresponding boundary conditions. u, v, and w represent the x-, y-, and z- components of u.

It should be noted that the thermal expansion rate of LBE is large, and the buoyancy should not be ignored under many operating conditions in LFRs. The physical properties of LBE are dependent on the temperature. Besides, Re in LFRs varies from zero to hundreds of thousands. However, every consideration mentioned previously causes extra burden on computational cost of DNS. Therefore, constant physical properties and moderate Re (Re = U_∞D/ν = 500, where ν is the kinematic viscosity) without buoyancy are taken into consideration in this article as the beginning of a series of studies. Even in such cases, the present study still provides significantly important information for the liquid metals with very low Pr, especially when the temperature variation is within a limited range.

2.2 Numerical Schemes

The governing equations are discretized by the finite volume method and solved via the open-source CFD software OpenFOAM. The convergence criterion for all equations is 10⁻⁷. The time derivative term is discretized by Euler method. The convection and diffusion terms are discretized by Gauss QUICK scheme and Gauss linear corrected scheme, respectively. The pressure–velocity decoupling is dealt by PISO (pressure implicit with splitting of operators) algorithm. The preconditioned conjugate gradient method with geometric–algebraic multigrid (GAMG) as the preconditioner and diagonal incomplete Cholesky as the smoother are used to solve the pressure equation. The merge level in GAMG is chosen to be 2 to speed up the solving process.

2.3 Numerical Settings and Grid Independence Validation

Two sets of mesh with different resolutions are generated, and three cases are carried out: Pr = 0.71 with mesh A, Pr = 0.71 with mesh B, and Pr = 0.025 with mesh B, where the two cases of the air (Pr = 0.71) are used for mesh independence validation. The detailed settings of mesh A and B are listed in Table 1, and a view of mesh B is presented in Supplementary Figure S1. Uniform nodes are configured in the spanwise direction. Both sets of mesh are refined near the wall and in the wake region. The time step for the cases with mesh A and mesh B are set to 6.25 × 10⁻⁴ and 5 × 10⁻⁴, respectively, where the Courant–Friedrichs–Lewy (CFL) number is within 0.14 for both cases, meeting the CFL limit (Jiang, 2020). Each case was simulated for 10 flow-through times (500 dimensionless time); that is, 104 vortex shedding cycles after the statistically steady state of turbulence were reached. The results presented below are analyzed using the latest 500 dimensionless time. In total, 400,000 CPU hours were consumed for the three cases via Tianhe-2 platform, the national supercomputer center in Guangzhou, China.

TABLE 1

TABLE 1. Parameters of grid generation.

Table 2, Figure 2, and Supplementary Figure S2 provide some results for the case of Pr = 0.71. The meanings of involved symbols are as follows: dimensionless wall distance $y^{+}=\frac{y{u}_{\tau }}{\nu }$, drag coefficient ${\mathit{C}}_{\mathit{D}}\mathit{=}\frac{{\mathit{F}}_{\mathit{D}}}{\mathit{0}\mathit{.5}{\mathit{\rho }}_{\infty }{\mathit{U}}_{\infty }^{\mathit{2}}\mathit{DL}}$, and Strouhal number $\mathit{St=}\frac{\mathit{fD}}{{\mathit{U}}_{\infty }}$, $\mathit{Nu=}\frac{\mathit{hD}}{\mathit{\lambda }}$. Here, y is the distance from the center of the first cell to the wall; u_τ is the wall friction velocity; F_D is the drag force of cylinder; L is the height of the cylinder; f is the vortex shedding frequency; h is the heat transfer coefficient; and λ is the thermal conductivity of the fluid. $\overline{{\mathit{C}}_{\mathit{D}}}$ and $\overline{Nu}$ are the time-averaged C_D and time-averaged Nu, respectively, and $\overline{N{u}_0}$ stands for the value of $\overline{Nu}$ at the stagnation point.

TABLE 2

TABLE 2. y⁺, St, $\overline{C_D}$ and Nu (Pr = 0.71).

FIGURE 2

FIGURE 2. Statistical convergence of $\overline{C_D}$ (Pr = 0.71).

Evidences are found from Table 2 that both sets of grids meet the number and refinement requirements in the boundary layer as the circumferentially averaged y⁺ in both cases is smaller than 0.1. The simulated results of St, $\overline{N{u}_0}$, $\overline{Nu}$, and $\overline{C_D}$ are in good agreement with reference values with small relative discrepancies listed in Table 2. It is obvious that 500 dimensionless time is long enough for the statistical convergence of $\overline{C_D}$ for both mesh A and mesh B cases, as proven by the convergence tolerances in the last 100 dimensionless time shown in Figure 2. In addition, the grid size of mesh B is closer to the local Kolmogorov length scale, and the maximum of the ratio of the local mesh size to local Kolmogorov length scale is 2.7, located in the wake region, as shown in Supplementary Figure S2. The local mesh size is smaller than the local Kolmogorov length scale in many locations.

Therefore, mesh B was selected as the mesh for the case of Pr = 0.71. In a forced convection, the mesh resolution is determined by the velocity field when Pr < 1; therefore, there is no need to carry out the grid independence validation for the case with LBE. Accordingly, the data and analysis in the following sections are based on mesh B for both Pr = 0.025 and Pr = 0.71 cases. The above validation shows evidences that the numerical mesh resolution used in this study is adequate to simulate the fluid flow and heat transfer in the near wall region and the main stream region.

3 Results and Discussion

3.1 Forces on the Cylinder

In this article, the velocity and pressure relevant results are discussed regardless of Pr, as the temperature is considered as a passive scalar; that is, the heat transfer under different Pr has no effect on the flow field.

Temporal evolutions of the lift coefficient C_L and drag coefficient C_D are shown in Supplementary Figure S3 and Supplementary Figure S4, where ${\mathit{C}}_{\mathit{L}}\mathit{ = }\frac{{\mathit{F}}_{\mathit{L}}}{\mathit{0}\mathit{.5}{\mathit{\rho }}_{\infty }{\mathit{U}}_{\infty }^{\mathit{2}}\mathit{DL}}$ and F_L is the lift force of cylinder. Supplementary Figure S5 shows the spectrum of C_L. A dominant frequency of 0.208 can be obtained, as listed in Table 2, giving a result of St in good accordance with the empirical formula ($St=0.2139-\frac{4.0}{Re}$, when 325 < Re < 1,600) summarized from certain experimental and numerical data by Norberg (2003). The root mean square (R.M.S.) of C_L is C_Lrms = 0.3195.

In Supplementary Figure S6, the variations of the time-averaged skin-friction coefficient $\overline{C_f}$ along the circumference of the cylinder are plotted, where C_f is defined as ${\mathit{C}}_{\mathit{f}}\mathit{ = }\frac{{\mathit{\tau }}_{\mathit{w}}}{\mathit{0}\mathit{.5}{\mathit{\rho }}_{\infty }{\mathit{U}}_{\infty }^{\mathit{2}}}$, and τ_w is the wall shear stress. The time-averaged flow separation angle φ₀ is 102.5° according to the location where $\overline{C_f}$ reaches zero. The formula φ₀ = 78.8 + 505Re^−0.5 (when 270 ≤ Re ≤ 10⁵) concluded by Jiang (2020) gives a result of φ₀ = 101.4°. The separation angle in this article is consistent with it, and the relative difference is 1.1%.

3.2 Instantaneous Fields and Vortex Structure

Instantaneous fields and the vortex structure of the two cases are demonstrated in Figure 3 and Figure 4, wherein the vortex structure is visualized via Q method (Jinhee and Hussain, 1995). The isosurface of Q = 0.2 indicates that the flow develops three-dimensionally in the near-wake region, where the vortices form a wavy spanwise structure, as revealed in Figure 3. For the case of air, a similarity among the wake structure of instantaneous temperature, fluctuating temperature, and velocity exists as Pr is close to 1 (Figure 4). The larger Pr gives a result that the influence of wall temperature spreads to a thinner region. Therefore, the temperature rapidly recovers to close to T_∞ within about 2D downstream of the cylinder. On the contrary, the Pr of LBE is much smaller than 1, which leads to a significant enhancement of the diffusion effect. The instantaneous temperature field and the fluctuating temperature field differ severely from the velocity field (Figure 4).

FIGURE 3

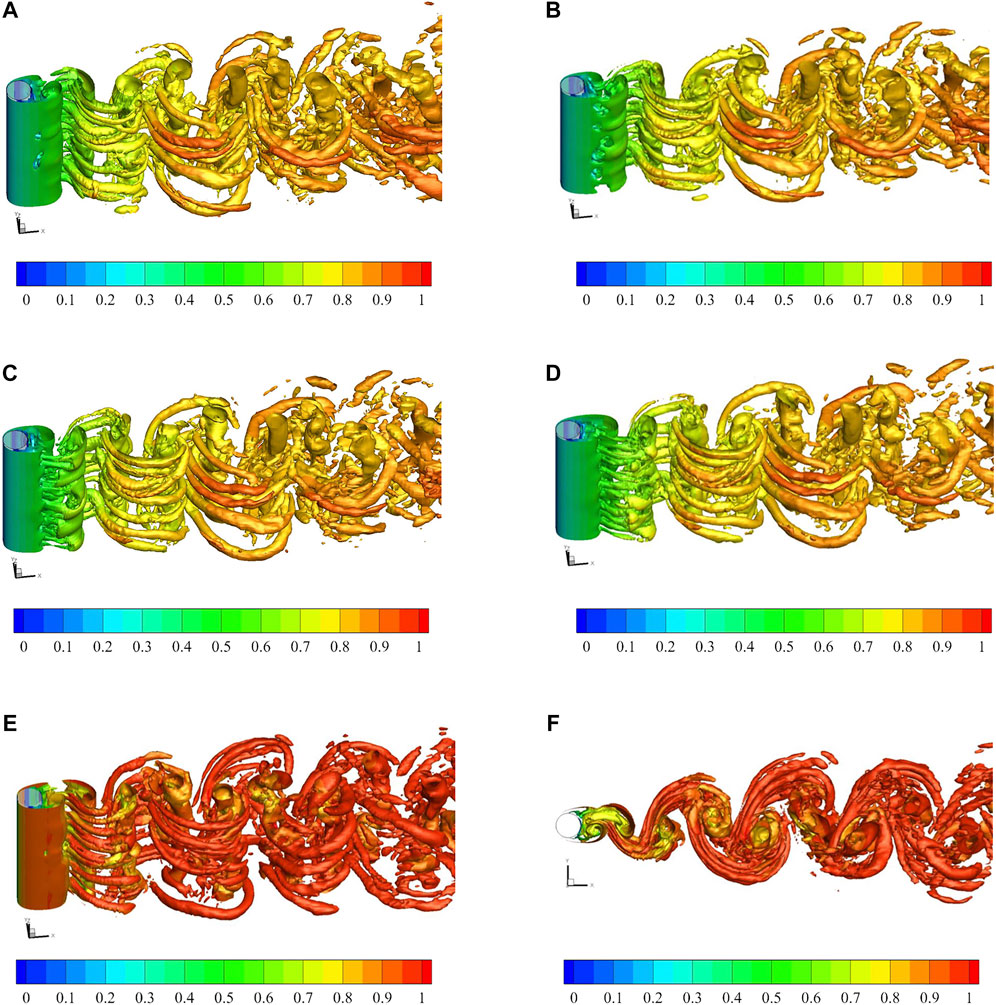
FIGURE 3. Instantaneous vortex shown by isosurfaces of Q = 0.2 for five instants of time. Note that these five instants stand for five typical moments in one vortex shedding period since the vortex shedding period t_vs is 4.854 (according to the value of St in Table 2). In A–D, the isosurfaces are colored by the temperature for the case of LBE (Pr = 0.025). In E and F, the isosurfaces are colored by the temperature for the case of air (Pr = 0.71). (A) t = t₀ (a typical moment), (B) t = t₀ + 1, (C) t = t₀ + 2, (D) t = t₀ + 3, (E) t = t₀ + 4, and (F) t = t₀ + 4.

FIGURE 4

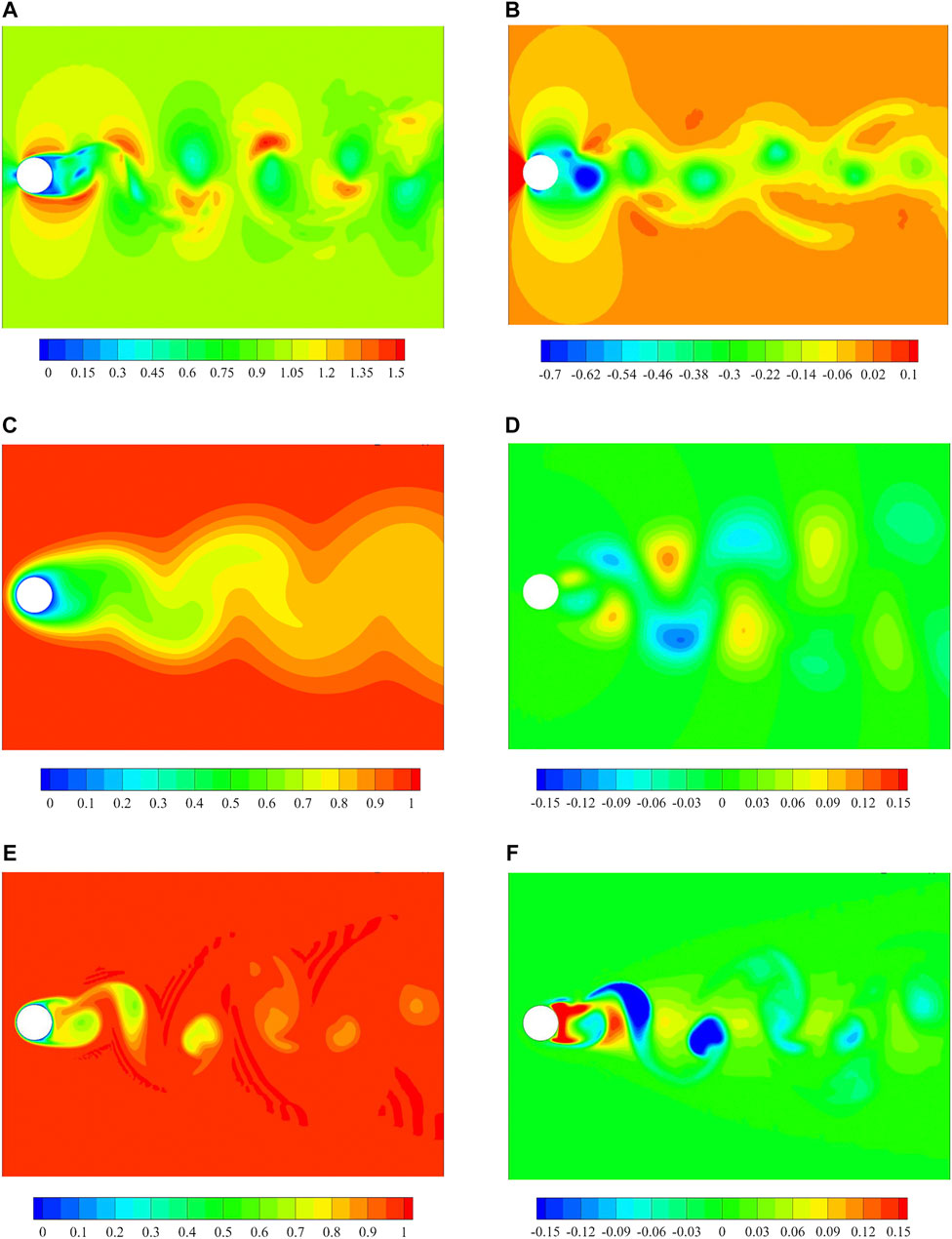
FIGURE 4. Distributions of pressure, velocity and temperature at a typical moment (at z = 0 plane). (A) Magnitude of velocity; (B) pressure; (C) transient temperature (LBE, Pr = 0.025); (D) fluctuating temperature T′ (T′ = T − $\overline{T}$) (LBE, Pr = 0.025); (E) transient temperature (air, Pr = 0.71); (F) fluctuating temperature T′ (air, Pr = 0.71).

3.3 Nusselt Number

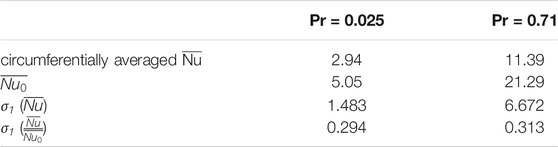
Figure 5A and Table 3 show the information of the local $\overline{Nu}$ on the cylinder surface. It is obvious that the heat transfer characteristics of fluid passing a cylinder are affected by both Re and Pr. Smaller Pr causes a thicker temperature boundary layer, which results in smaller local $\overline{Nu}$ and circumferentially averaged $\overline{Nu}$. $\overline{Nu}$ decreases gradually due to the thickening of the boundary layer in the range of φ = 0°–117° for both cases, then the trends of these two cases differ after that. For the case of air, the turbulence and Karman vortex shedding enhance the mixing; therefore, $\overline{Nu}$ has a significant rise when φ > 117°. The diffusion coefficient of air is small, so the turning point of declining and ascending φ₁ (φ₁ = 117°) is larger than the time-averaged flow separation angle φ₀. However, $\overline{Nu}$ almost keeps declining until φ = 180° for the case of LBE because the increase in diffusion coefficient weakens the effect of convection. The following correlation formula (Churchill and Bernstein, 1977), that is, Eq. 4, concluded from a large amount of experimental data, is an estimation of the lower bound for the circumferentially averaged $\overline{Nu}$ for RePr > 0.4. It gives a result that the ${\overline{Nu}}_{lb}$ of air and LBE are 11.33 and 2.80, respectively, which is obviously consistent with the results in Table 3. It should be noted that the relative discrepancy between the simulation results and the correlation formula is 5.0% for LBE, which is a little larger than that of air, resulting from the fact that the experimental data of fluids with low Pr are insufficient, and the applicability of this formula for low Pr conditions may have not been fully verified yet.

${\overline{\mathrm{Nu}}}_{\mathrm{lb}}\mathit{= 0}\mathit{.3+0}\mathit{.62}{\text{Re}}^{\frac{\mathit{1}}{\mathit{2}}}{\text{Pr}}^{\frac{\mathit{1}}{\mathit{3}}}{\left[\mathit{1+}{\left(\frac{\text{Re}}{\mathit{282000}}\right)}^{\frac{\mathit{5}}{\mathit{8}}}\right]}^{\frac{\mathit{4}}{\mathit{5}}}{\left[\mathit{1+}{\left(\frac{\mathit{0}\mathit{.4}}{\text{Pr}}\right)}^{\frac{\mathit{2}}{\mathit{3}}}\right]}^{\mathit{-}\frac{\mathit{1}}{\mathit{4}}}.(4)$

FIGURE 5

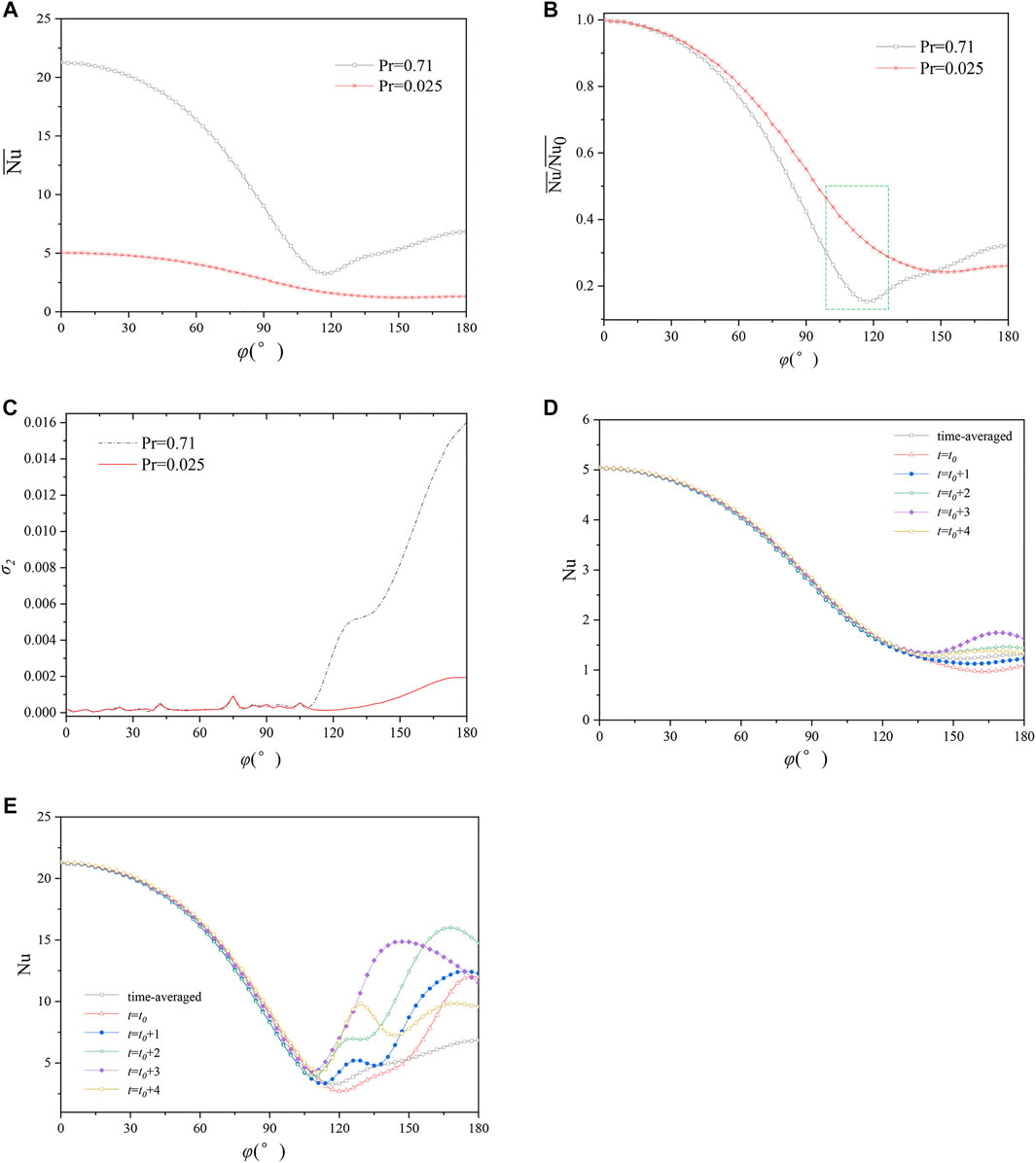
FIGURE 5. Distribution of Nu. The five instants of time in D and E are explained in Figure 3. (A) Variation of local $\overline{Nu}$ on the cylinder surface (at z = 0 plane); (B) circumferentially variations of $\frac{\overline{Nu}}{\overline{N{u}_0}}$; (C) the spanwise standard deviation σ₂ with the angle φ; (D) distribution of local time-averaged and instantaneous Nu for LBE (Pr = 0.025) (at z = 0 plane); (E) distribution of local time-averaged and instantaneous Nu for air (Pr = 0.71) (at z = 0 plane).

TABLE 3

TABLE 3. $\overline{Nu}$ and circumferentially standard deviations (at z = 0 plane).

The parameter σ₁ in Table3 is the circumferentially standard deviation, which reflects the circumferential uniformity. Results show that σ₁ ($\overline{Nu}$) and σ₁ ($\frac{\overline{Nu}}{\overline{N{u}_0}}$) in the LBE are smaller than those of air, which indicates a more uniform circumferential distribution and is consistent with Figure 5B.

On the other hand, the two curves in Figure 5B almost coincide with each other when φ < 50° and then separate beyond this range, which can be explained together with Supplementary Figure S6 and Eq. 3. In the regions of φ < 50°, $\overline{C_f}$ increases monotonously, and no flow separation occurs, so $\frac{\partial T}{\partial t}\approx 0$ and the transport of temperature can be written as

$\text{RePr }\mathit{u}\cdot \nabla \mathit{T=}\nabla \cdot \left(\nabla \mathit{T}\right).(5)$

Considering

$\mathrm{Nu}\mathit{=}\frac{\left(\nabla {\mathit{T}}_{\mathit{n}}\right)\mathit{D}}{{\mathit{T}}_{\infty }\mathit{-}{\mathit{T}}_{\mathit{w}}}\propto \nabla {\mathit{T}}_{\mathit{n}},(6)$

where the subscript “n” represents the normal component, it is obvious that $\nabla T$ or Nu is dependent on $(\text{RePr} \mathit{u})$. Therefore, for each condition with different Pr, $\frac{\overline{Nu}}{\overline{N{u}_0}}$ is dependent on u as the influence of Pr is eliminated via the denominator $\overline{N{u}_0}$. When φ > 50°, $\overline{C_f}$ starts declining, which means that instantaneous flow separation occurs, and the flow becomes turbulent, both indicating that the unsteady term of temperature transport $\frac{\partial T}{\partial t}$ should be considered. Under such conditions, $\frac{\overline{Nu}}{\overline{N{u}_0}}$ is dependent on u and Pr; therefore, the discrepancy of these two curves can be observed when φ > 50°. The areas with 99° < φ < 126° and relative difference greater than 50% are marked by dotted box in Figure 5B. Supplementary Figure S6 shows that $\overline{C_f}$ is negative within this region, implying that $\frac{\partial T}{\partial t}$ is quite large, and the influence of Pr on $\frac{\overline{Nu}}{\overline{N{u}_0}}$ is remarkable.

The parameter σ₂ in Figure 5C represents the standard deviations in the spanwise direction. For both cases, the values of σ₂ are almost equal and smaller than 0.001 when φ < 110°, demonstrating a uniform spanwise distribution of $\frac{\overline{Nu}}{\overline{N{u}_0}}$. After that, σ₂ increases sharply for both cases, reflecting a nonuniform distribution brought by the three-dimensional vortex structure as shown and discussed in Section 3.2. Similar to previous discussion, the larger diffusivity weakens the effect of convection, so σ₂ in the LBE is significantly smaller than that of the air when φ > 110°.

The comparison between local $\overline{Nu}$ and local instantaneous Nu at different angles at five instants in one vortex shedding period is presented in Figures 5D and E, which in fact matches Figures 5A and B to a certain extent. It can be seen from Figures 5D and E that the distribution in the case of LBE almost overlaps, except for the position where φ > 135°, because its thermal diffusion coefficient is much greater than the momentum diffusion coefficient, which makes the temperature field less affected by the flow field. In the case of air, a larger difference appears after φ > 108° where flow separation occurs. These features correspond to the dotted box region in Figure 5B.

3.4 Characteristics of Temperature Field

The characteristics of the time-averaged temperature field are shown in Figure 6. The mean temperature boundary layer is thicker for the case of LBE; therefore, the time-averaged temperature $\overline{T}$ in the downstream is lower compared with the case of air, but it increases monotonically with the increase in the distance from the cylinder. Only 80% of T_∞ can be recovered at x/D ≈ 7 and 88% of T_∞ in the far field (x/D = 30), where x represents the streamwise distance from the center of the cylinder to the location interested. In the case of air, different phenomena will occur. The air temperature experiences a region of slight decrease in the range of x/D = 1–1.5, where a similar declining can be observed for the time-averaged x-component velocity $\overline{u}$ as the air temperature is more influenced by the velocity (Figure 6C). The influence of wall temperature on the air temperature is mainly limited to a short distance. Eighty percent of T_∞ can be recovered at x/D ≈ 2 and approximately 98% of T_∞ in the far field (x/D = 30).

FIGURE 6

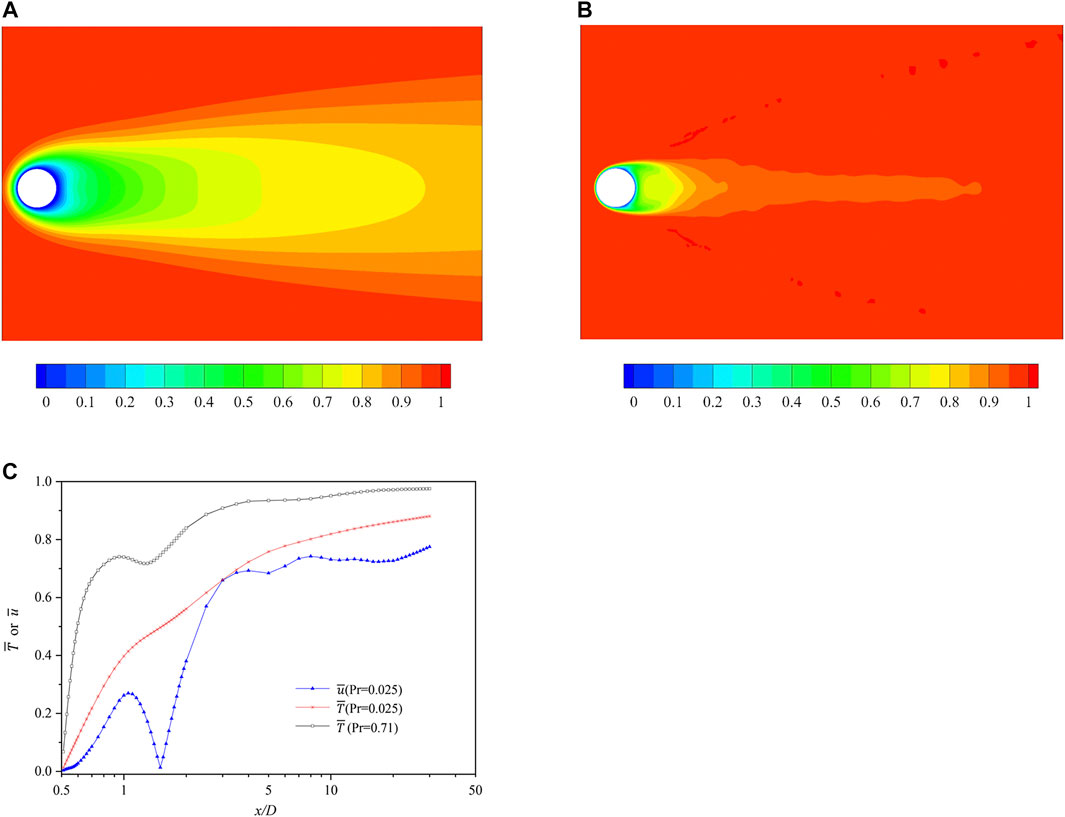
FIGURE 6. Distributions of time-averaged temperature fields. (A) $\overline{T}$ around cylinder at z = 0 plane (LBE, Pr = 0.025); (B) $\overline{T}$ around cylinder at z = 0 plane (air, Pr = 0.71); (C) variation of $\overline{T}$ and $\overline{u}$ along the wake axis at z = 0 plane.

The R.M.S. of T′ and the turbulence kinetic energy k ($k=\frac{1}{2}\overline{u_i^{\text{'}}{u}_i^{\text{'}}}$) for the two cases are calculated to compare and discuss the fluctuation of temperature quantitatively. Figure 7 shows that T′_rms is almost symmetric with respect to y = 0 for both cases. For LBE, T′_rms is smaller than 0.03 at all locations and remains nearly constant within a long distance (x = 0.7D∼5D). For the case of air, T′_rms is larger than that in the LBE at all locations, which is consistent with the results observed in pipe flows (Redjem-Saad, 2007). Two significant local maxima can be observed. T′_rms rises sharply in the boundary layer, decreases to a local minimum of 0.054 at x/D = 1, and then reaches a local maximum at x = 2D.

FIGURE 7

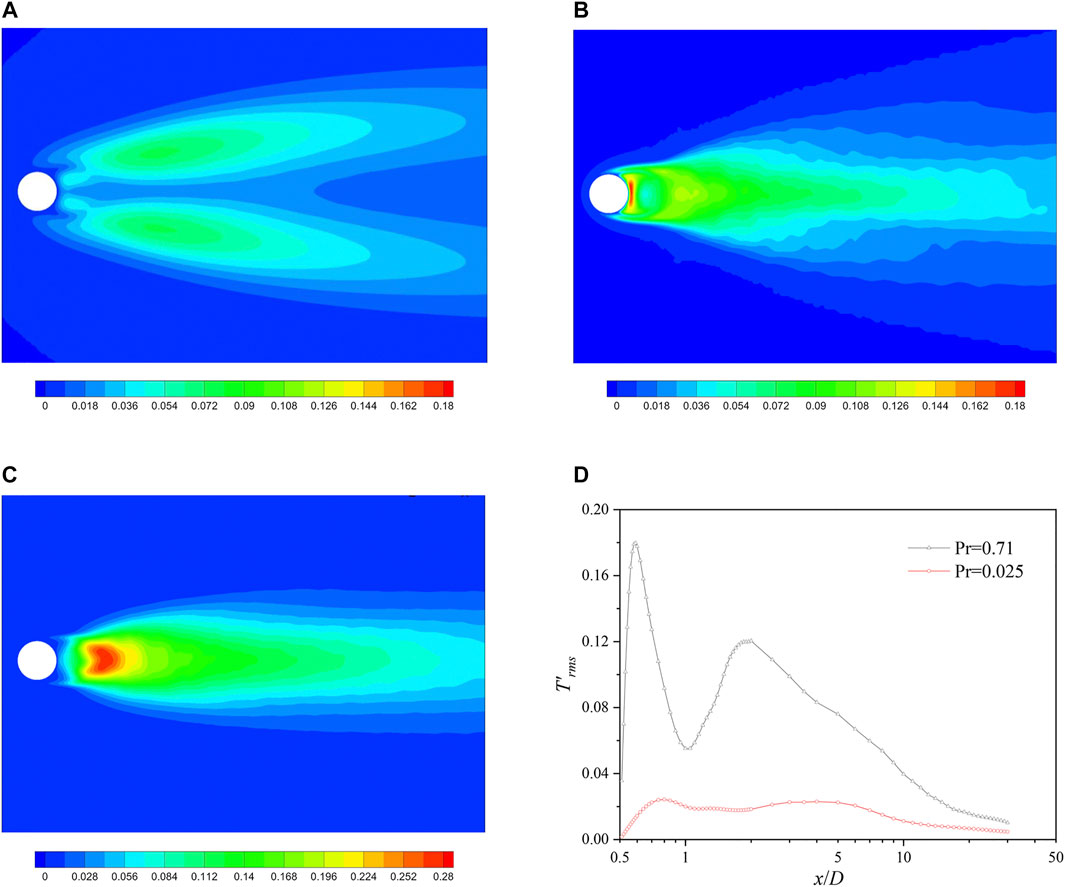
FIGURE 7. Distributions of root mean square fields. (A) T′_rms on the plane of z = 0 (LBE, Pr = 0.025); (B) T′_rms on the plane of z = 0 (air, Pr = 0.71); (C) k on the plane of z = 0; (D) variation of T′_rms along the wake axis.

The transverse distribution of mean temperature and T′_rms at different downstream locations are displayed in Figure 8. For the case of LBE, the distribution of $\overline{T}$ along the transverse direction is single peaked, except for the locations at x/D = 1 and x/D = 1.2, where the temperature in the wake axis is slightly lower than the maximum temperature. This differs from the phenomenon in the air, where there are two or more peaks along the transverse direction (e.g., x/D = 0.6–1.2). The descent rate of mean temperature along the y direction in the LBE is relatively mild compared with air, proving that the thermal conductivity of LBE is larger than that of air.

FIGURE 8

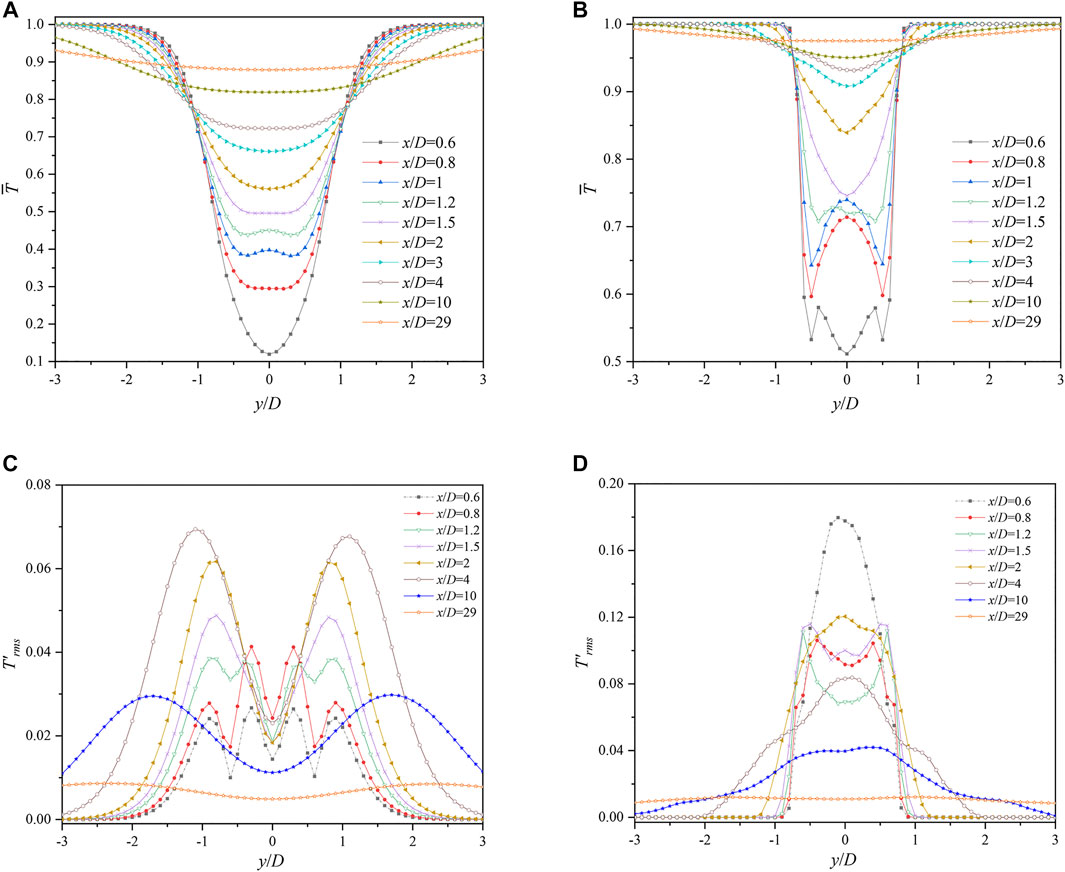
FIGURE 8. Transverse distributions of $\overline{T}$ and T′_rms at different downstream locations. (A) $\overline{T}$ (LBE, Pr = 0.025); (B) $\overline{T}$ (air, Pr = 0.71). (C) T′_rms (LBE, Pr = 0.025); (D) T′_rms (air, Pr = 0.71).

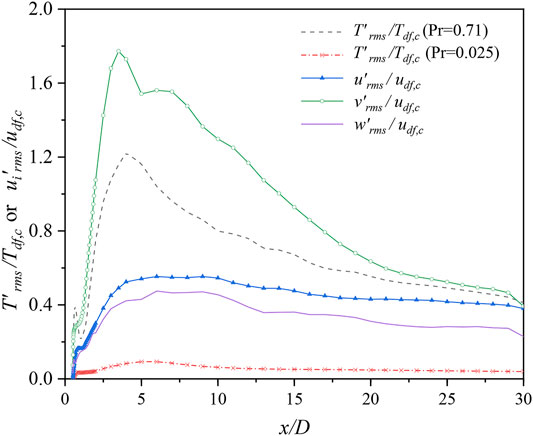
For LBE, T′_rms near the cylinder (x/D = 0.6–1) is smaller than those at x/D = 1.5–4. Four peaks appear at x/D ≤ 1.2, and double peaks for other locations. However, only one peak occurs for air at almost all x-locations, except for x/D = 0.8–1.5. T′_rms near the wall (x/D = 0.6) is the largest. The attenuation rate of T′_rms in the transverse direction in the LBE is smaller than that in the air.

These circumstances match with Figure 7 and Figure 4. The fluctuation of the temperature in the air is mostly dependent on the fluctuation of velocity; hence, a resemblance between the distribution of T′_rms and k can be recognized. The wake structure of instantaneous and fluctuating temperature is close to Karman vortex, and the vortices on both sides affect the wake axis. Therefore, the transverse maxima of T′_rms appears on the wake axis for most of streamwise locations. However, none of such wake structures can be observed from the fields of instantaneous temperature and fluctuating temperature for the case of LBE. The temperature fluctuation mainly occurs on both sides of the wake axis, resulting in four or double peaks in the transverse direction as shown in Figure 8C.

The fluctuations of typical variables near the cylinder wall are also discussed. In general, there is one local maximum for the cases with small angles, whereas two for other curves with larger angles, as illustrated in Figure 9, where Δr is the radial distance to the wall. The first local maximum or the first plateau is attributed to the wall effect, and the second one is due to vortex shedding. However, the characteristics of temperature fluctuations in the air and LBE are different.

FIGURE 9

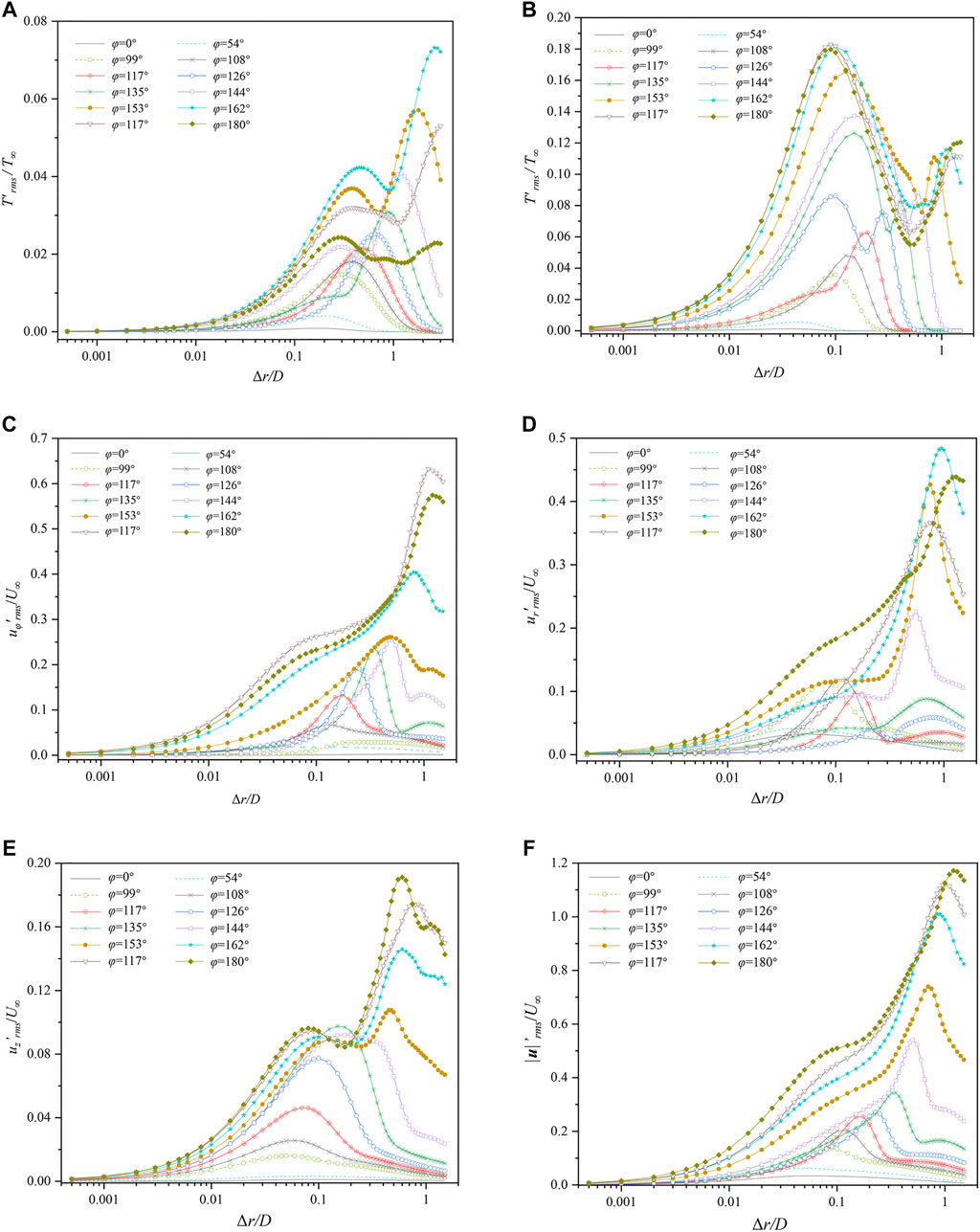
FIGURE 9. Distributions of several variables along different angles near the cylinder wall. (A) T′_rms/T_∞ for the case of LBE; (B) T′_rms/T_∞ for the case of air; (C) u_φ′_rms/U_∞, where u_φ means the circumferential component of velocity; (D) u_r′_rms/U_∞, where u_r means the radial component of velocity; (E) w′_rms/U_∞; (F) |u|′_rms/U_∞.

The transition angle from one maximum to two maxima for T′_rms/T_∞ in the air is approximately 117°, a little larger than the flow separation angle, which is comparable with Figure 5E. T′_rms/T_∞ almost increases with the increase in φ, and the first maximum occurs where Δr/D = 0.05–0.15. The radial component of the gradient of temperature is quite large, as can be seen from the contours of temperature (Figure 4), so that the radial variations of temperature are relevant to the fluctuations of u_r. Therefore, between Figure 9B and Figure 9D, some similarities of the transition angle and the locations where the first maximum or the first plateau occurs can be observed. It should be noted that first peaks in the near wall region in the graph of u_φ′_rms/U_∞ (Figure 9C), u_r′_rms/U_∞ (Figure 9D), and |u|′_rms/U_∞ (Figure 9F) are not obvious, resulting from the fact that the diffusion and convection are significantly enhanced in the flow separation region.

T′_rms/T_∞ of LBE is smaller than that of air. The transition angle from one maximum to two maxima for T′_rms/T_∞ in the LBE is approximately 135°, which is much larger than the flow separation angle, and the phenomenon is comparable with Figure 5D. Unlike the case of air, the second peak of T′_rms/T_∞ is larger than the first peak/plateau for the case of LBE, because the smaller Pr of LBE causes a more significant suppression of temperature fluctuation by the wall. The locations where the first maximum or the first plateau of T′_rms/T_∞ occurs are Δr/D = 0.2–0.6, further than T′_rms/T_∞ in air and u_φ′_rms/U_∞ for both cases.

3.5 Temperature and Velocity Defect Laws in Wake

The velocity and temperature profiles in the near-wake region are determined by the boundary layer, the shape of the object, and whether a flow separation occurs. There exists a similarity of the velocity or temperature profile in the far wake of a bluff body such as x/D > 50 (Zdravkovich, 1997) or x/D > 100 (Chen, 2002), where the disturbance of the object on the flow or temperature field tends to vanish. It should be noted that this location where the self-preserving flow exists depends on how far it needs to develop the profile from a boundary layer type at the trailing edge of the object to a fully developed similar wake profile. Therefore, this distance is closely related to the specific working conditions. In other words, it has been well established that there exists a velocity scale and a length scale, which are the universal function of x/D, scaled by which the mean velocity profiles and the mean temperature profiles may be self-similar (Wygnanski et al., 1986). The existence of such similar temperature scale under a specific condition or not is a matter to be discussed.

The transverse profile of velocity defect follows the Gaussian distribution for a small-defect wake in a two-dimensional plate wake, detailed deductions of which can be found in the references (Wygnanski et al., 1986; Chen, 2002). In this section, the self-preserving states of the temperature and velocity in the wake are discussed according to the simulation cases by introducing the velocity defect as the velocity scale, the temperature defect as the temperature scale, and the defect width as the length scale, respectively. The similarity or deviation between the Gaussian distribution and the transverse profiles of velocity defect and temperature defect are also discussed.

3.5.1 Velocity Defect, Temperature Defect and Defect Width

The velocity defect along the transverse direction at the downstream position of x/D is defined as follows:

${\mathit{u}}_{\mathit{df}}\mathit{=}\overline{{\mathit{u}}_{\mathit{e}}}\mathit{-}\overline{\mathit{u}},(7)$

where the defect variable u_df is marked by the subscript “df”, and $\overline{u_e}$ is $\overline{u}$ at the outer edge of the wake (y = 20D) marked by the subscript “e.” u_df is normalized to u_df⁺ according to:

${\mathit{u}}_{\mathit{df}}^{\mathit{+}}\mathit{=}\frac{{\mathit{u}}_{\mathit{df}}}{{\mathit{u}}_{\mathit{df,c}}}\mathit{ = }\frac{{\mathit{u}}_{\mathit{df}}}{\overline{{\mathit{u}}_{\mathit{e}}}\mathit{-}\overline{{\mathit{u}}_{\mathit{c}}}},(8)$

where u_df⁺ is the normalized velocity defect, u_df,c is the velocity defect on the wake axis, that is, the transverse center of the wake, at the downstream location of x/D, and $u_{df,c} = \overline{u_e}-\overline{u_c}$. Note that the superscript “+” indicates the variable normalized by the defect variable on the wake axis.

Correspondingly, the temperature defect T_df and normalized temperature defect T_df⁺ are calculated as follows:

${\mathit{T}}_{\mathit{df}}\mathit{=}\overline{{\mathit{T}}_{\mathit{e}}}\mathit{-}\overline{\mathit{T}},(9)$

${\mathit{T}}_{\mathit{df}}^{\mathit{+}}\mathit{=}\frac{{\mathit{T}}_{\mathit{df}}}{{\mathit{T}}_{\mathit{df,c}}}\mathit{ = }\frac{{\mathit{T}}_{\mathit{df}}}{\overline{{\mathit{T}}_{\mathit{e}}}\mathit{-}\overline{{\mathit{T}}_{\mathit{c}}}},(10)$

where $\overline{T_e}$ is the average temperature at the outer edge of wake (y = 20D), T_df,c is the temperature defect on the wake axis at the location of x/D (y = 0), and $T_{df,c} = \overline{T_e}-\overline{T_c}$.

Assume that the transverse profile of velocity defect follows the Gaussian distribution, as expressed in Eq. 11. Then the Gaussian parameter σ_U can be obtained by fitting Eq. 11 with the simulation results of y and u_df⁺. The velocity defect width of wake W_U is defined as half of the wake width where u_df⁺ = 1%; that is, W_U satisfies that $\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{\sigma }_U}{x}{W}_U^2\right)=0.01$. Therefore, W_U can be calculated by Eq. 12. Similarly, the temperature defect width of wake W_T is defined as half of the wake width where T_df⁺ = 1%; see Eqs 13 and 14.

${\mathit{u}}_{\mathit{df}}^{\mathit{+}}\mathrm{=exp}\left(\mathit{-}\frac{{\mathit{\sigma }}_{\mathit{U}}}{\mathit{x}}{\mathit{y}}^{\mathit{2}}\right),(11)$

${\mathit{W}}_{\mathit{U}}\mathit{=}\sqrt{\frac{\mathit{x}}{{\mathit{\sigma }}_{\mathit{U}}}\mathrm{2ln10}},(12)$

${\mathit{T}}_{\mathit{df}}^{\mathit{+}}\mathrm{=exp}\left(\mathit{-}\frac{{\mathit{\sigma }}_{\mathit{T}}}{\mathit{x}}{\mathit{y}}^{\mathit{2}}\right),(13)$

${\mathit{W}}_{\mathit{T}}\mathit{=}\sqrt{\frac{\mathit{x}}{{\mathit{\sigma }}_{\mathit{T}}}\mathrm{2ln10}}.(14)$

Figure 10A presents how W_U and W_T vary with the distance from the cylinder. The variation trends of W_{T (Pr=0.71)} and W_U are similar. They increase near the cylinder, experience a plateau in the range of x/D = 3–6, and then keep increasing along the downstream. However, no plateau can be observed for W_{T (Pr=0.025)}. In the entire wake, W_{T (Pr=0.025)} > W_{T (Pr=0.71)} > W_U, which is consistent with the results shown in the contour of time-averaged temperature field (Figures 6A, B). In LBE, the region where the cylinder influences the temperature in the transverse direction is large. On the contrary, the effect is confined in a very narrow range for the case of air. The transverse influence range of temperature in the LBE is 1.4–2.2 times of that for the air case.

FIGURE 10

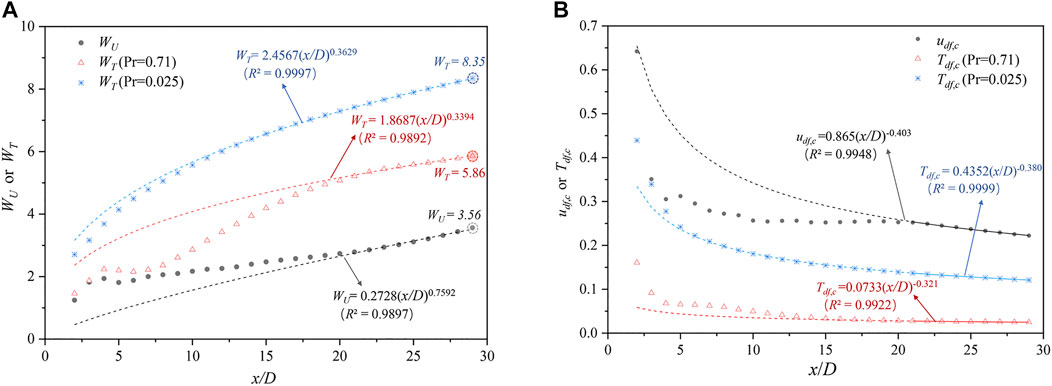
FIGURE 10. Variations of velocity defect width, temperature defect width, velocity defect, and temperature defect in wake. The curves and formulas are fitting results according to the data at locations of x/D ≥ 21 and R² represents the coefficient of determination. (A) Defect width; (B) velocity defect and temperature defect.

The defect width should be proportional to (x/D)^0.5 according to the mathematical model of the far wake with the introduction of linear hypothesis during deduction (Zdravkovich, 1997) and the unknown influence of Pr bring about a necessity of studies on whether the relationship is still established for the wake of cylinder and the scope of the establishment. The power–law relationships fitted by the data of far wake (x/D ≥ 21) are shown in Figure 10A. For the case of LBE, it is obvious that W_T = 2.4567 (x/D)^0.3629 is almost valid in the whole wake, except for slight deviations at x/D < 5. However, the results for W_{T (Pr=0.71)} and W_U deviate sharply from the fitting curves when x/D < 21. It can be concluded that the self-preserving state of temperature appears from the near-wake region (x/D ≥ 5) for the case of LBE, while only in far wake (x/D ≥ 21) for the self-preserving states of temperature in the air and velocity.

Another notable thing is that even though the data of defect width in far wake satisfy the power–law relationships well, which has been validated in Figure 10A by the fact that R² is close to 1 for the three cases, especially for W_{T (Pr=0.025)}, the power–law coefficients differ from the theoretical value 0.5. The main reason is that some assumptions derived from the theory are different from the calculation conditions in this article. For example, the flow and temperature fields in this article are three-dimensional, not two-dimensional, and the observed region is not small-defect wake. This also reflects that the results of the theoretical derivation based on assumptions are not always applicable to the complicated situations such as the flow and heat transfer around a circular cylinder.

The following is to discuss the velocity scale and temperature scale. Figure 10B shows the relationships between u_df,c or T_df,c and x/D on the wake axis. The exponents of formulas for u_df,c, T_df,c (Pr = 0.71), and T_df,c (Pr = 0.025) are −0.403, −0.321, and −0.380, respectively, which are close to −0.5 with some deviations. As shown in Figure 10A, the power law describes the distribution of T_df,c well within the range of x/D = 5–30 in the LBE, but x/D > 15 for the case of air.

3.5.2 Transverse Profiles and Fluctuation Attenuation

As explained previously, the transverse profiles of velocity defect follow the Gaussian distribution for a small-defect wake (Wygnanski et al., 1986), that is, the region where u_df,c $\ll$ U_∞. The transverse profile of temperature will follow the Gaussian distribution as well, provided that Pr = 1, but show different patterns if Pr ≠ 1. In the following, the relationship between the profiles of defect variables and the Gaussian distribution is discussed.

The normalized transverse coordinates Y_T and Y_U, defined as follows, are introduced to illustrate the difference of profiles more clearly,

${\mathit{Y}}_{\mathit{T}}\mathit{=}\frac{{\mathit{y}}_{\mathit{i}}}{{\mathit{W}}_{\mathit{T,i}}},(15)$

${\mathit{Y}}_{\mathit{U}}\mathit{=}\frac{{\mathit{y}}_{\mathit{i}}}{{\mathit{W}}_{\mathit{U,i}}},(16)$

where y_i is the y-coordinate at the location of x_i; W_T,i and W_U,i are the temperature defect width and velocity defect width at the location of x_i, respectively. The profiles of normalized temperature defect T_df⁺ and normalized velocity defect u_df⁺ with Y_U and Y_T are plotted in Figures 11A–C, respectively. Considering the symmetry of the time-averaged field, the results of Y_U < 0 or Y_T < 0 are not shown here. According to Eq. 11–Eq. 16, these profiles collapse quite neatly onto a single curve described by the following formula:

${\mathit{T}}_{\mathit{df}}^{\mathit{+}}\mathit{=}{\mathrm{e}}^{\left(\mathrm{-2ln10}\right){\mathit{Y}}_{\mathit{T}}^{\mathit{2}}},(17)$

${\mathit{u}}_{\mathit{df}}^{\mathit{+}}\mathit{=}{\mathrm{e}}^{\left(\mathrm{-2ln10}\right){\mathit{Y}}_{\mathit{U}}^{\mathit{2}}}.(18)$

FIGURE 11

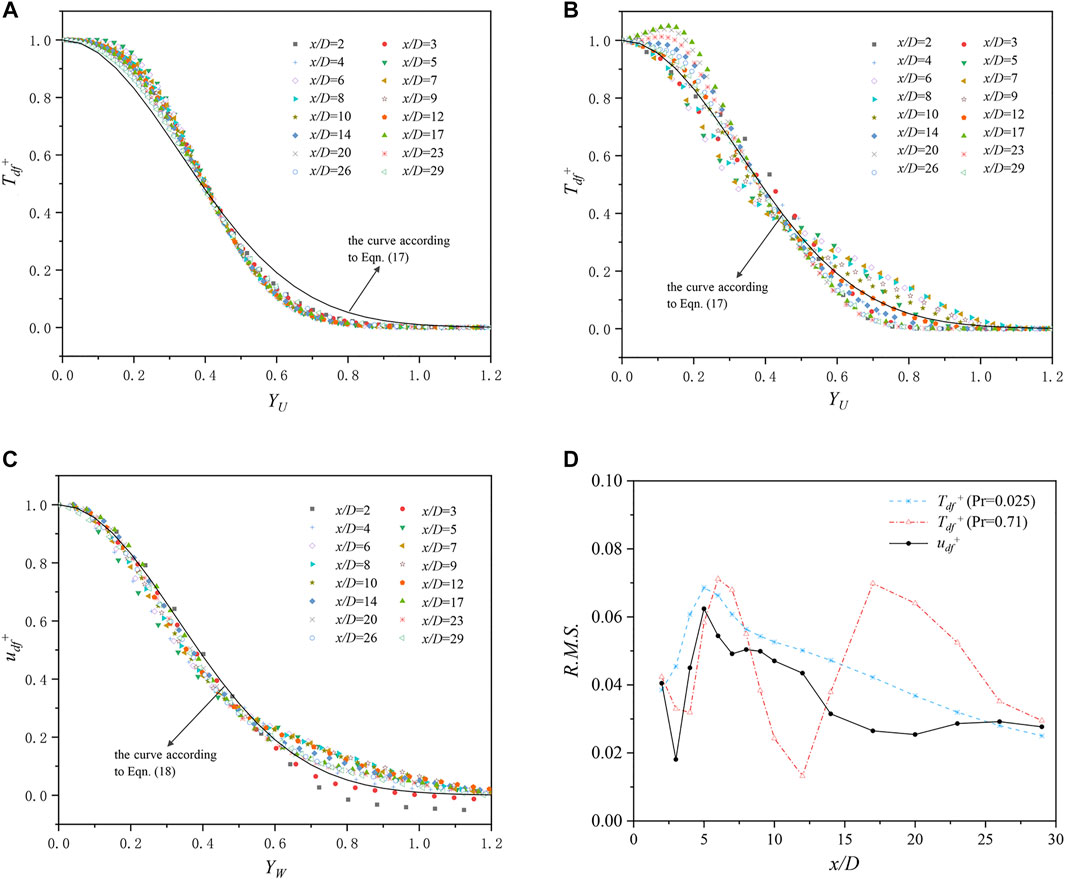
FIGURE 11. Transverse profiles of normalized temperature defect and normalized velocity defect. (A) T_df⁺ in the LBE, Pr = 0.025; (B) T_df⁺ in the air, Pr = 0.71; (C) u_df⁺; (D) R.M.S. of differences.

Figure 11 illustrates that the Gaussian distribution describes the profiles roughly with certain deviations presented by the R.M.S. of differences shown in Figure 11D.

The pattern of how the relative fluctuations on the wake axis decay, which stands for the dynamic similarity, is investigated before the discussions about the reasons of the deviations in Figure 11. The attenuation profiles of T′_rms/T_df,c, u′_rms/u_df,c, v′_rms/u_df,c, and w′_rms/u_df,c on the wake axis are given in Figure 12, where three stages can be generally observed. First, all relative fluctuations increase rapidly in the near-wake vortex street formation zone until x/D ≈ 5, and then different trends appear after that. Apart from a slight decrease near the location of x/D ≈ 5, T′_rms/T_df,c in the LBE almost maintains until the end of the computational domain, which means that the temperature of LBE experiences self-preserving state in this region. T′_rms/T_df,c in the air keeps declining rapidly after the peak at x/D ≈ 5, and the attenuation rate decreases from x/D ≈ 25, implying that the self-preserving state for the temperature in the air does not appear until x/D ≈ 25. Three components of velocity differ significantly in the entire wake and converge gradually at the end of the computational domain, indicating that the self-preserving state for the velocity does not show up within x/D < 30.

FIGURE 12

FIGURE 12. Distribution of T′_rms/T_df,c, u′_rms/u_df,c, v′_rms/u_df,c and w′_rms/u_df,c on wake axis.

The fact that the linear hypothesis introduces an assumption that u_df,c $\ll$ U_∞ when deducing the transverse profile (Wygnanski et al., 1986) results that the difference between the profiles and the Gaussian distribution is proportional to (u_df,c/U_∞)² in a small-defect far wake. Unignorable u_df,c/U_∞ leads to the deviations between the profile of velocity and the Gaussian distribution. Therefore, the R.M.S. of u_df⁺ in Figure 11D is noticeable. Nevertheless, the convergence of profile scatters improves after x/D > 15, which is consistent with Figure 12, where the distribution of three components of velocity tends to be flat.

The distribution of T_df⁺ for the air in Figure 11B is not centralized; therefore, the R.M.S. in Figure 11D is quite large until x/D > 25. The Gaussian distribution tends to overestimate T_df⁺ when Y_T < 0.4 and underestimate it when Y_T > 0.4 in the region of x/D < 10. Opposite phenomenon is observed in the region of x/D > 12. A local descent appears in the region of 6 < x/D < 12 in Figure 11D due to the presence of transition region 10 < x/D < 12. The descent of the attenuation rate of T′_rms/T_df,c (shown in Figure 12) corresponds to the smaller R.M.S. of difference for air in Figure 11D when x/D > 25.

The R.M.S. of T_df⁺ for the case of LBE in Figure 11D declines continuously when x/D > 5; therefore, the transversal profiles are well centered as it is under a self-preserving state. Even so, differences from the Gaussian distribution can be observed in Figure 11A, in which it tends to overestimate T_df⁺ when Y_T > 0.4 and underestimate it near the center of the wake. However, the differences are reasonable, considering that Pr of LBE is much smaller than unity.

3.5.3 Summary

As can be seen from Figure 12 and Figure 11D, the attenuation of relative fluctuation is consistent with the trend of the deviation between normalized temperature/velocity defect and the Gaussian distribution for the temperature in the LBE, the temperature in the air, and the velocity, except for the local descent in Figure 11D as explained above. In addition, Figure 10 shows that the sum of the exponents of temperature defect and temperature defect width is close to zero for both LBE and air cases, which is in good agreement with the law of “velocity defect width*velocity defect = constant” obtained from the wake of two-dimensional plate (Wygnanski et al., 1986; Zdravkovich, 1997), whereas the sum for the velocity deviates from zero. These results demonstrate that the velocity field has not entered the self-preserving state yet, whereas the self-preserving state starts from x/D = 5 for the temperature in the LBE and x/D = 21 for the temperature in the air, from another point of view.

It is obtained that the recovering length and the defect width of the temperature field of LBE flow show much larger than that of the conventional fluid flow (Pr close to 1). It indicates that in a helical coil steam generator, the flow and thermal boundaries may vary for pipes at different locations, and its performance will be significantly affected by the diameter, distance, and arrangement of the bundles. Improper design of bundle geometry may lead to uneven heat transfer, affect the heat exchange efficiency, and result in temperature hotspots. Therefore, a more adequate experimental/numerical verification is needed during the design of helical coil steam generators with LBE as the working fluid.

4 Conclusion

In this article, the flow and heat transfer characteristics of LBE (Pr = 0.025) and air (Pr = 0.71) passing a circular cylinder at Re = 500 are investigated by DNS method. The agreement of the numerical results with the literature verifies the effectiveness of the methodology. For the case of air, there exists a similarity among the instantaneous temperature, fluctuating temperature, and velocity fields in the wake downstream the cylinder, whereas these fields differ severely for the case of LBE. The temperature boundary layer of LBE is thicker than that of air. The downstream temperature is more affected by the wall temperature of the cylinder, and a large region of low temperature can be recognized. The main conclusions are as follows:

1) The circumferentially averaged $\overline{Nu}$ is 2.94 and 11.39 for LBE and air, respectively. Local $\overline{Nu}$ decreases gradually because of the thickening of the boundary layer in the range of φ = 0°–117° for both cases, and then the trends of the two cases differ beyond that. Both the local $\overline{Nu}$ and circumferentially averaged $\overline{Nu}$ are smaller in the LBE. The circumferential and spanwise distributions of $\overline{Nu}$ in the LBE are more uniform than that of air. The region with larger circumferential or spanwise inhomogeneity appears in the flow separation zone for both cases.

2) The temperature fluctuation of LBE is smaller in both the bulk region and the near wall region. A resemblance between the distribution of the R.M.S. of fluctuation temperature T′_rms and the turbulence kinetic energy k can be recognized in the air, but it disappears for the case of LBE.

3) By introducing the velocity defect as the velocity scale, the temperature defect as the temperature scale and the defect width as the length scale, the self-preserving state and the similarity or deviation between the Gaussian distribution and the transverse profiles of velocity defect and temperature defect are fully discussed. It is found that the velocity field has not entered the self-preserving state yet, whereas the self-preserving state starts from x/D = 5 for the temperature in the LBE and x/D = 21 for the temperature in the air.

To obtain a more general database, the temperature calculated in this article is nondimensionalized. If extended to dimensional situations, these data will have a certain degree of confidence under the cases within a small temperature variation, where the influence of buoyancy can be ignored. For the case of large temperature difference, the influence of buoyancy cannot be ignored, and constant physical properties are inappropriate. In that way, further simulations are needed to determine the error quantitatively. Considering the amount of calculation, this will be carried out in future work.

In a reactor, LBE experiences various working conditions, including different flow rates and different temperatures. In the initial stage of the research, a series of databases with different Prs and an Re at low/medium level are carried out. Generation of a database with high Res and different Prs is ongoing. In the engineering field, database under an Re of 500 and different Prs can be used not only for comparison and verification with experimental results and RANS simulation, but also for the development of turbulence heat flux models, which will be extended to more complex conditions with higher Re with the supplementation of databases under other Re.

In conclusion, a fruitful description of the flow and heat transfer of the LBE passing a circular cylinder is presented, which is a typical flow in a helical coil steam generator of an LFR. Even without consideration of buoyancy, these highly resolved data on velocity and temperature are valuable for turbulence and heat fluxes modeling in the future, especially for liquid–metal flow with extremely low Prs within a limited variation range of operating temperature.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Methodology, L-XC and H-NZ; Software, H-NZ, L-XC, and CY; Formal Analysis, L-XC, and J-LZ; Investigation, F-CL, L-XC, CY, and J-LZ; Supervision and resources, YM and F-CL; Writing—Original Draft, L-XC and CY; Writing—Review and Editing, L-XC, H-NZ, YM, and F-CL; Funding acquisition, J-LZ, H-NZ, YM and F-CL All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant numbers 51976238, 51776057, 52006249 and U1830118) and the open fund project of Key Laboratory of Thermal Power Technology (Grant number TPL2018B02).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.823590/full#supplementary-material

References

Abram, T., and Ion, S. (2008). Generation-IV Nuclear Power: A Review of the State of the Science. Energy Policy 36, 4323–4330. doi:10.1016/j.enpol.2008.09.059

CrossRef Full Text | Google Scholar

Batta, A., Class, A. G., Litfin, K., Wetzel, T., Moreau, V., Massidda, L., et al. (2015). Experimental and Numerical Investigation of Liquid-Metal Free-Surface Flows in Spallation Targets. Nucl. Eng. Des. 290, 107–118. doi:10.1016/j.nucengdes.2014.11.009

CrossRef Full Text | Google Scholar

Chen, M. (2002). Fundamentals of Viscous Fluid Dynamics (Chinese). Beijing: Higher Education Press.

Google Scholar

Cho, J. H., Batta, A., Casamassima, V., Cheng, X., Choi, Y. J., Hwang, I. S., et al. (2011). Benchmarking of thermal Hydraulic Loop Models for Lead-Alloy Cooled Advanced Nuclear Energy System (LACANES), Phase-I: Isothermal Steady State Forced Convection. J. Nucl. Mater. 415, 404–414. doi:10.1016/j.jnucmat.2011.04.043

CrossRef Full Text | Google Scholar

Churchill, S. W., and Bernstein, M. (1977). A Correlating Equation for Forced Convection from Gases and Liquids to a Circular cylinder in Crossflow. J. Heat Transf. 99, 300–306. doi:10.1115/1.3450685

CrossRef Full Text | Google Scholar

Concetta, F. (2015). Handbook on Lead-bismuth Eutectic Alloy and Lead Properties, Materials Compatibility, Thermal-hydraulics and Technologies. 2015 Edition. Paris: OECD.

Google Scholar

De Santis, A., and Shams, A. (2018). Application of an Algebraic Turbulent Heat Flux Model to a Backward Facing Step Flow at Low Prandtl Number. Ann. Nucl. Energ. 117, 32–44. doi:10.1016/j.anucene.2018.03.016

CrossRef Full Text | Google Scholar

Greenspan, E., Hong, S. G., Lee, K. B., Monti, L., Okawa, T., Susplugas, A., et al. (2008). Innovations in the ENHS Reactor Design and Fuel Cycle. Prog. Nucl. Energ. 50, 129–139. doi:10.1016/j.pnucene.2007.10.022

CrossRef Full Text | Google Scholar

Guo, C., Lu, D., Zhang, X., and Sui, D. (2015). Development and Application of a Safety Analysis Code for Small Lead Cooled Fast Reactor SVBR 75/100. Ann. Nucl. Energ. 81, 62–72. doi:10.1016/j.anucene.2015.03.021

CrossRef Full Text | Google Scholar

Habibi Khalaj, A., and Halgamuge, S. K. (2017). A Review on Efficient thermal Management of Air- and Liquid-Cooled Data Centers: From Chip to the Cooling System. Appl. Energ. 205, 1165–1188. doi:10.1016/j.apenergy.2017.08.037

CrossRef Full Text | Google Scholar

Ince, N. Z., and Launder, B. E. (1989). On the Computation of Buoyancy-Driven Turbulent Flows in Rectangular Enclosures. Int. J. Heat Fluid Flow 10, 110–117. doi:10.1016/0142-727X(89)90003-9

CrossRef Full Text | Google Scholar

Jeong, J., and Hussain, F. (1995). On the Identification of a Vortex. J. Fluid Mech. 285, 69–94. doi:10.1017/s0022112095000462

CrossRef Full Text | Google Scholar

Jiang, H. Y. (2020). Separation Angle for Flow Past a Circular cylinder in the Subcritical Regime. Phys. Fluids 32, 014106. doi:10.1063/1.5139479

CrossRef Full Text | Google Scholar

Kawamura, H., Abe, H., and Matsuo, Y. (1999). DNS of Turbulent Heat Transfer in Channel Flow with Respect to Reynolds and Prandtl Number Effects. Int. J. Heat Fluid Flow 20, 196–207. doi:10.1016/s0142-727x(99)00014-4

CrossRef Full Text | Google Scholar

Kawamura, H., Ohsaka, K., Abe, H., and Yamamoto, K. (1998). DNS of Turbulent Heat Transfer in Channel Flow with Low to Medium-High Prandtl Number Fluid. Int. J. Heat Fluid Flow 19, 482–491. doi:10.1016/S0142-727X(98)10026-7

CrossRef Full Text | Google Scholar

Knebel, J. U., Müller, G., and Konys, (2002). “Lead-Bismuth Activities at the Karlsruhe Lead Laboratory KALLA,” in International Conference on Nuclear Engineering (Arlington, VA: ASME). doi:10.1115/icone10-22240

CrossRef Full Text | Google Scholar

Krall, K. M., and Eckert, E. R. G. (1973). Local Heat Transfer Around a Cylinder at Low Reynolds Number. J. Heat Transf. 95, 273–275. doi:10.1115/1.3450044

CrossRef Full Text | Google Scholar

Lefhalm, C.-H., Tak, N.-I., Piecha, H., and Stieglitz, R. (2004). Turbulent Heavy Liquid Metal Heat Transfer along a Heated Rod in an Annular Cavity. J. Nucl. Mater. 335, 280–285. doi:10.1016/j.jnucmat.2004.07.028

CrossRef Full Text | Google Scholar

Ma, W., Bubelis, E., Karbojian, A., Sehgal, B. R., and Coddington, P. (2006). Transient Experiments from the thermal-hydraulic ADS lead Bismuth Loop (TALL) and Comparative TRAC/AAA Analysis. Nucl. Eng. Des. 236, 1422–1444. doi:10.1016/j.nucengdes.2006.01.006

CrossRef Full Text | Google Scholar

Marocco, L., Loges, A., Wetzel, T., and Stieglitz, R. (2012). Experimental Investigation of the Turbulent Heavy Liquid Metal Heat Transfer in the thermal Entry Region of a Vertical Annulus with Constant Heat Flux on the Inner Surface. Int. J. Heat Mass Transfer 55, 6435–6445. doi:10.1016/j.ijheatmasstransfer.2012.06.037

CrossRef Full Text | Google Scholar

Muhammad, A., Selvakumar, D., and Wu, J. (2020). Numerical Investigation of Laminar Flow and Heat Transfer in a Liquid Metal Cooled Mini-Channel Heat Sink. Int. J. Heat Mass Transfer 150, 119265. doi:10.1016/j.ijheatmasstransfer.2019.119265

CrossRef Full Text | Google Scholar

Norberg, C. (2003). Fluctuating Lift on a Circular cylinder: Review and New Measurements. J. Fluids Structures 17, 57–96. doi:10.1016/s0889-9746(02)00099-3

CrossRef Full Text | Google Scholar

Redjem-Saad, L., Ould-Rouiss, M., and Lauriat, G. (2007). Direct Numerical Simulation of Turbulent Heat Transfer in Pipe Flows: Effect of Prandtl Number. Int. J. Heat Fluid Flow 28, 847–861. doi:10.1016/j.ijheatfluidflow.2007.02.003

CrossRef Full Text | Google Scholar

Roelofs, F., Shams, A., Otic, I., Böttcher, M., Duponcheel, M., Bartosiewicz, Y., et al. (2015). Status and Perspective of Turbulence Heat Transfer Modelling for the Industrial Application of Liquid Metal Flows. Nucl. Eng. Des. 290, 99–106. doi:10.1016/j.nucengdes.2014.11.006

CrossRef Full Text | Google Scholar

Roelofs, F. (2019). Thermal Hydraulics Aspects of Liquid Metal Cooled Nuclear ReactorsCambridge. Cambridge: Woodhead Publishing.

Google Scholar

Shams, A., De Santis, A., and Roelofs, F. (2019). An Overview of the AHFM-NRG Formulations for the Accurate Prediction of Turbulent Flow and Heat Transfer in Low-Prandtl Number Flows. Nucl. Eng. Des. 355, 110342. doi:10.1016/j.nucengdes.2019.110342

CrossRef Full Text | Google Scholar

Shen, Y., Peng, S., Yan, M., Zhang, Y., Deng, J., Yu, H., et al. (2021). Study of Flow and Heat Transfer Characteristics of Lead-Based Liquid Metals in a Turbulent Tube Flow and the Impacts of Roughness. Front. Energ. Res. 9, 634964. doi:10.3389/fenrg.2021.634964

CrossRef Full Text | Google Scholar

Tarantino, M., De Grandis, S., Benamati, G., and Oriolo, F. (2008). Natural Circulation in a Liquid Metal One-Dimensional Loop. J. Nucl. Mater. 376, 409–414. doi:10.1016/j.jnucmat.2008.02.080

CrossRef Full Text | Google Scholar

Todreas, N. E., and Kazim, M. S. (2011). Nuclear Systems Volume I: Thermal Hydraulic Fundamentals. 2nd edn. Boca Raton: CRC Press.

Google Scholar

Versteeg, H. K., and Malalasekera, W. (2007). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Second Edition. Harlow: Pearson Education Limited.

Google Scholar

Weigand, B., Ferguson, J. R., and Crawford, M. E. (1997). An Extended Kays and Crawford Turbulent Prandtl Number Model. Int. J. Heat Mass Transfer 40, 4191–4196. doi:10.1016/S0017-9310(97)00084-7

CrossRef Full Text | Google Scholar

Wygnanski, I., Champagne, F., and Marasli, B. (1986). On the Large-Scale Structures in Two-Dimensional, Small-Deficit, Turbulent Wakes. J. Fluid Mech. 168, 31–71. doi:10.1017/S0022112086000289

CrossRef Full Text | Google Scholar

Zdravkovich, M. M. (1997). Flow Around Circular Cylinders Volume 1 Fundamentals. New York: Oxford University Press.

Google Scholar

Zhang, Y., Wang, C., Cai, R., Lan, Z., Shen, Y., Zhang, D., et al. (2020). Experimental Investigation on Flow and Heat Transfer Characteristics of lead-bismuth Eutectic in Circular Tubes. Appl. Therm. Eng. 180, 115820. doi:10.1016/j.applthermaleng.2020.115820

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, C., Lan, Z., Wei, S., Chen, R., Tian, W., et al. (2020). Review of Thermal-Hydraulic Issues and Studies of Lead-based Fast Reactors. Renew. Sustainable Energ. Rev. 120, 109625. doi:10.1016/j.rser.2019.109625

CrossRef Full Text | Google Scholar

Zhao, P., Ge, Z., Zhu, J., Liu, J., and Ye, M. (2018). Quasi-direct Numerical Simulation of Forced Convection over a Backward-Facing Step: Effect of Prandtl Number. Nucl. Eng. Des. 335, 374–388. doi:10.1016/j.nucengdes.2018.05.012

CrossRef Full Text | Google Scholar