Production Analysis of Horizontal Wells in a Two-Region Composite Reservoir Considering Formation Damage

The horizontal well is extensively used to exploit oil at the Bohai offshore oilfield, China. It has been proved by practice that formation damage always happens during the production of wells. However, it is a challenging task to evaluate the formation damage for horizontal wells. In this paper, a flow model considering formation damage is established for horizontal wells. The reservoir geometry is divided into two regions: the inner region represents the region of formation damage and the outer region that without damage. The finite element method is used to solve the flow model. The well production rate can be determined by using the material balance method. For different scenarios, such as when the horizontal well is completely in the inner region or when the horizontal well passes through two regions, the effects of some key parameters such as damage radius, damage region permeability, and well position on the oil production rate and pressure distribution characteristics are analyzed. The results show that a smaller damage radius, higher damage zone permeability, and a horizontal well closer to or in greater contact with the outer region result in a higher oil production rate and faster pressure drop propagation. The presented model and obtained results enrich production analysis of horizontal wells in a two-region composite reservoir considering formation damage, which has significance for efficient offshore reservoir development.

Introduction

Formation damage is a condition most commonly caused by wellbore fluids used during drilling, completion, and workover operations (Krueger, 1988; Civan, 2015; Xu et al., 2016). It impairs the permeability of reservoir rocks, thereby reducing the natural productivity of reservoirs (The Defining Series: Formation Damage, Schlumberger, slb.com). Before drilling the reservoir, the rocks, clay minerals, and fluids are at an equilibrium. After opening the reservoir, the original equilibrium state is broken due to the external fluid, which will harm the oil and gas reservoir and reduce the production capacity of oil and gas. Changes in the physical and chemical properties of rocks and fluids in the formation are the most fundamental causes of formation damage. The categories of formation damage mechanisms can be divided into mechanical, chemical, biological, and thermal.

Field development practice on onshore oilfields indicates that formation damage can lead to low production efficiency for wells, and the effect of formation damage on reservoir properties and well performance should be carefully evaluated. Shen et al. studied the effects of key reservoir and production parameters (matrix porosity and permeability, fracture porosity and permeability, Langmuir pressure and volume, diffusion coefficient, shut-in time, drawdowns, and injection rate) on the process of water retention and gas production in the shale gas reservoirs (Shen et al., 2016). Zhang et al. investigated the effects of the related reservoir properties and production parameters on the characteristics of effective reserve utilization in tight sandstone reservoirs, which provide a better understanding of reservoir pressure distribution and effective utilization of reserves to optimize the gas recovery and development (Zhang et al., 2020).

Commonly, transient pressure responses and rate decline analysis are applied to inverse the formation parameters such as skin factor, damage zone radius, and damage zone permeability. As the parameters in the damaged zone and undamaged zone are always different, a composite reservoir model must be established. A large number of previous studies have focused on the curves type of horizontal wells. In 1973, Gringarten and Ramey proposed source function and green function methods which are used as powerful tools in solving unsteady flow problems for horizontal wells (Gringarten and Ramey, 1973). Clonts and Ramey presented an analytical solution for a uniform flux horizontal drainhole in an anisotropic reservoir (Clonts and Ramey, 1986). Log-log type curves are presented for various drainhole radii and can be used to determine reservoir parameters such as permeability or drainhole half length. Goode and Thambynayagam proposed an analytical solution by solving the three-dimensional diffusion equation with successive integral transforms for the pressure response during drawdown and buildup of a horizontal well (Goode and Thambynayagam, 1987). Daviau et al. (Daviau et al., 1988) proposed a new solution to analyze the pressure response by semi-log and log-log curves. They found that a circular radial flow will happen in early time and a horizontal pseudo-radial flow will happen in late time. Then, Ozkan and Raghavan (Ozkan and Raghavan, 1991a; Ozkan and Raghavan, 1991b; Ozkan, 1994) proposed a new source function approach to study transient pressure behaviors of different well patterns, such as those of vertical wells and horizontal wells, in various reservoirs. This method remains one of the primary solving methods in the performance analysis family. Park and Zhan simplified the horizontal well into a line source and analyzed the wellbore storage and skin effect (Park and Zhan, 2002). Ezulike and Igbokoyi achieved a three-dimensional point source semi-analytical solution in composite reservoir systems (Ezulike and Igbokoyi, 2012). Shi et al. (Shi et al., 2012) developed the well test model for horizontal wells in a two-zone composite reservoir and presented the field interpretation example. Nie et al. established a new transient well test and rate decline analysis model for a horizontal well in multiple-zone composite reservoirs. The negative skin is considered in their model (Nie et al., 2011). Zhao et al. established a composite model to describe the stimulated reservoir volume for multiple hydraulic fractured horizontal wells (Zhao et al., 2014). Yuan et al. (Yuan et al., 2018) proposed a semi-analytical solution for well pressure transient analysis and transient rate analysis of multistage fractured horizontal wells in composite reservoirs in which two regions with different formation parameters are considered. By now, the semi-analytical methods have been widely used for transient pressure responses and rate decline analysis in unconventional oil and gas reservoirs (Jiang et al., 2014; Xu et al., 2015; Zeng et al., 2015; Zhang et al., 2016; Ren and Guo, 2017; Zhao et al., 2018; Zhang et al., 2019; Yao et al., 2020).

To the best of our knowledge, although it has been decades since people started studying well performance analysis theories of horizontal wells, there exists a little model that can successfully calculate the performance behavior for reservoirs with formation damage. In this paper, the composite reservoir model is extended to evaluate the formation damage effect on well production. The mathematical equation is derived for the inner region and outer region. The inner region characterizes the damaged zone. The damaged zone can have an irregular boundary. To solve the flow model, the finite element method is employed. The horizontal well production rate is calculated by using the material balance method. The effect of damage radius, damage region permeability, and well position on oil production rate is analyzed.

The paper is organized as follows: section 1 is the introduction; section 2 is the mathematical model; section 3 is the solution workflow; section 4 is the sensitivity analysis.

System Description

Physical Model

The schematic diagram for a horizontal well in a composite reservoir is shown in Figure 1. The reservoir has two regions, the inner and outer region, each of which have different reservoir properties. The model assumptions are as follows: 1) the interface between the inner region and outer region is irregular (commonly, the inner region can be assumed to have a circular shape and the radius can be assumed to be r₁); 2) the reservoir is horizontal with a uniform thickness of h and original pressure pi; 3) for the inner region, the horizontal permeability is K_h1, the vertical permeability is Kv1, the compressibility C_t1, and the porosity is φ₁ while for the outer region, they are K_h2, K_v2, C_t2, and φ₂, respectively; 4) the influence of gravity and capillary forces is ignored. In this paper, assuming that the inner region is the damage region, we considered the scenario when the horizontal well is entirely in the inner region (Figure 1A) and when the horizontal well passes through two regions (Figures 1B,C).

FIGURE 1

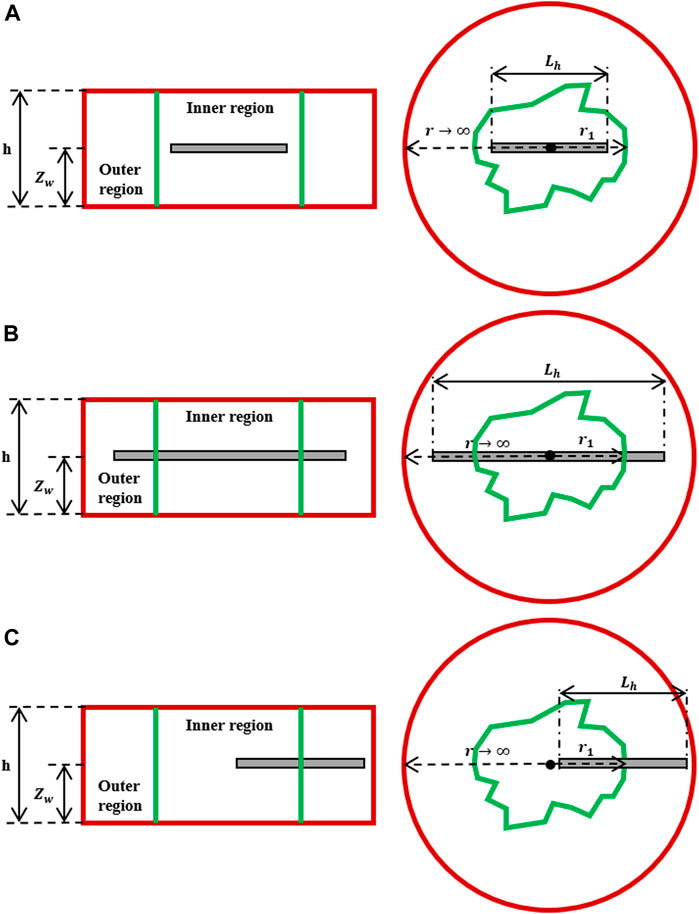
FIGURE 1. Schematic of a horizontal well. (A) Horizontal well in the inner region. (B) Horizontal well passing through both inner region and outer region on both sides. (C) Horizontal well passing through both inner region and outer region on single side.

Mathematical Model

With an orthogonal coordinate system, the flow equation can be expressed as follows:

The flow equation in the inner region is

$\frac{\partial }{\partial x}\left(\frac{K_{1h}}{\mu }\frac{\partial p_1}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{1h}}{\mu }\frac{\partial p_1}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{1v}}{\mu }\frac{\partial p_1}{\partial z}\right)={\varphi }_1{C}_{t1}\frac{\partial p_1}{\partial t}+q(1)$

The flow equation in the outer region is

$\frac{\partial }{\partial x}\left(\frac{K_{2h}}{\mu }\frac{\partial p_2}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{2h}}{\mu }\frac{\partial p_2}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{2v}}{\mu }\frac{\partial p_2}{\partial z}\right)={\varphi }_2{C}_{t2}\frac{\partial p_2}{\partial t}+q(2)$

If the sink or source is ignored, Eqs. 1, 2 can be simplified into the following:

The flow equation in the inner region is

$\frac{\partial }{\partial x}\left(\frac{K_{1h}}{\mu }\frac{\partial p_1}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{1h}}{\mu }\frac{\partial p_1}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{1v}}{\mu }\frac{\partial p_1}{\partial z}\right)={\varphi }_1{C}_{t1}\frac{\partial p_1}{\partial t}(3)$

The flow equation in the outer region is

$\frac{\partial }{\partial x}\left(\frac{K_{2h}}{\mu }\frac{\partial p_2}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{2h}}{\mu }\frac{\partial p_2}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{2v}}{\mu }\frac{\partial p_2}{\partial z}\right)={\varphi }_2{C}_{t2}\frac{\partial p_2}{\partial t}(4)$

With initial condition

$p\left(x,y,z,t=0\right)=p_i(5)$

and outer boundary

$\begin{array}{cc}\frac{\partial p_1}{\partial z}=\frac{\partial p_2}{\partial \tilde{z}}=0,& z=0\text{or}\text{h}\end{array}(6)$

$\begin{array}{cc}{p}_2=0,& r=\infty \end{array}(7)$

and interface condition

$\begin{array}{cc}{p}_1=p_2,& r=r_1\end{array}(8)$

$\begin{array}{cc}\frac{k_{1h}}{\mu }\frac{\partial p_1}{\partial r}=\frac{k_{2h}}{\mu }\frac{\partial p_2}{\partial r},& r=r_1\end{array}(9)$

Here, x, y, and z are the directional coordinates, m; r is the radial distance from the origin of a point in the XY plane; L is the well length, m; k₁ and k₂ are the permeability in inner and outer regions, respectively,m²; p_1,2 are reservoir pressure in inner and outer regions, respectively, Pa; p_i is reference pressure, Pa; μ is viscosity, Pa·s; t is time, sec; C_t is the compressibility factor, 1/Pa; and φ_1,2 are the formation porosity in inner and outer regions, respectively, fraction.

Model Solution

Solution Method

In this study, we use the finite element method to solve the equation system. The basic function is defined as follows:

$N=\left(N_1,N_2\dots N_n\right)(10)$

The displacement function is

$\tilde{p}={\displaystyle \sum _{i=1}^n{N}_i{p}_i}(11)$

We can get the integrating form for the inner region and outer region:

${\displaystyle \underset{{\text{Ω}}_e}{\iiint }{N}_i\left[\frac{\partial }{\partial x}\left(\frac{K_{1h}}{\mu }\frac{\partial {\tilde{p}}_1}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{1h}}{\mu }\frac{\partial {\tilde{p}}_1}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{1v}}{\mu }\frac{\partial {\tilde{p}}_1}{\partial z}\right)\right]}dV={\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left({\varphi }_1{C}_{t1}\right)N_i\frac{\partial {\tilde{p}}_1}{\partial t}dV}(12)$

${\displaystyle \underset{{\text{Ω}}_e}{\iiint }{N}_i\left[\frac{\partial }{\partial x}\left(\frac{K_{2h}}{\mu }\frac{\partial {\tilde{p}}_2}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{2h}}{\mu }\frac{\partial {\tilde{p}}_2}{\partial y}\right)+\frac{\partial }{\partial z}\left(\frac{K_{2v}}{\mu }\frac{\partial {\tilde{p}}_2}{\partial z}\right)\right]}dV={\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left({\varphi }_2{C}_{t2}\right)N_i\frac{\partial {\tilde{p}}_2}{\partial t}dV}(13)$

The final equation form is as follos:

$\begin{array}{l}{\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left\{\left(\frac{K_{1h}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial x}\\ \frac{\partial N_2}{\partial x}\\ ⋮\\ \frac{\partial N_n}{\partial x}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial x}& \frac{\partial N_2}{\partial x}& \cdots & \frac{\partial N_n}{\partial x}\end{array}\right)+\left(\frac{K_{1h}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial y}\\ \frac{\partial N_2}{\partial y}\\ ⋮\\ \frac{\partial N_n}{\partial y}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial y}& \frac{\partial N_2}{\partial y}& \cdots & \frac{\partial N_n}{\partial y}\end{array}\right)+\left(\frac{K_{1v}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial z}\\ \frac{\partial N_2}{\partial z}\\ ⋮\\ \frac{\partial N_n}{\partial z}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial z}& \frac{\partial N_2}{\partial z}& \cdots & \frac{\partial N_n}{\partial z}\end{array}\right)\right\}\left(\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_n\end{array}\right)dV}\\ +{\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left({\varphi }_1{C}_{t1}\right)\left(\begin{array}{c}{N}_1\\ N_2\\ ⋮\\ N_n\end{array}\right)\left(\begin{array}{cccc}{N}_1& N_2& \cdots & N_n\end{array}\right)\left(\begin{array}{c}\frac{p_1^n-p_1^{n-1}}{\text{Δ}t}\\ \frac{p_2^n-p_2^{n-1}}{\text{Δ}t}\\ ⋮\\ \frac{p_n^n-p_n^{n-1}}{\text{Δ}t}\end{array}\right)dV}=0\end{array}(14)$

$\begin{array}{l}{\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left\{\left(\frac{K_{2h}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial x}\\ \frac{\partial N_2}{\partial x}\\ ⋮\\ \frac{\partial N_n}{\partial x}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial x}& \frac{\partial N_2}{\partial x}& \cdots & \frac{\partial N_n}{\partial x}\end{array}\right)+\left(\frac{K_{2h}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial y}\\ \frac{\partial N_2}{\partial y}\\ ⋮\\ \frac{\partial N_n}{\partial y}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial y}& \frac{\partial N_2}{\partial y}& \cdots & \frac{\partial N_n}{\partial y}\end{array}\right)+\left(\frac{K_{2v}}{\mu }\right)\left(\begin{array}{c}\frac{\partial N_1}{\partial z}\\ \frac{\partial N_2}{\partial z}\\ ⋮\\ \frac{\partial N_n}{\partial z}\end{array}\right)\left(\begin{array}{cccc}\frac{\partial N_1}{\partial z}& \frac{\partial N_2}{\partial z}& \cdots & \frac{\partial N_n}{\partial z}\end{array}\right)\right\}\left(\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_n\end{array}\right)dV}\\ +{\displaystyle \underset{{\text{Ω}}_e}{\iiint }\left({\varphi }_2{C}_{t2}\right)\left(\begin{array}{c}{N}_1\\ N_2\\ ⋮\\ N_n\end{array}\right)\left(\begin{array}{cccc}{N}_1& N_2& \cdots & N_n\end{array}\right)\left(\begin{array}{c}\frac{p_1^n-p_1^{n-1}}{\text{Δ}t}\\ \frac{p_2^n-p_2^{n-1}}{\text{Δ}t}\\ ⋮\\ \frac{p_n^n-p_n^{n-1}}{\text{Δ}t}\end{array}\right)dV}=0\end{array}(15)$

Material Balance Method

Combined with the natural energy production calculation formula, the finite element numerical method is used to solve and analyze the oil production rate under different damage degrees in the process of oilfield development. Natural energy production means the volume of fluid displaced by natural energy due to pore compression and liquid expansion.

Oil production of reservoir driven by natural energy can be obtained from the following formula:

$\text{Δ}V=C_t{V}_f\left(p_i-p_b\right)(16)$

The finite element numerical solution method introduced in Section 3.1 can obtain the pressure values of each position in the composite reservoir at each time. However, because the pressure values at different positions in the composite reservoir are not equal at different times, volume integration is performed over the entire reservoir. The production rate considering formation damage can be obtained by the following formula:

$N_p={\displaystyle {\iiint }_{V_f}{C}_t\left(p_t-p_w\right)d{V}_f}(17)$

$C_t=C_f+\varphi C_l(18)$

Where △V is the reserves, m³; C_t is the comprehensive compressibility, 1/Pa; V_f is the composite reservoir volume, m³; p_i is the original pressure of reservoir, Pa; p_b is reservoir saturation pressure, Pa; N_p is the cumulative oil production corresponding to the total pressure drop, m³; p_t is the pressure at a certain position in the reservoir at time t, Pa; p_w is bottom hole pressure, Pa; φ are the formation porosity; C_f is the formation fluid compressibility, 1/Pa; and C_l is the formation rock compressibility, 1/Pa.

Discussion and Analysis

Typical Transient Pressure Distribution and production Rate Decline Curve

Basic parameters to be paid attention to: r₂ = 600 m, K_h1 = K_v1 = 0.002 μm² and h = 10 m.

Typical case 1: r₁ = 300 m and the center coordinate of horizontal well is (0, 0, 5).

Typical case 2: r₁ = 150 m and the center coordinate of horizontal well is (0, 0, 5).

Typical case 3: r₁ = 200 m, and the center coordinate of horizontal well is (200, 0, 5).

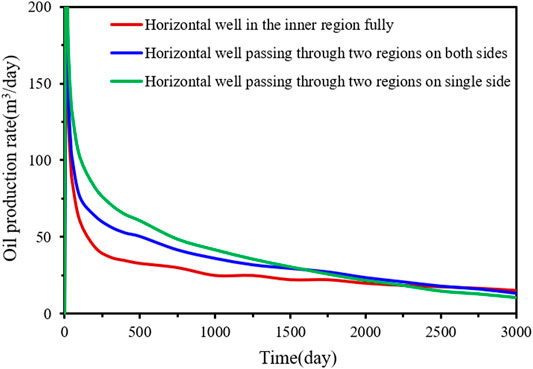
Figures 2A–C shows the typical transient pressure distribution of horizontal well in the inner region, horizontal well passing through two regions on both sides and horizontal well passing through two regions on single sides, respectively. The transient pressure profiles of the three typical cases describe the pressure distributions at different times in the three typical cases. By comparison, the pressure drops when the horizontal well passing through two regions on a single side propagates faster. Figure 3 shows the production rate decline curves for the above three cases. As shown in Figure 3, the oil production rate of the horizontal well entirely in the inner region is basically lower than that of the other two scenarios. The reason for this is that the permeability of the inner region is lower than that of the outer region, whereas when a horizontal well is entirely in the inner region, the pressure drop propagation is more affected by the damage of the inner region and becomes slower.

FIGURE 2

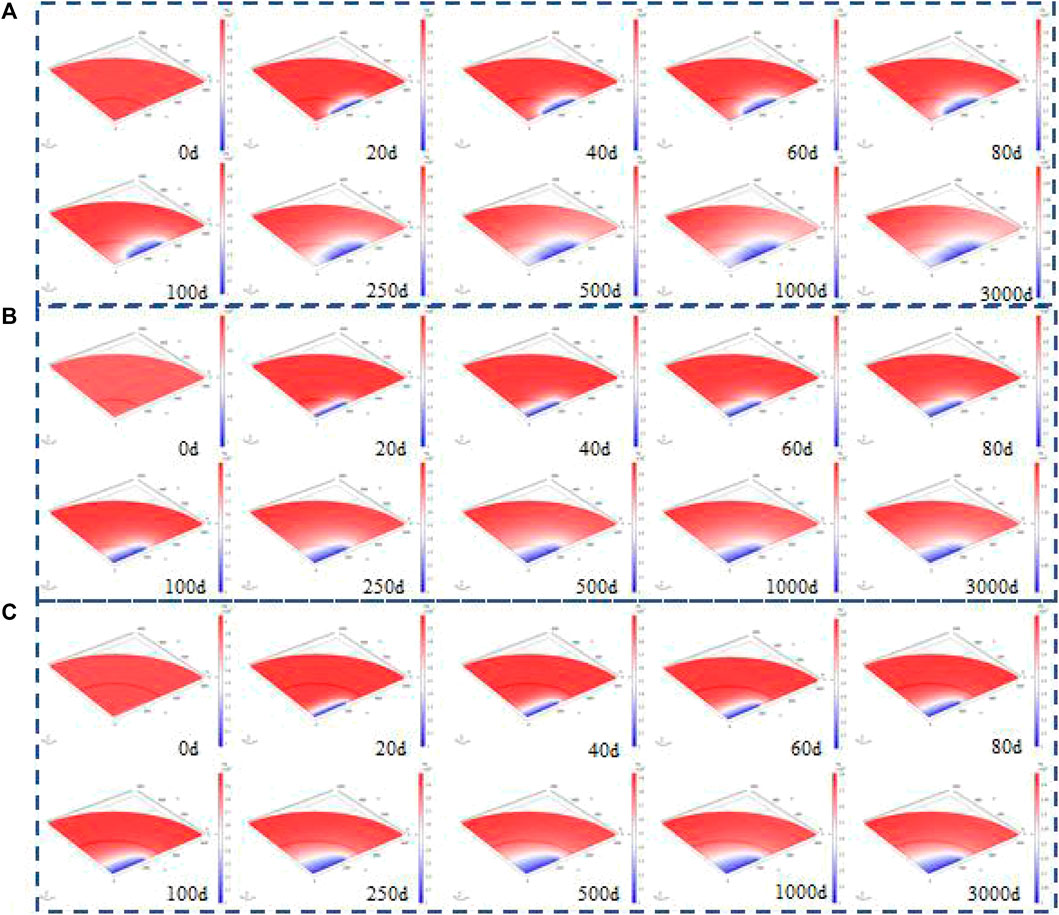
FIGURE 2. Typical transient pressure distribution of (A) a horizontal well fully in the inner region, (B) a horizontal well passing through two regions on both sides, and (C) a horizontal well passing through two regions on a single side.

FIGURE 3

FIGURE 3. Production rate decline curves for the above three cases.

Effects of Different Parameters

In this section, the effects that various reservoirs parameters have on the performance (transient pressure distribution and production rate decline performance) of a composite reservoir described mathematically in the previous section are discussed. The effects of damage radius, damage region permeability, and well position on oil production rate are discussed for the scenario when the horizontal well is entirely in the inner region (Figure 1A) and when the horizontal well passes through two regions (Figures 1B,C).

Case 1. Horizontal well completely in the inner regionThe effects of damage radius, damage region permeability, and well position on oil production rate are discussed. The parameters used are shown in Table 1.Sensitivity analysis of different parameters are as follows:

(1) Effect of inner region radius

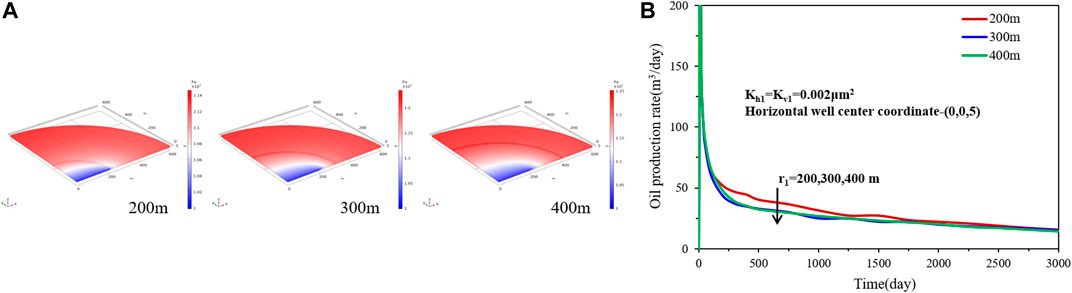
To analyze the effect of inner radius, three different inner region radii, 200 m, 300 m, and 400 m, are considered. The horizontal well center coordinate is (0,0,5), and the inner region permeability is 0.002 μm².Figure 4 compares the differences in the transient pressure distribution and the rate decline performance for case 1. The transient pressure distribution shows that the damage radius has an effect on pressure drop propagation. As the damage radius becomes great, the pressure drop will propagate slowly. From the rate decline curves, it can be seen that the bigger the inner region radius, the smaller the production rate, but the decline rate will be slower. The reason is that a higher outer region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. It should be noted that when the damage radius reaches a certain size, its influence on the production rate is not obvious. In the later stage, different damage radius has little effect on the oil production rate.

(2) Effect of inner region permeability

To analyze the effect of inner region permeability, three different damage region permeability, 0.001 μm², 0.002 μm², and 0.003 μm² are considered. The horizontal well center coordinate is (0,0,5) and the inner region radius is 300 m.Figure 5 shows the effect of inner region permeability on the transient pressure distribution as well as on the rate performance for case 1. For different damage region permeability, the pressure drops propagate at different rates. It can be seen that the greater inner region permeability results in a faster pressure drop propagation rate. The reason is that a higher inner region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. The comparison of the results of the production rate shows that the damage region radius has an obvious effect on the production rate and decline rate. A higher inner region permeability causes a bigger production rate but a faster decline rate.

(3) Effect of horizontal well position

To analyze the effect of horizontal well position, three different well positions, (0, 0, 5, 0, 100, 5), and (0,200,5), are considered. The inner region radius is 300 m, and the inner region permeability is 0.002 μm².Figure 6 shows the effect of the horizontal well position on the transient pressure distribution as well as on the rate performance for case 1. The horizontal well position has an effect on the pressure drop propagate rates. A horizontal well farther from the center of the reservoir will cause a bigger pressure drop. The comparison of the results of the production rate shows that well position has an obvious effect on the production rate and decline rate. A horizontal well farther from the center of the reservoir results in a bigger production rate in the earlier stage but a faster decline rate in the whole process. In the later stage, a horizontal well, whose center is located at (0, 200, 5), causes a lower production rate than the other two positions.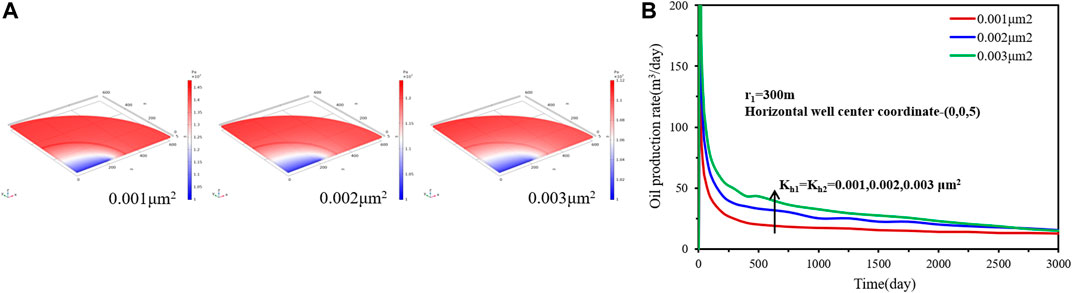

TABLE 1

TABLE 1. Input parameters for horizontal well entirely in the inner region.

FIGURE 4

FIGURE 4. Effect of inner region radius on (A) transient pressure and (B) rate decline performance.

FIGURE 5

FIGURE 5. Effect of inner region permeability on (A) transient pressure and (B) rate decline performance.

FIGURE 6

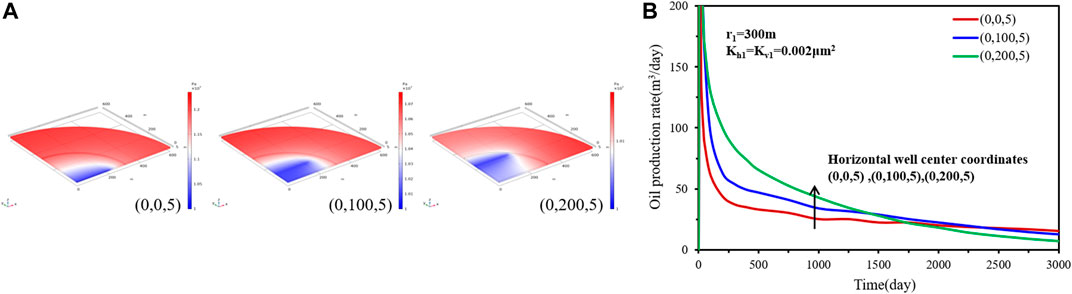
FIGURE 6. Effect of horizontal well position on (A) transient pressure and (B) rate decline performance.

Case 2. Horizontal well passing through both inner region and outer region on both sides.The effects of damage radius, damage region permeability, and well position on oil production rate are discussed. The parameters used are shown in Table 2.The sensitivity analyses of the different parameters are as follows:

(1) Effect of inner region radius.

To analyze the effect of inner radius, four different inner region radii, 50 m, 10 0m, 150m and 190 m are considered. The horizontal well center coordinate is (0, 0, 5) and the inner region permeability is 0.002 μm².Figure 7 compares the differences in the transient pressure distribution and the rate decline performance for case 2. The transient pressure distribution shows that damage radius has an effect on pressure drop propagation. As the damage radius becomes small, the damage region has less influence on pressure drop propagations and the pressure drop will propagate quickly. From the rate decline curves, it can be seen that the smaller the inner region radius, the bigger the production rate, but the decline rate will be faster. The reason is that a higher outer region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. It should be noted that in the later stage, different damage radius has little effect on the oil production rate.

(2) Effect of inner region permeability.

To analyze the effect of inner region permeability, three different damage region permeability, 0.001μm², 0.002μm², and 0.004 μm² are considered. The horizontal well center coordinate is (0, 0, 5) and the inner region radius is 150 m.Figure 8 shows the effect of inner region permeability on the transient pressure distribution as well as on the rate performance for case 2. For different damage region permeability, the pressure drops propagate at different rates. It can be seen that the greater inner region permeability results in a faster pressure drop propagation rate. The reason is that a higher inner region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. The comparison of the results of the production rate shows that damage region radius has an obvious effect on the production rate and decline rate. A higher inner region permeability causes a bigger production rate but a faster decline rate.

(3) Effect of horizontal well position.

To analyze the effect of horizontal well position, three different well positions, (0, 0, 5), (0, 50, 5) and (0, 100, 5) are considered. The inner region radius is 150 m and the inner region permeability is 0.002 μm².Figure 9 shows the effect of the horizontal well position on the transient pressure distribution as well as on the rate performance for case 2. The horizontal well position has an effect on the pressure drop propagate rates. A horizontal well farther from the center of the reservoir will cause a bigger pressure drop. The reason is that a higher inner region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. The comparison of the results of the production rate shows that the well position has an obvious effect on the production rate and decline rate. A horizontal well farther from the center of the reservoir results in a bigger production rate in the earlier stage but a faster decline rate in the whole process. In the later stage, the horizontal well, whose center is located at (0, 0, 5), causes a higher production rate than the other two positions.

TABLE 2

TABLE 2. Input parameters for horizontal well passing through both inner region and outer region on both sides.

FIGURE 7

FIGURE 7. Effect of inner region radius on (A) transient pressure and (B) rate decline performance.

FIGURE 8

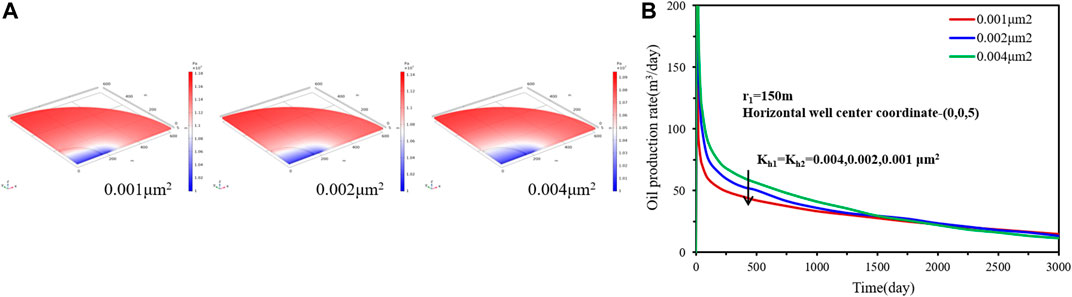
FIGURE 8. Effect of inner region permeability on (A) transient pressure and (B) rate decline performance.

FIGURE 9

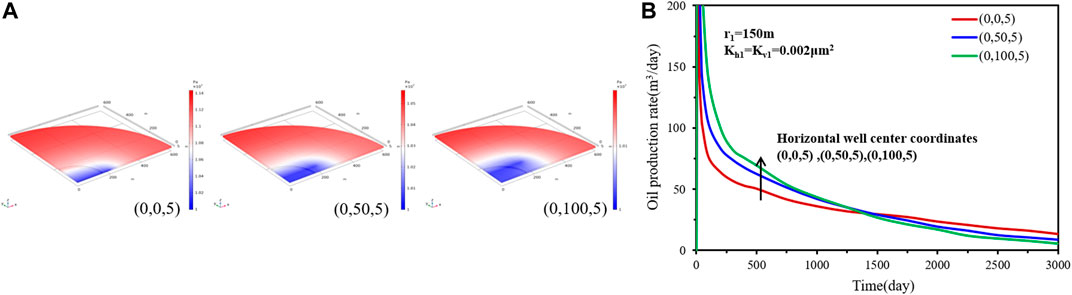
FIGURE 9. Effect of horizontal well position on (A) transient pressure and (B) rate decline performance.

Case 3. Horizontal well passing through both inner region and outer region on a single side.The effects of damage radius, damage region permeability, and well position on oil production rate are discussed. The parameters used are shown in Table 3.Sensitivity analysis of different parameters is as follows:

(1) Effect of inner region radius.

To analyze the effect of the inner radius, four different inner region radii, 150 m, 200 m, and 250 m are considered. The horizontal well center coordinate is (200, 0, 5) and the inner region permeability is 0.002 μm².Figure 10 compares the differences in the transient pressure distribution and the rate decline performance for case 2. The transient pressure distribution shows that damage radius has an effect on pressure drop propagation. As the damage radius becomes small, the damage region has less influence on pressure drop propagations and the pressure drop will propagate quickly. From the rate decline curves, it can be seen that the smaller the inner region radius, the bigger the production rate, but the decline rate will be faster. The reason is that a higher outer region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. It should be noted that in the later stage, different damage radius has little effect on the oil production rate.

(2) Effect of inner region permeability.

To analyze the effect of inner region permeability, three different damage region permeability, 0.001, 0.002, and 0.004 μm² are considered. The horizontal well center coordinate is (200, 0, 5) and the inner region radius is 200 m.Figure 11 shows the effect of inner region permeability on the transient pressure distribution as well as on the rate performance for case 2. For different damage region permeability, the pressure drops propagate at different rates. It can be seen that the greater inner region permeability results in faster pressure drop propagation rate. The reason is that a higher inner region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. The comparison of the results of the production rate shows that damage region radius has obvious effect on the production rate and decline rate. A higher inner region permeability causes a bigger production rate but a faster decline rate.

(3) Effect of horizontal well position.

To analyze the effect of the horizontal well position, three different well positions, (200, 0, 5), (200, 50, 5), and (200, 100, 5) are considered. The inner region radius is 200 m and the inner region permeability is 0.002 μm².Figure 12 shows the effect of the horizontal well position on the transient pressure distribution as well as on the rate performance for case 2. The horizontal well position has an effect on the pressure drop propagate rates. A horizontal well farther from the center of the reservoir will cause a bigger pressure drop. The reason is that a higher inner region permeability can increase the flow capacity of fluid flow from the outer region to the inner region. The comparison of the results of the production rate shows that the well position has an obvious effect on the production rate and decline rate. A horizontal well farther from the center of the reservoir results in a bigger production rate in the earlier stage but a faster decline rate in the whole process. In the later stage, the horizontal well, whose center is located at (200, 0, 5), causes a lower production rate than the other two positions.

TABLE 3

TABLE 3. Input parameters for horizontal well passing through both inner region and outer region on single sides.

FIGURE 10

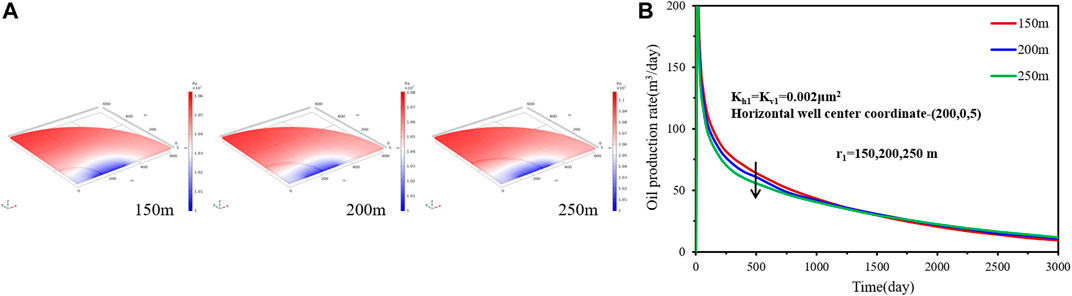
FIGURE 10. Effect of inner region radius on (A) transient pressure and (B) rate decline performance.

FIGURE 11

FIGURE 11. Effect of inner region permeability on (A) transient pressure and (B) rate decline performance.

FIGURE 12

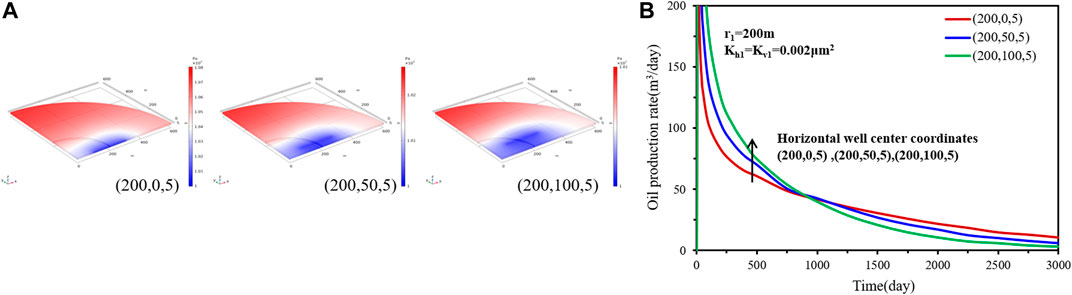
FIGURE 12. Effect of horizontal well position on (A) transient pressure and (B) rate decline performance.

Conclusion

In this paper, we investigated the pressure distribution characteristics and oil production rate decline curve of horizontal wells in a composite reservoir when the well passes through the inner region or in the inner region fully. From the above analysis, the following conclusions can be drawn:

1. The mathematical model is solved by finite element method and the oil production rate is calculated using the material balance method in the composite reservoir. There are different pressure distribution characteristics and oil production rate decline trend for horizontal well when in the inner region fully or passing through two different regions on both sides or single side.

2. The inner region radius, inner region permeability, and well position all have an important effect on transient pressure distribution and production rate decline curves. When the inner region radius becomes smaller or the inner region permeability becomes bigger, the production rate will increase but decline faster. Horizontal wells closer to or in greater contact with the outer region result in faster pressure drops propagation and higher oil production rate but faster decline rates. In the later stage, there will be a significant difference in production rate due to the well location compared to the influence of radius and permeability.

3. For the reservoir considering the damage, the corresponding technological measures should be taken to reduce the damage range and damage degree to increase the production rate. Although changing well location is of great help to increase oil production performance, it is difficult and time-consuming to determine a well location mainly based on careful analysis of geological structure, hydrogeological conditions, and geophysical exploration data.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JL: Conceptualization and Methodology. TW: Software and Writing—Original Draft Preparation. All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

Author TW was employed by the company China oilfield services limited (Research Institute of Oilfield Production, COSL).

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author’s contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

References

Civan, F. (2015). Reservoir Formation Damage. Houston, TX: Gulf Professional Publishing.

Google Scholar

Clonts, M. D., and Ramey, H. J. (1986). Pressure Transient Analysis for wells with Horizontal drainholes[C]//SPE California Regional Meeting. Richardson, TX: OnePetro.

Google Scholar

Daviau, F., Mouronval, G., Bourdarot, G., and Curutchet, P. (1988). Pressure Analysis for Horizontal Wells. Eval 3 (04), 716–724. doi:10.2118/14251-pa

CrossRef Full Text | Google Scholar

Ezulike, O., and Igbokoyi, A. (2012). Horizontal Well Pressure Transient Analysis in Anisotropic Composite Reservoirs-A Three Dimensional Semi-analytical Approach. J. Pet. Sci. Eng. 96-97, 120–139. doi:10.1016/j.petrol.2012.09.002

CrossRef Full Text | Google Scholar

Goode, P. A., and Thambynayagam, R. K. M. (1987). Pressure Drawdown and Buildup Analysis of Horizontal wells in Anisotropic media. SPE Form. Eval. 2 (04), 683–697. doi:10.2118/14250-pa

CrossRef Full Text | Google Scholar

Gringarten, A. C., and Ramey, H. J. (1973). The Use of Source and Green's Functions in Solving Unsteady-Flow Problems in Reservoirs. Soc. Pet. Eng. J. 13 (05), 285–296. doi:10.2118/3818-pa

CrossRef Full Text | Google Scholar

Jiang, R., Xu, J., Sun, Z. J., Guo, C., and Zhao, Y. (2014). Rate Transient Analysis for Multistage Fractured Horizontal Well in Tight Oil Reservoirs Considering Stimulated Reservoir Volume. Math. Probl. Eng. 2014, 1–11. doi:10.1155/2014/489015

CrossRef Full Text | Google Scholar

Krueger, R. F. (1988). An Overview of Formation Damage and Well Productivity in Oilfield Operations: An update[C]//SPE California Regional Meeting. Richardson, TX: OnePetro.

Google Scholar

Nie, R.-S., Guo, J.-C., Jia, Y.-L., Zhu, S.-Q., Rao, Z., and Zhang, C.-G. (2011). New Modelling of Transient Well Test and Rate Decline Analysis for a Horizontal Well in a Multiple-Zone Reservoir. J. Geophys. Eng. 8 (3), 464–476. doi:10.1088/1742-2132/8/3/007

CrossRef Full Text | Google Scholar

Ozkan, E. (1994). New Solutions for Well-Test-Analysis Problems: Part III-Additional algorithms[C]//SPE Annual Technical Conference and Exhibition. Richardson, TX: OnePetro.

Google Scholar

Ozkan, E., and Raghavan, R. (1991). New Solutions for Well-Test-Analysis Problems: Part 1-Analytical Considerations. Eval 6 (03), 359–368. doi:10.2118/18615-pa

CrossRef Full Text | Google Scholar

Ozkan, E., and Raghavan, R. (1991). New Solutions for Well-Test-Analysis Problems: Part 2 - Computational Considerations and Applications. Eval 6 (03), 369–378. doi:10.2118/18616-pa

CrossRef Full Text | Google Scholar

Park, E., and Zhan, H. (2002). Hydraulics of a Finite-Diameter Horizontal Well with Wellbore Storage and Skin Effect. Adv. Water Resour. 25 (4), 389–400. doi:10.1016/s0309-1708(02)00011-8

CrossRef Full Text | Google Scholar

Ren, J., and Guo, P. (2017). Nonlinear Flow Model of Multiple Fractured Horizontal wells with Stimulated Reservoir Volume Including the Quadratic Gradient Term. J. Hydrol. 554, 155–172. doi:10.1016/j.jhydrol.2017.09.005

CrossRef Full Text | Google Scholar

Shen, W., Xu, Y., Li, X., Huang, W., and Gu, J. (2016). Numerical Simulation of Gas and Water Flow Mechanism in Hydraulically Fractured Shale Gas Reservoirs. J. Nat. Gas Sci. Eng. 35, 726–735. doi:10.1016/j.jngse.2016.08.078

CrossRef Full Text | Google Scholar

Shi, G., Nie, R., Lu, J., Ji, C., and Fan, S. (2012). Well Test Model of Horizontal Well in 2-zoned Composite Reservoir and Example Interpretation. J. Southwest Pet. Univ. (Science Tech. Edition) 34 (5), 99–106. doi:10.3863/j.issn.1674-5086.2012.05.015

CrossRef Full Text | Google Scholar

Xu, C., Kang, Y., You, Z., and Chen, M. (2016). Review on Formation Damage Mechanisms and Processes in Shale Gas Reservoir: Known and to Be Known. J. Nat. Gas Sci. Eng. 36, 1208–1219. doi:10.1016/j.jngse.2016.03.096

CrossRef Full Text | Google Scholar

Xu, J., Guo, C., Teng, W., Wei, M., and Jiang, R. (2015). Production Performance Analysis of Tight Oil/gas Reservoirs Considering Stimulated Reservoir Volume Using Elliptical Flow. J. Nat. Gas Sci. Eng. 26, 827–839. doi:10.1016/j.jngse.2015.06.057

CrossRef Full Text | Google Scholar

Yao, S., Wang, X., and Yuan, Q. J. (2020). Production Analysis of Multifractured Horizontal wells with Composite Models: Influence of Complex Heterogeneity. J. Hydrol. 583, 124–542. doi:10.1016/j.jhydrol.2020.124542

CrossRef Full Text | Google Scholar

Yuan, J., Jiang, R., and Zhang, W. (2018). The Workflow to Analyze Hydraulic Fracture Effect on Hydraulic Fractured Horizontal Well Production in Composite Formation System. Adv. Geo-energy Res. 2 (3), 319–342. doi:10.26804/ager.2018.03.09

CrossRef Full Text | Google Scholar

Zeng, H., Fan, D., Yao, J., and Sun, H. (2015). Pressure and Rate Transient Analysis of Composite Shale Gas Reservoirs Considering Multiple Mechanisms. J. Nat. Gas Sci. Eng. 27, 914–925. doi:10.1016/j.jngse.2015.09.039

CrossRef Full Text | Google Scholar

Zhang, J., Fang, F., and Shen, W. (2020). Experimental Study on the Effective Utilization of Reserves in Tight Sandstone Gas Reservoirs and Their Applications. Geofluids. doi:10.1155/2020/8854299

CrossRef Full Text | Google Scholar

Zhang, R.-h., Zhang, L.-h., Wang, R.-h., Zhao, Y.-l., and Huang, R. (2016). Simulation of a Multistage Fractured Horizontal Well with Finite Conductivity in Composite Shale Gas Reservoir through Finite-Element Method. Energy Fuels 30 (11), 9036–9049. doi:10.1021/acs.energyfuels.6b01565

CrossRef Full Text | Google Scholar

Zhang, W., Cui, Y., Jiang, R., Xu, J., Qiao, X., Jiang, Y., et al. (2019). Production Performance Analysis for Horizontal wells in Gas Condensate Reservoir Using Three-Region Model. J. Nat. Gas Sci. Eng. 61, 226–236. doi:10.1016/j.jngse.2018.11.004

CrossRef Full Text | Google Scholar

Zhao, Y.-L., Zhang, L.-H., Luo, J.-X., and Zhang, B.-N. (2014). Performance of Fractured Horizontal Well with Stimulated Reservoir Volume in Unconventional Gas Reservoir. J. Hydrol. 512, 447–456. doi:10.1016/j.jhydrol.2014.03.026

CrossRef Full Text | Google Scholar

Zhao, Y.-L., Zhang, L.-H., and Shan, B.-C. (2018). Mathematical Model of Fractured Horizontal Well in Shale Gas Reservoir with Rectangular Stimulated Reservoir Volume. J. Nat. Gas Sci. Eng. 59, 67–79. doi:10.1016/j.jngse.2018.08.018

CrossRef Full Text | Google Scholar