
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Energy Res. , 01 July 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.811690
This article is part of the Research Topic Design, Simulation and Optimization of Hydraulic Machinery View all 25 articles
Addressing the cavitation prevention requirements for a longer service life of the high-speed centrifugal pump in the temperature control system of aerospace, the effect of blade inlet width on cavitation performance is studied on the premise of consistency of impeller outlet diameter D2, impeller outlet width b2, volute inlet diameter D3, pump interface and other structural parameters. Therefore, the corrected coefficient k1 of blade inlet exclusion coefficient is introduced; four groups of centrifugal impellers with inlets of different geometric structures blades are put forward. To begin with, based on the D# pump performance test and Pumplinx simulation, the cavitation performance of high-speed pump with four different groups of impellers is studied under five working conditions of negative inlet pressure (Pj=(−20, −30, −40, −50, −60)kPa) on the premise that energy characteristics agree well with cavitation performance. According to the results, when Pj drops from −50 kPa to −60 kPa, the cavitation perform changes the most significantly. This indicates that the method of twisting the centrifugal impeller of the suspended forward-extended blade shows a significant effect in preventing cavitation performance under such working conditions of high speed and negative pressure. Its application in aerospace power systems can effectively reduce the impact of low pressure in the system and significantly improve the cavitation performance.
Aerospace systems often require miniaturized high speed centrifugal pumps, which are prone to cavitation, a phenomenon degrading the hydraulic performance of pumps, especially at the blade inlet areas (Guan, 1995; Wang, 2004). Under continuous high-frequency and high-pressure blow by the cavitation bubble, the metal surfaces of flow passage components such as volute casing could sustain metal damage that shortens their service life. Therefore, cavitation prevention in high-speed pumps became an urgent requirement. However, conventional analysis of civil or industrial centrifugal pumps is mainly conducted with clean water or at low speed. No research have been conducted on the different types of impellers with overhung forward-extended blades at high speed in ethylene glycol aqueous solution. Research on the cavitation characteristics of high-speed centrifugal pumps in ethylene glycol aqueous solution is rare. Thus, this study focused on the cavitation under high-speed operation with multi-component non-Newtonian ethylene glycol aqueous solution to address the urgent need for analyzing the effect of impeller shapes on cavitation characteristics of high-speed centrifugal pumps for aerospace temperature control systems in special media.
Cavitation characteristics of centrifugal pumps have been extensively studied. Zhang et al., Feng, and Chao et al. (Feng, 2016; Zhang et al., 2017; Chao and Wang, 2019) investigated the influence of impeller type on cavitation (splitter blade and composite impeller). Zhao et al. and Wang et al. (Wang and Xie, 2016; Zhao and Zhao, 2017) studied the influence of blade adjustment (obstacle arrangement and slotting) on cavitation. Wei et al., Fu et al., and Chao et al. (Fu and Shen, 2016; Wei and Song, 2016; Chao and Wang, 2018) explored the centrifugal pump inlet backflow cavitation characteristics under different working conditions. Hu et al. (Hu and Song, 2017) studied the cavitation characteristics of micro-pump under low flow. Pei et al. (Pei and Yin, 2017) examined the influence of impeller geometric parameters on cavitation performance with the orthogonal experimental design based on Computational Fluid Dynamics (CFD).
Current cavitation prevention measures, such as changing the pump inlet structure and adopting a front inducer, are not applicable to aerospace systems due to their internal structure, shapes, and dimensions. Measures such as reducing the flow resistance of the pipeline and increasing the medium pressure in front of the pump are not applicable due to pipeline structure and pressure specification in the aerospace system. Measures such as using anti-cavitation materials are restricted by the anti-redundancy requirements.
Under the promise that existing cavitation and hydraulic tests conform well to the Pumplinx three-dimensional full flow channel vapor-liquid two-phase numerical simulation, we conducted numerical simulation and explored the internal cavitation characteristics of high-speed centrifugal pumps with four different types of impellers in ethylene glycol aqueous solution (Zindani et al., 2016; Yao and Luo, 2019; Han et al., 2021; Liao and Wuruikang, 2021; Tang et al., 2021) and obtained the influence of different geometric shapes of the blade on the external characteristics and cavitation flow characteristics of high-speed centrifugal pumps. This study could provide a theoretical basis for the better application of high-speed centrifugal pumps in aerospace systems.
Parameters of the research object are follows: the rated flow Qv = 400 L/h, the boost value ΔP = 170 kPa, the rated speed n = 9,400 r/min, and the impellers are four Long and four short blade semi-open compound type. Table 1 shows the geometrical parameters of the pump, and Figures 1, 2 presents the structure diagrams of four centrifugal impeller types.
The fluid passing through the impeller follows the velocity triangle. The axial plane component velocity vm is the component of the fluid flowing out of the impeller along the axis and is related to the fluid flow passing through the impeller. With the same fluid flow, a larger flow area means smaller velocity and minimal energy loss.
With consistent outlet diameters and outlet widths of volute and impeller, we designed four groups of impellers, namely, twisted overhung forward-extended backswept composite impeller (A), cylindrical overhung forward-extended backswept composite impeller (B), twisted backswept composite impeller (C) and cylindrical backswept composite impeller (D), respectively, using four long blades and four short blades, as shown in Figure 2.
When designing the twisted overhung forward-extended backswept composite impeller (A) with four short blades and four long blades, the corrected blade excretion coefficient k1 was introduced (Eq. (1)). The conventional calculation method for blade inlet velocity of centrifugal pump only considers the blade thickness and ignores the blade width b. This paper proposed to consider both the thickness (k in Eq. 1) and width of the blade when calculating the blade excretion coefficient.
The revise corrected coefficient k1 takes into account the thickness and width of the blade,So K1 is smaller than K.Reduce the blade inlet working face, increase the opening area and flow capacity of the inlet between blades, According to the Bernoulli Equation,The flow rate decreases, the pressure increases,So as to improve the anti cavitation performance.
Formula:F1 is the discharge section area of the calculation point, k is the blade excretion coefficient at the calculation point, k1 is the corrected blade excretion coefficient at the calculation point, D1 is the diameter of the diameter at the calculation point, Su1 is the circumferential thickness of the blade at the calculation point, ?v is the volumetric efficiency, b is the width of the blade at the calculation point, b’ is the width of the forward-extended blade at the calculation point, δb is the width coefficient, Z is the number of blades, and V is the inlet velocity at the calculation point.
The motion of the ethylene glycol aqueous solution in the high-speed centrifugal pump is an unsteady three-dimensional complex turbulent flow with the following Reynolds time-averaged N-S equations:
Formula:
Pumplinx numerical simulation software operates with the Singhal full cavitation model “Cavitation” based on the idea of the two-phase flow model. The “Cavitation” model solves the dynamic process of the phase transition of the cavitation bubble with the bubble dynamics Rayleigh-plesset equation and introduces the concept of mixing density, which integrates the non-condensable gas, evaporation condensation processes and the compressibility of liquids (Wen et al., 2018; Ma and Pan, 2020; Bai and Ma, 2021). This model has also been tested and verified by a large number of engineering projects.
The Singhal full cavitation model and the N-S equation were combined, and the RNG k-ε turbulence model was adopted to solve the equation. By combining the Singhal model with the continuity equation, the relationship between the changing rates of density and vapor phase volume fraction was obtained as follows:
where vapor volume fraction αv is related to cavitation bubble number density and cavitation bubble diameter RB:
Singhal model is based on the Rayleigh-Plesset bubble dynamics equation:
The expression for the phase transition rate is obtained by neglecting the viscosity and surface tension effects and combining the continuity equation of each phase:
Where: PB is the saturation vapor pressure, σ is the surface tension coefficient.
In the simulation of internal flow cavitation of centrifugal pump, the phase change rate is related to vapor phase density, liquid density and mixture density. The Singhal model takes into account the effects of turbulence and non-condensable gas. The Singhal vapor phase mass fraction transport equation is as follows:
Where:
The flow in the centrifugal pump is mainly three-dimensional viscous and incompressible unsteady turbulent flow. Reynolds time averaged N-S equations, RNG K-andepsi; two-side turbulence model and SIMPLE algorithm are selected, Singhal full Cavitation model. The first phase is the ethylene glycol aqueous solution, and the second phase is the bubble. The saturated vapor pressure of ethylene glycol aqueous solution is 1.41 kPa.
During the calculation, the speed of centrifugal pump impeller n = 9,400 r/min and volute outlet volume flow rate Qv = 400 L/h(0.000111 m3/s)and inlet pressure (Pj=(−20, −30, −40, −50, −60)kPa). During the numerical calculation, the NPSH of the pump is changed by gradually decreasing the inlet pressure from 0 Pa to control the cavitation degree in the pump.
The quality of the fluid domain grid is decisive for the accuracy of the numerical simulation results. PumpLinx uses the finite volume method for CFD simulation solution, that is, the unstructured grid. PumpLinx grid generator uses a proprietary CAB geometric equirectangular height adaptive binary tree Cartesian coordinate algorithm and a more regular Cartesian hexahedral mesh, which can generate body-fitted grid near wall surfaces. The CAB algorithm can automatically adjust the grid size to fit the geometric surfaces and geometric boundary lines by continuously splitting the grid. Adaptive algorithm was also incorporated when generating grids for automatic encrypted resolution of the geometry of complex details. At the same accuracy level, the proprietary grid generation algorithm has a smaller grid number than the tetrahedral mesh.
Figure 3 shows the three-dimensional diagram of the flow channel of the flow passage component, and Figure 4 shows the grid diagram of the impeller, where the computational domain consists of the impeller, the volute, and the tip clearance layer of the impeller. Since this study focuses on the cavitation characteristics of high-speed centrifugal pumps, the grid topology, number of grids, and the grid aspect ratio are controlled to ensure a relatively smaller size difference between adjacent grid nodes and more accurate numerical simulation results. Following the grid independence verification, the total number of grids in the computational domain is finally determined to be approximately 2.6 million considering the computer capability and efficiency. Table 2 verification of grid independence.
In this paper, the hydraulic performance characteristics of a semi-open composite impeller low-specific speed centrifugal pump used for cryogenic circulation in a certain space station with a shrinkage coefficient of one were tested on the AECC Xi’an Engine Control Co. Ltd. open test bench, of which glass rotameter type: LZB-20D, 60–600 L/h, class 2.5 level, sensor type: MPM 480, 0–0.6 MPa, class 0.25 level.as shown in Figure 5. The working medium of the test was low-temperature glycol aqueous solution.
The cavitation test was carried out on a hydraulic test bench with a four Long and four short blade composite centrifugal pump according to the test standard GB/T3216-2005. The ethylene glycol aqueous solution density ρ = 1,030 kg/m3, the temperature t = 7.6°C, and the flow rate QV = 400 L/h. The initial inlet pressure Pj = 0 kPa. The inlet pressure of the pump was gradually reduced by adjusting the inlet valve until the decreased value of inlet and outlet pressure difference was 3% of the rated inlet and outlet pressure difference. At this time, the critical cavitation margin was reached. The cavitation test results were compared with the numerical simulation results to verify the accuracy of the numerical simulation. The test setup is shown in Figure 5.
Figure 6 shows the error between the experimental performance value and the performance parameter predicted by the numerical simulation of the cylindrical backswept compound impeller (D) at the design operation point under the non-cavitation condition. It can be seen that the errors between the head value and the test value are all below 5%, indicating that the numerical calculation simulation can simulate the internal flow field of the centrifugal pump at the design operation point and the numerical simulation results in this paper are accurate. Although the power error did not exceed 10%, the error is still large because the mechanical friction loss of various bearings and friction pairs in the operation of the centrifugal pump is not considered in the numerical simulation process.
Figure 7 shows the error between the experimental performance value and the performance parameter predicted by the numerical simulation of the cylindrical backswept compound impeller (D) under the cavitation condition. It can be seen that the errors between the head value and the test value are all less than 5%, indicating that the numerical calculation simulation can simulate the internal flow field of the centrifugal pump at the design operation point and numerical simulation results in this paper are accurate. When the inlet negative pressure Pj = −50 kPa, the inlet and outlet pressure difference ∆p = 155 kPa and is close to 3% of the rated pressure difference. At this time, the pump outlet pressure P2 = 105 kPa, which is critical cavitation outlet pressure.
Figure 8 shows that when the inlet negative pressure is −50 kPa, the pump outlet flow rate remains at 400 L/h, but when the inlet negative pressure is −60 kPa, the outlet flow rate decrease to 300 L/h, indicating that a large amount of steam has been generated in the centrifugal pump at this time, with the largest volume of steam in the blade and the most intense bubble activity.
Figure 9 shows the cavitation bubble volume distribution diagrams of the midsections of the four types of pumps when the inlet negative pressure (Pj = −50 kPa; Pj = −60 kPa) and the design flowrate. In general, cavitation regions of the four types of pumps show a similar pattern. They all appear at the inlets of impellers and are mainly concentrated on the blade back (non-working surface). However, the cavitation regions vary due to the difference in impeller type. When Pj = −50 kPa, the cavitation regions of type A and type C are round, the volume fractions are both below 0.5; the cavitation regions of type B and type D are rectangular, the volume fractions are both below 0.875. The cavitation severity is ranked as B > D > A > C. When Pj = −60 kPa, the cavitation regions of the four types of impellers expand from the back of the blade to the working surface of the blade and gradually expand from the low-pressure area of the blade to the flow channel. The cavitation strength is obviously deepened, especially for type C, whose volume fraction increases from a level below 0.5 to 0.875. The cavitation regions of type A and type C are still round, and the volume fraction of type A is below 0.625. The cavitation regions of type B and type D gradually turn into round, and the volume fractions are still within the range of below 0.875. The cavitation severity ranking becomes C > D > B > A. Therefore, the non-forward-extended blade has a weaker cavitation resistance than the forward-extended blade.
Due to the asymmetry of the volutes of the centrifugal pumps, the pressure and velocity at the dynamic and static coupling are non-uniformly distributed. In addition, the blades are arranged in a 4 × 4 staggered layout, resulting in the asymmetry distribution of the cavitation region. The most serious cavitation is at four in Figure E, followed by that at 3 and 2, and the lightest at 1, forming a reciprocating 4, 3, 1, two cavitation bubble cycle. As the inlet negative pressure of the high-speed centrifugal pump increases from Pj = −50 kPa (critical point) to Pj = −60 kPa, the distribution area of cavitation bubbles on the blade surface gradually expands.
To analyze the cavitation evolution process in different types of impellers, the cavitation region with the volume fraction larger or equal to the 0.5 iso-surface in impeller axial view and the lateral view is extracted under the rated operating condition with the same speed and different inlet negative pressure values Taking a pair of blades in Figure 10 as an example. In Figure 10, the cavitation characteristics of the high-speed.
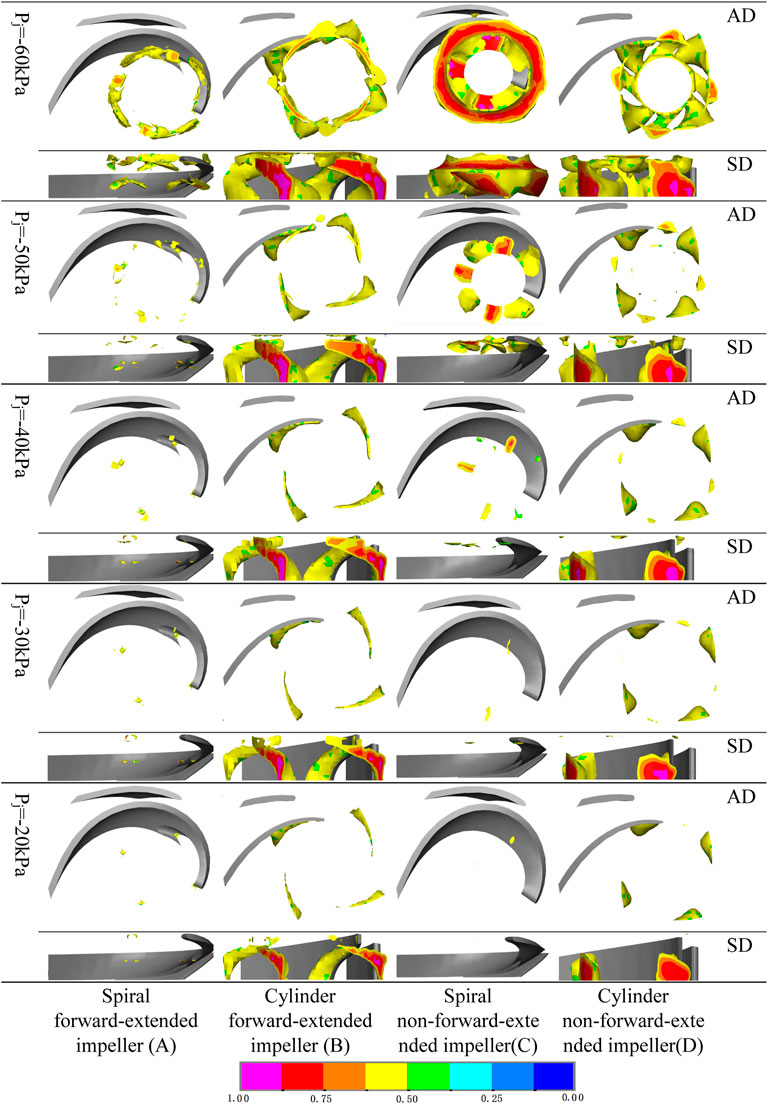
FIGURE 10. The distribution cloud diagrams of gas-phase volume fractions of different types of pumps at different inlet negative pressures under the design flow. (A) Spiral forward-extended impeller (B) Cylinder forward-extended impeller (C) Spiral non-forward-extended impeller (D) Cylinder non-forward-extended impeller.
centrifugal pump can be divided into three processes:1) Cavitation bubble first appears at the head of the suction surface of the blade and at the rear of the blade inlet. The distribution of cavitation bubbles at the four blades is different. This is the initial stage of the cavitation bubble, except the cavitation bubbles at type A blade suction surface, which are few and sporadic-dot-shaped and initially occur everywhere except the contact between the blade and the back shroud. 2) As the inlet negative pressure continues to increase, the cavitation bubbles gradually grow and increase, and there is no obvious sharp increase. At this time, the performance of the pump does not change. The number of cavitation bubbles at the suction surface of the type A blade increases more uniformly, the increase is small. The cavitation bubbles of the type A blade are sporadic spot-shaped. The lateral view shows that cavitation bubbles appear at the area from the blade inlet to the middle of the blade. When the inlet negative pressure reaches Pj = −50 kPa, the increase becomes significant, and the cavitation bubbles are star-shot-shaped. The cavitation bubble with a strength level of 0.875 does not occur until the negative inlet pressure reaches this level. Type B cavitation bubbles are tadpole-shaped and opposite to the direction of rotation of the impeller. Four tadpole shapes form a ring shape attached to the forward-extended section of the blade in the lateral view. With the increase of inlet negative pressure, the tadpole-shaped cavitation bubbles become longer and wider, the cavitation strength deepens, and the ring gradually closes. When Pj = −20 kPa, type B has the cavitation bubble with a strength level of 0.875, and when Pj = −40 kPa, the cavitation bubble with a strength level of one appears. Type C cavitation bubbles occur at the inlet of the blade. When Pj = −20 kPa, there is almost no cavitation bubble; when Pj = −40 kPa, cavitation bubbles increase, and the ring-type cavitation bubbles are more obvious; when Pj = -50 kPa, eight cavitation bubble rounds are presented, each having two rounds, underside of the blade tip has one round, and the rear of the blade tip at the suction surface has one round. The two cavitation bubbles are laterally zygomorphic at 45°; when Pj = −40 kPa, the cavitation bubble with a strength level of 0.875 appears. Type D cavitation bubbles present four lentil shapes, forming a ring. When Pj = −30 kPa, small cavitation bubbles of different sizes appear in the middle of the four lentil shapes in the axial view. In the lateral view, the four lentil shapes are at the root of the blade, and small cavitation bubbles are at the tip of the blade. With the increase of the inlet negative pressure, the tadpole-like cavitation bubbles become longer and wider, the cavitation strength deepens, and the ring is closed. Type D blade has the cavitation bubble with a strength level of 0.87 when Pj = −20 kPa, and when Pj = −40 kPa, the cavitation bubble with a strength level of one appears. Cavitation bubble volume change of type C impeller is more significant than cavitation bubble volume changes of other types of impellers before Pj = −50 kPa. Type B and type D impellers have larger cavitation volumes than type A and type C impellers. This stage is called the development of cavitation. (3) When Pj = −60 kPa, the cavitation bubble volumes of the four types of impellers increase suddenly, forming complete cavitation or severe cavitation. The sudden increments are ranked as C > D > B > A. The bottom layers of type B and type D cavitation bubbles become thickened, and the cavitation bubble trails at the outlet of the impeller completely block the outflow of the liquid flow. The bottom layers of type C cavitation bubbles become thickened, and the cavitation bubble trail at the inlet of the impeller completely blocks the outflow of the liquid flow. The outflow blocked by the three types of cavitation bubbles accounts for 3/4 of the impeller flow. At this time, the performance of the centrifugal pump is severely degraded. Although type A cavitation bubbles have a sudden increase, the increase is one order of magnitude less than the increases of the other three types.
It can be seen from Figure 7 and Figure 8 that when the inlet negative pressure is reduced from Pj = −20 kPa to Pj = −60 kPa, type A and type C impellers reduce the impact loss of the blade on the medium with the impact changing from the axial direction to the radial direction, and reduce the energy loss at the inlet, improving the fuel flow characteristics. The forward-extended sections of type A and type B blades occupy a smaller inlet space and have a smaller excretion towards the medium compared to those of type C and type D blades, which makes the inlet velocity small. In conventional inlet velocity calculation, the excretion coefficient, such as coefficient k in Eq. (1), is calculated by considering only the blade thickness and ignoring the blade width. In this paper, the corrected inlet excretion coefficient, such as the coefficient k1 in Eq. (1), is proposed after considering the blade width.
In general, impellers with forward-extended blades (type A and type B) have less variation in cavitation strength and cavitation region compared to those without forward-extended blades (type C and type D), indicating that impellers with forward-extended blades (type A and type B) have stronger cavitation resistance.
Under the condition that the design parameters, such as the outlet diameter of the volute and the impeller and the specific speed, remain unchanged, we designed four sets of impellers with different blade forms and studied the anti-cavitation characteristics of the high-speed centrifugal pump using ethylene glycol aqueous solution as the medium in the aerospace temperature control system under different inlet negative pressures. The following conclusions are drawn:
(1) For the design of blades in the centrifugal pump, while ensuring the blade thickness and taking into account the blade inlet width, the corrected coefficient k1 of the blade was introduced to obtain the twisted, overhung and forward-extended blade beyond the conventional design.
(2) When the inlet negative pressure decreased from Pj = −50 kPa to Pj = −60 kPa, the volume fraction of type A was below 0.625, and the volume fractions of other types were increased to 0.875. The cavitation severity changed from B > D > A > C to C > D > B > A.
(3) When the inlet negative pressure decreased from Pj = −20 kPa to Pj = −60 kPa, type A had the smallest cavitation area and cavitation strength. The shape, size, and position of the cavitation regions of the four types of impellers varied significantly. The change of type C subject to inlet negative pressure gradient was the most sensitive. Type B and type D both had cavitation bubbles with the strength level of 0.875 when Pj = −20 kPa and cavitation bubbles with the strength level of one when Pj = −40 kPa.
(4) The width of the blade inlet was reduced so that the excretion strength of the blade inlet to the medium was weakened, the inlet energy loss of the blade was improved, and the flow loss at the blade inlet was reduced, improving the anti-cavitation characteristics, especially when Pj = −60 kPa.
Chao Wenxiong (1985-), male, postgraduate, associate professor, mainly engaged in the research and optimization of the int-ernal fluid drive and control of aerospace centrifugal pumps.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
W-xC:Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; B-lS:Data Curation, Writing—Original Draft; HR: Visualization, Investigation; WD:Resources, Supervision.
National Natural Science Foundation of China (52009114); Natural Science Foundation of Shaanxi Provincial Department of Science and Technology (2021JM-525); Xi’an Aeronautical University Foundation (2020KY1227).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bai, K., and Ma, X. (2021). Nume-rical Simulations of Internal Flow Fieldand Mass Flow Characteristic of Gear Pumps in torpedo Based on Pumplinx[J]. Ship Sci. Technology 43 (3), 56–59.
Chao, W., and Wang, J. (2018). Hydraulic Characteristics Analysis of Centrifugal Pump with Unshrouded Composite Impeller at Different Tip Clearances[J]. Chin. Hydraulics Pn-eumatics (11), 89–93.
Chao, W., and Wang, J. (2019). Numerical Simulation and Experimental Analysis for Cavitation in Compos-Ite Centrifugal Pump. [J].Chinese SpaceScience and Technolongy. 39 (3), 64–70. doi:10.16708/j.cnki.1000-758X.2019.0020
Feng, J. (2016). Numerical Analysis of Unsteady Flow Field of Centrifugal Pump under Different Impeller Type[J]. China Pet. Chem. Stand-ard Qual. 36 (11), 9–11.
Fu, Y., and Shen, C. (2016). Cav-itation Characteristic Induced by Inlet Back Flow in a Centrifugal Pump[J]. J. Drainage Irrigation Machinery Eng. (10), 841–846. doi:10.3969/j.issn.1674-8530.15.0183
Han, Y., Zhou, L., Bai, L., Shi, W., and Agarwal, R. (2021). Comparison and Validation of Various Turbulence Models for U-bend Flow with a Magnetic Resonance Velocimetry experiment. Phys. Fluids 33, 125117. doi:10.1063/5.0073910
Hu, S., and Song, W. (2017). Numerical Analysis of Cavitation Characteristics of High Speed Micro-pump in Low Flow[J]. J. Eng. Therm. Energ. Power 32 (8), 100–106. doi:10.16146/j.cnki.rndlgc.2017.08.0016
Liao, W., and Wuruikang, F. (2021). The Hydraulic Design and Opt-Imization for Ultra-thin Centrifugal Micropump[J]. J. Eng. Thermophys. 42 (5), 1251–1256.
Ma, H., and Pan, Y. (2020). Research on Influence of Blade Outlet Angle on Int-Ernal and External Performance of Centrifugal Pump Based on Pumplinx[J]. Coal Mine Machinery 41 (05), 60–63. doi:10.13436/j.mkjx.202005020
Pei, J., and Yin, T. (2017). Cavitation Optimization for a Centrifugal Pump Impeller by Using Orthogonal Designof Experiment[J]. Chin. J. Mech. Eng. 30 (01), 103–109. doi:10.3901/cjme.2016.1024.125
Tang, S., Zhu, Y., and Yuan, S. (2021). An Improved Convolutional Neural Network with an Adaptable Learning Rate towards Multi-Signal Fault Diagnosis of Hydraulic Piston Pump. Adv. Eng. Inform. 50, 101406. doi:10.1016/j.aei.2021.101406
Wang, F. (2004). Computational Fluid Dy-Namics Analysis-CFD Software Princip-Le and application[M]. Beijing: TsinghuaUniversity Press.
Wang, Y., and Xie, S. (2016). Nu-merical Simulation of Cavitation Performance of Low Specific Speed Centrifu-Gal Pump with Slotted Blades[J]. Journ-al Drainage Irrigation Machin-ery Eng. 34 (3), 210–215. doi:10.3969/j.issn.1674-8530.15.0009
Wei, L., and Song, W. (2016). Num-erical Simulation and Analysis of the Flow at the Inlet of a High Speed Centrifugal Pump Based on the Soft ware CFD[J]. J. Eng. Therm. Energ. Power 31 (7), 103–109. doi:10.16146/j.cnki.rndlgc.2016.07.017
Wen, C., Zhang, C., and Li, Y. (2018). Simulation of Internal Flow Field of Gear Pump Based on Pump-Linx[J]. J. Chengdu Univ. 37 (3), 307–312.
Yao, W., and Luo, J. (2019). A Novel Bezier Method for Continuous Thrust Maneuver Orbit Optimal Design[J]. Jour-nalof Astronautics 40 (11), 1274–1285.
Zhang, X., Lai, X., and Liao, J. (2017). Analysis of Influence of Splitter Bladeon Unsteady Cavitation Flow Character-Istics of Centrifugal Pump[J]. J. Eng. Therm. Energ. Power 32 (4), 109–114. doi:10.16146/j.cnki.rndlgc.2017.04.017
Zhao, W., and Zhao, G. (2017). Numerical Simulation and Experi-Mentof Obstacle Arrangement on Centrifugalpump Blade to Suppress Cavitation[J]. Trans. Chin. Soc. Agric. Machinery 48 (9), 111–120. doi:10.6041/j.issn.1000-1298.2017.09.014
Keywords: impeller type, twisted overhung forward-extended, high-speed centrifugal pump, cavitation, ethylene glycol aqueous solution, numerical simulation CLC number: TH137, TH311 document code: A 0 preface
Citation: Chao W-x, Shi B-l, Ruan H and Dong W (2022) The Cavitation Characteristics of High Speed Centrifugal Pumps With Different Impeller Types. Front. Energy Res. 10:811690. doi: 10.3389/fenrg.2022.811690
Received: 09 November 2021; Accepted: 07 March 2022;
Published: 01 July 2022.
Edited by:
Ling Zhou, Jiangsu University, ChinaReviewed by:
Baoling Cui, Zhejiang Sci-Tech University, ChinaCopyright © 2022 Chao, Shi, Ruan and Dong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wen-xiong Chao, Y3d4Mzg2MDYwNUAxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.