Optimal Peak Regulation Strategy of Virtual and Thermal Power Plants

To achieve the national carbon-peak and carbon-neutral strategic development goals, it is necessary to build power systems dominated by renewable and sustainable energy. The future power system with a high proportion of renewable and sustainable energy is required to have large-scale, low-cost, flexible, and adjustable resources. To this end, this article aggregates user-side distributed energy storage and electric vehicles into a virtual power plant, considering the uncertainty of wind power fluctuations and the uncertainty of electric vehicle charging and discharging to establish a day-ahead and intra-day peak regulation model for combined peak regulation of virtual and thermal power plants. The bounding algorithm seeks the optimal strategy for the two-stage model of joint peak regulation and obtains the day-ahead and intra-day two-stage optimal peak regulation strategy. The simulation example shows that the virtual power plant and its day-ahead and intra-day optimal peak regulation strategy can reduce the peak regulation cost of the power system, as compared with the deep peak regulation of thermal power plants with a special supporting energy storage power station. This work provides a global perspective for virtual power plants to participate in the formulation of power system peak regulation rules.

1 Introduction

In recent years, carbon-peak and carbon-neutral has gradually become a heated term. Carbon-peak and carbon-neutral refers to China’s efforts to reach the peak of carbon dioxide emissions by 2030 and strive to achieve neutralization by 2060. To achieve the carbon-peak and carbon-neutral strategic development goals in China, it is necessary to build power systems dominated by renewable and sustainable energy (Wiryadinata et al., 2019; Zhao and You, 2020; Zhang Y. et al., 2021). The future power system with a high proportion of renewable and sustainable energy is required to have large-scale, low-cost, flexible, and adjustable resources (Li et al., 2020; Zou et al., 2021). To enlarge the regulation capacity of the power system, some thermal power plants have a specially built energy storage system for peak regulation. However, building energy storage systems specifically on the side of thermal power plants has a relatively high investment cost (Lai et al., 2021).

With the deepening of power market reform in China, the price gap between peaks and valleys has gradually increased, and user-side energy storage used for peak and valley arbitrage has continued to increase; at the same time, electric vehicles will also usher in large-scale development to reduce carbon emissions and reduce fuel consumption (Gammon and Sallah, 2021; Xing et al., 2021; Xue et al., 2021). User-side distributed energy storage and electric vehicles are both flexible and adjustable resources with good performance (Vithayasrichareon et al., 2016; Mou et al., 2019). These existing flexible and adjustable resources are used to participate in the regulation of the power system so that the originally distributed energy storage can further improve its utilization efficiency. On the premise of meeting its traffic needs, electric vehicles act as a regulating resource for the power system, which is more economical than the construction of a supporting energy storage system in thermal power plants. Moreover, the energy storage system sitting in thermal power plants can only participate in the peak and frequency modulation services of the power system and cannot provide localized power supply reliability guarantees for various power supply areas. However, a single demand-side resource has problems such as small capacity, scattered geographical location, and intermittent output and cannot accept grid dispatch. The emergence of virtual power plants provides new ideas for solving this problem. The virtual power plant is composed of controllable units, uncontrollable units, energy storage, electric vehicles, and other resources and further consider factors such as demand response and uncertainty through information communication with the control center, cloud center, power trading center, etc., to achieve energy interaction with the grid. Therefore, the distributed energy storage and existing electric vehicle resources that have been invested on the user side for peak shifting, and valley filling and the existing electric vehicle resources are aggregated into a virtual power plant through advanced communication methods, enabling these two types of high-quality distributed resources to respond to grid dispatching, and it can provide effective help for the construction of a new power system approach with renewable and sustainable energy as the main body.

Scholars have researched the participation of virtual power plants in peak regulation. The work of Ya et al. (2019) based on the response characteristics of distributed energy and using deep learning algorithms proposed an optimal scheduling method for virtual power plants to participate in peak regulation auxiliary services. The work of Cui et al. (2021) refers to the operating rules of the Shanghai peak regulation auxiliary service market and proposes a multitime scale clearing model in which virtual power plants participate in peak regulation auxiliary services. Zhang H. et al. (2021) established an optimal dispatch model for virtual power plants to participate in the peak regulation auxiliary service market in northeast China. Guili et al. (2021) considered the multiple uncertainties of virtual power plants participating in deep peak regulation bidding and established a two-stage optimal scheduling model for virtual power plants to maximize their own benefits. Yang et al. (2021) built a virtual power plant for electric vehicles and built an operational decision model for the virtual power plant to assist thermal power plants with deep peak regulation. Guo et al. (2021) clarified the structure and market transaction mechanism of the electrothermal coupling virtual power plant and proposed an optimal scheduling method for the electrothermal coupling virtual power plant to participate in market transactions. Li J. et al. (2021) compared and analyzed the construction of the market mechanism of peak regulation and frequency modulation service by virtual power plants in different provinces and cities from the four perspectives of market composition, market access, quotation clearance, and settlement. Wang et al. (2020) proposed the optimal bidding strategy for virtual power plants to participate in energy, reserve, and flexible peak regulation markets and established a joint clearing model for virtual power plants to participate in the main and auxiliary markets. Zhao et al. (2020) designed the peak regulation auxiliary service market mechanism that considers the participation of virtual power plants and gives the day-ahead and real-time clearing models of the deep peak regulation market. The aforementioned research mostly considered the virtual power plant’s participation in the peak regulation auxiliary service market and did not consider the possibility of virtual power plant participating in the peak regulation from the perspective of demand response. To this end, the work of Yun et al. (2019) aggregates wind power, photovoltaic, and electric vehicles into a virtual power plant to accept grid dispatch, establishes a virtual power plant optimal dispatch model, and obtains the optimal operation strategy of the virtual power plant’s internal resources. Xiuyun et al. (2019) constructed three models of virtual power plants accepting single dispatch, coordinated dispatch, and jointly optimized dispatch and established a virtual power plant-grid company distribution plan based on cooperative game theory. The work of Yao et al. (2017) aggregates wind power, photovoltaics, gas turbines, and energy storage into a virtual power plant and establishes an optimal scheduling model for the virtual power plant after considering demand response.

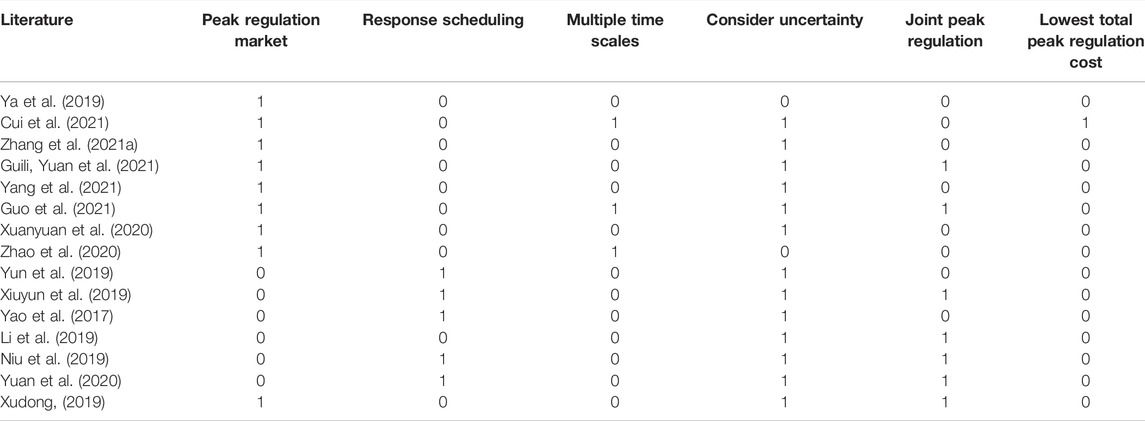
With the further research of scholars, the virtual power plant began to combine peak regulation with other adjustable resources. Li et al. (2019) combined the power generation side and demand side peak regulation resources and established a nuclear-fire-virtual power plant three-stage joint peak regulation model. Niu et al. (2019) built a two-tier optimal scheduling model for virtual power plants and energy-efficient power plants to achieve peak regulation and valley-filling of load curves and improve the system’s ability to absorb random power. The work of Yuan et al. (2020) aimed to maximize the expected economic benefits of virtual power plants and establishes a stochastic optimal scheduling model of virtual power plants based on real-time electricity prices through bilateral joint optimization. The work of Xudong Li, (2019) combines the power generation side and demand side peak regulation resources and establishes a multiresource joint peak regulation optimization model that considers the carbon trading mechanism. The comparison of references is shown in Table 1. 1 represents the document considered the content, and 0 represents the document did not consider the content. Most of the abovementioned research started from the perspective of the highest individual adjustment benefits of virtual power plants and did not consider the fast peak regulation characteristics of virtual power plants. The fast peak regulation characteristics of the virtual power plant means that the virtual power plant has a faster second-level adjustment response capability than the thermal power plant, and it can also jointly peak regulate with thermal power plants in the day-ahead and intra-day two phases, which can minimize the overall peak regulation cost of the power system. To this end, this paper proposes to aggregate two types of user-side high-quality adjustable resources of distributed energy storage and electric vehicles into a virtual power plant and studies the optimization strategy of the virtual and thermal power plants’ joint participation in day-ahead and intra-day peak regulation.

TABLE 1

TABLE 1. Reference comparison table.

The key contributions of this work are listed as follows:

1) We proposed a framework for joint peak regulation of the virtual and thermal power plant based on the perspective of response dispatch, which considers the fast peak regulation characteristics of the virtual power plant.

2) We proposed an intra-day dispatch strategy for the virtual and thermal power plant combined peak regulation. It is considered that the virtual power plant has a fast peak regulation capability based on the work of Yang et al. (2021). With this strategy, the thermal power plant does not need to perform deep peak regulation.

3) We conducted case studies in a power system scenario with renewable and sustainable energy as the mainstay in a certain area to verify the effectiveness of the proposed model and strategy and compared the economics and environmental protection of the virtual and thermal power plant peak regulation through calculation examples.

This study is organized as follows: Section 2 first introduces the rules of China’s peak regulation market, then proposes the mechanism of joint peak regulation of the virtual and thermal power plant in this paper, and finally proposes the handling of uncertain factors in the peak regulation process. Section 3 proposes a day-ahead and intra-day peak regulation model for combined peak regulation of the virtual and thermal power plant. Section 4 proposed a day-ahead and intra-day peak regulation strategy for the virtual and thermal power plant. Section 5 describes the feasibility of joint peak regulation of the virtual and thermal power plant based on the proposed strategy. Section 6 summarizes the contributions of this article.

2 Joint Peak Regulation Process and Uncertainty Treatment of Virtual and Thermal Power Plant

In order to help achieve a carbon-peak and be carbon-neutral, it is imperative to build a power system dominated by renewable and sustainable energy. However, the large amount of renewable and sustainable energy connected to the grid will lead to antipeak regulation, which puts the system security to the test. Virtual power plants can aggregate multiple types of high-quality peak regulation resources and participate in system peak regulation. This section first introduces China’s peak regulation market mechanism and proposes methods to deal with the uncertain factors in the peak regulation process to lay the foundation for follow-up research.

2.1 Day-Ahead and Intra-Day Peak Regulation Process

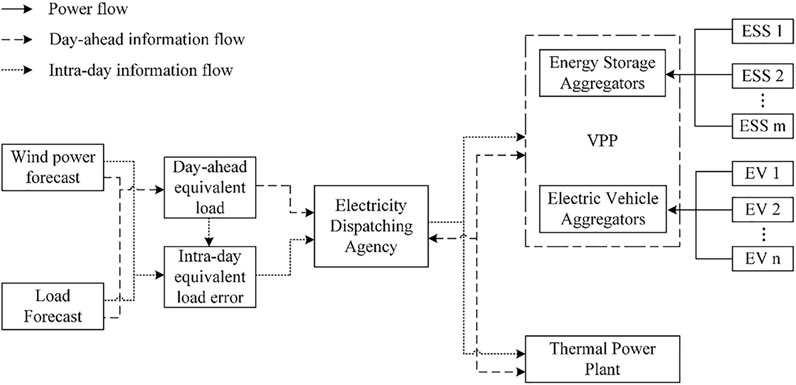
In this paper, the virtual power plant adopts a centralized control method. Through the control and coordination center, the virtual power plant can fully grasp and control all the information of the internal energy storage and electric vehicles. Through the centralized control method, the virtual power plant can simply solve the optimization problem of each distributed unit to meet the peak regulation demand.

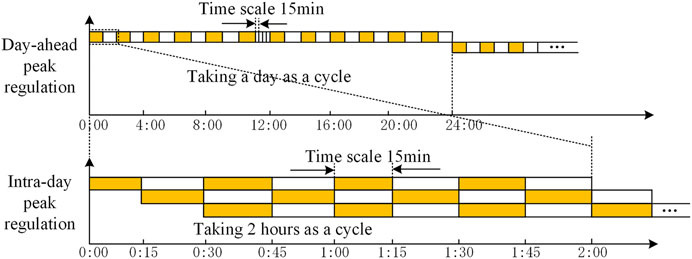
The joint optimization of peak regulation of virtual and thermal power plants refers to the behavior of virtual and thermal power plant to optimize their own power curve or output curve according to the change in the load curve. At present, North China and Shanghai have clarified that virtual power plants can participate in the local peak regulation market as a third-party independent entity, and have issued corresponding rules and documents detailing the organization process of virtual power plants participating in peak regulation auxiliary services (Li Z. et al., 2021). The document stipulates that in the day-ahead phase, the dispatch agency completed the preparation of the 96-point power generation preplanning of the provincial network throughout the day in accordance with the provincial network market rules, and formed the charge and discharge curves of each third-party independent entity and the third-party independent aggregate entity. In the intra-day phase, the provincial network determines the peak regulation resources that each resource can provide every 15 min based on the intra-day power generation plan of each resource, and issues peak regulation instructions for the next 2 h. In summary, based on the rules of the domestic peak regulation market, this article proposes a joint peak regulation mechanism for virtual and thermal power plants.

1) Day-ahead peak regulation plan: taking a day as a cycle and 15 min as a time scale, we determine the start-stop and output status of 96 points of the thermal power plant and the output status of 96 points of various resources inside the virtual power plant

2) Intra-day peak regulation plan: taking 2 h as a cycle and 15 min as the time scale, the output of 96 points of various resources in the virtual power plant is rolling optimization

The day-ahead and intra-day peak regulation timeline is shown in Figure 1.

FIGURE 1

FIGURE 1. Day-ahead and intra-day peak regulation timeline chart.

The day-ahead and intra-day peak regulation process is shown in Figure 2.

FIGURE 2

FIGURE 2. Day-ahead and intra-day peak regulation flowchart.

2.2 Uncertainty Treatment of Joint Peak Regulation

The uncertainty of the joint peak regulation of the virtual and the thermal power plant mainly comes from the volatility of wind power and the uncertainty of the electric vehicle charging and discharging inside the virtual power plant. When dealing with the aforementioned uncertain issues, this paper first uses Monte Carlo simulation to sample the wind power prediction error and the start time of electric vehicle charging to generate a large number of uncertainty scenarios. Similar scenarios are further reduced by comparing the probability distances between the various scenarios (Minghao, 2021), and finally, the CvaR risk theory is used to quantitatively evaluate the possible risks. On this basis, the joint peak regulation optimization of the virtual and thermal power plant is carried out to minimize the peak regulation cost while reducing the system risk as much as possible.

3 Joint Peak Regulation Model of Virtual and Thermal Power Plant

Based on the foregoing, the uncertainty of wind power output and the uncertainty of electric vehicle charging and discharging will affect the joint peak regulation optimization problem of virtual and thermal power plants, which also turns the joint peak regulation optimization problem of virtual and thermal power plants into risk management problem. In summary, this paper establishes a day-ahead and intra-day two-stage virtual and thermal power plant joint peak regulation optimization model considering CvaR.

3.1 Day-Ahead Joint Peak Regulation Model

The main objectives are to obtain the highest overall reliability and lowest total cost of the virtual power plant combined with thermal power plants participating in peak regulation. The day-ahead peak regulation model needs to consider the power upregulation and downregulation characteristics of the virtual power plant and its adjustment cost, and arrange the day-ahead peak regulation plan for the virtual and thermal power plant in advance, so as to reliably meet the demand of load changes (Zhao et al., 2021). Based on the equation of the relationship between the output power of thermal power plants, the output power of virtual power plants, the actual output power of wind turbines, the load value; the load prediction curve is used as the input while the planned output power of 96 points of adjustable resources and the actual output power of wind turbines are the output. The day-ahead joint peak regulation model of the virtual and thermal power plants is

${\displaystyle \sum _{n=1}^{N_G}{P}_{gn,t}}+P_{VPP,t}+P_{wind,t}=P_{load,t},(1)$

$P_{VPP,t}={\displaystyle \sum _{k=1}^{N_{ESS}}{P}_{ESS,k,t}}+{\displaystyle \sum _{l=1}^{N_{EV}}{P}_{EV,l,t}}.(2)$

In these equations, $P_{VPP,t}$ represents the output power of the virtual power plant at time t, $P_{gn,t}$ represents the output power of the thermal power plant at time t. $N_G$ represents the number of thermal power plants, $N_{ESS}$ represents the number of energy storage devices, and $N_{EV}$ represents the number of electric vehicles. $P_{ESS,k,t}$ represents the output power of energy storage device k at time t, and $P_{EV,l,t}$ represents the output power of electric vehicle l at time t. $P_{wind,t}$ represents the actual output power of wind turbines at time t. $P_{load,t}$ represents the actual power value of the load at time t.

3.2 Intra-Day Joint Peak Regulation Model

The objectives of the virtual power plant combined with thermal power plants are to obtain the fastest peak regulation response, the highest reliability, and the lowest adjustment cost. The intra-day peak regulation model needs to consider the power regulation characteristics and regulation costs of virtual and thermal power plants, and adjust the output of virtual and thermal power plants to reliably compensate for load errors. The model uses an equation to describe the relationship between the output power of thermal power plants, the output power of the virtual power plant, and the predicted error value, where the predicted error is the input and the planned regulated output power of 96 points of adjustable resources is the output. The intra-day joint peak regulation model of the virtual and thermal power plants is shown as follows:

$P_{load,t}^{ID}-P_{wind,t}^{ID}={\displaystyle \sum _{k=1}^{N_{ESS}}\text{Δ}{P}_{ESS,k,t}+{\displaystyle \sum _{l=1}^{N_{EV}}\text{Δ}{P}_{EV,l,t}+{\displaystyle \sum _{n=1}^{N_G}\text{Δ}{P}_{gn,n,t}+{\displaystyle \sum _{n=1}^{N_G}{P}_{gn,t}+P_{VPP,t}}}}}.(3)$

In this equation, $P_{load,t}^{ID}$ represents the value of the load at time t in the intra-day. $P_{wind,t}^{ID}$ represents the value of the wind power at time t in the intra-day. $\Delta P_{ESS,k,t}$ represents the regulated power of energy storage device k at time t, $\Delta P_{EV,l,t}$ represents the regulated power of electric vehicle l at time t, and $\Delta P_{gn,n,t}$ represents the regulated power of thermal power plant n at time t.

4 Jointly Optimized Peak Regulation Strategy of Virtual and Thermal Power Plant

Based on the day-ahead and intra-day peak regulation model of the virtual and thermal power plants established in section 1, the model can be solved with reasonable objective function and constraint conditions, and finally its day-ahead and intra-day peak regulation optimization strategy is obtained.

4.1 The Day-Ahead Joint Peak Regulation Phase

In the day-ahead phase, it is necessary to determine the start-stop plan of thermal power plants, the output of 96 points of various peak regulation resources, and the amount of abandoned wind power. Under the day-ahead joint peak regulation phase, the objective is to minimize the cost of adjustable resource peak regulation:

$\min F_1={\displaystyle \sum _{w=1}^{N_w}{\pi }_w(F_{gn}+F_{VPP}+F_{wind,Loss}^{DA}+F_{EV,Loss}^{DA}+F_{CVaR}^{DA})},(4)$

$F_{gn}={\displaystyle \sum _{n=1}^{N_G}{\displaystyle \sum _{t=1}^T(a_n{P}_{gn,t}^2+b_n{P}_{gn,t}+c_n)}}+{\displaystyle \sum _{n=1}^{N_G}{\displaystyle \sum _{t=1}^T(C_g^u{u}_{gn,t}+C_g^v{v}_{gn,t})}},(5)$

$F_{VPP}={\displaystyle \sum _{k=1}^{N_{ESS}}{\displaystyle \sum _{t=1}^T{C}_{ES}(P_{ESS,k,t}^{in}+P_{ESS,k,t}^{out})}}+{\displaystyle \sum _{t=1}^{N_{EV}}{\displaystyle \sum _{t=1}^T{C}_{EV}(P_{EV,l,t}^{in}+P_{EV,l,t}^{out})}},(6)$

$F_{wind,Loss}^{DA}={\displaystyle \sum _{t=1}^T{\lambda }_{wind,t,loss}\text{Δ}{P}_{wind,t,loss}^{DA}},(7)$

$F_{EV,Loss}^{DA}={\displaystyle \sum _{l=1}^{N_{EV}}{\lambda }_{EV,l,loss}\text{Δ}{E}_{EV,l,loss}^{DA}},(8)$

$F_{CVaR}^{DA}={\mu }^{DA}(\zeta -\frac{1}{N_w(1-\beta )}){\displaystyle \sum _{w=1}^{N_w}{z}_w}).(9)$

In these equations, $F_{gn}$, $F_{VPP}$, $F_{wind,Loss}^{DA}$, $F_{EV,Loss}^{DA}$ and $F_{CVaR}^{DA}$ represents the peak regulation cost of thermal power plants, the peak regulation cost of virtual power plants, wind curtailment penalty cost, electric vehicles charging capacity deviation penalty cost, and CVaR risk cost in the day-ahead phase, respectively. $T$ represents the cycle of joint peak regulation in the day-ahead phase. $N_w$ represents the total number of scenes. ${\pi }_w$ represents the probability of each scene. $a_n$, $b_n$, and $c_n$ represent the cost coefficient of conventional peak regulation thermal power plants. $C_g^u$ and $C_g^v$ represent the start and stop costs of thermal power plants, respectively. $u_{gn,t}$ and $v_{gn,t}$ represent the startup and shutdown state variables of thermal power plants, respectively, which are 0–1 variables. $C_{ES}$ represents the cost coefficient of charge and discharge power of the energy storage device. $P_{ESS,k,t}^{in}$ and $P_{ESS,k,t}^{out}$ represents the charge and discharge power of energy storage, respectively. $C_{EV}$ represents the cost coefficient of charge and discharge power of electric vehicles. $P_{EV,l,t}^{in}$ and $P_{EV,l,t}^{out}$ represents the charge and discharge power of electric vehicles, respectively. ${\lambda }_{wind,t,loss}$ represents the abandonment penalty coefficient. $\mathrm{\Delta }{P}_{wind,t,loss}^{DA}$ represents the power of abandoned wind in the day-ahead phase. ${\lambda }_{EV,l,loss}$ represents the penalty cost coefficient of electric vehicles charging capacity deviation. $\mathrm{\Delta }{E}_{EV,l,loss}^{DA}$ represents the capacity deviation value at the end of electric vehicles charging in the day-ahead phase. ${\mu }^{DA}$ represents the risk preference coefficient of the day-ahead phase. $\beta$ represents confidence level. $\zeta$ and $z_w$ both represent auxiliary variables.

In the day-ahead joint peak regulation phase, the constraint conditions are as follows:

1) The power system must meet the requirements of power balance during peak regulation of the virtual and thermal power plants, so the system’s active power balance constraint is

${\displaystyle \sum _{n=1}^{N_G}{P}_{gn,t}+{\displaystyle \sum _{k=1}^{N_{ESS}}{P}_{ESS,k,t}+{\displaystyle \sum _{l=1}^{N_{EV}}{P}_{EV,l,t}+P_{wind,t}=P_{load,t}}}}.(10)$

2) When thermal power plants participate in peak regulation, the upper and lower limits of their power are restrained, the working state cannot change rapidly and the climbing speed is limited, so thermal power plants are restricted as follows:

$u_{gn,t}{P}_{gn,\min }\le P_{gn,t}\le u_{gn,t}{P}_{gn,\max },(11)$

$-v_{gn,dn}\le P_{gn,t}-P_{gn,t-1}\le v_{gn,un},(12)$

$u_{gn,t}+v_{gn,t}\le 1,(13)$

$\begin{array}{l}\{\begin{array}{l}{T}_t^D-(I_t-I_{t-1})T_D\ge 0\\ T_t^D={\displaystyle \sum _{k=t-T_D}^{t-1}(1-I_k)}\end{array},\\ \{\begin{array}{l}{T}_t^U-(I_{t-1}-I_t)T_U\ge 0\\ T_t^U={\displaystyle \sum _{k=t-T_U}^{t-1}{I}_k}\end{array}.\end{array}(14)$

In these equations, Equation 11 represents the upper and lower limits of the thermal power plant output. Equation 12 represents the climbing constraint of the thermal power plant. Equation 13 represents the constraint of the charge and discharge state variables of the thermal power plant. Equation 14 represents the minimum startup and shutdown time constraints of the thermal power plant. $v_{gn,un}$ and $v_{gn,dn}$ represents maximum upward and downward climb rates of the thermal power plant n. $T_D$ and $T_U$ represent minimum continuous operating time and minimum continuous shutdown time of the thermal power plant n. $I_t$ represents the state variable of thermal power plants at time t. $P_{gn,\max }$ and $P_{gn,\min }$ represent the maximum and minimum output power limits of the thermal power plant n.

3) When the virtual power plant participates in peak regulation, the upper and lower limits of the energy storage capacity are limited, the charging and discharging power is limited, the working state cannot change rapidly, and there is a certain relationship between the state of charge at the time before and after, so energy storage devices constraints are

$S_{oc,k,t+1}^{ESS}=\frac{({\eta }_{ESS}^{in}{P}_{ESS,k,t}^{in}-\frac{P_{ESS,k,t}^{out}}{{\eta }_{ESS}^{out}})\text{Δ}t}{C_{ESS}^{Cap}}+S_{oc,k,t}^{ESS}(1-{\delta }_{ESS}),(15)$

$S_{oc,k,\min }^{ESS}\le S_{oc,k,t+1}^{ESS}\le S_{oc,k,\max }^{ESS},(16)$

${\delta }_{ESS}^{in}{P}_{ESS,k,\min }^{in}\le P_{ESS,k,t}^{in}\le {\delta }_{ESS}^{in}{P}_{ESS,k,\max }^{in},(17)$

${\delta }_{ESS}^{out}{P}_{ESS,k,\min }^{out}\le P_{ESS,k,t}^{out}\le {\delta }_{ESS}^{out}{P}_{ESS,k,\max }^{out},(18)$

${\delta }_{ESS}^{in}+{\delta }_{ESS}^{out}\le 1.(19)$

In these equations, Equation 15 represents the SOC state constraint of energy storage. Equation 16 represents the upper and lower limits of SOC for energy storage. Equations 17, 18 represent the charge and discharge power constraints of energy storage. Equation 19 represents the state variable constraints of the charge and discharge of energy storage. $P_{ESS,k,\max }^{in}$ and $P_{ESS,k,\min }^{in}$ represent upper and lower limits of charging power of the energy storage device k. $P_{ESS,k,\max }^{out}$ and $P_{ESS,k,\min }^{out}$ represent upper and lower limits of discharging power of the energy storage device k. $S_{oc,k,t+1}^{ESS}$ and $S_{oc,k,t}^{ESS}$ represent the state of charge at time t + 1 and time t of energy storage devices, respectively. ${\eta }_{ESS}^{in}$ and ${\eta }_{ESS}^{out}$ represent the charging and discharging efficiency of energy storage devices, respectively. $C_{ESS}^{Cap}$ represents the capacity of energy storage devices. ${\delta }_{ESS}$ represents the selfdischarge rate of energy storage devices. $S_{oc,k,\min }^{ESS}$ and $S_{oc,k,\max }^{ESS}$ represent energy storage devices’ minimum and maximum limits of the state of charge, respectively. ${\delta }_{ESS}^{in}$ and ${\delta }_{ESS}^{out}$ represent the variable of the charge and discharge state of the electric vehicle, respectively, which is a variable of 0–1, when ${\delta }_{ESS}^{in}$ is equal to 1, it represents electric vehicles charging, when ${\delta }_{ESS}^{out}$ is equal to 1, it represents electric vehicles discharging.

4) This paper divides electric vehicles into three categories according to their needs. The first type of electric vehicle has always been charged at the rated power, which corresponds to the actual demand for a full charge at the fastest speed, and the corresponding charging costs are relatively high. The second type of electric vehicle allows the charging power to be less than the rated power, but cannot be discharged, and must be fully charged within 4 h. The charging cost is relatively low and it is not urgent to correspond to the actual use of the car. It is hoped that the demand for charging costs can be reduced. The third type of electric vehicle allows the charging power to be lower than the rated power and is allowed to discharge, but the charging must be completed within 6 h, and the charging cost is the lowest. It corresponds to the requirement that there is plenty of time for charging in practice, and it is hoped that the charging cost can be minimized (Zhang et al., 2021). The constraints that distinguish the first type of electric vehicle from other electric vehicles are as follows:

$P_{EV,l,t}^{in}=P_{rated},(20)$

$S_{oc,l,t+1}^{EV}=S_{oc,l,t}^{EV}(1-{\delta }_{EV})+\frac{P_{EV,l,t}^{in}{\eta }_{EV}^{in}\text{Δ}t}{C_{EV}^{Cap}}.(21)$

In these equations, Equation 20 represents the charging power constraint of the first type of electric vehicle. Equation 21 represents the SOC state constraint of the first type of electric vehicle and $P_{rated}$ represents the rated power of the charging pile. $S_{oc,l,t+1}^{EV}$ and $S_{oc,l,t}^{EV}$ represent the state of charge at time t + 1 and time t of electric vehicles, respectively. ${\delta }_{EV}$ represents the selfdischarge rate of electric vehicles. $C_{EV}^{Cap}$ represents the capacity of electric vehicles. ${\eta }_{EV}^{in}$ represents the charge efficiency of electric vehicles.

The constraints that distinguish the second type of electric vehicle from other electric vehicles are as follows:

$0\le P_{EV,l,t}^{in}\le P_{rated},(22)$

$S_{oc,l,t+1}^{EV}=S_{oc,l,t}^{EV}(1-{\delta }_{EV})+\frac{P_{EV,l,t}^{in}{\eta }_{EV}^{in}\text{Δ}t}{C_{EV}^{Cap}},(23)$

$S_{oc,l,T_0+4}^{EV}\ge S_{oc,l,need}^{EV}.(24)$

In these equations, Equation 22 represents the charging power constraint of the second type of electric vehicle. Equation 23 represents the SOC state constraint of the second type of electric vehicles. Equation 24 represents the SOC value constraint at the end of the second type of electric vehicle charging. $S_{oc,l,T_0+4}^{EV}$ represents the SOC value of the electric vehicle after 4 h of charging. $S_{oc,l,need}^{EV}$ represents the SOC value required by the user when using the car. $T_0$ represents the time when the electric vehicle starts to charge.

The constraints that distinguish the third type of electric vehicles from other electric vehicles are as follows:

$0\le P_{EV,l,t}^{in}\le {\delta }_{EV}^{in}{P}_{rated},(25)$

$0\le P_{EV,l,t}^{out}\le {\delta }_{EV}^{out}{P}_{rated},(26)$

$S_{oc,l,t+1}^{EV}=S_{oc,l,t}^{EV}(1-{\delta }_{EV})+\frac{(P_{EV,l,t}^{in}{\eta }_{EV}^{in}-\frac{P_{EV,l,t}^{out}}{{\eta }_{EV}^{out}})\text{Δ}t}{C_{EV}^{Cap}},(27)$

$S_{oc,l,T_0+6}^{EV}\ge S_{oc,l,need}^{EV}.(28)$

In these equations, Equations 25, 26 represent the charge and discharge power constraints of the third type of electric vehicles. Equation 27 represents the SOC state constraint of the third type of electric vehicles. Equation 28 represents the SOC value constraint at the end of the third type of electric vehicle charging. ${\eta }_{EV}^{out}$ represents the discharge efficiency of electric vehicles. ${\delta }_{EV}^{in}$ and ${\delta }_{EV}^{out}$ represent the variable of the charge and discharge state of the electric vehicle, which is a variable of 0–1, when ${\delta }_{EV}^{in}$ is equal to 1, it represents electric vehicles charging, when ${\delta }_{EV}^{out}$ is equal to 1, it represents electric vehicles discharging.

The three types of electric vehicles have common constraints, such as SOC value upper and lower limit constraints, charge and discharge state variable constraints, and the capacity deviation constraints that exist at the end of electric vehicle charging.

$S_{oc,l,\min }^{EV}\le S_{oc,l,t}^{EV}\le S_{oc,l,\max }^{EV},(29)$

${\delta }_{EV}^{in}+{\delta }_{EV}^{out}\le 1,(30)$

$\text{Δ}{E}_{EV,l,loss}^{DA}\le E_{EV,l,rated}-E_{EV,l,need}.(31)$

In these equations, Equation 29 represents the upper and lower limits of the SOC value of electric vehicles. Equation 30 represents the constraint of the charge and discharge state variables of electric vehicles. Equation 31 represents the capacity deviation constraint at the end of electric vehicle charging. $S_{oc,l,\min }^{EV}$ and $S_{oc,l,\max }^{EV}$ represent electric vehicles’ minimum and maximum limits of the state of charge, respectively. $E_{EV,l,rated}$ represents the rated capacity of electric vehicles. $E_{EV,l,need}$ represents the capacity value required by the user when using the car.

5) There are related constraints on auxiliary variables in CVaR cost:

$z_w\ge 0,(32)$

$z_w\ge \zeta -(F_{gn}+F_{ESS}+F_{EV}+F_{wind,Loss}^{DA}+F_{EV,Loss}^{DA}).(33)$

Equations 32, 33 represent the related constraints of auxiliary variables $z_w$ and $\zeta$.

6) The constraints of wind power are

$0\le P_{wind,t}\le P_{wind,max}.(34)$

Equation 34 represents wind power constraint. $P_{wind,max}$ represents the maximum power of the wind turbine at time t.

4.2 The Intra-Day Joint Peak Regulation Phase

Under the intra-day phase, the goal is to minimize the total cost of the adjustable resource adjustment output power of the power system based on the planned output power of the day-ahead phase. The objective function is as follows:

$\min F_2={\displaystyle \sum _{w=1}^{N_w}{\pi }_w}\left(\text{Δ}{F}_{ESS}+\mathrm{\Delta }{F}_{EV}+\mathrm{\Delta }{F}_{gn}+F_{wind,Loss}^{ID}+F_{EV,Loss}^{ID}+F_{CVaR}^{ID}\right),(35)$

$\text{Δ}{F}_{ESS}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{k=1}^{N_{ESS}}{\delta }_{ESS,k}\mathrm{\Delta }{P}_{ESS,k,t}\mathrm{\Delta }t}},(36)$

$\text{Δ}{F}_{EV}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^{N_{EV}}{\delta }_{EV,l}\mathrm{\Delta }{P}_{EV,l,t}\mathrm{\Delta }t}},(37)$

$\text{Δ}{F}_{gn}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{n=1}^{N_G}{\delta }_{gn}\mathrm{\Delta }{P}_{gn,n,t}\mathrm{\Delta }t}},(38)$

$F_{wind,Loss}^{ID}={\displaystyle \sum _{t=1}^T{\lambda }_{wind,t,loss}\mathrm{\Delta }{P}_{wind,t,loss}^{ID}},(39)$

$F_{EV,Loss}^{ID}={\displaystyle \sum _{t=1}^{N_{EV}}{\lambda }_{EV,l,loss}\mathrm{\Delta }{E}_{EV,l,loss}^{ID}},(40)$

$F_{CVaR}^{ID}={\mu }^{ID}(\epsilon -\frac{1}{N_w(1-\beta )}{\displaystyle \sum _{w=1}^{N_w}{\rho }_w}).(41)$

In these equations, $\text{Δ}{F}_{ESS}$, $\mathrm{\Delta }{F}_{EV}$, $\mathrm{\Delta }{F}_{gn}$, $F_{wind,Loss}^{ID}$, $F_{EV,Loss}^{ID}$, $F_{CVaR}^{ID}$ represent the adjustment cost of energy storage, the adjustment cost of electric vehicles, the adjustment cost of thermal power plants, the penalty cost of abandonment of wind power, the penalty cost of electric vehicle charging capacity deviation, and the cost of CVaR in the intra-day phase, respectively. ${\delta }_{ESS,k}$ represents the cost of unit compensation for adjustment output power of the energy storage device k. $\mathrm{\Delta }{P}_{ESS,k,t}$ represents the regulated power of output power of the energy storage device k at time t. ${\delta }_{EV,l}$ represents the cost of unit compensation for adjustment output power of the electric vehicle l. $\mathrm{\Delta }{P}_{EV,l,t}$ represents the regulated power of output power of the electric vehicle l at time t. ${\delta }_{gn}$ represents the cost of unit compensation for adjustment output power of the thermal power plant n. $\mathrm{\Delta }{P}_{gn,n,t}$ represents the regulated power of output power of the thermal power plant n. $\mathrm{\Delta }{P}_{wind,t,loss}^{ID}$ represents the power of abandoned wind in the intra-day phase. $\mathrm{\Delta }{E}_{EV,l,loss}^{ID}$ represents the deviation of electric vehicles charging capacity in the intra-day phase. ${\mu }^{ID}$ represents the risk preference coefficient of the intra-day phase. $\epsilon$ and ${\rho }_w$ both represent auxiliary variables. $\mathrm{\Delta }t$ represents the interval of scheduling time, the interval of scheduling time in this article represents 15 min.

In the intra-day joint peak regulation phase, the constraint conditions are as follows:

1) When it comes to adjusting the output power of various resources during the intra-day phase, the power system must meet the requirements of power balance, so the power balance constraint is

${\displaystyle \sum _{n=1}^{N_G}{P}_{gn,t}+{\displaystyle \sum _{k=1}^{N_{ESS}}{P}_{ESS,k,t}}+{\displaystyle \sum _{l=1}^{N_{EV}}{P}_{EV,l,t}}+{\displaystyle \sum _{k=1}^{N_{ESS}}\mathrm{\Delta }{P}_{ESS,k,t}}}+{\displaystyle \sum _{t=1}^{N_{EV}}\mathrm{\Delta }{P}_{EV,l,t}}+{\displaystyle \sum _{n=1}^{N_G}\mathrm{\Delta }{P}_{gn,n,t}}=P_{load,t}^{ID}-P_{wind,t}^{ID}.(42)$

2) When the virtual power plant combined with thermal power plants participates in intra-day peak regulation, the output power adjustment range of its internal energy storage devices is limited, the charging and discharging power is limited, and the working state change is restricted. And there is a certain relationship between the state of charge at the time before and after. Therefore, the output power regulation capacity of energy storage devices is restricted as

$0\le \mathrm{\Delta }{P}_{ESS,k,t}^{up}\le {\delta }_{ESS,k,t}^{up}(P_{ESS,k,\max }^{out}-P_{ESS,k,t}),(43)$

$0\le \mathrm{\Delta }{P}_{ESS,k,t}^{down}\le {\delta }_{ESS,k,t}^{down}(P_{ESS,k,t}-P_{ESS,k,\min }^{in}),(44)$

$\mathrm{\Delta }{P}_{ESS,k,t}=\mathrm{\Delta }{P}_{ESS,k,t}^{up}-\Delta P_{ESS,k,t}^{down},(45)$

$S_{oc,k,t+1}^{ESS}=\frac{({\eta }_{ESS}^{in}\mathrm{\Delta }{P}_{ESS,k,t}^{down}-\frac{\mathrm{\Delta }{P}_{ESS,k,t}^{up}}{{\eta }_{ESS}^{out}})\mathrm{\Delta }t}{C_{ESS}^{cap}}+S_{oc,k,t}^{ESS}(1-{\delta }_{ESS}),(46)$

${\delta }_{ESS,k,t}^{up}+{\delta }_{ESS,k,t}^{down}\le 1.(47)$

In these equations, Equations 43, 44 represent the positive and negative spinning reserve capacity constraints of energy storage. Equation 46 represents the SOC state constraint of energy storage. Equation 47 represents the positive and negative rotation state variable constraints of energy storage. $\mathrm{\Delta }{P}_{ESS,k,t}^{up}$ and $\mathrm{\Delta }{P}_{ESS,k,t}^{down}$ represent the upregulated output power and the downregulated output power of the energy storage k at time t, respectively. ${\delta }_{ESS,k,t}^{up}$ and ${\delta }_{ESS,k,t}^{down}$ are the state variable of upregulated output and the state variable of downregulated output at time t of energy storage k, respectively.

3) When the virtual power plant combined with the thermal power plant participates in the peak regulation in the intra-day phase, all three types of electric vehicles have the state of charge constraints, the state variable constraints of charge and discharge, and the constraints of the allowable deviation of the capacity at the end of the charge (Zhao et al., 2019).

$S_{oc,l,t+1}^{EV}=\frac{({\eta }_{EV}^{in}\mathrm{\Delta }{P}_{EV,l,t}^{down}-\frac{\mathrm{\Delta }{P}_{EV,l,t}^{up}}{{\eta }_{EV}^{out}})\mathrm{\Delta }t}{C_{EV}^{cap}}+S_{oc,l,t}^{EV}(1-{\delta }_{EV}),(48)$

$\mathrm{\Delta }{P}_{EV,l,t}=\mathrm{\Delta }{P}_{EV,l,t}^{up}-\mathrm{\Delta }{P}_{EV,l,t}^{down},(49)$

$E_{EV,l,rated}-E_{EV,l,need}\ge \mathrm{\Delta }{E}_{EV,l,loss}^{ID},(50)$

${\delta }_{EV,l,t}^{down}+{\delta }_{EV,l,t}^{up}\le 1.(51)$

In these equations, Equation 48 represents the SOC state constraint of electric vehicles. Equation 50 represents the capacity deviation constraint at the end of electric vehicle charging. Equation 51 represents the constraints of the positive and negative rotation state variables of the electric vehicle. ${\delta }_{EV,l,t}^{up}$ and ${\delta }_{EV,l,t}^{down}$ are the state variable of upregulated output and the state variable of downregulated output at time t of electric vehicle l, respectively.

The first type of electric vehicle can only be charged at rated power, so there is no regulation capacity constraint, only the second and third types of electric vehicles have regulation capacity constraints.

The second category of electric vehicles adds the following constraints to the common constraints:

$0\le \mathrm{\Delta }{P}_{EV,l,t}^{up}\le {\delta }_{EV,l,t}^{up}{P}_{EV,l,t}^{in},(52)$

$0\le \mathrm{\Delta }{P}_{EV,l,t}^{down}\le {\delta }_{EV,l,t}^{down}(P_{rated}-P_{EV,l,t}^{in}).(53)$

Equations 52, 53 represent the positive and negative spinning reserve capacity constraints of the second type of electric vehicle.

The third category of electric vehicles adds the following constraints to the common constraints:

$0\le \mathrm{\Delta }{P}_{EV,l,t}^{up}\le {\delta }_{EV,l,t}^{up}(P_{rated}-P_{EV,l,t}),(54)$

$0\le \mathrm{\Delta }{P}_{EV,l,t}^{down}\le {\delta }_{EV,l,t}^{down}(P_{EV,l,t}+P_{rated}).(55)$

Equations 54, 55 represent the positive and negative spinning reserve capacity constraints of the third type of electric vehicles.

4) When thermal power plants participate in peak regulation, their output power adjustment range is limited, the output power range is limited, and the climbing speed is limited. And there are restrictions on the change of working status, which are the problems that thermal power plants face when adjusting the output. Therefore, the positive and negative spinning reserve capacity of thermal power plants is restricted as

$0\le P_{u,n,t}\le (P_{gn,\max }-P_{gn,t}){\delta }_{gn,t}^{up},(56)$

$0\le P_{d,n,t}\le (P_{gn,t}-P_{gn,\min }){\delta }_{gn,t}^{down},(57)$

$\mathrm{\Delta }{P}_{gn,n,t}=P_{u,n,t}-P_{d,n,t},(58)$

${\delta }_{gn,t}^{up}+{\delta }_{gn,t}^{down}\le 1,(59)$

$-v_{gn,dn}\le P_{u,n,t}-P_{u,n,t-1}\le v_{gn,un},(60)$

$-v_{gn,dn}\le P_{d,n,t}-P_{d,n,t-1}\le v_{gn,un}.(61)$

In these equations, Equations 56, 57 represent the positive and negative spinning reserve capacity constraints of thermal power plants. Equation 59 represents the positive and negative rotation state variable constraints of the thermal power plant. Equations 60, 61 represent the climbing constraint that exists when adjusting the output of the thermal power plant. $P_{u,n,t}$ and $P_{d,n,t}$ represents the upregulated and downregulated power of the thermal power plant, respectively. ${\delta }_{gn,t}^{up}$ and ${\delta }_{gn,t}^{up}$ represent the upward rotating state variables and the downward rotating state variables of the thermal power plant n at time t, respectively.

5) There are related constraints on auxiliary variables in CVaR cost:

${\rho }_w\ge 0,(62)$

${\rho }_w\ge \epsilon -(\mathrm{\Delta }{F}_{ESS}+\mathrm{\Delta }{F}_{EV}+\mathrm{\Delta }{F}_{gn}+F_{wind,Loss}^{ID}+F_{EV,Loss}^{ID}).(63)$

Equations 62, 63 represent the related constraints of auxiliary variables ${\rho }_w$ and $\epsilon$

6) The constraints of wind power are

$0\le P_{wind,t}\le P_{wind,max}.(64)$

Equation 64 represents wind power constraint. $P_{wind,max}$ represents the maximum power of the wind turbine at time t.

4.3 Jointly Optimized Peak Regulation Strategy for Day-Ahead and Intra-Day

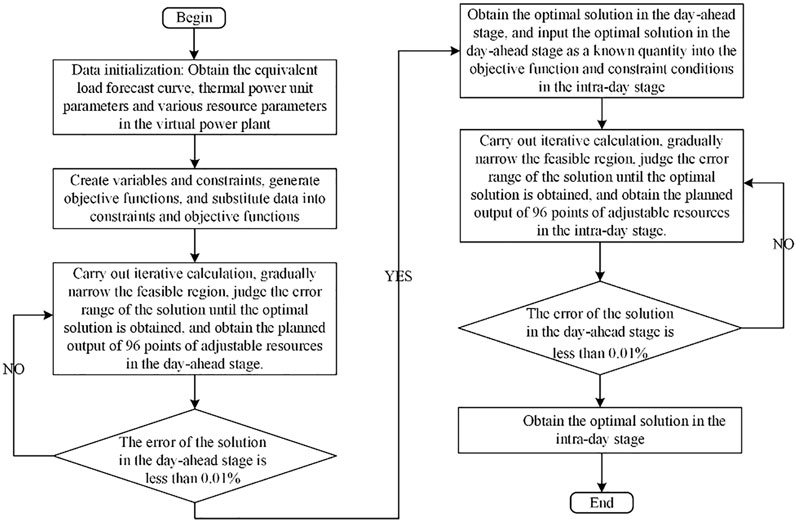
Compared with other algorithms, the branch and bound algorithm have the advantages of occupying less memory and reusing the parent node information and it is more suitable for two-stage optimization strategy solving (Li J. et al., 2021). Therefore, the day-ahead and intra-day joint peak regulation model can be solved and the optimal strategy for joint peak regulation can be obtained by using the branch and bound algorithm. The specific algorithm flow is shown in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of branch and bound algorithm.

5 Case Study

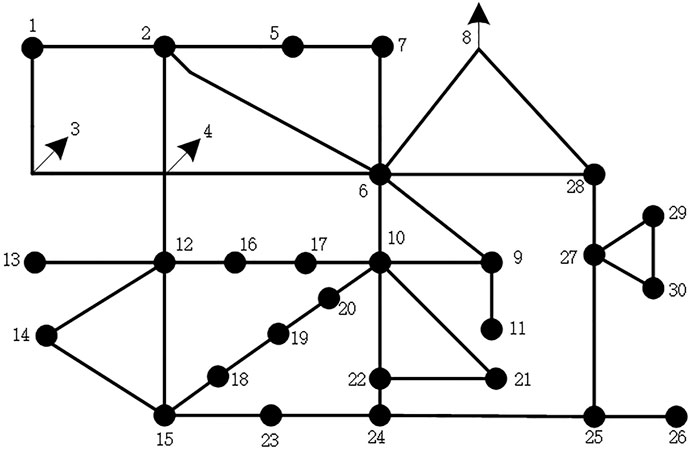
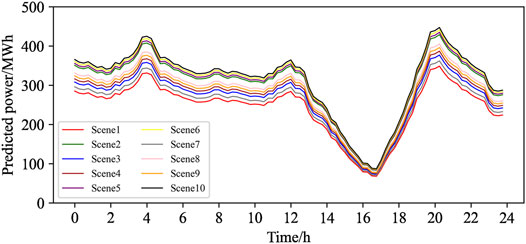
To prove the effectiveness of the strategy proposed in this article, a calculation example of a virtual power plant combined with a thermal power plant participating in peak regulation is designed for a power system with renewable and sustainable energy as the main part in a certain area. This area includes a thermal power plant with a capacity of 600 MW, five wind farms with a capacity of 100 MW, a total installed wind power capacity of 500 MW, a total load of 650 MW, and distributed energy storage capacities of 15, 25, 20 and 20 MW for access nodes. The virtual power plant aggregates 1,000 electric vehicles with a total capacity of 50 MW. In this article, the capacity of the three types of electric vehicles is allocated according to 1:3:6. The power network structure in this area is shown in Figure 4. Node 1 serves as the connection location of the thermal power plant, and nodes 13, 26, 23, 11, and 18 serve as the connection location of the wind farm. Energy storage aggregators 1, 2, 3, and 4 are connected at nodes 8, 21, 29, and 30, respectively. The first type of electric vehicle aggregator is connected at node 19. The second type of electric vehicle aggregator is connected at node 7. The third type of electric vehicle aggregator is connected at node 15. The wind power forecast error and the start time of electric vehicle charging generally obey a normal distribution with a mean value of 0. However, considering the actual situation, the first type of electric vehicle corresponds to the situation where the owner’s demand for the car is relatively urgent, so the charging start time of the first type of electric vehicle is set between 7:00–21:00. The charging start time of the second type of electric vehicle is between 1:00–23:00. The charging start time of the third type of electric vehicle is at any time throughout the day. Considering the volatility of wind power and the randomness of the start time of electric vehicle charging, this article first generates ten classic scenarios of wind power output prediction errors according to the steps described in section 1.2, and by sampling and clustering, the charging start time of electric vehicles, the charging start times for the three types of electric vehicles are 15:00, 17:00 and 21:00, respectively. The randomly generated wind output curve is shown in Figure 5. After considering the uncertainty, this article considers two scenarios, namely, a virtual power plant combined with thermal power unit peak regulation and a thermal power plant side building energy storage system for peak regulation. The total cost of peak regulation at different stages can be obtained with the profits at different stages of the virtual power plant, and the profits at different stages of energy storage on the side of the thermal power plant under each scenario, conduct a comparative analysis, and analyze the impact of different risk preference coefficients and wind power forecast errors on the results.

FIGURE 4

FIGURE 4. Node diagram of regional power network.

FIGURE 5

FIGURE 5. Wind power curve graphs in different scenarios.

5.1 Model Parameter Setting

This article regards the wind power in this area as a negative load, the wind power forecast curve and the load forecast curve are superimposed to obtain the equivalent load forecast curve. The current equivalent load forecast curve for this area will be shown in various resource output power curve diagrams. This article assumes that the SOC value when the electric vehicle is connected to the charging station to start charging should be 0.25, The SOC value at the end of charging needs to be greater than 0.8. The maximum and minimum output of the thermal power plant is 600 and 300 MW, respectively and the climbing constraint power is 400 MWh. The three coefficients of coal consumption cost ai is 0.0375 ¥/(MW)², bi is 20 ¥/(MW)², and ci is 372.5 ¥/(MW)², the compensatory costs for the positive and negative spinning reserve capacity of the thermal power plants are 230 ¥/MWh, respectively. The abandonment penalty coefficient is 150 ¥/(MWh). The parameters of energy storage devices and electric vehicles inside the virtual power plant are shown in Table 2. The self-discharge rate of all energy storage devices is 0.005%. The initial state of charge is 0.3, 0.4, 0.5, 0.6. The charge and discharge cost of all energy storage devices is 50 ¥/MWh. The compensatory prices for energy storage devices participating in auxiliary services are 192, 204, 216, and 216 ¥/MWh, respectively. The self-discharge rate of electric vehicles is 0.005%. The initial state of charge is 0.3. The charge and the discharge cost of electric vehicles is 50 ¥/MWh. The compensatory price for electric vehicles participating in auxiliary services is 210 ¥/MWh, and the capacity deviation penalty coefficient at the end of charging is 0.5 ¥/kWh. In this article, the confidence level is 0.95, and the risk preference coefficient is 0.7.

TABLE 2

TABLE 2. Parameters of internal resources of the virtual power plant.

5.2 Modelling Results

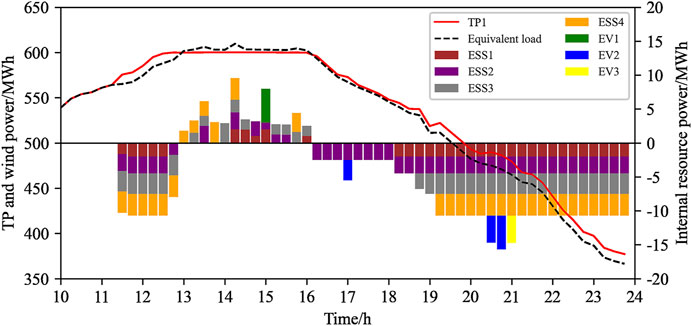
Comparing the sampling results, it is found that the probability of scene 8 is the largest, so scene 8 is selected as a typical scene for result analysis. The day-ahead and intra-day peak regulation costs of the system are shown in Table 3, and the day-ahead adjustable resource output power curve of the system is shown in Figure 6.

TABLE 3

TABLE 3. System peak regulation cost.

FIGURE 6

FIGURE 6. Day-ahead planned output power curve of adjustable resources.

It can be seen from Table 3 that in the day-ahead joint peak regulation phase, the peak regulation cost of the virtual power plant accounted for 6.36% of the total cost. The peak regulation cost of the virtual power plant accounted for 8.05% of the total cost under the intra-day joint peak regulation phase. This shows that the virtual power plant plays a vital role in different peak regulation phases, and shares the peak regulation pressure of the thermal power plant to a large extent.

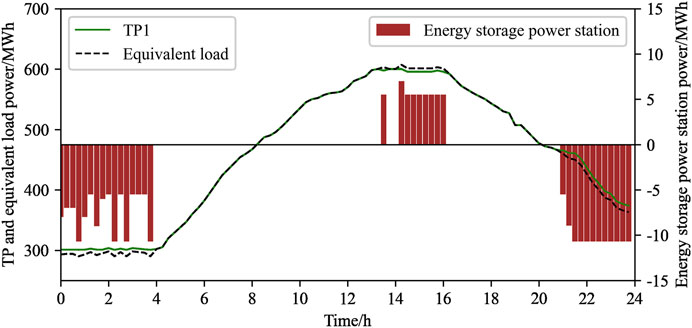
It can be seen from Figure 6 that the thermal power plant is started to meet the system power balance in the day-ahead phase. During the peak period of equivalent load (4:00–16:00) and the period of low equivalent load (20:00–24:00), the output power of the thermal power plant reaches the limit, leading to the result that the peak regulation demand of the system cannot be met. At this moment, various resources within the virtual power plant need to be combined with the thermal power plant to participate in peak regulation. Through the comparative analysis of the results, we found that during the low equivalent load period (0:00–6:00), because the output of the thermal power plant reaches the limit, and energy storage and electric vehicles can no longer store energy, wind abandonment occurs at this time.

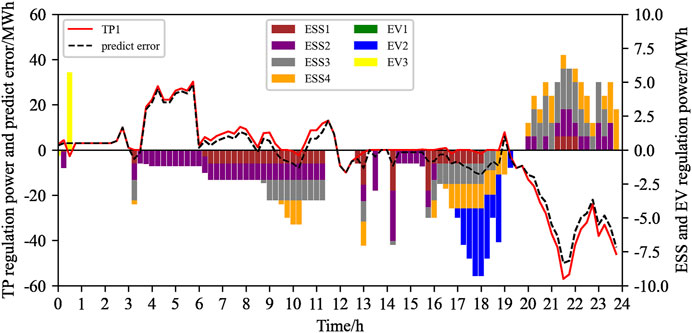
In the intra-day phase, the handling of uncertain factors is the same as the day-ahead method, so this section will not go into detail. The regulation of the output power of the system in the intra-day phase is shown in Figure 7. It can be seen from Figure 7 that during the period of 4:00–14:00, the equivalent load prediction error is relatively large. The first type of electric vehicle can only be charged with a constant charging power, so power regulation cannot be performed. At this moment, the internal energy storage of the virtual power plant and the thermal power plant simultaneously adjust the output to compensate for the load error. During 17:00–20:00 and 0:00–2:00, electric vehicles participate in system peak regulation and adjust output power together with energy storage to compensate for load errors with the thermal power plant.

FIGURE 7

FIGURE 7. Wind power consumption curve.

In summary, the joint peak regulation of the virtual and thermal power plant in the day-ahead and intra-day two phases can not only improve the economics of peak regulation but also be an effective way to improve the power grid regulation capability.

5.3 Comparative Analysis

5.3.1 Comparative Analysis 1

To reflect the economy of the joint peak regulation of virtual and thermal power plants compared with thermal power plants alone, and to verify the effectiveness of the method proposed in this article, the model in this paper is compared with the traditional peak regulation model that only has a thermal power plant and requires deep peak regulation to meet load changes.

1) Model 1: jointly optimized peak regulation model of the virtual and thermal power plant in this article.

2) Model 2: the traditional peak regulation model only considers the thermal power plants participating in peak regulation. Also, the thermal power plants need to perform deep peak regulation.

The day-ahead and intra-day output power curves of the thermal power plant in Model 2 are shown in Figure 8. Comparing Figure 8 with Figure 6, during the period of 0:00–4:00, the thermal power plant has entered deep peak regulation during the day-ahead and intra-day phases.

FIGURE 8

FIGURE 8. The output power curve of the deep peak regulation of the thermal power plant.

The day-ahead and intra-day peak regulation costs of different models are shown in Table 3.

Comparing the costs of Model 1 and Model 2 in Table 3, we find that in the day-ahead phase, Model 1 is more economical than Model 2, the total system peak regulation cost is reduced by 22.89%, and the wind abandonment cost is reduced by 76.4%. In the intra-day phase, the trend of the comparison results of the two models is similar to the day-ahead phase. In summary, the model proposed in this article can improve the economy of the system at different peak regulation phases, reduce the peak regulation pressure of the thermal power plant, increase the grid connection of renewable and sustainable energy, and make the system cleaner.

5.3.2 Comparative Analysis 2

The model in this article is compared with the traditional model of thermal power plant side energy storage combined with the thermal power plant to participate in peak regulation.

1) Model 1: jointly optimized peak regulation model of the virtual and thermal power plant in this article

2) Model 2: the traditional peak regulation model of thermal power plant side energy storage combined with the thermal power plant to participate in peak regulation

The output power curve of the thermal power plant and thermal power plant side energy storage in Model 2 is shown in Figure 9.

FIGURE 9

FIGURE 9. Peak regulation resource output power curve in Model 2.

In Model 1, the profit of the virtual power plant in the day-ahead phase was 37,000 ¥, and the profit in the intra-day phase was 97,000 ¥. the profit of the energy storage at the thermal power plant side in the day-ahead phase was only 14,000 ¥, and the profit in the intra-day phase was only 38,000 ¥. A comparative analysis of the profit between the day-ahead and intra-day phases of Model 1 and Model 2 shows that the former has the advantage of low original investment costs. The investment cost of the virtual power plant has been covered by the revenue from peak regulation and valley filling of distributed energy storage and the revenue from the participation of electric vehicles in transportation, but the investment cost of energy storage on the thermal power plant side needs to be recovered in peak regulation. Therefore, it can be seen that the daily profit of the energy storage on the side of the thermal power plant is much lower than the daily peak regulation profit of the virtual power plant.

5.3.3 Comparative Analysis 3

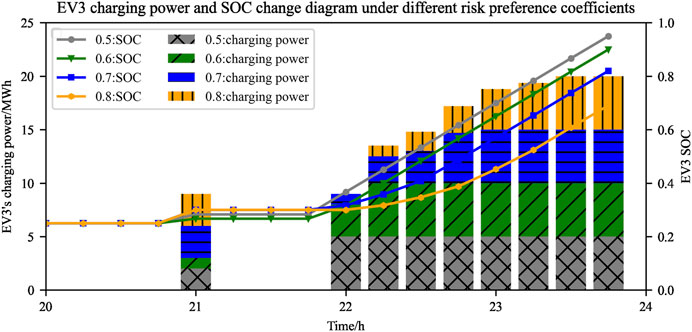
In order to compare the impact of different risk preference coefficients on system strategy and cost, Table 4 shows the relationship between the total peak regulation cost, wind curtailment cost, and capacity deviation cost of the virtual and the thermal power plant under different risk preference coefficients. Figure 10 shows the changes in the charging power and SOC value of the third type of electric vehicle under different risk preference coefficients.

TABLE 4

TABLE 4. Cost analysis table under different risk preference coefficients.

FIGURE 10

FIGURE 10. EV3 charging power and SOC change diagram under different risk preference coefficients.

It can be seen from Table 4 that as the risk preference coefficient increases, the total peak regulation cost of the system increases accordingly, and the cost of wind abandonment and the penalty cost of capacity deviation also increase. This is because the risk preference coefficient reflects the importance of the peak regulation strategy to uncertain factors. The greater the risk preference coefficient, the higher the system’s requirements for safety, and the more the system peak regulation strategy is biased towards reducing the risk loss during system peak regulation. According to Figure 10, as the risk preference coefficient increases, in order to reduce the influence of system uncertainties, the system peak regulation depends more on the thermal power plant and energy storage. Therefore, the greater the risk preference coefficient, the greater the power involved in peak regulation of the thermal power plant and energy storage, the smaller the response capacity of electric vehicles, the smaller the amount of wind power consumption.

5.3.4 Comparative Analysis 4

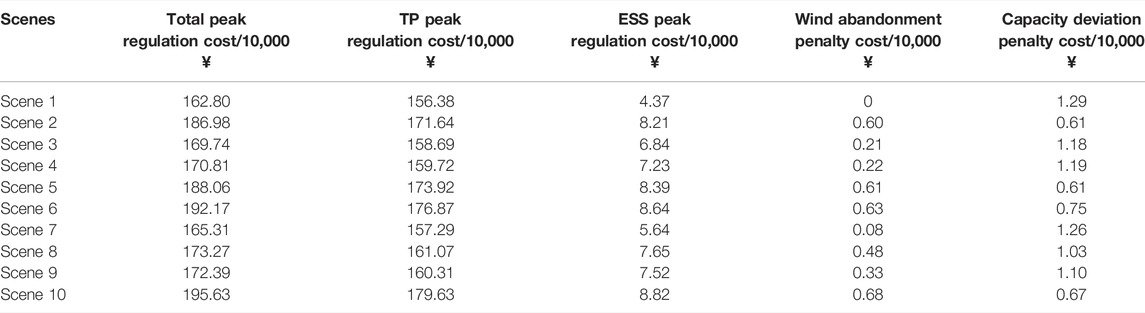
In order to analyze the impact of different wind power forecast accuracy on the peak regulation results, Table 5 shows the system peak regulation results under ten scenarios. It can be seen from Table 5 that the greater the positive forecast error of wind power, the greater the total peak regulation cost of the system, which requires more power from the thermal power plant and energy storage to participate in peak regulation, and the higher the cost of wind curtailment and the penalty cost of capacity deviation at this time. This is because during the low load period, when the positive error of wind power is greater, and the thermal power reaches the lower limit of the minimum output, it still cannot meet the peak regulation demand, and more energy storage is needed to participate in peak regulation. When neither energy storage nor the thermal power plant can meet the demand for peak regulation, wind power will generate more wind abandonment power, and the overall capacity deviation at the last moment of electric vehicle charging will be smaller.

TABLE 5

TABLE 5. System peak regulation results in different scenarios.

6 Conclusion and Future Work

In order to further improve the economy of peak regulation, this article constructs a day-ahead and intra-day two-stage joint peak regulation model for virtual and thermal power plants. The specific contributions are as follows:

1) The joint peak regulation of the virtual and thermal power plant can significantly reduce the peak regulation cost of the system, further improve resource utilization efficiency, and at the same time promote the integration of renewable and sustainable energy into the grid, making the system cleaner.

2) The virtual power plant combined with the thermal power plant to participate in peak regulation can relieve part of the peak regulation pressure of the thermal power plant.

3) The joint peak regulation of the virtual and thermal power plant can not only improve system economy but also enhance system regulation ability.

4) The thermal power plant has built a supporting energy storage system. The energy storage system can participate in power system peak and frequency modulation. However, the energy storage system cannot participate in the trade of multiple power system varieties on the user side, nor can it provide localized power supply reliability guarantees for various regions. Its economy is lower than that of the virtual power plant combined with the thermal power plant to participate in peak regulation.

Meanwhile, in view of the problems reflected in the research, this article considers the following aspects to further expand:

1) In this paper, the virtual power plant aggregates energy storage devices and electric vehicles but does not aggregate high-quality adjustable resources such as interruptible loads and shiftable loads.

2) The peak regulation strategy proposed in this paper only includes two phases, day-ahead, and intra-day, and does not maximize the ability of fast peak regulation of virtual power plants. Therefore, this article will further consider real-time peak regulation in the future.

3) The objects involved in peak regulation in this article are only virtual and thermal power plants, and other high-quality peak regulation resources such as pumped storage are not considered. Therefore, this article will consider a variety of objects to participate in peak regulation in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

PL conceptualized the study, contributed to the study methodology, and wrote the original draft. YC managed and investigated data and assisted in establishing models and improving strategies. KY wrote programs, assisted in data analysis and wrote the original draft. PY carried out project management and supervision. JY verified the correctness of the method and carried out project management. SY and ZZ contributed to the validation and writing—review and editing. CSL, LLL, and AFZ contributed to the writing—review and editing.

Funding

This work was supported by the Research Project of Digital Grid Research Institute, China Southern Power Grid under Grant YTYZW20010.

Conflict of Interest

Authors PL, YC, JY, and SY are employed by China Southern Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cui, Y., Xiao, F., Wang, W., Sun, Z., Ai, Q., Jin, M., et al. (2021). “The Mechanism of Virtual Power Plant Participating in the Peak Regulation Auxiliary Service Market,” in 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), 1010–1015. doi:10.1109/AEEES51875.2021.9403008

CrossRef Full Text | Google Scholar

Gammon, R., and Sallah, M. (2021). Preliminary Findings from a Pilot Study of Electric Vehicle Recharging from a Stand-Alone Solar Minigrid. Front. Energy Res. 8, 374. doi:10.3389/fenrg.2020.563498

CrossRef Full Text | Google Scholar

Guili, Y., Sixuan, C., and Xiaoxuan, D. (2021). Research on Two-Stage Game Strategy of Virtual Power Plant in Deep Peak Regulation Auxiliary Service Market. E3S Web Conf. 256, 01026. doi:10.1051/e3sconf/202125601026

CrossRef Full Text | Google Scholar

Guo, W., Liu, P., and Shu, X. (2021). Optimal Dispatching of Electric-Thermal Interconnected Virtual Power Plant Considering Market Trading Mechanism. J. Clean. Prod. 279, 123446. doi:10.1016/j.jclepro.2020.123446

CrossRef Full Text | Google Scholar

Lai, C. S., Locatelli, G., Pimm, A., Wu, X., and Lai, L. L. (2021). A Review on Long-Term Electrical Power System Modeling with Energy Storage. J. Clean. Prod. 280, 124298. doi:10.1016/j.jclepro.2020.124298

CrossRef Full Text | Google Scholar

Li, J., Ai, Q., and Yin, S. (2021). “Market Mechanism and Foreign Experience of Virtual Power Plant Participating in Peak-Regulation and Frequency-Regulation,” in Proceedings of The Chinese Society for Electrical Engineering, 1–21.

Google Scholar

Li, X., Ai, X., Hu, J., Zhou, B., and Lin, Z. (2019). Three-stage Combined Peak Regulation Strategy for Nuclear-Thermal-Virtual Power Plant Considering Carbon Trading Mechanism. Power Syst. Technol., 2460–2470.

Google Scholar

Li, Y., Wang, C., and Li, G. (2020). A Mini-Review on High-Penetration Renewable Integration into a Smarter Grid. Front. Energy Res. 8, 84. doi:10.3389/fenrg.2020.00084

CrossRef Full Text | Google Scholar

Li, Z., Li, Y., Liu, Y., Wang, P., Lu, R., and Gooi, H. B. (2021). Deep Learning Based Densely Connected Network for Load Forecasting. IEEE Trans. Power Syst. 36, 2829–2840. doi:10.1109/TPWRS.2020.3048359

CrossRef Full Text | Google Scholar

Minghao, G. (2021). Research on Optimal Dispatch of Park Integrated Energy System Based on Conditional Value at Rsik Theory. Master's Thesis. Xi'an University of Technology.

Google Scholar

Mou, X., Zhang, Y., Jiang, J., and Sun, H. (2019). Achieving Low Carbon Emission for Dynamically Charging Electric Vehicles through Renewable Energy Integration. IEEE Access 7, 118876–118888. doi:10.1109/ACCESS.2019.2936935

CrossRef Full Text | Google Scholar

Niu, D., Zhao, D., Yang, S., and Liu, L. (2019). Cooperative Scheduling Optimization Model and Simulation Application for Virtual Power Plant and Efficiency Power Plant Considering Uncertainty and Energy Storage System. J. Central South Univ. Sci. Technol., 1736–1743.

Google Scholar

Vithayasrichareon, P., Mills, G., and MacGill, I. (2016). “Impact of Electric Vehicles and Solar PV on Future Generation Portfolio Investment,” in 2016 IEEE Power and Energy Society General Meeting (PESGM) (IEEE), 1. doi:10.1109/PESGM.2016.7741123

CrossRef Full Text | Google Scholar

Wiryadinata, S., Morejohn, J., and Kornbluth, K. (2019). Pathways to Carbon Neutral Energy Systems at the University of California, Davis. Renew. Energy 130, 853–866. doi:10.1016/j.renene.2018.06.100

CrossRef Full Text | Google Scholar

Xing, Q., Cheng, M., Liu, S., Xiang, Q., Xie, H., and Chen, T. (2021). Multi-Objective Optimization and Dispatch of Distributed Energy Resources for Renewable Power Utilization Considering Time-Of-Use Tariff. Front. Energy Res. 9, 68. doi:10.3389/fenrg.2021.647199

CrossRef Full Text | Google Scholar

Xiuyun, G., Ying, W., Feng, Z., Yan, J., Chengzhi, S., Yimiao, Y., et al. (2019). “Research on Cooperative Scheduling Model of Wind-Solar-Thermal Virtual Power Plant Based on Thermal Load Demand Response,” in 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia) (IEEE), 3810–3814. doi:10.1109/ISGT-Asia.2019.8881358

CrossRef Full Text | Google Scholar

Xuanyuan, W., JianXiao, W., Zhaoyuan, W., Zhen, L., and Yonghua, S. (2020). Virtual Power Plant's Optimal Bidding Strategy for Flexible Ramping Products Based on a Hybrid Stochastic/Robust Optimization. Renew. Energy Resour., 539–544. doi:10.13941/j.cnki.21-1469/tk.2020.04.018

CrossRef Full Text | Google Scholar

Xudong, L. (2019). Research on Combined Peak Regulation Strategy of Multiple Power Supply with High Proportion Unconventional Units. doi:10.27140/d.cnki.ghbbu.2019.001249

CrossRef Full Text | Google Scholar

Xue, P., Xiang, Y., Gou, J., Xu, W., Sun, W., Jiang, Z., et al. (2021). Impact of Large-Scale Mobile Electric Vehicle Charging in Smart Grids: A Reliability Perspective. Front. Energy Res. 9, 241. doi:10.3389/fenrg.2021.688034

CrossRef Full Text | Google Scholar

Ya, L., Deliang, Z., and Xuanyuan, W. (2019). “A Peak Regulation Ancillary Service Optimal Dispatch Method of Virtual Power Plant Based on Reinforcement Learning,” in 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia) (IEEE), 4356–4361. doi:10.1109/ISGT-Asia.2019.8881083

CrossRef Full Text | Google Scholar

Yang, X., Niu, D., Sun, L., Wang, K., and De, G. (2021). Participation of Electric Vehicles in Auxiliary Service Market to Promote Renewable Energy Power Consumption: Case Study on Deep Peak Load Regulation of Auxiliary Thermal Power by Electric Vehicles. Energy Sci. Eng. 9, 1465–1476. doi:10.1002/ese3.907

CrossRef Full Text | Google Scholar

Yao, W., Zheng, S., Zheng, W., Jiawei, W., Xuxia, L., Yuming, Z., et al. (2017). “Dynamic Scheduling Optimization Model for Virtual Power Plant Connecting with Wind-Photovoltaic-Energy Storage System,” in 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2) (IEEE), 1–6. doi:10.1109/EI2.2017.8244411

CrossRef Full Text | Google Scholar

Yuan, G., Jia, X., Fang, F., and Don, J. (2020). Joint Stochastic Optimal Scheduling of Heat and Power Considering Source and Load Sides of Virtual Power Plant. Power Syst. Technol., 2932–2940.

Google Scholar

Yun, Q., Gao, W., Zhang, F., Cheng, L., and Tian, L. (2019). “Optimization of Operation Strategy of Virtual Power Plants Involved in Peak Shaving,” in 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC) (IEEE), 1786–1791. doi:10.1109/CIEEC47146.2019.CIEEC-2019619

CrossRef Full Text | Google Scholar

Zhang, H., Li, D., Tian, Z., Guo, L., and Chen, J. (2021a). Optimal Scheduling Model of Virtual Power Plant and Thermal Power Units Participating in Peak Regulation Ancillary Service in Northeast China. J. Phys. Conf. Ser. 1887, 012046. doi:10.1088/1742-6596/1887/1/012046

CrossRef Full Text | Google Scholar

Zhang, X., Guo, C., Jin, G., Yin, K., Gao, Y., and Zhou, Y. (2021). Collaborative Optimal Dispatch of Multi-Station Integration Based on Affine Robust Optimization. Mod. Electr. Power, 1–10. doi:10.19725/j.cnki.1007-2322.2021.0139

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, X., and Feng, S. (2021b). Power to Gas: an Option for 2060 High Penetration Rate of Renewable Energy Scenario of China. Environ. Sci. Pollut. Res. 29, 6857–6870. doi:10.1007/s11356-021-16137-x

CrossRef Full Text | Google Scholar

Zhao, J., Yang, Y., Sun, Z., Ye, H., Ling, X., and Wang, X. (2020). Deep Peak Regulation Market Mechanism and Clearing Model Considering Participation of Virtual Power Plants. J. Glob. Energy Interconnect., 469–476. doi:10.19705/j.cnki.issn2096-5125.2020.05.006

CrossRef Full Text | Google Scholar

Zhao, N., and You, F. (2020). Can Renewable Generation, Energy Storage and Energy Efficient Technologies Enable Carbon Neutral Energy Transition? Appl. Energy 279, 115889. doi:10.1016/j.apenergy.2020.115889

CrossRef Full Text | Google Scholar

Zhao, Z., Guo, J., Lai, C. S., Xiao, H., Zhou, K., and Lai, L. L. (2021). Distributed Model Predictive Control Strategy for Islands Multimicrogrids Based on Noncooperative Game. IEEE Trans. Ind. Inf. 17, 3803–3814. doi:10.1109/TII.2020.3013102

CrossRef Full Text | Google Scholar

Zhao, Z., Yang, P., Wang, Y., Xu, Z., and Guerrero, J. M. (2019). Dynamic Characteristics Analysis and Stabilization of PV-Based Multiple Microgrid Clusters. IEEE Trans. Smart Grid 10, 805–818. doi:10.1109/TSG.2017.2752640

CrossRef Full Text | Google Scholar

Zou, C., Xiong, B., Xue, H., Zheng, D., Ge, Z., Wang, Y., et al. (2021). The Role of New Energy in Carbon Neutral. Petroleum Explor. Dev. 48, 480–491. doi:10.1016/S1876-3804(21)60039-3

CrossRef Full Text | Google Scholar