- 1Arizona State University LightWorks® and the School of Sustainability (former address: Sandia National Laboratories, Albuquerque, New Mexico, USA), Tempe, AZ, United States
- 2Sandia National Laboratories, Thermal Sciences and Engineering Department, Albuquerque, NM, United States
- 3Sandia National Laboratories, Advanced Materials Laboratory, Albuquerque, NM, United States
- 4The George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, United States
- 5Arizona State University LightWorks® and the School of Molecular Sciences, Tempe, AZ, United States
- 6Sandia National Laboratories, Concentrating Solar Technologies, Albuquerque, NM, United States
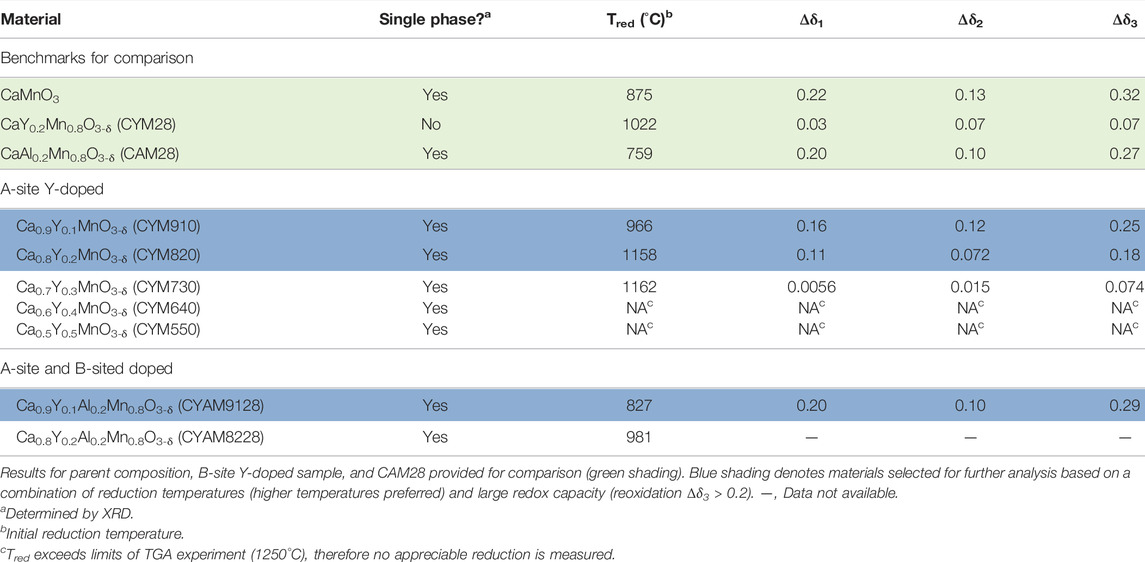
CaAl0.2Mn0.8O3-δ (CAM28) and CaTi0.2Mn0.8O3-δ (CTM28) are perovskite metal oxides developed for high-temperature thermochemical energy storage (TCES) applications, e.g., in support of air Brayton power generation. Previous reports for these compounds focus on the equilibrium non-stoichiometry (δ) as a function of temperature and oxygen partial pressure (pO2) and the endotherm (or exotherm) accompanying changes in δ resulting from thermal reduction (or re-oxidation). Herein, we report results for elemental substitution and doping (Al, Co, Fe, La, Sr, Ti, Y, Zn, and Zr) of calcium manganites (CM) that establish the preference for CAM28 and CTM28. Techniques employed include conventional (screening and equilibrium) and ballistically heated multi-cycle thermogravimetric analysis (TGA), conventional and high temperature (in-situ) X-ray diffraction (XRD), and differential scanning calorimetry (DSC). Forward-looking results for A-site Y-doped materials, e.g., Ca0.9Y0.1MnO3-δ (CYM910), establish a route to increasing the reduction enthalpy relative to CAM28 and CTM28, albeit at the expense of increased reduction temperatures and raw materials costs. A thermodynamic model presented for CAM28, but extendable to related materials, provides values for the reaction enthalpy and extent of reduction as a function of temperature and oxygen partial pressure for use in design efforts. Taken as a whole, the results support the choice of Al-doped CaMnO3-δ as a low-cost material for TCES in a high temperature air Brayton application, but point the way to achieving higher stored energy densities that could lead to overall cost savings.
Introduction
It is widely understood that reliable and cost effective hourly, daily, and seasonal energy storage solutions are absolutely critical to achieving deep penetration of renewable technologies into the energy ecosystem. Thermal energy storage (TES) is the approach generally applied to concentrating solar power (CSP) technology, as it is highly efficient, readily scalable, and provides power on demand while “right sizing” the power generating subsystem to cost-saving high capacity factors. Sensible heat storage in molten salts is the state of the art technology for CSP and provides an energy density of approximately ∼410 kJ/kg (Wu et al., 2011; Stekli et al., 2013). However, better solutions are actively sought after due to several short-comings. These include upper temperature limits that preclude higher efficiency power cycles and the relatively low energy densities that increase system volumes and hence associated costs. Furthermore, molten salts present significant materials and operational challenges, as they tend to be corrosive and are subject to solidification if temperatures are allowed to fall too low. Indeed, problems with the salt storage system are often cited in discussions of the disappointing performance and financial failures of the Crescent Dunes CSP plant in Nevada, USA (Chamberlain, 2020; Mehos et al., 2020).
Thermochemical energy storage (TCES) is an alternative approach in which at least a fraction of the energy storage is achieved through the use of selective and reversible chemical reactions; the remaining fraction is stored as sensible heat. Interest in this approach is motivated by the potential to store and deliver heat at higher temperatures for more efficient power generation, the potential for more cost-effective, higher energy density storage, and of course the possibility to avoid the materials compatibility and handling issues of molten salts. Furthermore, at least some TCES approaches appear to be cost competitive with molten salt (Bayon et al., 2018). These factors have helped fuel a recent boom in interest in solar TCES; a Scopus search produces over 250 publications for the search terms “solar” AND “thermochemical energy storage” for the 5 years spanning 2015–2020, and only 52 for the preceding 5 years. Additionally, general reviews for TCES were published in each of the previous 3 years (Chen et al., 2018; Prasad et al., 2019; Laurie and Abanades, 2020), along with reviews targeting specific chemistries (see below) and implementations (Almendros-Ibáñez et al., 2019).
Briefly, though details vary, TCES technologies are commonly sorted into categories based on the reaction chemistry or substrate, or in some cases phases involved in the reaction (gas, gas-solid, gas-liquid). Examples include hydrides, oxides, and gas phase reactions. Oxides are further categorized into carbonate formation/decomposition, hydration/dehydration, and oxidation/reduction systems. Gas phase reactions include ammonia synthesis/decomposition (sometimes considered as a hydride system), sulfur based chemistries, reforming, and dehydrogenation/hydrogenation chemistries. Oxide systems account for much of the recent work. In particular, calcium oxide looping, which also has applications beyond TCES, has been the subject of intense interest, with both options (CO2 and H2O) under development as discussed in several recent reviews (Yuan et al., 2018; Ortiz et al., 2019; Yan et al., 2020). Redox systems are also the subject of many efforts and can further be divided into those which undergo a stoichiometric reduction to a new crystal phase, and mixed-ionic/electronic conducting (MIEC) materials that are capable of supporting a large number of oxygen vacancies without undergoing a crystallographic phase change. Manganese, cobalt and to some extent copper oxides account for much of the effort on the stoichiometric approach, with work typically directed towards one or more of the following topics: characterization, tuning performance and operating conditions, enhancing reversibility, measuring and improving reaction kinetics and stability (e.g., sinter resistance), and developing systems for implementation of TCES at scale with these materials. The reader is directed to recent reviews for additional information (Dizaji and Hosseini, 2018; Wu et al., 2018). Note that these stoichiometric redox reactions are discrete. That is, thermodynamically, the reduction can proceed to completion at a single transition temperature for a specific oxygen partial pressure (pO2). For example, Co3O4 reduces to CoO (releasing O2) endothermically (ΔHred = 844 kJ/kg Co3O4 (Carillo et al., 2014)) at ∼885°C in air (Hutchings et al., 2006), while reoxidation in air will take place at any temperature below that. Of course, increasing or decreasing the pO2 shifts the temperature separating the oxidizing region from the reducing region up or down, respectively. Detailed kinetic studies of reduction and oxidation as function temperature and pO2 have been reported (Muroyama et al., 2015). Generally, oxidation kinetics are sluggish at temperatures <700°C (Agrafiotis et al., 2014).
In contrast to stoichiometric oxides, the redox-active MIEC materials of interest, often of the perovskite structural family, transition through a continuum of redox states (oxygen stoichiometries) without undergoing major structural rearrangements. This is accomplished through the creation and destruction of oxygen vacancies in the crystal lattice with the thermodynamic equilibrium composition of the solid being a function of both the temperature and pO2 of the surrounding gas phase. As there is no fundamental change in structure, the reaction is represented by the parameter δ, denoting the deviation in oxygen stoichiometry from the fully oxidized state. For a perovskite, this can be represented as
As suggested by the AB notation, there is an almost endless array of compositions that can be produced via cation variation and substitution (of a metal with the same oxidation state) or doping (introducing a metal with a different oxidation state) on both the A and B sites (Pena and Fierro, 2001). In other words, the materials and their thermodynamics (i.e., δ as a function of T and pO2), are highly tunable. The principle limitation of this class of materials is that the redox capacity, embodied by δ, tends to be small in comparison to the stoichiometric oxides. However, the combination of high ionic and electronic conductivities in an MIEC facilitate reaction and oxygen transport throughout the bulk of the material thereby promoting reaction kinetics and complete utilization of the available redox capacity. This makes them more competitive with the stoichiometric reactions which do not have similar beneficial properties. Additionally, MIECs tend to be very stable at high temperatures. In total, this combination of properties makes them attractive materials candidates across a broad application space beyond TCES including water and carbon dioxide splitting (Miller, et al., 2014; Bayon et al., 2020), separating or removing O2 from air (Ezbiri et al., 2015; Vieten et al., 2016; Bush et al., 2019) and pumping oxygen from reactive systems (Brendelberger et al., 2017, 2018, 2019). Each application has a unique set of priorities and hence materials and thermodynamic requirements or targets. As a result, compositions of interest for different applications tend to vary significantly.
Our materials development efforts in the TCES space have primarily been directed towards the specific application of producing a heated pressurized air stream for power generation via an air Brayton turbine. Conceptually, the combustion section in the system is replaced by a gas-solid heat exchanger wherein compressed air is heated from 300–400°C to >1000°C (preferably 1200°C) (Miller et al., 2016; Gorman et al., 2021) by direct and counter-current contact with hot, reduced MIEC particles (Babiniec, et al., 2016a). The heat is drawn from both the oxidation exotherm and the sensible heat of the oxide particle. In some cases, e.g., if a large oxidation exotherm occurs at a high enough temperature range, the air outlet temperature can exceed the particle storage temperature (Babiniec, et al., 2016a). We began our efforts with ABO3-δ (A = La, Ba, Sr, K; B = Co, Mn, Fe) perovskites (Babiniec, et al., 2015; Babiniec, et al., 2016b). Gokon et al. have reported on similar materials targeting temperatures >600°C (Gokon et al., 2019). We then transitioned to calcium manganites (CaBxMn1-xO3, B = Al, Ti) with improved storage capacity and cost profiles (Babiniec, et al., 2016c). Sr-subsituted calcium manganites targeting similar applications with slightly different targets and implementations have been reported (Imponenti, et al., 2018; Albrecht et al., 2018; Vieten et al., 2016). Cr-doped calcium manganites synthesized by ball-milling have also be examined (Lucio et al., 2019), as have La-doped calcium manganites (Mastronardo et al., 2021). Herein, we present results for elemental substitution and doping that helped establish the preference for aluminum doping and titanium substitution in the calcium manganites, along with forward-looking results focused on A-site Y-doped materials. These latter compounds establish a route to higher reduction enthalpy, albeit at the expense of increased reduction temperatures and raw materials costs. We also present a thermodynamic model for calcium manganites, and related materials, that provide values for the reaction enthalpy and extent of reduction as a function of temperature and pO2, appropriate for use in analysis and design efforts.
Materials and Methods
All perovskite oxides were synthesized using the previously described modification of Pechini’s method, as reported in (Babiniec et al., 2015). All constituent elements (Ca, Al, Co, Fe, Mn, Zn, Zr, Sr, and La) with the exception of Ti, were sourced from nitrates and dissolved in DI water in the desired stoichiometric cation ratios, along with excess citric acid as a chelating agent. The solution was dried, the recovered material combusted, and then calcined in a furnace with an air environment. For compositions containing Ti, an analogous procedure was followed, however the Ti was sourced as an isopropoxide and ethylene glycol was used in place of DI water to circumvent hydrolysis of the precursor. In either case, the resulting powder was recovered and pressed into a pellet and calcined at high temperature (1000–1250°C) to produce a dense solid which was subsequently ground in a mortar and pestle to a fine power. Sieves were used to recover particles falling in a specific size range for evaluation. As previously reported, optimal particle sizes for heat recovery in a counter-flow direct-contact gas-solid heat exchanger concept are 100–200 μm (Babiniec et al., 2016a). For convenience, a shorthand notation indicative of the constituent elements and their relative stoichiometries is adopted. For example, CaAl0.2Mn0.8O3-δ is CAM28 and Ca0.8La0.2Ti0.2Mn0.8O3-δ is CLTM8228. Refer to Tables 1, 2 for a complete listing.
Room temperature crystallographic data were typically recorded using PANalytical X’Pert and Bruker AXS D8 Advance X-ray diffractometers (XRDs) with CuKα radiation. Crystal structure and phase composition were determined by analyzing XRD patterns using Jade software (Materials Data Inc. Jade+, Livermore, CA, United States). Materials with a calculated impurity of <5% were categorized as single-phase. In-situ XRD experiments were performed using a previously-described Scintag PAD X diffractometer (Thermo Electron Inc., Waltham, MA, United States) using a similar method (Coker et al., 2012). Scans were collected at 100°C increments while heating from ambient to 1200°C (e.g., 25, 200, 300, 400, …, 1100, 1200) and then back (1200, 1100, …, 50) under controlled environment (air or 500 ppm O2 in N2).
Three previously developed and reported thermogravimetric (TGA) methods were applied in this study. The first is a relatively simple screening procedure performed using a TA Instruments Q600 TG/DSC (Babiniec et al., 2015). In short, an initial break-in cycle to ensure a common starting point for all materials was performed by ramping the material at 20°C/min to 1250°C in air and holding for 30 min, then cooling back to 200°C and holding for 30 min. This is immediately followed an evaluation cycle consisting of an identical ramp in air to 1250°C with a 10 min hold in air, then a 20 min hold in Ar, 20 more minutes hold in air, and then cooling to 200°C in air (the final temperature typically deviates by 25–50°C above the 200°C target as there is no active cooling and no hold). Four different descriptive metrics are extracted from this evaluation for comparison: the temperature at which reduction is initially observed during the ramp, and the change in oxygen stoichiometry (Δδ) occurring during each stage of the process (Δδ1 reduction in air, Δδ2 further reduction in argon, and Δδ3 reoxidation in air while cooling). A tangent line method was used when the data was amenable (presented reasonably linear slopes) to determine the initial temperatures. In each case the Δδ values are calculated as
Where Δm is the mass change measured by TGA, minit is the initial mass set as that after the break in cycle, MWABO3 is the molecular weight of the perovskite assuming that the initial state of the material is stoichiometric ABO3 (δ = 0), and MWO is the molecular weight of monatomic oxygen.
In the second method, a Netzsch STA 449 F3 Jupiter TGA was used to obtain equilibrium measurements of mass over a range of temperatures and O2 partial pressures (Babiniec et al., 2015; 2016b; 2016c). Following a single break-in cycle and an initial mass measurement at a low temperature (e.g., 200°C) and pO2 of 0.9 atm to establish an assumed δ = 0 condition, samples were given adequate time to equilibrate at temperatures of 950, 1025, 1100, 1175, and 1250°C, with O2 partial pressures of 0.9, 0.1, 0.01, and 0.001 atm at each temperature. (Note this is different set of temperatures than the referenced work; this set is skewed more towards higher temperatures.) The complete set of measurements was completed three times on individual samples and the results averaged. The resulting data sets were subjected to van’t Hoff analysis to extract an enthalpy and entropy for each oxygen content (δ). These enthalpies were subsequently integrated from zero up to the δ of interest to determine the energy storage profile for the continuous reaction (Mizusaki et al., 1991; Babiniec et al., 2015, 2016b, 2016c).
This instrument was also used in DSC mode with simultaneous TGA to characterize apparent phase transitions for several materials. Powder samples weighing ca. 45 mg were ramped from ambient temperature to 1250°C and back down to 200°C at 25°C/min in an environment of 90% O2 in an Ar balance to limit interference from the endothermic reduction reaction. Similar analyses were conducted in gaseous environments of 20% O2 and 500 ppm O2 with ramp rates of 50°C/min. These latter tests were repeated at least three times to confirm the results reported herein are typical.
The third thermogravimetric method was used to assess multi-cycle and cycle-to-cycle stability and repeatability and employed a TA Instruments Discovery TGA with ballistic heating capabilities. Approximately 100 mg samples of perovskite powders, sieved to 75–150 μm particle size, were subjected to a break-in cycle and then cycled up to 100 times between 400 and 1050°C (the upper limit of the furnace), with 5 min dwell times. The heating and cooling rates were 400 and 200 K/min, respectively. The high temperature (reductive) dwell was carried out under flowing Ar, or a 10/90 (v/v) air/Ar mixture. Oxidation (low temperature dwell) was carried out under flowing air. The method deviates slightly from that previously reported through the use of shorter dwell times and different gaseous environments for oxidation and reduction rather than a constant air flow throughout (Babiniec et al., 2016b).
Heat capacities were measured by DSC in a Netzsch STA 409CD with a highly stable and thermally-uniform PtRh furnace and additional isothermal jacketing (30°C) to improve the precision of the measurement. In these experiments, the material was pre-reduced at 1000°C and then cooled in argon. The heat capacity experiment was then carried out in argon by ramping from 200 to 1000°C. The pre-reduction is critical so that no reaction occurs that would contribute to the heat signal and render the heat capacity determination difficult and unreliable. However, the resulting compromise is that there are fewer chemical bonds to store energy, and thus the measured heat capacity measured likely yields a lower-bound result.
Thermodynamic models were developed in Wolfram Mathematica using a two-parameter compound energy formalism, i.e., with no δ or temperature dependence in the enthalpy or entropy of formation. Parameterization was accomplished using a least squares fit. The derivation was validated against the well-known Zinkevich model (Zinkevich et al., 2006) for ceria. For further validation, we developed a method to map the results from the compound energy formalism to the correlation developed by Bulfin and co-workers (Bulfin, et al., 2013).
Results
Materials Screening
In an earlier publication, we reported two doped calcium manganites with promise for high-temperature TCES, CaAl0.2Mn0.8O3-δ (CAM28), and CaTi0.2Mn0.8O3-δ (CTM28) (Babiniec, et al., 2016c). The baseline material for comparison was La0.3Sr0.7Co0.9Mn0.1O3-δ (LSCM3791), which had been identified in an earlier study (Babiniec, et al., 2015; 2016b). These two formulations were identified as alternatives for development through a design and screening process described here. The principal metric is storage capacity (i.e., thermodynamics). Other concerns include applicable temperature range, stability (thermal, physical, chemical), reaction kinetics, and cost. The energy contribution of the thermal reduction depends on two parameters: the reduction extent in each cycle, Δδ, and the associated reduction enthalpy in that δ range. (For simplicity, in our calculations we generally assume δ = 0 for the material in the fully oxidized state and adjust the MW and stoichiometry to account for vacancies arising from doping, i.e., Δδ = δ unless otherwise indicated.)
The approach to maximize δ was to increase the average B-site oxidation state by using non-labile, low oxidation state cations on the A-sites. The approach to maximize the enthalpy was to manipulate the B-site (primarily) and A-site (secondarily) composition to drive the reduction to the high end of the temperature range of interest. Materials that require higher temperatures (or lower pO2) to drive reaction typically have larger reaction enthalpies. This follows from a basic conceptualization and reports that the entropy change varies over a fairly small range and is largely attributable to O2 gas formation (Meredig and Wolverton, 2009), recent advances in manipulating the entropy for thermochemical applications via configurational contributions from the solid notwithstanding (Zhai et al., 2018; Gautam et al., 2020). In any case, a balance must be achieved, because too large an increase in the enthalpy can compromise the reaction extent under conditions of interest. In search of this balance we combined elements known to form stronger and weaker metal oxygen bonds into single compounds.
Regarding the sensible heat component of the energy storage, heat capacities scale with the number of atoms. Thus, the molar and volumetric sensible heat can reasonably be expected to vary little from one perovskite to another. That is, this property is not subject to significant manipulation. However, the mass-normalized energy storage densities (sensible and thermochemical) scale proportionally to molecular weight. To the degree that stored mass impacts system design, cost, and efficiencies, molecular weight can be a consideration. In practice, we focused on and applied TGA to screen for materials with the goal of identifying materials with as high an initial reduction temperature as possible with reasonable extents of reduction (Δδ3 > 0.2), giving preference to low-cost, earth abundant elements with lower molecular weights.
Calcium manganite (CaMnO3, CM) perovskites were selected as the basis for materials studies aimed at improved performance relative to LSCM3791 due to their adherence to the criteria. Calcium is a +2 cation, requiring the B-site cation to be at the maximum oxidation state of +4 in the stoichiometric material. Calcium is a relatively low molecular weight, low cost, abundant element, as is manganese. Additionally, previous studies showed that CaMnO3-δ materials reduced at high temperatures (∼800°C in air, Bakken et al., 2005a) and were amenable to substitution, e.g., with non-labile metals such as Al and Ti. However the parent CM has also been reported to have limited thermal stability (Bakken et al., 2005b; Leonidova et al., 2011). Therefore, in addition to manipulating the redox thermodynamics, an additional goal of substituting other elements into the manganites was to improve the thermal stability.
The pre-screen data for CM and for each doped CaMnO3 perovskite are found in Table 1, along with LSCM3791 data for comparison. Note that the procedure should not be understood as providing equilibrium values of δ, but rather as an efficient method for identifying promising candidates for further study. The data provide an indication of the relative reduction enthalpy (higher reaction onset is an indication of larger enthalpy), redox capacity (Δδ1 and Δδ2) and reversibility (Δδ3), and reasonable kinetics (the values are obtained after limited hold times, or in the case of Δδ3, at the end of the ramp cycle time). The first set of samples evaluated included CM and similarly B-site substituted/doped materials containing one of two relatively labile cations (Fe, Co), each with a range of known oxidation states in metal oxides (+4, +3, and +2), or one of two non-labile cations, Al and Ti, expected to be present in the 3+ and 4+ oxidation states, respectively. Note that replacing Mn4+ with Al3+ requires either the oxidation of Mn4+ to Mn5+ (possibly facilitating reduction), the formation of oxygen vacancies to maintain electric neutrality (possibly inhibiting reduction), or some balance of the two. The 20% doping/substitution level was selected as being large enough to discern an impact, but likely small enough to preserve the ABO3−δ single phase stoichiometry of the product.
Each material in this set was single phase by XRD and crystallized in an orthorhombic space group (Supplementary Material, Supplementary Figure S1). In this case, the a and b lattice parameters are very similar, closely relating the observed structures to tetragonal. As anticipated, each member of this initial set of materials displayed reduction onset temperatures higher than LSCM3791, while retaining significant redox capacity (Δδ3 > 0.2). However, the ferrite compositions CFM28 and CFM46 had significantly lower reduction onset temperatures than the other formulations and the parent material, an indication that the Fe was initially present in a highly reducible Fe4+ state. CFM formulations were dropped from further consideration based on this result.
Each of the remaining materials, CM, CTM28, CCM28, and CAM28, was annealed in flowing Ar for 5 h at 1000°C to evaluate the possible effects of deep reduction (Supplementary Figure S2). XRD was conducted on the annealed material to determine any phase changes due to the reduction process. CM and CCM28 were found to have decomposed (Supplementary Figures S2A,B), consistent with previous reports for CM, and excluded from further study. CTM28 and CAM28 did not decompose, but rather converted from the orthorhombic structure to the tetragonal (distorted cubic) perovskite phase with a corresponding increase in lattice parameters (Supplementary Figures S2C,D). CTM28 and CAM28 were advanced forward for further study.
Based on the results for CTM28 and CAM28, second and third sets of compounds were synthesized for evaluation (Table 1). The goals and metrics remained the same--further increases in reduction temperature without excessive loss of reaction extent. The second set of compounds expanded the selection of non-labile compounds to include Zn, Y, and Zr, which were anticipated to assume the +2, +3, and +4 oxidation states, respectively. The materials from the second set of compounds did not form single phases by XRD. The Y-doped material, CYM28, segregated into at least two phases that index to an A-site doped orthorhombic perovskite and A-site doped tetragonal Ca2MnO4 phase (Supplementary Figure S3A). The reduction temperature of CYM28 increased significantly above that of CM, but the redox capacity was very limited. In CZnM28 samples, ZnO precipitated out, at least in part, leaving a presumably-redox-active tetragonal calcium manganite phase (Supplementary Figure S3B). CZrM28 also phase segregated, in this case into two orthorhombic ABO3 perovskites (CaMnO3, CaZrO3) (Supplementary Figure S3C). CZnM28 and CZrM28 each have initial reduction temperatures similar to CM and satisfy the reaction extent criteria. Of the two, CZrM28 was chosen for further study, despite crystallizing in two phases, because it displayed the most promising redox capacity as well as rapid kinetics, and circumvented the possibility of volatility issues often encountered with Zn compounds at high temperature.
The third set of samples expanded the range of Ti substitution and combined Ti substitution with La or Sr A-site doping/substitution. Each of the synthesized materials are single-phase and adopt the same orthorhombic perovskite structure as the parent CTM28 compound. CTM46 and CTM64 exhibit increased reduction onset temperatures over CTM28, but the redox capacity of the materials declined significantly and were eliminated from further study. On the other hand, the initial reduction temperature of CTM0595 decreased compared to CTM28, but its redox capacity improved. As the net enthalpic trade-off between those two properties was not known, CTM0595 was selected for additional analysis. However, the material was found to decompose at high temperature and low pO2, similar to the parent CM, indicating that doping at the 5% level is inadequate to provide the required stabilization. As a result the material was eliminated from further evaluation. Regarding the A- and B-site modified materials, CSTM8228 exhibited redox properties very similar to CTM28, suggesting there would be little or no benefit for the added expense. Nonetheless this material was selected for further evaluation as it met the screening criteria. On the other hand, La, likely substituting as a 3+ cation, significantly increased the reduction temperature albeit at the expense of a collapse in the redox capacity. As a result, the two La-doped materials were eliminated from further consideration.
Since the completion of this work, a detailed study of CTM55 in the context of water splitting has been published. An enthalpy of 400–560 kJ/mol O2 and a maximum δ of 0.225 were reported, e.g., at T = 1500°C and pO2 = 0.00082 atm (Qian, et al., 2021). This is consistent with our observations regarding CTM46 and CTM64.
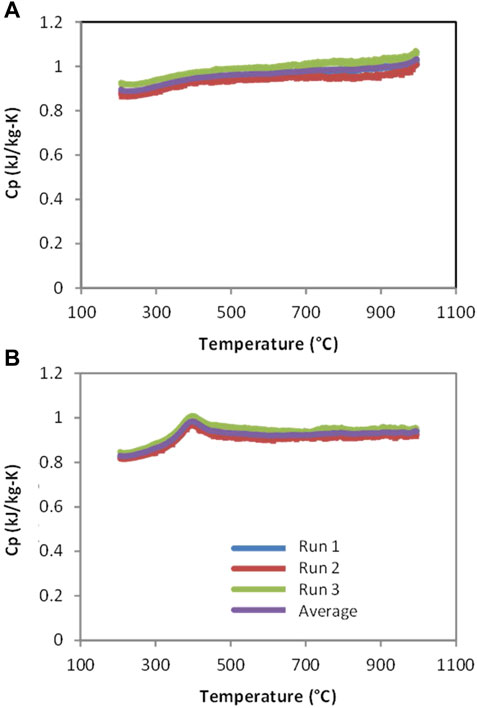
Screening of A-Site Y-Doping
In the screening studies described above, only Y-doping and La A-site doping resulted in reduction temperatures above that achievable with Ti alone. It was also observed that Y appeared to prefer to reside on the A-site of the calcium manganites. These observations prompted screening studies of intentional Y A-site doping. The results are presented in Table 2 alongside data for CM, CAM28, and CYM28 for ease of comparison. Each of the A-site doped materials crystallized as a single phase by XRD rather than the multiphase composition that comprised CYM28. The CYM patterns exhibit peak splitting that becomes more pronounced as the concentration of Y increases (Supplementary Figure S4). In pure CM, similar splitting has been attributed to oxygen vacancy ordering as oxygen is removed from the lattice (Chiang and Poeppelmeier, 1991). However, the inclusion of Y3+ cations on the A-site does not require vacancy formation to achieve charge neutrality for these materials, though it cannot be ruled out. (Mn can assume the +3 oxidation state to balance the Y.) Thus, we suggest the splitting is possibly the result of distortion in the crystal lattice arising from the presence of the slightly smaller Y cation. The doubly-doped materials CYAM9128 and CYAM8228 do not exhibit similar splitting, suggesting the presence of Al on the B-site balances or stabilizes the lattice against distortion.
The data in Table 2 further illustrate the success of this approach. Each of the A-site Y-doped materials exhibits a higher initial reduction temperature than its parent (CM for CYM samples and CAM for CYAM samples). Additionally the reduction temperature adheres to a clear pattern of increasing with yttrium concentration. (CYM550 is a possible exception as the reduction temperature of both CYM640 and CYM550 exceed the upper limit of the screening, 1250°C.) As expected, the redox capacity shows a trend of decreasing with increasing initial reduction temperature. However, as the highest of these temperatures are so near the temperature limit of the experiment, it is possible, perhaps even likely, that these materials have significant reduction capacity which is not sampled by this screen. In any case, CYM910 and CYAM9128 fully meet the screening criteria and were further evaluated. CYM820 was also selected for further study as it exhibited significant redox capacity even though reduction began within <100°C from the upper temperature limit.
Reduction Enthalpies by TGA
The δ-dependent enthalpies extracted via van’t Hoff analysis are plotted in Figure 1A, while the cumulative molar reduction enthalpies (i.e., integrated from 0 to δ) are plotted in Figure 1B for CZrM28, CSTM8228, CYM910, CYAM9128, and CYM820. Previously reported values for CTM28 and CAM28 are included for comparison (Babiniec et al., 2016c). Results normalized on a mass basis are provided in Supplementary Figure S5 and Supplementary Table S1 alongside literature values for related CM materials. The data in each plot extends to the δ value corresponding to the most extreme experimental condition: 1250°C, and pO2 = 0.001 atm. The data in Figure 1B reflect differences in volumetric storage capacities since each material should have very similar molar volumes and molar sensible heat capacities. That said, the relative results on a mass basis are quite similar given that the molecular weights for this group of materials varies by only 12.5% from least (CAM28) to greatest (CYM820).
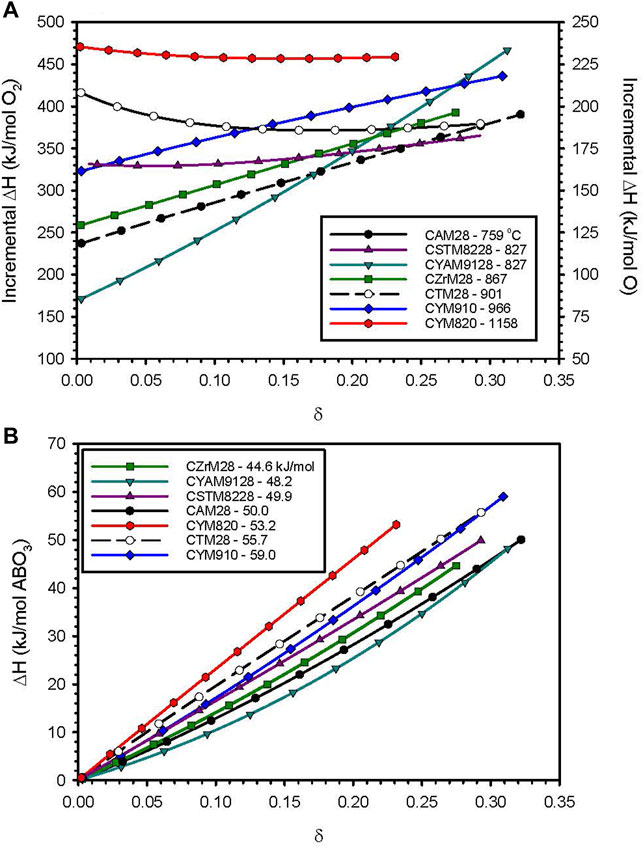
FIGURE 1. Results from van’t Hoff analysis of TGA data for selected perovskite formulations. (A) Incremental reduction enthalpy as a function of δ. Captions list the initial reduction temperature observed by TGA (°C). (B) Cumulative reduction enthalpy data from Figure 1A integrated from 0 to δ. Captions indicate the measured value at the largest realized value of δ. Supplementary Figure S5 provides these same results on a mass basis and includes data points taken from the literature for other calcium manganites.
The initial reduction temperature (provided in the figure legend) and the low-δ enthalpies do not show a 1:1 correlation in Figure 1A. This is likely reflective of the fact that a somewhat subjective method of determination (particularly in cases where the data exhibited significant curvature and baseline drift) of the initial temperature was applied to data collected during a rapid temperature ramp where small differences in kinetics may have a significant impact. Differences in entropy terms for the materials may also play a role. Nonetheless, Figures 1A,B show that the initial reduction temperature is a fairly coarse, but effective, screen for identifying materials of interest. The highest cumulative enthalpies correspond to the three materials with the highest initial reduction temperatures. And, with the exception of one, the materials show higher enthalpic potential than the previously identified CAM28 across the range of δ, and two also show improvements over CTM28. The highest total enthalpy is observed for CYM910, however, CYM820 shows potential to eclipse that if δ is increased, e.g., through higher reduction temperatures. This trend highlights the ability to influence reduction thermodynamics via A-site doping, with implications for the design of future materials.
Note that the thermodynamic data in Figure 1A are informative of the reduction behavior beyond the reduction onset temperatures. A large variation in ΔH over the range of δ values, i.e., a material that seemingly becomes increasingly difficult to reduce with increases in δ (see discussion in Thermodynamic Modeling section regarding δ and T dependence), is an indication that for a given pO2 the material reduces incrementally over a larger temperature range than one with a more uniform (small slope with δ) enthalpy. That is, a relatively constant ΔH indicates that a large portion of the reduction, i.e., change in δ, will take place over a relatively small, but specific, range of ΔT for a given pO2. This is illustrated in Figure 2 and Supplementary Figure S6 wherein the experimental 3-δ values (assuming no native vacancies) for CYM820, CYM910, CYAM9128 are plotted as a function of T and various pO2 values. For a given pO2, the dependence of δ with T (the slope) is seen to increase in the order CYAM9128 < CYM910 < CYM820. These three samples are seen in Figure 1A to have enthalpy values that have large, intermediate, and little dependence on δ, respectively, thereby illustrating the point.
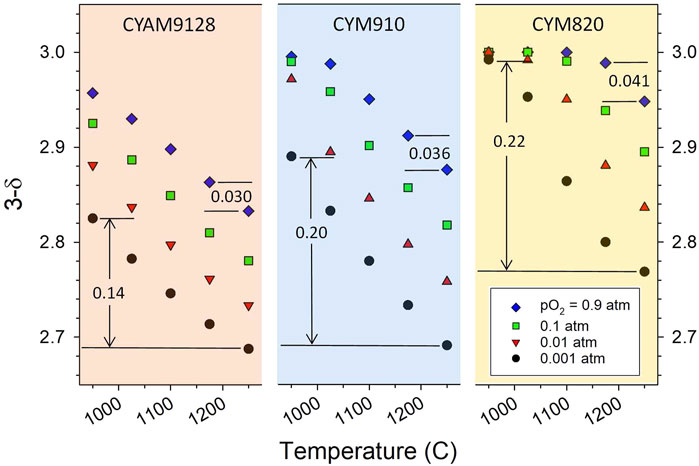
FIGURE 2. Measured oxygen stoichiometry (3-δ) of CYAM9128, CYM910 and CYM820 as a function of temperature and pO2 (assumes δ = 0 in fully oxidized state). Numbers in the graphs indicate Δδ values for the associated temperature interval and illustrate that for a given pO2, the dependence of δ with T (the slope) increases in the order CYAM9128 < CYM910 < CYM820, the opposite of the trend for ΔH with δ (Figure 1A). See also Supplementary Figure S6.
DSC Analysis
In an earlier publication we reported that preliminary results for CAM28 and CTM28 suggested that the heat capacities are consistent with theoretical values (Miller et al., 2016). The theoretical Dulong-Petit limit of 3NR or 15R for perovskites is 125 J/mol-K. After accounting for the molecular weights, this works out to 0.89 and 0.91 kJ/kg-K, for CAM28 and CTM28, respectively. The specific heats of thermally reduced CAM28 and CTM28 determined by differential scanning calorimetry (DSC) over the range of 200–1000°C and shown in Figure 3 confirm our earlier report. Note the measurements were highly reproducible, with a maximum deviation between runs of ∼0.035 kJ/kg-K for CAM28 and ∼0.019 kJ/kg-K for CTM28. The heat capacities depicted in Figure 3 likely represent a lower-bound result, as the reduction necessary to accomplish the measurement decreases the number of atoms in the material. The curve for CAM28 is well-behaved (Figure 3A), with a small inflection observed near the beginning and a more prominent one approaching the ending at each curve, i.e., at 200°C and approaching 1000°C. The former may result from the establishment of temperature equilibrium while the latter may represent the onset of a transition (see below). The possibility of reaction onset is unlikely due to the pretreatment and the absence of a similar observation for CTM28, which would be expected if residual O2 in the argon allowed for partial reoxidation of the samples after pretreatment. In contrast to CAM28, CTM28 has a clear and reproducible peak at ∼375°C (Figure 3B). The area under the peak accounts for an endotherm of approximately 5 J/g. This behavior is suggestive of the material undergoing reversible phase transition or ordering. The low temperature for this transition relative to those reported immediately below and in the In-Situ XRD section may be attributable to the pre-reduction and presence of vacancies.
During TGA/DSC prescreening of CZrM28 and CYM910, small peaks not corresponding to reduction phenomena were noted in the DSC signals. In each case, an endothermic peak was observed during the ramps to high temperature, and corresponding exothermic peaks were observed during cooling. Careful DSC measurements were made to better characterize these observations. Initially, high pO2 conditions were employed to prevent or minimize interference from the reduction reaction. For CYM910, endothermic and exothermic peaks were observed at 1076 and 1081°C, respectively (Figure 4 and Supplementary Table S2), and for CZrM28 at 950 and 958°C (Supplementary Figure S7 and Supplementary Table S2). Careful peak integration with background subtraction gave values of 8.3 J/g for CZrM28 and 9.3 J/g for CYM910, similar in magnitude to the peak observed for CTM28, suggesting a similar origin, likely a phase transition (vide infra) The potential contribution to the total storage capacity from these transitions is very small, less than 5% of the reduction endotherm. The apparent features found at higher temperature, e.g., in the 90% O2 traces, are believed to be artifacts as they are not reproduced under other conditions and not readily correlated with other observations. However, we cannot entirely rule out the possibility that these features are the result of a low energy transition such as vacancy ordering, lattice distortion, or very minor impurity.
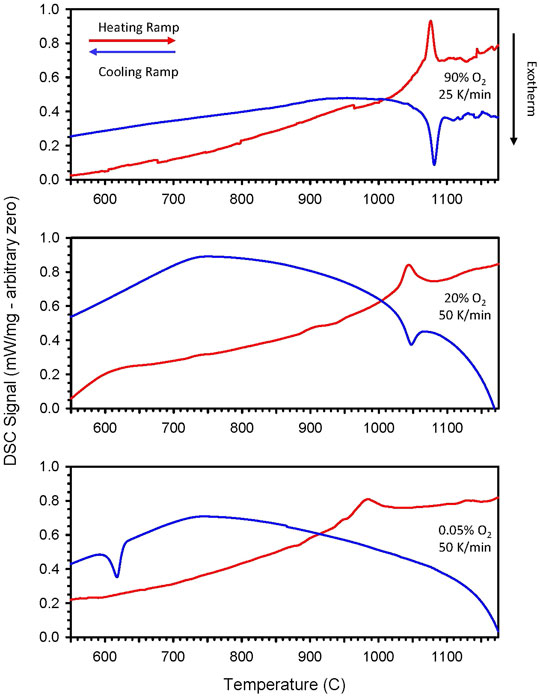
FIGURE 4. Individual DSC traces of CYM910 show small endothermic and corresponding exothermic peaks during ramp up and ramp down of temperature, respectively. Peak positions vary as a function of ramp rate and gaseous environment (pO2). (Top: 90% O2, 25°C/min; middle: 20% O2, 50°C/min, bottom: 500 ppm O2, 50°C/min). Peak positions and corresponding δ values elucidated via concurrent TGA are given in Supplementary Table S2. These peaks are likely indicators of phase changes that take place as a function of temperature and reduction state of the oxide. The depicted behavior is reproducible over several cycles. Similar behavior is observed for CZrM28 (Supplementary Figure S7 and Supplementary Table S2).
Additional DSC data was collected for these materials under 20% and 500 ppm O2 at a ramp rate of 50°C/min. Representative traces for these conditions are also shown in Figure 4 and Supplementary Figure S7, and summarized in Supplementary Table S2. Under 20% O2, the peaks shift to a lower temperature but remain relatively closely spaced. Even larger shifts towards lower temperatures are observed under 500 ppm O2, and the peak positions during the heating and cooling ramps vary significantly from one another. In fact, a peak is not observed during the cooling ramp for CZrM28 under 500 ppm O2. These trends are indicative that the events responsible for the peaks are not only a function of the temperature, but of the reduction state of the material as well. As is readily seen in Supplementary Table S2, a deeper reduction state (larger δ) correlates with lower temperature DSC features. The divergence of the peaks under 500 ppm O2 results in part from the fact that the materials begin in a highly oxidized state and are reduced during the heating ramp, but do not return or even approach that state during reoxidation (cooling) at low pO2. Complicating this is the fact that the temperature ramps are rapid so that the material composition is not at thermodynamic equilibrium with the gas phase at all points during the ramps. The temperature increase outpaces the move towards equilibrium via reduction, and the decrease likewise outpaces the oxidation, particularly in the lower temperature regions. That is, in the case of 500 ppm O2, δ is quite asymmetric and not at equilibrium as a function of temperature for heating and cooling, resulting in the divergence in the DSC from one another. In contrast, for 90 and 20% O2, where oxidation and reduction are only expected at the highest temperatures, δ is fairly consistent (symmetric) as a function of T during the heating and cooling ramps.
In-Situ XRD
In-situ XRD characterization was done for samples of CAM28, CYM910, CYAM9128 and CZrM28. CAM28, CYM910, and CYAM9128 were heated and cooled in flowing gas containing 500 ppm O2. CYM910 was also heated and cooled under air. The biphasic CZrM28 material was heated and cooled under both low pO2 and in air, the latter to avoid possible decomposition of the CM phase. A representative example is shown for CYM910 in Figure 5 and Supplementary Figures S8, S9. In each case, samples were observed to convert from an orthorhombic perovskite phase to a tetragonal (slightly-distorted-cubic) phase in high temperature scans. These transitions were observed to occur in the ranges 800 ≤ T ≤ 900°C for CAM28; 1000 ≤ T ≤ 1100°C for CYM910 in air and 800 ≤ T ≤ 900°C in 500 ppm O2; 900 ≤ T ≤ 1000°C for CYAM9128; and 800 ≤ T ≤ 900°C for CZrM28 in 500 ppm O2 and 900 ≤ T ≤ 1000°C in air. In the particular case of CZrM28, both of the constituent perovskites were maintained as distinct materials throughout the entire temperature scan with only the CM phase undergoing a phase change (Supplementary Figures S10, S11). The center of these temperature ranges are within 17–123°C of the observed initial reduction temperatures (Tables 1, 2). More significantly, the peaks observed in DSC for CZrM28 and CYM910 in 20% O2 (Supplementary Table S2) fall within the respective ranges observed by in-situ XRD in air. For the 500 ppm O2 evaluations, the regions overlap in both cases. These results provide strong evidence that the “additional” energetic events observed in DSC are associated with phase transformations of the various perovskites.
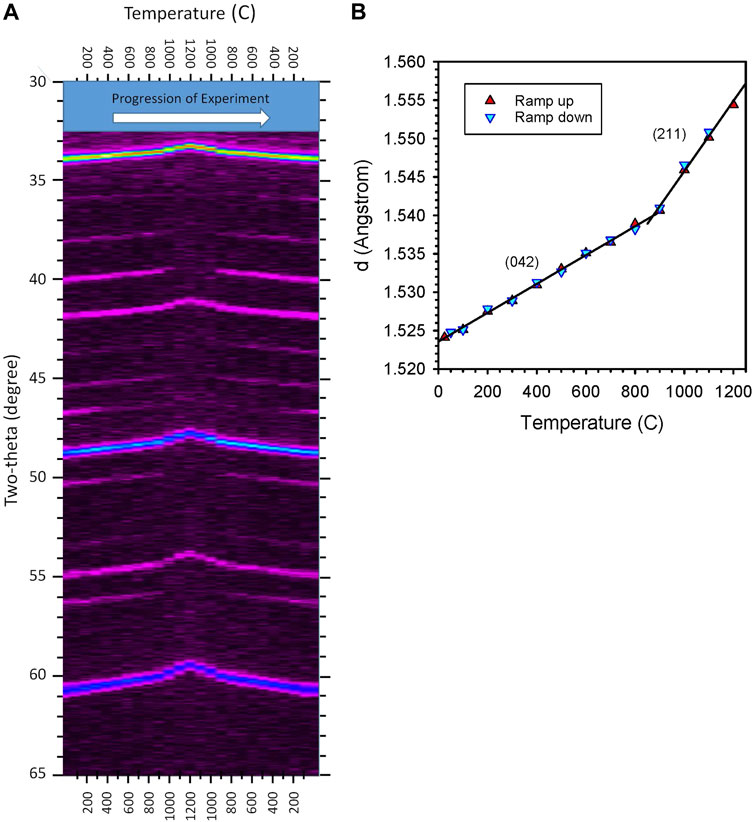
FIGURE 5. Results for in-situ XRD of CYM910 under flowing N2 with 500 ppm O2. Aside from end points, scans were done in 100°C increments (25, 100, 200 … 1100, 1200, 1100 … 200, 100, 50°C). (A) XRD intensity plot. Reversible peak shifts are attributable to a combination of thermal expansion across the temperature range and a phase (symmetry) change at the highest temperatures. The disappearance and reappearance of peaks are attributable to symmetry (phase) changes. Elapsed time increases from left to right. (B): Variation in d-spacing calculated for the intense peak appearing between 59 and 61° two-theta for the experiment shown in (A). With the lines provided to guide the eye, and taking (A) into account, it is clear that a transition from an orthorhombic to tetragonal phase occurs at a temperature near 900°C. The peak index changes accordingly, as shown. See Supplementary Figure S8 for an alternate visualization of the data.
Multi-Cycle TGA
We previously reported the results from ballistically heated, multi-cycle TGA evaluations of CAM28 and CTM28 (50 and 100 cycles, respectively, between 400 and 1050°C in air) (Miller et al., 2016). These results demonstrate the substantial stability of these materials, and the qualitatively rapid redox kinetics. The observed changes in Δδ were +0.0004, for CTM28 over 100 cycles, and −0.002 in 50 cycles for CAM28. CTM28 reoxidized fully during cool-down in less than 5 min. Furthermore, the particles exhibit no changes in structure (by XRD) nor particle morphology (by SEM) after cycling (the particles begin and end in a “fully oxidized” state) (Babiniec et al., 2016b). Stability was further verified over 10 cycles in a rapidly heated up-flow reactor (UFR) (Bush et al., 2017) for CAM28, CTM28, and LSCM3791 (Supplementary Figure S12). Reduction kinetics were observed to be so rapid that they could be modeled assuming a heat-transfer limited reaction under some conditions (Schrader et al., 2020). Additionally, sintering was characterized via dilatometry. Sintering temperatures were determined by the tangent line method to be 1197 and 1211°C for CAM28 and CTM28, respectively. The sintering results likely represent a worst case as the measurements were conducted with a particle packing density orders of magnitude higher than what is expected in particle storage (Miller et al., 2016). Taken as a whole, these results verify that the transition events seen in XRD and DSC for CAM28 do not present a barrier to repeated cycling; the transitions are complete and reversible over the cycle. Furthermore they are suggestive that similar observations for other materials are not necessarily indications of stability issues.
Similar multi-cycle TGA studies were completed for CYAM9128, CYM910, and CZrM28. An example illustrating the procedure and demonstrating cycle-to-cycle repeatability for CYAM9128, reduced in Ar and oxidized in air, is provided as Figure 6. In the case of CYM910, reduced in 90:10 Ar:air and oxidized in air, an increase in mass was observed over the course of the experiment. As post-reaction XRD showed no phase changes, it is presumed this is the result of an inadequate break-in time (the sample was not quite in an equilibrium “fully oxidized” state after break-in), or a baseline shift, or most likely a combination of both. This latter possibility is supported by two observations. First, Δδ is observed to increase primarily over the first 20 cycles or so with weight gain being larger than weight loss (Supplementary Figure S13). The divergence between gain and loss diminishes with increasing cycles. That is, the sample was slowing moving towards a more fully oxidized state in the earlier cycles. The process required multiple cycles as the oxidation temperature was low and the hold times short. It is reasonable to assume Δδ will eventually reach a steady state plateau constrained by equilibrium and kinetic considerations. Second, while the Δδ curve flattens after the early cycles, the reported mass for the oxidized state increases steadily over the latter half of the experiment (Figure 6). This is consistent with a slight baseline shift taking place over the second day of the lengthy evaluation. In any case, the experiment demonstrates cycling is reversible, rapid, and resists degradation.
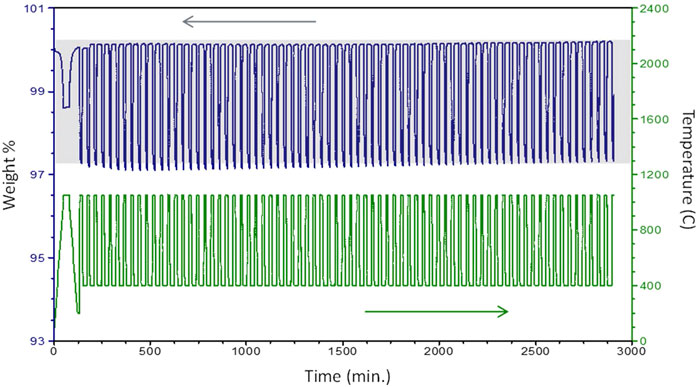
FIGURE 6. Multi-cycle TGA of CYAM9128 illustrating stability over 74 cycles (reduction in Ar, oxidation in air). First cycle is a break-in to bring sample to a known condition and not counted. Shading is provided as an aid to the eye due to slight baseline shifts.
The results for CZrM28, reduced in Ar and oxidized in air, stand in sharp contrast to the others. Supplementary Figure S14 shows that the measured Δδ increases over the first 15 cycles and then exhibits a decline that becomes severe by cycle 20. The rate of decline has significantly slowed by the final (100th) cycle. However, the Δδ capacity has been reduced to <30% of its peak value. Recalling that this sample is composed of a mixture of CaZrO3 and CaMnO3 phases, and assuming, as above, that CaZrO3 is irreducible under these conditions, the result is consistent with the decomposition of CaMnO3 under high temperature reducing conditions (Supplementary Figure S2A), though this could not be confirmed by XRD due to insufficient sample recovery. This result illustrates the importance of evaluating the stability of candidate materials over a large number of cycles at the extremes of the conditions they might be subjected to (e.g., temperatures, reducing atmospheres, and rapid transients).
Thermodynamic Modeling
The simplified van’t Hoff relationship is a convenient and simple method for fitting TGA data and extracting thermodynamic parameters from sets of TGA data. It lacks utility for design and analysis work, however, as it does not provide an equation set predicting δ as a function of T and pO2, for example. Nonetheless, it is theory-based in that the linearized van’t Hoff relationship is derived from the equilibrium expression for the reduction reaction, assuming that the gas phase is ideal, the activities of the oxidized and reduced phases are nearly identical, and the thermodynamic parameters are functions of only δ and not temperature. That is, the temperature dependence is convoluted into the δ dependence.
The van’t Hoff analysis requires T and pO2 data pairs at constant δ. Unfortunately, TGA does not lend itself well to collecting constant δ data. Rather, as described in Materials and Methods, δ is measured across the T and pO2 ranges of interest. Lines of constant δ are then numerically generated by interpolation from the typically sparse data set (e.g., 20 points spanning >600°C, and nearly four orders of magnitude for pO2). In our case, this analysis is done by fitting a line to each constant pO2 data set (δ = mT+b), and then applying these fits to generate constant δ data sets in ln(pO2), 1/T format. Performing linear regression on these generated data sets yields the van’t Hoff parameters; ΔH and ΔS are extracted from the slope and intercept, respectively. While we find linear fits to constant pO2 data (in our case five points) are generally quite good, there is nothing physical supporting this choice. Any reasonable numerical approach to describing the pO2, T, δ surface could be adapted, and non-linear approaches may be needed, especially for cases where larger data sets are available.
Given the significant assumptions and limitations inherent to the van’t Hoff approach, we sought to develop an alternate, potentially more rigorous, method of analyzing TGA data sets, giving preference to one tied to predictive computational methods. We began with the widely known compound energy formalism (CEF) (Hillert, 2001). The CEF is a method for computing the thermodynamic properties for solid solution phases, i.e., those with two or more sublattices with possible variations in composition, including variations in reduction state. The CEF offers a theory-backed basis to derive an improved general functional relationship for fitting TGA data that supports the derivation of thermodynamic parameters with their δ- and T-dependence. The resulting models are functional for systems and analysis efforts.
As a solution based approach, the CEF combines weighted contributions from simple end members, accounts for configurational entropy (mixing), and corrects from these simple linear combinations (regular solution) *with “excess terms.”
To elaborate, the set of end members in the CEF consists of all possible combinations with a single constituent species on each sublattice; constituent species include all the elements and possible charge states in the composition of interest and lattice vacancies. For the ABO3 perovskites, there are three sublattices, A, B and X, represented as
For CAM28, the weighting terms are:
An Important Simplification Is
The configurational entropy contribution to the CEF is constructed around the assumption of ideal random mixing on each sublattice, i.e., a random* solution model, which is:
Where
With this background, we return to the goal of deriving a useful expression from the CEF that relates the equilibrium composition of the solid (δ) to the externally imposed or constrained pO2 of the gas phase and temperature (T). Phase equilibria requires that the oxygen chemical potential (OCP) or a related state function be equivalent in the solid and gas phases. Here we opt for a unitless state function that we refer to as
Where G, S, and H, are the Gibbs free energy, entropy, and enthalpy, respectively. The OCP in the gas phase is
We choose reference values of significance to the TGA campaign and compounds of interest,
For any metal oxide, we derived the following form, truncated to three temperature terms, for the solid phase:
Given the limited range in
The reduction enthalpy and entropy of the solid then rigorously follow from the variational principle and Gibbs relationship, respectively as:
For the gas phase, we use an analytic fit to tabulated data for temperature (
Or alternately in a linear approximation,
With both sides of the phase equilibrium equation defined, the tools are in place to derive parameters from TGA or similar data to apply to modeling and development efforts. Note that the CEF-derived model physically limits the fitting parameters and functional form and enables semi-empirical and/or computational parameterization (Gautam et al., 2020). First, by way of validation, we have confirmed (see “Model Validation” in supporting material) that we are able to invert the data and infer the parameters for ceria from the well-known Zinkevich model (Zinkevich et al., 2006). Returning to CAM28, we find that, despite the possibility of using nine parameters, we achieve a good fit to the previously published data with just two fitting parameters in a linear least squares fit and could not get statistically significant additional terms,
Where (recalling x = 0.2 for CAM28)
Note that
An alternative to our approach is to derive an analytic expression for
Where
Then, the mapping yields the following expressions in place of our polynomials.
Where,
Figure 7 shows both the quality of the fit as well as the comparison between the two fits. For practical purposes, the results are indistinguishable; the derived reduction enthalpy and entropy are the same in each case. However, the CEF fit requires only two parameters while the Bulfin approach uses four: n,
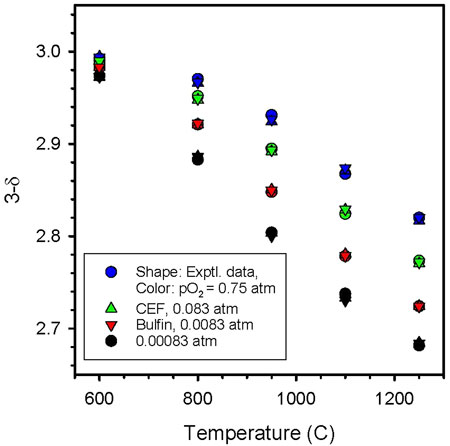
FIGURE 7. Comparison of CEF and Bulfin fits to CAM28 data. The shape of the data point indicates the data set (experimental - circle, CEP–up triangle, Bulfin–down triangle) while the color indicates the pO2 (blue – 0.75 atm, green – 0.083 atm, red – 0.0083 atm, black – 0.00083 atm). Both approaches fit the data well. No distinction between approaches can be discerned, given the currently available data.
To summarize, the CEF approach yields thermodynamic equations that are grounded in theory and that are not only useful for materials comparisons, but directly applicable to systems studies. If the data support it, the approach will accommodate both δ- and T-dependence for the thermodynamic parameters. The Bulfin approach also has a physical basis. We postulate that the CEF approach should be more robust than Bulfin as it offers the possibility of more parameters. However, if true, this potential advantage will only become evident over time as more data sets are evaluated. In the current instance, the primary difference is that the CEF model provides a two parameter fit that is indistinguishable from the four parameter Bulfin model. For a similar quality fit, it is reasonable to conclude fewer parameters is an improvement. A note of caution: as formulated, both the CEF and Bulfin approaches assume no phase transitions occur, such as those we have observed and reported herein. That is, both approaches essentially average through the transition.
Discussion and Summary
Calcium manganites were studied as alternatives to the previously identified LSCM379 for TCES with the primary goal of increasing the thermal storage capacity. This family of perovskites was selected as the basis based on several properties: 1) a reducible B-site element (Mn) in the +4 oxidation state supports large redox capacity, 2) reports of high reduction temperatures suggest large reduction endotherms, and 3) elemental constituents that are relatively low molecular weight, low cost, and abundant support cost and mass energy density metrics. Compositions wherein 20% of the B-site element Mn were replaced Al, Co, Fe, Ti, Zn, Zr, and Y were synthesized and evaluated with the goal of maximizing the storage capacity and stabilizing the perovskite in high-temperature reducing conditions. A 40% Fe sample was also examined. Of these, only the Al, Co, Fe and Ti yielded single-phase materials at room temperature. The parent CM was also single phase in the as-prepared form. The presence of Fe (CFM28 and CFM46) decreased the reduction temperatures relative to CM, an indication of a decrease in reduction enthalpy. This is also suggestive of the presence of a highly reducible Fe4+ or Mn5+ species in the as-prepared material. CM and CCM28 decompose when exposed to reducing conditions, i.e., Co does not adequately stabilize CM for this application. Based on these results CM, CCM, and CFM compositions were excluded from further investigation.
CYM28 not only consisted of multiple phases but was largely irreducible when screened at 1250°C under flowing Ar. Therefore, B-site doped CYM compositions were also eliminated from further consideration. However, the results also suggested that Y prefers to occupy an A-site, prompting further investigation. Multiple phases in the as-prepared material, lack of clear advantage over CM in screening, and potential for Zn volatilization also discouraged further evaluations of CZnM formulations. As the most promising of the three multi-phase samples, CZrM28 was advanced for further evaluation, but found to deactivate during multicycle studies. This is consistent with CM being the active phase. Additionally it serves as an excellent illustration of the importance of evaluating samples over larger numbers of cycles and at the extremes of anticipated conditions.
In preliminary results, not presented here, decreasing the Ti content from 20 to 10% (CTM19) produced a sample with behavior very similar to CTM28. Further decreasing the Ti to 5% (CTM0595) produced a material that met screening criteria, but was found to be unstable under further examination. Increasing Ti content from 20 to 40 and 60% greatly decreased the redox capacity in the temperature range of interest. The introduction of La onto the A-site with Ti on the B-site (CLTM8228 and CLTM5555) likewise led to collapse of the redox capacity, at least in the temperature range of interest. These negative results are likely linked to the irreducibility of the Ti and La cations and the replacement of a portion of the Ca2+ cation with La3+ which requires partial reduction of the Mn to the 3+ state to maintain charge balance. The substitution of Sr2+ onto the A-site (CSTM8228) had little impact.
A-site Y-doped CM samples (CYM) are single phase by XRD. XRD peak splitting, which increased with Y content, was observed for these samples, presumably due to distortion of the crystal lattice. Y-doping pushed the reduction temperatures higher without catastrophic loss of redox capacity. Seemingly, the reduction temperature increases in a regular fashion with Y-content, although further verification is required as the reduction temperatures were pushed above the upper range of the experiments for the higher doping levels. For this reason, only CYM910 and CYM820 were studied further. However, the materials with higher Y content remain of potential interest for higher temperature applications. Doubly doping, with Y on the A-site, and Al on the B-site (CYAM9128, CYAM8228) results in initial reduction temperatures situated between those of the respective singly-doped compounds (CYM910, CYM82, and CAM28). It also eliminates peak splitting in XRD. This presents something of a contrast to somewhat analogous CLTM materials. Further inquiry is required to fully elucidate the differences, but note that the Y3+ can be charge balanced by Al3+ in the CYAM materials rather than the manganese alone. CYAM9128 was selected for further study.
Figure 1 depicts the reduction endotherms for each of the remaining materials, along with CZrM28 which had not yet been identified as unstable. The highest thermal capacity attributable to the redox reaction, 59 kJ/mol for CYM91, is 34% higher than that of LSCM3791 (44.1 kJ/mol) (Babiniec et al., 2015). Figure 1B shows that the cumulative reduction enthalpy over the range of interest are grouped in a narrow range across the set. Putting aside CZrM28, the smallest value (for CYAM9128) is 82% of the largest (for CYM910). The top four candidates from this evaluation, CYM910, CTM28, CYM820, and CAM28, are all singly modified with the best exhibiting a capacity that is only 18% larger than the worst performing of the group (or the worst 15% smaller than the best). However, as this difference can impact design parameters such as vessel sizes and flow rates throughout a solar power facility, it should not be dismissed as insignificant. On the other hand, though higher storage capacity decreases the required amount of material and potentially component sizes, the cost of the constituent elements should not be overlooked (Table 3). As can be seen, Y is the most costly element and it replaces the least costly, Ca. Aluminum, on the other hand, replaces a more expensive element, Mn. Ti may also decrease the cost of elemental constituents, depending on the source. Materials cost therefore favors CAM28 and CTM28 over the CYM options.
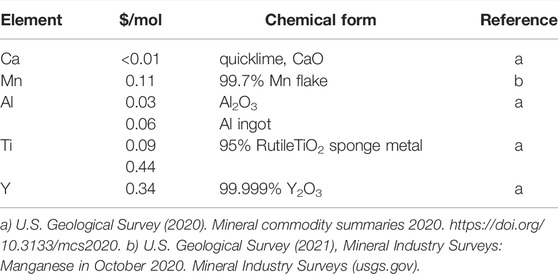
TABLE 3. Recent prices (in US dollars per mole) reported for the metals comprising the evaluated MIECs.
Given these complexities, the most economical choice for a given application therefore can best be determined by evaluating the apparent tradeoffs within a system model. A basic thermodynamic model relating T, pO2, δ, and ΔH of the perovskites is an essential tool for this exercise. Using CAM28 as an example, we have demonstrated that the CEF provides a good framework for developing these models from TGA. In the case of CAM28, the model provides good fits with only two parameters, though more can be applied as necessary. Heat capacities are also needed for this process. In this regard, CAM28 and CTM28 were demonstrated to conform to theoretical expectations. Similar materials will likely do so as well. Other important considerations for cost and operability include the long term stability and compatibility with materials of construction. Regarding the latter, previously reported studies with CAM and CTM materials indicate reaction can occur with commonly used insulating materials, necessitating the use of a zirconia-based liner, e.g., in hot storage bins (Miller et al., 2016).
There are many aspects to stability. Stable cycle-to-cycle performance is of course paramount. Our multicycle results help to establish the redox stability of CAM28, CTM28, CYM910, and CYAM9128. But given the experience with CZrM28, and the observation that small changes are still detectable after 100 cycles for example for CYM910, they also illustrate the importance of extended testing and/or understanding the changes occurring in the materials over time at a fundamental level. Our results illustrate the utility of in-situ, high-temperature XRD and DSC analyses in detecting and probing bulk changes (and verifying reversibility) in the perovskites occurring during the redox reaction that might not be apparent, for example, in a limited number of TGA cycles.
High-temperature deactivation/instability is often raised as a concern. However, many of the mechanisms by which active materials, such as catalysts, deactivate are not relevant here. For example, there are no highly-dispersed, high-surface area active materials to sinter or volatilize. Nor is there porosity that must be protected from thermally-driven collapse. Rather, the high temperatures promote rapid reaction, even with low surface area materials, and the inherent oxygen conductivity of this class of materials renders the entire particle accessible without porosity. As such, redox performance is relatively free from small changes in particle size. That said, bulk sintering or agglomeration which could impact flows, and attrition, which imposes a replacement cost and may require the installation of filters and other equipment, are significant concerns for operability and cost. Agglomeration has not been observed for any material in this study, and sintering onset temperatures for CAM28 and CTM28 are 1197 and 1211°C, respectively. As the test samples were highly dense and produced under high compressive loads, these results are very encouraging.
Techniques for evaluating and comparing attrition resistance are numerous but can be difficult to interpret without direct experience for some of the materials in the application environment to anchor the results. Fortunately, the attrition resistance of substituted calcium manganites has been evaluated in the context of fluidized chemical looping combustion and found to be very favorable (Rydén et al., 2014). For example, CaMg0.1Mn0.9O(3-δ) was tested in a 10 kWth reactor with a generation of fines between 0.02 and 0.002%/h and was considered likely suitable for commercial use in this challenging environment.
In summary, substituted/doped calcium manganites, particularly CYM910, CTM28, CYM820, and CAM28, remain excellent candidates for high-temperature TCES (≤1250°C). CYM910 exhibits the highest chemical storage capacity of the group: 59 kJ/mol via reduction at 1250°C and pO2 = 0.001 atm. CYM820, and potentially other A-site Y-doped compositions (e.g., CYM730), appear poised to eclipse this value if higher temperatures are used. While the materials may undergo minor structural changes during cycling, these appear to be fully reversible and more of an interest to science than barrier to application. While CAM28 is likely the least costly material, only an analysis with the full system context can determine the overall most economical choice.
Looking forward, and setting aside the need to eventually demonstrate materials and operations at the pilot scale we recommend several additional studies that could further lower barriers to implementation. First, characterization of the sensitivity of the results to the synthesis method and the batch-to-batch or lab-to-lab variability for a given method would further validate the results, as well as provide useful information for scaling-up the production. Careful XRD studies including Rietveld analysis would benefit this effort. Further, adding more data points to the T, pO2, δ map for materials of greatest interest would also be recommended. Second, the robustness of the various materials should be evaluated. That is, operational limits for combinations of temperature, pO2 and time, maximum achievable δ values before decomposition, etc., can be established by testing the material to failure. Options for recovery or regeneration can also be evaluated. This information has implications for full system design and operations, e.g., establishing how tightly different unit operations must be controlled, and identifying potential areas of concern when operations are upset or out of spec. Finally, validated kinetic expressions for reduction and oxidation across a broad range of temperatures and pO2 values would be invaluable for system design and analysis. Given the difficulties associated with characterizing an extremely rapid batch reaction in a transient thermal and gaseous environment, this will require the application of specialized techniques and equipment, accounting for the paucity of this type of information.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
JM: project conception, management, and direction; analysis; principle author. SB: materials conception, synthesis, characterization, and analysis. EC: Materials characterization and analysis. PL: project conception, supervision ES: project conception, thermodynamic modeling. AA: project conception, management, and direction; supervision; materials synthesis, characterization, and analysis.
Funding
The U.S. Department of Energy (DOE) SunShot Initiative provided funding for the project entitled High Performance Reduction/Oxidation Metal Oxides for Thermochemical Energy Storage (PROMOTES) under award number DE-FOA-0000805-1541 as part of the CSP:ELEMENTS program. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank all the members of the PROMOTES team for useful conversations and insights.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.774099/full#supplementary-material
References
Agrafiotis, C., Roeb, M., Schmücker, M., and Sattler, C. (2014). Exploitation of Thermochemical Cycles Based on Solid Oxide Redox Systems for Thermochemical Storage of Solar Heat. Part 1: Testing of Cobalt Oxide-Based Powders. Solar Energy 102, 189–211. doi:10.1016/j.solener.2013.12.032
Albrecht, K. J., Jackson, G. S., and Braun, R. J. (2018). Evaluating Thermodynamic Performance Limits of Thermochemical Energy Storage Subsystems Using Reactive Perovskite Oxide Particles for Concentrating Solar Power. Solar Energy 167, 179–193. doi:10.1016/j.solener.2018.03.078
Almendros-Ibáñez, J. A., Fernández-Torrijos, M., Díaz-Heras, M., Belmonte, J. F., and Sobrino, C. (2019). A Review of Solar thermal Energy Storage in Beds of Particles: Packed and Fluidized Beds. Solar Energy 192, 193–237. doi:10.1016/j.solener.2018.05.047
Babiniec, S. M., Coker, E. N., Ambrosini, A., and Miller, J. E. (2016b). ABO3 (A = La, Ba, Sr, K; B = Co, Mn, Fe) Perovskites for Thermochemical Energy Storage. AIP Conf. Proc. 1734, 050006. doi:10.1063/1.4949104
Babiniec, S. M., Coker, E. N., Miller, J. E., and Ambrosini, A. (2016c). Doped Calcium Manganites for Advanced High-Temperature Thermochemical Energy Storage. Int. J. Energ. Res. 40, 280–284. doi:10.1002/er.3467
Babiniec, S. M., Coker, E. N., Miller, J. E., and Ambrosini, A. (2015). Investigation of La Sr1−Co M1−O3− (M = Mn, Fe) Perovskite Materials as Thermochemical Energy Storage media. Solar Energy 118, 451–459. doi:10.1016/j.solener.2015.05.040
Babiniec, S. M., Miller, J. E., Ambrosini, A., Stechel, E., Coker, E. N., Loutzenhiser, P. G., et al. (2016a). “Considerations for the Design of a High-Temperature Particle Reoxidation Reactor for Extraction of Heat in Thermochemical Energy Storage Systems,” in Proceedings of ASME International Conference on Energy Sustainability (Charlotte, NC, USA). doi:10.1115/ES2016-59646
Bakken, E., Boeriogoates, J., Grande, T., Hovde, B., Norby, T., Rormark, L., et al. (2005a). Entropy of Oxidation and Redox Energetics of CaMnO. Solid State Ionics 176, 2261–2267. doi:10.1016/j.ssi.2005.06.009
Bakken, E., Norby, T., and Stolen, S. (2005b). Nonstoichiometry and Reductive Decomposition of CaMnO. Solid State Ionics 176, 217–223. doi:10.1016/j.ssi.2004.07.001
Bayon, A., Bader, R., Jafarian, M., Fedunik-Hofman, L., Sun, Y., Hinkley, J., et al. (2018). Techno-economic Assessment of Solid-Gas Thermochemical Energy Storage Systems for Solar thermal Power Application. Energy 149, 473e484. doi:10.1016/j.energy.2017.11.084
Bayon, A., de la Calle, A., Ghose, K. K., Page, A., and McNaughton, R. (2020). Experimental, Computational and Thermodynamic Studies in Perovskites Metal Oxides for Thermochemical Fuel Production: A Review. Int. J. Hydrogen Energ. 45, 12653–12679. doi:10.1016/j.ijhydene.2020.02.126
Brendelberger, S., Vieten, J., Roeb, M., and Sattler, C. (2019). Thermochemical Oxygen Pumping for Improved Hydrogen Production in Solar Redox Cycles. Int. J. Hydrogen Energ. 44, 9802–9810. doi:10.1016/j.ijhydene.2018.12.135
Brendelberger, S., Vieten, J., Vidyasagar, M. J., Roeb, M., and Sattler, C. (2018). Demonstration of Thermochemical Oxygen Pumping for Atmosphere Control in Reduction Reactions. Solar Energy 170, 273–279. doi:10.1016/j.solener.2018.05.063
Brendelberger, S., von Storch, H., Bulfin, B., and Sattler, C. (2017). Vacuum Pumping Options for Application in Solar Thermochemical Redox Cycles - Assessment of Mechanical-, Jet- and Thermochemical Pumping Systems. Solar Energy 141, 91–102. doi:10.1016/j.solener.2016.11.023
Bulfin, B., Lowe, A. J., Keogh, K. A., Murphy, B. E., Lübben, O., Krasnikov, S. A., et al. (2013). Analytical Model of CeO2 Oxidation and Reduction. J. Phys. Chem. C 117, 24129–24137. doi:10.1021/jp406578z
Bush, H. E., Datta, R., and Loutzenhiser, P. G. (2019). Aluminum-doped Strontium Ferrites for a Two-step Solar Thermochemical Air Separation Cycle: Thermodynamic Characterization and Cycle Analysis. Solar Energy 188, 775–786. doi:10.1016/j.solener.2019.06.059
Bush, H. E., Schlichting, K.-P., Gill, R. J., Jeter, S. M., and Loutzenhiser, P. G. (2017). Design and Characterization of a Novel Upward Flow Reactor for the Study of High-Temperature thermal Reduction for Solar-Driven Processes. ASME. J. Sol. Energ. Eng. 139, 051004. doi:10.1115/1.4037191
Carrillo, A. J., Moya, J., Bayón, A., Jana, P., de la Peña O’Shea, V. A., Romero, M., et al. (2014). Thermochemical Energy Storage at High Temperature via Redox Cycles of Mn and Co Oxides: Pure Oxides versus Mixed Ones. Solar Energ. Mater. Solar Cell 123, 47–57. doi:10.1016/j.solmat.2013.12.018
Chamberlain, K. (2020). HeliosCSP “New Concentrated Solar Power Report Offers Learnings from Crescent Dunes Flop. Available at: https://helioscsp.com/new-concentrated-solar-power-report-offers-learnings-from-crescent-dunes-flop/ (Accessed November 10, 2021).
Chen, X., Zhang, Z., Qi, C., Ling, X., and Peng, H. (2018). State of the Art on the High-Temperature Thermochemical Energy Storage Systems. Energ. Convers. Manag. 177, 792–815. doi:10.1016/j.enconman.2018.10.011
Chiang, C. C. K., and Poeppelmeier, K. R. (1991). Structural Investigation of Oxygen-Deficient Perovskite CaMnO2.75. Mater. Lett. 12, 102–108. doi:10.1016/0167-577X(91)90066-F
Coker, E. N., Rodriguez, M. A., Ambrosini, A., Miller, J. E., and Stechel, E. B. (2012). Using In-Situ Techniques to Probe High-Temperature Reactions: Thermochemical Cycles for the Production of Synthetic Fuels from CO2 and Water. Powder Diffr. 27, 117–125. doi:10.1017/S0885715612000255
Dizaji, H. B., and Hosseini, H. (2018). A Review of Material Screening in Pure and Mixed-Metal Oxide Thermochemical Energy Storage (TCES) Systems for Concentrated Solar Power (CSP) Applications. Renew. Sust. Energ. Rev. 98, 9–26. doi:10.1016/j.rser.2018.09.004
Ezbiri, M., Allen, K. M., Gàlvez, M. E., Michalsky, R., and Steinfeld, A. (2015). Design Principles of Perovskites for Thermochemical Oxygen Separation. ChemSusChem 8, 1966–1971. doi:10.1002/cssc.201500239
Gokon, N., Yawata, T., Bellan, S., Kodama, T., and Cho, H.-S. (2019). Thermochemical Behavior of Perovskite Oxides Based on LaxSr1-x(Mn, Fe, Co)O3-δ and BaySr1-yCoO3-δ Redox System for Thermochemical Energy Storage at High Temperatures. Energy 171, 971–980. doi:10.1016/j.energy.2019.01.081
Gorman, B. T., Lanzarini-Lopes, M., Johnson, N. G., Miller, J. E., and Stechel, E. B. (2021). Techno-economic Analysis of a Concentrating Solar Power Plant Using Redox-Active Metal Oxides as Heat Transfer Fluid and Storage media. Front. Energy Res. 9, 734288. doi:10.3389/fenrg.2021.734288
Hillert, M. (2001). The Compound Energy Formalism. J. Alloys Comp. 320, 161–176. doi:10.1016/S0925-8388(00)01481-X
Hutchings, K., Wilson, M., Larsen, P., and Cutler, R. (2006). Kinetic and Thermodynamic Considerations for Oxygen Absorption/desorption Using Cobalt Oxide. Solid State Ionics 177, 45–51. doi:10.1016/j.ssi.2005.10.005
Imponenti, L., Albrecht, K. J., Kharait, R., Sanders, M. D., and Jackson, G. S. (2018). Redox Cycles with Doped Calcium Manganites for Thermochemical Energy Storage to 1000 °C. Appl. Energ. 230, 1–18. doi:10.1016/j.apenergy.2018.08.044
Laurie, A., and Abanades, S. (2020). Recent Advances in Thermochemical Energy Storage via Solid–Gas Reversible Reactions at High Temperature. Energies 13, 5859. doi:10.3390/en13225859
Leonidova, E. I., Leonidov, I. A., Patrakeev, M. V., and Kozhevnikov, V. L. (2011). Oxygen Non-stoichiometry, High-Temperature Properties, and Phase Diagram of CaMnO3-δ. J. Solid State. Electrochem. 15, 1071–1075. doi:10.1007/s10008-010-1288-1
Lucio, B., Romero, M., and González-Aguilar, J. (2019). Analysis of Solid-State Reaction in the Performance of Doped Calcium Manganites for thermal Storage. Solid State Ionics 338, 47–57. doi:10.1016/j.ssi.2019.05.007
Mastronardo, E., Qian, X., Coronado, J. M., and Haile, S. M. (2021). Impact of La Doping on the Thermochemical Heat Storage Properties of CaMnO3-δ. J. Energ. Storage 40, 102793. doi:10.1016/j.est.2021.102793
Mehos, M., Price, H., Cable, R., Kearney, D., Kelly, B., Kolb, G., et al. (2020). Concentrating Solar Power Best Practices Study. Golden, CO: National Renewable Energy Laboratory. NREL/TP-5500-75763. Available at: www.nrel.gov/docs/fy20osti/75763.pdf.
Meredig, B., and Wolverton, C. (2009). First-principles Thermodynamic Framework for the Evaluation of thermochemicalH2O- orCO2-Splitting Materials. Phys. Rev. B 80, 245119-1–245119-8. doi:10.1103/PhysRevB.80.245119
Miller, J. E., Ambrosini, A., Coker, E. N., Ho, C. K., Al-Ansary, H., Jeter, S. M., et al. (2016). “High Performance Reduction/Oxidation Metal Oxides for Thermochemical Energy Storage (PROMOTES),” in Proceedings of ASME International Conference on Energy Sustainability (Charlotte, NC, USA). doi:10.1115/ES2016-59660
Miller, J. E., McDaniel, A. H., and Allendorf, M. D. (2014). Considerations in the Design of Materials for Solar-Driven Fuel Production Using Metal-Oxide Thermochemical Cycles. Adv. Energ. Mater. 4, 1300469. doi:10.1002/aenm.201300469
Mizusaki, J., Tagawa, H., Naraya, K., and Sasamoto, T. (1991). Nonstoichiometry and Thermochemical Stability of the Perovskite-type La1−xSrxMnO3−δ. Solid State Ionics 49, 111–118. doi:10.1016/0167-2738(91)90076-N
Muroyama, A. P., Schrader, A. J., and Loutzenhiser, P. G. (2015). Solar Electricity via an Air Brayton Cycle with an Integrated Two-step Thermochemical Cycle for Heat Storage Based on Co3O4/CoO Redox Reactions II: Kinetic Analyses. Solar Energy 122, 409–418. doi:10.1016/j.solener.2015.08.038
Ortiz, C., Valverde, J. M., Chacartegui, R., Perez-Maqueda, L. A., and Giménez, P. (2019). The Calcium-Looping (CaCO3/CaO) Process for Thermochemical Energy Storage in Concentrating Solar Power Plants. Renew. Sust. Energ. Rev. 113, 109252. doi:10.1016/j.rser.2019.109252
Peña, M. A., and Fierro, J. L. G. (2001). Chemical Structures and Performance of Perovskite Oxides. Chem. Rev. 101, 1981–2018. doi:10.1021/cr980129f
Qian, X., He, J., Mastronardo, E., Baldassarri, B., Yuan, W., Wolverton, C., et al. (2021). Outstanding Properties and Performance of CaTi0.5Mn0.5O3-δ for Solar-Driven Thermochemical Hydrogen Production. Matter 4, 688–708. doi:10.1016/j.matt.2020.11.016
Redlich, O., and Kister, A. T. (1948). Algebraic Representation of Thermodynamic Properties and the Classification of Solutions. Ind. Eng. Chem. 40, 345–348. doi:10.1021/ie50458a036
Rydén, M., Moldenhauer, P., Lindqvist, S., Mattisson, T., and Lyngfelt, A. (2014). Measuring Attrition Resistance of Oxygen Carrier Particles for Chemical Looping Combustion with a Customized Jet Cup. Powder Tech. 256, 75–86. doi:10.1016/j.powtec.2014.01.085
Sai Gautam, G., Stechel, E. B., and Carter, E. A. (2020). Exploring Ca-Ce-M-O (M = 3d Transition Metal) Oxide Perovskites for Solar Thermochemical Applications. Chem. Mater. 32, 9964–9982. doi:10.1021/acs.chemmater.0c02912
Schrader, A., Bush, H. E., Ranjan, D., and Loutzenhiser, P. G. (2020). Aluminum-doped Calcium Manganite Particles for Solar Thermochemical Energy Storage: Reactor Design, Particle Characterization, and Heat and Mass Transfer Modeling. Int. J. Heat Mass Transfer 152, 119461. doi:10.1016/j.ijheatmasstransfer.2020.119461
Stekli, J., Irwin, L., and Pitchumani, R. (2013). Technical Challenges and Opportunities for Concentrating Solar Power with thermal Energy Storage. J. Therm. Sci. Eng. Appl. 5, 021011. doi:10.1115/1.4024143
Sunku Prasad, J., Muthukumar, P., Desai, F., Basu, D. N., and Rahman, M. M. (2019). A Critical Review of High-Temperature Reversible Thermochemical Energy Storage Systems. Appl. Energ. 254, 113733. doi:10.1016/j.apenergy.2019.113733
Vieten, J., Bulfin, B., Call, F., Lange, M., Schmücker, M., Francke, A., et al. (2016). Perovskite Oxides for Application in Thermochemical Air Separation and Oxygen Storage. J. Mater. Chem. A. 4, 13652–13659. doi:10.1039/c6ta04867f
Wu, S., Zhou, C., Doroodchi, E., Nellore, R., and Moghtaderi, B. (2018). A Review on High-Temperature Thermochemical Energy Storage Based on Metal Oxides Redox Cycle. Energ. Convers. Manag. 168, 421–453. doi:10.1016/j.enconman.2018.05.017
Wu, Y.-t., Ren, N., Wang, T., and Ma, C.-f. (2011). Experimental Study on Optimized Composition of Mixed Carbonate Salt for Sensible Heat Storage in Solar thermal Power Plant. Solar Energy 85, 1957–1966. doi:10.1016/j.solener.2011.05.004
Yan, Y., Wang, K., Clough, P. T., and Anthony, E. J. (2020). Developments in Calcium/chemical Looping and Metal Oxide Redox Cycles for High-Temperature Thermochemical Energy Storage: A Review. Fuel Process. Tech. 199, 106280. doi:10.1016/j.fuproc.2019.106280
Yuan, Y., Li, Y., and Zhao, J. (2018). Development on Thermochemical Energy Storage Based on CaO-Based Materials: A Review. Sustainability 10, 2660. doi:10.3390/su10082660
Zhai, S., Rojas, J., Ahlborg, N., Lim, K., Toney, M. F., Jin, H., et al. (2018). The Use of Poly-Cation Oxides to Lower the Temperature of Two-step Thermochemical Water Splitting. Energy Environ. Sci. 11, 2172–2178. doi:10.1039/C8EE00050F
Keywords: thermochemical energy storage, metal oxides, mixed ionic electronic conductor, MIEC, calcium manganite CaMnO3, concentrating solar power (CSP), compound energy formalism
Citation: Miller JE, Babiniec SM, Coker EN, Loutzenhiser PG, Stechel EB and Ambrosini A (2022) Modified Calcium Manganites for Thermochemical Energy Storage Applications. Front. Energy Res. 10:774099. doi: 10.3389/fenrg.2022.774099
Received: 10 September 2021; Accepted: 09 February 2022;
Published: 14 April 2022.
Edited by:
Emanuela Mastronardo, University of Messina, ItalyReviewed by:
Xin Qian, Georgia Institute of Technology, United StatesJuan M. Coronado, Spanish National Research Council (CSIC), Spain
Copyright © 2022 Miller, Babiniec, Coker, Loutzenhiser, Stechel and Ambrosini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James E. Miller, SmltLkUuTWlsbGVyQGFzdS5lZHU=
 James E. Miller
James E. Miller Sean M. Babiniec2
Sean M. Babiniec2 Eric N. Coker
Eric N. Coker Peter G. Loutzenhiser
Peter G. Loutzenhiser Ellen B. Stechel
Ellen B. Stechel Andrea Ambrosini
Andrea Ambrosini