The integrated modeling of microgrid cyber physical system based on hybrid automaton

To fully reveal the interplay of the cyber system and physical system in the microgrid, this paper proposes a generic hierarchical modeling framework for cyber-physical integration modeling of microgrid, including two layers: physical device layer and controller layer. Each layer includes two parts: the continuous part (characterizing the physical system in the microgrid) and the discrete part (characterizing the cyber system in the microgrid). In this paper, firstly, detailed mathematical expressions describing the dynamic characteristics of each layer (including continuous characteristics and discrete characteristics) and describing the interplay of the continuous part and discrete part in each layer are given, which contributes to a better understanding of the interplay of the information flow and energy flow in the microgrid. Secondly, the cyber-physical integration modeling of each unit in the proposed framework is established using hybrid automaton, which can clearly present the operation state of each unit of the microgrid and its state transfer process, which is beneficial to design the optimal operation state trajectory of the system. The proposed modeling framework is generic and can be extended to any dynamic system with cyber-physical integration. Finally, a typical microgrid system is taken as an example to verify the feasibility of the proposed modeling approach.

1 Introduction

Cyber physical system (CPS) is a multidimensional heterogeneous complex system that integrates computing, network and physical environment (Zonouz et al., 2014; Gao et al., 2021). Compared with the traditional single physical system, CPS improves the operating efficiency of the system by integrating network, computing and physical resources (Poovendran, 2010). In recent years, the coupling of cyber space and energy system has become increasingly close with the rapid development of communication technology, sensor technology, computer technology and automatic control theory. The microgrid proposed to solve the problem of renewable energy grid-connection has increasingly possessed the key features of CPS (Cheng and Chow, 2020) and has developed into a typical microgrid CPS (MCPS). The cyber-physical coupling characteristic of MCPS has the function of energy management but it also brings the shortage that faults on any side will affect the safe and stable operation of the entire MCPS. Therefore, it is important to promote the development of MCPS that studies the coupling relationship from the perspective of CPS. The model is the basis for studying its coupling relationship (Ilic et al., 2010), so this paper mainly studies from the perspective of MCPS model.

There is a body of research that has focused extensively on the cyber-physical integration modeling of the power grid CPS. For example, Ref (Wei et al., 2014). established a power grid CPS (PGCPS) model that conforms to the characteristics of the actual PGCPS structure based on the analysis of the component configuration and coupling rules of the cyber network. Refs (Xin et al., 2015; Xin et al., 2017). proposes a two-layer multi-agent PGCPS framework that divides CPS clusters through cluster theory to achieve distributed control of PGCPS using less information. Refs (Yu et al., 2016; Li et al., 2020). built a PGCPS model based on the node-branch correlation matrix, which described the coupling of information and energy flows more comprehensively in the PGCPS, but it was difficult to quantitatively describe and analyze the stochastic events and complex response processes in the cyber system. Refs (Xue and Yu, 2017; Xu et al., 2019). used the matrix formed by multi-element tuple to quantitatively describe the association relationship of information processing layer, communication layer, secondary equipment layer, and physical space, which can effectively describe the coupling relationship within the PGCPS. Ref (Wang et al., 2017). established an integrated PGCPS model considering the correlation and coupling characteristics of the power network, communication network, and cyber network, which reveals the multilayer coupling association mechanism of PGCPS more clearly.

In summary, the above studies have proposed modeling methods for PGCPS from different perspectives, which can reveal the interaction between information flow and energy flow to a certain extent, but the objects of their studies are mainly PGCPS, and there are few studies involving the modeling of MCPS in the literature. Meanwhile, there are still some limitations that need to be solved in the above models:

a) The above modeling approaches are mainly performed from a task-specific perspective, not a generic modeling approach for the system, so their application fields are limited.

b) The existing modeling methods mostly focus on the static relationships in the system, lacking the modeling of dynamic process and evolution. Meanwhile, the above models cannot clearly present the operating status of each unit of the microgrid and its state transfer process.

The research in this paper attempts to address above issues. Therefore, in this paper, taking microgrid as the research object, a generic hierarchical modeling framework for integration modeling of MCPS, including two layers: physical device layer and controller layer, is proposed. To the best of the authors’ knowledge, the original contributions of this paper are summarized as follows:

1) Detailed mathematical expressions describing the dynamic characteristics of each layer (including continuous dynamic characteristics and discrete characteristics) and describing the interactions between the continuous part and discrete part within each layer are given, which contributes to a better understanding of the interplay of the information flow and energy flow in the MCPS;

2) In the established modeling framework, the cyber-physical integration modeling of each unit is established by using hybrid automaton (HA), which can clearly present the operating state, state transfer process, and transfer conditions of each unit in the microgrid. This is beneficial to design the optimal operation state trajectory of the microgrid and explore the optimal control strategy;

3) The proposed modeling framework divides the microgrid system modeling into different layers, which makes modeling more intuitive. Moreover, the proposed modeling framework is generic and can be extended to any dynamic system with cyber-physical integration.

2 Microgrid CPS architecture

2.1 The architecture of microgrid CPS

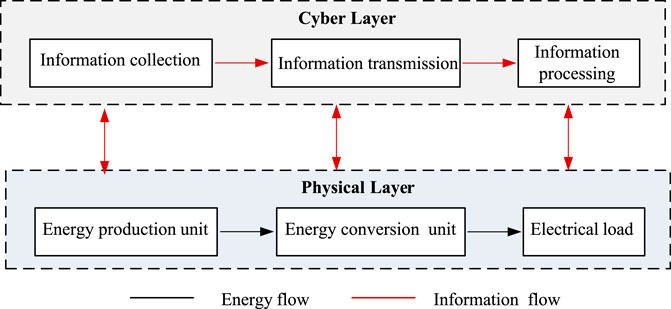
Figure 1 shows a typical MCPS architecture, which consists of two parts: the physical layer and the cyber layer. The physical layer is composed of energy production units (photovoltaic, wind power, energy storage, etc.), energy conversion units, various types of loads and other physical equipment, and the power network connecting these physical devices. The cyber layer is composed of cyber equipment such as sensing equipment, distributed computing equipment, control decision equipment and a communication network connecting these cyber devices.

FIGURE 1

FIGURE 1. The CPS-based architecture of microgrid.

In MCPS, the cyber layer and the physical layer have the function of the energy management of the microgrid through the tight coupling of information flow and energy flow. Cyber-physical coupling is manifested in that the cyber layer perceives the operating status of the equipment in the physical layer through sensors, converts the energy flow into an information flow, transmits it to the cyber layer through the communication network and the information flow is processed by the cyber processing unit as the input of the decision-making control unit. The decision-making control unit converts the input information into control instructions and sends them to the physical equipment in the physical layer to control the operation of the physical equipment. It can be seen that the information input of the cyber layer to make decisions comes from the operating status of the equipment in the physical layer. The operating status of the physical layer equipment depends on the control commands issued by the cyber layer, indicating that the cyber layer and the physical layer in the MCPS are tightly coupled.

2.2 The description of the hybrid system

The hybrid system (HS) can be formally described by the following multi-element tuple (Petreczky and Schuppen, 2297).

$H=\left\{M,\mathrm{\Sigma },P,\delta ,R,X\right\}(1)$

Where: M denotes the set of discrete states of the system (also called the mode of operation of the system), and for any one discrete state, there are $m=m\left(t\right)\in M$;

$\Sigma =\left\{e_1,e_2,\cdots ,e_N\right\}$ denotes the set of discrete events of the system, and for any one discrete event, it can be expressed as $e=e\left(t\right)\in \Sigma$;

P denotes the parameter variable of the system;

$\delta$ denotes the system discrete state transition function;

R denotes the reset function, which determines the initial value of the continuous variable after the discrete state transition of the system occurs;

$X={\left\{A^{\left(m\right)}\right\}}_{m\in M}$ is the set of state spaces of the CVDS, Among them, $A^{\left(m\right)}=\left(X^{\left(m\right)},G^{\left(m\right)},f^{\left(m\right)},{\lambda }^{\left(m\right)}\right)$, the elements of $A^{\left(m\right)}$ is defined as follows:

$X^{\left(m\right)}$ denotes the continous state space of the system in mode $m\in M$, and $x\left(t\right)\in X^{\left(m\right)}$ denotes the state variables of the CVDS;

$G^{\left(m\right)}:X^{\left(m\right)}\times M\times \Sigma \to \left\{true,false\right\}$ is the transition condition under the mode $m\in M$;

$f^{\left(m\right)}$ denotes the evolution rule of the CVDS under mode m, characterizing the dynamic behavioral properties of the CVDS;

${\lambda }^{\left(m\right)}$ indicates the output function of the system.

The dynamics of the HS can be described by the following equations.

${\dot{x}}^{\left(m\right)}\left(t\right)=f^{\left(m\right)}\left(x^{\left(m\right)}\left(t\right),u\left(t\right),p\right)(2)$

$y\left(t\right)={\lambda }^{\left(m\right)}\left(x^{\left(m\right)}\left(t\right),u\left(t\right),p\right)(3)$

$m_{+}\left(t\right)=\delta \left(m_{-}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e\right)(4)$

$x_{+}^{\left(m_{+}\right)}\left(t\right)=R\left(m_{-}\left(t\right),m_{+}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e\right)(5)$

Where the subscripts "+" denotes the state after the event e occurs and subscripts "−" denotes the state before the event e occurs, $m_{-}\left(t\right)$ and $x_{-}^{\left(m_{-}\right)}\left(t\right)$ denote the state mode and continuous state before the event e occurs, respectively, $m_{+}\left(t\right)$ and $x_{+}^{\left(m_{+}\right)}\left(t\right)$ denote the state mode and continuous state after the event e occurs, respectively.

Let t be the initial moment and the initial state of the system is $\left(m_0,x_0^{\left(m_0\right)}\right)$. In the discrete state m(t) = m₀, the continuous dynamics are described by the differential Equation 2. At any time $t\in T$, the occurrence of an event may lead to a change in the operating mode of the system. The change of system operation mode is described by Eq. 3, which indicates that at time t, the event e changes the system from mode $m_{-}\left(t\right)$ to $m_{+}\left(t\right)$. Also, as the system changes to operate in the successor mode, the state variables of the system may undergo a jump, i.e., change from system state $\left(m_{-}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right)\right)$ to system state $\left(m_{+}\left(t\right),x_{+}^{\left(m_{+}\right)}\left(t\right)\right)$, and the change of state is described by Eq. 5. After the HS transitions to the successor mode, the system will continue to evolve along the trajectory described by Equations 2–5 if a new event occurs.

3 Hierarchical modeling framework for microgrid CPS

3.1 The hybrid characteristics of microgrid CPS

The MCPS presents a hybrid system characteristic during operation. For example, the energy flow in the physical system varies continuously with time according to a certain rule, which has the characteristics of a continuous variable dynamic system (CVDS). The cyber system controls the physical system through the information flow, including information collection, communication, processing, and control processes, all of which work digitally and consist of various types of events and their responses, which has the characteristics of a discrete event dynamic system (DEDS). Moreover, there is an interaction between the above two characteristics.

From the above analysis, it is clear that the physical system in the MCPS can be regarded as a CVDS, while the cyber system in the MCPS can be regarded as a DEDS. Therefore, the analysis of the interplay of information flow and energy flow in the MCPS can be converted into the analysis of the interplay of the CVDS and the DEDS in the MCPS.

3.2 The CPS-based modeling framework for microgrid

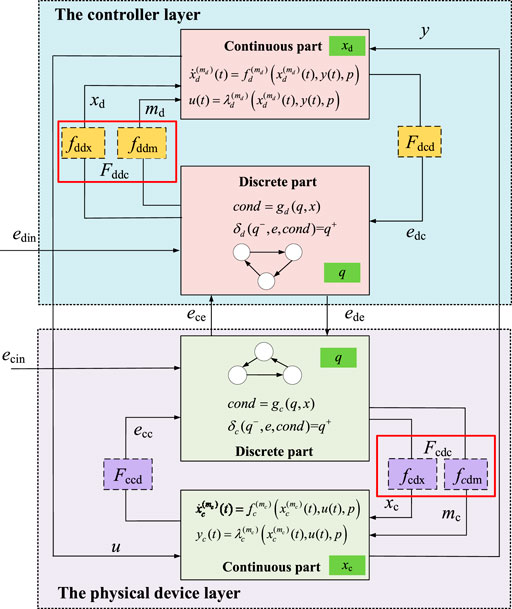
To accurately characterize the interplay of the information flow and energy flow in the MCPS, a generic hierarchical modeling framework for cyber-physical integration modeling of MCPS is proposed, as shown in Figure 2.

FIGURE 2

FIGURE 2. The hierarchical modeling framework for the MCPS.

In Figure 2, the modeling framework of MCPS includes two layers: the physical device layer and the controller layer.

1) Physical device layer: This layer mainly includes some PV unit, WT unit, BSS unit, etc., which can be considered as a unit-level CPS. The unit-level CPS can optimize the allocation of resources within the working capacity of the device through the physical device, its control system, and communication modules. At this layer, each device in the physical device layer transmits information related to its state and sensed environmental information to the controller layer and executes control commands issued by the controller layer.

2) Controller layer: As the upper layer of the microgrid CPS, this layer, on the one hand, mainly issues control commands to the physical device layer to drive the actions of the units in the physical device layer. On the other hand, it mainly uses data fusion, distributed computing, big data analysis, and other technologies to monitor, analyze and control the whole working status of the system in real-time, to achieve the optimal configuration, decision, and operation of the system.

In Figure 2, both the physical device layer and the controller layer consist of two parts: the continuous part and the discrete part. The continuous part is used to describe the characteristics of the continuous change of the device state over time. While the discrete part is used to describe the transfer process of the device between different operating states. The continuous part and the discrete part interact with each other through interface functions.

4 Microgrid CPS modeling based on hybrid automaton

4.1 The mathematical description of each layer

4.1.1 The physical device layer.

i) The continuous part

In the continuous part, the continuous dynamic behavior of the device is characterized by the following equation.

$\{\begin{array}{l}{\dot{x}}_c^{\left(m\right)}\left(t\right)=f_c^{\left(m\right)}\left(x_c^{\left(m\right)}\left(t\right),u\left(t\right),p\right)\\ y_c\left(t\right)={\lambda }_c^{\left(m\right)}\left(x_c^{\left(m\right)}\left(t\right),u\left(t\right),p\right)\end{array}(6)$

Where, $f_c^{\left(m\right)}$ denotes the continuous dynamic change relationship function of the device, ${\lambda }_c^{\left(m\right)}$ denotes the output function of the device, $x_c^{\left(m\right)}\left(t\right)$ is the continuous state variable of the device, $u\left(t\right)$ denotes the control input variable of the device, m denotes the current operating state mode of the device, and p denotes a time-independent parameter variable.

ii) The discrete part

The discrete part is used to describe the transfer process of the device between different discrete states q, which can be described by the state transfer condition function g_c and the state transfer function ${\delta }_{\text{c}}$.

The function g_c

$g_c:Cond=\left\{true,false\right\},cond=g_c\left(q,x\right)(7)$

The (7) indicates whether the system satisfies the condition of operating state transfer by function g_c under the condition of discrete state q and continuous state x.

The function ${\delta }_c$

${\delta }_c:{\delta }_c\left(q^{-},e,cond\right)=q^{+},\left\{e_{cd1},e_{cd2},\cdots \right\}(8)$

The event e can be a state event e_cc generated by the continuous part, or an internal control input event e_de of the system, or an event e_cin generated by the environment. The (8) indicates that the system will transfer from state q⁻ to state q⁺ and generate a series of discrete events e_cdi when event e occurs and the transfer condition cond of the state is true.

iii) The interface layers

The interface layers include the discrete-continuous system interface and the continuous-discrete system interface. Define F_ccd to denote the continuous-discrete interface layer function that represents the action of the continuous part on the discrete part. Similarly, define F_cdc to denote the discrete-continuous interface layer function that represents the action of the discrete part on the continuous part.

① The F_ccd represents the action of the continuous part on the discrete part, which manifests in triggering an event e_cc generated when the state trajectory of the x traverses the hypersurface h_m, which acts on the discrete part through the event e_cc, thus changing the value of q. For each mode $m\in M$, define a hypersurface h_m.

$h_m:H_m\left(x\left(t\right),u\left(t\right)\right)=0(9)$

Then the expression that generates the event e_cc is shown in Eq. 10.

$e_{cc}=F_{ccd}\left(x\left(t\right),h_m\right)(10)$

② The F_cdc represents the action of the discrete part on the continuous part and consists of two parts, as follows.

$F_{cdc}=\left[f_{cdx},f_{cdm}\right](11)$

In Eq. 11, the function f_cdm manifests in affecting the dynamic evolution relationship of continuous variables x through the discrete state q, and its expression is as follows:

$m_{+}\left(t\right)=f_{cdm}\left(m_{-}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),q\right)(12)$

The (12) shows that the state mode m of the system is affected by q, while the device operates in different state modes m, there are corresponding differential equations to describe the dynamic behavior of the continuous part, i.e., the function f_cdm influences the differential equations of the dynamic behavior of the continuous part through m.

When the system undergoes a state transfer, the value of the continuous state variable x may undergo a jump. The process is described by the function f_cdx, and its expression is as follows

$x_{+}^{\left(m_{+}\right)}\left(t\right)=f_{cdx}\left(m_{-}\left(t\right),m_{+}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e_{cdi}\right)(13)$

Where "+" indicates the state after the event and "−" indicates the state before the event. As can be seen from Eq. 13. The discrete part acts on the continuous part by generating the discrete event e_cdi, which changes the value of the x.

In summary, the mathematical description of the dynamic characteristics of the continuous part, the discrete part, and the interface layers in the physical device layer are summarized as follows:

$\{\begin{array}{l}\{\begin{array}{l}{\dot{x}}_c^{\left(m\right)}\left(t\right)=f_c^{\left(m\right)}\left(x_c^{\left(m\right)}\left(t\right),u\left(t\right),p\right)\\ y_c\left(t\right)={\lambda }_c^{\left(m\right)}\left(x_c^{\left(m\right)}\left(t\right),u\left(t\right),p\right)\end{array}\\ \\ \{\begin{array}{l}\begin{array}{l}{h}_m:H_m\left(x\left(t\right),u\left(t\right)\right)=0\\ e_{cc}=F_{ccd}\left(x\left(t\right),h_m\right)\end{array}\}\to F_{ccd}\\ \begin{array}{l}{x}_{+}^{\left(m_{+}\right)}\left(t\right)=f_{cdx}\left(m_{-}\left(t\right),m_{+}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e_{cdi}\right)\\ m_{+}\left(t\right)=f_{cdm}\left(m_{-}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e\right)\end{array}\}\to F_{cdc}\end{array}\\ \\ \{\begin{array}{l}Cond=\{true,false\},cond=g_c(q,x)\\ {\delta }_c(q^{-},e,cond)=q^{+}\text{,}\{e_{cd1},e_{cd2},\cdots \}\end{array}\end{array}(14)$

4.1.2 The controller layer

Similar to the physical device layer, the dynamic characteristics of each part in the controller layer can be described in Eq. 5:

$\{\begin{array}{l}\{\begin{array}{l}{\dot{x}}_d^{\left(m\right)}\left(t\right)=f_d^{\left(m\right)}\left(x_d^{\left(m\right)}\left(t\right),y\left(t\right),p\right)\\ u\left(t\right)={\lambda }_d^{\left(m\right)}\left(x_d^{\left(m\right)}\left(t\right),y\left(t\right),p\right)\end{array}\\ \{\begin{array}{l}\begin{array}{l}{h}_m:H_m\left(x\left(t\right),y\left(t\right)\right)=0\\ e_{dc}=F_{dcd}\left(x\left(t\right),h_m\right)\end{array}\}\to F_{dcd}\\ \begin{array}{l}{x}_{+}^{\left(m_{+}\right)}\left(t\right)=f_{ddx}\left(m_{-}\left(t\right),m_{+}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e_{ddi}\right)\\ m_{+}\left(t\right)=f_{ddm}\left(m_{-}\left(t\right),x_{-}^{\left(m_{-}\right)}\left(t\right),e\right)\end{array}\}\to F_{ddc}\end{array}\\ \{\begin{array}{l}Cond=\{true,false\},cond=g_d\left(q,x\right)\\ {\delta }_d\left(q^{-},e,cond\right)=q^{+}\text{,}\left\{e_{dd1},e_{dd2},\cdots \right\}\end{array}\end{array}(15)$

4.2 CPS modeling of microgrid based on hybrid automaton

In this section, to clearly present the operation status, state transfer conditions, and state transfer process of each unit in the microgrid under the conditions of external control commands or various events, the cyber-physical integration modeling of MCPS is established using hybrid automaton (HA) (Lin et al., 2021). The HA is an extension of the original Finite State Machine (FSM) (Li et al., 2014), that is, continuous variables are added to the variables of the system and the influence of continuous variables is added to the state transfer process of the system.

The HA can describe the continuous dynamic behavior of the system as well as the discrete dynamic behavior of the system. An HA usually includes the following elements: 1) present state (the current state of the system), 2) conditions (also called events, when a condition is met, it will trigger the state transition of the system), 3) action (referring to the action executed after the system state transition condition is met) 4) second state (referring to the next state to be transitioned after the system state transition condition is met).

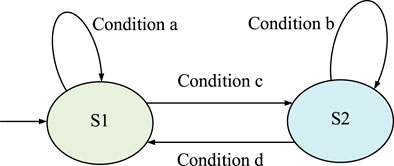
An HA is often represented by a directed graph and the state of the HA is represented by a circle. In each state, there is a function that describes how the continuous state changes. A directed curve is used to represent the state transition process of the system. The starting point of the directed curve represents the current state of the system and the end point represents the next state after the transition. At the same time, mark the transition conditions of the system state transition on the edge of the directed curve. Take an HA with two states as an example to illustrate the working principle of HA, as shown in Figure. 3.

FIGURE 3

FIGURE 3. The directed graph of hybrid automaton.

The HA in Figure. 3 includes two states S1 and S2. The arrow pointing to S1 on the left indicates that the initial state of the system is S1. Above S1, draw a directed curve with the start and end points on S1. The condition a of state transition is marked on the curve, which means that when the system state is S1 and condition a is met, the state of HA remains unchanged; the directed curve marked with condition c from S1 to S2 shows that when the system state is S1 and condition c is satisfied, the system state is converted to S2. Similarly, according to the directed graph, when the system is in the S2 state, and the condition b is satisfied, the state of HA remains unchanged; when the condition b is satisfied, the system state changes to S1.

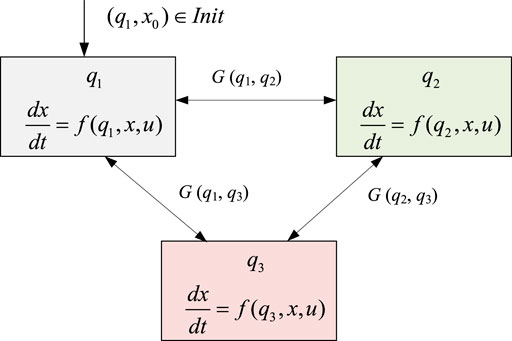
Taking the three states of a device in the MCPS as an example, the CPS model of the device is established using HA as shown in Figure. 4.

FIGURE 4

FIGURE 4. The CPS model of device using HA.

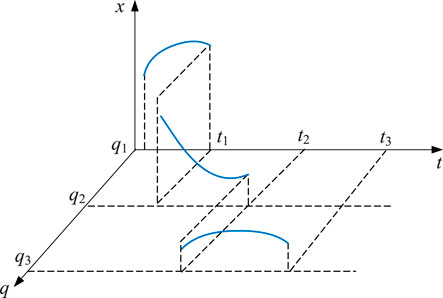
As seen from Figure 4, the transfer process between different states of the device can be described as follows: the trajectory of the device starts from the initial state, and the transfer process includes continuous state evolution and discrete state transfer. The initial discrete state of the device is q1, then the continuous variable x evolves according to the following differential equation.

$\frac{dx}{dt}=f\left(q_1,x\right),x\left(0\right)=x_0(16)$

As long as the state transfer condition function g () is not satisfied, the device keeps evolving in the current operating state, i.e., the discrete state q remains unchanged with q(t) = q₁. And when the state transfer condition function G (q₁, q₂) is satisfied for some reason, the discrete state transfer of the system is triggered and the system changes from the discrete state q₁ to the discrete state q₂ according to the state transfer function $\delta$. The x jumps from the current value of the continuous variable to the new value according to the reset function and evolves according to the corresponding differential equation in the new discrete state q₂. The switching between other modes is similar to the above process, and by repeating this process continuously, the device runs continuously.

The evolution of the above device can be described by the evolutionary trajectory shown in Figure 5.

FIGURE 5

FIGURE 5. The evolution trajectory of the device.

The transfer conditions between the different modes can be divided into two categories: internal state events due to the evolution of internal state variables across a specific threshold or state plane, and external state events due to the influence of external inputs (e.g., command issuance) on the system. These two types of events can act on the MCPS either individually or simultaneously.

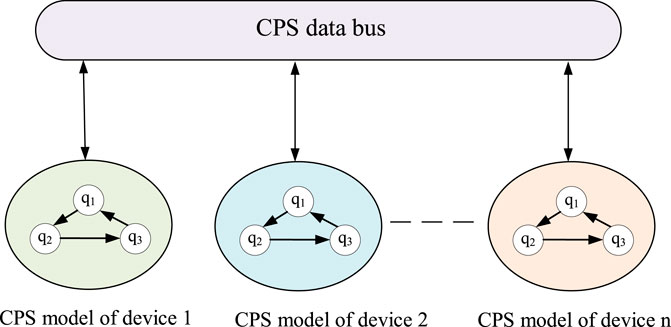
By connecting CPS models of the multiple devices established using HA in the MCPS through the CPS data bus, the CPS model of the entire microgrid system (i.e., the system-level CPS model) can be obtained, as shown in Figure 6.

FIGURE 6

FIGURE 6. The CPS model of the entire microgrid system.

As can be seen from Figure 6 that the operating process of the microgrid system can be characterized and analyzed by multiple state transfer models, and the transfer between different states is achieved using HA. In each operating state, the device’s continuous variation characteristics are described using differential or algebraic equations.

In summary, the microgrid model established in this paper is completely different from the conventional microgrid state space model in terms of the modeling approach and thinking and has more advantages in terms of observability. On the one hand, no matter what operating state the microgrid is in, the operating state of each unit in the microgrid can be known. On the other hand, during the transfer of the microgrid operating state, the operation state transfer process of each unit in the microgrid and the conditions of transfer can be clearly presented and observed, which is not available in the conventional state space model.

5 Model validation

5.1 Case description

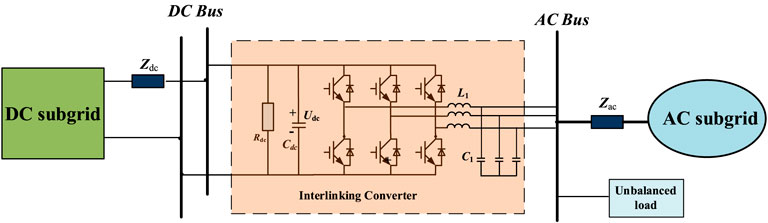
This paper takes the operating mode of Interlinking Converter (ILC) in hybrid AC/DC microgrids (HMs) as an example to verify the modeling method proposed in this paper. Figure 7 corresponds to the topological structure diagram of the HMs in this example, which consists of an AC subgrid, a DC subgrid, and ILC connecting the AC subgrid and the DC subgrid.

FIGURE 7

FIGURE 7. The topology structure of HMs.

Among them, an unbalanced load is connected to the AC bus. The unbalanced load will make the AC bus voltage u_ac and the ILC current i_ILC unbalanced. The DC bus voltage u_dc will produce ripple through the coupling effect of ILC. Since ILC does not run at rated power most of the time, we can make full use of the remaining available capacity of ILC to realize HMs power quality control, including balancing u_ac, i_ILC and suppressing ripple in u_dc. The specific principles are beyond the scope of this paper and are referred to the references (Nejabatkhah et al., 2018; Wang et al., 2018). Among them, ILC can be divided into different operating modes according to different control objectives.

The different operating modes of ILC are realized by adjusting the equivalent impedance zILC of ILC. Different zILC corresponds to different operating modes. The switching between the different operating modes of ILC is determined by the imbalance degree of u_ac, i_ILC and the ripple ratio of u_dc. B_iILC represents the unbalance degree of i_ILC. B_uac represents the unbalance degree of u_ac. R_udc represents the ripple ratio of u_dc. B_iILC-up represents the upper limit of B_iILC. B_uac-up represents the upper limit of B_uac. R_udc-up represents the upper limit of R_udc. When B_iILC is greater than B_iILC-up, which means that the current imbalance of ILC exceeds the upper limit, ILC needs to switch to current imbalance compensation mode. Other situations are similar. The situation that two or three of i_ILC, u_ac, and u_dc exceed the upper limit is defined as an ILC fault state, and it is necessary to switch to the ILC fault state.

B_iILC-stan represents the standard value of B_iILC. B_uac-stan represents the standard value of B_uac. R_udc-stan represents the standard value of R_udc When ILC works in the current unbalance compensation mode, the ILC current balances. The condition that B_iILC equals to B_iILC-stan is satisfied. Other situations are similar and not mentioned here.

5.2 HA-based ILC model

According to the modeling method of part of the MCPS model in Section 4.2, the modeling process of ILC can be obtained as follows.

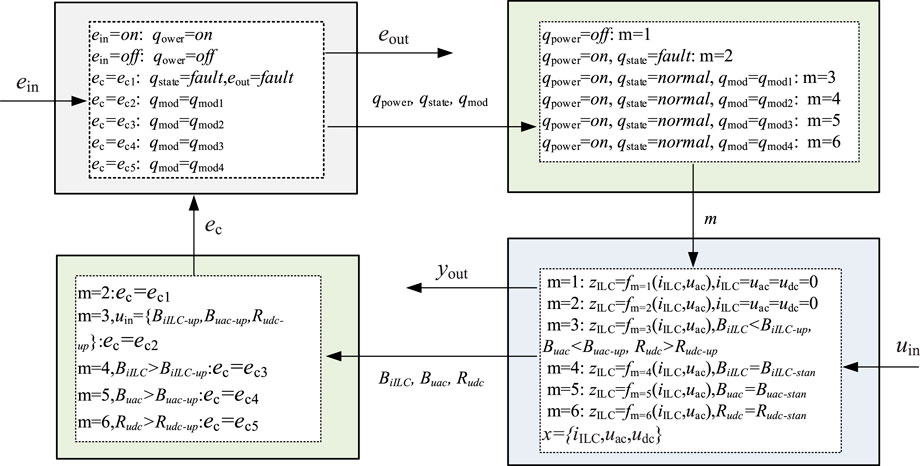
① Determine the input and output variables of ILC:

Input variables include external input control command e_in and continuous input variable u_in. Among them, $e_{in}=\left\{off,on\right\}$ represents the start and stop running commands of ILC, and.

$u_{in}=\left\{B_{iILC-up},B_{uac-up},R_{udc-up},B_{iILC-s\tan },B_{uac-s\tan },R_{udc-s\tan }\right\}$.

The output variables include y_out and the output event signal e_out which indicates ILC failure, among them $y_{out}=\left\{u_{ac},u_{dc},i_{ILC}\right\}$.

② Determine the state variables of the ILC:

Discrete variable $q=\left\{q_{power},q_{state},q_{\mathrm{mod}}\right\}$ includes:

$q_{power}=\left\{off,on\right\}$ represents the running and stopping status of ILC;

$q_{state}=\left\{fault,normal\right\}$ represents the fault and normal running status of the ILC;

$q_{\mathrm{mod}}=\left\{q_{\mathrm{mod}1},q_{\mathrm{mod}2},q_{\mathrm{mod}3},q_{\mathrm{mod}4}\right\}$ represents that ILC respectively works in uncontrolled mode, AC bus voltage negative sequence compensation mode, current imbalance compensation mode and DC bus voltage ripple suppression mode.

Continuous variables $x=\left\{u_{ac},u_{dc},i_{ILC},z_{ILC}\right\}$.

③ Determine the transition function of continuous system and discrete system and the function of interaction between the two: define the value of parameter m as 5, and continuous system has different update functions under different values. The realization of the multi-mode operation of ILC is essentially achieved by adjusting the equivalent impedance z_ILC of ILC, so the update function of the continuous system is the function of adjusting the ILC equivalent impedance z_ILC, that is f_m (z_ILC, i_ILC, u_ac). The discrete system acts on the continuous part by the value of m.

Define five hypersurfaces h_i, which are used to generate five continuous events e_c, and influence the discrete system through e_c. Among them, $e_c=\left\{e_{c1},e_{c2},e_{c3},e_{c4},e_{c5}\right\}$ includes: e_c1 represents the fault of ILC. e_c2 represents uncontrolled event. e_c3 represents ILC current balance. e_c4 represents voltage balance in AC bus. e_c5 represents no ripple in DC bus voltage.

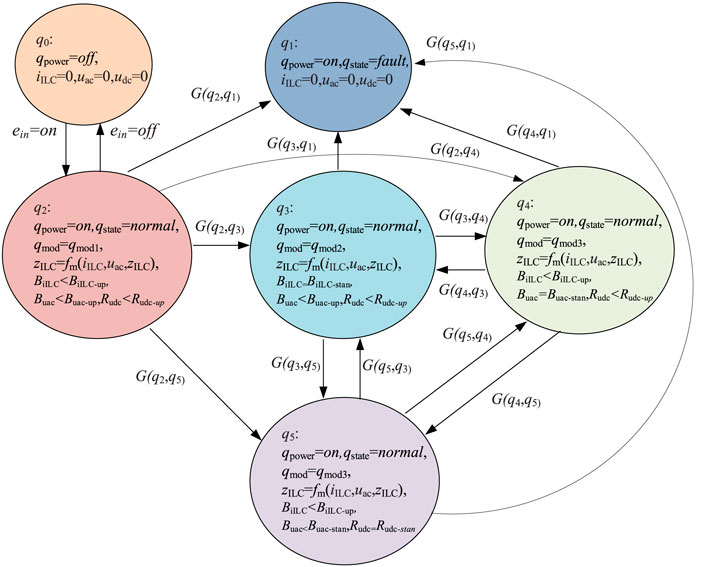
The model of ILC can be obtained as shown in Figure 8 according to the definition of the above elements. The above model can describe the effect of external input on ILC, and the relationship between internal state and input-output. The transition process and conditions of ILC between different states can be described by the model in Figure 9.

FIGURE 8

FIGURE 8. The model of ILC.

FIGURE 9

FIGURE 9. The conversion process of different operating states of ILC.

The conversion conditions between the different modes in Figure 9 are shown in Table 1

TABLE 1

TABLE 1. The conversion conditions of ILC.

5.3 Simulation analysis

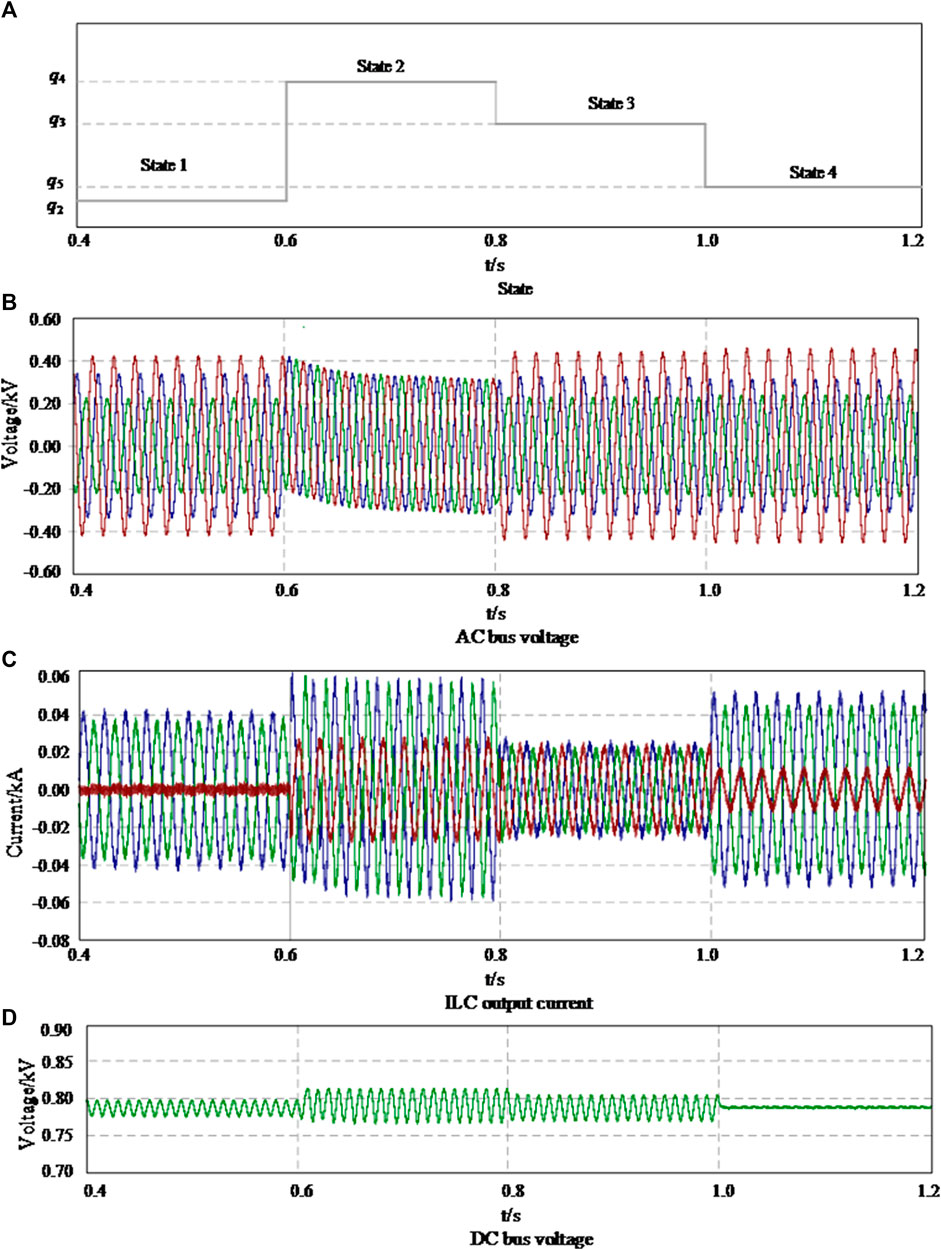
Take the transition from state 3 to state 4 as an example to illustrate the transition process of ILC between different modes. When ILC is in state 3, ILC works in the current imbalance compensation mode. The output current of ILC is basically balanced, as shown in Figure 8C, but the AC bus voltage u_ac is unbalanced, as shown in Figure 8B. The DC bus voltage u_dc produces ripple, as shown in Figure 8D. When B_uac is greater than B_uac-up for some reason, adjust the impedance z_ILC of the ILC to make ILC run from state three to state four. At this time, ILC works in AC bus voltage negative sequence compensation mode, AC bus voltage u_ac is basically balanced, but ILC output current i_ILC becomes unbalanced, and DC bus voltage u_dc produces ripple. The transition process between the other modes is similar. The waveform of the conversion process of ILC in different working states in Figure 7 above is obtained as shown in Figure 10, based on the simulation model shown in Figure 9 built by the PSCAD simulation software. Among them, state 1, state 2, state 3 and State 4 respectively correspond to the uncontrolled mode, ILC output current imbalance compensation mode, AC bus voltage imbalance compensation mode and DC bus voltage ripple suppression mode.

FIGURE 10

FIGURE 10. The conversion process of different operating states of ILC.

Take the transition from state 3 to state 4 as an example to illustrate the transition process of ILC between different modes. When ILC is in state 3, ILC works in the current imbalance compensation mode. The output current of ILC is basically balanced, as shown in Figure 10C, but the AC bus voltage u_ac is unbalanced, as shown in Figure 10B. The DC bus voltage u_dc produces ripple, as shown in Figure 10D. When B_uac is greater than B_uac-up for some reason, adjust the impedance z_ILC of the ILC to make ILC run from state three to state four. At this time, ILC works in AC bus voltage negative sequence compensation mode, AC bus voltage u_ac is basically balanced, but ILC output current i_ILC becomes unbalanced, and DC bus voltage u_dc produces ripple. The transition process between the other modes is similar.

6 Conclusion

To fully reveal the interplay of the cyber system and physical system in the microgrid and present the operation state of each unit in the microgrid and its state transfer process, this paper takes the continuous operation characteristics and discrete process of the microgrid into consideration and establishes the cyber-physical integration modeling of MCPS. The main conclusions are as follows:

1) A generic hierarchical modeling framework applicable to the modeling of the MCPS is proposed, which is divided into the physical device layer and controller layer. And detailed mathematical expressions describing the dynamic characteristics of each layer and the interactions between layers are given, which contributes to a better understanding of the interplay of the information flow and energy flow in the MCPS;

2) The cyber-physical integration modeling of the MCPS is established using HA, which can clearly present the operation state of each unit in the microgrid and its state transfer process. This is beneficial to design the optimal operation state trajectory of the system and explore the optimal control strategy; The model established from the perspective of generality can be extended to any dynamic system of cyber-physical integration, and the model established is more intuitive and easy to extend.

The CPS model of the MCPS established in this paper will be applied in detail in the future work, including the use of the established model to guide the planning of the microgrid system, the design of the optimal system strategy, etc.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

PL: methodology, conceptualization and funding acquisition. FZ: software and writing—original draft preparation. XM: formal analysis. SY: investigation and resources. PY: writing—review and editing. YY: reference searching and visualization. ZZ: validation. CL: supervision. LL: data curation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by The Research Project of Digital Grid Research Institute, China Southern Power Grid under Grant YTYZW20010, and in part by the National High Technology Research and Development Program of China (863 Program) under Grant 2014AA052001.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cheng, Z., and Chow, M. Y. (2020). Resilient collaborative distributed energy management system framework for cyber-physical DC microgrids. IEEE Trans. Smart Grid 11 (6), 4637–4649. doi:10.1109/TSG.2020.3001059

CrossRef Full Text | Google Scholar

Gao, C., Wang, T., Cao, H., Wang, Z., Yu, T., Cheng, R., et al. (2021). Concepts, structure and developments of high-reliability cyber-physical fusion based coordinated planning for distribution system. Front. Energy Res. 9, 697959. doi:10.3389/fenrg.2021.697959

CrossRef Full Text | Google Scholar

Ilic, M. D., Xie, L., Khan, U. A., and Moura, J. M. F. (2010). Modeling of future cyber–physical energy systems for distributed sensing and control. IEEE Trans. Syst. Man. Cybern. A 40 (4), 825–838. doi:10.1109/TSMCA.2010.2048026

CrossRef Full Text | Google Scholar

Li, H., Dimitrovski, A., Song, J. B., Han, Z., and Qian, L. (2014). Communication infrastructure design in cyber physical systems with applications in smart grids: A hybrid system framework. IEEE Commun. Surv. Tutorials 16 (3), 1689–1708. doi:10.1109/surv.2014.052914.00130

CrossRef Full Text | Google Scholar

Li, M., Xue, Y., Ni, M., and Li, X. (2020). Modeling and hybrid calculation architecture for cyber physical power systems. IEEE Access 8 (99), 138251–138263. doi:10.1109/ACCESS.2020.3011213

CrossRef Full Text | Google Scholar

Lin, T., Chen, Z., Zheng, C., Huang, D., and Zhou, S. (2021). Fault diagnosis of lithium-ion battery pack based on hybrid system and dual extended Kalman filter algorithm. IEEE Trans. Transp. Electrific. 7 (1), 26–36. doi:10.1109/tte.2020.3006064

CrossRef Full Text | Google Scholar

Nejabatkhah, F., Li, Y., and Sun, K. (2018). Parallel three-phase interfacing converters operation under unbalanced voltage in hybrid AC/DC microgrid. IEEE Trans. Smart Grid 9 (2), 1310–1322. doi:10.1109/TSG.2016.2585522

CrossRef Full Text | Google Scholar

Petreczky, Mihály, and Schuppen, J. H. V. (22972010). Realization theory for linear hybrid systems. IEEE Trans. Autom. Contr. 55 (10), 2282–2297. doi:10.1109/tac.2010.2044258

CrossRef Full Text | Google Scholar

Poovendran, R. (2010). Cyber–physical systems: Close encounters between two parallel worlds [point of view]. Proc. IEEE 98 (8), 1363–1366. doi:10.1109/JPROC.2010.2050377

CrossRef Full Text | Google Scholar

Wang, T., Nian, H., Zhu, Z. Q., Ding, L., and Zhou, B. (2018). Flexible compensation strategy for voltage source converter under unbalanced and harmonic condition based on a hybrid virtual impedance method. IEEE Trans. Power Electron. 33 (9), 7656–7673. doi:10.1109/TPEL.2017.2768381

CrossRef Full Text | Google Scholar

Wang, Y., Liu, D., and Sun, C. (2017). A cyber physical model based on a hybrid system for flexible load control in an active distribution network. Energies 10 (3), 267. doi:10.3390/en10030267

CrossRef Full Text | Google Scholar

Wei, J., Kundur, D., Zourntos, T., and Butler-Purry, K. L. (2014). A flocking-based paradigm for hierarchical cyber-physical smart grid modeling and control. IEEE Trans. Smart Grid 5 (6), 2687–2700. doi:10.1109/TSG.2014.2341211

CrossRef Full Text | Google Scholar

Xin, S., Guo, Q., Sun, H., Zhang, B., Wang, J., and Chen, C. (2015). Cyber-physical modeling and cyber-contingency assessment of hierarchical control systems. IEEE Trans. Smart Grid 6 (5), 2375–2385. doi:10.1109/tsg.2014.2387381

CrossRef Full Text | Google Scholar

Xin, S., Guo, Q., Sun, H., Zhang, B., Wang, J., and Chen, C. (2017). Cyber-physical modeling and cyber-contingency assessment of hierarchical control systems. IEEE Trans. Smart Grid 6 (5), 2375–2385. doi:10.1109/TSG.2014.2387381

CrossRef Full Text | Google Scholar

Xu, L., Guo, Q., Yang, T., and Sun, H. (2019). Robust routing optimization for smart grids considering cyber-physical interdependence. IEEE Trans. Smart Grid 10 (5), 5620–5629. doi:10.1109/TSG.2018.2888629

CrossRef Full Text | Google Scholar

Xue, Y., and Yu, X. (2017). Beyond smart grid—Cyber–physical–social system in energy future [point of view]. Proc. IEEE 105 (12), 2290–2292. doi:10.1109/JPROC.2017.2768698

CrossRef Full Text | Google Scholar

Yu, W., Xue, Y., Luo, J., Ni, M., Tong, H., and Huang, T. (2016). An UHV grid security and stability defense system: Considering the risk of power system communication. IEEE Trans. Smart Grid 7 (1), 491–500. doi:10.1109/TSG.2015.2392100

CrossRef Full Text | Google Scholar

Zonouz, S., Davis, C. M., Davis, K. R., Berthier, R., Bobba, R. B., and Sanders, W. H. (2014). Socca: A security-oriented cyber-physical contingency analysis in power infrastructures. IEEE Trans. Smart Grid 5 (1), 3–13. doi:10.1109/TSG.2013.2280399

CrossRef Full Text | Google Scholar