- 1School of Mathematics and Statistics, Central South University, Changsha, China
- 2School of Mathematics and Statistics, Hunan First Normal University, Changsha, china
Facing the rapidly changing domestic and foreign futures markets, how to accurately and immediately predict the price trend of crude oil futures in order to avoid the risks caused by price fluctuations is very important for all participants in the crude oil futures market. Based on the 5-min high-frequency trading data of China’s crude oil futures market in recent 3 years, this paper uses the EMD-MFDFA model combined with multifractal detrended fluctuation analysis (MF-DFA) and empirical mode decomposition unsupervised K-means clustering and Gaussian mixture model (GMM) to identify the risk status of each trading day. Further, Support vector machine (SVM), extreme gradient lifting (XGBoost) and their improved algorithms are used to predict the risk state of China’s crude oil futures market. The empirical results are as follows: first, There are obvious multifractal features in the return rate series of China’s crude oil futures market and its single trading day; Second, compared with the traditional SVM model, the improved Twin Support Vector Machine (TWSVM) based on solving the sample imbalance issue has better prediction ability for China’s crude oil futures risk.; Third, The XGBoost has a great impact on the prediction of China’s crude oil risk, and the Focal-XGBoost with focal loss function performs the best in predicting the risk of China’s crude oil futures market.
Introduction
With the rapid development of economy, energy issues have become the focus of the world. Energy is indispensable to the world economic development, and crude oil plays an important role in the energy market. According to the 2019–2020 Blue Book of China’s Oil and Gas Industry Development Analysis and Prospect Report, China ranks among the top in both crude oil imports and consumption. Specifically, China’s crude oil imports reached 506 million tons in 2019, with a year-on-year growth of 9.5%, and its external dependence reached 70.8%. In terms of crude oil consumption, China consumed 696 million tons in 2019, with a year-on-year growth of 6.8%. The data indicate that the crude oil market has a huge impact on China’s energy economic market, and its price fluctuation often brings huge consequences.
With the rapid development of economy, energy issues have become the focus of the world. Energy is indispensable to the world economic development, and crude oil plays an important role in the energy market. According to the 2019–2020 Blue Book of China’s Oil and Gas Industry Development Analysis and Prospect Report, China ranks among the top in both crude oil imports and consumption. Specifically, China’s crude oil imports reached 506 million tons in 2019, with a year-on-year growth of 9.5%, and its external dependence reached 70.8%. In terms of crude oil consumption, China consumed 696 million tons in 2019, with a year-on-year growth of 6.8%. With the sustained and rapid growth of China’s economy, the demand for crude oil import and consumption is increasing, the fluctuation of crude oil price has an increasing impact on China.
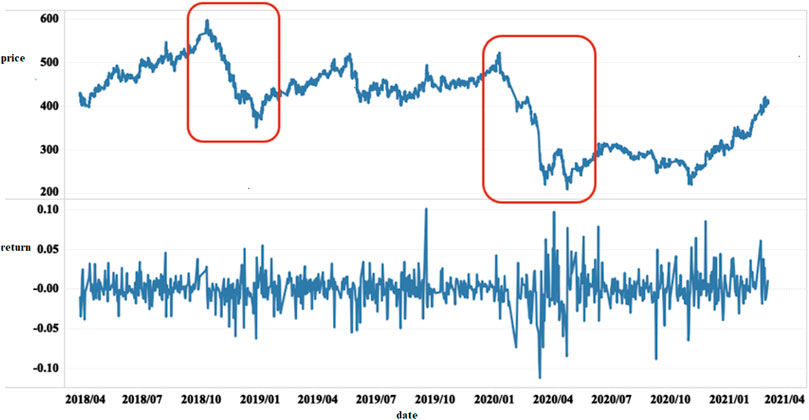
After years of development, the crude oil market, which is closely related to the economic development of each country, has formed a relatively authoritative price system, and its supply and demand as well as trade are carried out in the global scope. Before the official launch of Chinese crude futures, West Texas Intermediate (WTI) of the United States and Brent of the United Kingdom dominated the pricing system for global oil prices. After 17 years of careful planning, China’s crude oil futures market was officially listed on the Shanghai International Energy Exchange on 26 March 2018, denominated in RMB, and filled the gap of domestic crude oil futures market. Less than half a year after listing, China’s crude oil futures trading volume has reached 17 million contracts, accounting for 12% of the global crude oil futures market volume, and its accumulated trading volume reached 8.57 trillion yuan, ranking among the top three in the world. As can be seen from the data, China’s crude oil futures market is developing rapidly. Up to now, China’s crude oil futures market has exceeded 6% of the international market share, and the market activity has been continuously improved, becoming the third largest crude oil futures variety in the world after WTI and Brent.
China’s oil futures is of great significance to the global oil futures market. It sets a benchmark for Asian oil futures markets and provides a channel for Chinese companies to hedge their oil consumption and avoid risks. At the same time, the establishment of a crude oil price benchmark level that reflects the relationship between demand and supply in China and the Asia-Pacific market has filled the gap in the existing international crude oil pricing system and increased China’s participation in the international market. However, compared with the mature crude oil futures market, China’s crude oil futures market, which has been established for a short time, has many aspects to be improved and the demand for risk aversion has become increasingly urgent. Therefore, it is necessary to study the risk status of China’s crude oil futures market from the perspective of market price fluctuation.
However, traditional risk research models, such as VaR (Value at Risk), are mainly based on the efficient market hypothesis (EMH) proposed by Fama. EMH believes that investors can respond to information rationally and linearly, so market prices can timely and fully reflect information changes in the system, that is, prices in the financial market have no long-term memory, and price fluctuations are unpredictable. However, a lot of research found that financial market usually shows nonlinear structural characteristics, and its complex operation mechanism, which cannot reflect the actual situation of the market, is contrary to the efficient market hypothesis. Therefore (Altman, 1967), proposed the nonlinear fractal theory for measuring financial investment risk. Further (Peters, 1994a), proposed the Fractal Market Hypothesis (FMH) on the basis of Mandelbrot’s theory. From the practical point of view, he regarded the capital market as a complex nonlinear dynamic system with the characteristics of interaction and self-adaptability. Therefore, FMH, with the characteristics of interaction and self-adaptability, can better describe the complexity of the market, analyze the nonlinear dynamic characteristics of market price fluctuations, measure the impact of information on prices, and explore the predictability of the market. A large number of studies also show that fractal features are indeed universal in financial markets.
Furthermore, with the development of computer technology, machine learning algorithms, such as Decision Tree, Support Vector Machine (SVM) and Artificial Neural Network (ANN) came into being. With the further development of technology, the integration algorithm, which combines several weak learners into strong learners, has received more and more attention. The main ways to synthesize weak learners are bagging, boosting and stacking. For example, Random Forest is the representative of bagging algorithm, and Extreme Gradient Boosting (XGBoost) is a boosting algorithm. Machine learning models have been widely used in the research of risk prediction due to their outstanding advantages in dealing with nonlinear complex systems.
Taking China’s crude oil futures market as the research object, this paper introduces the multifractal feature parameters into the machine learning model, and carries out risk status recognition and prediction of China’s crude oil futures market. In the turbulent economic situation, futures with its unique hedging function is favored by more and more investors, and has become a crisis management means to deal with the economic recession. By predicting the risk of China’s crude oil futures market, relevant investors can find the potential risk in advance and formulate preventive and control measures in time, so as to avoid the risk reasonably and reduce the loss to a large extent.
Literature Review
Existing relevant literature mainly focuses on four aspects, namely, the characteristics of crude oil futures, multifractal method, multifractal spectrum parameters and financial market risk prediction.
The first is to study the risk features of crude oil futures. At present, more and more scholars study China’s crude oil futures, China’s crude oil market environment and oil policy. Sun et al. (2018) used GARCH and TARCH models to study the fluctuation characteristics of China’s crude oil futures returns rate based on high-frequency data, and they found that the changes of China’s crude oil futures returns rate in the current as well as the lag period were mainly influenced by itself, and the influence coefficient of one period lag was larger and the influence time was longer. Ji and Zhang (2019) analyzed the initial characteristics of China’s crude oil futures market, laying a good foundation for subsequent studies. Li et al. (2019) proposes a new, novel crude oil price forecasting method based on online media text mining, with the aim of capturing the more immediate market antecedents of price fluctuations, the empirical results suggest that the proposed topic-sentiment synthesis forecasting models perform better than the older benchmark models. Liu et al. (2019a) constructed Copula-POT-CoVaR model to study the Risk Spillover Effect of crude oil market on BRIC stock markets, and found that there was significant risk spillover. Özdurak (2021) constructed DCC-GARCH model to study the spillover effect of crude oil price on clean energy investment, and found that with the rise of oil price, renewable energy investment will also tend to decrease. Weng et al. (2021) proposed a modeling framework, genetic algorithm regularization online extreme learning machine with forgetting factor (GA-RFOS-ELM), to estimate the effects of news during the COVID-19 pandemic on the volatility of crude oil futures which could be effective and efficient in volatility forecasting of crude oil futures.
The second is to study the multifractal method. Since the traditional efficient market theory does not conform to the objective facts, Mandelbrot (Altman, 1967) first proposed the concept of fractal in the 1970s. On this basis, Peters (1994a) proposed the fractal market hypothesis (FMH). R/S method was first proposed by Hurst in hydrological analysis in 1951, and was first used in the analysis of financial time series by Mandelbrot (Mandelbrot and Wheeler, 1983) in 1983. However, the research of Lo (1989) and Peters (1994b), Peters (1996) found that the length of sample interval and the short-term correlation of samples will affect the analysis results of R/s method. In order to solve this defect, Peng et al. (1994) proposed detrended fluctuation analysis (DFA) when studying the chimeric tissue of DNA, which distinguishes local correlation from long-term correlation, so as to remove the pseudo correlation phenomenon, and can effectively analyze the long-term power-law correlation of unstable time series, which is widely used in financial time series analysis. On this basis (Kantelhardt et al., 2002), generalized the DFA method and obtained the multifractal detrended fluctuation analysis (MF-DFA) method. In 2008, podobnik and Stanley (Podobnik and Stanley, 2008; Podobnik et al., 2009) formed detrended cross correlation analysis (DCCA) on DFA method, which expanded it into a method that can measure the long-term correlation of two non-stationary time series. Jiang and Zhou (2011) and others further improved the MF-DCCA method and proposed multifractal detrended moving average correlation analysis (MF-X-DMA) (Wang et al., 2012). Combined statistical moment with multifractal cross-correlation analysis to test the cross multifractality between the two sequences. Ruan et al. (2016) used the price and trading volume data of gold spot and futures to study the cross-correlation and time-varying characteristics of price and trading volume. Zhang et al. (2019) and others studied the multifractal characteristics of bitcoin market with MF-DCCA, and further analyzed the multifractal correlation between bitcoin price and other financial market prices. Feng and Cao (2022) used multifractal detrended cross-correlation analysis (MF-X-DFA) and multifractal detrended partial cross-correlation analysis (MF-DPXA) to explore the fluctuation characteristics of cross-correlation between China and the United States agricultural futures market before and after canceling the price of West Texas medium crude oil futures, as well as the impact and cross-correlation on the market.
The third is to study the multifractal spectrum parameters. In the field of engineering, multifractals are mostly used to extract the characteristics of signals, and then the extracted parameters are used in the research of signal recognition and classification. Li and Xie (2013) identified the multifractal spectrum characteristics of radar signals and discussed the identification mechanism of multifractal spectrum parameters. The empirical study shows that the feature parameters are effective to recognize signals. Li et al. (2020a) verified the validity of multifractal spectral parameters by analyzing the multifractal features of friction signals and quantitatively describing the friction vibration characteristics under different friction states through the calculated spectral parameters. In the field of finance, multifractal parameters have also been widely used. Sun et al. (2001) found that the main parameter
The fourth aspect is the financial market risk prediction research. At present, the risk prediction models of financial market can be divided into two categories: one is the statistical approach, which mainly includes linear models such as univariate, multivariate and logistic regression. The idea of multivariate linear early warning model was first proposed by (Altman, 1967), whose Z-score model is the most classic and representative linear risk prediction model at present. Dong et al. (2019) use the CAViaR method to forecast the oil return risks, and further depict the dynamic and heterogeneous features during the crisis (or non-crisis) period, as well as in different markets via DCC-GARCH models. Latunde et al. (2020) uses the CAPM and some statistical tools (variance, covariance and mean) to study risks on the expected return of investing in four common Deutsche Bank (DB) crude oil assets, the result reveals that DTO-DB Crude oil Double Short has the highest beta risk and highest expected return. And the higher the risk, the higher the expected return, and vice versa, that is, the risk is directly proportional to the expected return. Liu et al. (2019b) extend the Copula-CoVaR models by introducing the Peak-over-Threshold and construct the Copula-POT-CoVaR model to investigate the risk spillover effect from crude oil market to BRICS stock markets. By using the crude oil market and BRICS stock market data from 2006 to 2016 as the sample, the empirical study results show that: there is a significant risk spillover from crude oil market to BRICS stock markets, and the risk of crude oil market explains more than 50 percent of BRICS stock markets’ risk. Li et al. (2021) use the Conditional Autoregressive Value at Risk models (CAViaR) approach to forecast the risk of Bitcoin’s returns, the results show that Bitcoin’s volatility is significantly related to the volatility of the crypto-asset’s return and the main determinants of volatility are speculation, investor attention, market interoperability and the interaction between speculation and market interoperability. Li et al. (2020b) measure the return risks of the cryptocurrencies by using the CAViaR model, the results show that they have similar risk tendencies, the risk spillover directions are highly correlative with the market capitalizations of the cryptocurrencies. However, the statistical approach, which mainly includes linear models, is difficult to describe the nonlinear relationship in the financial market. The second category is the machine learning approach. With the rapid development of machine learning algorithms, many scholars begin to combine computer technology with relevant knowledge of financial markets to do interdisciplinary research on the risk prediction of financial markets, with algorithms such as Support Vector Machine (SVM) and Extreme Gradient Boost (XGBoost). Tam and Kiang (1990) compared the neural network model and the traditional statistical model in predicting the risks of banks, and he found that the prediction accuracy of the BP (back propagation) neural network was higher. Later, in order to make the results more reliable (Tam, 1991), compared the prediction results of the BP neural network with those of other algorithms (such as logistic regression, decision tree and feed-forward artificial neural network), and he found that the prediction effect of the BP neural network was the best. Uthayakumar et al. (2020) proposed a cluster-based classification model, including improved K-means clustering and fitness-scaling chaotic genetic ant colony algorithm (FSCGACA) classification model to predict financial crises. Zhao et al. (2018) used least squares support vector machine (LSSVM) to predict systemic financial risks, and Particle Swarm Optimization (PSO) was used to optimize the parameters of the model, and the results show that LSSVM is better at accurate prediction and generalization. Ma and Lv (2019) took the objective function of machine learning algorithms such as support vector machine and neural network as the basis function to carry out the weighted average, and used the constructed Multi-Lingual Information Access (MLIA) model to predict the credit risk of Internet finance. The empirical results show that this model has a higher prediction accuracy compared with logistic regression. Li and Quan (2019) used BP neural network to predict the financial risks of manufacturing enterprises, optimized the model parameters by using improved particle swarm optimization (IPSO), and established a financial risk prediction model based on the IPSOBP model.
Throughout the above literature, although the existing literature has carried out a large number of studies on the multifractal theory and analysis methods, multifractal spectrum parameters and risk prediction models, there is still room for further research. ① Since China’s crude oil futures market is an emerging market, there are few studies on it at present. Most of the existing research focus on price fluctuations of China’s crude oil futures, or comparison with other markets through econometric models by studying the co-integration relationship, Granger causality relationship or linkage effect between markets. Although (Wang et al., 2011) introduced the multifractal method into the research of China’s crude oil futures market, they did not study the risk of this market from the perspective of multifractal spectrum parameters. ② A large number of existing studies focus on the confirmation and generation mechanism of multifractal features of financial markets, but the achievements of fractal theories applied to financial markets are relatively scattered. Although some scholars have substituted the fractal indirect index (fractal spectral parameter) for variance to measure the financial market risk, there are few studies that combine the multi-fractal parameters with clustering algorithm to carry out pattern recognition of market risk. ③ Although the machine learning method has been introduced into the research of financial market risk prediction, it mainly focuses on the analysis and measurement of the overall risk of the market, instead of using the multi-fractal parameters to predict the risk status of the financial market from the perspective of the multifractal features. In this paper, therefore, with China’s crude oil futures as the research object, we employ the multifractal theory framework and introduce multifractal feature parameters into the machine learning model to identify and predict China’s oil futures market risk, so as to provide relevant investors a more effective reference for risk management by helping them identify potential risks in advance and promptly formulate prevention and control measures.
The marginal contribution of this paper is mainly reflected in the following two aspects. First, this paper studies the multifractal features of China’s crude oil futures market from the perspective of high frequency. This paper calculates the intra-day multifractal spectrum parameters through the improved EMD-MFDFA method, and combines it with the unsupervised clustering algorithm to identify as well as define the risk status of the market in each trading day. Second, this paper adopts SVM and XGBoost as well as their improved algorithms based on sample imbalance issue to predict the risk status of China’s crude oil futures market, so that relevant investors can identify potential risks in advance and formulate prevention and control measures in time.
The overall framework of this paper is as follows: Section 3 analyzes the risk characteristics of China’s crude oil futures market, providing sample data for the risk prediction of energy futures market; Section 4 identifies and measures the risk of China’s crude oil futures market; Section 5 is about the risk prediction of China’s crude oil futures market. The main conclusions of this paper are in Section 6.
Risk Features of China’s Crude Oil Futures Market
Data Sources and Basic Analysis of China’s Crude Oil Futures Market
This paper selects China’s crude oil futures issued in March 2018 as the research object, and the sample data time span is from 26 March 2018 to 1 March 2021, with a total of 73,575 5-min high-frequency trading records of 712 trading days (excluding weekends and holidays; data are from Shanghai Futures Exchange). Data collection starts at 21:00 p.m. on the day before trading and ends at 15:00 p.m. on the day of trading, recording once every 5 min, then 111 pieces of data can be collected on each trading day (Note: the trading time of each trading day is 21:00-02:30, 09:00-11:30, 13:30-15:00).
This paper defines the logarithmic return rate as:
In addition, Table 1 displays the descriptive statistics of sample data. The series skewness and kurtosis shown in the table are obviously not zero, indicating obvious non-normality of both the price series and the return rate series. Specifically, the skewness values of price and returns are both less than 0, and the kurtosis values are greater than 0. According to the skewness value, the distribution of the return rate series is slightly to the left. The kurtosis value indicates that the return rate series presents the characteristic of sharp peak and thick tail. What’s more, the Jarque-Bena (JB) statistic is used to test the normality of the sequence, and it is found that the JB statistic is relatively large, which indicates that the hypothesis of the sequence obeying normal distribution is rejected at the 1% confidence level.
Multifractal Features of China’s Crude Oil Futures Market
Although the MF-DFA method can effectively analyze the multifractal features of non-stationary time series, there are still some shortcomings in this method. Firstly, the MF-DFA method requires the time series to be detrended. Specifically, it is found that when the MF-DFA method is used to segment the whole sequence, the segmented interval length is not always an integral multiple of the original sequence length, so the segmented interval is not always continuous. This uncertainty will lead to the discontinuity of the fitting polynomials of adjacent segmented intervals, which may produce new pseudo-random fluctuation error, and then make the fluctuation function produce a certain deviation, resulting in the distortion of the scale index. Therefore, in this paper, the sliding-window method is adopted to improve the discontinuity problem of the segmented interval, so that the segmentation of the non-overlapping interval is optimized into continuous overlapping interval, and the error caused by the discontinuity of the segmented interval is avoided. Secondly, in the MF-DFA method, the polynomial fitting method is used to estimate the local trend of the sequence, and each interval should be de-trended. But the polynomial fitting needs to determine the order of polynomial artificially in advance, and there is no certain standard for the choice of order, so it is subject to great random interference. Therefore, this paper combines the empirical mode decomposition (EMD) with multifractal detrended fluctuation analysis to improve the shortcomings of MF-DFA. The improved EMD-MFDFA method eliminates the trend term extracted by empirical mode decomposition from the original series, so as to eliminate the trend in the time series and avoid the error caused by the unfixed order of polynomial fitting.
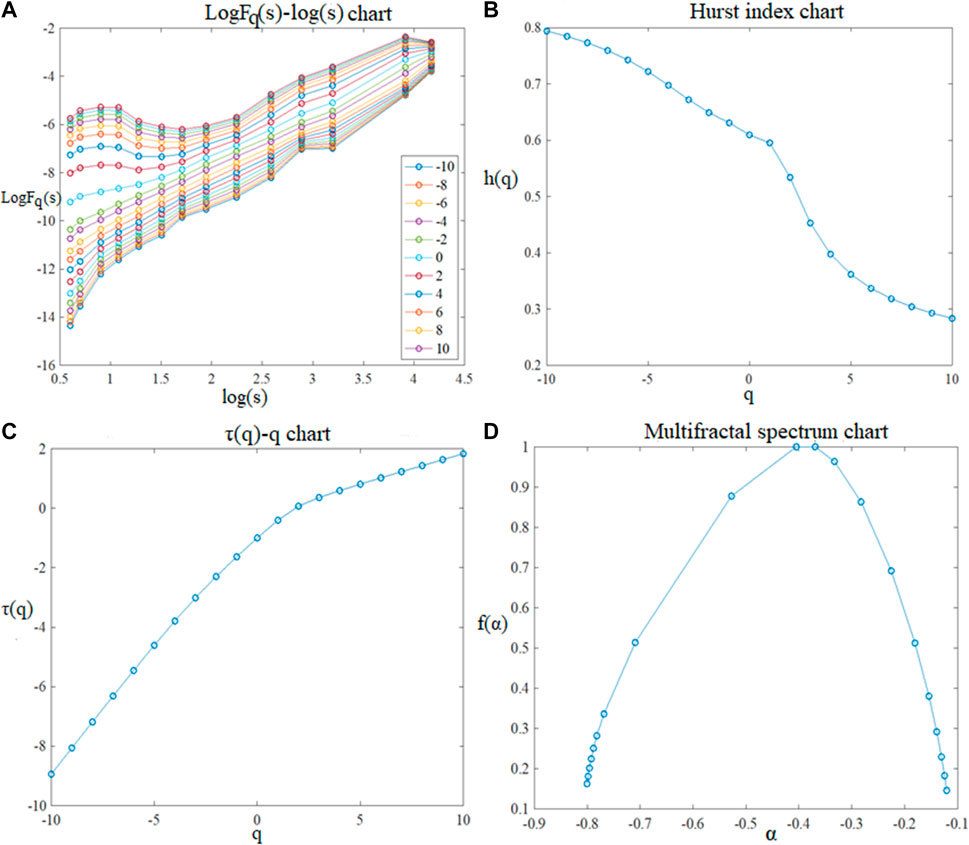
To sum up, this paper combines the advantages of the sliding-window technology and the EMD method to improve the original MF-DFA method, and uses the improved EMD-MFDFA method to analyze the multifractal features of the return rate series of China’s crude oil futures market, which are shown in Figure 2.
The following conclusions can be drawn from Figure 2:
① Figure2A shows the double logarithm relationship between the scale s and the fluctuation function
② As is known to all, when the value of
③ It can also be seen from Figure 2C that there is an obvious nonlinear relationship between the Renyi index
④ Figure 2D shows the multifractal spectrum of the sequence. It can be seen from the figure that the multifractal spectrum changes with
The above analysis of the generalized Hurst index and multifractal spectrum is only a direct and qualitative analysis on multifractal features. On this basis, we also need to carry out quantitative analysis to accurately describe the multifractal degree. Because the multifractal parameters
Since
Risk Identification and Measurement of China’s Crude Oil Futures Market
Risk Identification of China’s Crude Oil Futures Market Based on Fractal Characteristics
The price fluctuation of China’s crude oil futures market has obvious multifractal characteristics. On this basis, this paper divides the whole sample data into daily trading data and calculates the daily multifractal spectrum parameters, so as to effectively identify the daily risk pattern of the market. In order to make the research more rigorous, this paper first analyzes the multifractal features of each trading-day series with the EMD-MFDFA by selecting a trading day at random, and the results are shown in Figure 3.
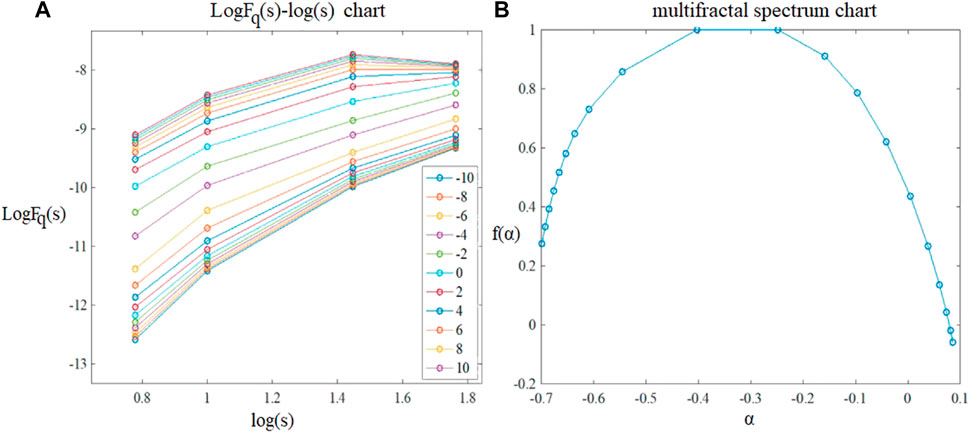
FIGURE 3. Multifractal analysis of the return rate of China’s crude oil futures market under day granularity (taking 2018/05/24 as an example).
Taking the 5-min high-frequency trading data on 24 May 2018 as an example, the double logarithm graph and multifractal spectrum are drawn. It can be seen from Figure 3A that the daily return rate series of China’s crude oil futures market has obvious power-law relationship under different
The definition of
To sum up,
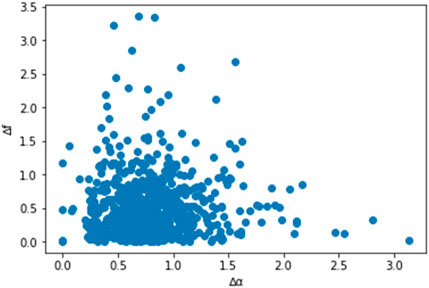
Obviously, the data distribution in the lower left corner of the figure is relatively concentrated. In combination with the above theoretical analysis, it can be seen that the larger the values of
In this paper, the K-means clustering and the Gaussian Mixture Model (GMM) are used to cluster the parameters
In short, the Gaussian Mixture Model (GMM) can be regarded as an optimization of the K-means algorithm. It is not only a kind of technical means commonly used in industry, but also belongs to a generation model. The GMM is to mix the probability distribution of multi-dimensional Gaussian model, so as to fit different sample data sets, so it has strong generalization ability and good fitting effect. In the K-means algorithm, the probability that the sample belongs to each cluster is qualitative, only “yes” or “no,” and the corresponding probability value cannot be output. The GMM method, on the other hand, gives the probability of these sample data points being assigned to each cluster, and it can assign samples to different clusters according to artificial threshold values. Therefore, the information obtained by the GMM method is more. Figure 5 shows the risk pattern recognition results with K-means clustering and GMM clustering algorithms for China’s crude oil futures market. It is also obvious from the clustering results in the figure that the results gathered by the GMM are more accurate and more in line with the actual situation of the market. Therefore, this paper uses the GMM algorithm to identify the risks of China’s crude oil futures market and defines the market risk status into two categories: the normal status and the risk status, providing a label basis for subsequent risk prediction model.
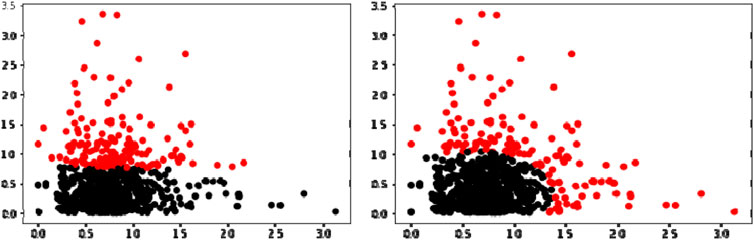
FIGURE 5. Risk identification of China’s crude oil futures market by K-means clustering (left) and GMM clustering (right).
Selection of Risk Feature Indicators
After obtaining the risk status indicator variables of China’s crude oil futures market, it is also necessary to select appropriate feature indicator variables for the market risk prediction model. Since there are many factors that affect market volatility, in order to get as much information as possible, this paper selects the risk feature indicators from two aspects: basic indicators and technical indicators.
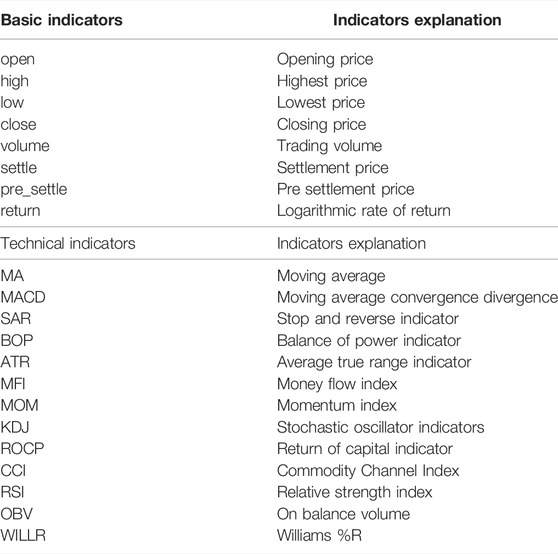
To be specific, This paper selects eight basic indicators (open, high, low, close, volume, settle, pre_settle, return) and 16 technical indicators (MA5, MA10, MACD, SAR, BOP, ATR, MFI, MOM, K, D, J, ROCP, CCI, RSI, OBV, WILLR) as the eigenvectors of the prediction model. Among them, most of the technical indicators in this paper are calculated from the quantified transaction package Ta-Lib in Python. The basic meanings of indicators are shown in Table 3.
Data Processing
Through the above analysis, this paper transforms and processes eight basic indicators to calculate 17 technical indicators, obtaining the feature indicator variables of China’s crude oil futures market in each trading day from 26 March 2018 to 1 March 2021; then, this paper combines the variables with the risk pattern recognition results (label index) in Section 4.2 to form a sample data set of risk prediction model. The feature indicators and the label indicators can be expressed as
Because the selected feature indicators have different orders of magnitude, if they are not processed, the information extraction of the data will be incomplete, and the effect of the model will also be greatly affected. In order to narrow the magnitude gap among feature data and improve the accuracy of model prediction, this paper adopts the Min-Max method to normalize the sample feature data, that is, to make linear changes to the original feature data so that the processed data results can be mapped to a unified interval. The specific formula is as follows:
After data normalization, the prediction accuracy and convergence speed of the model can be improved.
Screening of Risk Feature Indicators
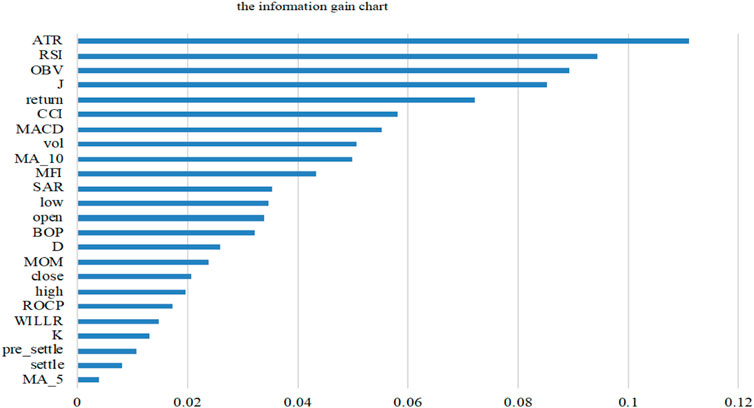
The prediction model is a complex model with multiple indicators. Only by accurately extracting the feature vectors that affect market risks can we make the risk prediction more accurate. It is worth noting that many technical indicators are calculated based on the basic indicators, so the feature indicators we select may have obvious correlation between each other, and the information contained in one indicator may be relatively similar with another. Therefore, choosing more indicators will not make the model better, but will reduce the learning efficiency and increase the time cost of the model. At the same time, there may be some unclassifiable feature indicators in the initial ones. Thus, in order to simplify the complexity of the model and improve its prediction efficiency and accuracy, we need to further screen the selected initial feature indicators, so that the selected ones can contain the information of the majority of features, and achieve the effect of dimensionality reduction and denoising. Therefore, in order to extract the representative risk measurement indicators of China’s crude oil futures market from the initial indicators, this paper adopts the decision tree algorithm and calls the feature_importances interface in the decision tree model to obtain the importance of the features. This method mainly measures whether a feature is important or not from two aspects: first, the total number of features split; Second, the total (average) information gain from features. The more the total number of feature splits or the greater the total (average) information gain, the higher the importance of the feature is, and vice versa. In this paper, information gain will be used to calculate the importance of each feature, and the results are shown as follows:
In the decision tree construction, the larger the information gain of a feature, the stronger the ability of classification, that is, the higher the importance of the feature. Therefore, we need to select features with large information gain from the original features as the feature indicator variables. As can be seen from Figure 6, the top 10 variables of information gain are ATR, RSI, OBV, J, return, CCI, MACD, vol, MA_10 and MFI, so this paper takes them as the feature indicators in the risk prediction model of China’s crude oil futures market.
Risk Prediction of China's Crude Oil Futures Market
Risk Prediction Evaluation Criteria
After the above data processing, this paper obtained a complete data set for risk prediction, including 10 characteristic indicators and label indicators obtained by multi-fractal spectral parameter clustering. According to the statistics, among the 691 trading days included in the sample, 550 trading days are in the normal state and 141 trading days are in the risk status. The proportion of risk samples and normal samples is close to 1:4, so the samples are unbalanced. Therefore, the accuracy of classification can not be used as an evaluation criterion of the quality of the model, and some other evaluation criteria are necessary to measure the training ability and generalization ability of the classification model. Based on the confusion matrix, this paper calculates two comprehensive evaluation indexes as model evaluation criteria to solve the problem of sample imbalance in this paper. The specific meaning of confusion matrix is shown in Table 4:
According to the results of the confusion matrix, the accuracy, precision, recall rate and specificity of the risk prediction model can be calculated. The specific meanings and formulas are as follows:
Accuracy: The proportion of all correctly predicted samples to the total number of samples.
Precision: the proportion of true minorities in all samples predicted to be minorities.
Recall rate: The percentage of a sample that is actually a minority category that is predicted to be a minority category.
Specificity: a measure of how many samples that are actually in the majority class are correctly predicted to be majority.
To sum up, there is a trade-off between accuracy and recall rate, and the balance between the two means that we should try not to miss the majority class while capturing the minority. Therefore, in order to meet the above requirements, the harmonic mean of the two is calculated as a comprehensive index and expressed by F1. According to the characteristics of the harmonic mean which tends to favor the index with a smaller value, when the accuracy and recall rate are both large, the closer the value of F1 is to 1, the better the classification effect of the model. The specific formula of F1 is as follows:
In addition, according to the calculation formulas of recall rate and specificity, recall rate can be used to measure the classification accuracy of the minority class, while specificity can represent the classification accuracy of most classes. Similarly, in order to take both recall rate and specificity into account, the geometric mean of both are constructed as a comprehensive evaluation index G, that is, only when both recall rate and specificity are high, the corresponding G value will be relatively ideal.
To sum up, F1 and G, the two comprehensive evaluation indexes, can be used to measure the prediction ability of the model for samples of the minority class and the comprehensive prediction ability for two classes of samples, respectively. The larger the F1 is, the better the prediction ability of the model is in predicting the minority class samples, and vice versa. If G is large, it indicates that the model has high accuracy in predicting both classes of samples. Therefore, this paper measures the effect of the classification model of unbalanced samples by using two comprehensive evaluation indexes, F1 and G, which are calculated from the confusion matrix.
Selection of Risk Prediction Methods and Comparison of Prediction Results
Based on the sample data set constructed by the feature indicator variables and the label indicator variables constructed above, and considering the advantages of the support vector machine (SVM) model in dealing with such problems, this paper firstly uses the SVM model to forecast the risks of China’s crude oil futures market. The empirical process is completed in Python, mainly using Numpy, Pandas, Sklearn and other libraries. At the same time, in order to make the experimental prediction results more accurate, this paper also uses the five-fold cross validation method, and adopts the StratifiedKFold sampling method when dividing the training set and the test set to ensure that the proportion of normal samples and risk samples in the training set and the test set is consistent with the original data set. In the empirical study, the function SVC in Sklearn library, which is used to classify support vectors, is used to process the sample data in this paper. Considering the imbalance of samples in this paper, the class_weight parameter in the SVC function is set to balanced to make the results of the model more accurate.
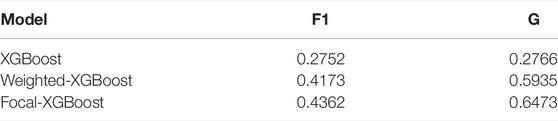
After empirical adjustment, the values of F1 and G are 0.1356 and 0.1387, respectively, both of which are relatively small, indicating that the prediction ability of the model is poor. Although the class_weight parameter has been processed, the decision hyperplane of SVM will still automatically bias to the minority class when processing asymmetric data sets, which will result in weak prediction ability of the model and failure to accurately identify the risk samples in this paper. Therefore, twin support vector machine (TWSVM) is introduced in this paper on the basis of SVM. One decision hyperplane in SVM is extended into two decision hyperplanes, making each hyperplane close to the sample points of this class and far away from the sample points of the other class, so as to overcome the defect of SVM when dealing with the problem of sample imbalance.
The Twin Support Vector Machine (TWSVM) method was first proposed by Khemchandani and Chandra (2007) Its basic idea is similar to the traditional SVM algorithm. It transforms a large classification problem into two small classification problems, so that the constraints of each quadratic programming problem become half of the original. Specifically, two non-parallel decision hyperplanes are determined by solving two related SVM classification problems, and samples are classified according to the closest decision hyperplane of a given sample point. This improvement not only solves the error caused by the sample imbalance to some extent, but also improves the generalization ability and iteration speed of the model.
In order to make the prediction results of the two models comparable, the same training set and test set are also adopted in TWSVM, and the prediction results of SVM and TWSVM are compared, as shown in Table 5:
It can be found from the results in Table 5 that the F1 and G values of the TWSVM in the test set are significantly higher than those of traditional SVM model, that is, the prediction ability of the TWSVM model for samples of the minority class as well as the comprehensive class are better than that of SVM, indicating that TWSVM can effectively solve the problem of sample imbalance to some extent, and has high prediction accuracy.
Risk Prediction Algorithm Selection and Prediction Results Comparison
For the problem of sample imbalance, most existing studies start from the data set level and solve the sample imbalance by over-sampling and under-sampling. However, over-sampling will lead to the problem of over-fitting, and under-sampling will lose important information in the data, so they are not advisable. At the algorithm level, in addition to changing the decision-making ideas of the algorithm (such as the TWSVM method mentioned above), we can start from the loss function of the algorithm. Lin et al. (2017) introduced the Focal loss function and weighted loss functions on the basis of XGBoost, an extreme gradient lifting algorithm proposed by Chen Tianqi, and proposed an algorithm of Imbalance- XGBOOST for unbalanced samples. On this basis, Wang et al. (2020) derived the theory in detail, and verified that the method could effectively solve the problem of sample imbalance through practical application, and expanded the use scenarios of XGBoost. For the convenience of understanding, two loss functions used in the improved algorithm are listed. It should be noted that since this paper is aimed at classification problems, the activation functions are all sigmoid functions.
For the focal loss function:
For the weighted loss function:
Where
In the empirical study of this section, this paper mainly calls the integrated libraries such as Sklearn and Imbalance-XGboost in Python to predict the risks of China’s crude oil futures market. Similarly, the samples used in this section are the same as those in the previous section, and the training set and the test set are also the same. When adjusting the parameters of the model, GridSearch is used to optimize the parameters of the above loss function within the range of (Altman, 1967; Li et al., 2019), and the optimal parameters (
According to the empirical results, both F1 and G values of the original XGBoost are low, indicating that the non-equilibrium samples have a great impact on the prediction effect of the XGBoost algorithm. After the improvement of its loss function, the values of F1 and G are significantly improved, and when the focal loss function is used, the F1 and G of Focal-XGBoost are the best, indicating that Focal-XGBoost could effectively solve the problem of sample imbalance existing in this paper and improve the prediction accuracy of the model.
Conclusion
This paper takes the return rate series of China’s crude oil futures market as the research object, and uses the EMD-MFDFA method to study the multifractal characteristics based on 5-min high-frequency trading data. At the same time, the multifractal analysis is carried out on 111 trading data generated in each trading day, and the calculated daily multifractal spectral parameters are used to analyze the risk status of each trading day. The unsupervised clustering algorithms K-means and Gaussian Mixture Model (GMM) are further used to cluster the obtained spectral parameters. Each trading day is identified as the risk status or the normal status, and the identified risk status is used as the label data and combined with the corresponding technical indicators. SVM, XGBoost and their improved algorithms are used to predict the risks of China’s crude oil futures market, Based on the calculation results of confusion matrix, the prediction effects of each model are compared, and the optimal model is selected to predict the risks of China’s crude oil futures market, so that relevant investors can identify potential risks in advance and formulate prevention and control measures in time. The following conclusions are drawn:
① There are obvious multifractal characteristics in the return rate series of both China’s crude oil futures market and its single trading day, and the calculated daily multifractal parameters can effectively show the fluctuation of the series.
② Due to the imbalance of sample data, twin support vector machine (TWSVM) model has better prediction ability than the traditional support vector machine (SVM) model for the risk prediction of China’s crude oil futures market.
③ The XGBoost algorithm has a great impact on the risk prediction, and the Focal-XGBoost is better for China’s crude oil market risk prediction.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
Conceptualization, YG, SZ, and YL; Data curation, SZ and YL; Formal analysis, YG, SZ, and YL; Methodology, YG, SZ, and YL; Software, SZ; Validation, YG, SZ, and YL; Writing–original draft, YG, SZ, and YL; Writing–review and editing, YG, SZ, and YL.
Funding
This research was funded by Natural Science Foundation of Hunan Province of China (2021JJ30175).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Altman, E. I. (1967). The Prediction of Corporate Bankruptcy: A Discriminant Analysis. Los Angeles: University of California.
Dong, H., Liu, Y., Liu, Y., and Chang, J. (2019). The Heterogeneous Linkage of Economic Policy Uncertainty and Oil Return Risks. Green Financ. 1, 46–66. doi:10.3934/gf.2019.1.46
Feng, Y. S., and Cao, B. M. (2022). Multifractal Fluctuation Analysis of Correlations between Agricultural Futures Markets in China and the US Based on MF-X-DFA and MF-DPXA Methods[J]. Fluctuation Noise Lett. 21 (01). doi:10.1142/s0219477522500067
Ji, Q., and Zhang, D. (2019). China's Crude Oil Futures: Introduction and Some Stylized Facts. Finance Res. Lett. 28, 376–380. doi:10.1016/j.frl.2018.06.005
Jiang, Z. Q., and Zhou, W. X. (2011). Multifractal Detrending Moving-Average Cross-Correlation Analysis. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 84, 016106. doi:10.1103/PhysRevE.84.016106
Kantelhardt, Jan W., Zschiegner, Stephan A., Koscielny-Bunde, Eva, Havlin, Shlomo, Bunde, Armin, and Eugene Stanley, H. (2002). Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Phys. A Stat. Mech. its Appl. 316 (1). doi:10.1016/s0378-4371(02)01383-3
Khemchandani, R., and Chandra, S. (2007). Twin Support Vector Machines for Pattern Classification. IEEE Trans. Pattern Anal. Mach. Intell. 29 (5), 905–910.
Latunde, T., Akinola, L. S., Shina Akinola, L., and Deborah Dare, D. (2020). Analysis of Capital Asset Pricing Model on Deutsche Bank Energy Commodity. Green Financ. 2 (1), 20–34. doi:10.3934/gf.2020002
Li, J. M., Wei, H. J., Wei, L. D., Zhou, D. P., and Qiu, Y. (2020). Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition. Symmetry-Basel 12 (2), 22. doi:10.3390/sym12020272
Li, Q., and Xie, W. (2013). Classification of Aircraft Targets with Low-Resolution Radars Based on Multifractal Spectrum Features. J. Electromagn. Waves Appl. 27 (16), 2090–2100. doi:10.1080/09205071.2013.832394
Li, S., and Quan, Y. (2019). Financial Risk Prediction for Listed Companies Using IPSO-BP Neural Network. Int. J. Perform. Eng. 15 (4), 1209. doi:10.23940/ijpe.19.04.p16.12091219
Li, X., Shang, W., and Wang, S. (2019). Text-based Crude Oil Price Forecasting: A Deep Learning Approach. Int. J. Forecast. 35 (4), 1548–1560. doi:10.1016/j.ijforecast.2018.07.006
Li, Z. H., Dong, H., Floros, C., Charemis, A., and Failler, P. (2021). Re-examining Bitcoin Volatility: A CAViaR-Based Approach. Emerg. Mark. Financ. Trade, 1–19. doi:10.1080/1540496x.2021.1873127
Li, Z., Wang, Y., and Huang, Z. (2020). Risk Connectedness Heterogeneity in the Cryptocurrency Markets. Front. Phys. 8, 243. doi:10.3389/fphy.2020.00243
Lin, T. Y., Goyal, P., Girshick, R., He, K., and Dollár, P. (2017). “Focal Loss for Dense Object Detection,” in Proceedings of the IEEE International Conference on Computer Vision, 2980–2988.
Liu, K., Luo, C., Luo, C., and Li, Z. (2019). Investigating the Risk Spillover from Crude Oil Market to BRICS Stock Markets Based on Copula-POT-CoVaR Models. Quantitative Finance Econ. 3 (4), 754–771. doi:10.3934/qfe.2019.4.754
Liu, K., Luo, C. Q., Luo, C., and Li, Z. (2019). Investigating the Risk Spillover from Crude Oil Market to BRICS Stock Markets Based on Copula-POT-CoVaR Models. Quant. Financ. Econ. 3, 754–771. doi:10.3934/qfe.2019.4.754
Ma, X., and Lv, S. (2019). Financial Credit Risk Prediction in Internet Finance Driven by Machine Learning. Neural Comput. Applic 31 (12), 8359–8367. doi:10.1007/s00521-018-3963-6
Mandelbrot, B. B., and Wheeler, J. A. (1983). The Fractal Geometry of Nature. Am. J. Phys. 51 (3). doi:10.1119/1.13295
Özdurak, C. (2021). Nexus between Crude Oil Prices, Clean Energy Investments, Technology Companies and Energy Democracy. Gf 3 (3), 337–350. doi:10.3934/gf.2021017
Peng, C. K., Buldyrev, S. V., Havlin, S., Simons, M., Stanley, H. E., and Goldberger, A. L. (1994). Mosaic Organization of DNA Nucleotides. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 49 (2), 1685–1689. doi:10.1103/physreve.49.1685
Peters, E. E . (1994). Fractal Market Analysis : Applying Chaos Theory to Investment and Economics. John Wiley & Sons. Vol. 24.
Peters, E. E. (1996). Chaos and Order in the Capital Markets: A New View of Cycles, Prices,and Market Volatility. John Wiley & Sons.
Peters, E. E. (1994). Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. John Wiley & Sons.
Podobnik, B., Horvatic, D., Petersen, A. M., and Stanley, H. E. (2009). Cross-correlations between Volume Change and Price Change. Proc. Natl. Acad. Sci. U. S. A. 106 (52), 22079–22084. doi:10.1073/pnas.0911983106
Podobnik, B., and Stanley, H. E. (2008). Detrended Cross-Correlation Analysis: a New Method for Analyzing Two Nonstationary Time Series. Phys. Rev. Lett. 100 (8), 084102. doi:10.1103/PhysRevLett.100.084102
Ruan, Q., Jiang, W., and Ma, G. (2016). Cross-correlations between Price and Volume in Chinese Gold Markets. Phys. A Stat. Mech. its Appl., 451. doi:10.1016/j.physa.2015.12.164
Sun, H. G., and Li, W. H. (2018). “Analysis of the Fluctuation of Chinese Crude Oil Futures- Based on GARCH-type Model,” in Proceedings of the 2018 3rd International Conference on Modelling, Simulation and Applied Mathematics. Editors A. LuevanosRojas, G. Ilewicz, D. J. Jakobczak, and K. Weller (Paris: Atlantis Press), 160, 110–112. doi:10.2991/msam-18.2018.25
Sun, X., Chen, H. P., Wu, Z. Q., and Yuan, Y. Z. (2001). Multifractal Analysis of Hang Seng Index in Hong Kong Stock Market. Phys. A 291 (1-4), 553–562. doi:10.1016/s0378-4371(00)00606-3
Tam, K. (1991). Neural Network Models and the Prediction of Bank Bankruptcy. Omega 19 (5), 429–445. doi:10.1016/0305-0483(91)90060-7
Tam, K. Y., and Kiang, M. (1990). Predicting Bank Failures: A Neural Network Approach. Appl. Artif. Intell. 4 (4), 265–282. doi:10.1080/08839519008927951
Uthayakumar, J., Metawa, N., Shankar, K., and Lakshmanaprabu, S. K. (2020). Intelligent Hybrid Model for Financial Crisis Prediction Using Machine Learning Techniques. Inf. Syst. E-Bus Manage 18 (4), 617–645. doi:10.1007/s10257-018-0388-9
Wang, C., Deng, C., and Wang, S. (2020). Imbalance-XGBoost: Leveraging Weighted and Focal Losses for Binary Label-Imbalanced Classification with XGBoost. Pattern Recognit. Lett. 136, 190–197.
Wang, J., Shang, P., and Weijie, G. E. (2012). Multifractal Cross-Correlation Analysis Based on Statistical Moments. Fractals 20. doi:10.1142/s0218348x12500259
Wang, Y., Wei, Y., and Wu, C. (2011). Detrended Fluctuation Analysis on Spot and Futures Markets of West Texas Intermediate Crude Oil. Phys. A Stat. Mech. its Appl. 390 (5), 864–875. doi:10.1016/j.physa.2010.11.017
Wei, Y., and Huang, D. S. (2005). Multifractal Analysis of SSEC in Chinese Stock Market: A Different Empirical Result from Heng Seng Index. Phys. A 355 (2-4), 497–508. doi:10.1016/j.physa.2005.03.027
Weng, F., Zhang, H., and Yang, C. (2021). Volatility Forecasting of Crude Oil Futures Based on a Genetic Algorithm Regularization Online Extreme Learning Machine with a Forgetting Factor: The Role of News during the COVID-19 Pandemic. Resour. Policy 73, 102148. doi:10.1016/j.resourpol.2021.102148
Yuan, Y., Zhuang, X.-t., and Jin, X. (2009). Measuring Multifractality of Stock Price Fluctuation Using Multifractal Detrended Fluctuation Analysis. Phys. A Stat. Mech. its Appl. 388 (11), 2189–2197. doi:10.1016/j.physa.2009.02.026
Zhang, X., Yang, L., and Zhu, Y. (2019). Analysis of Multifractal Characterization of Bitcoin Market Based on Multifractal Detrended Fluctuation Analysis. Phys. A Stat. Mech. its Appl., 523. doi:10.1016/j.physa.2019.04.149
Zhao, D. D., Ding, J. C., and Chai, S. C. (2018). Systemic Financial Risk Prediction Using Least Squares Support Vector Machines. Mod. Phys. Lett. B 32 (17), 15. doi:10.1142/s021798491850183x
Keywords: China’s crude oil futures, multifractal, clustering, sample imbalance, risk prediction
Citation: Guo Y, Zhang S and Liu Y (2022) Research on Risk Features and Prediction of China’s Crude Oil Futures Market Based on Machine Learning. Front. Energy Res. 10:741018. doi: 10.3389/fenrg.2022.741018
Received: 14 July 2021; Accepted: 08 June 2022;
Published: 07 July 2022.
Edited by:
Xun Zhang, Academy of Mathematics and Systems Science (CAS), ChinaReviewed by:
Vidya C. T., Centre for Economic and Social Studies (CESS), IndiaNarottam Das, Central Queensland University, Australia
Wendong Yang, Shandong University of Finance and Economics, China
Copyright © 2022 Guo, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yanqiong Liu, c3h5bGl1eXFAaG5mbnUuZWR1LmNu
 Yaoqi Guo1
Yaoqi Guo1 Yanqiong Liu
Yanqiong Liu