Optimality Condition and Distributed Optimization for Economic Dispatch Using a Novel Weighted Incremental Cost Consensus Approach

This research report investigates a novel optimization approach for the economic dispatch problem (EDP) based on the weighted sum of generators’ costs under supply-demand balance. Unlike conventional approaches, we present a distributed optimization approach that ensures optimality using weighted incremental cost (IC) consensus and sign-consensus error convergence. We can apply the optimization of a weighted sum of generators’ costs to address several constraints, such as capacity and environmental constraints, in addition to the supply-demand balance. The proposed distributed weighted incremental cost consensus approach has been applied to the IEEE-30 bus and IEEE-118 bus systems over a communication topology. The results indicate the efficacy of weights to address generation constraints and the convergence of weighted ICs under supply-demand balance.

Introduction

Technological progress and changes in ecological policies around the world are forcing the energy markets to follow distributed generation models (El-Baz et al., 2019; Flore et al., 2019) and (Schubert and Stadelmann, 2015). To this end, economic dispatch becomes a fundamental problem [see and (Guozden et al., 2020; Mao et al., 2019)] in which total power generation cost of all distributed generating units is minimized over a micro-grid (Chansareewittaya, 2018). Most of the existing economic dispatch problem (EDP) algorithms use a centralized approach (Krishnamurthy et al., 2017; McLarty et al., 2019), which however cannot be applied to distributed generation scenarios (Liu et al., 2016; Zhang et al., 2019; Wang et al., 2020). Recently, a lot of work has been focused on solving EDP problem in a distributed scenario. For example, the study in Guodong Liu et al. (2019) developed a distributed energy management system for a public micro-grid to schedule distributed energy resources and energy storage systems, based on price signals. Yun et al. (2019) resolved the EDP in a distributed manner through a simple algorithm that required no particular initialization. The work in Yi et al. (2020) proposed a distributed method for the economic multi-energy system by considering numerous equality and inequality constraints for recurrent renewable generations. The authors in Lü et al. (2020) developed a directed and distributed Lagrangian momentum algorithm that joined the gradient-tracking technique with momentum terms by using nonuniform step-sizes. It has been observed that machine learning and optimization methods have several engineering and biomedical applications, as observed in the recent studies (Rehan and Hong, 2011; Ansari et al., 2019; Wu et al., 2019; Hou et al., 2020; Zafar and Hong, 2020; Zhu et al., 2021). Such bioinspired and learning schemes have their applications in artificial intelligence and adaptive systems (Rehan et al., 2011; Iqbal et al., 2018; Gomez-Tames et al., 2019; Ma et al., 2019; Manzanera et al., 2019; Yang et al., 2019; Chiarelli et al., 2020; Liu et al., 2020; Wei et al., 2020; Dalin Yang et al., 2020).

Recently, consensus algorithms have been applied to attain a distributed EDP (Yun et al., 2019; Wang and Liu, 2020), which are simple to realize and guarantee an optimal solution by respecting various communication topologies in a micro-grid. A robust consensus-based approach has been investigated in Zhang et al. (2016) for studying the potentials of distributed methods over environmental constraints, ramp-rate limit, prohibited zones, and switching topologies, in addition to box and equality constraints. An advanced concept of learning and adaptation has been employed in Zhang et al. (2018) via a two-layer and leader-based approach. In Chen et al. (2019), the authors considered an economical distributed control approach for the battery energy storage system under frequency control, and an incremental cost (IC) consensus algorithm was developed. Wang and Liu (2020) represented two distributed IC consensus-based optimization algorithms to answer EDPs without and with generation constraints via small gain theorem. Chen et al. (2020) presented a distributed consensus approach for cost-effective load dispatch under frequency regulation. The works in Wang et al. (2019), Yu et al. (2020), and Xing et al. (2019) proposed EDP methods under random delay, for time-varying step-sizes, and transmission losses. The role of control theories and Lyapunov analysis (us Saqib et al., 2018; Tang and Li, 2019; Zhao et al., 2019; Gao and Liu, 2020; Santos et al., 2020; Yao et al., 2020) can be useful in attaining optimization issues. The stability analysis, as observed in Dev and Sarkar (2019), Perng et al. (2020), Souza et al. (2020), Xie et al. (2020), and Yin et al. (2020), can be applied to attain coordination in generation systems.

The above-mentioned central, distributed, and IC consensus-based distributed methods consider optimization of total cost of generation, which is the sum of costs of all generating units. It should be noted that rather than achieving optimal generation, optimization of weighted sum of generations is more meaningful, as it can be applied to comply with several constraints, such as capacity constraints, environmental restraints, and other auxiliary restrictions. The idea of inclusion of weights in optimization is interesting, as it can provide freedom to designers for appropriately minimizing the total generation cost and to define and apply user-defined constraints as per requirements of the generation system. However, the solution to this problem is equally challenging for a distributed EDP environment, as the conventional optimality conditions and the conventional consensus methods cannot be applied in this situation. Motivated by these concerns, the present work is a step toward formulating and establishing conditions for distributed EDP with weighted cost function under supply-demand constraints, which can consider various generation constraints as well. Specifically, the contributions in the paper are as follows.

• A new problem of distributed optimization in EDP has been formulated to optimize the weighted costs of generators, for which the conventional EDP can be written as a specific case. To the best of our knowledge, a distributed optimization approach for solving weighted EDP (Eq. 3) has been provided for the first time. The proposed optimization approach is also advantageous, as it can be applied to attain several constraints in a simple manner by adjusting weights.

• Two optimality conditions for the said problem are investigated: The first condition provides the generic optimality condition, based on Lagrangian methods, and it shows that the optimal weighted EDP can be resolved by addressing weighted IC consensus, rather than the conventional IC consensus. The second condition investigates the optimality condition from a distributed optimization point of view over a network, based on sign-consensus error convergence, rather than applying the conventional consensus error.

• A novel protocol for the distributed weighted EDP has been provided. The condition on the protocol parameters for attaining EDP’s optimal solution is provided by applying graph theory and Lyapunov analysis. The proposed weighted EDP has been applied to the IEEE-30 bus and IEEE-118 bus systems, and the comparison of the proposed method with the existing ones is studied.

• It is worth mentioning that the proposed approach supports the signed graphs for the weighted cost optimization. The signed graphs can arise between two generators due to transmission of information via amplification through inverting amplifiers.

• By the application of the recent results in Pourbabak et al. (2020) for optimal power flow (OPF), a modified weighted cost function-based approach is also provided to resolve a more advanced and complicated problem, considering the practical constraints in addition to the cost optimization.

Problem Formulation

The neighborhood connections between generators can be modeled by means of a bidirectional graph $\mathcal{G}=\mathcal{(V,\; E,A)}$, where $\mathcal{V}$, $\mathcal{E}$, and $\mathcal{A}$ represent sets of nodes, edges, and adjacency matrix, respectively. The entries of $\mathcal{A}$ are represented by a_ij to depict communication links between generators. Consider the following equation (Krishnamurthy et al., 2017):

$C_i\left(P_{G_i}\right)={\alpha }_i+{\beta }_i{P}_{G_i}\left(t\right)+{\gamma }_i{P}_{G_i}^2\left(t\right),(1)$

which represents the cost expression of ith power generator with α_i, β_i and γ_i as coefficients. The weighted total cost can be written as

$C_{wt}\left(P_{G_i}\right)=\sum _{i=1}^N{w}_i{C}_i\left(P_{G_i}\right),(2)$

where w_i for i = 1, 2, … , N are positive weights and C_wt shows the weighted cost of generation. In relation (2), we have considered a modified cost function with weights for attaining the constraints. The use of weights is interesting and has found applications in the literature. For instance, weights have been considered in the cost functions (Shadmand et al., 2019) for attaining multiple control objectives for power electronic interfaces. Co-variance weighted nonlinear least-square cost functions are presented in Pintelon et al. (1997) for model identification applications. Time-delay estimation over highly oscillatory objective functions, with applications in sonar, as observed in Wu and Li (1998), has been attained for Cramer–Rao bounds [see also Toh and Eng (2008) for weighted least-square learning]. Even weights have also been used in economic dispatch problem over multiple objective functions of cost and environment (Dong and Wang, 2020), which motivates us to use weights for attaining EDP constraints.

Remark 1 The total generation cost can be written as $C_t\left(P_{G_i}\right)=\sum _{i=1}^N{C}_i\left(P_{G_i}\right)$. Note that the minimization of $C_{wt}\left(P_{G_i}\right)$ can ensure reduction of $C_t\left(P_{G_i}\right)$. If w_i = 1, we have $C_{wt}\left(P_{G_i}\right)=C_t\left(P_{G_i}\right)$, that is, the weighted cost function reduces to the conventional (nonweighted) cost function. The weights can be selected such that $\frac{1}{N}\sum _{i=1}^N{w}_i=1$. Here, the advantage is that these weights can be selected for attaining user-defined requirements. For instance, if a generator is likely to reach its upper generation constraint, its weight can be adjusted to a higher value to give more weight contribution to the minimization of the generator’s cost function. If a generator (say generator 10) is environmental friendly, its weight w₁₀ can be taken smaller for less weight on the optimization of $C_{10}\left(P_{G_{10}}\right)$. Hence, power generation $P_{G_i}$ of a generator i can be reduced by increasing its weight w_i, and vice versa.Consider the problem of minimization of weighted cost of generators under supply-demand constraint for generator capacity constraint, given by

$\left\{\begin{array}{c}\min C_{wt}\left(P_{G_i}\right)=\sum _{i=1}^N{w}_i{C}_i\left(P_{G_i}\right),\hfill \\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}{P}_D=\sum _{i=1}^N{P}_{G_i},\hfill \end{array}\right.(3)$

$P_{G_i}\in \left[\begin{array}{cc}\hfill P_{G_i}^m\hfill & \hfill P_{G_i}^M\hfill \end{array}\right].(4)$

The relation (Eq. 3) represents the proposed optimization problem, aiming to minimize the weighted cost (C_wt) in such a way that the power demand remains equal to summation of generated power by all generators. Condition (Eq. 4) shows that generated power should belong to maximum $(P_{G_i}^M)$ and minimum $(P_{G_i}^m)$ power of generator, called capacity constraint. In the present work, we have considered the minimization of weighted cost function $C_{wt}\left(P_{G_i}\right)$ under the supply demand equality constraint $P_D=\sum _{i=1}^N{P}_{G_i}$. The box constraint of (Eq. 4) is not explicitly considered in the work. Rather, this constraint is indirectly ensured via selection of weights w_i and w_j. Generally, the power generation limits can be determined by the minimum and maximum capacity of a generator, based on the design, technology used, and type and amount of fuel applicable for a distributed generator. These details are provided by the manufacturers/vendors. It should be noted that the weights w_i cannot be unified in the objective function of (Eq. 3), because the box constraint in (Eq. 3) cannot be considered a weighted supply-demand constraint. The optimization problem (Eq. 3) becomes complex owing to different formats of objective function (weighted) and constraints (nonweighted) and due to consideration of distributed as well as dynamic optimization over a graph. Similar to He et al. (2019), the total power generation mismatch (ΔP) is given by

$\mathrm{\Delta }P=P_D-\sum _{i=1}^N{P}_{G_i}.(5)$

If we take the derivative of Eq. 1 with respect to $P_{G_i}$, we obtain the IC of ith unit as

${\eta }_i\left(t\right)=\frac{d{C}_i\left(P_{G_i}\right)}{d{P}_{G_i}}={\beta }_i+2{\gamma }_i{P}_{G_i}.(6)$

Main Results

Investigation of Optimality Condition

This subsection investigates the optimality conditions for the proposed EDP problem in Eq. 3.

Lemma 1 The optimal solution $P_{G_i}^{\ast }$ for the weighted EDP in (Eq. 3) can be attained if

$w_i\frac{d{C}_i\left(P_{G_i}\right)}{d{P}_{G_i}}=w_j\frac{d{C}_j\left(P_{G_j}\right)}{d{P}_{G_j}},\forall i,j=\mathrm{1,2},\dots ,N,(7)$

$P_D=\sum _{i=1}^N{P}_{G_i}.(8)$

Proof Consider the Lagrangian function as

$L\left(P_{G_i},\lambda \right)=\sum _{i=1}^N{w}_i{C}_i\left(P_{G_i}\right)+\lambda \left(P_D-\sum _{i=1}^N{P}_{G_i}\right).(9)$

Taking the derivative of $L\left(P_{G_i},\lambda \right)$ with respect to $P_{G_i}$ and λ, we obtain

$\frac{\partial L\left(P_{G_i},\lambda \right)}{\partial P_{G_i}}=w_i\frac{\partial C_i\left(P_{G_i}\right)}{\partial P_{G_i}}-\lambda =0.(10)$

$\frac{\partial L\left(P_{G_i},\lambda \right)}{\partial \lambda }=P_D-\sum _{i=1}^N{P}_{G_i}=0.(11)$

For optimality condition, we require $\frac{\partial L\left(P_{G_i},\lambda \right)}{\partial P_{G_i}}=0$ and $\frac{\partial L\left(P_{G_i},\lambda \right)}{\partial \lambda }=0$, which lead from (Eq. 10)-(Eq. 11) that

$w_i\frac{\partial C_i\left(P_{G_i}\right)}{\partial P_{G_i}}=\lambda .(12)$

$P_D-\sum _{i=1}^N{P}_{G_i}=0.(13)$

The conditions in Eqs 12 and 13 are equivalent to (Eqs 7, 8), respectively, which completes the proof.

Remark 2 Lemma 1 applies the Lagrangian function approach to provide a generic optimality condition for (Eq. 3). It states that the optimization of weighted EDP (Eq. 3) can be attained by attaining weighted IC consensus (Eq. 7) and supply-demand balance condition (Eq. 8). For w_i = w_j = 1 with i, j = 1, 2, … , N, the conventional IC consensus scheme as in Chen et al. (2019) and Yu et al. (2020) can be derived a specific result.Now, we derive an optimality condition from distributed optimization over a network point of view. Let us define the weighted IC consensus error as

$e_i\left(t\right)=w_i{\eta }_i\left(t\right)-\frac{1}{N}\sum _{j=1}^N{w}_j{\eta }_j\left(t\right).(14)$

Lemma 2 The optimal solution $P_{G_i}^{\ast }$ for the weighted EDP (Eq. 3) can be attained if $e_i(t)=w_i{\eta }_i(t)-\frac{1}{N}\sum _{j=1}^N{w}_j{\eta }_j(t)$ converges to the zero and $\sum _{i=1}^N{P}_{G_i}$ reaches at P_D.

Proof Let us define $e(t)={\left[e_1^T,e_2^T,\dots ,e_N^T\right]}^T$, $\eta (t)=\left[{\eta }_1^T,{\eta }_2^T,\dots ,{\eta }_N^T\right]$, 1_N = [1,1, … ,1]^T ∈ R^N, and $W=\mathrm{diag}\left\{w_1,w_2,\dots ,w_N\right\}$, the condition (Eq. 14) gives

$e\left(t\right)=\left(I-\frac{1}{N}{1}_N{1}_N^T\right)W\eta \left(t\right).(15)$

It can be observed that zero is a simple eigenvalue of $\left(I-\frac{1}{N}{1}_N{1}_N^T\right)$, corresponding to right eigenvector I_N. The remaining eigenvalues are one with multiplicity N − 1. Hence, e(t) = 0 if and only if w_iη_i(t) = w_jη_j(t), for all i, j = 1, 2, … , N. Convergence of e(t) to zero ensures w_iη_i(t) = w_jη_j(t), which is equivalent to (Eq. 7). The other condition is the same as (Eq. 8).

Remark 3 In Lemma 2, we define an error $e_i(t)=w_i{\eta }_i(t)-\frac{1}{N}\sum _{j=1}^N{w}_j{\eta }_j(t)$, the convergence of which leads to an optimal solution of (Eq. 3). Conventionally, when w_i = w_j = 1 with i, j = 1, 2, … , N, the error $e_i(t)={\eta }_i(t)-\frac{1}{N}\sum _{j=1}^N{\eta }_j(t)$ is applied for complete consensus in ICs; however, the proposed weighted EDP does not require the complete consensus, rather it needs a different sign-consensus treatment between ICs of DGs, which means that the signs of ICs of DGs should have a consensus. Thanks to the recently investigated study on sign-consensus (Jiang et al., 2017), which can be applied as a tool to achieve optimal solution in the present case.

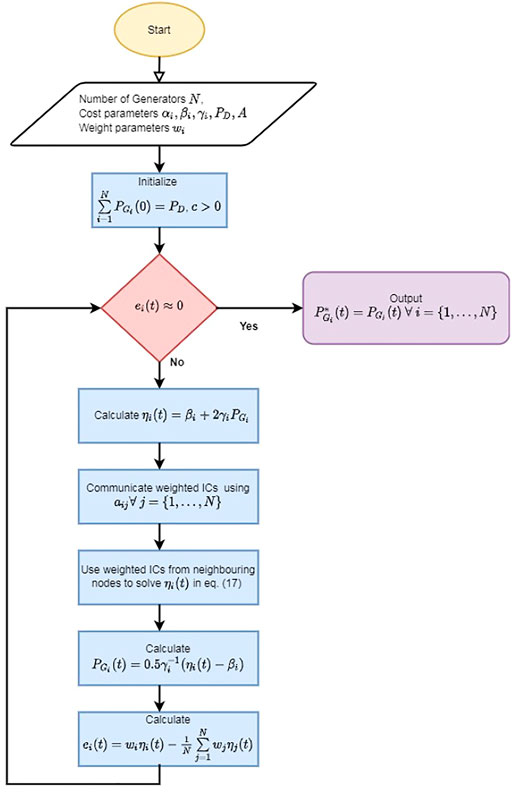
Proposed Distributed Optimization Approach

We take a balanced initial condition that can be achieved as seen in Xing et al. (2019), Yu et al. (2020), and references therein.

$\sum _{i=1}^N{P}_{G_i}\left(0\right)=P_D.(16)$

Assumption 1 The bidirectional graph $\mathcal{G}$ is strongly connected.The proposed optimization protocol has the form

$\left\{\begin{array}{c}{\dot{\eta }}_i\left(t\right)=2c{\gamma }_i\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(w_i{\eta }_i\left(t\right)-w_j{\eta }_j\left(t\right)\right),\hfill \\ H_{ij}=\left\{\begin{array}{cc}\hfill \frac{1}{a_{ij}},\hfill & \hfill \mathrm{i}\mathrm{f}{a}_{ij}\ne 0,\hfill \\ \hfill 0,\hfill & \hfill \mathrm{i}\mathrm{f}{a}_{ij}=0,\hfill \end{array}\right.\hfill \end{array}\right.(17)$

where c is a coupling weight and H_ij is used to normalized the entries a_ij. This normalization can be helpful for normalizing the large or small strengths of connection between nodes. Furthermore, we can have signed graphs with negative entries of a_ij. Practically, signed graphs can appear due to transmitting information with amplification through inverting amplifiers. In such a case, gains H_ij are necessary for normalizing the weights. Owing to the modification of H_ij, the presented approach can be applied to signed graphs. Each generator i can update its IC, η_i(t), by using its own weighted IC, w_iη_i(t), and the weighted IC, w_jη_j(t), of neighboring generator.

Remark 4 The proposed distributed optimization protocol has two distinctions compared to the existing methods (Xing et al., 2019; Yu et al., 2020; Chen et al., 2019). First, the IC of a generator can be updated based on local information of weighted IC (rather than IC), which is applied to resolve weighted EDP (Eq. 3). Second, we have introduced a normalization factor H_ij, through which the proposed approach can be applied to bidirectional (even signed) graphs, while the existing studies are limited to the conventional graphs. Note that in a realistic communication scenario, two generators can share weighted ICs with different strengths, leading to a bidirectional connection. The connection strength can also be negative due to use of inverting amplifiers, often used in signal transmissions.The following theorem provides the optimal solution of (Eq. 3).

Theorem 1 Consider the N generators satisfying Assumption 1 and validating (Eq. 16). The distributed protocol (Eq. 17) for c > 0 ensures convergence of $P_{G_i}$ to the optimal solution $P_{G_i}^{*}$ for the constrained weighted EDP (Eq. 3).

Proof Selecting $\varphi =\sum _{j=1}^N{w}_j{\eta }_j(t)$, we have

$\begin{array}{c}\hfill w_i{\eta }_i\left(t\right)-w_j{\eta }_j\left(t\right)=w_i{\eta }_i\left(t\right)+\varphi -\varphi -w_j{\eta }_j\left(t\right)\hfill \\ \hfill =e_i\left(t\right)-e_j\left(t\right).\hfill \end{array}(18)$

Putting (Eq. 18) in (Eq. 17) obtains

${\dot{\eta }}_i\left(t\right)=2c{\gamma }_i\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(e_i\left(t\right)-e_j\left(t\right)\right).(19)$

Taking the time-derivative of (Eq. 14) leads to

${\dot{e}}_i\left(t\right)=w_i{\dot{\eta }}_i\left(t\right)-\frac{1}{N}\sum _{j=1}^N{w}_j{\dot{\eta }}_j\left(t\right).(20)$

Using (Eq. 19) into (Eq. 20), we have

$\begin{array}{c}\hfill {\dot{e}}_i\left(t\right)=2c{\gamma }_i{w}_i\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(e_i\left(t\right)-e_j\left(t\right)\right)-\frac{2c}{N}\sum _{j=1}^N{\gamma }_j{w}_j\sum _{i=1}^N{H}_{ji}{a}_{ji}\left(e_j\left(t\right)-e_i\left(t\right)\right).\hfill \end{array}(21)$

The last term of Eq. 21 can be evaluated as

$\sum _{j=1}^N{\gamma }_j{w}_j\sum _{i=1}^N{H}_{ji}{a}_{ji}\left(e_j\left(t\right)-e_i\left(t\right)\right)=0.(22)$

Substituting (Eq. 22) into (Eq. 21) leads to

${\dot{e}}_i\left(t\right)=2c{\gamma }_i{w}_i\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(e_i\left(t\right)-e_j\left(t\right)\right).(23)$

For a positive scalar p, consider a Lyapunov function as

$V\left(e_i\left(t\right)\right)=0.25\sum _{i=1}^N{\gamma }_i^{-1}{w}_i^{-1}{e}_i^2.(24)$

Taking the time-derivative of (Eq. 24), we obtain

$\dot{V}\left(e_i\left(t\right)\right)=0.5\sum _{i=1}^N{\gamma }_i^{-1}{w}_i^{-1}{e}_i{\dot{e}}_i.(25)$

From Eq. 23, Eq. 25 becomes

$\dot{V}\left(e_i\left(t\right)\right)=c\sum _{i=1}^N{e}_i\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(e_i\left(t\right)-e_j\left(t\right)\right).(26)$

Under Assumption 1, we have H_ija_ij = H_jia_ji. Let us define a symmetric matrix as $\tilde{\mathcal{L}}={\left[{\tilde{l}}_{ij}\right]}_{N\times N}$, where

${\tilde{l}}_{ij}=\left\{\begin{array}{cc}\hfill -H_{ij}{a}_{ij},\hfill & \hfill i\ne j,\hfill \\ \hfill \sum _{j=1}^N{H}_{ij}{a}_{ij},\hfill & \hfill i=j.\hfill \end{array}\right.(27)$

Using the information of normalized Laplacian into (Eq. 26) leads to

$\begin{array}{c}\hfill \dot{V}\left(e_i\left(t\right)\right)=-c{e}^T\left(t\right)\tilde{\mathcal{L}}e\left(t\right)\le -c{e}^T\left(t\right)\alpha \left(\tilde{\mathcal{L}}\right)e\left(t\right)<0.\hfill \end{array}(28)$

As $\dot{V}(e_i(t))<0$, the convergence of e_i(t) to the origin is attained, that is to say, the first condition in Lemma 2 holds. To consider the second condition, we apply the analysis of (Eq. 17). Under $\bar{\gamma }=\sum _{j-1}^N{\left(2{\gamma }_j\right)}^{-1}$, dividing Eq. 17 by $\bar{\gamma }{\gamma }_i$, we obtain

$\frac{1}{{\gamma }_i\bar{\gamma }}{\dot{\eta }}_i\left(t\right)=\frac{c}{\bar{\gamma }}\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(w_i{\eta }_i\left(t\right)-w_j{\eta }_j\left(t\right)\right).(29)$

Let us assign $\mathrm{\Psi }=\sum _{i=1}^N\frac{1}{{\gamma }_i\bar{\gamma }}{\eta }_i(t)$, its derivative along (Eq. 29) becomes

$\dot{\mathrm{\Psi }}=\frac{c}{\bar{\gamma }}\sum _{i=1}^N\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(w_i{\eta }_i\left(t\right)-w_j{\eta }_j\left(t\right)\right).(30)$

Note that $\sum _{i=1}^N\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(w_i{\eta }_i(t)-w_j{\eta }_j(t)\right)=0$; therefore, $\dot{\mathrm{\Psi }}=0$. It further implies that there exists a constant χ such that Ψ = χ. Consequently, we have

$\sum _{i=1}^N\frac{1}{{\gamma }_i\bar{\gamma }}{\eta }_i\left(t\right)=\chi .(31)$

which by substituting (Eq. 6) implies

$\sum _{i=1}^N\left(\frac{{\beta }_i}{2}+P_{G_i}\left(t\right)\right)=2\bar{\gamma }\chi .(32)$

For investigating total generation from (Eq. 32), we have

$\sum _{i=1}^N{P}_{G_i}\left(t\right)=2\bar{\gamma }\chi -\frac{1}{2}\sum _{i=1}^N{\beta }_i=P_D.(33)$

It shows that the second condition of convergence of $\sum _{i=1}^N{P}_{G_i}$ to P_D is also attained. By the application of Lemma 2, $P_{G_i}$ will converge to $P_{G_i}^{\ast }$, which completes the proof.Although the presented approach in Theorem 1 provides the convergence condition, the rate of convergence has not been investigated in the presented study. Here we provide guidelines to improve the convergence rate. By selecting the larger control parameter c in (Eq. 17), fast convergence of the proposed approach can be attained. However, careful attention should be accounted in selecting the larger gain, as it can cause sensitivity of the algorithm against noises by amplifying their effects. The convergence of the protocol (Eq. 17) can also be faster for the large value of $\alpha (\tilde{\mathcal{L}})$, which can be increased by having more edges (connections between nodes) in a graph topology.The flowchart of the proposed weighted IC consensus approach is shown in Figure 1. After initialization, the value of IC at each node is calculated based on $P_{G_i}$ at the previous iteration. Subsequently, the nodes communicate their IC values to the connected node, where the connections among nodes are defined through an adjacency matrix. A new value of IC and $P_{G_i}$ is calculated by the node based on the weighted ICs from the nodes. Finally, a check is introduced to continuously monitor the convergence of weighted ICs that will ensure the optimal values of $P{G}_{G_i}$, i.e., $P_{G_i}^{\ast }$. The algorithmic form of the distributed optimization approach for weighted IC consensus is also given in Algorithm 1.

FIGURE 1

FIGURE 1. Flow chart of weighted IC consensus approach.

ALGORITHM 1

Algorithm 1. Weighted IC Consensus Algorithm.

Remark 5 Theorem 1 provides the main optimization results for resolving the weighted EDP (Eq. 3). To the best of our knowledge, a distributed optimization approach for solving weighted EDP (Eq. 3) has been provided for the first time. The results are attained by the application of a different sign-consensus theory along with the generation and weighted IC dynamical analysis. The proposed approach is also advantageous as it can be applied to attain several constraints in a simple manner by adjusting weights. The consensus control approaches like Sun et al. (2015) consider the attainment of agents’ same behavior by applying feedback. While the consensus-based optimization methods can be considered the progress of these control approaches for a distributed optimization, an objective function is optimized, like the cost of generation is optimized, and constraints like generation constraint.

Remark 6 In a network, electrical losses over transmission lines can be a challenging problem, which should be considered for a realistic EDP problem. Let P_L be an estimate of the electrical losses in the transmission lines, then we require $P_D+P_L-\sum _{i=1}^N{P}_{G_i}=0$, instead of (Eq. 13). This condition can be attained by simply using the modified initial condition as $\sum _{i=1}^N{P}_{G_i}(0)=P_D+P_L$.

Remark 7 Recently, economic dispatch has been addressed in Zhao et al. (2018) and Shi et al. (2020) for saving the communication bandwidth through an even-triggering mechanism. Another interesting study of Shi et al. (2021) has developed an optimization protocol for exponential convergence. Compared to these results, the presented approach considers an optimization problem by considering a different weighted cost function. Based on the studies Zhao et al. (2018) and Shi et al. (2020), the present approach can be extended for event-triggered communication, rather than the time-triggered approach, for the efficient bandwidth utilization. Furthermore, the presented approach can be extended for exponential rate of the optimization, based on the results of Shi et al. (2021), for controlling the convergence rate parameter.

Extension to OPF Problem

OPF is an advanced optimization problem in micro-grids, the aim of which is to minimize the cost of generated power under EDP constraints along with the practical constraints, like bus voltage limits, bus power limits, and bus losses. Compared with EDP, OPF considers the cost minimization along with implementation aspects of power flow in a grid. Generally, OPF is a complex problem due to 1) additional nonlinear constraints, 2) non-convexity of the new constraints, 3) requirement of more computational resources, and 4) uncertain environment in large-scale systems, as observed in Pourbabak et al. (2019). In addition, attainment of a distributed OPF solution for a distributed optimization issue further complicates this problem, as seen in Pourbabak et al. (2019), Pourbabak et al. (2020), Liu et al. (2017), Yun Liu et al. (2019), Linfeng Yang et al. (2020), and Wang et al. (2017).

Here, we modify the proposed EDP approach in Theorem 1 for OPF by the application of the recent results in Pourbabak et al. (2020) for the weighted cost function, based on weighted IC consensus. Let N_dl, N_g, N_load, and N_b represent the sets of distributed lines, generators, load lines, and all lines over a DC micro-grid. For active generation $P_{G_i}$ and demand $P_{D_i}$ of ith generator, the OPF problem can be represented as

$\min C_{wt}\left(P_{G_i}\right)=\sum _{i=1}^N{w}_i{C}_i\left(P_{G_i}\right),$

such that

$\begin{array}{c}\hfill \sum _{i=1}^N{P}_{D_i}=\sum _{i=1}^N{P}_{G_i},\hfill \\ \hfill P_{net,i}=\left\{\begin{array}{cc}\hfill P_{G_i}-P_{D_i},\hfill & \hfill \forall i\in \left(N_g+N_l\right),\hfill \\ \hfill 0,\hfill & \hfill \forall i\notin \left(N_g+N_l\right),\hfill \end{array}\right.\hfill \\ \hfill P_{net,i}=\sum _{n\in \left(N_b-i\right)}^N{P}_{in},\forall i\in N_b,\hfill \\ \hfill v_i^{\min }\le v_i\le v_i^{\max },\forall i\in N_g\hfill \\ \hfill P_{in}=G_{in}\left(v_i{v}_i-v_i{v}_n\right),\forall i,n\in N_b,\hfill \\ \hfill P_{in}\le P_{in}^{\max },\forall i,n\in N_{dl},\hfill \end{array}(34)$

where v_i denotes the ith generator bus voltage with minimum and maximum limits as $v_i^{\min }$ and $v_i^{\max }$, respectively. G_in represents the conductance of a line between buses i and n. P_net,i shows the net power injected in ith bus. The power flow between i and n buses is represented by P_in with limit $P_{in}^{\max }$. The discretized first-order approximation form of (Eq. 17) with sample time T_s is given as

$\left\{\begin{array}{c}{\eta }_i\left(j,k+1\right)=-{\eta }_i\left(j,k\right)+2c{\gamma }_i{T}_s\sum _{j=1}^N{H}_{ij}{a}_{ij}\left(w_i{\eta }_i\left(j,k\right)-w_j{\eta }_j\left(j,k\right)\right),\hfill \\ H_{ij}=\left\{\begin{array}{cc}\hfill \frac{1}{a_{ij}},\hfill & \hfill \mathrm{i}\mathrm{f}{a}_{ij}\ne 0,\hfill \\ \hfill 0,\hfill & \hfill \mathrm{i}\mathrm{f}{a}_{ij}=0.\hfill \end{array}\right.\hfill \end{array}\right.(35)$

Upon convergence of η_i(j, k + 1) → η_c,i(j) from (Eq. 35), we can determine the generations as

$\begin{array}{c}\hfill {\mu }_{i,mn}\left(j+1\right)={\mu }_{i,mn}\left(j\right)+s_1{\vartheta }_{mn}\left(P_{mn}-P_{mn}^{\max }\right),\hfill \\ \hfill P_{G_i}\left(j\right)=\frac{{\eta }_i\left(j\right)-{\beta }_i+{\mu }_{i,mn}\left(j\right)}{2{\gamma }_i},i\in N_g,\hfill \end{array}(36)$

where s₁ is a small value and ϑ_mn shows sensitivity between m and n buses. Here, μ_i,mn(j) is the state for controlling the power flow limit between two buses. Let us assign X_in = v_iv_n, the following approach for small scalars s₂ and s₃ can be used for validating the practical constraints through OPF (see details in Pourbabak et al. (2020)):

$\begin{array}{c}\hfill X_{in}\left(j+1\right)=X_{in}\left(j\right)+s_2\left(X_{ii}\left(j\right)X_{nn}\left(j\right)-X_{in}\left(j\right)\right),\hfill \\ \hfill \forall i\in N_b,n\in \left(N_b-\left\{i\right\}\right),\hfill \end{array}(37)$

$X_{ii}\left(j+1\right)=\left(P_{G_i}\left(j\right)-P_{D_i}+\sum _{n\in \left(N_b-\left\{i\right\}\right)}^N{G}_{in}{X}_{in}\left(j\right)\right){\left(\sum _{n\in \left(N_b-\left\{i\right\}\right)}^N{G}_{in}\right)}^{-1},(38)$

$\begin{array}{c}\hfill {\eta }_i\left(j+1,k\right)={\eta }_{c,i}\left(j\right)+s_3\left(P_{G_i}\left(j\right)-P_{D_i}\left(j\right)-\sum _{n\in \left(N_b-\left\{i\right\}\right)}^N{G}_{in}\left(X_{ii}\left(j\right)-X_{in}\left(j\right)\right)\right),\hfill \\ \hfill \forall i\in N_b.\hfill \end{array}(39)$

The OPF problem for $\min C_{wt}\left(P_{G_i}\right)=\sum _{i=1}^N{w}_i{C}_i\left(P_{G_i}\right)$ under (Eq. 34) can be resolved by the application of (Eqs 35–39) for a new weighted cost function. In the future, the detailed analysis of such an algorithm along with the practical model for OPF for analyzing the results can be investigated.

Remark 8 The conventional EDP methods (Xing et al., 2019; Yu et al., 2020; Chen et al., 2019) cannot be applied practically to resolve the OPF issue in a distributed way. There are very limited distributed methods, as seen in Pourbabak et al. (2019), Pourbabak et al. (2020), Liu et al. (2017), Yun Liu et al. (2019), Linfeng Yang et al. (2020), and Wang et al. (2017), which deal with the OPF problem over a micro-grid using distributed algorithms. It is worth mentioning that the proposed approach in Theorem 1 has been extended for a distributed OPF protocol by considering these exceptional works.

Simulation Results

Here, we provide the simulation results of the proposed optimization methodology for the IEEE-30 bus system and for a large-scale IEEE-118 bus system. The IEEE-30 bus system is selected to emphasize basic understanding of the proposed technique and for the comparison of our approach with the existing methods. The IEEE-118 bus system has been adapted to test the application of the proposed approach to a complex system and to investigate adjustment in the resultant method for the application to a large-scale system.

Application to IEEE-30 Bus System

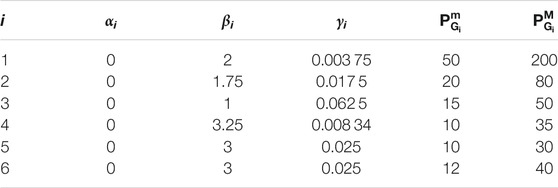
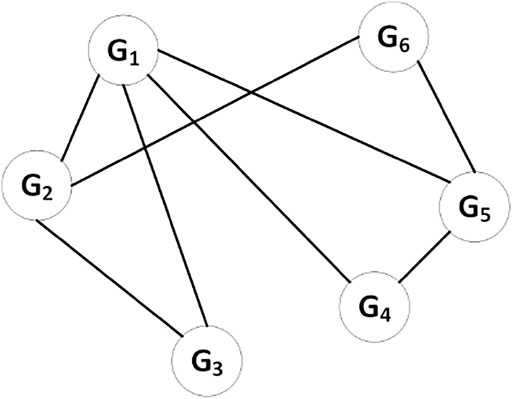
We consider IEEE-30 bus system (He et al., 2019) for testing the proposed weighted EDP approach, which consists of six distributed generators. The simulations are carried out in MATLAB environment, motivated by the approaches of Wang et al. (2021) and Hu et al. (2021), by considering a total demand of P_D = 360 MW. The parameters are taken as α_i = 0 for all generators, β_i are given by 2, 1.75, 1, 3.25, 3, and 3, and γ_i are taken as 0.003 75, 0.017 5, 0.062 5, 0.008 34, 0.025, and 0.025, for i = 1, 2, … , 6, respectively. The minimum and maximum generation constraints are given by sets {50, 20, 15, 10, 10, 12} and {200, 80, 50, 35, 30, 40}. All the cost coefficients of IEEE-30 bus system are shown in Table 1. The graph between DGs of IEEE-30 bus system is shown in Figure 2 (Lewis et al., 2014). The location of generators and the connection between DGs can be represented via an adjacency matrix. The adjacency matrix $\mathcal{A}$ has the form

$\mathcal{A}=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right].(40)$

TABLE 1

TABLE 1. Parameters for IEEE-30 bus system.

FIGURE 2

FIGURE 2. Six generators connected in IEEE-30 bus system.

All the simulations are carried out in MATLAB. The initial conditions for the generation are taken as $P_{G_1}(0)=180$ MW, $P_{G_2}(0)=70$ MW, $P_{G_3}(0)=40$ MW, $P_{G_4}(0)=20$ MW, $P_{G_5}(0)=20$ MW, and $P_{G_5}(0)=30$ MW. In the following, we first apply the conventional approach by taking w_i = 1 ∀ i = {1, 2, … , 6}. Afterward, we show the effectiveness of appropriate weight selection in dealing with the capacity and environmental constraints. By solving Theorem 1 for unity weights, we have selected c = 100.

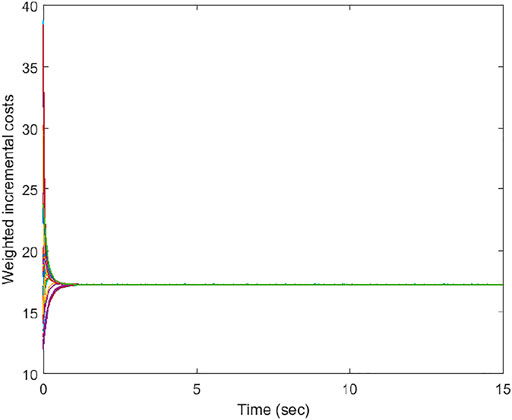
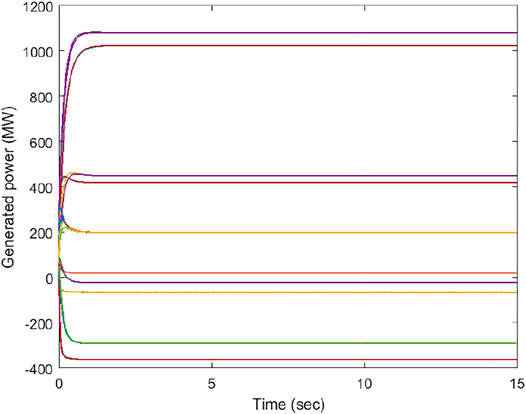
Figure 3 shows the results of weighted ICs for a special case, in which w₁ = w₂ = w₃ = w₄ = w₅ = w₆ = 1. This special scenario is equivalent to the conventional IC consensus scenario depicted in Xing et al. (2019), Yu et al. (2020), and Chen et al. (2019) without generation constraints. The IC curves of all the generators converge rapidly to a common value. For the unity weights, the corresponding generation plots are shown in Figure 4. The results are optimal for $C_t\left(P_{G_i}\right)$; however, generator G₁ crosses the upper limit of 200 MW, violating the constraints in (Eq. 4). Also note that the power generation of G₅ and G₆ converges to 20 MW. As mentioned earlier that the existing methods (Xing et al., 2019; Yu et al., 2020; Chen et al., 2019) are special case of the proposed approach in terms of weights, the same violation of the capacity constraint while achieving IC consensus can be observed. In addition, if G₆ is environmental friendly, we cannot increase its generation under reduced cost using the existing distributed methods.

FIGURE 3

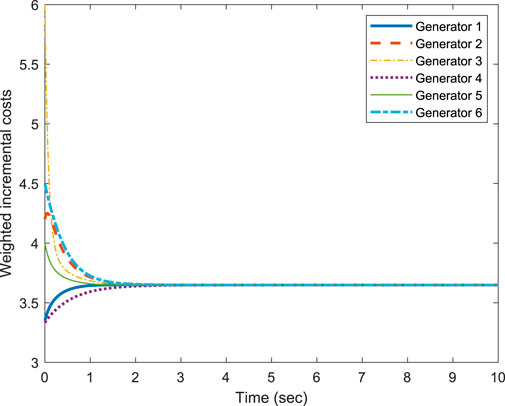
FIGURE 3. Weighted ICs of individual generators versus time (sec) under the conventional approach (unity weights).

FIGURE 4

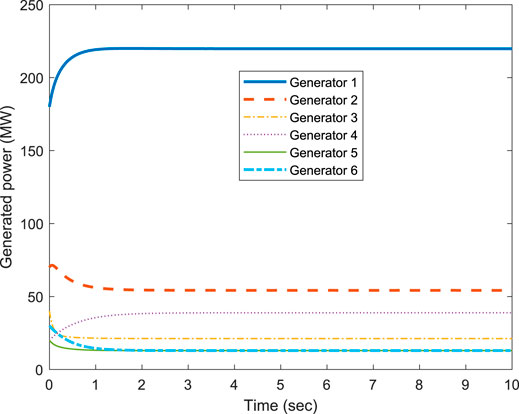
FIGURE 4. Power generations (MW) of individual generators versus time (sec) under the conventional approach (unity weights).

For the verification of the proposed method, we assume that the generator G₆ is environment friendly. Therefore, we increase its generation in addition to (Eq. 4) for G₁. For that, we can select our weights w_i (which is not possible in conventional approaches). Let us choose w₁ = 1.1, w₂ = w₃ = w₄ = w₅ = 1.025 and w₆ = 0.8. The weight w₁ is assigned a higher value to reduce G₁ generation below 200 MW. The smaller value of w₆ is assigned to increase the generation of G₆ due to its environment friendly nature. Under these weights, the results of the proposed approach for weighted ICs and generations are demonstrated in Figure 5 and Figure 6. Clearly, the weighted IC consensus has been achieved as demonstrated in Figure 5. In addition, the steady-state generation for G₁ is around 192 MW, validating the capacity constraint, and for G₆, we are able to increase its generation to around 34 MW by simply reducing the weight to 0.8. Hence, the optimal solution to the proposed weighted EDP (Eq. 3) can be achieved through the proposed methods for validating additional constraints such as capacity and environment constraints.

FIGURE 5

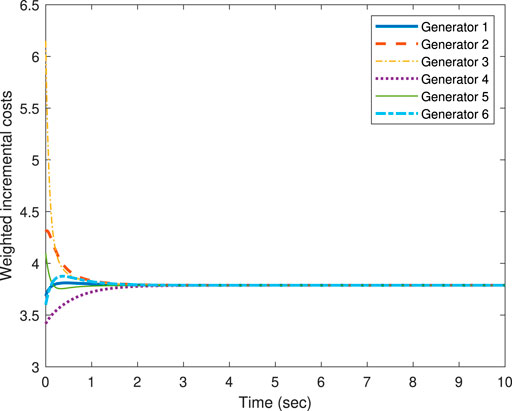
FIGURE 5. Weighted ICs of individual generators versus time (sec) using the proposed approach (via weight selection), w₁ = 1.1, w₂ = w₃ = w₄ = w₅ = 1.025 and w₆ = 0.8.

FIGURE 6

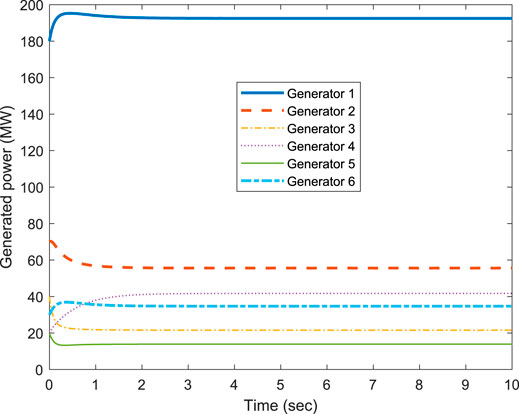
FIGURE 6. Power generations (MW) of individual generators versus time (sec) using the proposed approach (via weight selection), w₁ = 1.1, w₂ = w₃ = w₄ = w₅ = 1.025 and w₆ = 0.8.

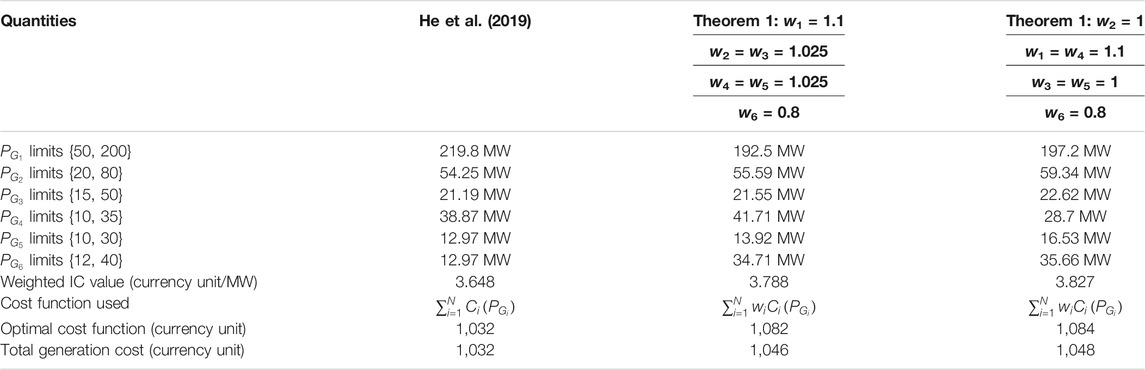
Here, we compare the proposed approach in Theorem 1 with the existing methods of Krishnamurthy et al. (2017), McLarty et al. (2019), and Yu et al. (2015). The conventional approaches (Krishnamurthy et al., 2017) and (McLarty et al., 2019) are based on the central methods, for which data sharing with dispatch center is needed along with central computation. In contrast, the proposed approach applies the distributed computation of the optimal solution to attain a quick solution with several processors, installed at the generator levels, without sharing the data with a central unit. Hence, the distributed computation applied in the proposed method has a simple advantage over Krishnamurthy et al. (2017) and McLarty et al. (2019) for fast computation using distributed processors, based on first-order simple differential equations. In addition, the proposed method also avoids data transmission delays caused by data transmission from/to the central unit, and it ensures data confidentiality as well. The comparison of the proposed method with Yu et al. (2015) [see also similar works (He et al., 2019; Xing et al., 2019; Yu et al., 2020), and (Chen et al., 2019) without weights] is provided in Table 2 for generations, cost functions, incremental costs, and total cost. For this purpose, the total demand is selected as P_D = 360 MW. First, we consider weights as w₁ = 1.1, w₂ = w₃ = w₄ = w₅ = 1.025, and w₆ = 0.8 for the proposed method, as per the previous study. It can be observed that the proposed method respects the generation constraint of generator 1, as $P_{G_1}$ satisfies the generation limits for the optimal solution. In addition, $P_{G_6}$ can be increased through the proposed method for increasing the generation of unit 6. Mainly, the proposed method has a different (weighted) cost function compared to He et al. (2019), which is capable of handling several generation constraints. The optimal solutions of both cost functions are also provided herein. It should be noted that the total cost has been increased from 1,032 to 1,046 units. There is only 1.36% increase in the total generation cost, which is quite minimal for attaining the benefits handling the capacity and environmental constraints.

TABLE 2

TABLE 2. Comparison of the proposed method with the existing study.

In the first experiment for weights w₁ = 1.1, w₂ = w₃ = w₄ = w₅ = 1.025 and w₆ = 0.8, the focus was on considering the generation units 1 and 6, and their weights were considered to be different from the rest of the units. For this weight selection, it can be observed that the generation of unit 4 crosses the maximum limit, which was also observed in the original approach of He et al. (2019). To consider the capacity constraint for generator 4, we have reconsidered the weights w₂ = 1, w₁ = w₄ = 1.1, w₃ = w₅ = 1, and w₆ = 0.8. For the increased weight of unit 4, the capacity constraint is also validated as observed in the last column of Table 2 and as mentioned in Remark 1. It can be concluded that the weights can play a critical role in handling the network constraints. For further studies, we recommend a generation-dependent weight selection via $w_i={\mathrm{\Upsilon }}_i(P_{G_i})$, where the function ${\mathrm{\Upsilon }}_i(P_{G_i})$ can be taken as ${\mathrm{\Upsilon }}_i(P_{G_i})=1$ in the normal operating conditions, ${\mathrm{\Upsilon }}_i(P_{G_i})>1$ can be accounted for reducing the increase in generation, and ${\mathrm{\Upsilon }}_i(P_{G_i})<1$ can be chosen to limit the decrease in generation. Such a generation-dependent selection of weights through functions ${\mathrm{\Upsilon }}_i(P_{G_i})$ requires rigorous analysis and investigation, which can be considered in the future works.

Application to IEEE-118 Bus System

IEEE-118 bus system is a 54 unit, 24 h system with 118 buses and 94 loads (IIT-Power-Group, 2003). The generators in this system are thermal units. It is a large-scale generation system and highly complex model owing to the involvement of constraints on several units. The values for parameters α_i, β_i, γ_i, and minimum $P_{G_i}^m$ and maximum generation $P_{G_i}^M$ capacity are taken from IIT-Power-Group (2003). The range of values is given as follows: ${\alpha }_i\in \left[6.7874.33\right]$, ${\beta }_i\in \left[8.339137.6968\right]$, ${\gamma }_i\in \left[0.00240.0697\right]$, $P_{G_i}^m\in \left[20150\right]$, and $P_{G_i}^M\in \left[5420\right]$.

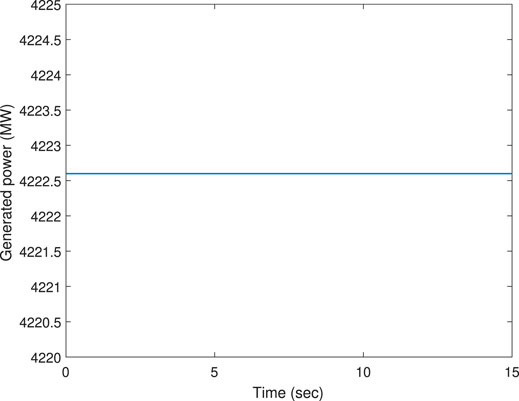
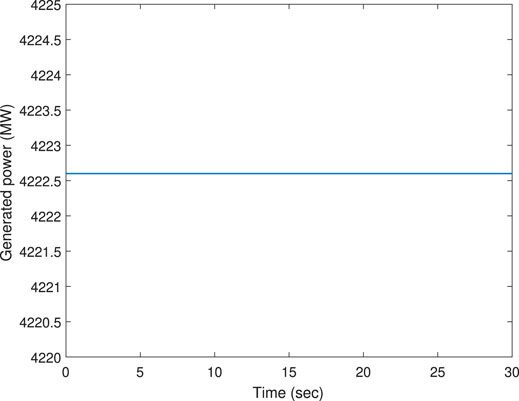
The system operates in three zones, and the parameters have been calculated on the basis of 24 h system at a fuel price of 1 USD/MBtm. For our study, we consider the connections between generators as random to accommodate the stochastic nature of the algorithm, such that the graph remains undirected. The approach has been tested for a demand of P_D = 4,222.59 MW. Each connection strength is taken as either zero or unity. The initial generation conditions are also selected randomly based on uniform distribution. Owing to a large-scale system, it is challenging to design a distributed approach for such a system, ensuring the generation constraints.

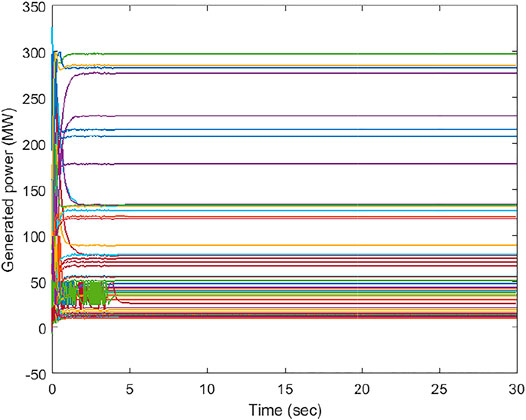
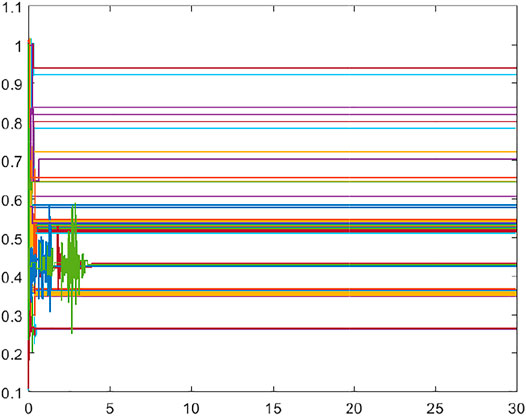
If we select w_i = 1 similar to the methods (Yu et al., 2015) (see also similar works (He et al., 2019; Xing et al., 2019; Yu et al., 2020), and (Chen et al., 2019) without weights), the approach in Theorem 1 provides the relevant graphs in Figure 7, Figure 8, and Figure 9. Figure 7 shows that the IC consensus has been achieved, and Figure 9 demonstrates that the required initial demand does not alter. However, the diagram of Figure 8 reveals that the generation values are beyond the upper or lower limits for many generators. Such a solution cannot be employed for the EDP. The existing methods suggest the saturation of generations (limiting to $P_{G_i}^M$); however, it can reduce the total generation without meeting the demand. The IEEE-118 bus system is a complex system and the results for a distributed handling are not easy for a real-world situation.

FIGURE 7

FIGURE 7. IC consensus for unity weights of IEEE-118 bus system.

FIGURE 8

FIGURE 8. Generation obtained under unity weights for IEEE-118 bus system.

FIGURE 9

FIGURE 9. Total generation under unity weights for IEEE-118 bus system.

To handle this dilemma, we consider two approaches 1) inclusion of weights w_i and 2) updating weights w_i dynamically. The updating of weights can be more meaningful for a complex system like IEEE-118 bus system. The weights are updated dynamically such that if we are going close to the upper limit of a generator, the corresponding weight can be increased, and vice versa. The results obtained through these two modifications are shown in Figures 10–13. The weighted IC consensus is achieved, which is shown in Figure 10 in the case of dynamic weights. The generations remain within the predefined ranges and updated for an optimal solution (Figure 11). The profiles for weights for the proposed modified approach are demonstrated in Figure 12, while the total demand remains unchanged, as per Figure 13. Hence, the use of weights can be more meaningful for a distributed EDP; however, at the same time, it can require more efforts and investigation to attain distributed EDP for complex systems, such as IEEE-118 bus system.

FIGURE 10

FIGURE 10. Weighted IC consensus using the proposed approach for IEEE-118 bus system.

FIGURE 11

FIGURE 11. Generation obtained using the proposed approach for IEEE-118 bus system.

FIGURE 12

FIGURE 12. Dynamic weights using the proposed method for IEEE-118 bus system.

FIGURE 13

FIGURE 13. Total generation using the proposed approach for IEEE-118 bus system.

Conclusion

In this paper, a distributed EDP has been solved under bidirectional communication topology by incorporating weight adjustment. Two optimality conditions are provided: First condition encompasses a generic case and second condition encompasses distributed optimization. A distributed optimization protocol by using weighted ICs has been provided to deal with several constraints. A coupling weight selection approach for optimal solution of the weighted EDP has been derived via the sign-consensus method, supply-demand balance realization, proposed protocol analysis, generation dynamics investigation, and Lyapunov analysis. The proposed method has been applied to IEEE-30 bus and IEEE-118 bus systems, and it was observed that the proposed method can be applied to attain an environmentally friendly solution of EDP. In addition, it can be used for the validation of capacity constraints when compared with the existing schemes. In the future, the proposed study can be extended to deal with the optimization of a more general objective function, containing the environmental effects.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author Contributions

WA, K-SH, and MR conceived of the idea. U-E-HA and WA developed the theoretical framework. U-E-HA, WA, K-SH, and MR verified the analytical methods. U-E-HA and SA performed the simulation results. U-E-HA, WA, and MR wrote the manuscript with support from K-SH and SA. U-E-HA, WA, and K-SH checked the paper. All authors discussed the results and contributed to the final manuscript.

Funding

This work was supported by the Higher Education Commission (HEC) of Pakistan through indigenous PhD scholarship of the first author and by the National Research Foundation (NRF) of Korea under the auspices of the Ministry of Science and ICT, Korea (grant no. NRF-2020R1A2B5B03096000).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ansari, A. H., Cherian, P. J., Caicedo, A., Naulaers, G., De Vos, M., and Van Huffel, S. (2019). Neonatal Seizure Detection Using Deep Convolutional Neural Networks. Int. J. Neur. Syst. 29, 1850011. doi:10.1142/s0129065718500119

PubMed Abstract | CrossRef Full Text | Google Scholar

Chansareewittaya, S. (2018). “Hybrid Ba/ats for Economic Dispatch Problem,” in 2018 22nd International Computer Science and Engineering Conference (ICSEC), Chiang Mai, Thailand, 21–24 November 2018 (IEEE), 1–4. doi:10.1109/icsec.2018.8712630

CrossRef Full Text | Google Scholar

Chen, C., Bao, Y.-Q., Wu, X.-H., Wang, B., and Shen, C. (2019). Battery Energy Storage System Based on Incremental Cost Consensus Algorithm for the Frequency Control. IEEE Access 7, 147362–147372. doi:10.1109/access.2019.2946458

CrossRef Full Text | Google Scholar

Chen, C., Bao, Y.-Q., Wu, X.-H., and Wang, B. (2020). Incremental Cost Consensus Algorithm for On/off Loads to Enhance the Frequency Response of the Power System. IEEE Access 8, 67687–67697. doi:10.1109/access.2020.2985782

CrossRef Full Text | Google Scholar

Chiarelli, A. M., Croce, P., Assenza, G., Merla, A., Granata, G., Giannantoni, N. M., et al. (2020). Electroencephalography-Derived Prognosis of Functional Recovery in Acute Stroke through Machine Learning Approaches. Int. J. Neural Syst. 30, 2050067. doi:10.1142/s0129065720500677

PubMed Abstract | CrossRef Full Text | Google Scholar

Dev, A., and Sarkar, M. K. (2019). Robust Higher Order Observer Based Non-Linear Super Twisting Load Frequency Control for Multi Area Power Systems via Sliding Mode. Int. J. Control. Autom. Syst. 17, 1814–1825. doi:10.1007/s12555-018-0529-4

CrossRef Full Text | Google Scholar

Dong, R., and Wang, S. (2020). New Optimization Algorithm Inspired by Kernel Tricks for the Economic Emission Dispatch Problem with Valve point. IEEE Access 8, 16584–16594. doi:10.1109/ACCESS.2020.2965725

CrossRef Full Text | Google Scholar

El-Baz, W., Tzscheutschler, P., and Wagner, U. (2019). Evaluation of Energy Market Platforms Potential in Microgrids: Scenario Analysis Based on a Double-Sided Auction. Front. Energ. Res. 7, 41. doi:10.3389/fenrg.2019.00041

CrossRef Full Text | Google Scholar

Flore, A., Clausen, M., and Uslar, M. (2019). Migration Paths for Smart Grids and Their Evaluation Using a Case Study. Front. Energ. Res. 7, 134. doi:10.3389/fenrg.2019.00134

CrossRef Full Text | Google Scholar

Gao, Y.-F., and Liu, L. (2020). Lyapunov-Based Triggering Mechanisms for Event-Triggered Control. Int. J. Control. Autom. Syst. 18, 1392–1398. doi:10.1007/s12555-019-0340-x

CrossRef Full Text | Google Scholar

Gomez-Tames, J., Hirata, A., Tamura, M., and Muragaki, Y. (2019). Corticomotoneuronal Model for Intraoperative Neurophysiological Monitoring during Direct Brain Stimulation. Int. J. Neur. Syst. 29, 1850026. doi:10.1142/s0129065718500260

PubMed Abstract | CrossRef Full Text | Google Scholar

Guozden, T., Carbajal, J. P., Bianchi, E., and Solarte, A. (2020). Optimized Balance between Electricity Load and Wind-Solar Energy Production. Front. Energ. Res. 8, 16. doi:10.3389/fenrg.2020.00016

CrossRef Full Text | Google Scholar

He, X., Yu, J., Huang, T., and Li, C. (2019). Distributed Power Management for Dynamic Economic Dispatch in the Multimicrogrids Environment. IEEE Trans. Contr. Syst. Technol. 27, 1651–1658. doi:10.1109/tcst.2018.2816902

CrossRef Full Text | Google Scholar

Hou, H., Zhang, X., and Meng, Q. (2020). Olfactory Eeg Signal Classification Using a Trapezoid Difference-Based Electrode Sequence Hashing Approach. Int. J. Neur. Syst. 30, 2050011. doi:10.1142/s0129065720500112

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, X., Zhang, H., Ma, D., and Wang, R. (2021). A Tngan-Based Leak Detection Method for Pipeline Network Considering Incomplete Sensor Data. IEEE Trans. Instrum. Meas. 70, 1–10. doi:10.1109/TIM.2020.3045843

PubMed Abstract | CrossRef Full Text | Google Scholar

IIT-Power-Group (2003). Ieee-118 Bus System Data by IIT Power Group, Electrical and Computer Engineering Department. Chicago: Illinois Institute of Technology.

Google Scholar

Iqbal, M., Rehan, M., and Hong, K.-S. (2018). Robust Adaptive Synchronization of Ring Configured Uncertain Chaotic FitzHugh-Nagumo Neurons under Direction-Dependent Coupling. Front. Neurorobot. 12, 6. doi:10.3389/fnbot.2018.00006

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., Zhang, H., and Chen, J. (2017). Sign-Consensus of Linear Multi-Agent Systems over Signed Directed Graphs. IEEE Trans. Ind. Electron. 64, 5075–5083. doi:10.1109/tie.2016.2642878

CrossRef Full Text | Google Scholar

Krishnamurthy, S., Tzoneva, R., and Apostolov, A. (2017). Method for a Parallel Solution of a Combined Economic Emission Dispatch Problem. Electric Power Components Syst. 45, 393–409. doi:10.1080/15325008.2016.1265614

CrossRef Full Text | Google Scholar

Lewis, F. L., Zhang, H., Hengster-Movric, K., and Das, A. (2014). Cooperative Control of Multi-Agent Systems: Optimal and Adaptive Design Approaches. London: Springer Publishing Company, Incorporated.

Google Scholar

Liu, J., Chen, W., and Dai, H. (2016). Sampled-Data Based Distributed Convex Optimization with Event-Triggered Communication. Int. J. Control. Autom. Syst. 14, 1421–1429. doi:10.1007/s12555-015-0133-9

CrossRef Full Text | Google Scholar

Liu, Y., Qu, Z., Xin, H., and Gan, D. (2017). Distributed Real-Time Optimal Power Flow Control in Smart Grid. IEEE Trans. Power Syst. 32, 3403–3414. doi:10.1109/TPWRS.2016.2635683

CrossRef Full Text | Google Scholar

Liu, G., Jiang, T., Ollis, T. B., Zhang, X., and Tomsovic, K. (2019). Distributed Energy Management for Community Microgrids Considering Network Operational Constraints and Building thermal Dynamics. Appl. Energ. 239, 83–95. doi:10.1016/j.apenergy.2019.01.210

CrossRef Full Text | Google Scholar

Liu, Y., Li, Y., Xin, H., Gooi, H. B., and Pan, J. (2019). Distributed Optimal Tie-Line Power Flow Control for Multiple Interconnected Ac Microgrids. IEEE Trans. Power Syst. 34, 1869–1880. doi:10.1109/TPWRS.2018.2883407

CrossRef Full Text | Google Scholar

Liu, X., Sun, C.-X., Gao, J., and Xu, S.-Y. (2020). Controllability of Networks of Multiple Coupled Neural Populations: An Analytical Method for Neuromodulation's Feasibility. Int. J. Neur. Syst. 30, 2050001. doi:10.1142/s012906572050001x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lü, Q., Liao, X., Li, H., and Huang, T. (2020). Achieving Acceleration for Distributed Economic Dispatch in Smart Grids over Directed Networks. IEEE Trans. Netw. Sci. Eng. 7, 1988–1999. doi:10.1109/tnse.2020.2965999

CrossRef Full Text | Google Scholar

Ma, X., Yu, N., and Zhou, W. (2019). Using Dictionary Pair Learning for Seizure Detection. Int. J. Neur. Syst. 29, 1850005. doi:10.1142/s0129065718500053

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzanera, O. M., Meles, S. K., Leenders, K. L., Renken, R. J., Pagani, M., Arnaldi, D., et al. (2019). Scaled Subprofile Modeling and Convolutional Neural Networks for the Identification of parkinsonâ€^TMs Disease in 3d Nuclear Imaging Data. Int. J. Neural Syst. 29, 1950010. doi:10.1142/s0129065719500102

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, S., Dong, Z., Schultz, P., Tang, Y., Meng, K., Dong, Z. Y., et al. (2019). A Finite-Time Distributed Optimization Algorithm for Economic Dispatch in Smart Grids. IEEE Trans. Syst. Man, Cybernetics: Syst. 51 (4), 2068–2079. doi:10.1109/TSMC.2019.2931846

CrossRef Full Text | Google Scholar

McLarty, D., Panossian, N., Jabbari, F., and Traverso, A. (2019). Dynamic Economic Dispatch Using Complementary Quadratic Programming. Energy 166, 755–764. doi:10.1016/j.energy.2018.10.087

CrossRef Full Text | Google Scholar

Perng, J.-W., Kuo, Y.-C., and Lu, K.-C. (2020). Design of the Pid Controller for Hydro-Turbines Based on Optimization Algorithms. Int. J. Control. Autom. Syst. 18, 1758–1770. doi:10.1007/s12555-019-0254-7

CrossRef Full Text | Google Scholar

Pintelon, R., Schoukens, J., and Vandersteen, G. (1997). Model Selection through a Statistical Analysis of the Global Minimum of a Weighted Nonlinear Least Squares Cost Function. IEEE Trans. Signal. Process. 45, 686–693. doi:10.1109/78.558486

CrossRef Full Text | Google Scholar

Pourbabak, H., Alsafasfeh, Q., and Su, W. (2020). A Distributed Consensus-Based Algorithm for Optimal Power Flow in Dc Distribution Grids. IEEE Trans. Power Syst. 35, 3506–3515. doi:10.1109/TPWRS.2020.2974957

CrossRef Full Text | Google Scholar

Pourbabak, H., Alsafasfeh, Q., and Su, W. (2019). Fully Distributed Ac Optimal Power Flow. IEEE Access 7, 97594–97603. doi:10.1109/ACCESS.2019.2930240

CrossRef Full Text | Google Scholar

Rehan, M., Hong, K.-S., and Aqil, M. (2011). Synchronization of Multiple Chaotic FitzHugh-Nagumo Neurons with gap Junctions under External Electrical Stimulation. Neurocomputing 74, 3296–3304. doi:10.1016/j.neucom.2011.05.015

CrossRef Full Text | Google Scholar

Rehan, M., and Hong, K.-S. (2011). LMI-Based Robust Adaptive Synchronization of FitzHugh-Nagumo Neurons with Unknown Parameters under Uncertain External Electrical Stimulation. Phys. Lett. A 375, 1666–1670. doi:10.1016/j.physleta.2011.03.012

CrossRef Full Text | Google Scholar

Santos, C., Espinosa, F., Santiso, E., and Gualda, D. (2020). Lyapunov Self-Triggered Controller for Nonlinear Trajectory Tracking of Unicycle-type Robot. Int. J. Control. Autom. Syst. 18, 1829–1838. doi:10.1007/s12555-018-0576-x

CrossRef Full Text | Google Scholar

Schubert, R., and Stadelmann, M. (2015). Energy-Using Durables €" Why Consumers Refrain from Economically Optimal Choices. Front. Energ. Res. 3, 7. doi:10.3389/fenrg.2015.00007

CrossRef Full Text | Google Scholar

Shadmand, M. B., Jain, S., and Balog, R. S. (2019). Autotuning Technique for the Cost Function Weight Factors in Model Predictive Control for Power Electronic Interfaces. IEEE J. Emerg. Sel. Top. Power Electron. 7, 1408–1420. doi:10.1109/JESTPE.2018.2849738

CrossRef Full Text | Google Scholar

Shi, X., Zheng, R., Lin, Z., and Yan, G. (2020). Distributed Optimization for Economic Power Dispatch with Event‐Triggered Communication. Asian J. Control. 22, 2412–2421. doi:10.1002/asjc.2140

CrossRef Full Text | Google Scholar

Shi, X., Zheng, R., Lin, Z., Yang, T., and Yan, G. (2021). An Exponentially Convergent Distributed Algorithm for Resource Allocation Problem. Asian J. Control. 23, 1072–1082. doi:10.1002/asjc.2341

CrossRef Full Text | Google Scholar

Souza, M. B. A., de Melo Honório, L., de Oliveira, E. J., and Moreira, A. P. G. M. (2020). Recursive Approach of Sub-Optimal Excitation Signal Generation and Optimal Parameter Estimation. Int. J. Control. Autom. Syst. 18, 1965–1974. doi:10.1007/s12555-019-0164-8

CrossRef Full Text | Google Scholar

Sun, Q., Han, R., Zhang, H., Zhou, J., and Guerrero, J. M. (2015). A Multiagent-Based Consensus Algorithm for Distributed Coordinated Control of Distributed Generators in the Energy Internet. IEEE Trans. Smart Grid 6, 3006–3019. doi:10.1109/TSG.2015.2412779

CrossRef Full Text | Google Scholar

Tang, L., and Li, D. (2019). Time-varying Barrier Lyapunov Function Based Adaptive Neural Controller Design for Nonlinear Pure-Feedback Systems with Unknown Hysteresis. Int. J. Control. Autom. Syst. 17, 1642–1654. doi:10.1007/s12555-018-0745-y

CrossRef Full Text | Google Scholar

Toh, K.-A., and Eng, H.-L. (2008). Between Classification-Error Approximation and Weighted Least-Squares Learning. IEEE Trans. Pattern Anal. Mach. Intell. 30, 658–669. doi:10.1109/TPAMI.2007.70730

PubMed Abstract | CrossRef Full Text | Google Scholar

us Saqib, N., Rehan, M., Iqbal, N., and Hong, K.-S. (2018). Static Antiwindup Design for Nonlinear Parameter Varying Systems with Application to Dc Motor Speed Control under Nonlinearities and Load Variations. IEEE Trans. Contr. Syst. Technol. 26, 1091–1098. doi:10.1109/TCST.2017.2692745

CrossRef Full Text | Google Scholar

Wang, A., and Liu, W. (2020). Distributed Incremental Cost Consensus-Based Optimization Algorithms for Economic Dispatch in a Microgrid. IEEE Access 8, 12933–12941. doi:10.1109/access.2020.2966078

CrossRef Full Text | Google Scholar

Wang, J., Li, H., and Wang, Z. (2019). Distributed Event‐Triggered Scheme for Economic Dispatch in Power Systems with Uncoordinated Step‐Sizes. IET Generation, Transm. Distribution 13, 3612–3622. doi:10.1049/iet-gtd.2019.0144

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). Soc-based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 36, 7866–7879. doi:10.1109/TPEL.2021.3049241

CrossRef Full Text | Google Scholar

Wang, Y., Wu, L., and Wang, S. (2017). A Fully-Decentralized Consensus-Based Admm Approach for Dc-Opf with Demand Response. IEEE Trans. Smart Grid 8, 2637–2647. doi:10.1109/TSG.2016.2532467

CrossRef Full Text | Google Scholar

Wang, Z., Zheng, L., and Li, H. (2020). Distributed Optimization over General Directed Networks with Random Sleep Scheme. Int. J. Control. Autom. Syst. 18, 2534–2542. doi:10.1007/s12555-018-9543-9

CrossRef Full Text | Google Scholar

Wei, Q., Zhu, S., Wang, Y., Gao, X., Guo, H., and Wu, X. (2020). A Training Data-Driven Canonical Correlation Analysis Algorithm for Designing Spatial Filters to Enhance Performance of Ssvep-Based Bcis. Int. J. Neur. Syst. 30, 2050020. doi:10.1142/s0129065720500203

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Q., Zhang, Y., Liu, J., Sun, J., Cichocki, A., and Gao, F. (2019). Regularized Group Sparse Discriminant Analysis for P300-Based Brain-Computer Interface. Int. J. Neur. Syst. 29, 1950002. doi:10.1142/s0129065719500023

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, R., and Li, J. (1998). Time-Delay Estimation via Optimizing Highly Oscillatory Cost Functions. IEEE J. Oceanic Eng. 23, 235–244. doi:10.1109/48.701196

CrossRef Full Text | Google Scholar

Xie, M., Gulzar, M. M., Tehreem, H., Javed, M. Y., and Rizvi, S. T. H. (2020). Automatic Voltage Regulation of Grid Connected Photovoltaic System Using Lyapunov Based Sliding Mode Controller: A Finite - Time Approach. Int. J. Control. Autom. Syst. 18, 1550–1560. doi:10.1007/s12555-019-0563-x

CrossRef Full Text | Google Scholar

Xing, H., Zeng, P., Mou, Y., and Wu, Q. (2019). Consensus-Based Distributed Approach to Lossy Economic Power Dispatch of Distributed Energy Resources. Int. Trans. Electr. Energ. Syst. 29, e12041. doi:10.1002/2050-7038.12041

CrossRef Full Text | Google Scholar

Yang, D., Hong, K.-S., Yoo, S.-H., and Kim, C.-S. (2019). Evaluation of Neural Degeneration Biomarkers in the Prefrontal Cortex for Early Identification of Patients with Mild Cognitive Impairment: An Fnirs Study. Front. Hum. Neurosci. 13, 317. doi:10.3389/fnhum.2019.00317

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, D., Huang, R., Yoo, S.-H., Shin, M.-J., Yoon, J. A., Shin, Y.-I., et al. (2020). Detection of Mild Cognitive Impairment Using Convolutional Neural Network: Temporal-Feature Maps of Functional Near-Infrared Spectroscopy. Front. Aging Neurosci. 12, 141. doi:10.3389/fnagi.2020.00141

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, L., Luo, J., Xu, Y., Zhang, Z., and Dong, Z. (2020). A Distributed Dual Consensus Admm Based on Partition for Dc-Dopf with Carbon Emission Trading. IEEE Trans. Ind. Inf. 16, 1858–1872. doi:10.1109/TII.2019.2937513

CrossRef Full Text | Google Scholar

Yao, L., Wang, Z., Wang, Q., Xia, J., and Shen, H. (2020). Exponential Stabilization of Delayed Complex-Valued Neural Networks with Aperiodic Sampling: A Free-Matrix-Based Time-Dependent Lyapunov Functional Method. Int. J. Control. Autom. Syst. 18, 1894–1903. doi:10.1007/s12555-019-0706-0

CrossRef Full Text | Google Scholar

Yi, Z., Xu, Y., Hu, J., Chow, M.-Y., and Sun, H. (2020). Distributed, Neurodynamic-Based Approach for Economic Dispatch in an Integrated Energy System. IEEE Trans. Ind. Inf. 16, 2245–2257. doi:10.1109/tii.2019.2905156

CrossRef Full Text | Google Scholar

Yin, Z., Jiang, X., and Wang, F. (2020). Stability Criteria for Systems with Multiple Probabilistic Intervals Time-Varying Delay. Int. J. Control. Autom. Syst. 18, 877–885. doi:10.1007/s12555-019-0309-9

CrossRef Full Text | Google Scholar

Yu, M., Song, C., Feng, S., and Tan, W. (2020). A Consensus Approach for Economic Dispatch Problem in a Microgrid with Random Delay Effects. Int. J. Electr. Power Energ. Syst. 118, 105794. doi:10.1016/j.ijepes.2019.105794

CrossRef Full Text | Google Scholar

Yu, W., Li, C., Yu, X., Wen, G., and Lü, J. (2015). “Distributed Consensus Strategy for Economic Power Dispatch in a Smart Grid,” in 2015 10th Asian Control Conference (ASCC), 1–6. doi:10.1109/ASCC.2015.7244550

CrossRef Full Text | Google Scholar

Yun, H., Shim, H., and Ahn, H.-S. (2019). Initialization-Free Privacy-Guaranteed Distributed Algorithm for Economic Dispatch Problem. Automatica 102, 86–93. doi:10.1016/j.automatica.2018.12.033

CrossRef Full Text | Google Scholar

Zafar, A., and Hong, K.-S. (2020). Reduction of Onset Delay in Functional Near-Infrared Spectroscopy: Prediction of Hbo/hbr Signals. Front. Neurorobot. 14, 10. doi:10.3389/fnbot.2020.00010

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Gong, Z., Yang, Z., and Chen, Z. (2019). Distributed Convex Optimization for Flocking of Nonlinear Multi-Agent Systems. Int. J. Control. Autom. Syst. 17, 1177–1183. doi:10.1007/s12555-018-0191-x

CrossRef Full Text | Google Scholar

Zhang, X. S., Li, Q., Yu, T., and Yang, B. (2018). Consensus Transfer Q -Learning for Decentralized Generation Command Dispatch Based on Virtual Generation Tribe. IEEE Trans. Smart Grid 9, 2152–2165. doi:10.1109/TSG.2016.2607801

CrossRef Full Text | Google Scholar

Zhang, X., Xu, H., Yu, T., Yang, B., and Xu, M. (2016). Robust Collaborative Consensus Algorithm for Decentralized Economic Dispatch with a Practical Communication Network. Electric Power Syst. Res. 140, 597–610. doi:10.1016/j.epsr.2016.05.014

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, Y., and Lee, J. (2019). Lyapunov and Sliding Mode Based Leader-Follower Formation Control for Multiple mobile Robots with an Augmented Distance-Angle Strategy. Int. J. Control. Autom. Syst. 17, 1314–1321. doi:10.1007/s12555-018-0194-7

CrossRef Full Text | Google Scholar

Zhao, Z., Chen, G., and Dai, M. (2018). Distributed Event-Triggered Scheme for a Convex Optimization Problem in Multi-Agent Systems. Neurocomputing 284, 90–98. doi:10.1016/j.neucom.2017.12.060

CrossRef Full Text | Google Scholar

Zhu, M., Yang, Q., Dong, J., Zhang, G., Gou, X., Rong, H., et al. (2021). An Adaptive Optimization Spiking Neural P System for Binary Problems. Int. J. Neural Syst. 31, 2050054. doi:10.1142/s0129065720500549

PubMed Abstract | CrossRef Full Text | Google Scholar