Distributionally robust transactive control for active distribution systems with SOP-connected multi-microgrids

The increasing demand for distributed energy and active load increases the risk of voltage violations in active distribution systems. This paper proposes a distributionally robust transactive control method for local energy trading and network operation management of active distribution systems with interconnected microgrids. In particular, the emerging SOP technology is used for the flexible connection of the multi-microgrids (MMGs). First, the local energy interactive market between distribution network operator (DNO) and regional microgrids is constructed to simultaneously solve the economic and security problems of distribution networks considering the energy trading scenarios and various operational constraints. Then, the dual relaxation technique is used to transform the two-layer structure model into a single-layer model. Furthermore, the single-layer game model is further transformed into a two-stage distributed robust problem considering the uncertainties of load demand and renewable power outputs, and the second stage of the problem is decomposed into multiple parallel subproblems without dual information. Finally, numerical simulations on IEEE-33 test system verify the advantages and effectiveness of the proposed method.

1 Introduction

The improvement of renewable energy penetration has promoted the transformation of traditional distribution network to active distribution systems, which puts forward higher requirements for efficiency, flexibility and responsiveness of the system. MMGs are considered as an emerging network design in active distribution systems (Yang et al., 2020a; Xu et al., 2020). Information exchange and energy sharing can be achieved through flexible interconnection of MGs (Yang et al., 2020b). It has significant advantages in power loss reduction, operation cost saving, and system reliability enhancement. The existing researches on MGs often pursues the economic benefits of individual microgrid, merely considering this objective could undermine the operation performance by causing nodal voltage violations. Therefore, it is imperative to resolve the economic and operational problems of the active distribution systems with MMGs in a holistic manner through joint optimization of energy trading and system operation.

Recent efforts have focused on the transactive control method for active distribution systems with MMGs, which can be classified into two categories: direct control-based and local energy market-based methods. The control-based methods (Yang et al., 2020a; Zhou et al., 2020) are designed from the point of view of the DNO to determine direct control commands for all controllable parts by collecting all the information from MGs. Although this kind of methods are easy to be implemented, it has potential shortcomings such as poor scalability and low transparency, and it cannot give play to the flexibility of the users. The method based on the local energy market is different from the above method. This method ensures the consistency of control decisions by decentralized coordination of different entities in the distribution network (Yan et al., 2021). Thus, the regional microgrid can effectively manage the internal distributed energy, and protect the interests of the system (Liu et al., 2020). Recent studies about local energy markets mainly includes multiagent-based (Jadhav et al., 2019), game theory-based (Anoh et al., 2020), auction theory-based (El-Baz et al., 2019; Esfahani et al., 2019) methods, and semi-market-based method under supervision (Park et al., 2016). Although the above research provides a reference for building a local energy market, there are still many limitations.

1) Neglecting the joint research on the economic problems of multi-microgrid transactions and the technical problems of distribution network operation. The voltage regulation and the economy of the whole system may not play an optimal role simultaneously (Ji et al., 2019).

2) Neglecting the uncertainty of distributed energy and demand of users. The deviation between the result and the actual existence will increase, which will lead to improper regulation of physical components in the system. This situation not only makes the result of economic optimization deviate from the reality, but also may bring security problems to the distribution network system.

Therefore, an optimization model of energy interactive regulation based on the local energy market is constructed. This model can not only eliminate voltage violations, but also maximize the flexibility and economy of distribution network.

As for the interactive control of distribution network constraints, the early research mainly focused on resource management of microgrid and market clearing algorithm (Esfahani et al., 2019; Yang X et al., 2021). The interactive operation between agents is often ignored, and the application of SOP associated with energy trading has not been fully studied. As a new type of fully controlled power electronic device, SOP has fast response speed (Ji et al., 2019; Yang Z et al., 2021), and can accurately and continuously realize the characteristics of active/reactive power regulation of connected feeders (Yan et al., 2021). Therefore, this paper introduces SOP in the distribution system of local energy market to reduce the impact of distributed energy transactions on system power flow and improve the economy of the overall distribution network operation.

Secondly, as for how to effectively deal with the problem that the uncertainty of renewable energy and demand of users has a serious impact on the system (Park et al., 2016), the existing research schemes mainly include stochastic optimization (Liu et al., 2017; Guo et al., 2021), robust optimization (Zhao et al., 2020; Li et al., 2021) and distributed robust optimization (Wang et al., 2016; Liu et al., 2019; Ding et al., 2022). Among them, stochastic optimization depends on the known probability distribution, and it is easy to ignore the external influences such as risks and the characteristics of different internal distributions, which will lead to too little consideration in decision-making. Although robust optimization only needs to use the set reflecting the change range of uncertain factors (Li et al., 2021), it only optimizes the goal in the worst case, which will lead to the result being too conservative and the income cannot reach the optimal value. Based on the above two methods, this paper uses the distributed robust optimization method to solve the optimal value under the uncertainty environment. The results obtained are robust while avoiding excessive conservatism.

The contributions of this work are summarized as follows:

1) A two-stage distributed robust energy trading regulation model is proposed for active distribution system. The two-level problem is decomposed into several parallel subproblems to avoid the need for dual information like traditional distributed robust optimization (DRO) according to the special two-phase scenario designed in this paper.

2) This paper considers various operation constraints, which is different from most existing researches that only focus on the transaction mechanism, and proposes a comprehensive decision-making method. SOP technology is introduced for flexible interconnection between multi-regional microgrids to actively improve system power flow and achieve security regulation of voltage and economic operation of transactions.

3) This paper uses KKT conditions, duality, linearization and relaxation techniques to transform the two-layer game problem into a single-layer MISOCP problem. In the case of many uncertain individuals as in this paper, this method is conducive to improving the efficiency of decision-making.

The rest of the paper is organized as follows. Section 2 introduces the transactive control architecture for active distribution systems with SOP-connected MMGs. In Section 3, the formulas of DNO and multi-microgrid optimization models and the conversion process of two-layer models are described in detail. The system uncertainty model based on distributed robustness is introduced in Section 4. In Section 5, the case study of interactive regulation architecture is introduced and discussed. Finally, conclusions are drawn in Section 6.

2 Proposed transactive control framework

The active distribution system with MMGs is built, as shown in Figure 1.

FIGURE 1

FIGURE 1. Architecture of distribution network system with MMGs.

In this paper, the on-load tap changer (OLTC) is used to connect the distribution network with high voltage (HV) system, and the distribution network is divided into three regional microgrids. The regional microgrid includes distributed energy [mainly including photovoltaic array (PV) and wind turbine (WT)], energy storage system (ESS), general load and transferable load. SOPs are also used in the distribution network system to connect the regional microgrids, so as to conduct more accurate and rapid power regulation, and prevent transaction congestion.

Distribution network operator (DNO) is introduced as the intermediary between the HV and the regional microgrids, which is mainly responsible for the following: 1) Monitor and manage the operation of the distribution network to ensure that the system meets the constraints of safe operation and the stability of system voltage; 2) Different from other studies in which the microgrid directly trades with the HV, DNO is given the right to control and manage the trading volume between the distribution network and the HV, so that it can dynamically distribute the internal energy of the distribution network and improve the local energy consumption; 3) Participate in the local energy market between DNO and the regional microgrid, and dynamically adjust the clearing price by referring to the power demand of users, so as to minimize the operating cost.

As the main body participating in the local energy market on behalf of users, the regional microgrid is mainly responsible for the following: 1) Collect the electricity demand of all users in the region, and use it as a bargaining chip with DNO. The electricity demand is adjusted independently and flexibly to minimize the cost for users according to the clearing electricity price; 2) Manage the charging and discharging of energy storage systems to improve the local utilization rate of distributed energy.

In the transaction process of the local energy market, DNO needs to fully consider the dynamic feedback from users due to the price. Microgrids can decide their own power consumption strategy dynamically and flexibly according to the price (Lei et al., 2022). This process achieves the efficient operation of the overall system and improve the local consumption capacity of distributed energy (Xu et al., 2022). Furthermore, due to the uncertainty of distributed energy and load demand, there will be large deviation between the results obtained and the expected results, which will result in voltage deviation. In order to balance the interactive benefits and scheduling performance, this paper constructs a transactive control architecture for active distribution systems with SOP-connected MMGs.

3 Model formulation

3.1 Optimization model of DNO

For the DNO, its objective is to achieve power loss reduction and voltage regulation, and minimize the system operation cost. Therefore, the optimization model of the DNO can be expressed as follows.

$\mathit{min}{F}_{DN\mathrm{O}}\left(x\right)={\alpha }_o\left(f_{\mathrm{H}\mathrm{V}}+f_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}}-f_{\mathrm{M}\mathrm{G}\mathrm{s}}\right)+{\beta }_v{f}_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}}(1)$

where ${\alpha }_o$ and ${\beta }_v$ are the weight coefficients which can be determined by a subjective weighting method (Li et al., 2017). $f_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$, $f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}}$, $f_{\mathrm{H}\mathrm{V}}$ and $f_{\mathrm{M}\mathrm{G}\mathrm{s}}$ are the network losses cost, adjusting cost of OLTC, grid cost, and the income from MGs, respectively. $f_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}}$ represents accumulated voltage deviation, the specific expression above is as follows.

$\left\{\begin{array}{l}{f}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=C_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\left({\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{ij\in {\Omega }_B}{r}_{ij}{I}_{t,ij}^2+{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^N{P}_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)\Delta t\\ f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}}={\displaystyle \sum }_{ij\in {\Omega }_O}{\displaystyle \sum }_{t=1}^T\left(C_{\mathrm{O}\mathrm{L}\mathrm{T}\mathrm{C}}\left|K_{t,ij}-K_{t-1,ij}\right|\right)\\ f_{\mathrm{H}\mathrm{V}}={\displaystyle \sum }_{t=1}^{N_T}\left\{{\left[{\mathrm{g}}_t\right]}^{+}{\gamma }_t^b-{\left[-{\mathrm{g}}_t\right]}^{+}{\gamma }_t^s\right\}\Delta t\\ f_{\mathrm{M}\mathrm{G}\mathrm{s}}={\displaystyle \sum }_{t=1}^{N_T}{\displaystyle \sum }_{n=1}^{N_{mg}}{\lambda }_t{P}_{t,n}^{\mathrm{n}\mathrm{e}\mathrm{t}}\Delta t\\ f_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}}={\displaystyle \sum }_{t=1}^{N_T}{\displaystyle \sum }_{t=1}^{N_N}\left|{\mathrm{U}}_{t,i}^2-\stackrel{\sim }{U_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}\right|\end{array}\right.(2)$

where ${\left[.\right]}^{+}$ represents a projection operator on a non-negative orthogonal. For example, ${\left[P\right]}^{+}=\max \left(P,0\right)$.

1) Network constraints of the DN. The widely used Distflow branch model is adopted to model the DN as described in the following (Li et al., 2017; Cao et al., 2022).

${\displaystyle \sum }_{ik\in {\Omega }_l}{P}_{t,ik}-{\displaystyle \sum }_{ji\in {\Omega }_l}\left(P_{t,ji}-r_{ji}{I}_{t,ji}^2\right)=P_{t,i}(3)$

${\displaystyle \sum }_{ik\in {\mathrm{\Omega }}_l}{Q}_{t,ik}-{\displaystyle \sum }_{ji\in {\mathrm{\Omega }}_l}\left(Q_{t,ji}-x_{ji}{I}_{t,ji}^2\right)=Q_{t,i}(4)$

$U_{t,i}^2-U_{t,j}^2-2\left(r_{ij}{P}_{t,ij}+x_{ij}{Q}_{t,ij}\right)+\left(r_{ij}^2+x_{ij}^2\right)I_{ij}^2=0(5)$

$I_{t,ij}^2{U}_{t,i}^2=P_{t,ij}^2+Q_{t,ij}^2(6)$

$P_{t,i}=P_{t,i}^{\mathrm{P}\mathrm{V}}+P_{t,i}^{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{d}}+P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}-P_{t,i}^{\mathrm{L}}+\left(d_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s}}-c_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s}}\right)(7)$

$Q_{t,i}=Q_{t,i}^{\mathrm{P}\mathrm{V}}+Q_{t,i}^{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{d}}+Q_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}-Q_{t,i}^{\mathrm{L}}(8)$

$Q_{t,i}^{\mathrm{P}\mathrm{V}}=P_{t,i}^{\mathrm{P}\mathrm{V}}\tan {\theta }_k^{\mathrm{P}\mathrm{V}}(9)$

$\sqrt{{\left(P_{t,i}^{\mathrm{P}\mathrm{V}}\right)}^2+{\left(Q_{t,i}^{\mathrm{P}\mathrm{V}}\right)}^2}\le S_i^{\mathrm{P}\mathrm{V}}(10)$

The security constraints of the DN are presented as

${\underset{\_}{U}}^2\le U_{t,i}^2\le {\overline{U}}^2(11)$

$I_{t,ij}^2\le {\overline{I}}^2,\forall t,\left(i,j\right)\in {\Omega }_l(12)$

Constraint Eq. 11) represents the system voltage limits, and Constraint Eq. 12) represents the maximum line current capacity.

2) SOP operation constraints. In this work, the back-to-back voltage source converters (VSCs)-based SOP device is utilized (Li et al., 2017). The optimization variables of the SOP consist of the active and reactive power outputs of the two VSCs, the relevant operational optimization constraints are as follows.

i) Active/reactive power constraints.

$P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}+P_{t,j}^{\mathrm{S}\mathrm{O}\mathrm{P}}+P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+P_{t,j}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=0(13)$

$P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=A_i^{\mathrm{S}\mathrm{O}\mathrm{P}}\sqrt{{\left(P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}\right)}^2+{\left(Q_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}\right)}^2}(14)$

${\underset{\_}{Q}}_i^{\mathrm{S}\mathrm{O}\mathrm{P}}\le Q_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}\le {\overline{Q}}_i^{\mathrm{S}\mathrm{O}\mathrm{P}}(15)$

ii) Capacity constraints.

$\sqrt{{\left(P_{t,i}^{SOP}\right)}^2+{\left(Q_{t,i}^{SOP}\right)}^2}\le S_i^{SOP}(16)$

3) Constraints of the OLTC.

The variables of the OLTC are considered as the action series of its tap steps. For the constraint formula of OLTC, this paper refers to (Li et al., 2017).

4) Transaction price constraint.

${\lambda }_t^{\mathit{min}}\le {\lambda }_t\le {\lambda }_t^{\mathit{max}}(17)$

$\frac{1}{T}{\displaystyle \sum }_{t=1}^T{\lambda }_t\le \frac{1}{T}{\displaystyle \sum }_{t=1}^T{\lambda }_t^{\mathit{max}}(18)$

Eq. (18) indicates that the average price of internal electric energy is not higher than the average price of power purchased from the superior grid to protect the interests of power users.

3.2 Optimization model of microgrids

The Multi-microgrid optimization model includes the power consumption plan of load demand in the trading market and the charging/discharging regulation of ESS. The optimization model of individual MG is given as follows.

$\begin{array}{l}\min F_{\mathrm{M}\mathrm{G}}={\displaystyle \sum }_{t=1}^{{\mathrm{N}}_{\mathrm{T}}}{\lambda }_t{P}_{t,n}^{\mathrm{n}\mathrm{e}\mathrm{t}}\Delta t-{\displaystyle \sum }_{t=1}^{N_T}{\displaystyle \sum }_{i\in S_n}{v}_n^{\mathrm{D}}\left(P_{t,i}^{\mathrm{L},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}+P_{t,i}^{\mathrm{L},\mathrm{u}\mathrm{p}}\right)\Delta t+{\displaystyle \sum }_{\forall \mathrm{t}}{\displaystyle \sum }_{e=1}^{{\mathrm{N}}_{\mathrm{e}}}\left(C_{\mathrm{deg}}{P}_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}}{\eta }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}}+\frac{P_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}}}{{\eta }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}}}\right)\Delta t\\ s.t.P_{t,n}^{\mathrm{n}\mathrm{e}\mathrm{t}}={\displaystyle \sum }_{i\in S_n}\left(P_{t,i}^{L,unc}+P_{t,i}^{L,up}+P_{t,i}^{L,do}\right)-P_{t,i}^{\mathrm{P}\mathrm{V}}+{\displaystyle \sum }_{e=1}^{N_e}\left(c_{t,e}^{ess}-d_{t,e}^{ess}\right)\end{array}(19)$

In Eq. (19), the first part represents the total cost of trading with DNO, the second part represents the dissatisfaction with the transferable load, and the third part represents the compensation cost for ESS aging and degradation. $v_n^D$ is the inconvenience sensitivity coefficient of MG n (Yang et al., 2019), $v_n^D\ge 0$.

This paper refers to (Xu et al., 2019; Yang X et al., 2021) for the constraints of the charging/discharging power and charging state of ESS. Similarly, the constraint conditions of demand response (DR) refer to (Yang et al., 2019).

3.3 Transformation of the bilevel model

The decision optimization of DNO and microgrids is a two-layer optimization, which can be solved through Stackelberg game. The regional microgrid determines the operation status and the power exchange according to the received electricity price. The power exchange must meet the network constraints and match the optimal solution of the microgrids. This requires an iterative process to obtain the equilibrium solution

Compared with the iterative solution of traditional two-layer game, this paper considers that the decision-making optimization of the game is affected by uncertain factors and the convergence of regional microgrids is asynchronous. In order to get the optimization results more quickly and effectively, the two-layer optimization problem is transformed into a single-layer optimization problem by constructing Lagrangian functions and using KKT conditions and dual theory (Jin et al., 2021).

Because there are complementary constraints in the microgrids, such as the energy storage system cannot discharge and charge simultaneously, the relevant non-linear constraints are complementary relaxed. Finally, the following single-layer master-slave game problem can be obtained.

$\begin{array}{c}\min F_{lequ}=\left\{{\alpha }_o\left(f_{\mathrm{H}\mathrm{V}}-{\displaystyle \sum }_t{\displaystyle \sum }_n{\displaystyle \sum }_{i\in S_n}\left({P_{t,i}^{\mathrm{L},\mathrm{f}\mathrm{i}\mathrm{x}}-P}_{t,i}^{\mathrm{P}\mathrm{V}}-P_{t,i}^{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\right)\Delta t+f_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}}\right)+{\beta }_v{F}_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}}\right\}\\ +{\displaystyle \sum }_t{\displaystyle \sum }_i\left\{+{\sum }_e\left(\left[{-\mu }_{2,t,i}^{\mathrm{L},\mathrm{u}\mathrm{p}}{L}_{t,i}^{\max }-{\mu }_{2,t,i}^{\mathrm{L},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}{L}_{t,i}^{\max }\right]-{\mu }_{2,t,e}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}}{P}_e^{\mathrm{c},\mathrm{r}\mathrm{a}\mathrm{t}}-{\mu }_{2,t,\mathrm{e}}^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}}{P}_e^{\mathrm{d},\mathrm{r}\mathrm{a}\mathrm{t}}+{\mu }_{1,t,\mathrm{e}}^{\mathrm{e}\mathrm{s}\mathrm{s}}{S}_e^{\min }-{\mu }_{2,t,e}^L{S}_e^{\max }\right)\right\}\end{array}(20)$

s.t. Eqs. 3–18

$0\le \mu \perp h\left(x\right)\ge 0(21)$

In Eq. (20), decision variables are ${\lambda }_t$, $K_{t,ij}$, $P_{t,i}^{\mathrm{s}\mathrm{o}\mathrm{p}}$, $Q_{t,i}^{\mathrm{s}\mathrm{o}\mathrm{p}}$, $P_{t,i}^{L,\mathrm{u}\mathrm{p}}$, $P_{t,i}^{L,\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}$, $P_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},c}$, $P_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},d}$. The decision variables of DNO include clearing electricity price ${\lambda }_t$, the regulation of OLTC $K_{t,ij}$, the active/reactive power of SOP in each period $P_{t,i}^{\mathrm{s}\mathrm{o}\mathrm{p}}/Q_{t,i}^{\mathrm{s}\mathrm{o}\mathrm{p}}$; The decision variables of microgrids include the load demand of DR $P_{t,i}^{L,\mathrm{u}\mathrm{p}}/P_{t,i}^{L,\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}$, and charging and discharging power of ESS in each period $P_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},c}/P_{t,i}^{\mathrm{e}\mathrm{s}\mathrm{s},d}$.

4 Reformulation based on distributed robustness

4.1 Distributed robust model

Multi-scenario method is used to describe the uncertainty of load, PV and WT. The above deterministic optimization model (i.e., Eq. (20)) is transformed into uncertain model. The conversion result is as follows.

$\begin{array}{l}\min {\mathbb{E}}_{\pi }\left[{\mathcal{J}}_D\right]={\displaystyle \sum }_{\omega \in N_{\omega }}{p}_{\omega }{F}_{lequ,\omega }=\\ {\displaystyle \sum }_{\omega \in N_{\omega }}{p}_{\omega }\times \left\{{\alpha }_o\left(f_{\mathrm{H}\mathrm{V},\omega }-{\displaystyle \sum }_t{\displaystyle \sum }_n{\displaystyle \sum }_{i\in S_n}\left(P_{t,i,\omega }^{\mathrm{L},\mathrm{f}\mathrm{i}\mathrm{x}}-P_{t,i,\omega }^{\mathrm{P}\mathrm{V}}-P_{t,i,\omega }^{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\right)\Delta t+f_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s},\omega }+f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h},\omega }\right)+{\beta }_v{F}_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e},\omega }\right\}\\ +{\displaystyle \sum }_t{\displaystyle \sum }_i\left\}\left[{-\mu }_{2,t,i,\omega }^{\mathrm{L},\mathrm{u}\mathrm{p}}{L}_{t,i}^{\max }-{\mu }_{2,t,i,\omega }^{\mathrm{L},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}{L}_{t,i}^{\max }\right]+{\sum }_e\left(-{\mu }_{2,t,e,\omega }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{c}}{P}_e^{\mathrm{c},\mathrm{r}\mathrm{a}\mathrm{t}}-{\mu }_{2,t,\mathrm{e},\omega }^{\mathrm{e}\mathrm{s}\mathrm{s},\mathrm{d}}{P}_e^{\mathrm{d},\mathrm{r}\mathrm{a}\mathrm{t}}+{\mu }_{1,t,\mathrm{e},\omega }^{\mathrm{e}\mathrm{s}\mathrm{s}}{S}_e^{\min }-{\mu }_{2,t,e,\omega }^L{S}_e^{\max }\right)\right\}\end{array}(22)$

Discrete adjustment variables, such as OLTC’s tap steps, are set as the first stage variables z according to the flexibility and real-time of the adjustment of each resource equipment, other continuous variables, such as active and reactive power of SOP, clearing electricity price and transferable load power, are set as variables in the second stage $x_{\omega }$, The following functions can be obtained.

$\begin{array}{l}\min {\mathbb{E}}_{\pi }\left[{\mathcal{J}}_D\right]=\\ \underset{z}{\min }\underset{p_{\omega }\in {\Omega }^p}{\max }{\displaystyle \sum }_{\omega \in N_{\omega }}{p}_{\omega }\underset{x_{\omega }}{\min }\left\{{\alpha }_o\left(f_{\mathrm{H}\mathrm{V},\omega }-{\displaystyle \sum }_t{\displaystyle \sum }_n{{\displaystyle \sum }}_{i\in S_n}\left({P_{\mathrm{t},\mathrm{i},\omega }^{\mathrm{L},\mathrm{f}\mathrm{i}\mathrm{x}}-P}_{t,i,\omega }^{\mathrm{P}\mathrm{V}}-P_{t,i,\omega }^{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\right)\Delta t+f_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s},\omega }+f_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h},\omega }\right)+{\beta }_v{F}_{\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e},\omega }\right\}\\ +{\displaystyle \sum }_t\left\{{\displaystyle \sum }_i\left[-{\mu }_{2,t,i,\omega }^{\mathrm{L},\mathrm{u}\mathrm{p}}{L}_{t,i}^{\max }-{\mu }_{2,\mathrm{t},\mathrm{i},\omega }^{\mathrm{L},\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}{L}_{t,i}^{\max }\right]+{\sum }_e\left(-{\mu }_{2,t,e,\omega }^{ess,c}{P}_e^{c,rat}-{\mu }_{2,t,\mathrm{e},\omega }^{ess,d}{P}_e^{d,rat}+{\mu }_{1,t,\mathrm{e},\omega }^{ess}{S}_e^{\min }-{\mu }_{2,t,e,\omega }^L{S}_e^{\max }\right)\right\}\end{array}(23)$

In order to ensure that the probability distribution of each scenario from historical data is close to the actual operation scenario, the uncertainty set of probability distribution is constructed by using the comprehensive method of norm-1 and norm-inf to limit the allowable fluctuation range of the probability distribution of discrete scenarios. The uncertainty set is as follows.

$\psi =\left\{\left\{p_{\omega }\right\}\left|\begin{array}{c}{p}_{\omega }\ge 0\\ {\displaystyle \sum }_{\omega =1}^{{\mathrm{N}}_{\omega }}{p}_{\omega }=1\\ {\displaystyle \sum }_{\omega =1}^{{\mathrm{N}}_{\omega }}\left|p_{\omega }-p_{\omega }^0\right|\le {\delta }_1\\ \underset{1\le \omega \le N_{\omega }}{\max }\left|p_{\omega }-p_{\omega }^0\right|\le {\delta }_{\infty }\end{array}\right.\right\}(24)$

$\left\{\begin{array}{l}{\delta }_1=\frac{N_{\omega }}{2K}\ln \frac{2N_{\omega }}{1-{\alpha }_1}\\ {\delta }_{\infty }=\frac{1}{2K}\ln \frac{2N_{\omega }}{1-{\alpha }_{\infty }}\end{array}\right.(25)$

Eq. (24) and Eq. (25) are the comprehensive constraints of norm-1 and norm-inf.

4.2 Model linearization and cone relaxation transformation

1) Linearization. The Boolean variable $\kappa$ is introduced to transform the complementary relaxation constraint in Eq. (21) into a linear inequality. The form is as follows.

$0\le \mu \le M\kappa (26)$

$0\le h\left(x\right)\le M\left(I-\kappa \right)(27)$

Furthermore, variable replacement is used for linearization, that is, $l_{t,ij}$ and $v_{t,i}$ are used to replace $I_{t,ij}^2$ and $U_{t,i}^2$ in Eq. (3)–(5), (11) and (12), respectively; The non-linear voltage deviation term in Eq. (2) is replaced by the auxiliary variable ${\mathrm{A}\mathrm{u}\mathrm{x}}_{t,i}$. The specific process is shown in (Li et al., 2017).

Because of the absolute value constraint in Eq. (24), the auxiliary variables $z_{\omega }^{+}$ and $z_{\omega }^{-}$ are introduced to linearize the norm-1 constraint. The norm-inf constraint is linearized, similarly. The obtained linear constraint conditions are as follows.

$z_{\omega }^{+}+z_{\omega }^{-}\le 1,\forall \omega (28)$

$\left\{\begin{array}{l}0\le p_{\omega }^{+}\le z_{\omega }^{+}{\delta }_1,\forall \omega \\ 0\le p_{\omega }^{-}\le z_{\omega }^{-}{\delta }_1,\forall \omega \\ p_{\omega }=p_{\omega }^0+p_{\omega }^{+}-p_{\omega }^{-},\forall \omega \end{array}\right.(29)$

${\displaystyle \sum }_{\omega =1}^{N_{\omega }}\left(p_{\omega }^{+}+p_{\omega }^{-}\right)\le {\delta }_1(30)$

$p_{\omega }^{+}+p_{\omega }^{-}\le {\delta }_{\infty },\forall \omega (31)$

2) Cone relaxation. Eq. (6) can be transformed into a second-order cone constraint through convex relaxation. The transformed equality constraint is as follows.

${‖\begin{array}{l}2P_{t,ij}\\ 2Q_{t,ij}\\ l_{t,ij}-v_{t,i}\end{array}‖}_2\le l_{t,ij}+v_{t,ij},\forall t(32)$

${\left(P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}\right)}^2+{\left(Q_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P}}\right)}^2\le 2\frac{P_{t,\mathrm{i}}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}{\sqrt{2}{A}_i^{\mathrm{S}\mathrm{O}\mathrm{P}}}\frac{P_{t,i}^{\mathrm{S}\mathrm{O}\mathrm{P},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}{\sqrt{2}{A}_i^{\mathrm{S}\mathrm{O}\mathrm{P}}}(33)$

${\left(P_{t,i}^{alt}\right)}^2+{\left(Q_{t,i}^{alt}\right)}^2\le 2\frac{S_{t,i}^{alt}}{\sqrt{2}}\frac{S_{t,i}^{alt}}{\sqrt{2}},alt\in \left\{SOP,PV,wind\right\}(34)$

Through above transformation processes, the non-linear programming problem is transformed into MISOCP model, which can be effectively solved by optimization solver (such as Gurobi and CPLEX).

4.3 Distributed robust model solving

Eq. (23) is a min-max-min three-layer two-stage model. Columns and constraints generation (C&CG) algorithm is used for iterative solution (Li et al., 2022).

The main problem is to solve the first stage optimal solution $z^{*}$ and provide the updated lower bound value under the condition that the worst probability distribution is known. The matrix vector form of the original formula is used for the convenience of expression. The expression is as follows.

$\underset{z\in Z,x\in X^s,G}{\mathit{min}}G(35)$

$G\ge {\displaystyle \sum }_{\omega =1}^{N_{\omega }}{p}_{\omega }^{{\mathrm{m}}^{\ast }}{A}^T{x}_{\omega }^m,\forall r=\mathrm{1,2},...,M(36)$

$C{x}_{\omega }^m\le y(37)$

$E{x}_{\omega }^m=u(38)$

${‖Q_i{x}_{\omega }^m+H_i‖}_2\le c_i^T{x}_{\omega }^m+{\rho }_i(39)$

$D{x}_{\omega }^m+Fz=f(40)$

where ${\displaystyle \sum }_{\omega =1}^{N_{\omega }}{p}_{\omega }^{m^{\ast }}{A}^T{x}_{\omega }^m$ represents the max-min part of Eq. (23); A, C, E, D, F, Q, H, c, y, u, ρ, f represent the matrix or vector forms of the corresponding models; Eq. (37) and (38) represent the relevant constraints of variables in the second stage; Eq. (39) represents the second-order cone relaxation constraints; Eq. (40) represents the coupling constraints in the first stage and the second stage.

The subproblem solves the worst probability distribution value $p_{\omega }^{m^{\ast }}$ of each scenario based on the $z^{*}$ given by the main problem, and provides the updated upper bound value. The subproblem expression is as follows.

$\underset{p_{\omega }\in {\Omega }^p}{\mathit{max}}\underset{x_{\omega }}{\mathit{min}}{\displaystyle \sum }_{\omega =1}^{N_{\omega }}{p}_{\omega }^m{A}^T{x}_{\omega }^m(41)$

It can be judged that each scenario in the second stage is independent of each other, and the probability distribution values and variables are independent of each other according to the structural characteristics and scenario characteristics of the subproblem. The subproblem can be divided into two parts. The expression is as follows.

$\left\{\begin{array}{l}{f}_{\omega }=\underset{x_{\omega }}{\min A^T{x}_{\omega }^m}\\ \underset{p_{\omega }\in {\mathrm{\Omega }}^p}{\max }{\displaystyle \sum }_{\omega =1}^{N_{\omega }}{p}_{\omega }^m{f}_{\omega }\end{array}\right.(42)$

If Eq. (42) has a feasible solution, a group of additional variables $x_{\omega }^m$ and related constraints need to be generated and added to the main problem of the next iteration (Ding et al., 2018). The specific iterative solution process is shown in Table 1.

1) It is high efficiency. The transformation of two-stage game model and the use of the modified DRO method avoid mutual coupling factors and improve the overall decision efficiency.

2) It has better robustness and economy. It can improve power flow distribution, achieve voltage and reactive power regulation, and take into account the overall interests of the active distribution systems in a flexible trading market.

TABLE 1

TABLE 1. PROCEDURE of modified C&CG ALGORITHM.

5 Simulation studies

5.1 Base data

In this paper, IEEE-33 node system is used for testing, which is divided into three regional microgrids (Li and Xu, 2019; Zhou et al., 2019; Li et al., 2020) as shown in Figure 2.

FIGURE 2

FIGURE 2. Topology diagram of the IEEE 33-bus test system with three microgrids and three SOPs.

The whole system includes four PVs, two WTs, three ESSs and three SOPs. The relevant parameters are shown in Table 2. The loads of the microgrid in each region, the output of PVs and WTs, and the net loads are shown in Figure 3. The capacity of the installed SOPs is set as 1.0 MVA. The percentage of demands that participates the DR is assumed to be 20% (Yang et al., 2019; Cruz et al., 2020). The price of electricity purchased by the distribution network from the HV is set according to the reference (Jin et al., 2021), and the selling price of the distribution network is set at 400 ¥/MWh. ${\lambda }_t^{\mathit{min}}$ is equal to the price of electricity sold by the active distribution systems to the HV. ${\lambda }_t^{\mathit{max}}$ is equal to the price of electricity purchased by the active distribution systems from the HV. All the installed renewable generators are operated at a unit power factor without considering the localized reactive power support of renewables (Yang Z et al., 2021). $\Delta t$ is set to 1 h. Referring to the setting in (Li et al., 2017), ${\alpha }_o$ and ${\beta }_v$ are set to .833 and .167, respectively; the limiting voltages $\overline{U}/\underset{\_}{U}$ are set to 1.05 p.u. and .95 p.u.; the correlation coefficient of network loss $C_{loss}$ is set to .08; the charging and discharging coefficient of ESS $C_{\mathit{deg}}$ is set to 18.741 ¥/MWh; the allowable operation number of OLTC ${\overline{\Delta }}^{OLTC}$ is set to 4 times/day; and the initial tap step $k_{ij,0}$ and tap step increment $\Delta k_{ij}$ are set to 1.0% and 1%, respectively. The proposed method in this paper was implemented in the YALMIP optimization toolbox with MATLAB R2020a, and solved by GUROBI 9.1.2.

TABLE 2

TABLE 2. Relevant parameters of IEEE 33 bus test system.

FIGURE 3

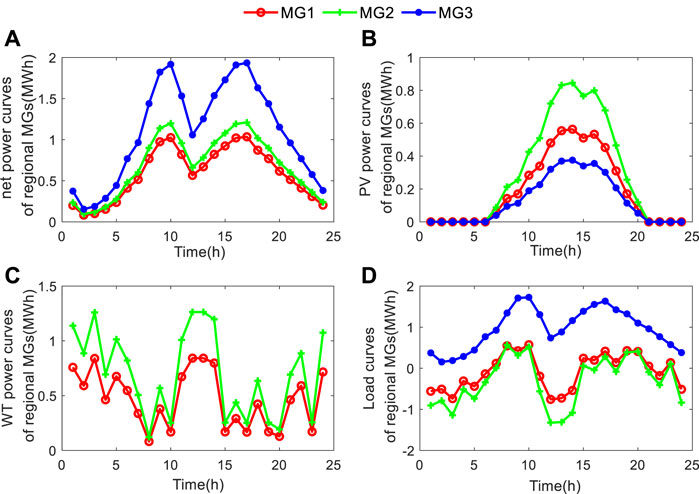
FIGURE 3. Initial data of microgrid in each region: (A) Total load of microgrid in each region; (B) Photovoltaic output of microgrid in each region; (C) Output of microgrid fans in each region; (D) Net load of microgrid in each region.

5.2 Results and analysis

5.2.1 Impact analysis of local energy interaction market

The energy storage system charging/discharging control and the transferable load control are important regulation means for microgrids to respond the DNO’s decision in local interactive market. The results are shown in Figure 4 and Figure 5, respectively.

FIGURE 4

FIGURE 4. Control result diagram of energy storage charge and discharge.

FIGURE 5

FIGURE 5. Control result of transferable load.

In the local interactive market, the price of electricity acts as a “bridge” for DNO to transfer its decisions to the microgrids. The transaction price is shown in Figure 6. The transaction volume of the microgrids is shown in Figure 7.

FIGURE 6

FIGURE 6. Dynamic chart of clearing price.

FIGURE 7

FIGURE 7. Transaction volume of each market entity.

Figures 4–7 show that the power generation of renewable energy does not reach the peak, and the supply is less than the demand, which makes the electricity price rise continuously in the peak period of power consumption (6:00-10:00 and 15:00-20:00). Therefore, users have to dynamically adjust their own power consumption strategy (i.e., ESS discharge, load demand decreases) to maintain their own interests in this period of time; The supply exceeds the demand, the microgrid’s own power generation can meet the demand, and DNO does not need to purchase power from the HV in the low peak period of power consumption (0:00-6:00) and the peak period of renewable energy power generation (11:00-14:00). This situation makes the electricity price drop significantly, which attracts users to dynamically adjust their own power consumption strategy (i.e., ESS charging, load demand increase).

To sum up, the local consumption of distributed energy can be achieved flexibly and the stability impact of the grid connection of distributed energy can be reduced by building a local trading market composed of DNO and regional microgrids. The electricity price is used to indirectly mobilize users to participate in dispatching of active distribution system by introducing market factors. This method effectively prevents the operation safety problems, such as blockage of grid lines during peak power consumption and low energy utilization during low peak power consumption.

5.2.2 Model validation analysis

In order to verify the accuracy of the second-order cone relaxation of the proposed model, the validation analysis of the model is carried out in this section (Li et al., 2017). Gap value of the whole system in each period is shown in Figure 8. It can be seen that the error values of the whole system are all at 10^–4. Therefore, the results calculated by the proposed method achieve acceptable accuracy.

FIGURE 8

FIGURE 8. Diagram of Gap value.

5.2.3 Case studies

This section compares the proposed decision-making method with the other two models to prove its effectiveness. Specific cases are defined as follows.

Case I. Economy-oriented transactive control. In this case, only economy-concerned factors are considered, thus the power flow, line power losses and voltage deviation are not included (Liu et al., 2020).

Case II. Compared with Case III, this case does not consider the use of SOPs.

Case III. The proposed method in previous sections.The comparison results of maximum and minimum voltage are shown in Figure 9, the comparison results of OLTC control are shown in Figure 12, and the comparison results of the relevant performances are shown in Table 3.The active/reactive power control results of SOPS in Case III are shown in Figure 10. SOP1 is connected to microgrid one and microgrid 3, SOP2 is connected to microgrid one and microgrid 2, SOP3 is connected to microgrid two and microgrid 3. The voltage fluctuation is shown in Figure 11.Table 3 shows that the energy storage system and demand response have been fully mobilized thanks to Case I does not need to consider the violation of network constraints, which reduces the cost of the microgrid. However, the results, which are compared with Case III, have greater line loss and voltage deviation. And Figure 10 shows that voltage violation is increased, which causes a big potential safety hazard to the operation of the actual active distribution system and affects whether the actual transaction can be completed smoothly and timely.Compared with Case III, the line power losses and the cost in Case II increase to a greater extent. Figure 9 and Figure 11 show that SOP keeps the voltage amplitude strictly within the safe range (i.e., [.96, 1.04] p.u.), which adjusts the system power to eliminate voltage violations and alleviates the problem of voltage rise. It proves the advantages of SOP in solving the security problems of active distribution system. Figure 10 and Figures 4–7 show that active power control of the SOP is consistent with the action of energy storage systems and the transferable loads in each regional microgrid. This situation reflects that SOP can adjust the active power flow distribution of the system flexibly and rapidly. The problem of transaction delay or failure caused by route congestion can be avoided through the connection between SOP and DNO. Therefore, the power flow fluctuation caused by renewable energy can be eliminated rapidly, and the economy of the overall operation of the distribution network can be improved indirectly. Furthermore, Figure 12 shows that the OLTC has less switching actions. The economic cost of active distribution system can be effectively reduced through the cooperation of SOP and OLTC.To sum up, it can be verified that the proposed comprehensive regulation method can give consideration to both operating economy and voltage security, and propose a more efficient scheme for consuming local distributed energy.

FIGURE 9

FIGURE 9. Comparison of the maximum and minimum voltages in the three cases.

TABLE 3

TABLE 3. Comparison results under different cases.

FIGURE 10

FIGURE 10. SOP active/reactive power control result.

FIGURE 11

FIGURE 11. Voltage magnitudes of all the 33 nodes.

FIGURE 12

FIGURE 12. Comparison diagram of OLTC control results.

5.3 Convergence analysis of distributed robust optimization

In this section, the DRO solution is tested and analyzed. Table 4 shows that the deviation between the main problem and the subproblem in the algorithm reaches 10^–3 levels of accuracy after three iterations. This shows that C&CG algorithm can quickly solve the distributed robust optimization model proposed in this paper.

TABLE 4

TABLE 4. Results of iterative convergence.

5.4 Comparison of distributed robust optimization methods

This paper assumes that the prediction errors of PV, WT and DR follow the Normal Distribution which the mean is set to 0 and the variance is set to .4 times of the predicted value (Ding et al., 2018). 3000 error scenario data are generated by fitting to represent the historical data. Finally, five typical scenarios are selected for simulation analysis of distributed robust optimization methods.

5.4.1 Comparative analysis of results under different confidence intervals

In order to show the influence trend of different confidence on the optimization results, and to prove the effectiveness of the comprehensive norm compared with the single norm, the following comparative analysis is made.

First, the results of distributed robust optimization under different confidence intervals are compared when the comprehensive norm constraint is adopted. Here, the range of α₁ is [.2, .8], and the range of ${\alpha }_{\infty }$ is [.5, .99]. The results are shown in Table 5.

TABLE 5

TABLE 5. The results of Comparison under different confidence intervals.

It can be observed from Table 5 that the value of the total cost increases with the increase of the comprehensive norm confidence α₁ and ${\alpha }_{\infty }$. This situation shows that the increase of confidence interval will increase the uncertainty contained in the system. This also means that the distribution network system needs to optimize the transaction content and call more resources (such as SOP) to eliminate the adverse impact of uncertainty on the system operation. This is the reason why the total cost of the system increases.

The results of comprehensive norm and single norm-inf are compared. Here ${\alpha }_{\infty }$ selects .99. The results are shown in Table 6.

TABLE 6

TABLE 6. Comparison of result between comprehensive norm and norm-inf.

It is shown that the results obtained by using the constraint condition of comprehensive norm are smaller than those obtained by using the norm-inf method. This means that comprehensive norm has better economy. Moreover, the comprehensive norm and single norm-1 results are compared. Here, α₁ is selected as .5. The results are shown in Table 7.

TABLE 7

TABLE 7. Comparison of result between comprehensive norm-inf and norm-1.

It can be observed from Table 7 that the calculated results of comprehensive norm are smaller thanks to the constraint of comprehensive norm further limits the fluctuation range of uncertainty. This also means that the overall cost of the system is lower and the conservatism of the results is improved.

According to the above conclusions, it can be proved that the comprehensive norm is more effective than the single norm.

5.4.2 Analysis and comparison of distributed robust optimization and other methods

This part will compare the stochastic optimization, robust optimization and the DRO adopted in this paper. Here, the stochastic optimization is calculated based on the scenarios known by the distributed robust method, where the probability values of each scenario are .2; The robust optimization uses .4 times of the predicted value as the fluctuation range; The comprehensive norm constraint of DRO that ${\alpha }_{\infty }$ selects .99 and α₁ selects .8. The comparison results are shown in Table 8.

TABLE 8

TABLE 8. Comparison of result between DRO and other methods.

To prove the effectiveness of the distributed robust optimization method in this paper, 6000 random probability distribution combinations are randomly generated based on the prediction scenario, and three result schemes are implemented to obtain the mean value of the expected cost of the probability distribution. The results are shown in Table 9.

TABLE 9

TABLE 9. Comparison of results of different algorithms.

According to Table 8 and Table 9, although the optimization result of stochastic optimization based on known scenarios is the smallest, the result is always greater than that of distributed robust optimization when the randomness of scenarios is fully considered. This situation indicates that its robustness is obviously insufficient to that of distributed robust optimization. Because robust optimization only considers the worst scenario information, the result of network loss and cost is the largest.

Compared with the other two methods, the performance and cost of DRO are in the middle, and the expected mean value of the probability distribution cost is lower than the other two methods. This shows that its probability distribution average performance is better than the other two methods, which reflects its good balance in economy, conservatism and security and have better adaptability under the actual uncertainty environment.

6 Conclusion

In this paper, a distributionally robust transactive control method for active distribution systems with SOP-connected MMGs is proposed. First of all, the constructed local energy interactive market fully considers the system operation safety factors such as voltage quality, so that it can operate more safely, while ensuring the overall economy and the flexibility and autonomy of users. Secondly, SOP is introduced into the active distribution systems based on the local energy market, and associate it with DNO. This significantly reduces the line loss and voltage deviation, maintains the economic interests of each subject, and further improves the flexibility of internal transactions of active distribution systems. Then, KKT conditions, relaxation techniques and other techniques are used to transform the two-layer game problem into a single-layer MISOCP problem. The optimization of the complex coupling model is achieved, and the efficiency of the operation is improved. Thirdly, the modified DRO optimization method is combined with the active distribution system. Compared with the traditional stochastic and robust methods, the DRO method achieves a better balance in terms of economy and conservatism, and has better economy and uncertainty adaptability. Finally, the conservative strategy of the integrated regulation method can be flexibly adjusted by changing the confidence level of the ambiguity set. This situation shows that the decision-making level can reasonably choose between the operation economic cost and the operation safety risk according to the actual situation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YH: Conceptualization, investigation, methodology, software, validation, writing—Original draft, writing—review and editing; YXi: Conceptualization, methodology, data curation; ZY: Supervision, project administration; YX: Supervision, project administration; GW: Supervision, project administration; LJ: Validation.

Funding

The authors gratefully acknowledge the support of the National Natural Science Foundation of China (52007074, U22B20116).

Conflict of interest

YZ was employed by Economic and Technological Research Institute of State Grid Anhui Electric Power Co., Ltd. and GW was employed by State Grid Anhui Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anoh, K., Maharjan, S., Ikpehai, A., Zhang, Y., and Adebisi, B. (2020). Energy peer-to-peer trading in virtual microgrids in smart grids: A game-theoretic approach. IEEE Trans. Smart Grid 11 (2), 1264–1275. doi:10.1109/tsg.2019.2934830

CrossRef Full Text | Google Scholar

Cao, Y., Zhou, B., Chung, C. Y., Shuai, Z., Hua, Z., and Sun, Y. (2022). Dynamic modelling and mutual coordination of electricity and watershed networks for spatio-temporal operational flexibility enhancement under rainy climates. IEEE Trans. Smart Grid 2022, 1. doi:10.1109/TSG.2022.3223877

CrossRef Full Text | Google Scholar

Cruz, M. R. M., Fitiwi, D. Z., Santos, S. F., Mariano, S. J. P. S., and Catalao, J. P. S. (2020). Multi-flexibility option integration to cope with large-scale integration of renewables. IEEE Trans. Sustain. Energy 11 (1), 48–60. doi:10.1109/tste.2018.2883515

CrossRef Full Text | Google Scholar

Ding, T., Yang, Q., Yang, Y., Li, C., Bie, Z., and Blaabjerg, F. (2018). A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method. IEEE Trans. Smart Grid 9 (5), 4994–5004. doi:10.1109/tsg.2017.2677481

CrossRef Full Text | Google Scholar

Ding, X., Ma, H., Yan, Z., Xing, J., and Sun, J. (2022). Distributionally robust capacity configuration for energy storage in microgrid considering renewable utilization. Front. Energy Res. 10, 896. doi:10.3389/fenrg.2022.923985

CrossRef Full Text | Google Scholar

El-Baz, W., Tzscheutschler, P., and Wagner, U. (2019). Evaluation of energy market platforms potential in microgrids: Scenario analysis based on a double-sided auction. Front. Energy Res. 7, 41. doi:10.3389/fenrg.2019.00041

CrossRef Full Text | Google Scholar

Esfahani, M. M., Hariri, A., and Mohammed, O. A. (2019). A multiagent-based game-theoretic and optimization approach for market operation of multimicrogrid systems. IEEE Trans. Industrial Inf. 15 (1), 280–292. doi:10.1109/tii.2018.2808183

CrossRef Full Text | Google Scholar

Guo, Z., Pinson, P., Chen, S., Yang, Q., and Yang, Z. (2021). Chance-constrained peer-to-peer joint energy and reserve market considering renewable generation uncertainty. IEEE Trans. Smart Grid 12 (1), 798–809. doi:10.1109/tsg.2020.3019603

CrossRef Full Text | Google Scholar

Jadhav, A. M., Patne, N. R., and Guerrero, J. M. (2019). A novel approach to neighborhood fair energy trading in a distribution network of multiple microgrid clusters. IEEE Trans. Industrial Electron. 66 (2), 1520–1531. doi:10.1109/tie.2018.2815945

CrossRef Full Text | Google Scholar

Ji, H., Wang, C., Li, P., Ding, F., and Wu, J. (2019). Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration. IEEE Trans. Sustain. Energy 10 (1), 280–289. doi:10.1109/tste.2018.2833545

CrossRef Full Text | Google Scholar

Jin, X., Wu, Q., Jia, H., and Hatziargyriou, N. (2021). Optimal integration of building heating loads in integrated heating/electricity community energy systems: A Bi-level mpc approach. IEEE Trans. Sustain. Energy 12 (3), 1741–1754. doi:10.1109/tste.2021.3064325

CrossRef Full Text | Google Scholar

Lei, W., Sun, W., and Zhao, Y. (2022). Research on market trading strategy of multi-microgrid intelligent power distribution system based on Bi-level optimization[J]. Front. Energy Res. 1587, 1032051. doi:10.3389/fenrg.2022.1032051

CrossRef Full Text | Google Scholar

Li, J., Khodayar, M. E., Wang, J., and Zhou, B. (2021). Data-Driven distributionally robust Co-optimization of P2P energy trading and network operation for interconnected microgrids. IEEE Trans. Smart Grid 12 (6), 5172–5184. doi:10.1109/tsg.2021.3095509

CrossRef Full Text | Google Scholar

Li, P., Ji, H., Wang, C., Zhao, J., Song, G., Ding, F., et al. (2017). Coordinated control method of voltage and reactive power for active distribution networks based on soft open point. IEEE Trans. Sustain. Energy 8 (4), 1430–1442. doi:10.1109/tste.2017.2686009

CrossRef Full Text | Google Scholar

Li, P., Qin, Y., Wu, Z., Quan, X., Han, J., and Chen, M. (2022). Distributionally robust energy trading among multi-microgrids with consideration of network constraints[J]. Front. Energy Res. 1774.

Google Scholar

Li, Z., Xu, Y., Feng, X., and Wu, Q. (2020). Optimal stochastic deployment of heterogeneous energy storage in a residential multienergy microgrid with demand-side management. IEEE Trans. Industrial Inf. 17 (2), 991–1004. doi:10.1109/tii.2020.2971227

CrossRef Full Text | Google Scholar

Li, Z., and Xu, Y. (2019). Temporally-coordinated optimal operation of a multi-energy microgrid under diverse uncertainties. Appl. energy 240, 719–729. doi:10.1016/j.apenergy.2019.02.085

CrossRef Full Text | Google Scholar

Liu, N., Yu, X., Wang, C., Li, C., Ma, L., and Lei, J. (2017). Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 32 (5), 3569–3583. doi:10.1109/tpwrs.2017.2649558

CrossRef Full Text | Google Scholar

Liu, Y., Li, Y., Gooi, H. B., Jian, Y., Xin, H., Jiang, X., et al. (2019). Distributed robust energy management of a multimicrogrid system in the real-time energy market. IEEE Trans. Sustain. Energy 10 (1), 396–406. doi:10.1109/tste.2017.2779827

CrossRef Full Text | Google Scholar

Liu, Z., Wang, L., and Ma, L. (2020). A transactive energy framework for coordinated energy management of networked microgrids with distributionally robust optimization. IEEE Trans. Power Syst. 35 (1), 395–404. doi:10.1109/tpwrs.2019.2933180

CrossRef Full Text | Google Scholar

Park, S., Lee, J., Bae, S., Hwang, G., and Choi, J. K. (2016). Contribution-based energy-trading mechanism in microgrids for future smart grid: A game theoretic approach. IEEE Trans. Industrial Electron. 63 (7), 4255–4265. doi:10.1109/tie.2016.2532842

CrossRef Full Text | Google Scholar

Wang, Z., Glynn, P. W., and Ye, Y. (2016). Likelihood robust optimization for data-driven problems. Comput. Manag. Sci. 13 (2), 241–261. doi:10.1007/s10287-015-0240-3

CrossRef Full Text | Google Scholar

Xu, D., Zhong, F., and Bai, Z. (2022). A two-layer multi-energy management system for microgrids with solar, wind, and geothermal renewable energy[J]. Front. Energy Res. 1598, 1030662. doi:10.3389/fenrg.2022.1030662

CrossRef Full Text | Google Scholar

Xu, D., Zhou, B., Chan, K. W., Li, C., Wu, Q., Chen, B., et al. (2019). Distributed multienergy coordination of multimicrogrids with biogas-solar-wind renewables. IEEE Trans. Industrial Inf. 15 (6), 3254–3266. doi:10.1109/tii.2018.2877143

CrossRef Full Text | Google Scholar

Xu, D., Zhou, B., Liu, N., Wu, Q., Voropai, N., Li, C., et al. (2020). Peer-to-Peer multienergy and communication resource trading for interconnected microgrids. IEEE Trans. Industrial Inf. 17 (4), 2522–2533. doi:10.1109/tii.2020.3000906

CrossRef Full Text | Google Scholar

Yan, M., Shahidehpour, M., Paaso, A., Zhang, L., Alabdulwahab, A., and Abusorrah, A. (2021). Distribution network-constrained optimization of peer-to-peer transactive energy trading among multi-microgrids. IEEE Trans. Smart Grid 12 (2), 1033–1047. doi:10.1109/tsg.2020.3032889

CrossRef Full Text | Google Scholar

Yang, X., He, H., Zhang, Y., Chen, Y., and Weng, G. (2019). Interactive energy management for enhancing power balances in multi-microgrids. IEEE Trans. Smart Grid 10 (6), 6055–6069. doi:10.1109/tsg.2019.2896182

CrossRef Full Text | Google Scholar

Yang, X., Xu, C., He, H., Yao, W., Wen, J., and Zhang, Y. (2020a). Flexibility provisions in active distribution networks with uncertainties[J]. IEEE Trans. Sustain. Energy 12 (1), 553–567. doi:10.1109/TSTE.2020.3012416

CrossRef Full Text | Google Scholar

Yang, X., Xu, C., Zhang, Y., Yao, W., Wen, J., and Cheng, S. (2021). Real-time coordinated scheduling for ADNs with soft open points and charging stations. IEEE Trans. Power Syst. 36 (6), 5486–5499. doi:10.1109/tpwrs.2021.3070036

CrossRef Full Text | Google Scholar

Yang, X., Zhang, Y., Wu, H., Wen, J., and Cheng, S. (2020b). Enabling online scheduling for multi-microgrid systems: An event-triggered approach. IEEE Trans. Smart Grid 12 (3), 1836–1852. doi:10.1109/tsg.2020.3038436

CrossRef Full Text | Google Scholar

Yang, Z., Hu, J., Ai, X., Wu, J., and Yang, G. (2021). Transactive energy supported economic operation for multi-energy complementary microgrids. IEEE Trans. Smart Grid 12 (1), 4–17. doi:10.1109/tsg.2020.3009670

CrossRef Full Text | Google Scholar

Zhao, C., Wan, C., and Song, Y. (2020). An adaptive bilevel programming model for nonparametric prediction intervals of wind power generation. IEEE Trans. Power Syst. 35 (1), 424–439. doi:10.1109/tpwrs.2019.2924355

CrossRef Full Text | Google Scholar

Zhou, Q., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2020). Flexible division and unification control strategies for resilience enhancement in networked microgrids. IEEE Trans. power Syst. 35 (1), 474–486. doi:10.1109/tpwrs.2019.2932939

CrossRef Full Text | Google Scholar

Zhou, Q., Tian, Z., Shahidehpour, M., Liu, X., Alabdulwahab, A., and Abusorrah, A. (2019). Optimal consensus-based distributed control strategy for coordinated operation of networked microgrids. IEEE Trans. Power Syst. 35 (3), 2452–2462. doi:10.1109/tpwrs.2019.2954582

CrossRef Full Text | Google Scholar

Glossary

${\mathit{N}}_{\mathit{T}}$ Total number of time periods.

${\mathit{N}}_{\mathit{N}}$ Total number of nodes.

${\mathit{N}}_{\mathit{m}\mathit{g}}$ Total number of microgrids (MGs) inside the distribution network (DN).

${\mathbf{\Omega }}_{\mathit{l}}$ Set of all the branches.

${\mathbf{\Omega }}_{\mathit{o}}$ Set of all the branches with on-load tap changer (OLTC).

${\mathit{S}}_{\mathit{n}}$ Node set of MG n.

${\mathit{N}}_{\mathit{e}}$ Total number of energy storage system (ESS) inside the MG.

${\mathit{N}}_{\mathit{\omega }}$ Total number of discrete scenarios.

$\mathit{\omega }$ Index of scenarios.

$\mathit{\psi }$ Feasible region of $p_{\omega }$.

${\mathit{\gamma }}_{\mathit{t}}^{\mathit{b}}/{\mathit{\gamma }}_{\mathit{t}}^{\mathit{s}}$ Trading prices with HV grid.

${\mathit{g}}_{\mathit{t}}$ Net load of DN system.

${\mathit{C}}_{\mathit{l}\mathit{o}\mathit{s}\mathit{s}}/{\mathit{C}}_{\mathit{O}\mathit{L}\mathit{T}\mathit{C}}$ Cost coefficients associated with power losses and OLTC, respectively.

${\mathit{r}}_{\mathit{i}\mathit{j}}$ Resistance of branch ij.

${\mathit{I}}_{\mathit{t},\mathit{i}\mathit{j}}$ Current of branch ij at period t.

$\Delta \mathit{t}$ Discrete time interval

${\stackrel{\sim }{\mathit{U}}}_{\mathit{r}\mathit{e}\mathit{f}}$ Reference voltage point.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{P}\mathit{V}}/{\mathit{Q}}_{\mathit{t},\mathit{i}}^{\mathit{P}\mathit{V}}$ Active/reactive power injected by PV array at node i at period t.

${\mathit{\theta }}_{\mathit{k}}^{\mathit{P}\mathit{V}}$ Power factor angle of PV k.

${\mathit{S}}_{\mathit{i}}^{\mathit{P}\mathit{V}}$ Capacity of PV i.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{W}\mathit{i}\mathit{n}\mathit{d}}/{\mathit{Q}}_{\mathit{t},\mathit{i}}^{\mathit{W}\mathit{i}\mathit{n}\mathit{d}}$ Active/reactive power injected by wind turbine at node at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{L},\mathit{u}\mathit{n}\mathit{c}}$ General load at node i at period t

$\overline{\mathit{I}}$ Upper current limit.

$\overline{\mathit{U}}/\underset{\_}{\mathit{U}}$ Upper/lower limits of statutory voltage range.

${\mathit{S}}_{\mathit{i}}^{\mathit{S}\mathit{O}\mathit{P}}$ Capacity of VSC at node i.

${\underset{\_}{\mathit{Q}}}_{\mathit{i}}^{\mathit{S}\mathit{O}\mathit{P}}/{\overline{\mathit{Q}}}_{\mathit{i}}^{\mathit{S}\mathit{O}\mathit{P}}$ Reactive power boundaries of VSC at node i.

${\mathit{\lambda }}_{\mathit{t}}^{\mathbf{min}}/{\mathit{\lambda }}_{\mathit{t}}^{\mathbf{max}}$ Upper and lower bounds of the internal transaction price at period t.

${\mathit{C}}_{\mathbf{deg}}$ Coefficients concerning ESS degradation.

${\mathit{\eta }}^{\mathit{e}\mathit{s}\mathit{s},\mathit{c}}/{\mathit{\eta }}^{\mathit{e}\mathit{s}\mathit{s},\mathit{d}}$ Power exchange efficiencies of the ESS.

${\mathit{S}}_{\mathit{e}}^{\mathit{min}}/{\mathit{S}}_{\mathit{e}}^{\mathit{max}}$ SoC boundaries of ESS e.

$\mathit{\mu }/\mathit{\lambda }$ Dual variables of inequality/equality constraints in optimization model of MGs.

${\mathit{p}}_{\mathit{\omega }}$ Probability of scenario ω.

${\mathit{\delta }}_{\mathbf{1}}/{\mathit{\delta }}_{\mathit{\infty }}$ Tolerant limit of norm-1/norm-inf of the ambiguity set in the distributed robust optimization (DRO) model.

$\mathit{p}$ vector of element $p_{\omega }$.

$\mathit{m}$ Number of iterations.

$\mathit{M}$ Infinite positive integer

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{s}\mathit{o}\mathit{p},\mathit{l}\mathit{o}\mathit{s}\mathit{s}}$ Active power losses caused by SOP at period t.

${\mathit{\lambda }}_{\mathit{t}}$ Clearing price of the energy trading market at period t.

${\mathit{P}}_{\mathit{t},\mathit{n}}^{\mathit{n}\mathit{e}\mathit{t}}$ Net load of MG n at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}}/{\mathit{Q}}_{\mathit{t},\mathit{i}}$ Sum of active/reactive power injection at node i at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}\mathit{j}}/{\mathit{Q}}_{\mathit{t},\mathit{i}\mathit{j}}$ Active/reactive power flow of branch ij at period t.

${\mathit{U}}_{\mathit{t},\mathit{i}}$ Voltage magnitude of node i at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{L}}/{\mathit{Q}}_{\mathit{t},\mathit{i}}^{\mathit{L}}$ Active/reactive load consumptions of node i at period t.

${\mathit{c}}_{\mathit{t},\mathit{i}}^{\mathit{e}\mathit{s}\mathit{s}}/{\mathit{d}}_{\mathit{t},\mathit{i}}^{\mathit{e}\mathit{s}\mathit{s}}$ Charging/discharging power of ESS i at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{S}\mathit{O}\mathit{P}}/{\mathit{Q}}_{\mathit{t},\mathit{i}}^{\mathit{S}\mathit{O}\mathit{P}}$ Active/reactive power injection by VSC at node i at period t.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{L},\mathbf{u}\mathbf{p}}/{\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{L},\mathbf{d}\mathbf{o}\mathbf{w}\mathbf{n}}$ Increased/decreased load demands due to the demand response (DR) program.

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathbf{e}\mathbf{s}\mathbf{s},\mathit{c}}/{\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathbf{e}\mathbf{s}\mathbf{s},\mathit{d}}$ Charging/discharging power of ESS.

${\mathit{p}}_{\mathit{\omega }}^{+}/{\mathit{p}}_{\mathit{\omega }}^{-}$ Positive/negative probability value offset of $p_{\omega }$.

${\mathit{K}}_{\mathit{t},\mathit{i}\mathit{j}}$ Number of the tap steps and turns ratio of the OLTC connected to branch ij at period t.