Abstract
To be consistent with the actual production, this paper establishes the 2-D steady-state mathematical model of the porous media to numerically analyze influences of structural and operational parameters on the vertical cooling process by applying particle characteristic parameters, and heat transfer and resistance correlations of the multi-size sinter. Considering comprehensive effects of the temperature and pressure drop, the operating and structural parameters are optimized with the objective of the maximum income exergy of the gas. Results show that the numerical model established in this paper can well predict the gas-solid heat transfer process in the sinter bed with the maximum error of 7%. Besides, the income exergy of the gas increases and decreases with the sinter outlet temperature and gas outlet temperature increasing, respectively. The reduction in the equivalent particle diameter is conducive to improving the income exergy. What’s more, the income exergy of the gas first ascends and then descends with the increase of the flow rate ratio of gas to sinter and the height of the sinter layer. Therefore, optimal values of the flow rate ratio of the gas to sinter and the height of the sinter layer are 1,050–1,540 m3·h−1 and 7–11.5 m within the scope of this study, respectively.
Introduction
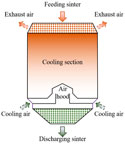
With the formulation of the double carbon strategy (Xiong et al., 2022), the industrial production should take some necessary measures, such as improving the utilization rate of the clean energy and the combustion efficiency of fossil fuels (Xu et al., 2020a; Xu et al., 2021). As the energy consumption of the iron and steel industry accounts for about 20% of the whole industry, it has become an important focus of the low-carbon development of the economy. With the gradual optimization of various processes, the efficient recovery of the waste heat has become an important way to achieve the green development for the iron and steel industry (Xu et al., 2020b), especially in the sintering process (Zhang et al., 2021a). The energy consumption of the sintering process accounts for 10–15% of the whole iron and steel industry (Zhang et al., 2013). As the horizontal structure, the sinter annular cooling process has inevitable shortcomings, making the utilization rate of the waste heat less than 30% (Zhang, 2022). Therefore, the sinter vertical cooling process is proposed by imitating the coke dry quenching process (Sun et al., 2015), as shown in Figure 1. The new process as the vertical structure not only reduces the air leakage rate, but also improves the gas-solid heat transfer efficiency. Thus, the recovery rate and the quality of the waste heat are improved from 30% to 80% and from 150 to 350°C to 450–550°C, respectively (Zhang, 2022).
FIGURE 1
Schematic diagram of the sinter vertical cooling process.
At present, the test run indicates that the improvement effect of the waste heat recovery is lower than the expected target (Bi and Sun, 2018), which is attributed to the unreasonable design of operating parameters and structural parameters. To popularize the new technology in the iron and steel field, a lot of researches have been done on pressure drop characteristics, heat transfer characteristics and the numerical optimization of the new process. Moreover, the research on pressure drop characteristics and heat transfer characteristics of the sinter has been very mature, fitting the corresponding empirical correlations. In previous studies, the pressure drop correlation of the sinter was modified by considering the effects of the particle shape (Feng et al., 2015a; Tian et al., 2016a), bed voidage (Feng et al., 2015b), equivalent particle diameter (Feng et al., 2014), confined wall (Tian et al., 2016b; Feng et al., 2019; Zhang et al., 2022a) and particle size distribution (Pan et al., 2015; Tian et al., 2016c; Zhang et al., 2021b). The results showed that the pressure drop had a linear relationship with the height of the material layer, increased in a quadratic relationship with the increase of the gas velocity, and declined exponentially with the increase of the equivalent particle diameter and bed voidage or the decrease of the shape factor. In addition, Tian et al. (Tian et al., 2016b) found that the influence of the confined wall can be neglected when the diameter ratio of bed to particle was larger than 19. When the diameter ratio of bed to particle was less than 19, the wall effect played a dominant role, reducing the pressure drop of the gas in the bed. Zhang et al. (Zhang et al., 2022a) also found that the wall effect would only reduce the pressure drop no matter what the gas flow state was. Moreover, the more irregular the sinter particles were, the weaker the wall effect was. What’s more, the research of Tian et al. (Tian et al., 2016c) showed that the resistance coefficient of the binary-size sinter was larger than that of the mono-size sinter, and the turbulent degree of the gas flow was more significant. Furthermore, Pan et al. (Pan et al., 2015) found that the 17% increase in the proportion of small particles (0–10 mm) in the sinter mixture caused the pressure drop to increase by 2–3 times. The study of Zhang et al. (Zhang et al., 2021b) also indicated that the change of the pressure drop in the multi-size sinter bed with the equivalent particle diameter was completely different from that in the mono-size sinter bed. The decreasing amplitude of the pressure drop for the multi-size sinter ascended first and then descend with the increase of the equivalent particle diameter. Also, the bed permeability of the multi-size sinter was lower than that of the mono-size sinter under the same equivalent particle diameter. In addition, the layered distribution mode of dividing the wide particle size into the narrow particle size was conducive to reducing the pressure drop (Zhang, 2022).
What’s more, previous studies (Jang and Chiu, 2009; Pan et al., 2015; Feng et al., 2016a; Liu et al., 2016; Zheng et al., 2019; Zhang, 2021; Zhang et al., 2022b) showed that the gas-solid heat transfer intensity increased with the increase of the gas velocity, bed height and sinter velocity or the decrease of the particle size. Among them, the gas velocity and the particle size had the most significant influence (Zheng et al., 2019). Additionally, Zheng et al. (Zheng et al., 2019) obtained the heat transfer coefficient of the mono-size sinter by the logarithmic mean temperature difference method based on the moving bed, and fitted it into the heat transfer correlation by the dimensionless method. It was also found that the change trend of the measured heat transfer coefficient with the Reynolds number was similar to that of the predicted value calculated by Wakao et al. (Wakao et al., 1979). However, the irregular shape of the sinter led to the large deviation in the value. Besides, Feng et al. (Feng et al., 2016a) measured the gas temperature at the inlet and outlet of the sinter fixed bed. The arithmetic mean value of them was taken as the mean temperature of the whole bed. Then the logarithmic mean temperature difference method was used to obtain the heat transfer correlation of the mono-size sinter. Based on the heat-mass transfer analogy method, Liu et al. (Liu et al., 2016) applied the naphthalene sublimation technology to obtain the heat transfer coefficient of the mono-size sinter, and found that it was about 40% lower than the predicted value of previous correlations (Wakao et al., 1979). By combining experimental and numerical methods, Jang et al. (Jang and Chiu, 2009) fitted the heat transfer correlation of the mono-size sinter for the cross-flow heat transfer mode of the annular cooling process. In addition, Pan et al. (Pan et al., 2015) showed that the heat transfer performance of the sinter mixture with 17% small particles was lower than that of the sinter mixture without small particles. This indicated that widening the range of the particle size distribution was not conducive to the gas-solid heat transfer. Therefore, Zhang et al. (Zhang, 2021) considered the influence of the particle size distribution to obtain the heat transfer correlation of the multi-size sinter by using the inverse problem method (Zhang et al., 2022b), which was more consistent with the actual heat transfer law. Besides, the heat transfer performance of the multi-size sinter was lower than that of the mono-size sinter, which was attributed to the heterogeneous stacking structure (Zhang, 2021).
The above experimental studies on pressure drop and heat transfer characteristics lay a foundation for the numerical study of the sinter vertical cooling process. First of all, Dong et al. (Dong et al., 2012) showed that the flow rate ratio of gas to sinter and the height of the material layer were the most significant parameters affecting the waste heat recovery. It was also found that the gas exergy had a maximum value with the change of the flow rate ratio of gas to sinter and the height of the material layer. This indicated that these two parameters had an optimal value. However, the empirical correlation of the coke was used for the calculation of the heat transfer coefficient. The meaning of the gas exergy and geometric parameters of the sinter were not also clarified. Considering the combined effect of the temperature and pressure drop, Zhang et al. (Zhang et al., 2019) found that the most significant parameter affecting the dimensionless exergy consumption was the bed diameter, followed by the gas flow rate, bed height and sinter flow rate. However, the pressure drop and temperature fields were numerically predicted by the pressure drop and heat transfer correlations and particle characteristic parameters of the mono-size sinter. Feng et al. (Feng et al., 2016b; Feng et al., 2020) also only applied the heat transfer and pressure drop correlations of the mono-size sinter to optimize the structural and operating parameters of the vertical cooling process. When only considering the influence of the temperature on the gas exergy, the optimal values of the bed diameter, bed height, and gas flow rate for the sinter with an annual output of 3.9 million tons were 10 m, 8 m, 150 kg·s−1, respectively (Feng et al., 2016b). Based on the comprehensive influence of the temperature and pressure drop, the optimal values of the bed diameter, bed height, and gas flow rate for an annual output of 3.9 million tons are 9 m, 8 m, 180 kg·s−1, respectively (Feng et al., 2020). This indicated that the optimization results would change with different optimization objectives. However, the pressure drop determined the energy consumption and gas flow characteristics, which affected the gas-solid heat transfer process and the gas outlet temperature. Moreover, the heights of the material layer in the vertical cooler and the annular cooler were 7–10 m (Feng et al., 2016b; Zhang et al., 2019; Feng et al., 2020) and .8–1.5 m (Liu et al., 2014; Feng et al., 2016c), respectively. The difficulty of the gas flowing through the vertical cooler was much higher than that of the annular cooler. It further indicated that the effect of the pressure drop on the waste heat recovery could not be ignored.
It can be seen that previous numerical studies did not consider the influence of the particle size distribution, and only applied pressure drop and heat transfer correlations of the mono-size sinter to investigate the vertical cooling process. This was inconsistent with the multi-size distribution characteristic in the actual production (Tian et al., 2016a; Zhang et al., 2021b). Moreover, previous studies (Pan et al., 2015; Tian et al., 2016c; Zhang et al., 2021b; Zhang, 2021) showed that the heat transfer performance and pressure drop of the multi-size sinter were lower and higher than those of the mono-size sinter, respectively. In addition, Koekemoer et al. (Koekemoer and Luckos, 2015) and Rong et al. (Rong et al., 2014) showed that the wide particle size distribution enhanced the inhomogeneity of the local structure and gas flow. Byon et al. (Byon and Kim, 2013) found that the permeability decreased in a quasi-linear relationship with the particle size range broadening. Keyser et al. (Keyser et al., 2006) also indicated that the wider the particle size distribution, the greater the pressure drop in the bed, and the more uneven the distribution of the gas flow. Wu et al. (Wu et al., 2016) found that the viscous and inertial resistance coefficients were totally different under the uniform and non-uniform particles. What’s more, Yang et al. (Yang et al., 2016) showed that the flow and temperature fields under the uniform and non-uniform particles were different. Besides, the heat transfer performance of non-uniform particles was significantly lower than that of uniform particles (Yang et al., 2012). This was attributed to that the pressure drop and heat transfer performance under the ordered packing mode was lower and better than those under the disordered packing mode, respectively (Wang et al., 2018).
The above studies prove that the particle size distribution affects the uniformity of the packed structure and gas flow, determining heat transfer and pressure drop characteristics. Therefore, this paper established a 2-D steady-state porous medium model to numerically analyze the influence of operating and structural parameters on the outlet temperature and pressure drop by using the heat transfer and pressure drop correlations of the multi-size sinter. Considering the comprehensive influence of the temperature and pressure drop, the optimization is carried out with the objective of the maximum income exergy of the gas, providing the theoretical reference for the engineering practice.
Establishment of numerical methods
Assumptions and physical models
During the sinter cooling process, the countercurrent convection heat transfer between the hot sinter and the cooling air is essentially carried out in the porous medium formed by the accumulation of sinter particles. To facilitate the study, the following assumptions are made (
Feng et al., 2016b).
(1) Under the stable operation, the temperature in the vertical furnace basically does not change with the time, which can be regarded as a steady heat transfer process.
(2) As the size of the sinter is much smaller than that of the vertical furnace, the sinter layer can be seen as the homogeneous porous media.
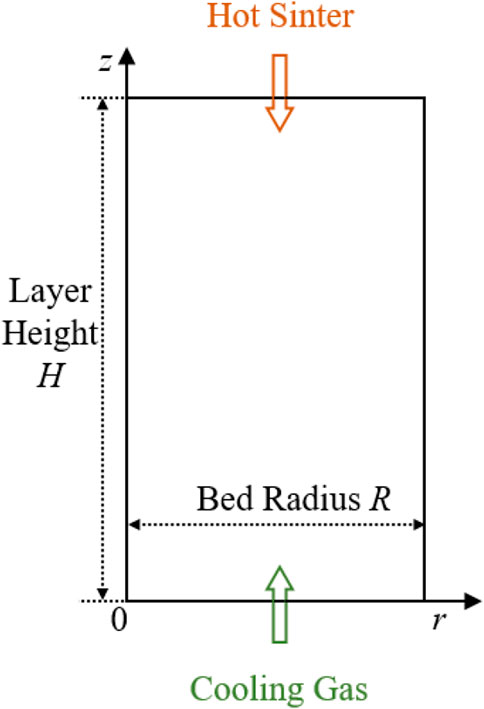
(3) On the basis of ignoring the air hood, it is considered that the inner diameters of the inlet and outlet of the cooling section are the same.
(4) The sinter and gas only flow evenly along the vertical direction, ignoring the circumferential and radial velocities and the circumferential heat transfer.
(5) There is the local thermal non-equilibrium between the sinter and gas, which transfers the heat through the forced convection.
Based on the above assumptions, the cooling section of the vertical furnace can be simplified as a two-dimensional physical model, as shown in Figure 2.
FIGURE 2
Physical model of the cooling section of the sinter vertical cooling process.
Mathematical model
Based on the reasonable assumptions, this paper establishes a two-dimensional steady-state mathematical model of the porous media.
(1) Energy equation of the gas
where
rand
zare the axial direction and radial direction of the material layer, respectively, m;
is the bed voidage;
and
are the gas temperature and the sinter temperature, respectively, K.
,
,
and
are the coefficient of the heat conductivity, velocity, specific heat, and density of the gas, respectively, W·m
−1·K
−1, m·s
−1, J·kg
−1·K
−1, and kg·m
−3.
(2) Energy equation of the sinter
where
,
,
and
are the coefficient of the heat conductivity, velocity, specific heat, and density of the sinter, respectively, W·m
−1·K
−1, m·s
−1, J·kg
−1·K
−1, and kg·m
−3;
is the specific surface area, m
−1;
is the surface heat transfer coefficient calculated by Eq.
3, W·m
−2·K
−1:
where
is the equivalent particle diameter of the sinter, m;
represents the Nusselt number of the convective heat transfer intensity. For the Nusselt number of the multi-size sinter, the experimental correlation obtained by the inverse problem method in our previous work (
Zhang, 2021) is used, as follows:
where
is the Prandtl number of the gas;
is the particle Reynolds number representing the gas flow state, which is calculated by:
where
is the viscosity coefficient of the gas, Pa·s
−1.
The boundary conditions set for the gas-solid energy equation are described as:
(i) Boundary conditions of the gas
where
is the inlet temperature of the gas, K.
(ii) Boundary conditions of the sinter
where
is the inlet temperature of the sinter, K.
(3) Momentum equation
In our previous work (Zhang et al., 2021b), the empirical correlation of the pressure drop for the multi-size sinter was obtained through the experimental method. Based on the above assumptions, this paper uses the pressure drop equation instead of the momentum equation, as follows:where is the pressure drop of the gas through the sinter bed, Pa; H is the height of the material layer, m.
Solution method and verification of the mesh independence
The solution method of the numerical model consists of three steps, which are the discretization of meshes, discretization of the differential energy equation and solution of the algebraic equation system, respectively (Zhang et al., 2022b). Firstly, the physical model is meshed by the external node method to determine the node position and mesh element. What’s more, the differential energy equations of the gas and solid for each mesh element are discretized into the algebraic equation by using the control volume method. By sorting out the discrete equation of each mesh element, two sets of tridiagonal algebraic equation systems on the gas temperature and solid temperature can be obtained. The initial value of the gas and solid temperature is assigned by reasonable assumptions. Based on the assumptions, two sets of algebraic equation systems are solved by the tridiagonal matrix algorithm, obtaining the new value of the temperature. Based on the new value, the tridiagonal matrix algorithm is used to solve the algebraic equation system repeatedly until the temperature difference between the two results is less than 10−3. Finally, this paper uses the computer language C# to write the program to realize the above algorithm and calculation process.
To obtain the solution independent of meshes, two limiting conditions are selected in this paper with the equivalent particle diameter of 11.45 mm and 30.95 mm, respectively. The outlet temperature of the sinter and gas that significantly affects the process feasibility are taken as parameters to verify the mesh independence, as shown in Figure 3. It is observed that the effect of increasing the number of meshes on the outlet temperature of the gas and sinter is no longer significant when the number of meshes is greater than 280,000. The further increase of meshes will greatly increase the amount of the calculation, while the improvement of the calculation accuracy is limited to less than 0.5%. Therefore, the mesh number is set to 280,000 in the numerical simulation.
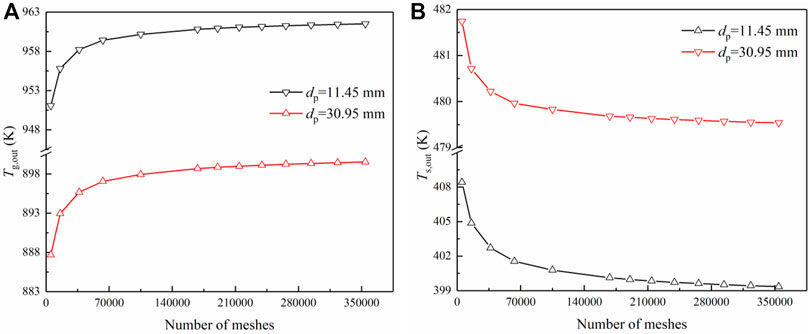
FIGURE 3
Variation of the temperature with the number of meshes: (A) Outlet temperature of the gas ; (B) Outlet temperature of the sinter .
Verification of the numerical model
At present, there are few successful cases of the sinter vertical cooling technology applied in the engineering. Therefore, this paper applies the pilot experimental data of three kinds of the mono-size sinters in Ref (Dong, 2015). to verify the accuracy of the numerical model. The particle sizes of three kinds of the mono-size sinter are 5–10 mm, 10–15 mm and 15–20 mm, respectively. The height of the material layer is 0.4 m. The inlet temperatures of the sinter and gas are 873 K and 293 K, respectively. The moving speed of the sinter is 0.95 mm s−1. The gas flow velocities are 1.38, 1.58, 1.73 and 1.92 m s−1, respectively. According to the above conditions, the sinter outlet temperature and the gas outlet temperature are calculated by using the numerical model in this paper, which are compared with the measured values, as shown in Figure 4. It can be observed that the maximum errors of and are within 6% and 7%, respectively. This indicates that the numerical model established in this paper is accurate, which can well predict the gas-solid heat transfer process of the sinter.
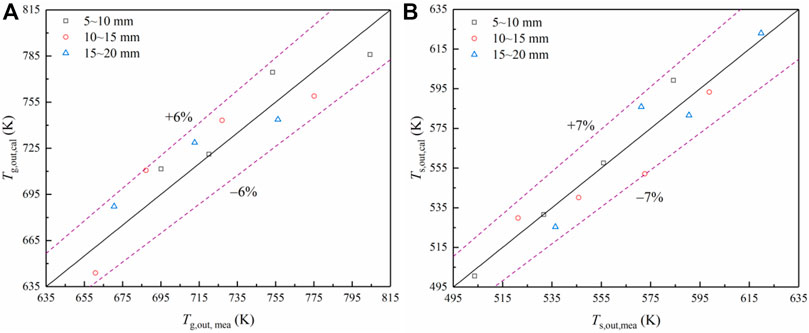
FIGURE 4
(A) Comparison between predicted values and measured values of the gas outlet temperature; (B) Comparison between predicted values and measured values of the sinter outlet temperature.
Basic parameters and optimization criteria of the vertical cooling process
Basic parameters of the vertical cooling process
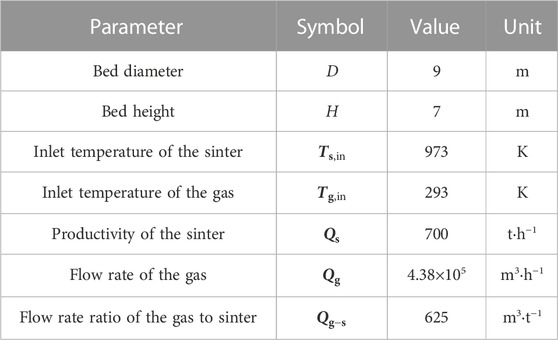
Based on the production site, the process parameters and particle characteristic parameters applied in the numerical model are designed and measured so as to provide the effective guidance. First of all, the structure parameters and operating parameters set in the numerical study are from the production site of HBIS Group Co., Ltd., as shown in Table 1. Moreover, five batches of the sinter mixture are selected from the sintering production site. From our previous work (Zhang et al., 2021b), it can be seen that the sinter with the particle size of 5–60 mm accounts for more than 85% of the total weight. Therefore, this paper studies the multi-size sinter mixture with this typical particle size, as shown in Figure 5. To adapt to the production fluctuation, six types of the multi-size sinter composed of 11 kinds the mono-size sinter are designed based on the original particle size distribution (Zhang et al., 2021b), as shown in Figure 6.
TABLE 1
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Bed diameter | D | 9 | m |
| Bed height | H | 7 | m |
| Inlet temperature of the sinter | 973 | K | |
| Inlet temperature of the gas | 293 | K | |
| Productivity of the sinter | 700 | t·h−1 | |
| Flow rate of the gas | 4.38×105 | m3·h−1 | |
| Flow rate ratio of the gas to sinter | 625 | m3·t−1 |
Structural and operating parameters of the sinter vertical cooling process.
FIGURE 5
(A) Multi-size sinter of 5–60 mm; (B) Mono-size sinter of 5–10 mm; (C) Mono-size sinter of 20–25 mm; (D) Mono-size sinter of 55–60 mm.
FIGURE 6
Mass fraction of each mono-size sinter in six types of the multi-size sinters.
To obtain accurate particle characteristic parameters, the thermophysical and geometric properties of the sinter are measured, respectively. First of all, the specific heat and thermal conductivity of the sinter at different temperatures are measured by the simultaneous thermal analyzer (DSC 404F3) and laser thermal conductivity instrument (LFA 467HT), which are fitted into the following equation:
For the multi-size particle composed of various mono-size irregular particles, the equivalent particle diameter and apparent density can be calculated by the weighted harmonic mean method with Eq. 15 (Keyser et al., 2006; Koekemoer and Luckos, 2015) and the weighted mean method with Eq. 16 (Tian et al., 2016c; Zhang et al., 2021b):where is the mass fraction of each mono-size particle in the multi-size particle, wt%; is the equivalent particle diameter of each mono-size sinter, mm; is the apparent density of each mono-size sinter, kg·m−3. The apparent density represents the mass of the material per unit apparent volume. The apparent volume includes the solid volume of particles and the volume of closed pores inside particles. In our previous work (Zhang et al., 2021c), the equivalent particle diameter and apparent density of the mono-size sinter are measured by the equal volume sphere method and drainage method, respectively. The bed voidage is calculated by the bulk density and apparent density as follows:where is the bulk density, kg·m−3, which is measured by the weighing method with the known-volume container (Tian et al., 2016a; Zhang et al., 2021c). The bulk density refers to the mass of the material per unit bulk volume, which consists of the volume of closed pores inside particles, the solid volume of particles and the volume of voids between particles. The geometric parameters of the multi-size sinter obtained by the above method are shown in Figure 7. First of all, the equivalent particle diameters of the six kinds of the multi-size sinters are 11.45, 15.35, 19.25, 23.15, 27.05, and 30.95 mm, respectively. What’s more, the apparent density decreases with the increase of the equivalent particle diameter. The previous work (Zhang et al., 2021c) shows that the number of closed pores inside particles increases with the increase of the particle size. This makes of the mono-size sinter decrease with the increase in the particle size. Additionally, Figure 6 shows that the content of small particles and large particles in the multi-size sinter decreases and increases with the increase of , respectively. Moreover, it is observed that the bulk density also declines with the increase of . Firstly, the apparent density shows a similar trend. Secondly, the content of large particles in the multi-size sinter gradually increases. This makes the void between particles increase. Meanwhile, this is the reason why the bed voidage increases with the increase in .
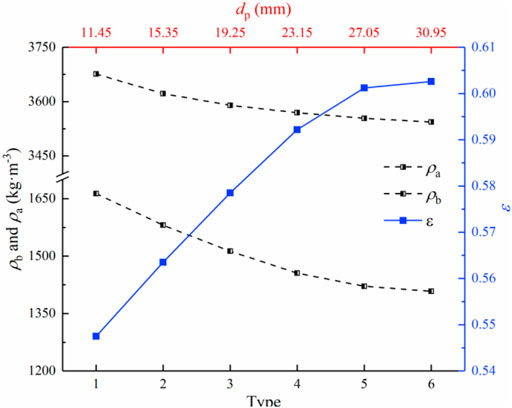
FIGURE 7
Equivalent particle diameter , apparent density , bulk density and bed voidage of six kinds of multi-size sinters.
In addition, Figure 8 compares the bed voidage of the mono-size and multi-size sinters under the same equivalent particle diameter. First of all, the bed voidage of the multi-size sinter is lower than that of the mono-size sinter. For the multi-size sinter, the small particles will fill the gaps between large particles, making the packing denser. In addition, the voidage difference reduces with increasing from 19.25 mm to 30.95 mm. The voidage difference corresponding to 19.25 mm and 30.95 mm are 0.0296 and 0.0175 with the reducing extent of 40.88%, respectively. With the increase in , the content of small particles in the multi-size sinter declines. It reduces the mixing degree of particles and improves the uniformity of the void structure. Therefore, the particle size composition has a significant impact on the size and distribution uniformity of the void in the sinter bed. This further indicates that it is necessary to carry out the numerical research on the cooling process of the multi-size sinter.
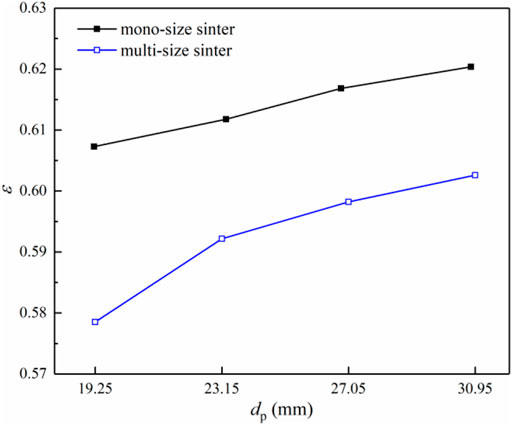
FIGURE 8
Comparison of the bed voidage between the mono-size sinter and multi-size sinter under the same equivalent particle diameter .
Optimization criteria of the vertical cooling process
In this paper, the exergy is applied to analyze the effect of the process parameter based on the quantity and quality of the waste heat. From the inlet to the outlet of the vertical furnace, the change of the gas exergy includes the temperature exergy and pressure exergy . and are related to the temperature rise and pressure drop of the gas, which can be given by Eqs. 18, 19 (Feng et al., 2020):where and are the temperature exergy and pressure exergy of the gas per unit time, MW; is the mass flow rate of the gas, kg·s−1; and represent the temperature and pressure of the gas, K and Pa; and are the gas temperature at the outlet and inlet of the vertical furnace, K; and are the gas pressure at the inlet and outlet of the vertical furnace, Pa; and represent the ambient temperature and the ambient pressure, K and Pa; is the pressure drop of the gas through the sinter layer in the vertical furnace, Pa; = 287.05 is the gas constant, J·kg−1·K−1.
Based on the comprehensive influence of the temperature and pressure drop, the process parameters are numerically optimized based on the income exergy of the gas, as follows (Feng et al., 2020):where represents the income exergy of the gas, MW.
Results and discussion
Analysis of temperature fields in the sinter bed
The sinter vertical cooling process is calculated by the numerical model. Taking the multi-size sinter with the equivalent particle diameter of 11.45 mm as an example, Figure 9 analyses the temperature field of the sinter and gas. First of all, it is observed that the gas temperature increases from 293 K to 935.79 K from the bottom to the top of the bed. Moreover, the sinter temperature decreases from 973 K to 341.10 K from the bed top to the bed bottom. There exists the temperature difference between the gas and solid, leading to the convection heat transfer. Therefore, the cooling gas gains the amount of the heat, increasing the gas temperature. While the hot sinter loses the amount of the heat, making the sinter temperature reduce.
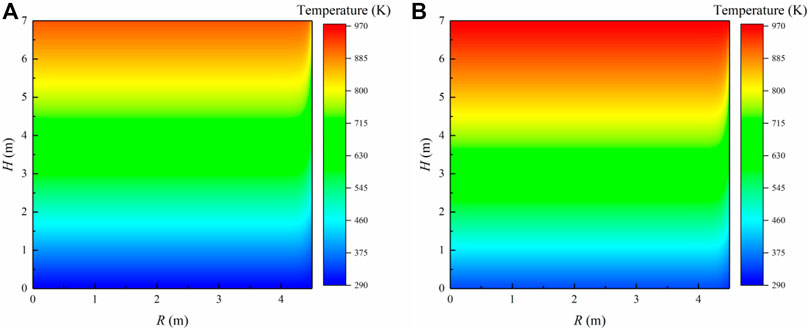
FIGURE 9
Temperature fields of the multi-size sinter bed with the equivalent particle diameter of 11.45 mm: (A) Gas; (B) Sinter.
Effect of the sinter inlet temperature on the cooling process
Figure 10 illustrates the influence of the sinter inlet temperature on the sinter outlet temperature , gas outlet temperature , pressure drop , temperature exergy , pressure exergy and income exergy . First of all, Figure 10A shows that both and increase with the increase of . This indicates that the increase of is beneficial to the improvement of the quality of the waste heat. The gas-solid temperature difference increases with increasing. Therefore, the increase in the quantity of the heat exchange makes improve. Meanwhile, this is the reason why the increasing extent of is lower than that of . When increases from 873 K to 1073 K, only increases from 351.07 K to 384.11 K.
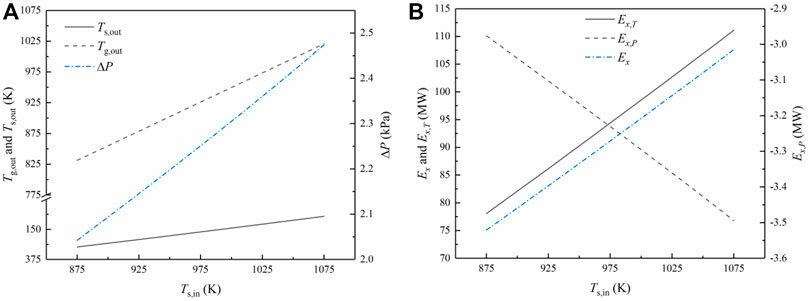
FIGURE 10
Influences of the sinter inlet temperature on the cooling process: (A) Change of the sinter outlet temperature , gas outlet temperature and pressure drop with ; (B) Change of the temperature exergy , pressure exergy and income exergy with .
Moreover, the increase of leads to the increase in the pressure drop . The gas temperature in the sinter bed improves with increasing. Therefore, the gas density reduces, making the gas flow velocity increase. It makes the gas flow more disordered, increasing the pressure drop of the gas through the sinter layer (Feng et al., 2015b; Zhang et al., 2021c). Additionally, it can be seen from Figure 10B that the temperature exergy and pressure exergy increase with the increase of . This is attributed to an increase in and . Besides, the increasing extent of is less than that of . It leads to the improvement of the income exergy with increasing . Therefore, the heat loss of the hot sinter during the transportation process shall be cut down as much as possible so as to improve the sinter temperature at the inlet.
Effect of the gas inlet temperature on the cooling process
Figure 11 illustrates the influence of the gas inlet temperature on the sinter outlet temperature , gas outlet temperature , pressure drop , temperature exergy , pressure exergy and income exergy . First of all, it can be observed from Figure 11A that improves with the increase of . The gas-solid temperature difference declines with the increase of , leading to the reduction of the released heat from the hot sinter. It is also found that increases with increasing. This implies that the quality of the waste heat is improved. However, the reduction of the temperature difference would reduce the amount of the absorbed heat for the gas. Therefore, the increasing extent of is lower than that of . With increasing from 293 K to 423 K, only increases from 874.59 K to 895.62 K. Moreover, increases as increases. The gas temperature improves with the increase in . As a result, the gas density reduces, making the gas velocity increase.
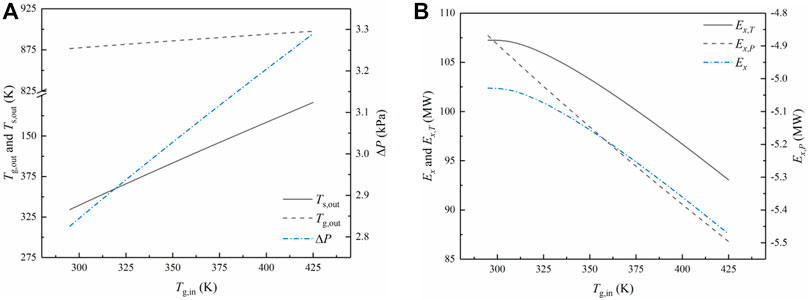
FIGURE 11
Influences of the gas inlet temperature on the vertical cooling process: (A) Change of the sinter outlet temperature , gas outlet temperature and pressure drop with ; (B) Change of the temperature exergy , pressure exergy and income exergy with .
In addition, Figure 11B shows that the temperature exergy reduces with increasing. This is caused by the fact that the increasing extent of is lower than that of . Besides, the increase of leads to the increase in the pressure exergy . Therefore, the income exergy declines with increasing. It can be concluded that the increase of not only causes a limited increase in the quality of the waste heat, but also significantly reduces . Therefore, the fresh air should be supplemented at the gas inlet to minimize the gas inlet temperature as much as possible.
Effects of the equivalent particle diameter on the cooling process
Figure 12 shows the change of the sinter outlet temperature , gas outlet temperature , pressure drop , temperature exergy , pressure exergy , and income exergy with the equivalent particle diameter . First of all, it can be observed from Figure 12A that and increase and decrease with increasing, respectively. The heat transfer intensity of the gas-solid convection declines with the increase of (Zhang et al., 2022b). Firstly, the specific surface area of particles declines with increasing, reducing the total area of the gas-solid heat transfer. Secondly, the bed voidage increases as increases. The reduction of the gas velocity makes the turbulent degree of the gas decrease. It can increase the thickness of the boundary layer of particles, improving the heat transfer resistance. These two aspects reduce the amount of the gas-solid heat exchange with the increase of . This makes the temperature drop of the sinter and the temperature rise of the gas decrease. Moreover, the pressure drop declines exponentially with the increase of (Feng et al., 2015b). First of all, the decrease in the gas velocity reduces the collision frequency between particles and gases, and the velocity gradient of the boundary layer. It leads to the reduction in the inertial and viscous resistance of the gas flow. Secondly, the gas-solid contact is insufficient, further reducing the viscous resistance.
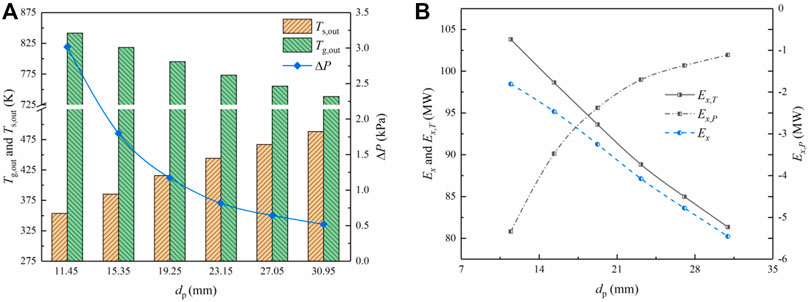
FIGURE 12
The influence of the equivalent particle diameter on the vertical cooling process: (A) Change of the sinter outlet temperature , gas outlet temperature and pressure drop with ; (B) Change of the temperature exergy , pressure exergy and income exergy with .
Additionally, Figure 12B indicates that both the temperature exergy and pressure exergy decline with the increase of , which is attributed to the reduction of and . However, the decreasing extent of is lower than that of , making the income exergy decline with increasing. Therefore, the reduction of increases the quality of the waste heat and the income exergy. On the premise of ensuring the particle size of the sinter applied in the ironmaking process, the particle size of the sinter produced by the sintering machine should be reduced as much as possible.
Effect of the flow rate ratio of gas to sinter on the cooling process
The influence factors of the sinter cooling process also include the sinter flow rate and gas flow rate. Moreover, both of them have a significant impact on the gas flow rate per ton of the sinter. Thus, Figure 13 analyses the influence of the flow rate ratio of gas to sinter on the sinter outlet temperature , gas outlet temperature , pressure drop , temperature exergy , pressure exergy and income exergy . It can be discovered from Figure 13A that both and reduces with the increase of . Moreover, the change range of and gradually decreases and increases, respectively. The increase of has a significant impact on the two aspects. Firstly, the increase of the gas velocity improves the intensity and amount of the gas-solid heat transfer. Secondly, the increase in the gas flow rate means the increase of the total heat required to heat the gas to the same temperature. These two reasons make decline with the increase of . However, gradually approaches the gas inlet temperature with increasing. Therefore, the decreasing extent of gradually declines. In addition, the sinter heat has not been released completely when is relatively low. Therefore, the improvement of the heat transfer intensity makes the decreasing extent of relatively low. When is very high, the sinter heat is completely released, resulting in an increase in the decreasing extent of .
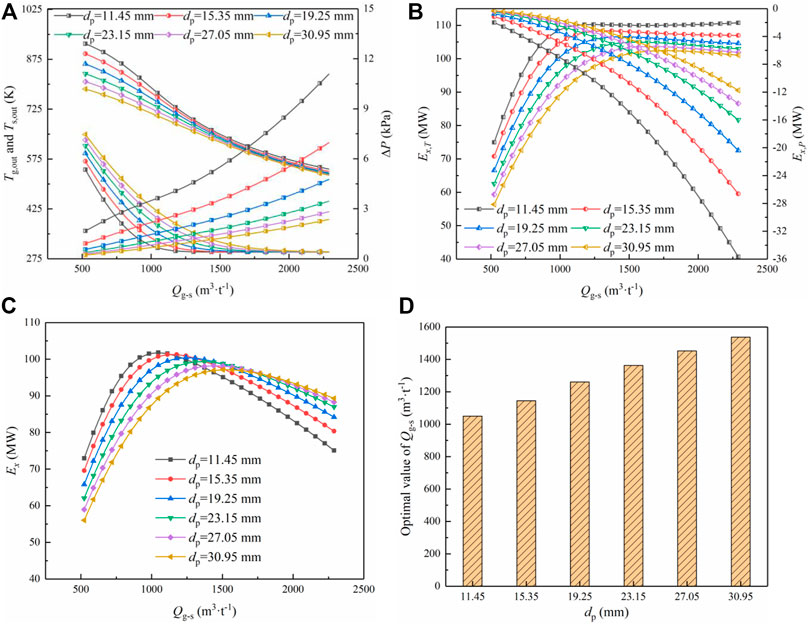
FIGURE 13
The influence of the flow rate ratio of gas to sinter on the vertical cooling process under different multi-size sinters: (A) Change of the sinter outlet temperature , gas outlet temperature and pressure drop with ; (B) Change of the temperature exergy , and pressure exergy with ; (C) Change of the income exergy with ; (D) Change of the optimal value of with the equivalent particle diameter .
Also, the pressure drop increases approximately in a quadratic relationship with increasing (Feng et al., 2015b). The gas temperature reduces with the increase in . So the gas density in the bed becomes large, making the gas velocity reduce. But the increase in means the direct increase in the gas velocity, which is far greater than the influence of the gas temperature. Therefore, the gas velocity improves as increases, resulting in the increase of the inertial and viscous resistance.
Figure 13B shows that the temperature exergy first increases and then decreases slightly with the increase of . According to Eq. 18, is mainly affected by the flow rate and outlet temperature of the gas. When is relatively low, the gas outlet temperature is relatively high and the change range is very small. Under this working condition, is mainly controlled by the gas flow rate, which increases rapidly with the increase of . When is very high, the gas outlet temperature is relatively low and the variation range increases. This makes the outlet temperature and flow rate of the gas have the same influence on . Therefore, it makes only slightly decline with the continuous increase of . Besides, it is found that the pressure exergy increases in a quadratic relationship with increasing, which is similar to the change trend of the pressure drop.
Moreover, Figure 13C indicates that the income exergy first ascends and then descends with the increase of . This indicates that there exists an optimal value of when is adjusted to an appropriate value. When is relatively small, the increasing extent of is lower than that of . At the large , tends to be unchanged, while continues to increase. Furthermore, the increasing rate and decreasing rate of increase with the equivalent particle diameter reducing. The reduction of improves the intensity of the heat transfer and the turbulent degree of the gas. Therefore, the change rate of and also increases with the decrease in . Figure 13D illustrates the change of the optimal value of with the equivalent particle diameter . It is found that the optimal value of is 1,050–1,540 m3 h−1 within the scope of this study, and increases with the increase in . The heat transfer intensity improves with the reduction of . Therefore, the smaller the equivalent particle diameter is, the lower the flow rate ratio of gas to sinter required to achieve the same heat transfer effect. The quantitative relationship between the optimal value of and can provide the theoretical guidance for the engineering application. Thus, the waste heat recovery effect can be maximized with the minimum energy consumption.
Effect of the height of the sinter layer on the cooling process
The height of the material layer also has a significant impact on the waste heat recovery. Firstly, the height of the material layer determines the time of the gas-solid heat transfer, affecting the quality and quantity of the waste heat. Secondly, the height of the material layer significantly influences the pressure drop of the gas through the bed, determining the pressure and energy consumption of the fan. Thirdly, the height of the material layer determines the height of the cooling section, affecting the construction cost. Thus, Figure 14 studies the influence of the height of the material layer H on the sinter outlet temperature , gas outlet temperature , pressure drop , temperature exergy , pressure exergy and income exergy .
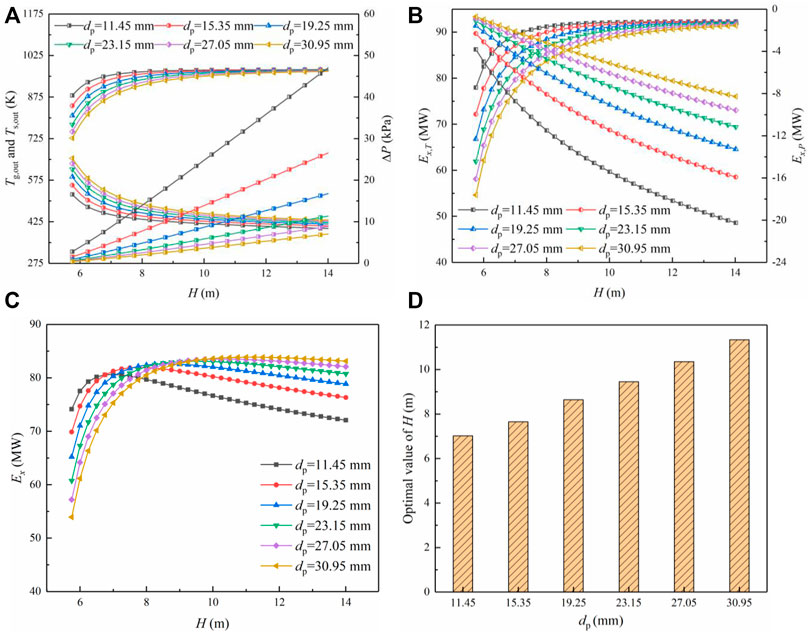
FIGURE 14
The influence of the height of the sinter layer H on the vertical cooling process under different multi-size sinters: (A) Change of the sinter outlet temperature , gas outlet temperature and pressure drop with H; (B) Change of the temperature exergy , and pressure exergy with H; (C) Change of the income exergy with H; (D) Change of the optimal value of H with the equivalent particle diameter .
Figure 14A shows that both and first increase and then tend to be constant with the increase of H. When other parameters remain unchanged, and depends on the heat transfer time and the water equivalent ratio of gas to sinter. First of all, the heat transfer time increases with H increasing, which makes and decrease and increase, respectively. As H continues to increase, the gas-solid heat transfer is completely sufficient. This makes and tend to be constant. Secondly, the water equivalent of the sinter is greater than that of the gas under this flow rate ratio of gas to sinter. Therefore, is close to the sinter inlet temperature. While the asymptotic value of is 423 K, which is higher than the gas inlet temperature. Besides, the pressure drop increases in an approximate linear relationship with the increase of H, which is in line with previous studies (Feng et al., 2015a; Zhang et al., 2021c).
It can be also discovered from Figure 14B that the temperature exergy first ascends and then tends to be constant with H increasing, which is attributed to the similar change of . Besides, the pressure exergy improves with the increase in H, which is caused by the increase of the pressure drop. Figure 14C shows that the income exergy first ascends and then descends with the increase in H. It indicates that there is an optimum value for the height of the sinter layer. When H is relatively low, both and increase with H increasing. However, the increasing extent of is smaller than that of . This leads to the increase in the income exergy with the increase of H. As H continues to increase, tends to be constant, while continues to increase. It causes to decline with the continuous increase of H. In addition, the ascending speed of is higher than that of descending speed of . is mainly affected by the pressure drop and outlet temperature of the gas . Moreover, the change range of is far higher than that of . When H is relatively low, changes greatly so much that it becomes the dominant factor. With H continuing to increase, is basically unchanged, making become the controlling factor.
Figure 14D shows that the optimal value of H is 7–11.5 m within the scope of this study, and declines with the reduction of the equivalent particle diameter . The smaller is, the larger the heat transfer intensity is. To achieve the same heat transfer effect, the gas-solid contact time required for the small-size sinter is shortened. The optimization of the height of the material layer not only contributes to reducing the energy consumption, but also helps to obtain the maximum waste heat recovery effect with the minimum investment cost.
Conclusion
To realize the dual carbon strategy in the iron and steel industry, it is necessary to study the vertical waste heat recovery technology of the sinter. At present, previous numerical studies are inconsistent with the non-uniform particle size distribution in the actual production. Therefore, a 2-D steady-state numerical model is established to analyze the gas-solid heat transfer process by using the heat transfer and pressure drop correlations, and particle characteristic parameters of the multi-size sinter. Considering the effects of the pressure drop and temperature, the operating parameters and structural parameters are optimized with the objective of the income exergy.
With the increase in the sinter inlet temperature , the increasing extent of the temperature exergy is higher than that of the pressure exergy , improving in the income exergy . Therefore, the heat loss of the sinter during the transmission process should be reduced as much as possible. In addition, and decrease and increase with the gas inlet temperature increasing, respectively, which makes decline. Therefore, the fresh air shall be supplemented at the inlet as much as possible. Moreover, the decreasing extent of is lower that of with the increase in the equivalent particle diameter , causing to decline. Therefore, the sinter size should be reduced as much as possible on the premise of ensuring the size of the sinter in ironmaking process.
With the flow rate ratio of gas to sinter increasing, first increases and then decreases slightly, while increases approximately in a quadratic relationship. This makes first increase and then decrease with the increase of . Therefore, the optimal value of is 1,050–1,540 m3·h−1 within the scope of this study, and increases with the increase of . Besides, first increases and then tends to remain unchanged with the increase in the bed height H, while has been increasing. This makes first ascend and then descend with the increase of H. Therefore, the optimal value of H is 7–11.5 m within our investigated conditions, and increases with the increase of .
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
SZ: Writing-Original Draft, Investigation. LH: Writing-Review and Editing. XL: Supervision. HW: Conceptualization.
Acknowledgments
This work is supported by Fundamental Research Funds for the Central Universities (FRF-TP-22-077A1).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Bi C. Sun J. (2018). Application of process to recycle sensible heat of sinter using vertical cooling furnace in Meisteel. Sinter. Pelletizing43 (4), 69. (in Chinese). 10.13403/j.sjqt.2018.04.061
2
Byon C. Kim S. J. (2013). The effect of the particle size distribution and packing structure on the permeability of sintered porous wicks. Int. J. Heat. Mass Transf.61, 499–504. 10.1016/j.ijheatmasstransfer.2013.02.025
3
Dong H. (2015). Experimental study on gas-solid heat transfer coefficient of layer in vertical tank for recovering sintering waste heat in some working conditions. Shenyang: Northeastern University. (Dissertation of Master Degree).
4
Dong H. Li L. Cai J. Li J. (2012). Numerical simulation of heat exchange in vertical tank of waste heat recovery. J. Northeast. Univ. Nat. Sci.33 (9), 1299–1302. (in Chinese). 10.12068/j.issn.1005-3026.2012.09.020
5
Feng H. Chen L. Liu X. Xie Z. Sun F. (2016). Constructal optimization of a sinter cooling process based on exergy output maximization. Appl. Therm. Eng.96, 161–166. 10.1016/j.applthermaleng.2015.11.089
6
Feng J. Dong H. Dong H. (2015). Modification of Ergun’s correlation in vertical tank for sinter waste heat recovery. Powder Technol.280, 89–93. 10.1016/j.powtec.2015.04.033
7
Feng J. Dong H. Gao J. Li H. Liu J. (2016). Numerical investigation of gas-solid heat transfer process in vertical tank for sinter waste heat recovery. Appl. Therm. Eng.107, 135–143. 10.1016/j.applthermaleng.2016.06.175
8
Feng J. Dong H. Gao J. Liu J. Liang K. (2016). Experimental study of gas-solid overall heat transfer coefficient in vertical tank for sinter waste heat recovery. Appl. Therm. Eng.95, 136–142. 10.1016/j.applthermaleng.2015.11.058
9
Feng J. Dong H. Li M. Cai J. (2014). Resistance characteristics of fixed bed layer in vertical tank for recovering sinter waste heat. J. Central South Univ. Sci. Technol.45 (8), 2566–2571. (in Chinese).
10
Feng J. Dong H. Liu J. Liang K. Gao J. (2015). Experimental study of gas flow characteristics in vertical tank for sinter waste heat recovery. Appl. Therm. Eng.91, 73–79. 10.1016/j.applthermaleng.2015.07.050
11
Feng J. Zhang S. Dong H. Pei G. (2019). Frictional pressure drop characteristics of air flow through sinter bed layer in vertical tank. Powder Technol.344, 177–182. 10.1016/j.powtec.2018.12.013
12
Feng J. Zhao L. Zhang S. Dong H. (2020). Exergy analysis and parameter optimization of sinter cooling process in vertical moving bed for waste heat recovery. Appl. Therm. Eng.175, 115370. 10.1016/j.applthermaleng.2020.115370
13
Jang J. Chiu Y. (2009). 3-D Transient conjugated heat transfer and fluid flow analysis for the cooling process of sintered bed. Appl. Therm. Eng.29, 2895–2903. 10.1016/j.applthermaleng.2009.02.012
14
Keyser M. J. Conradie M. Coertzen M. Van Dyk J. C. (2006). Effect of coal particle size distribution on packed bed pressure drop and gas flow distribution. Fuel85, 1439–1445. 10.1016/j.fuel.2005.12.012
15
Koekemoer A. Luckos A. (2015). Effect of material type and particle size distribution on pressure drop in packed beds of large particles: Extending the Ergun equation. Fuel158, 232–238. 10.1016/j.fuel.2015.05.036
16
Liu Y. Wang J. Cheng Z. Yang J. Wang Q. (2016). Experimental investigation of fluid flow and heat transfer in a randomly packed bed of sinter particles. Int. J. Heat. Mass Transf.99, 589–598. 10.1016/j.ijheatmasstransfer.2016.03.107
17
Liu Y. Yang J. Wang J. Cheng Z. Wang Q. (2014). Energy and exergy analysis for waste heat cascade utilization in sinter cooling bed. Energy67, 370–380. 10.1016/j.energy.2013.11.086
18
Pan L. Wei X. Peng Y. Shi X. Liu H. (2015). Experimental study on convection heat transfer and air drag in sinter layer. J. Cent. South Univ.22, 2841–2848. 10.1007/s11771-015-2816-z
19
Rong L. W. Dong K. J. Yu . A. B. (2014). Lattice-Boltzmann simulation of fluid flow through packed beds of spheres: Effect of particle size distribution. Chem. Eng. Sci.116, 508–523. 10.1016/j.ces.2014.05.025
20
Sun K. Tseng C. Wong D. S. Shieh S. Jang S. Kang J. et al (2015). Model predictive control for improving waste heat recovery in coke dry quenching processes. Energy80, 275–283. 10.1016/j.energy.2014.11.070
21
Tian F. Huang L. Fan L. Qian H. Gu J. Yu Z. et al (2016). Pressure drop in a packed bed with sintered ore particles as applied to sinter coolers with a novel vertically arranged design for waste heat recovery. J. Zhejiang Univ.-SCI A17, 89–100. 10.1631/jzus.A1500088
22
Tian F. Huang L. Fan L. Qian H. Yu Z. (2016). Wall effects on the pressure drop in packed beds of irregularly shaped sintered ore particles. Powder Technol.301, 1284–1293. 10.1016/j.powtec.2016.07.073
23
Tian F. Huang L. Fan L. Yu Z. Hu Y. (2016). Experimental study on pressure drop of packed beds with binary sintered ore particle mixtures. J. Zhejiang Univ. Eng. Sci.50 (11), 2077–2086. (in Chinese). 10.3785/j.issn.1008-973X.2016.11.006
24
Wakao N. Kaguei S. Funazkri T. (1979). Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds: Correlation of nusselt numbers. Chem. Eng. Sci.34 (3), 325–336. 10.1016/0009-2509(79)85064-2
25
Wang J. Yang J. Cheng Z. Liu Y. Chen Y. Wang Y. (2018). Experimental and numerical study on pressure drop and heat transfer performance of grille-sphere composite structured packed bed. Appl. Energy227, 719–730. 10.1016/j.apenergy.2017.07.140
26
Wu G. Xing Y. Lü Y. Qi H. Li D. (2016). Experimental analysis of resistance coefficient of oil and water flow in porous media. Exp. Technol. Manag.33 (10), 34–37. (in Chinese). 10.16791/j.cnki.sjg.2016.10.010
27
Xiong Y. Yao C. Ren J. Wu Y. Xu Q. Nie B. et al (2022). Waste semicoke ash utilized to fabricate shape-stable phase change composites for building heating and cooling. Constr. Build. Mat.361, 129638. 10.1016/j.conbuildmat.2022.129638
28
Xu Q. Liu L. Feng J. Qiao L. Yu C. Shi W. et al (2020). A comparative investigation on the effect of different nanofluids on the thermal performance of two-phase closed thermosyphon. Int. J. Heat. Mass Transf.149, 119189. 10.1016/j.ijheatmasstransfer.2019.119189
29
Xu Q. Wang K. Zou Z. Zhong L. Akkurt N. Feng J. et al (2021). A new type of two-supply, one-return, triple pipe-structured heat loss model based on a low temperature district heating system. Energy218, 119569. 10.1016/j.energy.2020.119569
30
Xu Q. Zou Z. Chen Y. Wang K. Du Z. Feng J. et al (2020). Performance of a novel-type of heat flue in a coke oven based on high-temperature and low-oxygen diffusion combustion technology. Fuel267, 117160. 10.1016/j.fuel.2020.117160
31
Yang J. Wang J. Bu S. Zeng M. Wang Q. (2012). Experimental study of forced convective heat transfer in structured packed porous media of particles. J. Eng. Thermophys.33 (5), 851–855. (in Chinese).
32
Yang J. Wu J. Zhou Z. Wang Q. (2016). Computational study of fluid flow and heat transfer in composite packed beds of spheres with low tube to particle diameter ratio. Nucl. Eng. Des.300, 85–96. 10.1016/j.nucengdes.2015.10.030
33
Zhang S. (2022). Effects of the layered distribution pattern on the gas flow resistance through the bed with the multisize irregular particle for the waste heat recovery. Int. J. Photoenergy2022, 1–15. 10.1155/2022/3727937
34
Zhang S. (2021). Study on flow and heat transfer characteristics in the sinter vertical cooling process. Beijing: University of Science and Technology Beijing. (Dissertation of Doctor Degree).
35
Zhang S. Wen Z. Liu X. Liu X. Wang S. Zhang H. (2021). Experimental study on the permeability and resistance characteristics in the packed bed with the multi-size irregular particle applied in the sinter vertical waste heat recovery technology. Powder Technol.384, 304–312. 10.1016/j.powtec.2021.02.027
36
Zhang S. Wen Z. Liu X. Xing Y. Zhang H. (2022). Gas flow characteristics through irregular particle bed with the vertical confined wall for waste heat recovery. Int. J. Photoenergy2022, 1890541–1890616. 10.1155/2022/1890541
37
Zhang S. Wen Z. Liu X. Zhang H. Liu X. Wang S. (2021). Effects of particle shape on permeability and resistance coefficients of sinter packed bed. 52(4), 1066–1075. 10.11817/j.issn.1672-7207.2021.04.003(in Chinese)
38
Zhang S. Wen Z. Wang G. Lou G. Liu X. (2021). Kinetic analyses of coke combustion and thermal decompositions of limestone and dolomite based on the sintering atmosphere. Fuel289, 119870. 10.1016/j.fuel.2020.119870
39
Zhang S. Wen Z. Xing Y. Liu X. Zhang H. Xiong Y. (2022). Experimental study on gas-solid heat transfer characteristics for the vertical waste heat recovery using the inverse problem method. Int. J. Photoenergy2022, 1–21. 10.1155/2022/4053105
40
Zhang S. Zhao L. Feng J. Luo X. Dong H. (2019). Thermal analysis of sinter vertical cooler based on waste heat recovery. Appl. Therm. Eng.157, 113708. 10.1016/j.applthermaleng.2019.04.118
41
Zhang X. Chen Z. Zhang J. Ding P. Zhou J. (2013). Simulation and optimization of waste heat recovery in sinter cooling process. Appl. Therm. Eng.54, 7–15. 10.1016/j.applthermaleng.2013.01.017
42
Zheng Y. Dong H. Cai J. Feng J. Zhao L. Liu J. et al (2019). Experimental investigation of volumetric heat transfer coefficient in vertical moving-bed for sinter waste heat recovery. Appl. Therm. Eng.151, 335–343. 10.1016/j.applthermaleng.2019.01.055
Summary
Keywords
operational parameter, structural parameter, multi-size, optimization, waste heat
Citation
Zhang S, Huang L, Liu X and Wang H (2023) Optimization of structural and operational parameters for the multi-size sinter vertical waste heat recovery with the objective of the income exergy. Front. Energy Res. 10:1114270. doi: 10.3389/fenrg.2022.1114270
Received
02 December 2022
Accepted
16 December 2022
Published
05 January 2023
Volume
10 - 2022
Edited by
Yaxuan Xiong, Beijing University of Civil Engineering and Architecture, China
Reviewed by
Songhua Hao, Sichuan University, China
Kai Xie, Weifang University of Science and Technology, China
Updates
Copyright
© 2023 Zhang, Huang, Liu and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sizong Zhang, 513865909@qq.com
This article was submitted to Energy Storage, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.